Abstract
This manuscript develops for the first time a mathematical formulation of the dynamical behavior of bi-directional functionally graded porous plates (BDFGPP) resting on a Winkler–Pasternak foundation using unified higher-order plate theories (UHOPT). The kinematic displacement fields are exploited to fulfill the null shear strain/stress at the bottom and top surfaces of the plate without needing a shear factor correction. The bi-directional gradation of materials is proposed in the axial (x-axis) and transverse (z-axis) directions according to the power-law distribution function. The cosine function is employed to define the distribution of porosity through the transverse z-direction. Equations of motion in terms of displacements and associated boundary conditions are derived in detail using Hamilton’s principle. The two-dimensional differential integral quadrature method (2D-DIQM) is employed to transform partial differential equations of motion into a system of algebraic equations. Parametric analysis is performed to illustrate the effect of kinematic shear relations, gradation indices, porosity type, elastic foundations, geometrical dimensions, and boundary conditions (BCs) on natural frequencies and mode shapes of BDFGPP. The effect of the porosity coefficient on the natural frequency is dependent on the porosity type. The natural frequency is dependent on the coupling of gradation indices, boundary conditions, and shear distribution functions. The proposed model can be used in designing BDFGPP used in nuclear, marine, aerospace, and civil structures based on their topology and natural frequency constraints.
Keywords:
unified plate theories; free vibration; 2D-FG Pate; elastic foundation; porous materials; 2D-DIQM MSC:
65M22
1. Introduction
Nowadays, many studies have been performed on the design and manufacture of plates for use in different loading conditions (i.e., tremendously high loading and high-heat and -moisture environmental conditions) and a wide range of engineering applications such as aerospace, nuclear reactors, marine, automobiles, electronics, and biomedical structures [1]. Functionally graded materials (FGMs) with enhanced properties are new materials invented in 1984 [2] whose constituents are changed continuously within the body through spatial directions [3]. FGMs gain unique characteristics that do not exist in classical composites such as elimination of high stress concentrations, delamination, crack formation, and moisture sensitivity [4]. FGMs can sustain a temperature of 2000 K and temperature gradient of 1000 K across a cross-section of <10 mm [5]. Certainly, it is difficult to discover the exact gradation in FGMs as it requires an experimental control, which leads to some imperfect products [6].
Some engineering applications may need enhanced composite materials with properties that vary continuously in more than one direction [7]. Lieu et al. [8] evaluated the mechanical responses of BDFG plates with variable thickness. Wu and Yu [9] derived 3D solutions for a free vibration of BDFG plates with assorted boundary conditions (BCs) using finite annular prism methods. Hashemi and Jafari [10] considered the nonlinear vibration responses of in-plane 2D-FG plates with temperature-dependent properties. Ghatage [11] introduced a comprehensive review on the modelling, simulation, and analysis of multi-directional FG structures. Pham et al. [12] studied the free vibration of 2D-FG rectangular plates in the fluid medium using isogeometric analysis (IGA). Chen et al. [13] evaluated the nonlinear responses of BDFG Kirchhoff plates with geometrical imperfections including von Kármán’s nonlinear strain under external force. Mohammadian [14] obtained closed-form analytical solutions of the nonlinear vibration of damped 2D-FG beams using a cubic-quintic nonlinear model. Abo-Bakr et al. [15,16] found the optimum weight of 2D-FG macro/micro-beams under a constraint of maximum frequency and critical buckling load using a multi-objective particle swarm optimization technique. Karamanli et al. [17] investigated numerically mechanical responses of multi-directional FG modified strain gradient microplates in the framework of 3D shear deformation theory. Patpatiya et al. [18] investigated the state of the art of polyjet 3D printing of polymers, multi-material structures, and FGMs, with an emphasis on its applications in a range of industrial domains. Attia and Shanab [19,20] evaluated the natural frequencies and dynamic responses of 2D-FG nanobeams under a moving harmonic load with couple stress and surface energy.
The accuracy of the obtained results in the study of beams, plates, and shell theories is dependent on the selection of the displacement and shear functions. Although the classical Kirchhoff–Love plate theory ignores the influence of shear strain, it may be used in the analysis of very thin structures with acceptable accuracy, [21]. Reddy [22] implemented Mindlin’s plate theory to consider shear deformation, rotary inertia, and lamination scheme effects. In 1991 Touratier [23] utilised a classic Kirchhoff–Love plate theory with a cosine shear stress distribution to examine the mechanical responses of laminated/sandwiched composite plates. Based on unified shear theories, Assie and Mahmoud [24] studied the buckling response of BDFG porous plates embedded in an elastic environment. Assie et al. [25,26] used Mindlin’s theory to investigate the viscoelastic response of laminated plates under transient loads and optimize its weight according to a rigidity constraint. Malikan et al. [27] studied thermal buckling of functionally graded piezomagnetic micro- and nanobeams presenting the flexomagnetic effect using Timoshenko shear deformation theory.
Brischetto et al. [27] studied the free vibration of FG plates and cylinders using a 3D elasticity model. Vu et al. [28] explored the mechanical responses of FG plates resting on elastic foundation using a refined quasi-3D logarithmic shear deformation theory. Raissi [29] examined stresses in adhesive layers of a sandwich plate under to different temperature environments using layerwise plate theory. Based on a hybrid quasi-3D plate theory, Van [30] studied the bending and vibration responses of BDFGM plates resting on Pasternak foundations. Considering the Reddy and Touratier shear plate theories, Daikh et al. [31,32] explored the static and vibration responses of sigmoidal FG/multilayer FG carbon-reinforced composite nanoplates. Using a new logarithmic shape function, quasi-3D HSDT, Li et al. [33] evaluated the vibration behavior of FGM plates resting on elastic foundations described by a Winkler/Pasternak/Kerr model. Duc and Minh [34] exploited Shi’s third-order shear theory to study the free vibration of cracked FG plates. Tran et al. [35] studied the natural frequencies and vibrations of FG FOSDT plates in the thermal environment. Sadgui and Tati [36] analyzed the buckling and vibration response of FG plates using a trigonometric shear deformation plate theory. Naghsh et al. [37] investigated the instability of sandwich tapered plates under uniform/non-uniform in-plane loadings utilizing higher-order zigzag shear theory. Under different moisture conditions, Brischetto and Torre [38] developed a 3D stress analysis of multilayered FG plates utilizing an exact layerwise approach. Melaibari et al. [39,40] exploited hyperbolic sine function shear deformation theory to study the dynamic behavior of randomly oriented FG laminated plates and shells with different geometries.
Porosities and voids may arise inside materials through the manufacturing process of FGMs owing to the large differences in solidification temperatures between material constituents during the process of sintering [41,42,43]. On the basis of classical and first-order shear deformation plate theories, Kim et al. [44] studied the mechanical response of FG porous microplates. Esmaeilzadeh and Kadkhodayan [2] investigated the dynamic response of porous 2D-FG plates reinforced by stiffeners under a dynamic moving load. Babaei et al. [45] examined static and dynamic behaviors of FG porous elliptical sector plates based on the 3D finite element method (FEM). Esmaeilzadeh et al. [46] presented the nonlinear dynamic response of BDFG porous nanoplates using a nonlocal strain gradient model. Li et al. [47] exploited FOSDT as well as IGA in analyzing the bending, buckling, and vibration of porous 2D-FG plates. Katiyar and Gupta [48] examined the dynamic response of FG porous refined non-polynomial trigonometric higher-order shear plates resting on elastic foundations under different thermal environments. Ansari et al. [49] studied the free vibration of post-buckled arbitrary-shaped FG porous nanocomposite plates using the Reddy plate theory. Using a power law with a uniform porosity distribution, Abdollahi et al. [50] investigated the aeroelastic response of honeycomb sandwich plates. Akbaş et al. [51,52] examined the transient vibration behaviors of FG porous beams with viscoelastic cores under pulse loads. Sah and Ghosh [53] presented the dynamic and buckling responses of multi-directional FG sandwich porous plates.
According to the previous articles surveyed, the free vibration response of BDFG unified higher-order shear plates with porous materials placed on elastic foundations has not been considered. Thus, this paper aims to illustrate this topic in comprehensively. This analysis will be limited to the one- or two-dimensional gradation functions. The following sections will present the problem formulations, kinematic and constitutive relations, porosity distribution functions, and equations of motion (Section 2). The solution methodology, two-dimensional differential integral quadrature method, and formulations of stiffness/mass matrices will be presented in Section 3. Section 4 presents the model validations and discusses the influences of kinematic fields, porosity distribution, gradation indices, aspect ratio, slenderness ratio, elastic foundation, and boundary conditions on the natural frequencies and mode shapes. Section 5 presents the main features and conclusions.
2. Mathematical Formulation
2.1. Displacement Field and Constitutive Relations
The displacement field of unified plate theory can be represented by
in which are the displacements defined with respect to the midplane. is a shape shear distribution function through the thickness directions that satisfies a zero shear at the top and bottom surfaces as [23,54,55,56,57]
The unified higher order shear theories are proposed to describe adequately the variation in transverse shear strain within the thickness of the plate. Based on Equations (1)–(3), the normal and shear strains can be represented by
By considering isothermal conditions and neglecting the transverse normal strain , the constitutive relations for 2D shear deformation plate theory are
in which the stiffness coefficients are
The Young’s modulus and Poisson’s ratio are and , respectively. Properties of the material including porosity and voids are graded in both axial and transverse directions by power law as
where signifies a generic graded material property such as (density). and are the graded indices through the z- and x-directions. Subscripts and represent a ceramic and a metal, respectively. The porosity distribution function through the thickness has the following distributions:
where the porosity parameter is .
2.2. Governing Equations of Motion
The governing equations of motion are derived based on Hamilton’s Principles as
The virtual work of applied loads, is evaluated by
in which
where .
The variation in potential energy of the Winkler–Pasternak elastic foundation (displayed in Figure 1) is
where: .
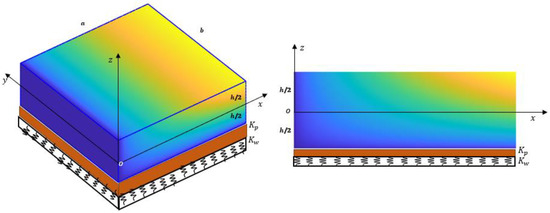
Figure 1.
BDFG plate resting on Winkler–Pasternak elastic foundation.
The virtual kinetic energy is prescribed by
Manipulating Equation (9) leads to the following:
The virtual strain energy
In terms of stress resultants, virtual strain energy () is obtained by
in which the stress resultants in terms of generalized displacements by
and the rigidity terms are
where are defined by Equations (4) and (5).
Substituting Equations (22)–(24), (27) and (28) for into Equation (21), the equations of FGM porous plates are:
where the boundary conditions are:
Substituting Equations (2), (3) and (11) into Equation (13), the governing equations of motion in terms of displacements are
The superscripts indicate the first derivative and second derivatives, respectively, w.r.t. To have nontrivial solutions (Eigenfrequencies, ) for the free vibration analysis, it is essential to ignore the in-plane forces, in Equations (46)–(49). The boundary conditions used are presented in Appendix A.
3. Solution Methodology
The derived equations of motion (Equation (15a–d)) are very complicated to be solved analytically since they are partial differential equations with variable coefficients. Thus, the efficient differential-integral quadrature method (DIQM) is modified to solve derived equations of motion. Major applications of DQM and DIQM in science and engineering are discussed in [58,59,60,61,62,63]. The applicability of DQM in the analysis of 1D problems, 2D problems, and the discretization of stress resultants and governing equations can be referred to in [24].
Using these terminologies, the stress resultants (Equations (29) and (30)) can be discretized using DIQM as
[24]
The kinetic terms in the right-hand side of Equations (33)–(36) can be represented by
Finally, DQM discretization of Equations (33)–(36) can be put in matrix form
where the entries of matrices , and are the stiffness, load, and mass, respectively. For free vibration analysis, in-plane and transversal loads are neglected, and the governing equation reduces to a generalized eigenvalue problem
where the element mass and stiffness matrices are presented in Appendix B.
4. Numerical Results
This section is divided into two main subsections. The first one presents the validation of the present model with many previous peer works. The second subsection illustrates parametric studies to present the influence of the number of nodes of DQM on the solution conversion, effects of shear functions, boundary conditions, gradation indices, porosity types, and elastic foundation on the natural frequencies (eigenvalues) and associated mode shapes (eigenvectors) of bi-directional functionally graded porous unified plates. The material properties for metal and ceramic ingredients used in the analysis are presented in Table 1, and the notation for boundary conditions of the plate are illustrated in Figure 2.

Table 1.
Material properties of BDFGM plates.
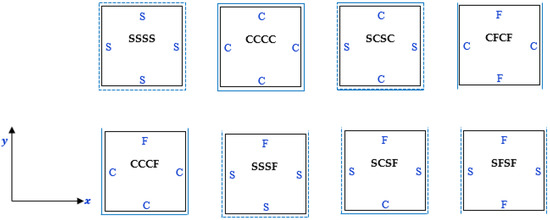
Figure 2.
The notations of plate boundary conditions.
4.1. Model Validations
The variation in the first natural frequency for a 1D-FG SSSS square plate at different gradation indices through the thickness direction and different slenderness ratios () is presented in Table 2, to validate the one-dimensional gradation with previous works published by Nguyen et al. [65], Matsunaga [66], and Thai and Choi [67]. As shown, for isotropic pure ceramics at , the present results are very close to the results obtained by Thai and Choi [67] and between the results of Nguyen et al. [65] and Matsunaga [66] at and the results are identical with Thai and Choi [67] for . It is noted that, by increasing the gradation index through the thickness, the material constituent changes from fully ceramic to grade to fully metal; therefore, the stiffness decreased and hence the natural frequency also decreased. It is observed that among the different shear theories, the results from the Reddy, Karama, and Thai and Kim theories are identical; however, the Touratier and Taibi theories are overestimated and underestimated, respectively, compared to the other theories.

Table 2.
1st nondimensional frequencies of isotropic SSSS square plates.
The validation of the 1D-FG plate model for higher modes is presented in Table 3. As seen, the obtained results are very close to those obtained by Reddy [69], Nguyen et al. [65], Hosseini et al. [68], and Thai and Vo [70] for the first, second, and third modes under the same conditions.

Table 3.
The first three non-dimensional frequencies of isotropic SSSS plates.
Figure 3 presents the validation of the porosity model with that developed by Coskun et al. (2019). Figure 3a illustrates the variation in the first natural frequency with porosity coefficients for the three porosity models. It is noted that by increasing the porosity coefficient the natural frequency increases in porosity Type 3, decreases in porosity Type 2, and approximately remains constant in porosity Type 1. Therefore, the effect of the porosity coefficient on the natural frequency is dependent on the porosity type. The influence of the gradation index through thickness on the natural frequency for the different porosity models is portrayed in Figure 3b. As seen, the natural frequencies for all porosity models decreased as the gradation index increased from 0 to 2, then the reverse effect dominated (i.e., the natural frequency increased linearly by increasing the gradation index from 2 to 10). The obtained results for different porosity coefficients and gradation indices are confirmed with those obtained by Coskun et al. [64].
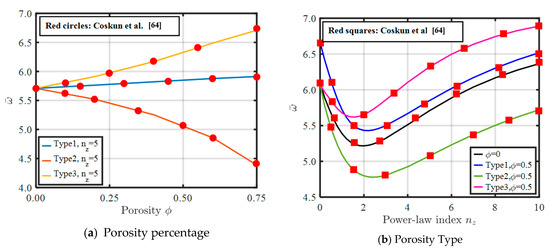
Figure 3.
Validation of dimensionless fundamental frequency of SSSS plates at different TFG indices and different porosity types.
The effects of the foundation parameters on the first natural frequency of 1D-FG SSSS plate are presented in Table 4. By increasing the coefficient of and the natural frequency is increased due to the increase in the overall stiffness. The has a significant effect rather than on the natural frequency. As seen from Table 5, the obtained results are very close to those obtained by Vu et al. [28] and Baferani et al. [71] at various gradation indices and elastic foundation parameters.

Table 4.
The dimensionless frequencies of square plates. , , with SSSS boundary conditions.

Table 5.
The non-dimensional frequency , of the Si3N4/SUS3O4 square BDFG SSSS plates .
Table 5 is presented to verify the 2D gradation functions with previous work for the SSSS plate case. As shown, by fixing the gradation through the thickness direction and varying the material constituents through the axial direction, the natural frequency is deceased. By increasing the gradation index through the axial direction from 0 to 2, the fundamental frequency reduced by around 24%. The same results were obtained previously by Pham et al. [12] and Li et al. [47] with different plate theories and solution techniques.
4.2. Parametric Analysis
- a.
- Convergence Study
To use a DQM in solving the proposed model, the convergence of solutions should be presented (see Table 6 and Figure 4). It is noted that the natural frequencies are overestimated in the case of small numbers of discretization points. The natural frequencies for all BCs are convergent after . Hence, is used to confirm the convergence of the solutions in the analysis.

Table 6.
Convergence of DQM of the fundamental frequency for a FG square plate for various boundary conditions.
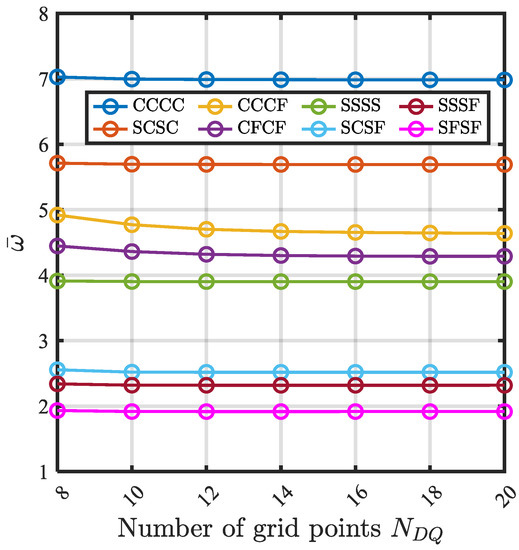
Figure 4.
Convergence of DQM of the fundamental frequency for BDFG square plates under compression with various BCs .
- b.
- Effect of Shear shape functions
Assessment of the first three natural frequencies using transverse shear shape functions in Equations (4)–(8) for SSSS plates at without an elastic foundation is shown in Table 7. As indicated, the results of the Reddy and Thai–Kim functions are the same for any mode and slenderness ratio. All shear functions give identical values for the third natural frequency at a/h = 5. The Karama shear function gives overestimated natural frequencies for all modes and all slenderness ratios.

Table 7.
Comparison of the non-dimensional frequencies of isotropic . SSSS square plates. .
- c.
- Effect of Slenderness ratio
The variation in fundamental frequency of a clamped plate against gradation indices at different side-to-thickness ratios () is illustrated in Figure 5 and Figure 6. As presented, the gradation indices in both the thickness and axial directions tend to reduce the natural frequencies, due to decreasing the percentage of ceramic phase in the constituent, which causes a reduction in the stiffness. The maximum natural frequency is noticed at and the minimum natural frequency is observed at . The variation in natural frequency vs. the gradation indices can be described by exponential decaying functions. From the figures, increasing in a/h tends to increase the natural frequency, which indicates the increasing stiffness of structures relative to their density.
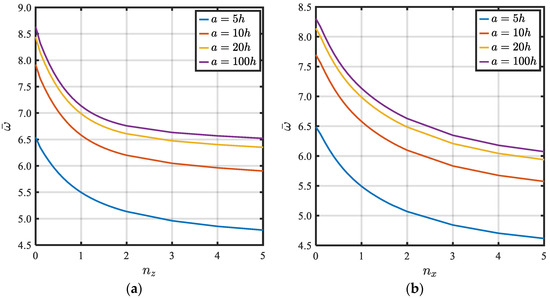
Figure 5.
Variation in the first natural frequency vs gradation indices through the thickness and axial directions. (a) versus (); (b) versus ().
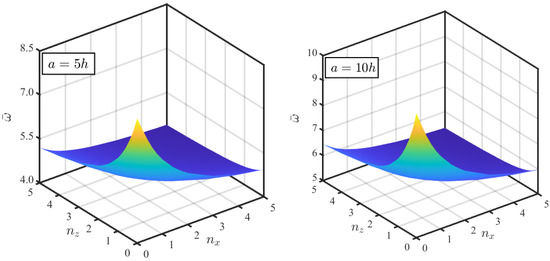
Figure 6.
The effect of the gradient indices and on the dimensionless fundamental frequency of BDFG CCCC plates at = 5,10,20 and 100.
- d.
- Effect of Boundary Conditions
The variation in the natural frequency of BDFG plates vs. the boundary conditions, shear distribution functions, and axial gradation index are presented in Table 8. By fixing the gradation index and shear functions, the highest natural frequency is observed in the CCCC case and the minimum is recorded for SFSF boundary conditions. It is found that the natural frequencies for CCCF, CFCF, and SSSS boundary conditions are very close to each other. Based on this table, the natural frequency is dependent on the coupling of gradation indices, boundary conditions, and shear distribution functions.

Table 8.
Comparison of the non-dimensional frequencies of BDFG square plates. .
The variation in the first four mode shapes with gradation indices for a CCCC BDFG plate is shown in Figure 7. The second and third modes are approximately identical from a profile perspective because the plate is symmetric in boundary conditions (CCCC) and geometrical dimensions (). For each profile of the four modes, no significant effect is noticed. However, there is a small deviation in peaks’ values and their spatial coordinates due to changing of the material gradations. Figure 8 illustrates the influence of different boundary conditions on the first three mode shapes of BDFG plates at . As is clear, the first, second, and third mode shapes are varied completely according to boundary conditions. Therefore, the response of the structure is dependent significantly on the type of constraints.
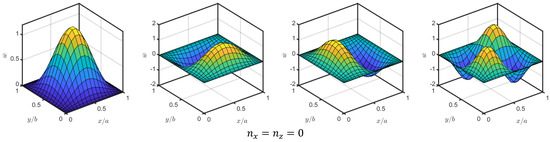
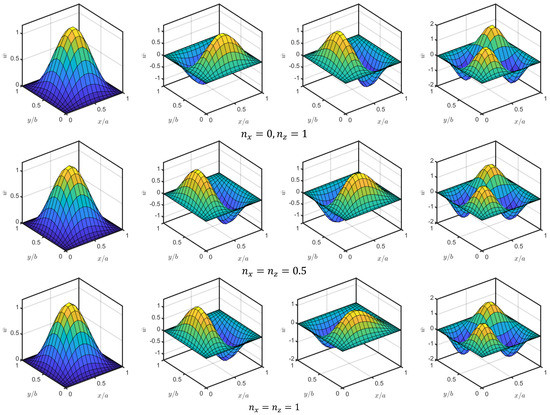
Figure 7.
Influence of gradient indices and on the mode shapes of BDFG CCCC plates at = 5, and .
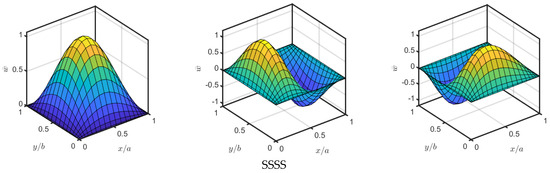
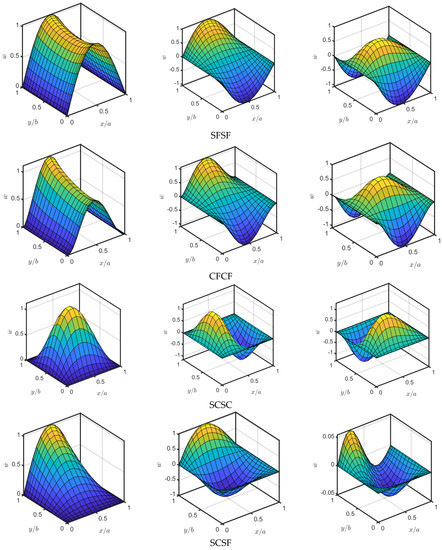
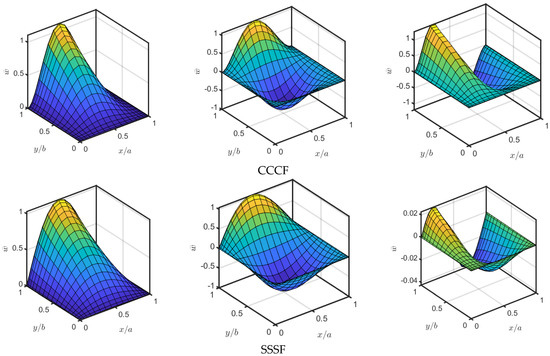
Figure 8.
Influence of BCs on the first three mode shapes of BDFG plates at .
- e.
- Effect of Geometrical Dimensions
The influence of side ratio (b/a) on the natural frequency versus gradation indices is presented in Figure 9. As shown, the natural frequency is decreased by increasing the gradation indices for both thickness and axial directions and by increasing the side ratio (b/a). It is found that the influence of side ratio (b/a) on the natural frequency is decreased for higher side ratios. This means that, by increasing b/a from 1 to 1.5, the natural frequency is reduced by 24%; however, when increasing b/a from 1.5 to 2 the natural frequency is reduced by 10%.
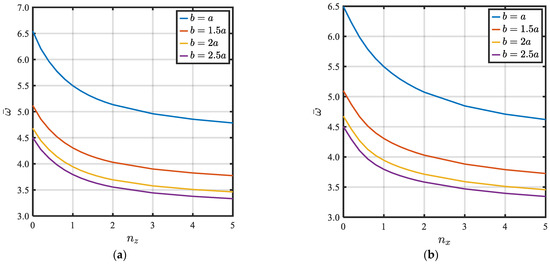
Figure 9.
Effect of plate dimensions (b/a) on the fundamental frequency vs. gradation indices in thickness and axial directions. (a) versus (); (b) versus ().
- f.
- Effect of porosity type
The dimensionless fundamental frequencies of a clamped square BDFG porous plate against gradation indices, porosity types, and porosity values are presented in Figure 10 and Figure 11. As concluded from these figures, the natural frequency is dependent on the coupled effects of porosity type, porosity value, and gradation indices. At gradation index = 0, the natural frequency increases with increasing porosity coefficient for both porosity Types 1 and 2, and the natural frequency is reduced for porosity Type 3. However, at gradation index = 5, by increasing the porosity value, the natural frequency is increased for porosity Type 1 and is decreased for Type 2 and Type 3.
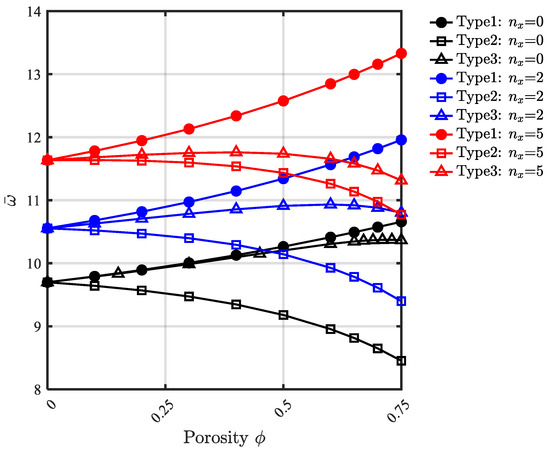
Figure 10.
Dimensionless fundamental frequency of CCCC plates at different gradient indices and different porosity types at .
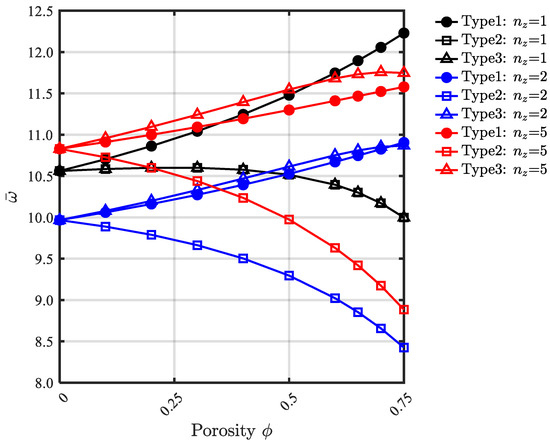
Figure 11.
Dimensionless fundamental frequency of CCCC plates at different gradient indices and different porosity types at .
Figure 12 illustrates the variation in fundamental frequency vs. gradation indices for different porosity types at porosity value . As shown in Figure 12a, the natural frequency is decreased a little bit by increasing the gradation index from 0 to 0.5, then it increased by increasing the gradation index for all porosity types. However, in the case of variation in the gradation index , the natural frequency is decreased by increasing from 0 to 1.5 for porosity types 1 and 2 increased for . For Type 3, the natural frequency decreases in the range of and increases in the other domain as illustrated in Figure 12b.
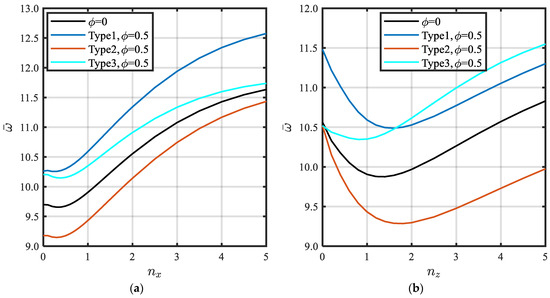
Figure 12.
Dimensionless fundamental frequency of CCCC plates at different gradient indices and different porosity types at a constant porosity value . (a) ; (b) .
- g.
- Effect of Elastic foundation parameters
The variation in fundamental frequency of SSSS BDFG plates vs. the elastic foundation parameters on are represented in Figure 13. As seen in this figure, the frequency is raised by raising both . The effect of is more substantial than the effect of on the frequency. At , by raising from 0 to 100, the natural frequency is raised from 3.9 to 7.55 (raised by 93%). If is raised from 0 to 100, the natural frequency is raised from 3.9 to 4.2 (raised by 7%).
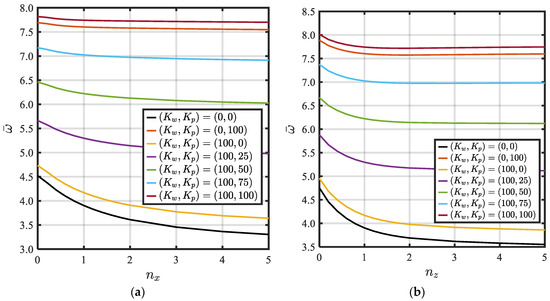
Figure 13.
Dimensionless fundamental frequency of a SSSS BDFG plate against gradation indices . (a) ; (b) .
5. Conclusions
A mathematical model for analyzing the free vibration of BDFG porous plates resting on elastic foundations is derived in this manuscript. The BDFG material varied through the axial and transverse directions is depicted by a power function with three types of porosity. From parametric studies, it can be concluded that
- ➢
- The natural frequencies for all BCs are convergent after .
- ➢
- The Reddy and Thai–Kim shear functions are identical for any modes and slenderness ratios. All shear functions give identical values for the third natural frequency at a/h = 5. The Karama shear function gives overestimated natural frequencies for all modes and all slenderness ratios.
- ➢
- The gradation indices in both thickness and axial directions tend to reduce the natural frequencies, due to the decreasing percentage of ceramic phase in the constituent, which causes a reduction in the stiffness.
- ➢
- The greatest natural frequency is noticed in the CCCC case and the minimum is recorded for SFSF boundary conditions. It was found that the natural frequencies for CCCF, CFCF, and SSSS boundary conditions are very close to each other.
- ➢
- It was found that the influence of the side ratio (b/a) on the natural frequency is decreased for higher side ratios.
- ➢
- The natural frequency is dependent on the coupled effects of porosity type, porosity value, and gradation indices.
- ➢
- The fundamental frequency is raised by raising the elastic foundation parameters . However, it is observed that the impact of is more significant than the impact of on the fundamental frequency.
Author Contributions
A.M. (project administration, funding acquisition, data curation, resources); S.A.M. (software, validation, formal analysis, investigation, original draft); A.E.A. (formal analysis, investigation, resources, original draft); R.A.S. (software, visualization, data curation, formal analysis); M.A.E. (Conceptualization, methodology, review and editing). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Institutional Fund Projects under grant no. IFPIP (1678-135-1443).
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This research was funded by the Institutional Fund Projects under grant no. IFPIP (1678-135-1443). The authors gratefully acknowledge technical and financial support provided by the Ministry of Education and King Abdulaziz University, DSR in Jeddah, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclatures
| The displacement field of unified plate theory | Thickness of the plate | ||
| Thickness coordinate | Metal material property | ||
| Shape shear distribution function | Ceramic material property | ||
| Young modulus | Shear correction factor | ||
| Poisson’s ratio | Winkler modulus parameter | ||
| density | First-order derivative weighting coefficient matrix | ||
| graded indices in the z-direction | Hadamard product operator | ||
| graded indices in the x-direction | Kronecker product | ||
| porosity distribution function | Stiffness and mass matrices, respectively | ||
| porosity coefficient | Fundamental linear frequency |
Appendix A
The used boundary conditions:
- Clamped edge:
- Simply supported edge:
- Free edge:
Appendix B
The elements of the mass matrix can be evaluated as
The elements of the stiffness matrix can be evaluated as
In which and are the zero and identity matrices of dimensions , respectively.
References
- Malikan, M.; Wiczenbach, T.; Eremeyev, V.A. Flexomagneticity in Functionally Graded Nanostructures. In Advanced Materials Modelling for Mechanical, Medical and Biological Applications; Springer: Cham, Germany, 2022; pp. 321–335. [Google Scholar]
- Sasaki, M.; Hirai, T. Thermal fatigue resistance of CVD SiC/C functionally gradient material. J. Eur. Ceram. Soc. 1994, 14, 257–260. [Google Scholar]
- Esmaeilzadeh, M.; Kadkhodayan, M. Dynamic analysis of stiffened bi-directional functionally graded plates with porosities under a moving load by dynamic relaxation method with kinetic damping. Aerosp. Sci. Technol. 2019, 93, 105333. [Google Scholar] [CrossRef]
- Dorduncu, M.; Olmus, I.; Rabczuk, A.T. Peridynamic approach for modeling of two dimensional functionally graded plates. Compos. Struct. 2022, 279, 114743. [Google Scholar] [CrossRef]
- Esen, I.; Özarpa, C.; Eltaher, M.A. Free vibration of a cracked FG microbeam embedded in an elastic matrix and exposed to magnetic field in a thermal environment. Compos. Struct. 2021, 261, 113552. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. A new hyperbolic-polynomial higher-order elasticity theory for mechanics of thick FGM beams with imperfection in the material composition. Compos. Struct. 2020, 249, 112486. [Google Scholar] [CrossRef]
- Nemat-Alla, M. Reduction of thermal stresses by developing two-dimensional functionally graded materials. Int. J. Solids Struct. 2003, 40, 7339–7356. [Google Scholar] [CrossRef]
- Lieu, Q.X.; Lee, S.; Kang, J.; Lee, J. Bending and free vibration analyses of in-plane bi-directional functionally graded plates with variable thickness using isogeometric analysis. Compos. Struct. 2018, 192, 434–451. [Google Scholar] [CrossRef]
- Wu, C.P.; Yu, L.T. Free vibration analysis of bi-directional functionally graded annular plates using finite annular prism methods. J. Mech. Sci. Technol. 2019, 33, 2267–2279. [Google Scholar] [CrossRef]
- Hashemi, S.; Jafari, A.A. Nonlinear Free and Forced Vibrations of In-Plane Bi-Directional Functionally Graded Rectangular Plate with Temperature-Dependent Properties. Int. J. Struct. Stab. Dyn. 2020, 20, 2050097. [Google Scholar] [CrossRef]
- Ghatage, P.S.; Kar, V.R.; Sudhagar, P.E. On the numerical modelling and analysis of multi-directional functionally graded composite structures: A review. Compos. Struct. 2020, 236, 111837. [Google Scholar] [CrossRef]
- Pham, Q.H.; Nguyen, P.C.; Tran, V.K.; Nguyen-Thoi, T. Isogeometric analysis for free vibration of bidirectional functionally graded plates in the fluid medium. Def. Technol. 2022, 18, 1311–1329. [Google Scholar] [CrossRef]
- Chen, X.; Chen, L.; Huang, S.; Li, M.; Li, X. Nonlinear forced vibration of in-plane bi-directional functionally graded materials rectangular plate with global and localized geometrical imperfections. Appl. Math. Model. 2021, 93, 443–466. [Google Scholar] [CrossRef]
- Mohammadian, M. Nonlinear free vibration of damped and undamped bi-directional functionally graded beams using a cubic-quintic nonlinear model. Compos. Struct. 2021, 255, 112866. [Google Scholar] [CrossRef]
- Abo-Bakr, H.M.; Abo-Bakr, R.M.; Mohamed, S.A.; Eltaher, M.A. Multi-objective shape optimization for axially functionally graded microbeams. Compos. Struct. 2021, 258, 113370. [Google Scholar] [CrossRef]
- Abo-Bakr, R.M.; Shanab, R.A.; Attia, M.A. Multi-objective optimization for lightweight design of bi-directional functionally graded beams for maximum frequency and buckling load. Compos. Struct. 2021, 278, 114691. [Google Scholar] [CrossRef]
- Karamanli, A.; Aydogdu, M.; Vo, T.P. A comprehensive study on the size-dependent analysis of strain gradient multi-directional functionally graded microplates via finite element model. Aerosp. Sci. Technol. 2021, 111, 106550. [Google Scholar] [CrossRef]
- Patpatiya, P.; Chaudhary, K.; Shastri, A.; Sharma, S. A review on polyjet 3D printing of polymers and multi-material structures. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 09544062221079506. [Google Scholar] [CrossRef]
- Attia, M.A.; Shanab, R.A. On the dynamic response of bi-directional functionally graded nanobeams under moving harmonic load accounting for surface effect. Acta Mech. 2022, 233, 3291–3317. [Google Scholar] [CrossRef]
- Attia, M.A.; Shanab, R.A. Vibration characteristics of two-dimensional FGM nanobeams with couple stress and surface energy under general boundary conditions. Aerosp. Sci. Technol. 2021, 111, 106552. [Google Scholar] [CrossRef]
- Whitney, J.M.; Pagano, N.J. Shear deformation in heterogeneous anisotropic plates. J. Appl. Mech. 1970, 37, 1031–1036. [Google Scholar] [CrossRef]
- Reddy, J.N. Free vibration of antisymmetric, angle-ply laminated plates including transverse shear deformation by the finite element method. J. Sound Vib. 1979, 66, 565–576. [Google Scholar] [CrossRef]
- Touratier, M. An efficient standard plate theory. Int. J. Eng. Sci. 1991, 29, 901–916. [Google Scholar] [CrossRef]
- Assie, A.E.; Mohamed, S.M.; Shanab, R.A.; Abo-bakr, R.M.; Eltaher, M.A. Static Buckling of 2D FG Porous Plates Resting on Elastic Foundation based on Unified Shear Theories. J. Appl. Comput. Mech. 2023, 9, 239–258. [Google Scholar] [CrossRef]
- Assie, A.E.; Eltaher, M.A.; Mahmoud, F.F. Behavior of a viscoelastic composite plates under transient load. J. Mech. Sci. Technol. 2011, 25, 1129–1140. [Google Scholar] [CrossRef]
- Assie, A.E.; Kabeel, A.M.; Mahmoud, F.F. Optimum design of laminated composite plates under dynamic excitation. Appl. Math. Model. 2012, 36, 668–682. [Google Scholar] [CrossRef]
- Malikan, M.; Wiczenbach, T.; Eremeyev, V.A. Thermal buckling of functionally graded piezomagnetic micro-and nanobeams presenting the flexomagnetic effect. Contin. Mech. Thermodyn. 2022, 34, 1051–1066. [Google Scholar] [CrossRef]
- Vu, T.V.; Nguyen, H.T.; Nguyen-Van, H.; Nguyen, T.P.; Curiel-Sosa, J.L. A refined quasi-3D logarithmic shear deformation theory-based effective meshfree method for analysis of functionally graded plates resting on the elastic foundation. Eng. Anal. Bound. Elem. 2021, 131, 174–193. [Google Scholar] [CrossRef]
- Raissi, H. Stress analysis in adhesive layers of a five-layer circular sandwich plate subjected to temperature gradient based on layerwise theory. Mech. Based Des. Struct. Mach. 2022, 50, 2274–2300. [Google Scholar] [CrossRef]
- Van Vinh, P. Deflections, stresses and free vibration analysis of bi-functionally graded sandwich plates resting on Pasternak’s elastic foundations via a hybrid quasi-3D theory. Mech. Based Des. Struct. Mach. 2021, 1–32. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari, M.S.A.; Eltaher, M.A. A novel nonlocal strain gradient Quasi-3D bending analysis of sigmoid functionally graded sandwich nanoplates. Compos. Struct. 2021, 262, 113347. [Google Scholar] [CrossRef]
- Daikh, A.A.; Houari, M.S.A.; Belarbi, M.O.; Mohamed, S.A.; Eltaher, M.A. Static and dynamic stability responses of multilayer functionally graded carbon nanotubes reinforced composite nanoplates via quasi 3D nonlocal strain gradient theory. Def. Technol. 2021, 18, 1778–1809. [Google Scholar] [CrossRef]
- Li, M.; Soares, C.G.; Yan, R. Free vibration analysis of FGM plates on Winkler/Pasternak/Kerr foundation by using a simple quasi-3D HSDT. Compos. Struct. 2021, 264, 113643. [Google Scholar] [CrossRef]
- Duc, N.D.; Minh, P.P. Free vibration analysis of cracked FG CNTRC plates using phase field theory. Aerosp. Sci. Technol. 2021, 112, 106654. [Google Scholar] [CrossRef]
- Tran, T.T.; Nguyen, P.C.; Pham, Q.H. Vibration analysis of FGM plates in thermal environment resting on elastic foundation using ES-MITC3 element and prediction of ANN. Case Stud. Therm. Eng. 2021, 24, 100852. [Google Scholar] [CrossRef]
- Sadgui, A.; Tati, A. A novel trigonometric shear deformation theory for the buckling and free vibration analysis of functionally graded plates. Mech. Adv. Mater. Struct. 2021, 1–16. [Google Scholar] [CrossRef]
- Naghsh, M.A.; Sarrami-Foroushani, S.; Azhari, M.; Mohajeri, S. Static and dynamic instability analysis of tapered CNTRC sandwich plates under uniform and non-uniform in-plane loadings using spline finite strip method. Aerosp. Sci. Technol. 2021, 110, 106514. [Google Scholar] [CrossRef]
- Brischetto, S.; Torre, R. 3D Stress Analysis of Multilayered Functionally Graded Plates and Shells under Moisture Conditions. Appl. Sci. 2022, 12, 512. [Google Scholar] [CrossRef]
- Melaibari, A.; Daikh, A.A.; Basha, M.; Abdalla, A.W.; Othman, R.; Almitani, K.H.; Eltaher, M.A. Free Vibration of FG-CNTRCs Nano-Plates/Shells with Temperature-Dependent Properties. Mathematics 2022, 10, 583. [Google Scholar] [CrossRef]
- Melaibari, A.; Daikh, A.A.; Basha, M.; Wagih, A.; Othman, R.; Almitani, K.H.; Eltaher, M.A. A Dynamic Analysis of Randomly Oriented Functionally Graded Carbon Nanotubes/Fiber-Reinforced Composite Laminated Shells with Different Geometries. Mathematics 2022, 10, 408. [Google Scholar] [CrossRef]
- Zhu, J.; Lai, Z.; Yin, Z.; Jeon, J.; Lee, S. Fabrication of ZrO2–NiCr functionally graded material by powder metallurgy. Mater. Chem. Phys. 2001, 68, 130–135. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Elastic buckling and static bending of shear deformable functionally graded porous beam. Compos. Struct. 2015, 133, 54–61. [Google Scholar] [CrossRef]
- Hamed, M.A.; Abo-Bakr, R.M.; Mohamed, S.A.; Eltaher, M.A. Influence of axial load function and optimization on static stability of sandwich functionally graded beams with porous core. Eng. Comput. 2020, 36, 1929–1946. [Google Scholar] [CrossRef]
- Kim, J.; Żur, K.K.; Reddy, J.N. Bending, free vibration, and buckling of modified couples stress-based functionally graded porous micro-plates. Compos. Struct. 2019, 209, 879–888. [Google Scholar] [CrossRef]
- Babaei, M.; Asemi, K.; Kiarasi, F. Static response and free-vibration analysis of a functionally graded annular elliptical sector plate made of saturated porous material based on 3D finite element method. Mech. Based Des. Struct. Mach. 2020, 1–25. [Google Scholar] [CrossRef]
- Esmaeilzadeh, M.; Golmakani, M.E.; Sadeghian, M. A nonlocal strain gradient model for nonlinear dynamic behavior of bi-directional functionally graded porous nanoplates on elastic foundations. Mech. Based Des. Struct. Mach. 2020, 1–20. [Google Scholar] [CrossRef]
- Li, S.; Zheng, S.; Chen, D. Porosity-dependent isogeometric analysis of bi-directional functionally graded plates. Thin Walled Struct. 2020, 156, 106999. [Google Scholar] [CrossRef]
- Katiyar, V.; Gupta, A. Vibration response of a geometrically discontinuous bi-directional functionally graded plate resting on elastic foundations in thermal environment with initial imperfections. Mech. Based Des. Struct. Mach. 2021, 1–29. [Google Scholar] [CrossRef]
- Ansari, R.; Hassani, R.; Gholami, R.; Rouhi, H. Free vibration analysis of postbuckled arbitrary-shaped FG-GPL-reinforced porous nanocomposite plates. Thin Walled Struct. 2021, 163, 107701. [Google Scholar] [CrossRef]
- Abdollahi, M.; Saidi, A.R.; Bahaadini, R. Aeroelastic analysis of symmetric and non-symmetric trapezoidal honeycomb sandwich plates with FG porous face sheets. Aerosp. Sci. Technol. 2021, 119, 107211. [Google Scholar] [CrossRef]
- Akbaş, Ş.D.; Bashiri, A.H.; Assie, A.E.; Eltaher, M.A. Dynamic analysis of thick beams with functionally graded porous layers and viscoelastic support. J. Vib. Control 2021, 27, 1644–1655. [Google Scholar] [CrossRef]
- Akbaş, Ş.D.; Fageehi, Y.A.; Assie, A.E.; Eltaher, M.A. Dynamic analysis of viscoelastic functionally graded porous thick beams under pulse load. Eng. Comput. 2022, 38, 365–377. [Google Scholar] [CrossRef]
- Sah, S.K.; Ghosh, A. Influence of porosity distribution on free vibration and buckling analysis of multi-directional functionally graded sandwich plates. Compos. Struct. 2022, 279, 114795. [Google Scholar] [CrossRef]
- Karama, M.; Afaq, K.S.; Mistou, S. Mechanical behaviour of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity. Int. J. Solids Struct. 2003, 40, 1525–1546. [Google Scholar] [CrossRef]
- Reddy, J.N. Theory and Analysis of Elastic Plates and Shells; CRC Press: Florida, CA, USA, 2006. [Google Scholar]
- Thai, H.T.; Kim, S.E. Closed-form solution for buckling analysis of thick functionally graded plates on elastic foundation. Int. J. Mech. Sci. 2013, 75, 34–44. [Google Scholar] [CrossRef]
- Taibi, F.Z.; Benyoucef, S.; Tounsi, A.; Bachir Bouiadjra, R.; Adda Bedia, E.A.; Mahmoud, S.R. A simple shear deformation theory for thermo-mechanical behaviour of functionally graded sandwich plates on elastic foundations. J. Sandw. Struct. Mater. 2015, 17, 99–129. [Google Scholar] [CrossRef]
- Bellman, R.; Kashef, B.G.; Casti, J. Differential quadrature: A technique for the rapid solution of nonlinear partial differential equations. J. Comput. Phys. 1972, 10, 40–52. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science Business Media: Berlin, Germany, 2012. [Google Scholar]
- Zong, Z. Advanced Differential Quadrature Methods; Chapman and Hall/CRC: London, UK, 2009. [Google Scholar]
- Mohamed, S.A.; Mohamed, N.A.; Abo-Hashem, S.I. A novel differential-integral quadrature method for the solution of nonlinear integro-differential equations. Math. Methods Appl. Sci. 2021, 44, 13945–13967. [Google Scholar] [CrossRef]
- Javani, M.; Kiani, Y.; Eslami, M.R. Application of generalized differential quadrature element method to free vibration of FG-GPLRC T-shaped plates. Eng. Struct. 2021, 242, 112510. [Google Scholar] [CrossRef]
- Javani, M.; Kiani, Y.; Eslami, M.R. Free vibration analysis of FG-GPLRC L-shaped plates implementing GDQE approach. ThinWalled Struct. 2021, 162, 107600. [Google Scholar] [CrossRef]
- Coskun, S.; Kim, J.; Toutanji, H. Bending, free vibration, and buckling analysis of functionally graded porous micro-plates using a general third-order plate theory. J. Compos. Sci. 2019, 3, 15. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Hong, T.T.; Vinh, P.V.; Quang, N.D.; Thom, D.V. A refined simple first-order shear deformation theory for static bending and free vibration analysis of advanced composite plates. Materials 2019, 12, 2385. [Google Scholar] [CrossRef]
- Matsunaga, H. Free vibration and stability of functionally graded plates according to a 2-D higher-order deformation theory. Compos. Struct. 2008, 82, 499–512. [Google Scholar] [CrossRef]
- Thai, H.T.; Choi, D.H. A simple first-order shear deformation theory for the bending and free vibration analysis of functionally graded plates. Compos. Struct. 2013, 101, 332–340. [Google Scholar] [CrossRef]
- Hosseini-Hashemi, S.; Fadaee, M.; Atashipour, S.R. A new exact analytical approach for free vibration of Reissner–Mindlin functionally graded rectangular plates. Int. J. Mech. Sci. 2011, 53, 11–22. [Google Scholar] [CrossRef]
- Reddy, J. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P. A new sinusoidal shear deformation theory for bending, buckling, and vibration of functionally graded plates. Appl. Math. Model. 2013, 37, 3269–3281. [Google Scholar] [CrossRef]
- Baferani, A.H.; Saidi, A.R.; Ehteshami, H. Accurate solution for free vibration analysis of functionally graded thick rectangular plates resting on elastic foundation. Compos. Struct. 2011, 93, 1842–1853. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).