Delayed Impulsive Control for μ-Synchronization of Nonlinear Multi-Weighted Complex Networks with Uncertain Parameter Perturbation and Unbounded Delays
Abstract
:1. Introduction
2. Mathematical Model and Preknowledge
3. Main Results
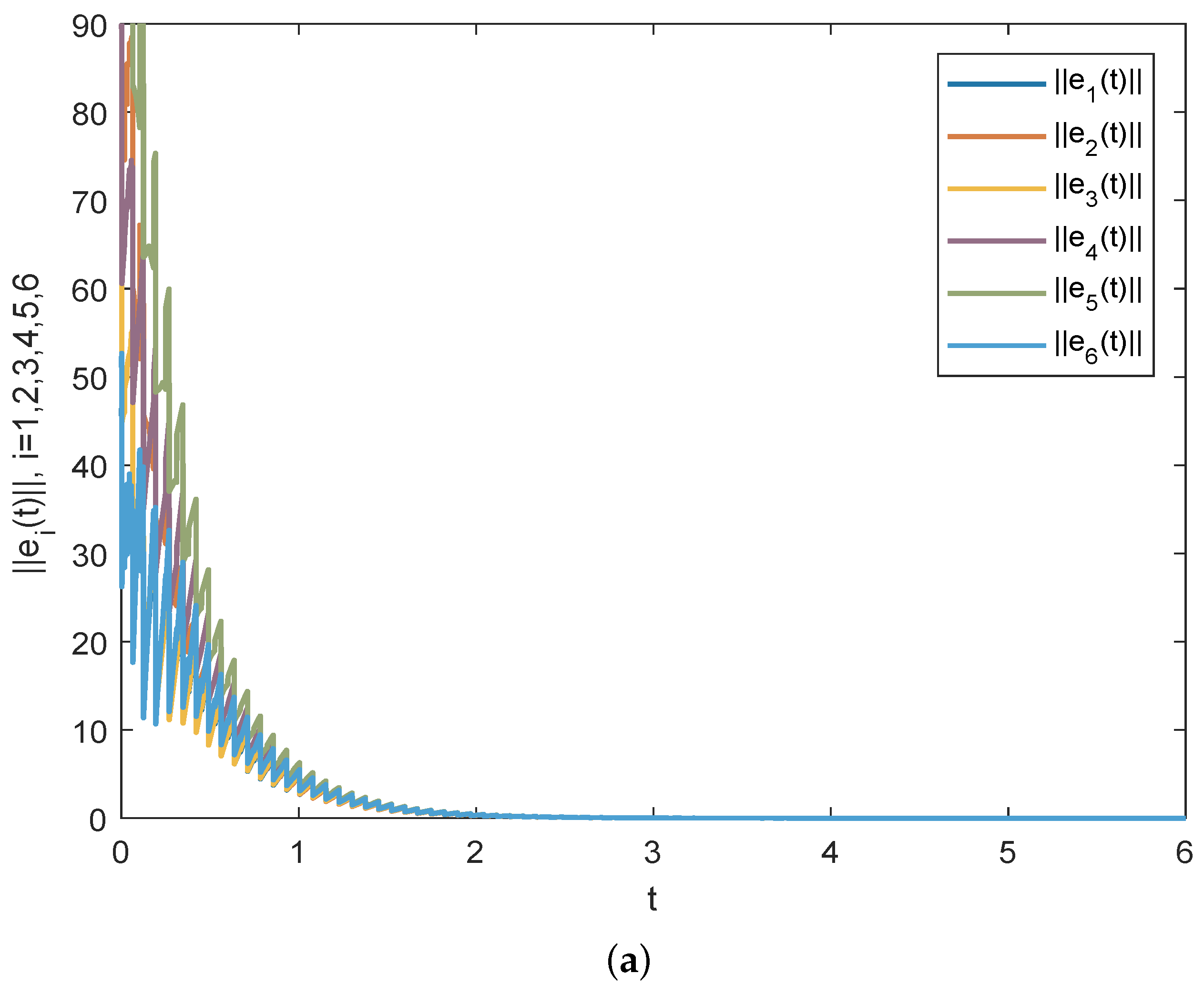
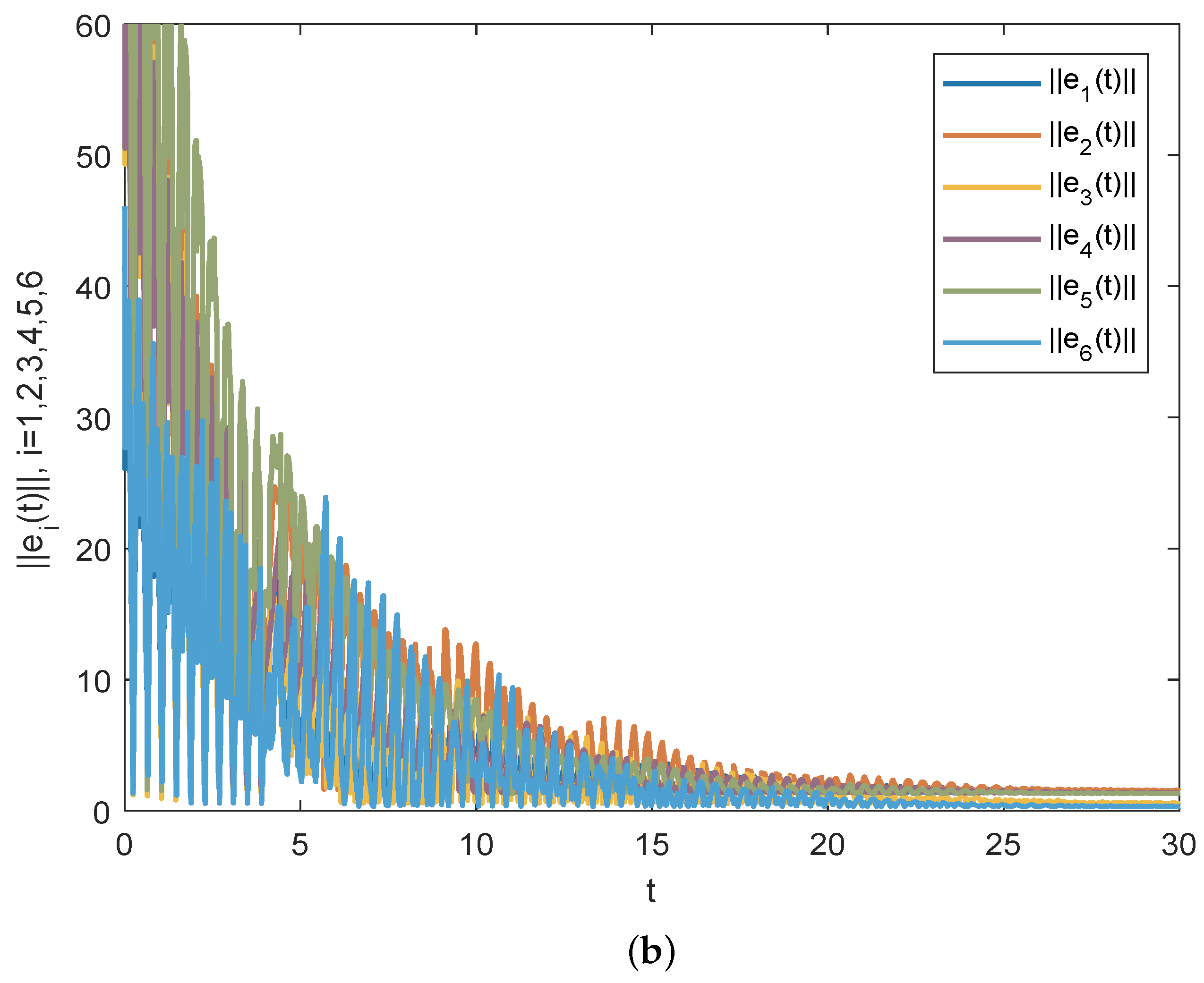
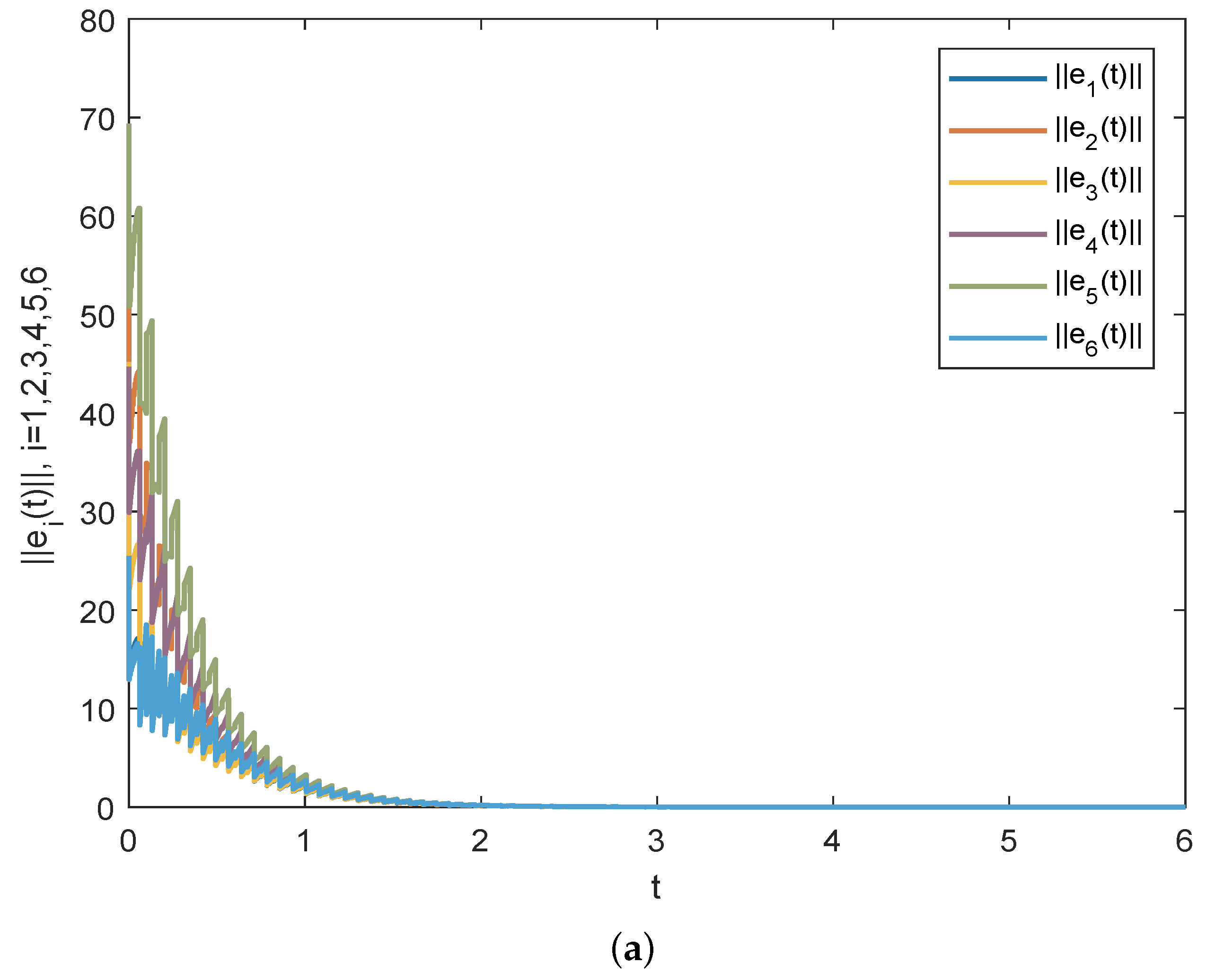
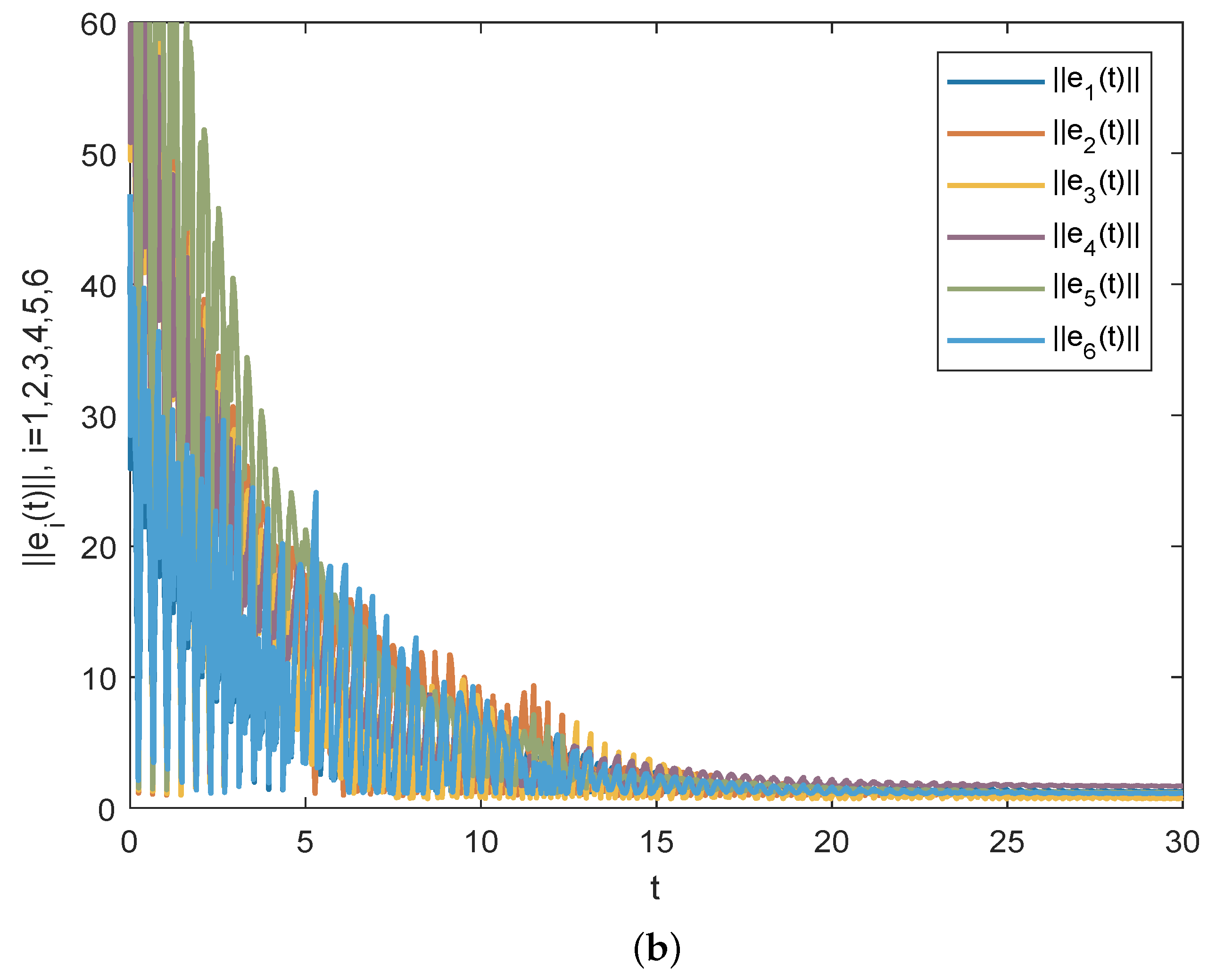
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mani, P.; Rajan, R.; Shanmugam, L.; Joo, Y.H. Adaptive control for fractional order induced chaotic fuzzy cellular neural networks and its application to image encryption. Inf. Sci. 2019, 491, 74–89. [Google Scholar] [CrossRef]
- Tang, Z.; Park, J.H.; Wang, Y.; Feng, J.W. Impulsive synchronization of derivative coupled neural networks with cluster-tree topology. IEEE Trans. Netw. Sci. Eng. 2020, 7, 1788–1798. [Google Scholar] [CrossRef]
- Shi, K.B.; Wang, J.; Zhong, S.M.; Tang, Y.Y.; Cheng, J. Non-fragile memory filtering of T-S fuzzy delayed neural networks based on switched fuzzy sampled-data control. Fuzzy Sets Syst. 2020, 394, 40–64. [Google Scholar] [CrossRef]
- Aliabadi, F.; Majidi, M.H.; Khorashadizadeh, S. Chaos synchronization using adaptive quantum neural networks and its application in secure communication and cryptography. Neural Comput. Appl. 2022, 34, 6521–6533. [Google Scholar] [CrossRef]
- Hu, W.; Zhu, Q.X.; Karimi, H.R. Some improved Razumikhin stability criteria for impulsive stochastic delay differential systems. IEEE Trans. Autom. Control 2019, 64, 5207–5213. [Google Scholar] [CrossRef]
- Fu, X.Z.; Zhu, Q.X. Stability of nonlinear impulsive stochastic systems with Markovian switching under generalized average dwell time condition. Sci. China Inf. Sci. 2018, 61, 112211. [Google Scholar] [CrossRef]
- Hu, W.; Zhu, Q.X. Stability criteria for impulsive stochastic functional differential systems with distributed-delay dependent impulsive effects. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2027–2032. [Google Scholar] [CrossRef]
- Sun, Y.G.; Liu, Y.H. Adaptive synchronization control and parameters identification for chaotic fractional neural networks with time-varying delays. Neural Process. Lett. 2021, 53, 2729–2745. [Google Scholar] [CrossRef]
- Yang, X.S.; Yang, Z.C. Synchronization of TS fuzzy complex dynamical networks with time-varying impulsive delays and stochastic effects. Fuzzy Sets Syst. 2014, 235, 25–43. [Google Scholar] [CrossRef]
- Xu, H.F.; Zhu, Q.X. New criteria on pth moment exponential stability of stochastic delayed differential systems subject to average-delay impulses. Syst. Control Lett. 2022, 164, 105234. [Google Scholar] [CrossRef]
- Xia, W.G.; Cao, J.D. Pinning synchronization of delayed dynamical networks via periodically intermittent control. Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 013120. [Google Scholar] [CrossRef] [PubMed]
- Rao, R.F.; Lin, Z.; Ai, X.Q.; Wu, J.R. Synchronization of Epidemic Systems with Neumann Boundary Value under Delayed Impulse. Mathematics 2022, 10, 2064. [Google Scholar] [CrossRef]
- Wang, J.L.; Wu, H.N.; Huang, T.W. Pinning control for synchronization of coupled reaction-diffusion neural networks with directed topologies. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 1109–1120. [Google Scholar] [CrossRef]
- Tang, Z.; Park, J.H.; Lee, T.H. Mean square exponential synchronization for impulsive coupled neural networks with time-varying delays and stochastic disturbances. Complexity 2016, 21, 190–202. [Google Scholar] [CrossRef]
- Shi, K.B.; Wang, J.; Zhong, S.M.; Tang, Y.Y.; Cheng, J. Hybrid-driven finite-time H∞ sampling synchronization control for coupling memory complex networks with stochastic cyber attacks. Neurocomputing 2020, 387, 241–254. [Google Scholar] [CrossRef]
- Fan, H.G.; Shi, K.B.; Zhao, Y. Pinning impulsive cluster synchronization of uncertain complex dynamical networks with multiple time-varying delays and impulsive effects. Phys. A 2022, 587, 126534. [Google Scholar] [CrossRef]
- Pan, L.; Cao, J.; Al-Juboori, U.A.; Abdel-Aty, M. Cluster synchronization of stochastic neural networks with delay via pinning impulsive control. Neurocomputing 2019, 366, 109–117. [Google Scholar] [CrossRef]
- Zhang, C.M.; Shi, L. Exponential synchronization of stochastic complex networks with multi-weights: A graph-theoretic approach. J. Frankl. Inst. 2019, 356, 4106–4123. [Google Scholar] [CrossRef]
- Zhang, C.M.; Yang, Y.H. Synchronization of stochastic multi-weighted complex networks with Lévy noise based on graph theory. J. Frankl. Inst. 2020, 546, 123496. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, B.D.; Wu, Y.B. Finite-time synchronization of stochastic multi-links dynamical networks with Markovian switching topologies. J. Frankl. Inst. 2020, 357, 359–384. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.X.; Ding, X.H. More general results of aperiodically intermittent synchronization for stochastic Markovian switching complex networks with multi-links and time-varying coupling structures. Neurocomputing 2020, 395, 39–55. [Google Scholar] [CrossRef]
- Li, S.; Lv, C.Y.; Ding, X.H. Synchronization of stochastic hybrid coupled systems with multi-weights and mixed delays via aperiodically adaptive intermittent control. Nonlinear Anal. Hybrid Syst. 2020, 35, 100819. [Google Scholar] [CrossRef]
- Zheng, M.W.; Li, L.X.; Peng, H.P.; Xiao, J.H.; Yang, Y.X.; Zhang, Y.P.; Zhao, H. General decay synchronization of complex multi-links time-varying dynamic network. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 108–123. [Google Scholar] [CrossRef]
- Liu, X.Z.; Zhang, K.X. Synchronization of linear dynamical networks on time scales: Pinning control via delayed impulses. Commun. Nonlinear Sci. Numer. Simul. 2016, 72, 147–152. [Google Scholar] [CrossRef]
- Li, X.D.; Song, S.J.; Wu, J.H. Exponential stability of nonlinear systems with delayed impulses and applications. IEEE Trans. Autom. Control 2019, 64, 4024–4034. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, X.S.; Xu, C.; Feng, J.W. Exponential synchronization of complex-valued complex networks with time-varying delays and stochastic perturbations via time-delayed impulsive control. Appl. Math. Comput. 2017, 306, 22–30. [Google Scholar] [CrossRef]
- Chen, T.P.; Wang, L.L. Global μ-Stability of delayed neural networks with unbounded time-varying delays. IEEE Trans. Neural Netw. 2007, 18, 1836–1840. [Google Scholar] [CrossRef]
- Fan, H.G.; Shi, K.B.; Zhao, Y. Global μ-synchronization for nonlinear complex networks with unbounded multiple time delays and uncertainties via impulsive control. Phys. A 2022, 599, 127484. [Google Scholar] [CrossRef]
- Xu, Z.L.; Li, X.D.; Duan, P.Y. Synchronization of complex networks with time-varying delays of unknown bound via delayed impulsive control. Neural Netw. 2020, 125, 224–232. [Google Scholar] [CrossRef]
- Cui, H.M.; Guo, J.; Feng, J.X.; Wang, T.F. Global μ-stability of impulsive reaction-diffusion neural networks with unbounded time-varying delays and bounded continuously distributed delays. Neurocomputing 2015, 157, 1–10. [Google Scholar] [CrossRef]
- Hu, B.X.; Song, Q.K.; Li, K.L.; Zhao, Z.J.; Alsaadi, F.; Fuad, E. Global μ-synchronization of impulsive complex-valued neural networks with leakage delay and mixed time-varying delays. Neurocomputing 2018, 307, 106–116. [Google Scholar] [CrossRef]
- Wang, H. Task-space synchronization of networked robotic systems with uncertain kinematics and dynamics. IEEE Trans. Autom. Control 2013, 58, 3169–3174. [Google Scholar] [CrossRef]
- Rakkiyappan, R.; Chandrasekar, A.; Petchiammal, G. Non-fragile robust synchronization for Markovian jumping chaotic neural networks of neutral-type with randomly occurring uncertainties and mode-dependent time-varying delays. ISA Trans. 2014, 53, 1760–1770. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.L.; Qiu, S.H.; Ren, S.Y.; Zheng, Z.W. Fixed-time synchronization of coupled Cohen-Grossberg neural networks with and without parameter uncertainties. Neurocomputing 2018, 315, 157–168. [Google Scholar] [CrossRef]
- Mao, K.; Liu, X.Y.; Cao, J.D.; Hu, Y.F. Finite-time bipartite synchronization of coupled neural networks with uncertain parameters. Phys. A 2022, 585, 126431. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, H.; Tang, J.; Shi, K.; Zhao, Y.; Wen, H. Delayed Impulsive Control for μ-Synchronization of Nonlinear Multi-Weighted Complex Networks with Uncertain Parameter Perturbation and Unbounded Delays. Mathematics 2023, 11, 250. https://doi.org/10.3390/math11010250
Fan H, Tang J, Shi K, Zhao Y, Wen H. Delayed Impulsive Control for μ-Synchronization of Nonlinear Multi-Weighted Complex Networks with Uncertain Parameter Perturbation and Unbounded Delays. Mathematics. 2023; 11(1):250. https://doi.org/10.3390/math11010250
Chicago/Turabian StyleFan, Hongguang, Jiahui Tang, Kaibo Shi, Yi Zhao, and Hui Wen. 2023. "Delayed Impulsive Control for μ-Synchronization of Nonlinear Multi-Weighted Complex Networks with Uncertain Parameter Perturbation and Unbounded Delays" Mathematics 11, no. 1: 250. https://doi.org/10.3390/math11010250
APA StyleFan, H., Tang, J., Shi, K., Zhao, Y., & Wen, H. (2023). Delayed Impulsive Control for μ-Synchronization of Nonlinear Multi-Weighted Complex Networks with Uncertain Parameter Perturbation and Unbounded Delays. Mathematics, 11(1), 250. https://doi.org/10.3390/math11010250






