Abstract
Bridge optimization is a significant challenge, given the huge number of possible configurations of the problem. Embodied energy and cost were taken as objective functions for a box-girder steel–concrete optimization problem considering both as single-objective. Embodied energy was chosen as a sustainable criterion to compare the results with cost. The stochastic global search TAMO algorithm, the swarm intelligence cuckoo search (CS), and sine cosine algorithms (SCA) were used to achieve this goal. To allow the SCA and SC techniques to solve the discrete bridge optimization problem, the discretization technique applying the k-means clustering technique was used. As a result, SC was found to produce objective energy function values comparable to TAMO while reducing the computation time by 25.79%. In addition, the cost optimization and embodied energy analysis revealed that each euro saved using metaheuristic methodologies decreased the energy consumption for this optimization problem by 0.584 kW·h. Additionally, by including cells in the upper and lower parts of the webs, the behavior of the section was improved, as were the optimization outcomes for the two optimization objectives. This study concludes that double composite action design on supports makes the continuous longitudinal stiffeners in the bottom flange unnecessary.
Keywords:
swarm intelligence; steel–concrete composite structures; bridges; optimization; metaheuristics; sustainability MSC:
05-04; 08-08; 05-11
1. Introduction
Structural engineering has been traditionally based on materialized safety solutions reducing the investment to the minimum. However, the current search for solutions that fall within the definition of sustainable development makes that criterion insufficient. Regarding this, other criteria have arisen to add the concept of sustainability to structures [1]. Introducing new design criteria in structural problems increases complexity, moving this problem to the decision-making field of knowledge. In order to assess the sustainability of solutions, life cycle assessment has become one of the most widely used tools to evaluate the social and environmental profile of a solution [2,3]. Nevertheless, in order to approximate an environmental assessment, one representative criterion can be chosen as an alternative. The most used criteria in these cases are the CO2 emissions and the energy consumption [4,5]. Regarding this, structural optimization research in recent years has focused on applying different techniques to obtain optimal designs considering CO2 emissions and embodied energy as well as cost as optimization objectives. In conclusion, in concrete structures, many research studies have shown a clear relation between the three criteria [6,7].
The energy required to build a structure, like CO2 emissions, is an indicator of sustainability [8]. However, there are different definitions of the energy required in the case of a structure. Each definition implies a different method of calculation. Therefore, there has yet to be a consensus in the scientific community regarding a single definition and calculation methodology [9,10]. Heuristic steel or composite structures were optimized in works such as Whitworth and Tsavdaridis [11]. In structures made of reinforced concrete, the reduction of the required energy can be accomplished optimizing the use of materials instead of directly changing traditional to new construction materials. Some authors have used energy as an objective function in structural optimization [12,13,14].
To address civil engineering optimization problems, particularly in the design of structures, heuristic methods have had interesting results [15]. One of the most representative structures of civil engineering is bridges because they can connect different geographical locations. This type of structure also stands out for its complexity in obtaining optimal solutions due to the high number of design possibilities. In order to obtain optimum designs, heuristic optimization techniques are put forth as an alternative to traditional experience-based design. These methods allow for reaching optimum designs ensuring compliance with the restrictions imposed by regulations, adding these as problem constraints. These methods were extensively applied in many types of structures, such as road vaults [16] or walls [17], among others.
Regarding bridge energy optimization, Penadés-Plà et al. [6] proposed a Kriging-based optimization approach that cut computing time by 99.06% and produced results that differed from heuristic optimization’s use of simulated annealing by just 2.54%. This research work was applied to optimize the embodied energy of a three-span 40–50–40 m continuous box-section footbridge.
However, recent review works highlight a lack of knowledge in applying heuristic and metaheuristic techniques to steel–concrete composite bridges (SCCB) [18] compared to concrete bridges. The techniques applied to that type of structure are: set-based parametric design [19], harmony search (HS) [20], genetic algorithm (GA), and imperialist competitive algorithm [21], among others. In addition, some particle swarm algorithms were applied to carry out SCCB optimizations [20]. However, in those studies, the unique criterion taken as an objective function is the cost. Thus, researchers have only considered the economic pillar of sustainability in some isolated studies. This shows a lack in SCCB sustainable designs research, which is not in line with the current policy of countries that seek economically viable solutions and are environmentally and socially friendly.
Therefore, this study proposes to optimize a composite steel and concrete bridge using embodied energy as the objective function. The main purpose of this research is to obtain an energy-embodied optimum design. For this, two types of metaheuristics were applied in order to use the one that reaches the best behavior for this optimization problem. Due to the large number of variables that the bridge presents, it is an important challenge for optimization algorithms. Since this energy optimization problem has not been solved before and there is no comparison baseline, it has been proposed to use and compare two groups of techniques. The first one is based on a global stochastic search (threshold accepting with a mutation operator algorithm) and was used before in solving similar problems with good results. The second is based on hybrid methods that integrate machine learning algorithms in the discretization process of continuous swarm intelligence methods. This technique has been used to solve combinatorial problems with a binary representation [22]. The current work proposes a variation to address the discrete problem. In this work, first, an analysis of the contribution of the hybrid method to the optimization result is carried out through the comparison with random discretization methods. Additionally, the main parameter () used in the hybrid method is analyzed in order to identify its contribution to the optimization result. Subsequently, the hybrid method is compared with the threshold accepting with a mutation operator algorithm. The comparison is made through the minimization of the embodied energy and of the costs. Finally, the different solutions found in both optimizations are analyzed and compared. For this, in Section 2, the optimization problem variables, parameters, and constraints were defined. Section 3 describes the different optimization algorithms used and their tuning. Subsequently, Section 4 and Section 5 show the results and the comparison with previous studies. As it can be seen in Section 6, results of the study show that the cost and the embodied energy are clearly related when optimizing cost; however, optimizing embodied energy does not necessarily result in a cost-optimal solution.
In conclusion, it should be mentioned that other types of particle swarm optimization algorithms [23,24] and other methods, such as differential evolution ones [25,26], can be applied in future research to study their behavior for this optimization problem. Moreover, in the new studies, new sustainability criteria, such as the complete life cycle assessment, will be chosen for carrying out multi-objective optimization. As the calculation of more and higher complexity objective functions can increase the computational time, the use of metamodels generated with machine learning techniques will be taken into account.
2. Optimization Problem Description
The problem posed in this study is the minimization of the objective function that evaluates the embodied energy and the cost of a steel–concrete composite bridge (SCCB). To deal with this problem, the bridge was parameterized. In this case, cost and embodied energy criteria were considered as a single objective in order to compare the designs obtained from both optimizations. In Equation (1), the embodied energy target function was defined. Data for embodied energy considers cradle-to-gate analysis; thus, it considers all processes necessary from obtaining raw materials, their conversion into those elements that will allow performing the bridge resistant section, and their final placement on-site. Data of embodied energy and costs in Table 1 were obtained from the Construction Technology Institute of Catalonia by the BEDEC database [27]. Furthermore, the cost objective function is formulated in Equation (2). Both objective functions must meet the regulation and recommendation constraints’ represented by Equation (3). Meeting these constraints will ensure the feasibility of the obtained solution from the optimization procedure. Expressions (1) and (2) represent the multiplication of each material measurement multiplied by the embedded energy () and price (), respectively.

Table 1.
Embodied energy and cost values for materials.
2.1. Variables and Parameters
A 220 m continuous three-span box-girder steel and concrete composite bridge was defined as the optimization problem. According to the variables, these correspond to each bridge element’s geometry, reinforcement, concrete, and steel grades. All of these variables were discretized in order to arrive at a real constructible solution, hence constituting a discrete optimization problem. The discretization of variables is defined in Table 2. The number of feasible optimization solutions is equal to 1.38 × 1046 when this variable discretization is considered. Metaheuristic methods are appropriate for locating the best answer when so many combinations are possible. This bridge optimization problem’s global formulation considers 34 different variables in total. These bridge variables are illustrated in Figure 1. The variables nature can be classified into six categories. First are the geometric variables of the transverse section, which are: distance between wings on top (b), angle between wings and flanges (), thickness of the upper slab (), depth of the steel section (), floor beam lower value (), upper flange thickness (), upper flange width (), upper cells height () and thickness (), wings thickness (), low cells height (), thickness (), and width (), and low slab thickness (). Beam depth limits are defined as L/40 and L/25, L being the longest length of the spans.
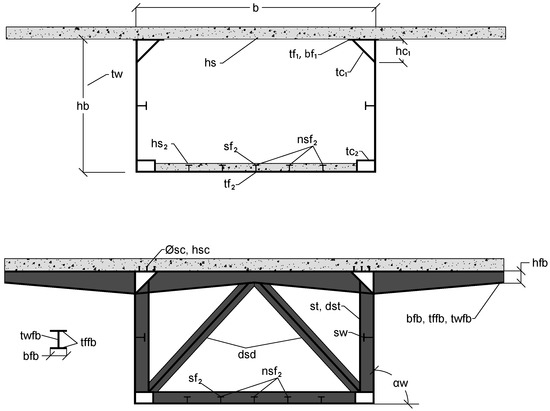
Figure 1.
Transverse section variables for the optimization problem.
SCCBs can utilize materials more effectively, profiting from the material location. This is true in statically determined girders. In this case, the upper concrete slab is materialized along the whole length of the bridge. This upper slab is attached to the upper flanges by shear connectors. This reinforces the flange plate, preventing it from buckling. Moreover, in the case of isostatics, the lower flanges would be subjected to tensile stress, avoiding buckling instability problems. In this problem, negative bending stresses will arise in supported portions under the typical loads (mostly gravitational) to which road bridges are subjected. This will cause a reversal of forces and tensile strains in the upper concrete slab and compression in the lower flange. In this instance, to improve the behavior of the bridge’s cross section, it was decided to realize a concrete bottom slab in this zone in addition to the reinforcement of the top slab. In order to optimize the reinforcement of the top slab, it was separated into a base reinforcement that is the least necessary by regulations [28,29,30] and two additional layers in negative bending sections, where the reinforcement is enhanced. Accordingly, the second group of variables corresponds to base reinforcement, first reinforcement and second reinforcement bar diameters (, , ), and the corresponding bar number of the reinforcement areas (, ).
In order to avoid buckling of steel plates, stiffeners were defined as the third category of the problem variables considering half IPE profiles for wings, bottom flange, and the transverse stiffeners (, , ). In order to allow the optimization procedure to define the number of stiffeners of the bottom flange (), this is considered as a variable placing them evenly distributed over the width.
To finalize the geometrical variables definition, the shear connectors and floor beam geometry were defined through the width of the floor beam (), thicknesses of the flanges () and webs (), and the shear connectors height () and diameter (). To determine the materials strength, the rolled steel tensile stress (), concrete strength (), and reinforcement steel tensile stress () were also defined as variables.

Table 2.
Optimization problem variables and boundaries.
Table 2.
Optimization problem variables and boundaries.
| Variables | Unit | Lower Limit | Upper Limit | Step Size | Possibilities |
|---|---|---|---|---|---|
| Geometrical variables | |||||
| b | m | 7 | 10 | 0.01 | 301 |
| deg | 45 | 90 | 1 | 46 | |
| mm | 200 | 400 | 10 | 21 | |
| cm | 250 (L/40) | 400 (L/25) | 1 | 151 | |
| mm | 400 | 700 | 100 | 31 | |
| mm | 25 | 80 | 1 | 56 | |
| mm | 300 | 1000 | 10 | 71 | |
| mm | 0 | 1000 | 1 | 101 | |
| mm | 16 | 25 | 1 | 10 | |
| mm | 16 | 25 | 1 | 10 | |
| mm | 0 | 1000 | 10 | 101 | |
| mm | 16 | 25 | 1 | 10 | |
| mm | 300 | 1000 | 10 | 71 | |
| mm | 25 | 80 | 1 | 56 | |
| mm | 150 | 400 | 10 | 26 | |
| Stiffeners | |||||
| u | 0 | 10 | 1 | 11 | |
| m | 1 | 5 | 0.1 | 41 | |
| m | 4 | 10 | 0.1 | 61 | |
| mm | IPE 200-IPE 600 * | 12 | |||
| mm | IPE 200-IPE 600 * | 12 | |||
| mm | IPE 200-IPE 600 * | 12 | |||
| Floor beams | |||||
| mm | 200 | 1000 | 100 | 9 | |
| mm | 25 | 35 | 1 | 11 | |
| mm | 25 | 35 | 1 | 11 | |
| Reinforcement | |||||
| u | 200 | 500 | 1 | 301 | |
| u | 200 | 500 | 1 | 301 | |
| mm | 6, 8, 10, 12, 16, 20, 25, 32 | 8 | |||
| mm | 6, 8, 10, 12, 16, 20, 25, 32 | 8 | |||
| mm | 6, 8, 10, 12, 16, 20, 25, 32 | 8 | |||
| Shear Connectors | |||||
| mm | 100, 150, 175, 200 | 4 | |||
| mm | 16, 19, 22 | 3 | |||
| Material strength | |||||
| MPa | 25, 30, 35, 40 | 4 | |||
| MPa | 275, 355, 460 | 3 | |||
| MPa | 400, 500 | 2 | |||
* Following the series of IPE profiles defined in [31].
Table 3 defines the parameters used for the bridge optimization problem. These parameters consider the Eurocode structural checks [28,29,30], the bridge spans length that corresponds to 60–100–60 m as can be seen in Figure 2, the deck width (B) of 16 m, and the upper and lower bound for the variables considering regulations [28,29,30] and design guides [32,33].

Table 3.
Parameters of the SCCB optimization problem.

Figure 2.
Bridge spans length of the SCC bridge.
Upper and lower slab reinforcements were set with the minimum amount required for reinforcement in Eurocode 2 [30]. The connection was obtained considering the concrete slab stresses. Effective widths due to shear lag are calculated considering Eurocode 4 [28] as only this part is considered as resistant. The steel bar reinforcements (, ) were placed only in the effective width. Lower slabs defined on supports are placed on the first and last third of every span corresponding to the shear lag negative bending areas defined in Eurocode 4 [28].
2.2. Structural Analysis and Constraints
The constraints of the optimization problem correspond to the structural safety and serviceability checks defined by the regulations [28,29,30]. Furthermore additional constraints were incorporated following some design guides [32,33].
Constraints defined by Eurocodes correspond to ultimate limit states (ULS) and serviceability limit states (SLS). ULS correspond to the structural resistance of bridge sections, while SLS correspond to the defined materials stresses and deflection limits. The loads and combination defined correspond to those imposed by Eurocode 1 [34] and are summarized in Table 3.
For ULS checks, both local and global analyses were performed. For global analysis, the checks corresponded to: shear, flexure, torsion, and flexure–shear interaction. To obtain the sections resistance, the reductions due to shear lag [28] and slenderness of Class 4 sections [30] were considered. The precision of the Class 4 reduction iterative process was defined in 10. Sections were homogenized considering the coefficient (n) between the longitudinal deflection modulus of concrete () and steel () as defined in Equation (4). Concrete creep and shrinkage were defined following the Eurocodes [28,29,30] standard. For developing the floor beams and diaphragm behavior to ULS, local modeling was performed.
Deflection, material’s tension limit, and fatigue were defined as SLS constraints. The deflection limit was defined following Spanish regulation IAP-11 [35], fixing as the maximum deflection value for live loads’ frequent combination. In this case, L l represents each span length. Furthermore, restrictions for construction and geometrical requirements were defined. All structural checks were defined using a numerical model programmed with Python language.
3. Optimization Algorithms
3.1. Trajectory-Based Algorithm: Threshold Accepting with a Mutation Operator (TAMO)
Duec and Scheuer [36] developed threshold accepting (TA), as an alternative to Kirpatricks’ simulated annealing (SA) [37]. Both metaheuristics are within the trajectory-based group. These algorithms vary the problem variables and compare the objective functions obtained. The rejection or acceptance of the new solution depends on the criteria chosen. SA applies an acceptation criteria formula that gives the new solution a probability of being chosen, even worsening the objective function value. TA applies a more specific criterion by applying a threshold where the solution is directly accepted if its objective function value is inside. Accepting bad solutions enhances the optimization process and allows for avoiding local optimums. While the optimization process is performed, the threshold is reduced to exploit the optimum neighborhood. This study has applied threshold accepting with a mutation operator (TAMO) [38]. As the original TA, this algorithm starts with a random solution and an initial threshold. According to Medina’s criterion [39], the initial threshold () is raised or lowered until the acceptability range is between 20% and 40%. The difference lies in the fact that in each iteration, the new solution can be modified, simulating the mutations of genetic algorithms. This modification allows adding exploration to the optimization process.
The TAMO algorithm has specific parameters that adjust it to the problem being solved. These parameters are variables number (), chain length (), standard deviation for mutation operator (), cooling coefficient (), and unimproved chains (). limits the number of variables changed in each iteration. defines the number of iterations run for each threshold. is related to the mutation operator’s probability of mutation of the solution. defines the threshold reduction when the is reached. Finally, the defines the number of chains without improvement allowed before the optimization process is ended. In addition to , if the threshold arrives at 0.05% of the initial, then the optimization process is also finished. The parameters chosen for this optimization problem are those described in Section 3.5.1.
3.2. Sine Cosine Algorithm (SCA)
In [40], the sine cosine algorithm (SCA) was proposed. When exploring and using the search space, the swarm intelligence algorithm considers the sine and cosine functions. The procedure additionally employs to relocate the solutions. It is the location of the final solution for iteration t and dimension j and is often the finest result thus far. Along with , the technique uses three random numbers, , with values ranging from zero to one. Equations (5) and (6) illustrate the update method employed.
3.3. Cuckoo Search Algorithm
The cuckoo species is distinguished by depositing their eggs in other bird species nests; this way of behaving inspired the CS algorithm. Cuckoos are so sophisticated that they can imitate the colors and patterns of their chosen host species’ eggs in some situations. An egg, in this instance, represents a solution. The analogy’s premise is that the best solutions (cuckoos) should be used to replace those that do not function adequately. The CS algorithm is based on three fundamental rules:
- 1.
- One egg is laid by each cuckoo at a time, and it is placed in a nest that is chosen at random.
- 2.
- The best nests, or those that produce eggs of a high caliber, will be taken into consideration for the succeeding generation.
- 3.
- The number of available nests is a fixed value. With a chance of , the cuckoo’s egg will be found by the host bird.
3.4. Hybrid Swarm Intelligence: SCA and CS
Because both metaheuristics perform naturally in continuous domains, the hybrid method is used in the case of swarm intelligence metaheuristics. It takes the metaheuristic, , the list of discrete solutions acquired in the previous iteration, , and a list of transition probabilities as input parameters. It returns a new list of discrete solutions, , as an output. In the first stage, the discretization method determines the ’s velocities. These velocities in the case of CSA and CS correspond to the component obtained by the difference between in Equations (5) to (7).
Following that, a k-means clustering technique is applied to convert the velocity values, which can take on values in , to transition probabilities values which take values in [0,1). The k-means technique clustering the velocities generating clusters in this specific case were five clusters. The clusters were sorted from the smallest to larger centroids. In the case of the smallest centroid, the smallest transition probability was assigned to all cluster velocities. The largest transition probability is assigned to all cluster points in the case of the largest centroid. Figure 3 shows a diagram with the k-means procedure. The values of transition probabilities used for this article were [0.1, 0.2, 0.4, 0.8, 0.9].
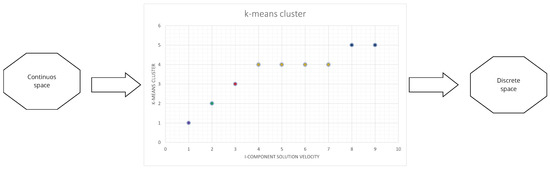
Figure 3.
K-means discretization technique chart.
Then, for each dimension of each solution, a transition probability is obtained. If this probability is more significant than a random number, , and a parameter is greater than a random number, , this dimension of the solution is updated with the value of the best solution obtained, until now. The procedure is updated with a random permitted value if the condition is not fulfilled. In the case neither transition probability nor condition is fulfilled, the dimension of the solution is not updated. This final option is intended to enhance the search space’s exploration.
3.5. Parameter Tuning
The metaheuristics’ results are dependent on the values of its parameters. As a result, a process of parameter selection is required to determine which parameters produce the greatest results for the goal function. This is highly dependent on the optimization problem. As a result, various optimization problems will provide a range of parameter values. Parameter tuning is the process of determining which parameters best fit the optimization problem.
3.5.1. TAMO Tuning
The number of parameters changes according to the metaheuristic. There are algorithms with more parameters than others, such as TAMO. Locating the most suitable ones might become a pretty hard job. As a result, current approaches enable the researcher to obtain the most statistically significant factors and concentrate the search on their variation. These are referred to as Design of Experiments (DoE). To obtain the TAMO parameter adjustment in this scenario, a 2k fractional factorial design was used.
In factorial designs, each trial or replication examines all potential combinations of the factor levels. This enables the evaluation of the response’s change as the factor level varies. This change is referred to as the factor’s effect, and it is proportional to the factor’s statistical significance [41]. Two levels must be allocated to the investigated algorithm parameters to carry out this operation. The parameters tested and the levels chosen are 100 and 100 for every step length, 0% and 30% for the standard deviation, 1 and 5 for the variable number change, 0.80 and 0.95 for the cooling coefficient, and 1 and 5 for the steps without improving.
Since each variable has two levels defined, 32 (25) runs are required to obtain a complete factorial design. Additionally, 5 replications are required to obtain the average and deviation for each experiment, resulting in a total of 160 runs. A fractional factorial DoE of resolution V was chosen to minimize the number of runs. This reduces the number of runs to 80 as the number of combinations is reduced to 16. Table 4, summarizes the parameter value combinations.

Table 4.
Results for each parameter combination of the DoE.
As shown in Table 4, the best results in terms of cost are obtained with Experiment 4. Furthermore, the deviation in cost is negligible. For these reasons, the parameters chosen for the TAMO algorithm correspond to those used in Experiment 4.
3.5.2. Hybrid Swarm Intelligence Methods Tuning
The process for choosing parameters employs four metrics to make an appropriate parameter selection: the best, the average, the worst value, and the time obtained in the different runs executed. Table 5 summarizes the parameters and their explored values. The Range column displays the values that were explored for each of the parameters. The Value column contains the currently selected value. We scanned eight parameter settings and repeated each setting five times.

Table 5.
Scanned parameters for the cuckoo search algorithm.
4. Results
This section details the results of the experiments carried out. Section 4.1 studies the contribution of the hybridization method to the final result of the optimization in addition to the value configured for the values of . In addition to the tables, descriptive statistical analyzes are considered. In particular, descriptive statistics are combined with violin plot visualizations for a comprehensive study. The statistical significance of the results is also determined using the Kolmogorov–Smirnov–Lilliefors and Wilcoxon signed-rank statistical tests. The statistical methods described in Figure 4 [42] were used to select these tests. Later, in Section 4.2, the proposed hybrid algorithms CS and SCA are compared with TA; the latter was successfully used to solve other related optimization problems. Finally, Section 4.3 analyzes the results of the best value obtained.
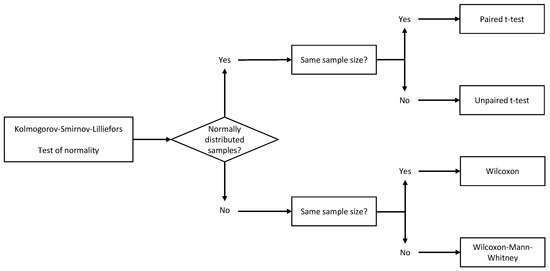
Figure 4.
Statistical method.
4.1. Parameters Exploration of the Hybrid Algorithm
This section aims to identify the contribution of the k-means technique in the discretization process as well as to explore the importance of the operator in the optimization result. To achieve the objective, two experiments were developed. The first corresponds to a comparison between the hybrid versions for SCA and CS with random discretization methods. The second involves comparing the results of using different values of the parameter. For the construction of the random operator, in Algorithm 1, the getClusterProbability function was replaced by a uniform random number generator in Line 8. This operation produces values ranging from zero to one. Line 9 of the method also sets up 2 values for ; it sets the initial value in (), which corresponds with a probability of transition of 50%. For the second value, the value is set to 0.7 (), corresponding to a probability transition of 30%. For this experiment, the value of used was 0.8. The result is displayed in Table 6.

Table 6.
Comparison of random with hybrid discretization algorithms in the embodied optimization problem.
Table 6 shows that for both CS and SCA the hybrid version is superior to both random versions. In the specific case of CS, which was the one that obtained the best result, when comparing it to its random versions, the average indicator in the hybrid version was 0.59% higher than and 0.6% for the case of . The Wilcoxon statistical test indicates that the difference is significant in all cases. The experiment’s main objective was to evaluate the impact of the clustering function (getClusterProbability); the experiment showed that the impact on the optimization results is significant for the CS and SCA cases. The second experiment, which is detailed in Table 7, evaluates the impact of the parameter used in Line 10 of Algorithm 1. Three conditions, , were verified. Both metaheuristics were again evaluated. The parameter determines if the movement is going to follow the best solution (Line 11) or considers a random movement (Line 13); the latter has the sense of developing an exploration of the search space. The higher the value is, the more limited the exploration will be. According to the results, the value that obtained the best results was 0.8. The differences were not as large as in the previous case; however, according to the Wilcoxon test, they were significant in all cases.
| Algorithm 1 Hybrid algorithm. |
|

Table 7.
Analysis of the parameter for hybrid CS and hybrid SCA algorithms in the embodied optimization problem.
4.2. Embodied Energy and Cost Optimization Methods Comparison
This section describes and analyzes the energy minimization results achieved by the TAMO, discrete CS, and discrete SCA algorithms. Table 8 shows the outcomes of the 30 executions of each of the algorithms. The results correspond to the minimization of the steel–concrete embodied energy of the structure. The minimum value of embodied energy obtained throughout the execution is represented in the Energy column. The Cost column represents the structure’s cost that was minimized. The Time corresponds to the amount of time it takes to achieve the minimum in seconds.

Table 8.
Embodied energy minimization results for 30 executions of TAMO, hybrid CS, and hybrid SCA algorithms.
When analyzing the table, it is observed that concerning the best value obtained, all three algorithms obtain the same value, 26,670,276.8 kW·h. In the case of the average indicator, TAMO obtained a slight superiority, with a value of 26,671,471.6 kW·h, followed by CS with a value of 26,677,980.8 kW·h, and finally SCA with 26,681,944.4 kW·h. In the case of the worst value obtained, TAMO again obtained the best value, followed by CS and finally SCA. The Wilcoxon test compared TAMO-CS and TAMO-SCA to determine whether this difference is significant. The result indicates that the difference is not significant since it delivers values greater than 0.05 in the p-value. When the times are analyzed, the situation changes. A notable difference is observed where CS obtains the best result with an average of 7305 s, CSA with an average of 7960 s, and TAMO with an average of 9399 s. In addition, in the table, we must highlight the dispersion of the results obtained for the costs in the three algorithms. For example, in the case of TAMO, some energy optimizations obtain costs of 3,822,723 and, in other cases, values of 4,422,594.
In Figure 5, the results of Table 8 are complemented with violin charts. The chart on the left shows the results of embodied energy, and the graph on the right shows the cost in euros for each configuration obtained. In the chart on the left, it can be seen that in the case of TAMO, the dispersion is less than that of CS and CSA; it should be noted that the scale is in the fourth digit. CS and SCA have similar distributions; however, according to the shape of the distribution obtained and the interquartile range, CS consistently produces better results than SCA. When analyzing the costs resulting from the configurations obtained by minimizing energy, we see that the dispersion of values is substantial and similar in the three algorithms. However, TAMO generates more sparse configurations than CS and SCA. In the case of CS and SCA, the distributions are similar.
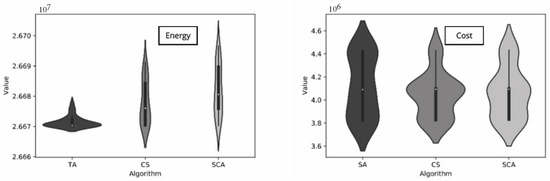
Figure 5.
Embodied energy and cost result violin plots.
In Table 9, the results of the cost optimization are shown. Regarding the algorithms and their results, something similar to the previous experiment occurs. In the best value, which corresponds to the minimum, they all obtain the value 3,822,723.1. Later in the average and the worst value, TA obtains the best results, closely followed by CS and then SCA. The statistical test indicates that the difference is not significant in the TAMO-CS and TAMO-SCA comparison. When analyzing the convergence times, the result is a little different since the best times in the minimum, average, and maximum are for the SCA, followed by the CS and at the end, TAMO. Another interesting point that marks a difference concerning the previous results is that in this case, the energy results for cost optima are good and very similar to those obtained in energy minimization. In this case, TAMO obtained the best values, but the values obtained by CS and SCA were very close. This effect will be analyzed in the next section.

Table 9.
Cost minimization results for 30 executions of TAMO, hybrid CS and hybrid SCA algorithms.
4.3. Optimization Results
The objective of this section is to compare the results obtained for embodied energy and cost optimizations. As it can be seen in Table 8 and Table 9, the three algorithms obtain the same best result. If the average results are compared, TAMO obtains the lower cost and energy values. However, if the computation time is taken into account, it can be seen that for cost optimization, SCA is 14.27% faster than TAMO, while CS results in a 25.79% faster energy optimization with little increase in the objective function. These variations correspond to 0.21% and 0.02% if SCA is considered for cost optimization and CS for energy optimization, respectively. For these reasons, SCA and CS were chosen to compare their optimization results. Results of the optimization problem variables are shown in Table 10.

Table 10.
Design variables minimum and maximum values for best cost and energy optimization results.
The first finding is related to the number of optimums found by both algorithms. Table 8 shows that CS found the same minimum value of energy several times but with different results in terms of costs. This is in line with Figure 6 that shows that the same results in energy can yield different cost values. This is because the embodied energy of steel does not depend on the yield stress. On the contrary, as the yield stress of steel rises, the cost increases. This comparison can be observed in Table 1. This allows the energy optimization to increase the yield stress without penalizing the objective function and, consequently, to obtain an optimum design with higher yield stress. On the contrary, the cost optimization searches for solutions with lower yield stresses to reduce the overall structure cost. Nevertheless, if we consider the relation between the cost and energy optimization obtained in the regression plots of Figure 6 we see that by reducing the cost by one EUR, the energy is reduced by 0.584 kW·h in this optimization problem.
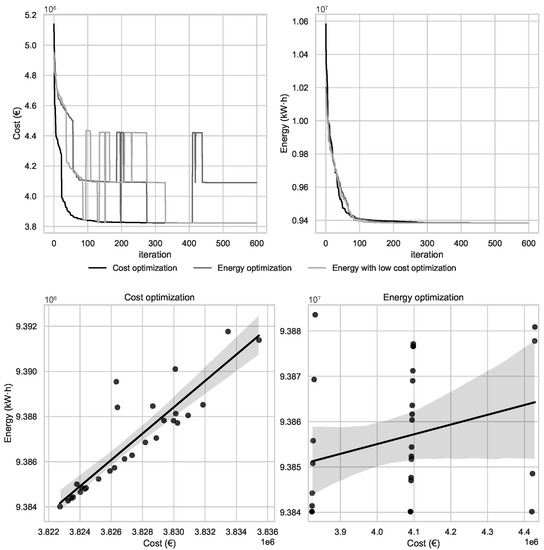
Figure 6.
Optimization results from both cost and energy optimization criteria.
Comparing the variables obtained from both optimizations, it can be observed that the upper part of the steel beam trends in every case to 7 m, matching the lower bound defined for this variable. Regarding the angle of the webs, it can be observed that the embodied energy profits more from the inertia of these elements obtaining, as a result, angles closer to 90 degrees which imply a greater perpendicularity between webs and flanges. Regarding the cells, the central part of the optimum designs gives a positive value for both upper and lower cells, which implies that these elements improve the cross section’s behavior. As can be seen, the optimum designs obtained by the two algorithms are pretty similar. The differences are mainly in the transverse beams and in the thicknesses of some elements. Finally, it is worth noting that the optimization removes the stiffeners of the lower wing. This is due to the double composite action of the slabs in the support zones.
5. Discussion
In the literature, three studies have optimized steel–concrete composite box-girder bridges. These studies are [20,43]. This section will compare the results obtained in Section 4 with those found in previous optimization studies. The value of concrete strength () obtained from both cost and energy optimizations were 25 MPa. The high inertia of the section produces this due to its height. In negative bending moment zones, the concrete is not considered in the calculation, following the method proposed by Eurocode 4 [28], while in positive bending moments, the high inertia of the cross section produces a reduction in the stresses. Because of this, higher concrete strength is not necessary.
In the comparison focused on steel yield stress (), it can be seen that in [20] the results give a design value for steel yield stress of 275 MPa when optimizing cost. This is in line with the results of this optimization problem when optimizing cost. In contrast, if the energy optimization steel stress results are compared, it can be seen that there is some disparity between the yield stress results. This is because the energy and the emissions produced for manufacturing different yield stress steels are the same. Optimizing energy has the same result as optimizing cost, depending on the yield stress chosen by the optimization procedure. Comparing the results with [43], it can be seen that the tensile stress chosen is a parameter and does not vary in this study. This yield stress corresponds with 355 MPa, the expected value for steel bridges.
Finally, a variable comparison was made with [20]. Regarding the lower flange stiffeners, these studies’ results align with the ones obtained in this study. In all cases, these elements are eliminated from the cross section. By comparing the different results, a compromise solution can be found that optimizes the costs and energy criteria by applying multi-objective optimization techniques.
6. Conclusions
There is a clear trend in bridge design to consider criteria other than cost to obtain new alternatives for structural design. Consequently, many studies consider different techniques and objectives in concrete bridge optimization to obtain more sustainable alternative bridges. In contrast, the optimization studies of steel–concrete composite bridges were focused on weight and cost reduction, leaving aside other pillars of sustainability (e.g., the environmental pillar). There are few studies of SCCB optimization. Three optimization algorithms were proposed to compare its results in terms of computation time and minimization results. One of these algorithms was a threshold accepting with a mutation operator (TAMO), which belongs to trajectory-based algorithms. The other two metaheuristics fit in the swarm intelligence algorithms family, the sine cosine algorithm (SCA) and the cuckoo search (CS). A hybridization machine learning strategy was applied to swarm algorithms to improve their performance.
This study shows a box-girder steel–concrete composite bridge optimization considering cost and embodied energy as single optimization objectives. The first part of the study compares the performance of the three algorithms proposed using the best tuning obtained for each algorithm. As a result of this part of the study, the SCA algorithm obtained similar results as TAMO, but on average, the computation time for cost optimization was higher. For energy optimization, the same occurs with CS compared with TAMO. Consequently, these algorithms were chosen to carry out both cost and energy single objective optimization. In both optimizations, the number of stiffeners defined at the end of the optimization process achieved the value of 0 due to the structural behavior produced by the double composite action design. Furthermore, in steel plates, upper and lower cells shorten the distance between non-stiffened zones and increase section stress resistances. Additionally, as demonstrated by past research on bridges, there is a direct connection between cost and energy optimization. In this case, 0.584 kW·h of energy reduction can be obtained for every EUR optimized when applying heuristic optimization techniques. This relation is only produced in the way of cost optimization. If embodied energy is optimized, it is not possible to ensure that an optimal solution will be found in relation to cost.
This work allows the structural researcher to enlarge their knowledge of SCCB optimization by considering new methods and target functions. It opens the door to using those elements to obtain new design criteria for more sustainable and efficient steel–concrete composite bridge alternatives. In future research, other machine learning techniques will be applied to study its performance and accelerate the computation time. Furthermore, this proposed study will consolidate or discard the addition of cells in the cross section and eliminate stiffeners in the bottom flange in this type of box-girder SCCB bridge.
Regarding the study of the algorithm, it is interesting to carry out a time complexity analysis. We must consider that the hybrid algorithm has a complexity of the metaheuristic plus (K-means), which is , plus the discretization process, which is also . The preceding suggests carrying out a time analysis study where, on the one hand, the structure can be varied by increasing its complexity to analyze how the different algorithms behave in convergence times. On the other hand, we can vary the analysis by maintaining the same design, but making the search space more complex, for example, increasing the number of discrete elements to evaluate the different algorithms at convergence times.
Author Contributions
Conceptualization, D.M.-M. and J.G.; methodology, D.M.-M., J.G. and V.Y.; software, D.M.-M. and J.G.; validation, D.M.-M., J.G., J.V.M. and V.Y.; formal analysis, D.M.-M. and J.G.; investigation, D.M.-M., J.G., J.V.M. and V.Y.; resources, J.G. and V.Y.; data curation, D.M.-M., J.G. and J.V.M.; writing—original draft preparation, D.M.-M. and J.G.; writing—review and editing, J.G., J.V.M. and V.Y.; visualization, D.M.-M. and J.G.; supervision, J.V.M. and V.Y.; project administration, J.G. and V.Y.; funding acquisition, J.G and V.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by: Grant PID2020-117056RB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”. Grant FPU-18/01592 funded by MCIN/AEI/10.13039/501100011033 and by “ESF invests in your future” and Grant CONICYT/FONDECYT/INICIACION/11180056.
Informed Consent Statement
Not applicable.
Data Availability Statement
The results of the experiments of this research are part of an ongoing study and can be accessed upon request to the authors.
Acknowledgments
The author gratefully acknowledge the fundings received by: Grant PID2020-117056RB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”. Grant FPU-18/01592 funded by MCIN/AEI/10.13039/501100011033 and by “ESF invests in your future” and Grant CONICYT/FONDECYT/INICIACION/11180056.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CS | Cuckoo Search |
| SCA | Sine Cosine Algorithm |
| TAMO | Threshold Accepting with a Mutation Operator |
| SCCB | Steel Concrete Composite Bridges |
| HS | Harmony Search |
| GA | Genetic Algorithm |
| TA | Threshold Accepting |
| SA | Simulated Annealing |
| DoE | Design of Experiments |
References
- Gervásio, H.; Simões da Silva, L. A probabilistic decision-making approach for the sustainable assessment of infrastructures. Expert Syst. Appl. 2012, 39, 7121–7131. [Google Scholar] [CrossRef]
- Yılmaz, Y.; Seyis, S. Mapping the scientific research of the life cycle assessment in the construction industry: A scientometric analysis. Build. Environ. 2021, 204, 108086. [Google Scholar] [CrossRef]
- Martínez-Muñoz, D.; Martí, J.V.; Yepes, V. Social Impact Assessment Comparison of Composite and Concrete Bridge Alternatives. Sustainability 2022, 14, 5186. [Google Scholar] [CrossRef]
- Abdou, N.; EL Mghouchi, Y.; Hamdaoui, S.; EL Asri, N.; Mouqallid, M. Multi-objective optimization of passive energy efficiency measures for net-zero energy building in Morocco. Build. Environ. 2021, 204, 108141. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, G.; Yan, C.; Wang, G.; Jiang, Y.; Zhao, K. A two-stage multi-objective optimization method for envelope and energy generation systems of primary and secondary school teaching buildings in China. Build. Environ. 2021, 204, 108142. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Accelerated optimization method for low-embodied energy concrete box-girder bridge design. Eng. Struct. 2019, 179, 556–565. [Google Scholar] [CrossRef]
- Martínez-Muñoz, D.; Martí, J.V.; García, J.; Yepes, V. Embodied energy optimization of buttressed earth-retaining walls with hybrid simulated annealing. Appl. Sci. 2021, 11, 1800. [Google Scholar] [CrossRef]
- Wang, T.; Lee, I.S.; Kendall, A.; Harvey, J.; Lee, E.B.; Kim, C. Life cycle energy consumption and GHG emission from pavement rehabilitation with different rolling resistance. J. Clean. Prod. 2012, 33, 86–96. [Google Scholar] [CrossRef]
- Casals, X.G. Analysis of building energy regulation and certification in Europe: Their role, limitations and differences. Energy Build. 2006, 38, 381–392. [Google Scholar] [CrossRef]
- Dixit, M.K.; Fernández-Solís, J.L.; Lavy, S.; Culp, C.H. Identification of parameters for embodied energy measurement: A literature review. Energy Build. 2010, 42, 1238–1247. [Google Scholar] [CrossRef]
- Whitworth, A.; Tsavdaridis, K. Embodied Energy Optimization of Steel-Concrete Composite Beams using a Genetic Algorithm. Procedia Manuf. 2020, 44, 417–424. [Google Scholar] [CrossRef]
- Yeo, D.; Gabbai, R.D. Sustainable design of reinforced concrete structures through embodied energy optimization. Energy Build. 2011, 43, 2028–2033. [Google Scholar] [CrossRef]
- Quaglia, C.; Yu, N.; Thrall, A.; Paolucci, S. Balancing energy efficiency and structural performance through multi-objective shape optimization: Case study of a rapidly deployable origami-inspired shelter. Energy Build. 2014, 82, 733–745. [Google Scholar] [CrossRef]
- Miller, D.; Doh, J.H.; Mulvey, M. Concrete slab comparison and embodied energy optimisation for alternate design and construction techniques. Constr. Build. Mater. 2015, 80, 329–338. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Shi, Y.; Li, J. Solving resource-constrained project scheduling problem via genetic algorithm. J. Comput. Civ. Eng. 2020, 34, 04019055. [Google Scholar] [CrossRef]
- Carbonell, A.; González-Vidosa, F.; Yepes, V. Design of reinforced concrete road vaults by heuristic optimization. Adv. Eng. Softw. 2011, 42, 151–159. [Google Scholar] [CrossRef]
- Molina-Moreno, F.; García-Segura, T.; Martí, J.V.; Yepes, V. Optimization of buttressed earth-retaining walls using hybrid harmony search algorithms. Eng. Struct. 2017, 134, 205–216. [Google Scholar] [CrossRef]
- Martínez-Muñoz, D.; Martí, J.V.; Yepes, V. Steel-concrete composite bridges: Design, life cycle assessment, maintenance, and decision-making. Adv. Civ. Eng. 2020, 2020, 8823370. [Google Scholar] [CrossRef]
- Rempling, R.; Mathern, A.; Tarazona Ramos, D.; Luis Fernández, S. Automatic structural design by a set-based parametric design method. Autom. Constr. 2019, 108, 102936. [Google Scholar] [CrossRef]
- Kaveh, A.; Bakhshpoori, T.; Barkhori, M. Optimum design of multi-span composite box girder bridges using cuckoo search algorithm. Steel Compos. Struct. 2014, 17, 703–717. [Google Scholar] [CrossRef]
- Pedro, R.L.; Demarche, J.; Miguel, L.F.F.; Lopez, R.H. An efficient approach for the optimization of simply supported steel–concrete composite i-girder bridges. Adv. Eng. Softw. 2017, 112, 31–45. [Google Scholar] [CrossRef]
- García, J.; Lemus-Romani, J.; Altimiras, F.; Crawford, B.; Soto, R.; Becerra-Rozas, M.; Moraga, P.; Becerra, A.P.; Fritz, A.P.; Rubio, J.M.; et al. A binary machine learning cuckoo search algorithm improved by a local search operator for the set-union knapsack problem. Mathematics 2021, 9, 2611. [Google Scholar] [CrossRef]
- Hama Rashid, D.N.; Rashid, T.A.; Mirjalili, S. ANA: Ant Nesting Algorithm for Optimizing Real-World Problems. Mathematics 2021, 9, 3111. [Google Scholar] [CrossRef]
- Pace, F.; Santilano, A.; Godio, A. A Review of Geophysical Modeling Based on Particle Swarm Optimization. Surv. Geophys. 2021, 42, 505–549. [Google Scholar] [CrossRef] [PubMed]
- Santucci, V.; Baioletti, M.; Di Bari, G. An improved memetic algebraic differential evolution for solving the multidimensional two-way number partitioning problem. Expert Syst. Appl. 2021, 178, 114938. [Google Scholar] [CrossRef]
- Deng, W.; Shang, S.; Cai, X.; Zhao, H.; Song, Y.; Xu, J. An improved differential evolution algorithm and its application in optimization problem. Soft Comput. 2021, 25, 5277–5298. [Google Scholar] [CrossRef]
- Catalonia Institute of Construction Technology. BEDEC ITEC Materials Database. Available online: https://metabase.itec.cat/vide/es/bedec (accessed on 15 January 2021).
- CEN. Eurocode 2: Design of Concrete Structures; European Committee for Standardization: Brussels, Belgium, 2013. [Google Scholar]
- CEN. Eurocode 3: Design of Steel Structures; European Committee for Standardization: Brussels, Belgium, 2013. [Google Scholar]
- CEN. Eurocode 4: Design of Composite Steel and Concrete Structures; European Committee for Standardization: Brussels, Belgium, 2013. [Google Scholar]
- CEN. EN 10365:2017: Hot Rolled Steel Channels, I and H Sections. Dimensions and Masses; European Committee for Standardization: Brussels, Belgium, 2017. [Google Scholar]
- Vayas, I.; Iliopoulos, A. Design of Steel-Concrete Composite Bridges to Eurocodes; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Monleón, S. Diseño estructural de puentes; Universitat Politècnica de València: València, Spain, 2017. (In Spanish) [Google Scholar]
- CEN. Eurocode 1: Actions on Structures; European Committee for Standardization: Brussels, Belgium, 2019. [Google Scholar]
- MFOM. IAP-11: Code on the Actions for the Design of Road Bridges; Ministerio de Fomento: Madrid, Spain, 2011. [Google Scholar]
- Dueck, G.; Scheuer, T. Threshold accepting: A general purpose optimization algorithm appearing superior to simulated annealing. J. Comput. Phys. 1990, 90, 161–175. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.J.; Vecchi, M.P. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Dueck, G.; Scheuer, T. Design of open reinforced concrete abutments road bridges with hybrid stochastic hill climbing algorithms. Inf. Construcción 2015, 67, e114. [Google Scholar]
- Medina, J.R. Estimation of incident and reflected waves using simulated annealing. J. Waterw. Port Coast. Ocean. Eng. 2001, 127, 213–221. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Lanza-Gutierrez, J.M.; Crawford, B.; Soto, R.; Berrios, N.; Gomez-Pulido, J.A.; Paredes, F. Analyzing the effects of binarization techniques when solving the set covering problem through swarm optimization. Expert Syst. Appl. 2017, 70, 67–82. [Google Scholar] [CrossRef]
- Briseghella, B.; Fenu, L.; Lan, C.; Mazzarolo, E.; Zordan, T. Application of topological optimization to bridge design. J. Bridge Eng. 2013, 18, 790–800. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).