Versatile Stochastic Two-Sided Platform Models

Abstract

This paper deals with the alternative mathematical modeling of the two-side platform. Two-sided platforms are specific multi-sided platforms that bring together two distinct groups of a model. The stochastic modeling by adapting various innovative mathematical methods including the first exceed theory and the stochastic pseudo-game theory has been applied for describing a two-sided platform more properly. A stochastic pseudo-game model is newly introduced to solve the two-sided platform more effectively. Analytically tractable results for operation thresholds for maximizing profits are provided and it also delivers the optimal balance of a two-sided platform. The paper includes how these innovative models are applied into various two-sided market situations. Additionally, users could conduct these multi-sided models to real business developments and the case practices of these unique models shall help the readers who want to find recommendations of their business situations easily even without having any mathematical background.

1. Introduction

Multi-sided platforms (or multi-side markets) are an important business phenomenon that has proliferated not only with classic business such as nightclubs and cable television but also with the rise of information technology and the Internet. Multi-sided markets bring together two or more distinct but business groups of customers [1,2,3,4]. Two-sided platforms are specific multi-sided platforms that bring together two distinct but interdependent groups of customers which are the consumed (i.e., the customer side) and the supplied customers (the supplier side). A two-sided platform has proliferated rapidly with the Internet and this has led to the development of new business models to monetize innovative value propositions not only in online but also offline markets [2,5,6,7]. Two different customer groups whose interactions are usually enabled over the platform. These two sides of the market represent the two primary sets of economic agents in the platform [8,9,10]. Both categories of economic agents have to be present on the platform in right proportions to create enough value to both sides and thereby accelerate and sustain the platform. In such market systems, participation from one side depends on the value created by presence of the other side over the platform [11,12]. Theoretical and mathematical approaches for the two-side platform models have been have widely studied by various contributors [13,14,15,16,17]. Additionally, the concept of the two-sided markets has been adapted for solving the specific situations [18,19,20,21,22,23]. Although there are several researches to use mathematical models to describe multi-sided platform, the stochastic modeling by adapting various innovative mathematical methods including the first exceed theory and the pseudo-stochastic game theory are never been studied before. This unique method enables to obtain analytically tractable solutions which determine the decision making factors including the moment of overflowing a platform capacity, one step prior to a platform overflow and optimum of a two-sided platform system.

This paper is constructed as follows: The stochastic pseudo-game model is newly introduced in Section 2. This section presents the stochastic models for two-sided markets. The original model has a limited resource and the open platform model, in the other hand, has an unlimited resource which indicates large enough to handle customers. The payoff function for the two-side platform has been constructed in Section 3. The visualization of a payoff function for a two-sided market is demonstrated in this section. Two practical application cases are introduced on Section 4. This section is written in a different style which is called case teaching materials which provide managerial questions to choose proper strategic decision. This section shall be even helpful for whom does not have a mathematical background to implement this two-sided model into their business domain. The conclusion of this paper is lastly provided on Section 5.

2. Stochastic Modelling for Two-Sided Platform

The innovative stochastic model has been adapted into the two-sided platform to analyze the behaviors of both sides. This analytical model consists of two sides (i.e., the customer and the supplier sides). This explicit function (Theorem–VTSP) gives the predicted moment of one step prior to hit the platform capacity by customers (simply called player A). The game theory framework makes complicated game types of problems simple to understand situations more clearly. Therefore, stochastic models with a game framework have been widely studied [24,25] and these models are applied for various areas including the blockchain [25,26,27] and the business strategy [28,29,30]. The recent game based stochastic model is adapted into the stock market exchanges [31]. A stochastic pseudo-game is not a stochastic game model but only adapts the stochastic game framework. The stochastic model in this research is a stochastic pseudo-game because this model does not describe a game type of situation but adapts the stochastic game framework for designing the two-sided platform more effectively because a stochastic pseudo-game makes the two-sided platform model solvable by using the mathematically proven processes from various research [24,32,33,34].

2.1. Stochastic Pseudo-Game

The antagonistic two-person pseudo-game (called “A” and “B”) describes the behavior of a two-sided platform between a customer (player A) and supplier (player B) sides. Both input flows to fill the capacity of the platform from either from a customer or a supplier sides. Let ($\Omega$, $\mathcal{F}\left(\Omega \right)$,$P)$ be probability space ${\mathcal{F}}_a,$${\mathcal{F}}_b,$ ${\mathcal{F}}_{\tau }\subseteq \mathcal{F}\left(\Omega \right)$ be independent $\sigma$-subalgebras. The processes represent the customer flow of player A (a customer side) $\mathit{A}$ and the number of suppliers of player B (a supplier side) $\mathit{B}$. Player A checks the number of customer input at times $s_1,$$s_2,\dots$ and sustain respective customers $X_1,$$X_2,\cdots$ formalized by the process $\mathit{A}$ as follows:

$$\mathit{A}:={\sum }_{k\ge 0}{X}_k{\epsilon }_{s_k},s_0\left(=0\right)<s_1<s_2<\cdots ,$$

(1)

and the number of suppliers to player B is similarly described by the process $\mathit{B}$ as follows:

$$\mathit{B}:={\sum }_{j\ge 0}{Y}_j{\epsilon }_{t_j},t_0\left(=0\right)<t_1<t_2<\cdots .$$

(2)

The numbers of supplier input at each epoch are $t_1,$$t_2,\dots$ with respective suppliers for player B are $Y_1,Y_2,\dots$. Both processes are $\mathcal{F}$-measurable marked Poisson processes (${\epsilon }_w$ is a point mass at w) with respective intensities ${\lambda }_a$ and ${\lambda }_b$ which are related with the input behaviors of both sides in the two-sided platform. Basically, player B counts the number of suppliers (or contents) to cover the customers in the platform. The processes $\mathit{A}$ and $\mathit{B}$ are specified by their transforms

$$\mathbb{E}\left[z^{\mathit{A}\left(s\right)}\right]=e^{{\lambda }_{a}s\left(z-1\right)},\mathbb{E}\left[g^{\mathit{B}\left(t\right)}\right]=e^{{\lambda }_{b}t\left(g-1\right)}.$$

(3)

The two-sided platform is monitored at random times in accordance with the point processin the two-side platform:

$$\mathit{T}:=\sum _{i\ge 0}{\epsilon }_{{\tau }_i},{\tau }_0\left(>0)\right),{\tau }_1,\dots ,$$

(4)

which is assumed to be delayed renewal process. If

$$\left(A\left(t\right),B\left(t\right)\right):=\mathit{A}\otimes \mathit{B}\left(\left[0,t\right]\right),t\ge 0,$$

(5)

then

$$\left(A_i,B_i\right):=\mathit{A}\otimes \mathit{B}\left(\left[0,{\tau }_i\right]\right),i=0,1,\dots ,$$

(6)

forms an observation process upon $\mathit{A}\otimes \mathit{B}$ embedded over $\mathit{T},$ with respective increments

$$\left(X_i,Y_i\right):=\mathit{A}\otimes \mathit{B}\left(\left[{\tau }_{i-1},{\tau }_i\right]\right),i=1,2,\dots ,$$

(7)

and

$$X_0=A_0,Y_0=B_0.$$

(8)

The observation process could be formalized as

$${\mathit{A}}_{\tau }\otimes {\mathit{B}}_{\tau }:=\sum _{i\ge 0}\left(X_i,Y_i\right){\epsilon }_{{\tau }_i},$$

(9)

where

$${\mathit{A}}_{\tau }=\sum _{i\ge 0}{X}_i{\epsilon }_{{\tau }_i},{\mathit{B}}_{\tau }=\sum _{i\ge 0}{Y}_i{\epsilon }_{{\tau }_i},$$

(10)

and it is with position dependent marking and with $X_k$ and $Y_k$ being dependent with the notation

$${\Delta }_k:={\tau }_k-{\tau }_{k-1},k=0,1,\dots ,{\tau }_{-1}=0,$$

(11)

and

$$\gamma \left(z,g\right)=\mathbb{E}\left[z^{X_i}·g^{Y_i}\right],\left|z\right|<1,\left|g\right|<1.$$

(12)

The setup of these processes from (1)–(4) are commonly used on various studies and the multi-variate processes from (5)–(8) have been conventionally used for antagonistic stochastic modeling and these processes haven been fully used confirmed from the various research [24,32,33,34]. It is noted the two-dimensional process (9) is not a simple process because each player contains the combination of several processes. For player A, the process $A\left(s\right)$ from (3) is a Poisson counting process with the continuous time parameter s; the process $A_k$ from (1) $\left(=A\left(s_k\right)\right)$ is a compound Poisson process which counts the values when the process is increased at the moment of $s_k$; the process $A_{\tau }$ from (9) $\left(=A\left(\tau \right)\right)$ is a compound Poisson process which counts the values at the moment of ${\tau }_i$ when the process is monitored by the observation process from (4). By using the double expectation,

$$\gamma \left(z,g\right)=\delta \left({\lambda }_a\left(1-z\right)+{\lambda }_b\left(1-g\right)\right),$$

(13)

and

$${\gamma }_0\left(z,g\right)=\mathbb{E}\left[z^{A_0}{g}^{B_0}\right]={\delta }_0\left({\lambda }_a^0\left(1-z\right)+{\lambda }_b^0\left(1-g\right)\right),$$

(14)

where

$$\delta \left(\theta \right)=\mathbb{E}\left[e^{-\theta {\Delta }_1}\right],{\delta }_0\left(\theta \right)=\mathbb{E}\left[e^{-\theta {\tau }_0}\right],$$

(15)

are the magical transform of increments ${\Delta }_1,{\Delta }_2,\dots$. The stochastic process ${\mathcal{A}}_{\tau }\otimes {\mathcal{B}}_{\tau }$ describes the status of the two-sided platform which has a connection between both sides and the supplier side is usually a dominant side. The attraction factor $\alpha$ is newly proposed which indicates the power of the dominant side to seduce the customers in the submissive side. Since we consider a supplier side is dominant which impacts on the input of customers, the customer input rate ${\lambda }_a$ becomes the function based on the given number of suppliers b and it could be assigned as follows:

$${\lambda }_a\left(b\right)={\lambda }_a\alpha ·\left(\frac{b}{\tilde{\delta }}\right),\alpha \ge 1,b\le M,$$

(16)

where $\tilde{\delta }=\mathbb{E}\left[{\Delta }_1\right]$ and $\alpha$ is the ratio between a supplier and a customer sides and this ratio is called the attraction factor which depends on the status of the dominant side. This value $\alpha$ is typically greater than 1 (i.e., $\alpha \ge 1$). The stochastic process ${\mathit{A}}_{\tau }\otimes {\mathit{B}}_{\tau }$ is completed when on the k-th observation epoch ${\tau }_k$, the collateral customers to player A exceeds the capacity of the platform M. To further formalize the game, the exit index is introduced:

$$\mu :=\inf \left\{k:A_k={\sum }_{k\ge 0}{X}_k\ge M,X_0=A_0\right\},$$

(17)

$$\nu :=\inf \left\{j:B_j={\sum }_{j\ge 0}{Y}_j\ge \frac{M}{\alpha },Y_0=B_0\right\}.$$

(18)

Since the platform shall be terminated at the time ${\tau }_{\mu },$ the number of customers may reach the capacity of the platform M. We shall be targeting the confined game in the view point of player A. The first passage time ${\tau }_{\mu }$ is the associated exit time from the confined game and the formula (7) will be modified as

$$\overline{{\mathit{A}}_{\tau }}\otimes \overline{{\mathit{B}}_{\tau }}:=\sum _{k\ge 0}^{\mu }\left(X_k,Y_k\right){\epsilon }_{{\tau }_k}$$

(19)

which the path of the game from $\mathcal{F}\left(\Omega \right)\cap \left\{\nu <\mu \right\}$, which gives an exact definition of the model observed until ${\tau }_{\mu }.$ The joint functional of the two-sided platform is as follows:

$$\begin{gathered} {\Phi }_M={\Phi }_M\left(\xi ,z_0,z_1,g_0,g_1\right) \\ =\mathbb{E}\left[{\xi }^{\mu }·z_0^{A_{\mu -1}}·z_1^{A_{\mu }}·g_0^{B_{\nu -1}}·g_1^{B_{\nu }}{\mathbf{1}}_{\left\{\mu <\nu \right\}}\right], \end{gathered}$$

(20)

where M indicates the platform capacity. This functional shall represent the status of the two-sided platform upon the exit time ${\tau }_{\mu }$. The latter is of particular interest, we are interested in not only the prediction of the moment of full but also one observation prior to this. The Theorem–VTSP: establishes an explicit formula ${\Phi }_M$ from (12)–(14). The $\mathcal{D}$-operator and its inverse operator $\mathfrak{D}$ from the first exceed model [35,36] have been adapted as follows:

$${\mathcal{D}}_{\left(x,y\right)}\left[f\left(x,y\right)\right]\left(u,v\right):=\left(1-u\right)\left(1-v\right)\sum _{x\ge 0}\sum _{y\ge 0}f\left(x,y\right)u^x{v}^y,$$

(21)

then

$$f\left(x,y\right)={\mathfrak{D}}_{\left(u,v\right)}^{\left(x,y\right)}\left[{\mathcal{D}}_{\left(x,y\right)}\left\{f\left(x,y\right)\right\}\right],$$

(22)

where $\left\{f\left(x,y\right)\right\}$ is a sequence, with the inverse

$${\mathfrak{D}}_{\left(u,v\right)}^{\left(m,n\right)}\left(•\right)=\left\{\begin{array}{cc}\left(\frac{1}{m!·n!}\right)\underset{\left(u,v\right)\to 0}{lim}\frac{{\partial }^m{\partial }^n}{\partial u^m\partial v^n}\frac{1}{\left(1-u\right)\left(1-v\right)}\left(•\right),\hfill & m\ge 0,n\ge 0,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(23)

Theorem–VTSP: The functional ${\Phi }_M$ of the process of (20) satisfies following expression:

$${\Phi }_M={\mathfrak{D}}_{\left(u,v\right)}^{\left(M,⌈\frac{M}{\alpha }⌉\right)}\left[{\varphi }_0^1-{\varphi }_0+\frac{\xi ·{\gamma }_0}{1-\xi \gamma }\left({\varphi }^1-\varphi \right)\right].$$

(24)

Proof. 

We find the explicit formula of the joint function ${\Phi }_m$. The joint functional (20) of player A is as following:

$$\begin{gathered} {\Phi }_m\left(\xi ,z_0,z_1,g_0,g_1\right)={\sum }_{k=0}^{\infty }{\xi }^k\mathbb{E}\left[{\mathbf{1}}_{\left\{\mu \left(m\right)=k\right\}}{z}_0^{A_{\mu -1}}·z_1^{A_{\mu }}·g_0^{B_{\nu -1}}·g_1^{B_{\nu }}{\mathbf{1}}_{\left\{\mu <\nu \right\}}\right] \\ ={\sum }_{k=0}^{\infty }{\sum }_{j=k+1}^{\infty }{\xi }^k\mathbb{E}\left[{\mathbf{1}}_{\left\{\mu \left(m\right)=k,\nu \left(n\right)=j\right\}}{z}_0^{A_{\mu -1}}·z_1^{A_{\mu }}·g_0^{B_{\nu -1}}·g_1^{B_{\nu }}\right] \end{gathered}$$

(25)

and, applying the operator $\mathcal{D}$ to random family $\left\{{\mathbf{1}}_{\left\{\mu \left(m\right)=k,\nu \left(n\right)=j\right\}}:m\ge 0\right\}$, we arrive at

$${\mathcal{D}}_{\left(x,y\right)}\left[{\mathbf{1}}_{\left\{\mu \left(m\right)=k,\nu \left(n\right)=j\right\}}\right]\left(u,v\right)=\left(u^{A_{k-1}}-u^{A_k}\right)\left(v^{B_{j-1}}-v^{B_j}\right)$$

(26)

and, from the previous research [24,26,27,28],

$$\begin{array}{l}\Psi \left(u,v\right)={\mathcal{D}}_{\left(x,y\right)}\left[{\Phi }_m\right]\left(u,v\right)\\ ={\sum }_{k=0}^{\infty }{\xi }^k{\sum }_{j>k}\mathbb{E}\left[z_0^{A_{\mu -1}}·z_1^{A_{\mu }}·g_0^{B_{\nu -1}}·g_1^{B_{\nu }}{u}^{A_{k-1}}{u}^{X_k}\left(1-u^{X_k}\right)\left(v^{B_{j-1}}-v^{B_j}\right)\right]\end{array}$$

(27)

$$={\sum }_{k=0}^{\infty }{D}_{1k}{D}_{2k}{\sum }_{j>k}{D}_{3kj}{D}_{4kj}$$

(28)

where

$$\begin{array}{ll}{D}_{1k}& ={\xi }^k\mathbb{E}\left[z_0^{A_{k-1}}·z_1^{A_{k-1}}·g_0^{B_{k-1}}·g_1^{B_{k-1}}{u}^{A_{k-1}}\right]\\ & =\left\{\begin{array}{cc}1,\hfill & k=0,\hfill \\ \xi {\gamma }_0{\left(\xi ·\gamma \right)}^{k-1},\hfill & k>0,\hfill \end{array}\right.\end{array}$$

(29)

$$\begin{array}{ll}{D}_{2k}& =\mathbb{E}\left[g_1^{X_k}{z}_1^{Y_k}{u}^{X_k}\left(1-u^{X_k}\right)\right]\\ & =\left\{\begin{array}{cc}{\varphi }_0^1-{\varphi }_0,\hfill & k=0,\hfill \\ {\varphi }^1-\varphi ,\hfill & k>0,\hfill \end{array}\right.\end{array}$$

(30)

$$D_{3kj}=\mathbb{E}\left[v^{\left(Y_{k+1}+\cdots +Y_{j-1}\right)}\right]=\gamma {\left(1,v\right)}^{j-\left(k+1\right)},$$

(31)

$$D_{4kj}=\mathbb{E}\left[1-v^{Y_j}\right]=1-\gamma \left(1,v\right),$$

(32)

and

$$\gamma :=\gamma \left(z_0{z}_{1}u,g_0{g}_{1}v\right),$$

(33)

$${\gamma }_0:={\gamma }_0\left(z_0{z}_{1}u,g_0{g}_{1}v\right),$$

(34)

$$\varphi :=\gamma \left(z_{1}u,g_{1}v\right),$$

(35)

$${\varphi }_0:={\gamma }_0\left(z_{1}u,g_{1}v\right),$$

(36)

$${\varphi }^1:=\gamma \left(z_1,g_{1}v\right),$$

(37)

$${\varphi }_0^1:={\gamma }_0\left(z_1,g_{1}v\right).$$

(38)

Adding up ${\Sigma }_{j>k}{D}_{3kj}{D}_{4kj}$ yields 1 due to $\left|\right|\gamma \left(u,v\right)\left|\right|<1$ [24,25] and summing ${\Sigma }_{k\ge 0}$$D_{1k}{D}_{2k}$ constructs:

$$\Psi \left(u,v\right)={\varphi }_0^1-{\varphi }_0+\frac{\xi ·{\gamma }_0}{1-\xi \gamma }\left({\varphi }^1-\varphi \right).$$

(39)

Finally, we have

$${\Phi }_M={\mathfrak{D}}^{\left(M,⌈\frac{M}{\alpha }⌉\right)}\left[{\varphi }_0^1-{\varphi }_0+\frac{\xi ·{\gamma }_0}{1-\xi \gamma }\left({\varphi }^1-\varphi \right)\right].$$

(40)

□

From (20) and (40), we can find the PGFs (probability generating functions) of $A_{\mu }$ and the exit index:

$$\mathbb{E}\left[{\xi }^{\mu }\right]={\Phi }_M\left(\xi ,1,1,1,1\right),$$

(41)

$$\mathbb{E}\left[z_1^{A_{\mu }}\right]={\Phi }_M\left(1,1,z_1,1,1\right),$$

(42)

$$\mathbb{E}\left[g_0^{B_{\nu -1}}\right]={\Phi }_M\left(1,1,1,g_0,1\right).$$

(43)

The mean for the number of customers in the platform $A_{\mu }$ could be found from (40), (42) and (43):

$$\mathbb{E}\left[A_{\mu }\right]=\mathbb{E}\left[\mathbb{E}\left[A_{\mu }|B_{\nu -1}\right]\right]=\underset{z_1\to 1}{lim}\sum _{k\ge 0}\left\{\frac{d}{d{z}_1}{\Phi }_M\left(1,1,z_1,1,1\right)p_k^b\right\}$$

(44)

where

$$p_k^b=\underset{g_0\to 0}{lim}\left(\frac{1}{k!}\right)\frac{{\partial }^k}{\partial g_0^k}{\Phi }_M\left(1,1,1,g_0,1\right)$$

(45)

and

$${\Phi }_M\left(1,1,1,g_0,1\right)={\mathfrak{D}}_{\left(u,v\right)}^{\left(M,⌈\frac{M}{\alpha }⌉\right)}\left[{\varphi }_0^1-{\varphi }_0+\frac{\xi ·{\gamma }_0}{1-\xi \gamma }\left({\varphi }^1-\varphi \right)\right],$$

(46)

where, from (33)–(38),

$$\gamma :=\gamma \left(u,g_{0}v\right),$$

(47)

$${\gamma }_0:={\gamma }_0\left(u,g_{0}v\right),$$

(48)

$$\varphi :=\gamma \left(u,v\right),$$

(49)

$${\varphi }_0:={\gamma }_0\left(u,v\right),$$

(50)

$${\varphi }^1:=\gamma \left(1,v\right),$$

(51)

$${\varphi }_0^1:={\gamma }_0\left(1,v\right).$$

(52)

2.2. Open Two-Sided Platform Model

This innovative two-sided platform model could have several variants. One of variants is the two-sided platform has an unlimited capacity. Practically speaking, it is not possible that a real system has unlimited capacity or resource of the platform. Unlike the original stochastic two-sided platform model, the capacity of an open two-sided platform is relatively a large number and both sides are not interrelated. Recalling from (1)–(15), the initial setup of the open model is the same as the previous section. The open two-sided platform means that the capacity of the platform is almost unlimited and the joint functional of the two-sided platform becomes:

$${\Phi }_M=\underset{M\to {\infty }^{-}}{lim}{\Phi }_M\left(\xi ,z_0,z_1,g_0,g_1\right).$$

(53)

Since the customer flow in a two-sided platform is given by the supplier flow from (16), the joint functional is modified only for the customer side to represent the open two-sided platform as follows:

$$\phi \left(b;z_0,z_1\right)=\mathbb{E}\left[z_0^{A_{\mu \left(b\right)-1}}·z_1^{A_{\mu \left(b\right)}}|B_{\nu -1}=b\right],$$

(54)

which is given by the flows from the supplier side. From (42)–(44), the PGFs (Probability Generating Functions) of $A_{\mu }$, $A_{\mu -1}$ are as follows:

$$\phi \left(b;z_0,z_1\right)={\gamma }_a^0\left(z_0{z}_1\right){\gamma }_a{\left(z_0{z}_1\right)}^{\mu \left(b\right)-1}{\gamma }_a\left(z_1\right),$$

(55)

where

$${\gamma }_a\left(z\right)=\delta \left({\lambda }_a\left(1-z\right)\right),{\gamma }_a^0\left(z\right)=\mathbb{E}\left[z^{A_0}\right]={\delta }_0\left({\lambda }_a\left(1-z\right)\right)$$

(56)

and the exit index of the customer side is:

$$\mu \left(b\right):=\mathbb{E}\left[\mu |B_{\nu }=b\right]\simeq ⌊\frac{b-b_0}{{\lambda }_b\tilde{\delta }}⌋,$$

(57)

($B_0$ is assumed as the fixed value $b_0=\mathbb{E}\left[B_0\right]$). It is noted that all index values $\nu -1$ and $\nu$ are almost the same (i.e., $\nu -1\simeq \nu$) when the resource of the supplier is almost unlimited (i.e., $0\ll M<\infty$ and $0\ll B_{\nu -1}\simeq B_{\nu }<\infty$). The mean number of customers $\mathbb{E}\left[A_{\mu }\right]$ in the two-sided platform could be found as follows:

$$\mathbb{E}\left[A_{\mu \left(B_{\nu -1}\right)}\right]=\mathbb{E}\left[\mathbb{E}\left[A_{\mu \left(B_{\nu -1}\right)}|B_{\nu -1}\right]\right],$$

(58)

where, from (16) and (57),

$$\mathbb{E}\left[A_{\mu \left(b\right)}|B_{\nu }=b\right]=\underset{z_1\to 1}{lim}\frac{d}{d{z}_1}\phi \left(b;1,z_1\right)={\lambda }_a\widetilde{{\delta }_0}+\mu \left(b\right)·{\lambda }_a\left(b\right)\tilde{\delta },$$

(59)

From (57) and (59), we have

$$\mathbb{E}\left[A_{\mu \left(B_{\nu -1}\right)}\right]=\sum _{k=0}^M\left\{{\lambda }_a\widetilde{{\delta }_0}+{\lambda }_a\left(k-b_0\right)\right\}{p}_k^b$$

(60)

and

$$p_k^b=P\left\{B_{\nu }=k\right\}=\left(\frac{1}{\mathit{A}}\right)\left\{\frac{{\left({\lambda }_a\tilde{\delta }\right)}^k}{k!}{e}^{-\left({\lambda }_a\tilde{\delta }\right)}\right\},$$

(61)

$$\mathit{A}=\sum _{k=0}^M\frac{{\left({\lambda }_a\tilde{\delta }\right)}^k}{k!}{e}^{-\left({\lambda }_a\tilde{\delta }\right)}.$$

(62)

Although the open platform model is relatively simple and easy to be analytically solvable, the open case is very practical for some specific cases. The practical real-world case for the open two-sided platform shall be provided on Section 4.2.

2.3. Memoryless Two-Sided Platform

It is assumed that the observation process has the memoryless properties which might be a special condition but very practical for actual implementation for analyzing the two-sided platform. It implies that the flow of suppliers does not contain any past information of the supplier side. We can find explicit solutions of $p_k^b$ and $\mathbb{E}\left[A_{\mu }\right]$ to build a proper payoff function for the optimization. Recall from (21), the $\mathcal{D}$-operator for single variable is defined as follows:

$$H\left(u\right)={\mathcal{D}}_x\left[w\left(x\right)\right]\left(u\right):=\left(1-u\right)\sum _{x\ge 0}w\left(x\right)u^x,$$

(63)

$$\begin{array}{l}{\mathcal{D}}_{\left(x,y\right)}\left[w_1\left(x\right)w_2\left(y\right)\right]\left(u,v\right)\\ :=\left(1-u\right)\left(1-v\right){\sum }_{x\ge 0}{\sum }_{y\ge 0}{w}_1\left(x\right)w_2\left(y\right)u^x{v}^y\\ ={\mathcal{D}}_x\left[w_1\left(x\right)\right]{\mathcal{D}}_y\left[w_2\left(y\right)\right],\end{array}$$

then

$$w\left(x,y\right)={\mathfrak{D}}_{\left(u,v\right)}^{\left(x,y\right)}\left[{\mathcal{D}}_{\left(x,y\right)}\left\{w\left(x,y\right)\right\}\right],$$

(64)

$$w_1\left(x\right)w_2\left(y\right)={\mathfrak{D}}_u^x\left[{\mathcal{D}}_x\left\{w_1\left(x\right)\right\}\right]{\mathfrak{D}}_v^y\left[{\mathcal{D}}_y\left\{w_2\left(y\right)\right\}\right],$$

(65)

where $\left\{f\left(x\right),\left(f_1\left(x\right)f_2\left(y\right)\right)\right\}$ are a sequence, with the inverse (101) and

$${\mathfrak{D}}_u^m\left(•\right)=\left\{\begin{array}{cc}\frac{1}{m!}\underset{u\to 0}{lim}\frac{{\partial }^m}{\partial u^m}\frac{1}{\left(1-u\right)}\left(•\right),\hfill & m\ge 0,\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(66)

and

$${\mathfrak{D}}_{\left(u,v\right)}^{\left(m,n\right)}\left[H_1\left(u\right)H_2\left(v\right)\right]={\mathfrak{D}}_u^m\left[H_1\left(u\right)\right]{\mathfrak{D}}_v^n\left[H_2\left(v\right)\right].$$

(67)

The $\mathfrak{D}$-operator is defined on the space of all analytic functions at 0 and this operator satisfies:

$${\mathfrak{D}}_u^m\sum _{k=0}^{\infty }{a}_k{u}^k=\sum _{k=0}^m{a}_k,$$

(68)

and the formulas (12)–(15) and (65) could be rewritten as follows:

$$\gamma \left(z,g\right)=\delta \left({\lambda }_a\left(1-z\right)+{\lambda }_b\left(1-g\right)\right)={\gamma }_a\left(z\right)·{\gamma }_b\left(g\right),$$

(69)

$${\gamma }_a\left(z\right)=\delta \left({\lambda }_a\left(1-z\right)\right),$$

(70)

$${\gamma }_b\left(z\right)=\delta \left({\lambda }_b\left(1-g\right)\right),$$

(71)

and

$${\gamma }_0\left(z,g\right)={\delta }_0\left({\lambda }_a\left(1-z\right)+{\lambda }_b\left(1-g\right)\right)={\gamma }_a^0\left(z\right)·{\gamma }_b^0\left(g\right),$$

(72)

$${\gamma }_a^0\left(z\right)=\mathbb{E}\left[z^{A_0}\right]={\delta }_0\left({\lambda }_a\left(1-z\right)\right),$$

(73)

$${\gamma }_b^0\left(z\right)=\mathbb{E}\left[g^{B_0}\right]={\delta }_0\left({\lambda }_b\left(1-g\right)\right),$$

(74)

from (33)–(38),

$$\gamma ={\gamma }_a·{\gamma }_b:={\gamma }_a\left(z_0{z}_{1}u\right){\gamma }_b\left(g_0{g}_{1}v\right),$$

(75)

$${\gamma }_0={\gamma }_a^0·{\gamma }_b^0:={\gamma }_a^0\left(z_0{z}_{1}u\right){\gamma }_b^0\left(g_0{g}_{1}v\right),$$

(76)

$$\varphi :={\gamma }_a\left(z_{1}u\right){\gamma }_b\left(g_{1}v\right),$$

(77)

$${\varphi }_0:={\gamma }_a^0\left(z_{1}u\right){\gamma }_b^0\left(g_{1}v\right),$$

(78)

$${\varphi }^1:={\gamma }_a\left(z_1\right){\gamma }_b\left(g_{1}v\right),$$

(79)

$${\varphi }_0^1:={\gamma }_a^0\left(z_1\right){\gamma }_b^0\left(g_{1}v\right).$$

(80)

$$\gamma ={\gamma }_a·{\gamma }_b:={\gamma }_a\left(z_0{z}_{1}u\right){\gamma }_b\left(g_0{g}_{1}v\right),$$

(81)

$${\gamma }_0={\gamma }_a^0·{\gamma }_b^0:={\gamma }_a^0\left(z_0{z}_{1}u\right){\gamma }_b^0\left(g_0{g}_{1}v\right),$$

(82)

$$\varphi :={\gamma }_a\left(z_{1}u\right){\gamma }_b\left(g_{1}v\right),$$

(83)

$${\varphi }_0:={\gamma }_a^0\left(z_{1}u\right){\gamma }_b^0\left(g_{1}v\right),$$

(84)

$${\varphi }^1:={\gamma }_a\left(z_1\right){\gamma }_b\left(g_{1}v\right),$$

(85)

$${\varphi }_0^1:={\gamma }_a^0\left(z_1\right){\gamma }_b^0\left(g_{1}v\right).$$

(86)

$${\gamma }_a^0\left(u\right)=\frac{1}{\left(1+\widetilde{{\delta }_0}·{\lambda }_a\right)-\widetilde{{\delta }_0}·{\lambda }_{a}u}=\frac{{\beta }_a^0}{1-{\alpha }_a^0·u},$$

(87)

$${\gamma }_a\left(u\right)=\frac{1}{\left(1+\tilde{\delta }·{\lambda }_a\right)-\tilde{\delta }·{\lambda }_{a}u}=\frac{{\beta }_a}{1-{\alpha }_a·u},$$

(88)

$${\gamma }_b^0\left(v\right)=\frac{1}{\left(1+\widetilde{{\delta }_0}·{\lambda }_b\right)-\widetilde{{\delta }_0}·{\lambda }_{b}v}=\frac{{\beta }_b^0}{1-{\alpha }_b^0·v},$$

(89)

$${\gamma }_b\left(v\right)=\frac{1}{\left(1+\tilde{\delta }·{\lambda }_b\right)-\tilde{\delta }·{\lambda }_{b}v}=\frac{{\beta }_b}{1-{\alpha }_b·v},$$

(90)

$${\beta }_a^0=\frac{1}{\left(1+\widetilde{{\delta }_0}·{\lambda }_a^0\right)},{\alpha }_a^0=\frac{\widetilde{{\delta }_0}·{\lambda }_a^0}{\left(1+\widetilde{{\delta }_0}·{\lambda }_a^0\right)},$$

(91)

$${\beta }_a=\frac{1}{\left(1+\tilde{\delta }·{\lambda }_a\right)},{\alpha }_a=\frac{\tilde{\delta }·{\lambda }_a}{\left(1+\tilde{\delta }·{\lambda }_a\right)},$$

(92)

$${\beta }_b^0=\frac{1}{\left(1+\widetilde{{\delta }_0}·{\lambda }_b^0\right)},{\alpha }_b^0=\frac{\widetilde{{\delta }_0}·{\lambda }_b^0}{\left(1+\widetilde{{\delta }_0}·{\lambda }_b^0\right)},$$

(93)

$${\beta }_b=\frac{1}{\left(1+\tilde{\delta }·{\lambda }_b\right)},{\alpha }_b=\frac{\widetilde{{\delta }_0}·{\lambda }_b}{\left(1+\tilde{\delta }·{\lambda }_b\right)},$$

(94)

$$\widetilde{{\delta }_0}=\mathbb{E}\left[{\tau }_0\right],\tilde{\delta }=\mathbb{E}\left[{\Delta }_k\right].$$

(95)

The function $\mathbb{E}\left[g_0^{B_{\nu -1}}\right]$ is the PGF (Probability Generating Function) of the number of suppliers at the prior moment of exceeding more than the platform capacity M. The probability distribution of $B_{\nu -1}$ could be found from (45) after obtaining the PGF from (43):

$$\mathbb{E}\left[g_0^{B_{\nu -1}}\right]={\Phi }_M\left(1,1,1,g_0,1\right)=L_1+\sum _{i\ge 0}\left\{Q_i^a-Q_{i+1}^a\right\}{Q}_i^b,$$

(96)

where

$$L_1=\frac{{\beta }_b^0\left(1-{\left({\alpha }_b^0\right)}^{M+1}\right)}{1-{\alpha }_b^0}-\frac{{\beta }_a^0{\beta }_b^0\left(1-{\left({\alpha }_a^0\right)}^{M+1}\right)\left(1-{\left({\alpha }_b^0\right)}^{M+1}\right)}{\left(1-{\alpha }_a^0\right)\left(1-{\alpha }_b^0\right)},$$

(97)

$$Q_i^a={\beta }_a^0{\left({\beta }_a\right)}^i{\sum }_{j_a\ge 0}{\Xi }_i^M\left(j_a,\frac{{\alpha }_a}{{\alpha }_a^0},{\alpha }_a^0\right),$$

(98)

$$Q_i^b=\left(\frac{{\beta }_a^0{\left({\beta }_a\right)}^{i+1}}{{\alpha }_b-{\alpha }_b^0{g}_0}\right){\sum }_{j_2\ge 0}\left\{\left({\alpha }_b\right){\Xi }_i^M\left(j_2,g_0,{\alpha }_b\right)-\left({\alpha }_b^0{g}_0\right){\Xi }_i^M\left(j_2,\frac{{\alpha }_b}{{\alpha }_b^0},{\alpha }_b^0{g}_0\right)\right\},$$

(99)

$${\Xi }_i^m\left(j,x,y\right)=\left(\genfrac{}{}{0pt}{}{i-1+j}{j}\right)x^j\left(\frac{y^j-y^{m+1}}{1-y}\right),\left|x\right|\le 1,\left|y\right|\le 1,$$

(100)

3. Stochastic Optimizations for Two-Sided Platform

The optimization practice in a two-sided platform is provided in this section. The best strategy for maximizing the payoff is determined by an attraction factor. Additionally, the optimization practice for an open two-sided platform is also introduced in this section because there are some special characteristics of this open platform.

3.1. Two-Sided Platform Payoff Function Design

The input ratio between two sides is a vital factor for a cost related function which includes the cost, the revenue and the payoff functions. The payoff function (i.e., a revenue function or a profit function) could be constructed based on the attraction factor $\alpha$ that indicates the customer coverage (i.e., the submissive side) by the supplier side (i.e., the dominant side). Practically, a typical range of the attraction factor $\alpha$ is up to 10 (i.e., $\alpha \in$ [1,10]) although it could reach up to the infinity ($\alpha <\infty$). The optimal value of $\alpha$ towards to maximize the payoff function $\mathfrak{S}$ of the two-sided platform and the payoff function is:

$$\begin{array}{l}\mathfrak{S}\left(\alpha ;M\right)\\ =\mathbb{E}\left[c_0·A_{\mu }-c_1·\left\{B_{\mu }·{\mathbf{1}}_{\left\{A_{\mu }+\alpha B_{\mu -1}\le M\right\}}+\left(M-A_{\mu }\right)·{\mathbf{1}}_{\left\{A_{\mu }+\alpha B_{\mu -1}>M\right\}}\right\}\right]\\ =c_0\mathbb{E}\left[A_{\mu }\right]-c_1\mathbb{E}\left[B_{\mu }·{\mathbf{1}}_{\left\{A_{\mu }+\alpha B_{\mu -1}\le M\right\}}\right]\\ -c_1\left\{M·\mathbb{E}\left[{\mathbf{1}}_{\left\{A_{\mu }+\alpha B_{\mu -1}>M\right\}}\right]-\mathbb{E}\left[A_{\mu }·{\mathbf{1}}_{\left\{A_{\mu }+\alpha B_{\mu -1}>M\right\}}\right]\right\},\end{array}$$

(101)

and the best value ${\alpha }^{*}$ could be found as follows:

$${\alpha }^{*}=\left\{{}^{\exists }\alpha \in [1,\infty ):\frac{\partial \mathfrak{S}\left(\alpha ;M\right)}{\partial \alpha }=0\right\},$$

(102)

where $c_0$ is the unit sales price from the customer side and $c_1$ is the unit cost price based on the suppliers. If $c_0\ge 0$ and $c_1\le 0$, the platform earns the money from both sides. If $c_0\le 0$ and $c_1\ge 0$, the platform spend the money from both sides. Although a payoff function could be constructed based on the attract factor in this section, other variables besides of the attraction factor could also construct payoff functions in different perspectives.

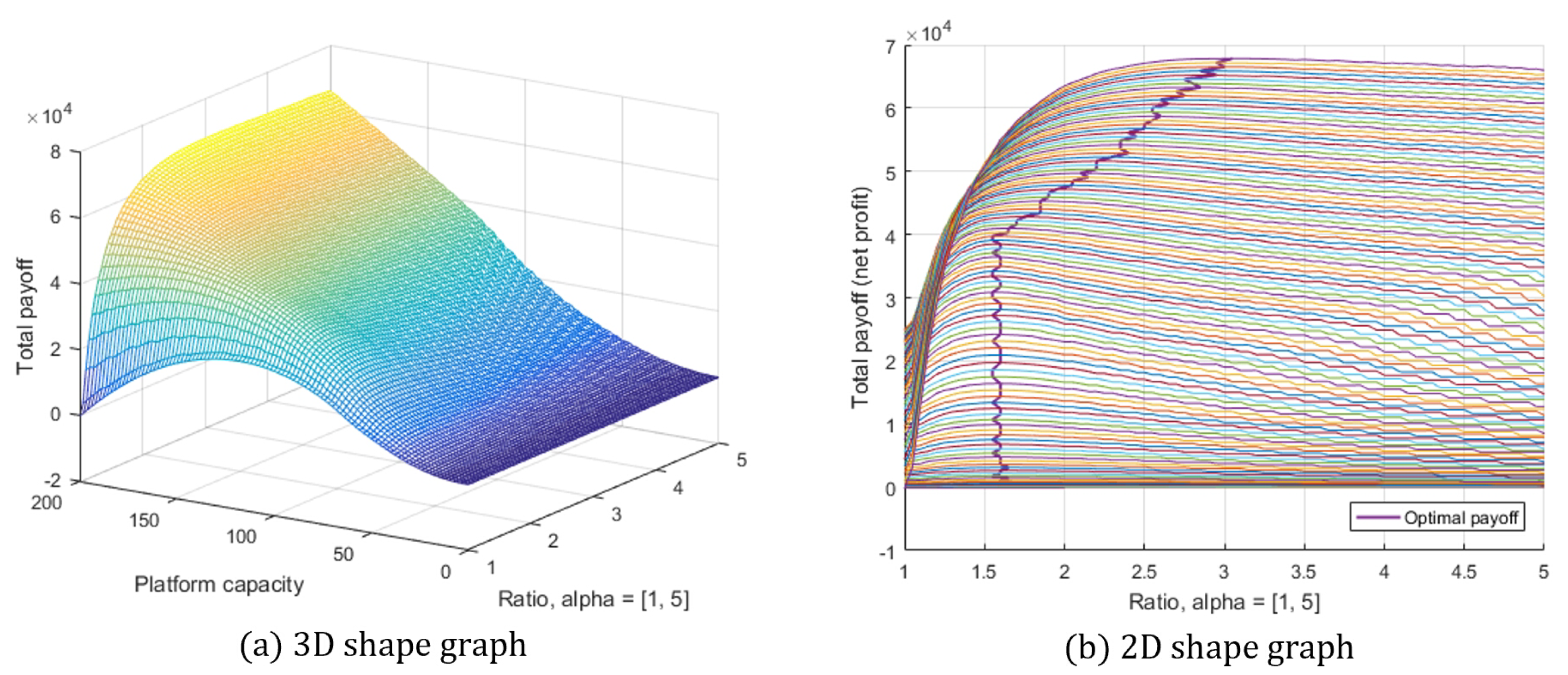
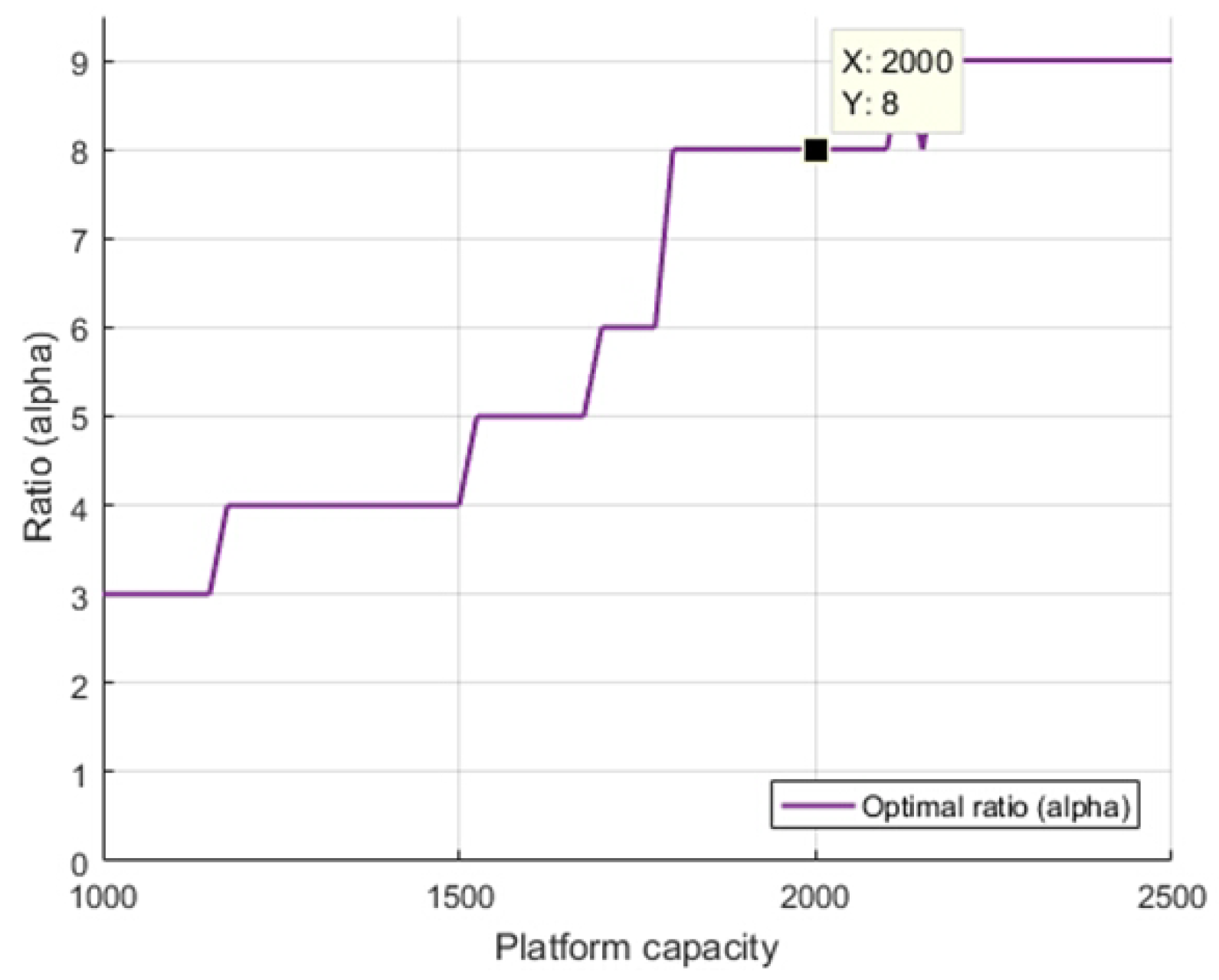
3.2. Two-Sided Platform Optimization Setup and Visualization

The several parameters shall be determined after constructing the payoff function (101) and the details of the setup for the payoff function are required to make an optimization problem solvable. Some of factors such as a platform capacity M and an attraction factor $\alpha$ are fixed and some of them are calculated (i.e., ${\lambda }_a\left(b\right),$$\mu$). The summary of all required parameter sets is shown in

Table 1. The parameters for Two-sided platform Setup.

Name	Formula	Description
M	–	Platform capacity
$\mu$	(17)	Termination index (i.e., first exceed level)
$\alpha$	–	Ratio between both sides of the platform
${\lambda }_a\left(b\right)$	(16)	The revised input rate of the men based on the dominant
$\mathfrak{S}\left(\alpha \right)$	(101)	Payoff function

.

The payoff function from (101) could be computationally implemented after all required parameters which are explained on Table 1 and these parameters are determined by actual data gathering. The practical real-world case (i.e., nightclub) shall be introduced on the next section. Although the payoff function in this section is constructed based on the attraction factor and the platform capacity, the payoff function could be designed in a different way.

The visualization of the payoff function for a two-sided platform model is shown in Figure 1. The payoff (i.e., reward) function from (101) is a two-variable function which could be maximized based on two variables which are the attraction factor (i.e., the ratio between a supplier and a customer sides) and the platform capacity. It is noted that a two-variable function such as a payoff function of a two-sided platform could be visualized either as a 3D shape (a) or a 2D shape (b) in Figure 1. A proper shape depends on the visualization objectives of a payoff function.

3.3. Properties of Open Two-Sided Platforms

As it has been mentioned on Section 2, an open two-sided platform is the two-sided platform (almost) without the limitation of the capacity. From (101) the payoff function is revised as follows:

$$\underset{M\to \infty }{lim}\mathfrak{S}\left(\alpha ;M\right)=c_0·\mathbb{E}\left[A_{\mu }\right]-c_1·\mathbb{E}\left[B_{\mu }\right]=\left(c_0-\frac{c_1}{\alpha }\right)\mathbb{E}\left[A_{\mu }\right],$$

(103)

where

$$\mathbb{E}\left[A_{\mu }\right]=\alpha \mathbb{E}\left[B_{\mu }\right].$$

(104)

Due to unlimited capacity, more suppliers attract more customers and more profits. It indicates that there are no turning points of the payoff function but the attract factor $\alpha$ should be greater than a certain value to start making the profit of the two-sided platform. Hence, the optimized attraction factor of an open two-sided platform could be terminated as follows:

$${\alpha }^{*}:=\inf \left\{\alpha :\underset{M\to \infty }{lim}\mathfrak{S}\left(\alpha ;M\right)\ge 0\right\},$$

(105)

From (104) and (105), we have

$${\alpha }^{*}=\frac{c_1}{c_0},$$

(106)

which indicates that the platform starts making benefits when the attraction factor is greater than ${\alpha }^{*}$. It is noted that the moment of making benefits depends on the cost ratio between the cost $c_1$ and the reward $c_0$ (i.e., $\alpha \ge \frac{c_1}{c_0}$).

One of interesting properties of an open two-sided platform is that an attraction factor only depends on the ratio between the cost/reward between two sides (see Figure 2). Additionally, there is no optimal value for maximizing profits because the resources for operating a two-sided platform are unlimited. In other words, the cost for operating the open platform is (almost) zero.

4. Applications Cases

In this section, two practical business cases are introduced which are classic and old situations of a two-sided platform model. Each subsection describes a specific situation and a versatile two-sided platform provides strategic recommendations to make proper decisions. First case is operating a nightclub which is a classic two-sided market: the supplier side is women and customer side is men because women are attracted by men and gather more men to come in a nightclub. Hence, nightclubs even recruit beautiful women to get more customers to come. The other case is constructing an application store (e.g., Google Play, App Store (Apple) Microsoft Apps) which mainly handles huge number of subscribers (i.e., customer side) and developers (i.e., supplier side). This case is suitable for an open two-sided platform because both sides are handling relatively large number of customers and suppliers. The open two-sided platform model is also applicable for OTT (Over-The-Top) services (e.g., Netflex, Amazon Prime, Disney+ and so on) because of the same reason. Unlike other parts of the paper, this section is written as a case method material for MBA students rather than a typical article style. Hence, the readers who only have business background without any mathematical background could even understand the situations and their recommendations more easily.

4.1. Khaos Nightclub

The Khaos (This nightclub is not real but the real one has been referenced to make this case more realistic (https://manilaclubbing.com/page/2/, accessed on 31 August 2022)) was one of most famous nightclubs in Manila which was capable up to 2000 people at once. Before grand opening, Mr. Bean who is a CEO of the Khaos, decided to do the soft launch for 1 month. The club charges 100 USD (5600 PHP) as an entrance fee and give the free for ladies with one free beverage which is equivalent with 1 USD (50 PHP). The guard of the club started monitoring 4 h before opening the club and checking every hour during the club operations. The Khaos found the following information during 1 month: Around 40 men are waiting on the queue before starting the club. And 8 men and 6 women had entered the club after opening the club (see

Table 2. Initial conditions of the Khaos nightclub.

Name	Value	Description
$c_0$	100 [USD/person]	Entry fee for men (i.e., a customer side)
$c_1$	1 [USD/person]	Reward for women’s entry
$\widetilde{{\delta }_0}$	4 [h]	Monitoring duration before the nightclub operation
$\tilde{\delta }$	1 [h]	Monitoring duration during the nightclub operation
${\lambda }_a$	8 [person/h]	The base input rate of men during the operation
${\lambda }_a^0$	10 [person/h]	The input rate of men before starting (waiting on the queue)
${\lambda }_b$	6 [person/h]	The base input rate of women during the operation
${\lambda }_b^0$	1 [person/h]	The input rate of women before starting (waiting on the queue)

). Additionally, average number of occupation of each monitoring time is full (2000 clubers) and 70 percent in the club is men.

After 1 month later, the Khaos needs to make proper strategies for better operations of the club. Hence, there are couple of managerial questions to be answered before the grand opening:

• Based on the data during the soft launch (see Table 1 for details), the club is operating good enough for the grand opening?
• How many ladies should be needed to maximize the profit with same number of clubers (2000 clubers)?
• What will be the proper managerial actions to improve the operation of the nightclub?
• The information (or data) for this nightclub case is reliable enough for making proper decision?

Regarding first question, we could get the current ratio between customers and suppliers (i.e., attraction factor) from the available data (Table 1). From (104), the attraction factor of the current status ${\alpha }_0$ is as follows:

$${\alpha }_0=\frac{\mathbb{E}\left[A_{\nu }\right]}{\mathbb{E}\left[B_{\nu }\right]}=\frac{0.7}{0.3}\simeq 2.33.$$

(107)

In the other hand, the optimal attraction factor ${\alpha }^{*}$ could be found from (101) and (102) with but it requires massive calculations. Hence, a numerical approach by coding is more suitable than an analytical approach. The result of a numerical approach for the Khaos nightclub is shown in Figure 3.

As illustrated on Figure 3, the optimal attraction factor is $8.0$ when the number of people in the club is 2000 (i.e., ${\alpha }^{*}=8.0$) during the soft launch. Compare to (107), the operation of the nightclub is not efficient enough to maximize the profit. Based on the information from Table 1 (and description of the Khaos nightclub in this section), we could find the proper number of ladies to optimize the profit as follows:

$${\alpha }^{*}\left(=8\right)=\frac{2000-x}{x}$$

(108)

where x is the number of required women who are supplied by the club and the optimal value becomes 222 (ladies) after doing simple algebra. In the managerial point of view, the Khaos should maintain around 222 ladies instead of 570 girls during the soft launch (i.e., 11 percent of 2000 clubers as an average). There are several ways to achieve the target (222 women from 570 women) as managerial actions. One of actions could be making more solid screening for girls at the gate. It is noted that all analysis in this section is valuable only if the data that gathered from the nightclub is reliable. The last managerial question shall remain unanswered for the readers to find answers themselves.

4.2. Omnia AppStore

The Omnia AppStore has been considered for the Android platform and the company who wants to launch the application store has gathered the data from the famous application store (The famous store is the Google Play of which the related data are publicly available from the following websites: https://buildfire.com/app-statistics/; https://42matters.com/google-play-statistics-and-trends; https://www.businessofapps.com/data/app-statistics/; https://www.appbrain.com/stats/android-app-downloads, accessed on 31 August 2022) and extract the information as seen in

Table 3. Initial conditions of the Omnia Appstore.

Name	Value	Description
B	[K app]	$\left(=\times {10}^3\right)$ The number of contents (i.e., dominant side)
$c_0$	0.345 [USD/app]	Download price
$c_1$	1.945 [USD/app]	Reword for app developers
$\tilde{\delta }$	1 [day]	Observation duration of the AppStore platform
${\lambda }_a$	7.67 [M app/day]	$\left(=\times {10}^6\right)$ The download rate per day during the operation
${\lambda }_a^0$	2.67 [M app/day]	$\left(=\times {10}^6\right)$ The download rate per day during the maintenance
${\lambda }_b$	2.33 [K app/day]	$\left(=\times {10}^3\right)$ The upload rate by app developers

.

The Omnia AppStore want to make the threshold to ban applications on the Omnia AppStore if applications are not popular. The managerial issue of the Omnia as follows:

• What is a proper threshold for optimizing this application store?

This issue is about the attraction factor for an open two-sided platform. Hence, we can easily find the proper attraction factor from (106) and the ratio between downloders and developers (i.e., uploaders) is as follows:

$${\alpha }^{*}\left(=\frac{c_1}{c_0}\right)=\frac{1.945}{0.345}=5.63,$$

(109)

which indicates that the attraction factor should be more than 5.63 to keep applications on the Omnia AppStore.

5. Conclusions

The new types of stochastic two-sided platform models are studied. A stochastic pseudo-game model is newly introduced to solve the two-sided platform more effectively. The players in a pseudo-game are the customer and the supplier sides of a two-sided market and a joint functional of the standard stopping game was designed to determine to analyze operation parameters which indicates the best strategies of a two-sided platform under a hybrid stochastic game framework which has been widely adapted in various applications [28,31,37]. The analytical approach enables to obtain analytically tractable solutions which determine the decision making factors including the moment of overflowing a platform capacity, one step prior to a platform overflow and optimum of a two-sided platform system. This unique method by applying the stochastic pseudo-game into the most practical cases was fully described as case method materials for teaching even in business and management classes. Furthermore, each application case provides key managerial questions to be faced by managers who could adapt the models even without mathematical knowledge. Variations of the versatile stochastic two-sided platform models are currently working as future research topics.