Dynamical Analysis and Adaptive Finite-Time Sliding Mode Control Approach of the Financial Fractional-Order Chaotic System
Abstract
1. Introduction
2. Mathematical Models of the Financial Chaotic System
3. Mathematical Model of Fractional-Order Financial Chaotic System
4. Finite-Time Fast Synchronization
4.1. Problem Formulation
4.2. Adaptive Finite-Time Fast Terminal Sliding Mode Control Approach
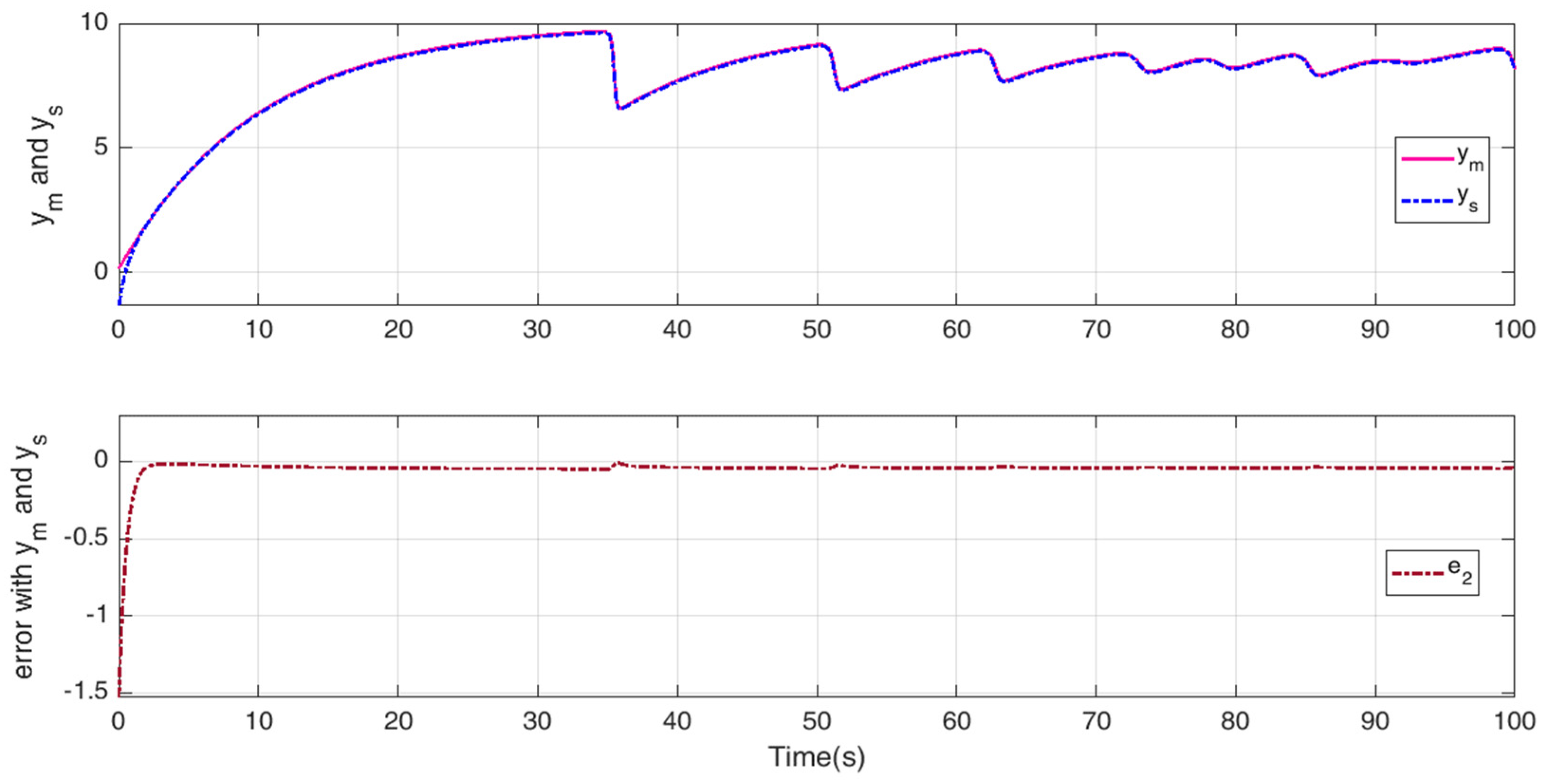
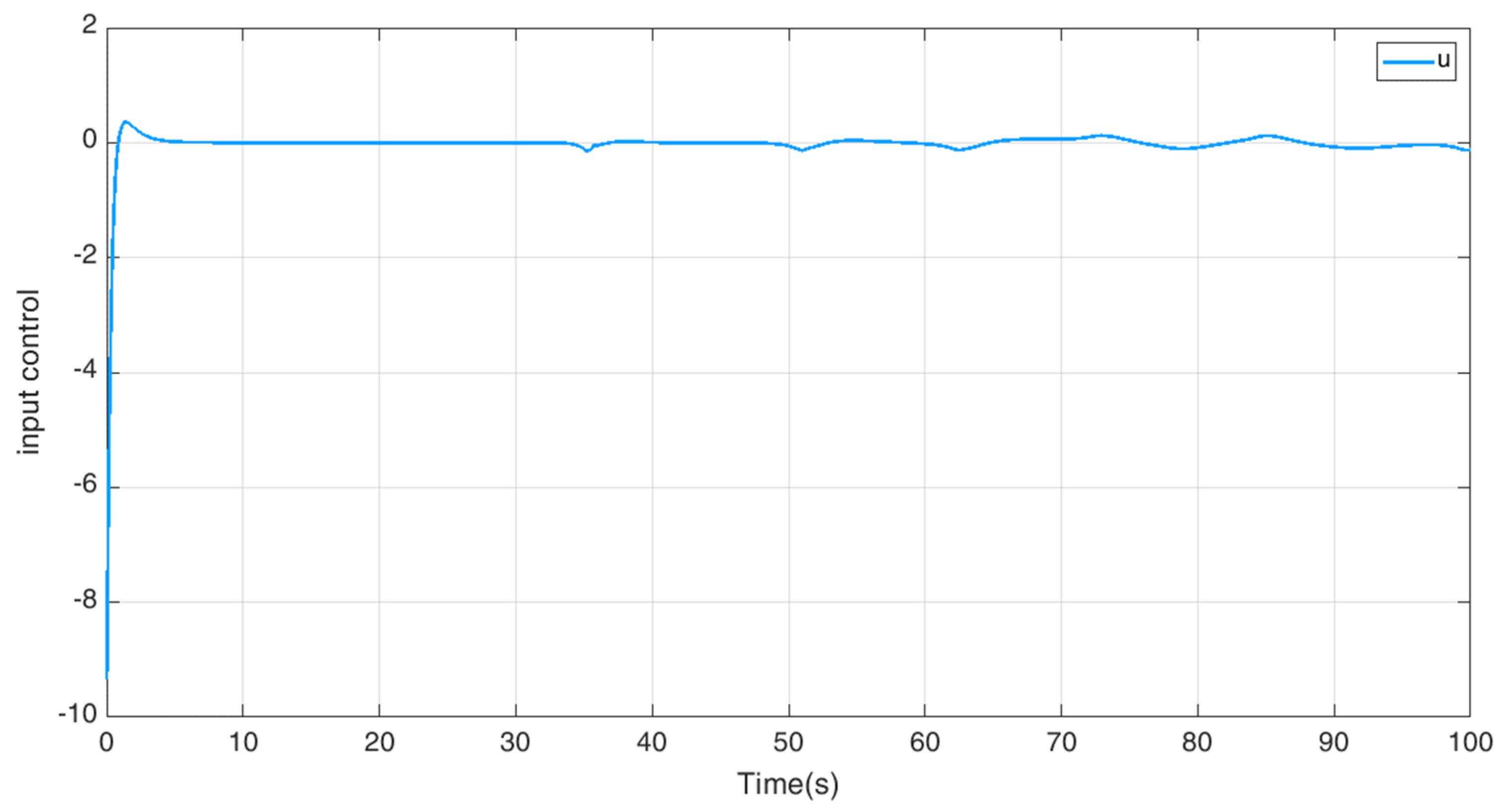
4.3. Simulation Results of Adaptive Finite-Time Fast Terminal Sliding Mode Control
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhuo, P.J.; Zhang, Z.X.; Gou, X.F. Chaotic motion of a magnet levitated over a superconductor. IEEE Trans. Appl. Supercond. 2016, 26, 1–6. [Google Scholar] [CrossRef]
- Abro, K.A. Numerical study and chaotic oscillations for aerodynamic model of wind turbine via fractal and fractional differential operators. Numer. Methods Partial. Differ. Equ. 2022, 38, 1180–1194. [Google Scholar] [CrossRef]
- Pappu, C.S.; Carroll, T.L.; Flores, B.C. Simultaneous radar-communication systems using controlled chaos-based frequency modulated waveforms. IEEE Access 2020, 8, 48361–48375. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Zhang, X.; Koyuncu, I.; Bonny, T.; Tuna, M.; Alcin, M.; Zhang, S.; Sulaiman, I.M.; Awwal, A.M.; et al. A Novel 3D Chaotic System with Line Equilibrium: Multistability, Integral Sliding Mode Control, Electronic Circuit, FPGA and its Image Encryption. IEEE Access 2022, 10, 68057–68074. [Google Scholar] [CrossRef]
- Mou, J.; Sun, K.; Ruan, J.; He, S. A nonlinear circuit with two memcapacitors. Nonlinear Dyn. 2016, 86, 1735–1744. [Google Scholar] [CrossRef]
- Naik, R.D.; Singru, P.M. Resonance, stability and chaotic vibration of a quarter-car vehicle model with time-delay feedback. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 3397–3410. [Google Scholar] [CrossRef]
- Fakhraei, J.; Khanlo, H.M.; Ghayour, M. Chaotic behaviors of a ground vehicle oscillating system with passengers. Sci. Iranica. Trans. B Mech. Eng. 2017, 24, 1051. [Google Scholar] [CrossRef][Green Version]
- Lim, T.S.; Lu, Y.; Nolen, J.H. Quantitative propagation of chaos in a bimolecular chemical reaction-diffusion model. SIAM J. Math. Anal. 2020, 52, 2098–2133. [Google Scholar] [CrossRef]
- Li, S.; He, Y.; Cao, H. Necessary conditions for complete synchronization of a coupled chaotic Aihara neuron network with electrical synapses. Int. J. Bifurc. Chaos 2019, 29, 1950063. [Google Scholar] [CrossRef]
- Sambas, A.; Vaidyanathan, S.; Bonny, T.; Zhang, S.; Hidayat, Y.; Gundara, G.; Mamat, M. Mathematical model and FPGA realization of a multi-stable chaotic dynamical system with a closed butterfly-like curve of equilibrium points. Appl. Sci. 2021, 11, 788. [Google Scholar] [CrossRef]
- Nakamura, Y.; Sekiguchi, A. The chaotic mobile robot. IEEE Trans. Robot. Autom. 2001, 17, 898–904. [Google Scholar] [CrossRef]
- Atangana, A.; Bonyah, E.; Elsadany, A.A. A fractional order optimal 4D chaotic financial model with Mittag-Leffler law. Chin. J. Phys. 2020, 65, 38–53. [Google Scholar] [CrossRef]
- Bekiros, S.; Jahanshahi, H.; Munoz-Pacheco, J.M. A new buffering theory of social support and psychological stress. PLoS one 2022, 17, e0275364. [Google Scholar] [CrossRef] [PubMed]
- Fanti, L.; Manfredi, P. Chaotic business cycles and fiscal policy: An IS-LM model with distributed tax collection lags. Chaos Solitons Fractals 2007, 32, 736–744. [Google Scholar] [CrossRef]
- Orlando, G. A discrete mathematical model for chaotic dynamics in economics: Kaldor’s model on business cycle. Math. Comput. Simul. 2016, 125, 83–98. [Google Scholar] [CrossRef]
- Barnett, W.A.; Bella, G.; Ghosh, T.; Mattana, P.; Venturi, B. Shilnikov chaos, low interest rates, and New Keynesian macroeconomics. J. Econ. Dyn. Control. 2022, 134, 104291. [Google Scholar] [CrossRef]
- Kyrtsou, C.; Labys, W.C. Evidence for chaotic dependence between US inflation and commodity prices. J. Macroecon. 2006, 28, 256–266. [Google Scholar] [CrossRef]
- Sukono; Sambas, A.; He, S.; Liu, H.; Vaidyanathan, S.; Hidayat, Y.; Saputra, J. Dynamical analysis and adaptive fuzzy control for the fractional-order financial risk chaotic system. Adv. Differ. Equ. 2020, 2020, 674. [Google Scholar] [CrossRef]
- Munoz-Pacheco, J.M.; Zambrano-Serrano, E.; Volos, C.; Tacha, O.I.; Stouboulos, I.N.; Pham, V.T. A fractional order chaotic system with a 3D grid of variable attractors. Chaos Solitons Fractals 2018, 113, 69–78. [Google Scholar] [CrossRef]
- Wang, Y.L.; Jahanshahi, H.; Bekiros, S.; Bezzina, F.; Chu, Y.M.; Aly, A.A. Deep recurrent neural networks with finite-time terminal sliding mode control for a chaotic fractional-order financial system with market confidence. Chaos Solitons Fractals 2021, 146, 110881. [Google Scholar] [CrossRef]
- Chen, W.C. Nonlinear dynamics and chaos in a fractional-order financial system. Chaos Solitons Fractals 2008, 36, 1305–1314. [Google Scholar] [CrossRef]
- Li, H.L.; Hu, C.; Zhang, L.; Jiang, H.; Cao, J. Complete and finite-time synchronization of fractional-order fuzzy neural networks via nonlinear feedback control. Fuzzy Sets Syst. 2022, 443, 50–69. [Google Scholar] [CrossRef]
- Li, H.L.; Jiang, H.; Cao, J. Global synchronization of fractional-order quater-nion-valued neural networks with leakage and discrete delays. Neurocomputing 2020, 385, 211–219. [Google Scholar] [CrossRef]
- Wang, S.; He, S.; Yousefpour, A.; Jahanshahi, H.; Repnik, R.; Perc, M. Chaos and complexity in a fractional-order financial system with time delays. Chaos Solitons Fractals 2020, 131, 109521. [Google Scholar] [CrossRef]
- Pan, I.; Korre, A.; Das, S.; Durucan, S. Chaos suppression in a fractional order financial system using intelligent regrouping PSO based fractional fuzzy control policy in the presence of fractional Gaussian noise. Nonlinear Dyn. 2012, 70, 2445–2461. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, X.; Zhao, Z. Synchronization of nonidentical chaotic fractional-order systems with different orders of fractional derivatives. Nonlinear Dyn. 2012, 69, 999–1007. [Google Scholar] [CrossRef]
- Hajipour, A.; Tavakoli, H. Dynamic analysis and adaptive sliding mode controller for a chaotic fractional incommensurate order financial system. Int. J. Bifurc. Chaos 2017, 27, 1750198. [Google Scholar] [CrossRef]
- Yousri, D.; Mirjalili, S. Fractional-order cuckoo search algorithm for parameter identification of the fractional-order chaotic, chaotic with noise and hyper-chaotic financial systems. Eng. Appl. Artif. Intell. 2020, 92, 103662. [Google Scholar] [CrossRef]
- Cao, Y. Chaotic synchronization based on fractional order calculus financial system. Chaos Solitons Fractals 2020, 130, 109410. [Google Scholar] [CrossRef]
- Wang, B.; Liu, J.; Alassafi, M.O.; Alsaadi, F.E.; Jahanshahi, H.; Bekiros, S. Intelligent parameter identification and prediction of variable time fractional derivative and application in a symmetric chaotic financial system. Chaos Solitons Fractals 2022, 154, 111590. [Google Scholar] [CrossRef]
- Subartini, B.; Vaidyanathan, S.; Sambas, A.; Zhang, S. Multistability in the Finance Chaotic System, Its Bifurcation Analysis and Global Chaos Synchronization via Integral Sliding Mode Control. IAENG Int. J. Appl. Math. 2021, 51, 995–1002. [Google Scholar]
- Xu, X.; Lee, S.D.; Kim, H.S.; You, S.S. Management and optimisation of chaotic supply chain system using adaptive sliding mode control algorithm. Int. J. Prod. Res. 2021, 59, 2571–2587. [Google Scholar] [CrossRef]
- Yin, C.; Dadras, S.; Zhong, S.M.; Chen, Y. Control of a novel class of fractional-order chaotic systems via adaptive sliding mode control approach. Appl. Math. Model. 2013, 37, 2469–2483. [Google Scholar] [CrossRef]
- Yan, J.J.; Hung, M.L.; Liao, T.L. Adaptive sliding mode control for synchronization of chaotic gyros with fully unknown parameters. J. Sound Vib. 2006, 298, 298–306. [Google Scholar] [CrossRef]
- Ghamati, M.; Balochian, S. Design of adaptive sliding mode control for synchronization Genesio–Tesi chaotic system. Chaos Solitons Fractals 2015, 75, 111–117. [Google Scholar] [CrossRef]
- Mohadeszadeh, M.; Delavari, H. Synchronization of fractional-order hyperchaotic systems based on a new adaptive sliding mode control. Int. J. Dyn. Control. 2017, 5, 124–134. [Google Scholar] [CrossRef]
- Li, W.L.; Chang, K.M. Robust synchronization of drive–response chaotic systems via adaptive sliding mode control. Chaos Solitons Fractals 2009, 39, 2086–2092. [Google Scholar] [CrossRef]
- Min, F.; Li, C.; Zhang, L.; Li, C. Initial value-related dynamical analysis of the memristor-based system with reduced dimensions and its chaotic synchronization via adaptive sliding mode control method. Chin. J. Phys. 2019, 58, 117–131. [Google Scholar] [CrossRef]
- Maeng, G.; Choi, H.H. Adaptive sliding mode control of a chaotic non-smooth-air-gap permanent magnet synchronous motor with uncertainties. Nonlinear Dyn. 2013, 74, 571–580. [Google Scholar] [CrossRef]
- Khan, A.; Singh, S. Generalization of combination-combination synchronization of n-dimensional time-delay chaotic system via robust adaptive sliding mode control. Math. Methods Appl. Sci. 2018, 41, 3356–3369. [Google Scholar] [CrossRef]
- Shang, Z.; Yu, Y.; Li, Y. Adaptive sliding mode control of chaotic oscilla-tion in power system based on relay characteristic function. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Weihai, China, 13–15 July 2020; pp. 1012–1016. [Google Scholar]
- Shukla, V.K.; Vishal, K.; Srivastava, M.; Singh, P.; Singh, H. Multi-switching compound synchronization of different chaotic systems with external disturbances and parametric uncertainties via two approaches. Int. J. Appl. Comput. Math. 2022, 8, 1–22. [Google Scholar] [CrossRef]
- Aqeel, M.; Ahmad, S.; Azam, A.; Ahmed, F. Dynamical and fractal properties in periodically forced stretch-twist-fold (STF) flow. Eur. Phys. J. Plus 2007, 132, 1–13. [Google Scholar] [CrossRef]
- Al-Azzawi, S.F. Stability and bifurcation of pan chaotic system by using Routh–Hurwitz and Gardan methods. Appl. Math. Comput. 2012, 219, 1144–1152. [Google Scholar] [CrossRef]
- Sun, K. Chaotic Secure Communication: Principles and Technologies. Tsinghua University Press and Walter de Gruyter GmbH: Beijing, China, 2016; pp. 119–135. [Google Scholar]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
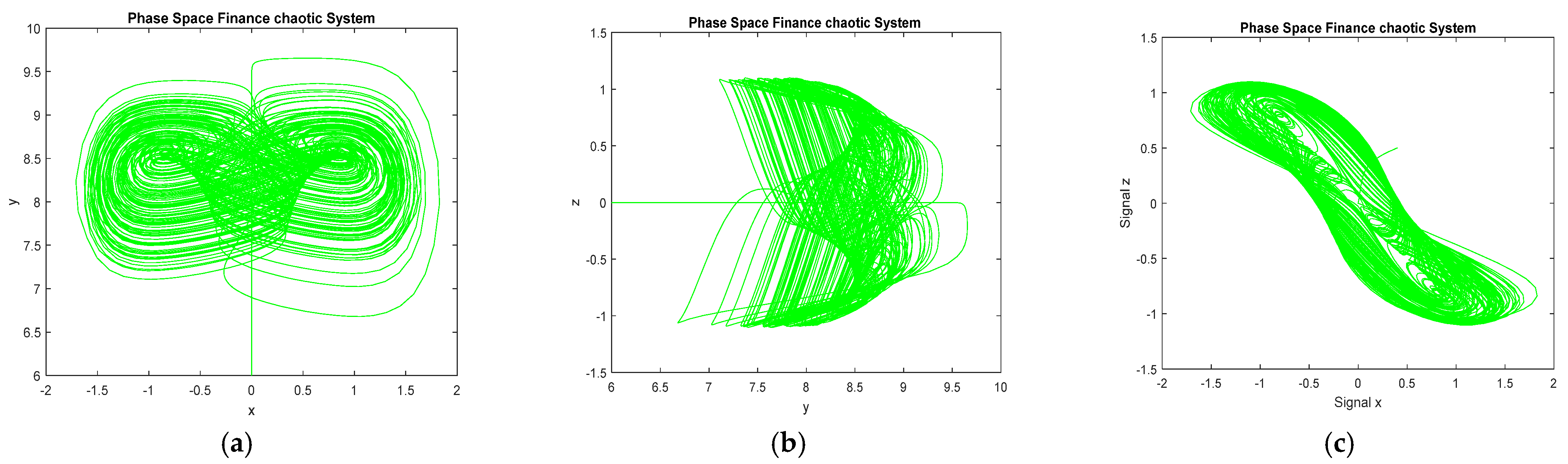
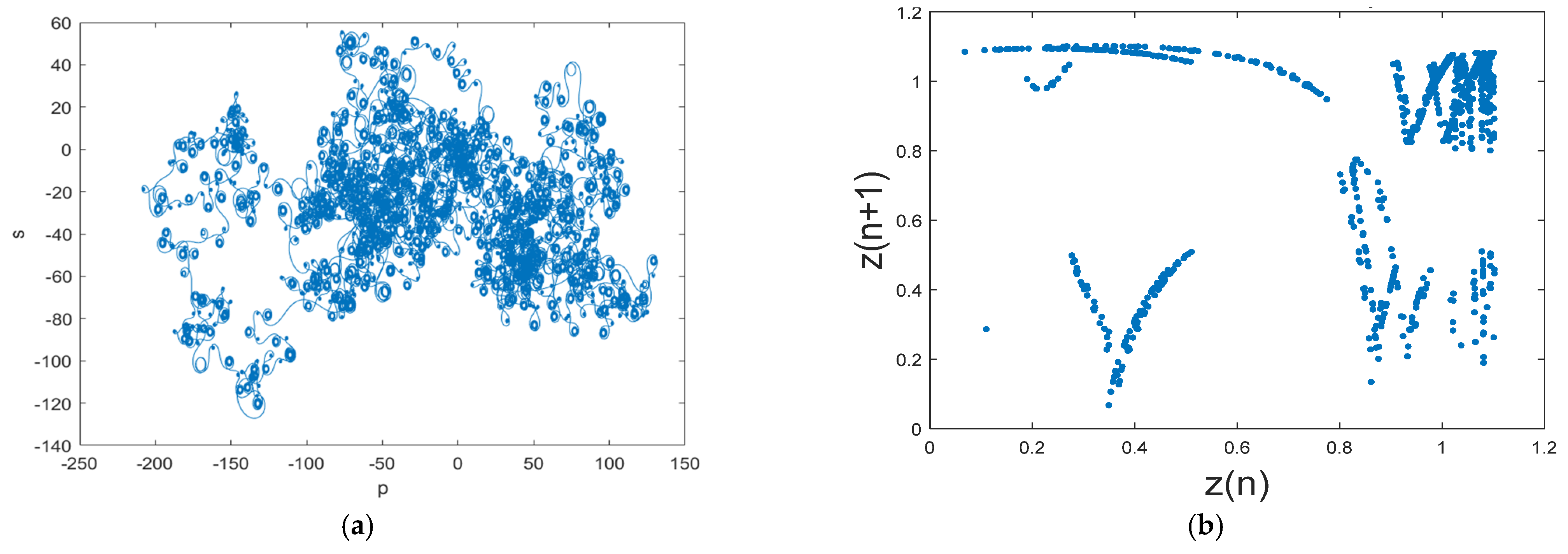
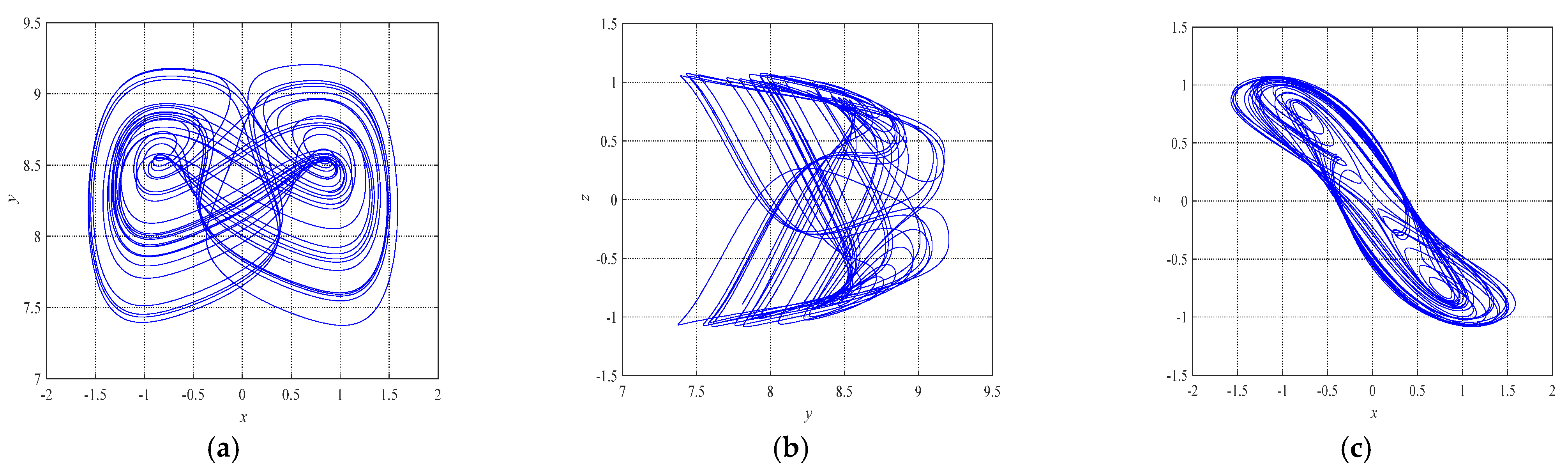
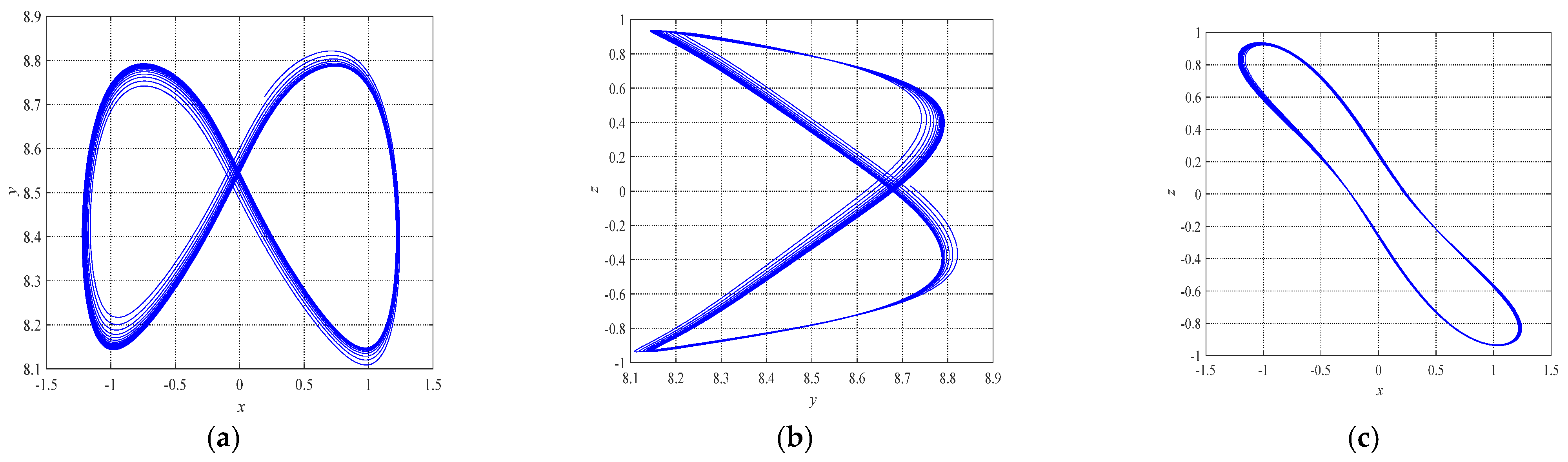



| Iteration | |||
|---|---|---|---|
| Parameter | Value |
|---|---|
| 0.24 | |
| 0.036 | |
| 37 | |
| 11 | |
| 21 | |
| 9 | |
| diag(0.5 1 1.5) | |
| diag(0.57 0.29 0.06) | |
| [3.2 0.5 4.8] | |
| [1 1 1] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johansyah, M.D.; Sambas, A.; Mobayen, S.; Vaseghi, B.; Al-Azzawi, S.F.; Sukono; Sulaiman, I.M. Dynamical Analysis and Adaptive Finite-Time Sliding Mode Control Approach of the Financial Fractional-Order Chaotic System. Mathematics 2023, 11, 100. https://doi.org/10.3390/math11010100
Johansyah MD, Sambas A, Mobayen S, Vaseghi B, Al-Azzawi SF, Sukono, Sulaiman IM. Dynamical Analysis and Adaptive Finite-Time Sliding Mode Control Approach of the Financial Fractional-Order Chaotic System. Mathematics. 2023; 11(1):100. https://doi.org/10.3390/math11010100
Chicago/Turabian StyleJohansyah, Muhamad Deni, Aceng Sambas, Saleh Mobayen, Behrouz Vaseghi, Saad Fawzi Al-Azzawi, Sukono, and Ibrahim Mohammed Sulaiman. 2023. "Dynamical Analysis and Adaptive Finite-Time Sliding Mode Control Approach of the Financial Fractional-Order Chaotic System" Mathematics 11, no. 1: 100. https://doi.org/10.3390/math11010100
APA StyleJohansyah, M. D., Sambas, A., Mobayen, S., Vaseghi, B., Al-Azzawi, S. F., Sukono, & Sulaiman, I. M. (2023). Dynamical Analysis and Adaptive Finite-Time Sliding Mode Control Approach of the Financial Fractional-Order Chaotic System. Mathematics, 11(1), 100. https://doi.org/10.3390/math11010100







