A Novel Dynamic Mathematical Model Applied in Hash Function Based on DNA Algorithm and Chaotic Maps
Abstract
:1. Introduction
2. Materials and Methods
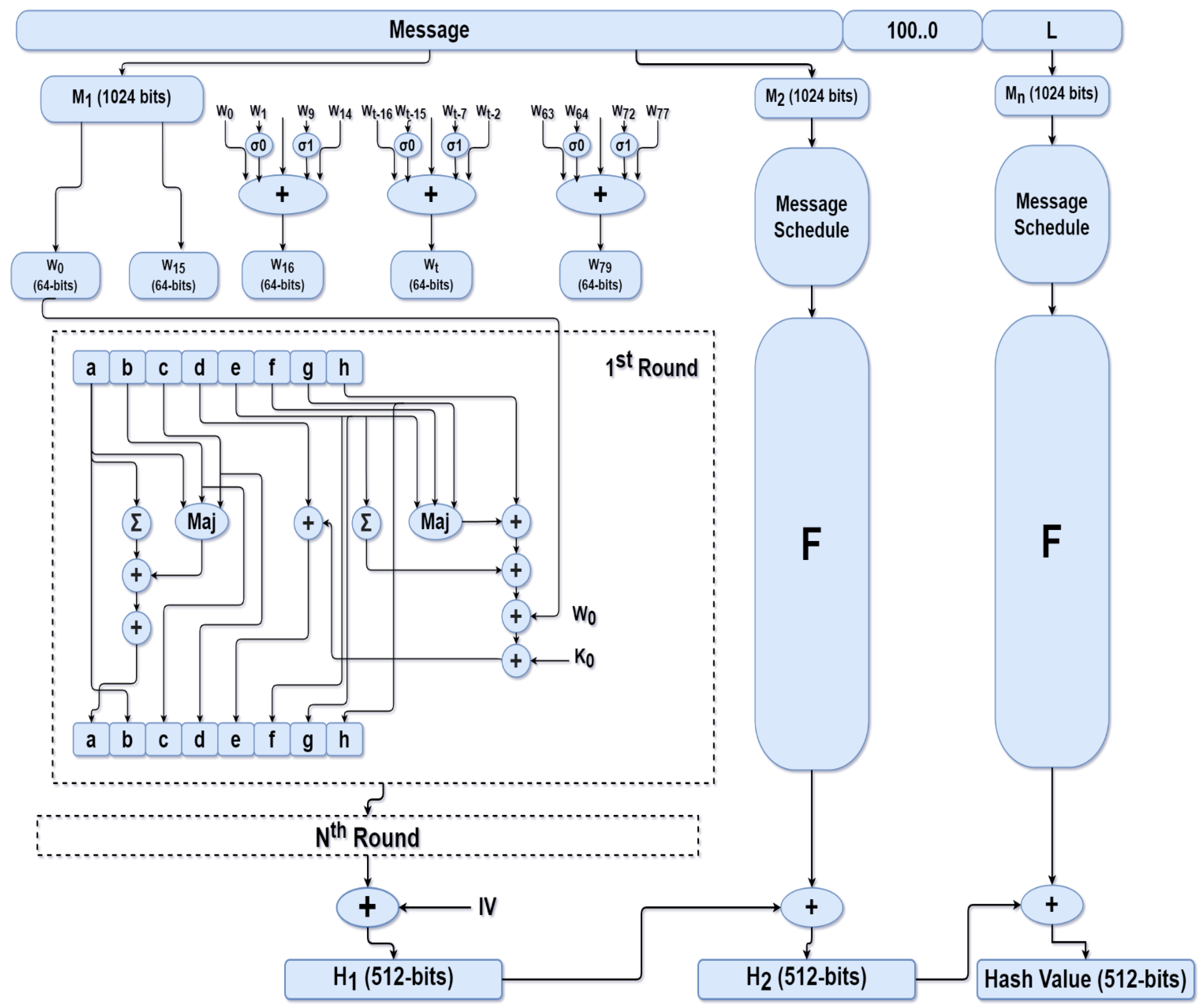
2.1. SHA-512 Hash Algorithm
- Step 1: Message preprocessing by padding and appending its length
- Step 2: Initializing hash buffer
- a = 6A09E667F3BCC908 b = BB67AE8584CAA73B
- c = 3C6EF372FE94F82B d = A54FF53A5F1D36F1
- e = 510E527FADE682D1 f = 9B05688C2B3E6C1F
- g = 1F83D9ABFB41BD6B h = 5BE0CDI9137E2179
- Step 3: Compression function
- Step 4: Output
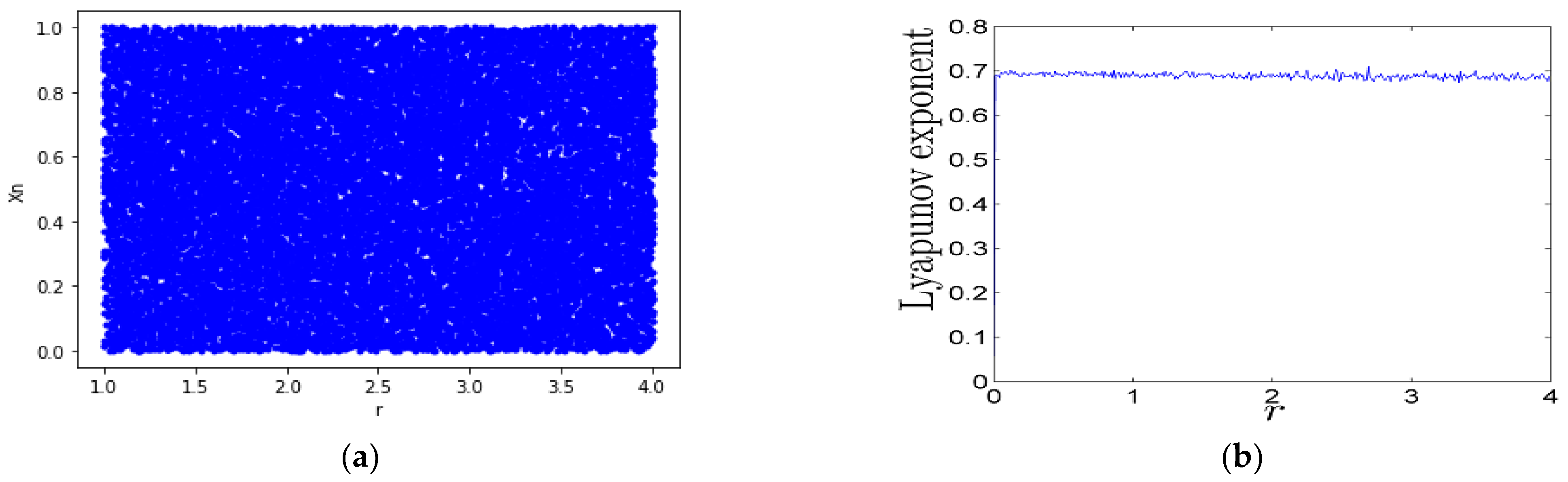
2.2. Chaotic Maps
- A limited range of chaotic behavior;
- Less possibility of computational analysis using iteration and correlation functions;
- Uneven distribution of chaotic output sequences.
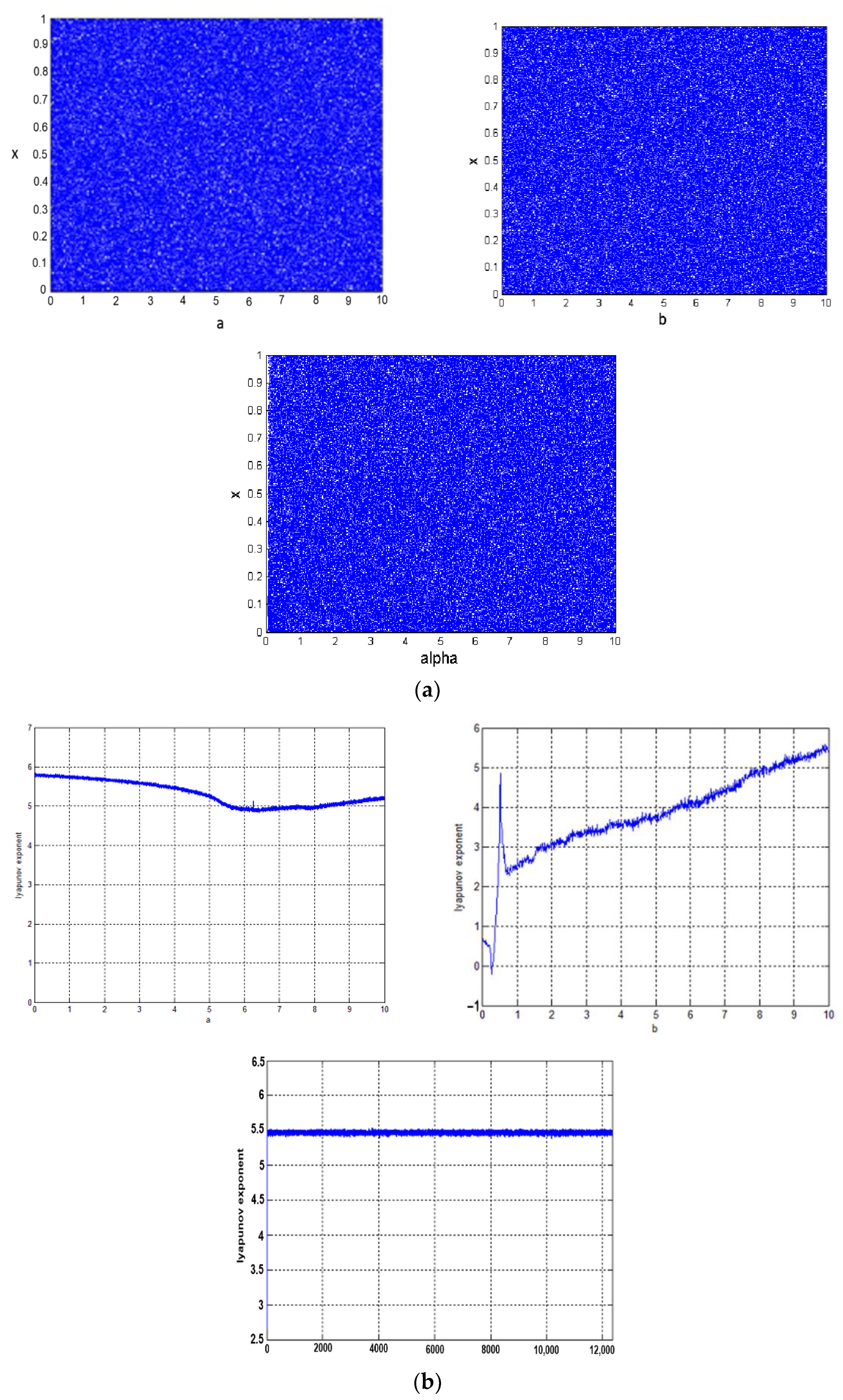
2.2.1. Improved Logistic Map
Xn+1 = f (Xn, a, b) × alpha − floor (f (Xn, a, b) × alpha)
2.2.2. Cosine Logistic System
2.2.3. Logistic Sine System
2.2.4. Tent Sine System
2.2.5. Hybrid Chaotic Map
2.3. DNA Sequence and Complementary Rules
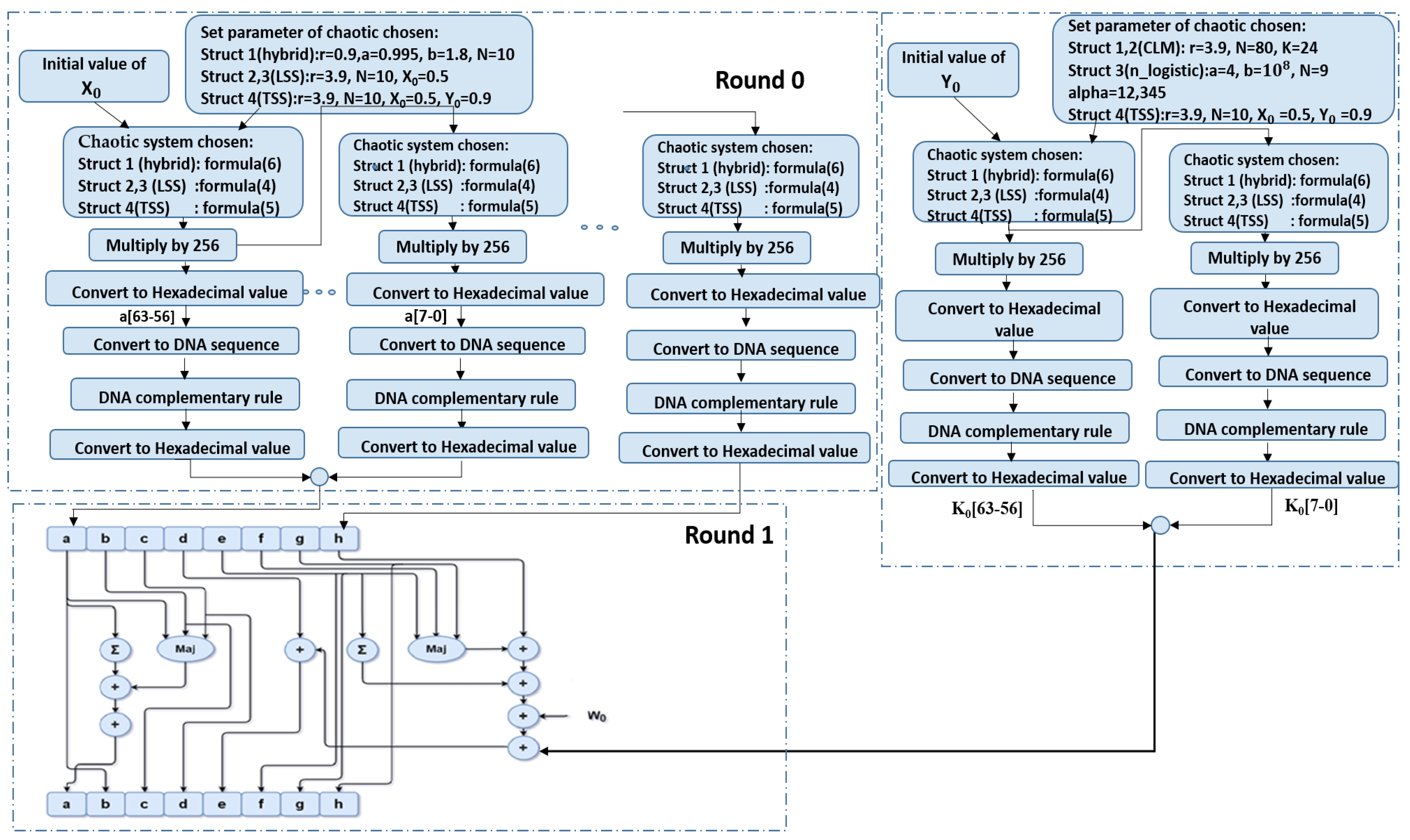
2.4. Method
- Step 1: The original message is encoded into an ASCII binary stream. The message is padded with a 1, followed by 0 values, and the length of the original message is appended at the final 128 bits. The number of zeroes is chosen so that the message length, after padding and appending the message length, is a multiple of 1024.
- Step 2: Chaotic maps are chosen for the hash buffers—either hybrid, LSS, or TSS—and for the additive constant—either CLM, improved logistic, or TSS.
- Step 3: The secret values for X0 ∈ [0, 1] are selected as initial values to obtain Xn+1 of the hash buffer (a, b, c, d, e, f, g, h) and Y0 ∈ [0, 1] to obtain Yn+1 additive constant Kt.
- Step 4: Xn+1 is multiplied by 256 and the output value, expressed in hexadecimal, is converted to a DNA sequence.
- Step 5: Complementary rule is applied to the output of the DNA sequence, and then it is turned back to hexadecimal value, which is written to the last eight bits in the hash buffer a.
- Step 6: Xn+1 from step 3 is used again to obtain the second 8 bits of hash buffer a, and the same process continues until 64 bits of buffer a are obtained; steps 4 and 5 are repeated for each eight-bit set.
- Step 7: The last Xn+1 obtained from buffer a is considered X0 for buffer b, and steps 4 and 5 are repeated until all remaining hash buffers (c, d, e, f, g, and h) are obtained.
- Step 8: Each round takes, as input, the 512-bit buffer value, and updates the buffer values using the 64-bit value derived from the current 1024-bit message schedule. Each round also makes use of an additive constant indicating which of the 80 rounds is currently in progress.
- Step 9: To obtain the first additive constant, steps 3 to 7 are repeated.
- Structure 1: a hybrid chaotic map is used by initializing buffer hash and CLM in adaptive constant kt and using DNA encoding rule 0 and G6 complementary rule;
- Structure 2: the buffer hash is initialized with LSS, CLM is applied to adaptive constant kt, and DNA encoding rule 5 and G1 complementary rule are used;
- Structure 3: the buffer hash is initialized with LSS, the improved logistic chaotic map is applied to adaptive constant kt, and DNA encoding rule 5 and G3 complementary rule are used;
- Structure 4: the buffer hash is initialized with TSS, which is then applied to adaptive constant kt, and DNA encoding rule 2 and G5 complementary rule are used.
3. Results
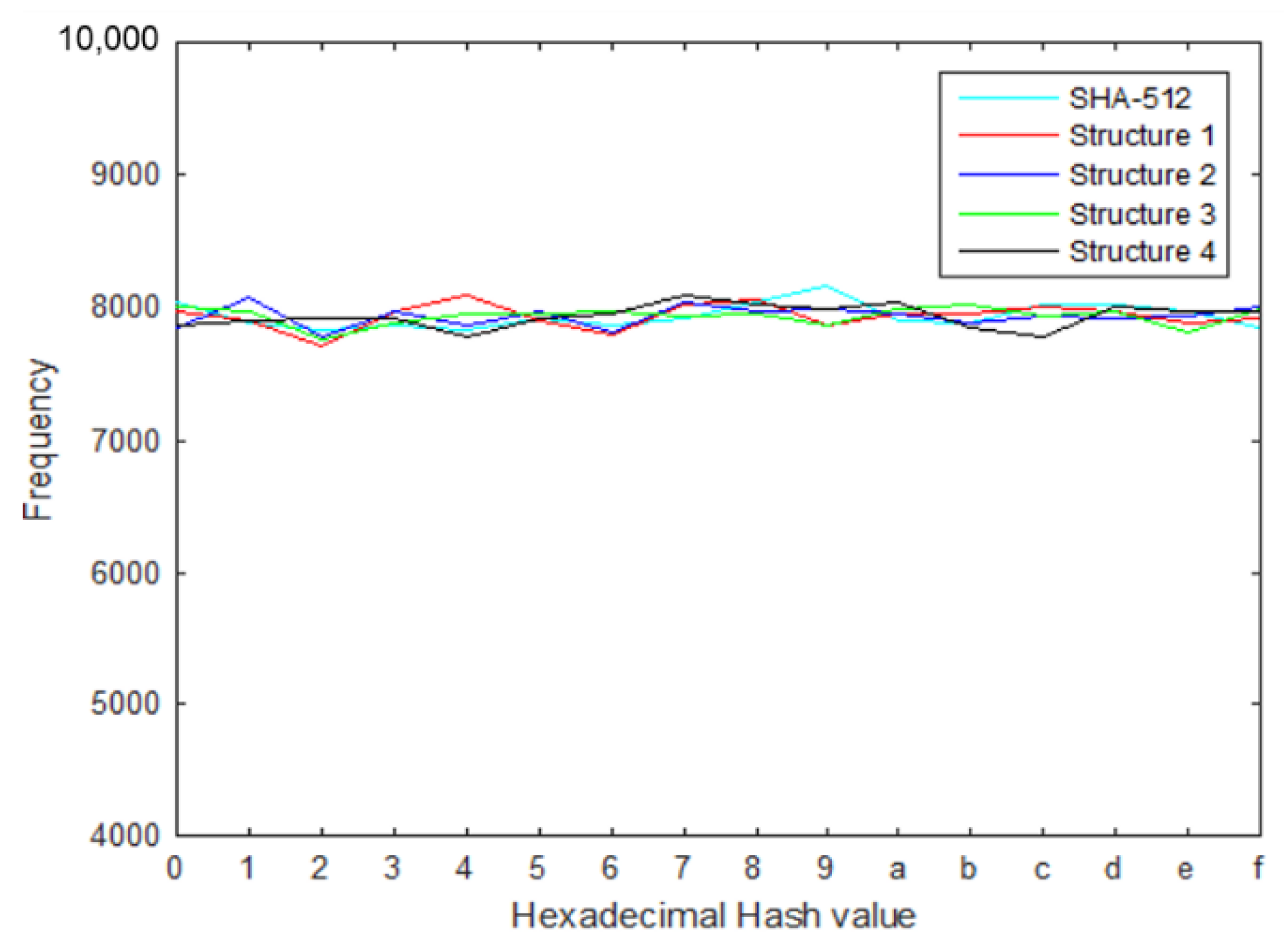
3.1. Hash Value Distribution
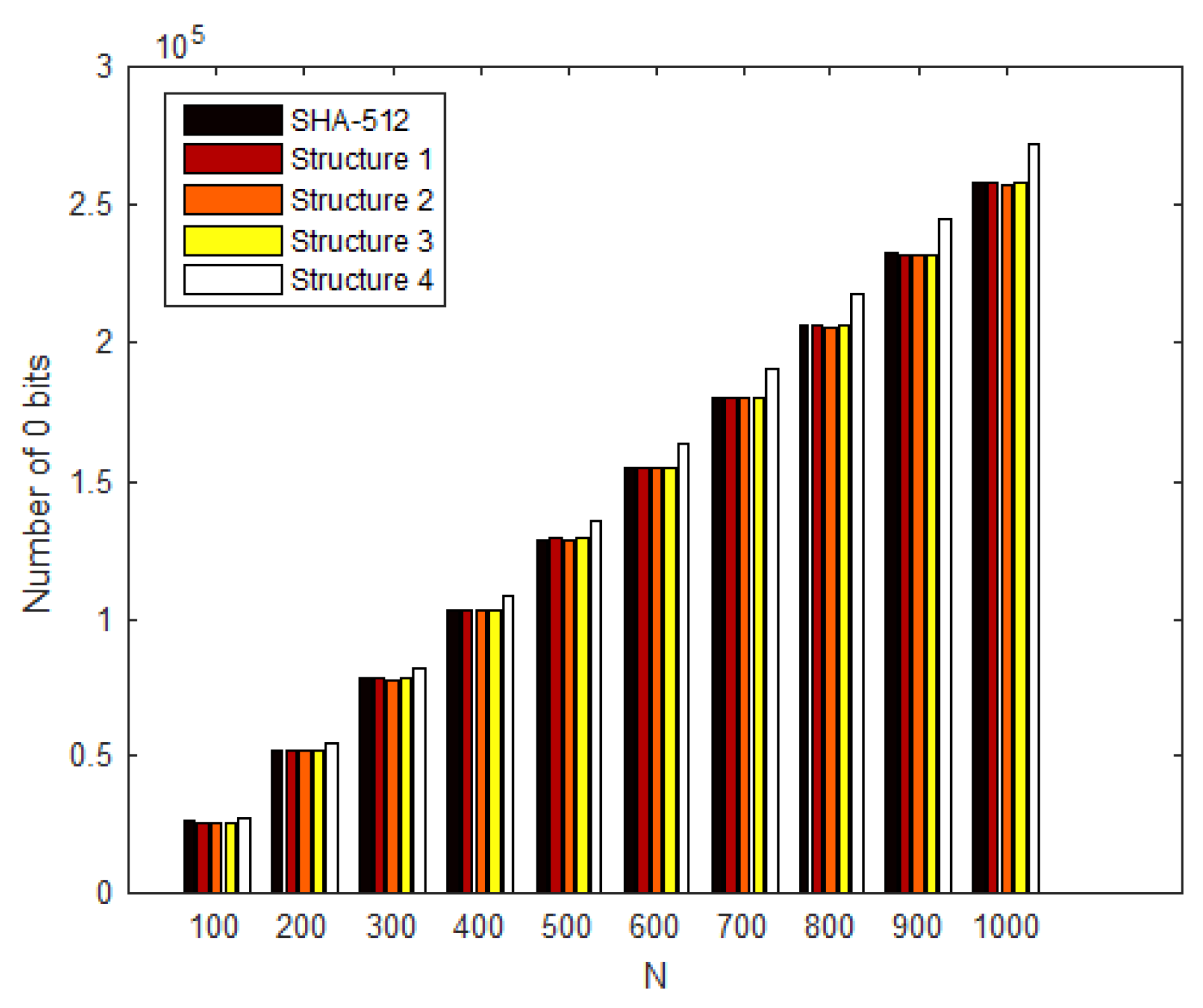
3.2. Linear Complexity
3.3. Sensitivity Analysis
- C1: The original plaintext message;
- C2: Alter ‘.’ At the end of a sentence to ‘/’;
- C3: Flip all letters (a) in a sentence to (o);
- C4: Change E in Egypt word to e;
- C5: Add 5 before history.
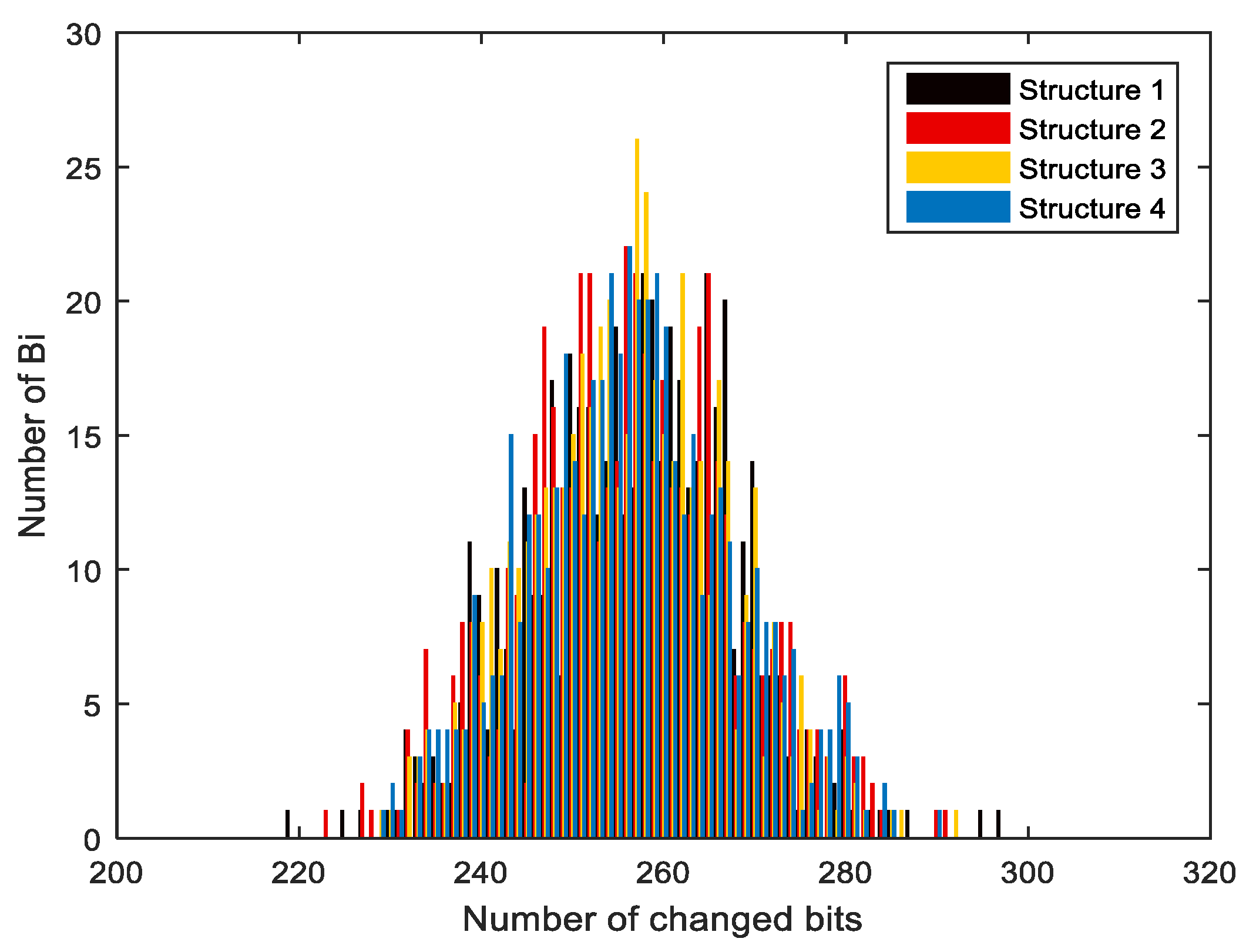
3.4. Confusion and Diffusion Analyses
- The hash value for an input message was calculated;
- Single bits in the message, and the hash value was calculated again;
- The two hashes were compared to identify the difference between them;
- Steps (1–3) were repeated for N times.
- Minimum number of changed bit: Bmin =min ;
- Maximum changed bit number: Bmax = max ;
- Mean number of changed bits: ;
- Mean changed probability: ;
- Standard variance of the changed bit number ΔB = ;
- Standard variance of probability ΔP= .
3.5. Hash Attacks
3.5.1. Brute Force Attack
Preimage and Second Preimage Attacks
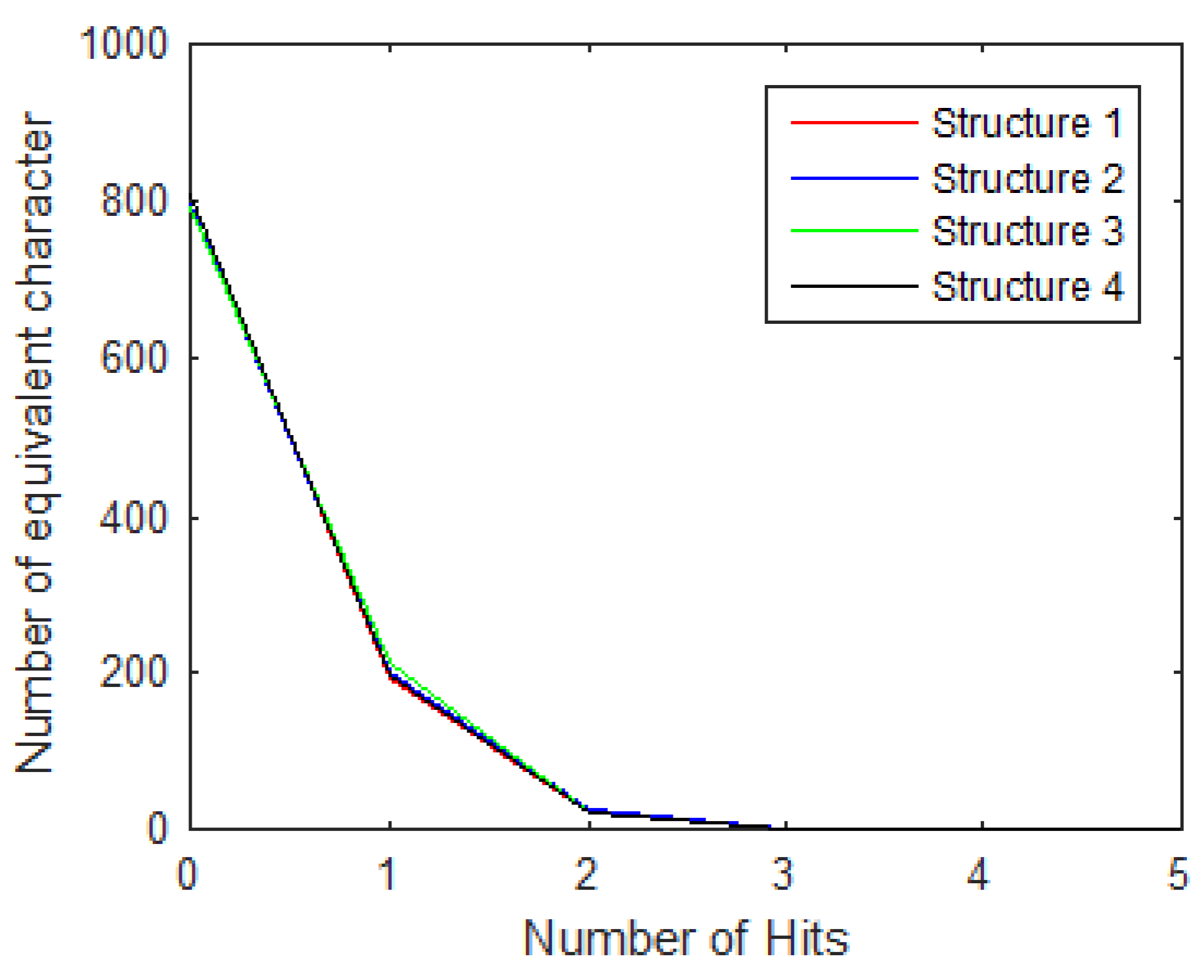
Collision Resist Attack
3.5.2. Cryptanalytic Attacks
Meet-in-the-Middle Attack
- Msg1 = (M1, M2, M3, …, Mn) can be replaced by Msg2 = (M1, M2, M3, …, Mn″). The second time, “advanced culture” was replaced with “civilization”;
- The hash value was calculated for both the original message and the replaced message;
- The number of bits different between the original and replaced message was counted.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohamed, M.H.; El Sobky, W.I.; Hamdy, S. Elliptic Curve Digital Signature Algorithm Challenges and Development Stages. Int. J. Innov. Technol. Explor. Eng. 2021, 10, 121–128. [Google Scholar] [CrossRef]
- Naif, J.R.; Abdul-Majeed, G.H.; Farhan, A.K. Secure IOT System Based on Chaos-Modified Lightweight AES. In Proceedings of the 2019 International Conference on Advanced Science and Engineering, Zakho-Duhok, Iraq, 2–4 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Farhan, A.K.; Mahdi, M.S. Proposal Dynamic Keys Generator for DES algorithms. Islamic Coll. Univ. J. 2014, 29, 25–48. [Google Scholar]
- Kadhim, A.; Salih, M. Proposal of New Keys Generator for DES Algorithms Depending on Multi Techniques. Eng. Technol. J. 2014, 32, 94–106. [Google Scholar]
- Yassein, H.; Al-Saidi, N.M.G.; Farhan, A. A new NTRU cryptosystem outperforms three highly secured NTRU-analog systems through an innovational algebraic structure. J. Discret. Math. Sci. Cryptogr. 2020, 25, 523–542. [Google Scholar] [CrossRef]
- Turner, J.M. The Keyed-Hash Message Authentication Code. FIPS Publications. 2008. Volume 2019, pp. 1–20. Available online: http://csrc.nist.gov/publications/fips/fips198-1/FIPS-198-1_final.pdf (accessed on 5 August 2019).
- An Advanced Signature Scheme: Schnorr Algorithm and its Benefits to the Bitcoin Ecosystem. 2018. Available online: https://www.politesi.polimi.it/bitstream/10589/144372/1/main.pdf (accessed on 22 January 2021).
- NIST. FIPS 186-2: Digital Signature Standard (DSS). FIPS Publications. 2000. Volume 2, pp. 86–92. Available online: http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:FIPS+186-3+Digital+Signature+Standard+(+DSS+)#0 (accessed on 19 May 2019).
- Kadhim, A.; Khalaf, S. New Approach for Security Chatting in Real Time. Int. J. Emerg. Trends Technol. Comput. Sci. 2015, 4, 30–36. [Google Scholar]
- Zheng, Z.; Xie, S.; Dai, H.; Chen, X.; Wang, H. An Overview of Blockchain Technology: Architecture, Consensus, and Future Trends. In Proceedings of the 2017 IEEE 6th International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017; pp. 557–564. [Google Scholar] [CrossRef]
- Delahaye, J.-P. Cryptocurrencies and Blockchains. Inference Int. Rev. Sci. 2016, 2, 1–86. [Google Scholar] [CrossRef]
- Wang, J.; Liu, G.; Chen, Y.; Wang, S. Construction and Analysis of SHA-256 Compression Function Based on Chaos S-Box. IEEE Access 2021, 9, 61768–61777. [Google Scholar] [CrossRef]
- Priyadarshini, I. Introduction to Blockchain Technology. In Cyber Security in Parallel and Distributed Computing: Concepts, Techniques, Applications and Case Studies; Scrivener Publishing LLC: Beverly, MA, USA, 2019; pp. 91–107. [Google Scholar] [CrossRef]
- Vujičić, D.; Jagodić, D.; Ranđić, S. Blockchain technology, bitcoin, and Ethereum: A brief overview. In Proceedings of the 2018 17th International Symposium INFOTEH-JAHORINA (INFOTEH), East Sarajevo, Bosnia and Herzegovina, 21–23 March 2018; pp. 1–6. [Google Scholar] [CrossRef]
- El Sobky, W.I.; Gomaa, S.H.; Hassan, A.Y. A-Survey-of-Blockchain-from-the-Viewpoints-of-Applications-Challenges-and-Chances. Int. J. Sci. Eng. 2021, 12, 11. [Google Scholar]
- FIPS Pub 180-1; Secure Hash Standard. NIST: Gaithersburg, MD, USA, 1995; Volume 17, p. 15.
- Stallings, W. Communications, the William Stallings Books on Computer Data and Computer Communications, 7th ed.; Pearson: Upper Saddle River, NJ, USA, 2011; p. 139. [Google Scholar]
- Ibrahim, A.F.S. New Secure Solutions for Privacy and Access Control in Health Information Exchange. Ph.D. Thesis, University of Kentucky, Lexington, KY, USA, 2016; p. 171. Available online: https://search.proquest.com/docview/1819468453?accountid=13460%0Ahttp://zp2yn2et6f.search.serialssolutions.com/directLink?&atitle=New+secure+solutions+for+privacy+and+access+control+in+Health+Information+Exchange&author=Ibrahim%2C+Ahmed+Fouad+Shedeed&issn (accessed on 20 March 2020).
- Seok, B.; Park, J.; Park, J.H. A Lightweight Hash-Based Blockchain Architecture for Industrial IoT. Appl. Sci. 2019, 9, 3740. [Google Scholar] [CrossRef] [Green Version]
- Martino, R.; Cilardo, A. Designing a SHA-256 processor for blockchain-based IoT applications. Internet Things 2020, 11, 100254. [Google Scholar] [CrossRef]
- Strogatz, S.; Friedman, M.; Mallinckrodt, A.J.; McKay, S. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Comput. Phys. 1994, 8, 532. [Google Scholar] [CrossRef]
- Ljupco, K.; Shiguo, L. Chaos-Based Cryptography; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 354. [Google Scholar] [CrossRef]
- Liu, Y.; Luo, Y.; Song, S.; Cao, L.; Liu, J.; Harkin, J. Counteracting Dynamical Degradation of Digital Chaotic Chebyshev Map via Perturbation. Int. J. Bifurc. Chaos 2017, 27, 1750033. [Google Scholar] [CrossRef]
- Abbasy, M.R.; Nikfard, P.; Ordi, A.; Torkaman, M.R.N. DNA Base Data Hiding Algorithm. Int. J. New Comput. Archit. Appl. 2012, 2, 183–192. [Google Scholar]
- Martino, R.; Cilardo, A. SHA-2 Acceleration Meeting the Needs of Emerging Applications: A Comparative Survey. IEEE Access 2020, 8, 28415–28436. [Google Scholar] [CrossRef]
- Ali, A.M.; Farhan, A.K. A Novel Improvement with an Effective Expansion to Enhance the MD5 Hash Function for Verification of a Secure E-Document. IEEE Access 2020, 8, 80290–80304. [Google Scholar] [CrossRef]
- Alawida, M.; Samsudin, A.; Teh, J.S. Enhanced digital chaotic maps based on bit reversal with applications in random bit generators. Inf. Sci. 2020, 512, 1155–1169. [Google Scholar] [CrossRef]
- Mohammed, A.A.; Ibadi, A. A Proposed Non Feistel Block Cipher Algorithm. Qalaai Zanist Sci. J. 2017, 2, 64–71. [Google Scholar] [CrossRef]
- Naif, J.R.; Abdul-Majeed, G.; Farhan, A.K. Internet of Things Security using New Chaotic System and Lightweight AES. J. Al-Qadisiyah Comput. Sci. Math. 2019, 11, 45–52. [Google Scholar] [CrossRef] [Green Version]
- Sadiq, A.T.; Farhan, A.K.; Hassan, S.A. A proposal to improve RC4 algorithm based on hybrid chaotic maps. J. Adv. Comput. Sci. Technol. Res. 2016, 6, 74–81. [Google Scholar]
- Fadhil, M.S.; Farhan, A.K.; Fadhil, M.N. Designing Substitution Box Based on the 1D Logistic Map Chaotic System. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1076, 012041. [Google Scholar] [CrossRef]
- Cao, J.; Chugh, R. Chaotic behavior of logistic map in superior orbit and an improved chaos-based traffic control model. Nonlinear Dyn. 2018, 94, 959–975. [Google Scholar] [CrossRef]
- Kadhim, A.; Emad, H. Mouse Movement with 3D Chaotic Logistic Maps to Generate Random Numbers. Diyala J. Pure Sci. 2017, 13, 24–39. [Google Scholar] [CrossRef] [Green Version]
- Farhan, A.K.; Ali, R.S.; Yassein, H.R.; Al-Saidi, N.M.G.; Abdul-Majeed, G.H. A new approach to generate multi S-boxes based on RNA computing. Int. J. Innov. Comput. Inf. Control. 2020, 16, 331–348. [Google Scholar] [CrossRef]
- Alzaidi, A.A.; Ahmad, M.; Doja, M.N.; Al Solami, E.; Beg, M.M.S. A New 1D Chaotic Map and $\beta$ -Hill Climbing for Generating Substitution-Boxes. IEEE Access 2018, 6, 55405–55418. [Google Scholar] [CrossRef]
- Al Solami, E.; Ahmad, M.; Volos, C.; Doja, M.N.; Beg, M.M.S. A New Hyperchaotic System-Based Design for Efficient Bijective Substitution-Boxes. Entropy 2017, 20, 525. [Google Scholar] [CrossRef] [Green Version]
- Alawida, M.; Samsudin, A.; Teh, J.S.; Alshoura, W.H. Digital Cosine Chaotic Map for Cryptographic Applications. IEEE Access 2019, 7, 150609–150622. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Chen, C.L.P. A new 1D chaotic system for image encryption. Signal Process. 2014, 97, 172–182. [Google Scholar] [CrossRef]
- Mazloom, S.; Moghadam, A.-M.E. Color image encryption based on Coupled Nonlinear Chaotic Map. Chaos Solitons Fractals 2009, 42, 1745–1754. [Google Scholar] [CrossRef]
- Zhang, T.; Li, S.; Ge, R.; Yuan, M.; Ma, Y. A Novel 1D Hybrid Chaotic Map-Based Image Compression and Encryption Using Compressed Sensing and Fibonacci-Lucas Transform. Math. Probl. Eng. 2016, 2016, 7683687. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Wang, X.; Kadir, A. Image encryption using DNA complementary rule and chaotic maps. Appl. Soft Comput. 2012, 12, 1457–1466. [Google Scholar] [CrossRef]
- Alawida, M.; Samsudin, A.; Alajarmeh, N.; Teh, J.S.; Ahmad, M.; Alshoura, W.H. A Novel Hash Function Based on a Chaotic Sponge and DNA Sequence. IEEE Access 2021, 9, 17882–17897. [Google Scholar] [CrossRef]
- Liu, H.; Kadir, A.; Liu, J. Keyed Hash Function Using Hyper Chaotic System with Time-Varying Parameters Perturbation. IEEE Access 2019, 7, 37211–37219. [Google Scholar] [CrossRef]
- Abdoun, N.; El Assad, S.; Hoang, T.M.; Deforges, O.; Assaf, R.; Khalil, M. Designing Two Secure Keyed Hash Functions Based on Sponge Construction and the Chaotic Neural Network. Entropy 2020, 22, 1012. [Google Scholar] [CrossRef] [PubMed]
- Todorova, M.; Stoyanov, B.; Szczypiorski, K.; Kordov, K. SHAH: Hash function based on irregularly decimated chaotic map. Int. J. Electron. Telecommun. 2018, 64, 457–465. [Google Scholar] [CrossRef]
- Sobti, R.; Geetha, G. Cryptographic Hash functions—A review. IJCSI Int. J. Comput. Sci. Issues 2012, 9, 461–479. [Google Scholar]
- Zhang, J.; Wang, X.; Zhang, W. Chaotic keyed hash function based on feedforward–feedback nonlinear digital filter. Phys. Lett. A 2007, 362, 439–448. [Google Scholar] [CrossRef]
- Li, Y.; Xiao, D.; Deng, S.; Han, Q.; Zhou, G. Parallel Hash function construction based on chaotic maps with changeable parameters. Neural Comput. Appl. 2011, 20, 1305–1312. [Google Scholar] [CrossRef]






| Binary\Rule | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 00 | C | C | G | G | T | T | A | A |
| 01 | T | A | T | A | C | G | C | G |
| 10 | A | T | A | T | G | C | G | C |
| 11 | G | G | C | C | A | A | T | T |
| ni\Group | G1 | G2 | G3 | G4 | G5 | G6 |
|---|---|---|---|---|---|---|
| A | T | T | C | C | G | G |
| T | C | G | G | A | C | A |
| C | G | A | T | G | A | T |
| G | A | C | A | T | T | C |
| Parameter | Initial Hash Buffer | Additive Constant | |
|---|---|---|---|
| Structure 1 | Hybrid: r = 0.9, a = 0.995, b = 1.8, N = 10, X0 = 0.5 CLM: r = 3.9, N = 80, K = 24, Y0 = 0.5 | a = 6d5b3ce95e42fd09 b = ac2bb11e816c5938 c = 8e6045061c786753 d = aa2fc0f52ebcfe05 e = 675227a241f91e7e f = 5a39e27c6b5835d3 g = 165f440108249951 h = 9c4c17654e1f836a | k1 = a99c8684073fdcf6 k2 = d708ff9ebf9cf7f4 k3 = 4ed248e568f52a86 k4 = 8be68516d917dbef k77 = fbb5fe2f58e7ef1b k78 = 830eeab0eff1aeae k79 = e8f8dfac50b5fe4d k80 = f88bfb8d813e7aed |
| Structure 2 | LSS: r = 3.9, N = 10, X0 = 0.5 CLM: r = 3.9, N = 80, K = 24, Y0 = 0.5 | a = fffffb1550d687fe b = 113bace070f3349d c = 52e070f33399f527 d = f4319af52883f336 e = db76fe081a5ceb4b f = 9bf335a4e753e070 g = 3299f42e9bf136aa h = 70f3349de854de6e | k1 = a99c8684073fdcf6 k2 = d708ff9ebf9cf7f4 k3 = 4ed248e568f52a86 k4 = 8be68516d917dbef k77 = fbb5fe2f58e7ef1b k78 = 830eeab0eff1aeae k79 = e8f8dfac50b5fe4d k80 = f88bfb8d813e7aed |
| Structure 3 | LSS: r = 3.9, N = 10, X0 = 0.5 Improved logistic: a = 4, b = 108, alpha = 12,345, N = 9, Y0 = 0.5 | a = fffffb1550d687fe b = 113bace070f3349d c = 52e070f33399f527 d = f4319af52883f336 e = db76fe081a5ceb4b f = 9bf335a4e753e070 g = 3299f42e9bf136aa h = 70f3349de854de6e | k1 = 64ca97e7026df731 k2 = f47e896ca60190e k3 = 5ea7206d450fa092 k4 = 4a6eca97e7026df7 k77 = fa092fc8ae5ac98 k78 = e5e5d4116787cf4c k79 = 3b131174ea4a6eca k80 = 8330a1437ff2982c |
| Structure 4 | TSS: r = 3.9 N = 10, X0 = 0.5, Y0 = 0.9 | a = 6b43d9f2a25da192 b = 30e087e0f925d9e c = caf3af5094d9c598 d = 9688d7e837d134cc e = 60ba87b1989540bf f = fe3e91c22e5f044c g = 6dad2a49859f1e18 h = f979897995e4d17 | k1 = 3139d540b95ff723 k2 = 90e8e811355ffc4b k3 = 6b173f9a382490e5 k4 = 6cf4fe2c859e63b0 k77 = 9dc80f916a938ed1 k78 = b21cc378aa9d2900 k79 = d6c101d634aff73a k80 = 9b087c315739b7c2 |
| Hash Value of 1st Case (Hash_Hybrid_CLM) | Changed Bits | |
|---|---|---|
| C1 | 76ec2e55956e3d03d56391b1db4ddadb7beb8b003 afcb8ad6fef744314f1ef55418a84c62c3a00ca6306 4686befa06aeca58cfaa0289a1dc0e915da54e42f333 | ___ |
| C2 | 54947ac5855264797ee1f4eee2b619a359548fd78c 8b640c5276793dff60e90b69e3d0a06fab29b2fc8f3 30cc6fc2530c6862e92ce331922c3482fa5cffa7151 | 257 |
| C3 | 39f72e29f55a7daa1b1fa0abbb595fba0f3f06f2e160 dd219022def05641ff0849689b9986a5e064e18a49 70ee8da76c47c3ff37fe8f4c7965f19f6e7d1f3b6f | 270 |
| C4 | 9bb66539582bf4d443e158aa565c111a924c113d07 16e5e42193ce3d9fdd31b183d09ed06f40e1f4d60ce 4d7b9117737dc74acbcae7f3817cce119adbb2994c8 | 259 |
| C5 | 54c94f2c6dc95bf68982a8519433161c48134ad6d8 d928c5173713f5e0d6915344f5b28c4e8e29c10404 0554faa512d8d8fae363d73e7c5b628603ddf2b9d0ae | 238 |
| Hash Value of 2nd Case (Hash_LSS_CLM) | Changed Bits | |
|---|---|---|
| C1 | 5cde39d1a7e0ce19e1550c37e8befc57551c4d2949b 864e2da0f714edd2941cd952dde5e7c780dfec773f4 4487d768929bf34cd731e2106a743312f475846bc5 | ___ |
| C2 | a954350f1ac222201c41176199ac7e6297075848b4 02e8a61048b6c76af076b3fb2f73c7af8ab69e14d2f 6049995654179cc2cd6e45af6049f0de757a5655168 | 257 |
| C3 | 7b923f81f921fa6d1ccef45d4f3d672c99d2a5775d6 5ef635c65fc24c4f4b483838417335603e72b31578 1d2fd4ee01a2ec297508c0e2f20447f15bb0feecfae | 265 |
| C4 | 797584a71b64c1a882d1d0d438ca9d9dc367ff5899a 48ade6ec2d3eae25cae60d594f04477a807c588b490 8deb9ca40e81022600328e767dbad5be0854daed21 | 261 |
| C5 | 7d64060613bb02ed718cbdbb901b6d2e61c898d0ed 3a549876047c8a94012900995d0abb5d826419f84e 0a6477d6be5d3f06cf07b813585f8e931d5e198a586 | 251 |
| Hash Value of the 3rd Structure (Hash_LSS_ Nlogistic) | Changed Bits | |
|---|---|---|
| C1 | a74901fcb8376c137a81a0c84deba7c4dc8781a5dd5 256736e755fdf33bf0873b9f7bdf62a9600051b1a68 7c3551d21890fcc7d87305a22557b6821f47608972 | ___ |
| C2 | 81c74c921f7f8e53dafb76c02c5e3e1a15537fefc791 4aab1f5886452a258ae6b972d24311c65c183a4ec0 997d46614baab20b6b59aef712e5e674553b13b011 | 245 |
| C3 | c0431d33acf8e118a0e8a2be0d1d7c67f43458f5f26 f92c70c028c970a4cf8b4f9b974cf8c2cae52aa393d 8a2cf221713061af521ae20b2718cac6225b3a6a5a | 254 |
| C4 | 512f1247e20d1b18d208300842071dfa72fa926c5c 1ac13d89f2c530e067e7c383067d5431d68395e661 a9e5e50a582b16c6238341d4b1c19cc3676752392768 | 259 |
| C5 | 26f05090636b04f1c123060f3655591fa315801c2d f47c6eea2330bf62041ae5f6d73d784b887ed9d2e35 310e097d1adce93db522785cee9eafa7dd206a59010 | 261 |
| Hash Value of the 4th Structure (Hash_TSS_TSS) | Changed Bits | |
|---|---|---|
| C1 | 9cbe1f41638067a6b10a1d53fdb51aea2fa0484c257 c22b8705daff6809c4247a1bcdd36b283a88b695bc 3cb493f045c5f509a1483b926b1fed846ffdb266e7d | ___ |
| C2 | fab43d0aeb737cff079a2a6f0885452780d0125cd92 bb89e9824136aec488a7ad1437c62e9f1aa4874aa4 83aff49438abd8a2b8ebdec6852babade2a01124496 | 262 |
| C3 | b5ee7a4a04add2922af173bb8fb171d5794683fd2e f715945fa94af9d2bf708930e9a5fd25e0cee19748 900e4ea3b0d7b2a92f91fcee7677762f1fd2a5a0ff16 | 270 |
| C4 | 66380959269b1de562517ea65a3ed64c4c042b5e2e6 050a73d16a07ae72a69c1e676180c321c56c1fb0b8b 0d3f14e415ce8320c61849b59b64a7d6e66336c6f5 | 244 |
| C5 | 24764345aa9f3895c5cd58acdcdfdfd3f7e024d4970 90c3c333926aefe0948ad1ed0d4122978d03d26a5d b8e917688a940b004f2043acac5e0c48f811fd38644 | 258 |
| Bmin | Bmax | Mean | P% | ΔB | ΔP | |
|---|---|---|---|---|---|---|
| SHA-512 | 212 | 297 | 256.09 | 50.018 | 11.13 | 2.174 |
| Structure1 | 219 | 291 | 256.0586 | 50.011 | 11.67 | 2.279 |
| Structure 2 | 219 | 293 | 256.032 | 50.006 | 10.92 | 2.133 |
| Structure 3 | 222 | 291 | 255.9648 | 49.993 | 11.34 | 2.214 |
| Structure 4 | 226 | 292 | 256.0244 | 50.0068 | 11.46 | 2.24 |
| Ref. [42]–Structure 1 | 223 | 291 | 256.496 | 50.05 | 11.41 | 2.229 |
| Ref. [42]–Structure 2 | 215 | 293 | 254.862 | 49.778 | 10.95 | 2.138 |
| Ref. [43] | 222 | 287 | 256.39 | 50.08 | 11.39 | 2.22 |
| Ref. [44]–Structure 1 | 217 | 293 | 256.2 | 50.04 | 11.20 | 2.18 |
| Ref. [44]–Structure 2 | 214 | 291 | 255.90 | 49.98 | 11.37 | 2.22 |
| Ref. [44]–Structure 3 | 215 | 296 | 255.53 | 49.90 | 11.41 | 2.23 |
| Ref. [45]–Structure 1 | 214 | 287 | 256.03 | 50.01 | 11.48 | 2.24 |
| Ref. [45]–Structure 2 | 229 | 292 | 256.45 | 50.08 | 11.32 | 2.21 |
| N = 256 | 512 | 1024 | 2048 | 10,000 | |
|---|---|---|---|---|---|
| Bmin | 228 | 224 | 219 | 214 | 210 |
| Bmax | 287 | 287 | 291 | 297 | 303 |
| Mean | 256.336 | 256.5 | 256.059 | 256.106 | 256.178 |
| P% | 50.066 | 50.098 | 50.011 | 50.021 | 50.034 |
| ΔB | 11.401 | 11.164 | 11.144 | 11.364 | 11.202 |
| ΔP | 2.227 | 2.180 | 2.176 | 2.220 | 2.20 |
| N = 256 | 512 | 1024 | 2048 | 10,000 | |
|---|---|---|---|---|---|
| Bmin | 227 | 219 | 219 | 219 | 217 |
| Bmax | 293 | 293 | 293 | 298 | 303 |
| Mean | 255.648 | 255.628 | 256.189 | 256.320 | 255.911 |
| P% | 49.931 | 49.928 | 50.037 | 50.062 | 49.983 |
| ΔB | 11.1031 | 10.791 | 10.907 | 11.073 | 10.80 |
| ΔP | 2.169 | 2.107 | 2.130 | 2.162 | 2.05 |
| N = 256 | 512 | 1024 | 2048 | 10,000 | |
|---|---|---|---|---|---|
| Bmin | 228 | 226 | 222 | 212 | 213 |
| Bmax | 290 | 290 | 291 | 294 | 300 |
| Mean | 256.402 | 255.978 | 255.965 | 255.668 | 256.024 |
| P% | 50.079 | 49.995 | 49.9931 | 49.935 | 50.005 |
| ΔB | 11.265 | 11.412 | 11.336 | 11.394 | 11.20 |
| ΔP | 2.200 | 2.229 | 2.214 | 2.225 | 2.110 |
| N = 256 | 512 | 1024 | 2048 | 10,000 | |
|---|---|---|---|---|---|
| Bmin | 226 | 226 | 226 | 225 | 207 |
| Bmax | 283 | 292 | 292 | 292 | 300 |
| Mean | 256.063 | 256.433 | 256.024 | 256.388 | 255.963 |
| P% | 50.012 | 50.085 | 50.005 | 50.076 | 49.993 |
| ΔB | 11.127 | 11.641 | 11.505 | 11.404 | 10.95 |
| ΔP | 2.173 | 2.274 | 2.247 | 2.227 | 2.175 |
| Number of Hits (ω) | ||||||
|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 64 | |
| Theoretical value | 797.10 | 200.05 | 24.71 | 2.00 | 0.11 | 1.42 × 10−56 |
| Structure 1 | 820 | 176 | 27 | 1 | 0 | 0 |
| Structure 2 | 812 | 187 | 23 | 2 | 0 | 0 |
| Structure 3 | 802 | 198 | 22 | 2 | 0 | 0 |
| Structure 4 | 809 | 194 | 0 | 0 | 0 | 0 |
| Absolute Difference | ||||
|---|---|---|---|---|
| Max. | Min. | Mean | Mean/Character | |
| SHA-512 | - | - | 5461.33 | 170.67 |
| Structure 1 | 6785 | 3863 | 5447.148 | 170.22 |
| Structure 2 | 7008 | 3946 | 5295.425 | 165.48 |
| Structure 3 | 6926 | 4143 | 5462.526 | 170.70 |
| Structure 4 | 6908 | 3801 | 5451.65 | 170.36 |
| Different Bits in Meet in the Middle Attack | |
|---|---|
| Structure 1 | 254 |
| Structure 2 | 259 |
| Structure 3 | 260 |
| Structure 4 | 245 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Meligy, N.E.; Diab, T.O.; Mohra, A.S.; Hassan, A.Y.; El-Sobky, W.I. A Novel Dynamic Mathematical Model Applied in Hash Function Based on DNA Algorithm and Chaotic Maps. Mathematics 2022, 10, 1333. https://doi.org/10.3390/math10081333
El-Meligy NE, Diab TO, Mohra AS, Hassan AY, El-Sobky WI. A Novel Dynamic Mathematical Model Applied in Hash Function Based on DNA Algorithm and Chaotic Maps. Mathematics. 2022; 10(8):1333. https://doi.org/10.3390/math10081333
Chicago/Turabian StyleEl-Meligy, Nada E., Tamer O. Diab, Ashraf S. Mohra, Ashraf Y. Hassan, and Wageda I. El-Sobky. 2022. "A Novel Dynamic Mathematical Model Applied in Hash Function Based on DNA Algorithm and Chaotic Maps" Mathematics 10, no. 8: 1333. https://doi.org/10.3390/math10081333
APA StyleEl-Meligy, N. E., Diab, T. O., Mohra, A. S., Hassan, A. Y., & El-Sobky, W. I. (2022). A Novel Dynamic Mathematical Model Applied in Hash Function Based on DNA Algorithm and Chaotic Maps. Mathematics, 10(8), 1333. https://doi.org/10.3390/math10081333






