Abstract
Information processing in the brain takes place in a dense network of neurons connected through synapses. The collaborative work between these two components (Synapses and Neurons) allows for basic brain functions such as learning and memorization. The so-called von Neumann bottleneck, which limits the information processing capability of conventional systems, can be overcome by the efficient emulation of these computational concepts. To this end, mimicking the neuronal architectures with silicon-based circuits, on which neuromorphic engineering is based, is accompanied by the development of new devices with neuromorphic functionalities. We shall study different memristor cellular nonlinear networks models. The rigorous mathematical analysis will be presented based on local activity theory, and the edge of chaos domain will be determined in the models under consideration. Simulations of these models working on the edge of chaos will show the generation of static and dynamic patterns.
Keywords:
memristor cellular nonlinear networks; local activity; edge of chaos; static and dynamic patterns MSC:
92B20; 65P20; 92C15
1. Introduction
The complexity phenomenon, the definition of which had been argued for a long time by many scientists, briefly refers to the emergence of complex patterns in homogeneous media and is thus strongly related to the neural computation concept. With the establishment of robust theoretical foundations for the local activity principle, it is now clear that various descriptions of complexity such as symmetry breaking, self-organization, and exchange of energy can be gathered under a unique framework. It was shown that the cells of a resistively coupled homogenous network have to be locally active for the emergence of complexity, which refers to static or dynamic pattern formation. In addition, if the equilibrium point of a locally active cell is asymptotically stable, then the cell is said to be at the edge of chaos. In other words, the edge of chaos refers to the scenario where the uncoupled cells are ‘silent’ but can be ‘potentially’ destabilized and generate complex behavior under dissipative coupling.
The ability to compute with memory is an essential property of nonlinear cellular networks. By incorporating memristor memory arrays [1,2] locally into the computing elements, one can achieve high flexibility in network learning algorithms due to the fact that they can provide high-density analog storage. This means that the memristive circuit has the behavior of conventional memory, i.e., the weight values can be calculated outside of the circuit and then be programmed to the corresponding addresses. In this way, one can retrieve the information when the algorithms need it.
Cellular Nonlinear Networks (CNN) [3,4,5] are defined as spatial arrangements of locally coupled dynamical systems, referred to as cells (see Figure 1). The CNN dynamics are determined by a dynamic law of an isolated cell, by the coupling laws between the cells, and by boundary and initial conditions. The state equations of CNN cells are described by nonlinear ordinary differential equations, which give the dynamic and coupling interactions of the cells. The mathematical presentation of CNN by a system of coupled ordinary differential equations is very compact, but nevertheless, these networks can have very complex behavior [4], such as chaotic behavior, self-organization, and pattern formation or nonlinear oscillation and wave propagation.
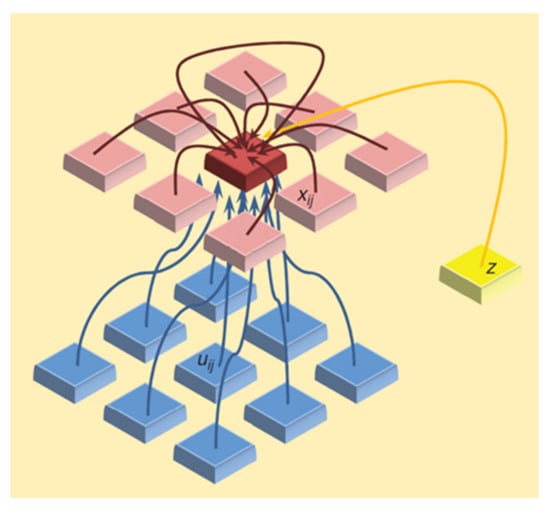
Figure 1.
Illustration of the CNN coupling structure.
Neural processing physically occurs both in space and time through a phenomenon called spatiotemporal pattern formation. The network dynamics behind the formation of these neural patterns are believed to underlie our high-level cognitive capabilities and therefore are of special interest in neuroscience. Similarly, the pattern formation phenomenon has been observed in other disciplines such as physical chemistry, biology, optics, thermodynamics, fluid mechanics as well as engineering systems, which shows that there has been a constant interest in pattern formation dynamics in various fields. However, there had not been a universal consensus on the definition of the mechanisms behind spatiotemporal pattern formation. In this work, we provide new results based on rigorous mathematical analysis of the edge of chaos phenomena and the pattern formation in such networks. In comparison to other works on memristor-based neural networks [6,7,8], here we determine the edge of chaos region by strong mathematical inequalities. In this region, complex phenomena and pattern generation can be observed.
Moreover, the memristor device model is integrated into the standard state equation of a CNN cell. Default parameter values of memristor models resulting from the analysis of different charge transportation phenomena are assumed. In a deep mathematical study, a niobium oxide memristor model replaces the cell resistor of a standard CNN cell. The aim of this work is to derive cell state equations and study their dynamics by applying local activity theory [9]. We prove that in the edge of chaos domain, the cell equilibrium points are both locally active and asymptotically stable. Based on this, we obtain different patterns, such as Turing static patterns, dynamic patterns, and chaotic patterns. Computer simulations show that such patterns can be obtained if the parameter sets are chosen on the edge of chaos domain. It is important to point out that memristor CNN models presented in the paper can have very promising applications, which is the aim of our future research.
2. Memristor CNN Modeling
Cellular Nonlinear Networks (CNN) [4] can describe different systems—physical, chemical, and biological. The operations inside CNN are continuous-time, and the interactions between the processing elements are local. Due to this, the networks can provide real-time signal processing with very high precision. CNN has many powerful applications [4,10,11], such as pattern recognition and signal processing, line detection, edge detection, noise removal, character recognition, etc. There are digital and analog implementations of CNN known in the literature in the form of VLSI chips. Usually, memristors can realize interactions between neighbor cells in the CNN circuit [11,12]. The proposed memristor model, which will replace the original linear resistor in the CNN cell circuit, has nonlinear current-voltage characteristics with locally negative differential resistance. We shall call such architecture memristor CNN (MCNN), which has nonvolatile and programmable synapse circuits [13,14,15,16,17]. In this way, the proposed model is more versatile and compact and with simple output function realization. In Figure 2, the implementation of the MCNN cell is given.
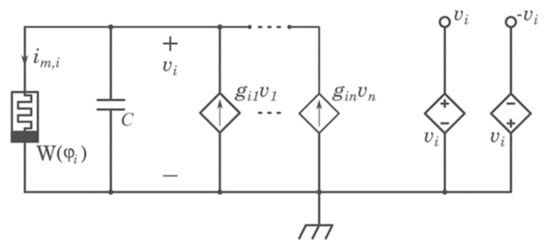
Figure 2.
Implementation of MCNN cell.
Hereby, we are planning to implement networks arranged in rectangular arrays of cells C(i,j). Each cell has neighboring cells; r denotes the radius of the neighborhood. The proposed MCNN state equation is given by [14].
where represents the cell capacitance, are cloning templates, is the state variable, is the input variable, and iM(t) is the current flowing through the current-controlled memristor according to the following law:
denotes memductance and is the state function of the considered memristor. We assume translation-invariant feedforward and feedback connections that mimic 2-D spatial diffusion of chemical substances, implemented by variable–gain current- controlled sources, the cell bias is given by I.
In the circuit analysis, a continuous-time autonomous network is stable if its solution is bounded and its energy function is damped. Since the state of a specific MCNN depends on the circuit parameters, it is straightforward to guarantee its boundedness. In order to prove the stability of MCNN [2], we shall introduce energy function E below, chosen by means of the Lyapunov stability theorem [18]:
It can be proved that the energy function is bounded (see [4]).
Again, methods from the theory of nonlinear systems [18] are applied, and a bifurcation analysis is provided for different feedforward and feedback coupling parameters.
We shall consider some MCNN models in the following. First, we shall consider the Gierer–Meinhardt system [19,20], which describes pattern formation in living cells:
where are positive constants, (.), denote the monotonically increasing.
Functions defined by:
where denotes the gain, and denote the minimum and maximum coupling strengths, respectively, denotes the variables for determining the coupling strength (l-leftward, r-rightward), is discretized Laplacian template, *-is the convolution operator [4].
= D().·()—is the memristive dynamics, denotes the polarity coefficient- = + 1: , = −1: , –is the time variable.
Next, we shall consider the following MCNN model with Brusselator [4,21,22] cell:
where = , , are positive constants.
In this paper, we shall present a two-dimensional grid in the form of a spatial lattice of identical cells positioned at the grid points. Their states are changed by local reaction-diffusion. This dynamical system implements kinetic equations in MCNN models. In the case when the diffusion coefficients > 0, l = 1, 2 complex phenomena can arise from the cell kinetic equations because the diffusion term in the above models has stabilizing effect. We shall prove that if the cell kinetic equations are not locally active in the parameters set, the complexity can not be exhibited regardless of the diffusion coefficients. Moreover, we shall derive rigorous mathematical inequalities for the local activity of the cell kinetic equation.
3. Edge of Chaos in Memristor CNN Models
Complex dynamics can arise in a locally-active cell kinetic equation in the case when all diffusion coefficients are zero, even if the single cells are uncoupled. Then limit cycles and chaos appear in the systems, and moreover, complex spatio-temporal phenomena arise.
We shall apply in our study the following definition of locally-active reaction-diffusion equations [9]: Let us consider a system of discrete reaction-diffusion equations. It is locally active if and only if its cells are locally active at the cell equilibrium point. If we denote by A the locally active domain of the parameter space, then the compliment is called the passive parameter domain in which we can obtain a homogeneous solution of the reaction-diffusion equations. The complexity can occur in active parameter region A, which is not an empty set in this case.
It is very important to have a physical implementation of the concept of local activity. The variables will be associated with the voltage and current of an electronic circuit (Figure 2) of a cell described by the same equations. The importance of the circuit model lies not only in the fact that it offers a convenient physical implementation but also in the fact that well-known results from classic circuit theory can be applied to test the cell for local activity. We shall suppose that each cell is operating near the equilibrium point. Then according to the theory of local activity [9], the circuit model of a cell is locally active if, in at least one equilibrium point, it behaves as a source of small-signal power.
We shall define the necessary and sufficient conditions for the local activity of a cell mathematically. For this purpose, we shall apply the following [9].
Test for local activity.
A cell with port state variables is locally-active at equilibrium point if, and only if, any one of the following conditions is true:
- (1)
- The complexity matrix has a pole in the open right-half plane ;
- (2)
- The complexity matrix has multiple poles on the imaginary axis;
- (3)
- The complexity matrix has a simple pole on the imaginary axis and is supposed to be a non-positive-definite matrix or a complex non- Hermitian matrix;
- (4)
- is a non-positive-definite matrix for some , T denotes the transpose and complex-conjugate operations.
In order to prove local activity in MCNN, we shall assume that the energy is zero when t = 0. Otherwise, some energy will be discharged outside the circuit, which leads to local passivity. The initial small input signal may cause a larger energy signal which comes from some external energy supply if the cell is a neuron.
We will be able to approximate the linear terms of the cell model by its Taylor series expansion if the signal is very small. By means of mathematics, we can derive an explicit analytical expression for the local activity of the cell based on the Taylor series computing. The system usually is highly nonlinear, and that is why under small perturbation, we can obtain complexity. If the discrete reaction-diffusion system has at least one spatio-temporal solution under homogeneous initial and boundary conditions, then it can exhibit complexity. It is very important to have initial conditions for the system of discrete reaction-diffusion equations with zero diffusion coefficients. Such a system can give rise to non-homogeneous static patterns when the initial condition corresponds to any pattern of cell equilibrium points (we can have one, two, or more equilibrium states).
Definition 1 (of the Edge of Chaos [9]).
In order for an uncoupled cell in MCNN to operate on the edge of chaos it is necessary that its equilibrium points are both locally active and asymptotically stable. Then the set of locally active parameters with this property is called the edge of chaos parameter set.
We shall develop a constructive algorithm for the determination of the edge of chaos in MCNN models [17,20,23]. These are the steps of the algorithm: (1). We approximate MCNN into discrete in space system; (2). We find the equilibrium points of the discrete system numerically or analytically. There might be one, two, or several real equilibrium points which are functions of the cell parameters and the diffusion coefficients; (3). We find the cell coefficients of the Jacobian matrix at each equilibrium point; (4). We calculate the trace and determinant of the Jacobian matrix at each equilibrium point; (5). We define the conditions for locally active and asymptotically stable equilibrium points by and ; (6). We define the edge of chaos region based on definition 1.
The following theorems from [9] are true:
Theorem 1 (of [9]).
Sharp Edge of Chaos ≡ edge of chaos for the one-port variable case. For the case where there is only one port variable, the sharp edge-of-chaos parameter domain is identical to the edge-of-chaos parameter domain of the complexity functionof any reaction–diffusion equation.
Theorem 2 (of [9]).
Sharp Edge of Chaos for the case of the two-port variables. For the case of two-port variables, the sharp edge of chaos parameter domain must satisfy at least one of the following three conditions involving the jk-th coefficients(iω), j, k = 1, 2, of the 2 × 2 complexity matrix, for at least one frequency:
- 1.
- 2.
- 3.
- +
We shall apply the following theorem from [5] for more general cases:
Theorem 3 (of [9]).
(Fast eigenvalue calculation algorithm). The eigenvalues of the Jacobian matrixare identical to the zeros of the admittance, i.e., the solution of the scalar polynomial equation of order .
The general conditions for the case are to be outlined during the simulation procedure of MCNN and will be based on the following conjecture: Only in this case, where the cell is locally active, can we have the homogeneous non-conservative system of equations apply complexity.
3.1. Edge of Chaos in Gierer–Meinhardt MCNN Model (1)
We shall determine the edge of chaos region of the MCNN model (1) by means of local activity theory [9]. We apply the following constructive algorithm [20,23]:
(A). We find the equilibrium points of (1). They are the solution of the following system [18]:
We calculate the equilibrium point of (3)- according to the local activity theory [9] when .
(B). We calculate the cell coefficients of the Jacobian matrix at the equilibrium point. In the equilibrium point we obtain the following results: , , .
(C). We define a locally active and stable region of cell parameters , such that:
or and and .
(D). We define the edge of chaos region in which there is at least one equilibrium point at which the isolated cell is both locally active and stable.
We obtain the simulation of the edge of chaos region for the Gierer–Meinhardt MCNN model given in Figure 3.
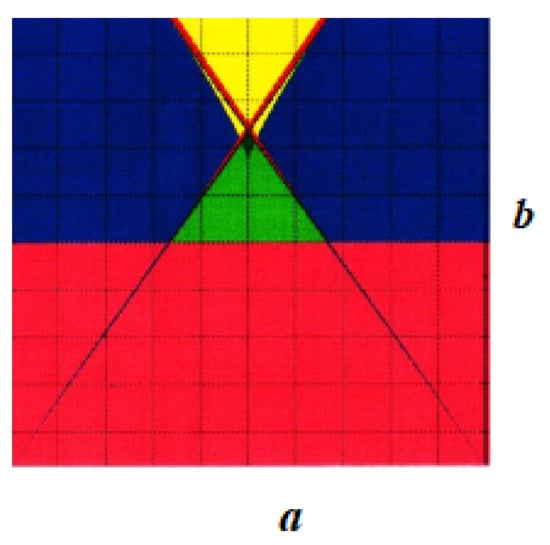
Figure 3.
Bifurcation diagram of the Gierer–Meinhardt MCNN model. Local activity region—dark pink, blue is a locally passive region, edge of chaos domain is red, green is a locally active and unstable region, yellow is the region in which no equilibrium point is both locally active and stable.
We present simulations of these regions for the parameter set and .
Remark 1.
In [19] Gierer and Meinhardt do rigorously prove the selected specific cell parameter points. Therefore we have proved here that these equilibrium points lie on the edge of chaos region based on the local activity theory.
3.2. Edge of Chaos in Brusselator MCNN (5)
We shall study the dynamics of the Brusselator MCNN (2) model by means of local activity theory [9], and we shall determine the edge of chaos region. Following the above-developed algorithm, we find the unique equilibrium point: . Then the cell coefficients are . The trace in our case is , and the determinant is .
In Figure 4 below, we present the simulation of the local activity region and the edge of chaos, as well as the locally passive region of the Brusselator MCNN model (2). The local activity test needs the estimation of ,which defines the profile of a cell parameter space. For this reason, we project the cell parameter space in Figure 4 below.
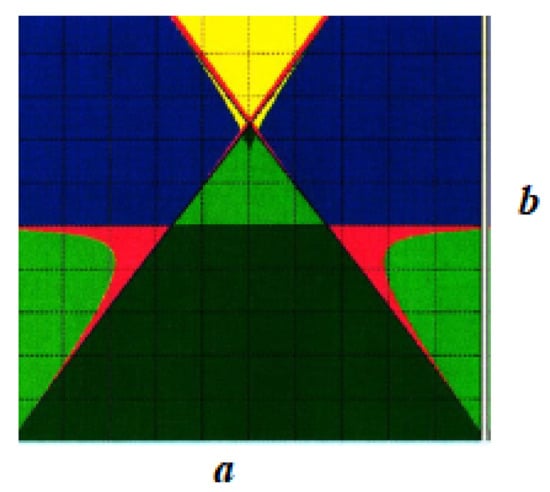
Figure 4.
Bifurcation diagram of the Brusselator MCNN model (2). The color indicates locally active and stable region (edge of chaos)—red, locally active and unstable region—green, locally passive region—blue, no equilibrium point is both locally active and stable—yellow.
Remark 2.
The Brusselator system [21] was defined in order to explain self-organization in chemical reactions. The theory of dissipative structures was developed based on this system, and it is operating far from thermodynamic equilibrium. However, this theory was not able to determine a more precise domain in which complex phenomena occur. Only the stability boundaries were found and it was ignored in the small subset of the edge of chaos in which emergence and complexity can emerge, which was performed in our analysis above.
4. Pattern Formation on the Edge of Chaos
We shall study the pattern formation dynamics in our MCNN models by approximating the dynamics in the spatial uniform equilibrium points [17,20,23]. It is very important for these models to be stable from the point of view of the simulations. This can be obtained by introducing a half-wave output nonlinearity which leads to spatial patterns.
We shall look for spatial pattern formation. That is why we derive conditions on the model parameters which exhibit spatial patterns. The simulations are conducted by using MATLAB based on the 4th order Runge–Kutta integration. We consider 256 cells’ MCNN architecture in order to obtain more accurate computations.
By applying a spatially random Gaussian distributed initial state which has zero mean and variance, we shall start the calculations. The positive and negative activity with characteristics bounds is obtained by means of the local activity theory [9].
In Figure 5 below, the simulations of the MCNN model (1) show that when Turing-like static patterns can occur if all equilibrium points are located in the locally active region (Figure 3). Let us consider the case and , then robust nonhomogeneous patterns may arise [20] (see Figure 5). The initial states used in all simulations of Figure 5 are chosen near the cell equilibrium point. The cell parameters are .
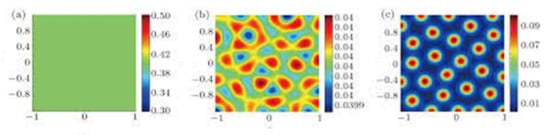
Figure 5.
Spatial patterns in Gierer- Meinhardt MCNN (1): (a) after 0 iterations; (b) after 1000 iterations; (c) after 5000 iterations.
In Figure 5, we can see the generation of static patterns, starting with (a), then after 1000 iterations (b) the Turing-like patterns are developed, and after 5000 iterations (c) when the equilibrium points are located on the edge of chaos region robust nonhomogeneous patterns arise.
Dynamic nonhomogeneous patterns (see Figure 6) occur when we choose the following diffusion coefficients and we are in the red region (Figure 3). We use the initial states near the equilibrium point, and the cell parameters are . The boundary, , plays an important role in the sense that for the cell parameter points located within the edge of chaos domain chaotic dynamic patterns usually emerge.
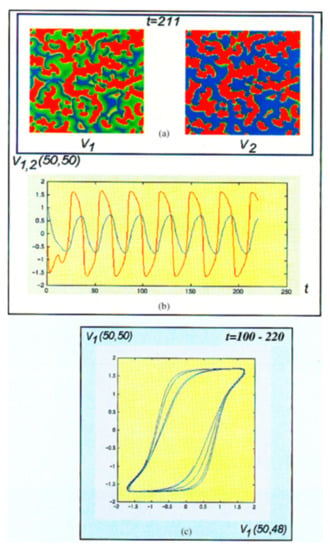
Figure 6.
Dynamic patterns of the Gierer–Meinhardt system. (a) snapshot of the dynamic pattern; (b) time evolution of the state variables; (c) projection of the high-dimensional attractor.
Remark 3.
Dynamic patterns arise when the cell parameters are in the locally active regions, which are very close to the edge of chaos. When the cell parameters are in the locally passive region, complex behavior is not observed in the case initial conditions are near the equilibrium points.
Following the analytical analysis of the MCNN model (2) in Section 3, we shall show the pattern generation in this model. The Brusselator equation is well known in chemical kinetics as an ideal system for studying dissipative structures. In some sense, this system behaves similarly to a harmonic oscillator. In [22], it is shown that the dynamics of the Brusselator equation have global periodicity, which depends on the initial and boundary conditions. In Figure 7, we present the complex behavior of MCNN (2) when the stable cells are on the edge of chaos region. It can be seen that in the locally active and stable regions, dynamic patterns occur. The initial states are near the equilibrium point, and the cell parameter values are .
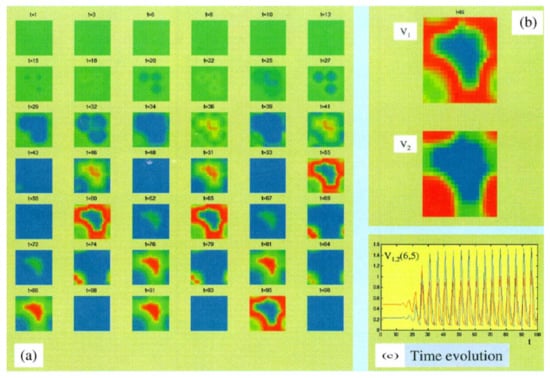
Figure 7.
Dynamic patterns in Brussellator MCNN model (2). (a) 42-time evolution snapshots of the state variable, (b) a snapshot of the dynamic patterns at t = 100, (c) time evolution of the state variables in red and in blue.
We can see in the figure above [22] that chaotic dynamic patterns arise in our model when it is working in the locally active region (Figure 5), which is very close to the edge of chaos. When the cell parameters are in the locally-passive region, no complex behavior occurs. Usually, it is not possible through the stability analysis to find the region in which the cells are locally passive.
5. Discussions
In this paper we consider two memristor CNN models, Gierer–Meinhardt and Brussellator. We develop a constructive algorithm for the determination of the edge of chaos region in which complex behavior arises. Pattern formation in the edge of chaos domain is presented for both models under investigation.
Possible applications of the proposed results can be found in neurobiology. Biological systems have additional features in common with engineered systems. These similarities hint at a deeper theory that can unify our understanding of natural and artificial systems. Engineered artificial systems of life open new avenues to future innovations in pharmacy, medicine, and technology, but they also provoke societal awareness, public perception, and ethical questions about artificial life.
Author Contributions
Conceptualization, A.S. and V.I.; methodology, A.S.; software, V.I.; validation, A.S. and V.I.; formal analysis, A.S.; investigation, A.S. and V.I.; resources, A.S.; data curation, A.S.; writing—original draft preparation, A.S. and V.I.; writing—review and editing, A.S. and V.I.; visualization, V.I.; supervision, A.S.; project administration, A.S.; funding acquisition, A.S. All authors have read and agreed to the published version of the manuscript.
Funding
The first author acknowledge the support of the project KP-06-H28/7.
Data Availability Statement
Not applicable.
Acknowledgments
The first author acknowledges the access provided to the e-infrastructure of the Centre for Advanced Computing and Data Processing, with the financial support by the Grant No BG05M2OP001-1.001-0003, financed by the Science and Education for Smart Growth Operational Program (2014–2020) and co-financed by the European Union through the European structural and Investment funds.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chua, L.O. Memristor—the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Chua, L.O.; Yang, Y. Cellular neural networks: Theory. IEEE Trans. Circuits Syst. 1988, 35, 1257–1272. [Google Scholar] [CrossRef]
- Slavova, A. Cellular Neural Networks: Dynamics and Modelling. In Mathematical Modelling: Theory and Applications 16; Kluwer Academic Publishers: Philip Drive Norwell, MA, USA, 2003; 225p. [Google Scholar]
- Slavova, A.; Zafirova, Z. Harmonic balance technique for studying CNN model of differential equations. AIP Conf. Proc. 2019, 2172, 030013. [Google Scholar]
- Sun, J.; Zhao, X.; Fang, J.; Wang, Y. Autonomous memristor chaotic systems of infinite chaotic attractors and circuitry realization. Nonlinear Dyn. 2018, 94, 2879–2887. [Google Scholar] [CrossRef]
- Sun, J.; Han, J.; Wang, Y.; Liu, P. Memristor-Based Neural Network Circuit of Emotion Congruent Memory with Mental Fa-tigue and Emotion Inhibition. IEEE Trans. Biomed. Circuits Syst. 2021, 15, 606–616. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Han, J.; Liu, P.; Wang, Y. Memristor-based neural network circuit of pavlov associative memory with dual mode switching. AEU—Int. J. Electron. Commun. 2021, 129, 153552. [Google Scholar] [CrossRef]
- Chua, L.O. Local Activity is the origin of complexity. Int. J. Bifurc. Chaos 2005, 15, 3435–3456. [Google Scholar] [CrossRef] [Green Version]
- Crounse, K.R.; Chua, L.O. Methods for image processing and pattern formation in cellular neural networks: A tutorial. IEEE Trans. Circuit Syst. I 1995, 42, 583–601. [Google Scholar] [CrossRef]
- Mazumder, P.; Li, S.-R.; Ebong, I.E. Tunneling-based cellular nonlinear network architectures for image processing. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2009, 17, 487–495. [Google Scholar] [CrossRef] [Green Version]
- Hu, X.; Duan, S.; Wang, L.; Liao, X. Memristive crossbar array with applications in image processing. Sci. China Inform. Sci. 2021, 55, 461–472. [Google Scholar] [CrossRef] [Green Version]
- Ascoli, A.; Tetzlaff, R.; Menzel, S. Exploring the dynamics of real-word memristors on the basis of circuit theoretic model pre-dictions. IEEE Circuits Syst. Mag. 2018, 18, 48–76. [Google Scholar] [CrossRef]
- Ascoli, A.; Tetzlaff, R.; Kang, S.; Chua, L.O. Theoretical Foundations of Memristor Cellular Nonlinear Networks: A DRM2-based Method to Design Memcomputers with Dynamic Memristors. IEEE Trans. Circuits Syst.–I Regul. Pap. 2020, 67, 2753–2766. [Google Scholar] [CrossRef]
- Hochstetter, J.; Zhu, R.; Loeffler, A.; Diaz-Alvarez, A.; Nakayama, T.; Kuncic, Z. Avalanches and edge-of-chaos learning in neuromorphic nanowire networks. Nat. Commun. 2021, 12, 4008. [Google Scholar] [CrossRef] [PubMed]
- Slavova, A. Memristor CNN Model for Image Denoising. In Proceedings of the 26th IEEE International Conference on Elec-tronics, Circuits and Systems, ICECS, Genoa, Italy, 27–29 November 2019. [Google Scholar] [CrossRef]
- Slavova, A.; Litsyn, E. Edge of chaos in CNN models with memristor synapses. In Memristor Computing Systems; Chua, L., Tetzlaff, R., Slavova, A., Eds.; Springer Nature: Cham, Switzerland, 2022. [Google Scholar]
- Vidyasagar, M. Nonlinear Systems Analysis, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- Gierer, A.; Meinhardt, H. A theory of biological pattern formation. Kybernetik 1972, 12, 30–39. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Slavova, A.; Ignatov, V. Universal Cellular Computing on the Edge of Chaos. In Proceedings of the 10th IEEE International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 5–7 July 2021. [Google Scholar]
- Britton, N.F. Reaction-Diffusion Equations and Their Applications to Biology; Academic Press: New York, NY, USA, 1986. [Google Scholar]
- Dogaru, R.; Chua, L.O. Edge of chaos and local activity domain of the Brusselator CNN. Int. J. Bifurc. Chaos 1998, 86, 1107–1130. [Google Scholar] [CrossRef]
- Slavova, A.; Tetzlaff, R. Edge of chaos in reaction-diffusion CNN model. Open Math. 2017, 15, 21–29. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).