Topology Adaptive Graph Estimation in High Dimensions
Abstract
:1. Introduction
Framework and Notation
2. Methodology
| Algorithm 1:Neighborhood selection with Lasso. |
Data: , ; Result: , ; Initialize a matrix ; for to p do Compute according to (2); Update the kth column of the matrix C according to ; end Set the estimated sets to and ; |
| Algorithm 2: GTREX. |
Data: , , ; Result: , ; Initialize all frequencies ; for to p do for to b do Generate sequential bootstrap sample of X; Compute according to (3); Update the frequencies for the edges adjacent to node k for to p do if then ; end end end end Set the estimated set of edges to ; |
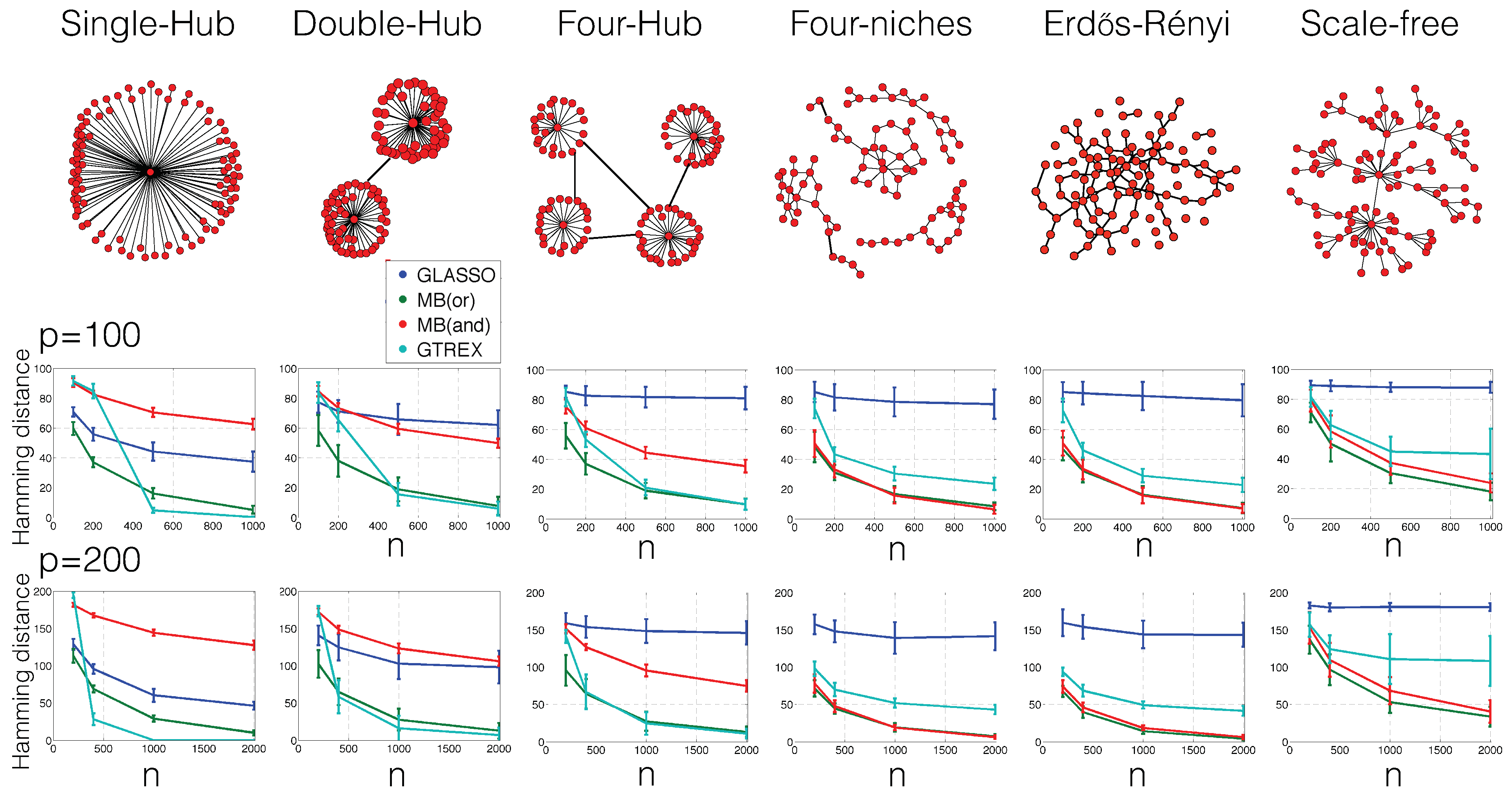
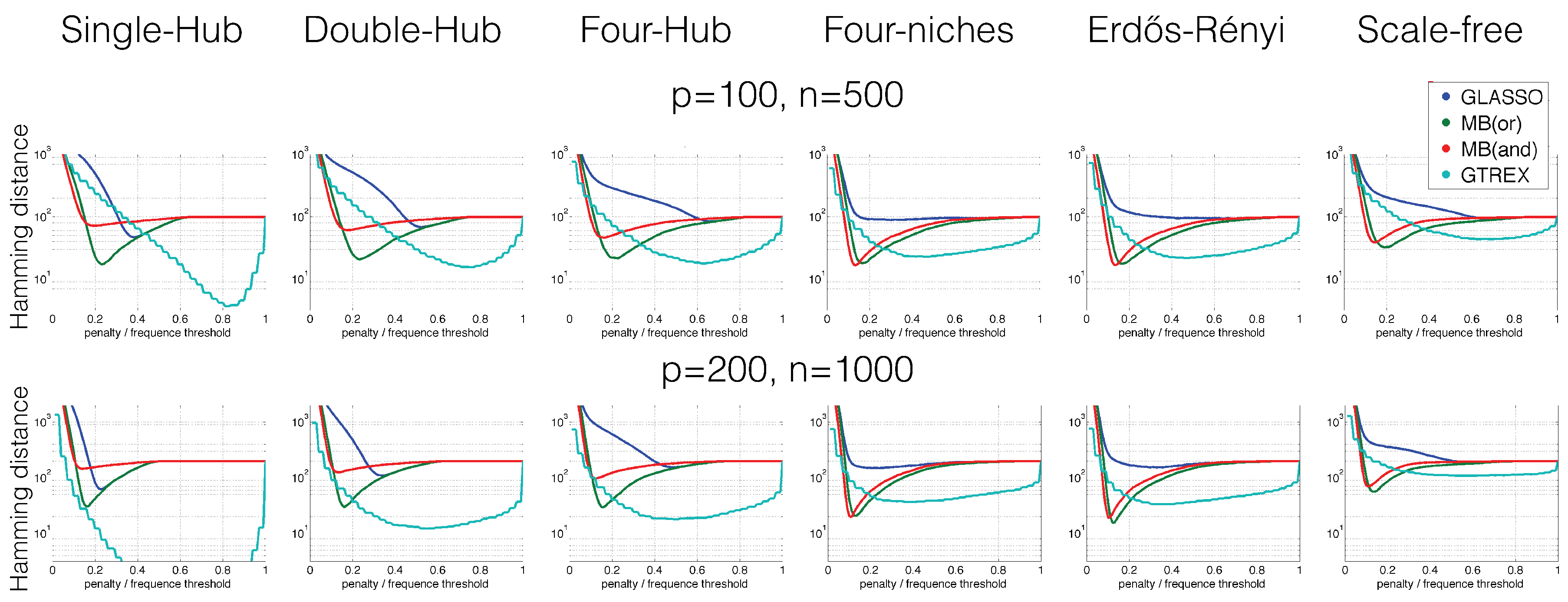
3. Experimental Scenarios
- Single-hub graph:The set of edges is first set to . Until the number of edges s is exhausted, edges are then uniformly at random added to ;
- Double-hub graphThe set of edges is first set to . Until the number of edges s is exhausted, edges are then uniformly at random added to ;
- Four-hub graphThe set of edges is first set to . Until the number of edges s is exhausted, edges are then uniformly at random added to ;
- Four-niche graph:Within each set of nodes , , , edges are uniformly selected at random and added to the set of edges. Until the number of edges s is exhausted, edges (connecting any nodes of the entire graph) are then uniformly at random added to ;
- Erdos–Rényi graph:Until the number of edges s is exhausted, edges are uniformly at random added to ;
- Scale-free graph:First, a set of edges is constructed with the preferential attachment algorithm [22]: The set of edges is first set to . For each node , an edge is then iteratively added to until the number of edges s is exhausted. The probability of selecting the edge is set proportional to the degree of node (that is, the number of edges at node j) in the current set of edges. One could also change this probability; for example, one could weight the degree more heavily, that is put more emphasis on nodes that already have edges connected to them. In general, the more weight on the degree, the more the graphs look the same as hub graphs and, therefore, the better the performance of our method relative to GLasso and MB.
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lederer, J. Fundamentals of High-Dimensional Statistics: With Exercises and R Labs; Springer Texts in Statistics: Heidelberg, Germany, 2022. [Google Scholar]
- Wille, A.; Zimmermann, P.; Vranová, E.; Fürholz, A.; Laule, O.; Bleuler, S.; Hennig, L.; Prelić, A.; von Rohr, P.; Thiele, L.; et al. Sparse graphical Gaussian modeling of the isoprenoid gene network in Arabidopsis thaliana. Genome Biol. 2004, 5, R92. [Google Scholar] [CrossRef] [Green Version]
- Friedman, N. Inferring Cellular Networks Using Probabilistic Graphical Models. Science 2004, 303, 799–805. [Google Scholar] [CrossRef]
- Jones, D.; Buchan, D.; Cozzetto, D.; Pontil, M. PSICOV: Precise structural contact prediction using sparse inverse covariance estimation on large multiple sequence alignments. Bioinformatics 2012, 28, 184–190. [Google Scholar] [CrossRef] [Green Version]
- Kurtz, Z.; Müller, C.; Miraldi, E.; Littman, D.; Blaser, M.; Bonneau, R. Sparse and Compositionally Robust Inference of Microbial Ecological Networks. arXiv 2014, arXiv:1408.4158. [Google Scholar] [CrossRef] [Green Version]
- Meinshausen, N.; Bühlmann, P. High Dimensional Graphs and Variable Selection with the Lasso. Ann. Stat. 2006, 34, 1436–1462. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, O.; El Ghaoui, L.; D’Aspremont, A. Model selection through sparse maximum likelihood estimation for multivariate gaussian or binary data. J. Mach. Learn. Res. 2008, 9, 485–516. [Google Scholar]
- Yuan, M.; Lin, Y. Model selection and estimation in the Gaussian graphical model. Biometrika 2007, 94, 19–35. [Google Scholar] [CrossRef] [Green Version]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 2008, 9, 432–441. [Google Scholar] [CrossRef] [Green Version]
- Hsieh, C.J.; Sustik, M.; Dhillon, I.; Ravkiumar, P. Sparse inverse covariance matrix estimation using quadratic approximation. NIPS 2011, 24, 1–18. [Google Scholar]
- Ravikumar, P.; Wainwright, M.; Lafferty, J. High-dimensional Ising model selection using L1-regularized logistic regression. Ann. Stat. 2010, 38, 1287–1319. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Lafferty, J.; Wasserman, L. The Nonparanormal: Semiparametric Estimation of High Dimensional Undirected Graphs. J. Mach. Learn. Res. 2009, 10, 2295–2328. [Google Scholar]
- Lam, C.; Fan, J. Sparsistency and Rates of Convergence in Large Covariance Matrix Estimation. Ann. Stat. 2009, 37, 4254–4278. [Google Scholar] [CrossRef] [PubMed]
- Ravikumar, P.; Wainwright, M.; Raskutti, G.; Yu, B. High-dimensional covariance estimation by minimizing ℓ1-penalized log-determinant divergence. Electron. J. Stat. 2011, 5, 935–980. [Google Scholar] [CrossRef]
- Liu, Q.; Ihler, A. Learning scale free networks by reweighted l1 regularization. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011. [Google Scholar]
- Liu, H.; Wang, L. Tiger: A tuning-insensitive approach for optimally estimating gaussian graphical models. arXiv 2012, arXiv:1209.2437. [Google Scholar] [CrossRef]
- Liu, H.; Roeder, K.; Wasserman, L. Stability approach to regularization selection (stars) for high dimensional graphical models. NIPS. 2010. Available online: https://proceedings.neurips.cc/paper/2010/file/301ad0e3bd5cb1627a2044908a42fdc2-Paper.pdf (accessed on 1 March 2022).
- Lederer, J.; Müller, C. Don’t fall for tuning parameters: Tuning-free variable selection in high dimensions with the TREX. arXiv 2014, arXiv:1404.0541. [Google Scholar]
- De Canditiis, D.; Guardasole, A. Learning Gaussian Graphical Models by symmetric parallel regression technique. arXiv 2019, arXiv:1902.03116. [Google Scholar]
- Meinshausen, N.; Bühlmann, P. Stability selection. J. R. Stat. Soc. Ser. (Stat. Methodol.) 2010, 72, 417–473. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [Green Version]
- Bien, J.; Gaynanova, I.; Lederer, J.; Müller, C.L. Non-convex global minimization and false discovery rate control for the TREX. J. Comput. Graph. Stat. 2018, 27, 23–33. [Google Scholar] [CrossRef]
- Combettes, P.; Müller, C. Perspective functions: Proximal calculus and applications in high-dimensional statistics. J. Math. Anal. Appl. 2018, 457, 1283–1306. [Google Scholar] [CrossRef]
- Chételat, D.; Lederer, J.; Salmon, J. Optimal two-step prediction in regression. Electron. J. Stat. 2017, 11, 2519–2546. [Google Scholar] [CrossRef]
- Li, W.; Lederer, J. Tuning parameter calibration for ℓ1-regularized logistic regression. J. Stat. Plan. Inference 2019, 202, 80–98. [Google Scholar] [CrossRef]
- Bien, J.; Gaynanova, I.; Lederer, J.; Müller, C.L. Prediction error bounds for linear regression with the TREX. Test 2019, 28, 451–474. [Google Scholar] [CrossRef] [Green Version]
| , | ||
| Method | P | R |
| GLasso | 0.99 | 0.35 |
| MB(or) | 0.99 | 0.48 |
| MB(and) | 0.99 | 0.49 |
| GTREX | 0.99 | 0.13 |
| , | ||
| Method | P | R |
| GLasso | 0.99 | 0.59 |
| MB(or) | 0.99 | 0.87 |
| MB(and) | 0.99 | 0.92 |
| GTREX | 1.00 | 0.99 |
| , | ||
| Method | P | R |
| GLasso | 1.00 | 0.25 |
| MB(or) | 1.00 | 0.30 |
| MB(and) | 1.00 | 0.29 |
| GTREX | 0.99 | 0.05 |
| , | ||
| Method | P | R |
| GLasso | 1.00 | 0.44 |
| MB(or) | 1.00 | 0.58 |
| MB(and) | 1.00 | 0.59 |
| GTREX | 1.00 | 0.60 |
| , | ||
| Method | P | R |
| GLasso | 1.00 | 0.17 |
| MB(or) | 1.00 | 0.55 |
| MB(and) | 0.99 | 0.59 |
| GTREX | 0.99 | 0.26 |
| , | ||
| Method | P | R |
| GLasso | 0.99 | 0.19 |
| MB(or) | 1.00 | 0.86 |
| MB(and) | 1.00 | 0.93 |
| GTREX | 1.00 | 0.80 |
| , | ||
| Method | P | R |
| GLasso | 1.00 | 0.15 |
| MB(or) | 1.00 | 0.36 |
| MB(and) | 1.00 | 0.40 |
| GTREX | 1.00 | 0.20 |
| , | ||
| Method | P | R |
| GLasso | 0.99 | 0.17 |
| MB(or) | 1.00 | 0.54 |
| MB(and) | 1.00 | 0.57 |
| GTREX | 1.00 | 0.53 |
| , | ||
| Method | P | R |
| GLasso | 1.00 | 0.31 |
| MB(or) | 1.00 | 0.61 |
| MB(and) | 0.99 | 0.69 |
| GTREX | 0.99 | 0.36 |
| , | ||
| Method | P | R |
| GLasso | 0.99 | 0.42 |
| MB(or) | 1.00 | 0.89 |
| MB(and) | 1.00 | 0.94 |
| GTREX | 1.00 | 0.71 |
| , | ||
| Method | P | R |
| GLasso | 1.00 | 0.30 |
| MB(or) | 1.00 | 0.43 |
| MB(and) | 1.00 | 0.46 |
| GTREX | 1.00 | 0.34 |
| , | ||
| Method | P | R |
| GLasso | 0.99 | 0.42 |
| MB(or) | 1.00 | 0.57 |
| MB(and) | 1.00 | 0.58 |
| GTREX | 1.00 | 0.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lederer, J.; Müller, C.L. Topology Adaptive Graph Estimation in High Dimensions. Mathematics 2022, 10, 1244. https://doi.org/10.3390/math10081244
Lederer J, Müller CL. Topology Adaptive Graph Estimation in High Dimensions. Mathematics. 2022; 10(8):1244. https://doi.org/10.3390/math10081244
Chicago/Turabian StyleLederer, Johannes, and Christian L. Müller. 2022. "Topology Adaptive Graph Estimation in High Dimensions" Mathematics 10, no. 8: 1244. https://doi.org/10.3390/math10081244
APA StyleLederer, J., & Müller, C. L. (2022). Topology Adaptive Graph Estimation in High Dimensions. Mathematics, 10(8), 1244. https://doi.org/10.3390/math10081244






