Exact Solution of Nonlinear Behaviors of Imperfect Bioinspired Helicoidal Composite Beams Resting on Elastic Foundations
Abstract
:1. Introduction
2. Problem Formulation
3. Bending Problem
- (a)
- S–S boundary conditions
- (b)
- C–C boundary conditions
4. Buckling Problem
4.1. Buckling of Perfect Beam
- (a)
- S–S boundary conditions
- (b)
- C–C boundary conditions
4.2. Buckling of Imperfect Beam
- (c)
- S–S boundary conditions
- (d)
- C–C boundary conditions
5. Numerical Analysis
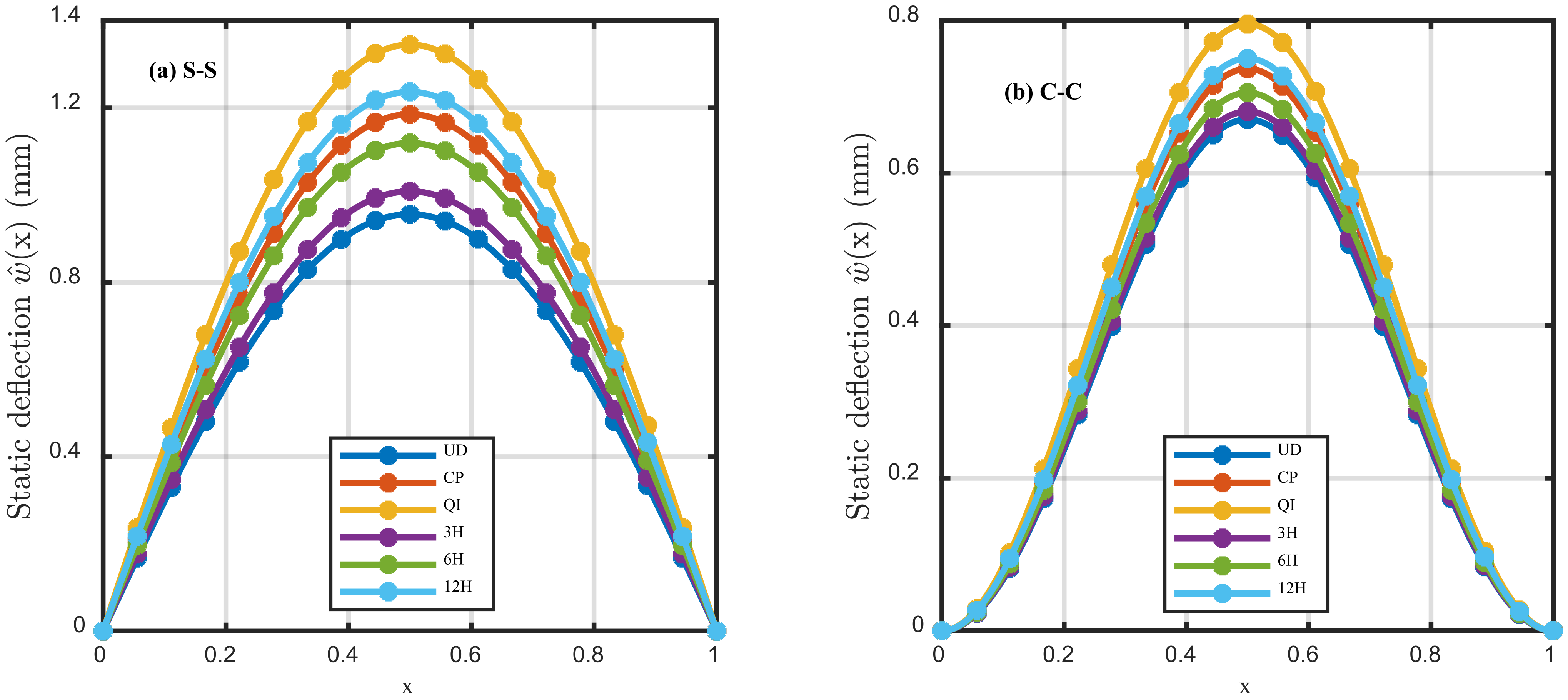
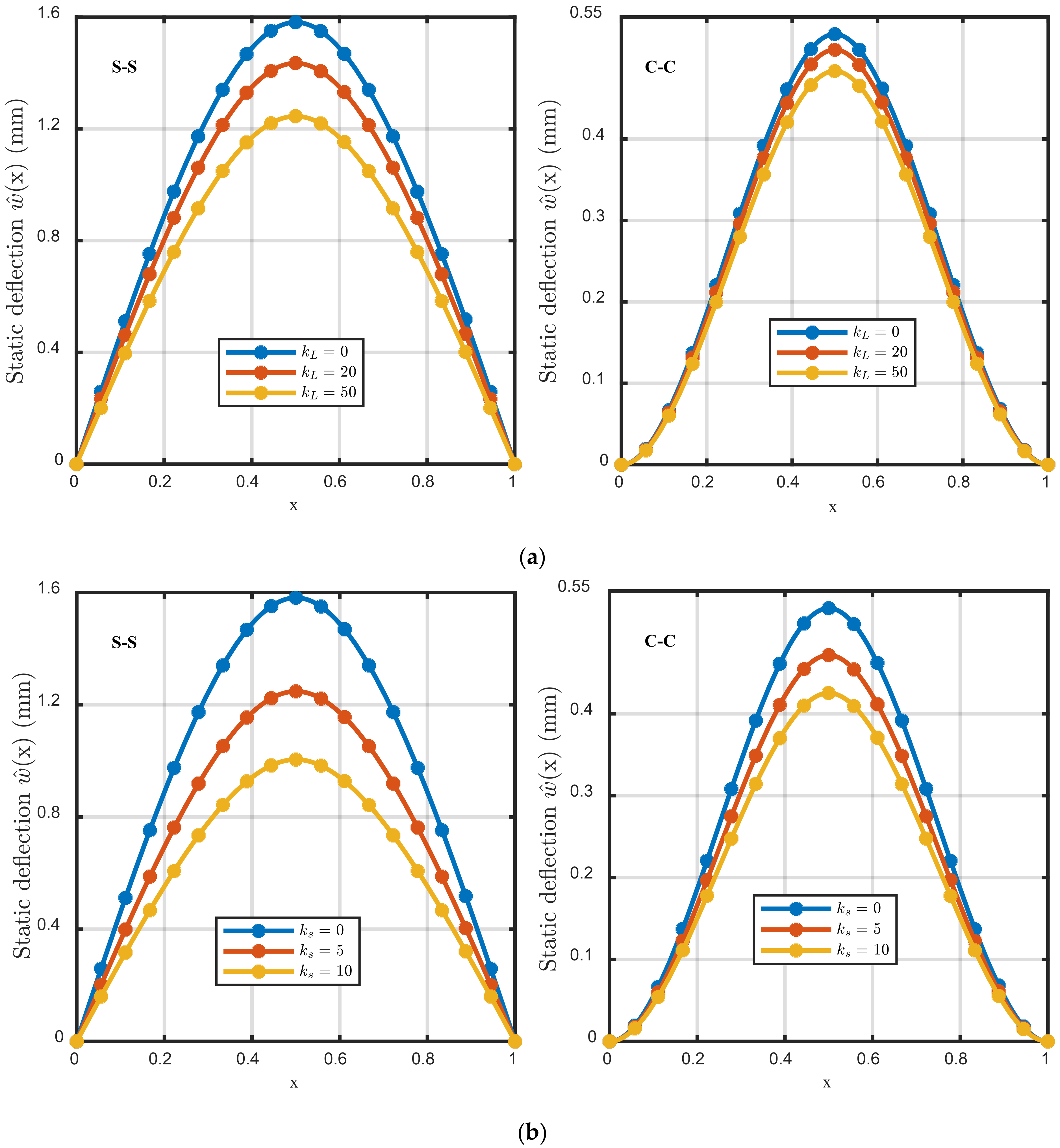
5.1. Results of Nonlinear Bending
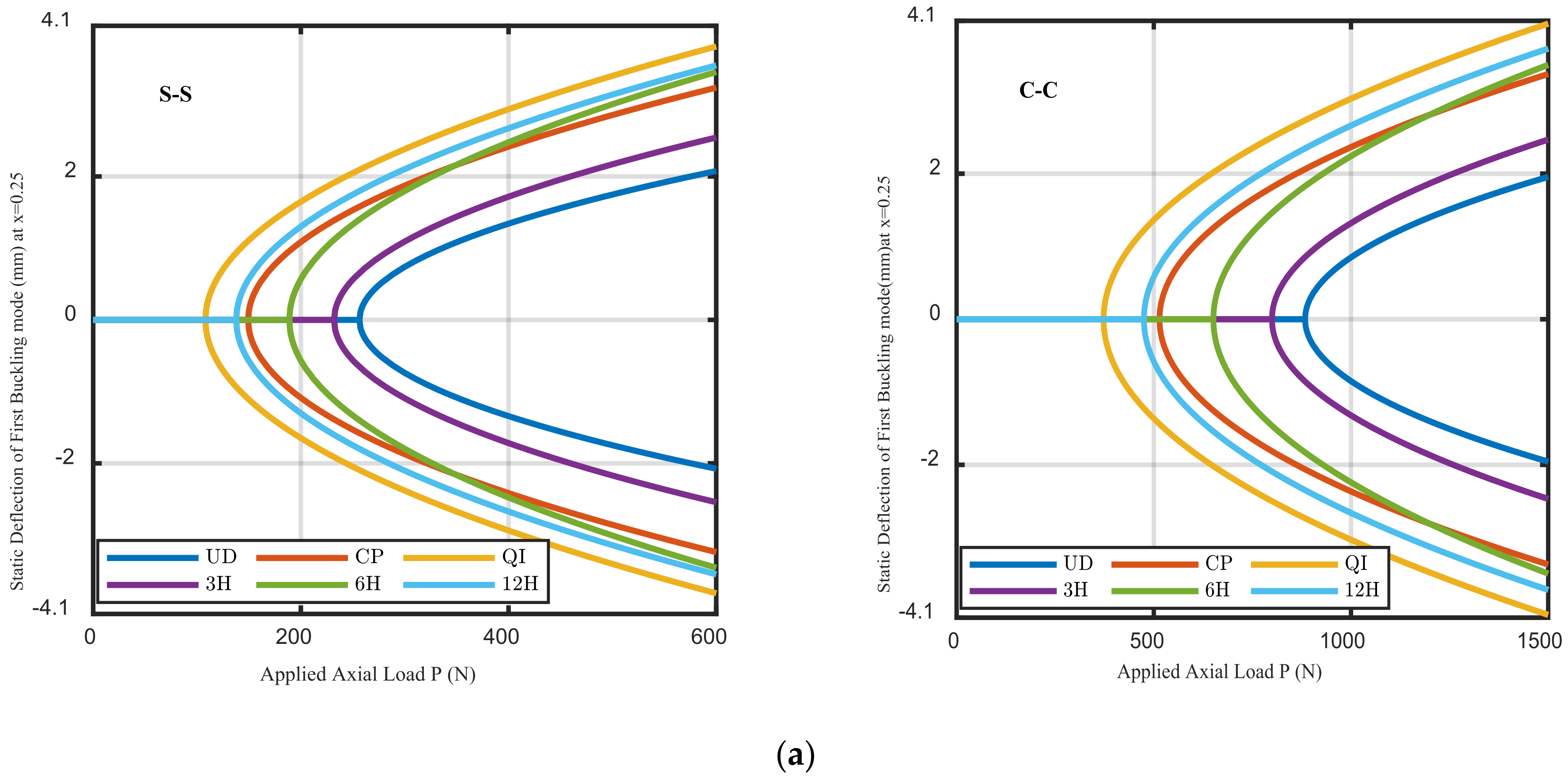
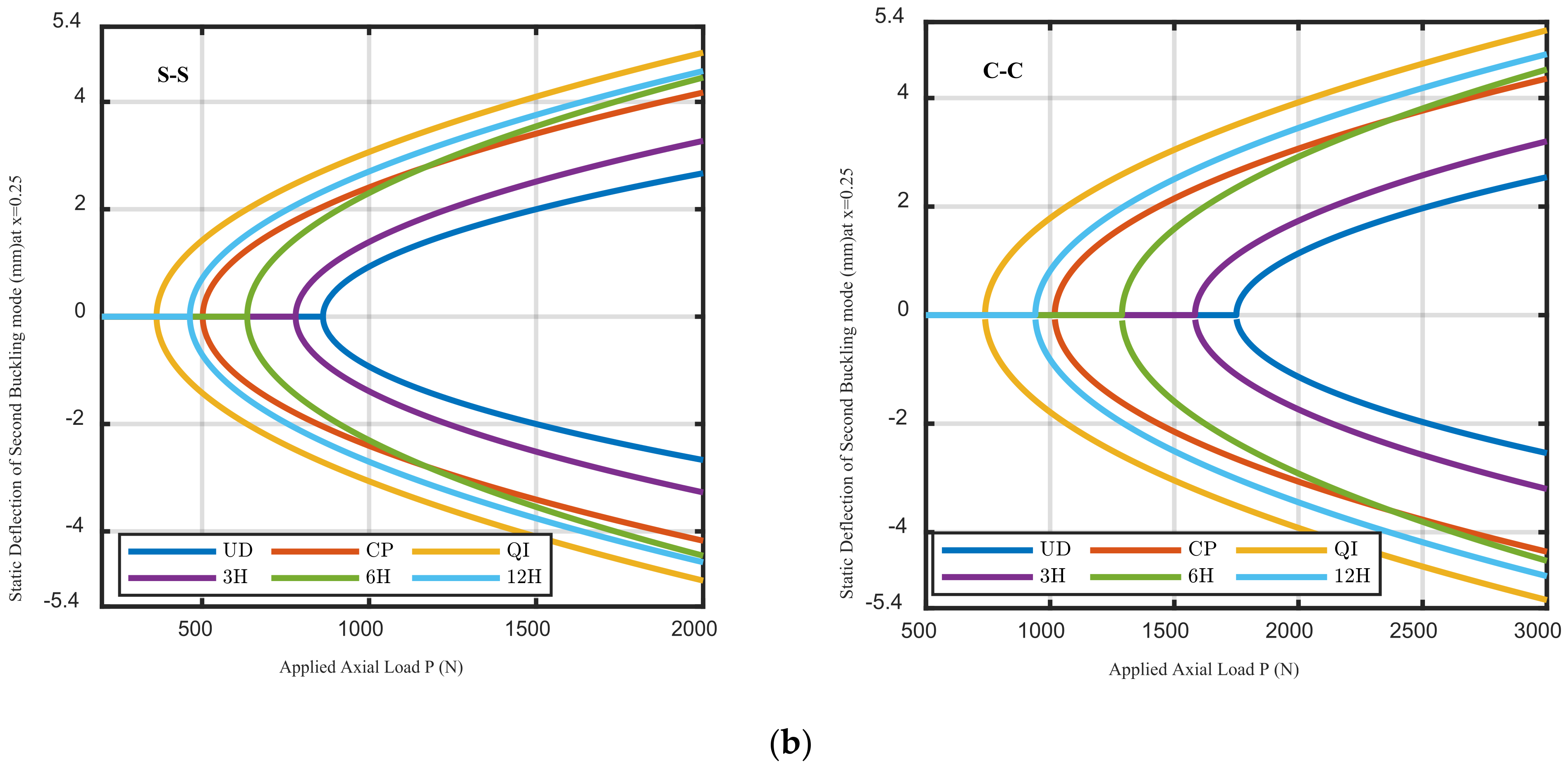
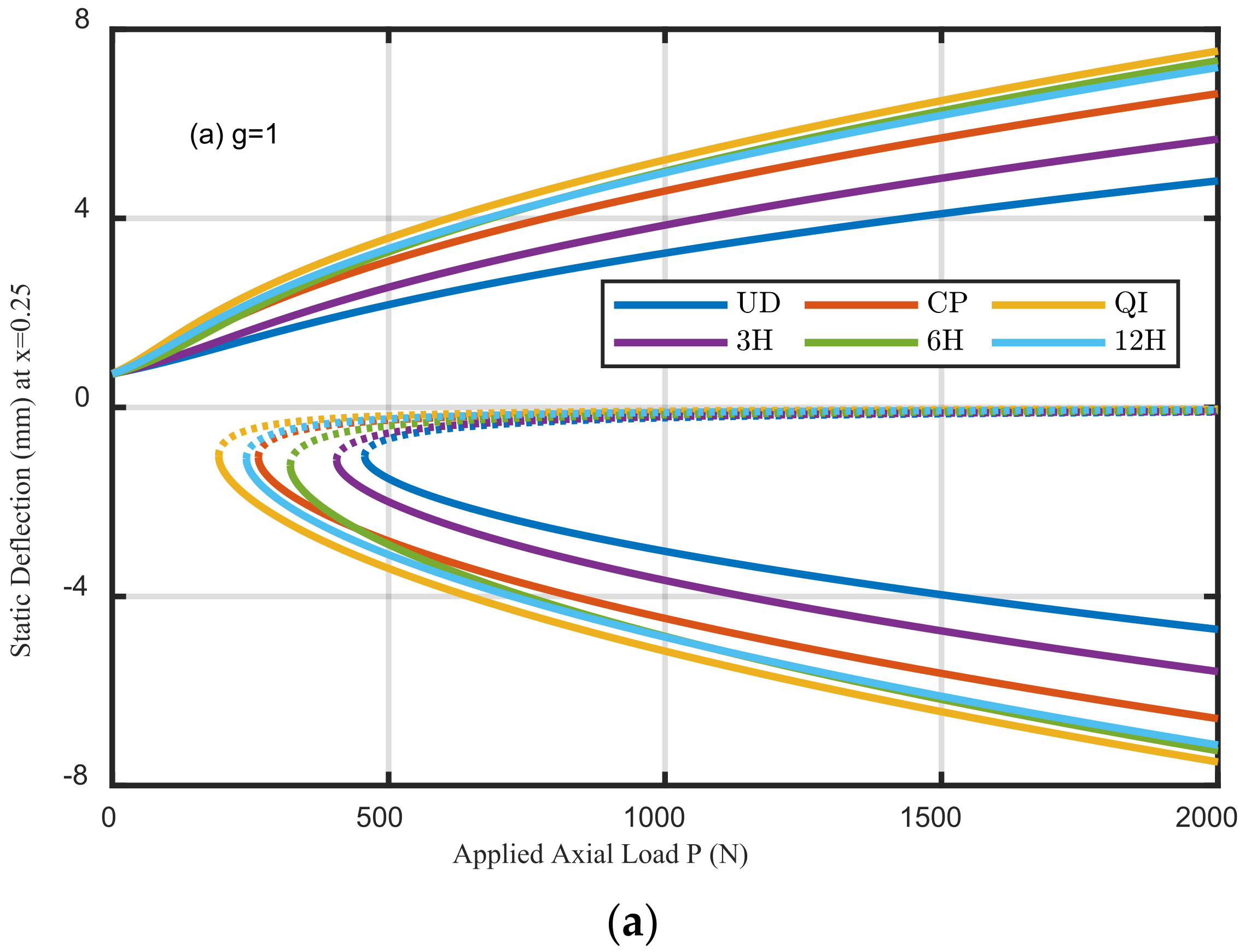
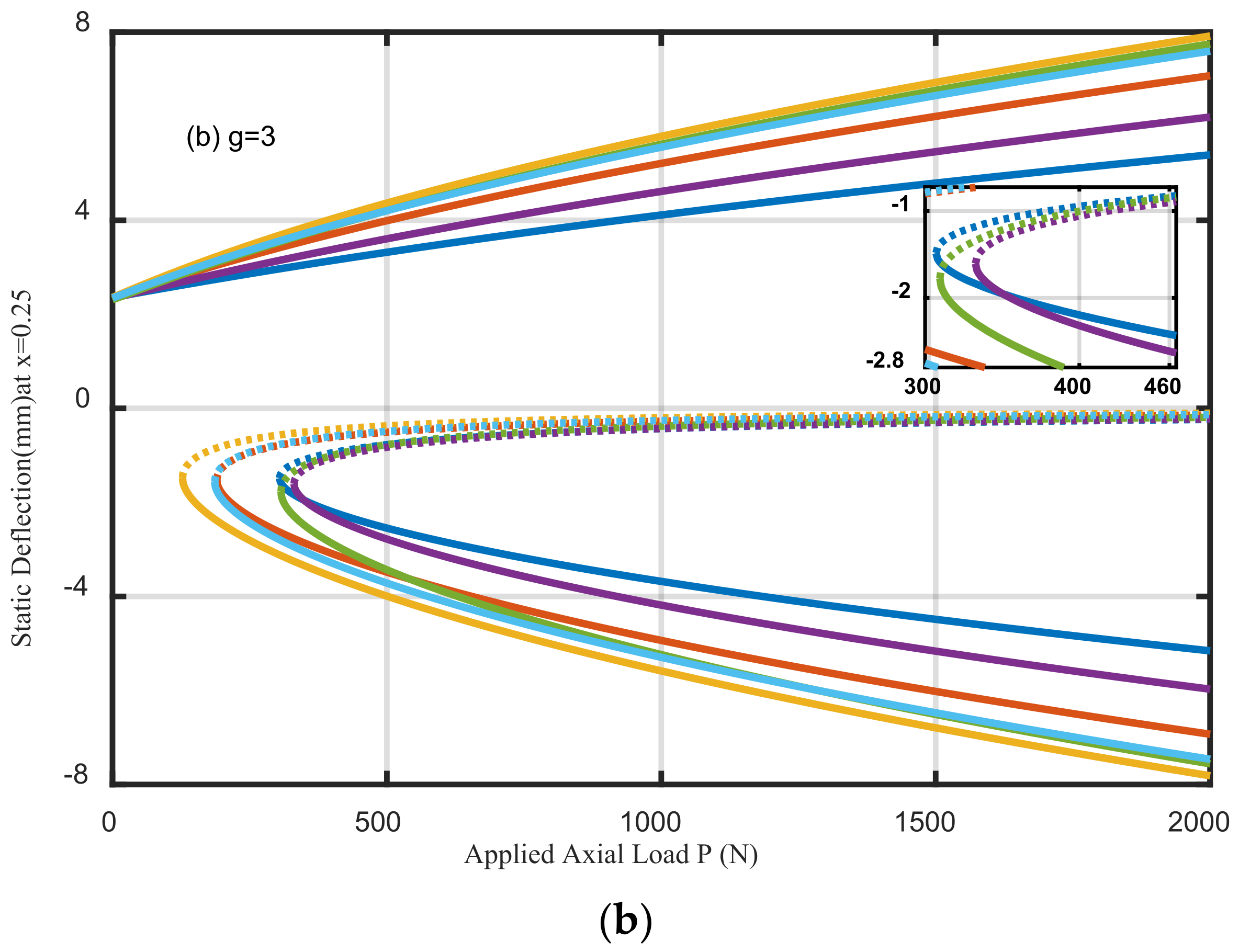
5.2. Buckling Analysis
6. Concluding Remarks
- The nonlinear bending deflection due to point load is highly dependent on the application position of the load.
- The hardening structural responses are associated with increasing the elastic foundation constants.
- The buckling strength is improved with an increase in the amplitude of initial imperfection; next, the critical values are continuously decreased with an increase in the initial imperfection amplitude.
- For larger values of amplitude of imperfection, the helicoidal composite beams can enhance the critical buckling loads.
- The layup configurations have a great influence on the nonlinear bending and buckling responses of perfect and imperfect beams.
- The proposed model can be exploited broadly in various engineering applications, such as airplane wings, helicopter blades, wind turbine blades, as well as many others in the aerospace, mechanical, and civil industries.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Melaibari, A.; Wagih, A.; Basha, M.; Kabeel, A.; Lubineau, G.; Eltaher, M. Bio-inspired composite laminate design with improved out-of-plane strength and ductility. Compos. Part A Appl. Sci. Manuf. 2021, 144, 106362. [Google Scholar] [CrossRef]
- Chen, B.; Peng, X.; Cai, C.; Niu, H.; Wu, X. Helicoidal microstructure of Scarabaei cuticle and biomimetic research. Mater. Sci. Eng. A 2006, 423, 237–242. [Google Scholar] [CrossRef]
- Ginzburg, D.; Pinto, F.; Iervolino, O.; Meo, M. Damage tolerance of bio-inspired helicoidal composites under low velocity impact. Compos. Struct. 2017, 161, 187–203. [Google Scholar] [CrossRef] [Green Version]
- Apichattrabrut, T.; Ravi-Chandar, K. Helicoidal Composites. Mech. Adv. Mater. Struct. 2006, 13, 61–76. [Google Scholar] [CrossRef]
- Cheng, L.; Thomas, A.; Glancey, J.L.; Karlsson, A.M. Mechanical behavior of bio-inspired laminated composites. Compos. Part A Appl. Sci. Manuf. 2011, 42, 211–220. [Google Scholar] [CrossRef] [Green Version]
- Morozov, E.; Lopatin, A.; Nesterov, V. Finite-element modelling and buckling analysis of anisogrid composite lattice cylindrical shells. Compos. Struct. 2011, 93, 308–323. [Google Scholar] [CrossRef]
- Kacar, I.; Yildirim, V. Free vibration/buckling analyses of noncylindrical initially compressed helical composite springs. Mech. Based Des. Struct. Mach. 2016, 44, 340–353. [Google Scholar] [CrossRef]
- Sabah, S.A.; Kueh, A.; Al-Fasih, M. Comparative low-velocity impact behavior of bio-inspired and conventional sandwich composite beams. Compos. Sci. Technol. 2017, 149, 64–74. [Google Scholar] [CrossRef]
- Sabah, S.A.; Kueh, A.; Bunnori, N.M. Failure mode maps of bio-inspired sandwich beams under repeated low-velocity impact. Compos. Sci. Technol. 2019, 182, 107785. [Google Scholar] [CrossRef]
- She, G.L.; Ren, Y.R.; Xiao, W.S.; Liu, H. Study on thermal buckling and post-buckling behaviors of FGM tubes resting on elastic foundations. Struct. Eng. Mech. Int. J. 2018, 66, 729–736. [Google Scholar] [CrossRef]
- She, G.-L.; Ren, Y.-R.; Yan, K.-M. On snap-buckling of porous FG curved nanobeams. Acta Astronaut. 2019, 161, 475–484. [Google Scholar] [CrossRef]
- She, G.L.; Liu, H.B.; Karami, B. On resonance behavior of porous FG curved nanobeams. Steel Compos. Struct. 2020, 36, 179–186. [Google Scholar] [CrossRef]
- Eltaher, M.; Mohamed, S.; Melaibari, A. Static stability of a unified composite beams under varying axial loads. Thin-Walled Struct. 2020, 147, 106488. [Google Scholar] [CrossRef]
- Qian, F.; Hajj, M.R.; Zuo, L. Bio-inspired bi-stable piezoelectric harvester for broadband vibration energy harvesting. Energy Convers. Manag. 2020, 222, 113174. [Google Scholar] [CrossRef]
- Kueh, A.; Siaw, Y. Impact resistance of bio-inspired sandwich beam with side-arched and honeycomb dual-core. Compos. Struct. 2021, 275, 114439. [Google Scholar] [CrossRef]
- Fani, M.; Taheri-Behrooz, F. Analytical study of thermal buckling and post-buckling behavior of composite beams reinforced with SMA by Reddy Bickford theory. J. Intell. Mater. Syst. Struct. 2021, 33, 121–135. [Google Scholar] [CrossRef]
- Lu, L.; She, G.-L.; Guo, X. Size-dependent postbuckling analysis of graphene reinforced composite microtubes with geometrical imperfection. Int. J. Mech. Sci. 2021, 199, 106428. [Google Scholar] [CrossRef]
- Hosseini, S.M.H.; Arvin, H. Thermo-rotational buckling and post-buckling analyses of rotating functionally graded microbeams. Int. J. Mech. Mater. Des. 2021, 17, 55–72. [Google Scholar] [CrossRef]
- Sojobi, A.; Liew, K. Multi-objective optimization of high performance bio-inspired prefabricated composites for sustainable and resilient construction. Compos. Struct. 2021, 279, 114732. [Google Scholar] [CrossRef]
- Melaibari, A.; Daikh, A.A.; Basha, M.; Abdalla, A.W.; Othman, R.; Almitani, K.H.; Hamed, M.A.; Abdelrahman, A.; Eltaher, M.A. Free Vibration of FG-CNTRCs Nano-Plates/Shells with Temperature-Dependent Properties. Mathematics 2022, 10, 583. [Google Scholar] [CrossRef]
- Petyt, M.; Fleischer, C. Free vibration of a curved beam. J. Sound Vib. 1971, 18, 17–30. [Google Scholar] [CrossRef]
- Wang, D.; Abdalla, M.M. Global and local buckling analysis of grid-stiffened composite panels. Compos. Struct. 2015, 119, 767–776. [Google Scholar] [CrossRef]
- Li, Z.-M.; Qiao, P. Buckling and postbuckling behavior of shear deformable anisotropic laminated beams with initial geometric imperfections subjected to axial compression. Eng. Struct. 2015, 85, 277–292. [Google Scholar] [CrossRef]
- Wu, H.; Yang, J.; Kitipornchai, S. Imperfection sensitivity of postbuckling behaviour of functionally graded carbon nanotube-reinforced composite beams. Thin-Walled Struct. 2016, 108, 225–233. [Google Scholar] [CrossRef]
- Wu, H.; Kitipornchai, S.; Yang, J. Thermo-electro-mechanical postbuckling of piezoelectric FG-CNTRC beams with geometric imperfections. Smart Mater. Struct. 2016, 25, 095022. [Google Scholar] [CrossRef]
- Wu, H.; Kitipornchai, S.; Yang, J. Imperfection sensitivity of thermal post-buckling behaviour of functionally graded carbon nanotube-reinforced composite beams. Appl. Math. Model. 2017, 42, 735–752. [Google Scholar] [CrossRef]
- Mohamed, N.; Eltaher, M.A.; Mohamed, S.; Seddek, L. Numerical analysis of nonlinear free and forced vibrations of buckled curved beams resting on nonlinear elastic foundations. Int. J. Non-Linear Mech. 2018, 101, 157–173. [Google Scholar] [CrossRef]
- Eltaher, M.; Mohamed, N.; Mohamed, S.; Seddek, L. Periodic and nonperiodic modes of postbuckling and nonlinear vibration of beams attached to nonlinear foundations. Appl. Math. Model. 2019, 75, 414–445. [Google Scholar] [CrossRef]
- Mohamed, N.; Eltaher, M.A.; Mohamed, S.A.; Seddek, L.F. Energy equivalent model in analysis of postbuckling of imperfect carbon nanotubes resting on nonlinear elastic foundation. Struct. Eng. Mech. 2019, 70, 737–750. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Mohamed, N.; Mohamed, S.; Seddek, L.F. Postbuckling of Curved Carbon Nanotubes Using Energy Equivalent Model. J. Nano Res. 2019, 57, 136–157. [Google Scholar] [CrossRef]
- Dabbagh, A.; Rastgoo, A.; Ebrahimi, F. Post-buckling analysis of imperfect multi-scale hybrid nanocomposite beams rested on a nonlinear stiff substrate. Eng. Comput. 2020, 38, 301–314. [Google Scholar] [CrossRef]
- Emam, S.; Lacarbonara, W. Buckling and postbuckling of extensible, shear-deformable beams: Some exact solutions and new insights. Int. J. Non-Linear Mech. 2021, 129, 103667. [Google Scholar] [CrossRef]
- Zhu, B.; Chen, X.-C.; Guo, Y.; Li, Y.-H. Static and dynamic characteristics of the post-buckling of fluid-conveying porous functionally graded pipes with geometric imperfections. Int. J. Mech. Sci. 2021, 189, 105947. [Google Scholar] [CrossRef]
- Xu, X.; Karami, B.; Shahsavari, D. Time-dependent behavior of porous curved nanobeam. Int. J. Eng. Sci. 2021, 160, 103455. [Google Scholar] [CrossRef]
- Mohamed, N.; Mohamed, S.A.; Eltaher, M.A. Buckling and post-buckling behaviors of higher order carbon nanotubes using energy-equivalent model. Eng. Comput. 2021, 37, 2823–2836. [Google Scholar] [CrossRef]
- Golewski, G.L. On the special construction and materials conditions reducing the negative impact of vibrations on concrete structures. Mater. Today Proc. 2021, 45, 4344–4348. [Google Scholar] [CrossRef]
- Zhang, Z.; Pei, K.; Wu, H.; Sun, M.; Chai, H.; Wu, H.; Jiang, S. Bistable characteristics of hybrid composite laminates embedded with bimetallic strips. Compos. Sci. Technol. 2021, 212, 108880. [Google Scholar] [CrossRef]
- Zhang, P.; Qing, H. Exact solutions for size-dependent bending of Timoshenko curved beams based on a modified nonlocal strain gradient model. Acta Mech. 2020, 231, 5251–5276. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Chen, Y.; Tan, Y.; Cao, H. Bending, buckling and free vibration of an axially loaded timoshenko beam with transition parameter: Direction of axial force. Int. J. Mech. Sci. 2020, 176, 105545. [Google Scholar] [CrossRef]
- Nazmul, I.; Devnath, I. Exact analytical solutions for bending of bi-directional functionally graded nanobeams by the nonlocal beam theory using the Laplace transform. Forces Mech. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Tang, Y.; Qing, H. Elastic buckling and free vibration analysis of functionally graded Timoshenko beam with nonlocal strain gradient integral model. Appl. Math. Model. 2021, 96, 657–677. [Google Scholar] [CrossRef]
- Emam, S.A. A static and dynamic analysis of the postbuckling of geometrically imperfect composite beams. Compos. Struct. 2009, 90, 247–253. [Google Scholar] [CrossRef]
- Boutahar, Y.; Lebaal, N.; Bassir, D. A Refined Theory for Bending Vibratory Analysis of Thick Functionally Graded Beams. Mathematics 2021, 9, 1422. [Google Scholar] [CrossRef]
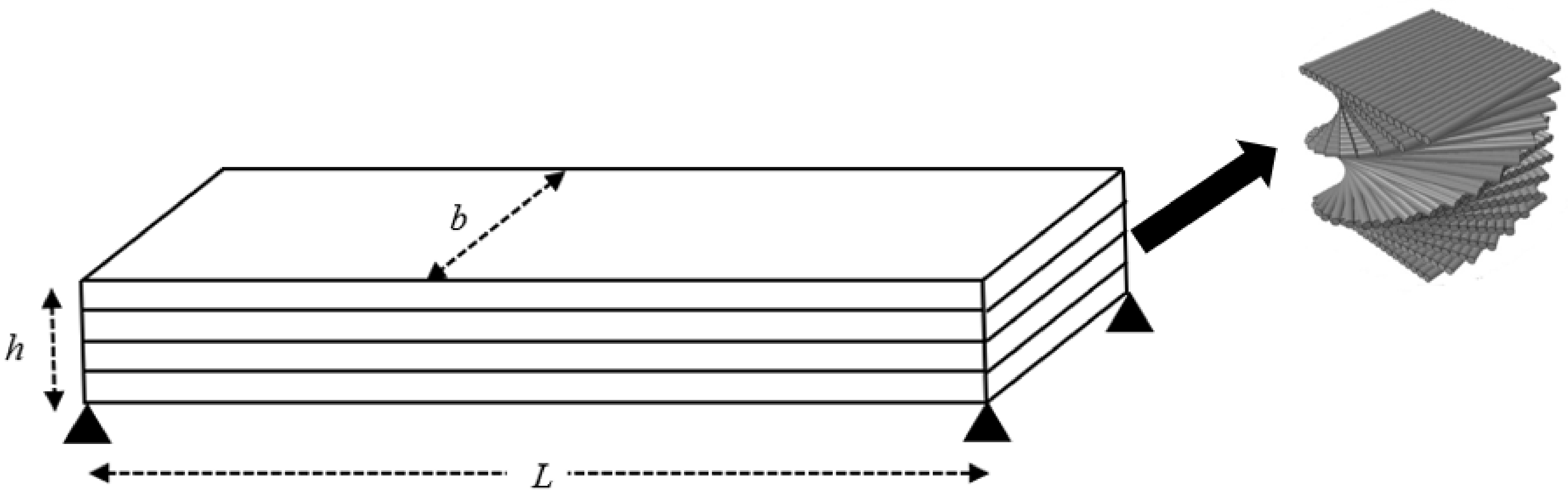


| Designation | Stacking Sequence | Description |
|---|---|---|
| UD | Unidirectional | |
| CP | Cross ply-symmetric | |
| QI | Quasi isotropic-symmetric | |
| 3H | Helicoidal (3°)-symmetric | |
| 6H | Helicoidal (6°)-symmetric | |
| 12H | Helicoidal (12°)-symmetric |
| Laminate | ||||||
|---|---|---|---|---|---|---|
| (a) S–S | ||||||
| UD | 256.4084 | 861.8419 | 1919.4286 | 321.9250 | 878.2210 | 1926.7082 |
| CP | 149.2720 | 501.7343 | 1117.4243 | 187.4135 | 511.2696 | 1121.6623 |
| QI | 108.1414 | 363.4857 | 809.5277 | 135.7733 | 370.3937 | 812.5979 |
| 3H | 232.0188 | 779.8635 | 1736.8525 | 291.3035 | 794.6846 | 1743.4397 |
| 6H | 188.9145 | 634.9810 | 1414.1813 | 237.1854 | 647.0487 | 1419.5447 |
| 12H | 137.8104 | 463.2093 | 1031.6245 | 173.0232 | 472.0125 | 1035.5370 |
| (b) C–C | ||||||
| UD | 883.6214 | 1749.6677 | 3411.9220 | 932.4433 | 1763.0029 | 3424.4339 |
| CP | 514.4136 | 1018.5955 | 1986.3019 | 542.8360 | 1026.3588 | 1993.5860 |
| QI | 372.6714 | 737.9303 | 1438.9936 | 393.2622 | 743.5545 | 1444.2706 |
| 3H | 799.5713 | 1583.2392 | 3087.3799 | 843.7493 | 1595.3060 | 3098.7017 |
| 6H | 651.0276 | 1289.1062 | 2513.8087 | 686.9981 | 1298.9312 | 2523.0271 |
| 12H | 474.9151 | 940.3841 | 1833.7866 | 501.1551 | 947.5513 | 1840.5113 |
| UD | CP | QI | 3H | 6H | 12H | |
|---|---|---|---|---|---|---|
| 358.9829 | 207.2039 | 151.5052 | 316.3949 | 249.3464 | 189.6495 | |
| 412.8145 | 238.8817 | 174.1865 | 366.2812 | 289.9060 | 219.1237 | |
| 402.0357 | 237.3041 | 169.3567 | 376.7940 | 312.7668 | 221.6148 | |
| 260.9025 | 164.7909 | 109.2545 | 291.3420 | 274.9440 | 162.9004 | |
| 0 | 27.3479 | −1.6466 | 118.7747 | 182.9625 | 48.3833 |
| UD | CP | QI | 3H | 6H | 12H | |
|---|---|---|---|---|---|---|
| 1239.6624 | 716.3208 | 523.1438 | 1096.6105 | 869.0241 | 656.4225 | |
| 1651.2582 | 955.5267 | 696.7461 | 1465.1250 | 1159.6239 | 876.4950 | |
| 1608.1426 | 949.2164 | 677.4268 | 1507.1759 | 1251.0673 | 886.4591 | |
| 1043.6099 | 659.1638 | 437.0182 | 1165.3680 | 1099.7761 | 651.6016 | |
| 0 | 109.3918 | −6.5864 | 475.0987 | 731.8499 | 193.5332 |
| (a) A0 = 0 | ||||||
| UD | 320.5012 | 364.1790 | 429.6956 | 428.2718 | 471.9496 | 537.4662 |
| CP | 186.5846 | 212.0123 | 250.1538 | 249.3249 | 274.7526 | 312.8941 |
| QI | 135.1728 | 153.5941 | 181.2261 | 180.6256 | 199.0469 | 226.6788 |
| 3H | 290.0151 | 329.5383 | 388.8230 | 387.5346 | 427.0577 | 486.3424 |
| 6H | 236.1363 | 268.3169 | 316.5877 | 315.5387 | 347.7192 | 395.9901 |
| 12H | 172.2580 | 195.7332 | 230.9461 | 230.1808 | 253.6561 | 288.8689 |
| (b) A0 = 4 | ||||||
| UD | 107.7706 | 151.4484 | 216.9650 | 215.5412 | 259.2189 | 324.7356 |
| CP | 90.0882 | 115.5159 | 153.6574 | 152.8285 | 178.2562 | 216.3977 |
| QI | 43.8061 | 62.2274 | 89.8594 | 89.2589 | 107.6802 | 135.3121 |
| 3H | 216.2941 | 255.8173 | 315.1020 | 313.8136 | 353.3367 | 412.6214 |
| 6H | 262.3648 | 294.5454 | 342.8162 | 341.7672 | 373.9477 | 422.2186 |
| 12H | 106.3061 | 129.7814 | 164.9943 | 164.2290 | 187.7042 | 222.9171 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almitani, K.H.; Mohamed, N.; Alazwari, M.A.; Mohamed, S.A.; Eltaher, M.A. Exact Solution of Nonlinear Behaviors of Imperfect Bioinspired Helicoidal Composite Beams Resting on Elastic Foundations. Mathematics 2022, 10, 887. https://doi.org/10.3390/math10060887
Almitani KH, Mohamed N, Alazwari MA, Mohamed SA, Eltaher MA. Exact Solution of Nonlinear Behaviors of Imperfect Bioinspired Helicoidal Composite Beams Resting on Elastic Foundations. Mathematics. 2022; 10(6):887. https://doi.org/10.3390/math10060887
Chicago/Turabian StyleAlmitani, Khalid H., Nazira Mohamed, Mashhour A. Alazwari, Salwa A. Mohamed, and Mohamed A. Eltaher. 2022. "Exact Solution of Nonlinear Behaviors of Imperfect Bioinspired Helicoidal Composite Beams Resting on Elastic Foundations" Mathematics 10, no. 6: 887. https://doi.org/10.3390/math10060887
APA StyleAlmitani, K. H., Mohamed, N., Alazwari, M. A., Mohamed, S. A., & Eltaher, M. A. (2022). Exact Solution of Nonlinear Behaviors of Imperfect Bioinspired Helicoidal Composite Beams Resting on Elastic Foundations. Mathematics, 10(6), 887. https://doi.org/10.3390/math10060887





