A More Realistic Markov Process Model for Explaining the Disjunction Effect in One-Shot Prisoner’s Dilemma Game

Abstract

The quantum model has been considered to be advantageous over the Markov model in explaining irrational behaviors (e.g., the disjunction effect) during decision making. Here, we reviewed and re-examined the ability of the quantum belief–action entanglement (BAE) model and the Markov belief–action (BA) model in explaining the disjunction effect considering a more realistic setting. The results indicate that neither of the two models can truly represent the underlying cognitive mechanism. Thus, we proposed a more realistic Markov model to explain the disjunction effect in the prisoner’s dilemma game. In this model, the probability transition pattern of a decision maker (DM) is dependent on the information about the opponent’s action, Also, the relationship between the cognitive components in the evolution dynamics is moderated by the DM’s degree of subjective uncertainty (DSN). The results show that the disjunction effect can be well predicted by a more realistic Markov model. Model comparison suggests the superiority of the proposed Markov model over the quantum BAE model in terms of absolute model performance, relative model performance, and model flexibility. Therefore, we suggest that the key to successfully explaining the disjunction effect is to consider the underlying cognitive mechanism properly.

1. Introduction

WON? CHEERS!

LOST? CHEER UP!

What time is it? It’s football time!

These lines are taken from a beer advertising campaign conducted during the English Premier League season (see Today, 2 September 2002; p. 42). The advertisement tries to tell soccer fans that it is always a good choice to drink a beer regardless of the outcome. This advertisement raises a question: if the fans do not know whether their team has won or lost, would they choose to drink? Savage suggested that if the fans choose to drink a beer when their team wins and when it loses, they will also choose to drink a beer if the outcome is uncertain [1]. This is referred to as the ‘sure-thing principle’. It states that if one prefers action A over action B under the state of the world X, and if one would also prefer action A over action B under the opposite state of the world ~X, then one should prefer action A over action B even if the state of the world is unknown [1]. The sure-thing principle is consistent with basic rational choice. However, researchers showed that people occasionally violate the sure-thing principle (e.g., [2,3]). Tversky and Shafir called such violation of the sure-thing principle the ‘disjunction effect’ [3]. One of the well-known examples is the disjunction effect in the one-shot prisoner’s dilemma (PD) [2]. In a PD game with a typical payoff matrix (as displayed in

Table 1. Payoff matrix of a typical PD game: in a typical PD game, the payoff matrix is set up in the way that no matter what move your opponent makes, you are better off to defect; the same is true for your opponent. The following table shows an example.

	The Opponent Defects	The Opponent Cooperates
You defect	You and your opponent each get 30 (x1)	You get 85 (x3) and your opponent gets 25 (x2)
You cooperate	You get 25 (x2) and your opponent gets 85 (x3)	You and your opponent each get 75 (x4)

), the payoff entries satisfy the inequalities x₃ > x₄ > x₁ > x₂ [4] so that defection is the dominant choice. Shafir and Tversky [2] made a key innovation by including trials that informed a player of the opponent’s action before they made a decision, in order to test the sure-thing principle. Their results were quite surprising. Many players defected when their opponent’s action was known: the defection rate was about 97% and 84% when the opponent was known to defect or to cooperate, respectively. However, they changed their decision to cooperation when their opponent’s choice was unknown, with a defection rate of about 63%. This presents a clear violation of the sure-thing principle in that the defection rate should not fall below 84% according to this principle.

Ever since the disjunction effect was found, it has attracted considerable interest. Several psychological theories, such as reluctance-to-think [2] and equate-to-differentiate [5] assumptions were originally proposed to qualitatively explain the disjunction effect. Later, as quantum models of cognition and decision making have become a popular new approach to psychology [6], one influential type of quantum model for decision making, the quantum belief–action entanglement (BAE) model, which is derived from quantum probability theory [7] and the Markov process model [8,9], was proposed to quantitatively account for the disjunction effect. A series of studies have suggested that the quantum probability based quantum BAE model can explain the disjunction effect, while the classical probability-based Markov process model (Markov BA model), with the identical cognitive setting, cannot (e.g., [10,11,12,13]). However, recent empirical studies suggest that the socio-economic decision making process can be regarded as a result of dual processes (one deliberate process and one intuitive process) (e.g., [14,15]), which can be well modelled by a drift diffusion model [16,17]. It should be noted that the drift diffusion model is also a Markov process model [18], and the mathematical difference between the Markov BA model and the diffusion model is that the Markov BA model is a discrete state Markov model, while the diffusion model is a continuous state model [19]. Given the validity of the Markov process model in explaining the socio-economic decision making process, it is worth investigating the failure of the Markov BA model in explaining the disjunction effect in the one-shot PD game by asking: it is really because of the inferiority of the Markov process model compared to the quantum BAE model or is it because the cognitive setting in the Markov BA model cannot properly reflect the realistic cognitive mechanism.

Driven by this question, the first aim of our study is to re-examine the Markov BA model, together with the similar quantum BAE model, focusing on the consistency between the model setting and the realistic cognitive mechanism. As the re-examination results in Section 3 revealed that several model settings are inconsistent with the realistic cognitive mechanism, the second aim of our study is to explore the effectiveness of a discrete state Markov model in explaining the disjunction effect. For this purpose, we developed an alternative discrete state Markov process model, which is corrected from those unrealistic settings, to account for the disjunction effect in the one-shot PD game.

The rest of the paper is structured as follows. Section 2 reviews the cognitive settings in the Markov BA model, the quantum BAE model and the recent relevant works. Then a re-examination of the quantum BAE and Markov BA models considering the underlying cognitive mechanism is conducted in Section 3. Based on the re-examination results, we propose an alternative, more realistic Markov model to account for the disjunction effect in the one-shot PD game in Section 4. The model application results are compared and discussed in Section 5. Finally, Section 6 comes to the conclusion.

2. Background

2.1. Cognitive Settings in Quantum BAE and Markov BA Models

The cognitive settings of the decision making process in the quantum BAE and Markov BA models can be displayed in Figure 1. $\varphi (·)$, is the probability distribution across belief–action states in the DM’s mind (see Supplementary Material or [20] for details), which evolves across the decision making process based on the information about the opponent’s action, payoff evaluation and cognitive dissonance. When receiving information about the opponent’s action at time $t_1$, the probability distribution across belief–action states changes to $\varphi \left(t_1|N\right)$ (where $N\in \left\{\mathrm{KD},\mathrm{KC},\mathrm{Ukn}\right\}$, hereinafter). Then, the dynamical evolution of decision process happens during $t_1$ and $t_2$ in which a DM adopts both payoff evaluation and cognitive dissonance (or so called BAE) strategies in order to make a decision. Payoff evaluation is a rational strategy representing that a DM evaluates the payoffs corresponding to different pairs of belief–action states to select an action with a higher payoff. Cognitive dissonance is a heuristical strategy that makes the DM’s belief and action more consistent: in the case of the PD game, when a DM believes that the opponent will defect/cooperate, then the DM will tend to defect/cooperate, and vice versa.

There are several characteristics in the settings of the quantum BAE and Markov BA models to be addressed. Firstly, the settings assume that there is no influence of the opponent’s information on the subsequent evolution dynamics, indicating that a DM will adopt the identical payoff evaluation and cognitive dissonance strategy to make a decision under decision conditions with different information about the opponent’s action. Secondly, the settings assume the independence between the payoff evaluation and cognitive dissonance during the decision process, indicating a DM will adopt these two strategies in a constant ratio through the decision making process. Thirdly, the models assume one fixed duration for the decision making processes of different decision conditions.

2.2. Dual Processing in Socio-Economic Decision Making

Dual processing theory states that there are two different cognitive components of processing involved in the socio-economic decision making: (1) the conscious, deliberative and analytic reasoning processing, (2) the intuitive, unconscious and heuristical reasoning processing [21,22]. These two components compete with each other, and the dominant component in the competition can be varied across different decision conditions (e.g., [23,24,25,26,27]) and different periods of the decision processes (e.g., [28,29,30]).

Many characteristics of the decision condition (e.g., time constraint, task complexity) can affect the competence between these two components. For example, researchers have found that under time pressure, people tend to adopt more heuristical strategy than under time free or time delay conditions, where they tend to adopt more deliberative strategy [27]. During the decision process, component 2 is believed to dominant the decision process at the very beginning, but as the decision process goes on, component 2 gradually gives way to component 1.

Recently, a biased drift diffusion model was proposed to capture the behavioral patterns in socio-economic decision making under different conditions [17]. To achieve the dual processing framework, the model regards component 2 as a starting point bias that is imposed on the very beginning of the decision process and component 1 as a drift rate determined by the utility difference between options that is imposed on the subsequent decision process. The model assumes that these two parameters can vary across different conditions. Such a model has proved to be an effective approach to quantitatively describe the decision process in the mini-dictator games. One might argue, why not just adopt this model to account for the disjunction effect? The reasons are as follows. Firstly, the drift diffusion model requires real decision time and many more model parameters to account for the decision process under different conditions (11 free parameters in the case of our study), which will cost much more computational resource and may lead to unnecessary model complexity. Secondly, and more importantly, the model fails to completely capture the intricate competence between these two components as their corresponding parameters are assumed to be independent with each other, which remains as the biggest challenge for our study.

Findings in other recent studies shed light on the solution of this challenge. It has been found that increased uncertainty about the behavior of the opponent and the payoff consequences cause DMs to use more heuristics in the socio-economic decision making process [31,32]. Under the framework of the Markov BA model, such uncertainty can be derived through measuring the uncertainty degree across the probability distribution across belief–action states (i.e., the subjective uncertainty degree, DSN, as mentioned in Section 4.1), as it reflects how certain a DM is about the opponent’s action and the payoff consequence after a specific action. Therefore, DSN may serve as an effective indicator of the competence between component 1 and 2.

2.3. Model Evaluation Metric

To evaluate the model performance for further model comparison, several model evaluation metrics are adopted and described in the following. The first, and also the most common metric is the root mean squared deviation (RMSD), which indicates the absolute model performance [33]. However, one important shortcoming of RMSD is that it fails to take model complexity into consideration, in that a model with more free parameters typically exhibits better absolute performance. The second model evaluation metric, the Bayesian information criterion (BIC) [34], considers the impact of model complexity on fitting performance and is used to show relative model performance [34]. The third model evaluation metric, model flexibility, refers to the ability of a model to fit different patterns of data [33]. We want a model to be flexible enough to capture the underlying cognitive process, which can be complicated; but, at the same time, the model must not be too flexible. An ideal model is parsimonious and generates only those choice patterns that are observed in experiments [35].

2.3.1. Root Mean Squared Deviation (RMSD)

A popular and simple model evaluation method is the (square root of the) average of the squared deviations (or root mean squared deviation (RMSD)) between observed data and model prediction. Specifically, RMSD was calculated as Equation (1), in which $J$ denotes the number of decision conditions, $o_i$ denotes the observed mean defection rate in condition i and $p_i$ denotes the mean defection rate predicted by the model. A smaller value of RMSD indicates a better absolute model performance.

$$\mathrm{RMSD}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^J{\left(o_i-p_i\right)}^2}{J}}$$

(1)

2.3.2. Bayesian Information Criterion (BIC)

The BIC considers the impact of model complexity on fitting performance. A lower value of the index indicates a better balance between goodness of fit and model complexity and thus suggests a more desirable model [34,36]. The BIC can be calculated as $G_i+k\ln \left(3N\right)$, where $k$ is the number of free parameters in the model, $G_i$ statistic expresses the badness of fit of the model predictions with the observed values, which can be defined as $2L{\displaystyle \sum }_{i=1}^J(o_i\ln \left(p_i\right)+\left(1-o_i\right)\ln \left(1-p_i\right))$, where L refers to the number of choices included in each condition [14]. A lower value of BIC indicates a better balance between goodness of fit and model complexity (in terms of the number of free parameters) and thus suggests a more desirable model.

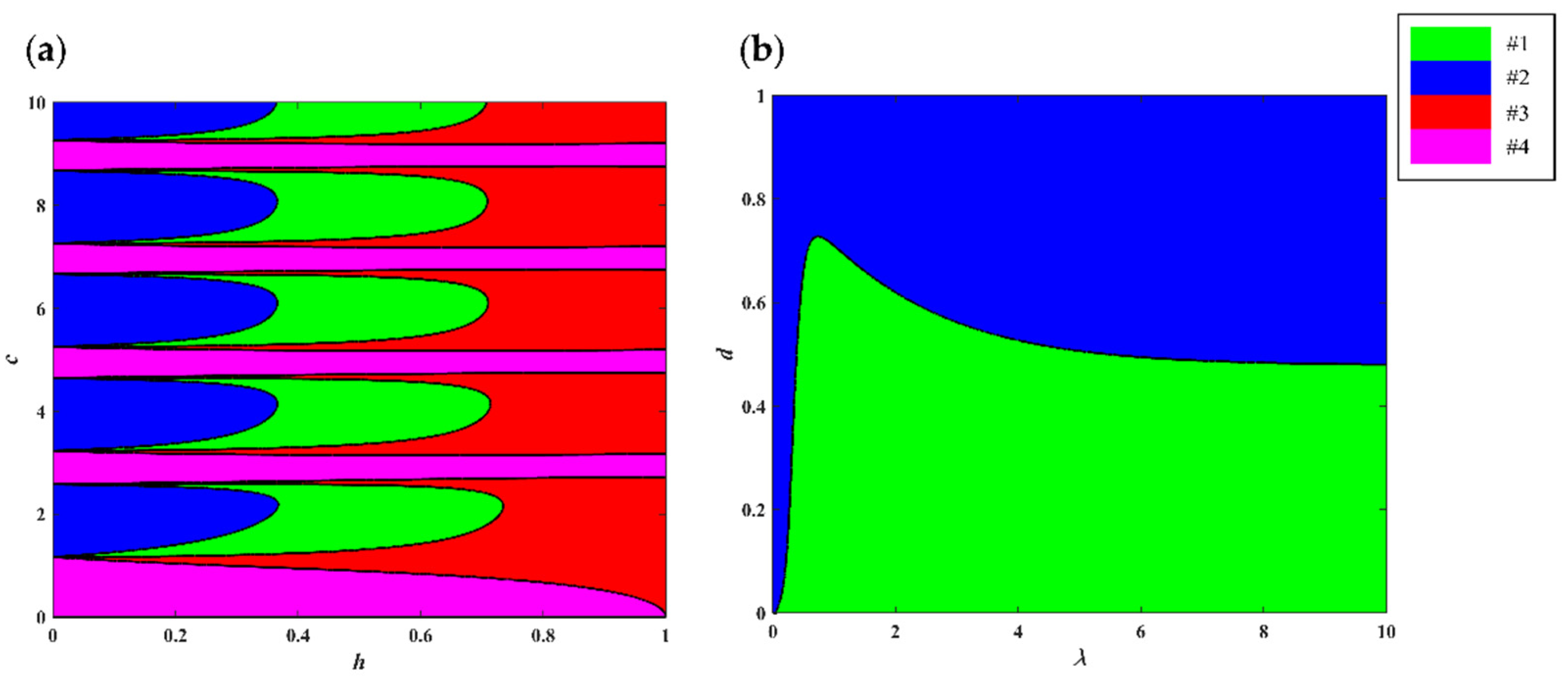
2.3.3. Model Flexibility

Model flexibility can be measured by the PSP (parameter space partitioning) method [37,38]. Such a method systematically assesses the choice patterns predicted by the models across the entire parameter space. A model is considered to be overly flexible when it can generate not only all choice patterns that are observed empirically but also choice patterns that are logically possible but never observed. Instead, one should prefer a less flexible model that only generates choice patterns that are actually frequently observed in experiments. In the case of the one-shot PD game, such patterns should be the disjunctive pattern ($p\left(\mathrm{D}|\mathrm{KD}\right)>p\left(\mathrm{D}|\mathrm{KC}\right)>p\left(\mathrm{D}|\mathrm{UK}\right)$, #1) and the non-disjunctive pattern ($p\left(\mathrm{D}|\mathrm{KD}\right)>p\left(\mathrm{D}|\mathrm{UK}\right)>p\left(\mathrm{D}|\mathrm{KC}\right)$, #2) [39,40,41]. To implement PSP, we used a grid search method [38] as follows. For each model and each parameter, we chose 100 values that were equally spaced over the corresponding parameter range. All combinations of these parameter values were used to generate data, which were then used to compute the proportions of each possible logical choice pattern.

3. Re-Examination of Quantum BAE and Markov BA Models

In this section, we conduct a thorough re-examination of quantum BAE and Markov BA models to test whether the settings in evolution dynamics can truly represent the underlying decision-making process. Specifically, we aim to examine whether the two cognitive components (i.e., payoff evaluation and cognitive dissonance), their mutual relation, and the decision time are properly represented in these two models.

3.1. Unrealistic Payoff Evaluation

3.1.1. The Preference for Higher Payoff Is Not Always Satisfied

The payoff evaluation represents the DM’s ‘rational’ preference for a higher payoff, which mathematically implies that for a pair of belief–action states with different payoffs, the probability of transitioning from one state with a higher payoff to the other state with a lower payoff is smaller than the transition probability in the opposite direction. The decision process dominated by payoff evaluation can be described by $Up\left(t\right)$ and $Tp\left(t\right)$ in the quantum BAE and Markov BA models, respectively (see Supplementary Material or [20] for details), in which $t$ represents the time in the decision process, and $h_D,h_C,k_D,k_C$ represents the utility differences between the payoffs corresponding to the different belief–action states.

$$\begin{gathered} Up\left(t\right)=e^{-i·t·Hp}=\left[\begin{array}{cc}U1\left(t\right)& 0\\ 0& U2\left(t\right)\end{array}\right] \\ U1\left(t\right)=\left[\begin{array}{cc}\cos \left(t\right)-\frac{i·\sin \left(t\right)}{\sqrt{1+h_D^2}}& -\frac{i·h_D·\sin \left(t\right)}{\sqrt{1+h_D^2}}\\ -\frac{i·h_D·\sin \left(t\right)}{\sqrt{1+h_D^2}}& \cos \left(t\right)+\frac{i·\sin \left(t\right)}{\sqrt{1+h_D^2}}\end{array}\right] \\ U2\left(t\right)=\left[\begin{array}{cc}\cos \left(t\right)-\frac{i·\sin \left(t\right)}{\sqrt{1+h_C^2}}& -\frac{i·h_C·\sin \left(t\right)}{\sqrt{1+h_C^2}}\\ -\frac{i·h_C·\sin \left(t\right)}{\sqrt{1+h_C^2}}& \cos \left(t\right)+\frac{i·\sin \left(t\right)}{\sqrt{1+h_C^2}}\end{array}\right] \end{gathered}$$

(2)

It is clear from this formulation that $Up\left(t\right)$ is a symmetric matrix so that ${\left|U{p}_{ij}\left(t\right)\right|}^2$ is always equal to ${\left|U{p}_{ji}\left(t\right)\right|}^2$ at any time point t, leading to the well-known consequence of the Hermiticity. This means that the probability of transitioning to state $i$ from state $j$ is always equal to the probability of transitioning to state $j$ from state $i$ during the decision process regardless of the differences in the payoffs corresponding to different states. Therefore, what we can infer from $Up\left(t\right)$ is that different payoffs are identical in the eyes of the DMs during the decision process. This is not only inconsistent with the intention of the preference for the higher payoff but is also against common sense.

$$\begin{gathered} Tp\left(t\right)=e^{t·Kp}=\left[\begin{array}{cc}T1\left(t\right)& 0\\ 0& T2\left(t\right)\end{array}\right] \\ T1\left(t\right)=\frac{1}{1+k_D}\left[\begin{array}{cc}{k}_D+e^{-\left(1+k_D\right)·t}& k_D-k_D·e^{-\left(1+k_D\right)·t}\\ 1-e^{-\left(1+k_D\right)·t}& 1+k_D·e^{-\left(1+k_D\right)·t}\end{array}\right] \\ T2\left(t\right)=\frac{1}{1+k_C}\left[\begin{array}{cc}{k}_C+e^{-\left(1+k_C\right)·t}& k_C-k_C·e^{-\left(1+k_C\right)·t}\\ 1-e^{-\left(1+k_C\right)·t}& 1+k_C·e^{-\left(1+k_C\right)·t}\end{array}\right] \end{gathered}$$

(3)

According to the intention of payoff evaluation, elements in $Tp\left(t\right)$ should satisfy $T{p}_{12}\left(t\right)>T{p}_{21}\left(t\right)$ and $T{p}_{34}\left(t\right)>T{p}_{43}\left(t\right)$. However, this can be violated when $0<k_D,k_C<1$, which implies that $Tp\left(t\right)$ in the Markov BA model still cannot fully serve its purpose. However, compared to the quantum BAE model, it is clear that the problem in the Markov BA model, as a result of the loose constraint on the relationship between $h_D/h_C$ and the constant parameter ‘1′ in $Kp\left(t\right)$, is much simpler than that in the quantum BAE model.

3.1.2. DMs Treat the Same Payoff Information Regardless of Opponent’s Actions

In the quantum BAE and Markov BA models, the matrices representing payoff evaluation ($Up\left(t\right)$ and $Tp\left(t\right)$) remain the same under different conditions. This setting means that DMs evaluate the same payoff information regardless of the opponent’s action. Moreover, the formulation of $Up\left(t\right)$ and $Tp\left(t\right)$ indicates that probability transitions can only happen between two pairs of states, ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{D}}\leftrightarrow {\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{C}}$ and ${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{D}}\leftrightarrow {\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{C}}$, as shown in Figure 2a. This further implies that DMs can only evaluate two pairs of payoffs ($x_1\leftrightarrow x_2$; $x_3\leftrightarrow x_4$), which is inconsistent with the real decision-making condition because DMs should pay attention to different pairs of payoffs depending on the opponent’s action [39,42]. When the opponent’s action is known, the DM’s belief about the opponent is fixed, and he/she only needs to consider one pair of payoffs corresponding to the fixed belief. Thus, the available probability transition can only happen between state ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{D}}$ and ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{C}}$(or state ${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{D}}$ and ${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{C}}$) as illustrated in Figure 2b (or Figure 2c). When the opponent’s action is unknown, payoffs corresponding to all the states are available for DMs for evaluation. Thus, the probability transitions can happen between all the possible pairs of states as illustrated in Figure 2d.

3.2. Unrealistic Belief and Action Entanglement

The highlight of both quantum BAE and Markov BA models is belief and action entanglement (produced by $Hb$ and $Kb$ in both models, see Supplementary Material or [20] for details), which in essence, is a matter of cognitive dissonance [20,43]. In the case of the one-shot PD game, when a DM believes the opponent will defect, then the DM will tend to choose to defect, and vice versa. Although $Hb$ and $Kb$ seem to function well to produce cognitive dissonance under Ukn [20,43], they lead to unrealistic model predictions under KD and KC. As a DM’s belief is fixed under KD/KC, in order to make belief and action agree with each other, the DM will tend to defect/cooperate, increasing the probability of observing state ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{D}}$/${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{C}}$. However, the outcomes in both models show otherwise. By setting the model parameters as previous studies suggested for testing the cognitive dissonance effect ($c=1$, $d=10$, $t_b=\pi /2$, [20]), one can obtain the probability distribution after a duration ($t_b$) of the decision process dominated by cognitive dissonance using the following equations.

For the quantum BAE model

$$\parallel \psi {\left(t_1+t_b|\mathrm{KD}\right)\parallel }^2=\parallel e^{-i·\pi /2·Hb\left(c=1\right)}·\psi {\left(t_1|\mathrm{KD}\right)\parallel }^2=\left[\begin{array}{c}0.25\\ 0.25\\ 0.25\\ 0.25\end{array}\right]$$

(4)

$$\parallel \psi {\left(t_1+t_b|\mathrm{KC}\right)\parallel }^2=\parallel e^{-i·\pi /2·Hb\left(c=1\right)}·\psi {\left(t_1|\mathrm{KC}\right)\parallel }^2=\left[\begin{array}{c}0.25\\ 0.25\\ 0.25\\ 0.25\end{array}\right]$$

(5)

For the Markov model

$$\varphi \left(t_1+t_b|\mathrm{KD}\right)=e^{\pi /2·Kb\left(d=10\right)}·\varphi \left(t_1|\mathrm{KD}\right)\approx \left[\begin{array}{c}0.454\\ 0.046\\ 0.046\\ 0.454\end{array}\right]$$

(6)

$$\varphi \left(t_1+t_b|\mathrm{KC}\right)=e^{\pi /2·Kb\left(d=10\right)}·\varphi \left(t_1|KC\right)\approx \left[\begin{array}{c}0.454\\ 0.046\\ 0.046\\ 0.454\end{array}\right]$$

(7)

As shown in Equations (4)–(7), the probability of observing state ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{D}}$/${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{C}}$ under KD/KC is 0.5 at time $t_1$. It then drops to 0.25 (quantum BAE model) and 0.454 (Markov BA model) after a duration $t_b$ of the decision process dominated by cognitive dissonance. Even more unrealistic is the occurrence of non-zero probabilities of the states in which the belief about the opponent’s action is not consistent with the known information. For example, when the DM knows that the opponent will defect, then the DM’s belief about the opponent’s action is fixed. Therefore, it is not likely that the DM’s belief will change to agree with his/her action, which means that the probability of observing states with the belief about the opponent’s action against the known information (${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{D}}$ and ${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{C}}$) after the process should remain zero.

We suggested the following causes for these unrealistic cognitive dissonance outcomes. First, $Hb$ and $Kb$ represent the probability transitions shown in Figure 3a, indicating that DMs can make their beliefs agree with their intended actions but cannot change their intended actions to agree with their beliefs. This is inconsistent with the definition of cognitive dissonance. [44]. Second, since the probability transition patterns of the cognitive dissonance process, as illustrated in Figure 3a for both quantum BAE and Markov BA models, remain unchanged under different conditions, the difference in the probability transition patterns across different conditions is not duly considered again. When DMs know their opponent’s action, their belief towards the opponent’s action is fixed. Under this circumstance, they only need to change their intended action to be consistent with their belief, as illustrated by the probability transitions in Figure 3b,c. Otherwise, DMs can either change their belief to agree with the intended action or change the intended action to agree with their belief as shown in Figure 3d.

3.3. Violation of the Dual Processing Framework

Though it has not been clearly stated, it should be clear that both the quantum BAE and Markov BA models are within the framework of the well-known dual processing theory. The payoff evaluation can be considered as a conscious component, while the cognitive dissonance as a heuristic component. According to the introduction of the dual processing framework in Section 2.2, the weight between payoff evaluation and cognitive dissonance should vary across different decision conditions and evolve through the decision process. For example, when a DM is confronted with a simple decision condition (e.g., KD or KC where a DM only needs to consider one pair of different payoffs, thus, less cognitive resource is required), payoff evaluation should play a more advantageous role in the decision-making process. When a DM is confronted with a complex decision condition (e.g., Ukn where a DM needs to consider multiple pairs of payoffs, thus, more cognitive resource is required), cognitive dissonance should play a more advantageous role. However, as the matrices determining payoff evaluation and cognitive dissonance remain unchanged across different conditions and periods in the decision process, indicating the constant relationship between payoff evaluation and cognitive dissonance, the dual processing framework is obviously violated in the quantum BAE and Markov BA models.

3.4. The Fixed Decision Time Parameter ‘π/2’

For quantum BAE models, the parameter t for decision time has always been fixed at π/2. The reasons are as follows. On the one hand, $\pi /2\approx 2$ stands for the average duration of decision making (2 s) for the DMs; on the other hand, and more importantly for the quantum model, final defection probabilities ($p\left(D,t_1+t|N,t_1\right)$) reach maxima when $t=\pi /2$ [11,20,44]. However, such explanations for the fixed decision time do raise a number of objections. First, whether parameter t can stand for the real decision time still remains unclear. Second, there is no empirical evidence supporting 2 s to be the average decision time, especially given the fact that the average decision time varies across different tasks and different participants. Third, and most importantly, the statement that the final defection choice probabilities reach their maxima when $t=\pi /2$ can be proven wrong as shown in Figure 4, from which we can see that the maximum time point of $p\left(D,t_1+t|\mathrm{Ukn},t_1\right)$ changes with different values of the parameter c.

3.5. Summary

This section presents a re-examination of the quantum BAE and Markov BA models, based on which we posit that both models fail to describe the decision process properly. Generally speaking, the major limitation of the Markov BA model, results from the lack of considerations of the real decision-making situations (e.g., identical probability transition patterns for different conditions), which can be corrected under proper consideration of the real decision-making situations. Moreover, for the quantum BAE model, the limitation also comes from the very nature of the quantum framework (e.g., the symmetry of $Up\left(t\right)$ caused by Hermiticity), which cannot be easily solved under the current theoretical framework. Therefore, it is feasible to develop a more realistic Markov model to account for the disjunction effect in a one-shot PD game.

4. Proposed Method

In this section, we construct a more realistic Markov model, which takes the key properties of realistic cognitive mechanisms into consideration, to account for the disjunction effect in the PD game. In Section 4.1, we first introduce the key settings in the proposed Markov model that make our model more consistent with the underlying cognitive mechanism we have discussed in previous Sections. Then, a detailed step-by-step model construction procedure is provided in Section 4.2.

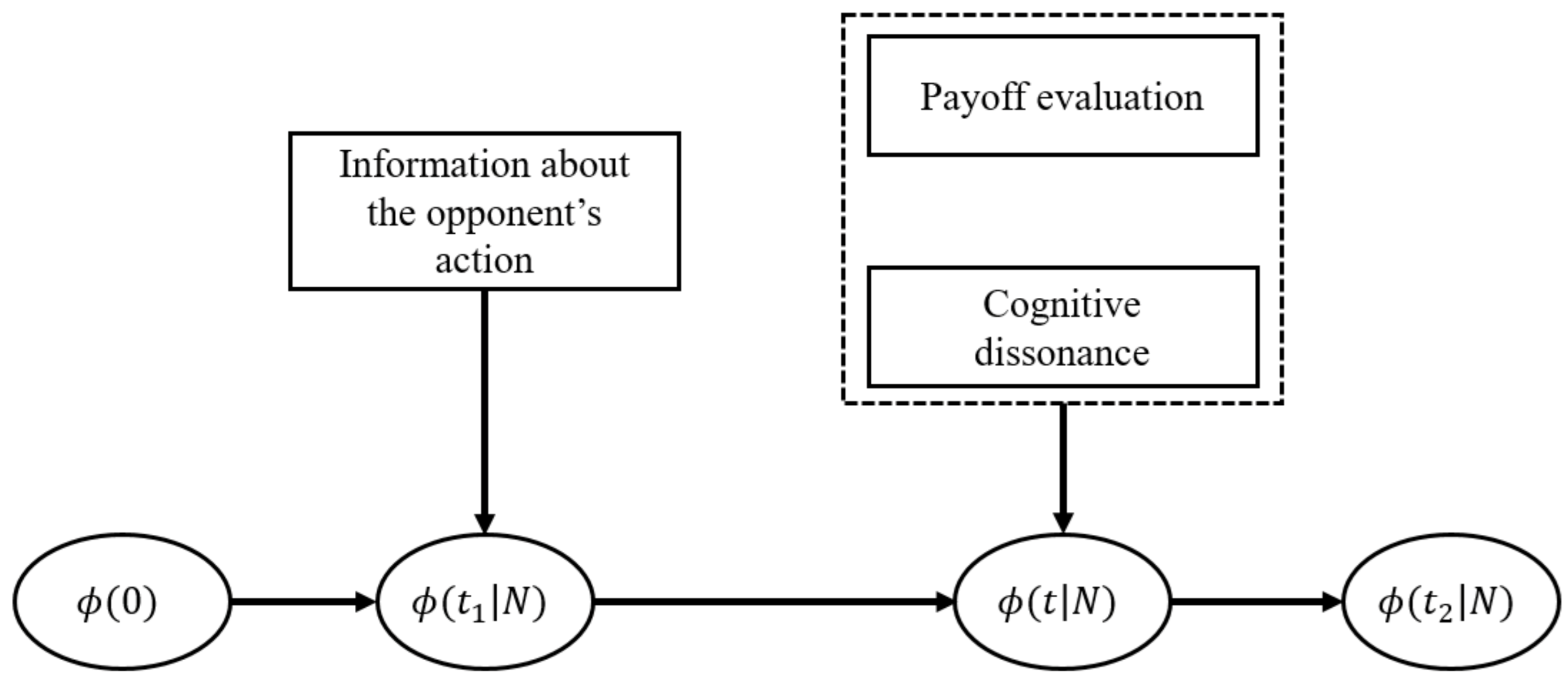
4.1. Model Highlights

The proposed Markov model includes the following unique key settings in the evolution dynamics of the decision process:

• The intensity matrices for payoff evaluation and cognitive dissonance are dependent on the information about the opponent’s action.
• The weight between payoff evaluation and cognitive dissonance is moderated by the DM’s DSN and is dynamically evolving during the decision process.
• The weight between payoff evaluation and cognitive dissonance can be considered as unchanged during a small period of time $∆\tau$.
• The final decision time is determined by the time when the probability distribution of a DM’s belief and action states reaches stationary.

The first setting is to make those matrices truly reflect the real probability transition patterns under different conditions as we have mentioned in Section 3.1 and Section 3.2. The second, also the most important setting, is to adopt DM’s DSN about belief and intended action as a moderator of the relationship between payoff evaluation and cognitive dissonance in order to fit the dual processing framework. The reasons for adopting DSN are not only because of the empirical findings as mentioned in Section 2.2, but also because it can correctly reflect the change in the relationship between payoff evaluation and cognitive dissonance across different decision conditions and different periods of the decision processes. Firstly, in the PD game, the increased task complexity in Ukn comes directly from the introduction of the information uncertainty, which will lead to the increase in DM’s DSN [39,42,45] and the consequential increase of the advantage on cognitive dissonance. Secondly, the decision-making process in some paradigms similar to the PD game is believed to be a process of evidence accumulation [46], where the DM’s DSN reduces as the accumulated evidence increases over time [47], exhibiting correspondence to the evolution of the weight between payoff evaluation and cognitive dissonance during the decision process. The third setting is to mimic the continuous decision process with a discrete process for computational simplicity [48], and the last setting is to agree with the fact that a DM has taken full consideration before making a decision, since a DM is not forced to respond before a certain time point.

The essential differences in cognitive settings between the former two models (quantum BAE and Markov BA models) and the proposed Markov model lie in the evolution dynamics of the decision process. Figure 5 presents a schematic of the cognitive settings in the proposed Markov model and highlights those differences. Two major differences are summarized as follows. Firstly, the former two models assume that there is no influence of the opponent’s information on the subsequent payoff evaluation and cognitive dissonance, leading to the invariance in the probability transition pattern across different conditions, which is inconsistent with a real decision-making situation as we have discussed in Section 3. In the proposed Markov model, however, the probability transition patterns for both payoff evaluation and cognitive dissonance depend on the information about the opponent’s action, and, therefore, the variation in the probability transition patterns across different condition (as illustrated in Figure 2 and Figure 3) can be naturally derived. Secondly, the former models assume a unilateral influence of cognitive components (payoff evaluation and cognitive dissonance) on the DM’s belief and action state and assume independence between each cognitive component, leading to the invariance in the weight between each cognitive component across different conditions and different periods of decision process, which is also against the dual processing framework mentioned before. In contrast, the proposed Markov model assumes a bilateral influence between the cognitive components and the DM’s belief and action states: at each moment during the decision process, the evolution of the probability distribution across the DM’s belief and action states toward the next moment is determined by the cognitive components, while the weight between each cognitive component is moderated by the uncertainty in the probability distribution across the DM’s belief and action states, which, as discussed, is an effective reflection of the dynamical relationship between these two cognitive components.

4.2. Model Construction

The flowchart of the construction of the proposed Markov model is illustrated in Figure 6, including eight steps.

Step 1: Define the initial belief and action state.

When playing a typical PD game, there exists a set of mutually exclusive and exhaustive belief states $\left\{{\mathrm{B}}_{\mathrm{D}},{\mathrm{B}}_{\mathrm{C}}\right\}$ and action states $\left\{{\mathrm{A}}_{\mathrm{D}},{\mathrm{A}}_{\mathrm{C}}\right\}$. Specifically, ${\mathrm{B}}_{\mathrm{C}}$ stands for the belief state in which the DM believes that the opponent will cooperate, while ${\mathrm{A}}_{\mathrm{D}}$ stands for the action state in which the DM intends to defect. Then, the four dimensional sets of belief and action states can be derived as $\left\{{\mathrm{B}}_{\mathrm{D}},{\mathrm{B}}_{\mathrm{C}}\right\}\otimes \left\{{\mathrm{A}}_{\mathrm{D}},{\mathrm{A}}_{\mathrm{C}}\right\}=\left\{{\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{D}},{\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{C}},{\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{D}},{\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{C}}\right\}.$ (The symbol $\otimes$ stands for the Kronecker product) in which, for example, ${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{D}}$ symbolizes the state in which the DM believes that the opponent will cooperate but the DM intends to defect. The initial probability distribution across those four states for the proposed Markov model can be set as $\psi \left(t=0\right)$ or simply $\varphi \left(0\right)$.

$$\varphi \left(0\right)=\left[\begin{array}{c}{\varphi }_{DD}\left(0\right)\\ {\varphi }_{DC}\left(0\right)\\ {\varphi }_{CD}\left(0\right)\\ {\varphi }_{CC}\left(0\right)\end{array}\right]$$

(8)

where, for example, ${\varphi }_{CD}\left(0\right)$ represents the probability of observing state ${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{D}}$ at the beginning of a game; ${\varphi }_{DD}\left(0\right)+{\varphi }_{CD}\left(0\right)$ represents the probability of observing state ${\mathrm{A}}_{\mathrm{D}}$ (i.e., probability of acting defection) at the beginning of a game. For simplicity, initial distribution is typically assumed as uniformed with ${\varphi }_i\left(0\right)=1/4$.

Step 2: Evolution of the state based on the information about the opponent’s action.

As the decision-making process goes on, the probability distribution across belief and action state evolves into a new distribution at time $t_1$, as the information about the opponent’s action changes the DM’s belief about the opponent’s action. If the opponent’s action is known to be defect, cooperate or is unknown, the probability distribution across belief–action states would change to $\varphi \left(t_1|\mathrm{KD}\right)$, $\varphi \left(t_1|\mathrm{KC}\right)$ and $\varphi \left(t_1|\mathrm{Ukn}\right)$, respectively

$$\begin{gathered} \varphi \left(t_1|\mathrm{KD}\right)=\frac{1}{{\varphi }_{DD}\left(0\right)+{\varphi }_{DC}\left(0\right)}\left[\begin{array}{c}{\varphi }_{DD}\left(0\right)\\ {\varphi }_{DC}\left(0\right)\\ 0\\ 0\end{array}\right] \\ \varphi \left(t_1|\mathrm{KC}\right)=\frac{1}{{\varphi }_{CD}\left(0\right)+{\varphi }_{CC}\left(0\right)}\left[\begin{array}{c}0\\ 0\\ {\varphi }_{CD}\left(0\right)\\ {\varphi }_{CC}\left(0\right)\end{array}\right] \\ \varphi \left(t_1|\mathrm{Ukn}\right)=\varphi \left(0\right) \end{gathered}$$

(9)

Step 3: Reconstruction of the intensity matrices for payoff evaluation and cognitive dissonance.

Substep 3.1: Reconstruction of payoff evaluation

To reconstruct the payoff evaluation process, the transition matrix was firstly made to agree with the fact that the probability of transitioning from the ith state with a higher payoff to the jth state with a lower payoff is always smaller than it is for the opposite transition direction. One can simply set $K{p}_{ji}^{\prime }\left(N\right)$ to be strictly smaller than $K{p}_{ij}^{\prime }\left(N\right)$ where $K{p}^{\prime }\left(N\right)$ is the intensity matrix determining the payoff evaluation under condition N. Therefore, the following equation is applied to define the off-diagonal elements in $K{p}^{\prime }\left(N\right)$

$$K{p}_{ij:i\ne j}^{\prime }\left(N\right)=\{\begin{array}{c}\frac{x_i{}^{\lambda }}{x_i{}^{\lambda }+x_j{}^{\lambda }} if {\varphi }_i\left(t_1|N\right)\ne 0 \wedge {\varphi }_j\left(t_1|N\right)\ne 0\hfill \\ 0 if {\varphi }_i\left(t_1|N\right)=0 \vee {\varphi }_j\left(t_1|N\right)=0\hfill \end{array}$$

(10)

$x_i$ represents the payoff corresponding to the ith belief and action state. The relationship between $\varphi \left(t_1|N\right)$ and $K{p}_{ij}^{\prime }\left(N\right)$ guarantees that the matrix will reflect the fact that DM will evaluate different payoff information under different conditions as we have mentioned in Section 3.1. $\lambda >0$ is the bounded rationality parameter indicating how well a DM can discriminate between the profitability of the different payoffs under a given condition [49]. By applying Equation (10) into different conditions, the intensity matrices representing the payoff evaluation process for different conditions can be reconstructed as follows.

For KD, the intensity matrix $K{p}^{\prime }\left(\mathrm{KD}\right)$, corresponding to the condition in which a probability transition can only happen between state ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{D}}$ and ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{C}}$, can be defined as

$$K{p}^{\prime }\left(\mathrm{KD}\right)=\left[\begin{array}{cccc}\frac{-x_2^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}& \frac{x_1^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}& 0& 0\\ \frac{x_2^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}& \frac{-x_1^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]$$

(11)

Additionally, the corresponding transition matrix $T{p}^{\prime }(t|\mathrm{KD})$ can be derived as

$$T{p}^{\prime }(t|\text{KD})=e^{K{p}^{\prime }\left(\text{KD}\right)·t}=\left[\begin{array}{cccc}\frac{x_1^{\lambda }+e^{-t}·x_2^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}& \frac{x_1^{\lambda }-e^{-t}·x_1^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}& 0& 0\\ \frac{x_2^{\lambda }-e^{-t}·x_2^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}& \frac{x_2^{\lambda }+e^{-t}·x_1^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

(12)

From the formulation of $T{p}^{\prime }(t|\mathrm{KD})$, it is easy to prove that given $x_1>x_2$, the probability of transiting from state ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{C}}$ to state ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{D}}$, $\frac{x_1^{\lambda }-e^{-t}·x_1^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}$, is always larger than the probability of transiting from state ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{D}}$ to state ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{C}}$, $\frac{x_2^{\lambda }-e^{-t}·x_2^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}$, demonstrating a valid correction of the preference for the state with a higher payoff.

Similarly, for KC, the intensity matrix $K{p}^{\prime }\left(\mathrm{KC}\right)$ can be similarly defined as

$$K{p}^{\prime }\left(\mathrm{KC}\right)=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& \frac{-x_4^{\lambda }}{x_3^{\lambda }+x_4^{\lambda }}& \frac{x_3^{\lambda }}{x_3^{\lambda }+x_4^{\lambda }}\\ 0& 0& \frac{x_4^{\lambda }}{x_3^{\lambda }+x_4^{\lambda }}& \frac{-x_3^{\lambda }}{x_3^{\lambda }+x_4^{\lambda }}\end{array}\right]$$

(13)

For Ukn, the intensity matrix $K{p}^{\prime }\left(\mathrm{Ukn}\right),$ representing probability transitions between all the possible pairs of states, can be set as

$$K{p}^{\text{'}}\left(\text{Ukn}\right)=\left[\begin{array}{cccc}\dots & \frac{x_1^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}& \frac{x_1^{\lambda }}{x_1^{\lambda }+x_3^{\lambda }}& \frac{x_1^{\lambda }}{x_1^{\lambda }+x_4^{\lambda }}\\ \frac{x_2^{\lambda }}{x_1^{\lambda }+x_2^{\lambda }}& \dots & \frac{x_2^{\lambda }}{x_2^{\lambda }+x_3^{\lambda }}& \frac{x_2^{\lambda }}{x_2^{\lambda }+x_4^{\lambda }}\\ \frac{x_3^{\lambda }}{x_1^{\lambda }+x_3^{\lambda }}& \frac{x_3^{\lambda }}{x_2^{\lambda }+x_3^{\lambda }}& \dots & \frac{x_3^{\lambda }}{x_3^{\lambda }+x_4^{\lambda }}\\ \frac{x_4^{\lambda }}{x_1^{\lambda }+x_4^{\lambda }}& \frac{x_4^{\lambda }}{x_2^{\lambda }+x_4^{\lambda }}& \frac{x_4^{\lambda }}{x_3^{\lambda }+x_4^{\lambda }}& \dots \end{array}\right]$$

(14)

where ‘$\cdots$’ stands for the diagonal elements $K{p}_{ii}^{\prime }\left(\mathrm{Ukn}\right)$, which is equal to $-{{\displaystyle \sum }}_{\underset{\left(j\ne i\right)}{j=1}}^{4}K{p}_{ij}^{\prime }\left(\mathrm{Ukn}\right)$ according to the property of the intensity matrix.

Substep 3.2: Reconstruction of cognitive dissonance

To reconstruct the cognitive dissonance process, we divide the belief and action states into two kinds: ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{D}}$ and ${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{C}}$ are the ‘stable’ states (SSt) in which belief and action agree with each other, while ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{C}}$ and ${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{D}}$ are the ‘unstable’ states (USt) in which belief and action do not agree. We propose the following general definitions to reflect the effect of cognitive dissonance on the probability transitions between a pair of belief and action states:

• A probability transition can only happen from one of any unstable states to one of any stable states.
• A probability transition can neither happen from one stable state to another nor from an unstable state to another.

The first definition guarantees those stable states are absorbing states, which, according to the property of the Markov process, ensures that the probability of observing any stable state is a monotonically increasing function of the transition parameter [50]. The second definition reflects the fact that the effect of cognitive dissonance cannot make a DM change both the belief and the action, and, therefore, there are no probability transitions between state ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{D}}$ and ${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{C}}$ or between state ${\mathrm{B}}_{\mathrm{C}}{\mathrm{A}}_{\mathrm{D}}$ and ${\mathrm{B}}_{\mathrm{D}}{\mathrm{A}}_{\mathrm{C}}$. Based on these definitions, we propose the definition of the off-diagonal elements in the intensity matrix $K{b}^{\prime }\left(N\right)$ representing cognitive dissonance in Equation (15), where $0<d<1$ is the scale transition parameter of the cognitive dissonance effect.

$$K{b}_{ij:i\ne j}^{\prime }\left(N\right)=\{\begin{array}{c}d i\in \left\{\mathrm{SSt}{{\displaystyle \cap }}^{}{\varphi }_i\left(t_1|N\right)\ne 0\right\} \wedge j\in \left\{\mathrm{USt}{{\displaystyle \cap }}^{}{\varphi }_i\left(t_1|N\right)\ne 0\right\}\hfill \\ 0 else\hfill \end{array}$$

(15)

The role of $\varphi \left(t_1|N\right)$ in Equation (15) is similar to that in Equation (10), which reflects the variation of probability transition pattern under different conditions as shown in Figure 3. Then, the intensity matrices of cognitive dissonance for different conditions can be derived as

$$K{b}^{\prime }\left(\mathrm{KD}\right)=\left[\begin{array}{cccc}0& d& 0& 0\\ 0& -d& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]$$

(16)

$$K{b}^{\prime }\left(\mathrm{KC}\right)=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& -d& 0\\ 0& 0& d& 0\end{array}\right]$$

(17)

$$K{b}^{\prime }\left(\mathrm{Ukn}\right)=\left[\begin{array}{cccc}0& d& d& 0\\ 0& -2d& 0& 0\\ 0& 0& -2d& 0\\ 0& d& d& 0\end{array}\right]$$

(18)

It should be noted that for the known conditions, since there is no probability transition to the states with the belief against the known information about the opponent’s action, which guarantees the probability of observing a stable state after a duration of cognitive dissonance is always greater than its initial probability, a valid correction of the unrealistic probability reduction in the Markov BA model, as described in Section 3.2, is therefore demonstrated.

Step 4: Calculate a DM’s DSN.

A DM’s DSN can be defined as how sure a DM is about the opponent’s action and the outcomes after a specific action: when the opponent’s action is known, the payoff information is quite clear and a DM is sure about the opponent’s action and the outcome following that action, so that the DSN is low in this circumstance; when the opponent’s action is unknown, the payoff information becomes complex and a DM feels uncertain about both the opponent’s action and its outcome, resulting in a higher DSN. Mathematically, the DM’s DSN can be defined as the uncertainty in the probability distribution across belief and action states, thus, it can be derived using entropy methods. In our study, the classical Shannon entropy is used to compute the DSN as follows

$$E\left(\tau |N\right)=-{{\displaystyle \sum }}^{}{\varphi }_i\left(\tau |N\right)·{\log }_2{\varphi }_i\left(\tau |N\right)$$

(19)

where $\varphi \left(\tau |N\right)$ represents the probability distribution across the DM’s belief and action states at time $\tau$ under the condition N, and higher $E\left(\tau |N\right)$ reflects a higher DSN. For example, at the beginning of the decision process ($t_1$), when the opponent’s action is known, the corresponding DSN $E\left(t_1|\mathrm{KD}\right)$ and $E\left(t_1|\mathrm{KC}\right)$ can be calculated as

$$E\left(t_1|\mathrm{KD}\right)=E\left(t_1|\mathrm{KC}\right)=-2\times \frac{1}{2}·{\log }_2\frac{1}{2}=1$$

(20)

In contrast, a higher DSN for Ukn at $t_1$ can be derived as

$$E\left(t_1|\mathrm{Ukn}\right)=-4\times \frac{1}{4}·{\log }_2\frac{1}{4}=2$$

(21)

The difference in the DSN across different conditions at $t_1$ is also a reflection of the complexity difference in different conditions because no cognitive processing is involved at the beginning of the decision process. As the decision process proceeds, the decrement in the DSN can also be naturally derived in our model, as illustrated in Figure S1 (Supplementary Material). This is because Markov-process-based decision-making models (including the proposed Markov model and Markov BA model) essentially represent a DSN-reduced evidence accumulation process [14,19].

Step 5: Calculate the weight between payoff evaluation and cognitive dissonance.

As mentioned before, the higher the DSN, the more weight on the heuristic cognitive dissonance and the less weight on the deliberative payoff evaluation. To achieve this purpose, a monotonic hyperbolic tangent function is adopted to map the DSN into the weight coefficient ranging from 0 to 1 as follows.

$$w_B\left(\tau |N\right)=\frac{2}{1+\exp \left(-2.5·E\left(\tau |N\right)\right)}-1$$

(22)

$$w_P\left(\tau |N\right)=1-w_B\left(\tau |N\right)$$

(23)

$w_B\left(\tau |N\right)$ and $w_P\left(\tau |N\right)$ represent the weights for cognitive dissonance and payoff evaluation, respectively, at time $\tau$ in condition N. If a DM is extremely sure about the opponent’s action and his/her intended action at time $\tau$ (this corresponds to the probability distribution where ${\varphi }_{i=m}\left(\tau |N\right)=1$, ${\varphi }_{i\ne m}\left(\tau |N\right)=0$), the lowest uncertainty degree is obtained ($E\left(\tau |N\right)=0$), and, therefore, the highest weight for payoff evaluation ($w_P\left(\tau |N\right)=1$) and the lowest weight for cognitive dissonance ($w_B\left(\tau |N\right)=0$) are derived. In contrast, when a DM is extremely uncertain about the opponent’s action and his/her intended action (this corresponds to the probability distribution where ${\varphi }_i\left(\tau |N\right)=1/4$), the highest uncertainty degree is obtained ($E\left(\tau |N\right)=2$), and the coefficient ‘2.5′ is used to generate the lowest weight for payoff evaluation and the highest weight for cognitive dissonance, approximately equal to 0 and 1, respectively, in this instance.

Step 6: Update the probability distribution of belief and action state.

After a small time increment $∆\tau$, the evolution of the probability distribution of the belief and action state from time $\tau$ to $\tau +∆\tau$ can be described by the following equation

$$\varphi \left(\tau +∆\tau |N\right)=e^{∆\tau ·\left(w_P\left(\tau |N\right)·K{p}^{\prime }\left(N\right)+w_B\left(\tau |N\right)·K{b}^{\prime }\left(N\right)\right)}·\varphi \left(\tau |N\right)$$

(24)

Step 7: Determine whether the distribution reaches stationary.

The absolute difference between $\varphi \left(\tau +∆\tau |N\right)$ and $\varphi \left(\tau |N\right)$ described in Equation (25) is used to determine whether the distribution reaches stationary at time $\tau$.

$$AD\left(\tau |N\right)={{\displaystyle \sum }}_i\left|{\varphi }_i\left(\tau +∆\tau |N\right)-{\varphi }_i\left(\tau |N\right)\right|$$

(25)

If $AD\left(\tau |N\right)>∆\tau /{10}^{10}$, the distribution $\varphi \left(\tau |N\right)$ is not stationary at time $\tau$, the decision process continues at time $\tau +∆\tau$ and then goes back to step 3; otherwise, the distribution is considered as stationary and then goes to the next step. In our study, $∆\tau$ is set to 0.01, a further test for the effect of the size of $∆\tau$ on the stationary distribution is displayed in Table S1 (Supplementary Material). The results show the consistency of the stationary distributions produced by the $∆\tau$ with varied sizes, demonstrating the reliabilities of the selection of $∆\tau$ and the application of discrete approximations to a continuous process.

Step 8: Calculate the final defection probabilities under different conditions.

Similar to the Markov BA model, the final defection probabilities for different conditions can be computed by Equation (26)

$$\begin{gathered} p\left(D|N\right)=L·M·\varphi \left(ts\left(N,∆\tau \right)|N\right) \\ M=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 0\end{array}\right] \end{gathered}$$

(26)

where $ts\left(N,∆\tau \right)$ represents the time of the final decision making (i.e., the time for $\varphi \left(\tau |N\right)$ reaching stationary) under the condition N given the defined value of $∆\tau$, and $\varphi \left(ts\left(N,∆\tau \right)|N\right)$ represents the stationary probability distribution of the belief and action states under condition N.

5. Model Fitting and Comparison

5.1. Model Fitting

A PSO (particle swarm optimization) algorithm was implemented to search for the parameter combination that can generate the minimal RMSD between the empirical data and model prediction. (To fit our model to the empirical data, the payoff parameters in our model inherit a classical setting with $x_1=30$, $x_2=25$, $x_3=85$ and $x_4=75$ [2]) In addition, in order to make comparisons between the quantum BAE model and our Markov model in the following section, the quantum BAE model is used to fit the empirical data. The optimized fitting results are shown in

Table 2. The empirical data and optimized fitting results of proposed Markov model and quantum BAE model.

Literature		$\mathit{p} \left(\mathit{D}|\mathbf{KD}\right)$	$\mathit{p} \left(\mathit{D}|\mathbf{KC}\right)$	$\mathit{p} \left(\mathit{D}|\mathbf{Ukn}\right)$
[2]	Obs a	0.97	0.84	0.63
	Q b	0.83	0.77	0.69
	M c	0.95	0.85	0.63
[45]	Obs	0.67	0.32	0.30
	Q	0.67	0.37	0.35
	M	0.72	0.34	0.32
[40]	Obs	0.82	0.77	0.72
	Q	0.82	0.77	0.73
	M	0.83	0.74	0.73
[52]	Obs	0.91	0.84	0.66
	Q	0.83	0.79	0.70
	M	0.94	0.82	0.66
[42]	Obs	0.97	0.93	0.88
	Q	0.95	0.91	0.93
	M	0.98	0.92	0.88
[39]	Obs	0.91	0.86	0.79
	Q	0.85	0.88	0.83
	M	0.94	0.84	0.79
[41]	Obs	0.94	0.89	0.88
	Q	0.93	0.87	0.90
	M	0.95	0.87	0.86
Average	Obs	0.88	0.78	0.69
	Q	0.83	0.77	0.73
	M	0.90	0.77	0.69

^a Obs represents the observed experiment results. ^b Q represents the quantum BAE model. ^c M represents the proposed Markov model.

. Generally, the results of our proposed Markov model are well fitted to the empirical data, and the disjunction effect is also well predicted in the cases of each part of the literature. In contrast, the quantum BAE model exhibits questionable fitting performances in the cases of [2,39,51] and this model even fails to predict the disjunction pattern in the cases of [41,42].

5.2. Model Comparison

The comparison results of RMSD and BIC for each model are shown in

Table 3. RMSD and BIC computed by the optimal model fitting results of quantum BAE and proposed Markov models.

Literature		k	$\mathit{L}$	RMSD	BIC
[2]	Q	3	444	0.0150	1219.46
	M	2	444	0.0002	1112.57
[45]	Q	3	80	0.0031	317.83
	M	2	80	0.0021	310.79
[40]	Q	3	210	<0.0001	692.86
	M	2	210	0.0007	687.90
[52]	Q	3	528	0.0074	1547.99
	M	2	528	0.0006	1473.06
[42]	Q	3	180	0.0018	298.92
	M	2	180	0.0001	286.16
[39]	Q	3	1500	0.0031	3756.77
	M	2	1500	0.0007	3705.17
[41]	Q	3	150	0.0008	308.37
	M	2	150	0.0001	295.52
Average	Q	2	441.72	0.0045	1163.17
	M	3	441.72	0.0005	1124.50

, it is evident that the results favor our Markov model since the proposed Markov model produced smaller RMSD and BIC values in most cases.

The PSP results presented in

Table 4. Proportions of choice patterns generated by each model.

Choice Pattern	Proportion of All Choice Patterns
	Q	M
#1: $p\left(\mathrm{D}|\mathrm{KD}\right)>p\left(\mathrm{D}|\mathrm{KC}\right)>p\left(\mathrm{D}|\mathrm{UK}\right)$	0.33	0.53
#2: $p\left(\mathrm{D}|\mathrm{KD}\right)>p\left(\mathrm{D}|\mathrm{UK}\right)>p\left(\mathrm{D}|\mathrm{KC}\right)$	0.15	0.47
#3: $p\left(\mathrm{D}|\mathrm{KC}\right)>p\left(\mathrm{D}|\mathrm{KD}\right)>p\left(\mathrm{D}|\mathrm{UK}\right)$	0.24	0.00
#4: $p\left(\mathrm{D}|\mathrm{KC}\right)>p\left(\mathrm{D}|\mathrm{UK}\right)>p\left(\mathrm{D}|\mathrm{KD}\right)$	0.28	0.00
#5: $p\left(\mathrm{D}|\mathrm{UK}\right)>p\left(\mathrm{D}|\mathrm{KD}\right)>p\left(\mathrm{D}|\mathrm{KC}\right)$	0.00	0.00
#6: $p\left(\mathrm{D}|\mathrm{UK}\right)>p\left(\mathrm{D}|\mathrm{KC}\right)>p\left(\mathrm{D}|\mathrm{KD}\right)$	0.00	0.00

show that the quantum BAE model can produce four different choice patterns including the frequently observed disjunctive pattern (#1) and non-disjunctive pattern (#2). However, the large residual part of the parameter space is occupied by logical but unreasonable choice patterns, i.e., #3 and #4, which have not been observed in empirical studies. For the proposed Markov model, the majority of the parameter space belongs to the frequently observed disjunctive and non-disjunctive patterns. Furthermore, from the visualized partitioned parameter space of the quantum BAE simplified model (quantum BAE simplified model, QS, refers to the model proposed by [43], assuming $h_D=h_C=h$) and the proposed Markov model as shown in Figure 7, one can see that the parameter space of choice patterns generated by QS exhibits an unreasonable periodic-like structure with multiple, non-contiguous areas representing each choice pattern, while that of the proposed Markov model shows a continuous structure for each choice pattern. Therefore, it is clear that the quantum BAE model is overly flexible and should not be preferred over the proposed Markov model.

In sum, the model comparison results show that the proposed Markov model outperforms the quantum BAE model in terms of absolute model performance, relative model performance and model flexibility, demonstrating the proposed Markov model is superior in modelling the disjunction effect in the one-shot PD game compared with the quantum BAE model.

5.3. Academic and Practical Implications

The excellent performance of the proposed Markov model demonstrates the effectiveness of the dual processing feature in explaining the decision process in the one-shot PD game, which is consistent with a series of research regarding socio-economic decision making as a result of dual processes [27,52,53,54,55]. The proposed Markov model partially supports the idea of the ‘equate-to-differentiate’ method, stating that a DM may focus more on an alternative perspective instead of the evaluation of their own payoffs to make a decision under Ukn [5]. Moreover, it demonstrates the effective role of the DSN between the rational cognitive component and the heuristic cognitive component, which is consistent with previous studies [29,30]. To some degree, it also supports the importance of adopting an extra degree of uncertainty in Ukn to model the disjunction effect [56,57], in that a higher DSN in Ukn does contribute to the production of the disjunctive pattern in the proposed Markov model.

Our proposed Markov model also has implications for the design of institutions that aim to control the ‘irrational’ behavior under uncertainty in social decision making. As DSN is an effective moderator between the rational cognitive component and heuristic cognitive component. Encouraging the DM to carefully consider the outcomes of his/her intended actions in the decision process under uncertain condition can reduce the DSN, thus, increasing the weight of the rational component and promoting the rational choice. In contrast, providing obscure information about the decision scenario may increase the DSN, thus, increasing the weight of the heuristic component and promoting the intuitive choice.

6. Concluding Remarks

In this study, we argue that the triumph of the quantum BAE model in explaining the disjunction effect may not be as convincing as it seems. We pointed out some unreasonable outcomes in the quantum BAE and Markov BA models. The occurrences of these problems are, on the one hand, a result of its quantum-like nature (e.g., the property of the Hermitian matrix and oscillatory and periodic solutions derived from the state evolution equations) and, on the other hand, resulting from a lack of consideration for the real decision-making scenario (e.g., identical state evolution dynamics across different conditions). It should be noted that the intention of this study is not to negate the quantum-like models. We believe that some ideas proposed by the quantum-like models, such as adopting the quantum concept of superposition to describe ‘fuzzy’ and ambiguous feelings under conditions of uncertainty [5], do provide novel insights into psychological issues. We also believe that the challenging findings against the quantum BAE model in our current study can help to improve this kind of model in the future.

Importantly, our study proposed a more realistic Markov model, which is demonstrated to better explain the disjunction effect than the quantum BAE model. The model takes realistic cognitive mechanism in decision making into account, especially the dual processing mechanism and its consequential effect that the evolution dynamics varied across different conditions and different periods in the decision process.

In broader terms, our study provides an alternative perspective to model the disjunctive pattern. The quantum BAE model posits the key to account for such ‘irrational’ behavior patterns is the ‘interference term’, which can be generated under the quantum theory framework. The essential setting for the generation of such an interference term is that the state evolution dynamics are identical for different conditions [20], which is inconsistent with a real decision-making situation, as we have discussed in Section 3. In contrast, our proposed Markov model admits the difference in evolution dynamics across different conditions, thus, the disjunction pattern can be naturally derived from a classical probability-based framework based on a comprehensive understanding of the corresponding cognitive process. We suggest the key to better model these ‘irrational’ behavioral patterns is to capture the realistic cognitive mechanisms underlying each specific behavioral pattern.

Finally, there are several limitations of our study to be addressed. Firstly, since our study only focused on the application of the Markov process model in one specific situation (i.e., the one-shot PD game), the advantages of quantum-like models in other fields should not be ignored. For example, Ikeda and his group proposed a quantum-like framework in the infinite repeated quantum game [58] and established infinitely repeated game of quantum prisoner’s dilemma and discovered a new Nash equilibrium in the presence of entanglement between players [59]. More recently, they applied repeated quantum games for theory of money, in which they verified the existence of the new Nash equilibrium that makes quantum information a commodity such as money [60]. In their most recent work, a quantum supremacy of quantum decision making was shown in a more simplified setting of adverse selection and principal-agent relation [61]. These works undoubtedly demonstrated the quantum advantages in this field. Secondly, as with similar decision-making models (e.g., [7,36]), the selection of the model parameters in our proposed Markov model is aimed at generating the optimal model performance. Such a selection method neglected the real-world scenarios, for example, the individual differences in personality and some cognitive capacity are highly related to the dual processing components (e.g., [62]). By measuring such individual characteristics, future study may develop empirical model parameters selection methods. Thirdly, because of the lack of data with real response time, our proposed Markov model still cannot take the real response time of decision making into consideration. Future research may extend the current framework of the proposed Markov model by applying data with real response time into our model.