Reconstructing Dynamic 3D Models with Small Data by Integrating Position-Based Dynamics and PDE-Based Modelling
Abstract
:1. Introduction
2. Related Work
2.1. Shape Deformations
- Geometric shape deformations relate skin shape changes to the underlying skeleton movements. Among various geometric shape deformation methods, Linear Blend Skinning [1] is most popular due to its efficiency and simplicity. Unfortunately, it has the artefacts of collapsing joints and candy-wrapper effects, etc. In order to overcome these artefacts, Dual Quaternion blending [2] was proposed. Although it eliminates the artefacts of collapsing joints and candy-wrapper effects, it causes a new problem called joint-bulging artefact. The Delta Mush algorithm [3] treats skinning as a problem of smoothing the low-frequency geometry while preserving detail to avoid manual weight painting, which is required in existing geometric skinning methods. Since the Delta Mush algorithm involves heavy iterative calculations, the Direct Delta Mush algorithm [4] was proposed to improve the efficiency and control of the Delta Mush algorithm at the cost of high storage requirements. In order to tackle this problem, a compression method was introduced into the Direct Delta Mush algorithm in [5] to reduce its storage and run-time computing costs.
- Data-driven shape deformations are proposed to improve the realism of shape changes. They treat the problem as a general data regression that learns the relationship between shape changes and skeleton movements from example shapes. Pose Space Deformation (PSD) [6] improves shape interpolation by representing shape changes as mappings from a pose space defined by a skeleton or a more abstract system of parameters to displacements. PSD requires a large amount of memory and is not suitable for use in interactive systems. This problem was tackled in [7] by fitting the parameters of a deformation model to best approximate the example data. The method proposed in [8] automatically extracts linear blending skinning by learning from a set of example poses. In recent years, machine learning has been introduced into data-driven methods. In [9], mesh deformations were split into linear and non-linear ones. The transformations of the skeleton underlying the mesh were used to determine the linear deformations, and deep learning was used to approximate remaining non-linear deformations. RigNet [10] predicted a skeleton to match an input 3D articulated character model and estimated surface skin weights by learning example data in a dataset.
- Physics-based shape deformations are introduced to tackle the problem of geometric methods in creating less realistic shapes and address the weakness of data-driven methods in requiring enough high-quality example shapes. Various physics-based shape deformation models have been developed as reviewed in [11]. Among these models, the three most important physics-based deformable models are mass-spring systems, the finite element method (FEM), and finite volume method. In [12], a mass-spring system of a facial muscle model was developed. For the simulation of elastic and elastoplastic fracturing materials, FEM is more effective and can generate more realistic results [13]. The finite volume method [14] employs a divergence-free vector field, representing solid shape deformations without losing self-interactions or features.
- Position-based dynamics makes a good compromise between realism and efficiency. It is initially proposed for solid simulation, such as cloth simulation [15]. Since bending constraints are determined by the dihedral angle rather than edge lengths, they and stretching constraints are separated into two independent parameters. Müller et al. have used this method to generate robust cloth simulation with high controllability. Macklin et al. have presented an alternative approach to simulate fluids in the PBD framework [16] by modelling the fluids as a particle system. Each particle is constrained by a minimum distance from others. Compared with force-based fluids simulation, the method of position-based fluids uses a larger time step with a comparable result, which significantly reduces the computation cost. Besides the particle-based models, the position-based method has also been applied in rigid body simulation by solving constraints between rigid bodies [17].
2.2. Parametric Surfaces-Based Reconstruction
2.3. ODE and PDE Based Modelling
- ODE-based modelling sweeps a curve defined by the solution to a vector-valued ODE along two boundary curves subject to continuity constraints on boundary curves to create an ODE surface. Various ODE-based modelling methods have been developed. For example, ODE-based sweeping surfaces were proposed in [24], ODE-based surface blending was investigated in [25], and ODE-based skin deformations were discussed in [26]. Since solving an ODE is easier than solving a PDE, ODE-based modelling is easier than PDE-based modelling. One weakness of ODE-based modelling is the difficulty of manipulating ODE sweeping surfaces since the manipulation is carried out on curves.
- PDE-based modelling uses the solution to a vector-valued PDE subject to given boundary constraints to define a PDE surface. PDE-based modelling has received a lot of research attention. Here we briefly review some work on PDE-based modelling using continuous PDE surfaces defined with analytical solutions to PDEs. PDE-based modelling of free form surfaces was pioneered in [27], where a vector-valued fourth-order PDE with one shape control parameter was used. Then it was used to develop the technique of interactive design [28] and achieve PDE surface-based reconstruction [29]. The current state in PDE-based modelling is analytical PDE-based skin deformation [30] and real-time PDE surface manipulation [31].
3. Deformation Simulation with Position-Based Dynamics
3.1. The Development of PBD
3.2. PBD Algorithm Overview
- Get the initial attributes of vertices of the mesh, including the initial coordinates , velocity , and weight ( denotes the mass of the vertex);
- Each vertex will update its velocity as well as its predicted position by the external force according to the following formula:
- After the predicted position has been gained, add constraints, including collisions, volume conservation, cloth balloons, and so on. The position will be directly modified to with a group of iterations:where stands for the number of constraints and denotes the solver iteration number;
- Finally, the position change will be reused to calculate the attributes and :where and will be used as the initial information of the vertices in the loop of the next timestep.
3.3. Our PBD Simulation Experiment
4. Mathematical Model and Closed-Form Solution
5. Reconstruction of Dynamic 3D Models
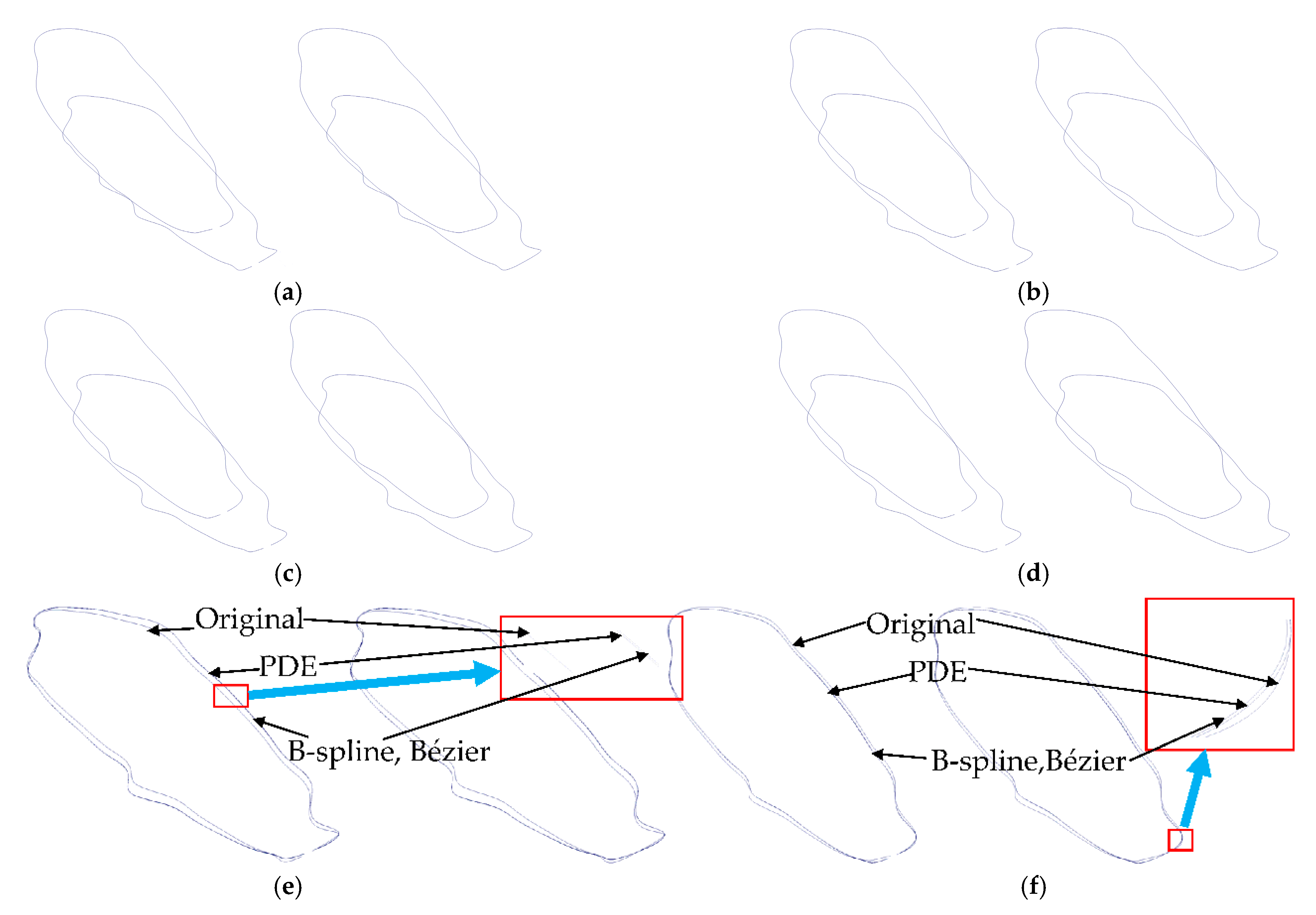
5.1. Comparison with Bézier and B-Spline Static Representations
5.2. Limitations of This Work
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Magnenat-Thalmann, N.; Laperrire, R.; Thalmann, D. Joint-dependent local deformations for hand animation and object grasping. In Proceedings of Graphics Interface ’88; Canadian Information Processing Society: Mississauga, ON, Canada, 1988. [Google Scholar]
- Kavan, L.; Collins, S.; Žára, J.; O’Sullivan, C. Geometric skinning with approximate dual quaternion blending. ACM Trans. Graph. 2008, 27, 1–23. [Google Scholar] [CrossRef]
- Mancewicz, J.; Derksen, M.L.; Rijpkema, H.; Wilson, C.A. Delta Mush: Smoothing deformations while preserving detail. In Proceedings of the Fourth Symposium on Digital Production; Association for Computing Machinery: New York, NY, USA, 2014; pp. 7–11. [Google Scholar]
- Le, B.H.; Lewis, J.P. Direct Delta Mush Skinning and Variants. ACM Trans. Graph. 2019, 38, 113. [Google Scholar] [CrossRef]
- Le, B.H.; Villeneuve, K.; Gonzalez-Ochoa, C. Direct delta mush skinning compression with continuous examples. ACM Trans. Graph. 2021, 40, 72. [Google Scholar] [CrossRef]
- Lewis, J.P.; Cordner, M.; Fong, N. Pose space deformation: A unified approach to shape interpolation and skeleton-driven deformation. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques; ACM Press/Addison-Wesley Publishing Co.: New York, NY, USA, 2000; pp. 165–172. [Google Scholar]
- Mohr, A.; Gleicher, M. Building efficient, accurate character skins from examples. ACM Trans. Graph. 2003, 22, 562–568. [Google Scholar] [CrossRef]
- Le, B.H.; Deng, Z. Smooth skinning decomposition with rigid bones. ACM Trans. Graph. 2012, 31, 199. [Google Scholar] [CrossRef]
- Bailey, S.W.; Otte, D.; Dilorenzo, P.; O’Brien, J.F. Fast and deep deformation approximations. ACM Trans. Graph. 2018, 37, 119. [Google Scholar] [CrossRef]
- Xu, Z.; Zhou, Y.; Kalogerakis, E.; Landreth, C.; Singh, K. RigNet: Neural rigging for articulated characters. ACM Trans. Graph. 2020, 39, 58. [Google Scholar] [CrossRef]
- Nealen, A.; Müller, M.; Keiser, R.; Boxerman, E.; Carlson, M. Physically based deformable models in computer graphics. Comput. Graph. Forum 2006, 25, 809–836. [Google Scholar] [CrossRef]
- Waters, K. A muscle model for animation three-dimensional facial expression. ACM SIGGRAPH Comput. Graph. 1987, 21, 17–24. [Google Scholar] [CrossRef]
- Terzopoulos, D.; Platt, J.; Barr, A.; Fleischer, K. Elastically deformable models. In Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques; Association for Computing Machinery: New York, NY, USA, 1987; pp. 205–214. [Google Scholar]
- Eymard, R.; Gallouët, T.; Herbin, R. Finite volume methods. In Handbook of Numerical Analysis; Elsevier: Amsterdam, The Netherlands, 2000; Volume 7, pp. 713–1018. [Google Scholar]
- Müller, M.; Heidelberger, B.; Hennix, M.; Ratcliff, J. Position based dynamics. J. Vis. Commun. Image Represent. 2007, 18, 109–118. [Google Scholar] [CrossRef] [Green Version]
- Macklin, M.; Müller, M. Position based fluids. ACM Trans. Graph. 2013, 32, 1–2. [Google Scholar] [CrossRef]
- Müller, M.; Dorsey, J.; McMillan, L.; Jagnow, R.; Cutler, B. Stable real-time deformations. In Proceedings of the 2002 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, San Antonio, TX, USA, 21–22 July 2002; pp. 49–54. [Google Scholar]
- Position Based Dynamics. Available online: https://github.com/InteractiveComputerGraphics/PositionBasedDynamics (accessed on 20 November 2021).
- Li, J.; Yao, F.; Liu, Y.; Wu, Y. Reconstruction of Broken Blade Geometry Model Based on Reverse Engineering. In 2010 Third International Conference on Intelligent Networks and Intelligent Systems; IEEE Computer Society Press: Washington, DC, USA, 2010; pp. 680–682. [Google Scholar]
- Prautzsch, H.; Wolfgang, B.; Marco, P. Bézier and B-spline Techniques; Springer: Berlin/Heidelberg, Germany, 2002; p. 6. [Google Scholar]
- Patrikalakis, N.M.; Maekawa, T. Shape Interrogation for Computer Aided Design and Manufacturing; Springer: Berlin/Heidelberg, Germany, 2002; p. 15. [Google Scholar]
- Hoschek, J.; Lasser, D. Fundamentals of Computer Aided Geometric Design; AK Peters Ltd.: Natick, MA, USA, 1993. [Google Scholar]
- Gálvez, A.; Iglesias, A. Particle swarm optimisation for non-uniform rational B-spline surface reconstruction from clouds of 3D data points. Inf. Sci. 2012, 192, 174–192. [Google Scholar] [CrossRef]
- You, L.H.; Yang, X.S.; Pachulski, M.; Zhang, J.J. Boundary constrained swept surfaces for modelling and animation. Comput. Graph. Forum 2007, 26, 313–322. [Google Scholar] [CrossRef]
- You, L.H.; Ugail, H.; Tang, B.P.; Jin, X.; You, X.Y.; Zhang, J.J. Blending using ODE swept surfaces with shape control and C1 continuity. Vis. Comput. 2014, 30, 625–636. [Google Scholar] [CrossRef] [Green Version]
- Chaudhry, E.; You, L.H.; Jin, X.; Yang, X.S.; Zhang, J.J. Shape modeling for animated characters using ordinary differential equations. Comput. Graph. 2013, 37, 638–644. [Google Scholar] [CrossRef]
- Bloor, M.I.; Wilson, M.J. Using partial differential equations to generate free-form surfaces. Comput. Aided Des. 1990, 22, 202–212. [Google Scholar] [CrossRef]
- Ugail, H.; Bloor, M.I.G.; Wilson, M.J. Techniques for interactive design using the PDE method. ACM Trans. Graph. 1999, 18, 195–212. [Google Scholar] [CrossRef]
- Ugail, H.; Kirmani, S. Method of surface reconstruction using partial differential equations. In Proceedings of the 10th WSEAS International Conference on Computers, Athens, Greece, 13–15 July 2006; pp. 51–56. [Google Scholar]
- Bian, S.H.; Deng, Z.; Chaudhry, E.; You, L.H.; Yang, X.S.; Guo, L.; Ugail, H.; Jin, X.; Xiao, Z.D.; Zhang, J.J. Efficient and realistic character animation through analytical physics-based skin deformation. Graph. Models 2019, 104, 201035. [Google Scholar] [CrossRef]
- Wang, S.B.; Xiang, N.; Xia, Y.; You, L.H.; Zhang, J.J. Real-time surface manipulation with C1 continuity through simple and efficient physics-based deformations. Vis. Comput. 2021, 37, 2741–2753. [Google Scholar] [CrossRef]
- Yun, S.; Sourin, A.; Castro, G.G.; Ugail, H. A PDE method for patchwise approximation of large polygon meshes. Vis. Comput. 2010, 26, 975–984. [Google Scholar]
- Bender, J.; Müller, M.; Macklin, M. A survey on position based dynamics. In Proceedings of the European Association for Computer Graphics: Tutorials, Lyon, France, 24–28 April 2017; pp. 1–31. [Google Scholar]
- Müller, M.; Keiser, R.; Nealen, A.; Pauly, M.; Gross, M.; Alexa, M. Point based animation of elastic, plastic and melting objects. In Proceedings of the 2004 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Grenoble, France, 27–29 August 2004; pp. 141–151. [Google Scholar]
- Bender, J.; Koschier, D.; Charrier, P.; Weber, D. Position-based simulation of continuous materials. Comput. Graph. 2014, 44, 1–10. [Google Scholar] [CrossRef]
- Macklin, M.; Müller, M.; Chentanez, N. XPBD: Position-based simulation of compliant constrained dynamics. In Proceedings of the 9th International Conference on Motion in Games, Burlingame, CA, USA, 10–12 October 2016; pp. 49–54. [Google Scholar]
- Hong, M.; Jung, S.; Choi, M.H.; Welch, S.W. Fast volume preservation for a mass-spring system. IEEE Comput. Graph. Appl. 2006, 26, 83–91. [Google Scholar] [CrossRef]
- Irving, G.; Schroeder, C.; Fedkiw, R. Volume conserving finite element simulations of deformable models. ACM Trans. Graph. 2007, 26, 13-es. [Google Scholar] [CrossRef]
- Kakadiaris, I.A. Physics-Based Modeling, Analysis and Animation; Technical Reports No. MS-CIS-93-45; University of Pennsylvania: Philadelphia, PA, USA, 1993. [Google Scholar]
- Kadleček, P.; Ichim, A.-E.; Liu, T.; Křivánek, J.; Kavan, L. Reconstructing personalised anatomical models for physics-based body animation. ACM Trans. Graph. 2016, 35, 213. [Google Scholar] [CrossRef] [Green Version]
- Bender, J.; Müller, M.; Macklin, M. Position-based simulation methods in computer graphics. In Proceedings of the 36th Annual Conference of the European Association for Computer Graphics, Eurographics 2015—Tutorials, Zurich, Switzerland, 4–8 May 2015. [Google Scholar]
- Barrielle, V.; Stoiber, N.; Cagniart, C. BlendForces: A dynamic framework for facial animation. Comput. Graph. Forum 2016, 35, 341–352. [Google Scholar] [CrossRef]
- Barrielle, V.; Stoiber, N. Realtime performance-driven physical simulation for facial animation. Comput. Graph. Forum 2019, 38, 151–166. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Lu, Y.; Liu, Q. Integrating viscoelastic mass spring dampers into position-based dynamics to simulate soft tissue deformation in real time. R. Soc. Open Sci. 2018, 5, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Kozlov, Y.; Bradley, D.; Bächer, M.; Thomaszewski, B.; Beeler, T.; Gross, M. Enriching facial blendshape rigs with physical simulation. Comput. Graph. Forum 2017, 36, 75–84. [Google Scholar] [CrossRef]
- Guo, J.; Li, J.; Narain, R.; Park, H.S. Inverse simulation: Reconstructing Dynamic Geometry of Clothed Humans via Optimal Control. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 14693–14702. [Google Scholar]
- Gladilin, E.; Zachow, S.; Deuflhard, P.; Hege, H.-C. Anatomy- and physics-based facial animation for craniofacial surgery simulations. Med. Biol. Eng. Comput. 2004, 42, 167–170. [Google Scholar] [CrossRef]
- Bauchau, O.A.; Craig, J.I. Euler-Bernoulli beam theory. In Structural Analysis; Springer: Dordrecht, The Netherlands, 2009; pp. 173–221. [Google Scholar]
- Polyanin, A.D.; Zhurov, A.I. Separation of Variables and Exact Solutions to Non-Linear PDEs; CRC Press; Taylor & Francis Group, LLC: Boca Raton, FL, USA, 2022; pp. 1–2. [Google Scholar]
- Abdel-Aziz, H.S.; Zanaty, E.A.; Ali, H.A.; Saad, M.K. Generating Bézier curves for medical image reconstruction. Results Phys. 2021, 23, 103996. [Google Scholar] [CrossRef]
- Ravari, A.N.; Taghirad, H.D. Reconstruction of B-spline curves and surfaces by adaptive group testing. Comput. Aided Des. 2016, 74, 32–44. [Google Scholar] [CrossRef]
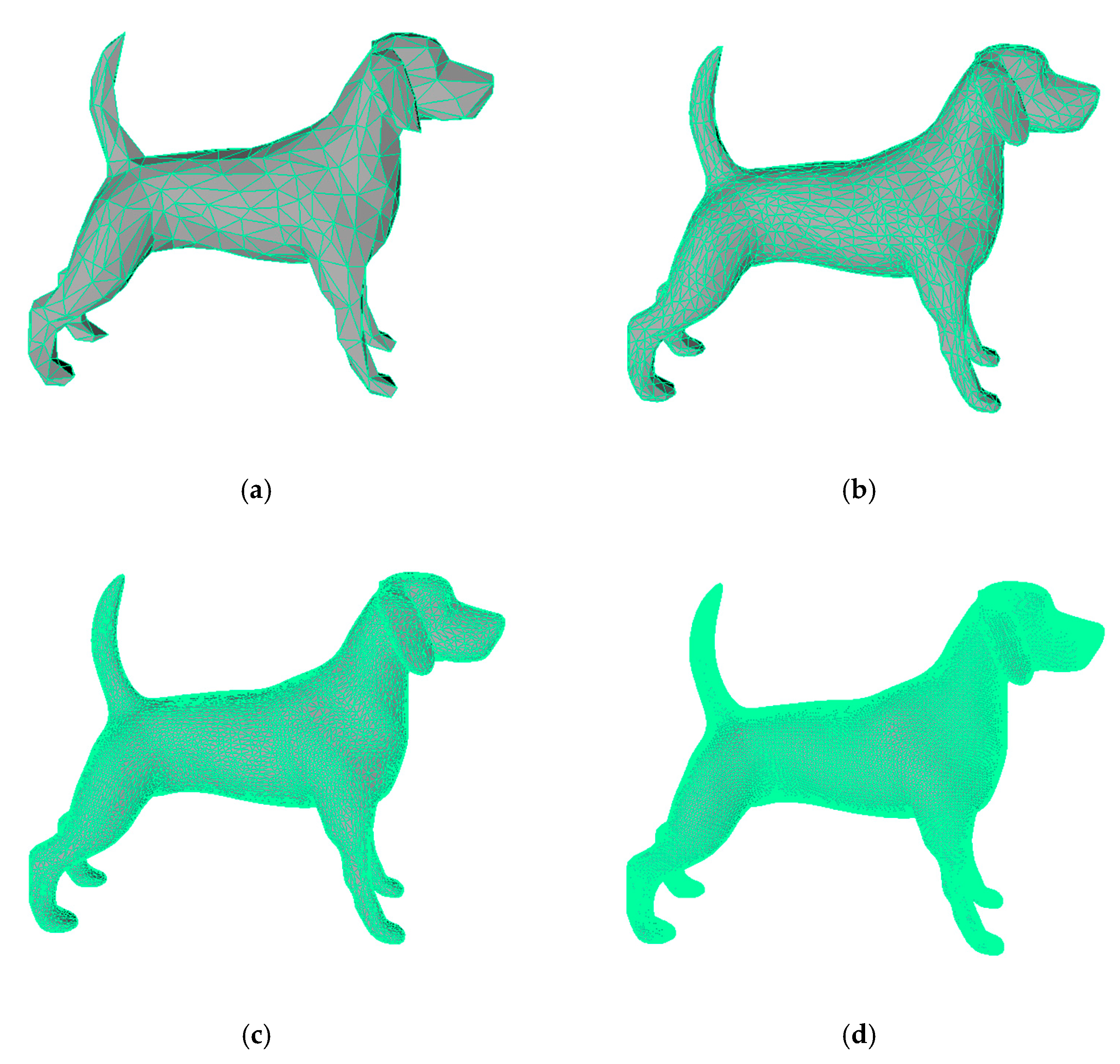
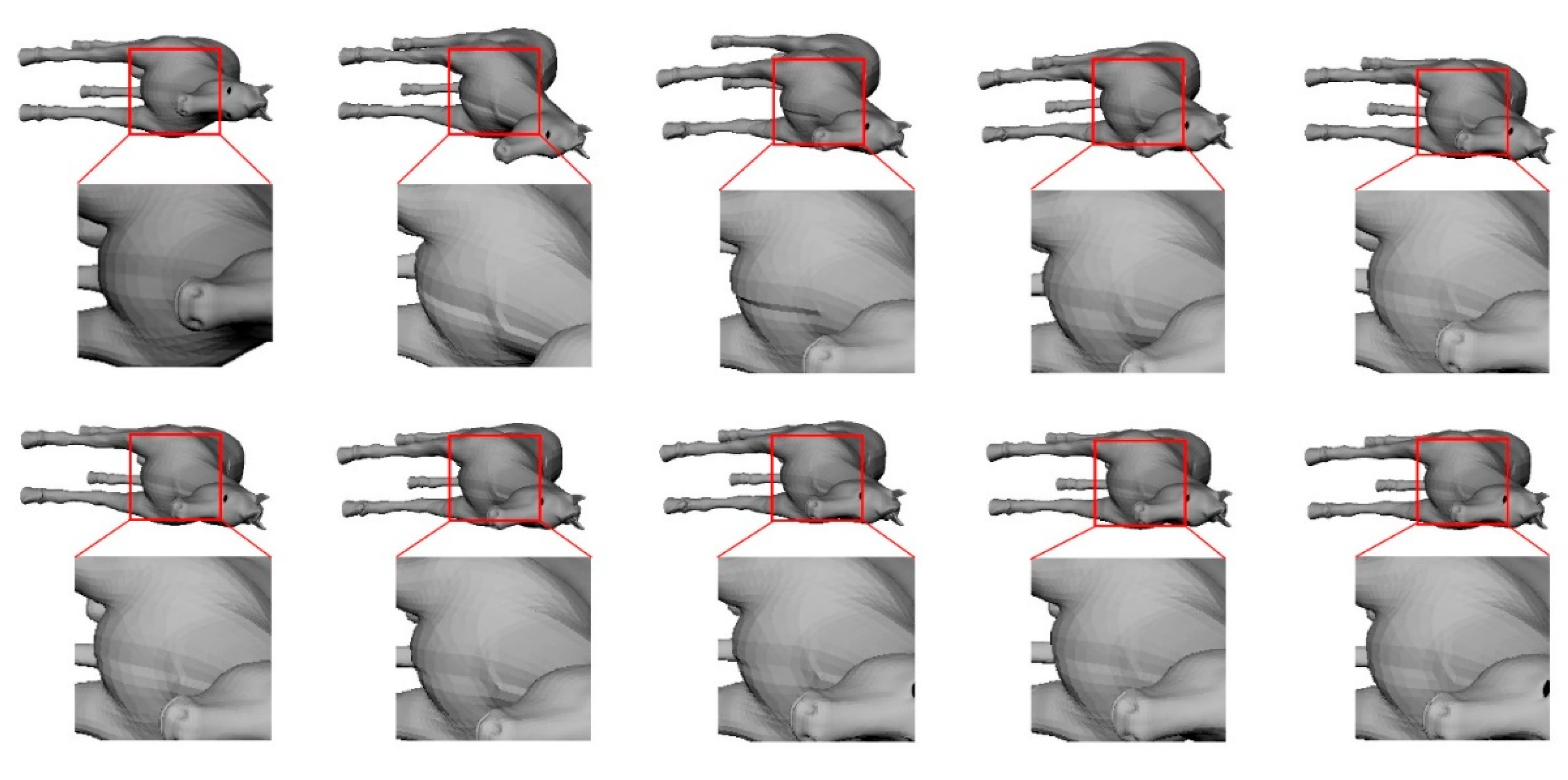




| Model\TET | 100,000 | 20,000 | 4000 | 1000 |
|---|---|---|---|---|
| 100,000 | 243.43 s | 76.74 s | 12.15 s | 3.51 s |
| 20,000 | / | 75.32 s | 13.19 s | 3.34 s |
| 4000 | / | / | 12.62 s | 3.25 s |
| 1000 | / | / | / | 3.15 s |
| PM | PBB | CPU (ms) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PDE | OC | 140 | 8 | 4.641821 | 3.811424 | 4.226623 | 71.60692 | 7.954821 | 71.60692 | 5.7532 |
| B-spline | OC | 140 | 8 | 4.631861 | 3.813969 | 4.222915 | 79.84222 | 7.796782 | 79.84222 | 3.3210 |
| Bézier | OC | 140 | 8 | 4.631861 | 3.813969 | 4.222915 | 79.84222 | 7.796782 | 79.84222 | 2.8257 |
| PDE | CC | 142 | 8 | 4.624602 | 3.810121 | 4.217362 | 71.00726 | 7.620819 | 71.00726 | 5.8322 |
| B-spline | CC | 142 | 8 | 4.615302 | 3.811597 | 4.213450 | 71.01385 | 7.470214 | 71.01385 | 3.5928 |
| Bézier | CC | 142 | 8 | 4.615302 | 3.811597 | 4.213450 | 71.01385 | 7.470214 | 71.01385 | 2.9644 |
| PM | PBB | CPU (ms) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PDE | OC | 132 | 8 | 2.638812 | 3.142145 | 2.890479 | 8.422275 | 19.07610 | 19.07610 | 5.4184 |
| B-spline | OC | 132 | 8 | 2.172167 | 2.181193 | 2.176680 | 80.48240 | 80.82564 | 80.48240 | 3.0592 |
| Bézier | OC | 132 | 8 | 2.172167 | 2.181193 | 2.176680 | 80.48240 | 8.082564 | 80.48240 | 2.6934 |
| PDE | CC | 134 | 8 | 2.632932 | 3.169087 | 2.901010 | 8.077028 | 18.39898 | 18.39898 | 5.4873 |
| B-spline | CC | 134 | 8 | 2.186633 | 2.195735 | 2.191184 | 80.73569 | 81.08065 | 81.08065 | 3.1072 |
| Bézier | CC | 134 | 8 | 2.186633 | 2.195735 | 2.191184 | 80.73569 | 81.08065 | 81.08065 | 2.8346 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, J.; Chaudhry, E.; Iglesias, A.; Macey, J.; You, L.; Zhang, J. Reconstructing Dynamic 3D Models with Small Data by Integrating Position-Based Dynamics and PDE-Based Modelling. Mathematics 2022, 10, 821. https://doi.org/10.3390/math10050821
Fang J, Chaudhry E, Iglesias A, Macey J, You L, Zhang J. Reconstructing Dynamic 3D Models with Small Data by Integrating Position-Based Dynamics and PDE-Based Modelling. Mathematics. 2022; 10(5):821. https://doi.org/10.3390/math10050821
Chicago/Turabian StyleFang, Junheng, Ehtzaz Chaudhry, Andres Iglesias, Jon Macey, Lihua You, and Jianjun Zhang. 2022. "Reconstructing Dynamic 3D Models with Small Data by Integrating Position-Based Dynamics and PDE-Based Modelling" Mathematics 10, no. 5: 821. https://doi.org/10.3390/math10050821
APA StyleFang, J., Chaudhry, E., Iglesias, A., Macey, J., You, L., & Zhang, J. (2022). Reconstructing Dynamic 3D Models with Small Data by Integrating Position-Based Dynamics and PDE-Based Modelling. Mathematics, 10(5), 821. https://doi.org/10.3390/math10050821








