Abstract
The purpose of this work was to conduct a numerical examination of mixed convective heat transfer in a three-dimensional triangular enclosure with a revolving circular cylinder in the cavity’s center. Numerical simulations of the hybrid Fe3O4/MWCNT-water nanofluid are performed using the finite element approach (FEM). The simulation is carried out for a range of parameter values, including the Darcy number (between 10−5 and 10−2), the Hartmann number (between 0 and 100), the angular speed of the rotation (between −500 and 1000), and the number of zigzags. The stream function, isotherms, and isentropic contours illustrate the impact of many parameters on motion, heat transfer, and entropy formation. The findings indicate that for enhancing the heat transfer rates of hybrid nanofluid in a three-dimensional triangular porous cavity fitted with a rotating cylinder and subjected to a magnetic field, Darcy number > 10−3, Hartmann number < 0, one zigzag on the hot surface, and rotation speed >500 in flow direction are recommended.
MSC:
76D05; 80A05; 80M10
1. Introduction
Nanofluids are a unique type of artificial fluid that incorporate nanoparticles. The unique and original properties of nanofluids that encourage us to use it instead of ordinary liquids as a coolant are its greater thermal conductivity and enhanced heat transmission capabilities. Heat pipes, solar receivers, petroleum exploration, chemical engineering, electronics cooling, mechanical engineering, and solar collectors are just a few of the key technologies that can utilize nanofluids to improve their performance [1,2,3]. Suspending nanoparticles in traditional working fluids has been shown to boost heat transfer rates by growing thermal conductivity. Nevertheless, the magnitude of the increment in heat transmission stated in the literature varies greatly. Numerous research articles (both experimental and computational) on application of nanofluids in various fields have been published [4,5,6,7,8].
Yazdanifard et al. [9] investigated the impact of using TiO2/water nanoliquids in a photovoltaic/thermal collector and found that it increased electricity production by 7% and heat output by 55%. Singh et al. [10] investigated the machining performance of a graphene nanoplatelet-based water-based nanoliquid while turning an AISI 304. The findings demonstrated that increasing particle concentrations resulted in a considerable decrease in cutting temperature and surface roughness. Zarifi et al. [11] simulated the neutronic behaviour of VVER-1000 reactors using a variety of water-based nanofluids. The effective multiplication factor was decreased in all nanoliquids; however, the effect varied according to the nanoparticle type. Jin et al. [12] enhanced solar energy collection and conveyance by using a water-based Au (gold) and MWCNTs nanoliquid. A significant increase in energy absorption was seen when nanoparticles were added to water; as compared to pure water, MWCNTs nanoliquid harvests about 5.5 times more energy. Additionally, studies have shown a significant increase in the thermal performance of heat pipes using hybrid nanofluids. Martin et al. [13] investigated the thermal performance of a simple heat pipe charged with an aqueous Fe:CuO hybrid nanoliquid at a 50:50 ratio. Triton X-100 was used as a surfactant to increase the stability of the produced sample. The findings indicated a maximum decrease in thermal resistance of 16.91% using the hybrid nanoliquid at a mass fraction of 2% compared to water.
Vazhnichaya et al. [14] demonstrated that an iron oxide nanoliquid was very successful in stimulating blood cells in healthy animals suffering from anemia due to significant blood loss. Yew et al. [15] conducted a review of the research on the uses of Fe3O4 nanoparticles in the biomedical sector, focusing on their potential for cancer therapy. According to their findings, biosynthesized Fe3O4 nanoparticles are capable of accumulating and delivering more medicines to the targeted location. More precisely, following injection into the bloodstream, these particles may be manipulated or steered by an external magnetic field [16,17]. Sun et al. [18] studied the cooling performance of a mini-channel heat sink using deionized copper and alumina nanofluids. It was discovered that tested nanofluids performed admirably and significantly improved heat sink cooling performance. When compared to deionized water, a temperature reduction of 4 to 18 °C was seen in the CPU chip. According to the literature about nanofluids, it is well-documented that they are greatly affected by various external factors such the presence of radiation, magnetic fields, porous media, geometrical parameters and operating parameters. Recent research has focused on the effect of spinning cylinders, porous media, and magnetic forces on the mixed convection flow of nanofluids, since these techniques are good for managing the flow and movement of energy within nanofluids.
Krishna et al. [19] used the Laplace transform to examine the unsteady MHD non-Newtonian Casson hybrid nanoliquid flow over an infinite exponentially accelerated vertical moving porous surface. The temperature may be increased by raising the nanoparticle concentration. Aly et al. [20] explored the fluctuations of magnetised Cu-water nanofluid confined inside a rectangular finned enclosure with a central obstruction and observed that the Hartmann number and fins had a major influence on the hydrothermal variations. Manna et al. [21] studied the impact of an intermittent banded magnetic field spatially applied over a porous enclosure filled with a hybrid nanofluid that was heated differentially. Their results suggest that using a partial magnetic band to passively adjust thermal parameters may be a viable strategy. Sheikholeslami et al. [22] investigated 3D MHD nanofluid flow and heat transfer using Buongiorno’s model, stating explicitly that the Reynolds number had the opposite influence on heat transfer rate as the thermophoretic and Brownian parameters did. Seyyedi et al. [23] examined the entropy of a magnetised Cu-water nanofluid contained inside a porous wavy hexagonal container. The findings suggested that the lack of a magnetic field increased heat transfer by 2.9%. Ghalambaz et al. [24] examined the non-uniform magnetic effects on a nanofluidic stream within a hexagonal chamber and concluded that when the Hartmann number increases, both the heat-mass transit and the Hartmann number decrease. Haq et al. [25] demonstrated a nanofluidic stream of CuO and water enclosed inside a trapezoidal compartment with a heated inner trapezoidal barrier. They observed significant thermal repercussions of the Rayleigh number, but reduced heat transfer with increasing nanoparticle concentration.
Numerous authors have examined the effects of spinning cylinders, and they all agree that the direction in which the cylinders revolve, their rotational speed, and their position all have an effect on heat transfer [26,27,28,29,30,31,32,33,34]. Siavashi et al. [35] examined mixed convection in a partially porous square container containing a non-Newtonian CuO/water nanoliquid and a revolving inner cylinder. They observed that boosting convection may result in an increase in heat transfer, while lowering viscosity can result in a decrease in heat transmission. Jasim et al. [36] studied an internally spinning adiabatic cylinder encased inside a vented chamber filled with a hybrid nanofluid. The findings indicate that increasing the volume percentage of solid particles in hybrid nanofluids improves energy transmission, albeit at the price of a larger pressure drop. Chatterjee et al. [37] investigated mixed convection in a cavity filled with a copper/water nanofluid and including a rotating adiabatic circular cylinder. According to legend, the top wall was cold and moving to the right, while the bottom wall stayed stationary and heated. It was discovered that when the nanofluid concentration increased and the cylinder’s spinning speed decreased, the Nusselt number increased. Hussain et al. [38] investigated the impact of spinning cylinders on the flow path of a channel that had been displaced by force. The findings suggested that the rotation of the cylinders had a noticeable effect on the flow. As a consequence of the cylinder’s clockwise spin, the running stream is pushed around it, modifying its flow pattern and temperature properties.
Arani et al. [39] investigated the flow, heat transmission, and creation of entropy in a triangular enclosure with a spinning adiabatic barrier. The blade form, they observed, has the greatest average Nusselt number, followed by the brick, platelet, and cylinder shapes. Haq et al. investigated the viscous fluid flow inside a partially heated lid-driven hexagonal enclosure with a heated circular barrier. [40] According to them, Reynolds and Richardson’s values are positively related to heat transfer amplification. Numerous investigations have also been conducted to determine the effect of the form of the contact surface on the thermal convection of flowing nanofluids. Alsabery et al. [41] investigated the buoyancy-induced convection of Al2O3-water nanoliquid flow inside a porous media in a side-cooled wavy cavity heated from below using a computer model. Their results indicate that wall waviness, as well as other flow-controlling properties, had a significant effect on thermal convection. Hamzah et al. [42] investigated the MHD thermal transport mechanism of an Al2O3-water nanoliquid in a wavy porous multilayer enclosure with varying temperatures. They observed that the waviness and porosity of the porous membrane had a significant effect on heat transfer. Cimpean et al. [43] simulated steady natural convection in an inclined square porous cavity filled with nanofluid and subjected to a sinusoidal temperature distribution using numerical simulations. They focused on the effects of heat and fluid flow on the inclination angle and periodic thermal boundary conditions.
According to the research stated before and to the best of the authors’ knowledge, the mixed convection flow and heat transfer within a three-dimensional triangular chamber with an internal rotating cylinder and zigzag-patterned hot wall have never been identified previously. As a result, it is considered that this research is unique and worthwhile. The current study used computational modeling to investigate the stable laminar mixed convection of a hybrid nanoliquid (Fe3O4 and MWCNT/water) inside a 3-D triangular porous chamber under the influence of an internal centrally located spinning circular cylinder and magnetic field. It is worth noting that the examined issue may be seen as a heat transfer performance study for a heat exchanger, an electronic heated element mounted vertically, or a solar collector operating under the effect of a smart working fluid (nanofluid). All of these issues are connected to the enhancement of convective energy transport and the advancement of heat transfer control systems.
2. Mathematical Model
The convective flow described in this work is constant, three-dimensional, and laminar. Figure 1 depicts the computational domain, which comprises porous media saturated with hybrid nanofluid, as well as the boundary conditions connected with it. The bottom wall and the cylinder are insulated, whereas the vertical side wall and inclined wall are heated and cooled, respectively. To test for the impact of enclosure geometry, various patterns for the zigzag wall on the vertical sidewall are investigated. Magnetic field effects are also taken into account by providing a steady magnetic field along the positive Z-axis. Water as a base liquid is combined with Fe3O4 and MWCNT nanoparticles to form the working suspensions. Table 1 summarizes the thermophysical characteristics of both the base fluid and nanoparticles. The one–energy equation model is used, with the assumption that the mixture density is a linear function of the temperature. Taking these assumptions into account, the governing equations for the studied case are as follows:
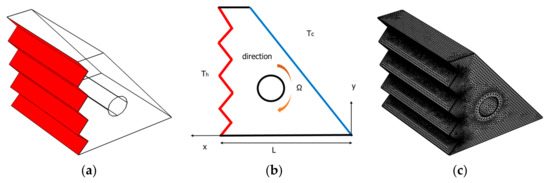
Figure 1.
The computational domain: (a) 3D view of the enclosure; (b) 2D view of the geometry with illustrations of the boundary conditions. (c) Grid mesh.
The mass, momentum, and energy conservation equations, as well as the entropy generation equation, may be expressed in a three-dimensional Cartesian coordinate system as follows [44]:
The conservation equations (CEs) are expressed in the porous area.
The non-dimensional parameters are denoted by the following:
It is noted that the last term on the right-hand side of Equations (3) and (4) represents the Lorentz force as a function of Hartmann number. The Hartmann number is taken as constant in our study.

Table 1.
Nanoparticles and base fluid thermos-physical properties [45].
Table 1.
Nanoparticles and base fluid thermos-physical properties [45].
| Pure Water | Fe3O4 | MWCNT | |
|---|---|---|---|
| (kg/m3) | 997.1 | 5180 | 2100 |
| Cp (J/kg k) | 4179 | 670 | 710 |
| (W/m k) | 0.613 | 9.7 | 2000 |
The governing equations’ boundary conditions are as follows:
Hypotenuse side walls:
Front and back walls:
Bottom wall:
Cylinder:
with .
Entropy generation can be written in dimensionless form as follows:
The correlations listed in Table 2 were utilized to determine the hybrid nanoliquid thermophysical properties, such as fluid density, viscosity, heat capacity, thermal conductivity, electrical conductivity, and so on, which are important to calculate flow and heat characteristic that are presented in the conservation equations. These equations are typically used in the literature to determine the properties of the nanofluids and hybrid nanofluids.

Table 2.
Properties of nanofluids and hybrid nanofluids.
The amount of entropy in a nanoliquid’s motion is predicted to change. Due to the fact that heat transfer is subject to specific variations, the total entropy may be characterized as follows:
and are estimated as:
While the entropy generation number is useful for creating entropy generation profiles or maps, it does not indicate whether fluid friction or heat transfer is dominant.
The Bejan number (Be), which is the ratio of heat transfer irreversibility to the total entropy generation, can be mathematically expressed as
The Bejan number is between 0 and 1.
Thus, Be = 1 is the limit at which irreversibility of heat transmission prevails, Be = 0 is the opposite limit at which fluid friction effects dominate irreversibility, and Be = 1/2 is the limit at which the rates of heat transfer and fluid friction entropy production are equal
3. Validation and Mesh Evaluation
Five distinct grids were employed to ensure that the findings were not grid-dependent. Nuavg and the Bejan number are used to establish the independence of heat transfer from the number of grids (see Table 3). Due to the variability of the findings, the fourth grid was chosen as the final grid in all situations, as seen in Figure 1. As a main criterion for reaching findings, Ghasemi et al.’s [46] past investigations were employed to validate our model, as seen in Figure 2.

Table 3.
Different mesh size for Ha = 0 and φ = 0.02.
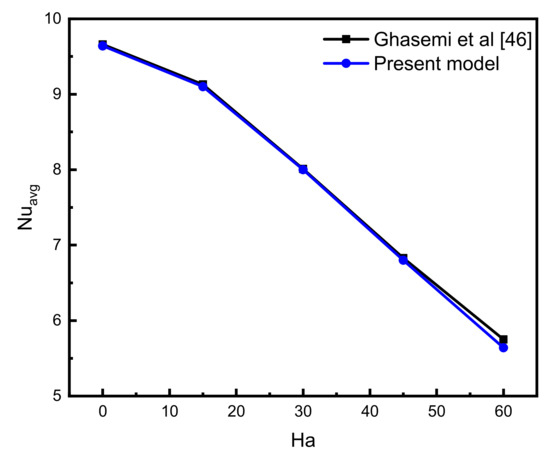
Figure 2.
Comparisons of present model with previous works [46].
It is critical to note that the governing equations and associated limitations are solved using the Galerkin finite element method. The Galerkin weighted residual finite element method solves the equations numerically. The programming environment is segregated in triangle pieces. Triangular Lagrange finite elements of different orders are employed on any of the flow variables inside the code domain. The residue is obtained by substituting the governing equations for the approximations.
4. Results and Discussion
To understand the thermal-hydraulic characteristics of a nanofluid’s flow in an enclosure (subjected to a magnetic field and having a porous medium and a moving cylinder), the following results in terms of 3-D surface plots are devoted to showing a complete picture about the thermal-hydraulic visualization inside the investigated cavity (see Figure 1). These massive visualizations expose the influence of essential parameters, such as the Darcy number (flow permeability in a porous medium), the Hartmann number (the effect of the magnetic field on the fluid flow), and the cylinder rotation speed and direction (for mixed convection heat transfer), on the fluid flow and heat transfer in terms of streamlines (flow streams), dimensionless isotherms (showing the hot and cold regions), and the Bejan number (evaluating the entropy generation by heat transfer to the total entropy generation).
Figure 3 depicts the effect of the Darcy number, Da, on the flow streamlines, isotherms, and the Bejan number. Four values of Da are selected, including 10−5, 10−4, 10−3, and 10−2,, to demonstrate the ease of flow at higher Da values due to increased permeability, resulting in enhanced heat transfer and minimized entropy generation. It is noted from the figure that flow streamlines pronounce themselves more with higher Da values, which is expected due to low flow resistance (more fluidity) with higher permeability (Da) values. Due to the zigzag feature at the hot surface, the streamlines are less smooth in the left region of the cavity compared to those closer to the colder surface (the right region)—two primary vortices are generated around the cylinder.
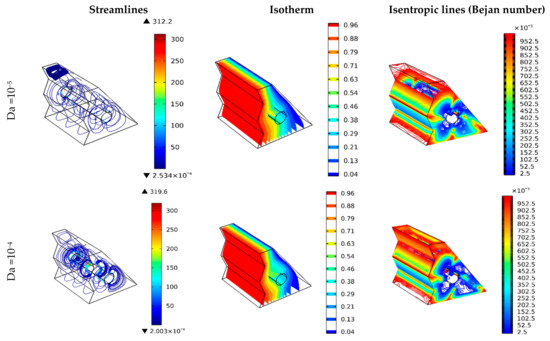
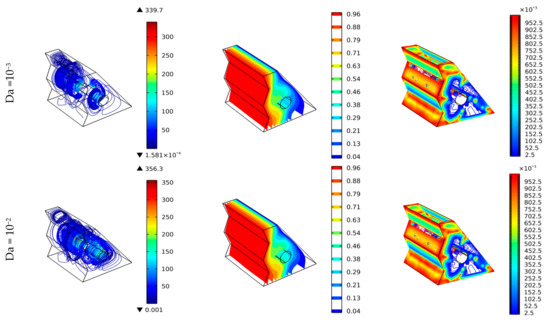
Figure 3.
Three-dimensional surface plots to show the effect of Darcy number (permeability) on the streamlines, temperature in terms of dimensionless isotherms, and Bejan number.
The effect of fluidity enhancements on the heat transfer with increased Da values is shown in the isotherm plots (second column in Figure 3). Instinctually, the heat transfer is from the hot surface to the cold surface, and due to the moving cylinder, the heat transfer is dominated by the mixed convection mechanism. Therefore, the isotherms show a consecutive temperature distribution from the hot surface to the cold one. By increasing Da values, the temperature values at the middle cavity (closer to the cylinder) illustrate better mixed hot and cold streams. This explains the increased heat transfer rates when Da is raised, which shows the influence of the cylinder rotation. The better heat transfer rates are obtained for Da > 10−3. Despite the fact that the cylinder rotation provides a mixed convection heat transfer, the lower value of Da increases the flow resistance. It may restrict the heat transfer to being the natural one. Thus, higher permeability values are recommended to improve flow and heat transfer characteristics.
The Bejan number as an indicator of the participation by heat transfer in the total entropy generation is an important guidance factor in helping minimize the irreversibility due to heat transfer. Therefore, Figure 3 (the 3rd column) visualizes the heat transfer contribution to the total entropy generation at different Da values. Since heat transfers from walls to the nanofluids, it is typical to see entropy generation closer to the walls (>0.7 Be), particularly when the heat transfer has lower values due to flow restrictions such as those at the corners (lower velocity) of the enclosure. For increasing Da values, both heat transfer entropy generation and friction entropy generation are anticipated to decrease due to increased flow velocity. However, the enhancement in the entropy generation drop due to heat transfer is more than that of the friction, lowering the Bejan number, as shown in Figure 3 (the 3rd column). To sum up, the higher Da values result in improved heat transfer and fluid flow, minimizing the entropy generation (majority of which is due to the friction) and improving the fluidity (flow movement) in the porous media.
The Hartmann number (Ha) is also an important index when a magnetic field (of an external transverse magnet) is applied to enhance heat transfer and fluid flow. It accounts for the hydromagnetic body force (Lorentz force) over the viscous resistance. Higher Ha values mean the hydromagnetic body force is dominant whereas the nanofluids viscosity effect is less. For such scenarios, Figure 4 shows the visualization plots of streamlines, isotherms, and Bejan number values under the impact of different Ha values (i.e., 0, 25, 50, and 100).
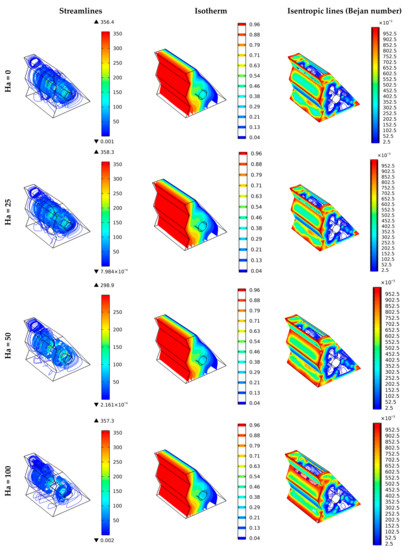
Figure 4.
Three-dimensional surface plots to show the effect of the Hartmann number on the streamlines, temperature in terms of dimensionless isotherms, and Bejan number.
It is shown in Figure 4 that the increase in Ha decreases the streamlines’ intensity due to hindering the typical flow direction (which should be clockwise) as the magnetic field is applied from the left to the right. Due to the circulation of the fluid inside the porous cavity affected by the cylinder rotation, even Ha = 100 does not significantly influence the fluid flow and heat transfer (as shown in the 2nd column). More details about the effect of Ha are shown in Figures 7 and 8. Bejan number plots (the 3rd column) demonstrate increased heat transfer participation in the total entropy generation since friction losses could be less minimized for higher Ha values.
The effect of cylinder rotation (clockwise and counter-clockwise) on the nanofluid’s flow and heat transfer characteristics in a cavity filled with porous media is shown in Figure 5. It is evident that streamlines have one vortex (around the cylinder) for Ω = 0 [rad/s] (no rotation), which is attributed to the natural convection heat transfer from right to left at the top and from left to right at the bottom of the cavity influenced by the nanofluid’s density minimized upwards closer to the hot zigzagged wall. For this reason, heat transfer amounts are also lower than other cases (i.e., rotating cylinder), and the associated entropy generation is high at the wall’s corners and even closer to the stationary cylinder. The scenario is different when Ω = ±500 [rad/s], in which two large vortices appear in the cavity: one at the left zone and one at the right zone owing to the cylinder rotation. The difference between clockwise rotation (Ω = −500 [rad/s]) and the opposite one (Ω = 500 [rad/s]) is that the streamlines and heat transfer rates are better for clockwise rotation due to increasing the nanofluid’s velocity in the typical direction (left to right at the top and right to left at the bottom of the cavity) resulting in better mixed convection heat transfer. In addition, the entropy generation participation of heat transfer is lower for the clockwise rotating cylinder, as shown by lower Bejan number values.
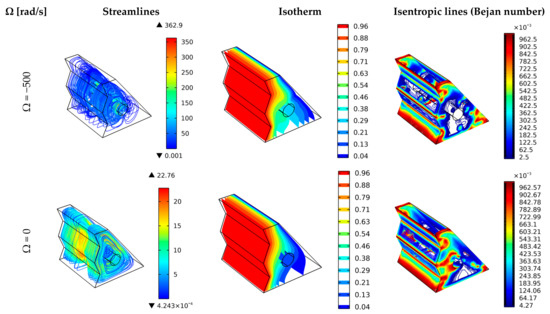
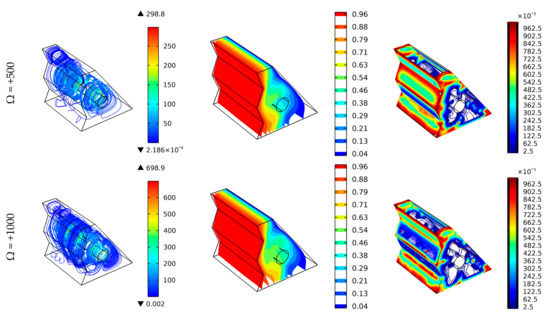
Figure 5.
Three-dimensional surface plots to show the effect of the cylinder rotation direction on the streamlines, temperature in terms of dimensionless isotherms, and Bejan number.
For higher values of cylinder rotation, such as in the case of Ω = 1000 [rad/s], mixing hot and cold streams is improved, resulting in better heat transfer rates and lower Bejan number values. From these results presented for Ω = ±500 [rad/s] and Ω = 1000 [rad/s], it can be expected that Ω = −1000 [rad/s] will lead to much better heat transfer and fluid flow characteristics due to increasing the flow velocity in the same direction of the cylinder rotation.
As the zigzagged wall is used, the number of zigzags (i.e., 1, 2, and 4) is investigated to show their effect on the flow and heat transfer behavior, as shown in Figure 6. As evident, increasing the number of zigzags makes the wall appear as a coarsely roughed flat wall where the isotherms are almost vertical (as in N = 4), and the effect of cylinder rotation is minimized. It is also due to the horizontal distance between the cylinder and hot wall being wider for the studied cases of N = 2 and 4. In other words, the higher flow area (between the cylinder and the hot wall) results in lower heat transfer rates. The heat transfer and streamlines behaviors have the same trends as the natural heat transfer mechanism for N = 2 and 4. In addition, the entropy generation closer to the cylinder is high (repeating a similar effect for Ω = 0 [rad/s] in Figure 5).
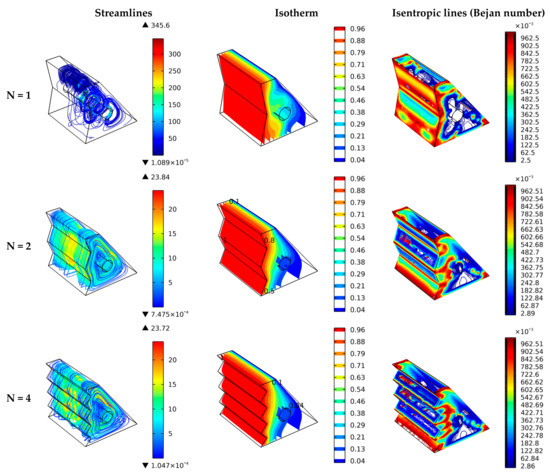
Figure 6.
Three-dimensional surface plots to show the effect of the zigzag number on the streamlines, temperature in terms of dimensionless isotherms, and Bejan number.
For N = 1, the fluid flow between the rotating cylinder and the hot wall is expected to be faster, leading to better streamlines and temperature mixture of hot and cold zones and thereby higher heat transfer rates. Thus, the increased zigzag number reduces the flow motion in porous media. The flow motion could be raised for the forced heat transfer mechanism when additional force is applied to circulate the flow on the roughened surface (like zigzag), yielding higher turbulence. For mixed convection heat transfer, it appears that N = 1 is sufficient. Bejan number values are higher in the regions closer to the hot surface (zigzags) for N = 1 case due to minimizing the friction effect at the hot surface.
To show the effect of the above-discussed parameters (Da, Ha, Ω, and N) on the heat transfer and its entropy generation contribution, the average Nusselt number (NuAvg) and average Bejan number (BeAvg) values profiles are highlighted.
Figure 7 shows the change in NuAvg with the variation in Ha and Ω values. It is clear that the increase in Ha values reduces the heat transfer rates, as discussed in Figure 4. The noticeable trend observed here is that the increase of Ha values up to 22 has a slight effect compared to those > 22, which means the Ha > 22 could show the flow hindering effect of the magnetic field (Lorentz force). However, the decrease in the heat transfer index (NuAvg) is not considered high for the mixed heat transfer mechanism due to the cylinder rotation. For example, at Ω = 1000 [rad/s], the NuAvg is equal to ~5.78 at Ha = 0, while it is about 5.20 for Ha = 100. The effect of rotation speed and direction on NuAvg are similar to those already discussed in Figure 5, in which the higher speed in the same flow direction improves the heat transfer rates.
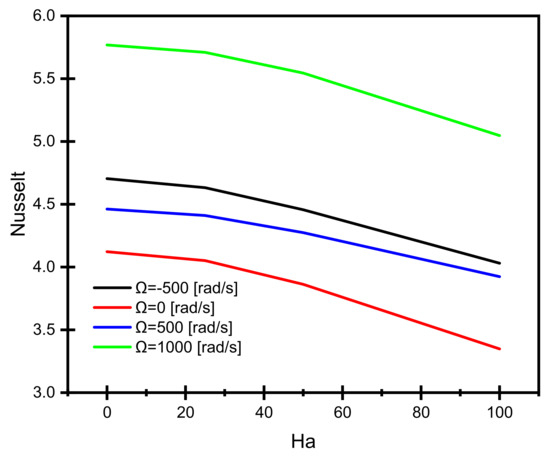
Figure 7.
Effect of the Hartmann number on the average Nusselt number at different values and directions of the cylinder rotation.
At the same conditions of Figure 7, BeAvg values slightly increase when Ha < 22 and then gradually rise for Ha > 22, as shown in Figure 8. Better BeAvg values are obtained with higher cylinder rotation speed, especially when the direction is clockwise, and lower Ha values due to improved mixed-convection heat transfer and decreased irreversible heat losses.
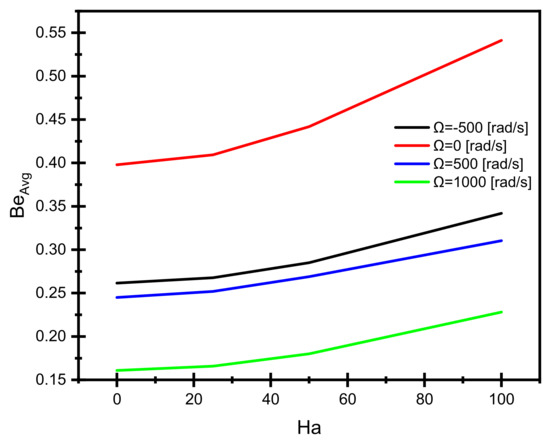
Figure 8.
Effect of the Hartmann number on the average Bejan number at different values and directions of the cylinder rotation.
Figure 9 repeats the facts discussed in Figure 3 that the heat transfer values (in terms of NaAvg) are increased with increased Da values due to improving the fluidity inside the porous media. Furthermore, because of increased fluidity, the improved heat transfer minimizes the Be values, as shown in Figure 10. Again, better NuAvg and lower BeAvg values are associated with higher Ω values having similar flow direction, as shown in Figure 9 and Figure 10, respectively.
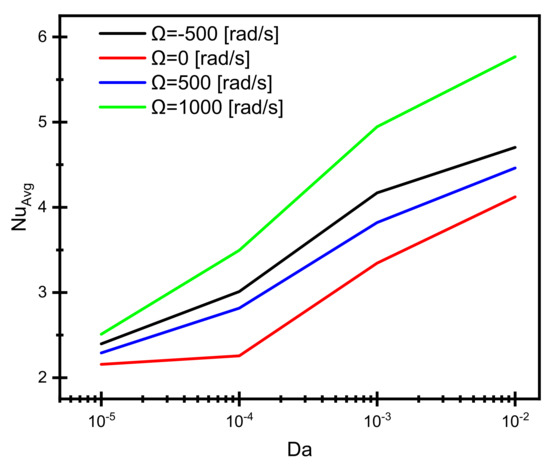
Figure 9.
Effect of the Darcy number on the average Nusselt number at different values and directions of the cylinder rotation.
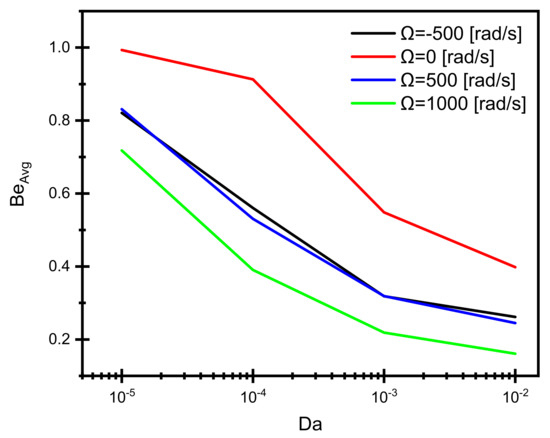
Figure 10.
Effect of the Darcy number on the average Bejan number at different values and directions of the cylinder rotation.
The zigzags number (N) is also important to improve heat transfer; however, for the investigated geometries, N = 1 results in more heat transfer rates and lower Bejan number values as shown in the visualization plots (Figure 6—the second and third columns) and confirmed again here in Figure 11 and Figure 12. This is valid for the mixed heat transfer and could be different for forced heat transfer in which more zigzags number could lead to more turbulence. Notably, Ω = −500 [rad/s] shows better performance than that of Ω = 500 [rad/s]. Thus, it is expected that Ω = −1000 [rad/s] will lead to better performance than Ω = 1000 [rad/s] (shown in the figure) due to increased flow velocity.
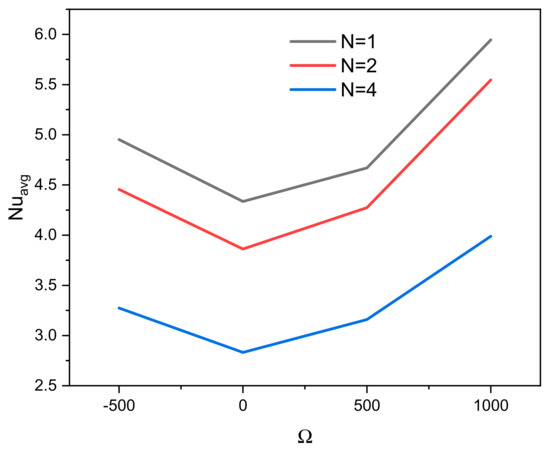
Figure 11.
Effect of the values and direction of the cylinder rotation on the average Nusselt number for three zigzags number of the hot wall.
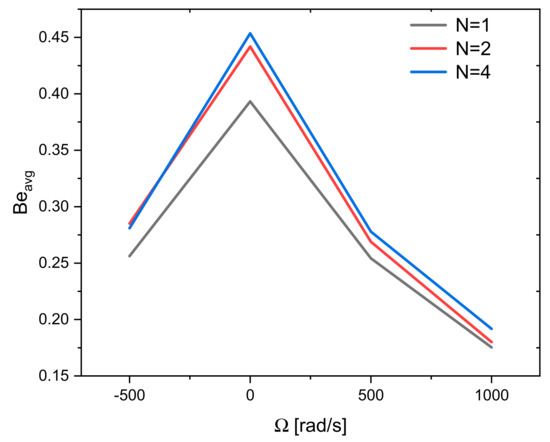
Figure 12.
Effect of the values and direction of the cylinder rotation on the average Bejan number for three zigzags number of the hot wall.
5. Conclusions
A porous cavity filled with Fe3O4/MWCNT-water hybrid nanofluid and equipped with a moving cylinder is investigated for thermal-hydraulic enhancements. The cavity is a trapezoid with a zigzagged hot wall on the left, while the right wall is cold, and the others are well-insulated. Three-dimensional CFD-based simulation was conducted using the Galerkin finite element (GFEM) method with a triangle element shape to simulate the investigated cavity. The developed model was validated against reported experimental data in the literature.
The fluid flow and heat transfer characteristics in terms of streamlines, isotherms, and Bejan number values are massively visualized in 3-D surface plots, while the average Nusselt number and average Bejan number profiles are plotted against Darcy number (10−5, 10−4, 10−3, and 10−2), Hartmann number (0, 20, 50 and 100), rotating cylinder speed (−500, 0, 500, 1000), and the number of zigzags of the hot wall (1, 2, and 4). Based on the investigated parameters, the following conclusions are drawn:
- -
- Higher Darcy number values enhance the fluid flow, temperature distribution, and heat transfer and minimize heat transfer’s contribution to the total entropy generation.
- -
- The effect of the Hartmann number on the flow characteristic is not high for mixed heat transfer flow in a porous cavity having a zigzagged wall; however, values of >22 (Hartmann number) could be avoided.
- -
- Clockwise rotation of the embedded cylinder enhances the heat transfer and fluidity better than a counter-clockwise one. However, both directions lead to a better heat transfer mechanism than the stationary cylinder (natural convection).
- -
- For the investigated geometries, one zigzag on the hot wall is sufficient to enhance the heat transfer rates and reduce the entropy generation contribution from the heat losses.
To sum up, for enhancing the heat transfer rates in a porous cavity having an embedded rotating cylinder and subjected to a magnetic field, Darcy number of >10−3, Hartmann number <0, one zigzag on the hot surface, and cylinder rotation of >500 in flow direction are recommended.
Author Contributions
Conceptualization, A.M. and A.A.; methodology, N.A.S. and J.D.C. software, A.M.; validation, O.Y. and N.A.A.Q.; formal analysis, R.M.; investigation, A.M.; resources, J.D.C.; data curation, O.Y.; writing—original draft preparation, A.M. and A.A.; writing—review and editing, all authors; visualization, R.M.; supervision, N.A.A.Q.; project administration, A.A.; funding acquisition, R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by King Khalid University, grant number RGP.1/173/42.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through the group research program under grant number R.G. P. 1/173/42. This work was supported by a Korea Institute of Energy Technology Evaluation and Planning (KETEP) grant funded by the Korea government (MOTIE) (No. 20192010107020, Development of hybrid adsorption chiller using unutilized heat source of low temperature).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| List of Symbols | |
| Specific heat capacity (Jkg−1 K−1) | |
| Dimensionless of triangular cavity (m) | |
| Pressure (Pa) | |
| Temperature (K) | |
| Dimensionless Cartesian coordinates | |
| Hartmann number | |
| Prandtl number | |
| Permeability | |
| Intensity of magnetic field | |
| Gravitational acceleration (ms−2) | |
| Thermal conductivity (Wm−1 K−1) | |
| Dimensionless pressure | |
| Velocity components (ms−1) | |
| Dimensional Cartesian coordinates (m) | |
| Rayleigh number | |
| Nu | Nusselt number |
| Radius of cylinder | |
| Forchheimer coefficient | |
| Greeks symbols | |
| Porosity | |
| Subscripts | |
| Fluid | |
| np | Solid particles |
| loc | Local |
| c | Cold |
| hnf | Hybrid nanofluid |
| avg | Average |
References
- Mahian, O.; Kianifar, A.; Kalogirou, S.A.; Pop, I.; Wongwises, S. A review of the applications of nanofluids in solar energy. Int. J. Heat Mass Transf. 2013, 57, 582–594. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Xu, B.; Yuan, M. Nanofluid research and applications: A review. Int. Commun. Heat Mass Transf. 2021, 127, 105543. [Google Scholar] [CrossRef]
- Okonkwo, E.C.; Wole-Osho, I.; Almanassra, I.W.; Abdullatif, Y.M.; Al-Ansari, T. An updated review of nanofluids in various heat transfer devices. J. Therm. Anal. 2021, 145, 2817–2872. [Google Scholar] [CrossRef]
- Pare, A.; Ghosh, S.K. A unique thermal conductivity model (ANN) for nanofluid based on experimental study. Powder Technol. 2021, 377, 429–438. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Javed, S.; Oztop, H.F.; Said, Z.; Pandya, N.S. Experimental and numerical investigation on the thermal performance of triple tube heat exchanger equipped with different inserts with WO3/water nanofluid under turbulent condition. Int. J. Therm. Sci. 2021, 164, 106861. [Google Scholar] [CrossRef]
- Mourad, A.; Abderrahmane, A.; Younis, O.; Marzouki, R.; Alazzam, A. Numerical Simulations of Magnetohydrodynamics Natural Convection and Entropy Production in a Porous Annulus Bounded by Wavy Cylinder and Koch Snowflake Loaded with Cu–Water Nanofluid. Micromachines 2022, 13, 182. [Google Scholar] [CrossRef] [PubMed]
- Al-Kouz, W.; Aissa, A.; Koulali, A.; Jamshed, W.; Moria, H.; Nisar, K.S.; Mourad, A.; Abdel-Aty, A.-H.; Khashan, M.M.; Yahia, I.S. MHD darcy-forchheimer nanofluid flow and entropy optimization in an odd-shaped enclosure filled with a (MWCNT-Fe3O4/water) using galerkin finite element analysis. Sci. Rep. 2021, 11, 22635. [Google Scholar] [CrossRef]
- Shahzad, F.; Jamshed, W.; Sathyanarayanan, S.U.D.; Aissa, A.; Madheshwaran, P.; Mourad, A. Thermal analysis on Darcy-Forchheimer swirling Casson hybrid nanofluid flow inside parallel plates in parabolic trough solar collector: An application to solar aircraft. Int. J. Energy Res. 2021, 45, 20812–20834. [Google Scholar] [CrossRef]
- Yazdanifard, F.; Ebrahimnia-Bajestan, E.; Ameri, M. Performance of a parabolic trough concentrating photovoltaic/thermal system: Effects of flow regime, design parameters, and using nanofluids. Energy Convers. Manag. 2017, 148, 1265–1277. [Google Scholar] [CrossRef]
- Singh, R.K.; Sharma, A.K.; Bishwajeet; Mandal, V.; Gaurav, K.; Nag, A.; Kumar, A.; Dixit, A.R.; Mandal, A.; Das, A.K. Influence of graphene-based nanofluid with minimum quantity lubrication on surface roughness and cutting temperature in turning operation. Mater. Today Proc. 2018, 5, 24578–24586. [Google Scholar] [CrossRef]
- Zarifi, E.; Jahanfarnia, G.; Veysi, F. Thermal–hydraulic modeling of nanofluids as the coolant in VVER-1000 reactor core by the porous media approach. Ann. Nucl. Energy 2013, 51, 203–212. [Google Scholar] [CrossRef]
- Jin, H.; Lin, G.; Zeiny, A.; Bai, L.; Cai, J.; Wen, D. Experimental study of transparent oscillating heat pipes filled with solar absorptive nanofluids. Int. J. Heat Mass Transf. 2019, 139, 789–801. [Google Scholar] [CrossRef]
- Martin, K.; Sözen, A.; Çiftçi, E.; Ali, H.M. An experimental investigation on aqueous Fe–CuO hybrid nanofluid usage in a plain heat pipe. Int. J. Thermophys. 2020, 41, 1–21. [Google Scholar] [CrossRef]
- Vazhnichaya, Y.; Mokliak, Y.; Zabozlaev, A. Effectiveness of magnetite nanoparticles stabilized by 3-hydroxypyridine derivative and polyvinyl pyrrolidone in experimental therapy of acute blood loss. Med. Technol. Med. 2015, 7, 84–91. [Google Scholar] [CrossRef][Green Version]
- Yew, Y.P.; Shameli, K.; Miyake, M.; Khairudin, N.B.B.A.; Mohamad, S.E.B.; Naiki, T.; Lee, K.X. Green biosynthesis of superparamagnetic magnetite Fe3O4 nanoparticles and biomedical applications in targeted anticancer drug delivery system: A review. Arab. J. Chem. 2020, 13, 2287–2308. [Google Scholar] [CrossRef]
- Tzirtzilakis, E. A mathematical model for blood flow in magnetic field. Phys. Fluids 2005, 17, 077103. [Google Scholar] [CrossRef]
- Boghi, A.; Russo, F.; Gori, F. Numerical simulation of magnetic nano drug targeting in a patient-specific coeliac trunk. J. Magn. Magn. Mater. 2017, 437, 86–97. [Google Scholar] [CrossRef]
- Sun, B.; Liu, H. Flow and heat transfer characteristics of nanofluids in a liquid-cooled CPU heat radiator. Appl. Therm. Eng. 2017, 115, 435–443. [Google Scholar] [CrossRef]
- Krishna, M.V.; Ahammad, N.A.; Chamkha, A.J. Radiative MHD flow of Casson hybrid nanofluid over an infinite exponentially accelerated vertical porous surface. Case Stud. Therm. Eng. 2021, 27, 101229. [Google Scholar] [CrossRef]
- Aly, A.M.; Mohamed, E.M.; Alsedais, N. The magnetic field on a nanofluid flow within a finned cavity containing solid particles. Case Stud. Therm. Eng. 2021, 25, 100945. [Google Scholar] [CrossRef]
- Manna, N.K.; Mondal, M.K.; Biswas, N. A novel multi-banding application of magnetic field to convective transport system filled with porous medium and hybrid nanofluid. Phys. Scr. 2021, 96, 065001. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.G.-D. Three dimensional heat and mass transfer in a rotating system using nanofluid. Powder Technol. 2014, 253, 789–796. [Google Scholar] [CrossRef]
- Seyyedi, S.M.; Dogonchi, A.; Hashemi-Tilehnoee, M.; Ganji, D.; Chamkha, A.J. Second law analysis of magneto-natural convection in a nanofluid filled wavy-hexagonal porous enclosure. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 4811–4836. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Sabour, M.; Sazgara, S.; Pop, I.; Trâmbiţaş, R. Insight into the dynamics of ferrohydrodynamic (FHD) and magnetohydrodynamic (MHD) nanofluids inside a hexagonal cavity in the presence of a non-uniform magnetic field. J. Magn. Magn. Mater. 2020, 497, 166024. [Google Scholar] [CrossRef]
- Haq, R.U.; Aman, S. Water functionalized CuO nanoparticles filled in a partially heated trapezoidal cavity with inner heated obstacle: FEM approach. Int. J. Heat Mass Transf. 2019, 128, 401–417. [Google Scholar] [CrossRef]
- Al-Farhany, K.; Abdulsahib, A.D. Study of mixed convection in two layers of saturated porous medium and nanofluid with rotating circular cylinder. Prog. Nucl. Energy 2021, 135, 103723. [Google Scholar] [CrossRef]
- Ahmed, A.; Khan, M.; Ahmed, J. Mixed convective flow of Maxwell nanofluid induced by vertically rotating cylinder. Appl. Nanosci. 2020, 10, 5179–5190. [Google Scholar] [CrossRef]
- Kareem, A.K.; Gao, S. A comparison study of mixed convection heat transfer of turbulent nanofluid flow in a three-dimensional lid-driven enclosure with a clockwise versus an anticlockwise rotating cylinder. Int. Commun. Heat Mass Transf. 2018, 90, 44–55. [Google Scholar] [CrossRef]
- Abdulsahib, A.D.; Al-Farhany, K. Numerical Investigation of the nanofluid mixed convection on two layers enclosure with rotating cylinder: High Darcy Number Effects. IOP Conf. Ser. Mater. Sci. Eng. 2020, 928, 22001. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Mixed convection of nanofluids in a three dimensional cavity with two adiabatic inner rotating cylinders. Int. J. Heat Mass Transf. 2018, 117, 331–343. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F.; Abu-Hamdeh, N.H. Mixed convection due to a rotating cylinder in a 3D corrugated cavity filled with single walled CNT-water nanofluid. J. Therm. Anal. 2018, 135, 341–355. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Chamkha, A.J. MHD mixed convection of nanofluid in a three-dimensional vented cavity with surface corrugation and inner rotating cylinder. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 1637–1660. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Öztop, H.F. Numerical study of MHD mixed convection in a nanofluid filled lid driven square enclosure with a rotating cylinder. Int. J. Heat Mass Transf. 2014, 78, 741–754. [Google Scholar] [CrossRef]
- Selimefendigil, F.; Ismael, M.; Chamkha, A.J. Mixed convection in superposed nanofluid and porous layers in square enclosure with inner rotating cylinder. Int. J. Mech. Sci. 2017, 124-125, 95–108. [Google Scholar] [CrossRef]
- Siavashi, M.; Karimi, K.; Xiong, Q.; Doranehgard, M.H. Numerical analysis of mixed convection of two-phase non-Newtonian nanofluid flow inside a partially porous square enclosure with a rotating cylinder. J. Therm. Anal. 2019, 137, 267–287. [Google Scholar] [CrossRef]
- Jasim, L.M.; Hamzah, H.; Canpolat, C.; Sahin, B. Mixed convection flow of hybrid nanofluid through a vented enclosure with an inner rotating cylinder. Int. Commun. Heat Mass Transf. 2021, 121, 105086. [Google Scholar] [CrossRef]
- Chatterjee, D.; Gupta, S.K.; Mondal, B. Mixed convective transport in a lid-driven cavity containing a nanofluid and a rotating circular cylinder at the center. Int. Commun. Heat Mass Transf. 2014, 56, 71–78. [Google Scholar] [CrossRef]
- Hussain, S.; Jamal, M.; Ahmed, S.E. Hydrodynamic forces and heat transfer of nanofluid forced convection flow around a rotating cylinder using finite element method: The impact of nanoparticles. Int. Commun. Heat Mass Transf. 2019, 108, 104310. [Google Scholar] [CrossRef]
- Arani, A.A.A.; Kazemi, M. Analysis of fluid flow and heat transfer of nanofluid inside triangular enclosure equipped with rotational obstacle. J. Mech. Sci. Technol. 2019, 33, 4917–4929. [Google Scholar] [CrossRef]
- Haq, R.U.; Soomro, F.A.; Wang, X.; Tlili, I. Partially heated lid-driven flow in a hexagonal cavity with inner circular obstacle via FEM. Int. Commun. Heat Mass Transf. 2020, 117, 104732. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Ismael, M.A.; Chamkha, A.J.; Hashim, I. Numerical investigation of mixed convection and entropy generation in a wavy-walled cavity filled with nanofluid and involving a rotating cylinder. Entropy 2018, 20, 664. [Google Scholar] [CrossRef] [PubMed]
- Hamzah, H.; Albojamal, A.; Sahin, B.; Vafai, K. Thermal management of transverse magnetic source effects on nanofluid natural convection in a wavy porous enclosure. J. Therm. Anal. 2021, 143, 2851–2865. [Google Scholar] [CrossRef]
- Cimpean, D.S.; Pop, I. Free convection in an inclined cavity filled with a nanofluid and with sinusoidal temperature on the walls: Buongiorno’s mathematical model. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 4549–4568. [Google Scholar] [CrossRef]
- Mourad, A.; Aissa, A.; Mebarek-Oudina, F.; Al-Kouz, W.; Sahnoun, M. Natural convection of nanoliquid from elliptic cylinder in wavy enclosure under the effect of uniform magnetic field: Numerical investigation. Eur. Phys. J. Plus 2021, 136, 1–18. [Google Scholar] [CrossRef]
- Mourad, A.; Aissa, A.; Mebarek-Oudina, F.; Jamshed, W.; Ahmed, W.; Ali, H.M.; Rashad, A. Galerkin finite element analysis of thermal aspects of FeO-MWCNT/water hybrid nanofluid filled in wavy enclosure with uniform magnetic field effect. Int. Commun. Heat Mass Transf. 2021, 126, 105461. [Google Scholar] [CrossRef]
- Ghasemi, K.; Siavashi, M. MHD nanofluid free convection and entropy generation in porous enclosures with different conductivity ratios. J. Magn. Magn. Mater. 2017, 442, 474–490. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).