Abstract
The model discussed in this paper provides an efficient mechanism for the selection and allocation of available limited spectra for transmission of heterogeneous data in a network. The data packets (customers), belonging to different classes, arrive according to a batch marked the Markovian arrival process (BMMAP). The inventory considered is of multi-type (different types of channels becoming available) and are generated according to a marked Markovian arrival process (MMAP). The number of distinct types of inventory and that of the customers are the same. Arriving customers are allowed to wait in finite buffers of each category which are reserved for distinct classes of customers except for the most general class, which is provided with an infinite waiting space. The number of servers also equals the number of distinct types of inventory. When items of a particular type arrive in the inventory, the service starts, providing the buffer of customers of the corresponding class is non-empty. The service can be viewed as a selection process with Coxian distributed service times. The system is analyzed using the matrix analytic method and performance measures are obtained. The model is illustrated with suitable numerical examples.
1. Introduction
In the current paper, we propose a model for a multiclass queueing inventory system into which customers belonging to different classes and items of different types arrive. The customers are packets, arriving at nodes in a network, for transmission. We assume that customers belonging to each class arrive in batches according to a batch marked the Markovian arrival process (BMMAP). It is a correlated arrival process with distinct categories of customers arriving in batches and so a very general case is considered. Queues with correlated arrival flow of customers are adequate mathematical models for various real systems addressing different needs of various class of customers for various demands [1]. The inventory items of a particular type are channels becoming available (inventory arrivals) for transmitting a particular class of packets (customers). The availability of channels is generated according to a marked Markovian arrival process (MMAP). The arriving customers are provided with finite capacity buffers for waiting, except for a particular class (most general, could be lowest priority/jobs requiring no specialization), which is given an infinite capacity waiting space. The service is a selection process, the service time follows distinct Coxian distribution for different classes.
The area of multi-type queueing inventory seems to have received very little attention even though many works on multi-type inventories are available. Benny, Chakravarthy, and Krishnamoorthy [2] studied a single server queueing-inventory system with two commodities in which the system has finite storage space for each type. This model is analyzed using the matrix analytic method. The analysis of a two commodity queueing inventory with two classes of customers was carried out by Ozkar and Kocer [3]. In [4] Altiok and Shiue discussed a manufacturing system with multiple products. In this model, a continuous review inventory control policy was adopted to each type of commodity. Krishnamoorthy, Iqbal, and Lakshmy B [5] investigated an inventory model with two types of commodities. Zhao and Lian [6] studied a queueing inventory with two classes of customers, modeled as level-dependent quasi-birth-death process and an extensive analysis was carried out. In [7], Krishnamoorthy, Manikandan, and Lakshmy described a queueing inventory model with distinct control policies for inventories and a set of optimization problems were analyzed.
In [8] Melikov, Ponomarenko, and Bagirova proposed models of queueing inventory with finite and infinite buffers for impatient customers. Yadavalli, Adetunji, Sivakumar, and Arivarignan [9] described a queueing inventory with three different types of customers with MAP for arrival and two distinct types of inventoried items. Chakravarthy [10] described queueing inventory models in which the customer demands a random number of items not exceeding a finite number and customer loss is also considered. Multi-item Queueing inventories can also be observed in [11]. Liu, Feng, and Wong [12] studied the Markov inventory system incorporated with flexible service policies and two classes of customers. A production inventory model with job shop routings and random arrivals was studied in [13].
Whereas we discuss in this paper a multi-type inventory (different types of jobs being created in employment scenario) with positive service time, Kalpakam and Arivarignan [14] consider a coordinated multi-commodity inventory system with negligible service time. In addition, the latter does not consider a very general model as we have done in the present paper, namely Batch Marked Markovian arrival of customers and Marked Markovian arrival process of different types (multi-commodity) of inventory. Meng and Heragu [15] investigate a batch size modeling of a multi-item, discrete manufacturing system via an open queuing network. However, these authors also do not consider positive service time to each customer before the inventory is provided to them. Nevertheless, theirs is modeled as a problem in an open queueing network. Ours is not as such a network problem. The service time that we assumed is Coxian of order, specified by the type of customer.
The highlights of the present model are
- The customer (packets for transmission) arrival process is the Batch Marked Markovian Arrival Process (BMMAP). It is a correlated arrival process with distinct categories of customers arriving in batches and so a very general case is considered.
- The channel availability is generated according to a Marked Markovian Arrival Process (MMAP).
- Customers of the least speciality (for example, messages requiring the lowest security measures) have an infinite capacity waiting room and the remaining ones are restricted to have finite capacity buffers.
- There are as many servers as the number of distinct types of channels.
Detailed descriptions of the matrix analytic method can be found in [16,17]. For phase-type distributions and the Markovian arrival process, we refer to [18,19]. Various Models with MAP arrivals and phase-type service time distributions can be seen in [20,21].
The paper is organized as follows: In Section 2, we describe the mathematical model of the system and analysis is carried out using the matrix analytic method. The stability condition is derived in Section 3. In Section 4, the steady state distribution of the system is given. Performance characteristics of the system are defined in Section 5. A linear profit function is defined in Section 6. A numerical illustration is provided in Section 7. Section 8 concludes the study.
2. Mathematical Model
In this system, customers belong to r different classes arrive in batches according to a batch marked Markovian Arrival Process (BMMAP). The BMMAP is defined by the sequences of matrices where and . The customers of class 1 (least priority) are the most general class and are allowed to wait in an infinite queue when they arrive. The customers belong to the classes are allowed to wait in finite buffers with capacities , respectively. The r different types of items arrive according to a Marked Markovian arrival process (MMAP). The MMAP is defined by the sequence of matrices . The arriving items form the inventory and maximum inventory level for a type i item is When the inventory of a type i is nonempty, the service for that class will be started if there is at least one customer of class i is waiting.
The service times for different classes are independent and identically distributed according to a Coxian random variable. For the class i the service times follow a Coxian distribution of order m with the phase-type representation , where is the initial probability distribution and is a matrix giving the transition rates among the m phases.
where , is the rate of transition from the phase j to j + 1 and the process moves from the phase j to j + 1 with probability qj or enters the absorption state with the complimentary probability 1 − qj.
The service of a customer may be interpreted as follows: from the first stage of service a customer either goes to next stage with probability or becomes absorbed with the complimentary probability . This happens at each of the consequent stages and if it goes to the last stage (last transient phase), then on completion, service is terminated. The service for each class of customers is provided in batches. The maximum permissible batch size for service of a class i is The service is a matching process, which assigns a batch of items of type i to equal number of customers(or maximum available and matching) of the corresponding class.
The following are the system descriptors at the time t.
- is the number of customers belonging to class the i, .
- ; is the number of inventoried items of the type i.
- ; is the phase of the Coxian distribution with representation
- is the phase of the batch marked Markovian arrival process.
- is the phase of the marked Markovian arrival process.
The process can be represented by a continuous time Markov chain
where
The state space of is described as follows.
Where
includes the states in which at least one selection process is going on and contains the state(s) with there is no selection process currently going on. The states in are the states with either the waiting line of a particular type or the corresponding inventory is empty.
The infinitesimal generator Q of takes the form
The transition rates are listed as follows.
In the following table, we use some abbreviations for certain component vectors for convenience. gives the vector of phases of the Coxian clock. is the numbers of items of various classes.
| From | To | Transition Rate |
The blocks of the matrix are as follows.
where
where
where
where
Let s be the state and be with h where
Let , the levels are redefined so that the levels to are merged together.
After merging of cells the modified form of Q take the structure
3. Stability Condition
Theorem 1.
Let be the steady state probability vector of the infinitesimal generator . The system is stable if and only if .
Proof.
The proof directly follows from [17]. The condition reduces to
where
where and
where .□
4. Stationary Distribution
The stationary distribution of the system process is obtained as follows.
Under the assumption of the stability condition, the steady state probability distribution exists. Let be the steady state probability vector of the Markov Chain , where .
where .
Then y is the unique solution to the system of equations and .
From and , we have the system of equations
Now, from the matrix analytic method, , , where R is the minimal non-negative solution, the matrix quadratic equation . R is computed algorithmically, using the logarithmic reduction algorithm [16].
5. Performance Measures
- Expected number of customers of class
- Expected number of inventoried items of type
- Probability that upon arrival a customer of class i finds inventoried items of type i
- Probability that type i items are unavailable in the inventory
- Probability that buffer for class i is empty and type i items are unavailable in the inventory
- Probability that buffer for class i is empty when type i items are available in the inventory
6. Profit Function
We constructed a profit function for optimally determining the buffer capacities and maximum inventory levels for each class of customers and corresponding inventory. In the following linear function , is the revenue per unit time for a customer of class i and is the revenue per unit time for an inventoried item of type i. Optimal values of various parameters may be numerically obtained using the Cost function.
7. Numerical Illustration
We consider a system with two class of arrivals of customers with two type of inventory. Here we assume items of type i arrive according to a Poisson process with parameter Service times for type i are exponentially distributed with parameter Customers of class i arrive in a batch of size j according to a Poisson process with parameter, where the inventory levels of both types are fixed as 3.
For the evaluation of performance measures listed in Table 1 we fix

Table 1.
Performance measures with increase in service rate .
Table 1 describes the variation in various performance measures of the system with the increase in the rate of service corresponding to class 1 customers. Clearly, customer accumulation in the infinite queue goes down and the type 1 inventory level decreases with an increase in Both these system behaviors are intuitively acceptable. Pictorial representation of this phenomenon is shown in Figure 1. The probability that type 1 inventory become available in the presence of the corresponding class of customers decreases with the increase in service rate. While increasing the measures corresponding to type 2 customers do not show any considerable change. In Table 2, changes in performance measures with the increase in the service rate for type 2 customers are shown. The accumulation of customers of type 2 and corresponding inventory level decreases with increase in the rate of the matching process. Probability of availability of type 2 items is inversely proportional to the service rate. Figure 2 shows the decreasing pattern of customer accumulation in the infinite queue with for different values of
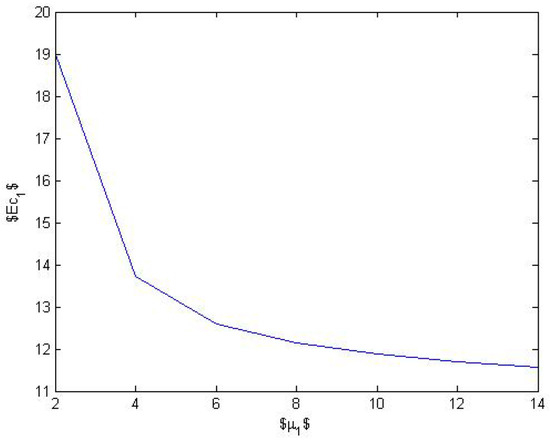
Figure 1.
with .

Table 2.
Performance measures with increase in service rate.
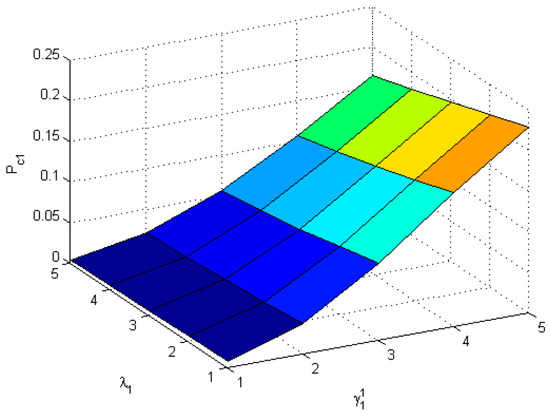
Figure 2.
with and .
In Figure 2, the congestion of general class with increase in service rate is plotted for distinct values of The variation in probability is such that a customer belongs to class 1, and finds type 1 inventory upon arrival with respect to arrival rates of customers and inventory. The elevation in this probability is obvious in the surface shown in Figure 2. The variation with respect to arrival rate and service rate is shown in Figure 3. Figure 4 shows the profit variation with and the rate of arrival of inventory items.
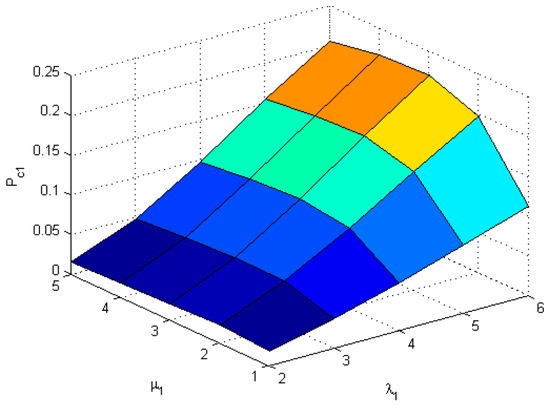
Figure 3.
with and .
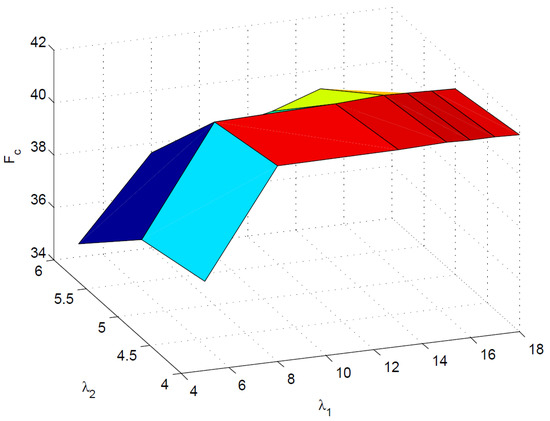
Figure 4.
with and .
8. Conclusions
The model discussed in this paper provides an efficient mechanism for the selection and allocation of available limited spectra for transmission of heterogeneous data in a network. The influence of various parameters in system performance characteristics are evaluated. In networking, one of the main advantages of this model is to maximize bandwidth use and minimize channel loss. This model can have further applications in many physical systems as well. For example, the model may be translated to that of employment providing platform as a queueing inventory system. The job aspirants (customers) belonging to different class arrive in the system and the multi type inventory considered is of different types of job vacancies generated. The number of distinct types of jobs and that of customers are the same. The service can be viewed as a selection process (exams, interviews, fitness test) which is started when job vacancies of a particular type arrive in the inventory, and the buffer of customers of the corresponding class is non-empty.
Author Contributions
Conceptualization, T.S.S.L. and A.K.; methodology, T.S.S.L. and V.C.J.; software, T.S.S.L.; validation, T.S.S.L., V.C.J. and A.K.; formal analysis, A.K., V.V. and D.K.; writing—original draft preparation, T.S.S.L. and V.C.J.; writing—review and editing, T.S.S.L., V.C.J., V.V. and D.K.; supervision, A.K.; project administration, A.K.; funding acquisition, V.V. and D.K. All authors have read and agreed to the published version of the manuscript.
Funding
This paper has been supported by the RUDN University Strategic Academic Leadership Program (recipient D.K., formal analysis) and funded by Russian Foundation for Basic Research according to the research project number 19-29-06043 (recipients V.V. and D.K., writing—review and editing).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors express their gratitude to the referees for valuable suggestions that improved the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Dudin, A.N.; Klimenok, V.I.; Vishnevsky, V.M. The Theory of Queuing Systems with Correlated Flows; Springer: Cham, Switzerland, 2020; pp. 1–410. [Google Scholar] [CrossRef]
- Benny, B.; Chakravarthy, S.R.; Krishnamoorthy, A. Queueing-Inventory System with Two Commodities. J. Indian Soc. Probab. Stat. 2018, 19, 437–454. [Google Scholar] [CrossRef]
- Ozkar, S.; Kocer, U.U. Two-commodity queueing-inventory system with two classes of customers. OPSEARCH 2021, 58, 234–256. [Google Scholar] [CrossRef]
- Altiok, T.; Shiue, G.A. Pull-type manufacturing systems with multiple product types. IIE Trans. 2000, 32, 115–124. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Iqbal, R.; Lakshmy, B. Analysis of a two commodity inventory problem. Int. J. Inf. Manag. Sci. 1994, 5, 127–136. [Google Scholar]
- Zhao, N.; Lian, Z. A queueing-inventory system with two classes of customers. Int. J. Prod. Econ. 2011, 129, 225–231. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.; Manikandan, R.; Lakshmy, B. A revisit to queueing-inventory system with positive service time. Ann. Oper. Res. 2015, 233, 221–236. [Google Scholar] [CrossRef]
- Melikov, A.Z.; Ponomarenko, L.A.; Bagirova, S.A. Analysis of queueing-inventory systems with impatient consume customers. Mezhdunarodnyi Nauchno-Tekhnicheskiy Zhurnal Probl. Upr. Inform. 2016, 48, 96–110. [Google Scholar] [CrossRef]
- Yadavalli, V.S.; Adetunji, O.; Sivakumar, B.; Arivarignan, G. Two-commodity perishable inventory system with bulk demand for one commodity. S. Afr. J. Ind. Eng. 2010, 21, 137–156. [Google Scholar] [CrossRef]
- Chakravarthy, S. Queueing-inventory models with batch demands and positive service times. Mat. Teor. Igr Prilozheniya 2019, 11, 95–120. [Google Scholar] [CrossRef]
- Balintfy, J.L. On a basic class of multi-item inventory problems. Manag. Sci. 1964, 10, 287–297. [Google Scholar] [CrossRef]
- Liu, M.; Feng, M.; Wong, C.Y. Flexible service policies for a Markov inventory system with two demand classes. Int. J. Prod. Econ. 2014, 151, 180–185. [Google Scholar] [CrossRef]
- Van Nyen, P.L.; Bertrand, J.W.; Van Ooijen, H.P.; Vandaele, N.J. A heuristic to control integrated multi-product multi-machine production-inventory systems with job shop routings and stochastic arrival, set-up and processing times. In Stochastic Modeling of Manufacturing Systems; Springer: Berlin/Heidelberg, Germany, 2006; pp. 253–288. [Google Scholar]
- Kalpakam, S.; Arivarignan, G. A coordinated multicommodity (s, S) inventory system. Math. Comput. Model. 1993, 18, 69–73. [Google Scholar] [CrossRef]
- Meng, G.; Heragu, S.S. Batch size modeling in a multi-item, discrete manufacturing system via an open queuing network. IIE Trans. 2004, 36, 743–753. [Google Scholar] [CrossRef]
- Latouche, G.; Ramaswami, V. Introduction to Matrix Analytic Methods in Stochastic Modeling; SIAM: Philadelphia, PA, USA, 1999; Volume 5. [Google Scholar]
- Neuts, M.F. Matrix-Geometric Solutions in Stochastic Models: An Algorithmic Approach; Courier Corporation: Chelmsford, MA, USA, 1994. [Google Scholar]
- Neuts, M.F. Probability Distributions of Phase Type; Amicorum, L., Florin, E.H., Eds.; Department Mathematics, University Louvain: Louvain, Belgium, 1975; pp. 173–206. [Google Scholar]
- Neuts, M.F. A versatile Markovian point process. J. Appl. Probab. 1979, 16, 764–779. [Google Scholar] [CrossRef]
- Sinu Lal, T.S.; Krishnamoorthy, A.; Joshua, V.C. A Queueing Inventory System with Search and Match—An Organ Transplantation Model. In Distributed Computer and Communication Networks (DCCN 2019); CCIS 1141; Springer: Berlin/Heidelberg, Germany, 2019; pp. 273–287. [Google Scholar]
- Sinu Lal, T.S.; Krishnamoorthy, A.; Joshua, V.C. A Disease Outbreak Managing Queueing System with Self-generation of Status and Random Clock for Quarantine Time. In Proceedings of the International Conference on Distributed Computer and Communication Networks, Moscow, Russia, 14–18 September 2020; Springer: Cham, Switzerland; pp. 195–205. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).