Parameter Identification and the Finite-Time Combination–Combination Synchronization of Fractional-Order Chaotic Systems with Different Structures under Multiple Stochastic Disturbances
Abstract
1. Introduction
2. Preliminaries
2.1. Definitions and Lemmas of Fractional Derivative
2.2. Stability Theories of Fractional Order System
3. Problem Description and Assumptions
| , | , | , | , | , | , | , |
4. Sliding Mode Synchronization Controller Design within Finite Time
| , | , |
| , | , |
| , | , |
| . |
- (i)
- Assume the matrix , then the drive systems (18), (19) achieve the finite-time combination synchronization (FTCS) with the response system (21) provided the following controller:and the adaptive updating laws,
- (ii)
- Assume the matrix , then the drive systems (18), (19) achieve the FTCS with the response system (20) provided the following controller:and the adaptive updating laws,
- (i)
- Assume the matrices , then the drive system (19) achieve the FTCS with the response system (21) provided the following controller:and the adaptive updating laws,
- (ii)
- Assume the matrices , then the drive system (19) achieve the FTCS with the response system (20) provided the following controller:and the adaptive updating laws,
- (iii)
- Assume the matrices , then the drive system (18) achieve the FTCS with the response system (20) provided the following controller:and the adaptive updating laws,
- (iv)
- Assume the matrices , then the drive system (18) achieve the FTCS with the response system (21) provided the following controller:and the adaptive updating laws,
- (i)
- Assume the matrices , then the equilibrium point of response system (21) is asymptotically stable provided the following controller:and the adaptive updating laws,
- (ii)
- Assume the matrices , then the equilibrium point of response system (20) is asymptotically stable provided the following controller:and the adaptive updating laws,
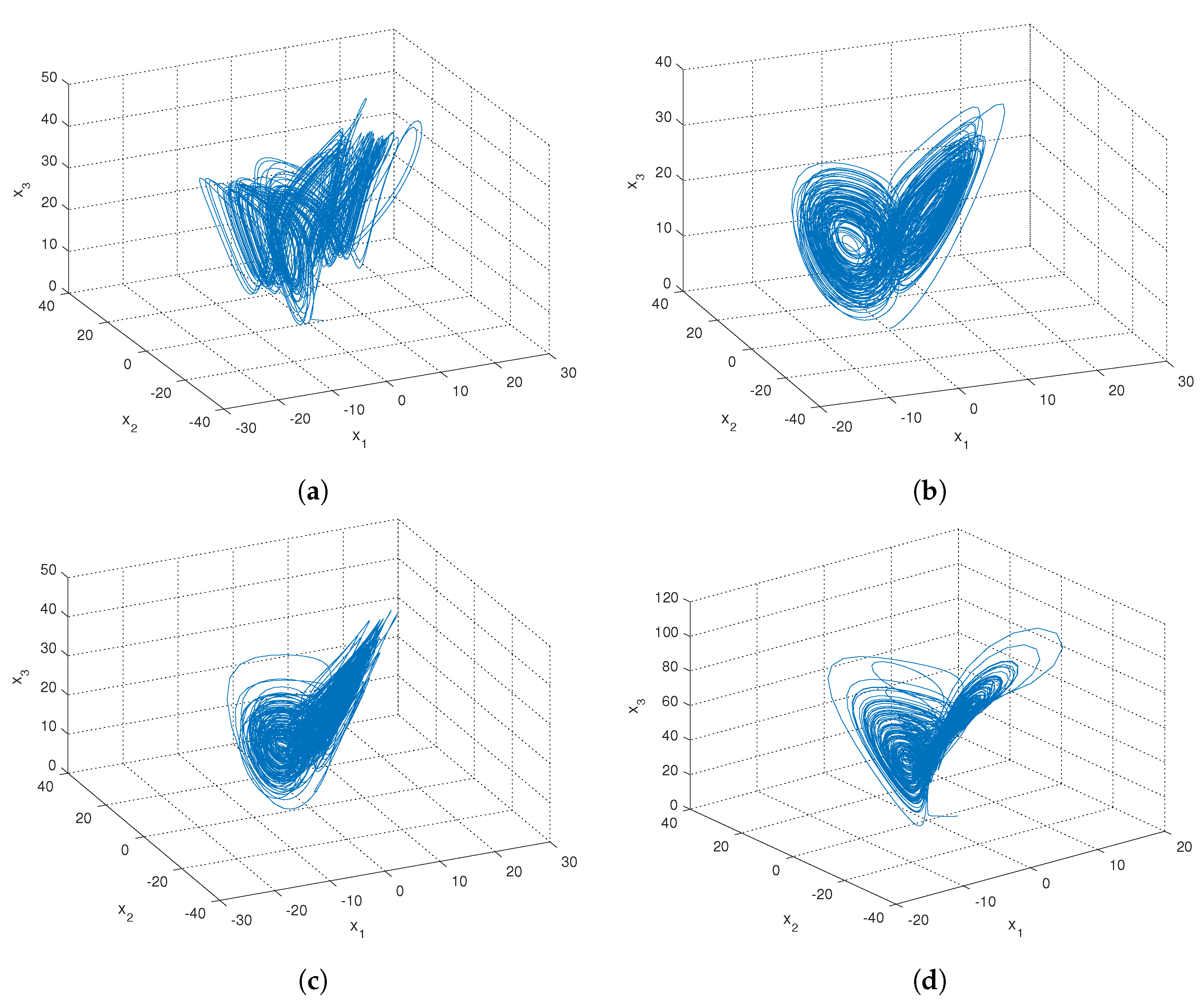
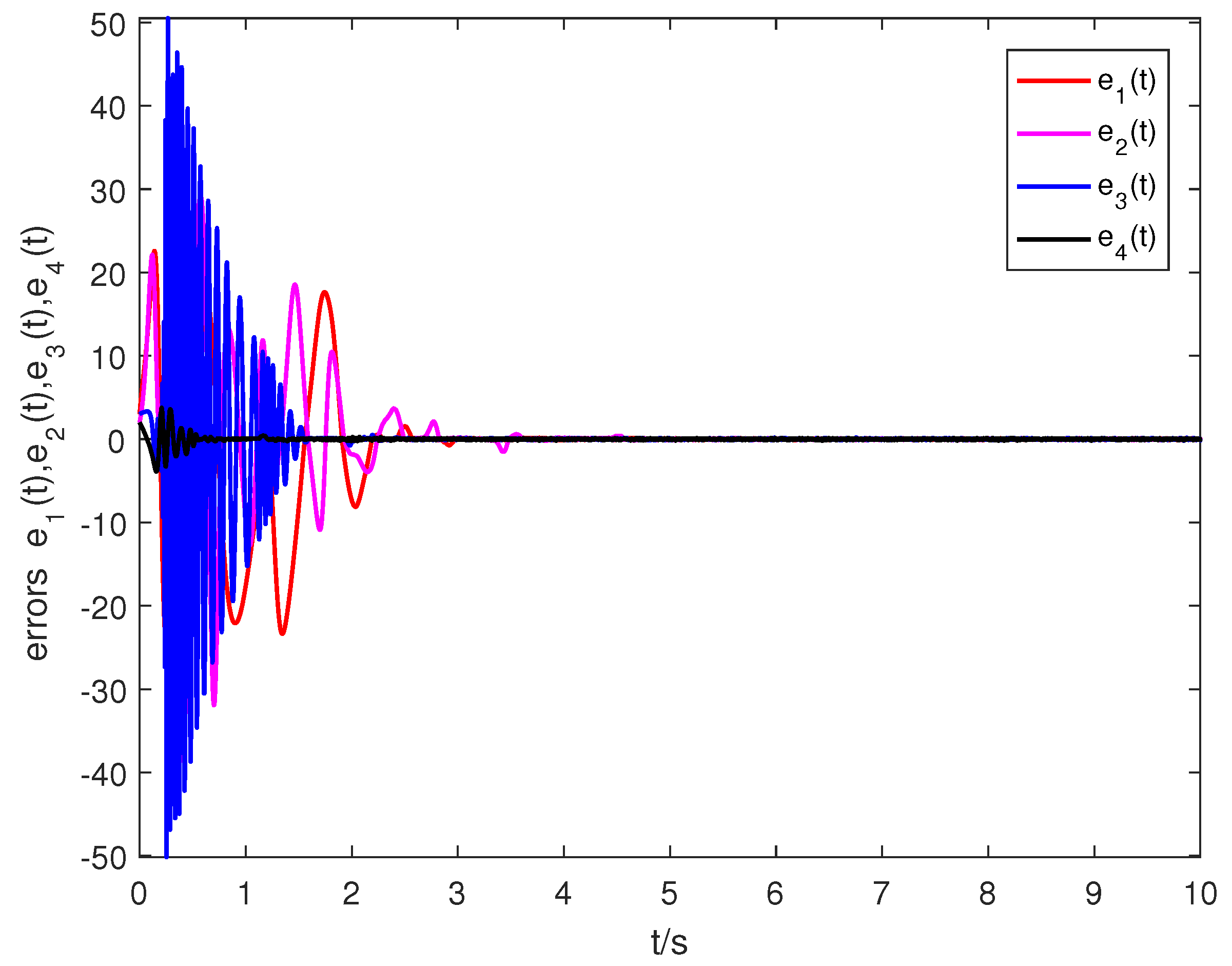
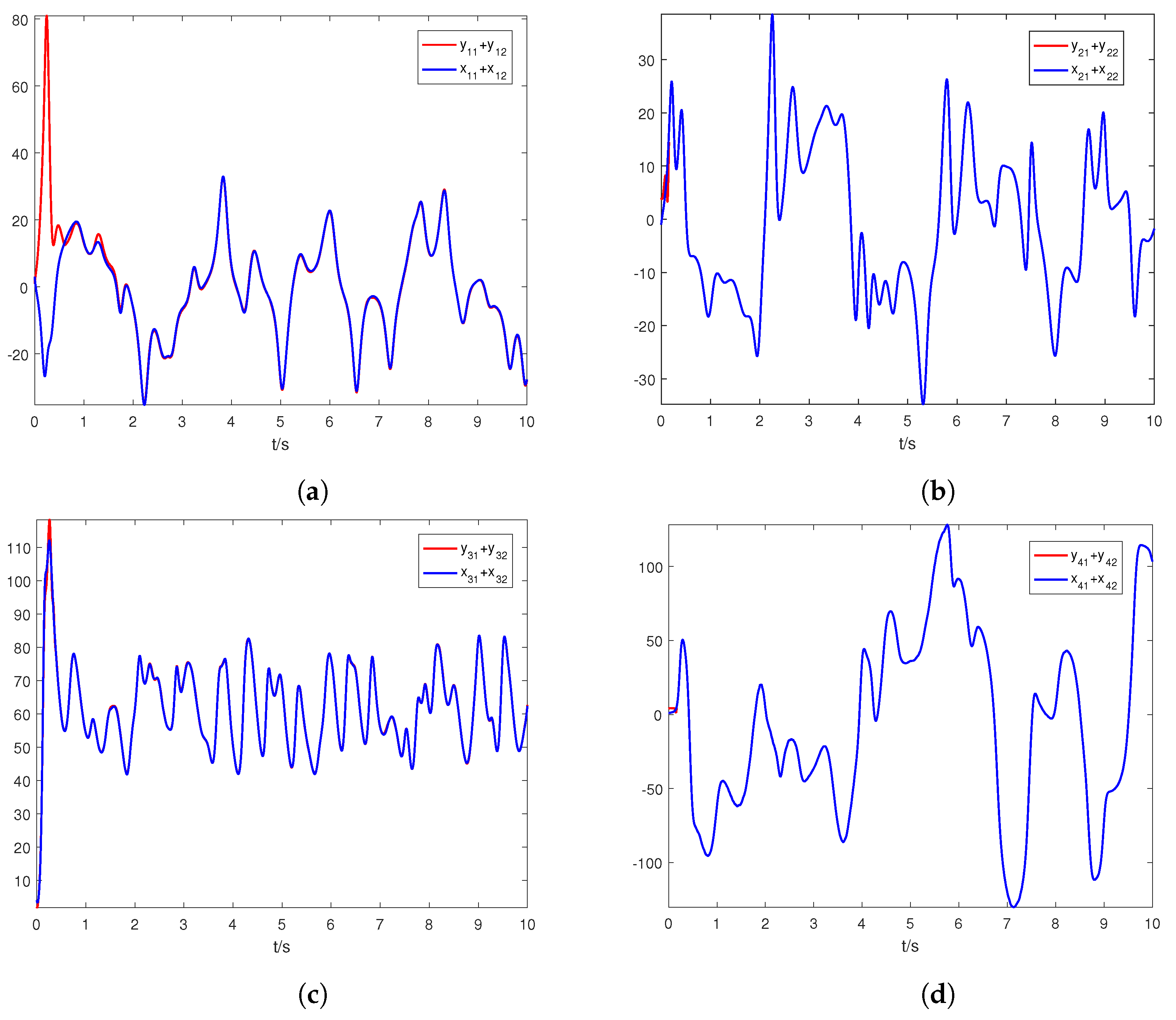
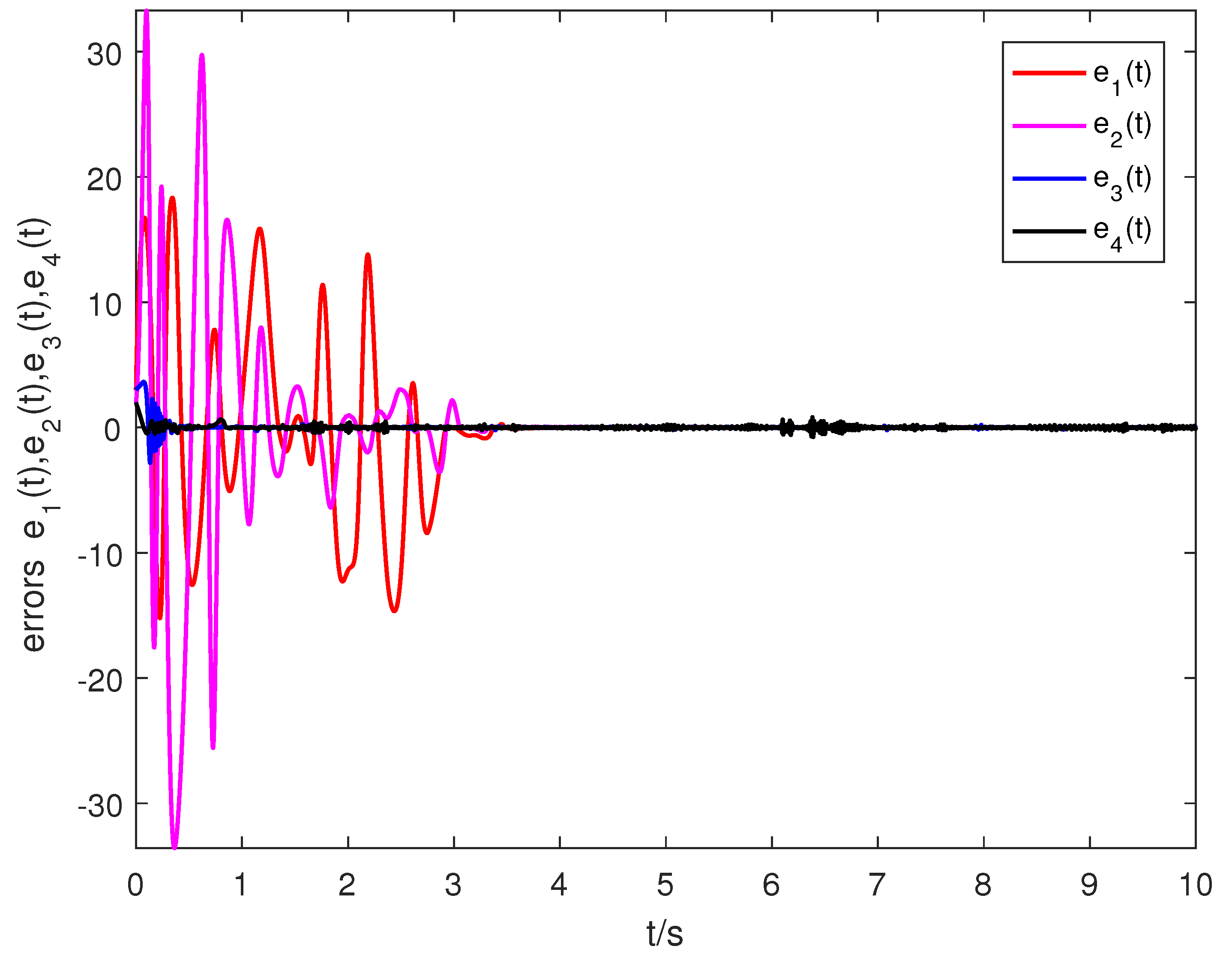
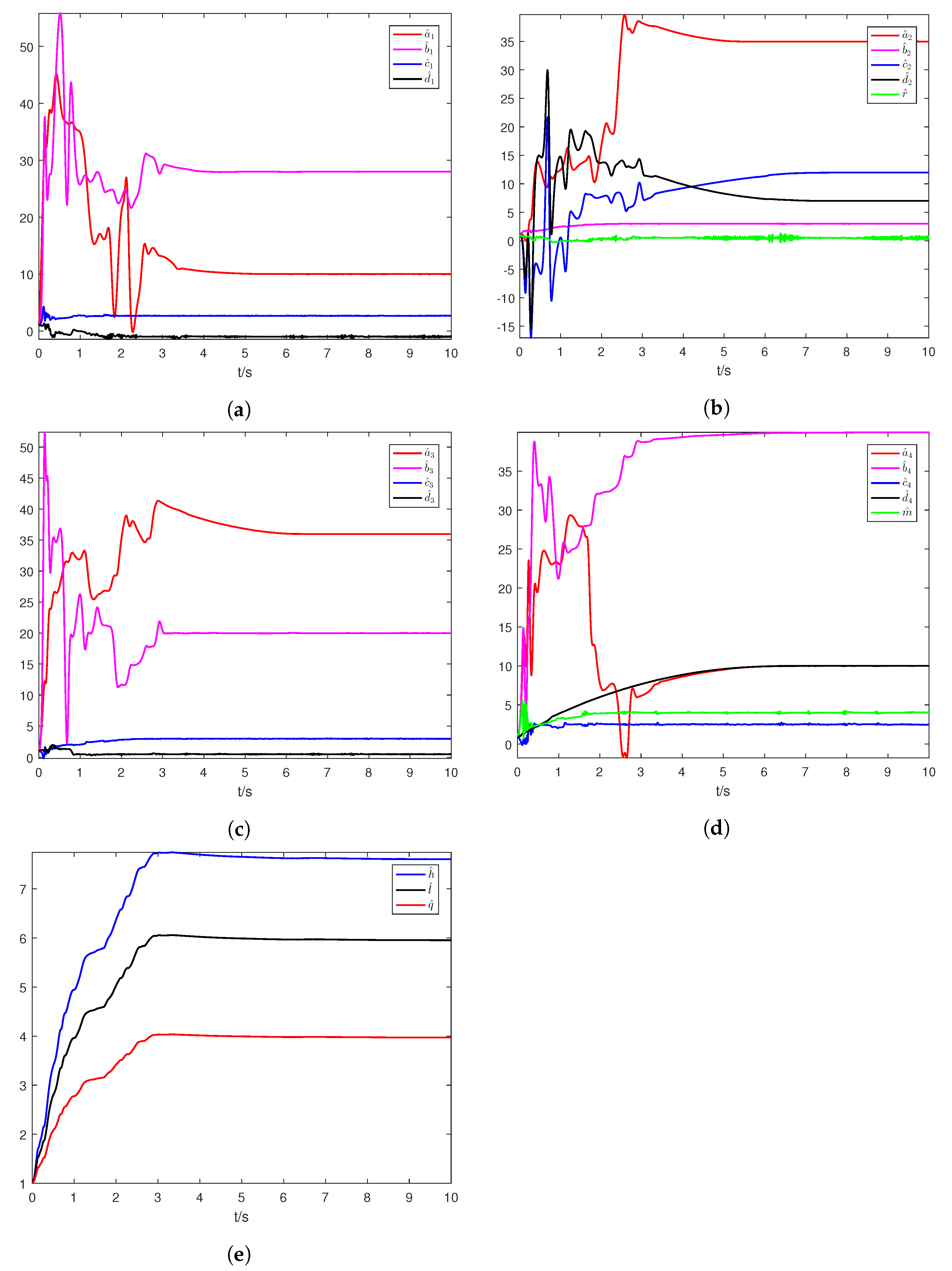
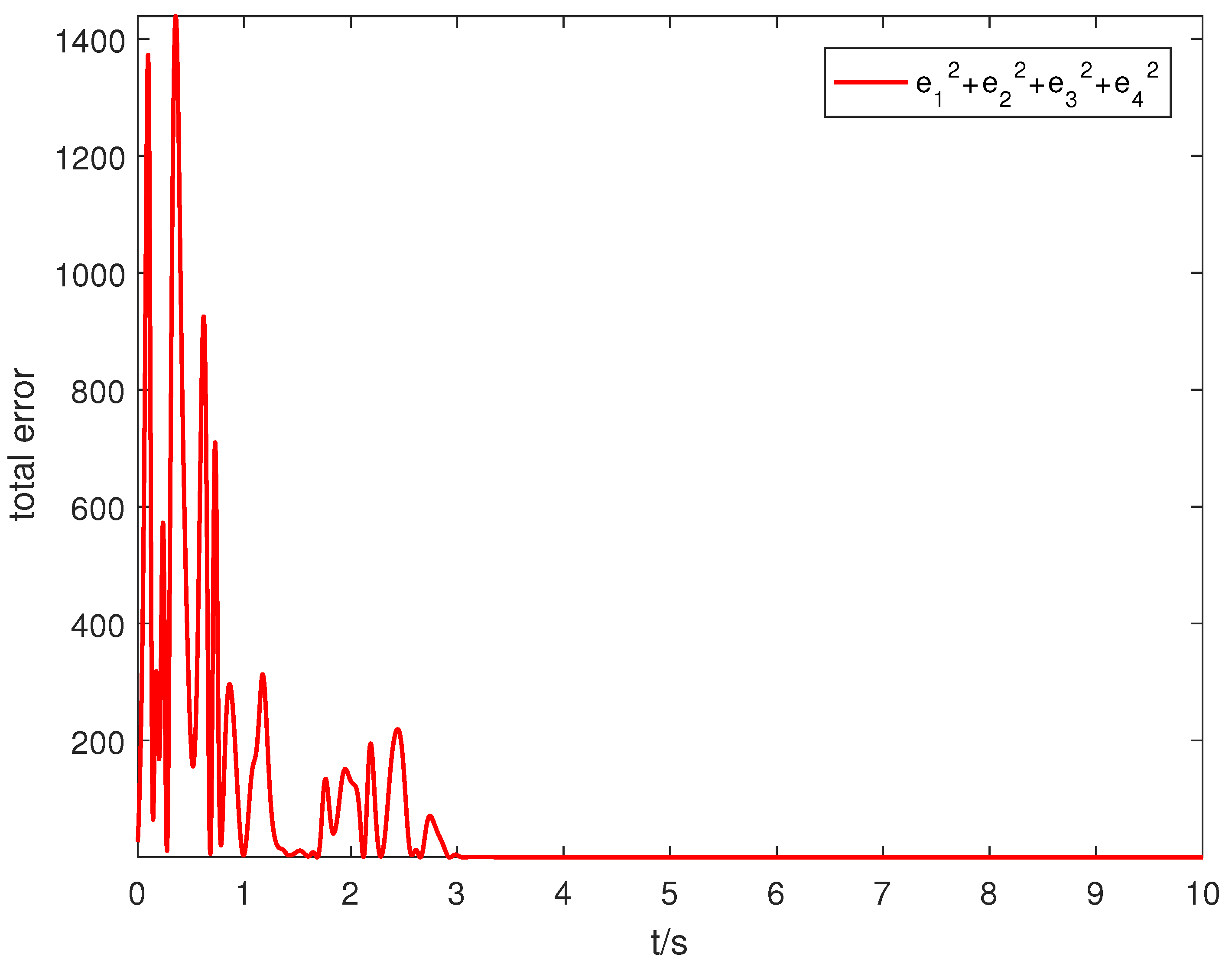
5. Numerical Simulation
| , | , |
| , | , |
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ping, Z.; Peng, Z. Drive-response synchronization for chaotic systems. J. Chong Qing Univ. 2002, 25, 77–79. [Google Scholar]
- Yu, J.; Hu, C.; Jiang, H. Projective synchronization for fractional neural networks. Neural Netw. 2014, 49, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Shao, K.; Guo, H.; Han, F. Finite-time projective synchronization of fractional-order chaotic systems via soft variable structure control. J. Mech. Sci. Technol. 2020, 34, 369–376. [Google Scholar] [CrossRef]
- Qin, X.; Li, S.; Liu, H. Adaptive fuzzy synchronization of uncertain fractional-order chaotic systems with different structures and time-delays. Adv. Diff. Equ. 2019, 2019, 174. [Google Scholar] [CrossRef]
- Bouzeriba, A.; Boulkroune, A.; Bouden, T. Fuzzy adaptive synchronization of a class of fractional-order chaotic systems. In Proceedings of the 2015 3rd International Conference on Control, Engineering & Information Technology (CEIT), Tlemcen, Algeria, 25–27 May 2015; Volume 7, pp. 1–16. [Google Scholar]
- Liu, Y.J.; Gong, M.; Tong, S.; Chen, C.P.; Li, D.J. Adaptive fuzzy output feedback control for a class of nonlinear systems with full state constraints. IEEE Trans. Fuzzy. Syst. 2018, 26, 2607–2617. [Google Scholar] [CrossRef]
- Ha, S.; Chen, L.; Liu, H. Command filtered adaptive neural network synchronization control of fractional-order chaotic systems subject to unknown dead zones. J. Frankl. Inst. 2021, 358, 3376–3402. [Google Scholar] [CrossRef]
- Zeng, H.B.; Teo, K.L.; He, Y.; Xu, H.; Wang, W. Sampled-data synchronization control for chaotic neural networks subject to actuator saturation. Neurocomputing 2017, 185, 1656–1667. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Stochastic feedback coupling synchronization of networked harmonic oscillators. Automatica 2018, 87, 404–411. [Google Scholar] [CrossRef]
- Li, H.L.; Jiang, Y.L.; Wang, Z.; Zhang, L.; Teng, Z. Parameter identification and adaptive-impulsive synchronization of uncertain complex networks with nonidentical topological structures. Optik-Int. J. Light Electron. Opt. 2015, 126, 5771–5776. [Google Scholar] [CrossRef]
- Li, X.F.; Chu, Y.D.; Leung, A.Y.; Zhang, H. Synchronization of uncertain chaotic systems via complete-adaptive-impulsive controls. Chaos Solitons Fractals 2017, 100, 24–30. [Google Scholar] [CrossRef]
- Kocamaz, U.E.; Cevher, B.; Uyaroğlu, Y. Control and synchronization of chaos with sliding mode control based on cubic reaching rule. Chaos Solitons Fractals 2017, 105, 92–98. [Google Scholar] [CrossRef]
- Vaidyanathan, S. Anti-synchronization of 3-cells cellular neural network attractors via integral sliding mode control. Int. J. PharmTech Res. 2016, 9, 193–205. [Google Scholar]
- Li, X.; Zhao, X.S. The chaotic synchronization of fractional-order and integer-order in a class of financial systems. J. Sci. Teach. Coll. Univ. 2020, 40, 1–4. [Google Scholar]
- Jing, W.; Guang, P. Design of a sliding mode controller for synchronization of fractional-order chaotic systems with different structures. J. Shanghai Jiaotong Univ. 2016, 50, 849–860. [Google Scholar]
- Jiang, N. The adaptive control synchronization of hyper-chaos lorenz system and hyper-chaos Rössler system. J. Taiyuan Norm Univ. 2014, 13, 47–50. [Google Scholar]
- Wei, X. Adaptive control and synchronization of Lü hyper-chaotic system. J. Honghe Univ. 2015, 13, 23–27. [Google Scholar]
- Li, T.; Wang, Y.; Zhao, C. Synchronization of fractional chaotic systems based on a simple Lyapunov function. Adv. Diff. Equ. 2017, 2017, 304. [Google Scholar] [CrossRef][Green Version]
- Wei, Y.H.; Chen, Y.Q. Lyapunov functions for nabla discrete fractional order systems. ISA Trans. 2019, 88, 82–90. [Google Scholar] [CrossRef]
- Tirandaz, H.; Tavakoli, H.R.; Ahmadnia, M. Modified projective synchronization of chaotic systems with noise disturbance, an active nonlinear control method. Int. J. Electr. Comput. Eng. 2017, 7, 3436–3445. [Google Scholar] [CrossRef]
- Khan, A.; Jahanzaib, L.S. Synchronization on the adaptive sliding mode controller for fractional order complex chaotic systems with uncertainty and disturbances. Int. J. Dyn. Control 2019, 7, 1419–1433. [Google Scholar] [CrossRef]
- Luo, R.; Su, H.; Zeng, Y. Synchronization of uncertain fractional-order chaotic systems via a novel adaptive controller. Chin. J. Phys. 2017, 55, 342–349. [Google Scholar] [CrossRef]
- Kekha Javan, A.A.; Shoeibi, A.; Zare, A.; Hosseini Izadi, N.; Jafari, M.; Alizadehsani, R.; Moridian, P.; Mosavi, A.; Acharya, U.R.; Nahavandi, S. Design of Adaptive-Robust Controller for Multi-State Synchronization of Chaotic Systems with Unknown and Time-Varying Delays and Its Application in Secure Communication. Sensors 2021, 21, 254. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Chaudhary, H. Hybrid projective combination-combination synchronization in non-identical hyperchaotic systems using adaptive control. Arab. J. Math. 2020, 9, 597–611. [Google Scholar] [CrossRef]
- Petras, I. Fractional-Order Nonlinear Systems, Modeling, Analysis and Simulation; Higher Education Press: Beijing, China, 2011. [Google Scholar]
- Mirrezapour, S.Z.; Zare, A.; Hallaji, M. A new fractional sliding mode controller based on nonlinear fractional-order proportional integral derivative controller structure to synchronize fractional-order chaotic systems with uncertainty and disturbances. J. Vib. Control 2021, 1–13. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, S. Robust chaos synchronization of fractional-order chaotic systems with unknown parameters and uncertain perturbations. Nonlinear Dyn. 2012, 69, 983–992. [Google Scholar] [CrossRef]
- Ma, S.J.; Shen, Q.; Jing, H. Modified projective synchronization of stochastic fractional order chaotic systems with uncertain parameters. Nonlinear Dyn. 2013, 73, 93–100. [Google Scholar] [CrossRef]
- Wang, Q.; Qi, D.L. Synchronization for fractional order chaotic systems with uncertain parameters. Int. J. Control Autom. Syst. 2016, 14, 211–216. [Google Scholar] [CrossRef]
- Nian, F.; Liu, X.; Zhang, Y. Sliding mode synchronization of fractional-order complex chaotic system with parametric and external disturbances. Chaos Solitons Fractals 2018, 116, 22–28. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Li, D.; Yang, D. Adaptive Synchronization for a Class of Fractional Order Time-delay Uncertain Chaotic Systems via Fuzzy Fractional Order Neural Network. Int. J. Control Autom. Syst. 2019, 17, 1209–1220. [Google Scholar] [CrossRef]
- Deepika, D.; Sandeep, K.; Shiv, N. Uncertainty and disturbance estimator based robust synchronization for a class of uncertain fractional chaotic system via fractional order sliding mode control. Chaos Solitons Fractals 2018, 115, 196–203. [Google Scholar] [CrossRef]
- Bhat, S.; Bernstein, D. Finite-time stability of homo-gencous systems. In Proceedings of the ACC, Albuquergue, NM, USA, 6 December 1997; pp. 2513–2514. [Google Scholar]
- Velmurugan, G.; Rakkiyappan, R.; Cao, J. Finite-time synchronization of fractional-order memristor-based neural networks with time delays. Neural Netw. 2016, 73, 36–46. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.L.; Yuan, Z.Z.; Cai, J.P. Finite-time synchronization between two different chaotic systems with uncertainties. J. Fujian Univ. Technol. 2019, 17, 77–82. [Google Scholar]
- Lan, T.L.; Wang, Y.J. Finite-time synchronization and parameters identification of a uncertain critical chaotic system. Math. Pract. Theory 2018, 48, 105–112. [Google Scholar]
- Rashidnejad, Z.; Karimaghaee, P. Synchronization of a class of uncertain chaotic systems utilizing a new finite-time fractional adaptive sliding mode control. Chaos Solitons Fractals 2020, 5, 100042. [Google Scholar] [CrossRef]
- Luo, Y.; Yao, Y. Finite-time synchronization of uncertain complex dynamic networks with time-varying delay. Adv. Diff. Equ. 2020, 2020, 32. [Google Scholar] [CrossRef]
- Mishra, A.K.; Das, S.; Yadav, V.K. Finite-time synchronization of multi-scroll chaotic systems with sigmoid non-linearity and uncertain terms. Chin. J. Phys. 2020, 75, 235–245. [Google Scholar] [CrossRef]
- Sweetha, S.; Sakthivel, R.; Harshavarthini, S. Finite-time synchronization of nonlinear fractional chaotic systems with stochastic actuator faults. Chaos Solitons Fractals 2020, 142, 110312. [Google Scholar] [CrossRef]
- Li, H.L.; Cao, J.; Jiang, H.; Alsaedi, A. Finite-time synchronization and parameter identification of uncertain fractional-order complex networks. Phys. A Stat. Mech. Appl. 2019, 533, 122027. [Google Scholar] [CrossRef]
- Sun, J.; Shen, Y.; Wang, X.; Chen, J. Finite-time combination-combination synchronization of four different chaotic systems with unknown parameters via sliding mode control. Nonlinear Dyn. 2014, 76, 383–397. [Google Scholar] [CrossRef]
- Luo, R.Z.; Wang, Y.L.; Deng, S.C. Combination synchronization of three classic chaotic systems using active back-stepping design. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 043114. [Google Scholar]
- Luo, R.Z.; Wang, Y.L. Finite-time stochastic combination synchronization of three different chaotic systems and its application in secure communication. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 821–824. [Google Scholar]
- Khan, A.; Khattar, D.; Prajapati, N. Dual combination combination multi switching synchronization of eight chaotic systems. Chin. J. Phys. 2017, 55, 1209–1218. [Google Scholar] [CrossRef]
- Ahmad, I.; Shafiq, M.; Al-Sawalha, M.M. Globally exponential multi switching-combination synchronization control of chaotic systems for secure communications. Chin. J. Phys. 2018, 56, 974–987. [Google Scholar] [CrossRef]
- Khan, A.; Nigar, U. Adaptive hybrid complex projective combination-combination synchronization in non-identical hyper-chaotic complex systems. Int. J. Dynam. Control 2019, 7, 1404–1418. [Google Scholar] [CrossRef]
- Vincent, U.E.; Saseyi, A.O.; Mcclintock, P. Multi-switching combination synchronization of chaotic systems. Nonlinear Dyn. 2015, 80, 845–854. [Google Scholar] [CrossRef]
- Sun, J.; Cui, G.; Wang, Y.; Shen, Y. Combination complex synchronization of three chaotic complex systems. Nonlinear Dyn. 2015, 79, 953–965. [Google Scholar] [CrossRef]
- Khan, A.; Budhraja, M.; Ibraheem, A. Combination-combination synchronisation of time-delay chaotic systems for unknown parameters with uncertainties and external disturbances. Pramana 2018, 91, 20. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic: New York, NY, USA, 1999. [Google Scholar]
- Hardy, G.H.; Littlewood, J.E.; Polya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Li, Y.; Chen, Y.Q.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput. Math. Appl. 2009, 59, 1810–1821. [Google Scholar] [CrossRef]
- Li, C.P.; Deng, W.H. Remarks on fractional derivatives. Appl. Math. Comput. 2007, 187, 777–784. [Google Scholar] [CrossRef]
- Li, J.L.; Xi, J.X.; Wang, L. Minimum-energy synchronization for interconnected networks with non-periodical information silence. Neurocomputing 2022, 481, 310–321. [Google Scholar] [CrossRef]
- Aleksandra, V.; Lazaros, M.; Vyacheslav, G. Fast synchronization of symmetric Hnon maps using adaptive symmetry control. Chaos Solitons Fractals 2022, 155, 111732. [Google Scholar]
- Kashkynbayev, A.; Issakhanov, A.; Otkel, M.; Kurths, J. Finite-time and fixed-time synchronization analysis of shunting inhibitory memristive neural networks with time-varying delays. Chaos Solitons Fractals 2022, 156, 111866. [Google Scholar] [CrossRef]
- Yuan, W.Y.; Ma, Y.C. Finite-time H∞ synchronization for complex dynamical networks with time-varying delays based on adaptive control. ISA Trans. 2021. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.N.; Zhang, J. Novel fractional-order decentralized control for nonlinear fractional-order composite systems with time delays. ISA Trans. 2021. [Google Scholar] [CrossRef]
- Li, Q.; Liu, S.; Chen, Y. Combination event-triggered adaptive networked synchronization communication for nonlinear uncertain fractional-order chaotic systems. Appl. Math. Comput. 2018, 333, 521–535. [Google Scholar] [CrossRef]
- Chen, X.; Park, J.H.; Cao, J.; Qiu, J. Adaptive synchronization of multiple uncertain coupled chaotic systems via sliding mode control. Neurocomputing 2017, 273, 9–21. [Google Scholar] [CrossRef]
- Khan, A. Chaotic analysis and combination-combination synchronization of a novel hyperchaotic system without any equilibria. Chin. J. Phys. 2018, 56, 238–251. [Google Scholar] [CrossRef]
- Sun, J.; Shen, Y.; Zhang, G.; Xu, C.; Cui, G. Combination-combination synchronization among four identical or different chaotic systems. Nonlinear Dyn. 2013, 73, 1211–1222. [Google Scholar] [CrossRef]
- Zerimeche, H.; Houmor, T.; Berkane, A. Combination synchronization of different dimensions fractional-order non-autonomous chaotic systems using scaling matrix. Int. J. Dyn. Control 2021, 9, 788–796. [Google Scholar] [CrossRef]
- Yadav, V.K.; Prasad, G.; Srivastava, M.; Das, S. Combination-combination phase synchronization among non-identical fractional order complex chaotic systems via nonlinear control. Int. J. Dyn. Control 2018, 7, 330–340. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Wang, Y.; Shen, Y. Finite-time synchronization between two complex-variable chaotic systems with unknown parameters via nonsingular terminal sliding mode control. Nonlinear Dyn. 2016, 85, 1105–1117. [Google Scholar] [CrossRef]
- Mossa Al-sawalha, M. Synchronization of different order fractional-order chaotic systems using modify adaptive sliding mode control. Adv. Differ. Equ. 2020, 2020, 417. [Google Scholar] [CrossRef]
- Ouannas, A.; Grassi, G.; Ziar, T. On a Function Projective Synchronization Scheme for non-identical Fractional-order chaotic (hyperchaotic) systems with different dimensions and orders. Optik 2017, 136, 513–523. [Google Scholar] [CrossRef]
- Zhang, W.W.; Chen, D.Y. Hybrid Projective Synchronization of Different Dimensional Fractional Order Chaotic Systems with Time Delay and Different Orders. Chin. J. Eng. Math. 2017, 34, 321–330. [Google Scholar]
- Song, S.; Song, X.N.; Pathak, N. Multi-switching adaptive synchronization of two fractional-order chaotic systems with different structure and different order. Int. J. Control Autom. Syst. 2017, 15, 1524–1535. [Google Scholar] [CrossRef]
- Zhen, W.; Xia, H.; Zhao, Z. Synchronization of nonidentical chaotic fractional-order systems with different orders of fractional derivatives. Nonlinear Dyn. 2012, 69, 999–1007. [Google Scholar]
- Si, G.; Sun, Z.; Zhang, Y.; Chen, W. Projective synchronization of different fractional-order chaotic systems with non-identical orders. Nonlinear Anal. Real World Appl. 2012, 13, 1761–1771. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, W.; Li, T.; Sajid, M.; Ali, S.; Pu, L. Parameter Identification and the Finite-Time Combination–Combination Synchronization of Fractional-Order Chaotic Systems with Different Structures under Multiple Stochastic Disturbances. Mathematics 2022, 10, 712. https://doi.org/10.3390/math10050712
Pan W, Li T, Sajid M, Ali S, Pu L. Parameter Identification and the Finite-Time Combination–Combination Synchronization of Fractional-Order Chaotic Systems with Different Structures under Multiple Stochastic Disturbances. Mathematics. 2022; 10(5):712. https://doi.org/10.3390/math10050712
Chicago/Turabian StylePan, Weiqiu, Tianzeng Li, Muhammad Sajid, Safdar Ali, and Lingping Pu. 2022. "Parameter Identification and the Finite-Time Combination–Combination Synchronization of Fractional-Order Chaotic Systems with Different Structures under Multiple Stochastic Disturbances" Mathematics 10, no. 5: 712. https://doi.org/10.3390/math10050712
APA StylePan, W., Li, T., Sajid, M., Ali, S., & Pu, L. (2022). Parameter Identification and the Finite-Time Combination–Combination Synchronization of Fractional-Order Chaotic Systems with Different Structures under Multiple Stochastic Disturbances. Mathematics, 10(5), 712. https://doi.org/10.3390/math10050712






