Color and Timbre Gestures: An Approach with Bicategories and Bigroupoids
Abstract
:1. Introduction
1.1. Mix and Comparisons
1.2. Some Empirical Evidence
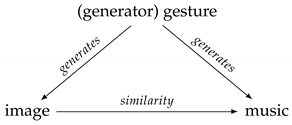

2. Categorical Depictions of Color and Timbre Gestures
In dimension 0 points of X will be identified if they can be joined by a path, i.e., a continuous map from the unit interval of real numbers such that and . This gives rise to the set of path-components, , of X. In dimension 1 the points of X will be retained, but paths between fixed points will be identified if there is a homotopy of rel end points between them. This gives rise to the fundamental groupoid, , of X. The class of a path will be called a 1-track. Hence, the most natural approach to 2-dimensional homotopical algebra of a space X is to retain points and paths between them and identify homotopies’ rel end points under a suitable homotopy relation. This gives rise to the notion of a 2-track. In this way we obtain a two-dimensional structure with points in dimension 0 (0-cells), paths in dimension 1 (1-cells), and 2-tracks in dimension 2 (2-cells). […] Horizontal pasting is neither strictly associative, nor do we have strict identities. However, horizontal pasting is still reasonably well-behaved in the sense that associativity does hold and strict inverses do exist up to coherent isomorphisms. Thus, we obtain a bicategory, , in the sense of Bénabou. The bicategory has the additional feature that the 2-cells are strictly invertible with respect to vertical pasting and the 1-cells are invertible up to coherent isomorphism, that is, is a bigroupoid which will be called the homotopy bigroupoid of the topological space X.
- There is a set of objects of COLOR, the points, that is, the 0-paths, or 0-cells (and similarly for TIMBRE);
- For each pair of objects in COLOR (TIMBRE), there is a 1-path between them, that is, an arrow or 1-cell;
- A morphism between two 1-paths exists and it is a 2-cell, here called a color band (timbre band);
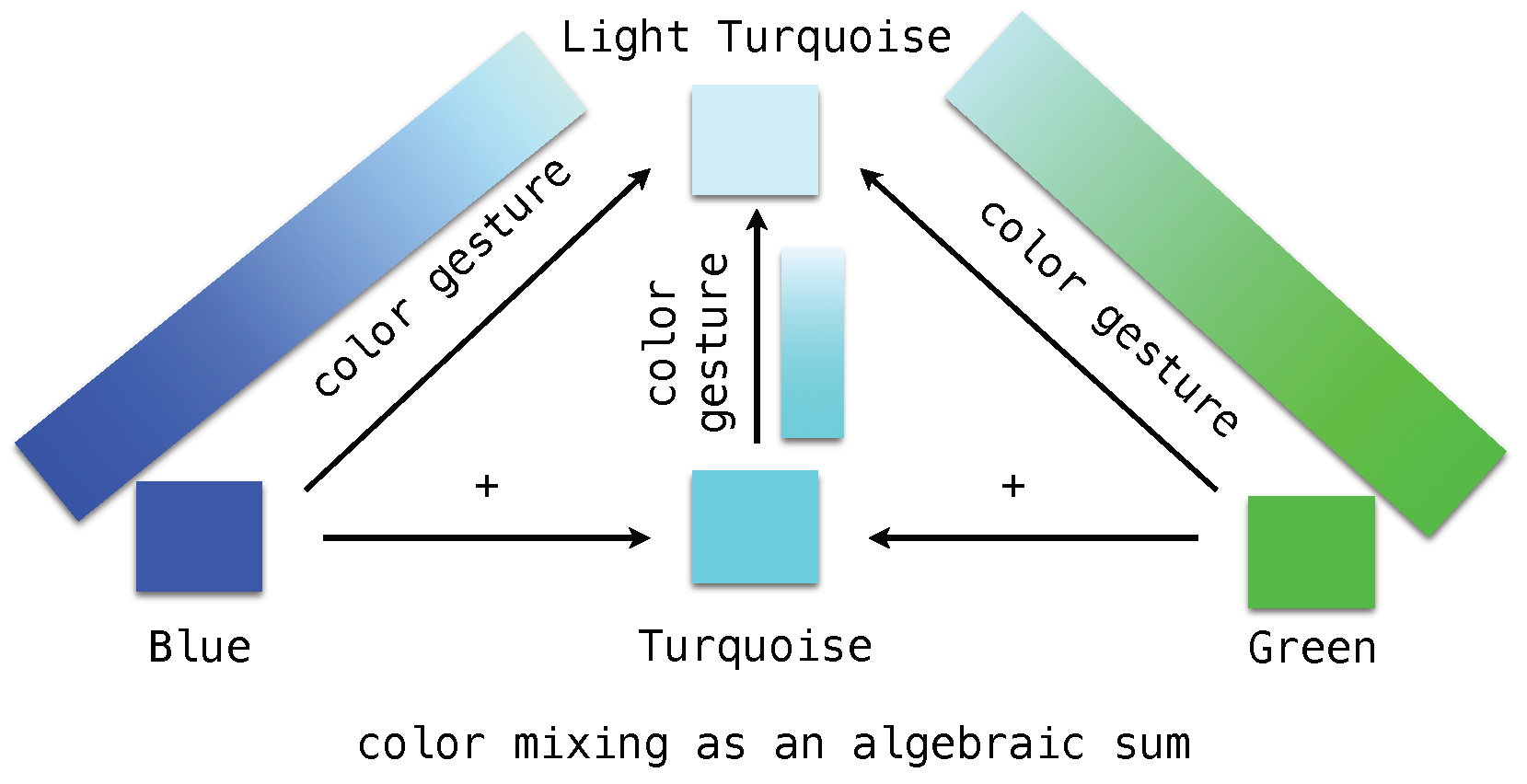
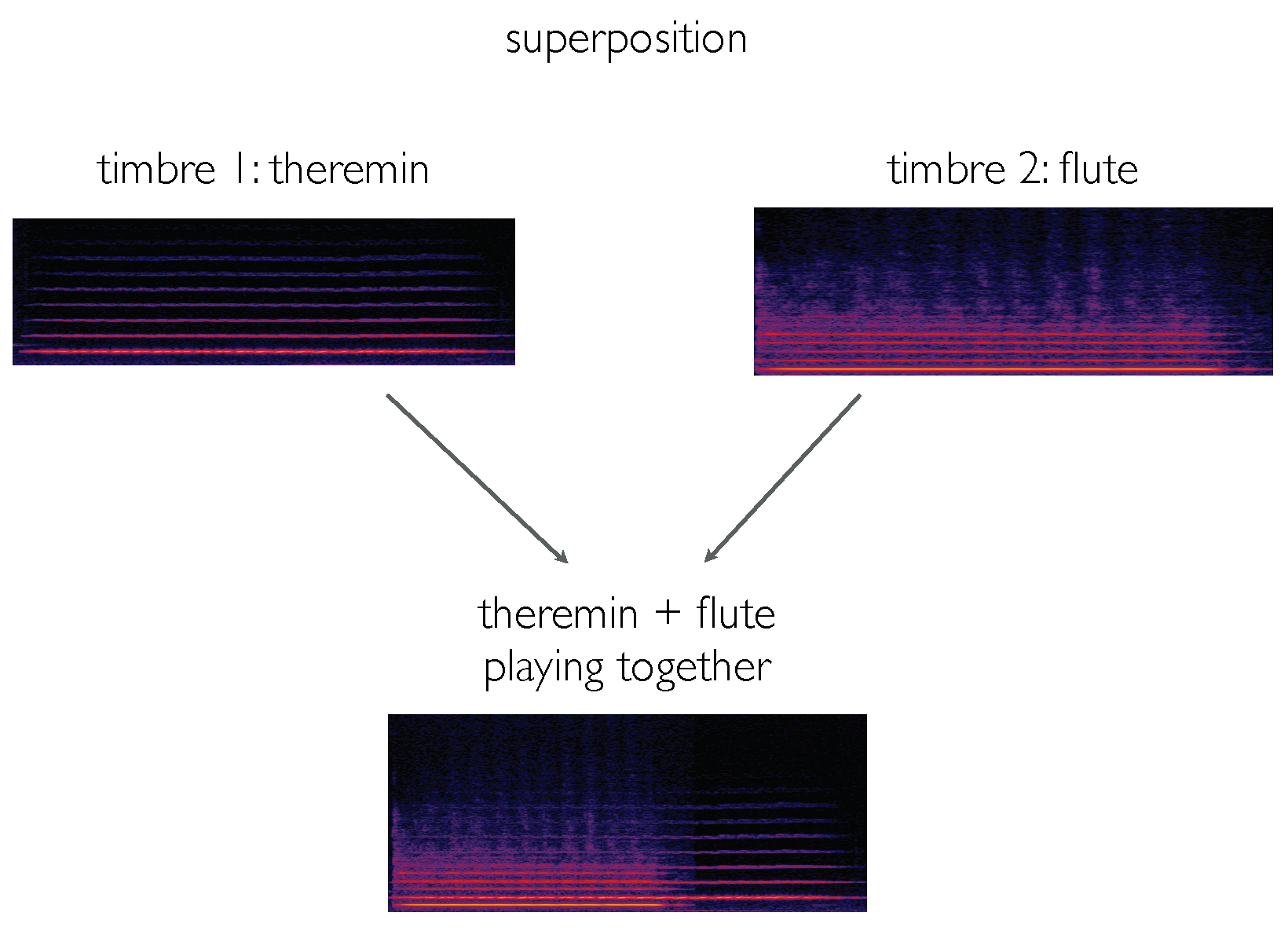
- The composition of two 2-paths and is additive: . In fact, we can add a color band to another adjacent one, creating a larger color band (similarly for timbre bands);
- The identity element exists and it is a 1-cell: it corresponds to the lazy path for colors (timbres);
- For each triple of color points (color1, color2, color3), there is a composition functor (same for timbres);
- The identity 2-cell (the identity 2-arrow) can be considered as a mapping from a 1-cell to itself (as the identity 1-cell maps a 0-cell to the same 0-cell);
- For each quadruple , there are natural isomorphisms, the associativity isomorphisms: , where , , (same for timbre paths);
- For each pair of objects of COLOR, there are two natural isomorphisms, the left and right identities: and (same for timbres);
- Isomorphisms satisfy pentagonal and triangular identities, similarly to the conditions required for monoidal categories.
- for each pair of objects of COLOR, the bicategory COLOR is a groupoid, that is, any 2-cell is invertible (same for TIMBRE);
- for each pair of COLOR, there is a (covariant) functor(and similarly for TIMBRE);
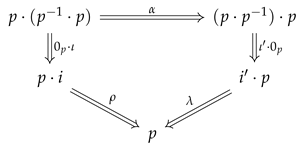
- for each pair of COLOR (same for TIMBRE) there are two natural isomorphisms, the cancellation isomorphisms: and , where is a 1-cell, that is, a 1-path, with the composition of verifying the pentagonal relationship of Diagram (3), where p stands for , i is the identity arrow from and to , is the identity arrow from and to , is the identity 2-cell .
- Our structure is a bigroupoid, and thus it is a special case of bicategory;
- We can define a tensor functor as , which in our case can be the following: adding two colors in COLOR gives as output another color in COLOR obtained as the weighted algebraic sum of the first two colors;
- The tensor product of a color (with itself) is the color itself: mixing white with white gives white;
- The tensor product of two objects is ;
- We have the associator ;
- The pentagonator of [47] (p. 272) is verified;
- Similarly, the associahedron [47] (p. 273) is verified as well, because there is no dependency on the organization of brackets;
- There is a monoidal unit I, for example, in this case mixing white with a transparent color, as a transparent acrylic;
- There are two unitor elements , ;
- There are two unitor invertible modifications verifying triangular correspondences as shown in the Reference [47] (p. 275);
- There are four equations of modifications as shown in the Reference [47] (p. 276).
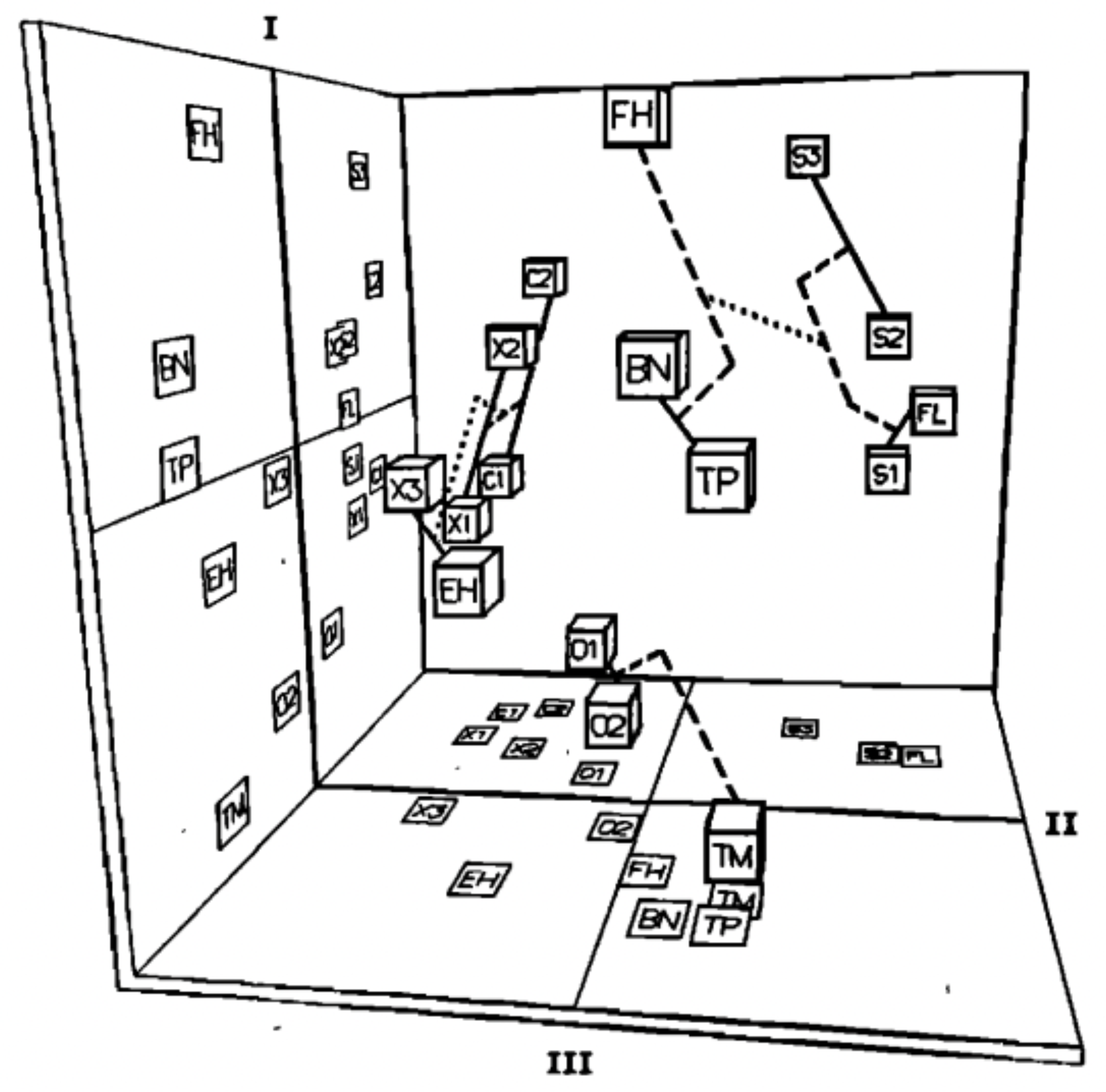
2.1. Timbre Spaces
3. Mapping of Color Classes onto Timbre Classes
- A map for the objects;
- For each pair of objects of , a functor for the morphisms.
4. Morphing versus Mixing

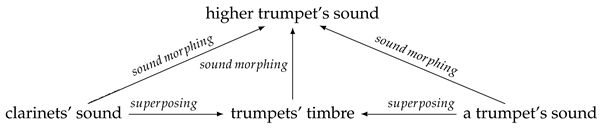
4.1. On Orchestration, Morphing and Hybridization
4.2. Assisted Orchestration and Sound Colors
5. The Souvenir Theorem
On Computer-Assisted Orchestration
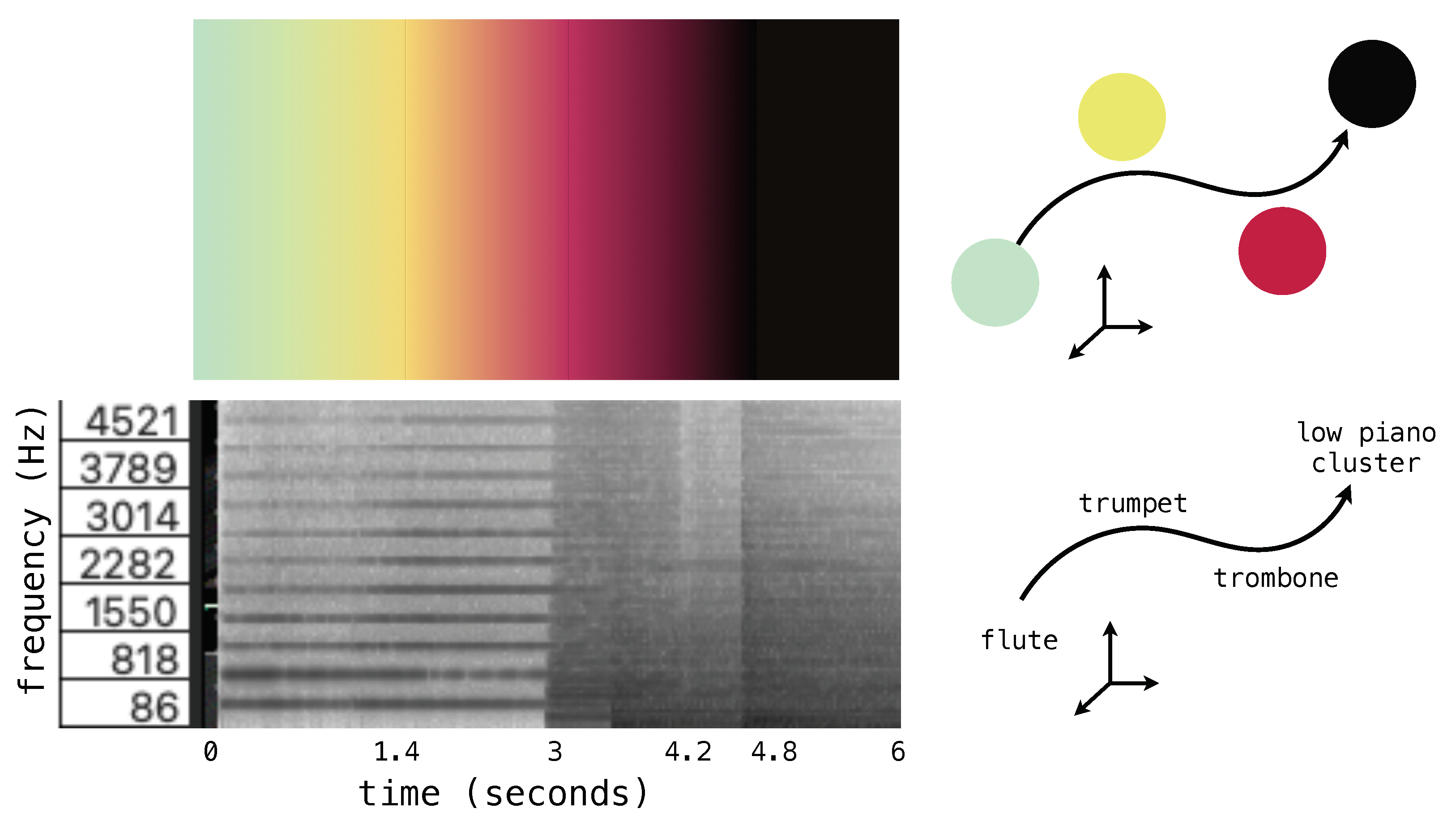
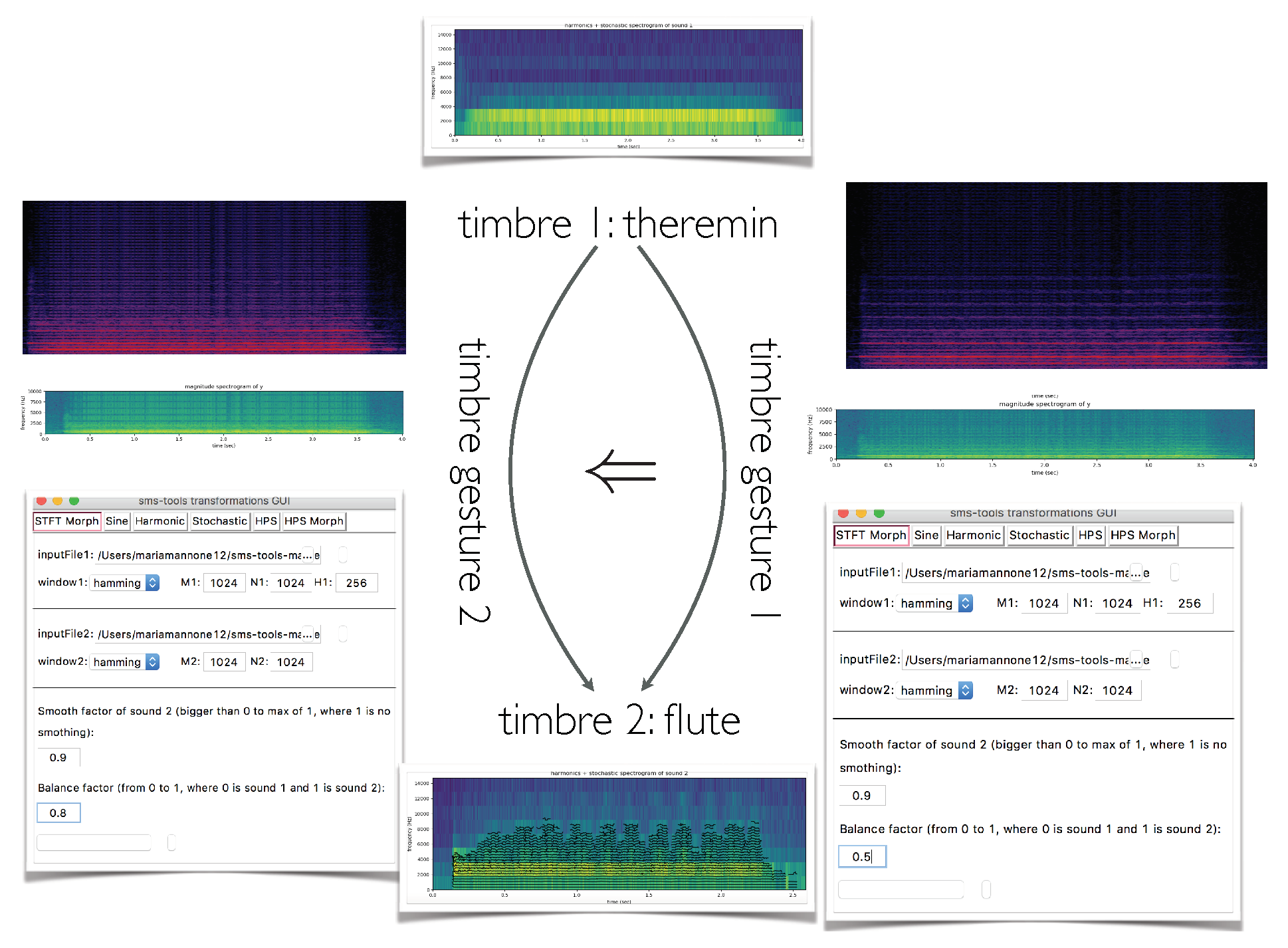
6. An Audio Example
7. Cultural Influences
| English | Blue | English | Yellow |
| Yoruba | Olomi Aro (blue) | Yoruba | Elezuru (yam special) |
| Igbo | Oji (something dark) | Igbo | Onashara (light white) |
| Tiv | Kwar Kwaodo (like sky) | Tiv | Oyha (like banana fruit) |
| Owan | Iblue (sky) | Owan | (paint of banana) |
| Urhobo | Oda dibo (paint of banana) | Ijaw | Pinapina (just like white) |
| English | Green | English | Red |
| Yoruba | Alawo ewe (color of leaves) | Yoruba | Pupa |
| Igbo | Akwukwo Ndu | Igbo | Uhie (color of blood) |
| Tiv | Ngu-er-ka Ikya uwer nahan | Tiv | Nyian |
| Owan | Ebesugbo (leaf) | Heusa | Ja |
| Ijaw | Deibide (like a particular cloth) | Urhobo | Oda Obara (blood-like) |
| Hausa | Igreen | Ijaw | Kwekwe |
8. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davis, J.; Leshko, J.; Fabing, S.J. Smith College Museum of Art: European and American Painting and Sculpture 1760–1960; Hudson Hills Press: Boston, MA, USA, 2000. [Google Scholar]
- Von Goethe, W. Theory of Colours (Zur Farbenlehre); J.G. Cotta’schen Buchhandlung: Stuttgart, Germany, 1810. [Google Scholar]
- Kandinsky, W. Complete Writings on Art; Lindsay, K.C., Vergo, P., Eds.; Da Capo Press: New York, NY, USA, 1994. [Google Scholar]
- Newton, I. Opticks, or, A Treatise of the Reflections, Refractions, Inflections and Colours of Light. 1704. Available online: https://www.loc.gov/resource/rbctos.2017gen39060/?st=gallery (accessed on 16 January 2022).
- Palmer, S.E.; Schloss, K.B.; Xu, Z.; Prado-Leon, L. Music-color associations are mediated by emotion. Proc. Natl. Acad. Sci. USA 2013, 110, 8836–8841. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pinna, B. What colour is it? Modal and amodal completion of colour in art, vision science and biology. Int. J. Arts Technol. 2010, 3, 2–3. [Google Scholar] [CrossRef]
- Provenzi, E. Geometry of color perception. Part 1, Structures and metrics of a homogeneous color space. J. Math. Neurosci. 2020, 10, 1–19. [Google Scholar] [CrossRef]
- Sethares, W. Tuning, Timbre, Spectrum; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Esfahlani, H.; Karkar, S.; Lissek, H.; Mosig, J.R. Acoustic dispersive prism. Nat. Sci. Rep. 2016, 6, 18911. Available online: https://www.nature.com/articles/srep18911 (accessed on 16 January 2022). [CrossRef] [PubMed] [Green Version]
- Lewis, D.; Larsen, M.J. The Measurement of Timbre. J. Acoust. Soc. Am. 1937, 8, 207. Available online: https://asa.scitation.org/doi/10.1121/1.1901995 (accessed on 16 January 2022). [CrossRef]
- Mac Lane, S. Categories for the Working Mathematician; Springer: New York, NY, USA, 1971. [Google Scholar]
- Grandis, M. Higher Dimensional Categories; World Scientific: Singapore, 2020. [Google Scholar]
- Eilenberg, S.; Mac Lane, S. General Theory of Natural Equivalences. Trans. Am. Math. Soc. 1945, 58, 231–294. Available online: https://www.ams.org/journals/tran/1945-058-00/S0002-9947-1945-0013131-6/S0002-9947-1945-0013131-6.pdf (accessed on 16 January 2022). [CrossRef] [Green Version]
- Mazzola, G.; Andreatta, M. Diagrams, gestures and formulae in music. J. Math. Music 2010, 1, 23–46. [Google Scholar] [CrossRef] [Green Version]
- Jedrzejewski, F. Hétérotopies Musicales: Modèles Mathématiques de la Musique; Hermann: Paris, France, 2019. [Google Scholar]
- Popoff, A.; Andreatta, M.; Ehresmann, A. A Categorical Generalization of Klumpenhouwer Networks. In Proceedings of the Conference Mathematics and Computation in Music (MCM 2015), London, UK, 22–25 June 2015; Collins, T., Volk, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Mannone, M. Introduction to Gestural Similarity in Music: An Application of Category Theory to the Orchestra. J. Math. Music 2018, 12, 63–87. [Google Scholar] [CrossRef]
- Mannone, M.; Turchet, L. Shall We (Math and) Dance? In Proceedings of the International Conference on Mathematics and Computation in Music (MCM 2019), Madrid, Spain, 18–21 June 2019; Montiel, M., Gómez-Martín, F., Agustín-Aquino, O.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Arias-Valero, J.S.; Lluis-Puebla, E. Simplicial Sets and Gestures: Mathematical Music Theory, iNfinity-Categories, Homotopy, and Homology. Compositionality (2020 to Appear). Available online: https://jusearva.files.wordpress.com/2020/08/simpgest.pdf (accessed on 16 January 2022).
- Mannone, M.; Arias-Valero, J.S. Some mathematical and Computational Relations between Timbre and Color. Math. Comput. Music. Conf. 2022. under review. [Google Scholar]
- Ward, J.; Huckstep, B.; Tsakanikos, E. Sound-Colour Synaesthesia: To What Extent Does it Use Cross-Modal Mechanisms Common to Us All? Cortex 2006, 42, 264–280. [Google Scholar] [CrossRef]
- Mannone, M. Knots, Music and DNA. J. Creat. Music Syst. 2018, 2, 32–54. Available online: https://www.jcms.org.uk/article/id/523/ (accessed on 16 January 2022). [CrossRef] [Green Version]
- Mannone, M.; Favali, F.; Di Donato, B.; Turchet, L. Quantum GestART: Identifying and applying correlations between mathematics, art, and perceptual organization. J. Math. Music 2020, 15, 62–94. [Google Scholar] [CrossRef] [Green Version]
- Santini, G. Synesthesizer: Physical Modelling and Machine Learning for a Color-Based Synthesizer in Virtual Reality. In Proceedings of the International Conference on Mathematics and Computation in Music MCM 2019, LNAI 11502, Madrid, Spain, 18–21 June 2019; Montiel, M., Gómez-Martín, F., Agustín-Aquino, O.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 229–235. [Google Scholar]
- Mannone, M.; (Department of Engineering, University of Palermo, Palermo, Italy); Santini, G.; (Ca’ Foscari University of Venice, Via Torino, 107, Venezia Mestre, Italy). Perceived Similarities between Classes of Colors and Classes of Timbres. Available from the Authors upon Request. 2020; unpublished. [Google Scholar]
- Rosenblum, L.D.; Dias, J.W.; Dorsi, J. The Supramodal Brain: Implications for Auditory Perception. J. Cogn. Psychol. 2016, 29, 65–87. [Google Scholar] [CrossRef]
- Parise, C.V. Crossmodal Correspondences: Standing Issues and Experimental Guidelines. Multisensory Res. 2016, 29, 7–28. [Google Scholar] [CrossRef] [PubMed]
- Itoh, K.; Sakata, H.; Kwee, I.L.; Nakada, T. Musical pitch classes have rainbow hues in pitch class-color synesthesia. Nat. Sci. Rep. 2017, 7, 17781. [Google Scholar] [CrossRef] [Green Version]
- Thoret, T.; Caramiaux, B.; Depalle, P.; McAdams, S. Learning metrics on spectrotemporal modulations reveals the perception of musical instrument timbre. Nat. Hum. Behav. 2020, 5, 369–377. [Google Scholar] [CrossRef]
- Favali, F. Shapes and Notes: Transforming Images into Musical Structures. Ph.D. Dissertation, University of Birmingham, Birmingham, UK, 2019. Available online: https://etheses.bham.ac.uk/id/eprint/9571/ (accessed on 16 January 2022).
- Crnjanski, N.; Tomas, D. Musical Perception and Visualization. Music and Spatiality. Paper read at Music and Spatiality. In Proceedings of the 13th Biennale International Conference on Music Theory and Analysis, Belgrade, Serbia, 4–6 October 2019. [Google Scholar]
- Christensen, E. The Musical Timespace: A Theory of Musical Listening; Aalborg University Press: Aalborg, Denmark, 1996. [Google Scholar]
- Seyler, F. “Michel Henry” The Stanford Encyclopedia of Philosophy (Fall 2019 Edition); Zalta, E.N., Ed.; Stanford University: Palo Alto, CA, USA, 2019; Available online: https://plato.stanford.edu/archives/fall2019/entries/michel-henry/ (accessed on 16 January 2022).
- Fortuna, S. Images to play: An Improvisation Model between Visual Arts and Music. In Konteksty Kultury I Edukacji Muzycznej; Parkita, E., Parkita, A., Sztejnbis-Zdyb, J., Eds.; Uniwersytetu Jana Kochanowskiego: Kielce, Poland, 2020; pp. 109–118. [Google Scholar]
- Arias-Valero, J.S.; Lluis-Puebla, E. Some Remarks on Hypergestural Homology of Spaces and Its Relation to Classical Homology. J. Math. Music 2020. [Google Scholar] [CrossRef]
- Grey, J. Multidimensional Perceptual Scaling of Musical Timbres. J. Acoust. Soc. Am. 1977, 61, 1270–1277. [Google Scholar] [CrossRef]
- McAdams, S.; Winsberg, S.; Donnadieu, S.; De Soete, G.; Krimphoff, J. Perceptual Scaling of Synthesized Musical Timbres: Common Dimensions, Specificities, and Latent Subject Classes. Psychol. Res. 1995, 58, 177–192. [Google Scholar] [CrossRef] [Green Version]
- Hatcher, A. Algebraic Topology; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Hardie, K.A.; Kamps, K.H.; Kieboom, R.W. A Homotopy Bigroupoid of a Topological Space. Appl. Categ. Struct. 2001, 9, 311–327. [Google Scholar] [CrossRef]
- Porter, T. Spaces as Infinity-Groupoids. In New Spaces in Mathematics Formal and Conceptual Reflections; Cambridge University Press: Cambridge, UK, 2021; pp. 258–321. Available online: http://nlab-pages.s3.us-east-2.amazonaws.com/nlab/files/Spaces+as+infinity-groupoids.pdf (accessed on 16 January 2022).
- Brandt, H. Über eine Verallgemeinerun des Gruppenbegriffes. Math. Ann. 1927, 96, 360–366. [Google Scholar] [CrossRef]
- Stevenson, D. The Geometry of Bundle Gerbes. Ph.D. Thesis, University of Adelaide, Adelaide, Australia, 2000. Available online: https://arxiv.org/pdf/math/0004117.pdf (accessed on 16 January 2022).
- Grothendieck, A. À la Poursuite des Champs; 1983. Typescript, English Translation in. Available online: https://thescrivener.github.io/PursuingStacks/ps-online.pdf (accessed on 16 January 2022).
- Kasangian, S.; Metere, G.; Vitale, E.M. The ziqqurath of exact sequences of n-groupoids. Cahiers de Topologie et Géométrie Différentielle Catégoriques 2011, 52, 2–44. Available online: http://www.numdam.org/item?id=CTGDC_2011__52_1_2_0 (accessed on 16 January 2022).
- Metere, G. The Ziqqurath of Exact Sequences of n-Groupoids. Ph.D. Thesis, University of Milano, Milano, Italy, 2008. Available online: https://arxiv.org/pdf/0802.0800.pdf (accessed on 16 January 2022).
- Pollard, H.F.; Jansson, E.V. A Tristimulus Method for the Specification of Musical Timbre. Acustica 1982, 51, 162–171. [Google Scholar]
- Schommer-Pries, C.J. The Classification of Two-Dimensional Extended Topological Field Theories. Ph.D. Dissertation, University of California, Berkeley, CA, USA, 2014. [Google Scholar]
- Hesse, J. Group Actions on Bicategories and Topological Quantum Field Theories. Ph.D. Dissertation, Staats-und Universitätsbibliothek Hamburg Carl von Ossietzky, Hamburg, Germany, 2017. Available online: https://d-nb.info/1137625104/34 (accessed on 16 January 2022).
- Calvo, M.; Cegarra, A.M.; Heredia, B.A. Structure and Classification of Monoidal Groupoids. Semigroup Forum 2013, 87, 35–79. [Google Scholar] [CrossRef]
- McAdams, S. Timbre as a structuring force in music. Proc. Meet. Acoust. 2013, 19, 035050. [Google Scholar]
- Xenakis, I. Formalized Music; Pendragon Press: New York, NY, USA, 2001. [Google Scholar]
- Wessel, D. Timbre Space as a Musical Control Structure. Comput. Music. J. 1974, 3, 45–52. Available online: https://www.cnmat.berkeley.edu/sites/default/files/attachments/Timbre-Space.pdf (accessed on 16 January 2022). [CrossRef]
- McAdams, S.; Giordano, B.L. The Perception of Musical Timbre. In The Oxford Handbook of Music Psychology; Hallam, S., Cross, I., Thaut, M., Eds.; Oxford University Press: New York, NY, USA, 2009; pp. 72–80. [Google Scholar]
- Siedenburg, K.; Saitis, C.; McAdams, S. The present, past, and future of timbre research. In Timbre: Acoustics, Perception, and Cognition; Siedenburg, K., Saitis, C., McAdams, S., Popper, A.N., Fay, R.R., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 1–19. [Google Scholar]
- Risset, J.C. Computer study of trumpet tones. J. Acoust. Soc. Am. 1965, 38, 912. [Google Scholar] [CrossRef] [Green Version]
- Mathews, M.V.; Miller, J.E.; Pierce, J.R.; Tenney, J. Computer study of violin tones. J. Acoust. Soc. Am. 1965, 38, 912–913. [Google Scholar] [CrossRef]
- Slawson, W. Sound Color; University of California Press: Berkeley, MA, USA, 1985. [Google Scholar]
- Siedenburg, S.; McAdams, S. Four distinctions for the auditory “wastebasket” of timbre. Front. Psychol. 2017, 8, 1747. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nouno, G.; Cont, A.; Carpentier, G.; Harvey, J. Making an Orchestra Speak. In Proceedings of the Sound and Music Computing, Porto, Portugal, 23–25 July 2009. [Google Scholar]
- Kendall, R.A.; Carterette, E.C. Identification and blend of timbres as a basis for orchestration. Contemp. Music. Rev. 1993, 9, 51–67. [Google Scholar] [CrossRef]
- Rose, F.; Hetrik, J.E. Enhancing Orchestration Technique via Spectrally Based Linear Algebra Methods. Comput. Music. J. 2009, 33, 32–41. [Google Scholar] [CrossRef]
- Caetano, M.; Rodet, X. Musical instrument sound morphing guided by perceptually motivated features. IEEE Trans. Audio Speech Lang. Process. 2013, 21, 1666–1675. [Google Scholar] [CrossRef]
- Grey, J.; Gordon, J.W. Perceptual effects of spectral modifications on musical timbres. J. Acoust. Soc. Am. 1978, 65, 1493–1500. [Google Scholar] [CrossRef]
- Grey, J.; Moorer, J.A. Perceptual evaluation of synthesized musical instrument tones. J. Acoust. Soc. Am. 1977, 62, 454–462. [Google Scholar] [CrossRef]
- Cella, C.-E. Orchidea: A comprehensive framework for target- based computer-assisted dynamic orchestration. J. New Music. Res. (JNMR). under review.
- Maresz, Y. On computer-assisted orchestration. Contemp. Music. Rev. 2013, 32, 99–109. [Google Scholar] [CrossRef]
- Anderson, J. A provisional history of spectral music. Contemp. Music. Rev. 2000, 9, 7–22. [Google Scholar] [CrossRef]
- Berlin, B.; Kay, P. Basic Color Terms: Their Universality and Evolution; California University Press: Berkeley, CA, USA, 1999. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mannone, M.; Santini, G.; Adedoyin, E.; Cella, C.E. Color and Timbre Gestures: An Approach with Bicategories and Bigroupoids. Mathematics 2022, 10, 663. https://doi.org/10.3390/math10040663
Mannone M, Santini G, Adedoyin E, Cella CE. Color and Timbre Gestures: An Approach with Bicategories and Bigroupoids. Mathematics. 2022; 10(4):663. https://doi.org/10.3390/math10040663
Chicago/Turabian StyleMannone, Maria, Giovanni Santini, Esther Adedoyin, and Carmine E. Cella. 2022. "Color and Timbre Gestures: An Approach with Bicategories and Bigroupoids" Mathematics 10, no. 4: 663. https://doi.org/10.3390/math10040663
APA StyleMannone, M., Santini, G., Adedoyin, E., & Cella, C. E. (2022). Color and Timbre Gestures: An Approach with Bicategories and Bigroupoids. Mathematics, 10(4), 663. https://doi.org/10.3390/math10040663





