Tail Conditional Moments for Location-Scale Mixture of Elliptical Distributions

Abstract

We present the general results on the univariate tail conditional moments for a location-scale mixture of elliptical distributions. Examples include the location-scale mixture of normal, location-scale mixture of Student’s t, location-scale mixture of logistic, and location-scale mixture of Laplace distributions. More specifically, we give the tail variance, the tail conditional skewness, and the tail conditional kurtosis of generalised hyperbolic distribution and Student–GIG mixture distribution. We give an illustrative example, which discusses the TCE, TV, TCS and TCK of three stocks, including Amazon, Google and Apple.

1. Introduction and Motivation

Let X be a random variable with a cumulative distribution function $F_X\left(x\right).$ Value-at-risk (VaR) of the random variable X, computed at a probability level $q\in (0,1)$, is defined as

$${\mathrm{VaR}}_q\left(X\right)=inf\{x\in \mathbb{R}|P(X\le x)\ge q\}.$$

VaR is one of the best known and the most frequently used measures of financial risk. Another important risk measure is the Tail Conditional Expectation (TCE), which is defined as

$${\mathrm{TCE}}_q\left(X\right)=\mathrm{E}\left(X\right|X>Va{R}_q\left(X\right)).$$

The TCE has already been discussed in many literatures. In this paper, we introduce the nth Tail Conditional Moments (TCM) for random variable X, which is defined as

$$\begin{array}{c}\hfill {\mathrm{TCM}}_q\left(X^n\right)=\mathrm{E}\left({[X-{\mathrm{TCE}}_q\left(X\right)]}^n\right|X>x_q),\end{array}$$

(1)

where

$$x_q=inf\{x\in \mathbb{R}|P(X\le x)\ge q\}.$$

We note that the proposed TCM takes the form of $\mathrm{E}\left[{(X-{\mathrm{TCE}}_q\left(X\right))}^n\right|X>x_q]$ instead of $\mathrm{E}\left[{(X-\mathrm{E}\left(X\right))}^n\right|X>x_q]$, because we think that these moments provide a better interpretation of tail trajectories. We care more about $X>x_q$ than X. It is interesting to note that TCM can be found in asymptotic expansion of the conditional characteristic function:

$${\phi }_q\left(t\right):=\mathrm{E}\left(e^{itX}\right|X>x_q)=1-{\mathrm{TV}}_q\left(X\right)\frac{t^2}{2}+\sum _{j=3}^k{\mathrm{TCM}}_q\left(X^j\right)\frac{{\left(it\right)}^j}{j!}+{o\left(\right|t|}^k),$$

where

$$\begin{array}{c}\hfill {\mathrm{TV}}_q\left(X\right):=\mathrm{Var}\left(X\right|X>{\mathrm{VaR}}_q\left(X\right))={\mathrm{TCM}}_q\left(X^2\right)\end{array}$$

(2)

is a special case of (1), which is a risk measure that examines the dispersion of the tail of a distribution for some quantile q. The tail variance risk measure (TV) was proposed by Furman and Landsman [1] and as a measure for the optimal portfolio selection in Landsman [2].

The risk measures, such as VaR, TCE and TV, do not provide sufficient information on skewness and kurtosis of the tail of a distribution. Therefore, we use the spread of the skewness and kurtosis of the tail of a distribution for some q-quantiles, which are proposed and studied by Landsman et al. (2016b). The Tail Conditional Skewness (TCS) and the Tail Conditional Kurtosis (TCK) are defined as follows, respectively,

$$\begin{array}{cc}\hfill {\mathrm{TCS}}_q\left(X\right)=& \frac{\mathrm{E}\left({[X-{\mathrm{TCE}}_q\left(X\right)]}^3\right|X>x_q)}{{\mathrm{TV}}_q{\left(X\right)}^{\frac{3}{2}}},\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\mathrm{TCK}}_q\left(X\right)=& \frac{\mathrm{E}\left({[X-{\mathrm{TCE}}_q\left(X\right)]}^4\right|X>x_q)}{{\mathrm{TV}}_q{\left(X\right)}^2}-3.\hfill \end{array}$$

(4)

The TCS can help us comprehend whether the distribution is left-skewed or right-skewed. If ${\mathrm{TCS}}_q\left(X\right)<0$, the tail is on the left side of the distribution, that is, the probability for X being below ${\mathrm{TCE}}_q\left(X\right)$ will be higher than that of being above it. If ${\mathrm{TCS}}_q\left(X\right)>0$, the tail is on the right side of the distribution, that is, the probability for X being above ${\mathrm{TCE}}_q\left(X\right)$ will be higher than that of being below it. By comparing the TCK of the normal distribution, we can know the shape of the probability distribution.

It is well-known that TCE describes the extreme expected losses. Recently, there have been many studies on TCE. For example, Landsman and Valdez [3] introduced tail conditional expectations for elliptical distributions. Ignatieva and Landsman [4] discussed conditional tail risk measures for the skewed generalised hyperbolic family. Deng and Yao [5] extended the Stein-type inequality to the multivariate generalized hyperbolic distribution. Li et al. [6] derived the conditional tail expectation for log-multivariate generalized hyperbolic distribution. In a more recent paper of Ignatieva and Landsman [7], where the location-scale mixture of elliptical distributions was introduced (and called the “generalised hyper-elliptical distributions”), they considered the tail conditional risk measures for that distributions; see also Zuo and Yin [8]. Kim [9] presented the conditional tail moments for an exponential family, and Landsman et al. [10] and Eini et al. [11] presented the conditional tail moments for elliptical distributions and generalized skew-elliptical distributions, respectively. In this paper, the main consideration is tail conditional moments for a location-scale mixture of elliptical distributions, which extends the conclusion of Zuo and Li. Since the location-scale mixture of elliptical distributions can be composed of any elliptical distribution and Generalised Inverse Gaussian distribution, which has generality, we found that location-scale mixtures of elliptical distributions are suitable for heavy-tailed distributions. Therefore, the location-scale mixture of elliptical distributions is more flexible, and we can choose different elliptic distributions and parameters to fit the models.

The paper is organized as follows. In Section 2 we introduce the location-scale mixture of elliptical distributions. In Section 3 we obtain the expression of the nth TCM for univariate cases of mixture of elliptical distributions. In Section 4 we give the expressions of TV, TCS, and TCK for some important cases of mixture of elliptical distributions. Section 5 offers the numerical analysis of GH and the mixture of the Student’s t distribution. Section 6 shows an illustrative example, and discusses the TCE, TV, TCS, TCK of three stocks. Section 7 gives concluding remarks.

2. Location-Scale Mixture of Elliptical Distributions

In this section, we introduce the mixture of elliptical distributions. Firstly, let us introduce the elliptical family distributions. The random vector $\mathbf{X}$ is said to have an elliptical distribution with parameters $\mathit{\mu }$ and $\mathsf{\Sigma }$ if its characteristic function can be expressed as

$$\begin{array}{c}\hfill {\phi }_{\mathit{X}}\left(t\right)=exp\left(i{\mathbf{t}}^T\mathit{\mu }\right)\psi \left(\frac{1}{2}{\mathbf{t}}^T\mathsf{\Sigma }\mathbf{t}\right),\end{array}$$

(5)

for some function $\varphi :\mathbb{R}\to \mathbb{R}$. Then we denote $\mathbf{X}\sim E_n(\mathit{\mu },\mathsf{\Sigma },\psi )$.

An elliptically distributed random vector $\mathbf{X}$ does not necessarily have a multivariate density function $f_{\mathbf{X}}$. If $\mathbf{X}\sim E_n(\mathit{\mu },\mathsf{\Sigma },\psi )$ has a density, then it will be of the form

$$\begin{array}{c}\hfill f_{\mathit{X}}\left(\mathit{x}\right):=\frac{c_n}{\sqrt{\left|\mathsf{\Sigma }\right|}}{g}_n\left\{\frac{1}{2}{(\mathit{x}-\mathit{\mu })}^T{\mathsf{\Sigma }}^{-1}(\mathit{x}-\mathit{\mu })\right\},\mathit{x}\in {\mathbb{R}}^n,\end{array}$$

(6)

where $\mathit{\mu }$ is an $n\times 1$ location vector, $\mathsf{\Sigma }$ is an $n\times n$ scale matrix, and $g_n\left(u\right)$, $u\ge 0$, is the density generator of $\mathbf{X}$. This density generator satisfies condition:

$$\begin{array}{c}\hfill {\int }_0^{\infty }{u}^{\frac{n}{2}-1}{g}_n\left(u\right)\mathrm{d}u<\infty ,\end{array}$$

(7)

and the normalizing constant $c_n$ is given by

$$\begin{array}{c}\hfill c_n=\frac{\Gamma (n/2)}{{\left(2\pi \right)}^{n/2}}{\left[{\int }_0^{\infty }{t}^{(n/2)-1}{g}_n\left(t\right)\mathrm{d}t\right]}^{-1}.\end{array}$$

(8)

A necessary condition for this covariance matrix to exist is

$$\begin{array}{c}\hfill |{\psi }^{\prime }\left(0\right)|<\infty ,\end{array}$$

(9)

(see Fang et al. [12]). Suppose $\mathbf{A}$ is a $k\times n$ matrix, and $\mathbf{b}$ is a $k\times 1$ vector. Then

$$\begin{array}{c}\hfill \mathbf{AX}+\mathbf{b}\sim E_k\left(\mathit{A}\mathit{\mu }+\mathit{b},\mathit{A}\mathsf{\Sigma }{\mathit{A}}^{\mathit{T}},g_{k,n}\right),\end{array}$$

(10)

where $g_{k,n}\left(u\right)={\int }_0^{\infty }{s}^{\frac{n-k}{2}-1}{g}_n(s+u)\mathrm{d}s$.

We denote the cumulative generator ${\overline{G}}_1\left(u\right)={\int }_u^{\infty }{g}_1\left(t\right)\mathrm{d}t$, and a sequence of cumulative generators

$${\overline{G}}_1\left(u\right)={\int }_u^{\infty }{g}_1\left(t\right)\mathrm{d}t,{\overline{G}}_2\left(u\right)={\int }_u^{\infty }{\overline{G}}_1\left(t\right)\mathrm{d}t,\dots ,{\overline{G}}_n\left(u\right)={\int }_u^{\infty }{\overline{G}}_{n-1}\left(t\right)\mathrm{d}t.$$

Meanwhile, assume the variance of $\mathbf{X}$ exists, and let $\mathbf{Z}=\frac{x-\mu }{\sigma },$ and

$$\frac{1}{2}{\sigma }_Z^2=c_1{\int }_0^{\infty }{z}^{2}g\left(\frac{1}{2}{z}^2\right)\mathrm{d}z={\int }_0^{\infty }{c}_{1}z\mathrm{d}{G}_1\left(\frac{1}{2}{z}^2\right)<\infty .$$

Consequently,

$${\int }_0^{\infty }{c}_1{\overline{G}}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z=\frac{1}{2}{\sigma }_Z^2,$$

and $\frac{c_1}{{\sigma }_Z^2}{\overline{G}}_1\left(\frac{1}{2}{z}^2\right)=f_{Z_1}\left(z\right)$, which is a density of random variable $Z_1$, defined on $\mathbb{R}$. Similarly,

$${\int }_0^{\infty }{c}_2{\overline{G}}_2\left(\frac{1}{2}{z}^2\right)\mathrm{d}z=\frac{1}{2}{\sigma }_Z^2,$$

and $\frac{c_2}{{\sigma }_Z^2}{\overline{G}}_2\left(\frac{1}{2}{z}^2\right)=f_{Z_2}\left(z\right)$ is a density of random variable $Z_2,$ defined on $\mathbb{R}$.

Next, we introduce the Location-Scale Mixture of Elliptical (LSME) distributions. $\mathbf{Y}\sim LSM{E}_n(\mathit{\mu },\mathsf{\Sigma },\mathit{\beta },\mathsf{\Theta },g_n)$ is an n-dimensional LSME distribution with location parameter $\mathit{\mu }$ and positive definite scale matrix $\mathsf{\Sigma }={\left({\sigma }_{i,j}\right)}_{i,j=1}^n$, if

$$\begin{array}{c}\hfill \mathbf{Y}=\mathit{\mu }+\mathsf{\Theta }\mathit{\beta }+{\mathsf{\Theta }}^{\frac{1}{2}}{\mathsf{\Sigma }}^{\frac{1}{2}}\mathbf{X},\end{array}$$

(11)

where $\mathit{\beta }\in {\mathbb{R}}^n$, and $\mathbf{X}\sim E_n(\mathbf{0},{\mathbf{I}}_n,g_n).$ Assuming that $\mathbf{X}$ is independent of non-negative scalar random variable $\mathsf{\Theta }$, we have

$$\begin{array}{c}\hfill \mathbf{Y}|\mathsf{\Theta }=\theta \sim E_n(\mathit{\mu }+\theta \mathit{\beta },\theta \mathsf{\Sigma },g_n).\end{array}$$

(12)

If ${\mathsf{\Theta }}^{1/\alpha }\ge 0,\alpha >1,$$\mathsf{\Theta }$ has a Generalised Inverse Gaussian distribution, $GIG(\lambda ,\chi ,\psi )$, given by pdf

$$\begin{array}{c}\hfill {\varpi }_{\lambda ,\chi ,\psi }\left(\theta \right)=f_{\lambda ,\chi ,\psi }\left(\theta \right)=\frac{{\chi }^{-\lambda }{\left(\sqrt{\chi \psi }\right)}^{\lambda }}{2K_{\lambda }\left(\sqrt{\chi \psi }\right)}{\theta }^{\lambda -1}exp\left\{-\frac{1}{2}\left(\chi {\theta }^{-1}+\psi \theta \right)\right\},\theta >0,\end{array}$$

(13)

where $K_{\lambda }(·)$ denotes a modified Bessel function of the third kind with index $\lambda$:

$$K_{\lambda }\left(\omega \right)=\frac{1}{2}{\int }_0^{\infty }{\chi }^{\lambda -1}exp\{-\frac{1}{2}\omega ({\chi }^{-1}+\chi )\}\mathrm{d}\chi .$$

Here the parameters satisfy $\chi >0$, $\psi \ge 0$ if $\lambda <0$; $\chi >0$, $\psi >0$ if $\lambda =0$; $\chi \ge 0$, $\psi >0$ if $\lambda >0$.

When ${\mathsf{\Theta }}^{-1}\sim B(\alpha ,1)$, the random vector $\mathbf{Y}$ has a new distribution, which is also a special case of LSME distributions. Here, $B(·,·)$ is the Beta function.

We list some examples of the mixture elliptical family, including the Location-Scale Mixture of Normal (LSMN), Location-Scale Mixture of Student’s t (LSMSt), Location-Scale Mixture of Logistic (LSMLo) and Location-Scale Mixture of Laplace (LSMLa) distributions.

Example 1.

(Mixture of normal distribution). An n-dimensional normal random vector $\mathbf{X}$ with location parameter μ and scale matrixΣhas density function

$$\begin{array}{c}\hfill f_{\mathit{X}}\left(\mathit{x}\right)=\frac{c_n}{\sqrt{\left|\mathsf{\Sigma }\right|}}exp\left\{-\frac{1}{2}{(\mathit{x}-\mathit{\mu })}^T{\mathsf{\Sigma }}^{-1}(\mathit{x}-\mathit{\mu })\right\},\mathit{x}\in {\mathbb{R}}^n,\end{array}$$

where $c_n={\left(2\pi \right)}^{-\frac{n}{2}}$, and is denoted by $\mathbf{X}\sim N_n\left(\mathit{\mu },\mathsf{\Sigma }\right)$. Therefore, the location-scale mixture of normal random vector $\mathbf{Y}\sim LSM{N}_n(\mathit{\mu },\mathsf{\Sigma },\mathit{\beta },\mathsf{\Theta })$ is defined as

$$\begin{array}{c}\hfill \mathbf{Y}=\mathit{\mu }+\mathsf{\Theta }\mathit{\beta }+{\mathsf{\Theta }}^{\frac{1}{2}}{\mathsf{\Sigma }}^{\frac{1}{2}}\mathbf{X},\end{array}$$

(14)

where $\mathbf{X}\sim N_n\left(\mathbf{0},{\mathit{I}}_{\mathit{n}}\right)$, and μ,Σ, Θ and β are the same as those in (11).

Example 2.

(Mixture of logistic distribution). Density function of an n-dimensional logistic random vector $\mathbf{X}$ with location parameter μ and scale matrixΣcan be expressed as

$$\begin{array}{c}\hfill f_{\mathit{X}}\left(\mathit{x}\right)=\frac{c_n}{\sqrt{\left|\mathsf{\Sigma }\right|}}\frac{exp\left\{-\frac{1}{2}{(\mathit{x}-\mathit{\mu })}^T{\mathsf{\Sigma }}^{-1}(\mathit{x}-\mathit{\mu })\right\}}{{\left[1+exp\left\{-\frac{1}{2}{(\mathit{x}-\mathit{\mu })}^T{\mathsf{\Sigma }}^{-1}(\mathit{x}-\mathit{\mu })\right\}\right]}^2},\mathit{x}\in {\mathbb{R}}^n,\end{array}$$

where

$$\begin{array}{cc}{c}_n\hfill & =\frac{\Gamma (n/2)}{{\left(2\pi \right)}^{n/2}}{\left[{\int }_0^{\infty }{t}^{n/2-1}\frac{exp(-t)}{{[1+exp(-t)]}^2}\mathrm{d}t\right]}^{-1}\hfill \\ \hfill & =\frac{1}{{\left(2\pi \right)}^{n/2}{\mathsf{\Psi }}_2^{*}(-1,\frac{n}{2},1)},\hfill \end{array}$$

and is denoted by $\mathbf{X}\sim L{o}_n\left(\mathit{\mu },\mathsf{\Sigma }\right)$. The location-scale mixture of logistic random vector $\mathbf{Y}\sim LSML{o}_n(\mathit{\mu },\mathsf{\Sigma },\mathit{\beta },\mathsf{\Theta })$ satisfies

$$\begin{array}{c}\hfill \mathbf{Y}=\mathit{\mu }+\mathsf{\Theta }\mathit{\beta }+{\mathsf{\Theta }}^{\frac{1}{2}}{\mathsf{\Sigma }}^{\frac{1}{2}}\mathbf{X},\end{array}$$

(15)

where $\mathbf{X}\sim L{o}_n\left(\mathbf{0},{\mathit{I}}_{\mathit{n}}\right)$, and μ,Σ, Θ and β are the same as those in (11).

Remark 1.

Here, ${\mathsf{\Psi }}_{\mathit{\mu }}^{*}(z,s,a)$ is the generalized Hurwitz–Lerch zeta function defined by (cf. Lin et al. (2006))

$${\mathsf{\Psi }}_{\mathit{\mu }}^{*}(z,s,a)=\frac{1}{\Gamma \left(\mu \right)}\sum _{n=0}^{\infty }\frac{\Gamma (\mu +n)}{n!}\frac{z^n}{{(n+a)}^s},$$

which has an integral representation

$${\mathsf{\Psi }}_{\mathit{\mu }}^{*}(z,s,a)=\frac{1}{\Gamma \left(s\right)}{\int }_0^{\infty }\frac{t^{s-1}{e}^{-at}}{{(1-z{e}^{-t})}^{\mu }}\mathrm{d}t,$$

where $\mathcal{R}\left(a\right)>0$, $\mathcal{R}\left(s\right)>0$ when $\left|z\right|\le 1(z\ne 1)$, $\mathcal{R}\left(s\right)>1$ when $z=1$.

Example 3.

(Mixture of Laplace distribution). The density of Laplace random vector $\mathbf{X}$ with location parameter μ and scale matrixΣis given by

$$\begin{array}{cc}\hfill f_{\mathit{X}}\left(\mathit{x}\right)=& \frac{c_n}{\sqrt{\left|\mathsf{\Sigma }\right|}}exp\left\{-{\left[{(\mathit{x}-\mathit{\mu })}^T{\mathsf{\Sigma }}^{-1}(\mathit{x}-\mathit{\mu })\right]}^{1/2}\right\},\mathbf{x}\in {\mathbb{R}}^n,\hfill \end{array}$$

where $c_n=\frac{\Gamma (n/2)}{2{\pi }^{n/2}\Gamma \left(n\right)}$, and is denoted by $\mathbf{X}\sim L{a}_n\left(\mathit{\mu },\mathsf{\Sigma }\right)$. Hence, the location-scale mixture of Laplace random vector $\mathbf{Y}\sim LSML{a}_n(\mathit{\mu },\mathsf{\Sigma },\mathit{\beta },\mathsf{\Theta })$ is defined as

$$\begin{array}{c}\hfill \mathbf{Y}=\mathit{\mu }+\mathsf{\Theta }\mathit{\beta }+{\mathsf{\Theta }}^{\frac{1}{2}}{\mathsf{\Sigma }}^{\frac{1}{2}}\mathbf{X},\end{array}$$

(16)

where $\mathbf{X}\sim L{a}_n\left(\mathbf{0},{\mathit{I}}_{\mathit{n}}\right)$, and μ,Σ, Θ and β are the same as those in (11).

3. Tail Conditional Moments

In this section, we present the $\mathrm{TCM}$ for a univariate case of the mixture of elliptical distributions. We assume that the conditional and mixture distributions are continuous.

Consider $Y\sim LSM{E}_1(\mu ,{\sigma }^2,\beta ,\mathsf{\Theta },g_1)$, then $Y|\mathsf{\Theta }\sim {\mathrm{E}}_1(\mu +\theta \beta ,\theta {\sigma }^2,g_1)$. Before giving the $\mathrm{TCM}$, we calculate the following conditional moments

$${\mathrm{E}}_{Y|\mathsf{\Theta }}\left[Y^n|Y>y_q\right],E\left[Y^n\right|Y>y_q].$$

Lemma 1.

Let $Y\sim LSM{E}_1(\mu ,{\sigma }^2,\beta ,\mathsf{\Theta },g_1)$ be a univariate location-scale mixture of an elliptical random variable defined as (11). Let $Y|\mathsf{\Theta }\sim {\mathrm{E}}_1(\mu +\theta \beta ,\theta {\sigma }^2,g_1)$, which implies

$$\begin{array}{c}\hfill {\int }_0^{\infty }{u}^{-1/2}{\overline{G}}_1\left(u\right)\mathrm{d}u<\infty .\end{array}$$

(17)

Then

$$\begin{array}{cc}\hfill {\mathrm{E}}_{Y|\mathsf{\Theta }}\left[Y^n\right|Y>y_q]=& {(\mu +\theta \beta )}^n+n\left(\sqrt{\theta }\sigma \right){(\mu +\theta \beta )}^{n-1}TC{E}_q\left(Z\right)+\sum _{k=2}^n{C}_n^k{\left(\sqrt{\theta }\sigma \right)}^k\hfill \\ \hfill & {(\mu +\theta \beta )}^{n-k}[c_1{\lambda }_{1,q}{z}_q^{k-1}+(k-1){\sigma }_Z^2{r}_{1,q}\left(z_q\right){\mathrm{TCE}}_{Z_1^{k-2}}\left(z_q\right)],\hfill \end{array}$$

where

$$\begin{array}{c}\hfill z=\frac{x-\mu -\theta \beta }{\sqrt{\theta }\sigma },{\lambda }_{1,q}=\frac{{\overline{G}}_1\left(\frac{1}{2}{z}_q^2\right)}{1-q},\end{array}$$

$$\begin{array}{c}\hfill r_{1,q}\left(z_q\right)=\frac{{\overline{F}}_{Z_1}\left(z_q\right)}{1-q},{\mathrm{TCE}}_{Z_1^{k-2}}\left(z_q\right)={\mathrm{E}}_{Z_1}\left(Z^{k-2}|Z>z_q\right).\end{array}$$

Proof. 

The nth conditional moments are

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathrm{E}}_{Y|\mathsf{\Theta }}\left[Y^n\right|Y>y_q]=& \frac{1}{{\overline{F}}_{Y|\mathsf{\Theta }}\left(y_q\right)}{\int }_{y_q}^{\infty }\frac{c_1}{\sqrt{\theta }\sigma }{y}^n{g}_1\left(\frac{1}{2}{\left(\frac{y-\mu -\theta \beta }{\sqrt{\theta }\sigma }\right)}^2\right)\mathrm{d}y\hfill \\ \hfill =& \frac{1}{1-q}{\int }_{z_q}^{\infty }{c}_1{\left(\sqrt{\theta }\sigma z+\mu +\theta \beta \right)}^n{g}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z\hfill \\ \hfill =& \frac{1}{1-q}\sum _{k=0}^n{C}_n^k{\int }_{z_q}^{\infty }{c}_1{\left(\sqrt{\theta }\sigma z\right)}^k{\left(\mu +\theta \beta \right)}^{n-k}{g}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z\hfill \\ \hfill =& \frac{1}{1-q}\left({\int }_{z_q}^{\infty }{c}_1{(\mu +\theta \beta )}^n{g}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z\right.\hfill \\ \hfill & \left.+\sum _{k=1}^n{C}_n^k{\int }_{z_q}^{\infty }{c}_1{\left(\sqrt{\theta }\sigma z\right)}^k{(\mu +\theta \beta )}^{n-k}{g}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z\right)\hfill \\ \hfill =& {(\mu +\theta \beta )}^n+\frac{1}{1-q}n{\int }_{z_q}^{\infty }{c}_1\left(\sqrt{\theta }\sigma z\right){(\mu +\theta \beta )}^{n-1}{g}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z\hfill \\ \hfill & +\frac{1}{1-q}\sum _{k=2}^n{C}_n^k{c}_1{\left(\sqrt{\theta }\sigma \right)}^k{(\mu +\theta \beta )}^{n-k}{\int }_{z_q}^{\infty }{z}^k{g}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z\hfill \\ \hfill =& {(\mu +\theta \beta )}^n+n\left(\sqrt{\theta }\sigma \right){(\mu +\theta \beta )}^{n-1}TC{E}_q\left(Z\right)+\sum _{k=2}^n{C}_n^k{\left(\sqrt{\theta }\sigma \right)}^k\hfill \\ \hfill & {(\mu +\theta \beta )}^{n-k}\left[c_1{\lambda }_{1,q}{z}_q^{k-1}+(k-1){\sigma }_Z^2{\int }_{z_q}^{\infty }{z}^{k-2}{f}_{Z_1}\left(z\right)\mathrm{d}z\right]\hfill \\ \hfill =& {(\mu +\theta \beta )}^n+n\left(\sqrt{\theta }\sigma \right){(\mu +\theta \beta )}^{n-1}TC{E}_q\left(Z\right)+\sum _{k=2}^n{C}_n^k{\left(\sqrt{\theta }\sigma \right)}^k\hfill \\ \hfill & {(\mu +\theta \beta )}^{n-k}\left[c_1{\lambda }_{1,q}{z}_q^{k-1}+(k-1){\sigma }_Z^2{r}_{1,q}\left(z_q\right)TC{E}_{Z_1^{k-2}}\left(z_q\right)\right].\hfill \end{array}\end{array}$$

□

Next, we calculate $\mathrm{E}\left[Y^n\right|Y>y_q]$, which plays an important role in TCM.

Lemma 2.

Let $Y\sim LSM{E}_1(\mu ,{\sigma }^2,\beta ,\mathsf{\Theta },g_1)$ be a univariate location-scale mixture of an elliptical random variable defined as (11). Then

$$\begin{array}{c}\hfill \mathrm{E}\left[Y^n\right|Y>y_q]={\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right){\mathrm{E}}_{Y|\mathsf{\Theta }}\left[Y^n\right|y>y_q]\mathrm{d}\theta .\end{array}$$

(18)

Proof. 

The nth conditional moments is

$$\begin{array}{cc}\hfill \mathrm{E}\left[Y^n\right|Y>y_q]=& \frac{1}{{\overline{F}}_Y\left(y_q\right)}{\int }_{y_q}^{\infty }{y}^n{f}_Y\left(y\right)\mathrm{d}y\hfill \\ \hfill =& \frac{1}{1-q}{\int }_{y_q}^{\infty }{y}^n{\int }_{{\Omega }_{\theta }}{f}_{Y|\mathsf{\Theta }}\left(y\right|\theta )\varpi \left(\theta \right)\mathrm{d}\theta \mathrm{d}y\hfill \\ \hfill =& \frac{1}{1-q}{\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right){\int }_{y_q}^{\infty }{y}^n{f}_{Y|\mathsf{\Theta }}\left(y\right|\theta )\mathrm{d}y\mathrm{d}\theta \hfill \\ \hfill =& \frac{1}{1-q}{\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right){\overline{F}}_{Y|\mathsf{\Theta }}\left(y_q\right)\frac{1}{{\overline{F}}_{Y|\mathsf{\Theta }}\left(y_q\right)}{\int }_{y_q}^{\infty }{y}^n{f}_{Y|\mathsf{\Theta }}\left(y\right|\theta )\mathrm{d}y\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right){\mathrm{E}}_{Y|\mathsf{\Theta }}\left[Y^n\right|Y>y_q]\mathrm{d}\theta ,\hfill \end{array}$$

where $Y|\mathsf{\Theta }\sim E_1(\mu +\theta \beta ,\theta {\sigma }^2,g_1).$ □

Remark 2.

In particular, when $n=1$, the above equation degenerates into

$$\begin{array}{cc}\hfill {\mathrm{TCE}}_{\mathrm{q}}\left(\mathrm{Y}\right)& =\mathrm{E}\left[Y\right|Y>y_q]\hfill \\ \hfill & ={\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right){\mathrm{E}}_{Y|\mathsf{\Theta }}\left[Y^n\right|Y>y_q]\mathrm{d}\theta \hfill \\ \hfill & =\mu +\frac{\beta }{1-q}{\int }_{{\Omega }_{\theta }}{\overline{F}}_{Y|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta +\frac{c_1{\sigma }^2}{c_2(1-q)}{\int }_{{\Omega }_{\theta }}{f}_{Y_1|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta \hfill \\ \hfill & =\mu +\frac{\beta }{1-q}{\delta }_1+\frac{c_1{\sigma }^2}{c_2(1-q)}{\delta }_2,\hfill \end{array}$$

(19)

where $c_2$ is the normalizing constant of $Y_1$,

$${\delta }_1={\int }_{{\Omega }_{\theta }}{\overline{F}}_{Y|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta ,{\delta }_2={\int }_{{\Omega }_{\theta }}{f}_{Y_1|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta ,$$

and $Y_1|\mathsf{\Theta }\sim E_1(\mu +\theta \beta ,\theta {\sigma }^2,{\overline{G}}_1).$

Theorem 1.

Let $Y\sim LSM{E}_1(\mathit{\mu },{\sigma }^2,\beta ,\mathsf{\Theta },g_1)$ be a univariate location-scale mixture of elliptical random variables defined as (11). Then

$$\begin{array}{cc}\hfill {\mathrm{TCM}}_q\left(Y^n\right)& =\mathrm{E}\left[{(Y-TC{E}_q)}^n\right|Y>y_q]\hfill \\ \hfill & =\sum _{i=0}^n{C}_n^i{(-1)}^{n-i}{(\frac{\beta }{1-q}{\delta }_1+\frac{c_1{\sigma }^2}{c_2(1-q)}{\delta }_2)}^{n-i}{\mu }_i,\hfill \end{array}$$

(20)

where

$$\begin{array}{cc}\hfill {\mu }_i=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{i,0}+i{\Lambda }_{i,1}{\lambda }_{1,q}+\sum _{l=2}^i{C}_i^l\right.\hfill \\ \hfill & \left.{\mathsf{\Lambda }}_{i,l}\left(c_1{z}_q^{l-1}{\lambda }_{1,q}+\left(l-1\right){\sigma }_Z^2{r}_{1,q}\left(z_q\right){\mathrm{TCE}}_{Z_1^{l-2}}\left(z_q\right)\right)\right)\mathrm{d}\theta ,\hfill \end{array}$$

$${\mathsf{\Lambda }}_{i,l}={\theta }^{i-\frac{l}{2}}{\sigma }^l{\beta }^{i-l},{\lambda }_{1,q}=\frac{{\overline{G}}_1\left(\frac{1}{2}{z}_q^2\right)}{1-q},r_{1,q}\left(z_q\right)=\frac{{\overline{F}}_{Z_1}\left(z_q\right)}{1-q}.$$

Proof. 

Using the Binomial Theorem, we can get

$$\begin{array}{cc}\hfill \mathrm{E}\left[{(Y-{\mathrm{TCE}}_q)}^n|Y>y_q\right]=& \mathrm{E}\left[{(Y-(\mu +\frac{\beta }{1-q}{\delta }_1+\frac{c_1{\sigma }^2}{c_2(1-q)}{\delta }_2))}^n\right|Y>y_q]\hfill \\ \hfill =& \mathrm{E}{[(Y-\mu )-(\frac{\beta }{1-q}{\delta }_1+\frac{c_1{\sigma }^2}{c_2(1-q)}{\delta }_2))}^n|Y>y_q]\hfill \\ \hfill =& \sum _{i=0}^n{(-1)}^{n-i}{(\frac{\beta }{1-q}{\delta }_1+\frac{c_1{\sigma }^2}{c_2(1-q)}{\delta }_2)}^{n-i}\mathrm{E}\left[{(Y-\mu )}^i\right|Y>y_q]\hfill \\ \hfill =& \sum _{i=0}^n{(-1)}^{n-i}{(\frac{\beta }{1-q}{\delta }_1+\frac{c_1{\sigma }^2}{c_2(1-q)}{\delta }_2)}^{n-i}{\mu }_i,\hfill \end{array}$$

where ${\mu }_0=\mathrm{E}\left[{(Y-\mu )}^0\right|Y>y_q]=1,$ ${\mu }_1=\mathrm{E}\left[(Y-\mu )\right|Y>y_q]={\int }_{{\Omega }_{\theta }}\varpi \left(\theta \beta +{\theta }^{\frac{1}{2}}\sigma {\lambda }_{1,q}\right)\mathrm{d}\theta ,$ and ${\mu }_i=\mathrm{E}\left[{(Y-\mu )}^i\right|Y>y_q],i\ge 2.$ The measures ${\mu }_i$ are calculated in the spirit of the proof of Lemma 1. Taking the transformation $z=\frac{x-\mu }{\sigma }$, we note that the tail function is ${\overline{F}}_Z\left(z_q\right)=1-q$, which is, in fact, the $1-q$ percentile. Furthermore, the transformation simplifies the integral in ${\mu }_i$, which is as follows:

$$\begin{array}{cc}\hfill {\mu }_i=& \mathrm{E}\left[{(Y-\mu )}^i\right|Y>y_q]\hfill \\ \hfill =& \frac{1}{{\overline{F}}_Y\left(y_q\right)}{\int }_{y_q}^{\infty }{(y-\mu )}^i{f}_Y\left(y\right)\mathrm{d}y\hfill \\ \hfill =& \frac{1}{{\overline{F}}_Y\left(y_q\right)}{\int }_{y_q}^{\infty }{(y-\mu )}^i{\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)f_{Y|\mathsf{\Theta }}\left(y\right|\theta )\mathrm{d}\theta \mathrm{d}y\hfill \\ \hfill =& \frac{1}{{\overline{F}}_Y\left(y_q\right)}{\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right){\int }_{y_q}^{\infty }{(y-\mu )}^i{f}_{Y|\mathsf{\Theta }}\left(y\right|\theta )\mathrm{d}y\mathrm{d}\theta \hfill \\ \hfill =& \frac{1}{{\overline{F}}_Y\left(y_q\right)}{\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right){\int }_{y_q}^{\infty }{(y-\mu )}^i\frac{c_1}{\sqrt{\theta }\sigma }{g}_1\left(\frac{1}{2}{\left(\frac{y-\mu -\theta \beta }{\sqrt{\theta }\sigma }\right)}^2\right)\mathrm{d}y\mathrm{d}\theta \hfill \\ \hfill =& \frac{1}{{\overline{F}}_Y\left(y_q\right)}{\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right){\int }_{z_q}^{\infty }{\left(\sqrt{\theta }\sigma z+\theta \beta \right)}^i{c}_1{g}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z\mathrm{d}\theta ,\hfill \end{array}$$

(21)

where

$$\begin{array}{cc}\hfill {\int }_{z_q}^{\infty }{\left(\sqrt{\theta }\sigma z+\theta \beta \right)}^i{c}_1{g}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z=& {\int }_{z_q}^{\infty }\sum _{l=0}^i{C}_i^l{\left(\sqrt{\theta }\sigma z\right)}^l{\left(\theta \beta \right)}^{i-l}{c}_1{g}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z\hfill \\ \hfill =& {\int }_{z_q}^{\infty }\sum _{l=0}^i{C}_i^l{\theta }^{i-\frac{l}{2}}{\sigma }^l{\beta }^{i-l}{z}^l{c}_1{g}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z\hfill \\ \hfill =& {\left(\theta \beta \right)}^i{\overline{F}}_Z\left(z_q\right)+i{\theta }^{i-\frac{1}{2}}\sigma {\beta }^{i-1}{c}_1{\overline{G}}_1\left(\frac{1}{2}{z}_q^2\right)\hfill \\ \hfill & -{\int }_{z_q}^{\infty }\sum _{l=2}^i{C}_i^l{\theta }^{i-\frac{l}{2}}{\sigma }^l{\beta }^{i-l}{c}_1{z}^{l-1}\mathrm{d}{\overline{G}}_1\left(\frac{1}{2}{z}^2\right)\hfill \\ \hfill =& {\Lambda }_{i,0}{\overline{F}}_Z\left(z_q\right)+i{\Lambda }_{i,1}{\overline{G}}_1\left(\frac{1}{2}{z}_q^2\right)+\sum _{l=2}^i{C}_i^l{\Lambda }_{i,l}\hfill \\ \hfill & \left(c_1{z}_q^{l-1}{\overline{G}}_1\left(\frac{1}{2}{z}_q^2\right)+(l-1){\sigma }_Z^2{\overline{F}}_{Z_1}\left(z\right){\mathrm{TCE}}_{{\mathrm{Z}}_1^{\mathrm{l}-2}}\left(z_q\right)\right),\hfill \end{array}$$

and here,

$${\Lambda }_{i,l}={\theta }^{i-\frac{l}{2}}{\sigma }^l{\beta }^{i-l}.$$

Taking into account (21), we get

$$\begin{array}{cc}\hfill {\mu }_i=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{i,0}+i{\Lambda }_{i,1}{\lambda }_{1,q}\right.\hfill \\ \hfill & \left.+\sum _{l=2}^i{C}_i^l{\Lambda }_{i,l}\left(c_1{z}_q^{l-1}{\lambda }_{1,q}+\left(l-1\right){\sigma }_Z^2{r}_{1,q}\left(z_q\right){\mathrm{TCE}}_{Z_1^{l-2}}\left(z_q\right)\right)\right)\mathrm{d}\theta .\hfill \end{array}$$

This ends the proof of Theorem 1. □

The GIG is involved in the mixture of elliptical distributions, resulting in different processes when calculating ${\mu }_i$. At the same time, there is some confusion in the normalization constants corresponding to different generating functions in Landsman (2016), which we pay special attention to when calculating.

Remark 3.

We can express $\mathrm{E}\left[{(Y-{\mathrm{TCE}}_q)}^n\right|Y>y_q]$ in another way.

$$\begin{array}{cc}\hfill \mathrm{E}\left[{(Y-{\mathrm{TCE}}_q)}^n|Y>y_q\right]=& \sum _{k=0}^n{(-1)}^{n-k}{\left({\mathrm{TCE}}_q\left(Y\right)\right)}^{n-k}\mathrm{E}\left[Y^k\right|Y>y_1]\hfill \\ \hfill =& \sum _{k=0}^n{(-1)}^{n-k}\frac{1}{1-q}{\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right){\mathrm{E}}_{Y|\mathsf{\Theta }}\left[Y^n\right|Y>y_q]\mathrm{d}\theta .\hfill \end{array}$$

Corollary 1.

The tail variance of the elliptical distribution can be derived by considering the cases $n=1$ and $n=2$. This risk measure takes the form

$$\begin{array}{c}\hfill {\mathrm{TV}}_q\left(Y\right)={\left(\frac{\beta }{1-q}{\delta }_1+\frac{c_1{\sigma }^2}{c_2(1-q)}{\delta }_2\right)}^2-2\left(\frac{\beta }{1-q}{\delta }_1+\frac{c_1{\sigma }^2}{c_2(1-q)}{\delta }_2\right){\mu }_1+{\mu }_2,\end{array}$$

(22)

where

$${\mu }_2={\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{2,0}+2{\Lambda }_{2,1}{\lambda }_{1,q}+{\Lambda }_{2,2}\left(c_1{z}_q{\lambda }_{1,q}+{\sigma }_Z^2{r}_{1,q}\right)\right)\mathrm{d}\theta .$$

Proof. 

$$\begin{array}{cc}\hfill {\mu }_2=& \mathrm{E}\left[{(Y-\mu )}^2\right|Y>y_q]\hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\theta }^2{\beta }^2+2{\theta }^{\frac{3}{2}}\sigma \beta {\lambda }_{1,q}+\theta {\sigma }^2\left(c_1{z}_q{\lambda }_{1,q}+{\sigma }_Z^2{r}_{1,q}\right)\right)\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{2,0}+2{\Lambda }_{2,1}{\lambda }_{1,q}+{\Lambda }_{2,2}\left(c_1{z}_q{\lambda }_{1,q}+{\sigma }_Z^2{r}_{1,q}\right)\right)\mathrm{d}\theta .\hfill \end{array}$$

For convenience, we write $\gamma =\frac{\beta }{1-q}{\delta }_1+\frac{c_1{\sigma }^2}{c_2(1-q)}{\delta }_2$, so $T{V}_q={\gamma }^2-2\gamma {\mu }_1+{\mu }_2$. □

Corollary 2.

The $\mathrm{TCS}$ of Y takes the form

$$\begin{array}{c}\hfill {\mathrm{TCS}}_q\left(Y\right)=\frac{{\sum }_{i=0}^3{C}_3^i{(-1)}^{3-i}{\gamma }^{3-i}{\mu }_i}{{({\gamma }^2-2\gamma {\mu }_1+{\mu }_2)}^{\frac{3}{2}}},\end{array}$$

(23)

where

$$\begin{array}{cc}\hfill {\mu }_3=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\hfill \\ \hfill & \left({\Lambda }_{3,0}+3{\Lambda }_{3,1}{\lambda }_{1,q}+3{\Lambda }_{3,2}\left(z_q{\lambda }_{1,q}+{\sigma }_Z^2{r}_{1,q}\left(z_q\right)\right)+{\Lambda }_{3,3}{c}_1\left(z_q^2{\lambda }_{1,q}+2{\lambda }_{2,q}\right)\right)\mathrm{d}\theta .\hfill \end{array}$$

(24)

Proof. 

Through (21), we can get

$$\begin{array}{cc}\hfill {\mu }_3=& \mathrm{E}\left({(Y-\mu )}^3|Y>y_q\right)\hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{3,0}+3{\Lambda }_{3,1}{\lambda }_{1,q}\right.\hfill \\ \hfill & \left.+\sum _{l=2}^3{C}_3^l{\Lambda }_{3,l}\left(c_1{z}_q^{l-1}{\lambda }_{1,q}+\left(l-1\right){\sigma }_Z^2{r}_{1,q}\left(z_q\right){\mathrm{E}}_{Z_1}\left(Z^{l-2}|Z>z_q\right)\right)\right)\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{3,0}+3{\Lambda }_{3,1}{\lambda }_{1,q}+3{\Lambda }_{3,2}\left(z_q{\lambda }_{1,q}+{\sigma }_Z^2{r}_{1,q}\left(z_q\right)\right)\right.\hfill \\ \hfill & \left.+{\Lambda }_{3,3}\left(c_1{z}_q^2{\lambda }_{1,q}+2{\sigma }_Z^2{r}_{1,q}\left(z_q\right){\mathrm{E}}_{Z_1}\left(Z|Z>z_q\right)\right)\right)\mathrm{d}\theta ,\hfill \end{array}$$

and we have

$$\begin{array}{cc}\hfill 2{\sigma }_Z^2{r}_{1,q}\left(z_q\right){\mathrm{E}}_{Z_1}\left(Z\right|Z>z_q)=& \frac{2}{1-q}{\int }_{z_q}^{\infty }{c}_{1}z{\overline{G}}_1\left(\frac{1}{2}{z}^2\right)\mathrm{d}z\hfill \\ \hfill =& 2c_1\frac{{\overline{G}}_2\left(\frac{1}{2}{z}_q^2\right)}{1-q}\hfill \\ \hfill =& 2c_1{\lambda }_{2,q},\hfill \end{array}$$

where

$${\lambda }_{2,q}=\frac{{\overline{G}}_2\left(\frac{1}{2}{z}_q^2\right)}{1-q}.$$

Thus, we get

$$\begin{array}{cc}\hfill {\mu }_3=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\hfill \\ \hfill & \left({\Lambda }_{3,0}+3{\Lambda }_{3,1}{\lambda }_{1,q}+3{\Lambda }_{3,2}\left(z_q{\lambda }_{1,q}+{\sigma }_Z^2{r}_{1,q}\left(z_q\right)\right)+{\Lambda }_{3,3}{c}_1\left(z_q^2{\lambda }_{1,q}+2{\lambda }_{2,q}\right)\right)\mathrm{d}\theta .\hfill \end{array}$$

□

Corollary 3.

The $\mathrm{TCK}$ of Y takes the form

$$\begin{array}{c}\hfill {\mathrm{TCK}}_q\left(Y\right)=\frac{{\sum }_{i=0}^4{C}_4^i{(-1)}^{4-i}{\gamma }^{4-i}{\mu }_i}{{({\gamma }^2-2\gamma {\mu }_1+{\mu }_2)}^2}-3,\end{array}$$

(25)

where

$$\begin{array}{cc}\hfill {\mu }_4=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left[{\Lambda }_{4,0}+\left(4{\Lambda }_{4,1}+6{\Lambda }_{4,2}{c}_1{z}_q+4{\Lambda }_{4,3}{c}_1{z}_q^2+{\Lambda }_{4,4}{c}_1{z}_q^3\right){\lambda }_{1,q}\right.\hfill \\ \hfill & \left.+\left(3{\Lambda }_{4,4}{c}_1{z}_q+8{\Lambda }_{4,3}\right){\lambda }_{2,q}+6{\Lambda }_{4,2}{\sigma }_Z^2{r}_{1,q}\left(z_q\right)+\frac{3}{c_2}{\Lambda }_{4,4}{\sigma }_Z^2{r}_{2,q}\left(z_q\right)\right]\mathrm{d}\theta .\hfill \end{array}$$

(26)

Proof. 

Letting i = 4 in (21), we get

$$\begin{array}{cc}\hfill {\mu }_4=& E\left[{(Y-\mu )}^4\right|Y>y_q]\hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{4,0}+4{\Lambda }_{4,1}{\lambda }_{1,q}\right.\hfill \\ \hfill & \left.+\sum _{l=2}^4{C}_4^l{\Lambda }_{4,l}\left(c_1{z}_q^{l-1}{\lambda }_{1,q}+(l-1){\sigma }_Z^2{r}_{1,q}\left(z_q\right){\mathrm{E}}_{Z_1}\left(Z^{l-2}|Z>z_q\right)\right)\right)\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left[{\Lambda }_{4,0}+4{\Lambda }_{4,1}{\lambda }_{1,q}+C_4^3{\Lambda }_{4,3}\left(c_1{z}_q^2{\lambda }_{1,q}+2{\lambda }_{2,q}\right)\right.\hfill \\ \hfill & \left.+{\Lambda }_{4,4}\left(c_1{z}_q^3{\lambda }_{1,q}+3{\sigma }_Z^2{r}_{1,q}\left(z_q\right){\mathrm{E}}_{Z_1}\left(Z^2|Z>z_q\right)\right)\right]\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left[{\Lambda }_{4,0}+\left(4{\Lambda }_{4,1}+6{\Lambda }_{4,2}{c}_1{z}_q+4{\Lambda }_{4,3}{c}_1{z}_q^2+{\Lambda }_{4,4}{c}_1{z}_q^3\right){\lambda }_{1,q}\right.\hfill \\ \hfill & \left.+\left(3{\Lambda }_{4,4}{c}_1{z}_q+8{\Lambda }_{4,3}\right){\lambda }_{2,q}+6{\Lambda }_{4,2}{\sigma }_Z^2{r}_{1,q}\left(z_q\right)+\frac{3}{c_2}{\Lambda }_{4,4}{\sigma }_Z^2{r}_{2,q}\left(z_q\right)\right]\mathrm{d}\theta ,\hfill \end{array}$$

where

$$r_{2,q}\left(z_q\right)=\frac{{\overline{F}}_{Z_2}\left(z_q\right)}{1-q}.$$

□

Corollary 4.

The nth moments of X takes the form

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathrm{E}}_{Y|\mathsf{\Theta }}\left[Y^n\right]={(\mu +\theta \beta )}^n+\sum _{k=1}^n{C}_n^k{\left(\sqrt{\theta }\sigma \right)}^k{(\mu +\theta \beta )}^{n-k}(k-1){\sigma }_Z^2{\mathrm{E}}_{Z^{*}}\left[Z^{k-2}\right].\end{array}\end{array}$$

Proof. 

$$\begin{array}{cc}\hfill {\mathrm{E}}_{Y|\mathsf{\Theta }}\left[Y^n\right]=& \underset{q\to 0}{lim}{\mathrm{E}}_{Y|\mathsf{\Theta }}\left[Y^n\right|Y>y_q]\hfill \\ \hfill =& {(\mu +\theta \beta )}^n+\sum _{k=1}^n{C}_n^k{\left(\sqrt{\theta }\sigma \right)}^k{(\mu +\theta \beta )}^{n-k}\hfill \\ \hfill & \underset{q\to 0}{lim}\left[c_1{\lambda }_{1,q}{z}_q^{k-1}+(k-1)r_{1,q}\left(z_q\right){\sigma }_Z^2{\mathrm{E}}_{Z^{*}}\left[Z^{k-2}\right|z>z_q]\right]\hfill \\ \hfill =& {(\mu +\theta \beta )}^n+\sum _{k=1}^n{C}_n^k{\left(\sqrt{\theta }\sigma \right)}^k{(\mu +\theta \beta )}^{n-k}(k-1){\sigma }_Z^2{\mathrm{E}}_{Z^{*}}\left[Z^{k-2}\right].\hfill \end{array}$$

Consider an $n\times$1 random vector $\mathbf{Y}=(Y_1,Y_2,\dots ,Y_n)$ with a location-scale mixture of elliptical distribution $Y\sim LSM{E}_n(\mathit{\mu },\mathsf{\Sigma },\mathit{\beta },\mathsf{\Theta },g_n).$ Then using Landsman and Valdez [3], the distribution of the return $R={\mathbf{y}}^T\mathbf{Y},$ where $\mathbf{y}\in {\mathbb{R}}^n,$ is as follows:

$$\begin{array}{c}\hfill R={\mathbf{y}}^T\mathbf{Y}\sim LSM{E}_1({\mu }_R={\mathbf{y}}^T\mathit{\mu },{\sigma }_R^2={\mathbf{y}}^T\mathsf{\Sigma }\mathbf{y},{\beta }_R,\mathsf{\Theta },g_1).\end{array}$$

(27)

Using (27) and by (19), (22), (23), (25) we obtain the $\mathrm{TV},\mathrm{TCS}$ and $\mathrm{TCK}$, respectively,

$${\mathrm{TCE}}_{\mathrm{q}}\left(\mathrm{R}\right)={\mathbf{y}}^T\mathit{\mu }+\frac{{\beta }_R}{1-q}{\delta }_{1,R}+\frac{c_1{\mathbf{y}}^T\mathsf{\Sigma }\mathbf{y}}{c_2(1-q)}{\delta }_{2,R},$$

where

$${\delta }_{1,R}={\int }_{{\Omega }_{\theta }}{\overline{F}}_{Y|\mathsf{\Theta }}\left(y_{q,R}\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta ,{\delta }_{2,R}={\int }_{{\Omega }_{\theta }}{f}_{Y_1|\mathsf{\Theta }}\left(y_{q,R}\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta ,$$

$$y_{q,R}=Va{R}_q\left(\frac{R-{\mu }_R}{{\sigma }_R}\right),$$

$${\mathrm{TV}}_{\mathrm{q}}\left(\mathrm{R}\right)={\left(\frac{{\beta }_R}{1-q}{\delta }_{1,R}+\frac{c_1{\mathbf{y}}^T\mathsf{\Sigma }\mathbf{y}}{c_2(1-q)}{\delta }_{2,R}\right)}^2-2\left(\frac{{\beta }_R}{1-q}{\delta }_{1,R}+\frac{c_1{\mathbf{y}}^T\mathsf{\Sigma }\mathbf{y}}{c_2(1-q)}{\delta }_{2,R}\right){\mu }_1+{\mu }_2,$$

$${\mathrm{TCS}}_{\mathrm{q}}\left(\mathrm{R}\right)=\frac{{\sum }_{i=0}^3{C}_3^i{(-1)}^{3-i}{\left(\frac{{\beta }_R}{1-q}{\delta }_{1,R}+\frac{c_1{\mathbf{y}}^T\mathsf{\Sigma }\mathbf{y}}{c_2(1-q){\delta }_{2,R}}\right)}^{3-i}{\mu }_i}{{\left({\left(\frac{{\beta }_R}{1-q}{\delta }_{1,R}+\frac{c_1{\mathbf{y}}^T\mathsf{\Sigma }\mathbf{y}}{c_2(1-q)}{\delta }_{2,R}\right)}^2-2\left(\frac{{\beta }_R}{1-q}{\delta }_{1,R}+\frac{c_1{\mathbf{y}}^T\mathsf{\Sigma }\mathbf{y}}{c_2(1-q)}{\delta }_{2,R}\right){\mu }_1+{\mu }_2\right)}^{\frac{3}{2}}},$$

and

$${\mathrm{TCK}}_q\left(R\right)=\frac{{\sum }_{i=0}^4{C}_4^i{(-1)}^{4-i}{\left(\frac{{\beta }_R}{1-q}{\delta }_{1,R}+\frac{c_1{\mathbf{y}}^T\mathsf{\Sigma }\mathbf{y}}{c_2(1-q){\delta }_{2,R}}\right)}^{4-i}{\mu }_i}{{\left({\left(\frac{{\beta }_R}{1-q}{\delta }_{1,R}+\frac{c_1{\mathbf{y}}^T\mathsf{\Sigma }\mathbf{y}}{c_2(1-q){\delta }_{2,R}}\right)}^2-2\left(\frac{{\beta }_R}{1-q}{\delta }_{1,R}+\frac{c_1{\mathbf{y}}^T\mathsf{\Sigma }\mathbf{y}}{c_2(1-q){\delta }_{2,R}}\right){\mu }_1+{\mu }_2\right)}^2}-3.$$

□

Remark 4.

Now we compare the different distributions of TCM form. The TCM for elliptical distributions (see Landsman et al. [10]) and the TCM for generalized skew-elliptical distributions (see Eini et al. [11]) are presented as follows, respectively,

$${\mathrm{TCM}}_q\left(X^n\right)=\sum _{i=0}^n{(-1)}^i{C}_n^i{\lambda }_{1,q}^{n-i}{\mu }_i,$$

where $X\sim E_1(\mu ,{\sigma }^2,g_1).$

$${\mathrm{TCM}}_q\left(Y^n\right)=\sum _{i=0}^n{(-1)}^i{\Lambda }_{1,q}{\sigma }^{n-i}{\mu }_i,$$

where $Y\sim S{E}_1(\mu ,{\sigma }^2,\gamma ,H).$ The mixture of elliptical distributions has a similar form as above. However, the three of them have different ${\mu }_i$ forms. Because the expectation and TCE of the mixture of ellipitical distributions lead to some differences in the calculation processes, the final form is different.

4. Some Special

In this section, we discuss some measures related to several mixtures of ellipitical distributions.

Example 4.

Let $Y\sim LSM{N}_1(\mu ,{\sigma }^2,\beta ,\mathsf{\Theta })$ be a univariate location-scale mixture of normal random variables, defined as (14). In this case, we notice that ${\overline{G}}_1\left(u\right)={\overline{G}}_2\left(u\right)=\dots =g_1\left(u\right)=e^{-u}$, and $c=c_1={\left(2\pi \right)}^{-\frac{1}{2}}$. We have ${\sigma }_Z^2=1$. Thus, we obtain the $\mathrm{TCE}$ for a location-scale mixture of normal distributions:

$$\begin{array}{c}\hfill {\mathrm{TCE}}_Y\left(y_q\right)=\mu +\frac{\beta }{1-q}{\delta }_1+\frac{{\sigma }^2}{1-q}{\delta }_2,\end{array}$$

(28)

where

$$\begin{array}{c}\hfill {\delta }_1={\int }_{{\Omega }_{\theta }}{\overline{F}}_{Y|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta ,{\delta }_2={\int }_{{\Omega }_{\theta }}{f}_{Y|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta \end{array}$$

and $Y|\mathsf{\Theta }\sim N_1(\mu +\theta \beta ,\theta {\sigma }^2)$.

Meanwhile, we have

$${\overline{G}}_j\left(\frac{1}{2}{u}^2\right)=\varphi \left(u\right),j=1,2,3\dots ,$$

$$f_{Z_1}\left(z\right)=f_{Z_2}\left(z\right),{\lambda }_{1,q}={\lambda }_{2,q}=\frac{\varphi \left(z_q\right)}{1-q},$$

$$r_{1,q}\left(z_q\right)=r_{2,q}\left(z_q\right)=\frac{\overline{\mathsf{\Phi }}\left(z_q\right)}{1-q}.$$

Accordingly, we have

$$\begin{array}{c}\hfill {\mu }_1={\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left(\theta \beta +{\theta }^{\frac{1}{2}}\sigma \frac{\varphi \left(z_q\right)}{1-q}\right)\mathrm{d}\theta ,\end{array}$$

(29)

$$\begin{array}{cc}\hfill {\mu }_2=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{2,0}+2{\Lambda }_{2,1}{\lambda }_{1,q}+{\Lambda }_{2,2}\left(c_1{z}_q{\lambda }_{1,q}+{\sigma }_Z^2{r}_{1,q}\right)\right)\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{2,0}+2{\Lambda }_{2,1}\frac{\varphi \left(z_q\right)}{1-q}+{\Lambda }_{2,2}\left({\left(2\pi \right)}^{-1}{z}_q\frac{\varphi \left(z_q\right)}{1-q}+\frac{\overline{\mathsf{\Phi }}\left(z_q\right)}{1-q}\right)\right)\mathrm{d}\theta ,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill {\mu }_3=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{3,0}+3{\Lambda }_{3,1}{\lambda }_{1,q}+3{\Lambda }_{3,2}\left(z_q{\lambda }_{1,q}+{\sigma }_Z^2{r}_{1,q}\left(z_q\right)\right)\right.\hfill \\ \hfill & \left.+{\Lambda }_{3,3}{c}_1\left(z_q^2{\lambda }_{1,q}+2{\lambda }_{2,q}\right)\right)\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{3,0}+3{\Lambda }_{3,1}\frac{\varphi \left(z_q\right)}{1-q}+3{\Lambda }_{3,2}\left(z_q\frac{\varphi \left(z_q\right)}{1-q}+\frac{\overline{\mathsf{\Phi }}\left(z_q\right)}{1-q}\right)\right.\hfill \\ \hfill & \left.+{\Lambda }_{3,3}{\left(2\pi \right)}^{-1}\frac{\varphi \left(z_q\right)}{1-q}(z_q^2+2)\right)\mathrm{d}\theta ,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill {\mu }_4=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left[{\Lambda }_{4,0}+\left(4{\Lambda }_{4,1}+6{\Lambda }_{4,2}{c}_1{z}_q+4{\Lambda }_{4,3}{c}_1{z}_q^2+{\Lambda }_{4,4}{c}_1{z}_q^3\right){\lambda }_{1,q}\right.\hfill \\ \hfill & \left.+\left(3{\Lambda }_{4,4}{c}_1{z}_q+8{\Lambda }_{4,3}\right){\lambda }_{2,q}+6{\Lambda }_{4,2}{\sigma }_Z^2{r}_{1,q}\left(z_q\right)+\frac{3}{c_2}{\Lambda }_{4,4}{\sigma }_Z^2{r}_{2,q}\left(z_q\right)\right]\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left[{\Lambda }_{4,0}+\left(4{\Lambda }_{4,1}+6{\Lambda }_{4,2}{\left(2\pi \right)}^{-1}{z}_q+4{\Lambda }_{4,3}{\left(2\pi \right)}^{-1}{z}_q^2+{\Lambda }_{4,4}{\left(2\pi \right)}^{-1}{z}_q^3\right)\right.\hfill \\ \hfill & \left.\frac{\varphi \left(z_q\right)}{1-q}+\left(3{\Lambda }_{4,4}{\left(2\pi \right)}^{-1}{z}_q+8{\Lambda }_{4,3}\right)\frac{\varphi \left(z_q\right)}{1-q}+6{\Lambda }_{4,2}\frac{\overline{\mathsf{\Phi }}\left(z_q\right)}{1-q}+6\pi {\Lambda }_{4,4}\frac{\overline{\mathsf{\Phi }}\left(z_q\right)}{1-q}\right]\mathrm{d}\theta .\hfill \end{array}$$

(32)

Then ${\mathrm{TV}}_q\left(Y\right),{\mathrm{TCS}}_q\left(Y\right),$ and ${\mathrm{TCK}}_q\left(Y\right)$ are obtained through substituting the above formulas in (22), (23) and (25).

Example 5.

Let $Y\sim LSMS{t}_1(\mu ,{\sigma }^2,\beta ,\mathsf{\Theta })$ be a univariate location-scale mixture of Student’s t random variables defined a (11). We know that there is a variance of Z for $m>2$ and ${\sigma }_Z^2=\frac{m}{m-2}$.

Thus, the cumulative generators of Y are shown as follows:

$$g_1\left(u\right)={\left(1+\frac{2u}{m}\right)}^{-(m+1)/2},{\overline{G}}_1\left(u\right)=\frac{m}{m-1}{\left(1+\frac{2u}{m}\right)}^{-(m-1)/2},$$

$$\begin{array}{cc}\hfill {\overline{G}}_2\left(u\right)=& {\int }_u^{\infty }{\overline{G}}_1\left(t\right)\mathrm{d}t\hfill \\ \hfill =& {\int }_u^{\infty }\frac{m}{m-1}{\left(1+\frac{2t}{m}\right)}^{-\frac{m-1}{2}}\mathrm{d}t\hfill \\ \hfill =& \frac{m}{m-1}\frac{m}{m-3}{\left(1+\frac{2u}{m}\right)}^{-\frac{m-3}{2}},\hfill \end{array}$$

and the normalizing constants are

$$c_1=\frac{\Gamma \left(\right(m+1)/2)}{\Gamma (m/2){\left(m\pi \right)}^{\frac{1}{2}}},c_2=\frac{m-1}{m^{\frac{3}{2}}B(\frac{1}{2},\frac{m-2}{2})}(m>2).$$

Thus,

$$f_{Z_1}\left(z\right)=\frac{m-2}{(m-1){\left(m\pi \right)}^{\frac{1}{2}}}\frac{\Gamma \left(\frac{m+1}{2}\right)}{\Gamma \left(\frac{m}{2}\right)}{\left(1+\frac{z^2}{m}\right)}^{\frac{m-1}{2}},$$

$$f_{Z_2}\left(z\right)=\frac{m-2}{m^{\frac{1}{2}}(m-3)B(\frac{1}{2},\frac{m-2}{2})}{\left(1+\frac{2z^2}{m}\right)}^{-\frac{m-3}{2}}.$$

Accordingly, we have

$${\lambda }_{1,q}=\frac{m}{(m-1)(1-q)}{\left(1+\frac{z_q^2}{m}\right)}^{-\frac{m-1}{2}},$$

$${\lambda }_{2,q}=\frac{m^2}{(m-1)(m-3)(1-q)}{\left(1+\frac{z_q^2}{m}\right)}^{-\frac{m-3}{2}},$$

$$r_{1,q}\left(z_q\right)=\frac{{\overline{F}}_{Z_1}\left(z_q\right)}{1-q},r_{2,q}\left(z_q\right)=\frac{{\overline{F}}_{Z_2}\left(z_q\right)}{1-q}.$$

Thus, we obtain the $\mathrm{TCE}$ for the location-scale mixture of Student’s t distributions:

$$\begin{array}{c}\hfill {\mathrm{TCE}}_Y\left(y_q\right)=\mu +\frac{\beta }{1-q}{\delta }_1+\frac{m^2{\sigma }^2}{(m-2)(1-q)}{\delta }_2,m>2,\end{array}$$

(33)

where

$$\begin{array}{c}\hfill {\delta }_1={\int }_{{\Omega }_{\theta }}{\overline{F}}_{Y|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta ,{\delta }_2={\int }_{{\Omega }_{\theta }}{f}_{Y_1|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta ,\end{array}$$

and $Y_1|\mathsf{\Theta }\sim E_1(\mu +\theta \beta ,\theta {\sigma }^2,{\overline{G}}_1).$

Meanwhile, we have

$$\begin{array}{cc}\hfill {\mu }_1=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left(\theta \beta +{\theta }^{\frac{1}{2}}\sigma {\lambda }_{1,q}\right)\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left(\theta \beta +{\theta }^{\frac{1}{2}}\sigma \frac{m}{(m-1)(1-q)}{\left(1+\frac{z_q^2}{m}\right)}^{-\frac{m-1}{2}}\right)\mathrm{d}\theta ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mu }_2=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{2,0}+2{\Lambda }_{2,1}\frac{\varphi \left(z_q\right)}{1-q}+{\Lambda }_{2,2}\left({\left(2\pi \right)}^{-1}{z}_q\frac{\varphi \left(z_q\right)}{1-q}+\frac{\overline{\mathsf{\Phi }}\left(z_q\right)}{1-q}\right)\right)\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{2,0}+2{\Lambda }_{2,1}\frac{m}{(m-1)(1-q)}{\left(1+\frac{z_q^2}{m}\right)}^{-\frac{m-1}{2}}\right.\hfill \\ \hfill & \left.+{\Lambda }_{2,2}\left(\frac{\Gamma \left(\right(m+1)/2)}{\Gamma (m/2){\left(m\pi \right)}^{\frac{1}{2}}}{z}_q\frac{{\overline{F}}_{Z_1}\left(z_q\right)}{1-q}+\frac{m}{m-2}\frac{{\overline{F}}_{Z_1}\left(z_q\right)}{1-q}\right)\right)\mathrm{d}\theta .\hfill \end{array}$$

The measures $u_i$ are calculated in the spirit of the Example 4. ${\mathrm{TV}}_q\left(Y\right),{\mathrm{TCS}}_q\left(Y\right),$ and ${\mathrm{TCK}}_q\left(Y\right)$ are obtained through substituting the above formulas in (22), (23) and (25).

Example 6.

Let $Y\sim LSML{o}_1(\mu ,{\sigma }^2,\beta ,\mathsf{\Theta })$ be a univariate location-scale mixture of a logistic random variable defined as (15). We find that ${\sigma }_Z^2=\frac{{\pi }^2}{3}.$ The cumulative generators of Y are shown as follows:

$$g_1\left(u\right)=\frac{exp(-u)}{{[1+exp(-u)]}^2},{\overline{G}}_1\left(u\right)=\frac{exp(-u)}{1+exp(-u)},$$

$$\begin{array}{cc}\hfill {\overline{G}}_2\left(u\right)=& {\int }_u^{\infty }{\overline{G}}_1\left(t\right)\mathrm{d}t\hfill \\ \hfill =& {\int }_u^{\infty }\frac{m}{m-1}{\left(1+\frac{2t}{m}\right)}^{-\frac{m-1}{2}}\mathrm{d}t\hfill \\ \hfill =& \frac{m}{m-1}\frac{m}{m-3}{\left(1+\frac{2u}{m}\right)}^{-\frac{m-3}{2}},\hfill \end{array}$$

and the normalizing constants are

$$c_1=\frac{1}{\sqrt{2\pi }{\mathsf{\Psi }}_2^{*}(-1,\frac{1}{2},1)},c_2=\frac{1}{\sqrt{2\pi }{\mathsf{\Psi }}_1^{*}(-1,\frac{1}{2},1)}.$$

Meanwhile, we have

$${\lambda }_{1,q}=\frac{exp\left(-\frac{1}{2}{z}_q^2\right)}{(1-q)\left(1+exp\left(-\frac{1}{2}{z}_q^2\right)\right)},{\lambda }_{2,q}=\frac{ln\left(1+exp\left(-\frac{1}{2}{z}_q^2\right)\right)}{1-q},$$

$$r_{1,q}=\frac{{\overline{F}}_{Z_1}\left(z_q\right)}{1-q},r_{2,q}=\frac{{\overline{F}}_{Z_2}\left(z_q\right)}{1-q}.$$

Accordingly, we have

$$f_{Z_1}\left(z\right)=\frac{3}{\sqrt{2}{\pi }^{\frac{5}{2}}{\mathsf{\Psi }}_2^{*}(-1,\frac{1}{2},1)}\frac{exp\left(-\frac{1}{2}{z}^2\right)}{1+exp\left(-\frac{1}{2}{z}^2\right)},$$

$$f_{Z_2}\left(z\right)=\frac{3}{\sqrt{x}{\pi }^{\frac{5}{2}}{\mathsf{\Psi }}_1^{*}(-1,\frac{1}{2},1)}ln\left(1+exp\left(-\frac{1}{2}{z}^2\right)\right).$$

Thus, we obtain the $\mathrm{TCE}$ for the location-scale mixture of Logistic distributions:

$$\begin{array}{c}\hfill {\mathrm{TCE}}_Y\left(y_q\right)=\mu +\frac{\beta }{1-q}{\delta }_1+\frac{{\mathsf{\Psi }}_1^{*}(-1,\frac{1}{2},1){\sigma }^2}{{\mathsf{\Psi }}_2^{*}(-1,\frac{1}{2},1)(1-q)}{\delta }_2,\end{array}$$

(34)

where

$$\begin{array}{c}\hfill {\delta }_1={\int }_{{\Omega }_{\theta }}{\overline{F}}_{Y|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta ,{\delta }_2={\int }_{{\Omega }_{\theta }}{f}_{Y_1|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta ,\end{array}$$

and $Y_1|\mathsf{\Theta }\sim E_1(\mu +\theta \beta ,\theta {\sigma }^2,{\overline{G}}_1)$.

Meanwhile,

$$\begin{array}{cc}\hfill {\mu }_1=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left(\theta \beta +{\theta }^{\frac{1}{2}}\sigma {\lambda }_{1,q}\right)\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left(\theta \beta +{\theta }^{\frac{1}{2}}\sigma \frac{exp\left(-\frac{1}{2}{z}_q^2\right)}{(1-q)\left(1+exp\left(-\frac{1}{2}{z}_q^2\right)\right)}\right)\mathrm{d}\theta ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mu }_2=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{2,0}+2{\Lambda }_{2,1}\frac{\varphi \left(z_q\right)}{1-q}+{\Lambda }_{2,2}\left({\left(2\pi \right)}^{-1}{z}_q\frac{\varphi \left(z_q\right)}{1-q}+\frac{\overline{\mathsf{\Phi }}\left(z_q\right)}{1-q}\right)\right)\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)[{\Lambda }_{2,0}+2{\Lambda }_{2,1}\frac{exp\left(-\frac{1}{2}{z}_q^2\right)}{(1-q)\left(1+exp\left(-\frac{1}{2}{z}_q^2\right)\right)}\hfill \\ \hfill & +{\Lambda }_{2,2}\left(\frac{1}{\sqrt{2\pi }{\mathsf{\Psi }}_2^{*}(-1,\frac{1}{2},1)}{z}_q\frac{exp\left(-\frac{1}{2}{z}_q^2\right)}{(1-q)\left(1+exp\left(-\frac{1}{2}{z}_q^2\right)\right)}+\frac{{\pi }^2}{3}\frac{{\overline{F}}_{Z_1}\left(z_q\right)}{1-q}\right)]\mathrm{d}\theta .\hfill \end{array}$$

The measures $u_i$ are calculated in the spirit of Example 4. ${\mathrm{TV}}_q\left(Y\right),{\mathrm{TCS}}_q\left(Y\right),$ and ${\mathrm{TCK}}_q\left(Y\right)$ are obtained through substituting the above formulas in (22), (23) and (25).

Example 7.

Let $Y\sim LSML{a}_1(\mu ,{\sigma }^2,\beta ,\mathsf{\Theta })$ be a univariate location-scale mixture of a Laplace random variable, defined as (15). We find that ${\sigma }_Z^2=2$, the cumulative generators of Y are shown as follows:

$$g_1\left(u\right)=exp(-\sqrt{2u}),{\overline{G}}_1\left(u\right)=(1+\sqrt{2u})exp(-\sqrt{2u}),$$

$${\overline{G}}_2\left(u\right)=(3+2u+3\sqrt{2u})exp(-\sqrt{2u}),$$

and the normalizing constants

$$c_1=\frac{1}{2},c_2=\frac{1}{4}.$$

Accordingly, we have

$$f_{Z_1}\left(z\right)={\overline{G}}_1\left(\frac{1}{2}{z}^2\right)=\left(1+\left|z\right|\right)exp\left(-\sqrt{2}\left|z\right|\right),$$

$$f_{Z_2}\left(z\right)=\frac{{\overline{G}}_2\left(\frac{1}{2}{z}^2\right)}{2}=\frac{3+z^2+3\left|z\right|}{2}exp(-2|z\left|\right),$$

$${\lambda }_{1,q}=\frac{1+|z_q|}{1-q}exp(-|z_q\left|\right),{\lambda }_{2,q}=\frac{\left(3+z_q^2+3\left|z_q\right|\right)}{1-q}exp(-|z_q\left|\right),$$

$$r_{1,q}\left(z_q\right)=\frac{{\overline{F}}_{Z_1}\left(z_q\right)}{1-q},r_{2,q}\left(z_q\right)=\frac{{\overline{F}}_{Z_2}\left(z_q\right)}{1-q}.$$

Thus, we obtain the $\mathrm{TCE}$ for a location-scale mixture of Laplace distributions:

$$\begin{array}{c}\hfill {\mathrm{TCE}}_Y\left(y_q\right)=\mu +\frac{\beta }{1-q}{\delta }_1+\frac{2{\sigma }^2}{1-q}{\delta }_2,\end{array}$$

(35)

where

$$\begin{array}{c}\hfill {\delta }_1={\int }_{{\Omega }_{\theta }}{\overline{F}}_{Y|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta ,{\delta }_2={\int }_{{\Omega }_{\theta }}{f}_{Y_1|\mathsf{\Theta }}\left(y_q\right)\theta \varpi \left(\theta \right)\mathrm{d}\theta ,\end{array}$$

and $Y_1|\mathsf{\Theta }\sim E_1(\mu +\theta \beta ,\theta {\sigma }^2,{\overline{G}}_1).$

Note that

$$\begin{array}{cc}\hfill {\mu }_1=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left(\theta \beta +{\theta }^{\frac{1}{2}}\sigma {\lambda }_{1,q}\right)\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left(\theta \beta +{\theta }^{\frac{1}{2}}\sigma \frac{1+|z_q|}{1-q}exp(-|z_q\left|\right)\right)\mathrm{d}\theta ,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mu }_2=& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{2,0}+2{\Lambda }_{2,1}{\lambda }_{1,q}+{\Lambda }_{2,2}\left(c_1{z}_q{\lambda }_{1,q}+{\sigma }_Z^2{r}_{1,q}\right)\right)\mathrm{d}\theta \hfill \\ \hfill =& {\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{2,0}+2{\Lambda }_{2,1}\frac{1+|z_q|}{1-q}exp(-|z_q\left|\right)\right.\hfill \\ \hfill & \left.+{\Lambda }_{2,2}\left(\frac{1}{2}{z}_q\frac{1+|z_q|}{1-q}exp(-|z_q\left|\right))+2\frac{{\overline{F}}_{Z_1}\left(z_q\right)}{1-q}\right)\right)\mathrm{d}\theta .\hfill \end{array}$$

The measures $u_i$ are calculated in the spirit of the Example 4. ${\mathrm{TV}}_q\left(Y\right),{\mathrm{TCS}}_q\left(Y\right),$ and ${\mathrm{TCK}}_q\left(Y\right)$ are obtained through substituting the above formulas in (22), (23) and (25).

5. Numerical Analysis

In this section, two numerical examples are presented. We first consider $\mathrm{TCE},\mathrm{TCS},$ $\mathrm{TCK}$ for a mixture of normal distributions and mixture of Student’s t distributions.

Example 8.

When $X\sim N(0,1)$ is a standard normal random variable, $\mathsf{\Theta }\sim GIG(\lambda ,\chi ,\psi )$. We denote $Y\sim GH(\lambda ,\chi ,\psi ,\mu ,\sigma ,\beta )$, and its pdf is

$$\begin{array}{c}\hfill f_X\left(x\right)=\frac{{\psi }^{\lambda }{(\psi +\frac{{\beta }^2}{{\sigma }^2})}^{\frac{1}{2}-\lambda }{\left(\sqrt{\chi \psi }\right)}^{-\lambda }{K}_{\lambda -\frac{1}{2}}\left(\sqrt{(\chi +\frac{{(x-\mathit{\mu })}^2}{{\sigma }^2})(\psi +\frac{{\beta }^2}{{\sigma }^2})}\right)}{\sqrt{2\pi }\sigma K_{\lambda }\left(\sqrt{\chi \psi }\right)\left(\sqrt{(\chi +\frac{{(x-\mathit{\mu })}^2}{{\sigma }^2})(\psi +\frac{{\beta }^2}{{\sigma }^2})}\right)}.\end{array}$$

Using Example 4, we obtain

$$\begin{array}{cc}\hfill & {\mathrm{TV}}_q\left(Y\right)\hfill \\ \hfill =& {(\frac{\beta }{1-q}{\delta }_1+\frac{{\sigma }^2}{(1-q)}{\delta }_2)}^2-2(\frac{\beta }{1-q}{\delta }_1+\frac{{\sigma }^2}{(1-q)}{\delta }_2){\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left(\theta \beta +{\theta }^{\frac{1}{2}}\sigma \frac{\varphi \left(z_q\right)}{1-q}\right)\mathrm{d}\theta \hfill \\ \hfill & +{\int }_{{\Omega }_{\theta }}\varpi \left(\theta \right)\left({\Lambda }_{2,0}+2{\Lambda }_{2,1}\frac{\varphi \left(z_q\right)}{1-q}+{\Lambda }_{2,2}\left({\left(2\pi \right)}^{-1}{z}_q\frac{\varphi \left(z_q\right)}{1-q}+\frac{\overline{\mathsf{\Phi }}\left(z_q\right)}{1-q}\right)\right)\mathrm{d}\theta .\hfill \end{array}$$

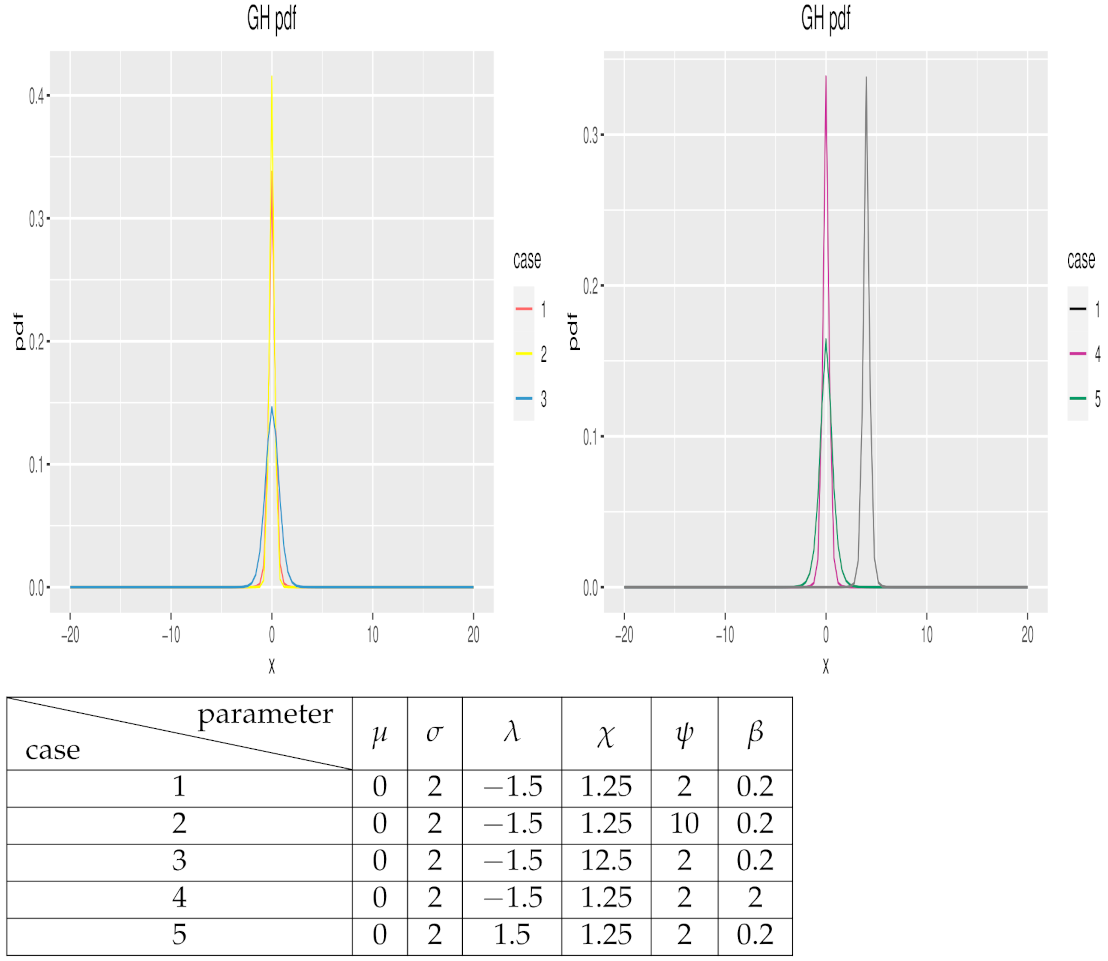
${\mathrm{TCS}}_q\left(Y\right),$ and ${\mathrm{TCK}}_q\left(Y\right)$ are obtained through substituting the above formulas in (22), (23) and (25). Next, we show the images of GH distribution under different parameters in Figure 1.

By assigning different values to each parameter, we can see the influence of each parameter, and adjust the appropriate parameters in the actual fitting to make the fitting effect better.

Example 9.

(Ignatieva and Landsman (2020)) Now, we consider the random variable X which has a Student’s t distribution, and $\mathsf{\Theta }\sim GIG(\lambda ,\chi ,\psi )$. Then Y has the following pdf:

$$\begin{array}{c}\hfill f_X\left(x\right)=\frac{c_p{\chi }^{-\lambda }{\left(\sqrt{\chi \psi }\right)}^{\lambda }}{2\sigma K_{\lambda }\left(\sqrt{\chi \psi }\right)}{\int }_0^{\infty }{(1+\frac{1}{m}{\left(\frac{x-\mu -\gamma \theta }{\sigma \sqrt{\theta }}\right)}^2)}^{-p}{\theta }^{\lambda -\frac{3}{2}}exp(-\frac{1}{2}(\frac{\chi }{\theta }+\psi \theta ))d\theta ,\end{array}$$

where $c_p=\frac{\Gamma \left(p\right)}{\sqrt{\pi m}\Gamma (p-\frac{1}{2})}.$

This case is the same as in Example 5, so we can get $\mathrm{TV}$, ${\mathrm{TCS}}_q\left(Y\right),$ and ${\mathrm{TCK}}_q\left(Y\right)$ from Example 5. Next, we show the images of Student-t-GIG distribution under different parameters in Figure 2.

Next, we consider TCE, TV, TCS and TCK for the universe GH distribution and mixture of Student’s t distribution. Let the parameters of GH:$\mu =0,\sigma =1.5,\lambda =1.7,\chi =2.1,\psi =6.7,\beta =-11\times {10}^{-3}$, and the parameters of Student’s t–GIG: $\mu =0,\sigma =1.5,\lambda =1.7,\psi =6.7,chi=2.1,\gamma =-11\times {10}^{-3}$. At the same time, we select the skew-normal distribution and skew Student’s t-normal distribution to compare with them. Let the parameters of skew-normal and skew Student’s t-normal be $\mu =0,\sigma =1.5,\gamma =1.7.$ We chose q = 0.75, 0.8, 0.9, 0.95, 0.98, and the results are given in the

Table 1. Comparison of different q-quantile values between different distributions.

Value	${\mathit{x}}_{\mathit{q}}$	TCE	TV	TCS	TCK
q-Quantile
GH distribution
0.75	0.9006	1.7999	0.6431	1.5854	3.5278
0.8	1.1346	1.9962	0.6101	1.6346	3.7742
0.9	1.7792	2.5642	0.5410	1.7404	4.3403
0.95	2.3514	3.0915	0.4992	1.8053	4.7143
0.98	3.0481	3.7514	0.4640	1.8593	5.0427
Skew-normal distribution
0.75	1.7187	2.4685	0.4122	1.3481	−2.1265
0.8	1.9186	2.6315	0.3815	1.3836	−2.2297
0.9	2.4667	3.0939	0.3108	1.4679	−2.4515
0.95	2.9398	3.5067	0.2626	1.5292	−2.5876
0.98	3.4895	3.9978	0.2179	1.5901	−2.7008
Student’s t-GIG distribution
0.75	0.9939	2.3330	2.5638	5.1605	∖
0.8	1.2761	2.6336	2.7512	5.3499	∖
0.9	2.1389	3.6097	3.5365	5.8106	∖
0.95	3.0408	4.6866	4.6877	6.1435	∖
0.98	4.3702	6.3318	6.9985	6.4558	∖
Skew Student’s t-normal distribution
0.75	1.6932	4.3558	6.3324	1.1997	∖
0.8	1.8918	4.9971	8.9551	0.5104	∖
0.9	2.4035	7.8632	39.5208	−0.5493	∖
0.95	2.7661	13.1504	252.5795	−0.5746	∖
0.98	3.0506	28.5219	$3.5449\times {10}^3$	−0.4057	∖

.

By doing the calculations, we found that the TCK of the Student’s t-GIG mixture distribution and skew Student’s t normal distribution tended to infinity. By comparing the TCK of the GH and skew-normal distribution, we found that GH is a heavy-tailed distribution and skew-normal is a light-tailed distribution. In general, the heavy-tailed distribution appears mainly in financial data, such as the return on securities. Comparing Student’s t–GIG to the skew Student’s t-normal distribution, we found that the Student’s t–GIG distribution was right-skewed and the skew Student’s t-normal distribution was left-skewed. It is easy to discover that the values of the measures of risk increase by raising the q-quantile value, which is not unexpected. Another phenomenon is that the measures of Student’s t–GIG are larger than that of GH.

6. Illustrative Example

We discuss TCE, TV, TCS and TCK of three stocks (Amazon, Google and Apple) covering a time frame from January 2016 to January 2019 by using the results of parameter estimates in Ignatieva and Landsman [4]. In order to fit GH distributions to the univariate data, we select parameter estimates from the univariate fit of the GH family of distributions to the losses arising from Amazon, Google and Apple stocks. Fixed parameter values are used: ${\mu }_1=1.1230,{\mu }_2=1.0584,{\mu }_3=1.1280,{\sigma }_1=1.1614,{\sigma }_2=0.9954,{\sigma }_3=0.9760.$ The results are shown in

Table 2. Comparison of univariate TCE, TV, TCS, and TCK computed for Amazon, Google, Apple at different quantile levels.

Stock	Amazon	Google	Apple
q-Quantile
TCE
0.8	0.6396	0.6673	0.5643
0.9	1.1881	1.1095	0.9236
0.95	1.3240	1.2017	1.1297
TV
0.8	0.4017	0.3506	0.3815
0.9	0.4459	0.4768	0.4108
0.95	0.4561	0.4977	0.4626
TCS
0.8	1.1881	1.1174	1.1565
0.9	1.2474	1.2576	1.3365
0.95	1.3240	1.3029	1.3407
TCK
0.8	3.2895	3.76601	3.3459
0.9	3.6603	4.0037	3.8228
0.95	3.9037	4.2550	4.0485

.

As we can see, the TCE, TV, TCS and TCK of Amazon, Google and Apple are increasing with the increase of q-quantile, which helps investors understand extreme losses by showing risk measures under different q-quantile values.

7. Concluding Remarks

In this paper, we have considered the univariate location-scale mixture of elliptical distributions, which has received much attention in finance and insurance applications, since this distribution not only includes the location-scale mixture of normal (LSMN) distributions, Student’s t (LSMSt) distributions, logistic (LSMLo) distributions and Laplace (LSMLa) distributions, but also includes the generalized hyperbolic distribution (GHD) and the slash distribution. We have given the general form of TCM and the expressions of TV, TCS, and TCK.