Resiliency and Nonlinearity Profiles of Some Cryptographic Functions

Abstract

Boolean functions are important in terms of their cryptographic and combinatorial properties for different kinds of cryptosystems. The nonlinearity and resiliency of cryptographic functions are crucial criteria with respect to protection of ciphers from affine approximation and correlation attacks. In this article, some constructions of disjoint spectra Boolean that function by concatenating the functions on a lesser number of variables are provided. The nonlinearity and resiliency profiles of the constructed functions are obtained. From the profiles of the constructed functions, it is observed that the nonlinearity of these functions is greater than or equal to the nonlinearity of some existing functions. Furthermore, in the security analysis of cryptosystems, 4th order nonlinearity of Boolean functions play a crucial role. It provides protection against various higher order approximation attacks. The lower bounds on 4th order nonlinearity of some classes of Boolean functions having degree 5 are provided. The lower bounds of two classes of functions have form $T{r}_1^n\left(\lambda x^d\right)$ for all $x\in {\mathbb{F}}_{2^n},$ $\lambda \in {\mathbb{F}}_{2^n}^{*},$ where (i) $d=2^i+2^j+2^k+2^{\ell }+1,$ where $i,j,k,\ell$ are integers such that $i>j>k>\ell \ge 1$ and $n>2i$, and (ii) $d=2^{4\ell }+2^{3\ell }+2^{2\ell }+2^{\ell }+1,$ where $\ell >0$ is an integer with property $\gcd (\ell ,n)=1$, $n>8$ are provided. The obtained lower bounds are compared with some existing results available in the literature.

1. Introduction

Boolean functions are useful in designing various cryptosystems. Boolean functions on n unknowns are functions from ${\mathbb{F}}_{2^n}$ to ${\mathbb{F}}_2,$ where ${\mathbb{F}}_{2^n}$ is an nth degree extension of ${\mathbb{F}}_2.$

Suppose ${\mathcal{B}}_n$ is collection of Boolean functions in n unknowns, and $|{\mathcal{B}}_n|=2^{2^n}$ is the cardinality of ${\mathcal{B}}_n$. Boolean functions have several applications in different types of cryptosystems. The functions used in various cryptosystems should possess some cryptographic criteria such as high nonlinearity, balancedness, high resiliency, low crosscorrelation, high algebraic immunity, and high higher order (rth-order) nonlinearity. It is not possible to optimize all criteria simultaneously, but there are some trade-offs among them. Almost all the cryptographic criteria of Boolean functions can be analyzed by using the Walsh–Hadamard transform (WHT). The WHT of $f\in {\mathcal{B}}_n$ is $W_f\left(b\right)={\sum }_{u\in {\mathbb{F}}_2^n}{(-1)}^{f\left(u\right)+b·u}$ at $b\in {\mathbb{F}}_{2^n}$. The nonlinearity is one of the important cryptographic properties of Boolean functions. The nonlinearity of $f\in {\mathcal{B}}_n$ is the minimum Hamming distance of function from all n-variable affine functions. The nonlinearity of $f\in {\mathcal{B}}_n$ is defined by $nl\left(f\right)=2^{n-1}-\frac{1}{2}{max}_{a\in {\mathbb{F}}_2^n}\left|W_f\left(a\right)\right|.$ The functions with maximum possible nonlinearity are called bent functions [1] and are the most resistant to the affine approximation attack [2,3].

The Boolean functions possessing good cryptographic properties are useful in the design of a secure cryptosystem. The Boolean functions which are highly nonlinear, resilient, correlation immune, balanced, with low cross-correlation, and having high higher order nonlinearity are eligible to provide protection against different kinds of cryptographic attacks. However, all of these properties can not be optimized simultaneously. However, some trade-off can be obtained among them. The researchers have analysed several classes of Boolean functions by considering some cryptographic criteria listed above. The resiliency and the nonlinearity are two important cryptographic properties for Boolean functions used in various cryptosystems. High resiliency provides protection against correlation attacks [4,5,6], whereas high nonlinearity helps to prevent the ciphers from linear cryptanalysis [7] and best affine approximation attacks [2,7]. A balanced function with high nonlinearity is considered to be a good candidate for various cryptographic applications. Such functions are used as combiner functions in LSFR (linear feedback shift register) based stream ciphers. For Boolean functions to be instrumental in cryptography, they must be balanced. The balancedness is presupposition of the resilient functions along with correlation immunity. Therefore, it is important to construct resilient functions having high nonlinearity. Several constructions of resilient functions satisfying some other important cryptographic criteria have been reported in the literature [2,4,5,6,7]. Sarkar-Maitra [8], Maitra-Pasalic [9] and Zhang-Xiao [10] have constructed some resilient function having high nonlinearity. For more study on constructions of resilient functions and their properties, we refer to [8,9,10,11,12,13,14]. Gao et al. [15] have provided a technique to construct resilient Boolean functions having high nonlinearity. Singh [16] have presented some classes of resilient functions which show good behavior with respect to nonlinearity profile. The Boolean functions were employed as the nonlinear combiner/filters in different stream ciphers required to bear both good nonlinearity and resiliency properties. Resiliency put a check for the system to verify that it is not prone towards correlation attacks. To enhance security against different linear cryptanalysis and higher order approximation attacks, there is a strong need to obtain functions which are resilient and have good nonlinearity profiles. The present article is an attempt in this direction. The article presents construction of some resilient functions with high nonlinearity. Moreover, two classes of Boolean functions with higher order (in particular, 4th order) nonlinearity are presented to enhance the security of the cryptosystems from higher order approximation attacks.

The rth order nonlinearity and nonlinearity profile is a generalization of a criterion of nonlinearity [3,17]. The rth order nonlinearity $n{l}_r\left(f\right)$ of a Boolean function f is given as the minimum Hamming distance of f to the functions of degree less than or equal to r (for r = 1, it becomes a nonlinearity of f). The concept of rth order nonlinearity is used in cryptoanalysis in [2,3,18]. Due to its deep relationship with Reed–Muller codes, it also has equal importance in coding theory. Computation of higher order nonlinearities for $r>1$ is an important problem. There is no efficient method to obtain the higher order nonlinearities for $r>1$. The most efficient algorithm is due to [19] which works up to $n=11$ and $r=2,$ and for some functions $n\le 13$. Therefore, it is crucial to obtain theoretically lower bounds for higher order nonlinearities of functions which are true for all values of $n.$ During the last few years, this problem has received attention from the researchers, and some interesting results have been produced. In 2008, Carlet has produced a remarkable work. He has introduced a recursive approach for computing lower bounds on higher order nonlinearities [17]. Using the Carlet’s recursive approach, Sun Wu [20] and Gode Gangopadhyay [21] have presented good lower bounds on higher order nonlinearities for various classes of Boolean functions. Recently, Singh and Paul [22] have presented lower bounds on $n{l}_4$ for a particular class of functions of the form $T{r}_1^n\left(\lambda x^s\right)$, $\lambda \in {\mathbb{F}}_{2^n}^{*},$ $s=2^{2t}-2^t+1$ and $gcd(n,t)=1,t=4.$ The higher order nonlinearity plays a crucial role to analyze the security of the cryptosystems with respect to higher order approximation attacks. Motivated through this, two classes of Boolean functions are identified which possess high 4th order nonlinearity.

The organization of the article is as follows: Section 2 provides some existing results required to derive the results in this article. In Section 3, some constructions of disjoint spectra Boolean functions by concatenating functions on a lesser number of variables are provided. The nonlinearity and resiliency profiles of the constructed functions are obtained. From the profiles of the constructed functions, it is observed that the nonlinearity of these functions is greater than or equal to the nonlinearity obtained for the functions presented in [15,16]. Section 4 provides the lower bounds on 4th order nonlinearity, and some classes of functions in ${\mathcal{B}}_n$ of degree 5 are obtained. The bounds for the functions having form $T{r}_1^n\left(\lambda x^d\right)$ for all $x\in {\mathbb{F}}_{2^n},$ $\lambda \in {\mathbb{F}}_{2^n}^{*},$ where (i) $d=2^i+2^j+2^k+2^{\ell }+1,$ where $i,j,k,\ell$ are integers such that $i>j>k>\ell \ge 1$ and $n>2i$, and (ii) $d=2^{4\ell }+2^{3\ell }+2^{2\ell }+2^{\ell }+1,$ where $\ell >0$ is an integer with $\gcd (\ell ,n)=1$ and $n>8$ is provided.

2. Preliminaries

This section presents some definitions and existing results required for further computation in the paper. The Hamming weight of $f\in {\mathcal{B}}_n$ is $wt\left(f\right)=\left|supp\right(f\left)\right|.$ The Hamming distance between functions h and k in ${\mathcal{B}}_n$ is given by $d(h,k)=\left|\right\{x\in {\mathbb{F}}_{2^n}:h\left(x\right)\ne k\left(x\right)\left\}\right|.$ There are various representations of Boolean functions used in coding theory and cryptography. The most common representation is the algebraic normal form (ANF) defined as ${\displaystyle f(x_1,x_2,\dots ,x_n)=\sum _{I\subseteq \{1,2,\dots ,n\}}{a}_I\left(\prod _{i\in I}{x}_i\right),}$ with $a_I\in {\mathbb{F}}_2$, and ${\prod }_{i\in I}{x}_i$ is called monomial. The largest degree of the monomial with nonzero coefficient in ANF is called its algebraic degree of $f.$

A function $\varphi \in {\mathcal{B}}_n$ is plateaued if, for every $u\in {\mathbb{F}}_2^n,$ $H_{\varphi }\left(u\right)\in \{0,\pm 2^k\},k\in \mathbb{N}$. Two functions $\varphi$ and $\psi$ in ${\mathcal{B}}_n$ satisfying the property $H_{\varphi }\left(\alpha \right)H_{\psi }\left(\alpha \right)=0$ for all $\alpha \in {\mathbb{F}}_2^n$ are called disjoint spectra functions. A function $\varphi \in {\mathcal{B}}_n$ is called balanced if $H_{\varphi }\left(0\right)=0$. If $H_{\varphi }\left(\alpha \right)=0$ for every $\alpha \in {\mathbb{F}}_2^n$ with $1\le wt\left(\alpha \right)\le r,$ then $\varphi$ is a correlation immune Boolean function of order $r.$ A correlation immune function of order r which is balanced is known as an r-resilient function.

The following result is due to Iwata and Kurosawa [3], which provide nonlinearity of a function in terms of nonlinearities of its subfunctions.

Lemma 1

([3]). Suppose ${\varphi }_0$ and ${\varphi }_1$ are restriction functions of $\varphi \in {\mathcal{B}}_n$ to the linear hyperplane $x_n=0$ and $x_n=1$, respectively. Then, the functions ${\varphi }_0$ and ${\varphi }_1$ are Boolean functions on $(n-1)$ variables and satisfy the relation

$$n{l}_r\left(\varphi \right)\ge n{l}_r\left({\varphi }_0\right)+n{l}_r\left({\varphi }_1\right).$$

For the construction of disjoint spectra functions, there is a concatenation of Boolean functions on less number of variables [23]. Suppose ${\varphi }_1$ and ${\varphi }_2$ are two Boolean functions on n-variables. Then, the concatenation $\varphi ={\varphi }_1\Vert {\varphi }_2$ of ${\varphi }_1$ and ${\varphi }_2$ is an $(n+1)$-variable function expressed by

$$\varphi ({\alpha }_{n+1},\dots ,{\alpha }_1)=(1+{\alpha }_{n+1}){\varphi }_1({\alpha }_n,\dots ,{\alpha }_1)+{\alpha }_{n+1}{\varphi }_2({\alpha }_n,\dots ,{\alpha }_1).$$

The profile of a Boolean function is represented by using 4-tupple $(p,q,r,s),$ where p represents number of variables, q resiliency order, r the algebraic degree, and s the nonlinearity of the selected function.

Sarkar and Maitra [8] have obtained the profile of a concatenated function on $(n+1)$ variables in terms of the profile of its subfunction on n variables.

Lemma 2

([8]). Suppose the profile of the function $\varphi \in {\mathcal{B}}_n$ is $(n,r,n-r-1,nl)$ and $\overline{\varphi }$ is the complement function of ϕ. Then, the profile of $\varphi \Vert \overline{\varphi }$ is given by $(n+1,r+1,n-r-1,2nl)$.

Siegenthaler [24] has provided the following relationship on resiliency of function obtained by the concatenation of two functions.

Lemma 3

([24]). If ${\varphi }_1$ and ${\varphi }_2,$ are two r-resilient functions, then the function $\varphi ={\varphi }_1\Vert {\varphi }_2$ is also r-resilient.

Let $v=(v_s,\dots ,v_1)$ and $\varphi \in {\mathcal{B}}_n$. The restriction function of $\varphi$ with respect to v is defined as

$${\varphi }_v({\alpha }_{n-s},\dots ,{\alpha }_1)=\varphi ({\alpha }_n=v_s,\dots ,{\alpha }_{n-s+1}=v_1,{\alpha }_{n-s},\dots ,{\alpha }_1).$$

Suppose $u=(u_s,\dots ,u_1)\in {\mathbb{F}}_2^s$ and $\alpha =({\alpha }_{n-s},\dots ,{\alpha }_1)\in {\mathbb{F}}_2^{n-s}.$ Then, the vector concatenation of u and $\alpha$ is defined as

$$u\alpha =(u,\alpha )=(u_s,\dots ,u_1,{\alpha }_{n-s},\dots ,{\alpha }_1).$$

Definition 1.

The spectrum characterization matrix $SM\left(\varphi \right)$ of $\varphi \in {\mathcal{B}}_n$ is a matrix whose rows are the vectors of ${\mathbb{F}}_2^n$ at which the WHS values of ϕ are non-zero, i.e.,

$$SM\left(\varphi \right)=\{\alpha \in {\mathbb{F}}_2^n:H_{\varphi }\left(\alpha \right)\ne 0\}.$$

Furthermore, if u is a string of some fixed length, then we denote the matrix $\{u\alpha :\alpha \in SM(\varphi \left)\right\}$ by $u\Vert SM\left(\varphi \right).$

Gao et al. [15] have provided a relationship between the WHT of function $\varphi$ and its subfunctions. Using this result, they have constructed highly nonlinear resilient Boolean functions.

Lemma 4

([15], Theorem 1). Suppose $\varphi \in {\mathcal{B}}_n,$$u=(u_s,\dots ,u_1)\in {\mathbb{F}}_2^s$ and $\alpha =({\alpha }_{n-s},\dots ,{\alpha }_1)\in {\mathbb{F}}_2^{n-s}.$ Then, the WHT of ϕ in terms of its subfunction is given by

$$H_{\varphi }\left(u\alpha \right)=\sum _{\mathbf{y}\in {\mathbb{F}}_2^s}{H}_{{\varphi }_y}\left(\alpha \right){(-1)}^{\langle u,y\rangle }.$$

For any subfield ${\mathbb{F}}_{2^t}$ of ${\mathbb{F}}_{2^n}\left(\mathrm{obviously}t\right|n)$, the function defined by $T{r}_t^n\left(x\right)=x+x^{2^t}+x^{2^{2t}}+\dots +x^{2^{(n-1)t}}$ is called trace function. For $t=1,$ the function $T{r}_1^n:{\mathbb{F}}_{2^n}\to {\mathbb{F}}_2$ defined by $T{r}_1^n\left(x\right)=x+x^2+x^{2^2}+\dots +x^{2^{n-1}}$ is called absolute trace function [25].

The derivative $D_{a}f\left(x\right)$ of a function f in ${\mathcal{B}}_n$ at $a\in {\mathbb{F}}_{2^n}$ is given as $D_{a}f\left(x\right)=f(x+a)+f\left(x\right)$ for all $x\in {\mathbb{F}}_{2^n}.$ Suppose U is a q-dimensional subspace in ${\mathbb{F}}_{2^n}$ generated using $b_1,\dots ,b_q,$ that is, $U=\langle b_1,\dots ,b_q\rangle .$ The qth order derivative of f in ${\mathcal{B}}_n$ with respect to U is defined as $D_{U}f\left(x\right)=D_{b_1}\dots D_{b_q}f\left(x\right),\mathrm{for}\mathrm{every}x\in {\mathbb{F}}_{2^n}.$ The bilinear form of f is given as $B(x,y)=f\left(x\right)+f\left(y\right)+f\left(0\right)+f(x+y).$ ${\mathcal{E}}_f=\{x\in {\mathbb{F}}_{2^n}:B(x,y)=0$ for every $y\in {\mathbb{F}}_{2^n}\}$ is a subspace of ${\mathbb{F}}_{2^n}$ and known as kernel of $B(x,y)$.

The following two results are due to Carlet [17], which are frequently used to draw lower bounds on rth order nonlinearities of functions.

Proposition 1

([17]). Let $f\in {\mathcal{B}}_n$ and $0<r<n$, an integer. Then, $n{l}_r\left(f\right)\ge \frac{1}{2}{max}_{a\in {\mathbb{F}}_{2^n}}n{l}_{r-1}\left(D_{a}f\right).$ In terms of higher-order derivatives, for all non negative $i<r,$

$$n{l}_r\left(f\right)\ge \frac{1}{2^i}\underset{a_1,a_2,\dots ,a_i\in {\mathbb{F}}_{2^n}}{max}n{l}_{r-i}(D_{a_1},D_{a_2}\dots D_{a_i}f).$$

Proposition 2

([17]). Let $h\in {\mathcal{B}}_n$ and $0<r<n$, an integer. Then,

$$n{l}_r\left(h\right)\ge 2^{n-1}-\frac{1}{2}\sqrt{2^{2n}-2\sum _{b\in {\mathbb{F}}_{2^n}}n{l}_{r-1}(D_{b}h}).$$

In terms of a higher-order derivative, for every positive integer $\ell <r,$

$$n{l}_r\left(h\right)\ge 2^{n-1}-\frac{1}{2}\sqrt{\sum _{a_1\in {\mathbb{F}}_{2^n}}\sqrt{\sum _{a_2\in {\mathbb{F}}_{2^n}}\cdots \sqrt{2^{2n}-2\sum _{a_{\ell }\in {\mathbb{F}}_{2^n}}n{l}_{r-1}(D_{a_1}\cdots D_{a_{\ell }}h)}}}.$$

Proposition 3

([26]). Suppose ${\displaystyle L\left(x\right)=\sum _{i=0}^v{c}_i{x}^{2^{ik}}}$ is a linearized polynomial in ${\mathbb{F}}_{2^n},$ where $v,k$ are positive integers with $\gcd (n,k)=1.$ Then, the zeros of the linearized polynomial in ${\mathbb{F}}_{2^n}$ are at most $2^v.$

Proposition 4

([25]). Let f be a quadratic function with its bilinear form as $B(x,y)$. Then, the weight distribution of spectrum of WHT of the function f is related to only dimension t of ${\mathcal{E}}_f$ of the bilinear form $B(x,y).$

${\mathit{W}}_{\mathit{f}}\mathbf{\left(}\mathit{\alpha }\mathbf{\right)}$		Number of$\mathit{\alpha }$
0		$2^n-2^{n-t}$
$2^{(n+t)/2}$		$2^{n-t-1}+{(-1)}^{f\left(0\right)}{2}^{(n-t-2)/2}$
$-2^{(n+t)/2}$		$2^{n-t-1}-{(-1)}^{f\left(0\right)}{2}^{(n-t-2)/2}$

3. Computation of Disjoint Spectra Resilient Functions Having Good Nonlinearity

The following theorem presents the construction of disjoint spectra Boolean functions on $n+4$ variables by using disjoint spectra functions on n variables.

Theorem 1.

Let ${\varphi }_0,{\psi }_0\in {\mathcal{B}}_n$ be optimal plateaued resilient Boolean functions having disjoint spectra. Define the functions $\varphi =(x_{n+1}+1){\varphi }_0+x_{n+1}{\psi }_0,$ $\psi =x_{n+1}+{\varphi }_0$ and $\kappa =x_{n+1}+{\psi }_0.$ Then, $\mathrm{\Phi }=\overline{\varphi }\Vert \varphi \Vert \varphi \Vert \overline{\varphi }\Vert \varphi \Vert \overline{\varphi }\Vert \overline{\varphi }\Vert \varphi$ and $\mathrm{\Psi }=\overline{\psi }\Vert \overline{\kappa }\Vert \kappa \Vert \psi \Vert \overline{\kappa }\Vert \overline{\psi }\Vert \psi \Vert \kappa$ are also disjoint spectra functions on ${\mathbb{F}}_2^{n+4}$.

Proof. 

Since ${\varphi }_0$ and ${\psi }_0$ are disjoint spectra functions, therefore, from a definition, it follows that $H_{{\varphi }_0}\left(\alpha \right)H_{{\psi }_0}\left(\alpha \right)=0$ for every $\alpha \in {\mathbb{F}}_2^n.$ It is easy to verify that $H_{\varphi }\left(\alpha \right)=-H_{\overline{\varphi }}\left(\alpha \right).$ Now, if $\alpha \in SM\left({\varphi }_0\right)$ or $SM\left({\psi }_0\right),$ then, by using Lemma 4, we obtain the Walsh–Hadamard transform of the function $\varphi$ as

$$\begin{array}{ccc}\hfill H_{\varphi }\left(0\alpha \right)& =& {\displaystyle \sum _{x\in {\mathbb{F}}_2}{H}_{{\varphi }_x}\left(\alpha \right){(-1)}^{0·x}}\hfill \\ & =& H_{{\varphi }_0}\left(\alpha \right)+H_{{\varphi }_1}\left(\alpha \right)\hfill \\ & =& H_{{\varphi }_0}\left(\alpha \right)+H_{{\psi }_0}\left(\alpha \right)\ne 0[as\varphi ={\varphi }_0\Vert {\psi }_0],\hfill \end{array}$$

(1)

and

$$\begin{array}{ccc}\hfill H_{\varphi }\left(1\alpha \right)& =& {\displaystyle \sum _{x\in {\mathbb{F}}_2}{H}_{{\varphi }_x}\left(\alpha \right){(-1)}^{1·x}}\hfill \\ & =& H_{{\varphi }_0}\left(\alpha \right)-H_{{\varphi }_1}\left(\alpha \right)\hfill \\ & =& H_{{\varphi }_0}\left(\alpha \right)-H_{{\psi }_0}\left(\alpha \right)\ne 0[as\varphi ={\varphi }_0\Vert {\psi }_0].\hfill \end{array}$$

(2)

According to Definition 1, the spectrum characterization matrix of $\varphi$ is a matrix whose rows are those vectors of ${\mathbb{F}}_2^{n+1}$ for which WHT values of $\varphi$ are nonzero. Therefore, on combining (1), (2), and Definition 1, the spectrum characterization matrix of $\varphi$ is given by

$$SM\left(\varphi \right)=\left(\begin{array}{cc}0& \Vert SM\left({\varphi }_0\right)\\ 1& \Vert SM\left({\varphi }_0\right)\\ 0& \Vert SM\left({\psi }_0\right)\\ 1& \Vert SM\left({\psi }_0\right)\end{array}\right).$$

In order to obtain the spectrum characterization matrix of function $\mathrm{\Phi }=\overline{\varphi }\Vert \varphi \Vert \varphi \Vert \overline{\varphi }\Vert \varphi \Vert \overline{\varphi }\Vert \overline{\varphi }\Vert \varphi$, the WHT values of $\mathrm{\Phi }$ are required. By using Lemma 4, the WHT values of $\mathrm{\Phi }$ in terms its subfunctions are given by

$$\begin{array}{ccc}{H}_{\mathrm{\Phi }}(u,\alpha )\hfill & =\hfill & {\displaystyle \sum _{y\in {\mathbb{F}}_{2^3}}{H}_{{\varphi }_y}\left(\alpha \right){(-1)}^{u.y}}\hfill \end{array}.$$

Taking $u=111,$ we obtain

$$\begin{array}{ccc}{H}_{\mathrm{\Phi }}\left(111\alpha \right)\hfill & =\hfill & H_{{\varphi }_{000}}\left(\alpha \right)+H_{{\varphi }_{001}}\left(\alpha \right)-H_{{\varphi }_{010}}\left(\alpha \right)+H_{{\varphi }_{011}}\left(\alpha \right)-H_{{\varphi }_{100}}\left(\alpha \right)\hfill \\ & & +H_{{\varphi }_{101}}\left(\alpha \right)+H_{{\varphi }_{110}}\left(\alpha \right)-H_{{\varphi }_{111}}\left(\alpha \right)\hfill \\ \\ & =\hfill & H_{{\varphi }_1}\left(\alpha \right)-H_{{\varphi }_2}\left(\alpha \right)-H_{{\varphi }_3}\left(\alpha \right)+H_{{\varphi }_4}\left(\alpha \right)-H_{{\varphi }_5}\left(\alpha \right)+H_{{\varphi }_6}\left(\alpha \right)\hfill \\ & & +H_{{\varphi }_7}\left(\alpha \right)-H_{{\varphi }_8}\left(\alpha \right)\hfill \end{array}$$

$$\begin{array}{ccc}\hfill H_{\mathrm{\Phi }}\left(111\alpha \right)& =& H_{\overline{\varphi }}\left(\alpha \right)-H_{\varphi }\left(\alpha \right)-H_{\varphi }\left(\alpha \right)+H_{\overline{\varphi }}\left(\alpha \right)-H_{\varphi }\left(\alpha \right)+H_{\overline{\varphi }}\left(\alpha \right)\hfill \\ & & +H_{\overline{\varphi }}\left(\alpha \right)-H_{\varphi }\left(\alpha \right)\hfill \\ & =& -H_{\varphi }\left(\alpha \right)-H_{\varphi }\left(\alpha \right)-H_{\varphi }\left(\alpha \right)-H_{\varphi }\left(\alpha \right)-H_{\varphi }\left(\alpha \right)-H_{\varphi }\left(\alpha \right)\hfill \\ & & -H_{\varphi }\left(\alpha \right)-H_{\varphi }\left(\alpha \right)\hfill \\ & =& -8H_{\varphi }\left(\alpha \right).\hfill \end{array}$$

(3)

Similarly, we can obtain the WHT of $\mathrm{\Phi }$ at other values of u as

$$\begin{array}{ccc}\hfill & & H_{\mathrm{\Phi }}\left(110\alpha \right)=0,H_{\mathrm{\Phi }}\left(101\alpha \right)=0,H_{\mathrm{\Phi }}\left(100\alpha \right)=0,H_{\mathrm{\Phi }}\left(011\alpha \right)=0,\hfill \\ & & H_{\mathrm{\Phi }}\left(010\alpha \right)=0,H_{\mathrm{\Phi }}\left(001\alpha \right)=0,H_{\mathrm{\Phi }}\left(000\alpha \right)=0.\hfill \end{array}$$

(4)

Now, by combining (3), (4), and Definition 1, the spectrum characterization matrix of $\mathrm{\Phi }$ is given by

$$SM\left(\mathrm{\Phi }\right)=111\Vert SM\left(\varphi \right)=\left(\begin{array}{cc}1110& \Vert SM\left({\varphi }_0\right)\\ 1111& \Vert SM\left({\varphi }_0\right)\\ 1110& \Vert SM\left({\psi }_0\right)\\ 1111& \Vert SM\left({\psi }_0\right)\end{array}\right).$$

Again, by using Lemma 4, the WHT values for the concatenated function $\mathrm{\Psi }=\overline{\psi }\Vert \overline{\kappa }\Vert \kappa \Vert \psi \Vert \overline{\kappa }\Vert \overline{\psi }\Vert \psi \Vert \kappa$ are given as $H_{\mathrm{\Psi }}\left(000\alpha \right)=0$, $H_{\mathrm{\Psi }}\left(001\alpha \right)=0$, $H_{\mathrm{\Psi }}\left(010\alpha \right)=-4H_{\psi }\left(\alpha \right)-4H_{\kappa }\left(\alpha \right)$, $H_{\mathrm{\Psi }}\left(011\alpha \right)=0$, $H_{\mathrm{\Psi }}\left(100\alpha \right)=0$, $H_{\mathrm{\Psi }}\left(101\alpha \right)=-4H_{\psi }\left(\alpha \right)+4H_{\kappa }\left(\alpha \right)$, $H_{\mathrm{\Psi }}\left(110\alpha \right)=0$, $H_{\mathrm{\Psi }}\left(111\alpha \right)=0.$

Therefore, the spectrum characterization matrix of $\psi ,\kappa$ and $\mathrm{\Psi }$ are given by

$$SM\left(\psi \right)=1\Vert SM\left({\varphi }_0\right),SM\left(\kappa \right)=1\Vert SM\left({\psi }_0\right),\mathrm{and}$$

$$SM\left(\mathrm{\Psi }\right)=\left(\begin{array}{cc}010& \Vert SM\left(\psi \right)\\ 101& \Vert SM\left(\psi \right)\\ 010& \Vert SM\left(\kappa \right)\\ 101& \Vert SM\left(\kappa \right)\end{array}\right)=\left(\begin{array}{cc}0101& \Vert SM\left({\varphi }_0\right)\\ 1011& \Vert SM\left({\varphi }_0\right)\\ 0101& \Vert SM\left({\psi }_0\right)\\ 1011& \Vert SM\left({\psi }_0\right)\end{array}\right).$$

From the spectrum characterization matrix of concatenated functions $\mathrm{\Phi }$ and $\mathrm{\Psi }$, it is observed that $\mathrm{\Phi }$ and $\mathrm{\Psi }$ are disjoint spectra Boolean functions on ${\mathbb{F}}_2^{n+4}$. □

In the following result, we obtain the profiles for the functions $\mathrm{\Phi }$ and $\mathrm{\Psi }$ as constructed in Theorem 1. We investigate the resiliency order and the nonlinearities of the constructed functions $\mathrm{\Phi }$ and $\mathrm{\Psi },$ and show that the disjoint spectra functions $\mathrm{\Phi }$ and $\mathrm{\Psi }$ are highly nonlinear and resilient on ${\mathbb{F}}_2^{n+4}$.

Theorem 2.

Suppose ${\varphi }_0,{\psi }_0\in {\mathcal{B}}_n$ are two optimal plateaued resilient functions of disjoint spectra having profile $(n,r,n-r-1,2^{n-1}-2^{r+1}),$ and $\varphi ,$ $\psi ,$ κ are the functions as in Theorem 1. Then, the functions Φ and Ψ are disjoint spectra resilient functions with good nonlinearity having profile $(n+4,r+3,n-r,2^{n+3}-2^{r+4})$ and $(n+4,r+2,n-r,2^{n+3}-2^{r+4}),$ respectively.

Proof. 

We have $\varphi ={\varphi }_0\Vert {\psi }_0;$ by Lemmas 2 and 3, it follows that the function $\overline{\varphi }\Vert \varphi$ is an $(r+1)$-resilient function and nonlinearity of $\overline{\varphi }\Vert \varphi$ is $nl\left(\overline{\varphi }\Vert \varphi \right)=2nl\left(\varphi \right).$ Suppose $P=\overline{\varphi }\Vert \varphi \Vert \varphi \Vert \overline{\varphi }.$ Then, in the view of Lemma 4, for any $\alpha \in {\mathbb{F}}_2^n,$ the WHT values of the function P are obtained as $H_P\left(00\alpha \right)=0$, $H_P\left(01\alpha \right)=0$, $H_P\left(10\alpha \right)=0$, $H_P\left(11\alpha \right)=-4H_{\varphi }\left(\alpha \right)$.

Clearly, when $wt\left(11\alpha \right)\le r+2,$ then $wt\left(\alpha \right)\le r$ and $\varphi$ is an r-resilient Boolean function; this implies $H_{\varphi }\left(\alpha \right)=0$, and therefore $H_P\left(11\alpha \right)=0$. Hence, resiliency order of P is $(r+2)$. In addition, by using Lemma 1, we obtain the nonlinearity $nl\left(P\right)=4nl\left(\varphi \right).$

Now, for the function $\mathrm{\Phi }=\overline{\varphi }\Vert \varphi \Vert \varphi \Vert \overline{\varphi }\Vert \varphi \Vert \overline{\varphi }\Vert \overline{\varphi }\Vert \varphi$, using Lemma 4, we obtain

$H_{\mathrm{\Phi }}\left(000\alpha \right)=0$, $H_{\mathrm{\Phi }}\left(001\alpha \right)=0,$$H_{\mathrm{\Phi }}\left(010\alpha \right)=0$, $H_{\mathrm{\Phi }}\left(011\alpha \right)=0$,

$H_{\mathrm{\Phi }}\left(100\alpha \right)=0$, $H_{\mathrm{\Phi }}\left(101\alpha \right)=0$, $H_{\mathrm{\Phi }}\left(110\alpha \right)=0$, $H_{\mathrm{\Phi }}\left(111\alpha \right)=-8H_{\varphi }\left(\alpha \right).$

If $wt\left(111\alpha \right)\le r+3$, then clearly $wt\left(\alpha \right)\le r$. Now, $\varphi$ is r-resilient function; therefore, $H_{\mathrm{\Phi }}\left(111\alpha \right)=0$, which implies $\mathrm{\Phi }$ is an $(r+3)$-resilient Boolean function on ${\mathbb{F}}_2^{n+4}$.

From the profile of the function $\varphi$, it is clear that ${max}_{\alpha \in {\mathbb{F}}_2^{n+1}}\left|H_{\varphi }\left(\alpha \right)\right|=2^{r+2}$, and the spectrum of $\mathrm{\Phi }$ shows that ${max}_{u\in {\mathbb{F}}_2^3,\alpha \in {\mathbb{F}}_2^{n+1}}|H_{\mathrm{\Phi }}(u,\alpha )|=8{max}_{\alpha \in {\mathbb{F}}_2^{n+1}}\left|H_{\varphi }\left(\alpha \right)\right|=2^3.2^{r+2}=2^{r+5}.$ Therefore, the nonlinearity of $\mathrm{\Phi }$ is given by $nl\left(\mathrm{\Phi }\right)=2^{n+3}-2^{r+4}.$ Hence, the profile of $\mathrm{\Phi }$ is $(n+4,r+3,n-r,2^{n+3}-2^{r+4})$.

From the definition of the functions, $\psi =\overline{{\varphi }_0}\Vert {\varphi }_0,$ $\kappa =\overline{{\psi }_0}\Vert {\psi }_0$ and Lemma 2, the profile of the functions $\psi$ and $\kappa$ is obtained as $(n+1,r+1,n-r-1,2^n-2^{r+2}).$ Now, on interchanging the position of the variables $x_{n+1}$ and $x_{n+2}$ in the function $\overline{\psi }\Vert \overline{\kappa }=\overline{{\varphi }_0}\Vert {\varphi }_0\Vert \overline{{\psi }_0}\Vert {\psi }_0,$ we obtain the function $\overline{{\varphi }_0}\Vert \overline{{\psi }_0}\Vert {\varphi }_0\Vert {\psi }_0,$ which is the same as the function concatenation $\overline{\varphi }\Vert \varphi .$ Using Lemma 2, we obtain the nonlinearity $nl\left(\overline{\psi }\Vert \overline{\kappa }\right)=2n{l}_{\varphi }.$

Now, take $Q=\overline{\psi }\Vert \overline{\kappa }\Vert \kappa \Vert \psi .$ By using Lemma 4, we obtain $H_Q\left(00\alpha \right)=0$, $H_Q\left(01\alpha \right)=-2H_{\psi }\left(\alpha \right)+2H_{\kappa }\left(\alpha \right)$, $H_Q\left(10\alpha \right)=-2H_{\psi }\left(\alpha \right)-2H_{\kappa }\left(\alpha \right)$, $H_Q\left(11\alpha \right)=0$. Now, if $wt\left(01\alpha \right),wt\left(10\alpha \right)\le r+2,$ then obviously $wt\left(\alpha \right)\le r+1.$ Now, both $\psi$ and $\kappa$ are $(r+1)$-resilient; therefore, $H_{\psi }\left(\alpha \right)=0,$$H_{\kappa }\left(\alpha \right)=0,$ and hence we obtain $H_Q\left(01\alpha \right)=0,H_Q\left(10\alpha \right)=0$. Thus, the order of resiliency of the function Q is $(r+2).$ Furthermore, the nonlinearity of Q is $nl\left(Q\right)=2nl\left(\overline{\psi }\Vert \overline{\kappa }\right)=4nl\left(\varphi \right).$

Now, consider the function $\mathrm{\Psi }=\overline{\psi }\Vert \overline{\kappa }\Vert \kappa \Vert \psi \Vert \overline{\kappa }\Vert \overline{\psi }\Vert \psi \Vert \kappa .$ Using Lemma 4, we obtain $H_{\mathrm{\Psi }}\left(000\alpha \right)=0$, $H_{\mathrm{\Psi }}\left(001\alpha \right)=0$, $H_{\mathrm{\Psi }}\left(010\alpha \right)=-4H_{\psi }\left(\alpha \right)-4H_{\kappa }\left(\alpha \right)$, $H_{\mathrm{\Psi }}\left(100\alpha \right)=0$, $H_{\mathrm{\Psi }}\left(011\alpha \right)=0$, $H_{\mathrm{\Psi }}\left(101\alpha \right)=-4H_{\psi }\left(\alpha \right)+4H_{\kappa }\left(\alpha \right)$, $H_{\mathrm{\Psi }}\left(110\alpha \right)=0$, $H_{\mathrm{\Psi }}\left(111\alpha \right)=0.$ Furthermore, $wt\left(010\alpha \right)\le (r+2)$ implies that $wt\left(\alpha \right)\le r+1.$ Since resiliency order of both $\psi$ and $\kappa$ is $(r+1),$ therefore $H_{\psi }\left(\alpha \right)=0$, $H_{\kappa }\left(\alpha \right)=0,$ from which it follows that $H_{\mathrm{\Psi }}\left(010\alpha \right)=0$, $H_{\mathrm{\Psi }}\left(101\alpha \right)=0$. Therefore, the resiliency order of $\mathrm{\Psi }$ is $r+2.$

From the profile of the functions $\psi$ and $\kappa$, it is clear that $ma{x}_{\alpha \in {\mathbb{F}}_2^{n+1}}\left\{|H_{\psi }\left(\alpha \right)|,|H_{\kappa }\left(\alpha \right)|\right\}=2^{r+3}.$ In addition, $\psi$ and $\kappa$ are functions of disjoint spectra; thus, from the Walsh–Hadamard spectrum of $\mathrm{\Psi }$, we obtain ${max}_{\mathbf{u}\in {\mathbb{F}}_2^3,\alpha \in {\mathbb{F}}_2^{n+1}}|H_{\mathrm{\Psi }}(\mathbf{u},\alpha )|=4{max}_{\alpha \in {\mathbb{F}}_2^{n+1}}\left\{\right|H_{\psi }\left(\alpha \right)|,|H_{\kappa }\left(\alpha \right)\left|\right\}=2^{r+5}.$ Hence, the nonlinearity of $\mathrm{\Psi }$ is $nl\left(\mathrm{\Psi }\right)=2^{n+3}-2^{r+4}.$ Therefore, the profile of $\mathrm{\Psi }$ is $(n+4,r+2,n-r,2^{n+3}-2^{r+4})$.

From spectrum characterization matrices and the constructions of the concatenated functions $\mathrm{\Phi }$ and $\mathrm{\Psi }$, it is clear that they are disjoint spectra plateaued resilient functions having good nonlinearity with profiles $(n+4,r+3,n-r,2^{n+3}-2^{r+4})$ and $(n+4,r+2,n-r,2^{n+3}-2^{r+4}),$ respectively. □

In the following result, another pair of concatenated functions is constructed. It is proved that the constructed functions are highly nonlinear resilient and have disjoint spectra. By analyzing the nonlinearity and resiliency of the constructed functions, their profiles are obtained.

Theorem 3.

Suppose ${\varphi }_0,{\psi }_0\in {\mathcal{B}}_n$ are two optimal plateaued resilient functions of disjoint spectra having profile $(n,r,n-r-1,2^{n-1}-2^{r+1}),$ and $\varphi ,$ $\psi ,$ κ are the functions as in Theorem 1. Then, the functions $\mathrm{\Phi }=\overline{\varphi }\Vert \overline{\varphi }\Vert \varphi \Vert \varphi \Vert \varphi \Vert \overline{\varphi }\Vert \varphi \Vert \overline{\varphi }$ and $\mathrm{\Psi }=\psi \Vert \kappa \Vert \kappa \Vert \psi \Vert \overline{\psi }\Vert \overline{\kappa }\Vert \overline{\kappa }\Vert \overline{\psi },$ are disjoint spectra resilient functions with good nonlinearity having profiles $(n+4,r+1,n-r,2^{n+3}-2^{r+3})$ and $(n+4,r+2,n-r,2^{n+3}-2^{r+4})$, respectively.

Proof. 

We have $\mathrm{\Phi }=\overline{\varphi }\Vert \overline{\varphi }\Vert \varphi \Vert \varphi \Vert \varphi \Vert \overline{\varphi }\Vert \varphi \Vert \overline{\varphi }$ and $\mathrm{\Psi }=\psi \Vert \kappa \Vert \kappa \Vert \psi \Vert \overline{\psi }\Vert \overline{\kappa }\Vert \overline{\kappa }\Vert \overline{\psi }$. By using Lemma 4, the Walsh–Hadamard transform values of concatenated function $\mathrm{\Phi }$ are given as follows:

$$\begin{array}{ccc}\hfill & & H_{\mathrm{\Phi }}\left(000\alpha \right)=0,H_{\mathrm{\Phi }}\left(001\alpha \right)=4H_{\varphi }\left(\alpha \right),H_{\mathrm{\Phi }}\left(010\alpha \right)=-4H_{\varphi }\left(\alpha \right),H_{\mathrm{\Phi }}\left(011\alpha \right)=0,\hfill \\ & & H_{\mathrm{\Phi }}\left(100\alpha \right)=0,H_{\mathrm{\Phi }}\left(101\alpha \right)=-4H_{\varphi }\left(\alpha \right),H_{\mathrm{\Phi }}\left(110\alpha \right)=-4H_{\varphi }\left(\alpha \right),H_{\mathrm{\Phi }}\left(111\alpha \right)=0,\hfill \end{array}$$

(5)

and the Walsh–Hadamard transform values of concatenated function $\mathrm{\Psi }$ are obtained as

$$\begin{array}{ccc}\hfill & & H_{\mathrm{\Psi }}\left(000\alpha \right)=0,H_{\mathrm{\Psi }}\left(001\alpha \right)=-4H_{\kappa }\left(\alpha \right),H_{\mathrm{\Psi }}\left(010\alpha \right)=0,H_{\mathrm{\Psi }}\left(011\alpha \right)=4H_{\kappa }\left(\alpha \right),\hfill \\ & & H_{\mathrm{\Psi }}\left(100\alpha \right)=0,H_{\mathrm{\Psi }}\left(101\alpha \right)=4H_{\psi }\left(\alpha \right),H_{\mathrm{\Psi }}\left(110\alpha \right)=0,H_{\mathrm{\Psi }}\left(111\alpha \right)=4H_{\psi }\left(\alpha \right).\hfill \end{array}$$

(6)

The remaining computation is similar to the computation made in Theorem 1 and Theorem 2. In view of (5), (6), and Definition 1, the spectrum characterization matrix of $\mathrm{\Phi }$ is obtained as follows:

$$SM\left(\mathrm{\Phi }\right)=\left(\begin{array}{cc}001& \Vert SM\left(\varphi \right)\\ 010& \Vert SM\left(\varphi \right)\\ 101& \Vert SM\left(\varphi \right)\\ 110& \Vert SM\left(\varphi \right)\end{array}\right)=\left(\begin{array}{cc}0010& \Vert SM\left({\varphi }_0\right)\\ 0011& \Vert SM\left({\varphi }_0\right)\\ 0100& \Vert SM\left({\varphi }_0\right)\\ 0101& \Vert SM\left({\varphi }_0\right)\\ 1010& \Vert SM\left({\varphi }_0\right)\\ 1011& \Vert SM\left({\varphi }_0\right)\\ 1100& \Vert SM\left({\varphi }_0\right)\\ 1101& \Vert SM\left({\varphi }_0\right)\\ 0010& \Vert SM\left({\psi }_0\right)\\ 0011& \Vert SM\left({\psi }_0\right)\\ 0100& \Vert SM\left({\psi }_0\right)\\ 0101& \Vert SM\left({\psi }_0\right)\\ 1010& \Vert SM\left({\psi }_0\right)\\ 1011& \Vert SM\left({\psi }_0\right)\\ 1100& \Vert SM\left({\psi }_0\right)\\ 1101& \Vert SM\left({\psi }_0\right)\end{array}\right),$$

and the spectrum characterization matrix of $\mathrm{\Psi }$ is given by

$$SM\left(\mathrm{\Psi }\right)=\left(\begin{array}{cc}100& \Vert SM\left(\psi \right)\\ 111& \Vert SM\left(\psi \right)\\ 100& \Vert SM\left(\kappa \right)\\ 111& \Vert SM\left(\kappa \right)\end{array}\right)=\left(\begin{array}{cc}1001& \Vert SM\left({\varphi }_0\right)\\ 1111& \Vert SM\left({\varphi }_0\right)\\ 1001& \Vert SM\left({\psi }_0\right)\\ 1111& \Vert SM\left({\psi }_0\right)\end{array}\right).$$

The matrices $SM\left(\mathrm{\Phi }\right)$ and $SM\left(\mathrm{\Psi }\right)$ show that the concatenated functions $\mathrm{\Phi }$ and $\mathrm{\Psi }$ have disjoint spectra. In addition, the profiles of $\mathrm{\Phi }$ and $\mathrm{\Psi }$ are $(n+4,r+1,n-r,2^{n+3}-2^{r+3})$ and $(n+4,r+2,n-r,2^{n+3}-2^{r+4})$, respectively. Here, it can be noted that the nonlinearity of the constructed function $\mathrm{\Phi }$ is efficiently high, which can be verified graphically from Figure 1 and numerically from

Table 1. Nonlinearity obtained in Theorems 2 and 3, and in [15,16] for $n\ge 7$.

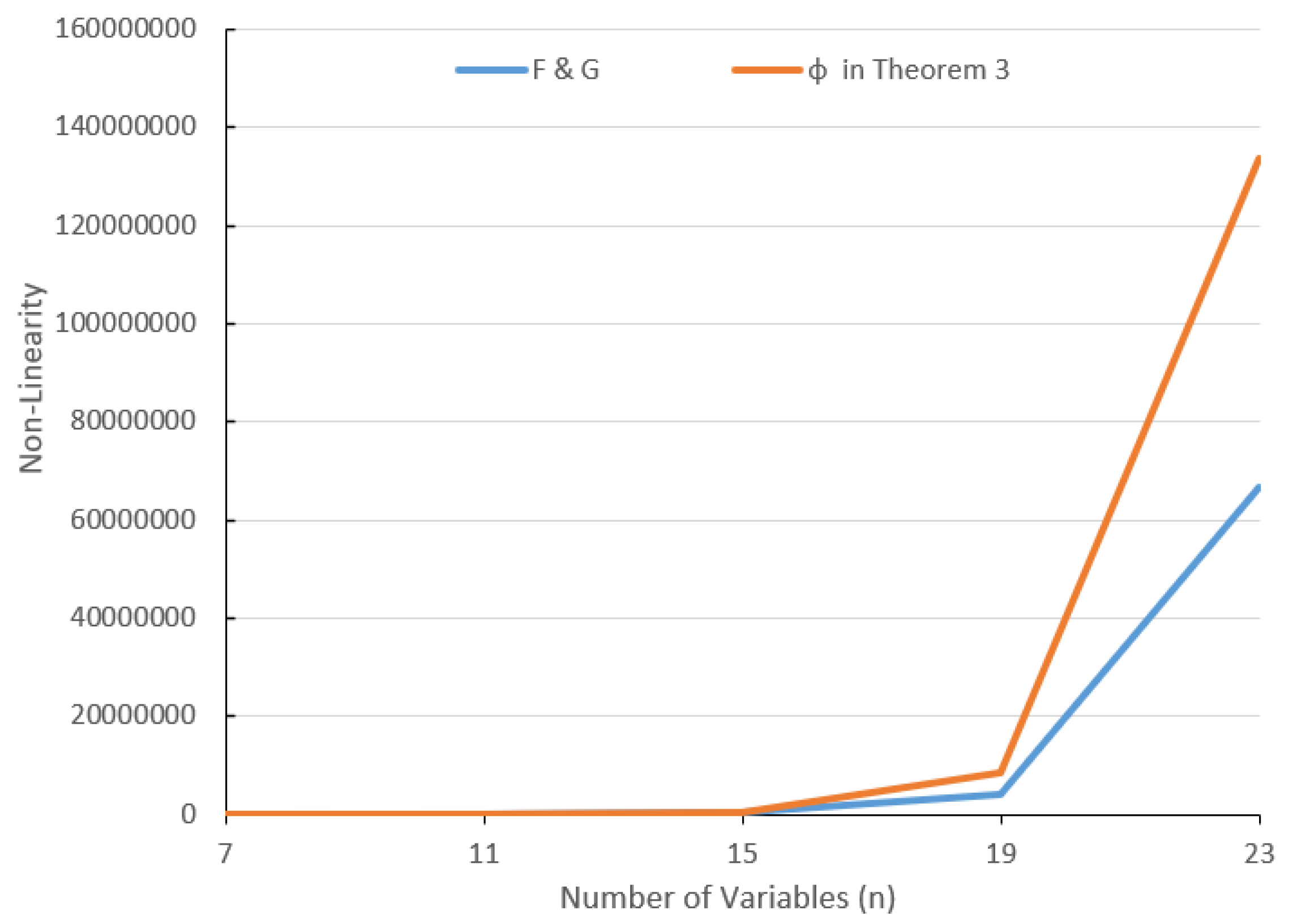
n	7	11	15	19	23
F and G in [15]	64	15,872	258,048	4,161,536	66,846,720
Functions in Theorem 3, [16]	64	15,872	258,048	4,161,536	66,846,720
$\mathrm{\Phi }$ in Theorem 3	96	16,128	260,096	4,177,920	66,977,792

. □

4. Lower Bounds for Fourth Order Nonlinearities of Two Classes of Monomial Functions Having Degree 5

This section provides lower bounds for 4th order nonlinearities of two classes of monomial functions having degree 5.

Theorem 4.

Let $f_{\lambda }\left(x\right)=T{r}_1^n\left(\lambda x^{2^i+2^j+2^k+2^{\ell }+1}\right),$ for all $x\in {\mathbb{F}}_{2^n},$ where $\lambda \in {\mathbb{F}}_{2^n}^{*},$ and $i,j,k$ and ℓ are integer with $i>j>k>\ell \ge 1$ and $n>2i.$ Then,

$$n{l}_4\left(f_{\lambda }\right)\ge \left\{\begin{array}{ccc}{2}^{n-4}-2^{\frac{n+2i-8}{2}}\hfill & for\hfill & n\equiv 0mod2\hfill \\ 2^{n-4}-2^{\frac{n+2i-9}{2}}\hfill & for\hfill & n\equiv 1mod2.\hfill \end{array}\right.$$

In particular, if $\gcd (n,j-k)=1$ and $\gcd (n,k-\ell )=1,$ then

$$n{l}_4\left(f_{\lambda }\right)\ge \left\{\begin{array}{ccc}{2}^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2){\left(2^{\frac{3n+2i}{2}}-3(2^n-2^{\frac{n+2i}{2}})\right)}^{1/2}}}\hfill & for\hfill & n\equiv 0mod2\hfill \\ 2^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2){\left(2^{\frac{3n+2i-1}{2}}-3(2^n-2^{\frac{n+2i-1}{2}})\right)}^{1/2}}}\hfill & for\hfill & n\equiv 1mod2.\hfill \end{array}\right.$$

Proof. 

The first order derivative $D_a{f}_{\lambda }$ of $f_{\lambda }$ at a in ${\mathbb{F}}_{2^n}^{*}$ is given as

$$\begin{array}{ccc}{D}_a{f}_{\lambda }\left(x\right)\hfill & =\hfill & f_{\lambda }(x+a)+f_{\lambda }\left(x\right)=T{r}_1^n\left(\lambda {(x+a)}^{2^i+2^j+2^k+2^{\ell }+1}\right)+T{r}_1^n\left(\lambda x^{2^i+2^j+2^k+2^{\ell }+1}\right)\hfill \\ & =\hfill & T{r}_1^n\left(\lambda \right(a{x}^{2^i+2^j+2^k+2^{\ell }}+a^{2^i}{x}^{2^j+2^k+2^{\ell }+1}+a^{2^j}{x}^{2^i+2^k+2^{\ell }+1}+a^{2^k}{x}^{2^i+2^j+2^{\ell }+1}\hfill \\ & & +a^{2^{\ell }}{x}^{2^i+2^j+2^k+1}\left)\right)+c\left(x\right),\hfill \end{array}$$

where $c\left(x\right)$ is cubic function. Now, the second order derivative $D_b\left(D_a{f}_{\lambda }\right)$ of $f_{\lambda }$ at b in ${\mathbb{F}}_{2^n}^{*}(b\ne a)$ is

$$\begin{array}{ccc}{D}_b\left(D_a{f}_{\lambda }\left(x\right)\right)\hfill & =\hfill & f_{\lambda }(x+a+b)+f_{\lambda }(x+b)+f_{\lambda }(x+a)+f_{\lambda }\left(x\right)\hfill \\ & =\hfill & T{r}_1^n\left[\lambda \right((a{b}^{2^{\ell }}+b{a}^{2^{\ell }})x^{2^i+2^j+2^k}+(a{b}^{2^i}+b{a}^{2^i})x^{2^j+2^k+2^{\ell }}\hfill \\ & & +(a{b}^{2^j}+b{a}^{2^j})x^{2^j+2^k+2^{\ell }}+(a{b}^{2^k}+b{a}^{2^k})x^{2^i+2^j+2^{\ell }}\hfill \\ & & +(a^{2^k}{b}^{2^{\ell }}+a^{2^{\ell }}{b}^{2^k})x^{2^i+2^j+1}+(a^{2^j}{b}^{2^{\ell }}+a^{2^{\ell }}{b}^{2^j})x^{2^i+2^k+1}\hfill \\ & & +(a^{2^j}{b}^{2^k}+a^{2^k}{b}^{2^j})x^{2^i+2^{\ell }+1}+(a^{2^i}{b}^{2^{\ell }}+a^{2^{\ell }}{b}^{2^i})x^{2^j+2^k+1}\hfill \\ & & +(a^{2^i}{b}^{2^k}+a^{2^k}{b}^{2^i})x^{2^j+2^{\ell }+1}+(a^{2^i}{b}^{2^j}+a^{2^j}{b}^{2^i})x^{2^k+2^{\ell }+1}\left)\right]+Q\left(x\right)\hfill \end{array}$$

where $Q\left(x\right)$ is a quadratic function.

The third order derivative $D_c\left(D_b{D}_a{f}_{\lambda }\right)$ of $f_{\lambda }$ at $c\in {\mathbb{F}}_{2^n}^{*}(a\ne c,b\ne c)$ is given as

$$\begin{array}{ccc}{D}_c\left(D_b{D}_a{f}_{\lambda }\left(x\right)\right)\hfill & =\hfill & f_{\lambda }(x+a+b+c)+f_{\lambda }(x+a+b)+f_{\lambda }(x+a+c)+f_{\lambda }(x+a)\hfill \\ & & +f_{\lambda }(x+b+c)+f_{\lambda }(x+b)+f_{\lambda }(x+c)+f_{\lambda }\left(x\right)\hfill \\ & =\hfill & h_{\lambda }\left(x\right)+l\left(x\right),\hfill \end{array}$$

where $l\left(x\right)$ is affine.

Since $D_c\left(D_b{D}_a{f}_{\lambda }\right)$ is quadratic, therefore WHS of $D_c\left(D_b{D}_a{f}_{\lambda }\right)$ is equivalent to the WHS of $h_{\lambda }\left(x\right),$ where

$$\begin{array}{ccc}{h}_{\lambda }\left(x\right)\hfill & =\hfill & T{r}_1^n\left[\lambda \right((a{b}^{2^{\ell }}{c}^{2^k}+b{a}^{2^{\ell }}{c}^{2^k}+a{b}^{2^k}{c}^{2^{\ell }}+b{a}^{2^k}{c}^{2^{\ell }}+a^{2^k}{b}^{2^{\ell }}c+a^{2^{\ell }}{b}^{2^k}c)x^{2^i+2^j}\hfill \\ & & +(a{b}^{2^{\ell }}{c}^{2^j}+b{a}^{2^{\ell }}{c}^{2^j}+a{b}^{2^j}{c}^{2^{\ell }}+b{a}^{2^j}{c}^{2^{\ell }}+a^{2^j}{b}^{2^{\ell }}c+a^{2^{\ell }}{b}^{2^j}c)x^{2^i+2^k}\hfill \\ & & +(a{b}^{2^j}{c}^{2^k}+a^{2^j}b{c}^{2^k}+a{b}^{2^k}{c}^{2^j}+a^{2^k}b{c}^{2^j}+a^{2^j}{b}^{2^k}c+a^{2^k}{b}^{2^j}c)x^{2^i+2^{\ell }}\hfill \\ & & +(a{b}^{2^{\ell }}{c}^{2^i}+a^{2^{\ell }}b{c}^{2^i}+a{b}^{2^i}{c}^{2^{\ell }}+a^{2^i}b{c}^{2^{\ell }}+a^{2^i}{b}^{2^{\ell }}c+a^{2^{\ell }}{b}^{2^i}c)x^{2^j+2^k}\hfill \\ & & +(a{b}^{2^k}{c}^{2^i}+a^{2^k}b{c}^{2^i}+a{b}^{2^i}{c}^{2^k}+a^{2^i}b{c}^{2^k}+a^{2^i}{b}^{2^k}c+a^{2^k}{b}^{2^i}c)x^{2^j+2^{\ell }}\hfill \\ & & +(a{b}^{2^i}{c}^{2^j}+a^{2^i}b{c}^{2^j}+a{b}^{2^j}{c}^{2^i}+a^{2^j}b{c}^{2^i}+a^{2^i}{b}^{2^j}c+a^{2^j}{b}^{2^i}c)x^{2^k+2^{\ell }}\hfill \\ & & +(a^{2^k}{b}^{2^{\ell }}{c}^{2^j}+a^{2^{\ell }}{b}^{2^k}{c}^{2^j}+a^{2^j}{b}^{2^{\ell }}{c}^{2^k}+a^{2^{\ell }}{b}^{2^j}{c}^{2^k}+a^{2^j}{b}^{2^k}{c}^{2^{\ell }}+a^{2^k}{b}^{2^j}{c}^{2^{\ell }})x^{2^i+1}\hfill \\ & & +(a^{2^k}{b}^{2^{\ell }}{c}^{2^i}+a^{2^{\ell }}{b}^{2^k}{c}^{2^i}+a^{2^i}{b}^{2^{\ell }}{c}^{2^k}+a^{2^{\ell }}{b}^{2^i}{c}^{2^k}+a^{2^i}{b}^{2^k}{c}^{2^{\ell }}+a^{2^k}{b}^{2^i}{c}^{2^{\ell }})x^{2^j+1}\hfill \\ & & +(a^{2^j}{b}^{2^{\ell }}{c}^{2^i}+a^{2^{\ell }}{b}^{2^j}{c}^{2^i}+a^{2^i}{b}^{2^{\ell }}{c}^{2^j}+a^{2^{\ell }}{b}^{2^i}{c}^{2^j}+a^{2^i}{b}^{2^j}{c}^{2^{\ell }}+a^{2^j}{b}^{2^i}{c}^{2^{\ell }})x^{2^k+1}\hfill \\ & & +(a^{2^j}{b}^{2^k}{c}^{2^i}+a^{2^k}{b}^{2^j}{c}^{2^i}+a^{2^i}{b}^{2^k}{c}^{2^j}+a^{2^k}{b}^{2^i}{c}^{2^j}+a^{2^i}{b}^{2^j}{c}^{2^k}+a^{2^j}{b}^{2^i}{c}^{2^k})x^{2^{\ell }+1}\left)\right]\hfill \end{array}$$

Let ${\mathcal{E}}_{h_{\lambda }}=\{x\in {\mathbb{F}}_{2^n}:B(x,y)=0\mathrm{for}\mathrm{every}y\in {\mathbb{F}}_{2^n}\},$ where $B(x,y)$ for $h_{\lambda }$ is

$$\begin{array}{ccc}B(x,y)\hfill & =\hfill & h_{\lambda }\left(0\right)+h_{\lambda }\left(y\right)+h_{\lambda }\left(x\right)+h_{\lambda }(x+y)\hfill \\ & =\hfill & T{r}_1^n\left[\lambda \right(y^{2^i}\{R_1{x}^{2^j}+R_2{x}^{2^k}+R_3{x}^{2^{\ell }}+R_{7}x\}+y^{2^j}\{R_1{x}^{2^i}+R_4{x}^{2^k}\hfill \\ & & +R_5{x}^{2^{\ell }}+R_{8}x\}+y^k\{R_2{x}^{2^i}+R_4{x}^{2^j}+R_6{x}^{2^{\ell }}+R_{9}x\}+y^{2^{\ell }}\{R_3{x}^{2^i}\hfill \\ & & +R_5{x}^{2^j}+R_6{x}^{2^k}+R_{10}x\}+y\{R_7{x}^{2^i}+R_8{x}^{2^j}+R_9{x}^{2^k}+R_{10}{x}^{2^{\ell }}\}\left)\right]\hfill \\ & =\hfill & T{r}_1^n\left(yP\left(x\right)\right),\hfill \end{array}$$

where the coefficients of different powers of x in the above expression are denoted by $R_1,R_2,\dots ,R_{10}$ and given as follows:

$$\begin{array}{ccc}{R}_1\hfill & =\hfill & a{b}^{2^{\ell }}{c}^{2^k}+b{a}^{2^{\ell }}{c}^{2^k}+a{b}^{2^k}{c}^{2^{\ell }}+b{a}^{2^k}{c}^{2^{\ell }}+a^{2^k}{b}^{2^{\ell }}c+a^{2^{\ell }}{b}^{2^k}c\hfill \\ R_2\hfill & =\hfill & a{b}^{2^{\ell }}{c}^{2^j}+b{a}^{2^{\ell }}{c}^{2^j}+a{b}^{2^j}{c}^{2^{\ell }}+b{a}^{2^j}{c}^{2^{\ell }}+a^{2^j}{b}^{2^{\ell }}c+a^{2^{\ell }}{b}^{2^j}c\hfill \\ R_3\hfill & =\hfill & a{b}^{2^j}{c}^{2^k}+a^{2^j}b{c}^{2^k}+a{b}^{2^k}{c}^{2^j}+a^{2^k}b{c}^{2^j}+a^{2^j}{b}^{2^k}c+a^{2^k}{b}^{2^j}c\hfill \\ R_4\hfill & =\hfill & a{b}^{2^{\ell }}{c}^{2^i}+a^{2^{\ell }}b{c}^{2^i}+a{b}^{2^i}{c}^{2^{\ell }}+a^{2^i}b{c}^{2^{\ell }}+a^{2^i}{b}^{2^{\ell }}c+a^{2^{\ell }}{b}^{2^i}c\hfill \\ R_5\hfill & =\hfill & a{b}^{2^k}{c}^{2^i}+a^{2^k}b{c}^{2^i}+a{b}^{2^i}{c}^{2^k}+a^{2^i}b{c}^{2^k}+a^{2^i}{b}^{2^k}c+a^{2^k}{b}^{2^i}c\hfill \\ R_6\hfill & =\hfill & a{b}^{2^i}{c}^{2^j}+a^{2^i}b{c}^{2^j}+a{b}^{2^j}{c}^{2^i}+a^{2^j}b{c}^{2^i}+a^{2^i}{b}^{2^j}c+a^{2^j}{b}^{2^i}c\hfill \\ R_7\hfill & =\hfill & a^{2^k}{b}^{2^{\ell }}{c}^{2^j}+a^{2^{\ell }}{b}^{2^k}{c}^{2^j}+a^{2^j}{b}^{2^{\ell }}{c}^{2^k}+a^{2^{\ell }}{b}^{2^j}{c}^{2^k}+a^{2^j}{b}^{2^k}{c}^{2^{\ell }}+a^{2^k}{b}^{2^j}{c}^{2^{\ell }}\hfill \\ R_8\hfill & =\hfill & a^{2^k}{b}^{2^{\ell }}{c}^{2^i}+a^{2^{\ell }}{b}^{2^k}{c}^{2^i}+a^{2^i}{b}^{2^{\ell }}{c}^{2^k}+a^{2^{\ell }}{b}^{2^i}{c}^{2^k}+a^{2^i}{b}^{2^k}{c}^{2^{\ell }}+a^{2^k}{b}^{2^i}{c}^{2^{\ell }}\hfill \\ R_9\hfill & =\hfill & a^{2^j}{b}^{2^{\ell }}{c}^{2^i}+a^{2^{\ell }}{b}^{2^j}{c}^{2^i}+a^{2^i}{b}^{2^{\ell }}{c}^{2^j}+a^{2^{\ell }}{b}^{2^i}{c}^{2^j}+a^{2^i}{b}^{2^j}{c}^{2^{\ell }}+a^{2^j}{b}^{2^i}{c}^{2^{\ell }}\hfill \\ R_{10}\hfill & =\hfill & a^{2^j}{b}^{2^k}{c}^{2^i}+a^{2^k}{b}^{2^j}{c}^{2^i}+a^{2^i}{b}^{2^k}{c}^{2^j}+a^{2^k}{b}^{2^i}{c}^{2^j}+a^{2^i}{b}^{2^j}{c}^{2^k}+a^{2^j}{b}^{2^i}{c}^{2^k},\hfill \end{array}$$

and the polynomial $P\left(x\right)$ is given as

$$\begin{array}{ccc}P\left(x\right)\hfill & =\hfill & {(\lambda R_1{x}^{2^j}+\lambda R_2{x}^{2^k}+\lambda R_3{x}^{2^{\ell }}+\lambda R_{7}x)}^{2^{n-i}}\hfill \\ & & +{(\lambda R_1{x}^{2^i}+\lambda R_4{x}^{2^k}+\lambda R_5{x}^{2^{\ell }}+\lambda R_{8}x)}^{2^{n-j}}\hfill \\ & & +{(\lambda R_2{x}^{2^i}+\lambda R_4{x}^{2^j}+\lambda R_6{x}^{2^{\ell }}+\lambda R_{9}x)}^{2^{n-k}}\hfill \\ & & +{(\lambda R_3{x}^{2^i}+\lambda R_5{x}^{2^j}+\lambda R_6{x}^{2^k}+\lambda R_{10}x)}^{2^{n-\ell }}\hfill \\ & & +(\lambda R_7{x}^{2^i}+\lambda R_8{x}^{2^j}+\lambda R_9{x}^{2^k}+R_{10}{x}^{2^{\ell }}).\hfill \end{array}$$

Let $L_{\lambda }\left(x\right)={\left(P\left(x\right)\right)}^{2^i}.$ Then, the polynomial $L_{\lambda }\left(x\right)$ becomes

$$\begin{array}{ccc}\hfill L_{\lambda }\left(x\right)& =& \lambda (R_1{x}^{2^j}+R_2{x}^{2^k}+R_3{x}^{2^{\ell }}+R_{7}x)+{\lambda }^{2^{i-j}}[R_1^{2^{i-j}}{x}^{2^{2i-j}}+R_4^{2^{i-j}}{x}^{2^{i+k-j}}+R_5^{2^{i-j}}{x}^{2^{i+\ell -j}}\hfill \\ & & +R_8^{2^{i-j}}{x}^{2^{i-j}}]+{\lambda }^{2^{i-k}}[R_2^{2^{i-k}}{x}^{2^{2i-k}}+R_4^{2^{i-k}}{x}^{2^{i+j-k}}+R_6^{2^{i-k}}{x}^{2^{i+\ell -k}}+R_9^{2^{i-k}}{x}^{2^{i-k}}]\hfill \\ & & +{\lambda }^{2^{i-\ell }}[R_3^{2^{i-\ell }}{x}^{2^{2i-\ell }}+R_5^{2^{i-\ell }}{x}^{2^{i+j-\ell }}+R_6^{2^{i-\ell }}{x}^{2^{i+k-\ell }}+R_{10}^{2^{i-\ell }}{x}^{2^{i-\ell }}]\hfill \\ & & +{\lambda }^{2^i}[R_7^{2^i}{x}^{2^{2i}}+R_8^{2^i}{x}^{2^{i+j}}+R_9^{2^i}{x}^{2^{i+k}}+R_{10}^{2^i}{x}^{2^{i+\ell }}]\hfill \end{array}$$

(7)

From $L_{\lambda }\left(x\right),$ in (7), the coefficient of x is zero if and only if $R_7=0,$ i.e., if and only if $a^{2^k}{b}^{2^{\ell }}{c}^{2^j}+a^{2^{\ell }}{b}^{2^k}{c}^{2^j}+a^{2^j}{b}^{2^{\ell }}{c}^{2^k}+a^{2^{\ell }}{b}^{2^j}{c}^{2^k}+a^{2^j}{b}^{2^k}{c}^{2^{\ell }}+a^{2^k}{b}^{2^j}{c}^{2^{\ell }}=0.$ If $a=1,$ then $b^{2^{\ell }}{c}^{2^j}+b^{2^k}{c}^{2^j}+b^{2^{\ell }}{c}^{2^k}+b^{2^j}{c}^{2^k}+b^{2^k}{c}^{2^{\ell }}+b^{2^j}{c}^{2^{\ell }}=0$ implies that $b\in {\mathbb{F}}_{2^{k-\ell }}$ and $c\in {\mathbb{F}}_{2^{k-\ell }}$. Thus, if $a=1,$ $b\in {\mathbb{F}}_{2^{k-\ell }}$ and $c\notin {\mathbb{F}}_{2^{k-\ell }},$ the degree of polynomial $L_{\lambda }\left(x\right)$ in x is at most $2^{2i}$. Hence, $k(1,b,c)\le 2i$ for even n and $k(1,b,c)\le 2i-1$ otherwise.

The Walsh–Hadamard transform of $D_c\left(D_b{D}_a{f}_{\lambda }\right)$ at $\mu \in {\mathbb{F}}_{2^n}$ is

$$W_{D_c\left(D_b{D}_a{f}_{\lambda }\right)}\left(\mu \right)\le \left\{\begin{array}{ccc}{2}^{\frac{n+2i}{2}}\hfill & \mathrm{for}\hfill & n\equiv 0mod2\hfill \\ 2^{\frac{n+2i-1}{2}}\hfill & \mathrm{for}\hfill & n\equiv 1mod2.\hfill \end{array}\right.$$

Therefore, by using the value of $W_{D_c\left(D_b{D}_a{f}_{\lambda }\right)}\left(\mu \right)$, we obtain the nonlinearity of the function $D_c\left(D_b{D}_a{f}_{\lambda }\right)$ as

$$\begin{array}{c}\hfill \begin{array}{ccc}nl\left(D_c\left(D_b{D}_a{f}_{\lambda }\right)\right)\hfill & =\hfill & 2^{n-1}-\frac{1}{2}\underset{\mu \in {\mathbb{F}}_2^n}{max}\left|W_{D_c\left(D_b{D}_a{f}_{\lambda }\right)}\left(\mu \right)\right|\hfill \\ & \ge \hfill & \left\{\begin{array}{ccc}\frac{1}{2}\left(2^n-·2^{\frac{n+2i}{2}}\right)\hfill & \mathrm{for}\hfill & n\equiv 0mod2\hfill \\ \frac{1}{2}\left(2^n-\frac{1}{2}·2^{\frac{n+2i-1}{2}}\right)\hfill & \mathrm{for}\hfill & n\equiv 1mod2.\hfill \end{array}\right.\hfill \end{array}\end{array}$$

(8)

From (8) and Proposition 1, we obtain 4th order nonlinearity of $f_{\lambda }$ as

$$\begin{array}{ccc}n{l}_4\left(f_{\lambda }\right)\hfill & \ge \hfill & \frac{1}{2^3}\underset{a,b,c\in {\mathbb{F}}_{2^n}}{max}nl\left(D_c\left(D_b{D}_a{f}_{\lambda }\right)\right)\hfill \\ \\ & \ge \hfill & \left\{\begin{array}{ccc}{2}^{n-4}-2^{\frac{n+2i-8}{2}}\hfill & \mathrm{for}\hfill & n\equiv 0mod2\hfill \\ 2^{n-4}-2^{\frac{n+2i-9}{2}}\hfill & \mathrm{for}\hfill & n\equiv 1mod2.\hfill \end{array}\right.\hfill \end{array}$$

In particular, if $\gcd (j-k,n)=1$ and $\gcd (k-\ell ,n)=1,$ then, by using Proposition 2, the improved 4th order nonlinearity of $f_{\lambda }$ is obtained as

• when $n\equiv 0mod2$

  $$\begin{array}{ccc}n{l}_4\left(f_{\lambda }\right)\hfill & \ge \hfill & 2^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2)\sqrt{2^{2n}-2(2^n-3)(2^{n-1}-2^{\frac{n+2i-2}{2}})}}}\hfill \\ & =\hfill & 2^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2){\left(2^{\frac{3n+2i}{2}}-3(2^n-2^{\frac{n+2i}{2}})\right)}^{1/2}}}.\hfill \end{array}$$
• when $n\equiv 1mod2$

  $$\begin{array}{ccc}n{l}_4\left(f_{\lambda }\right)\hfill & \ge \hfill & 2^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2)\sqrt{2^{2n}-2(2^n-3)(2^{n-1}-2^{\frac{n+2i-3}{2}})}}}\hfill \\ & =\hfill & 2^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2){\left(2^{\frac{3n+2i-1}{2}}-3(2^n-2^{\frac{n+2i-1}{2}})\right)}^{1/2}}}.\hfill \end{array}$$

and hence the result. □

Theorem 5.

Let $g_{\lambda }\left(x\right)=T{r}_1^n\left(\lambda x^{2^{4\ell }+2^{3\ell }+2^{2\ell }+2^{\ell }+1}\right)$ for all $x\in {\mathbb{F}}_{2^n},$ where $\lambda \in {\mathbb{F}}_{2^n}^{*}$ and ℓ is a positive integer with $\gcd (n,\ell )=1$ and $n>8.$ Then,

$$n{l}_4\left(g_{\lambda }\right)\ge \left\{\begin{array}{ccc}{2}^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2){\left(2^{\frac{3n+8}{2}}-3(2^n-2^{\frac{n+8}{2}})\right)}^{1/2}}}\hfill & if\hfill & n\equiv 0mod2\hfill \\ 2^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2){\left(2^{\frac{3n+7}{2}}-3(2^n-2^{\frac{n+7}{2}})\right)}^{1/2}}}\hfill & if\hfill & n\equiv 1mod2.\hfill \end{array}\right.$$

Proof. 

The proof is identical to Theorem 4 except the case $i=4\ell ,j=3\ell ,k=2\ell ,\ell =\ell$. Therefore, $L_{\lambda }\left(x\right)$ is obtained by replacing $i,j$ and k by $4\ell ,3\ell$ and $2\ell$, respectively, in (7).

$$\begin{array}{ccc}{L}_{\lambda }\left(x\right)\hfill & =\hfill & \lambda (R_1{x}^{2^{3\ell }}+R_2{x}^{2^{2\ell }}+R_3{x}^{2^{\ell }}+R_{7}x)+{\lambda }^{2^{\ell }}[R_1^{2^{\ell }}{x}^{2^{5\ell }}+R_4^{2^{\ell }}{x}^{2^{3\ell }}+R_5^{2^{\ell }}{x}^{2^{2\ell }}+R_8^{2^{\ell }}{x}^{2^{\ell }}]\hfill \\ & & +{\lambda }^{2^{2\ell }}[R_2^{2^{2\ell }}{x}^{2^{6\ell }}+R_4^{2^{2\ell }}{x}^{2^{5\ell }}+R_6^{2^{2\ell }}{x}^{2^{3\ell }}+R_9^{2^{2\ell }}{x}^{2^{2\ell }}]+{\lambda }^{2^{3\ell }}[R_3^{2^{3\ell }}{x}^{2^{7\ell }}+R_5^{2^{3\ell }}{x}^{2^{6\ell }}\hfill \\ & & +R_6^{2^{3\ell }}{x}^{2^{5\ell }}+R_{10}^{2^{3\ell }}{x}^{2^{3\ell }}]+{\lambda }^{2^{4\ell }}[R_7^{2^{4\ell }}{x}^{2^{8\ell }}+R_8^{2^{4\ell }}{x}^{2^{7\ell }}+R_9^{2^{4\ell }}{x}^{2^{6\ell }}+R_{10}^{2^{4\ell }}{x}^{2^{5\ell }}]\hfill \\ & =\hfill & x^{2^{6\ell }}[{\lambda }^{2^{2\ell }}{R}_2^{2^{2\ell }}+{\lambda }^{2^{3\ell }}{R}_3^{2^{3\ell }}+{\lambda }^{2^{4\ell }}{R}_9^{2^{4\ell }}]\hfill \\ & & +x^{2^{5\ell }}[{\lambda }^{2^{\ell }}{R}_1^{2^{\ell }}+{\lambda }^{2^{2\ell }}{R}_4^{2^{2\ell }}+{\lambda }^{2^{3\ell }}{R}_6^{2^{3\ell }}+{\lambda }^{2^{4\ell }}{R}_{10}^{2^{4\ell }}]\hfill \\ & & +x^{2^{3\ell }}[\lambda R_1+{\lambda }^{2^{\ell }}{R}_1^{2^{\ell }}+{\lambda }^{2^{2\ell }}{R}_6^{2^{2\ell }}+{\lambda }^{2^{3\ell }}{R}_{10}^{2^{3\ell }}]+x^{2^{2\ell }}[\lambda R_2+{\lambda }^{2^{\ell }}{R}_5^{2^{\ell }}+{\lambda }^{2^{2\ell }}{R}_9^{2^{2\ell }}]\hfill \\ & & +x^{2^{\ell }}[\lambda R_3+{\lambda }^{2^{2\ell }}{R}_8^{2^{\ell }}]+x\left[\lambda R_7\right]+x^{2^{8\ell }}\left[{\lambda }^{2^{4\ell }}{R}_7^{2^{4\ell }}\right]+x^{2^{7\ell }}[{\lambda }^{2^{3\ell }}{R}_3^{2^{3\ell }}+{\lambda }^{2^{4\ell }}{R}_8^{2^{4\ell }}]\hfill \end{array}$$

Now, the coefficient of x is zero if and only if $R_7=0$, i.e., if and only if $a^{2^{2\ell }}{b}^{2^{3\ell }}{c}^{2^{3\ell }}+a^{2^{2\ell }}{b}^{2^{2\ell }}{c}^{2^{2\ell }}+a^{2^{3\ell }}{b}^{2^{\ell }}{c}^{2^{2\ell }}+a^{2^{\ell }}{b}^{2^{3\ell }}{c}^{2^{2\ell }}+a^{2^{3\ell }}{b}^{2^{2\ell }}{c}^{2^{2\ell }}+a^{2^{2\ell }}{b}^{2^{3\ell }}{c}^{2^{2\ell }}=0$. If $a=1,$ then $b^{2^{2\ell }}{c}^{2^{3\ell }}+b^{2^{2\ell }}{c}^{2^{\ell }}+b^{2^{\ell }}{c}^{2^{2\ell }}+b^{2^{3\ell }}{c}^{2^{2\ell }}+b^{2^{2\ell }}{c}^{2^{\ell }}+b^{2^{3\ell }}{c}^{2^{\ell }}=0.$ If $b^{2^{2\ell }}=b$, then $b\in {\mathbb{F}}_{2^{2\ell }}$. Therefore, $b^{2^{2\ell }}=b$ implies that $c^{2^{2\ell }}=0,$ i.e., $c\in {\mathbb{F}}_{2^{2\ell }}$. If $a=1,$$b\in {\mathbb{F}}_{2^{2\ell }}$ and $c\notin {\mathbb{F}}_{2^{2\ell }},$ then the degree of $L_{\lambda }\left(x\right)$ is atmost $2^8.$ This implies $k(1,b,c)\le 8$ for even n and $k(1,b,c)\le 7$ otherwise.

The Walsh–Hadamard transform of $D_c\left(D_b{D}_a{g}_{\lambda }\right)$ at $\mu \in {\mathbb{F}}_{2^n}$ is

$$W_{D_c\left(D_b{D}_a{g}_{\lambda }\right)}\left(\mu \right)\le \left\{\begin{array}{ccc}{2}^{\frac{n+8}{2}}\hfill & \mathrm{for}\hfill & n\equiv 0mod2\hfill \\ 2^{\frac{n+7}{2}}\hfill & \mathrm{for}\hfill & n\equiv 1mod2.\hfill \end{array}\right.$$

Therefore, the nonlinearity of $D_c\left(D_b{D}_a{g}_{\lambda }\right)$ is

$$\begin{array}{c}\hfill nl\left(D_c\left(D_b{D}_a{g}_{\lambda }\right)\right)=\left\{\begin{array}{ccc}{2}^{n-1}-2^{\frac{n+6}{2}}\hfill & \mathrm{for}\hfill & n\equiv 0mod2\hfill \\ 2^{n-1}-2^{\frac{n+5}{2}}\hfill & \mathrm{for}\hfill & n\equiv 1mod2.\hfill \end{array}\right.\end{array}$$

(9)

From (9) and Proposition 1, the 4th order nonlinearity of function $g_{\lambda }$ is obtained as

$$\begin{array}{c}\hfill \begin{array}{ccc}n{l}_4\left(g_{\lambda }\right)\hfill & \ge \hfill & \frac{1}{2^3}\underset{a,b,c\in {\mathbb{F}}_{2^n}}{max}nl\left(D_c\left(D_b{D}_a{g}_{\lambda }\right)\right)\hfill \\ & \ge \hfill & \left\{\begin{array}{ccc}{2}^{n-4}-2^{\frac{n}{2}}\hfill & \mathrm{for}\hfill & n\equiv 0mod2\hfill \\ 2^{n-4}-2^{\frac{n-1}{2}}\hfill & \mathrm{for}\hfill & n\equiv 1mod2.\hfill \end{array}\right.\hfill \end{array}\end{array}$$

(10)

Now, by using Proposition 2 and (10), the improved 4th order nonlinearity of $g_{\lambda }$ is given by

• when $n\equiv 0mod2$

  $$\begin{array}{ccc}n{l}_4\left(g_{\lambda }\right)\hfill & \ge \hfill & 2^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2)\sqrt{2^{2n}-2(2^n-3)(2^{n-1}-2^{\frac{n+6}{2}})}}}\hfill \\ & \ge \hfill & 2^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2){\left(2^{\frac{3n+8}{2}}-3(2^n-2^{\frac{n+8}{2}})\right)}^{1/2}}}.\hfill \end{array}$$
• when $n\equiv 1mod2$

  $$\begin{array}{ccc}n{l}_4\left(g_{\lambda }\right)\hfill & \ge \hfill & 2^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2)\sqrt{2^{2n}-2(2^n-3)(2^{n-1}-2^{\frac{n+5}{2}})}}}\hfill \\ & \ge \hfill & 2^{n-1}-\sqrt{\frac{1}{4}(2^n-1)\sqrt{(2^n-2){\left(2^{\frac{3n+7}{2}}-3(2^n-2^{\frac{n+7}{2}})\right)}^{1/2}}}.\hfill \end{array}$$

and hence the result. □

5. Comparison

This section presents a numerical comparison of the results obtained in this article with the existing results. The nonlinearity of the function $\mathrm{\Phi }$ constructed in Theorem 3 is $2^{n+3}-2^{r+3}$, which is greater than the nonlinearity $2^{n+3}-2^{r+4}$ of the functions F and G given in [15], Theorem 3. Furthermore, the nonlinearity of the function $\mathrm{\Psi }$ constructed in Theorem 3, and the nonlinearity of the functions $\mathrm{\Phi }$ and $\mathrm{\Psi }$ constructed in Theorem 2 is the same as the nonlinearity of the functions given in [16], Theorem 3. The results are demonstrated numerically in Table 1 and graphically in Figure 1.

Table 2. Bounds due to Theorem 4 and [17] for $n\ge 9$, and $n\ge 2i$ with i an integer.

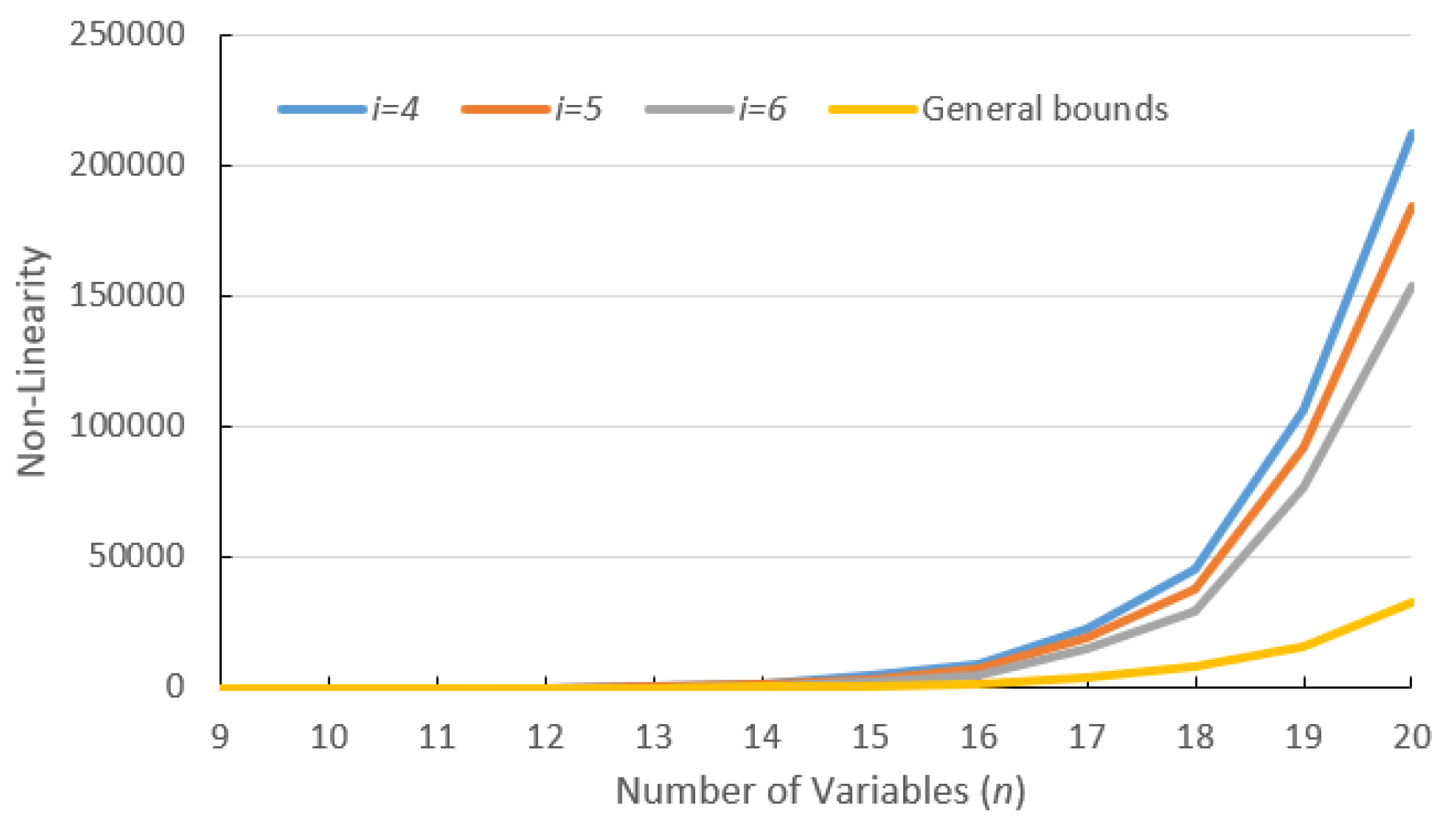
n		9	10	11	12	13	14	15	16	17	18	19	20
Bounds of Theorem 4	$i=4$	22	43	163	326	937	1874	4797	9596	23,038	46,079	106,266	212,538
	$i=5$	-	-	85	170	651	1303	3750	7499	19,193	38,388	92,161	184,326
	$i=6$	-	-	-	-	340	680	2606	5213	15,000	30,001	76,778	153,559
General bounds in [17]		16	32	64	128	256	512	1024	2048	4096	8192	16,384	32,768

and Figure 2 present a comparison of lower bounds obtained in Theorem 4 for $i=4,5,6$ with the general bounds on 4th order nonlinearity for Boolean functions of degree 5, i.e., $n{l}_4\left(f\right)\ge 2^{n-5}$ [17], since the formula for computation of bounds on 4th order nonlinearity is developed in terms of the integer i. In view of the condition $i>j>k>l\ge 1$ on the integers $i,j,k,l$, the smallest value that i can assume is 4. From Table 2 and Figure 2, it is clear that the bounds obtained in Theorem 4 for $i=4,5,6$ are efficiently large as compared to Carlet’s general bounds [17].

Furthermore,

Table 3. Comparison of bounds due to Theorem 5, [3,17] for $n\ge 9$.

n	9	10	11	12	13	14	15	16	17	18	19	20
Bounds of Theorem 5	22	43	163	326	937	1874	4797	9596	23,038	46,079	106,266	212,538
Bounds for inverse function [17]	-	-	-	-	-	-	-	-	2748	10,838	31,894	83,343
Carlet’s general bounds [17]	16	32	64	128	256	512	1024	2048	4096	8192	16,384	32,768
Iwata-Kurosawa’s bounds [3]	36	64	144	256	576	1024	2304	4096	9216	16,384	36,864	65,536

and Figure 3 provide a comparison of bounds obtained in Theorem 5 with the lower bounds for inverse function [17], general bounds [17], and the bounds due to Iwata-Kurosawa [3]. It is noted that the bounds in Theorem 5 are better than the bounds presented for above-mentioned classes of functions.

6. Conclusions

The nonlinearity and resiliency of cryptographic functions are crucial criteria with respect to protection of ciphers from affine approximation and correlation attacks. The article presents some constructions of disjoint spectra Boolean functions by concatenating functions on a lesser number of variables are provided. The nonlinearity and resiliency profiles of the constructed functions are analyzed. After analyzing the profiles of the constructed functions, it is observed that the nonlinearity of these functions is greater than (in the case of some functions) or the same as the nonlinearity obtained by Gao et al. [15] and Singh [16].

Furthermore, the higher order nonlinearity is instrumental in providing protection towards higher order approximation attacks. Therefore, identifying functions possessing higher order nonlinearity (in particular, 4th order nonlinearity) is a paramount research problem. It is evident from Table 2 that the bounds on 4th order nonlinearity obtained in Theorem 4 for $i=4,5,6$ are efficiently large as compared to Carlet’s general bounds [17]. Furthermore, Table 3 shows that the lower bounds obtained in Theorem 5 are better than the bounds obtained for inverse function [17], general bounds [17], and the bounds due to Iwata–Kurosawa [3].

On the basis of the properties satisfied by the functions presented in this article, it is expected that the results of this article will play an important role in analyzing security of cryptosystems with respect to linear cryptanalysis, affine approximation attacks, and higher order approximation attacks.

The good nonlinearity profile is predominant in ensuring the security of the cryptosystems. Along with the nonlinearity profile, it is considered equally important if the constructed functions owns properties of other cryptographic primitives such as balancedness, algebraic immunity, correlation immunity, algebraic degree, etc. In future work, our aim is to construct some more cryptographic functions with increased nonlinearity profiles that satisfy other cryptographic primitives.