A 3D Cuboid Image Encryption Algorithm Based on Controlled Alternate Quantum Walk of Message Coding
Abstract
1. Introduction
2. Preliminary Works
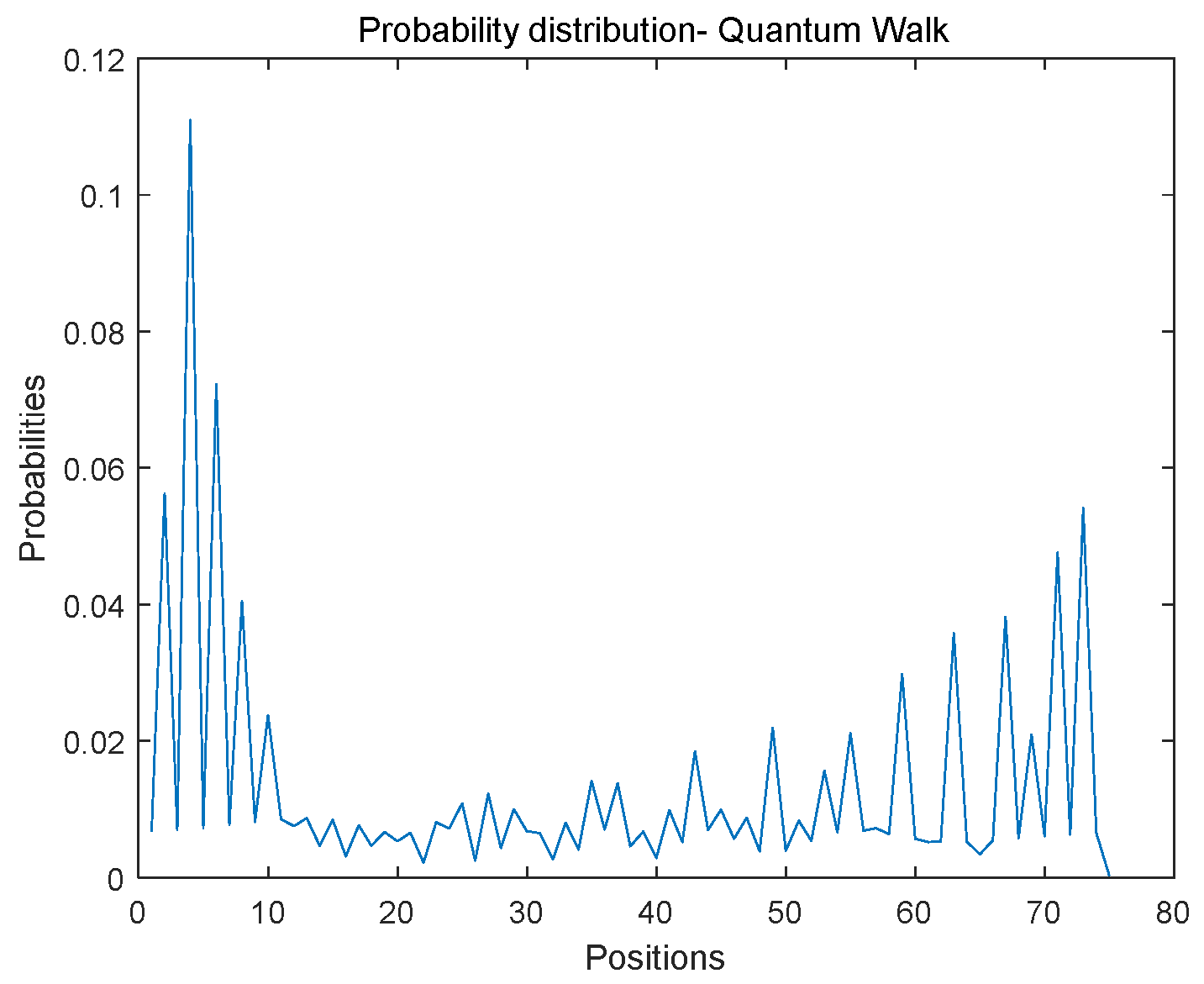
2.1. One-Dimensional Discrete Quantum Walks (1DQWs) on Circles
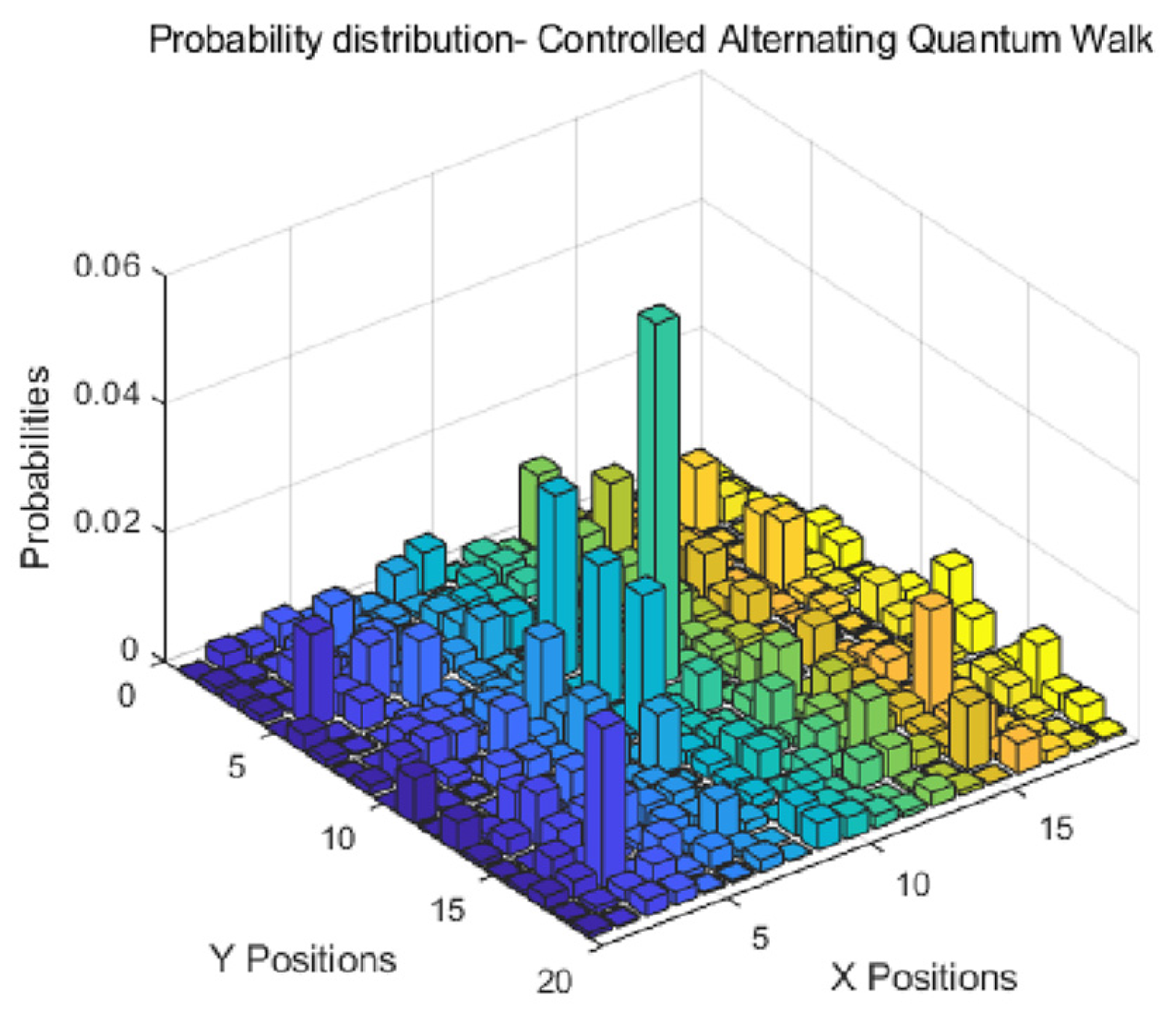
2.2. Controlled Alternate Quantum Walks (CAQWs) on Circles
3. Proposed Method
3.1. Generate Initial Key
3.1.1. Initial Parameters
3.1.2. Sum of Plaintext Image Pixel Values
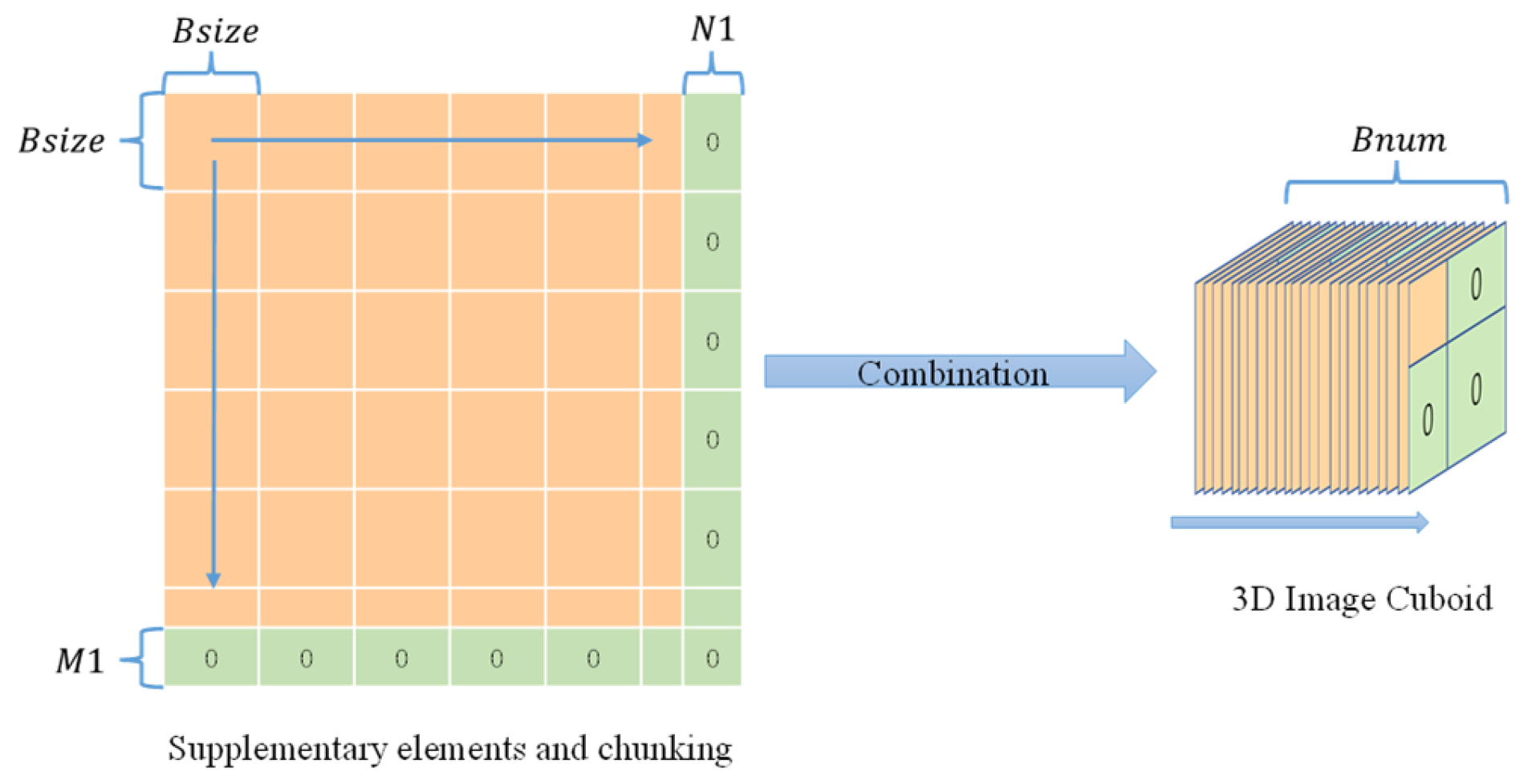
3.1.3. Image block size
3.1.4. Supplementary Parameters , and Number of Blocks
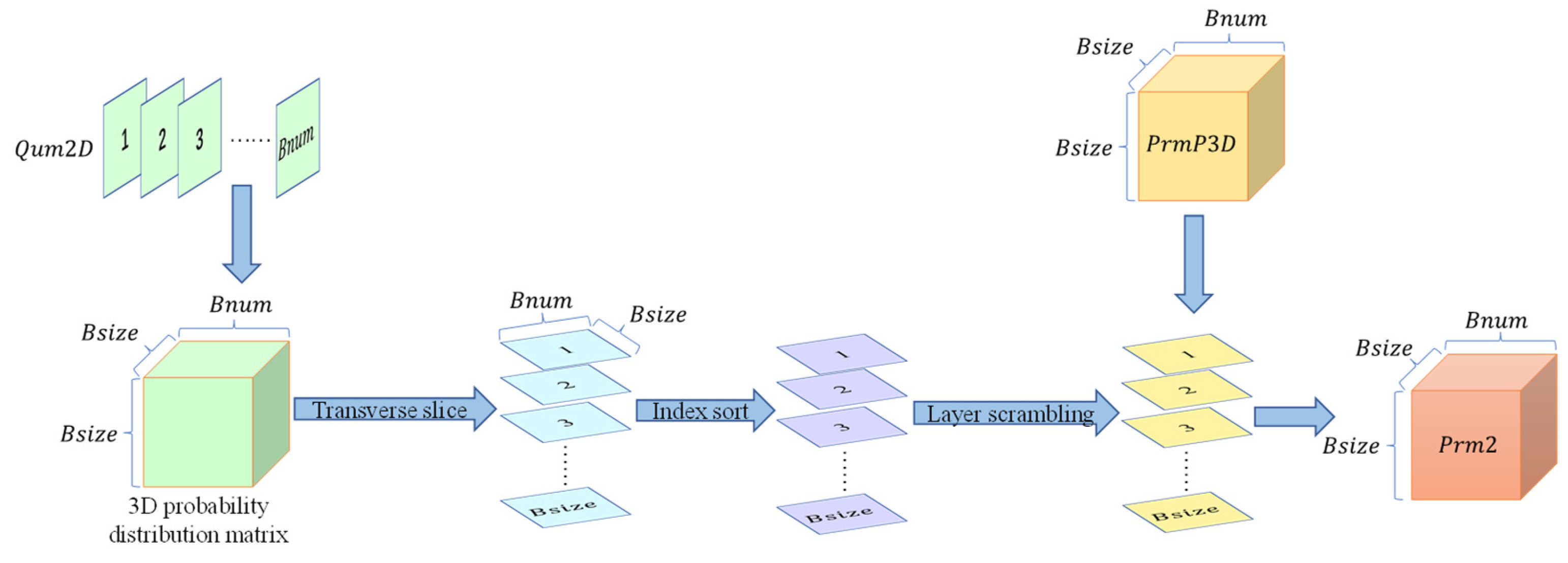
3.2. Generating 3D Probability Magnitude Matrix, 3D Probability Distribution Matrix, and 3D Quantum Hash Sequence by Using Quantum Walks
3.2.1. Generation of Initial Parameters for 1DQWs
- (1)
- Number of nodes on the circle
- (2)
- Coin parameter
- (3)
- The initial state of the coin
3.2.2. Generation of Initial Parameters of CAQWs
- (1)
- The number of nodes on the circle of CAQWs is equal to the block size .
- (2)
- Coin parameters
- (3)
- Initial state of the coin
3.2.3. Generating Probability Distribution Sequences Using 1DQWs
3.2.4. Message Encoding
3.2.5. Controlled Alternate Quantum Walks for Message Encoding
3.2.6. Three-Dimensional Probability Amplitude Matrix and Three-Dimensional Probability Distribution Matrix
3.2.7. Three-Dimensional Quantum Hash Sequence
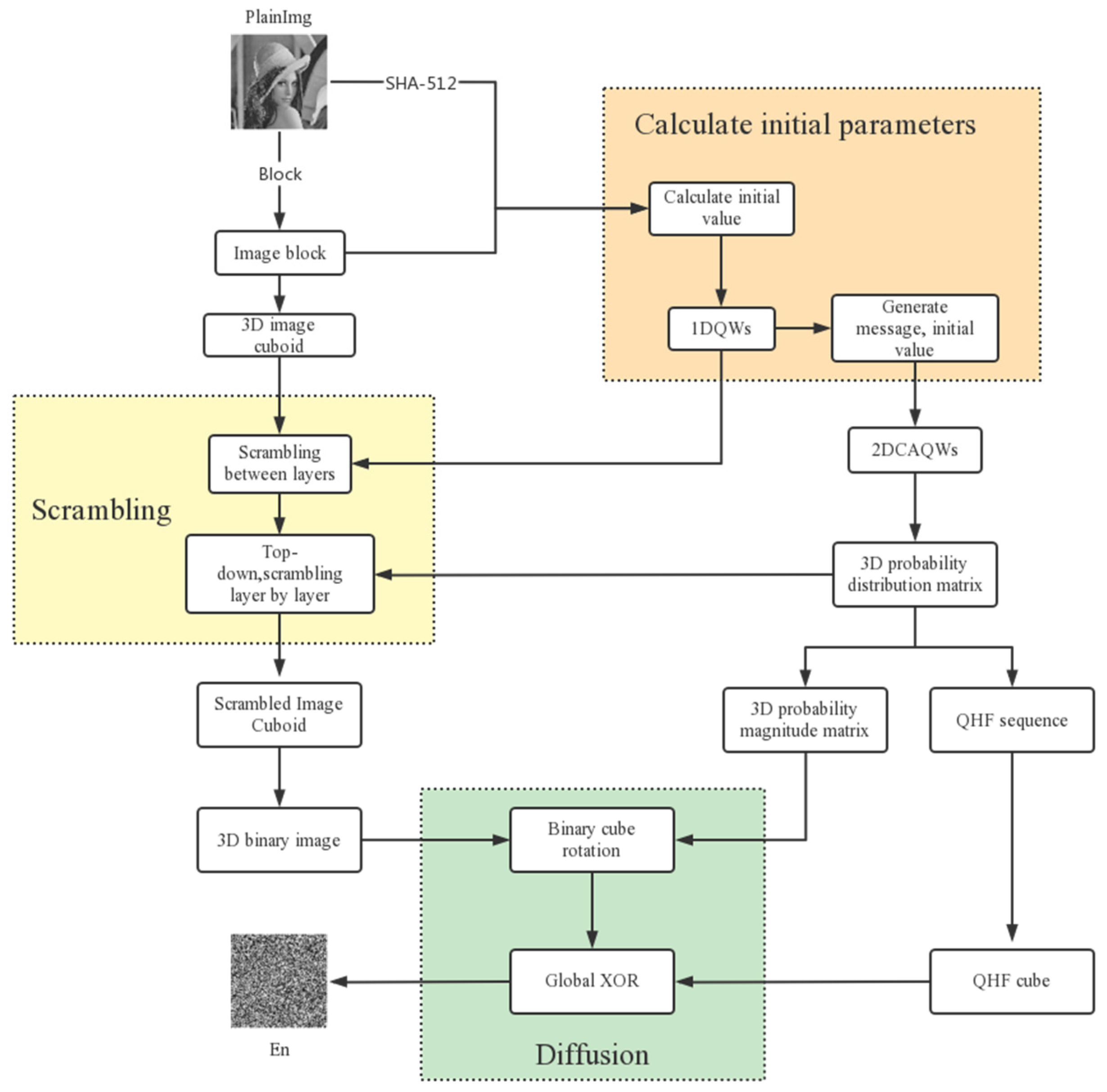
3.3. Image Encryption Process
| Algorithm 1. Sequence generation. |
| Input: Original image(PlainImg) Output 1 SHA-512(PlainImg) 2 Generate initial key parameters based on 3 Calculation of 1DQWs and 2DCAQWs 4 () // 1DQWs on a circle with node number 5 // Quadratic encoding 6 7 // Alternating quantum walks with sub-message encoding control on a circle 8 // Complete diffusion operation using 3D quantum hash sequence Btest |
| Algorithm 2. Encryption algorithms. |
| Input: Original image(PlainImg), , , , , Output: Encrypted images() 1 Image block (chunking the image 2 Integrating image blocks as rectangles 3 ; //Group summation 4 // Sort 5 Displacement between layers according to its index sequence for the image rectangle 6 Sorting and dislocation inside each depth layer using 7 for j 1 to B_num 8 ); 9 for i1 to x ∗ y do 10 reshape 11 If A > B 12 Bin_P3 Upper)// Upper layer rotated 90 degrees counterclockwise 13 else 14 Bin_P3 Lower) //Lower layer rotated clockwise by 90 degrees 15 end 16 P3bin(i,:) = reshape(Bin_P3); 17 end 18 P3bin1 = bin2dec(P3bin); 19 P3bin2 = reshape(P3bin1, x, y); 20 end 21 // Global xor 22 Tiling the image block |
3.3.1. Generation of Image Cuboid
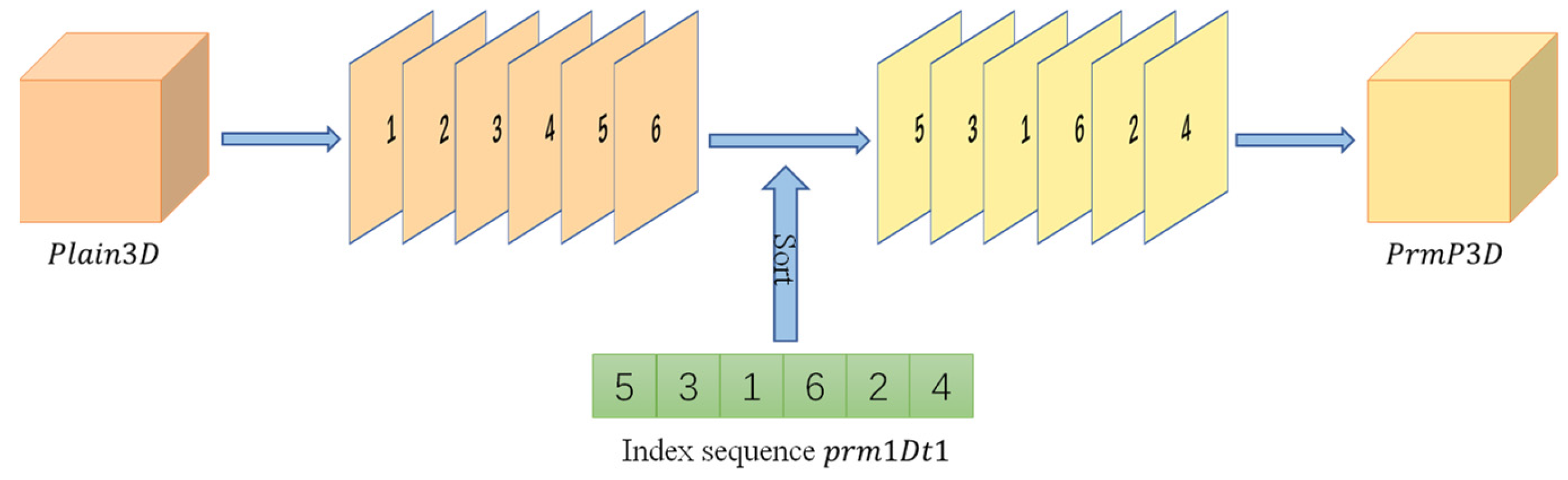
3.3.2. Two Rounds of Scrambling
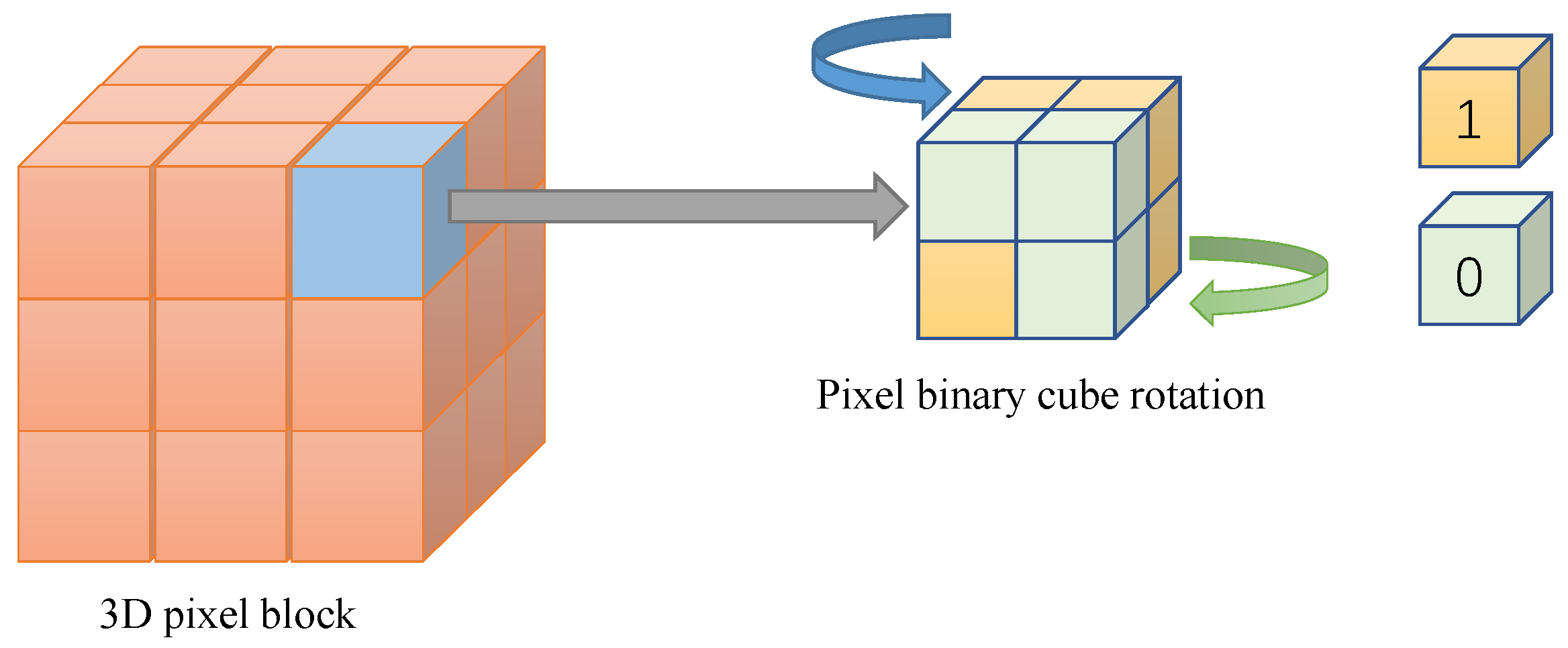
3.3.3. Two Rounds of Diffusion
3.4. Image Decryption Process
4. Simulation Results and Security Analysis
4.1. Encryption and Decryption Results
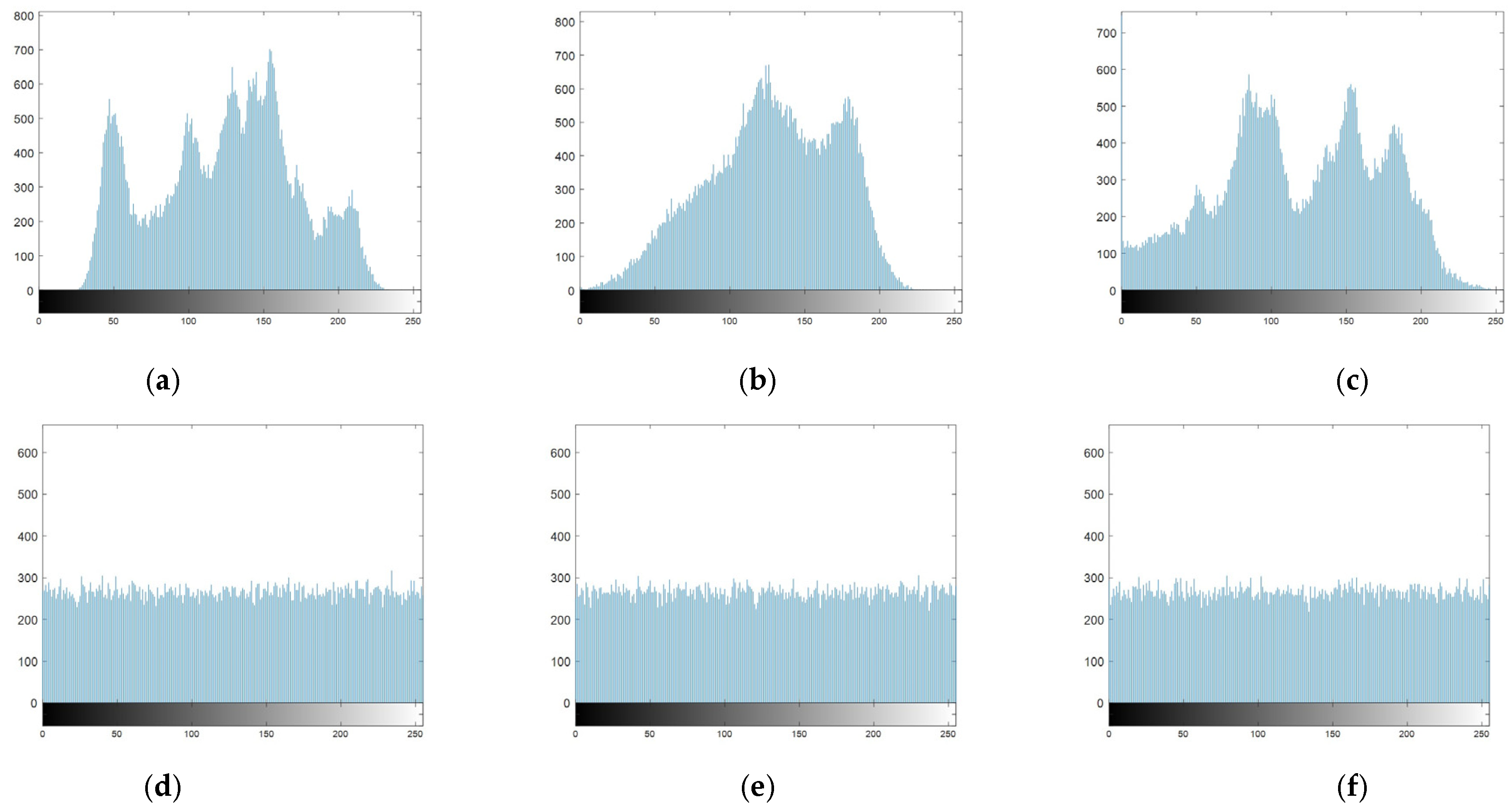
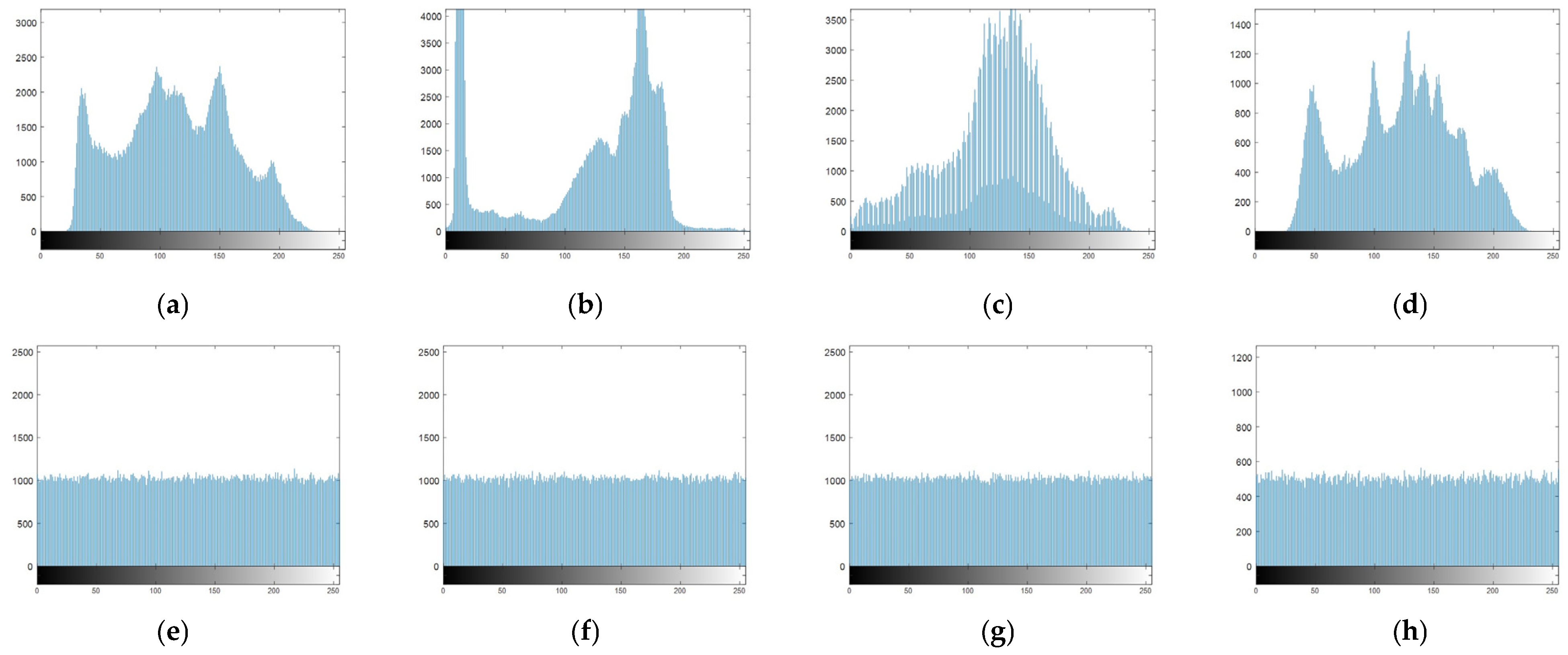
4.2. Histogram Analysis
4.3. Test
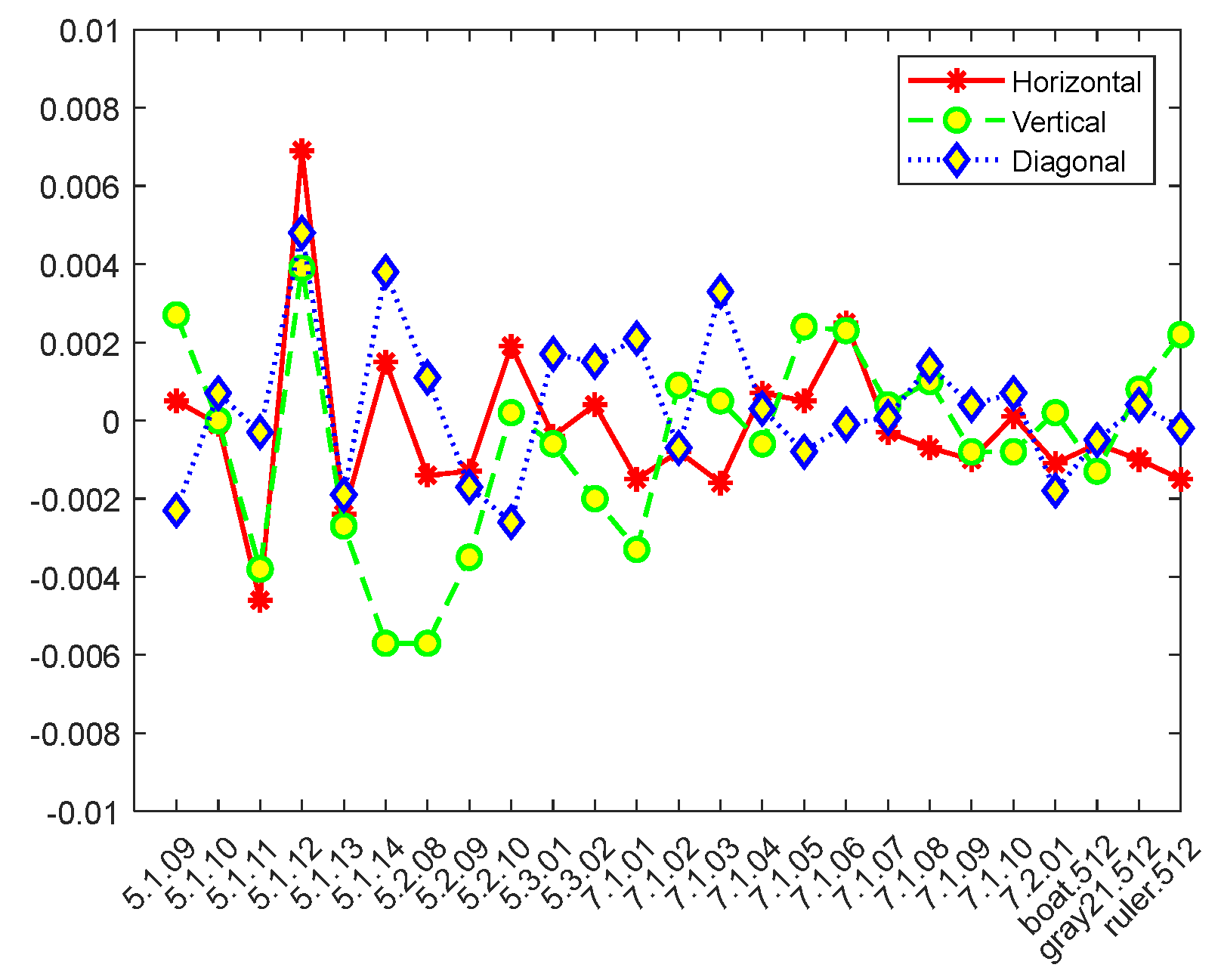
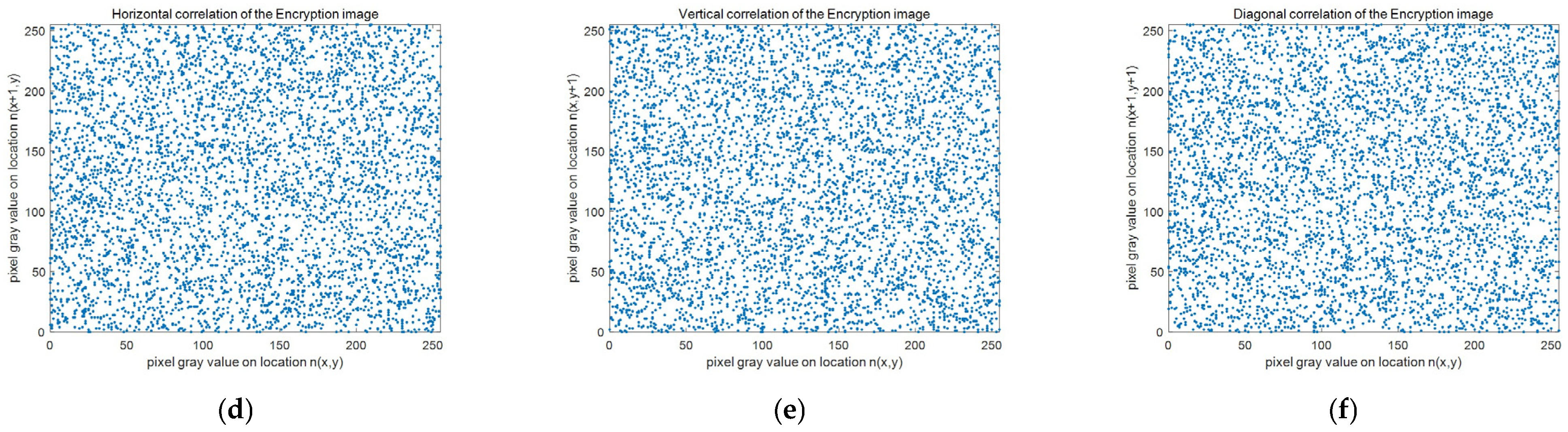
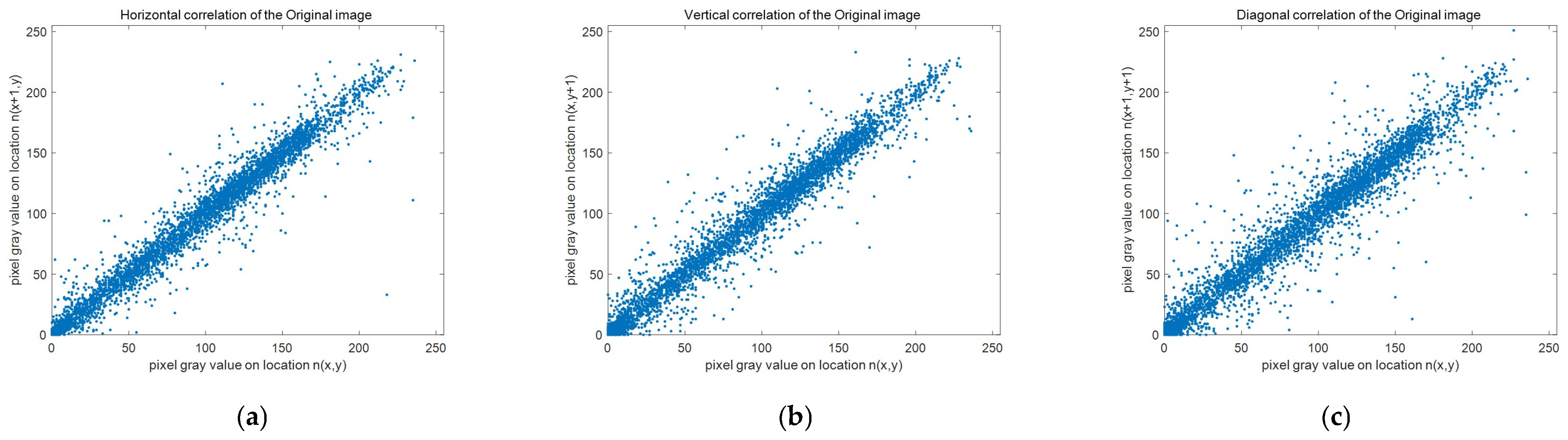
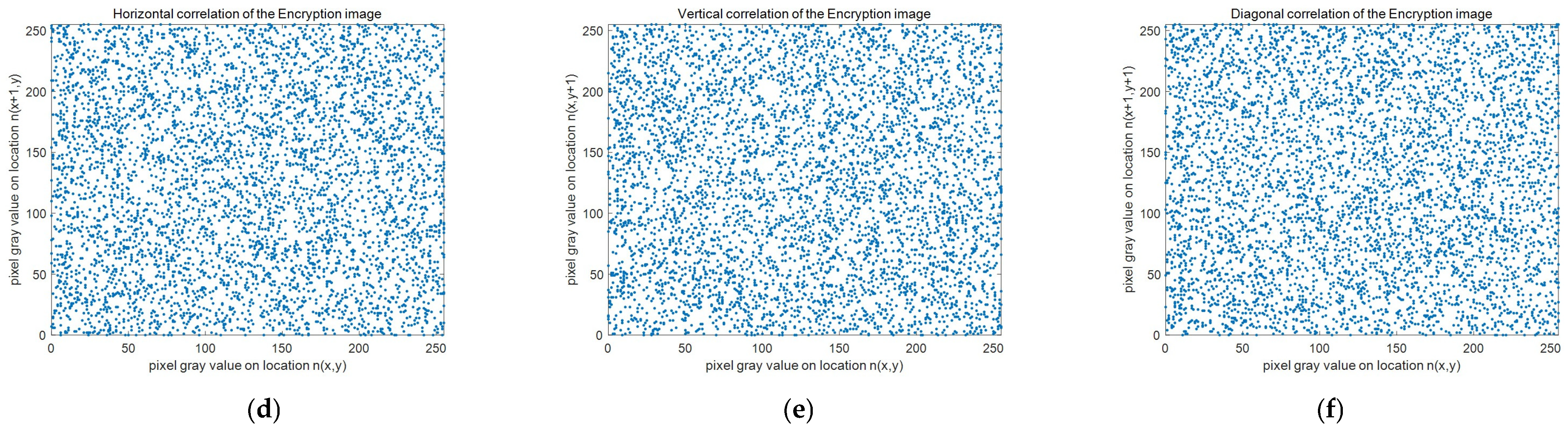
4.4. Correlation Coefficient Analysis
4.5. Information Entropy Analysis
4.6. Antidifferential Attack (NPCR and UACI Standard Evaluation)
4.7. Anticlipping and Noise Attacks
4.8. Key Space Analysis
4.9. Key Sensitivity Analysis
4.10. Computational Complexity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wan, W.; Wang, J.; Li, J.; Sun, J.; Zhang, H.; Liu, J. Hybrid JND model-guided watermarking method for screen content images. Multimed. Tools Appl. 2020, 79, 4907–4930. [Google Scholar] [CrossRef]
- Aminuddin, A.; Ernawan, F. AuSR2: Image watermarking technique for authentication and self-recovery with image texture preservation. Comput. Electr. Eng. 2022, 102, 108207. [Google Scholar] [CrossRef]
- Cao, W.; Mao, Y.; Zhou, Y. Designing a 2D infinite collapse map for image encryption. Signal Process. 2020, 171, 107457. [Google Scholar] [CrossRef]
- Man, Z.; Li, J.; Di, X.; Sheng, Y.; Liu, Z. Double image encryption algorithm based on neural network and chaos. Chaos Solitons Fractals 2021, 152, 111318. [Google Scholar] [CrossRef]
- Singh, K.N.; Singh, A.K. Towards integrating image encryption with compression: A survey. ACM Trans. Multimed. Comput. Commun. Appl. 2022, 18, 1–21. [Google Scholar] [CrossRef]
- Yan, X.; Liu, F.; Yan, W.Q.; Yang, G.; Lu, Y. Weighted visual cryptographic scheme with improved image quality. Multimed. Tools Appl. 2020, 79, 21345–21360. [Google Scholar] [CrossRef]
- Wang, T.; Wang, M.-H. Hyperchaotic image encryption algorithm based on bit-level permutation and DNA encoding. Opt. Laser Technol. 2020, 132, 106355. [Google Scholar] [CrossRef]
- Khalil, N.; Sarhan, A.; Alshewimy, M.A. An efficient color/grayscale image encryption scheme based on hybrid chaotic maps. Opt. Laser Technol. 2021, 143, 107326. [Google Scholar] [CrossRef]
- Zhou, S. A real-time one-time pad DNA-chaos image encryption algorithm based on multiple keys. Opt. Laser Technol. 2021, 143, 107359. [Google Scholar] [CrossRef]
- Zhang, Y. The fast image encryption algorithm based on lifting scheme and chaos. Inf. Sci. 2020, 520, 177–194. [Google Scholar] [CrossRef]
- Wang, X.; Guan, N.; Yang, J. Image encryption algorithm with random scrambling based on one-dimensional logistic self-embedding chaotic map. Chaos Solitons Fractals 2021, 150, 111117. [Google Scholar] [CrossRef]
- Alawida, M.; Teh, J.S.; Samsudin, A. An image encryption scheme based on hybridizing digital chaos and finite state machine. Signal Process. 2019, 164, 249–266. [Google Scholar] [CrossRef]
- Himeur, Y.; Boukabou, A. A robust and secure key-frames based video watermarking system using chaotic encryption. Multimed. Tools Appl. 2018, 77, 8603–8627. [Google Scholar] [CrossRef]
- Yu, J.; Xie, W.; Zhong, Z.; Wang, H. Image encryption algorithm based on hyperchaotic system and a new DNA sequence operation. Chaos Solitons Fractals 2022, 162, 112456. [Google Scholar] [CrossRef]
- Jasra, B.; Moon, A.H. Color image encryption and authentication using dynamic DNA encoding and hyper chatic system. Expert Syst. Appl. 2022, 206, 117861. [Google Scholar] [CrossRef]
- Qiu, H.; Xu, X.; Jiang, Z.; Sun, K.; Xiao, C. A color image encryption algorithm based on hyperchaotic map and Rubik’s Cube scrambling. Nonlinear Dyn. 2022, 1–19. [Google Scholar] [CrossRef]
- Mansouri, A.; Wang, X. A novel one-dimensional chaotic map generator and its application in a new index representation-based image encryption scheme. Inf. Sci. 2021, 563, 91–110. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, M. An image encryption algorithm based on hyperchaotic system and DNA coding. Opt. Laser Technol. 2021, 143, 107316. [Google Scholar] [CrossRef]
- Xian, Y.; Wang, X. Fractal sorting matrix and its application on chaotic image encryption. Inf. Sci. 2021, 547, 1154–1169. [Google Scholar] [CrossRef]
- Jithin, K.; Sankar, S. Colour image encryption algorithm combining Arnold map, DNA sequence operation, and a Mandelbrot set. J. Inf. Secur. Appl. 2020, 50, 102428. [Google Scholar] [CrossRef]
- Gao, W.; Sun, J.; Qiao, W.; Zhang, X. Digital image encryption scheme based on generalized Mandelbrot-Julia set. Optik 2019, 185, 917–929. [Google Scholar] [CrossRef]
- Gao, Y.; Jiao, S.; Fang, J.; Lei, T.; Xie, Z.; Yuan, X. Multiple-image encryption and hiding with an optical diffractive neural network. Opt. Commun. 2020, 463, 125476. [Google Scholar] [CrossRef]
- Chen, H.; Liu, Z.; Tanougast, C.; Liu, F. A novel chaos based optical cryptosystem for multiple images using DNA-blend and gyrator transform. Opt. Lasers Eng. 2021, 138, 106448. [Google Scholar] [CrossRef]
- Wang, F.; Ni, R.; Wang, J.; Zhu, Z.; Hu, Y. Invertible encryption network for optical image cryptosystem. Opt. Lasers Eng. 2022, 149, 106784. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, A.; Tang, Y.; Dang, J.; Wang, G. Plaintext-related image encryption algorithm based on perceptron-like network. Inf. Sci. 2020, 526, 180–202. [Google Scholar] [CrossRef]
- Ding, Y.; Wu, G.; Chen, D.; Zhang, N.; Gong, L.; Cao, M.; Qin, Z. DeepEDN: A deep-learning-based image encryption and decryption network for internet of medical things. IEEE Internet Things J. 2020, 8, 1504–1518. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, Z.; Shen, H.; Huang, Y.; Cai, S.; Du, S. FPGA implementation and image encryption application of a new PRNG based on a memristive Hopfield neural network with a special activation gradient. Chin. Phys. B 2022, 31, 020505. [Google Scholar] [CrossRef]
- Shi, Y.; Hu, Y.; Wang, B. Image encryption scheme based on multiscale block compressed sensing and Markov model. Entropy 2021, 23, 1297. [Google Scholar] [CrossRef]
- Sun, C.; Wang, E.; Zhao, B. Image encryption scheme with compressed sensing based on a new six-dimensional non-degenerate discrete hyperchaotic system and plaintext-related scrambling. Entropy 2021, 23, 291. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y. Chaotic image encryption algorithm based on hybrid multi-objective particle swarm optimization and DNA sequence. Opt. Lasers Eng. 2021, 137, 106393. [Google Scholar] [CrossRef]
- Abbasi, A.A.; Mazinani, M.; Hosseini, R. Chaotic evolutionary-based image encryption using RNA codons and amino acid truth table. Opt. Laser Technol. 2020, 132, 106465. [Google Scholar] [CrossRef]
- Liang, Z.; Qin, Q.; Zhou, C. An image encryption algorithm based on Fibonacci Q-matrix and genetic algorithm. Neural Comput. Appl. 2022, 34, 19313–19341. [Google Scholar] [CrossRef]
- Liu, X.; Xiao, D.; Huang, W.; Liu, C. Quantum block image encryption based on arnold transform and sine chaotification model. IEEE Access 2019, 7, 57188–57199. [Google Scholar] [CrossRef]
- Wang, J.; Chen, J.; Wang, F.; Ni, R. Optical image encryption scheme based on quantum s-box and meaningful ciphertext generation algorithm. Opt. Commun. 2022, 525, 128834. [Google Scholar] [CrossRef]
- Ma, Y.; Li, N.; Zhang, W.; Wang, S.; Ma, H. Image encryption scheme based on alternate quantum walks and discrete cosine transform. Opt. Express 2021, 29, 28338–28351. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.; Hussain, I.; Jamal, S.S.; Amin, M. A privacy scheme for digital images based on quantum particles. Int. J. Theor. Phys. 2019, 58, 4293–4310. [Google Scholar] [CrossRef]
- Yan, T.; Li, D. A Novel Quantum Color Image Encryption Scheme Based on Controlled Alternate Quantum Walks. In Proceedings of the International Conference on Security, Privacy and Anonymity in Computation, Communication and Storage, New York, NY, USA, 9–13 August 2021; Springer: Cham, Switzerland, 2021; pp. 519–530. [Google Scholar]
- Yang, Y.-G.; Pan, Q.-X.; Sun, S.-J.; Xu, P. Novel image encryption based on quantum walks. Sci. Rep. 2015, 5, 7784. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.-G.; Xu, P.; Yang, R.; Zhou, Y.-H.; Shi, W.-M. Quantum Hash function and its application to privacy amplification in quantum key distribution, pseudo-random number generation and image encryption. Sci. Rep. 2016, 6, 19788. [Google Scholar] [CrossRef] [PubMed]
- Abd EL-Latif, A.A.; Abd-El-Atty, B.; Abou-Nassar, E.M.; Venegas-Andraca, S.E. Controlled alternate quantum walks based privacy preserving healthcare images in internet of things. Opt. Laser Technol. 2020, 124, 105942. [Google Scholar] [CrossRef]
- Abd EL-Latif, A.A.; Abd-El-Atty, B.; Venegas-Andraca, S.E. Controlled alternate quantum walk-based pseudo-random number generator and its application to quantum color image encryption. Phys. A Stat. Mech. Appl. 2020, 547, 123869. [Google Scholar] [CrossRef]
- Boriga, R.E.; Dăscălescu, A.C.; Diaconu, A.V. A new fast image encryption scheme based on 2D chaotic maps. IAENG Int. J. Comput. Sci. 2014, 41, 249–258. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. Cyber J. Multidiscip. J. Sci. Technol. J. Sel. Areas Telecommun. 2011, 1, 31–38. [Google Scholar]
- Hore, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Li, Y. Research and Application of Deep Learning in Image Recognition. In Proceedings of the 2022 IEEE 2nd International Conference on Power, Electronics and Computer Applications (ICPECA), Shenyang, China, 21–23 January 2022; pp. 994–999. [Google Scholar]
- Falcetta, A.; Roveri, M. Privacy-preserving deep learning with homomorphic encryption: An introduction. IEEE Comput. Intell. Mag. 2022, 17, 14–25. [Google Scholar] [CrossRef]
- Chen, J.; Qiu, X.; Ding, C.; Wu, Y. SAR image classification based on spiking neural network through spike-time dependent plasticity and gradient descent. ISPRS J. Photogramm. Remote Sens. 2022, 188, 109–124. [Google Scholar] [CrossRef]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X. Synchronization of delayed fuzzy neural networks with probabilistic communication delay and its application to image encryption. IEEE Trans. Fuzzy Syst. 2022. [Google Scholar] [CrossRef]
- Li, J.; Liu, J.; Zhou, S.; Zhang, Q.; Kasabov, N.K. Learning a coordinated network for detail-refinement multi-exposure image fusion. IEEE Trans. Circuits Syst. Video Technol. 2022. [Google Scholar] [CrossRef]
- Feng, L.; Chen, X. Image recognition and encryption algorithm based on artificial neural network and multidimensional chaotic sequence. Comput. Intell. Neurosci. 2022, 2022, 9576184. [Google Scholar] [CrossRef]








| Image | Lena | Baboon | Peppers | White | Black | Avg. | Ref. [9] | Ref. [33] |
|---|---|---|---|---|---|---|---|---|
| Plaintext | 39,868.727 | 44,739.305 | 26,311.578 | 16,711,680 | 16,711,680 | - | - | - |
| Ciphertext | 219.269 | 216.589 | 225.765 | 259.881 | 241.390 | 232.579 | 244.159 | 254.078 |
| Image | Barbara | Cameraman | Livingroom | Irregular Lena | Avg. | Ref. [18] |
|---|---|---|---|---|---|---|
| Plaintext | 14,4101.119 | 418,530.147 | 276,815.883 | 74,075.357 | - | - |
| Ciphertext | 238.454 | 250.778 | 245.376 | 250.828 | 246.359 | 260.400 |
| Image | Plain Image | Cipher Image | Ref. [11] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H | V | D | H | V | D | H | V | D | |
| 5.1.09 | 0.9026 | 0.9406 | 0.9098 | 0.0005 | 0.0027 | −0.0023 | 0.0031 | −0.0016 | 0.0014 |
| 5.1.10 | 0.9016 | 0.8688 | 0.8311 | −0.0001 | 1.0819 × 10−6 | 0.0007 | 0.0044 | −0.0006 | −0.0052 |
| 5.1.11 | 0.9574 | 0.9480 | 0.8966 | −0.0046 | −0.0038 | −0.0003 | 0.0005 | −0.0019 | −0.0049 |
| 5.1.12 | 0.9576 | 0.9741 | 0.9408 | 0.0069 | 0.0039 | 0.0048 | 0.0068 | −0.0002 | −0.0055 |
| 5.1.13 | 0.8804 | 0.8497 | 0.7419 | −0.0024 | −0.0027 | −0.0019 | 5.76 × 10−6 | 0.0017 | −0.0072 |
| 5.1.14 | 0.9522 | 0.9018 | 0.8589 | 0.0015 | −0.0057 | 0.0038 | −0.0056 | 0.0001 | 0.0044 |
| 5.2.08 | 0.9289 | 0.8784 | 0.8472 | −0.0014 | −0.0057 | 0.0011 | 0.0028 | 0.0006 | −0.0027 |
| 5.2.09 | 0.9059 | 0.8701 | 0.8122 | −0.0013 | −0.0035 | −0.0017 | 0.0006 | −0.0123 | 0.0001 |
| 5.2.10 | 0.9409 | 0.9274 | 0.8948 | 0.0019 | 0.0002 | −0.0026 | −0.0024 | −0.0005 | 0.0031 |
| 5.3.01 | 0.9756 | 0.9811 | 0.9669 | −0.0004 | −0.0006 | 0.0017 | 0.0015 | 4.43 × 10−5 | −0.0017 |
| 5.3.02 | 0.9154 | 0.9053 | 0.8608 | 0.0004 | −0.0020 | 0.0015 | −0.0024 | −0.0011 | 0.0008 |
| 7.1.01 | 0.9635 | 0.9194 | 0.9080 | −0.0015 | −0.0033 | 0.0021 | −0.0021 | 0.0011 | 0.0067 |
| 7.1.02 | 0.9468 | 0.9478 | 0.9032 | −0.0008 | 0.0009 | −0.0007 | 0.0084 | 0.0017 | 0.0021 |
| 7.1.03 | 0.9410 | 0.9306 | 0.8998 | −0.0016 | 0.0005 | 0.0033 | 0.0045 | 8.67 × 10−5 | −0.0056 |
| 7.1.04 | 0.9762 | 0.9646 | 0.9546 | 0.0007 | −0.0006 | 0.0003 | −0.0031 | 0.0073 | 0.0002 |
| 7.1.05 | 0.9449 | 0.9193 | 0.8983 | 0.0005 | 0.0024 | −0.0008 | −0.0040 | −0.0004 | −0.0002 |
| 7.1.06 | 0.9378 | 0.9004 | 0.8791 | 0.0025 | 0.0023 | −0.0001 | 0.0002 | −0.0014 | −0.0057 |
| 7.1.07 | 0.8872 | 0.8735 | 0.8296 | −0.0003 | 0.0004 | 7.5782 × 10−5 | 0.0020 | −0.0009 | −0.0160 |
| 7.1.08 | 0.9563 | 0.9335 | 0.9245 | −0.0007 | 0.0010 | 0.0014 | 0.0083 | −0.0008 | 0.0057 |
| 7.1.09 | 0.9667 | 0.9277 | 0.9160 | −0.0010 | −0.0008 | 0.0004 | 0.0007 | −0.0005 | 0.0063 |
| 7.1.10 | 0.9659 | 0.9497 | 0.9341 | 0.0001 | −0.0008 | 0.0007 | 0.0058 | −0.0001 | 0.0050 |
| 7.2.01 | 0.9670 | 0.9468 | 0.9463 | −0.0011 | 0.0002 | −0.0018 | −0.0008 | −0.0031 | −0.0044 |
| boat.512 | 0.9371 | 0.9722 | 0.9220 | −0.0006 | −0.0013 | −0.0005 | 0.0024 | −6.53 × 10−7 | −0.0036 |
| gray21.512 | 0.9965 | 0.9998 | 0.9963 | −0.0010 | 0.0008 | 0.0004 | 0.0011 | 0.0007 | −0.0056 |
| ruler.512 | 0.4332 | 0.5068 | −0.0207 | −0.0015 | 0.0022 | −0.0002 | 0.0007 | 0.0120 | 3.59 × 10−5 |
| Mean | 0.9215 | 0.9095 | 0.8581 | −0.0014 | 0.0019 | 0.0014 | 0.0013 | 0.0020 | 0.0042 |
| Images | Size | Plain Image | Cipher Image | ||
|---|---|---|---|---|---|
| Ref. [6] | Ref. [12] | Ours | |||
| 5.1.09 | 256 ∗ 256 | 6.7093 | 7.9973 | 7.9971 | 7.9970 |
| 5.1.10 | 256 ∗ 256 | 7.3118 | 7.9973 | 7.9974 | 7.9977 |
| 5.1.11 | 256 ∗ 256 | 6.4523 | 7.9970 | 7.9969 | 7.9974 |
| 5.1.12 | 256 ∗ 256 | 6.7057 | 7.9975 | 7.9972 | 7.9974 |
| 5.1.13 | 256 ∗ 256 | 1.5483 | 7.9972 | 7.9969 | 7.9974 |
| 5.1.14 | 256 ∗ 256 | 7.3424 | 7.9970 | 7.9974 | 7.9977 |
| 5.2.08 | 512 ∗ 512 | 7.5237 | 7.9992 | 7.9993 | 7.9994 |
| 5.2.09 | 512 ∗ 512 | 6.9940 | 7.9994 | 7.9993 | 7.9993 |
| 5.2.10 | 512 ∗ 512 | 5.7056 | 7.9993 | 7.9993 | 7.9993 |
| 5.3.01 | 1024 ∗ 1024 | 7.5237 | 7.9998 | 7.9998 | 7.9998 |
| 5.3.02 | 1024 ∗ 1024 | 6.8303 | 7.9998 | 7.9998 | 7.9997 |
| 7.1.01 | 512 ∗ 512 | 6.0274 | 7.9993 | 7.9991 | 7.9993 |
| 7.1.02 | 512 ∗ 512 | 4.0045 | 7.9993 | 7.9992 | 7.9994 |
| 7.1.03 | 512 ∗ 512 | 5.4957 | 7.9993 | 7.9993 | 7.9994 |
| 7.1.04 | 512 ∗ 512 | 6.1074 | 7.9992 | 7.9993 | 7.9993 |
| 7.1.05 | 512 ∗ 512 | 6.5632 | 7.9993 | 7.9992 | 7.9993 |
| 7.1.06 | 512 ∗ 512 | 6.6953 | 7.9992 | 7.9993 | 7.9993 |
| 7.1.07 | 512 ∗ 512 | 5.9916 | 7.9993 | 7.9993 | 7.9992 |
| 7.1.08 | 512 ∗ 512 | 5.0534 | 7.9994 | 7.9993 | 7.9992 |
| 7.1.09 | 512 ∗ 512 | 6.1898 | 7.9993 | 7.9992 | 7.9994 |
| 7.1.10 | 512 ∗ 512 | 5.9088 | 7.9993 | 7.9993 | 7.9993 |
| 7.2.01 | 1024 ∗ 1024 | 5.6415 | 7.9998 | 7.9998 | 7.9998 |
| boat.512 | 512 ∗ 512 | 7.1914 | 7.9993 | 7.9994 | 7.9994 |
| gray21.512 | 512 ∗ 512 | 4.3923 | 7.9992 | 7.9994 | 7.9993 |
| ruler.512 | 512 ∗ 512 | 0.5000 | 7.9993 | 7.9992 | 7.9993 |
| Mean of 256 ∗ 256 | 256 ∗ 256 | - | 7.9972 | 7.9972 | 7.9974 |
| Mean of 512 ∗ 512 | 512 ∗ 512 | - | 7.9993 | 7.9993 | 7.9993 |
| Mean of 1024 ∗ 1024 | 1024 ∗ 1024 | - | 7.9998 | 7.9998 | 7.9998 |
| Image | NPCR | UACI | ||||||
|---|---|---|---|---|---|---|---|---|
| Ref. [6] | Ref. [7] | Ref. [8] | Proposed | Ref. [6] | Ref. [7] | Ref. [8] | Proposed | |
| 256 ∗ 256 | Theoretical NPCR | 99.5693 | Theoretical UACI | 33.2824~33.6447 | ||||
| 5.1.09 | 99.6109 | 99.603 | 99.5124 | 99.5787 | 33.4475 | 33.552 | 33.5214 | 33.3580 |
| 5.1.10 | 99.5972 | 99.636 | 99.6121 | 99.6565 | 33.4846 | 33.453 | 33.4215 | 33.5306 |
| 5.1.11 | 99.5865 | 99.942 | 99.5943 | 99.5860 | 33.4482 | 33.586 | 33.4014 | 33.5725 |
| 5.1.12 | 99.6323 | 99.792 | 99.5811 | 99.5992 | 33.4453 | 33.453 | 33.4158 | 33.5240 |
| 5.1.13 | 99.6216 | 99.792 | 99.5963 | 99.5802 | 33.4531 | 33.520 | 33.4236 | 33.4265 |
| 5.1.14 | 99.6078 | 99.621 | 99.5945 | 99.5831 | 33.4293 | 33.440 | 33.3951 | 33.5393 |
| 512 ∗ 512 | Theoretical NPCR | 99.5893 | Theoretical UACI | 33.3730~33.5541 | ||||
| 5.2.08 | 99.6105 | 99.960 | 99.5878 | 99.6136 | 33.5035 | 33.692 | 33.3978 | 33.5362 |
| 5.2.09 | 99.6033 | 99.876 | 99.5812 | 99.6022 | 33.4674 | 33.548 | 33.4182 | 33.3835 |
| 5.2.10 | 99.6101 | 99.654 | 99.6100 | 99.6147 | 33.4253 | 33.454 | 33.4263 | 33.4199 |
| 7.1.01 | 99.6136 | 99.957 | 99.6028 | 99.6310 | 33.4885 | 33.648 | 33.4474 | 33.5258 |
| 7.1.02 | 99.6040 | 99.918 | 99.6078 | 99.6151 | 33.4508 | 33.465 | 33.4326 | 33.4589 |
| 7.1.03 | 99.6101 | 99.849 | 99.5811 | 99.6124 | 33.4352 | 33.273 | 33.4836 | 33.4771 |
| 7.1.04 | 99.6178 | 99.991 | 99.5946 | 99.5930 | 33.5024 | 33.202 | 33.4782 | 33.4340 |
| 7.1.05 | 99.5979 | 99.942 | 99.5937 | 99.6136 | 33.4739 | 33.830 | 33.4716 | 33.4699 |
| 7.1.06 | 99.6269 | 99.670 | 99.5912 | 99.6041 | 33.4764 | 33.627 | 33.4365 | 33.4511 |
| 7.1.07 | 99.6193 | 99.983 | 99.6014 | 99.5995 | 33.4310 | 33.609 | 33.4313 | 33.4637 |
| 7.1.08 | 99.5979 | 99.818 | 99.6013 | 99.6170 | 33.4997 | 33.375 | 33.4460 | 33.4841 |
| 7.1.09 | 99.6113 | 99.874 | 99.6148 | 99.6109 | 33.4630 | 33.530 | 33.3856 | 33.4925 |
| 7.1.10 | 99.6166 | 99.697 | 99.6097 | 99.6079 | 33.4701 | 33.438 | 33.3941 | 33.4423 |
| boat.512 | 99.6227 | 99.715 | 99.6101 | 99.6212 | 33.4448 | 33.374 | 33.3973 | 33.4156 |
| gray21.512 | 99.6067 | 99.643 | 99.6034 | 99.5946 | 33.5113 | 33.507 | 33.4089 | 33.4367 |
| ruler.512 | 99.6124 | 99.637 | 99.5945 | 99.6056 | 33.4620 | 33.415 | 33.4635 | 33.4649 |
| 1024 ∗ 1024 | Theoretical NPCR | 99.5994 | Theoretical UACI | 33.4183~33.5088 | ||||
| 5.3.01 | 99.6067 | 99.950 | 99.6032 | 99.6294 | 33.5013 | 33.508 | 33.4392 | 33.5005 |
| 5.3.02 | 99.6015 | 99.982 | 99.6108 | 99.6128 | 33.4255 | 33.514 | 33.4547 | 33.4263 |
| 7.2.01 | 99.6005 | 99.980 | 99.6036 | 99.6088 | 33.4438 | 33.487 | 33.4301 | 33.4511 |
| Mean | 99.6098 | 99.8192 | 99.5957 | 99.6076 | 33.4634 | 33.5 | 33.4329 | 33.4674 |
| Std | 0.0103 | 0.2665 | 0.0200 | 0.0173 | 0.0268 | 0.0459 | 0.0328 | 0.0518 |
| Pass/All | 25/25 | 25/25 | 22/25 | 25/25 | 25/25 | 17/25 | 25/25 | 25/25 |
| Area | 1/16 | 1/8 | 1/4 | 1/2 |
|---|---|---|---|---|
| PSNR | 21.314192 | 18.380856 | 15.342343 | 12.250188 |
| Noise Level | 0.01 Level | 0.05 Level | 0.1 Level |
| PSNR | 28.971428 | 22.408105 | 19.258843 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, P.; Zhou, S.; Yan, W.Q. A 3D Cuboid Image Encryption Algorithm Based on Controlled Alternate Quantum Walk of Message Coding. Mathematics 2022, 10, 4441. https://doi.org/10.3390/math10234441
Liu P, Zhou S, Yan WQ. A 3D Cuboid Image Encryption Algorithm Based on Controlled Alternate Quantum Walk of Message Coding. Mathematics. 2022; 10(23):4441. https://doi.org/10.3390/math10234441
Chicago/Turabian StyleLiu, Pai, Shihua Zhou, and Wei Qi Yan. 2022. "A 3D Cuboid Image Encryption Algorithm Based on Controlled Alternate Quantum Walk of Message Coding" Mathematics 10, no. 23: 4441. https://doi.org/10.3390/math10234441
APA StyleLiu, P., Zhou, S., & Yan, W. Q. (2022). A 3D Cuboid Image Encryption Algorithm Based on Controlled Alternate Quantum Walk of Message Coding. Mathematics, 10(23), 4441. https://doi.org/10.3390/math10234441






