Proximity Effects in Matrix-Inclusion Composites: Elastic Effective Behavior, Phase Moments, and Full-Field Computational Analysis
Abstract
1. Introduction
2. Generation of Representative Volume Element of Matrix-Inclusion Composite with an Effective Minimal Distance between Inclusions
3. Elastic Properties and Homogenization
3.1. Stiffness Contrasts between Phases
3.2. Analytical Homogenization—Mori–Tanaka Estimates
3.2.1. The First Moment
3.2.2. The Second Moment
3.3. Computational Homogenization—Full-Field Simulations
4. Numerical Results
4.1. Results for the Effective Properties
4.2. Results for Phase Mean Fields
4.2.1. The First Moment
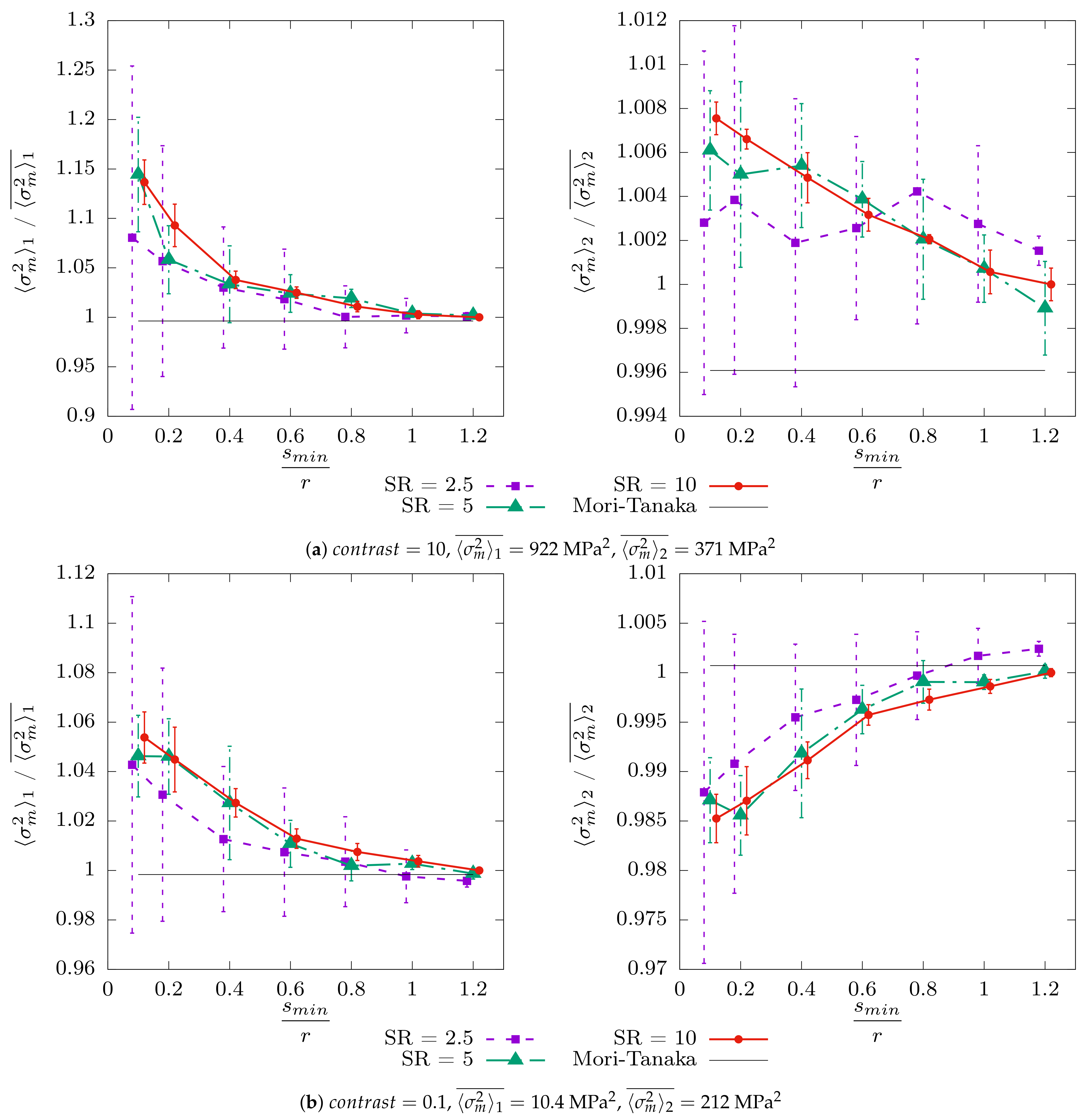
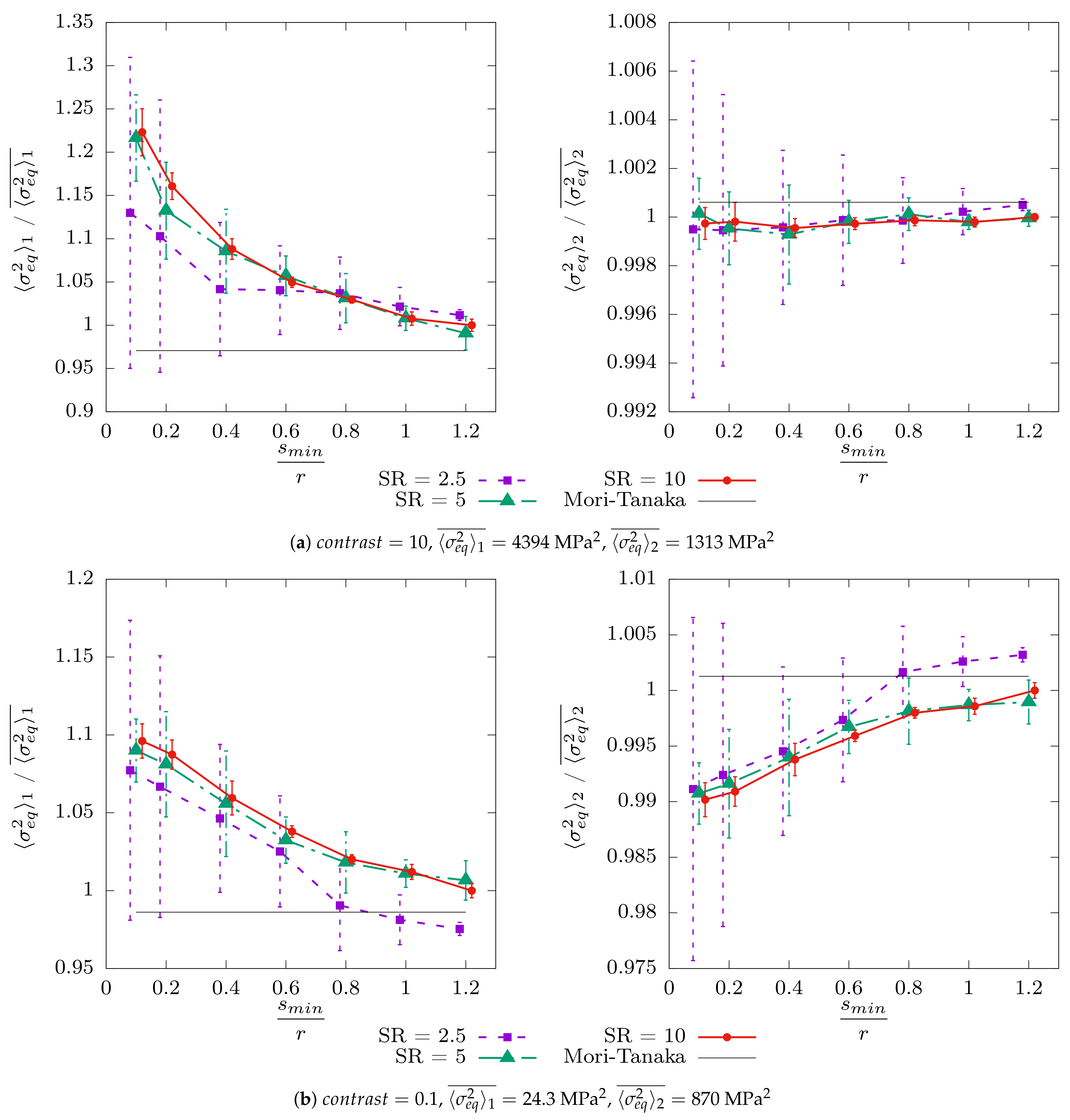
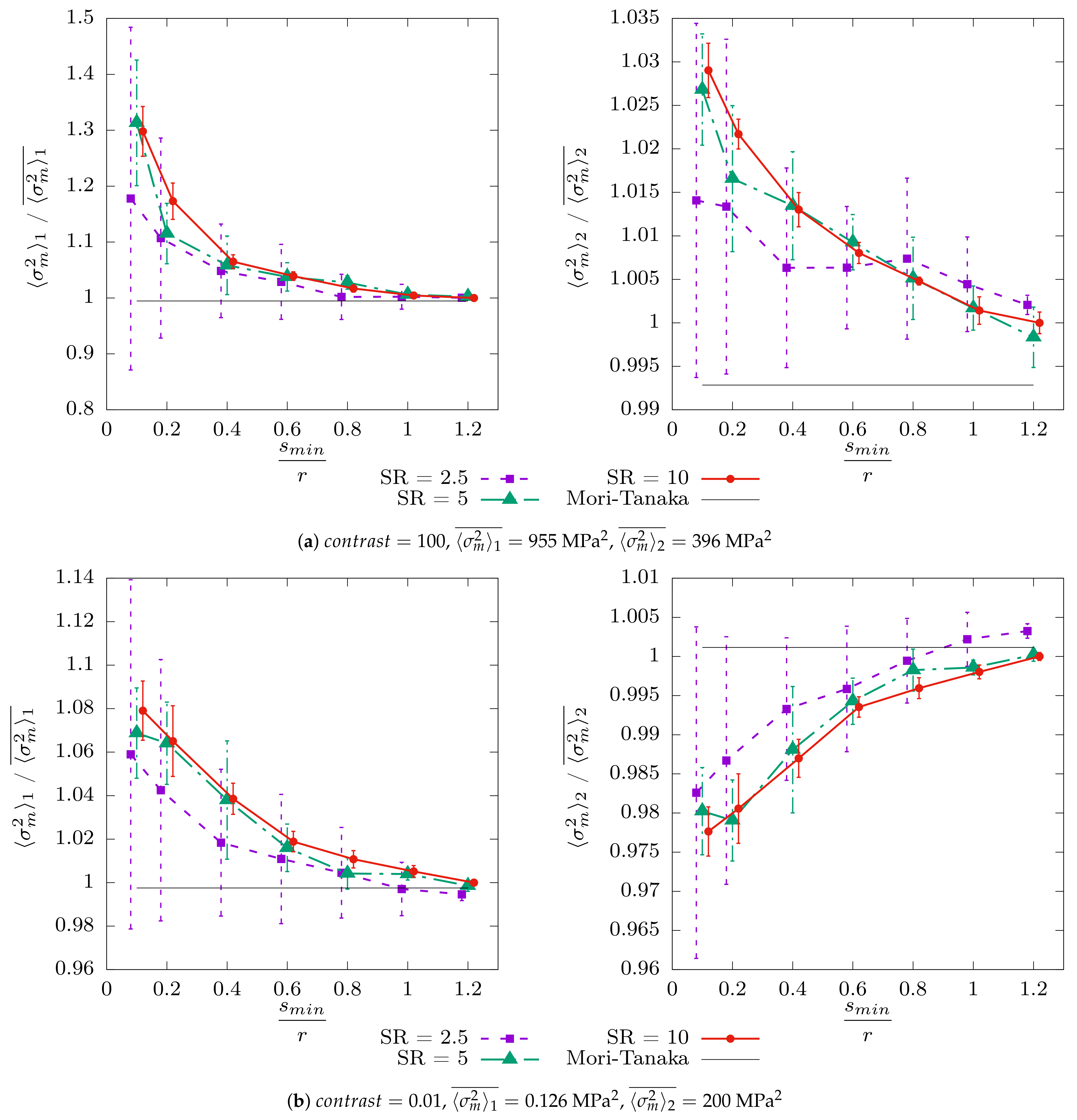
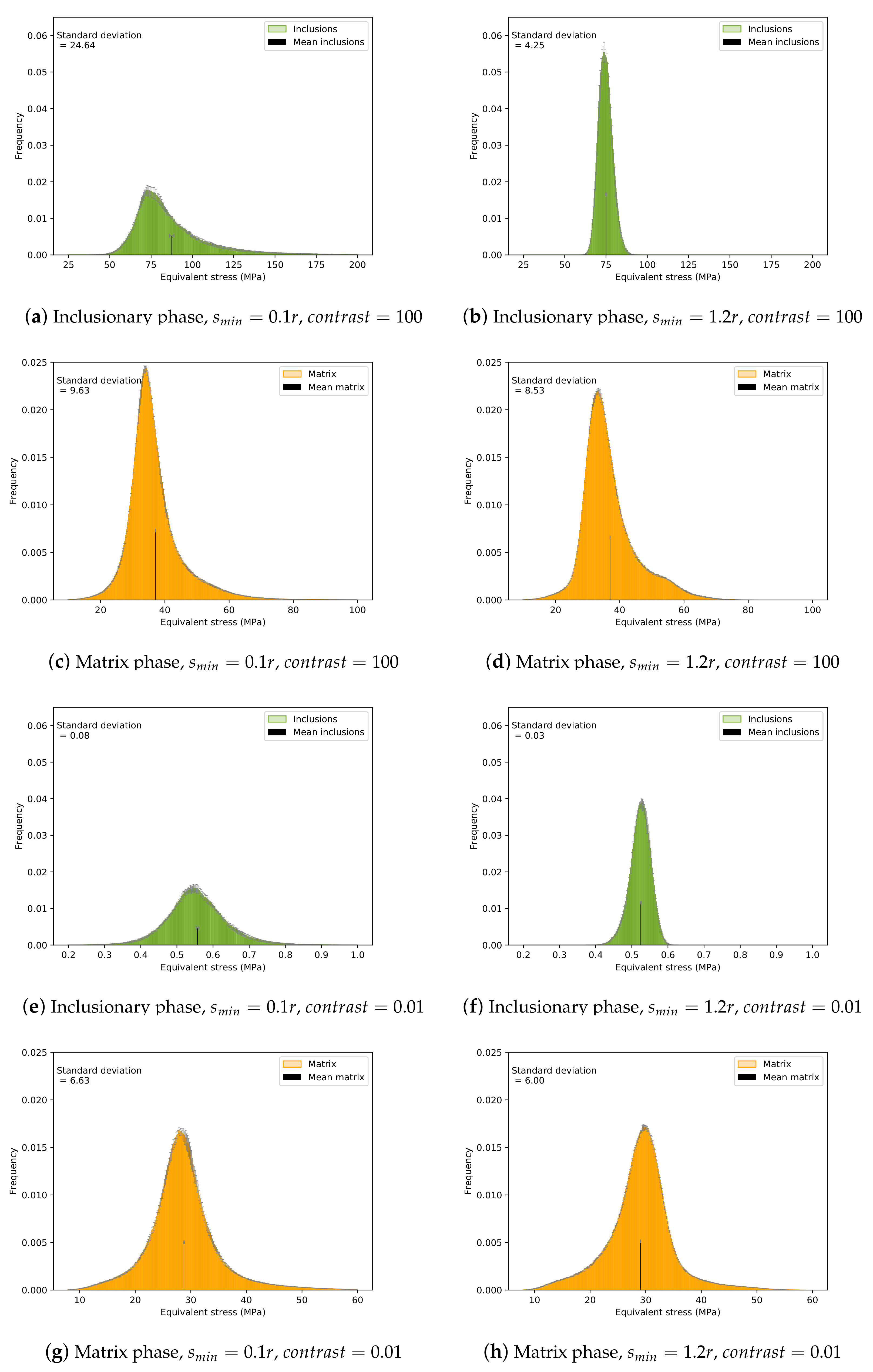
4.2.2. The Second Moment
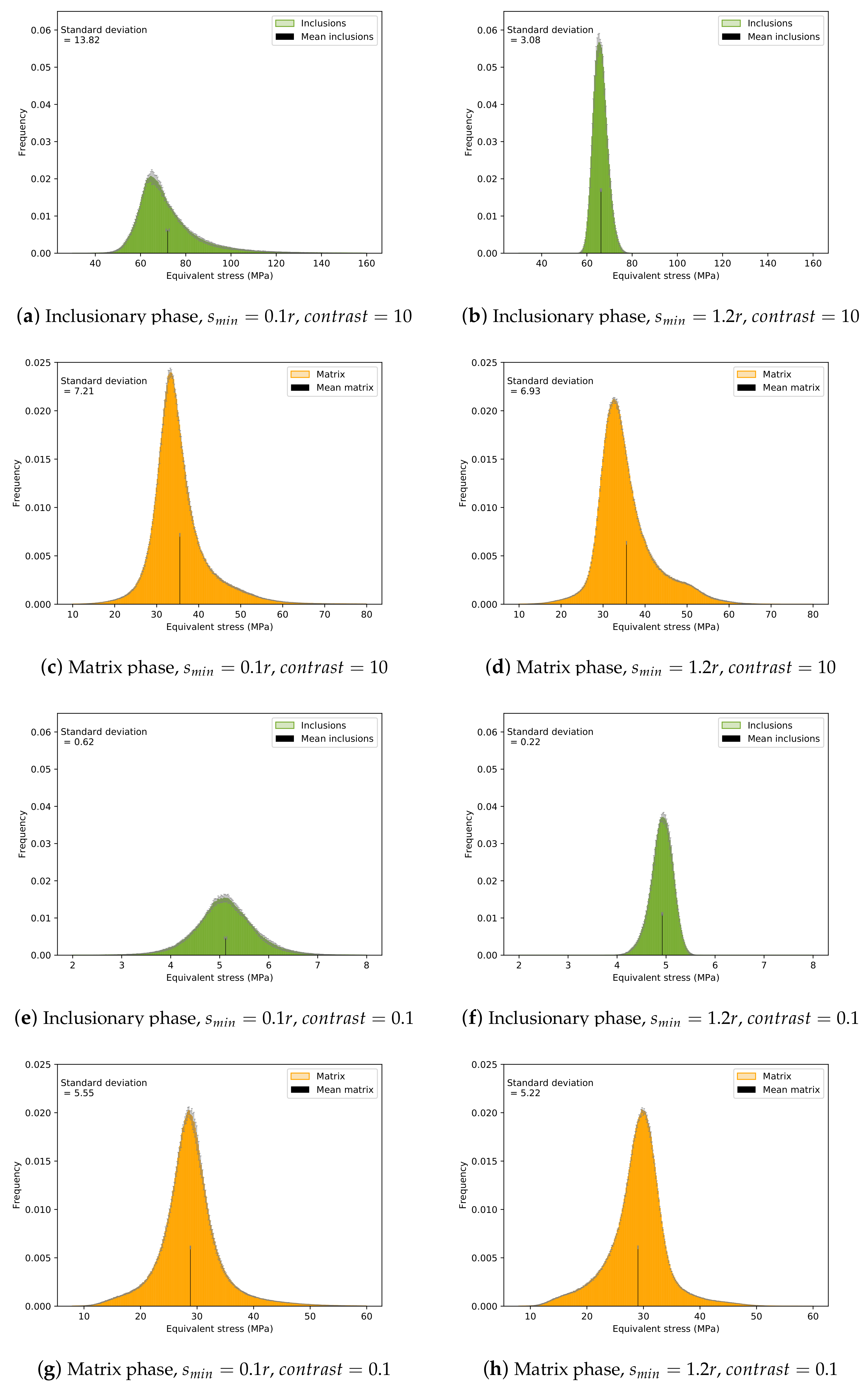
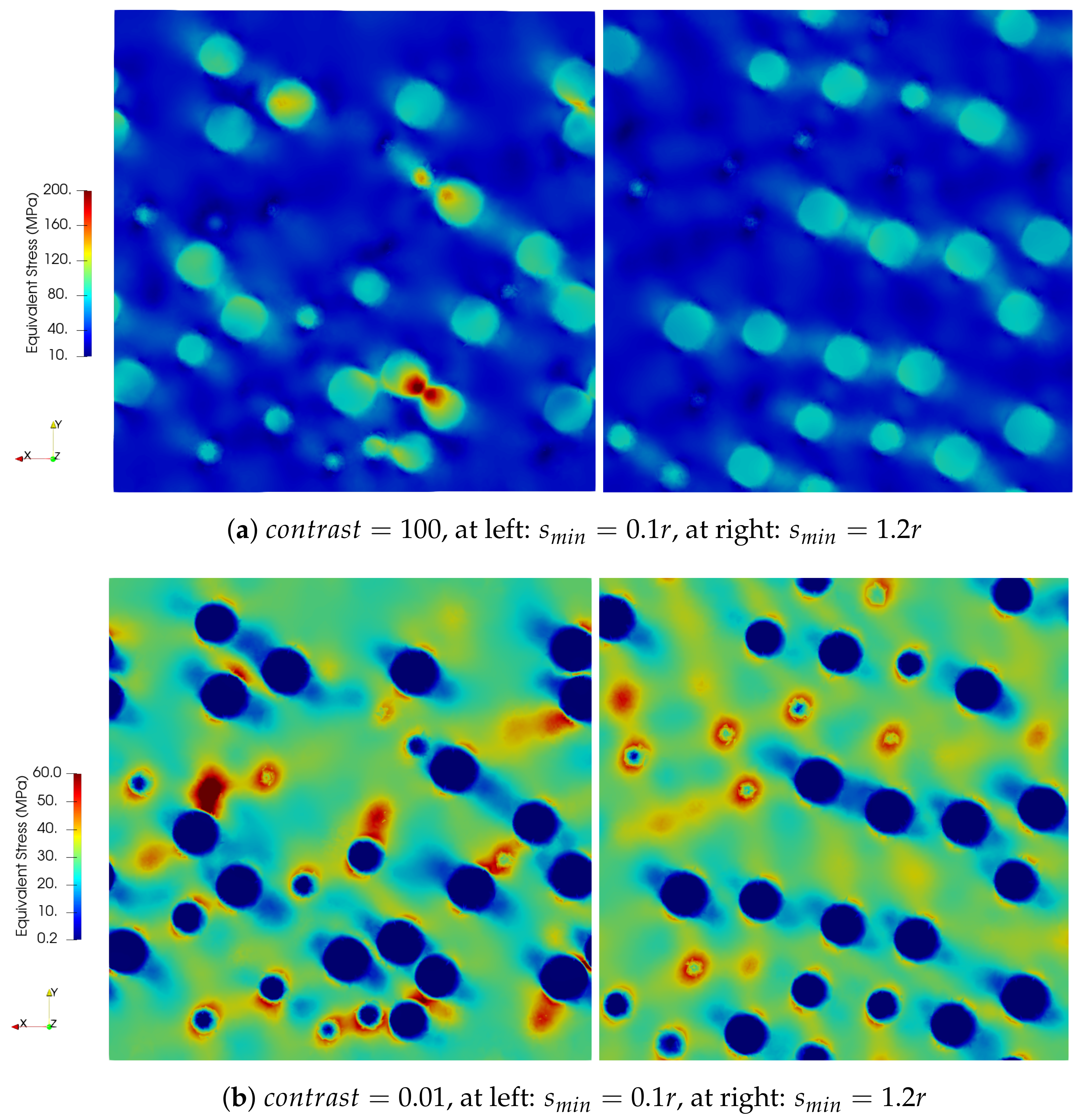
4.3. Results for the Local Fields
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation Formulas for Second-Moment Calculation
Appendix B. Complementary Results for the Effective Properties


Appendix C. Complementary Results for Mean Fields
Appendix C.1. First Moment



Appendix C.2. Second Moment

Appendix D. Complementary Results for Local Fields

References
- Gierden, C.; Kochmann, J.; Waimann, J.; Svendsen, B.; Reese, S. A Review of FE-FFT-Based Two-Scale Methods for Computational Modeling of Microstructure Evolution and Macroscopic Material Behavior. Arch. Comput. Methods Eng. 2022, 29, 4115–4135. [Google Scholar] [CrossRef]
- Hershey, A.V. The Elasticity of an Isotropic Aggregate of Anisotropic Cubic Crystals. J. Appl. Mech. 1954, 21, 236–240. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Christensen, R.; Lo, K. Solutions for effective shear properties in three phase sphere and cylinder models. J. Mech. Phys. Solids 1979, 27, 315–330. [Google Scholar] [CrossRef]
- Masson, R.; Seck, M.; Fauque, J.; Garajeu, M. A modified secant formulation to predict the overall behavior of elasto-viscoplastic particulate composites. J. Mech. Phys. Solids 2020, 137, 103874. [Google Scholar] [CrossRef]
- Ponte Castañeda, P. Stationary variational estimates for the effective response and field fluctuations in nonlinear composites. J. Mech. Phys. Solids 2016, 96, 660–682. [Google Scholar] [CrossRef]
- Feyel, F. A multilevel finite element method (FE2) to describe the response of highly non-linear structures using generalized continua. Comput. Methods Appl. Mech. Eng. 2003, 192, 3233–3244. [Google Scholar] [CrossRef]
- Abdulle, A.; Weinan, E.; Engquist, B.; Vanden-Eijnden, E. The heterogeneous multiscale method. Acta Numer. 2012, 21, 1–87. [Google Scholar] [CrossRef]
- Michel, J.; Suquet, P. Nonuniform transformation field analysis. Int. J. Solids Struct. 2003, 40, 6937–6955. [Google Scholar] [CrossRef]
- Liu, L.; Bessa, M.; Liu, W. Self-consistent clustering analysis: An efficient multi-scale scheme for inelastic heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2016, 306, 319–341. [Google Scholar] [CrossRef]
- Fritzen, F.; Leuschner, M. Reduced basis hybrid computational homogenization based on a mixed incremental formulation. Comput. Methods Appl. Mech. Eng. 2013, 260, 143–154. [Google Scholar] [CrossRef]
- Torquato, S. Morphology and effective properties of disordered heterogeneous media. Int. J. Solids Struct. 1998, 35, 2385–2406. [Google Scholar] [CrossRef]
- El Moumen, A.; Kanit, T.; Imad, A.; El Minor, H. Effect of overlapping inclusions on effective elastic properties of composites. Mech. Res. Commun. 2013, 53, 24–30. [Google Scholar] [CrossRef]
- Majewski, M.; Kursa, M.; Holobut, P.; Kowalczyk-Gajewska, K. Micromechanical and numerical analysis of packing and size effects in elastic particulate composites. Compos. Part B Eng. 2017, 124, 158–174. [Google Scholar] [CrossRef]
- Majewski, M.; Hołobut, P.; Kursa, M.; Kowalczyk-Gajewska, K. Packing and size effects in elastic-plastic particulate composites: Micromechanical modelling and numerical verification. Int. J. Eng. Sci. 2020, 151, 103271. [Google Scholar] [CrossRef]
- Bornert, M.; Stolz, C.; Zaoui, A. Morphologically representative pattern-based bounding in elasticity. J. Mech. Phys. Solids 1996, 44, 307–331. [Google Scholar] [CrossRef]
- Torquato, S. Single-Inclusion Solutions. In Random Heterogeneous Materials: Microstructure and Macroscopic Properties; Springer: New York, NY, USA, 2002; pp. 437–458. [Google Scholar] [CrossRef]
- Idiart, M.; Moulinec, H.; Ponte Castañeda, P.; Suquet, P. Macroscopic behavior and field fluctuations in viscoplastic composites: Second-order estimates versus full-field simulations. J. Mech. Phys. Solids 2006, 6, 201–208. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- El Moumen, A.; Kanit, T.; Imad, A. Numerical evaluation of the representative volume element for random composites. Eur. J. Mech. A/Solids 2021, 86, 104181. [Google Scholar] [CrossRef]
- Plancq, D.; Thouvenin, G.; Ricaud, J.; Struzik, C.; Helfer, T.; Bentejac, F.; Thévenin, P.; Masson, R. PLEIADES: A unified environment for multi-dimensional fuel performance modeling. In Proceedings of the International Meeting on LWR Fuel Performance, Orlando, FL, USA, 19–22 September 2004. [Google Scholar]
- Marelle, V.; Michel, B.; Sercombe, J.; Goldbronn, P.; Struzik, C.; Boulore, A. Advanced Simulation of Fuel Behavior Under Irradiation in the PLEIADES Software Environment. In Modelling of Water Cooled Fuel Including Design Basis and Severe Accidents, Proceedings of the Technical Meeting, Chengdu, China, 28 October–1 November 2013; IAEA TECDOC SERIES, IAEA-TECDOC-CD–1775; IAEA: Vienna, Austria, 2013. [Google Scholar]
- Williams, S.; Philipse, A. Random Packings of Spheres and Spherocylinders Simulated by Mechanical Contraction. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2003, 67, 051301. [Google Scholar] [CrossRef]
- Cooper, D. Random-sequential-packing simulations in three dimensions for spheres. Phys. Rev. A 1988, 38, 522–524. [Google Scholar] [CrossRef]
- Bourcier, C.; Dridi, W.; Chomat, L.; Laucoin, E.; Bary, B.; Adam, E. Combs: Open source python library for RVE generation. Application to microscale diffusion simulations in cementitious materials. In Proceedings of the Joint International Conference on Supercomputing in Nuclear Applications and Monte Carlo 2013 (SNA + MC 2013), Paris, France, 27–31 October 2013. [Google Scholar] [CrossRef]
- SALOME Platform. Available online: https://www.salome-platform.org/ (accessed on 1 July 2022).
- Schneider, M.; Josien, M.; Otto, F. Representative volume elements for matrix-inclusion composites—A computational study on the effects of an improper treatment of particles intersecting the boundary and the benefits of periodizing the ensemble. J. Mech. Phys. Solids 2022, 158, 104652. [Google Scholar] [CrossRef]
- Ramière, I.; Masson, R.; Michel, B.; Bernaud, S. Un schéma de calcul multi-échelles de type Éléments Finis au carré pour la simulation de combustibles nucléaires hétérogènes. In Proceedings of the 13e Colloque National en Calcul des Structures, Giens, France, 13–17 May 2013; Université Paris-Saclay, CSMA: Giens, Var, France, 2017. (In French). [Google Scholar]
- Ramière, I. Around Numerical Methods for Multiphysics and Multiscale Couplings in Solid Mechanics. Habilitation Thesis, Aix Marseille University (AMU), Marseille, France, 2021. [Google Scholar]
- Christensen, R.M. A critical evaluation for a class of micro-mechanics models. J. Mech. Phys. Solids 1990, 38, 379–404. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Cast3M. Available online: http://www-cast3m.cea.fr/ (accessed on 1 July 2022).
- Gloria, A.; Neukamm, S.; Otto, F. Quantification of ergodicity in stochastic homogenization: Optimal bounds via spectral gap on Glauber dynamics. Invent. Math. 2014, 199, 455–515. [Google Scholar] [CrossRef]
- Odegard, G.; Clancy, T.; Gates, T. Modeling of the mechanical properties of nanoparticle/polymer composites. Polymer 2005, 46, 553–562. [Google Scholar] [CrossRef]
- Zerhouni, O.; Brisard, S.; Danas, K. Quantifying the effect of two-point correlations on the effective elasticity of specific classes of random porous materials with and without connectivity. Int. J. Eng. Sci. 2021, 166, 103520. [Google Scholar] [CrossRef]
- Rasool, A.; Böhm, H.J. Effects of particle shape on the macroscopic and microscopic linear behaviors of particle reinforced composites. Int. J. Eng. Sci. 2012, 58, 21–34. [Google Scholar] [CrossRef]







| (MPa) | 20.916 | 20.918 | 20.920 | 20.914 | 20.919 |
| Standard deviation of (MPa) | 0.461 | 0.462 | 0.463 | 0.468 | 0.460 |
| Number of nodes | 279,000 | 65,300 | 32,500 | 88,900 | 158,700 |
| Number of nodes | 30,000 | 300,000 | 2,500,000 |
| Number of samples | 350 | 70 | 35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belgrand, L.; Ramière, I.; Largenton, R.; Lebon, F. Proximity Effects in Matrix-Inclusion Composites: Elastic Effective Behavior, Phase Moments, and Full-Field Computational Analysis. Mathematics 2022, 10, 4437. https://doi.org/10.3390/math10234437
Belgrand L, Ramière I, Largenton R, Lebon F. Proximity Effects in Matrix-Inclusion Composites: Elastic Effective Behavior, Phase Moments, and Full-Field Computational Analysis. Mathematics. 2022; 10(23):4437. https://doi.org/10.3390/math10234437
Chicago/Turabian StyleBelgrand, Louis, Isabelle Ramière, Rodrigue Largenton, and Frédéric Lebon. 2022. "Proximity Effects in Matrix-Inclusion Composites: Elastic Effective Behavior, Phase Moments, and Full-Field Computational Analysis" Mathematics 10, no. 23: 4437. https://doi.org/10.3390/math10234437
APA StyleBelgrand, L., Ramière, I., Largenton, R., & Lebon, F. (2022). Proximity Effects in Matrix-Inclusion Composites: Elastic Effective Behavior, Phase Moments, and Full-Field Computational Analysis. Mathematics, 10(23), 4437. https://doi.org/10.3390/math10234437








