Abstract
According to the World Health Organization updates, the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) caused a pandemic between 2019 and 2022, with millions of confirmed cases and deaths worldwide. There are various approaches to predicting the suspected, infected, and recovered (SIR) cases with different factual or epidemiological models. Some of the recent approaches to predicting the COVID-19 outbreak have had positive impacts in specific nations. Results show that the SIR model is a significant tool to cast the dynamics and predictions of the COVID-19 outbreak compared to other epidemic models. In this paper, we employ the Monte Carlo simulation to predict the spread of COVID-19 in the United Arab Emirates. We study traditional SIR models in general and focus on a time-dependent SIR model, which has been proven more adaptive and robust in predicting the COVID-19 outbreak. We evaluate the time-dependent SIR model. Then, we implement a Monte Carlo model. The Monte Carlo model uses the parameters extracted from the Time-Dependent SIR Model. The Monte Carlo model exhibited a better prediction accuracy and resembles the data collected from the Ministry of Cabinet Affairs, United Arab Emirates, between April and July 2020.
MSC:
65Z05
1. Introduction
The new SARS virus, SARS-CoV-2, responsible for causing the disease COVID-19, was declared a pandemic by the World Health Organization (WHO) on 11 March 2020 [1]. The United Arab Emirates announced a lockdown for schools, universities, and entertainment from 20 March 2020. The lockdown was extended several times to avoid the fatal spread of the virus. According to information published on the WHO website, there were more than 219 million confirmed cases, and more than 4 million deaths globally by September 2021 [2]. The infection was first identified by the Wellbeing Commission of the Hubei area, China. A number of unexplained instances of pneumonia of obscure etiology (obscure causes) [3], which was deadly, were first identified in Wuhan city of Hubei region, China, on 31 December 2019 [4]. After that, many patients were diagnosed as having COVID-19 in many states of China, goading the Chinese Government to control the pandemic [3]. Even though they implemented strict precautionary measures, the COVID-19 pandemic spread rapidly in the following months. Confirmed cases of COVID-19 showed some symptoms such as fever, a wet nose, dry cough, weakness, trouble breathing, and acute pneumonia. Because of the possibility of human transmission, this contagious infection has now spread worldwide, making the USA and Europe new focal points. The first indigenous instance of COVID-19 in the UAE was recorded in Dubai on 29 January 2020, when a group of tourists from Wuhan city tested positive. The UAE stopped all tourism as most of the validated COVID-19 cases were associated with different nations. It is too difficult for governments to diminish the fatality rate without high health costs and financial losses. The interventions at this time consolidated social distancing, separation, and closing schools, colleges, workplaces, houses of worship, bars, and other social places. Infected people were isolated and observed. Statistical or mathematical models assume a vital function in comprehending the spread of the pandemic and for planning systems to contain rapidly spreading irresistible sicknesses in the absence of particular antivirals or successful antibodies [5]. In the year 1927, Kermack and McKendrick [6] built a key pestilence model for human-to-human transmission to depict the elements of the population through three fundamentally unrelated compartments of disease, susceptible (S), infected (I), and removed (R). Mathematical models of irresistible infections are currently universal. Many of these models can exactly portray the dynamic spread of standard pandemics. The traditional SIR model for disease spread ignores the time-varying property, which is not precise and effective in predicting the trend of the disease. Therefore, a time-dependent SIR model was proposed in [7], where both the transmission rate and recovery rate are a function of time. Monte Carlo simulation can also be used to develop COVID-19 spread dynamics. It can be used as a decision-making tool in battling COVID-19 to respond to immediate needs and for modeling any other infectious diseases in the future [8]. Like the compartmental disease models (SIR) framework, the Monte Carlo model captures the population changes in each cohort but with different approaches. It is similar to a stochastic point process model because it treats each individual in a population as a random point, so the rationale is much more intuitive and easy to interpret. This paper implements a time-dependent SIR model and uses the output to present a Monte Carlo model to predict the number of active cases, new cases, and peak time. Additionally, we discuss other scenarios to predict the outbreak of COVID-19 in the UAE. Specifically, we try to answer the following research question: what are the active cases in the long run? Our results show good prediction accuracy for both time-dependent SIR and Monte Carlo models compared to real data collected from the United Arab Emirates Ministry of Cabinet Affairs. The structure of this paper is as follows: Section 2 displays the literature review about different simulation ways and proposes models to represent the outbreak of these diseases. In Section 3, we elaborate on the compartmental SIR models. The discussion of the implementation and the results is given in Section 4, and we conclude the paper and suggest avenues for future research in Section 5.
2. Literature Review
A few mathematical models have been developed to consider the transmission elements of the COVID-19 pandemic. Chen et al. [9] created a bats–hosts–reservoir–people network model to consider the transmission elements of COVID-19. Lin et al. [10] expanded the susceptible–exposed–infected–recovered (SEIR) compartment model to examine the elements of COVID-19 consolidating the public view of the danger and the number of aggregate cases. Khajanchi et al. [11] considered an all-inclusive SEIR model to contemplate the transmission elements of COVID-19 and play out a momentary expectation dependent on the information from India. A partial request by Khan et al. [12] concentrated on broadening the SEIR model in the attempt to portray the elements of COVID-19 infection in Wuhan, China, where the researchers determined the reproduction number (R0) to be 2.4829. Wu et al. [13] examined an SEIR model to research the elements of COVID-19 human–human transmission based on the information from Wuhan, China. Their study focused on the period from 31 December 2019 to 28 January 2020, and they found that the reproduction number (R0) was approximately 2.68. The authors in [14] proposed a non-autonomous nonlinear deterministic model to study the control of COVID-19. The model is divided into five compartments, namely susceptible, exposed, asymptomatic infected (not showing symptoms but can infect other healthy people), symptomatic infected (that has symptoms of disease and can infect other people), and recovered individuals. They used four COVID-19 controls in the absence of vaccination and proved that the disease can be reduced when individuals strictly stick to these proposed controls. Ref. [15] utilized an SIR model to outline the transmission elements of COVID-19 and gauge its clinical seriousness. To consider the elements of COVID-19, a stochastic transmission model was created by Kucharski et al. [16]. The examination of viral elements utilizing numerical models has helped integrate experiences into the comprehension of viral contamination, for example, in tuberculosis and dengue infection [17]. Observable endeavors include the openly accessible and constantly refreshed gauges by the Institute of Health Metrics and Evaluation (IHME) at the University of Washington [18] and the MRC Center for Global Infectious Disease Analysis at Imperial College London [19], among others, where there are free open COVID-19 prediction models for the world that utilize an assortment of factual or scourge infectious models. Faniran et al. [20] proposed a model of SARS-CoV-2 transmission dynamics in order to analyze the influence of a hypothetical imperfect anti-COVID-19 vaccination on the control of both the first and second variants of SARS-CoV-2. They took into account the influence of the escape rate of quarantined infected persons from isolation facilities. Their model consisted of nine mutually exclusive compartments representing COVID-19 dynamics. A few studies have focused on obtaining general information about future passings and accommodation needs [21], on disease cases and peaks [22], and others studied the effect of social separating, travel limitations, and isolation strategies [23]. Some distributed investigations have endeavored to approve the precision of explicit prediction techniques [22], where they used COVID-19 data from China. IHME has extracted a model which achieved 70 percent accuracy [24]. However, the accuracy fell the following day by 95 percent outside the predictions [25]. The IHME group later updated the model in a new approach in [26], even though the expected errors were high. Researchers and analysts worked to improve the strategies and techniques in a hurry to make an ever-increasing number of precise simulation models on the following developments of the COVID-19 pandemic [27]. Despite the unique nature of the COVID-19 disease, a few models have achieved good and positive impacts on educated strategy producers or decision makers [25]. Monte Carlo simulation approaches are limited in modeling and predicting the spread of COVID-19, however, the researchers used fixed values of the reproduction number (R0) extracted from the literature. Kharroubi investigated the problem of modeling the current COVID-19 pandemic trend in Lebanon for a long time [28]. He developed two different models using the Bayesian Markov chain and Monte Carlo simulation methods. The model was applied in Lebanon, and the results and data were published in [28]. Additionally, the model was applied to other countries in different periods. As a result, many researchers simulated the spread of the COVID-19 virus in different countries. However, they had different accuracy prediction results. Amro et al. [29] presented the Monte Carlo simulation model of COVID-19 spread inspired by physics variables such as temperature, cross-section, and interaction range, considering the Plank distribution of photons in the black body radiation to describe the mobility of individuals. Maltezos et al. [30] aimed to generate epidemiological data based on the natural mechanism of transmission of COVID-19, assuming the random interactions of a large finite number of individuals over very short distance ranges. These generated epidemic curves and proposed a methodology for determining the effective reproductive number during the main part of the daily new cases of the epidemic. In this paper, we implement and evaluate the performance of the time-dependent SIR model using real data (COVID-19 data from the United Arab Emirates), and establish a new Monte Carlo model to predict the COVID-19 outbreak based on the time-dependent SIR model outputs. We also study the effect of social separation and government interventions based on our new model.
3. Prediction Models
3.1. Traditional SIR Models
SIR models are compartmental models in epidemiology (mathematical modeling of infectious diseases). The model divides the population into susceptible, infected, and removed. Individuals may move between compartments. The labels’ arrangement often indicates the flow patterns between the compartments; for instance, SEIS stands for susceptible, exposed, infected, and then susceptible again.
As in Figure 1, the SIR model measures the gradual changes in the number of susceptible, infected, and removed populations over a period of time in a region. The incremental change can be represented by the following equations:
where s, r, i:

Figure 1.
SIR model.
The SIR model captures two directions of movements from susceptible to infected and infected to removed. Table 1 describes the variables of the SIR model.

Table 1.
Traditional SIR Model Variables.
The SIR model is based on the following assumptions:
- N is the population that may be affected by the disease. It gives the susceptible individuals at the beginning of the period. It is constant.
- is the number of individuals that are not yet infected, i.e., .
- is the number of individuals infected and removed (quarantined for treatment)—.
- is the number of infected individuals able to spread the disease to those who are still susceptible.
- The individuals belonging to can neither be infected again nor infect others.
- The contact and removal rates are constants.
- Throughout the assessment period, there have been no changes in the demographics.
- Because of the population’s diversity, an infected person is likely to come into touch with any susceptible person.
3.2. Time-Dependent SIR Model
The conventional SIR model ignores the time-varying property of the transmission rate and recovering rate . The authors in [7] proposed the time-dependent SIR model, where both and are functions of time. Such a time-dependent SIR model is much better at tracking the spread of the disease and controlling and predicting the future trend. A person in the susceptible state does not have an illness at time t, however, they might be infected if they come into contact with an individual infected with the disease. The contaminated state alludes to a person with the disease at time t which may conceivably infect an individual. The recovered state alludes to a person which has either recovered or died from the infection and is not, at this point, infectious at time t. Additionally, a recovered individual will not return to the susceptible state any longer. From an epidemiological perspective, the number of deaths is counted in the recovered state as recovery or death since these do not affect the spread of the infection. Accordingly, they can be viably disposed of from the likely host of the disease. Let and be the transmission rate and recovering rates, respectively, at time t. X(t) is the active cases at time t [7]. Substituting and by and in the equations of the conventional SIR model results in:
which verifies the following relation:
where n is the total population and is the number of active cases at time t.
Replacing and by and in the differential equations above yields:
These equations describe the difference in the number of susceptible persons at time t. According to [7], assuming that the total population is n, then the probability of a randomly chosen person being in the susceptible state is . Hence, an individual in the infected state will contact (on average) people in the susceptible state per unit of time, which implies that the number of newly infected persons is (as there are people in the infected state at time t). On the contrary, the number of people in the susceptible state will decrease by . Additionally, as every individual in the infected state will recover with rate , there are (on average) people recovered at time t. This explains the difference of at time t. The variables , and still satisfy Equations (11)–(13), and thus we have:
4. Modeling and Implementation
We apply the time-dependent SIR model to extract the values of , , and R0. We use the ridge regression model [31] to train the dataset, predict the active cases, and compare them with real data to check the model’s accuracy. The parameters extracted from this model will be used to implement the Monte Carlo approach.
4.1. Extracting R0 Values Based on Time-Dependent SIR Model
Due to the nature of COVID-19, the data are updated on a daily basis. Discrete-time difference equations were revised based on the rules described in the previous section.
The majority of the populace was in a vulnerable state during the start of the disease spread, and there were very few confirmed cases. The following equation is implied by the assumptions that S(t) = n, and t ≥ 0, for the analysis of COVID-19’s initial stage:
Based on Equations (15)–(18), we can easily derive the (t) and (t) of each day. The historical data from a certain period were given by X(t), R(t), 0 ≤t≤T− 1, then the corresponding (t), (t), 0 ≤t≤T− 2 can be measured [7]. With the above information, the regression model predicts the time-varying transmission and recovery rates.
where (t) and (t) are tracked and predicted by the commonly used finite impulse response (FIR) [32] filters in linear systems. From the FIR filters, they are predicted as follows:
where J and K are the orders of the two FIR filters (0 <J, K< T − 2), , j = 0, 1, . . . , J, and , k = 0, 1, . . . , K are the coefficients of the impulse responses of these two FIR filters [7]. The estimation approach that resolves the following optimization problem is the ridge regression, which is one of several frequently used machine learning techniques for the estimation of the coefficients of the impulse response of an FIR filter:
where and are the regularization parameters. This demonstrates how to track and predict the number of infected people and the number of recovered people in the time-dependent SIR model using the two FIR filters. Given a period of historical data X(t), R(t), 0 ≤t≤T− 1, we first find (t), (t), 0 ≤t≤T− 2. Then, the ridge regression is solved to learn the coefficients of the FIR filters, i.e., , j = 0, 1, . . . , J and , k = 0, 1, . . . , K. Once these coefficients are learned, (t) and (t) can be predicted at time t = T− 1 by the trained ridge regression. Denote by (respectively, ) the predicted number of infected (respectively, recovered) persons at time t. To predict and at time t = T, (t) and (t) are replaced by and [7]. This leads to:
Algorithm A1 in Appendix A presents the algorithm to train and estimate the , , and R0 values. We applied the algorithm on COVID-19 public data related to the United Arab Emirates. The data were downloaded from the Federal Competitiveness and Statistics Centre (FCSA) and WHO websites. The total population is N= 9,890,402.
We performed our experiment between 4 April 2020 and 20 July 2020. Figure 2, Figure 3 and Figure 4 show the rates of R0, , during the period from 7 April 2020 to 20 July 2020.
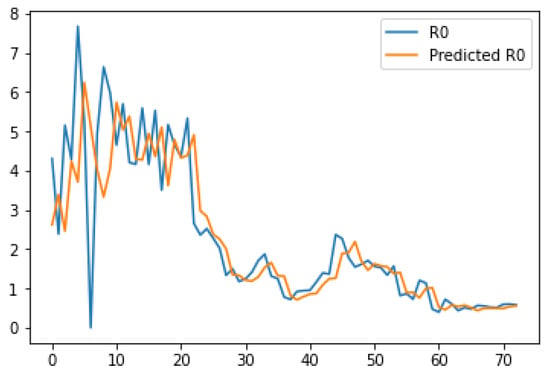
Figure 2.
R0 rates during given the period.
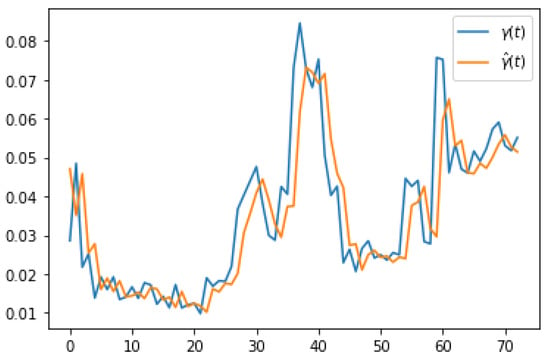
Figure 3.
rates during the given period.
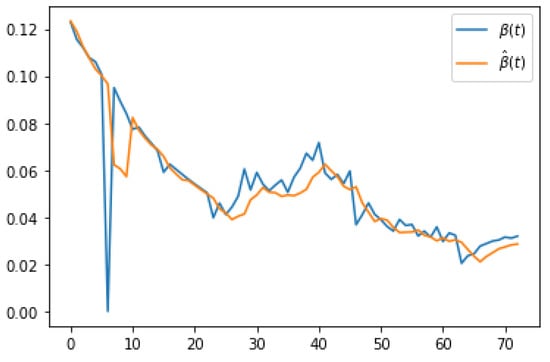
Figure 4.
rates during the given period.
Figure 5 shows the evaluation of the time-dependent SIR model of COVID-19 in the United Arab Emirates from 7 April 2020 to 20 August 2020. The model catches the same peak time with a very accurate value during the training period. However, Figure 6 shows an accurate comparison between the predicted and actual active cases. The model was not able to predict the next peak after finishing the simulation period (after 125 days). The regression model learns from a specific dataset, and these data contain one peak only.
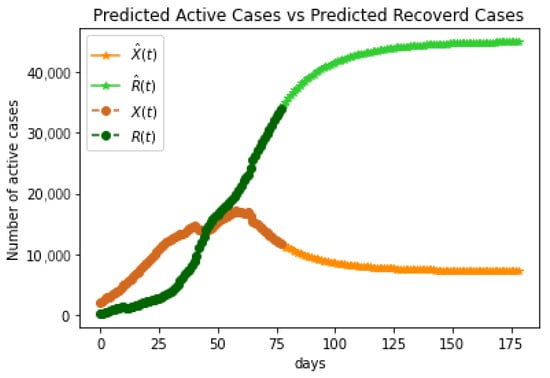
Figure 5.
Predicted active cases vs. predicted recovered cases based on the time-dependent SIR model. is the actual number of infected (active) cases; is the predicted number of infected cases; is the real number of recovered cases; and is the predicted number of recovered cases.
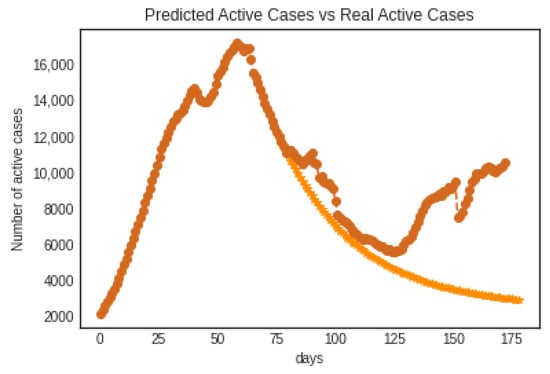
Figure 6.
Predicted infected cases (active) vs. real active cases based on the time-dependent SIR model. is the dark orange, and is the light orange.
To measure the accuracy of fitting for the time-dependent SIR model, we computed the mean absolute error () and root mean square error (). The and are defined in the following equations:
where represents the observed value, represents the simulation value, and n is the sample size. The values of and for the time-dependent SIR model during the simulation period (7 April 2020–20 August 2020) are 144 and 507, respectively, and their values after one–two months later (150 days) are 169 and 584, respectively. These results prove that the time-dependent SIR model cannot predict accurate values after training.
4.2. Applying Monte Carlo Simulation
Monte Carlo simulation follows a stochastic point process modeling approach based on algorithms that rely on repeated random sampling to compute their results. This paper uses this simulation procedure to represent the spread of COVID-19. We apply this simulation procedure to our data and compare its performance with the performance of the time-dependent SIR model. Firstly, we built our estimation algorithm to estimate the number of active and new cases based on dynamic R0 values. Subsequently, we built a Monte Carlo model to predict the active and new cases during the specific period. Then, we tested the model with real COVID-19 data reported by the United Arab Emirates. Finally, based on a number of arbitrary scenarios, we looked at several expected characteristics of the simulation model performance. The model output displays, for a given observation period, the estimated daily number of new confirmed cases and the daily number of active cases (i.e., new cases and carry-over infectious cases). The model output answers many questions asked by decision makers’ inquiries, e.g., What is the peak time? How many active cases fall back to a predefined level? What might be the outnumber of affirmed cases before the end of the COVID–19 flare-up? In this Section, we discuss our main approach. We use the values of R0, extracted from the time-dependent SIR model, to build the Monte Carlo model to simulate the outbreak of COVID-19 in the United Arab Emirates. The difference in this method is that we do not use a fixed value for R0 as in previous studies. Alternatively, we use different values, extracted from the time-dependent SIR model during the training period, and use them in the COVID-19 simulation by Monte Carlo approach. Finally, we discuss different assumptions and scenarios in order to prove our model’s effectiveness and compare the results with the real values. Our model outputs include the estimated daily number of newly confirmed and active infection cases over the observation period. The outputs of the model will answer our research questions. Our model was implemented using Python within the Jupiter notebook, and the source code is available at the following link (https://github.com/nrr-90/MonteCarlo-Simulation, accessed on 10 October 2022).
4.2.1. Model Assumptions and Parameters
The most important parameter in Monte Carlo simulation as the SIR model is the R0 (the number of cases resulting from the number of people a single infectious person can infect during their infectious period). Usually, it is defined from the literature, however, in our study, we used a strategy to define this number based on the implementation of the time-dependent SIR model which differs from the traditional SIR model. The assurance of the contamination rate R0 during a perception period relied upon numerous variables that accounted for various events including the integrity of the attack of the noticed number of affirmed COVID–19 cases; the understanding of the effect of government mediation/arrangements; the limit of the medical care framework; the assessment of the likely outcomes because of public reactions to government approaches; and individuals initiating behavior changes.
4.2.2. Estimation Algorithm
Because of the vulnerability presented by a probability distribution for deciding the number of infected cases and the time at which such an occasion would happen, we ought to permit the observation period generally more than the simulation time period. The analysis of the COVID–19 information revealed that 100 observation days were sufficient to obtain balanced-out reenactment results. The length of R0 values should be the same as the number of simulation days. Since Monte Carlo simulation processes involve the generation of random numbers, the simulation analysis results would be subject to random variation due to the different starting points intrinsically defined by a randomly selected seed value [33]. As such, when we would think about various situations of illness transmission utilizing the recreation model, a similar arbitrary seed was determined for every situation for a substantial correlation. The assurance of the infection rate designs was a blended methodology including the use of reproduction numbers extracted from the time-dependent SIR model. Algorithm A2 in Appendix A represents the procedure used to estimate and predict the number of new cases, active cases, and total cases during a specific observation and simulation period. The parameters of the algorithm are shown in Table 2.

Table 2.
Estimation Algorithm Parameters.
The first loop of the algorithm estimated the number of new cases infected by the initial number of infected cases, we use Poisson distribution with the first value of as a mean to estimate the number of new cases, and the negative binomial distribution to estimate the number of days before a new person is infected. Consequently, we add the number of new cases to the new cases array according to the estimated specific day. The second loop of the algorithm does the same by running for every new person added by the first loop, and the new cases infected by this person are also estimated by Poisson distribution, but this time by using different values over the simulation period. The values extracted from time-dependent SIR model. Estimation procedure assumptions:
- R0 values are extracted by time-dependent SIR model.
- The number of people getting infected by one person is estimated by Poisson distribution with the mean (R0 values).
- The number of days for anyone to get infected is estimated by a negative binomial distribution with a mean of 4 days.
- The limit of the number population is defined by the user.
- The immunity proportion in a population is defined by the user, and comprises the vaccinated and quarantined people who will be excluded from the infected proportion and the proportion that can infect others.
- The initial number of infectious people is defined by the user.
- The observation period is defined by the user.
- The simulation period is defined by the user.
- The spread of COVID–19 started with one person.
- We expect that at least one day is required for recently infected individuals to infect others.
- The times of infection are dependent, so more than one person could be infected by the same person on the same day.
- Once the number of infected people has been reached, it is generated by Poisson distribution, and the infectious person at the source is excluded from the transmission cycle.
- After the number of days determined by the negative binomial distribution, an infected person would be removed from the active case-cohort if they had no one else to spread the virus to.
4.2.3. Monte Carlo Model Implementation
To account for the uncertainty in a Monte Carlo simulation model, a bootstrap approach [34] was used to determine the estimated median and interquartile values of the number of active cases and the change in the total number of confirmed cases across the observation period. Each simulation model was run 10,000 times, the median values were considered the most likely estimation, and the uncertainty level was characterized by the interquartile range. Algorithm A3 in Appendix A represents the execution of the estimation procedure over the Monte Carlo Model.
We ran the simulation procedure 10,000 times, and then we predicted the active cases, new cases, and the median value for every day of the simulation period. We first examined the model’s theoretical performance using a few reasonable hypothetical infection rate patterns. Accepting the R0 values extracted from the time-dependent SIR model, Figure 7 shows the predicted active cases vs. the real active cases during the simulation period. The actual number of active people is represented by the solid curve in dark green. The predicted number of active people is represented by the dashed curve in light green. Figure 8 shows the predicted new cases vs. the real new cases during the simulation period. There is no training in the Monte Carlo simulation, which is based on selecting random sampling to compute the results. However, we can notice that the model is able to catch the peak time and peak values. The values of and for the Monte Carlo simulation model are 167 and 211, respectively. The values are better than those for the time-dependent SIR model, and the Monte Carlo model can be applied to any time slot and is able to catch different peak values in contrast to the time-dependent SIR model.
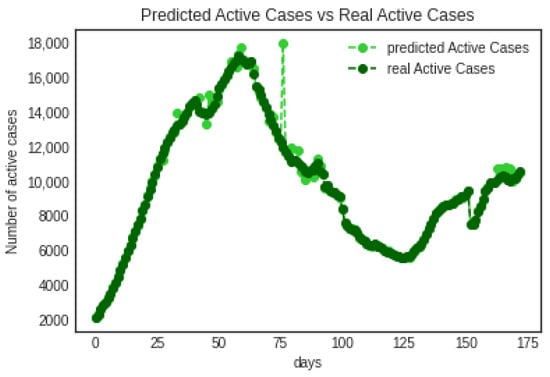
Figure 7.
Predicted Active Cases vs. Real Active Cases Based On Monte Carlo Simulation.
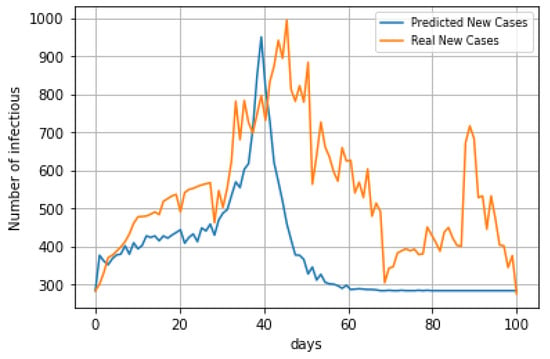
Figure 8.
Predicted New Cases vs. Real New Cases Based On Monte Carlo Simulation.
If we decrease the expected number of days for an existing infectious person to infect others, we will obtain fewer infected persons, but the peak time will not change (Figure 9).
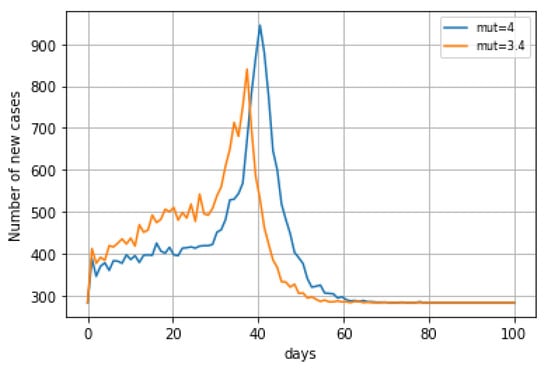
Figure 9.
Predicted New Cases with different Infected days values.
We want to see how the outbreak would have played out if the government’s action had come into effect five days earlier. The peak should be later and show less infected values (Figure 10).
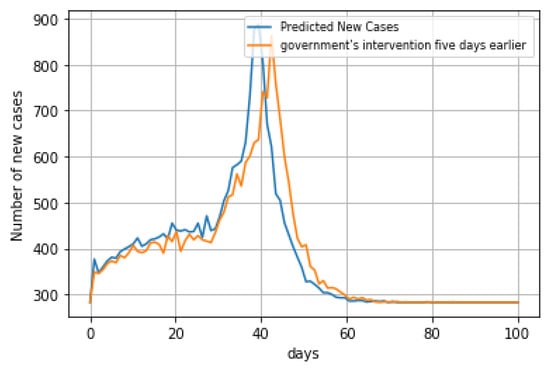
Figure 10.
Predicted New Cases if the Government interventions were 5 days earlier.
Finally, we looked at how things may change if the initial R0 values were less than 3. We can see that the peak will be at the same time and we will obtain a smaller number of infected cases (Figure 11).
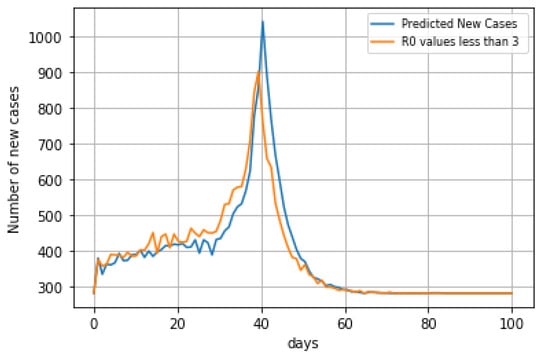
Figure 11.
Predicted New Cases with smaller. R0 rates.
4.3. Results Discussion
By comparing the proposed simulation model with the time-dependent SIR model, and by checking the results presented in Figure 9, Figure 10 and Figure 11, we conclude:
- Both the time-dependent SIR model and Monte Carlo model were able to catch the peak time and peak values.
- The values of and for Monte Carlo simulation were better than those for the time-dependent SIR model.
- Monte Carlo model can be applied to any time slot and it is able to catch different peak values in contrast to the time-dependent SIR model.
- By five days earlier of government intervention, the number of new cases would peak later and with much lower peak values.
- By reducing R0 to less than 3 for the first five days, the number of new cases would peak on the same day, however, with much lower peak values.
- Decreasing the expected number of days for an existing infectious person to infect others (3.4 versus 4 days) would considerably decrease the peak level.
- A higher value production rate or expected number of days for an existing infectious person to infect others would bring a higher number of peak values, keeping different things equivalent.
Each simulation model was run 10,000 times, and the median values of each simulation model were taken into consideration as the most likely estimate, and the interquartile range (i.e., the range between the 25th percentile and 75th percentile of the 10,000 values) was used to quantify the uncertainty level, as in Figure 12.
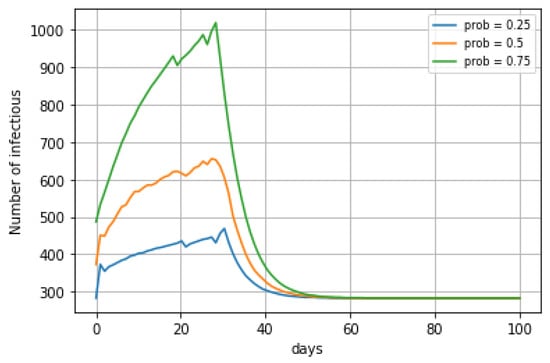
Figure 12.
Three hypothetical infection rate patterns of the number of new cases during the observation period.
The extracted results are reasonable and sufficient to answer our research question: What are the active cases in the long run?
We can see that, within our observation period, the model was able to predict the peak time and the peak values. The model was able to detect the effects of government interventions and social distancing. Regarding the number of active and daily new cases, our model showed adequate results compared to the real values, which are represented in Figure 7 and Figure 8.
5. Conclusions
This study developed a novel Monte Carlo simulation procedure to capture the essential virus transmission dynamics to model COVID-19 spread over time. The study implemented a stochastic point model in a Monte Carlo simulation based on R0 values extracted from the time-dependent SIR model. The proposed simulation model demonstrated a strong promise to be employed as an efficient and flexible tool in simulating the COVID-19 outbreak in both hypothetical and real-world instances. We built an SIR model strategy and novel Monte Carlo simulation technique through a hypothetical and genuine example of the United Arab Emirates data. The proposed models indicate a decent potential to be utilized as a compelling and versatile device in performing a scenario for specifically combating COVID–19 and might be explicitly used for some other irresistible illnesses in general. By studying the most basic COVID–19 spread component, the Monte Carlo model gives a legitimate and viable option compared to SIR models for predicting COVID-19 spread and then limiting the misfortunes brought about by its flare-up. The Monte Carlo model extracted accurate results and was proven to be more flexible than the time-dependent SIR model.
Author Contributions
Conceptualization, N.A., F.S. and S.H.; Data curation, N.A.; Formal analysis, N.A. and F.S.; Methodology, N.A. and F.S.; Software, N.A.; Validation, F.S., S.H. and M.A.; Writing—original draft, N.A.; Writing—review and editing, F.S., S.H. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this appendix, we listed the algorithms used in our research.
| Algorithm A1: Time-Dependent SIR Model. |
Input: { X(t),R(t), 0 ≤t≤ T − 1 }, Regularization parameters and , FIR filters J and K, prediction window W Output: { , , 0 ≤t≤T− 2 }, { , , t≥T− 1 }, and { (t), (t), 0 ≤t≤T− 2 }
|
| Algorithm A2: Estimation procedure. |
Input: R0 values, days, SimulationPeriod, pp, N0, , size, limit Output: arrays of daily new cases, daily active cases and all cases
|
| Algorithm 3: Monte Carlo Algorithm. |
|
References
- World Health Organization. Coronavirus Disease (COVID-19) Outbreak Situation; WHO: Geneva, Switzerland, 2020. [Google Scholar]
- Ghiasvand, S. Predicting the prevalence of COVID-19 pandemic in Germany; Technical Report, Working Paper 2020; Technical University of Dresden: Dresden, Germany, 2020. [Google Scholar]
- Chen, Q.; Zheng, Z.; Zhang, C.; Zhang, X.; Wu, H.; Wang, J.; Wang, S.; Zheng, C. Clinical characteristics of 145 patients with coronavirus disease 2019 (COVID-19) in Taizhou, Zhejiang, China. Infection 2020, 48, 543–551. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J.; Normile, D. New SARS-like virus in China triggers alarm. Science 2020, 367, 234–235. [Google Scholar] [CrossRef]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Chen, Y.C.; Lu, P.E.; Chang, C.S. A Time-dependent SIR model for COVID-19. arXiv 2020, arXiv:2003.00122. [Google Scholar]
- Hassanat, A.B.; Mnasri, S.; Aseeri, M.; Alhazmi, K.; Cheikhrouhou, O.; Altarawneh, G.; Alrashidi, M.; Tarawneh, A.S.; Almohammadi, K.; Almoamari, H. A Simulation Model for Forecasting COVID-19 Pandemic Spread: Analytical Results Based on the Current Saudi COVID-19 Data. Sustainability 2021, 13, 4888. [Google Scholar] [CrossRef]
- Chen, T.M.; Rui, J.; Wang, Q.P.; Zhao, Z.Y.; Cui, J.A.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9, 24. [Google Scholar] [CrossRef]
- Sanche, S.; Lin, Y.T.; Xu, C.; Romero-Severson, E.; Hengartner, N.; Ke, R. High contagiousness and rapid spread of severe acute respiratory syndrome Coronavirus 2. Emerg. Infect. Dis. 2020, 26, 1470. [Google Scholar] [CrossRef]
- Khajanchi, S.; Sarkar, K.; Mondal, J.; Perc, M. Dynamics of the COVID-19 pandemic in India. arXiv 2020, arXiv:2005.06286. [Google Scholar]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Wu, Z.; McGoogan, J.M. Characteristics of and important lessons from the coronavirus disease 2019 (COVID-19) outbreak in China: Summary of a report of 72 314 cases from the Chinese Center for Disease Control and Prevention. JAMA 2020, 323, 1239–1242. [Google Scholar] [CrossRef] [PubMed]
- Asamoah, J.K.K.; Okyere, E.; Abidemi, A.; Moore, S.E.; Sun, G.Q.; Jin, Z.; Acheampong, E.; Gordon, J.F. Optimal control and comprehensive cost-effectiveness analysis for COVID-19. Results Phys. 2022, 33, 105177. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.T.; Leung, K.; Bushman, M.; Kishore, N.; Niehus, R.; de Salazar, P.M.; Cowling, B.J.; Lipsitch, M.; Leung, G.M. Estimating clinical severity of COVID-19 from the transmission dynamics in Wuhan, China. Nat. Med. 2020, 26, 506–510. [Google Scholar] [CrossRef] [PubMed]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Flasche, S. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef] [PubMed]
- Das, D.K.; Khajanchi, S.; Kar, T.K. The impact of the media awareness and optimal strategy on the prevalence of tuberculosis. Appl. Math. Comput. 2020, 366, 124732. [Google Scholar] [CrossRef]
- Luo, J. Predictive monitoring of COVID-19. SUTD Data-Driven Innov. Lab 2020, 446. [Google Scholar]
- Eker, S. Validity and usefulness of COVID-19 models. Humanit. Soc. Sci. Commun. 2020, 7, 54. [Google Scholar] [CrossRef]
- Faniran, T.S.; Ali, A.; Al-Hazmi, N.E.; Asamoah, J.K.K.; Nofal, T.A.; Adewole, M.O. New Variant of SARS-CoV-2 Dynamics with Imperfect Vaccine. Complexity 2022, 2022, 1062180. [Google Scholar] [CrossRef]
- Murray, C.J. Forecasting COVID-19 impact on hospital bed-days, ICU-days, ventilator-days and deaths by US state in the next 4 months. MedRxiv 2020. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165. [Google Scholar] [CrossRef]
- Kissler, S.M.; Tedijanto, C.; Goldstein, E.; Grad, Y.H.; Lipsitch, M. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science 2020, 368, 860–868. [Google Scholar] [CrossRef] [PubMed]
- Woody, S.; Tec, M.G.; Dahan, M.; Gaither, K.; Lachmann, M.; Fox, S.; Meyers, L.A.; Scott, J.G. Projections for first-wave COVID-19 deaths across the US using social-distancing measures derived from mobile phones. medRxiv 2020. [Google Scholar] [CrossRef]
- Marchant, R.; Samia, N.I.; Rosen, O.; Tanner, M.A.; Cripps, S. Learning as we go: An examination of the statistical accuracy of COVID19 daily death count predictions. arXiv 2020, arXiv:2004.04734. [Google Scholar]
- Jewell, N.P.; Lewnard, J.A.; Jewell, B.L. Caution warranted: Using the Institute for Health Metrics and Evaluation model for predicting the course of the COVID-19 pandemic. Ann. Intern. Med. 2020, 173, 226–227. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Kharroubi, S.A. Modeling the spread of COVID-19 in Lebanon: A Bayesian perspective. Front. Appl. Math. Stat. 2020, 6, 40. [Google Scholar] [CrossRef]
- Amaro, J.E.; Orce, J.N. Monte Carlo simulation of COVID-19 pandemic using Planck’s probability distribution. Biosystems 2022, 218, 104708. [Google Scholar] [CrossRef]
- Maltezos, S.; Georgakopoulou, A. Novel approach for Monte Carlo simulation of the new COVID-19 spread dynamics. Infect. Genet. Evol. 2021, 92, 104896. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Neuvo, Y.; Cheng-Yu, D.; Mitra, S. Interpolated finite impulse response filters. IEEE Trans. Acoust. Speech Signal Process. 1984, 32, 563–570. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference; Cengage Learning: Boston, MA, USA, 2021. [Google Scholar]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; Chapman & Hall: London, UK, 1993; 436p. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).