An Enhanced Northern Goshawk Optimization Algorithm and Its Application in Practical Optimization Problems
Abstract
1. Introduction
- To improve the capacity of exploitation, this paper applies the quadratic interpolation function to each individual, to find a better solution.
- Different opposite learning methods are employed to help the algorithm search the space more fully, including opposite learning, quasi-opposite learning and quasi-reflected learning.
2. The Enhanced Northern Goshawk Optimization Algorithm
2.1. The Original Northern Goshawk Optimization
2.1.1. Initialization
2.1.2. Prey Identification
2.1.3. Prey Capture
2.2. The Improved Northern Goshawk Optimization
2.2.1. Polynomial Interpolation Strategy
2.2.2. Multi-Strategy Opposite Learning Method
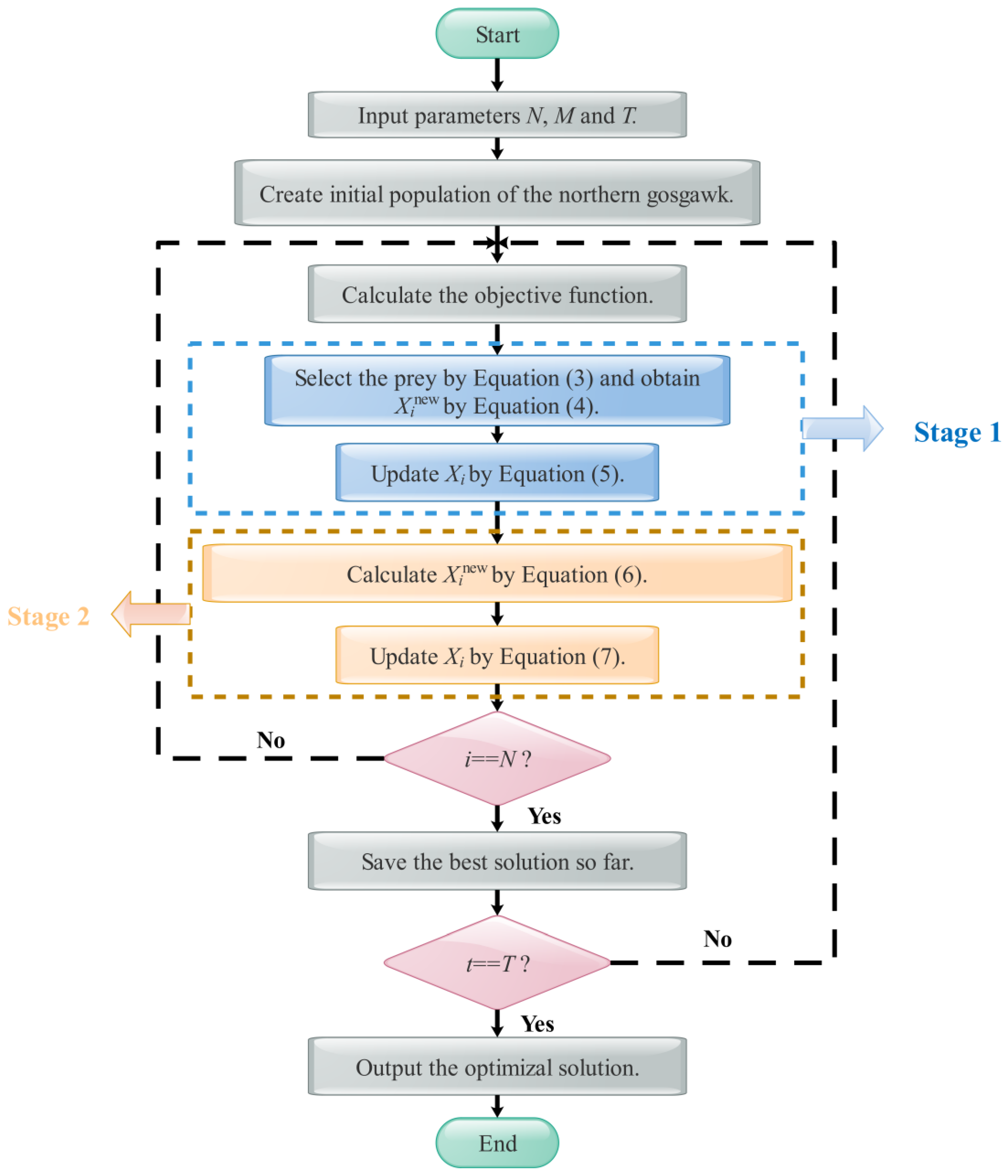
- Step 1. Initialize the parameters, such as the size of the northern goshawk population N, the dimension of the problem M, and the maximum iteration time T.
- Step 2. Create the initial northern goshawk population by Equation (2).
- Step 3. when t < T, calculate the fitness value of each individual in the population. Following the selection of the according prey of the i-th individual Xi by Equation (3), the updated solution can be obtained by Equations (4) and (5).
- Step 4. Divide the population into three equal groups.
- Step 5. Based on Equations (13)–(15), apply different opposite learning methods to the according group, and obtain new solutions.
- Step 6. Mix the new solutions with the population, and N better solutions are selected as the new population.
- Step 7. By simulating the behavior of chasing the prey, calculate the new solution by Equation (6). Then, update the solution by Equation (7).
- Step 8. Apply the polynomial interpolation strategy to each individual and update the individual by Equations (11) and (12).
- Step 9. if t < T, return to Step 3. Otherwise, output the best individual and its fitness value.
3. Numerical Experiment on the Test Functions
3.1. Test Functions and Parameters Setting
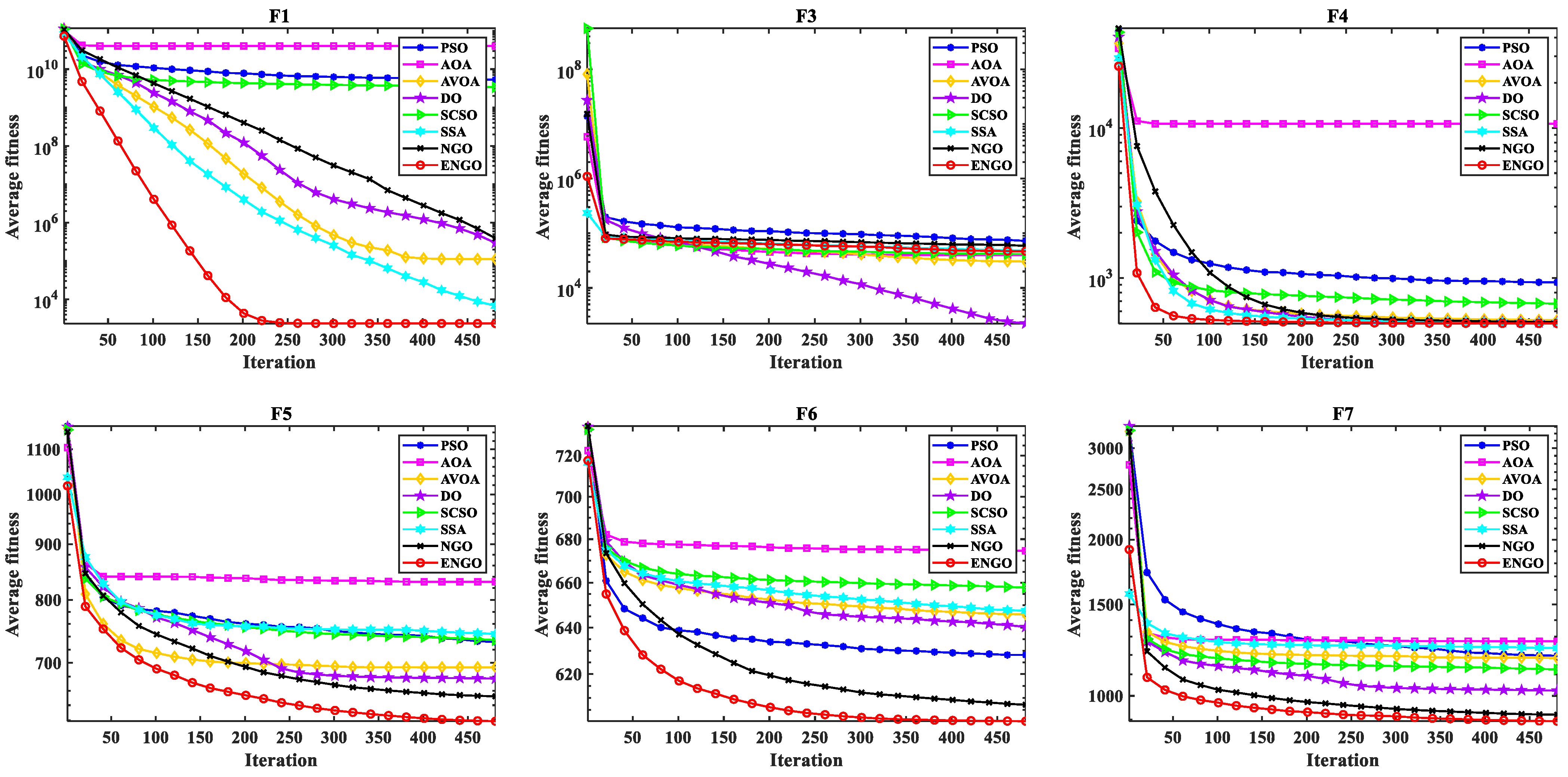
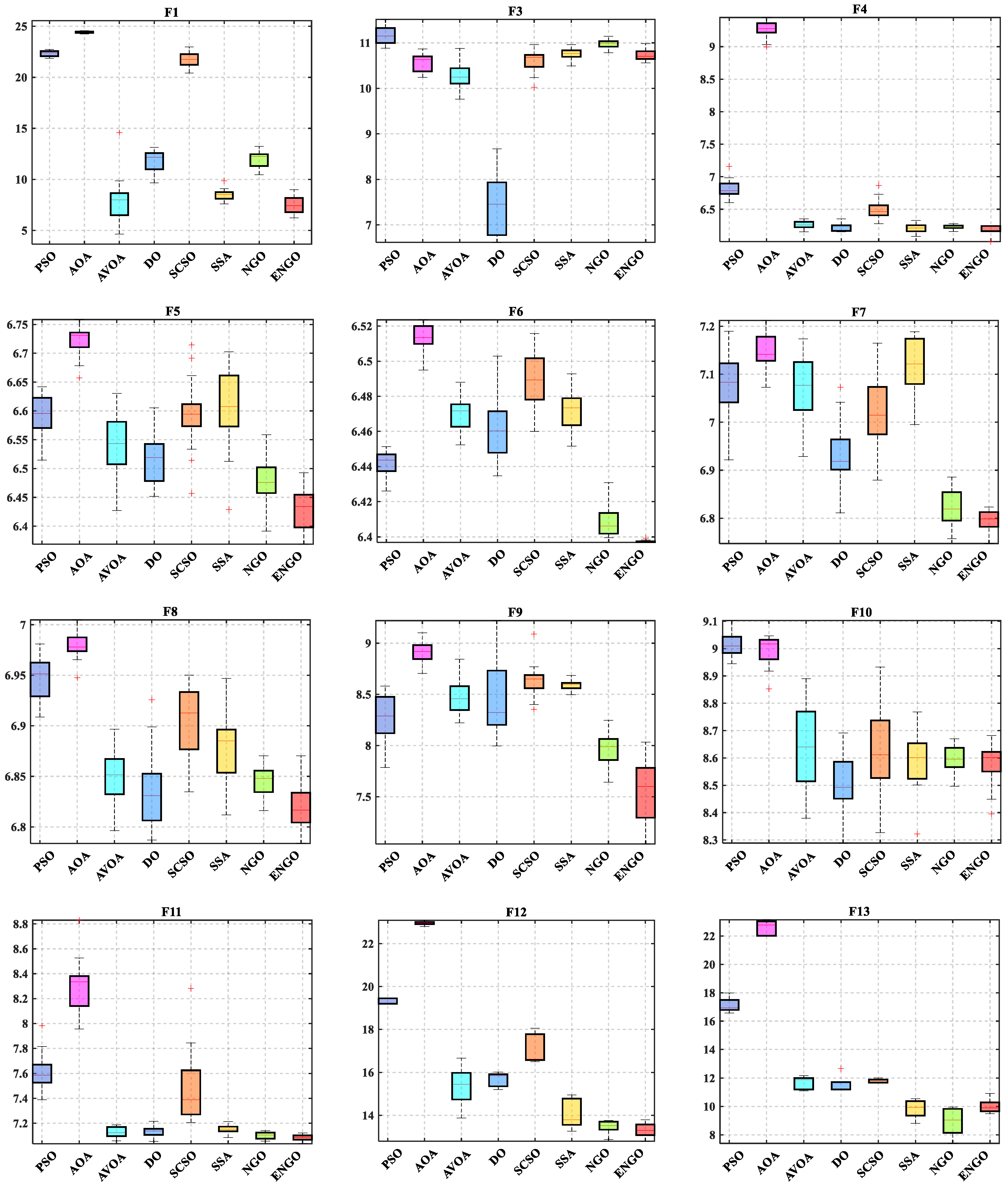
3.2. Results Analysis and Discussion
4. Practical Optimization Problems
4.1. Gear Train Design Problem
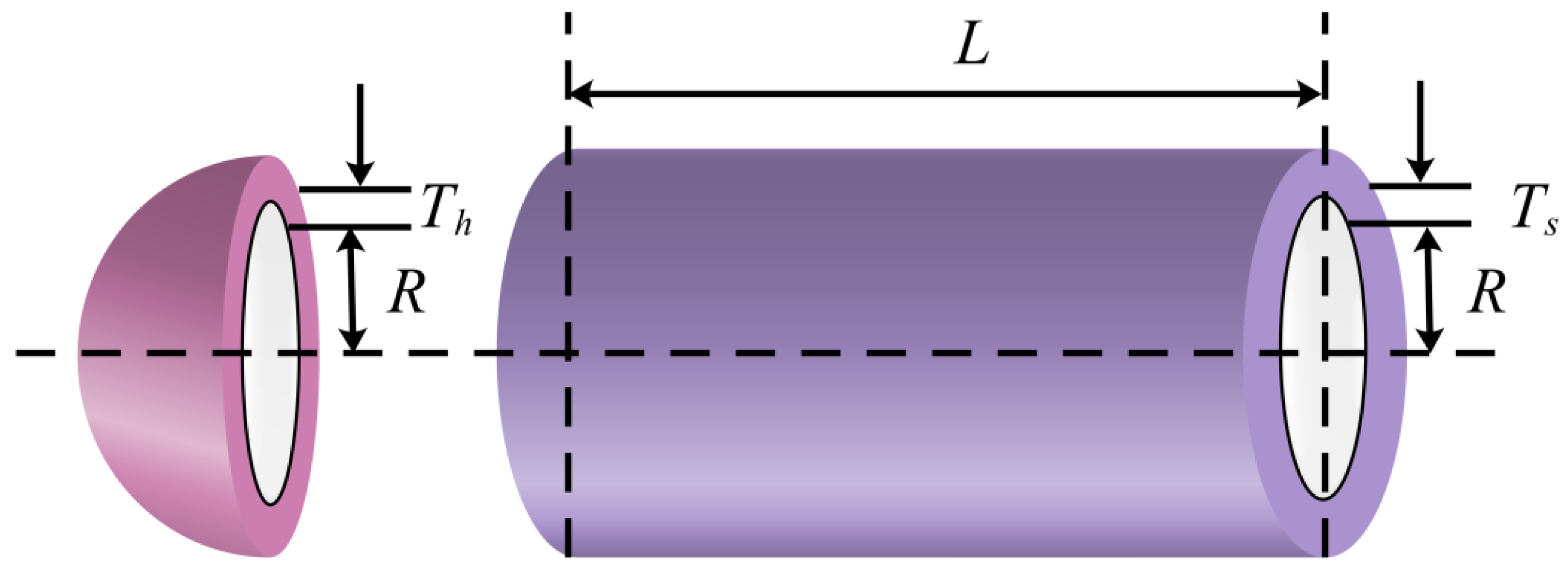
4.2. Pressure Vessel Design Problem
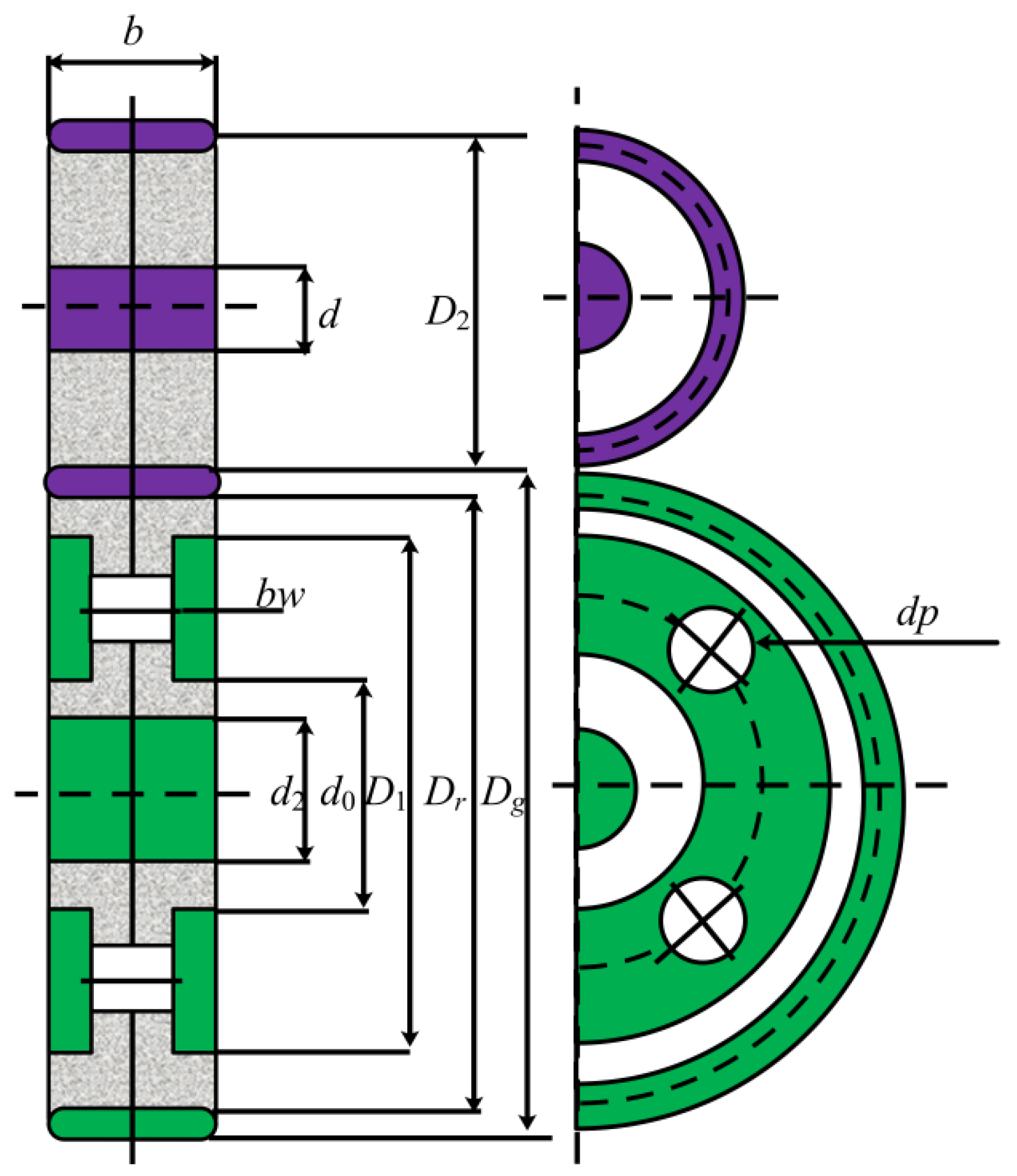
4.3. Four-Stage Gearbox Design Problem
4.4. 72-Bar Truss Design Problem
4.5. Traveling Salesman Problem
4.5.1. Two Traveling Salesmen and 80 Cities
4.5.2. Three Traveling Salesmen and 80 Cities
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Notations | Explanation |
| NGO | Northern goshawk optimization algorithm |
| ENGO | Enhanced goshawk optimization algorithm proposed in this paper |
| N | The size of the northern goshawk population |
| M | The dimension of the optimization problem |
| t | The number of current iterations of the algorithm |
| T | The maximum iterations |
| UB | The upper bound of the optimization problem |
| LB | The lower bound of the optimization problem |
| Xi | The i-th individual in the population |
| Xi,j | The j-th element of the i-th individual |
| preyi | The selected prey in the population |
| r | A random number in the goshawk optimization algorithm |
| I | A vector consisted of 1 or 2 |
| a0, a1, a2 | Three coefficients in the quadratic polynomial function |
| New solution obtained by opposite learning | |
| New solution obtained by quasi-opposite learning | |
| New solution obtained by quasi-reflected learning | |
| Xoppo | New population including the solutions after different opposite learning methods |
| TA, TB, TC, TD | Number of teeth in gears TA, TB, TC, TD |
| Ts | The thickness of the shell section |
| Th | The thickness of the head |
| R | The inner radius |
| L | The length of the cylindrical |
| The positions of the pinions | |
| The positions of the gears | |
| The thickness of the blanks | |
| The number of teeth of the different gears | |
| TSP | Traveling salesman problem |
| GA | Genetic algorithm |
| DE | Differential evolution algorithm |
| ICA | Imperialist competitive algorithm |
| MA | Memetic algorithm |
| BBO | Bio-geography optimization algorithm |
| SA | Simulated annealing algorithm |
| GSA | Gravitational search algorithm |
| SCA | Sine cosine algorithm |
| BOA | Billiards-inspired optimization algorithm |
| GBO | Gradient-based optimizer |
| PSO | Particle swarm optimization algorithm |
| WOA | Whale optimization algorithm |
| GWO | Grey wolf optimizer |
| AO | Aquila optimizer |
| SCSO | Sand cat swarm optimization algorithm |
| AOA | Archimedes optimization algorithm |
| AVOA | African vultures optimization algorithm |
| DO | Dandelion optimizer |
| SSA | Sparrow search algorithm |
| HHO | Harris hawks optimization algorithm |
| MRFO | Manta ray foraging optimization algorithm |
References
- Hu, G.; Yang, R.; Qin, X.Q.; Wei, G. MCSA: Multi-strategy boosted chameleon-inspired optimization algorithm for engineering applications. Comput. Methods Appl. Mech. Eng. 2023, 403, 115676. [Google Scholar] [CrossRef]
- Sotelo, D.; Favela-Contreras, A.; Avila, A.; Pinto, A.; Beltran-Carbajal, F.; Sotelo, C. A New Software-Based Optimization Technique for Embedded Latency Improvement of a Constrained MIMO MPC. Mathematics 2022, 10, 2571. [Google Scholar] [CrossRef]
- Hu, G.; Du, B.; Wang, X.; Wei, G. An enhanced black widow optimization algorithm for feature selection. Knowl.-Based Syst. 2022, 235, 107638. [Google Scholar] [CrossRef]
- Kvasov, D.E.; Mukhametzhanov, M.S. Metaheuristic vs. deterministic global optimization algorithms: The univariate case. Appl. Math. Comput. 2018, 318, 245–259. [Google Scholar] [CrossRef]
- Sotelo, D.; Favela-Contreras, A.; Kalashnikov, V.V.; Sotelo, C. Model Predictive Control with a Relaxed Cost Function for Constrained Linear Systems. Math. Probl. Eng. 2020, 2020, 7485865. [Google Scholar] [CrossRef]
- Yan, L.; Zou, X. Gradient-free Stein variational gradient descent with kernel approximation. Appl. Math. Lett. 2021, 121, 107465. [Google Scholar] [CrossRef]
- Rubio, J.d.J.; Islas, M.A.; Ochoa, G.; Cruz, D.R.; Garcia, E.; Pacheco, J. Convergent newton method and neural network for the electric energy usage prediction. Inf. Sci. 2022, 585, 89–112. [Google Scholar] [CrossRef]
- Gonçalves, M.L.N.; Lima, F.S.; Prudente, L.F. A study of Liu-Storey conjugate gradient methods for vector optimization. Appl. Math. Comput. 2022, 425, 127099. [Google Scholar] [CrossRef]
- Guan, G.; Yang, Q.; Gu, W.; Jiang, W.; Lin, Y. A new method for parametric design and optimization of ship inner shell based on the improved particle swarm optimization algorithm. Ocean Eng. 2018, 169, 551–566. [Google Scholar] [CrossRef]
- Rahman, I.; Mohamad-Saleh, J. Hybrid bio-Inspired computational intelligence techniques for solving power system optimization problems: A comprehensive survey. Appl. Soft. Comput. 2018, 69, 72–130. [Google Scholar] [CrossRef]
- Kiran, M.S.; Hakli, H. A tree–seed algorithm based on intelligent search mechanisms for continuous optimization. Appl. Soft. Comput. 2021, 98, 106938. [Google Scholar] [CrossRef]
- Montoya, O.D.; Molina-Cabrera, A.; Gil-Gonzalez, W. A Possible Classification for Metaheuristic Optimization Algorithms in Engineering and Science. Ingeniería 2022, 27, e19815. [Google Scholar] [CrossRef]
- Hu, G.; Zhong, J.; Du, B.; Wei, G. An enhanced hybrid arithmetic optimization algorithm for engineering applications. Comput. Methods Appl. Mech. Eng. 2022, 394, 114901. [Google Scholar] [CrossRef]
- Zhou, J.; Hua, Z. A correlation guided genetic algorithm and its application to feature selection. Appl. Soft. Comput. 2022, 123, 108964. [Google Scholar] [CrossRef]
- Gonçalves, E.N.; Belo, M.A.R.; Batista, A.P. Self-adaptive multi-objective differential evolution algorithm with first front elitism for optimizing network usage in networked control systems. Appl. Soft. Comput. 2022, 114, 108112. [Google Scholar] [CrossRef]
- Atashpaz-Gargari, E.; Lucas, C. Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 25–28. [Google Scholar]
- Seo, W.; Park, M.; Kim, D.-W.; Lee, J. Effective memetic algorithm for multilabel feature selection using hybridization-based communication. Expert Syst. Appl. 2022, 201, 117064. [Google Scholar] [CrossRef]
- Chen, X.; Tianfield, H.; Du, W.; Liu, G. Biogeography-based optimization with covariance matrix based migration. Appl. Soft. Comput. 2016, 45, 71–85. [Google Scholar] [CrossRef]
- Lee, J.; Perkins, D. A simulated annealing algorithm with a dual perturbation method for clustering. Pattern Recogn. 2021, 112, 107713. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, S.; Yu, Y.; Cai, Z.; Wang, Z. A gravitational search algorithm with hierarchy and distributed framework. Knowl.-Based Syst. 2021, 218, 106877. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Kaveh, A.; Khanzadi, M.; Rastegar Moghaddam, M. Billiards-inspired optimization algorithm; a new meta-heuristic method. Structures 2020, 27, 1722–1739. [Google Scholar] [CrossRef]
- Ahmadianfar, I.; Bozorg-Haddad, O.; Chu, X. Gradient-based optimizer: A new metaheuristic optimization algorithm. Inf. Sci. 2020, 540, 131–159. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, X.; Cao, X.; Wu, C. An efficient hybrid integer and categorical particle swarm optimization algorithm for the multi-mode multi-project inverse scheduling problem in turbine assembly workshop. Comput. Ind. Eng. 2022, 169, 108148. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, T.; Liu, Z. A whale optimization algorithm based on quadratic interpolation for high-dimensional global optimization problems. Appl. Soft. Comput. 2019, 85, 105744. [Google Scholar] [CrossRef]
- Yu, X.; Wu, X. Ensemble grey wolf Optimizer and its application for image segmentation. Expert Syst. Appl. 2022, 209, 118267. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-qaness, M.A.A.; Gandomi, A.H. Aquila Optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 1–25. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, K.; Zhou, Y.; Ma, L.; Zhang, Z. An immune algorithm for solving the optimization problem of locating the battery swapping stations. Knowl.-Based Syst. 2022, 248, 108883. [Google Scholar] [CrossRef]
- Reihanian, A.; Feizi-Derakhshi, M.-R.; Aghdasi, H.S. NBBO: A new variant of biogeography-based optimization with a novel framework and a two-phase migration operator. Inf. Sci. 2019, 504, 178–201. [Google Scholar] [CrossRef]
- Hu, G.; Du, B.; Wang, X. An improved black widow optimization algorithm for surfaces conversion. Appl. Intell. 2022, 1–42. [Google Scholar] [CrossRef]
- Kaveh, A.; Ghazaan, M.I.; Saadatmand, F. Colliding bodies optimization with Morlet wavelet mutation and quadratic interpolation for global optimization problems. Eng. Comput. 2022, 38, 2743–2767. [Google Scholar] [CrossRef]
- Yousri, D.; AbdelAty, A.M.; Al-qaness, M.A.A.; Ewees, A.A.; Radwan, A.G.; Abd Elaziz, M. Discrete fractional-order Caputo method to overcome trapping in local optima: Manta Ray Foraging Optimizer as a case study. Expert Syst. Appl. 2022, 192, 116355. [Google Scholar] [CrossRef]
- Lu, X.-l.; He, G. QPSO algorithm based on Lévy flight and its application in fuzzy portfolio. Appl. Soft. Comput. 2021, 99, 106894. [Google Scholar] [CrossRef]
- Jiang, F.; Xia, H.; Anh Tran, Q.; Minh Ha, Q.; Quang Tran, N.; Hu, J. A new binary hybrid particle swarm optimization with wavelet mutation. Knowl.-Based Syst. 2017, 130, 90–101. [Google Scholar] [CrossRef]
- Miao, F.; Yao, L.; Zhao, X. Symbiotic organisms search algorithm using random walk and adaptive Cauchy mutation on the feature selection of sleep staging. Expert Syst. Appl. 2021, 176, 114887. [Google Scholar] [CrossRef]
- Yang, D.; Wu, M.; Li, D.; Xu, Y.; Zhou, X.; Yang, Z. Dynamic opposite learning enhanced dragonfly algorithm for solving large-scale flexible job shop scheduling problem. Knowl.-Based Syst. 2022, 238, 107815. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubálovský, H.; Trojovský, A. Northern Goshawk Optimization: A New Swarm-Based Algorithm for Solving Optimization Problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Hu, G.; Du, B.; Li, H.; Wang, X. Quadratic interpolation boosted black widow spider-inspired optimization algorithm with wavelet mutation. Math. Comput. Simul. 2022, 200, 428–467. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, Y.; Tan, S.; Zhao, S.; Wu, J.; Gao, S.; Wang, Y.-G. An opposition learning and spiral modelling based arithmetic optimization algorithm for global continuous optimization problems. Eng. Appl. Artif. Intell. 2022, 113, 104981. [Google Scholar] [CrossRef]
- Li, B.; Li, Z.; Yang, P.; Xu, J.; Wang, H. Modeling and optimization of the thermal-hydraulic performance of direct contact heat exchanger using quasi-opposite Jaya algorithm. Int. J. Therm. Sci. 2022, 173, 107421. [Google Scholar] [CrossRef]
- Guo, W.; Xu, P.; Dai, F.; Zhao, F.; Wu, M. Improved Harris hawks optimization algorithm based on random unscented sigma point mutation strategy. Appl. Soft. Comput. 2021, 113, 108012. [Google Scholar] [CrossRef]
- Hu, G.; Zhu, X.; Wang, X.; Wei, G. Multi-strategy boosted marine predators algorithm for optimizing approximate developable surface. Knowl.-Based Syst. 2022, 254, 109615. [Google Scholar] [CrossRef]
- Houssein, E.H.; Gad, A.G.; Hussain, K.; Suganthan, P.N. Major Advances in Particle Swarm Optimization: Theory, Analysis, and Application. Swarm Evol. Comput. 2021, 63, 100868. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Abd Elaziz, M.; Gandomi, A.H. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Abdollahzadeh, B.; Gharehchopogh, F.S.; Mirjalili, S. African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Comput. Ind. Eng. 2021, 158, 107408. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Zheng, J.; Hu, G.; Ji, X.; Qin, X. Quintic generalized Hermite interpolation curves: Construction and shape optimization using an improved GWO algorithm. Comput. Appl. Math. 2022, 41, 115. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications. Eng. Appl. Artif. Intel. 2020, 87, 103300. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-Verse Optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Hu, G.; Li, M.; Wang, X.; Wei, G.; Chang, C.-T. An enhanced manta ray foraging optimization algorithm for shape optimization of complex CCG-Ball curves. Knowl.-Based Syst. 2022, 240, 108071. [Google Scholar] [CrossRef]
- Naruei, I.; Keynia, F. A new optimization method based on COOT bird natural life model. Expert Syst. Appl. 2021, 183, 115352. [Google Scholar] [CrossRef]
- Hu, G.; Zhu, X.; Wei, G.; Chang, C.-T. An improved marine predators algorithm for shape optimization of developable Ball surfaces. Eng. Appl. Artif. Intell. 2021, 105, 104417. [Google Scholar] [CrossRef]
- Gurrola-Ramos, J.; Hernàndez-Aguirre, A.; Dalmau-Cedeño, O. COLSHADE for Real-World Single-Objective Constrained optimization Problems. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
- Camp, C.V.; Farshchin, M. Design of space trusses using modified teaching-learning based optimization. Eng. Struct. 2014, 62–63, 87–97. [Google Scholar] [CrossRef]
- Hu, G.; Dou, W.; Wang, X.; Abbas, M. An enhanced chimp optimization algorithm for optimal degree reduction of Said-Ball curves. Math. Comput. Simul. 2022, 197, 207–252. [Google Scholar] [CrossRef]
- Uğur, A.; Aydin, D. An interactive simulation and analysis software for solving TSP using Ant Colony Optimization algorithms. Adv. Eng. Softw. 2009, 40, 341–349. [Google Scholar] [CrossRef]
- Skinderowicz, R. Improving Ant Colony Optimization efficiency for solving large TSP instances. Appl. Soft. Comput. 2022, 120, 108653. [Google Scholar] [CrossRef]









| Algorithms | Proposed Time | Parameters |
|---|---|---|
| PSO [44] | 1988 | Learning factors c1 = 2, c2 = 2.5, the inertia factor w = 2. |
| AOA [45] | 2021 | Control parameter µ = 0.499, Sensitive parameter a = 5. |
| AVOA [46] | 2021 | Hunger degrees z is a random value in [−1, 1]. |
| DO [47] | 2022 | Parameters β = 1.5, s = 0.01. |
| SCSO [28] | 2022 | The value of hearing characteristics SM = 2. |
| SSA [48] | 2017 | The update probability of the leader c3 = 0.5. |
| Function | Index | PSO | AOA | AVOA | DO | SCSO | SSA | NGO | ENGO |
|---|---|---|---|---|---|---|---|---|---|
| F1 | Ave | 5.1802E + 09 | 4.0462E + 10 | 1.1221E + 05 | 1.8277E + 05 | 3.3426E + 09 | 5.5010E + 03 | 2.0690E + 05 | 2.3466E + 03 |
| Std | 1.3161E + 09 | 3.5061E + 09 | 4.8240E + 05 | 1.3250E + 05 | 2.2407E + 09 | 3.6044E + 03 | 1.3089E + 05 | 1.8986E + 03 | |
| Rank | 7 | 8 | 3 | 4 | 6 | 2 | 5 | 1 | |
| F3 | Ave | 7.1287E + 04 | 3.9949E + 04 | 3.0323E + 04 | 2.1871E + 03 | 4.1388E + 04 | 4.7198E + 04 | 5.8724E + 04 | 4.5869E + 04 |
| Std | 1.3573E + 04 | 7.5639E + 03 | 9.2550E + 03 | 1.5687E + 03 | 8.6106E + 03 | 5.6481E + 03 | 5.3424E + 03 | 5.4097E + 03 | |
| Rank | 8 | 3 | 2 | 1 | 4 | 6 | 7 | 5 | |
| F4 | Ave | 9.1671E + 02 | 1.0676E + 04 | 5.2458E + 02 | 5.0657E + 02 | 6.6922E + 02 | 5.0147E + 02 | 5.0824E + 02 | 4.9688E + 02 |
| Std | 1.3168E + 02 | 1.2735E + 03 | 3.0283E + 01 | 2.7533E + 01 | 1.0356E + 02 | 3.2163E + 01 | 1.6062E + 01 | 2.8701E + 01 | |
| Rank | 7 | 8 | 5 | 3 | 6 | 2 | 4 | 1 | |
| F5 | Ave | 7.3096E + 02 | 8.3088E + 02 | 6.9320E + 02 | 6.7696E + 02 | 7.3262E + 02 | 7.4290E + 02 | 6.5192E + 02 | 6.1849E + 02 |
| Std | 2.3716E + 01 | 2.0645E + 01 | 3.8796E + 01 | 3.0970E + 01 | 4.2318E + 01 | 5.1374E + 01 | 2.6417E + 01 | 2.1285E + 01 | |
| Rank | 5 | 8 | 4 | 3 | 6 | 7 | 2 | 1 | |
| F6 | Ave | 6.2781E + 02 | 6.7466E + 02 | 6.4592E + 02 | 6.4002E + 02 | 6.5735E + 02 | 6.4691E + 02 | 6.0692E + 02 | 6.0030E + 02 |
| Std | 4.0829E + 00 | 4.6522E + 00 | 5.7921E + 00 | 1.2329E + 01 | 1.0318E + 01 | 8.0761E + 00 | 5.0220E + 00 | 4.5294E − 01 | |
| Rank | 3 | 8 | 5 | 4 | 7 | 6 | 2 | 1 | |
| F7 | Ave | 1.1906E + 03 | 1.2735E + 03 | 1.1822E + 03 | 1.0234E + 03 | 1.1217E + 03 | 1.2322E + 03 | 9.1927E + 02 | 8.9333E + 02 |
| Std | 7.9530E + 01 | 4.7253E + 01 | 8.5067E + 01 | 7.0898E + 01 | 9.2206E + 01 | 7.6023E + 01 | 3.4636E + 01 | 1.9863E + 01 | |
| Rank | 6 | 8 | 5 | 3 | 4 | 7 | 2 | 1 | |
| F8 | Ave | 1.0399E + 03 | 1.0744E + 03 | 9.4314E + 02 | 9.3114E + 02 | 9.9586E + 02 | 9.7208E + 02 | 9.3873E + 02 | 9.1502E + 02 |
| Std | 2.0781E + 01 | 1.3098E + 01 | 2.3945E + 01 | 3.4521E + 01 | 3.5091E + 01 | 3.1781E + 01 | 1.4437E + 01 | 1.9785E + 01 | |
| Rank | 7 | 8 | 4 | 2 | 6 | 5 | 3 | 1 | |
| F9 | Ave | 3.9823E + 03 | 7.4560E + 03 | 4.8178E + 03 | 4.9962E + 03 | 5.7009E + 03 | 5.3918E + 03 | 2.9437E + 03 | 1.9618E + 03 |
| Std | 8.1851E + 02 | 7.3024E + 02 | 8.2016E + 02 | 1.9850E + 03 | 9.5008E + 02 | 2.2118E + 02 | 4.5211E + 02 | 5.7069E + 02 | |
| Rank | 3 | 8 | 4 | 5 | 7 | 6 | 2 | 1 | |
| F10 | Ave | 8.2352E + 03 | 8.0569E + 03 | 5.7230E + 03 | 4.9592E + 03 | 5.6354E + 03 | 5.3943E + 03 | 5.4102E + 03 | 5.3437E + 03 |
| Std | 3.2222E + 02 | 4.0120E + 02 | 8.9928E + 02 | 4.9182E + 02 | 8.5290E + 02 | 4.9178E + 02 | 2.5354E + 02 | 3.8350E + 02 | |
| Rank | 8 | 7 | 6 | 1 | 5 | 3 | 4 | 2 | |
| F11 | Ave | 2.0359E + 03 | 4.0694E + 03 | 1.2502E + 03 | 1.2517E + 03 | 1.8404E + 03 | 1.2747E + 03 | 1.2135E + 03 | 1.1957E + 03 |
| Std | 2.8771E + 02 | 8.8072E + 02 | 5.1866E + 01 | 4.8974E + 01 | 6.1253E + 02 | 4.3691E + 01 | 3.4790E + 01 | 2.8866E + 01 | |
| Rank | 7 | 8 | 3 | 4 | 6 | 5 | 2 | 1 | |
| F12 | Ave | 2.5414E + 08 | 9.4131E + 09 | 6.7289E + 06 | 6.6982E + 06 | 3.2798E + 07 | 1.5966E + 06 | 7.3235E + 05 | 6.3577E + 05 |
| Std | 3.5963E + 07 | 9.5712E + 08 | 6.2126E + 06 | 2.1447E + 06 | 2.4691E + 07 | 1.1237E + 06 | 2.1315E + 05 | 2.3050E + 05 | |
| Rank | 7 | 8 | 5 | 4 | 6 | 3 | 2 | 1 | |
| F13 | Ave | 3.1682E + 07 | 7.2400E + 09 | 1.2733E + 05 | 1.2456E + 05 | 1.3647E + 05 | 2.1858E + 04 | 1.0714E + 04 | 2.5724E + 04 |
| Std | 1.9843E + 07 | 3.5318E + 09 | 5.4956E + 04 | 1.0581E + 05 | 1.9868E + 04 | 1.2436E + 04 | 8.5012E + 03 | 1.6919E + 04 | |
| Rank | 7 | 8 | 5 | 4 | 6 | 2 | 1 | 3 | |
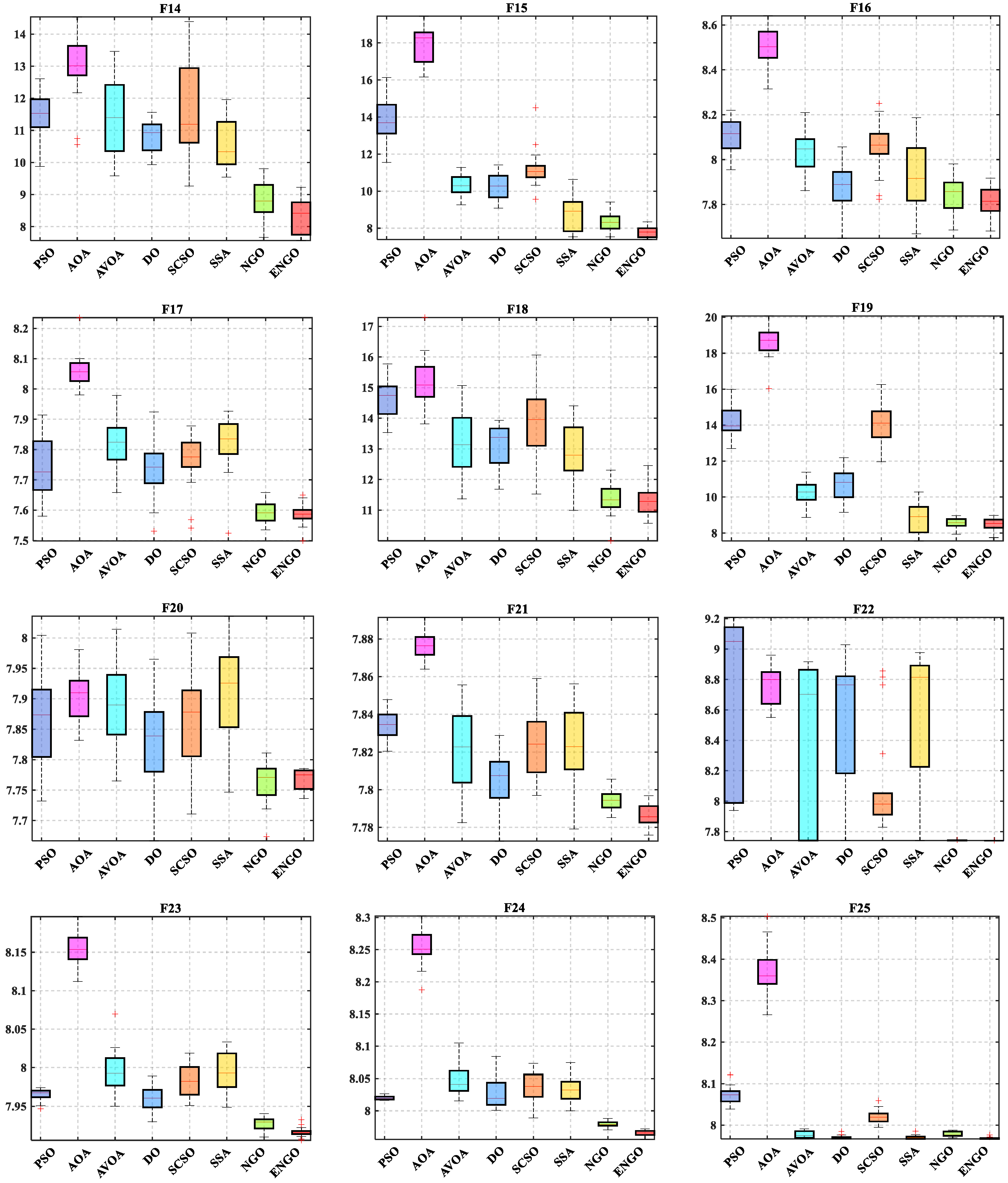
| F14 | Ave | 1.1780E + 05 | 6.2017E + 05 | 1.8606E + 05 | 5.7101E + 04 | 3.0132E + 05 | 5.1864E + 04 | 8.2371E + 03 | 4.6760E + 03 |
| Std | 8.0871E + 04 | 4.6962E + 05 | 2.2180E + 05 | 2.6573E + 04 | 4.7135E + 05 | 4.0322E + 04 | 4.6052E + 03 | 2.5158E + 03 | |
| Rank | 5 | 8 | 6 | 4 | 7 | 3 | 2 | 1 | |
| F15 | Ave | 1.8054E + 06 | 8.5030E + 07 | 3.4814E + 04 | 3.3985E + 04 | 1.7336E + 05 | 1.1045E + 04 | 4.6995E + 03 | 2.4524E + 03 |
| Std | 2.3121E + 06 | 6.6009E + 07 | 1.8818E + 04 | 2.2745E + 04 | 4.3157E + 05 | 1.2212E + 04 | 2.5192E + 03 | 6.9164E + 02 | |
| Rank | 7 | 8 | 5 | 4 | 6 | 3 | 2 | 1 | |
| F16 | Ave | 3.3186E + 03 | 4.9326E + 03 | 3.1043E + 03 | 2.6516E + 03 | 3.1768E + 03 | 2.8377E + 03 | 2.5559E + 03 | 2.4806E + 03 |
| Std | 2.7582E + 02 | 4.0993E + 02 | 3.0041E + 02 | 2.5849E + 02 | 3.3518E + 02 | 4.1478E + 02 | 1.9722E + 02 | 1.5468E + 02 | |
| Rank | 7 | 8 | 5 | 3 | 6 | 4 | 2 | 1 | |
| F17 | Ave | 2.3003E + 03 | 3.1673E + 03 | 2.5071E + 03 | 2.2951E + 03 | 2.3644E + 03 | 2.4993E + 03 | 1.9907E + 03 | 1.9748E + 03 |
| Std | 2.1638E + 02 | 1.8004E + 02 | 2.0256E + 02 | 2.0889E + 02 | 1.9855E + 02 | 2.1525E + 02 | 7.6050E + 01 | 6.6039E + 01 | |
| Rank | 4 | 8 | 7 | 3 | 5 | 6 | 2 | 1 | |
| F18 | Ave | 2.6966E + 06 | 5.6400E + 06 | 8.7903E + 05 | 5.9533E + 05 | 1.7970E + 06 | 5.9365E + 05 | 9.6472E + 04 | 9.4033E + 04 |
| Std | 1.6107E + 06 | 6.7615E + 06 | 9.5620E + 05 | 3.3879E + 05 | 2.1560E + 06 | 5.1722E + 05 | 4.6634E + 04 | 5.4539E + 04 | |
| Rank | 7 | 8 | 5 | 4 | 6 | 3 | 2 | 1 | |
| F19 | Ave | 2.1838E + 06 | 1.6601E + 08 | 3.3801E + 04 | 5.9278E + 04 | 2.0900E + 06 | 1.0631E + 04 | 5.3849E + 03 | 5.0245E + 03 |
| Std | 2.2968E + 06 | 1.1869E + 08 | 1.9333E + 04 | 4.8092E + 04 | 2.5655E + 06 | 9.8222E + 03 | 1.3140E + 03 | 1.4903E + 03 | |
| Rank | 7 | 8 | 4 | 5 | 6 | 3 | 2 | 1 | |
| F20 | Ave | 2.6074E + 03 | 2.7081E + 03 | 2.6796E + 03 | 2.5232E + 03 | 2.6236E + 03 | 2.7266E + 03 | 2.3560E + 03 | 2.3617E + 03 |
| Std | 1.9460E + 02 | 1.0941E + 02 | 1.9055E + 02 | 1.9280E + 02 | 2.1442E + 02 | 2.1721E + 02 | 7.4857E + 01 | 4.2260E + 01 | |
| Rank | 4 | 7 | 6 | 3 | 5 | 8 | 1 | 2 | |
| F21 | Ave | 2.5259E + 03 | 2.6337E + 03 | 2.4945E + 03 | 2.4552E + 03 | 2.4992E + 03 | 2.4968E + 03 | 2.4270E + 03 | 2.4084E + 03 |
| Std | 1.8736E + 01 | 2.0020E + 01 | 5.4731E + 01 | 3.3110E + 01 | 4.3535E + 01 | 5.5648E + 01 | 1.2745E + 01 | 1.3815E + 01 | |
| Rank | 7 | 8 | 4 | 3 | 6 | 5 | 2 | 1 | |
| F22 | Ave | 6.4159E + 03 | 6.4679E + 03 | 4.8378E + 03 | 5.5543E + 03 | 3.4848E + 03 | 5.7974E + 03 | 2.3034E + 03 | 2.3005E + 03 |
| Std | 3.2348E + 03 | 7.8528E + 02 | 2.3835E + 03 | 2.0029E + 03 | 1.4360E + 03 | 2.1210E + 03 | 1.9491E + 00 | 1.2498E + 00 | |
| Rank | 7 | 8 | 4 | 5 | 3 | 6 | 2 | 1 | |
| F23 | Ave | 2.8792E + 03 | 3.4845E + 03 | 2.9717E + 03 | 2.8672E + 03 | 2.9288E + 03 | 2.9679E + 03 | 2.7722E + 03 | 2.7413E + 03 |
| Std | 2.1797E + 01 | 7.5564E + 01 | 8.0333E + 01 | 4.7990E + 01 | 5.9829E + 01 | 7.6021E + 01 | 2.1701E + 01 | 1.6470E + 01 | |
| Rank | 4 | 8 | 7 | 3 | 5 | 6 | 2 | 1 | |
| F24 | Ave | 3.0411E + 03 | 3.8398E + 03 | 3.1300E + 03 | 3.0604E + 03 | 3.0968E + 03 | 3.0891E + 03 | 2.9197E + 03 | 2.8797E + 03 |
| Std | 9.3852E + 00 | 9.8943E + 01 | 8.3199E + 01 | 6.9980E + 01 | 7.1139E + 01 | 6.9832E + 01 | 1.4223E + 01 | 1.2927E + 01 | |
| Rank | 3 | 8 | 7 | 4 | 6 | 5 | 2 | 1 | |
| F25 | Ave | 3.2031E + 03 | 4.3262E + 03 | 2.9137E + 03 | 2.8939E + 03 | 3.0406E + 03 | 2.8956E + 03 | 2.9170E + 03 | 2.8886E + 03 |
| Std | 6.4161E + 01 | 2.5324E + 02 | 2.4682E + 01 | 1.3634E + 01 | 5.1759E + 01 | 1.3847E + 01 | 1.7329E + 01 | 6.2293E + 00 | |
| Rank | 7 | 8 | 4 | 2 | 6 | 3 | 5 | 1 | |
| F26 | Ave | 6.1568E + 03 | 9.9657E + 03 | 6.6772E + 03 | 5.7903E + 03 | 6.1648E + 03 | 6.3669E + 03 | 3.2578E + 03 | 3.5280E + 03 |
| Std | 4.9151E + 02 | 3.4324E + 02 | 1.0058E + 03 | 4.4628E + 02 | 1.0908E + 03 | 1.5443E + 03 | 7.6200E + 02 | 1.2912E + 03 | |
| Rank | 4 | 8 | 7 | 3 | 5 | 6 | 1 | 2 | |
| F27 | Ave | 3.3027E + 03 | 4.4396E + 03 | 3.2770E + 03 | 3.2687E + 03 | 3.3635E + 03 | 3.2875E + 03 | 3.2230E + 03 | 3.2184E + 03 |
| Std | 1.7512E + 01 | 2.0391E + 02 | 3.0678E + 01 | 4.2722E + 01 | 8.8901E + 01 | 4.2029E + 01 | 9.6877E + 00 | 6.4926E + 00 | |
| Rank | 6 | 8 | 4 | 3 | 7 | 5 | 2 | 1 | |
| F28 | Ave | 3.5240E + 03 | 6.3214E + 03 | 3.2690E + 03 | 3.2365E + 03 | 3.4941E + 03 | 3.2461E + 03 | 3.2798E + 03 | 3.2054E + 03 |
| Std | 7.3227E + 01 | 3.5836E + 02 | 2.2702E + 01 | 2.6406E + 01 | 1.1313E + 02 | 2.2172E + 01 | 1.4775E + 01 | 6.6437E + 00 | |
| Rank | 7 | 8 | 4 | 2 | 6 | 3 | 5 | 1 | |
| F29 | Ave | 4.3235E + 03 | 6.2964E + 03 | 4.2739E + 03 | 3.9694E + 03 | 4.4828E + 03 | 4.2342E + 03 | 3.8593E + 03 | 3.8632E + 03 |
| Std | 1.9360E + 02 | 5.6231E + 02 | 2.8515E + 02 | 1.9885E + 02 | 3.4699E + 02 | 3.4541E + 02 | 9.4104E + 01 | 1.5308E + 02 | |
| Rank | 6 | 8 | 5 | 3 | 7 | 4 | 1 | 2 | |
| F30 | Ave | 7.0571E + 06 | 8.7344E + 08 | 5.0128E + 05 | 6.2123E + 05 | 7.0001E + 06 | 2.0995E + 04 | 1.7041E + 04 | 6.8796E + 03 |
| Std | 5.5024E + 06 | 2.6904E + 08 | 3.0621E + 05 | 4.2992E + 05 | 4.9031E + 06 | 7.5318E + 03 | 1.4933E + 04 | 9.3090E + 02 | |
| Rank | 7 | 8 | 4 | 5 | 6 | 3 | 2 | 1 | |
| Average rank | 6.0000 | 7.7586 | 4.7931 | 3.3448 | 5.7586 | 4.4828 | 2.5172 | 1.3448 | |
| PSO | AOA | AVOA | DO | SCSO | SSA | NGO | |
|---|---|---|---|---|---|---|---|
| F1 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 5.255 × 10−5/+ | 2.960 × 10−7/+ | 6.796 × 10−8/+ | 4.540 × 10−6/+ | 6.796 × 10−8/+ |
| F3 | 6.796 × 10−8/+ | 6.796 × 10−8/− | 6.796 × 10−8/− | 5.979 × 10−1/− | 6.796 × 10−8/− | 6.796 × 10−8/+ | 6.796 × 10−8/+ |
| F4 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 5.979 × 10−1/= | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ |
| F5 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 1.481 × 10−3/+ | 2.184 × 10−1/= | 6.796 × 10−8/+ | 8.817 × 10−1/= | 7.712 × 10−3/+ |
| F6 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 1.657 × 10−7/+ | 1.431 × 10−7/+ | 7.898 × 10−8/+ | 1.235 × 10−7/+ | 1.803 × 10−6/+ |
| F7 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 8.585 × 10−2/= |
| F8 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 9.173 × 10−8/+ |
| F9 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 5.091 × 10−4/+ | 2.073 × 10−2/+ | 6.015 × 10−7/+ | 3.987 × 10−6/+ | 4.155 × 10−4/+ |
| F10 | 1.953 × 10−3/+ | 7.898 × 10−8/+ | 2.041 × 10−5/+ | 3.382 × 10−4/− | 1.376 × 10−6/+ | 1.201 × 10−6/+ | 3.942 × 10−1/= |
| F11 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 8.597 × 10−6/+ | 1.116 × 10−3/+ | 9.748 × 10−6/+ | 3.069 × 10−6/+ | 1.047 × 10−6/+ |
| F12 | 7.937 × 10−8/+ | 7.937 × 10−3/+ | 6.905 × 10−1/= | 8.413 × 10−1/= | 7.937 × 10−3/+ | 1.000 × 10−0/= | 5.476 × 10−1/= |
| F13 | 7.937 × 10−8/+ | 7.937 × 10−3/+ | 2.222 × 10−1/= | 3.175 × 10−2/+ | 7.937 × 10−3/+ | 3.095 × 10−1/= | 9.524 × 10−2/− |
| F14 | 7.937 × 10−8/+ | 7.937 × 10−3/+ | 7.937 × 10−3/+ | 7.937 × 10−3/+ | 7.937 × 10−3/+ | 8.413 × 10−1/= | 4.206 × 10−1/= |
| F15 | 4.903 × 10−1/= | 5.166 × 10−6/+ | 8.392 × 10−1/= | 1.058 × 10−2/+ | 9.246 × 10−1/= | 4.703 × 10−3/+ | 1.065 × 10−7/+ |
| F16 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 1.143 × 10−2/+ | 6.389 × 10−2/= | 2.062 × 10−6/+ | 7.113 × 10−3/+ | 4.540 × 10−6/+ |
| F17 | 6.917 × 10−7/+ | 6.796 × 10−8/+ | 1.600 × 10−5/+ | 2.616 × 10−1/= | 3.705 × 10−5/+ | 5.310 × 10−2/= | 7.353 × 10−1/= |
| F18 | 6.168 × 10−1/= | 6.796 × 10−8/+ | 6.220 × 10−4/+ | 5.428 × 10−1/= | 7.205 × 10−2/= | 6.868 × 10−4/+ | 1.014 × 10−3/+ |
| F19 | 6.220 × 10−4/+ | 3.069 × 10−6/+ | 1.719 × 10−1/= | 5.652 × 10−2/= | 5.428 × 10−1/= | 2.073 × 10−2/+ | 7.898 × 10−8/+ |
| F20 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 4.735 × 10−1/= | 1.929 × 10−2/+ | 6.796 × 10−8/+ | 2.341 × 10−3/+ | 1.294 × 10−4/− |
| F21 | 6.040 × 10−3/+ | 1.415 × 10−5/+ | 4.155 × 10−4/+ | 1.333 × 10−1/= | 8.355 × 10−3/+ | 1.610 × 10−4/+ | 2.393 × 10−1/= |
| F22 | 3.416 × 10−7/+ | 6.796 × 10−8/+ | 1.159 × 10−4/+ | 7.712 × 10−3/+ | 1.807 × 10−5/+ | 1.794 × 10−4/+ | 2.977 × 10−1/= |
| F23 | 5.979 × 10−1/= | 3.152 × 10−2/+ | 8.604 × 10−1/= | 2.503 × 10−1/= | 6.610 × 10−5/+ | 6.389 × 10−2/= | 6.796 × 10−8/+ |
| F24 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 1.657 × 10−7/+ | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 7.205 × 10−2/= |
| F25 | 9.127 × 10−7/+ | 6.796 × 10−8/+ | 1.235 × 10−7/+ | 4.539 × 10−7/+ | 3.939 × 10−7/+ | 1.918 × 10−7/+ | 1.436 × 10−2/+ |
| F26 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 5.255 × 10−5/+ | 1.556 × 10−1/= | 6.796 × 10−8/+ | 6.787 × 10−2/= | 6.796 × 10−8/− |
| F27 | 1.047 × 10−6/+ | 6.796 × 10−8/+ | 2.356 × 10−6/+ | 6.917 × 10−7/+ | 1.997 × 10−4/+ | 1.600 × 10−5/+ | 8.597 × 10−6/+ |
| F28 | 1.065 × 10−7/+ | 6.796 × 10−8/+ | 2.302 × 10−5/+ | 5.091 × 10−4/+ | 1.431 × 10−7/+ | 6.674 × 10−6/+ | 4.249 × 10−1/= |
| F29 | 6.796 × 10−8/+ | 6.796 × 10−8/+ | 9.620 × 10−2/= | 2.748 × 10−2/+ | 1.065 × 10−7/+ | 1.333 × 10−1/= | 2.561 × 10−3/− |
| F30 | 1.047 × 10−6/+ | 6.796 × 10−8/+ | 2.041 × 10−5/+ | 2.748 × 10−2/+ | 9.127 × 10−7/+ | 1.794 × 10−4/+ | 4.249 × 10−1/= |
| +/=/− | 26/3/0 | 28/0/1 | 21/7/1 | 16/11/2 | 25/3/1 | 21/8/0 | 15/10/4 |
| Algorithms | The Best | The Average | The Worst | The Std | Rank |
|---|---|---|---|---|---|
| NGO | 6059.99 | 6074.13 | 6127.80 | 30.01 | 2 |
| ENGO | 6059.73 | 6066.12 | 6090.62 | 13.70 | 1 |
| AOA | 6071.98 | 6545.79 | 7222.18 | 444.38 | 8 |
| AO | 6113.00 | 6199.99 | 6410.86 | 120.66 | 4 |
| HHO | 6118.61 | 6795.99 | 7306.63 | 449.83 | 9 |
| WOA | 6570.10 | 7922.69 | 10,623.26 | 1569.47 | 10 |
| PSO | 6059.72 | 6276.06 | 6439.73 | 197.57 | 5 |
| GWO | 6069.89 | 6076.51 | 6091.00 | 9.24 | 3 |
| MRFO | 6060.57 | 6276.27 | 6410.09 | 183.54 | 6 |
| MVO | 6327.37 | 6518.43 | 6821.12 | 213.74 | 7 |
| Algorithms | x1 | x2 | x3 | x4 |
|---|---|---|---|---|
| NGO | 0.7782 | 0.3847 | 40.3197 | 200.0000 |
| ENGO | 0.7782 | 0.3847 | 40.3201 | 200.0000 |
| AOA | 0.7788 | 0.3851 | 40.3452 | 199.6439 |
| AO | 0.7910 | 0.4106 | 40.8942 | 193.8638 |
| HHO | 0.8351 | 0.4132 | 43.2690 | 162.6520 |
| WOA | 0.8270 | 0.4523 | 42.2240 | 175.0869 |
| PSO | 0.7988 | 0.3948 | 41.3871 | 185.6578 |
| GWO | 0.7785 | 0.3850 | 40.3279 | 199.9139 |
| MRFO | 0.7799 | 0.3855 | 40.4039 | 198.8352 |
| MVO | 0.7850 | 0.3884 | 40.6637 | 195.3838 |
| Algorithms | The Best | The Average | The Worst | The Std | Rank |
|---|---|---|---|---|---|
| NGO | 5885.40 | 5891.23 | 5912.01 | 7.63 | 2 |
| ENGO | 5885.53 | 5889.23 | 5903.66 | 4.43 | 1 |
| AOA | 5888.21 | 6177.71 | 8486.53 | 579.23 | 4 |
| AO | 6015.94 | 6827.33 | 7996.55 | 649.54 | 9 |
| HHO | 5991.42 | 6529.04 | 7347.30 | 389.76 | 8 |
| WOA | 6191.17 | 8298.09 | 13,900.72 | 1763.29 | 10 |
| PSO | 5921.55 | 6192.62 | 6694.52 | 248.26 | 5 |
| GWO | 5885.32 | 6415.77 | 7318.93 | 543.48 | 7 |
| MRFO | 5889.04 | 5899.86 | 5927.37 | 11.37 | 3 |
| MVO | 5902.31 | 6376.45 | 7181.97 | 368.37 | 6 |
| Algorithms | x1 | x2 | x3 | x4 |
|---|---|---|---|---|
| NGO | 13.1101 | 6.7661 | 42.1004 | 176.6150 |
| ENGO | 13.3703 | 7.0200 | 42.0984 | 176.6376 |
| AOA | 12.0123 | 5.9525 | 40.3278 | 199.9302 |
| AO | 12.2204 | 6.1872 | 40.5586 | 196.7161 |
| HHO | 12.7969 | 5.5343 | 41.3533 | 186.0939 |
| WOA | 13.8206 | 6.6719 | 41.5674 | 183.3307 |
| PSO | 13.3587 | 6.7702 | 42.0985 | 176.6364 |
| GWO | 11.7017 | 6.0078 | 40.3203 | 200.0000 |
| MRFO | 13.1352 | 6.8732 | 42.0915 | 176.7231 |
| MVO | 14.9302 | 7.0317 | 48.6240 | 109.7093 |
| Algorithms | The Best | The Average | The Worst | The Std | Rank |
|---|---|---|---|---|---|
| NGO | 18,398.72 | 166,899.45 | 355,937.63 | 98,874.36 | 6 |
| ENGO | 40.29 | 31,057.83 | 118,898.03 | 38,591.38 | 2 |
| AOA | 236,593.12 | 593,321.31 | 1,367,729.52 | 318,308.48 | 9 |
| AO | 75,789.09 | 334,881.90 | 1,053,952.90 | 240,302.34 | 7 |
| HHO | 16,877.30 | 335,825.38 | 826,083.75 | 241,230.91 | 8 |
| WOA | 148,853.31 | 639,888.43 | 2,175,565.64 | 412,516.64 | 10 |
| PSO | 72.27 | 110,875.33 | 293,548.53 | 91,901.27 | 4 |
| GWO | 43.52 | 147,549.85 | 489,288.82 | 133,316.04 | 5 |
| MRFO | 40.09 | 29,320.84 | 126,516.25 | 42,610.57 | 1 |
| MVO | 61.07 | 103,131.19 | 363,070.87 | 128,562.16 | 3 |
| Algorithms | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 |
|---|---|---|---|---|---|---|---|---|
| NGO | 16.3597 | 43.4036 | 15.6042 | 20.7061 | 15.9103 | 45.3901 | 18.1319 | 37.3685 |
| ENGO | 16.3498 | 36.2778 | 18.0688 | 32.4697 | 13.9053 | 36.2515 | 15.7787 | 31.2109 |
| AOA | 7.3482 | 16.5814 | 9.7969 | 18.9440 | 8.9957 | 11.7763 | 6.7875 | 23.3493 |
| AO | 6.7509 | 26.2480 | 15.9342 | 28.5684 | 18.4118 | 42.2120 | 11.9579 | 14.9953 |
| HHO | 19.5464 | 53.4613 | 24.5021 | 44.3106 | 20.7301 | 44.8527 | 26.8726 | 52.5285 |
| WOA | 11.5902 | 27.4520 | 12.1870 | 32.3820 | 11.1318 | 20.5502 | 13.5990 | 23.5141 |
| PSO | 23.4903 | 54.2967 | 24.7237 | 51.7276 | 32.4498 | 54.2332 | 18.4690 | 43.6656 |
| GWO | 21.7829 | 59.0988 | 22.9404 | 33.5723 | 20.0176 | 47.8837 | 20.2588 | 42.3957 |
| MRFO | 22.1205 | 43.6337 | 17.6126 | 38.1229 | 20.9525 | 41.6324 | 21.0797 | 48.9074 |
| MVO | 32.4530 | 57.1252 | 22.4880 | 47.3220 | 22.7186 | 67.3639 | 13.1444 | 22.6758 |
| Algorithms | x9 | x10 | x11 | x12 | x13 | x14 | x15 | x16 |
| NGO | 0.7977 | 1.9562 | 1.2978 | 0.7257 | 1.5711 | 3.5749 | 5.1603 | 4.5826 |
| ENGO | 1.1626 | 1.0218 | 1.1244 | 1.2402 | 1.8459 | 3.5264 | 4.2182 | 4.8197 |
| AOA | 2.6529 | 1.2972 | 1.6242 | 1.9436 | 1.6410 | 2.7802 | 4.2547 | 3.5011 |
| AO | 2.4254 | 0.5351 | 1.0247 | 1.6666 | 1.7472 | 3.5758 | 2.1305 | 3.9710 |
| HHO | 0.7225 | 0.9587 | 1.2449 | 1.1576 | 6.2971 | 2.8094 | 4.5773 | 3.2258 |
| WOA | 0.8123 | 1.1016 | 1.4739 | 1.4853 | 0.7152 | 3.7964 | 3.5428 | 3.1702 |
| PSO | 1.2110 | 1.4161 | 1.1434 | 1.1996 | 1.6512 | 6.2798 | 2.9257 | 5.6438 |
| GWO | 0.6744 | 0.5895 | 0.6186 | 0.8372 | 8.0862 | 4.0926 | 5.5300 | 5.1202 |
| MRFO | 1.1778 | 1.1063 | 1.0636 | 1.0945 | 2.3573 | 5.2736 | 5.1814 | 4.8497 |
| MVO | 1.4973 | 1.0831 | 0.7566 | 1.9664 | 7.2887 | 5.9129 | 5.7797 | 5.5464 |
| Algorithms | x17 | x18 | x19 | x20 | x21 | x22 | ||
| NGO | 2.9657 | 1.1195 | 4.3970 | 2.4098 | 3.5683 | 3.6964 | ||
| ENGO | 4.8350 | 1.8115 | 5.3561 | 3.8104 | 3.7590 | 2.7212 | ||
| AOA | 4.5457 | 2.9304 | 5.6055 | 2.3556 | 1.6346 | 1.6271 | ||
| AO | 2.7660 | 6.2850 | 3.4033 | 2.7208 | 3.2026 | 2.8172 | ||
| HHO | 2.9383 | 4.7721 | 2.9564 | 2.4774 | 3.4950 | 2.9967 | ||
| WOA | 2.5494 | 1.0331 | 1.7917 | 2.8701 | 1.7390 | 2.7638 | ||
| PSO | 6.0429 | 7.3123 | 5.0504 | 3.1684 | 6.1872 | 3.9215 | ||
| GWO | 5.1050 | 6.3408 | 6.4331 | 3.6878 | 4.2577 | 5.0673 | ||
| MRFO | 6.2644 | 4.2654 | 4.1077 | 2.8940 | 3.6149 | 4.3536 | ||
| MVO | 3.6218 | 1.9314 | 5.9677 | 5.2745 | 6.1850 | 3.9999 |
| Case | Node | Px (Kips) | PY (Kips) | Pz (Kips) |
|---|---|---|---|---|
| 1 | 17 | 0.0 | 0.0 | −5.0 |
| 18 | 0.0 | 0.0 | −5.0 | |
| 19 | 0.0 | 0.0 | −5.0 | |
| 20 | 0.0 | 0.0 | −5.0 | |
| 2 | 17 | 5.0 | 5.0 | −5.0 |
| Algorithms | The Best | The Average | The Worst | The Std | Rank |
|---|---|---|---|---|---|
| NGO | 392.18 | 411.71 | 444.66 | 15.70 | 4 |
| ENGO | 364.94 | 369.08 | 374.79 | 2.37 | 1 |
| AOA | 521.87 | 633.25 | 797.57 | 79.64 | 8 |
| AO | 450.14 | 519.94 | 643.44 | 49.42 | 5 |
| HHO | 469.52 | 535.59 | 653.30 | 46.82 | 6 |
| WOA | 657.74 | 1276.02 | 2551.19 | 500.03 | 10 |
| PSO | 561.18 | 656.26 | 817.32 | 58.92 | 9 |
| GWO | 366.77 | 385.89 | 544.00 | 41.89 | 2 |
| MRFO | 374.05 | 387.49 | 398.93 | 6.14 | 3 |
| MVO | 403.42 | 631.44 | 818.15 | 130.68 | 7 |
| Variables | Elements | NGO | ENGO | AOA | AO | HHO | WOA | PSO | GWO | MRFO | MVO |
|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 (cm2) | 1–4 | 2.0920 | 1.8590 | 1.5676 | 1.1585 | 1.8381 | 1.1766 | 1.7266 | 1.9659 | 2.1464 | 2.0780 |
| A2 (cm2) | 5–12 | 0.4767 | 0.5651 | 0.5686 | 0.9007 | 0.5715 | 1.3878 | 0.5236 | 0.5256 | 0.4721 | 0.6499 |
| A3 (cm2) | 13–16 | 0.0947 | 0.0010 | 0.1243 | 0.0010 | 0.5927 | 1.0805 | 1.0676 | 0.0076 | 0.0282 | 0.4172 |
| A4 (cm2) | 17–18 | 0.1207 | 0.0036 | 0.5637 | 0.7380 | 0.0010 | 0.5005 | 0.4696 | 0.0116 | 0.0133 | 0.0010 |
| A5 (cm2) | 19–22 | 0.9872 | 1.1815 | 2.6426 | 0.8930 | 0.8664 | 1.0783 | 0.9505 | 1.3216 | 1.1074 | 1.3433 |
| A6 (cm2) | 23–30 | 0.5752 | 0.5100 | 0.7967 | 0.5979 | 0.3892 | 0.4719 | 1.0107 | 0.4859 | 0.5052 | 0.5199 |
| A7 (cm2) | 31–34 | 0.0220 | 0.0087 | 0.0677 | 0.0371 | 0.0010 | 0.3239 | 0.3293 | 0.0239 | 0.0035 | 0.0010 |
| A8 (cm2) | 35–36 | 0.0156 | 0.0027 | 0.6353 | 0.0010 | 0.9025 | 1.0858 | 0.2507 | 0.0553 | 0.0259 | 0.0066 |
| A9 (cm2) | 37–40 | 0.6838 | 0.5605 | 0.9351 | 0.5663 | 0.7672 | 0.3525 | 1.1277 | 0.5764 | 0.6552 | 0.8319 |
| A10 (cm2) | 41–48 | 0.5559 | 0.5261 | 0.3389 | 0.4346 | 0.6098 | 0.8691 | 0.6233 | 0.5201 | 0.5437 | 0.4748 |
| A11 (cm2) | 49–52 | 0.0664 | 0.0010 | 0.3367 | 0.0010 | 0.5841 | 0.2747 | 0.1287 | 0.0254 | 0.0472 | 0.0010 |
| A12 (cm2) | 53–54 | 0.0944 | 0.1566 | 0.6734 | 0.4884 | 0.0737 | 0.9883 | 0.4048 | 0.0536 | 0.0857 | 0.3795 |
| A13 (cm2) | 55–58 | 0.2149 | 0.1639 | 0.9447 | 0.1893 | 0.1440 | 0.5191 | 0.3632 | 0.1694 | 0.2025 | 0.1548 |
| A14 (cm2) | 59–66 | 0.5023 | 0.5753 | 0.5190 | 0.7363 | 0.5593 | 0.3495 | 0.3299 | 0.5391 | 0.5462 | 0.5078 |
| A15 (cm2) | 67–70 | 0.4853 | 0.3682 | 0.6180 | 0.5549 | 0.9750 | 1.0178 | 0.7666 | 0.4751 | 0.4264 | 0.2240 |
| A16 (cm2) | 71–72 | 0.8930 | 0.5086 | 0.5435 | 0.7684 | 0.5203 | 1.0450 | 1.3540 | 0.5289 | 0.7368 | 0.6657 |
| Algorithms | The Best | The Average | The Worst | The Std | Rank |
|---|---|---|---|---|---|
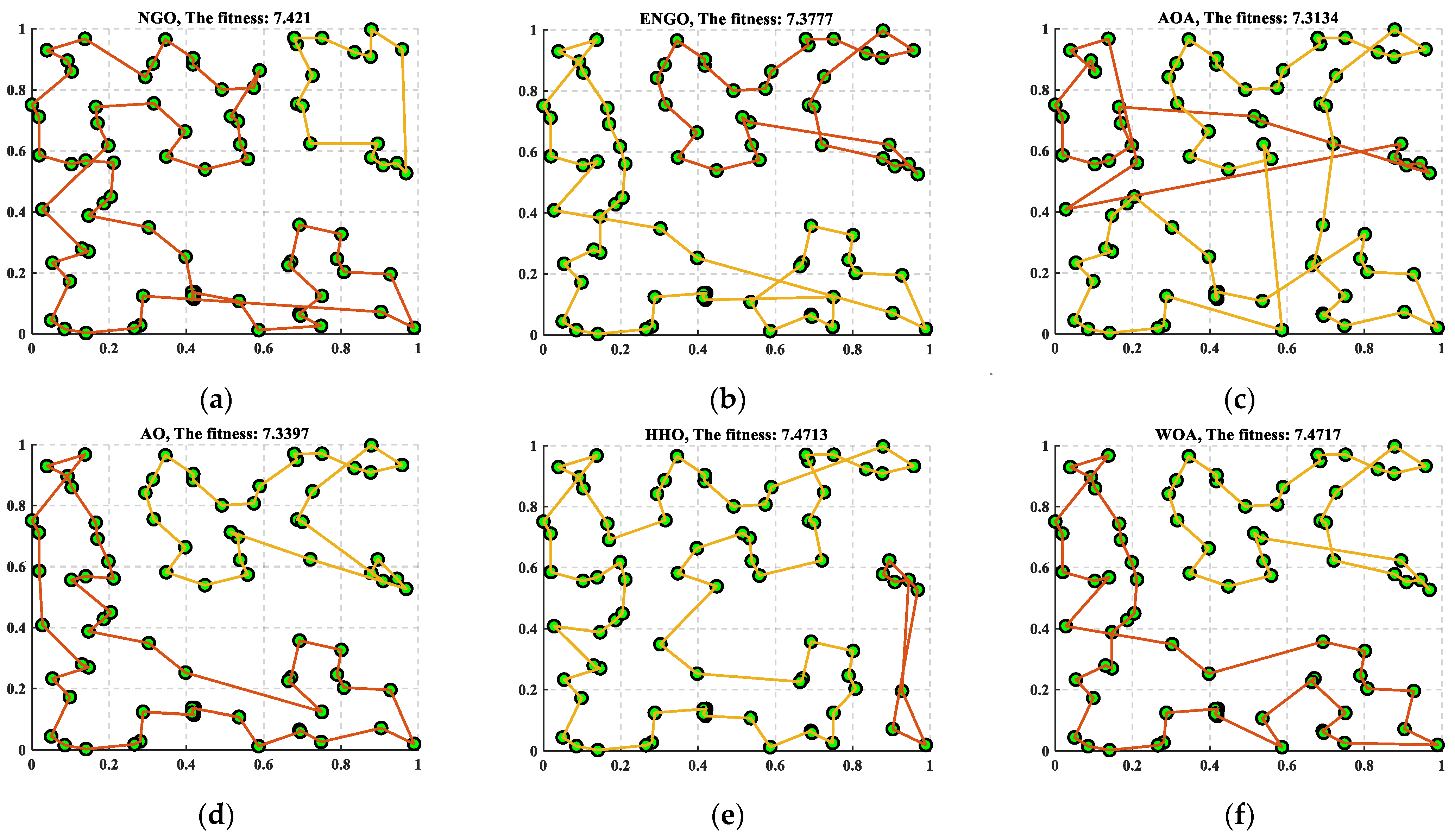
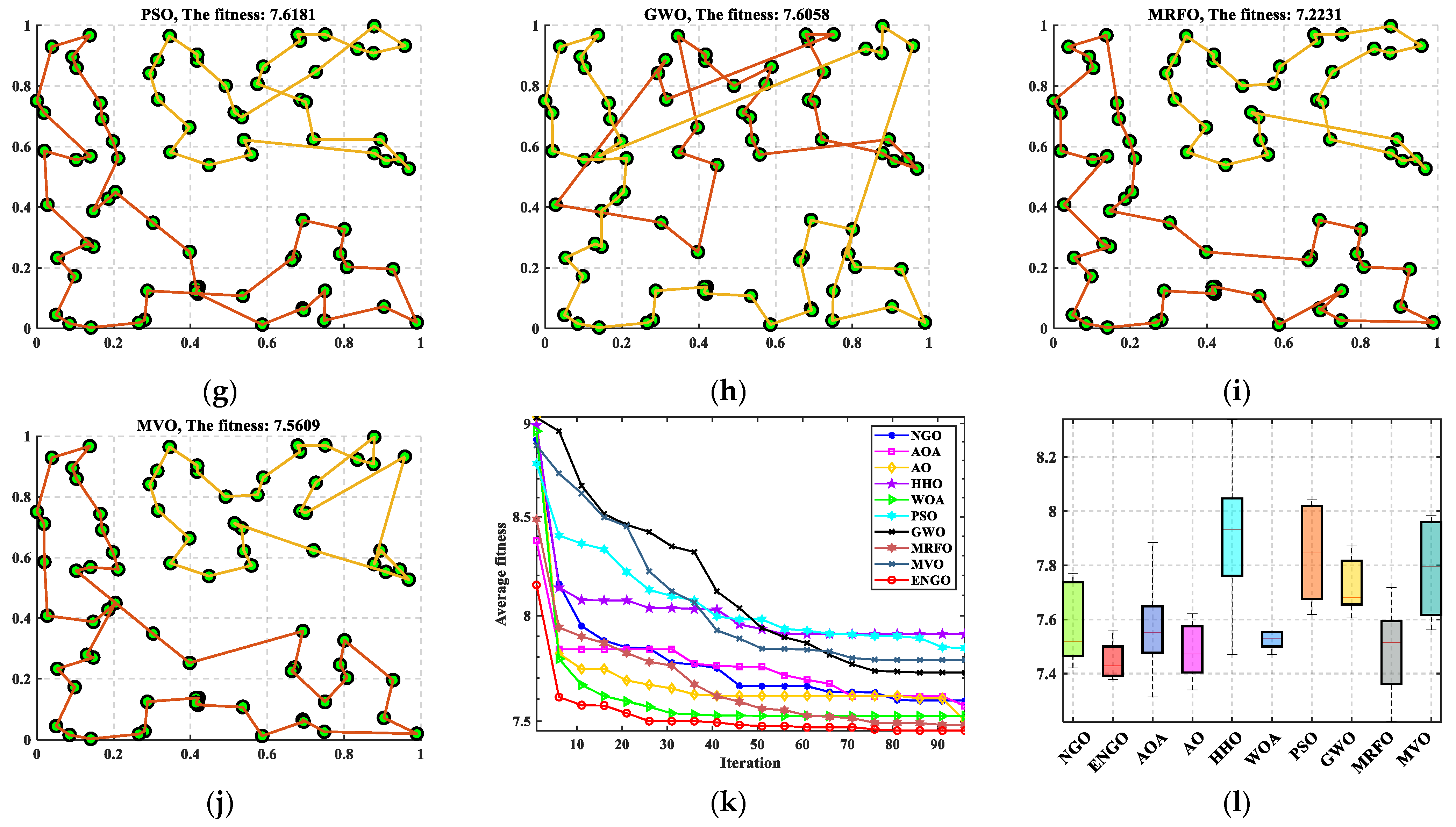
| NGO | 7.4210 | 7.5834 | 7.7711 | 0.1558 | 6 |
| ENGO | 7.3777 | 7.4481 | 7.5576 | 0.0727 | 1 |
| AOA | 7.3134 | 7.5703 | 7.8840 | 0.2039 | 5 |
| AO | 7.3397 | 7.4836 | 7.6206 | 0.1105 | 3 |
| HHO | 7.4713 | 7.9101 | 8.3391 | 0.3088 | 10 |
| WOA | 7.4717 | 7.5239 | 7.5539 | 0.0346 | 4 |
| PSO | 7.6181 | 7.8428 | 8.0443 | 0.1876 | 9 |
| GWO | 7.6058 | 7.7255 | 7.8716 | 0.1072 | 7 |
| MRFO | 7.2231 | 7.4833 | 7.7176 | 0.1832 | 2 |
| MVO | 7.5609 | 7.7854 | 7.9852 | 0.1874 | 8 |
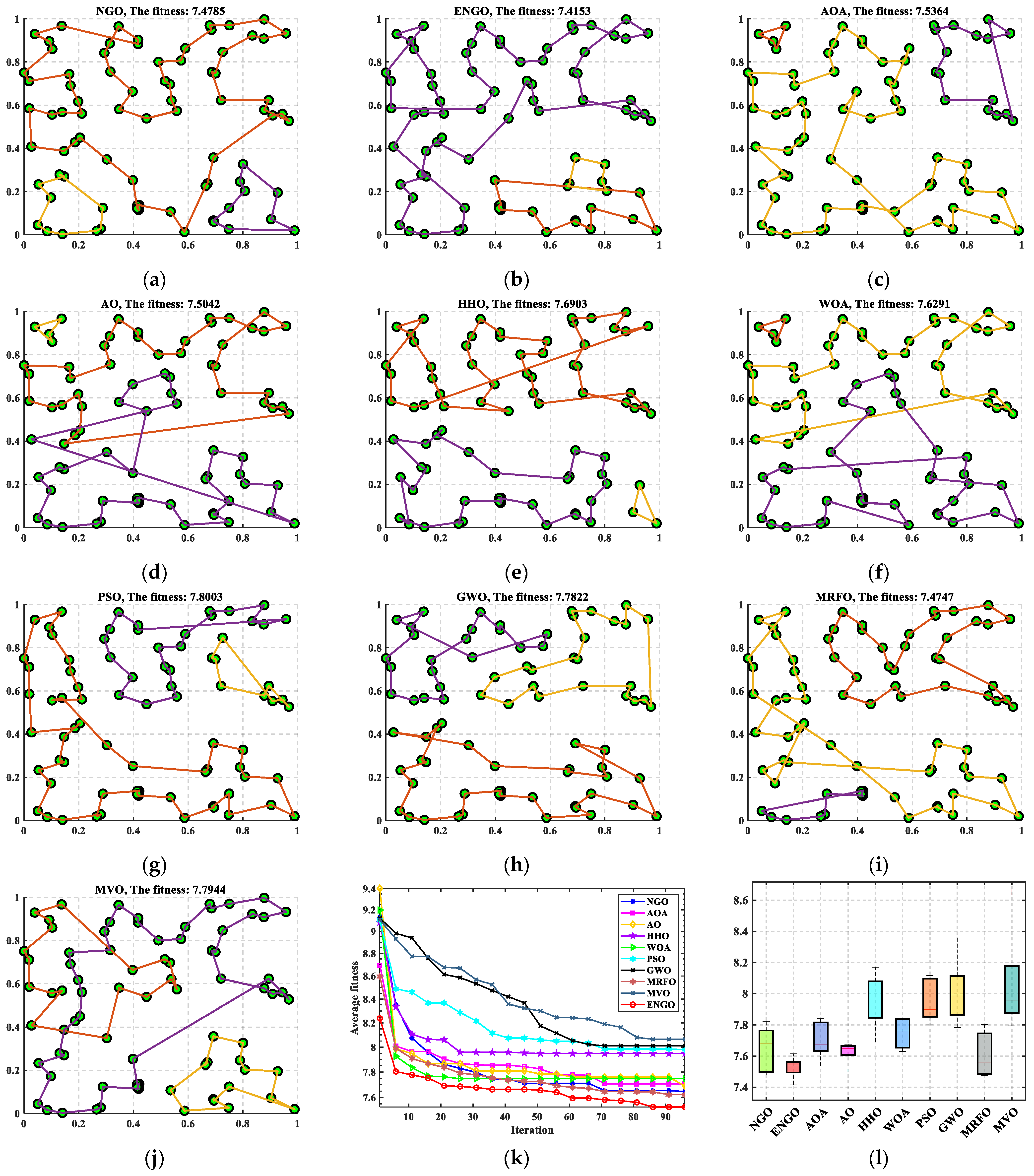
| Algorithms | The Best | The Average | The Worst | The Std | Rank |
|---|---|---|---|---|---|
| NGO | 7.4785 | 7.6461 | 7.8232 | 0.1497 | 4 |
| ENGO | 7.4153 | 7.5262 | 7.6154 | 0.0719 | 1 |
| AOA | 7.5364 | 7.7051 | 7.8416 | 0.1225 | 5 |
| AO | 7.5042 | 7.6262 | 7.6752 | 0.0695 | 3 |
| HHO | 7.6903 | 7.9476 | 8.1682 | 0.1786 | 7 |
| WOA | 7.6291 | 7.7467 | 7.8408 | 0.0973 | 6 |
| PSO | 7.8003 | 7.9549 | 8.1152 | 0.1396 | 8 |
| GWO | 7.7822 | 8.0106 | 8.3583 | 0.2167 | 9 |
| MRFO | 7.4747 | 7.6107 | 7.8013 | 0.1459 | 2 |
| MVO | 7.7944 | 8.0646 | 8.6528 | 0.3388 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Hu, X.; Hu, G.; Dou, W. An Enhanced Northern Goshawk Optimization Algorithm and Its Application in Practical Optimization Problems. Mathematics 2022, 10, 4383. https://doi.org/10.3390/math10224383
Liang Y, Hu X, Hu G, Dou W. An Enhanced Northern Goshawk Optimization Algorithm and Its Application in Practical Optimization Problems. Mathematics. 2022; 10(22):4383. https://doi.org/10.3390/math10224383
Chicago/Turabian StyleLiang, Yan, Xianzhi Hu, Gang Hu, and Wanting Dou. 2022. "An Enhanced Northern Goshawk Optimization Algorithm and Its Application in Practical Optimization Problems" Mathematics 10, no. 22: 4383. https://doi.org/10.3390/math10224383
APA StyleLiang, Y., Hu, X., Hu, G., & Dou, W. (2022). An Enhanced Northern Goshawk Optimization Algorithm and Its Application in Practical Optimization Problems. Mathematics, 10(22), 4383. https://doi.org/10.3390/math10224383







