A Class of Semilinear Parabolic Problems and Analytic Semigroups †
Abstract
1. Introduction and Main Theorem
- (1)
- and for all and all , and there exists a constant such thatwhere is the cotangent bundle of .
- (2)
- for all .
- (3)
- and in .
- (1)
- and are real-valued, functions on .
- (2)
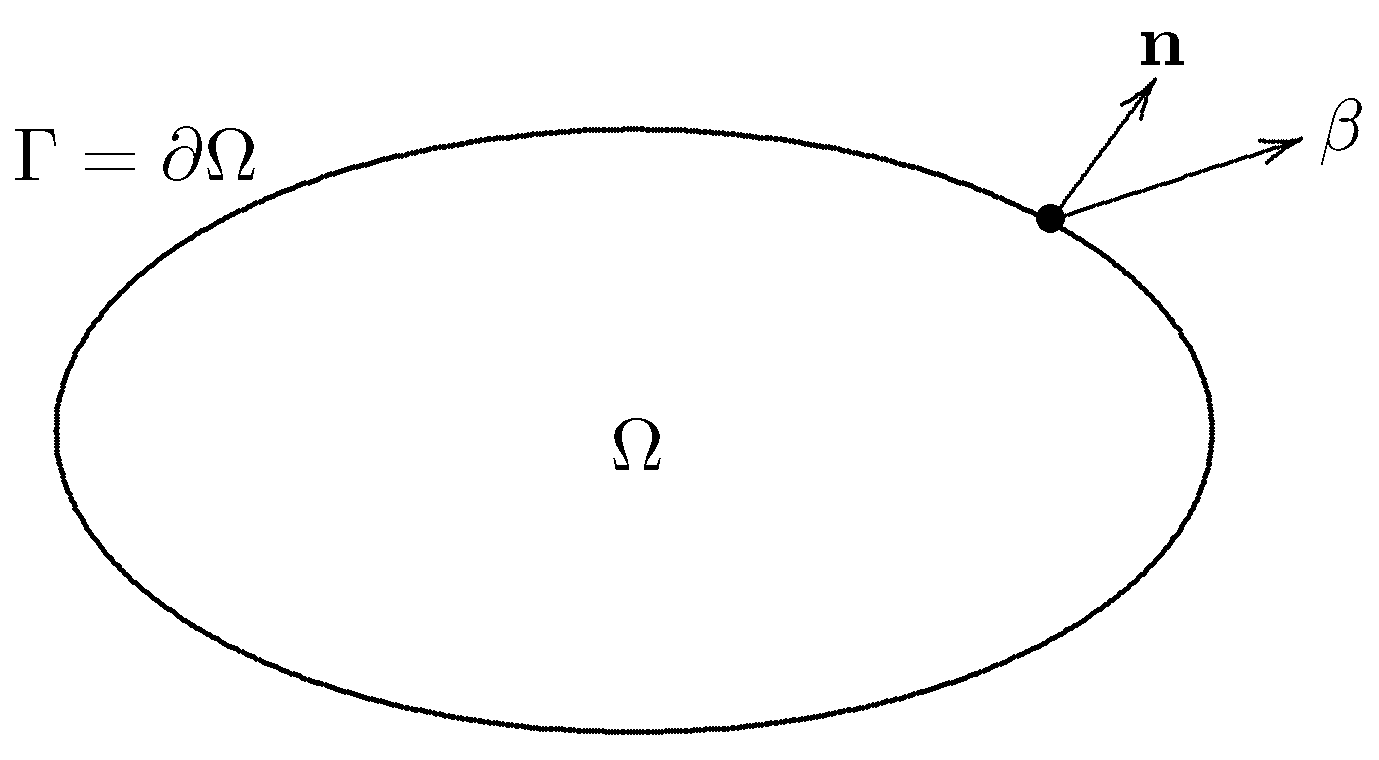
- is the conormal derivative associated with the differential operator A:being the unit outward normal to the boundary (see Figure 1).
- (a)
- The domain of definition of is the set
- (b)
- for every .
- (H.1)
- and on Γ.
- (H.2)
- on Γ.
- (i)
- For every , there exists a constant such that the resolvent set of contains the setand that the resolvent satisfies the estimatewhere is a constant depending on ε.
- (ii)
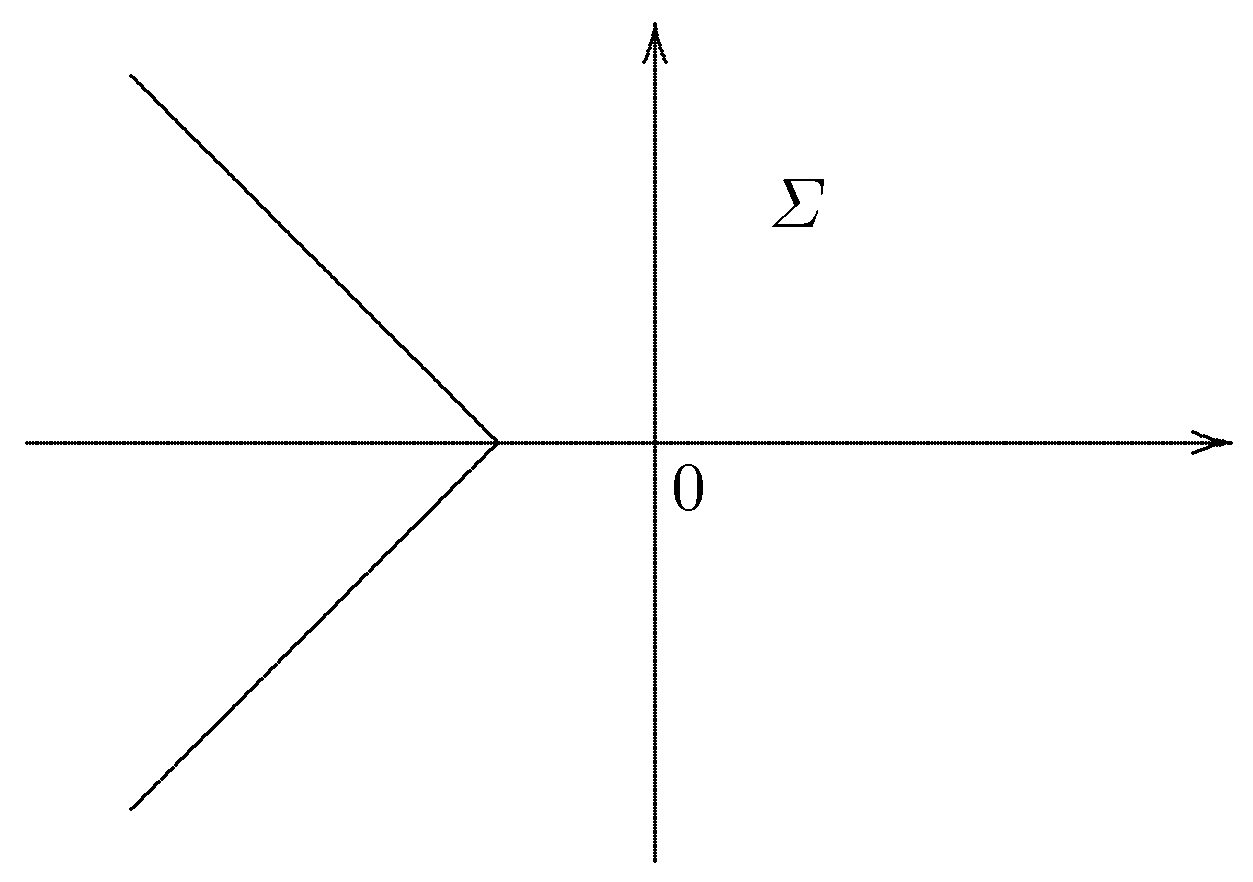
- The operator generates a semigroup on the space which is analytic in the sectorfor any (see Figure 2).
1.1. Statement of Main Theorem
- (H.1)
- and on Γ.
- (H.3)
- Either on Γ (regular Robin and Neumann cases) or and on Γ (Dirichlet case).
1.2. Outline of the Paper
2. Fractional Powers for Analytic Semigroups
- (1)
- The space is a Banach space.
- (2)
- (3)
- If , then we have with continuous injection.
3. Compactness Theorem for Spaces of Class
4. Proof of Theorem 2
5. Applications to Diffusive Logistic Equations in Population Dynamics
- (1)
- is the Laplacian.
- (2)
- d is a positive parameter.
- (3)
- is a real-valued function on .
- (4)
- is a non-negative function on .
- (5)
- Either and on (Neumann cases) or and on (Dirichlet case).
- (6)
- is the unit outward normal to the boundary (see Figure 1).
- (M1)
- The function belongs to the space and the set has positive measure.
- (i)
- The solution represents the population density of a species inhabiting a region .
- (ii)
- The members of the population are supposed to move about via the type of random walks occurring in Brownian motion that is modeled by the diffusive term ; hence d represents the rate of diffusive dispersal. For large values of d the population spreads more rapidly than for small values of d.
- (iii)
- The local rate of change in the population density is described by the density-dependent term .
- (iv)
- The term describes the rate at which the population would grow or decline at the location x in the absence of crowding or limitations on the availability of resources. The sign of will be positive on favorable habitats for population growth and negative on unfavorable ones. Specifically may be considered as a food source or any resource which will be good in some areas and bad in others.
- (v)
- The term describes the effects of crowding on the growth rate of the population at the location x; these effects are supposed to be independent of those determining the growth rate. The size of the coefficient of intraspecific competition describes the strength of the effects of crowding within the population.
- (vi)
- In terms of biology, the homogeneous Dirichlet condition represents that is surrounded by a completely hostile exterior such that any member of the population which reaches the boundary dies immediately; in other words, the exterior of the domain is deadly to the population ( and on ).
- (vii)
- If the boundary acts as a barrier, so that individuals reaching the boundary simply return to the interior, a Neumann boundary condition results ( and on ).
- (viii)
- If the exterior is hostile but not completely deadly, a mixed or Robin boundary condition results ( and on ), and the analysis is similar.
- (ix)
- A biological interpretation of our main results (Theorems 6 and 9) is that when the environment has an impassable boundary and is on the average unfavorable, then high diffusion rates have the same effect as they always have when the boundary is deadly; but if the boundary is impassable and the environment is on the average neutral or favorable, then the population can persist, no matter what its rate of diffusion.
5.1. Dirichlet Eigenvalue Problems with Indefinite Weights
- 1°
- By the Rayleigh principle (see Manes–Micheletti [17], de Figueiredo [18]), we know that the first eigenvalue is given by the variational formulaHere is the closure of smooth functions with compact support in Ω in the Sobolev space .
- 2°
- By Formula (64), we find that the first eigenvalue is strictly decreasing with respect to the weight in the following sense (see [19] (Proposition 8.3)): If almost everywhere in Ω, then the corresponding first eigenvalues and satisfy the relationIf the inequality is strict on a set of positive measure, it follows that .
- (i)
- If there is a favorable region, then the models we consider predict persistence for a population since the existence of the first positive eigenvalue is equivalent to the existence of a positive density function describing the distribution of the population of .
- (ii)
- The size of the first eigenvalue is of crucial importance; increasing imposes a more stringent condition on the diffusion rate d if the population is to persist, since (see Theorem 6).
- (iii)
- It is worthwhile to point out here that the first eigenvalue will tend to be smaller in situations where favorable and unfavorable habitats are closely intermingled (producing cancellation effects), and larger when the favorable region consists of a relatively small number of relatively large isolated components.
5.2. Diffusive Logistic Dirichlet Problems
- (Z1)
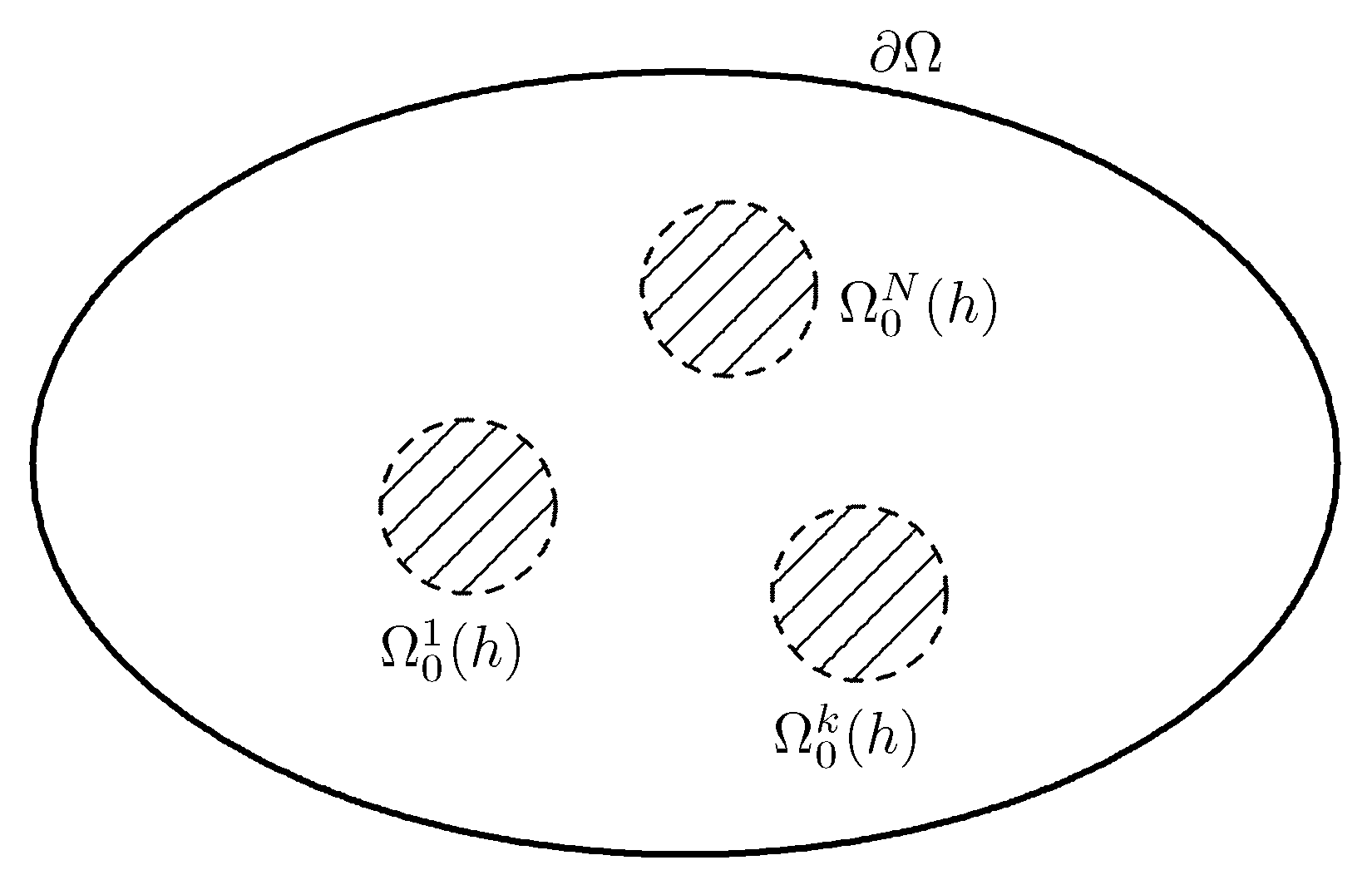
- The open set consists of a finite number of connected components with boundary of class , say , , which are bounded away from the boundary .
- (Z2)
- Each set has positive measure for ,
- (i)
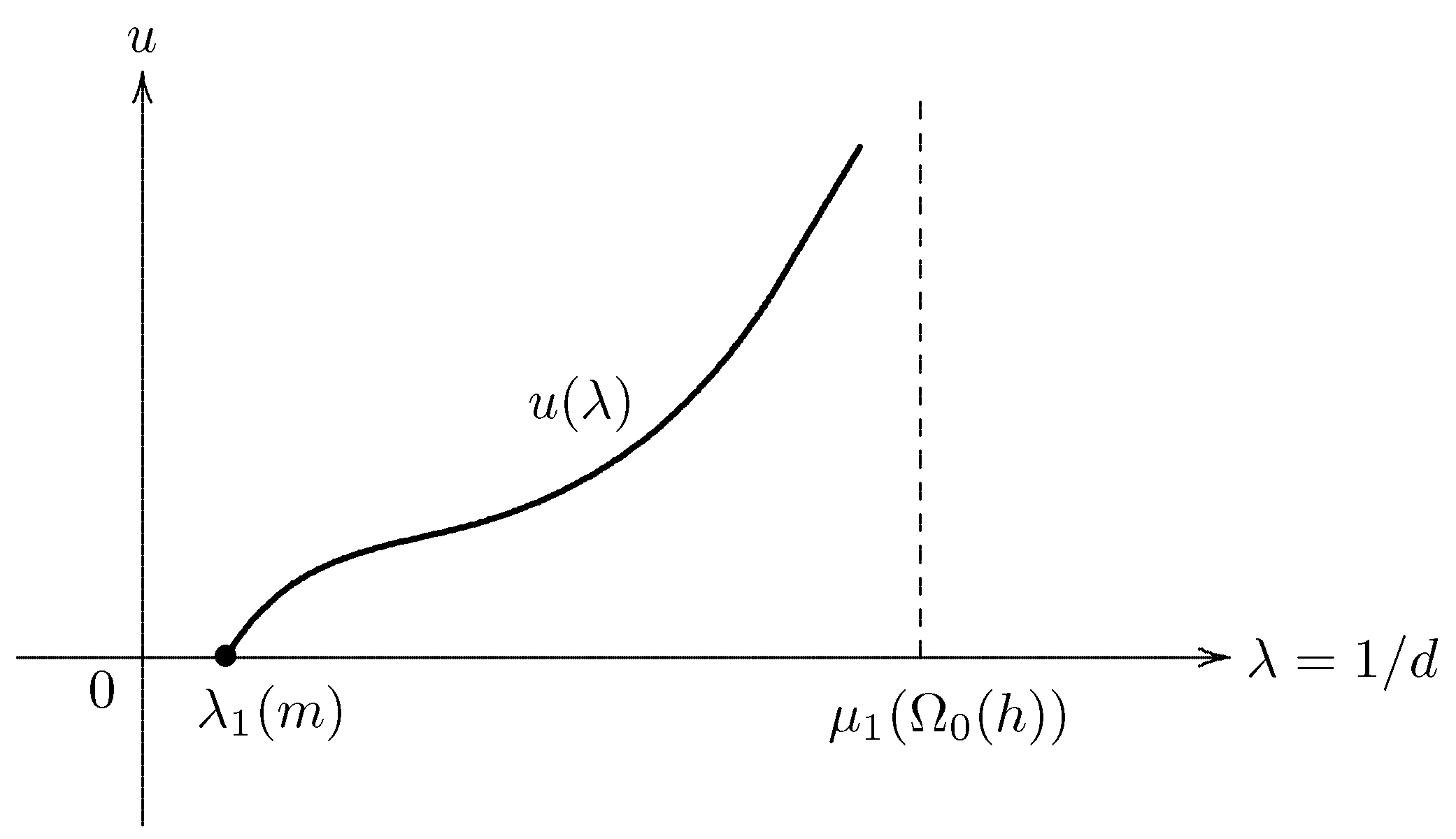
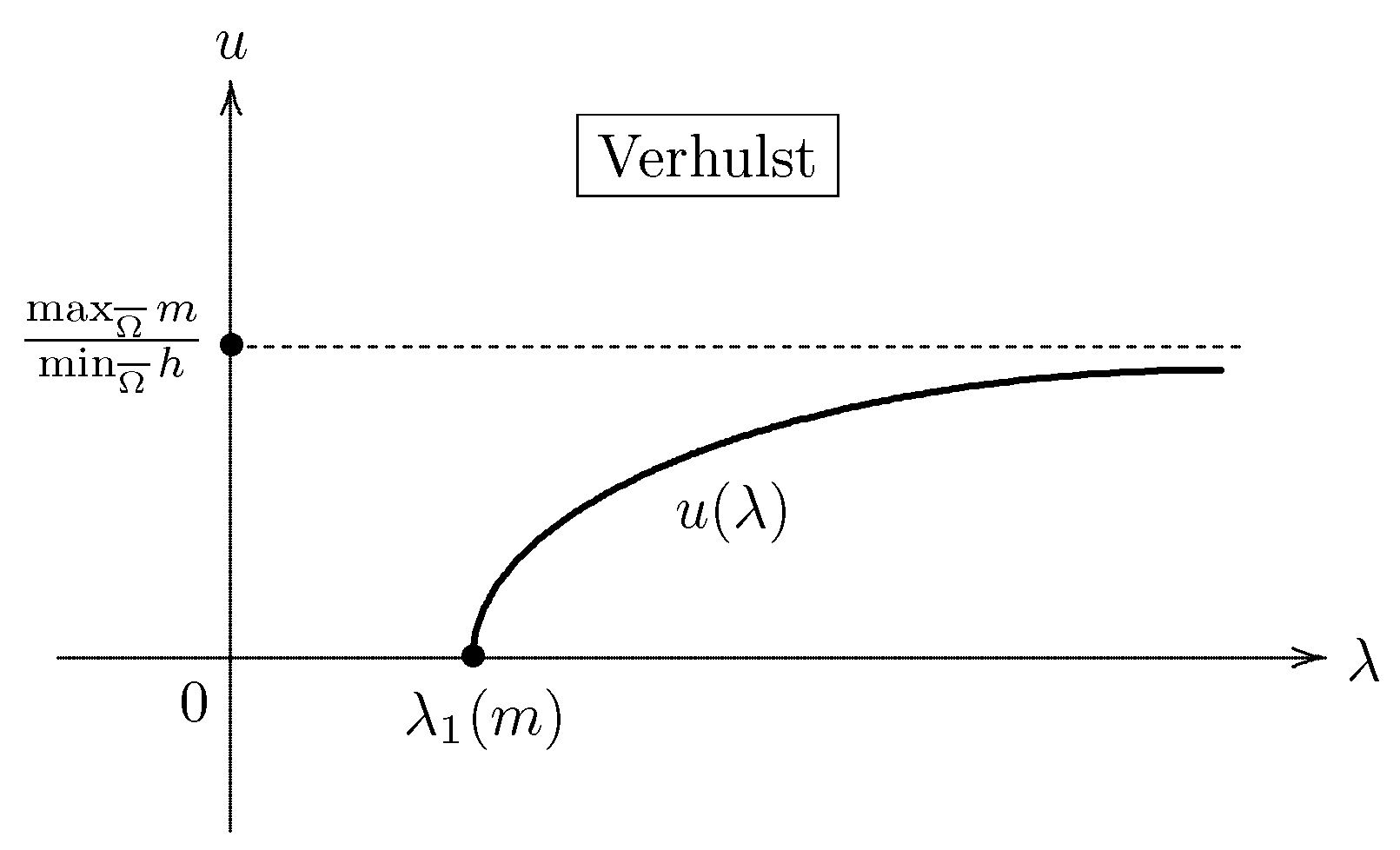
- If the environment has a completely hostile boundary, then the models we consider predict persistence for a population if its diffusion rate d is below the critical value depending on the intrinsic growth rate and if it is above the critical value depending on the coefficient describing the strength of the crowding effects.
- (ii)
- In a certain sense, the most favorable situations will occur if there is a relatively large favorable region (with good resources and without crowding effects) located some distance away from the boundary of .
- 1°
- Theorem 6 may be proved by using thesuper-sub-solution methodjust as in the proof of Fraile et al. [26] (Theorems 3.5 and 4.6), with a weaker assertion
- 2°
- Theorem 6 asserts that the assertions hold true if the dimension n is greater than 2 (). It should be emphasized that an estimate of the growth rate of the total size of the positive steady states as is of crucial importance from the viewpoint of population dynamics.
- 3°
- López-Gómez–Sabina de Lis [27] analyze the pointwise growth to infinity of positive solutions of the logistic Dirichlet problem in the case where in Ω (see [27], Theorems 4.2 and 4.3). Furthermore, García-Melián et al. [28] study the pointwise behavior and the uniqueness of positive solutions of nonlinear elliptic boundary value problems of general sublinear type, and give the exact limiting profile of the positive solutions (see [28], Theorem 3.1, Corollary 3.3 and Theorem 6.4). Their numerical computations confirm and illuminate the above bifurcation diagram (Figure 5).
5.3. Stability for Positive Solutions of Diffusive Logistic Dirichlet Problems
- (i)
- The zero solution of the logistic Dirichet problem (66) is globally asymptotically stable if λ is so small thatIn this case, we can give an estimate of the decay rate of the total size of the population
- (ii)
- A positive solution of the logistic Dirichlet problem (66) is globally asymptotically stable for each λ satisfying the condition
- (iii)
- If λ is so large thatthen we have the assertionfor each non-trivial initial value satisfying the compatibility conditions (72).
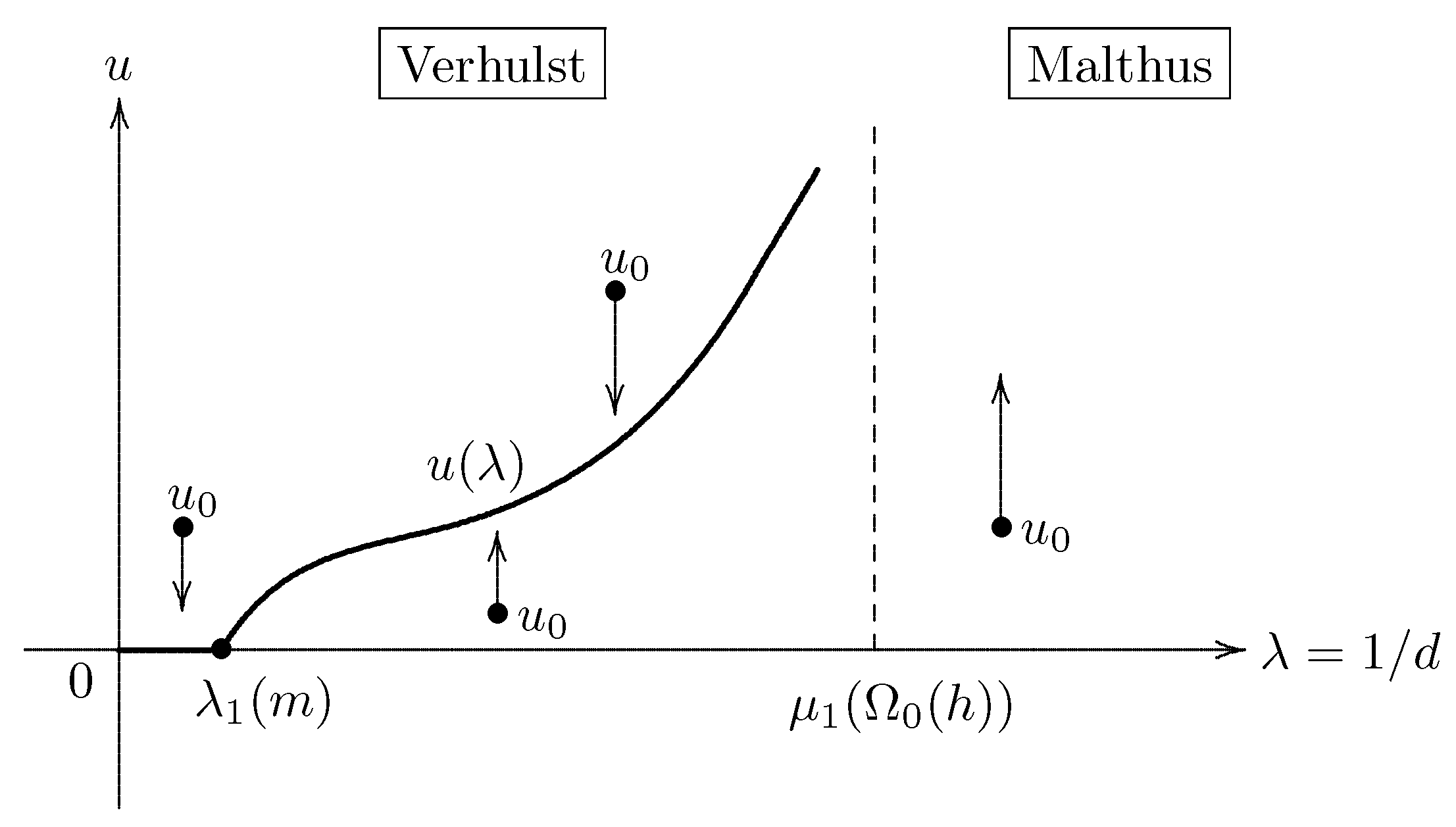
- (i)
- A population will grow exponentially until limited by lack of available resources if the diffusion rate is below the critical value (assertion (74) in part (iii)); this idea is generally credited to the English economist Thomas Robert Malthus (1776–1834).
- (ii)
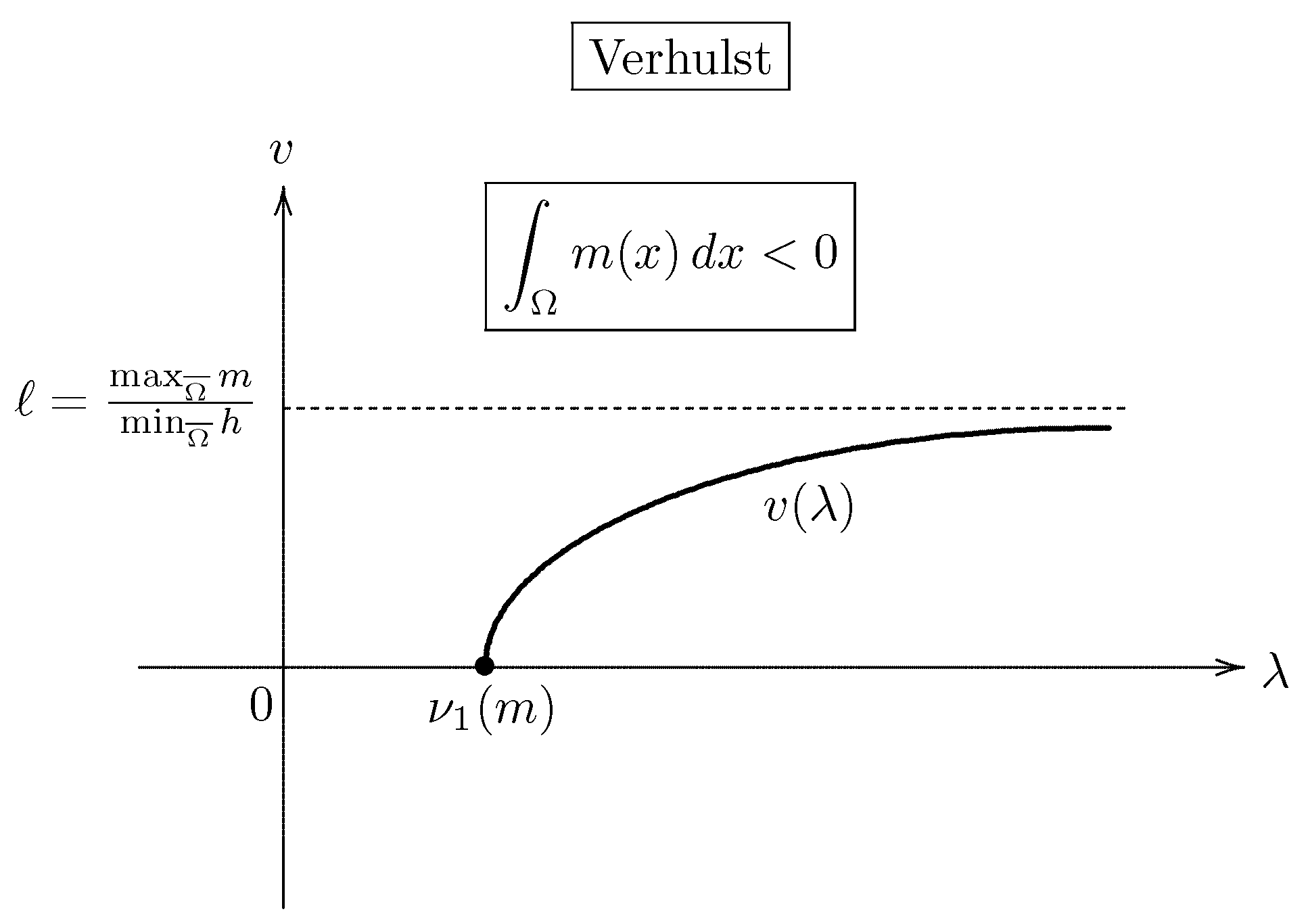
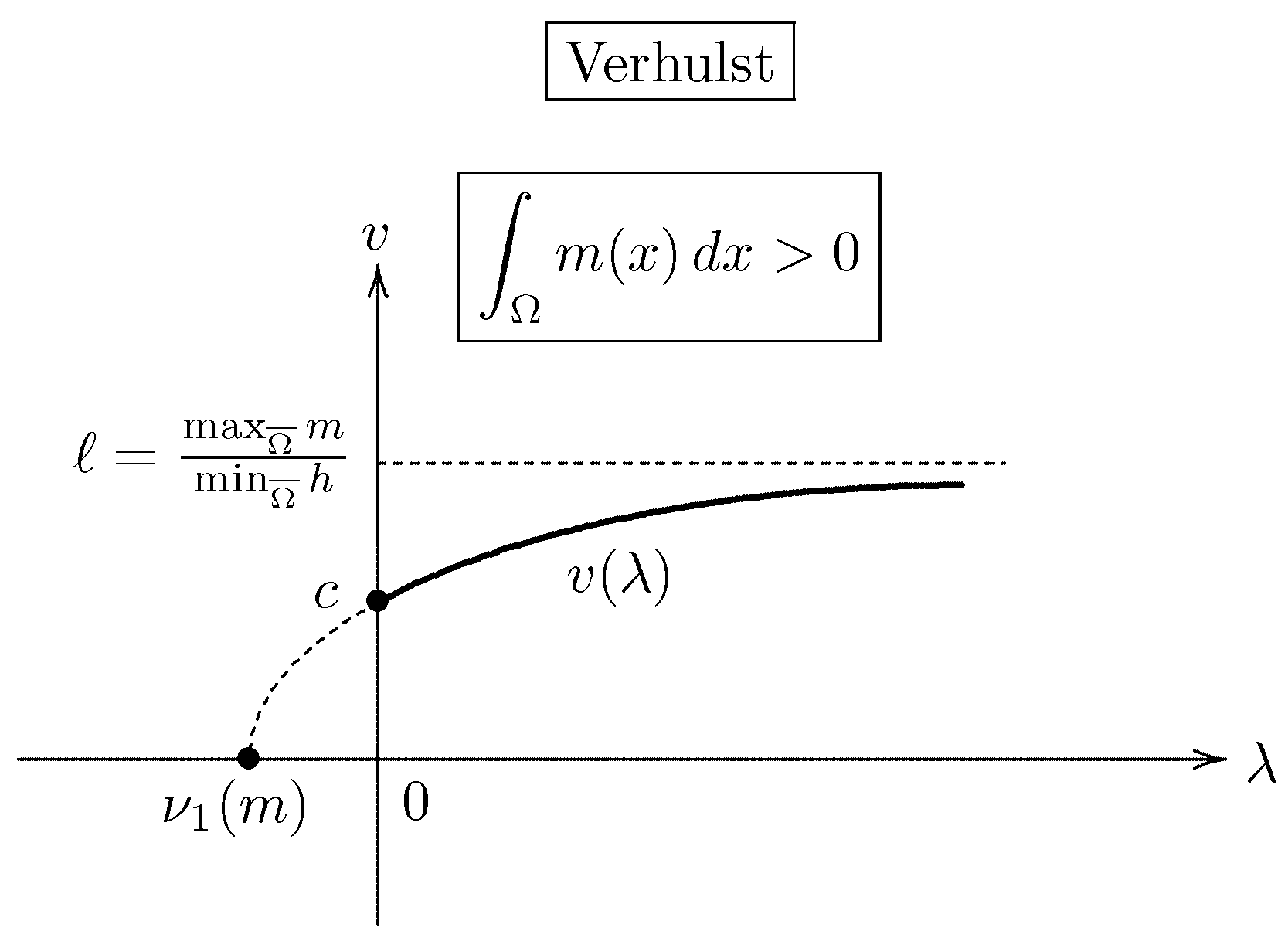
- If the diffusion rate is above the critical value , then the model obeys the logistic equation introduced by the Belgian mathematical biologist Pierre François Verhulst (1804–1849) around 1840 (the decay estimate (73) in part (i)).
5.4. Heuristic Approach to Diffusive Logistic Dirichlet Problems via the Semenov Approximation
5.5. Diffusive Logistic Neumann Problems
- (M2)
- The intrinsic growth rate belongs to the Hölder space for and it attains both positive and negative values in .
- (i)
- If , then the smallest, non-zero eigenvalue of the Neumann problem (79) is positive and simple, and its corresponding eigenfunction may be chosen to be strictly positive everywhere in Ω. Moreover, no other positive eigenvalues have positive eigenfunctions. The eigenvalue 0 is simple and has the positive eigenfunction in Ω.
- (ii)
- If , then the largest, non-zero eigenvalue of the Neumann problem (79) is negative and simple, and its corresponding eigenfunction may be chosen to be strictly positive everywhere in Ω. Moreover, no other negative eigenvalues have positive eigenfunctions. The eigenvalue 0 is simple and has the positive eigenfunction in Ω.
- (iii)
- If , then the eigenvalue 0 of the Neumann problem (79) is the only eigenvalue having the positive eigenfunction in Ω.
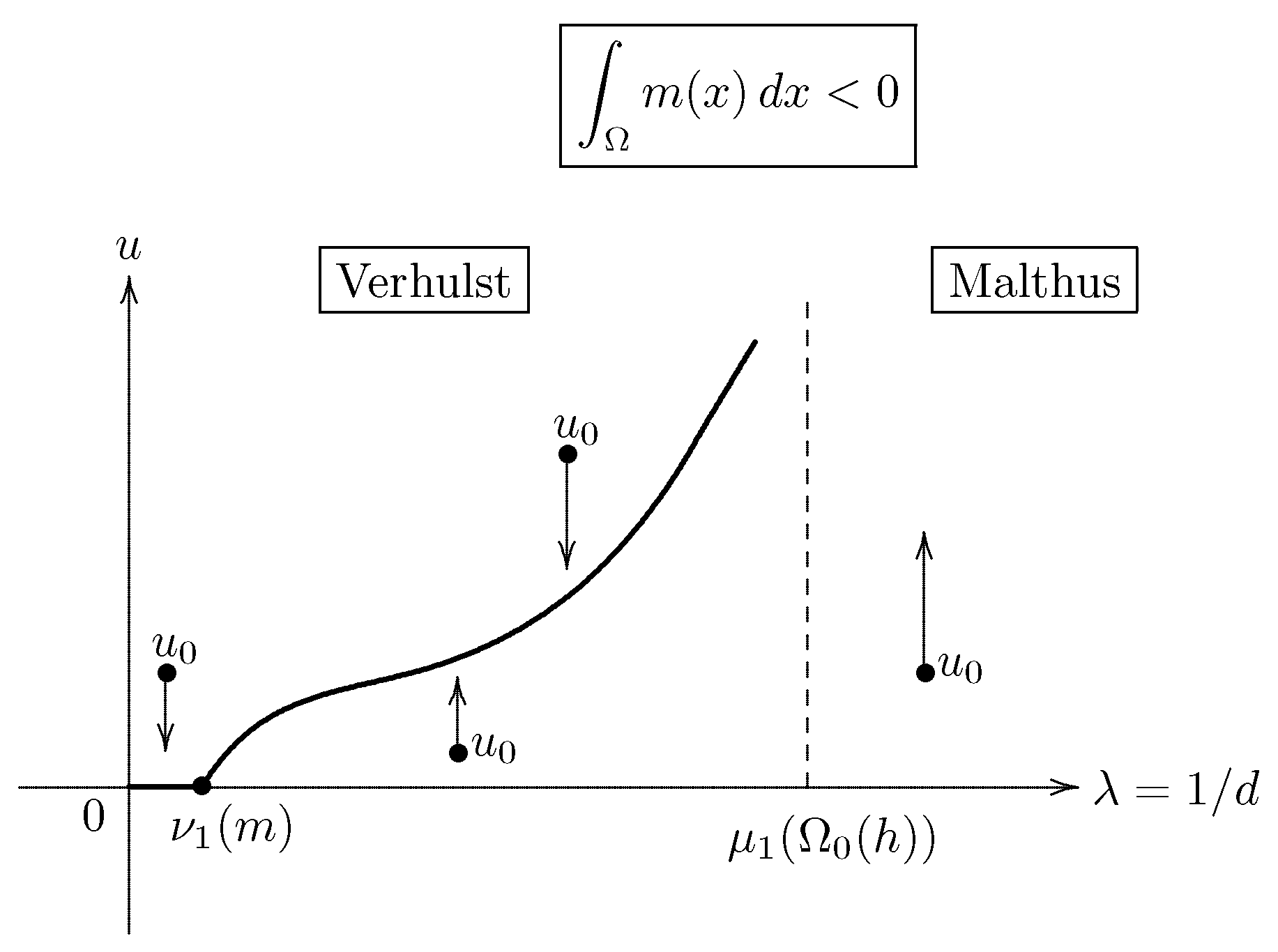
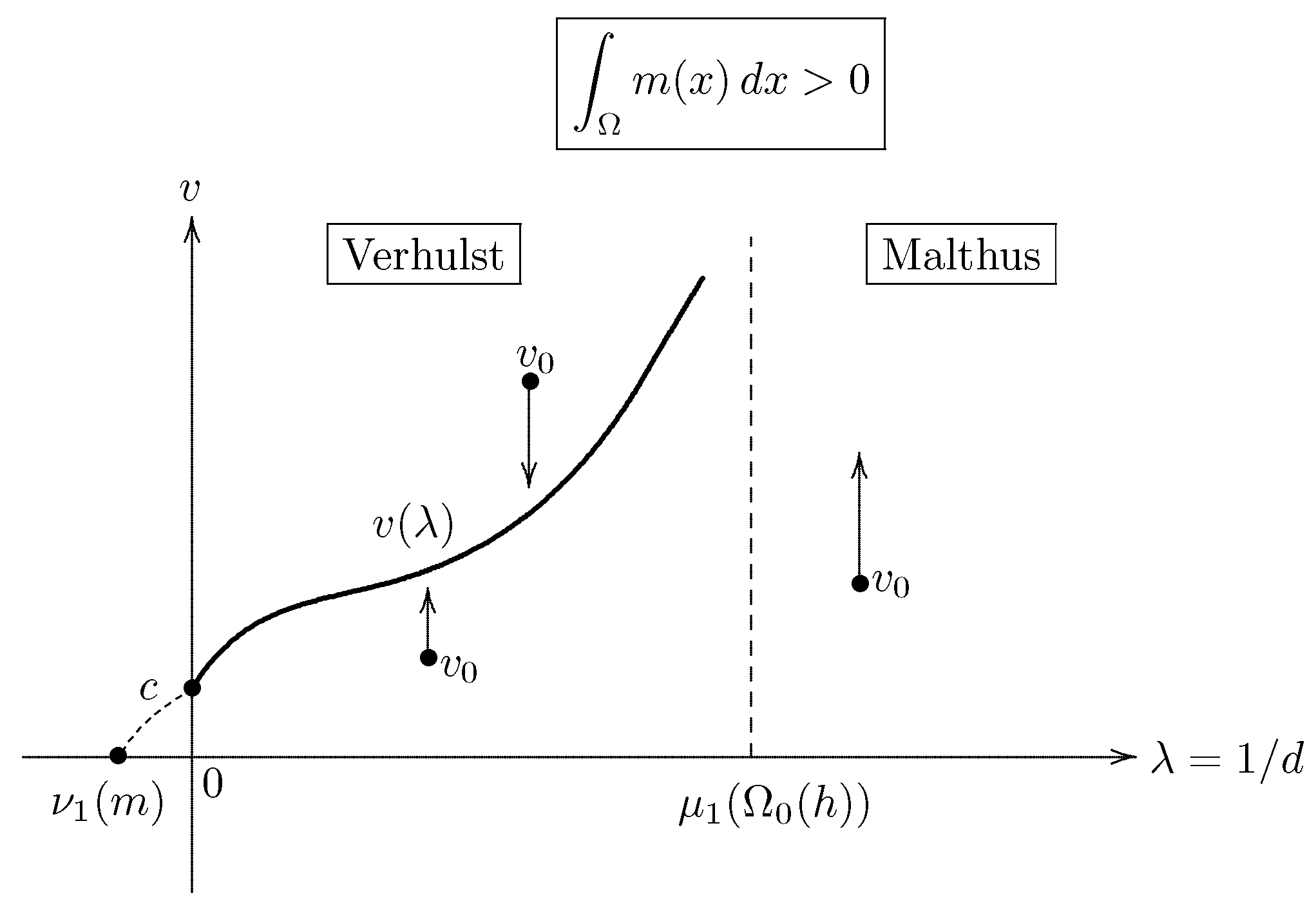
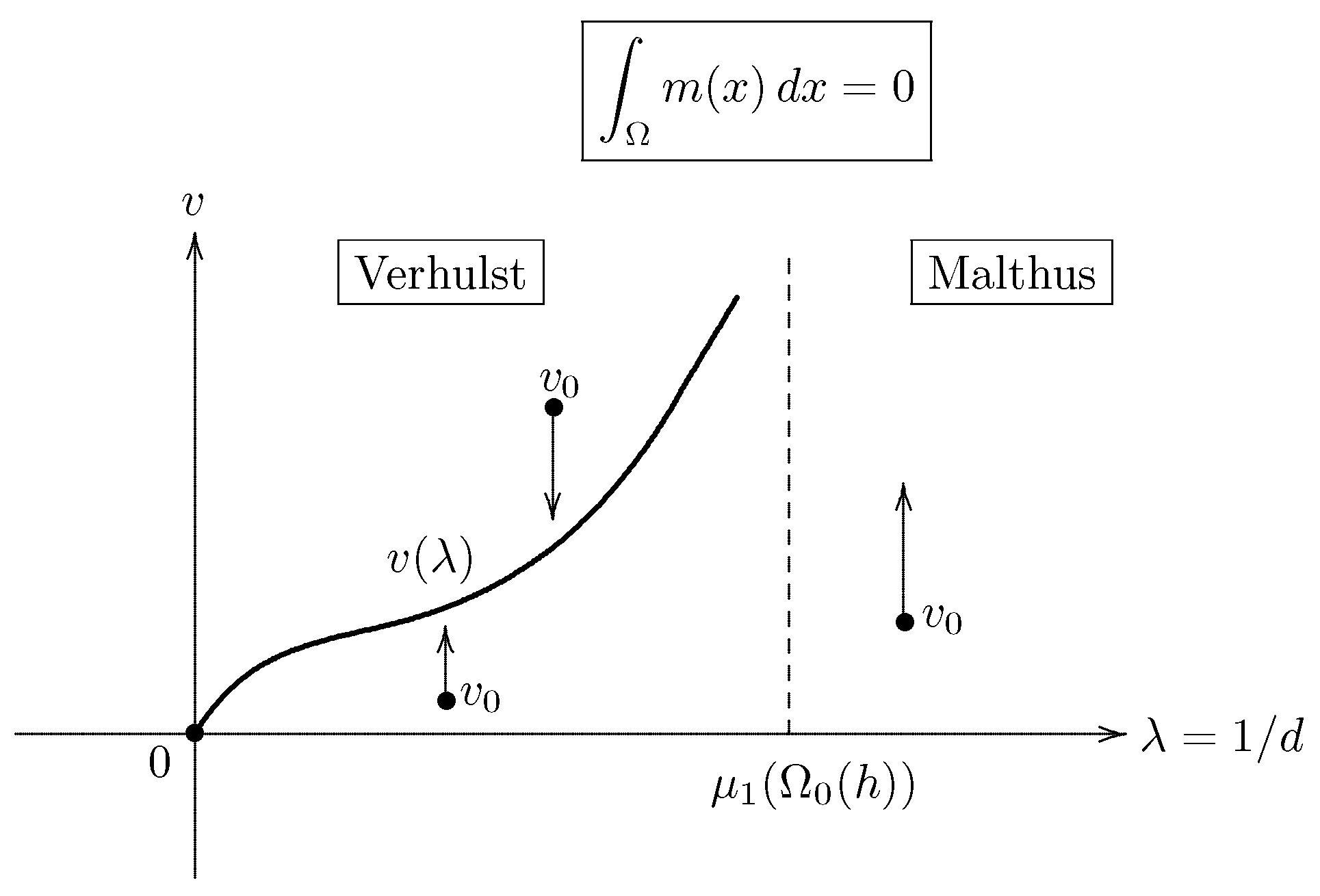
- (i)
- When the environment has an impassable boundary and is on the average unfavorable, then high diffusion rates have the same effect as they always have when the boundary is deadly (cf. Figure 5).
- (ii)
- (iii)
- If the boundary is impassable and the environment is on the average neutral or favorable, then the population can persist, no matter what its rate of diffusion.
- (iv)
- (v)
- If , there occurs a secondary bifurcation from the line of trivial solutions.
- (vi)
- If , there are two curves bifurcating at the point ; the line of trivial solutions and the curve .
- (i)
- If , then we have the following three assertions (a)–(c) (see Figure 11 below):
- (a)
- The zero solution of the logistic Neumann problem (80) is globally asymptotically stableif λ is so small that . In this case, we can obtain an estimate of the decay rate of the total size of the population
- (b)
- A positive solution of the logistic Neumann problem (80) is globally asymptotically stablefor each .
- (c)
- If λ is so large that , then we have the assertionfor each non-trivial initial value satisfying the compatibility conditions (78).
- (ii)
- (d)
- A positive solution of the logistic Neumann problem (80) is globally asymptotically stablefor each .
- (e)
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Classical Results for Linear Initial Boundary Value Problems of Parabolic Type
- (1)
- is an outward pointing, nowhere tangent vector field of class for on the boundary .
- (2)
- and on .
Appendix A.1. Function Spaces for Equations of Parabolic Type
- (1)
- .
- (2)
- .
- (1)
- .
- (2)
- .
- (1)
- .
- (2)
- .
Appendix A.2. Unique Solvability Theorems for Linear Initial Boundary Value Problems of Parabolic Type
References
- Taira, K. Analytic Semigroups and Semilinear Initial-Boundary Value Problems, 2nd ed.; London Mathematical Society Lecture Note Series; Cambridge University Press: Cambridge, UK, 2016; Volume 434. [Google Scholar]
- Lions, J.-L.; Peetre, J. Sur une classe d’espaces d’interpolation. Inst. Hautes Études Sci. Publ. Math. 1964, 19, 5–68. [Google Scholar] [CrossRef]
- Redlinger, R. Über die C2-Kompaktheit der Bahn von Lösungen semilinearer parabolischer Systeme. Proc. R. Soc. Edinb. Sect. A Math. 1982, 93, 99–103. [Google Scholar] [CrossRef]
- Taira, K. A mathematical study of diffusive logistic equations with mixed type boundary conditions. Discret. Contin. Dyn. Syst. S 2021. Available online: https://www.aimsciences.org/article/doi/10.3934/dcdss.2021166 (accessed on 1 December 2021). [CrossRef]
- Ladyženskaja, O.A.; Solonnikov, V.A.; Ural’ceva, N.N. Linear and Quasilinear Equations of Parabolic Type; Smith, S., Translator; Translated from the Russian, Translations of Mathematical Monographs; American Mathematical Society: Providence, RI, USA, 1968; Volume 23. [Google Scholar]
- Friedman, A. Partial Differential Equations of Parabolic Type; Dover Publications Inc.: Mineola, NY, USA, 2008. [Google Scholar]
- Henry, D. Geometric Theory of Semilinear Parabolic Equations; Lecture Notes in Mathematics No. 840; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Pazy, A. Semigroups of Linear Operators and Applications to Partial Differential Equations; Applied Mathematical Sciences; Springer: Berlin/Heidelberg, Germany, 1983; Volume 44. [Google Scholar]
- Lunardi, A. Analytic Semigroups and Optimal Regularity in Parabolic Problems; Reprint of the 1995 Original; Modern Birkhäuser Classics; Birkhüser/Springer Basel AG: Basel, Switzerland, 1995. [Google Scholar]
- Amann, H. Linear and Quasilinear Parabolic Problems, Volume I, Abstract Linear Theory; Monographs in Mathematics; Birkhäuser Boston: Boston, MA, USA, 1995; Volume 89. [Google Scholar]
- Wloka, J. Partial Differential Equations; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Adams, R.A.; Fournier, J.J.F. Sobolev Spaces, 2nd ed.; Pure and Applied Mathematics; Elsevier/Academic Press: Amsterdam, The Netherlands, 2003; Volume 140. [Google Scholar]
- Gilbarg, D.; Trudinger, N.S. Elliptic Partial Differential Equations of Second Order; Reprint of the 1998 Edition; Classics in Mathematics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Taira, K. Positive solutions of diffusive logistic equations. Taiwan. J. Math. 2001, 5, 117–140. [Google Scholar]
- Taira, K. Diffusive logistic equations in population dynamics. Adv. Differ. Equ. 2002, 7, 237–256. [Google Scholar] [CrossRef]
- Taira, K. Introduction to diffusive logistic equations in population dynamics. Korean J. Comput. Appl. Math. 2002, 9, 289–347. [Google Scholar] [CrossRef]
- Manes, A.; Micheletti, A.M. Un’estensione della teoria variazionale classica degli autovalori per operatori ellitici del secondo ordine. Boll. Un. Mat. Ital. 1973, 7, 285–301. [Google Scholar]
- de Figueiredo, D.G. Positive solutions of semilinear elliptic problems. In Differential Equations; Lecture Notes in Mathematics No. 957; Springer: Berlin/Heidelberg, Germany, 1982; pp. 34–87. [Google Scholar]
- López-Gómez, J. Linear Second Order Elliptic Operators; World Scientific Publishing: Hackensack, NJ, USA, 2013. [Google Scholar]
- Ouyang, T.-C. On the positive solutions of semilinear equations Δu + λu − hup = 0 on the compact manifolds. Trans. Am. Math. Soc. 1992, 331, 503–527. [Google Scholar]
- Taira, K. Degenerate elliptic boundary value problems with asymmetric nonlinearity. J. Math. Soc. Jpn. 2010, 62, 431–465. [Google Scholar] [CrossRef]
- Chavel, I. Eigenvalues in Riemannian Geometry; Pure and Applied Mathematics; Academic Press: Orlando, FL, USA, 1984; Volume 115. [Google Scholar]
- Cantrell, R.S.; Cosner, C. Diffusive logistic equations with indefinite weights: Population models in disrupted environments. Proc. R. Soc. Edinb. Sect. A Math. 1989, 112, 293–318. [Google Scholar] [CrossRef]
- Hess, P.; Kato, T. On some linear and nonlinear eigenvalue problems with an indefinite weight function. Commun. Partial Differ. Equ. 1980, 5, 999–1030. [Google Scholar] [CrossRef]
- Hess, P. Periodic-Parabolic Boundary Value Problems and Positivity; Pitman Research Notes in Mathematical Series 247; Longman Scientific & Technical: Harlow, UK, 1991. [Google Scholar]
- Fraile, J.M.; Medina, P.K.; López-Gómez, J.; Merino, S. Elliptic eigenvalue problems and unbounded continua of positive solutions of a semilinear elliptic equation. J. Differ. Equ. 1996, 127, 295–319. [Google Scholar] [CrossRef]
- López-Gómez, J.; de Lis, J.C.S. First variations of principal eigenvalues with respect to the domain and point-wise growth of positive solutions for problems where bifurcation from infinity occurs. J. Differ. Equ. 1998, 148, 47–64. [Google Scholar] [CrossRef]
- García-Melián, J.; Gomez-Renasco, R.; López-Gómez, J.; de Lis, J.C.S. Pointwise growth and uniqueness of positive solutions for a class of sublinear elliptic problems where bifurcation from infinity occurs. Arch. Ration. Mech. Anal. 1998, 145, 261–289. [Google Scholar] [CrossRef]
- Amann, H. Periodic solutions of semi-linear parabolic equations. In Nonlinear Analysis: A Collection of Papers in Honor of Erich H. Rothe; Cesari, L., Kannan, R., Weinberger, H., Eds.; Academic Press: New York, NY, USA, 2014; pp. 1–29. [Google Scholar]
- Taira, K. Semilinear degenerate elliptic boundary value problems via the Semenov approximation. Rendiconti del Circolo Matematico di Palermo Series 2 2021, 70, 1305–1388. [Google Scholar] [CrossRef]
- Semenov, N.N. Chemical Kinetics and Chain Reactions; Clarendon Press: Oxford, UK, 1935. [Google Scholar]
- Brown, K.J.; Lin, S.S. On the existence of positive eigenfunctions for an eigenvalue problem with indefinite weight function. J. Math. Anal. Appl. 1980, 75, 112–120. [Google Scholar] [CrossRef]
- Senn, S.; Hess, P. On positive solutions of a linear elliptic eigenvalue problem with Neumann boundary conditions. Math. Ann. 1982, 258, 459–470. [Google Scholar] [CrossRef]
- Senn, S. On a nonlinear elliptic eigenvalue problem with Neumann boundary conditions, with an application to population genetics. Commun. Partial. Differ. Equ. 1983, 8, 1199–1228. [Google Scholar] [CrossRef]
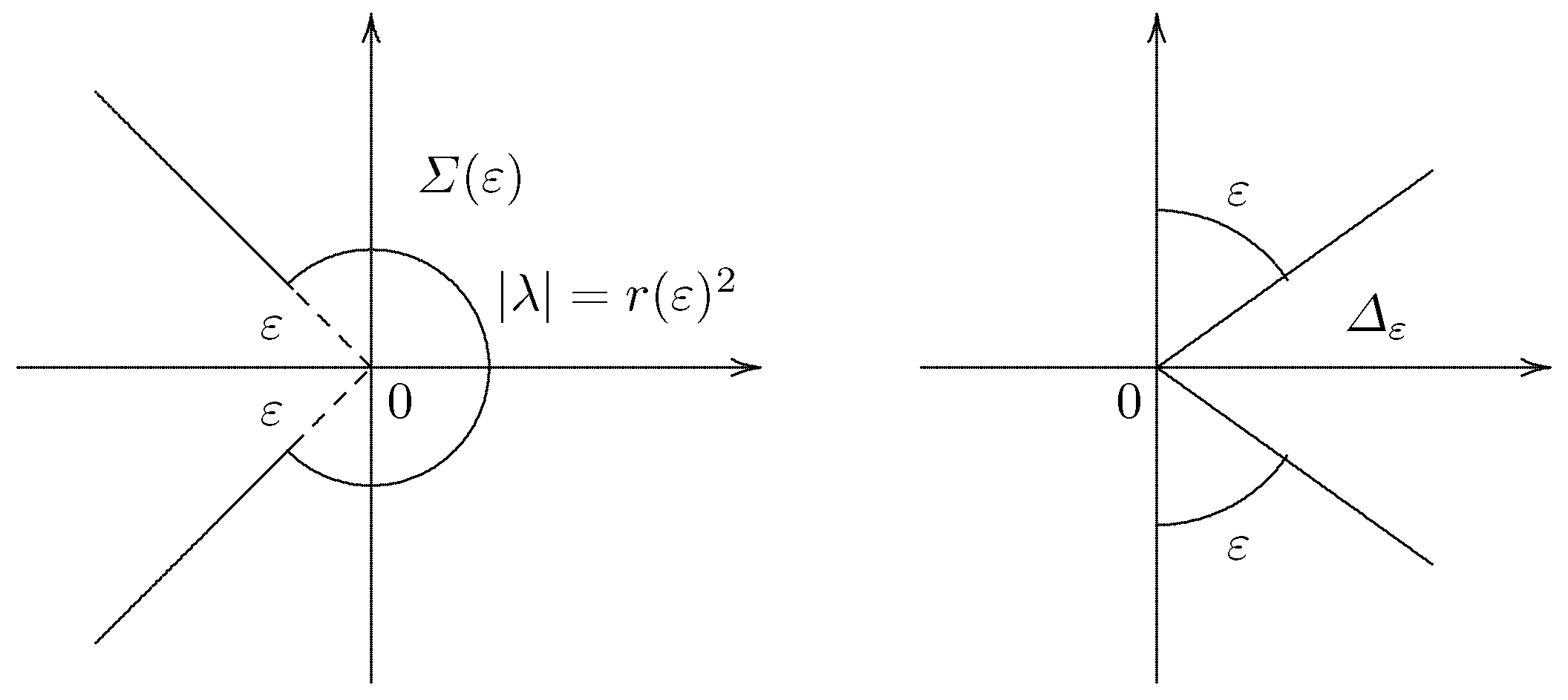

| Term | Biological Interpretation |
|---|---|
| Terrain | |
| Population density of a species inhabiting the terrain | |
| A member of the population moves about the terrain via the type of random walks occurring in Brownian motion | |
| d | Rate of diffusive dispersal |
| Intrinsic growth rate | |
| Coefficient of intraspecific competition |
| Boundary Condition | Biological Interpretation |
|---|---|
| Dirichlet case | Completely hostile (deadly) exterior |
| Neumann case | Barrier |
| Robin or mixed-type case | Hostile but not completely deadly exterior |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taira, K. A Class of Semilinear Parabolic Problems and Analytic Semigroups. Mathematics 2022, 10, 4381. https://doi.org/10.3390/math10224381
Taira K. A Class of Semilinear Parabolic Problems and Analytic Semigroups. Mathematics. 2022; 10(22):4381. https://doi.org/10.3390/math10224381
Chicago/Turabian StyleTaira, Kazuaki. 2022. "A Class of Semilinear Parabolic Problems and Analytic Semigroups" Mathematics 10, no. 22: 4381. https://doi.org/10.3390/math10224381
APA StyleTaira, K. (2022). A Class of Semilinear Parabolic Problems and Analytic Semigroups. Mathematics, 10(22), 4381. https://doi.org/10.3390/math10224381






