A Note on Some Weaker Notions of Cop-Win and Robber-Win Graphs

Abstract

The game of pursuit and evasion, when played on graphs, is often referred to as the game of cops and robbers. This classical version of the game has been completely solved by Nowakowski and Winkler, who gave the exact class of graphs for which the pursuer can win the game (cop-win). When the graph does not satisfy the dismantlability property, Nowakowski and Winkler’s Theorem does not apply. In this paper, we give some weaker notions of cop-win and robber-win graphs. In particular, we fix the number of cops to be equal to one, and we ask whether there exist sets of initial conditions for which the graph can be cop-win or robber-win. We propose some open questions related to this initial condition problem with the goal of developing both structural characterizations and algorithms that are computable in polynomial time (P) and that can solve weakly cop-win and weakly- robber-win graphs.

1. Introduction

The game of pursuit and evasion, when played on graphs, is often referred to as the game of cops and robbers, (e.g., Nowakowski and Winkler [1] and Quilliot [2]) and is considered to be the discrete version of pursuit–evasion differential games (e.g., the Lion and the Man problem developed by Rado and Besicovitch 1930s and the Homicidal Chauffeur game developed by Issacs in the 1960s). In its most common formulation, the pursuers and evader sequentially choose their positions on the graph under perfect visibility and, upon each move, each player can only move to some neighboring vertex. This classical game of cops and robbers was completely solved by Nowakowski and Winkler [1], who gave the exact class of graphs for which the pursuer can win the game (cop-win) and by Clarke and MacGillivray [3], who formalized this result for the case of any finite number of cops using the concept of the categorical product of a graph. The class of cop-win graphs, referred to as dismantlable graphs, was demonstrated to have rich graph theoretical properties by Brightwell and Winkler [4].

When the graph does not satisfy the dismantlability property, Nowakowski and Winkler’s Theorem does not apply. Then, a natural question that is often asked is what may the minimum number of cops (cop number) be that can be added to the game so that the graph becomes cop-win. The current state of the art in this literature now revolves around an unsolved conjecture (open problem) due to Meyniel [5] (Personal communication, (1985) [6]) about the number of cops in a graph. Chiniforooshan [7] gives an important bound on the number of cops. Although the Meyniel conjecture remains open, the best bound that can be found in the literature is given by Lu and Peng [8]. However, while it is well-known that the algorithm for deciding cop-win graphs runs in polynomial time (finding a corner runs in polynomial time and hence, deciding whether a graph is cop-win is in P), Fomin, Golovach, Kratochvil, Nisse, and Suchande [9] showed that when the graph is not dismantlable, the problem of finding the minimum number of cops as in the Meyniel’s conjecture is NP hard (e.g., as observed by Bonato and Nowakowski [10], chapter 5).

In this paper, we propose to look at the above problem from a different perspective. In our proposed approach, instead on focusing on the cop number (when the graph is not dismantlable), we fix the number of cops to be equal to one and ask whether there exist initial conditions for which the graph can be cop-win or robber-win. Initial-condition-dependent cops and robbers games were first studied by Ibragimov and Luckraz [11], who provided a class of graphs for which the game is strongly robber-win (that is, robber-win for all possible initial conditions). However, the class of graphs for which the graph is weakly robber-win or weakly cop-win (for fixed initial conditions) remains open. The following example is a simple illustration of this class of problems.

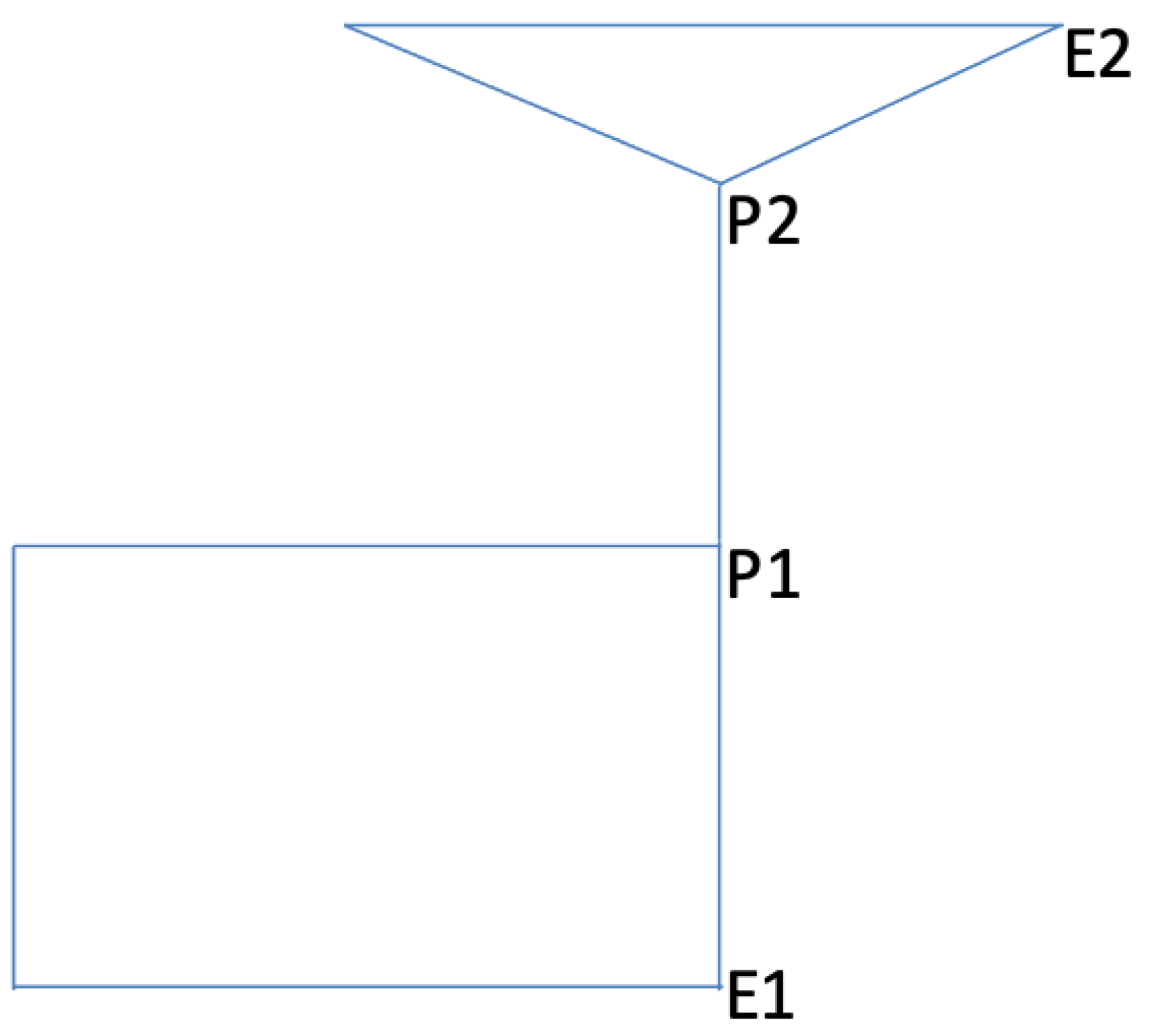
The above graph (Figure 1) is not dismantlable and hence not cop-win in the sense of Nowakowski and Winkler’ Theorem, since at the initial condition $(P1,E1)$, the robber can win (where P is cop’s position, while E is the robber’s position). Moreover, the above graph is not strongly robber-win in the Ibragimov–Luckraz sense. However, if we fix the initial conditions at $(P2,E2)$, then the cop can win. Several open questions related to this initial condition problem with the goal of developing both structural characterizations and computable in polynomial time (P) algorithms that can solve weakly cop-win and weakly robber-win graphs (undirected or directed with appropriate restrictions) can be studied. As the above example shows, while the complement of the class of cop-win graphs is robber-win graphs, the complement of strongly cop-win graphs is not strongly robber-win graphs.

2. Preliminaries

We let $G=(V,E)$ be a finite connected graph such that $|V\left(G\right)|\ge 2$. Let $e\in V$ denote the position of the robber and $p\in V$ denote the position of the cop. Time is discrete. The cop and the robber are initially located at vertices $v_{p_0}$ and $v_{e_0}$, respectively, where $v_{p_0}\ne v_{e_0}$. The robber moves in odd periods whereas the cops move in even periods (Note that, in the classical version of the game, the cop moves first as players are allowed to choose their initial conditions sequentially. In our version, the initial conditions are given and thus, in order to avoid trivial cop-win games, it makes sense to assume that the robber moves first.). Each player has perfect visibility at each move. At a designated move, the cop/robber can move to some neighboring vertex or remain at the same vertex.

Definition 1. 

A strategy for the cop is given by the function $s_p:V^2\times T^{even}\to V$, where $T^{even}$ is the set of all even numbers, whereas a strategy for the robber is given by the function $s_e:V^2\times T^{odd}\to V$, where $T^{odd}$ is the set of all odd numbers.

Let $S_p$ denote the set of all possible strategies of the cop and $S_e$ denote the set of all possible strategies of the robber.

2.1. New Notions of Cop-Win and Robber-Win Graphs

The novelty at the heart of our contribution is the distinction between the different notions of cop-win and robber-win graphs. Formally, we propose the three following notions of cop-win and robber-win graphs in decreasing order of strength.

Definition 2. 

We say that graph $G=(V,E)$ is strongly cop-win iff $\exists s_p\in S_p$ such that $\forall (v_{p_0},v_{e_0})\in V^2$ and $\forall s_e\in S_e$, we have $v_{p_t}=v_{e_t}$ for some t.

Definition 3. 

We say that graph $G=(V,E)$ is strongly robber-win iff $\exists s_e\in S_e$ such that $\forall (v_{p_0},v_{e_0})\in V^2$ and $\forall s_p\in S_p$, we have $v_{p_t}\ne v_{e_t}$ for all t.

Definition 4. 

We say that graph $G=(V,E)$ is cop-win iff $\exists s_p\in S_p$ and $\exists v_{p_0}\in V$ such that $\forall v_{e_0}\in V$ and $\forall s_e\in S_e$, we have $v_{p_t}=v_{e_t}$ for some t.

Definition 5. 

We say that graph $G=(V,E)$ is robber-win iff $\exists s_e\in S_e$ and $\exists v_{e_0}\in V$, such that $\forall v_{p_0}\in V$ and $\forall s_p\in S_p$, we have $v_{p_t}\ne v_{e_t}$ for all t.

Definition 6. 

We say that graph $G=(V,E)$ is weakly cop-win iff $\exists v_{p_0}\in V$ and $\exists s_p\in S_p$ such that $\forall s_e\in S_e$, we have $v_{p_t}=v_{e_t}$ for some t and for some $v_{e_0}\in V$.

Definition 7. 

We say that graph $G=(V,E)$ is weakly robber-win iff $\exists v_{e_0}\in V$ and $\exists s_e\in S_e$, such that $\forall s_p\in S_p$, we have $v_{p_t}\ne v_{e_t}$ for all t and for some $v_{p_0}\in V$.

Note that strongly and weakly cop/robber-win graphs are new in the literature and it is precisely these definitions that we expect will allow us to generalize Nowakowski and Winkler’s theorem.

2.2. Nowakowski and Winkler’s Dismantlability Condition for Cop-Win Graphs

Suppose that $H$ is an induced subgraph of G obtained after deleting one vertex from G, and that f is a homomorphism from G into ${\left(H\right)}^l$, where ${\left(H\right)}^l$ is the reflexive closure of H, then we call H a retract of G iff $f\left(x\right)=x$ for all $x\in V\left(H\right)$ and for the unique $y\notin V\left(H\right)$, we have $f\left(y\right)\in N\left(y\right)$.

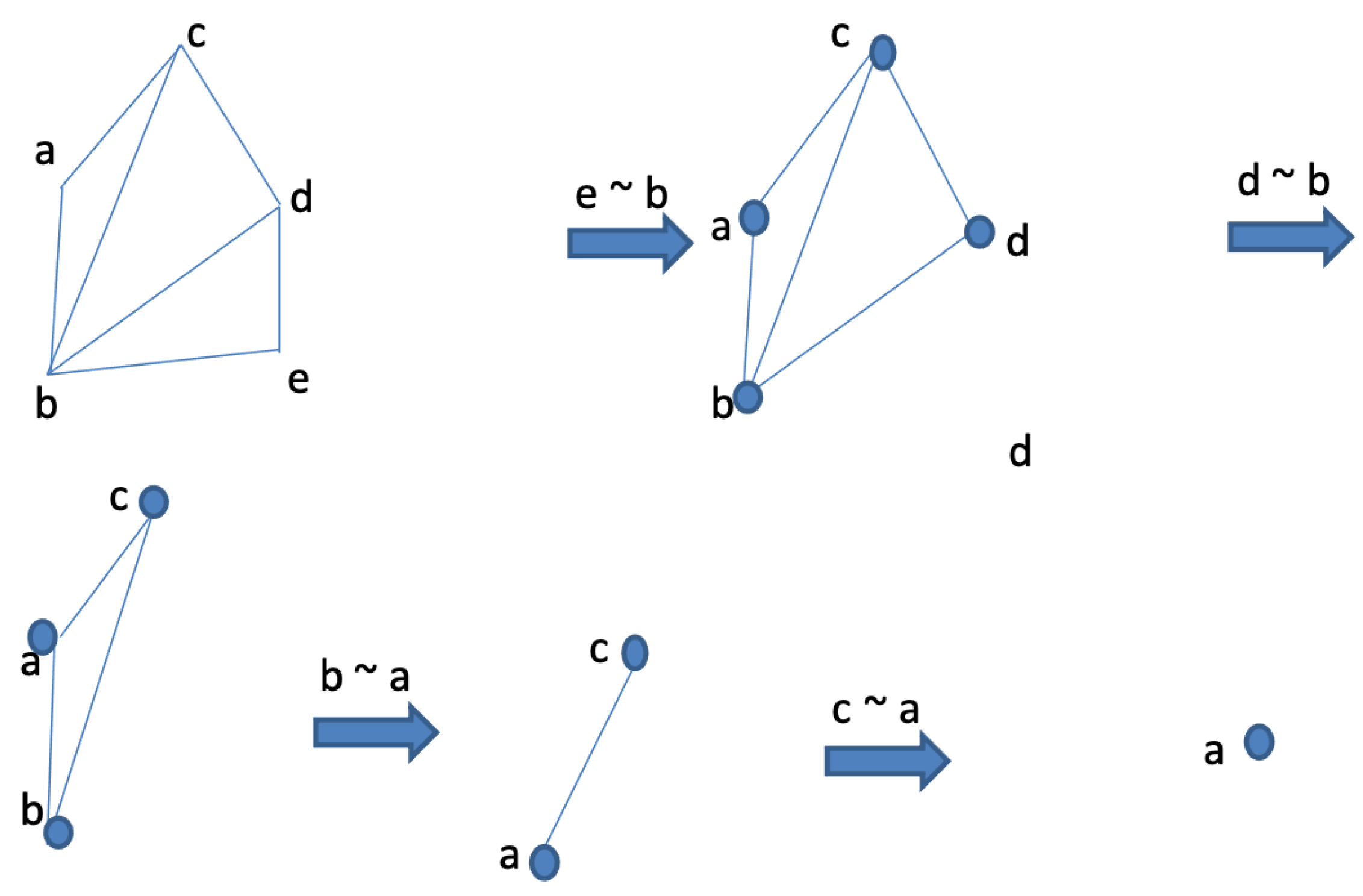
We say that graph G is dismantlable if there exists some sequence of retracts of G that reduces its vertex set to a singleton. Figure 2 gives an example of a dismantlable graph.

Theorem 1 

([1]). (Nowakowski and Winkler) G is cop-win iff it is dismantlable.

The theorem was generalized by Clarke and MacGillivray [3] for the case of k cops.

2.3. Conditions for Strongly Robber-Win Graphs

We say that $v\in V\left(G\right)$ is irreducible iff some $u=v$ exists such that $N\left[u\right]$⊇$N\left[v\right]$. $G=(V,E)$ is not irreducible everywhere iff each $v\in$V is not irreducible. Figure 3 gives an example of a graph that is not irreducible everywhere.

Theorem 2 

([11]). (Ibragimov and Luckraz) $G=(V,E)$ is a robber-win graph iff each $v\in V$ is not irreducible.

3. Open Problems

In this section, we pose some new problems for the aforementioned generalized class of game of cops and robbers for which the initial conditions are given. In particular, let $G=(V,E)$ be a general graph (undirected or directed, finite or infinite), and let $(I_{0C},I_{0R})\in V\times V$ denote the initial positions of the cop and the robber, respectively. We assume that the number of cops is fixed at 1. The justification for this formulation can be understood from Figure 1, where the graph is not dismantlable and hence, Theorem 1 does not apply. However, it can be easily verified that two cops can capture the robber on this graph. While the recent literature in the game of cops and robbers (see Luckraz (2019) [12]) have taken the approach of finding the minimum number of cops needed to make a non-dismantlable graph cop-win, we retain the one cop assumption (weaker) in our study of weakly cop-win graphs. Thus, we are interested in the class of non-dismantlable graphs that are weakly cop-win. For that, we use the following notion of the categorical product of graphs. From $G=(V,E)$, define $G_I=(V_I,E_I)$ as follows.

$$V_I=\left\{(I_{0C},I_{0R})\in V\times V:G\mathrm{is}\mathrm{weakly}\mathrm{cop}-\mathrm{win}\mathrm{for}(I_{0C},I_{0R})\right\}$$

$$E_I=\left\{\left\{(I_{0C},I_{0R}),(I_{0C}^{\prime },I_{0R}^{\prime })\right\}:\left\{I_{0C},I_{0C}^{\prime }\right\}\in E\mathrm{and}\left\{I_{0R},I_{0R}^{\prime }\right\}\in E\right\}$$

We pose the following problems.

• For which class of graphs G is $G_I$ a connected graph?
• For which class of graphs G is $G_I$ homomorphic to some dismantlable graph H?
  From $G=(V,E)$, define $G_{I^{\ast }}=(V_{I^{\ast }},E_{I^{\ast }})$ as follows.

  $$V_{I^{\ast }}=\left\{(I_{0C},I_{0R})\in V\times V:G\mathrm{is}\mathrm{weakly}\mathrm{robber}-\mathrm{win}\mathrm{for}(I_{0C},I_{0R})\right\}$$

  $$E_{I^{\ast }}^{}=\left\{\left\{(I_{0C},I_{0R}),(I_{0C}^{\prime },I_{0R}^{\prime })\right\}:\left\{I_{0C},I_{0C}^{\prime }\right\}\in E\mathrm{and}\left\{I_{0R},I_{0R}^{\prime }\right\}\in E\right\}$$
• For which class of graphs G is $G_{I^{\ast }}$ a connected graph?
• For which class of graphs G is $G_{I^{\ast }}$ homomorphic to some nowhere irreducible graph H?
• Which class of graphs G are bipartite graphs with independent sets A and B such that $(I_{0C},I_{0R})\in V\times V$ is a weakly cop-win initial condition if and only if $I_{0C}\in A$ and $I_{0R}\in B$?
• Suppose that $G=\left(V,E\right)$ is not dismantlable. What is the minimum number of edges that can be added/deleted to make the game cop-win?

4. Conclusions

We proposed weaker notions of cop-win and robber-win games for the classic of games of cops and robbers on graphs. The new definitions we consider allow us to look at Meyniel’s conjecture from a different perspective. We also proposed several open questions that our notions of cop-win and robber-win graphs could entail.