Modelling, Optimization, and Experimental Studies of Refrigeration CO2 Ejectors: A Review
Abstract
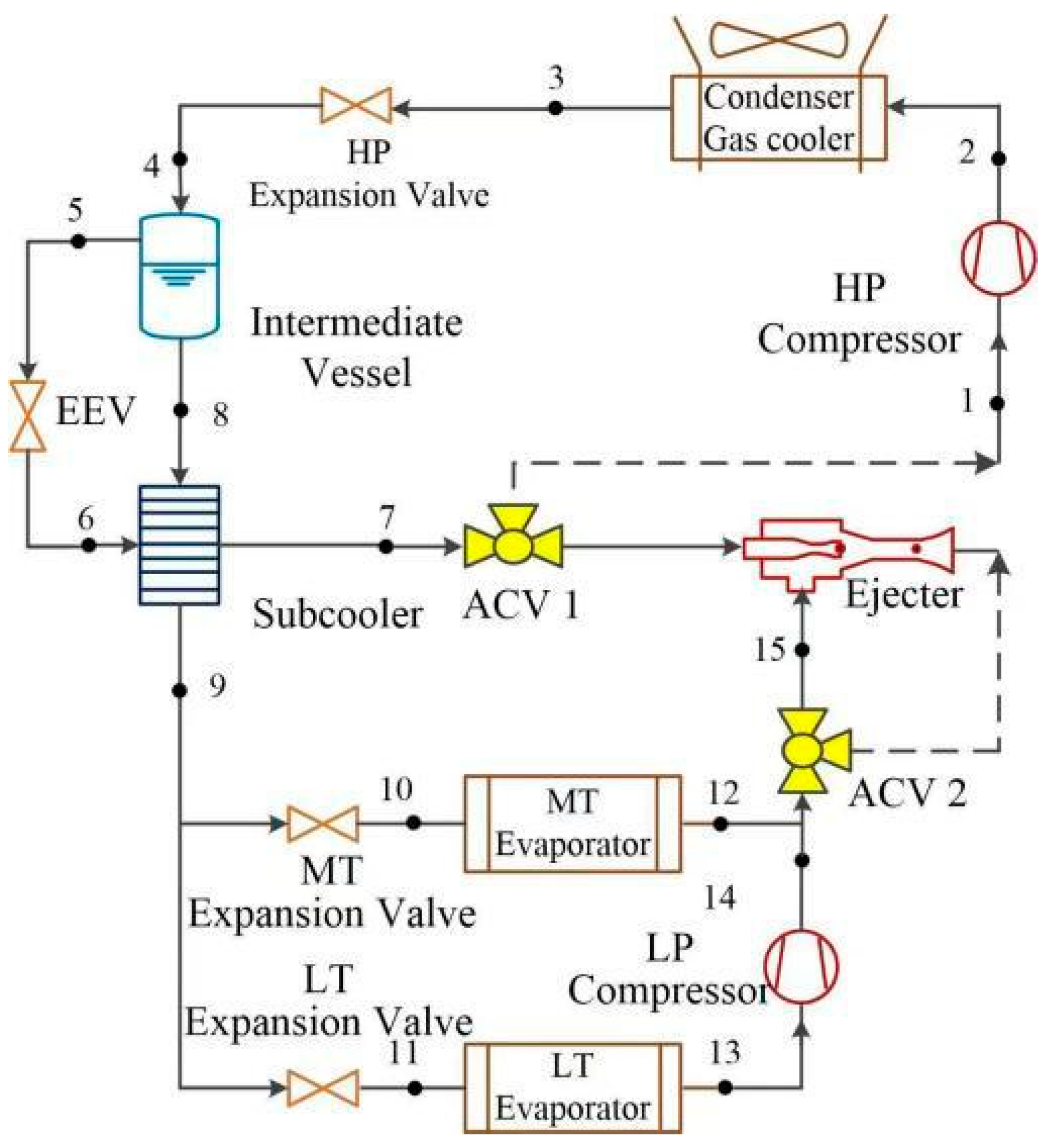
1. Introduction
2. Model and Simulation
2.1. HEM
2.2. HRM
2.3. Mixture Model
2.4. DEM
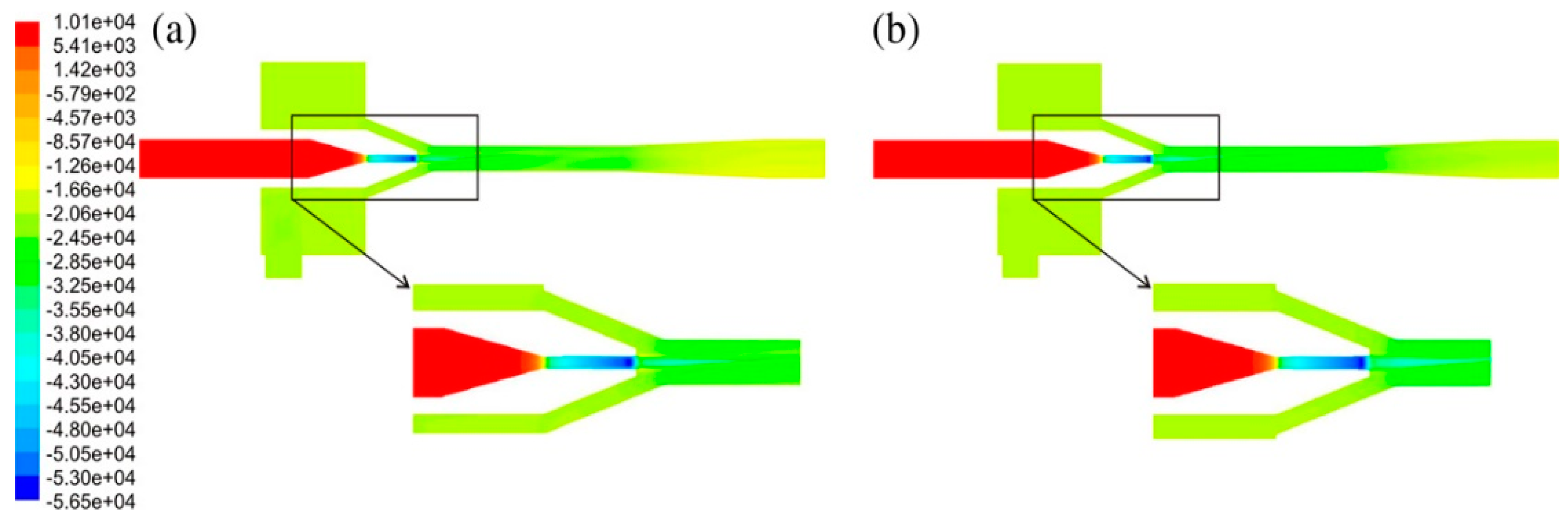
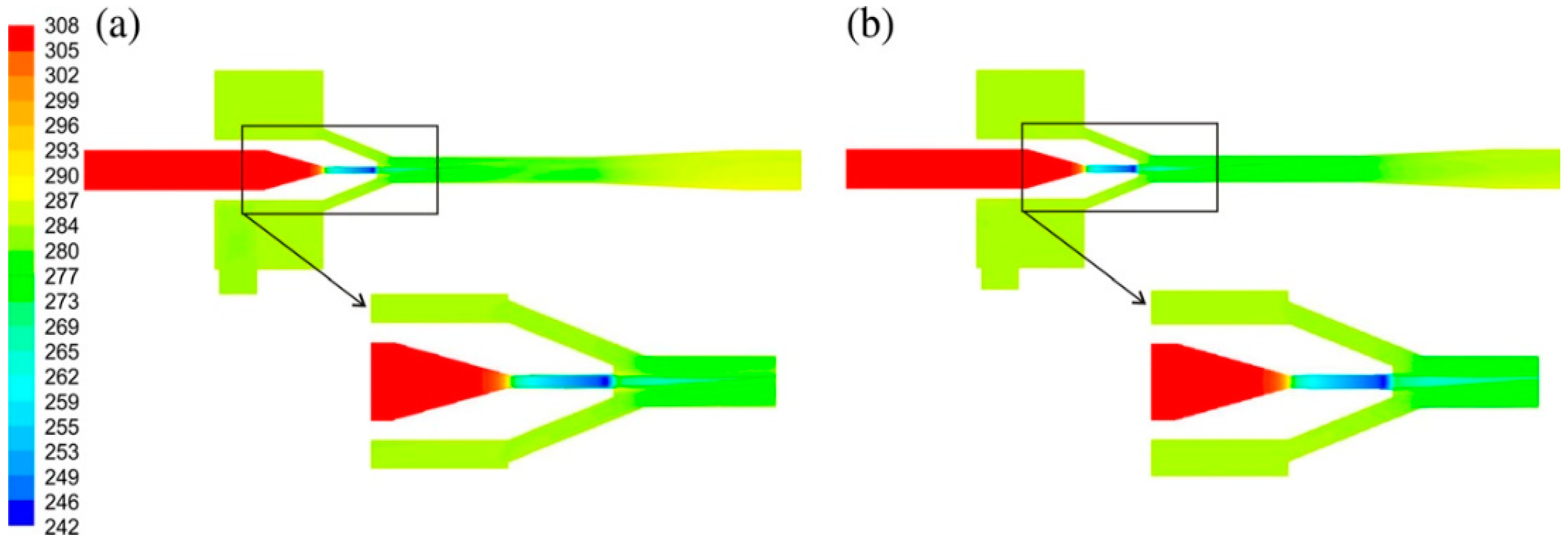
2.5. Shock Wave
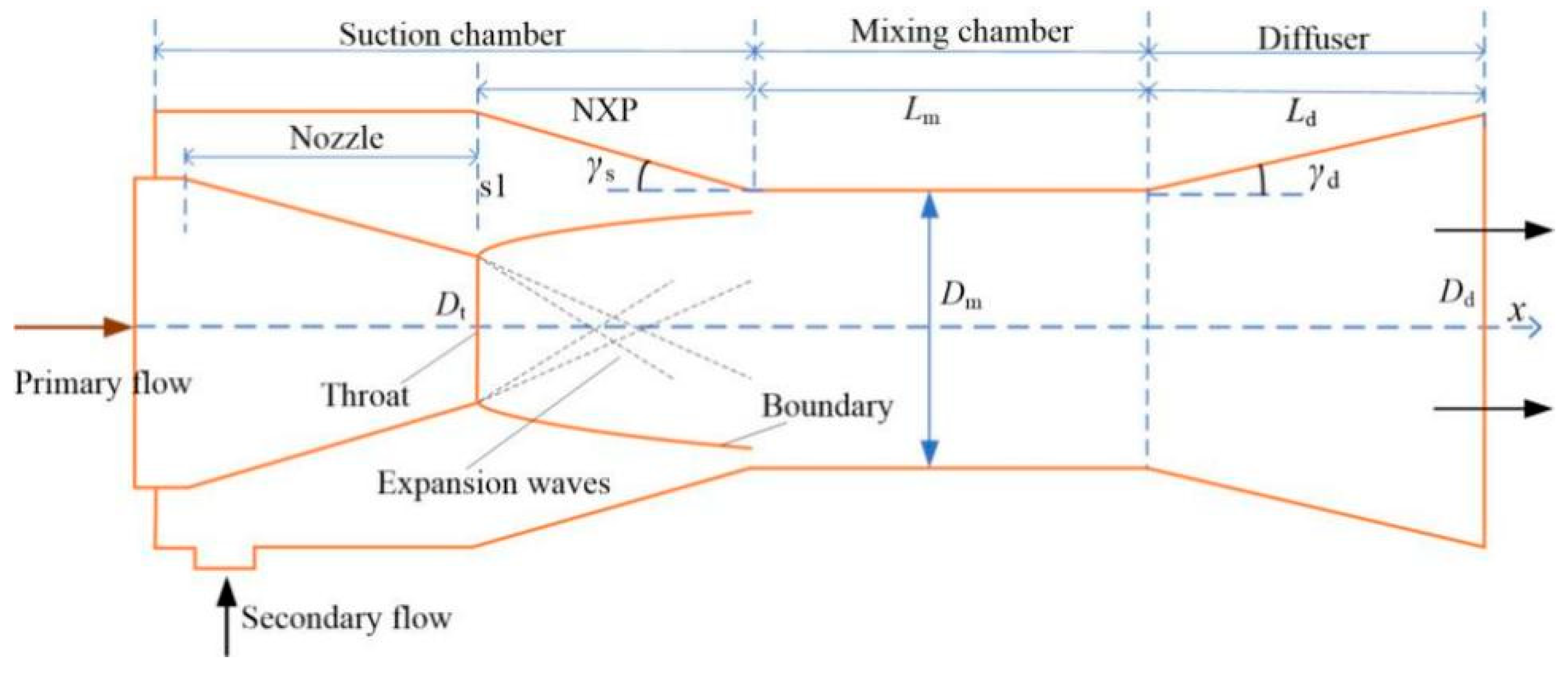
3. Optimization of Ejector Structure
3.1. Change the Geometry of the Motive Nozzle
3.2. Optimization of Mixing Chamber Structure
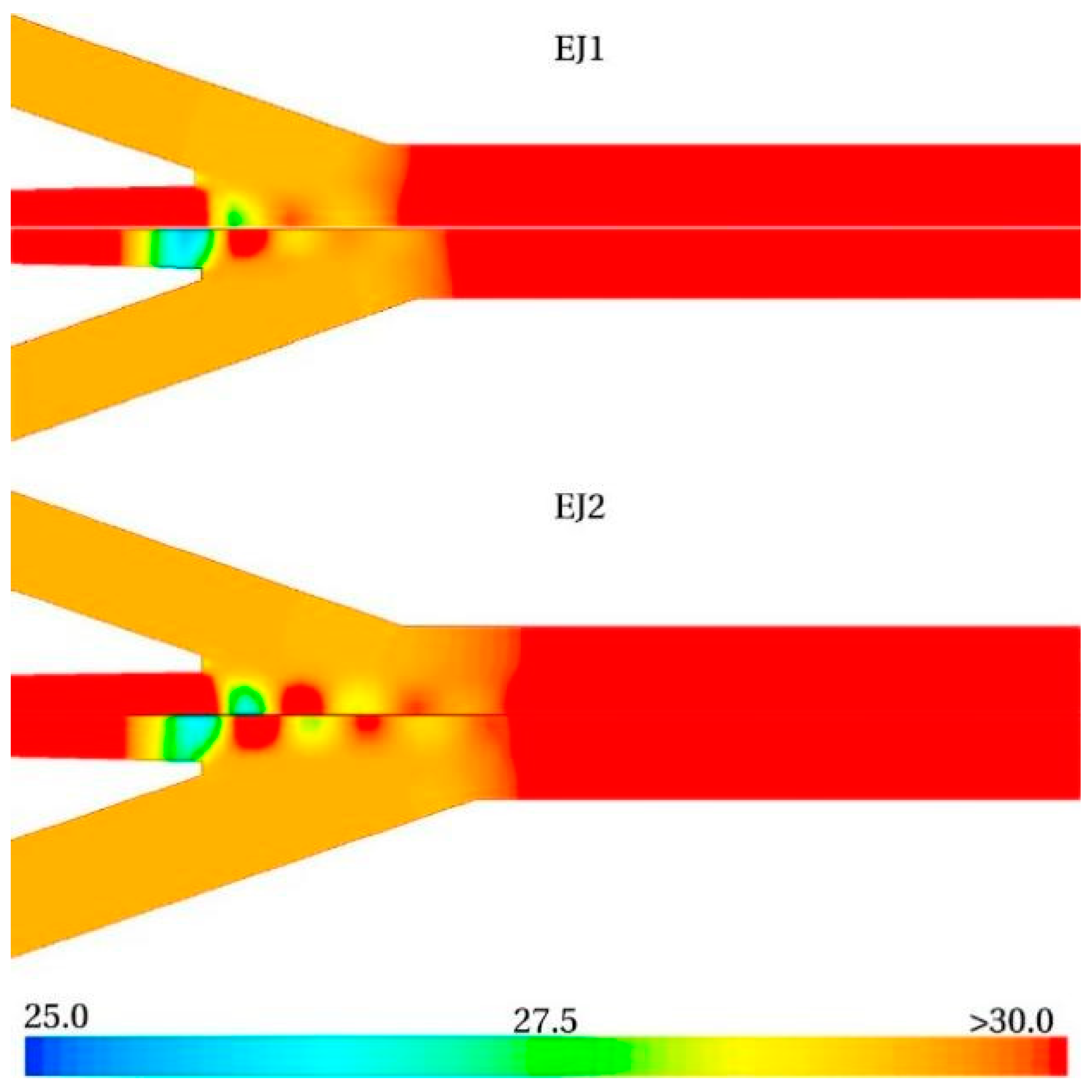
3.3. Method of Combining Multiple Ejectors
4. Visualization Experiments with the CO2 Ejector
5. Conclusions
- (1)
- It is demonstrated that the HEM technique produces more accurate calculations for CO2 ejectors at supercritical operating conditions, whereas the HRM model improves model accuracy in terms of the mass entrainment ratio at lower temperatures and pressures by accounting for unbalanced phase changes. The DEM considers the nonequilibrium phase change to improve the model accuracy of a CO2 ejector. In Section 2 of this paper, we collect four different turbulence models to provide a summary chart that is able to compare the differences between these turbulence models.
- (2)
- The numerical analysis enables a detailed analysis of the operating processes within the ejector and the optimized design of its overall performance. The mainstream optimal methods and techniques were presented to enhance ejector efficiency. In this section, the effects of the motive nozzle, mixing chamber structure, and multiple ejectors on the performance of CO2 ejectors are investigated in terms of their structural dimensions. The adjustable throat area method is an effective method for adjusting the optimum high pressure. In the mixing chamber, the turbulent mixing procedure causes the greatest irreversible losses, which means that the performance of the mixing chamber is significantly impacted by its structural design. Using multiple ejectors could flexibly and effectively manage the discharge pressure and revive the expansion work.
- (3)
- This paper also investigates the flow field in the nozzle of a CO2 ejector. The results of this study show that the supersonic flow of fluid within the ejector causes irreversible processes such as shock waves and such irreversible processes can have an impact on the operating characteristics of the ejector. The importance of surge waves in the nozzle is emphasized by observing the flow field within the injector under different operating conditions in a visualization experiment of the CO2 ejector, which investigates the effect of surge waves on the injector entrainment rate and the injector cooling system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bellos, E.; Tzivanidis, C. A comparative study of CO2 refrigeration systems. Energy Convers. Manag. 2019, 1, 100002. [Google Scholar] [CrossRef]
- Yu, B.B.; Yang, J.Y.; Wang, D.D.; Shi, J.Y.; Chen, J.P. An updated review of recent advances on modified technologies in transcritical CO2 refrigeration cycle. Energy 2019, 189, 116147. [Google Scholar] [CrossRef]
- Nebot-Andrés, L.; Del Duca, M.G.; Aprea, C.; Zerovnik, A.; Tusek, J.; Llopis, R.; Maiorino, A. Improving efficiency of transcritical CO2 cycles through a magnetic refrigeration subcooling system. Energy Convers. Manag. 2022, 265, 115766. [Google Scholar] [CrossRef]
- Thongtip, T.; Aphornratana, S. Impact of primary nozzle area ratio on the performance of ejector refrigeration system. Appl. Therm. Eng. 2021, 188, 116523. [Google Scholar] [CrossRef]
- Ghazizade-Ahsaee, H.; Askari, I.B. The application of thermoelectric and ejector in a CO2 direct-expansion ground source heat pump; energy and exergy analysis. Energy Convers. Manag. 2020, 226, 113526. [Google Scholar] [CrossRef]
- Deng, J.Q.; Jiang, P.X.; Lu, T.; Lu, W. Particular characteristics of transcritical CO2 refrigeration cycle with an ejector. Appl. Therm. Eng. 2007, 27, 381–388. [Google Scholar] [CrossRef]
- Zhu, Y.; Huang, Y.; Li, C.; Zhang, F.; Jiang, P.X. Experimental investigation on the performance of transcritical CO2 ejector–expansion heat pump water heater system. Energy Convers. Manag. 2018, 167, 147–155. [Google Scholar] [CrossRef]
- Santini, F.; Bianchi, G.; Di Battista, D.; Villante, C.; Orlandi, M. Experimental investigations on a transcritical CO2 refrigeration plant and theoretical comparison with an ejector-based one. Energy Procedia 2019, 161, 309–316. [Google Scholar] [CrossRef]
- Pérez, B.P.; Carrillo, J.; Flor, F.; Lissen, J.; Navarro, A.M. Thermoeconomic analysis of CO2 ejector-expansion refrigeration cycle (EERC) for low-temperature refrigeration in warm climates. Appl. Therm. Eng. 2021, 188, 116613. [Google Scholar] [CrossRef]
- Zou, H.; Yang, T.; Tang, M.; Tian, C.; Butrymowicz, D. Ejector optimization and performance analysis of electric vehicle CO2 heat pump with dual ejectors. Energy 2022, 239, 122452. [Google Scholar] [CrossRef]
- Ringstad, K.E.; Allouche, Y.; Gullo, P. A detailed review on CO2 two-phase ejector flow modeling. Therm. Sci. Eng. Prog. 2022, 20, 100647. [Google Scholar] [CrossRef]
- Yu, F.; Poncet, S.; Nesreddine, H.; Bartosiewicz, Y. An open-source density-based solver for two-phase CO2 compressible flows: Verification and validation. Int. J. Refrig. 2019, 106, 526–538. [Google Scholar]
- Al-Tameemi, M.R.J.; Yu, Z. Thermodynamic approach for designing the two-phase motive nozzle of the ejector for transcritical CO2 heat pump system. Energy Procedia 2017, 142, 1206–1212. [Google Scholar] [CrossRef]
- He, Y.; Deng, J.Q.; Li, Y.F.; Zhang, X.P. Synergistic effect of geometric parameters on CO2 ejector based on local exergy destruction analysis. Appl. Therm. Eng. 2021, 184, 116256. [Google Scholar] [CrossRef]
- He, Y.; Deng, J.Q.; Li, Y.F.; Ma, L. A numerical contrast on the adjustable and fixed transcritical CO2 ejector using exergy flux distribution analysis. Energy Convers. Manag. 2019, 196, 729–738. [Google Scholar] [CrossRef]
- Li, Y.F.; Deng, J.Q. Numerical investigation on the performance of transcritical CO2 two-phase ejector with a novel non-equilibrium CFD model. Energy 2022, 238, 121995. [Google Scholar] [CrossRef]
- Yazdani, M.; Alahyari, A.A.; Radcliff, T.D. Numerical modeling of two-phase supersonic ejectors for work-recovery applications. Int. J. Heat Mass Transf. 2012, 55, 5744–5753. [Google Scholar] [CrossRef]
- Palacz, M.; Smolka, J.; Fic, A.; Bulinski, Z. Application range of the HEM approach for CO2 expansion inside two-phase ejectors for supermarket refrigeration systems. Int. J. Refrig. 2015, 59, 251–258. [Google Scholar] [CrossRef]
- Smolka, J.; Bulinski, Z.; Fic, A.; Nowak, A.J.; Banasiak, K.; Hafner, A. A computational model of a transcritical R744 ejector based on a homogeneous real fluid approach. Appl. Math. Model. 2013, 37, 1208–1224. [Google Scholar] [CrossRef]
- Lucas, C.; Rusche, H.; Schroeder, A.; Koehleret, J. Numerical investigation of a two-phase CO2 ejector. Int. J. Refrig. 2014, 43, 154–166. [Google Scholar] [CrossRef]
- Giacomelli, F.; Banasiak, K.; Hafner, A.; Mazzelli, F.; Milazzo, A. Experimental and numerical investigation on a ejector for CO2 vapor compression systems. In Proceedings of the 13th IIR Gustav Lorentzen Conference, Valencia, Spain, 18–20 June 2018. [Google Scholar]
- Bodys, J.; Smolka, J.; Palacz, M.; Haida, M.; Banasiak, K.; Nowak, A.T.; Hafner, A. Performance of fixed geometry ejectors with a swirl motion installed in a multi-ejector module of a CO2 refrigeration system. Energy 2016, 117, 620–631. [Google Scholar] [CrossRef]
- Palacz, M.; Smolka, J.; Nowak, A.J.; Banasiak, K.; Hafneret, A. Shape optimisation of a two-phase ejector for CO2 refrigeration systems. Int. J. Refrig. 2017, 74, 212–223. [Google Scholar] [CrossRef]
- Gullo, P.; Hafner, A.; Banasiak, K. Transcritical R744 refrigeration systems for supermarket applications. Curr. Status Future Perspect. 2018, 93, 269–310. [Google Scholar]
- Liu, G.D.; Wang, Z.; Zhao, H.X.; Ali Abdulwahid, A. R744 ejector simulation based on homogeneous equilibrium model and its application in trans-critical refrigeration system. Appl. Therm. Eng. 2022, 201, 117791. [Google Scholar] [CrossRef]
- Bilicki, Z.; Kestin, J. Physical aspects of the relaxation model in two-phase flow. Math. Phys. Sci. 1990, 428, 379–397. [Google Scholar]
- Haida, M.; Smolka, J.; Hafner, A.; Palacz, M.; Banasiak, K.; Nowak, A.J. Modified homogeneous relaxation model for the R744 trans-critical flow in a two-phase ejector. Int. J. Refrig. 2018, 85, 314–333. [Google Scholar] [CrossRef]
- Angielczyk, W.; Bartosiewicz, Y.; Butrymowicz, D.; Seynhaeve, J.M. 1-D modeling of supersonic carbon dioxide two-phase flow through ejector motive nozzle. In Proceedings of the International Refrigeration and Air Conditioning Conference, Purdue, IN, USA, 12–15 July 2010. [Google Scholar]
- Colombo, A.; Conti, P.; Orlandi, M. CFD simulations of a two-phase ejector for transcritical CO2 cycles applied to supermarket refrigeration systems. In Proceedings of the 13th IIR Gustav Lorentzen Conference, Valencia, Spain, 18–20 June 2018. [Google Scholar]
- Schmidt, D.; Colarossi, M.; Bergander, M.J. Multidimensional modeling of condensing two-phase ejector flow. In Proceedings of the International Seminar on Ejector/Jet Pump Technology and Applications, Louvain-la-Neuve, Belgium, 7–9 September 2009. [Google Scholar]
- Palacz, M.; Haida, M.; Smolka, J.; Nowak, A.J.; Banasiak, K.; Hafner, A. HEM and HRM accuracy comparison for the simulation of CO2 expansion in two-phase ejectors for supermarket refrigeration systems. Appl. Therm. Eng. 2017, 115, 160–169. [Google Scholar] [CrossRef]
- Bodys, J.; Smolka, J.; Palacz, M.; Haida, M.; Banasiak, K.; Nowak, A.J. Effect of turbulence models and cavitation intensity on the motive and suction nozzle mass flow rate prediction during a non-equilibrium expansion process in the CO2 ejector. Appl. Therm. Eng. 2022, 201, 117743. [Google Scholar] [CrossRef]
- Ringstad, K.E.; Banasiak, K.; Ervik, A.; Hafner, A. Machine learning and CFD for mapping and optimization of CO2 ejectors. Appl. Therm. Eng. 2021, 199, 117604. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten years of industrial experience with the SST turbulence model. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Bartosiewicz, Y.; Aidoun, Z.; Mercadier, Y. Numerical assessment of ejector operation for refrigeration applications based on CFD. Appl. Therm. Eng. 2006, 26, 604–612. [Google Scholar] [CrossRef]
- Giacomelli, F.; Mazzelli, F.; Milazzo, A. A novel CFD approach for the computation of R744 flashing nozzles in compressible and metastable conditions. Energy 2018, 162, 1092–1105. [Google Scholar] [CrossRef]
- Song, Y.; Ma, Y.; Wang, H.; Yin, X.; Cao, F. Review on the simulation models of the two-phase-ejector used in the transcritical carbon dioxide systems. Int. J. Refrig. 2020, 119, 434–447. [Google Scholar] [CrossRef]
- Giacomelli, F.; Mazzelli, F.; Banasiak, K.; Hafner, A.; Milazzo, A. Experimental and computational analysis of a R744 flashing ejector. Int. J. Refrig. 2019, 107, 326–343. [Google Scholar] [CrossRef]
- Banasiak, K.; Hafner, A. 1D Computational model of a two-phase R744 ejector for expansion work recovery. Int. J. Therm. Sci. 2011, 50, 2235–2247. [Google Scholar] [CrossRef]
- He, Y.; Zhang, Z.X.; Xue, C.L.; Yang, Y.Z.; Deng, J.Q. A CO2 two-phase ejector model based on delayed equilibrium model. J. Refrig. 2016, 37, 1–6. [Google Scholar]
- Angielczyk, W.; Seynhaeve, J.M.; Gagan, J.; Bartosiewicz, Y.; Butrymowicz, D. Prediction of critical mass rate of flashing carbon dioxide flow in convergent-divergent nozzle. Chem. Eng. Process. Process Intensif. 2019, 143, 107599. [Google Scholar] [CrossRef]
- Banasiak, K.; Hafner, A. Mathematical modelling of supersonic two-phase R744 flows through converging–diverging nozzles: The effects of phase transition models. Appl. Therm. Eng. 2013, 51, 635–643. [Google Scholar] [CrossRef]
- Berana, M.S.; Nakagawa, M.; Harada, A. Shock waves in supersonic two-phase flow of CO2 in converging-diverging nozzles. HVACR Res. 2009, 15, 1081–1098. [Google Scholar] [CrossRef]
- Taleghani, S.T.; Sorin, M.; Poncet, S. Modeling of two-phase transcritical CO2 ejectors for on-design and off-design conditions. Int. J. Refrig. 2018, 87, 91–105. [Google Scholar] [CrossRef]
- Zheng, L.X.; Hu, H.W.; Wang, W.B.; Zhang, Y.Y.; Wang, L.M. Study on Flow Distribution and Structure Optimization in a Mix Chamber and Diffuser of a CO2 Two-Phase Ejector. Mathematics 2022, 10, 693. [Google Scholar] [CrossRef]
- Zheng, L.X.; Deng, J.Q. Research on CO2 ejector component efficiencies by experiment measurement and distributed-parameter modeling. Energy Convers. Manag. 2017, 142, 244–256. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Li, C.H.; Zhang, F.Z.; Jiang, P.X. Comprehensive experimental study on a transcritical CO2 ejector-expansion refrigeration system. Energy Convers. Manag. 2017, 151, 98–106. [Google Scholar] [CrossRef]
- Haberschill, P.; Nehdi, E.; Kairouani, L. Experimental study of a two-phase ejector for CO2 transcritical refrigeration system. Arch. Thermodyn. 2021, 42, 217–246. [Google Scholar]
- Chen, J.; Li, Y.; Chen, W.; Luo, X.; Ying, C.; Yang, Z.; Eames, I.W. Investigation of the ejector nozzle in refrigeration system. Energy 2018, 157, 571–587. [Google Scholar] [CrossRef]
- Huai, Y.S.; Guo, X.M.; Shi, Y.G. Experimental Study on Performance of Double-throttling Device Transcritical CO2 Ejector Refrigeration System. Energy Procedia 2017, 105, 5106–5113. [Google Scholar] [CrossRef]
- Liu, Y.F.; Yu, J.; Wu, Q. Current status of research on CO2 heat pump/cooling system with ejector. Build. Energy Effic. 2017, 46, 64–69, 78. [Google Scholar]
- He, Y.; Deng, J.Q.; Zheng, L.X.; Zhang, Z.X. Performance optimization of a transcritical CO2 refrigeration system using a controlled ejector. Int. J. Refrig. 2017, 75, 250–261. [Google Scholar] [CrossRef]
- Huang, H.L.; Liu, H.; Li, G. Performance optimization of transcritical CO2 ejectors based on boiling cavitation model. J. Sol. Energy 2020, 41, 233–240. [Google Scholar]
- Banasiak, K.; Hafner, A.; Andresen, T. Experimental and numerical investigation of the influence of the two-phase ejector geometry on the performance of the R744 heat pump. Int. J. Refrig. 2012, 35, 1617–1625. [Google Scholar] [CrossRef]
- Haida, M.; Banasiak, K.; Smolka, J.; Hafner, A.; Eikevik, T.M. Experimental analysis of the R744 vapor compression rack equipped with the multi-ejector expansion work recovery module. Int. J. Refrig. 2016, 64, 93–107. [Google Scholar] [CrossRef]
- Eskandari, M.F.; Cheraghi, M. Performance of a new two-stage transcritical CO2 refrigeration cycle with two ejectors. Appl. Therm. Eng. 2019, 156, 402–409. [Google Scholar] [CrossRef]
- Liu, X.; Yu, K.; Wan, X.; Li, X. Performance evaluation of CO2 supermarket refrigeration system with multi-ejector and dedicated mechanical subcooling. Energy Rep. 2021, 7, 5214–5227. [Google Scholar] [CrossRef]
- Bodys, J.; Palacz, M.; Haida, M.; Smolka, J.; Nowak, A.J.; Banasiak, K.; Hafner, A. Full-scale multi-ejector module for a carbon dioxide supermarket refrigeration system: Numerical study of performance evaluation. Energy Convers. Manag. 2017, 138, 312–326. [Google Scholar] [CrossRef]
- Gullo, P.; Hafner, A.; Banasiak, K.; Minetto, S. Multi-ejector concept: A comprehensive review on its latest technological developments. Energies 2019, 12, 406. [Google Scholar] [CrossRef]
- Liu, J.; Liu, Y.; Yu, J. Performance analysis of a modified dual-ejector and dual-evaporator transcritical CO2 refrigeration cycle for supermarket application. Int. J. Refrig. 2021, 131, 109–118. [Google Scholar] [CrossRef]
- Bai, T.; Yan, G.; Yu, J. Performance evolution on a dual-temperature CO2 transcritical refrigeration cycle with two cascade ejectors. Appl. Therm. Eng. 2017, 120, 26–35. [Google Scholar] [CrossRef]
- Huang, Z.; Zhao, H.; Yu, Z.; Han, J. Simulation and optimization of a R744 two-temperature supermarket refrigeration system with an ejector. Int. J. Refrig. 2018, 90, 73–82. [Google Scholar] [CrossRef]
- Li, Y.F.; Deng, J.Q.; Ma, L.; Zhang, Y.Z. Visualization of two-phase flow in primary nozzle of a transcritical CO2 ejector. Energy Convers. Manag. 2018, 171, 729–741. [Google Scholar] [CrossRef]
- Li, Y.F.; Deng, J.Q.; Ma, L. Experimental study on the primary flow expansion characteristics in transcritical CO2 two-phase ejectors with different primary nozzle diverging angles. Energy 2019, 186, 115839. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Z.; Yang, Y.; Jiang, P.X. Flow visualization of supersonic two-phase transcritical flow of CO2 in an ejector of a refrigeration system. Int. J. Refrig. 2017, 74, 354–361. [Google Scholar] [CrossRef]
- Palacz, M.; Bodys, J.; Haida, M. Two-phase flow visualisation in the R744 vapor ejector for refrigeration systems. Appl. Therm. Eng. 2022, 210, 118322. [Google Scholar] [CrossRef]

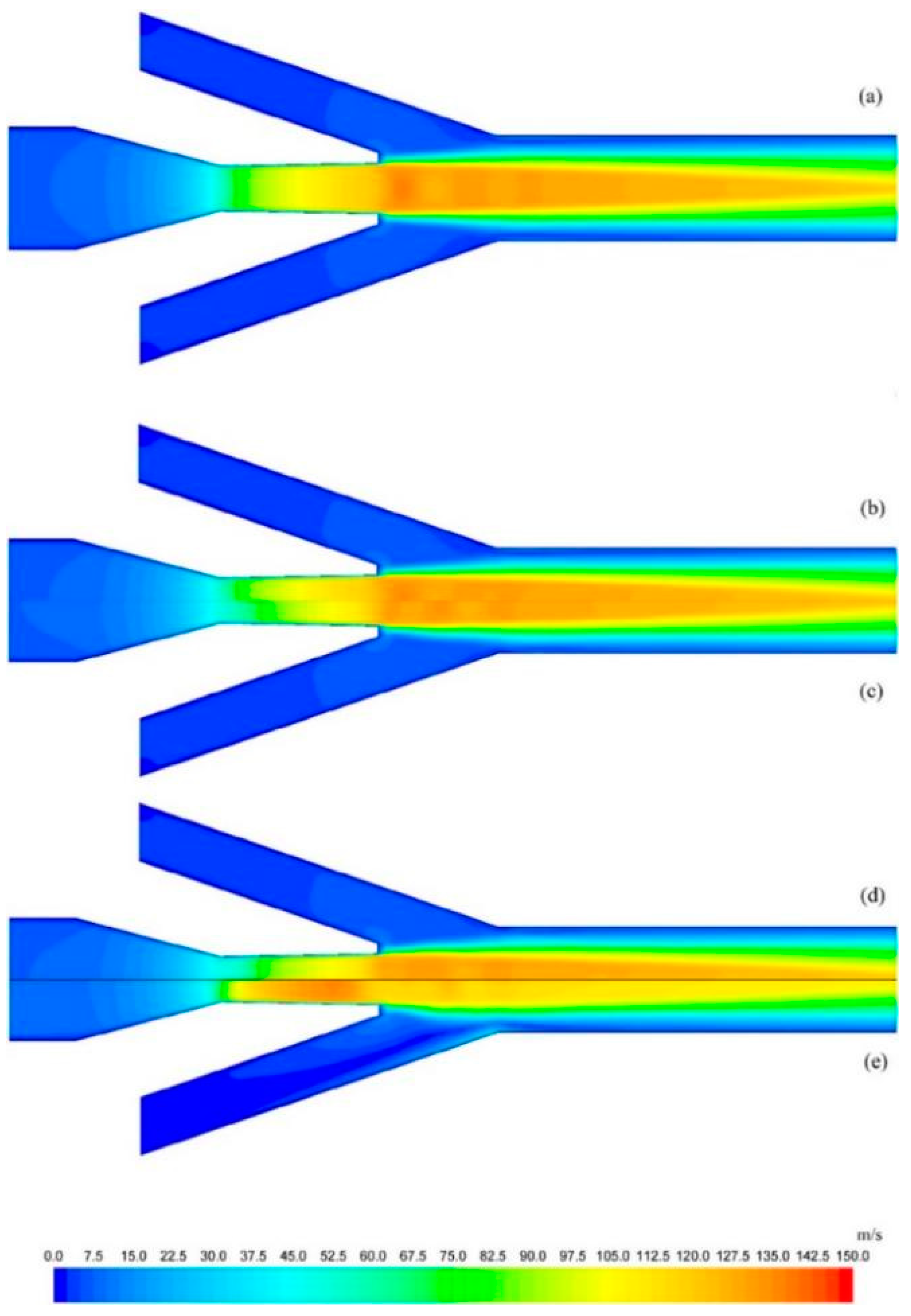

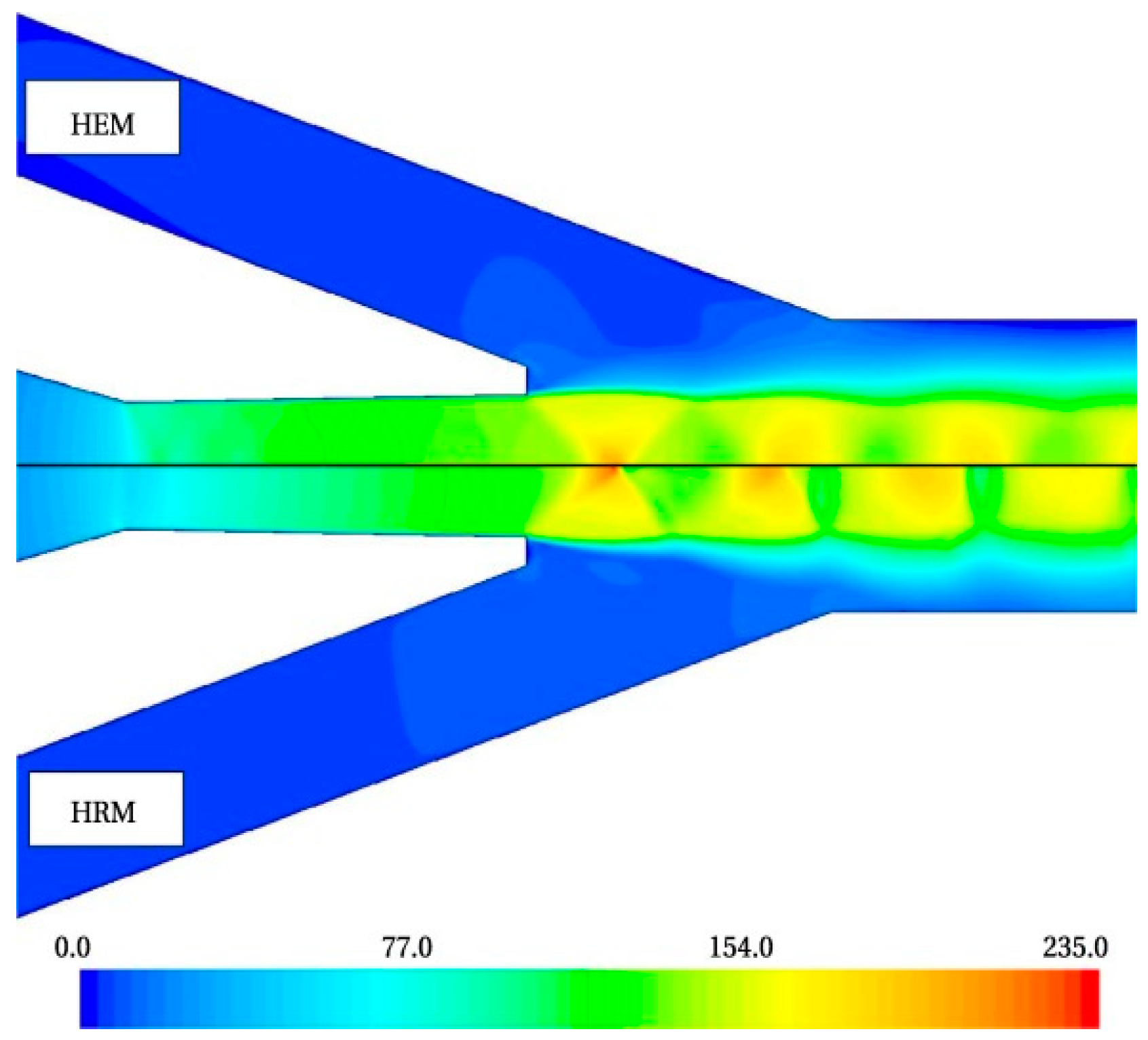
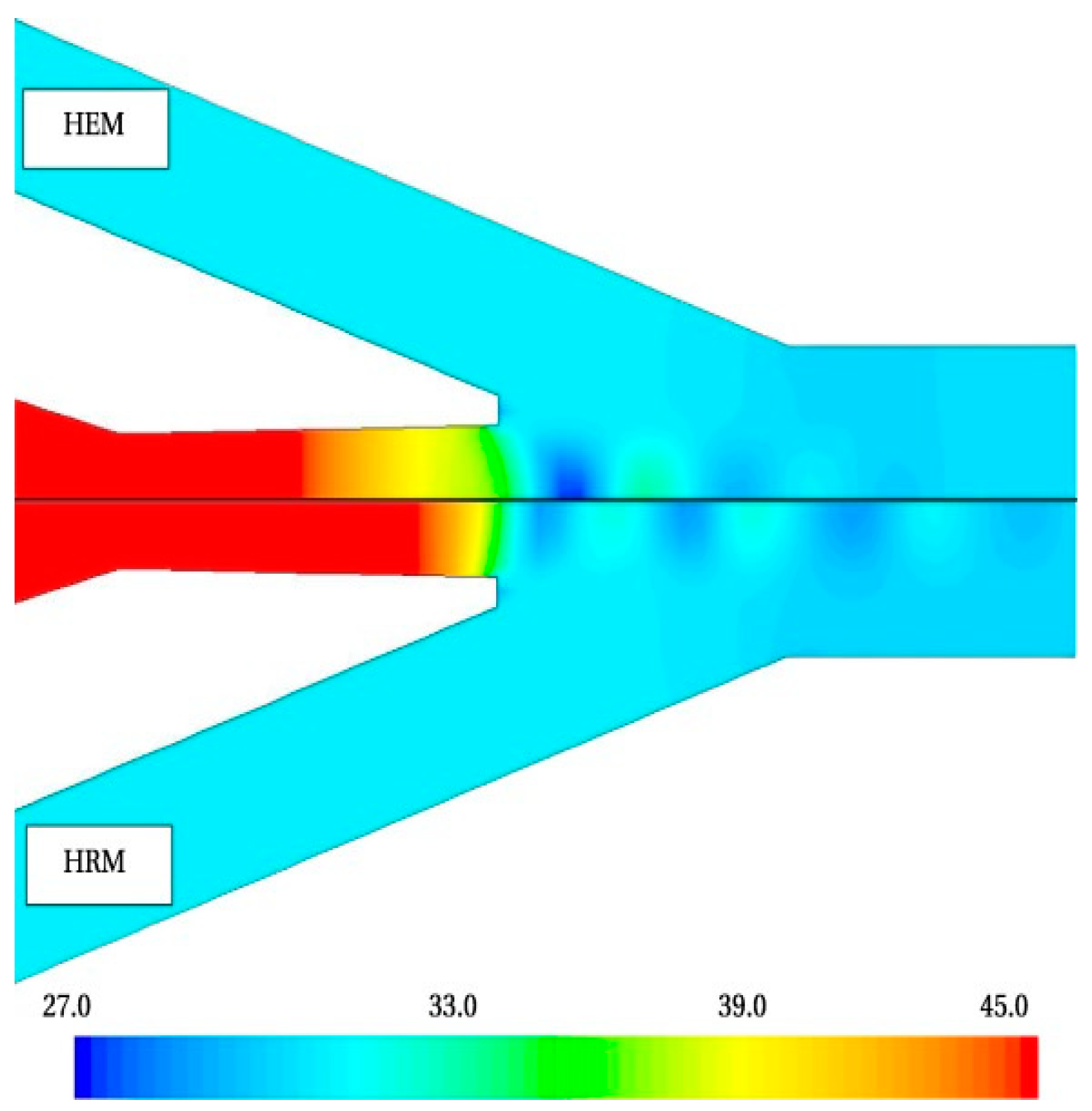

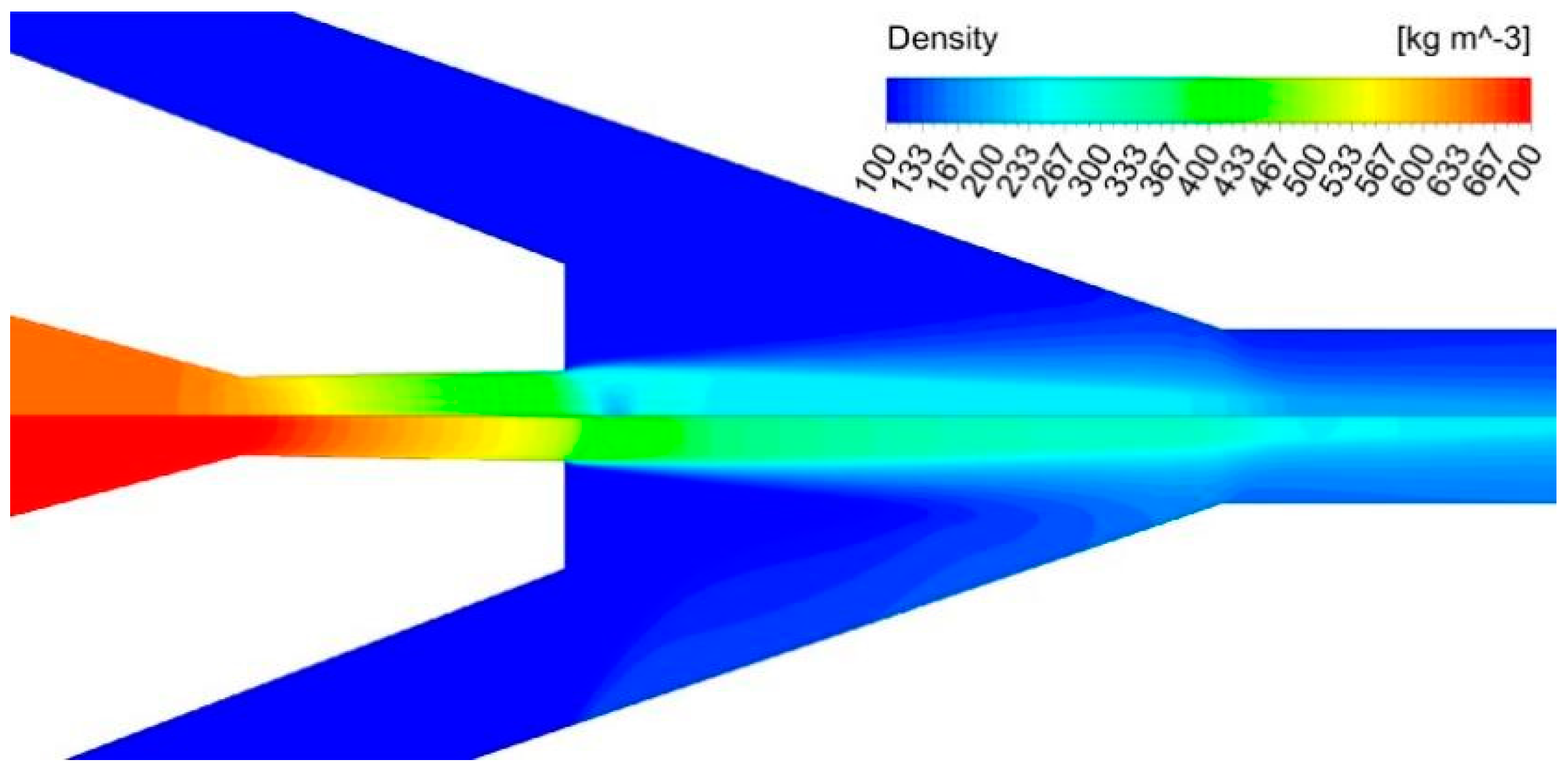
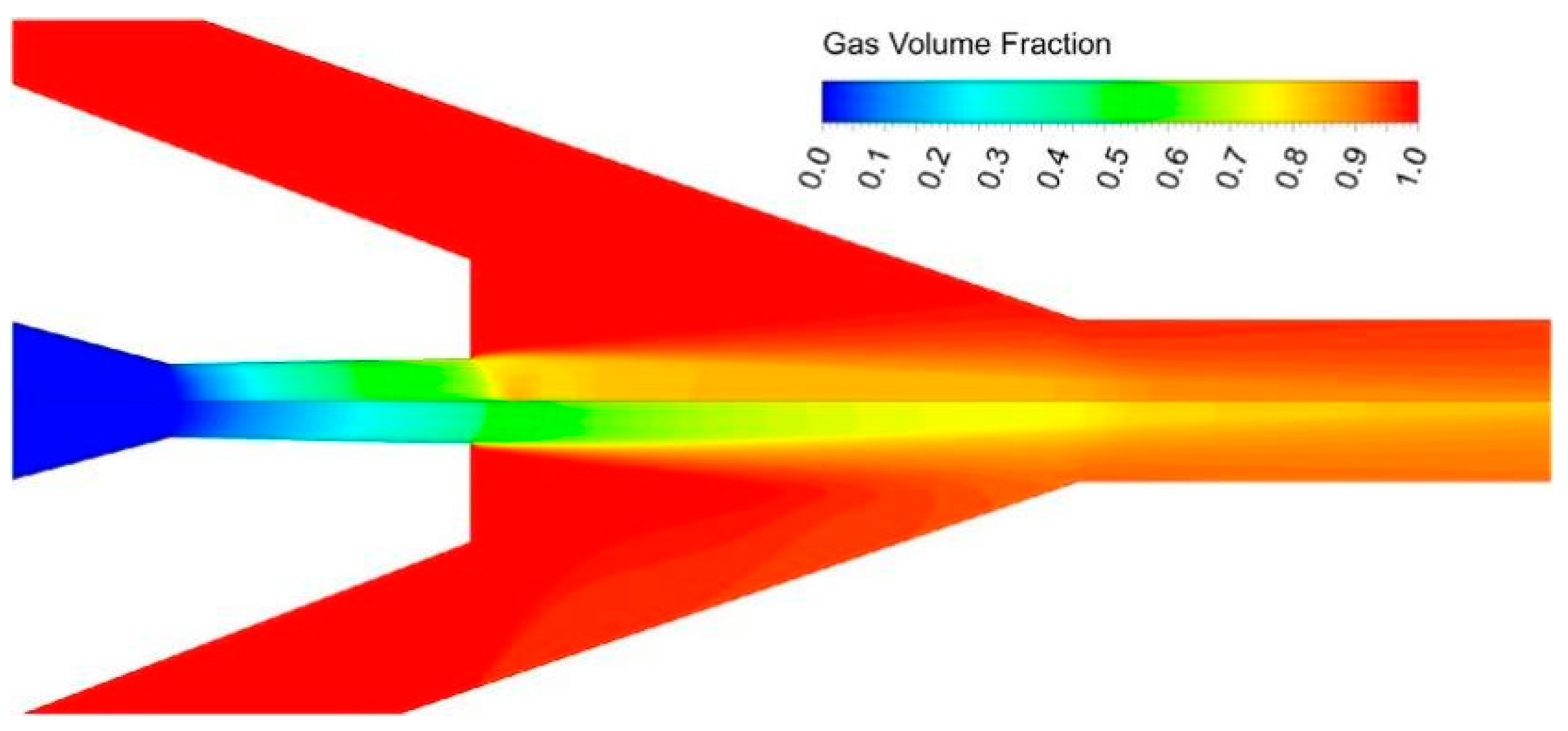

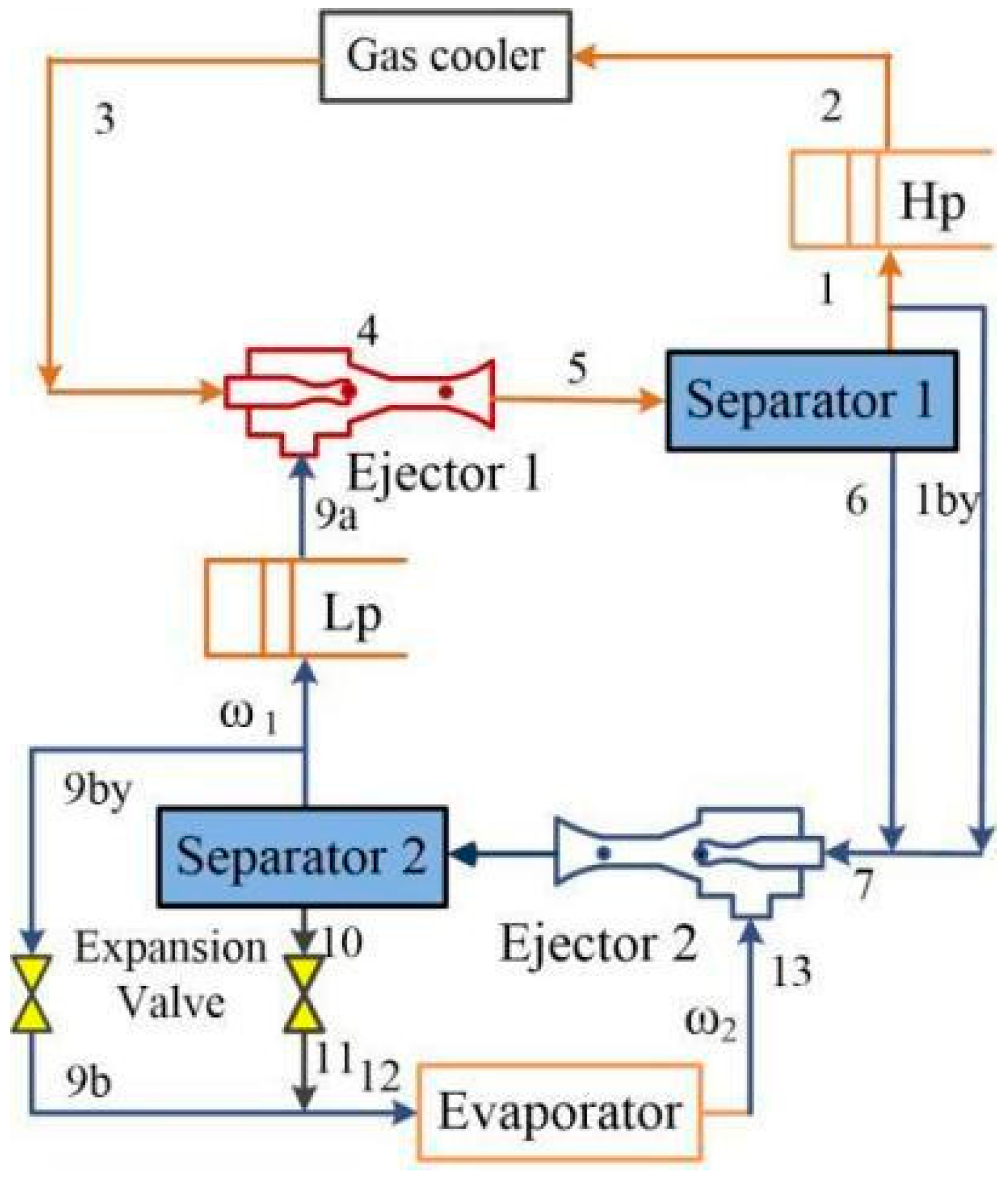


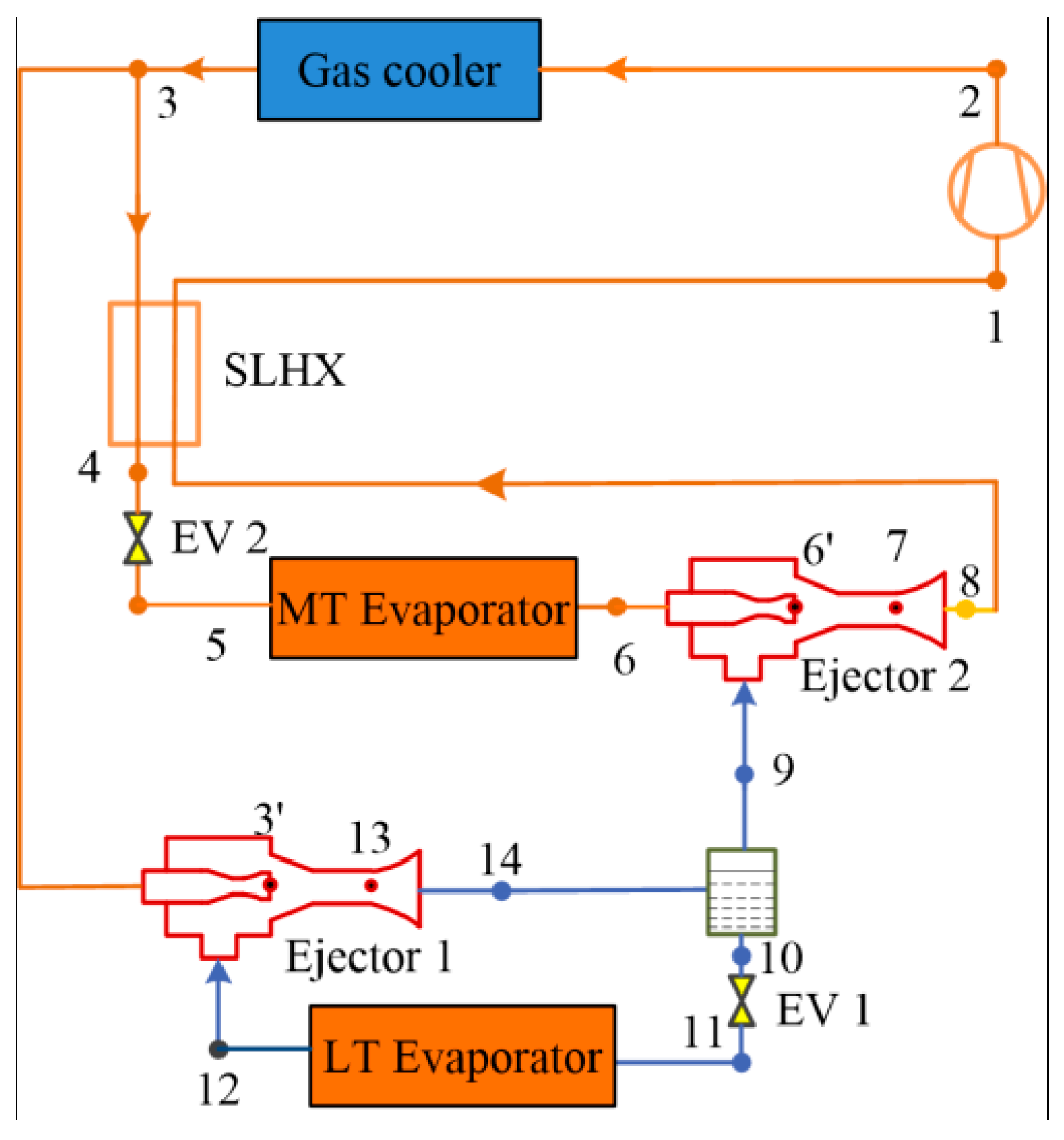
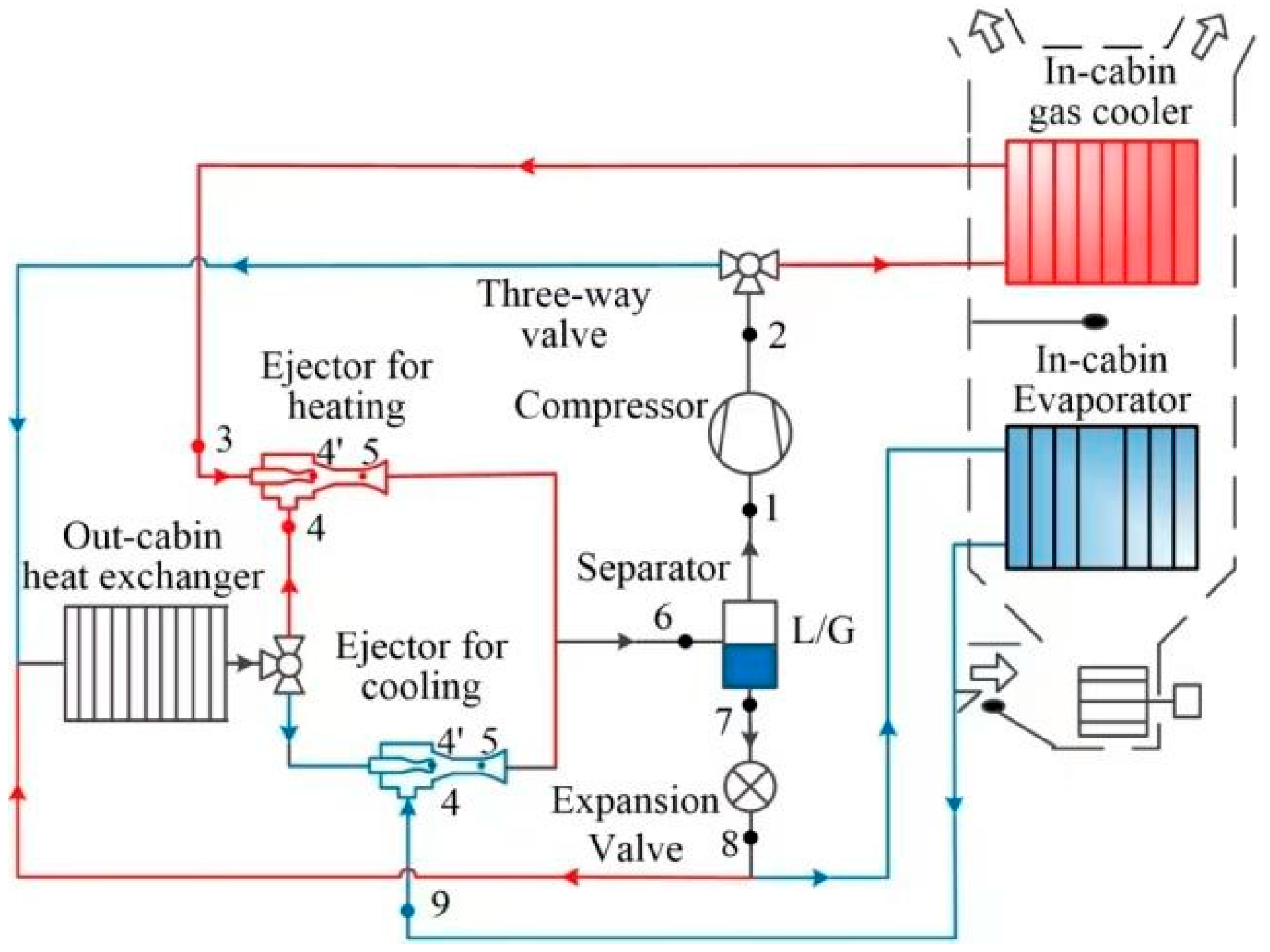



| Model | Study | Equations |
|---|---|---|
| k-ε | Smolka et al. [19] | k-ε turbulence equations: |
| k-ε Realizable | Ringstad et al. [33] | the collection of transport equations for turbulence: |
| k-ω SST | Menter et al. [34] | where the definitions of the mixing functions F1 and F2 are: The following is the definition of turbulent eddy viscosity: where S is an invariant measure of the strain rate. The SST model employed a production limiter to stop the formation of turbulence in standstill regions: |
| k-ε RNG | Bartosiewicz et al. [35] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, L.; Zhang, Y.; Hao, L.; Lian, H.; Deng, J.; Lu, W. Modelling, Optimization, and Experimental Studies of Refrigeration CO2 Ejectors: A Review. Mathematics 2022, 10, 4325. https://doi.org/10.3390/math10224325
Zheng L, Zhang Y, Hao L, Lian H, Deng J, Lu W. Modelling, Optimization, and Experimental Studies of Refrigeration CO2 Ejectors: A Review. Mathematics. 2022; 10(22):4325. https://doi.org/10.3390/math10224325
Chicago/Turabian StyleZheng, Lixing, Yiyan Zhang, Lifen Hao, Haojie Lian, Jianqiang Deng, and Wei Lu. 2022. "Modelling, Optimization, and Experimental Studies of Refrigeration CO2 Ejectors: A Review" Mathematics 10, no. 22: 4325. https://doi.org/10.3390/math10224325
APA StyleZheng, L., Zhang, Y., Hao, L., Lian, H., Deng, J., & Lu, W. (2022). Modelling, Optimization, and Experimental Studies of Refrigeration CO2 Ejectors: A Review. Mathematics, 10(22), 4325. https://doi.org/10.3390/math10224325







