Transient Dynamic Response Analysis of Two-Dimensional Saturated Soil with Singular Boundary Method
Abstract
1. Introduction
2. Governing Equations
3. Singular Boundary Method in Frequency-Domain
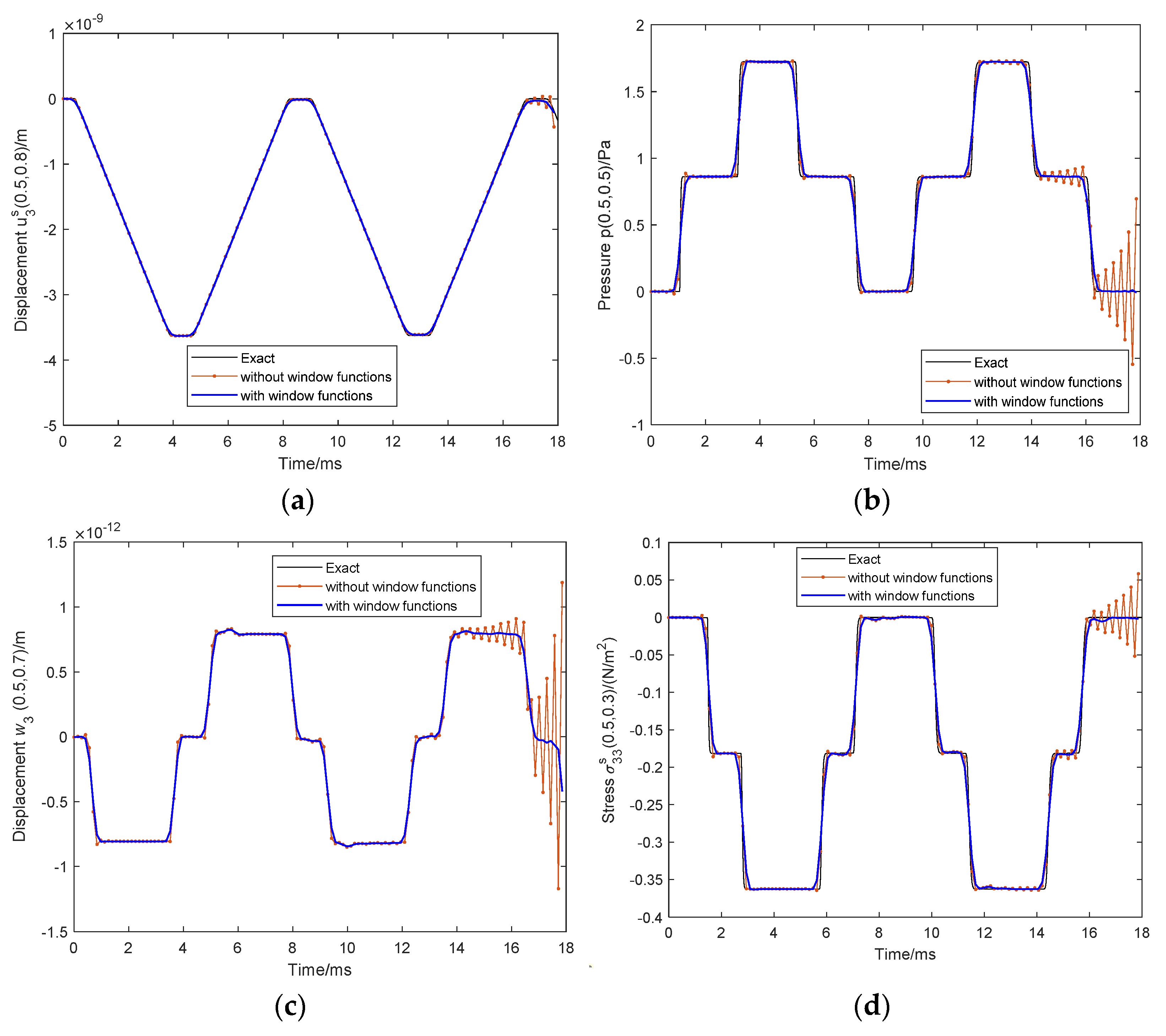
4. Exponential Window Method
- (1)
- Determine the total calculation time and the number of sampling frequencies , then to determine the angular frequency resolution with ;
- (2)
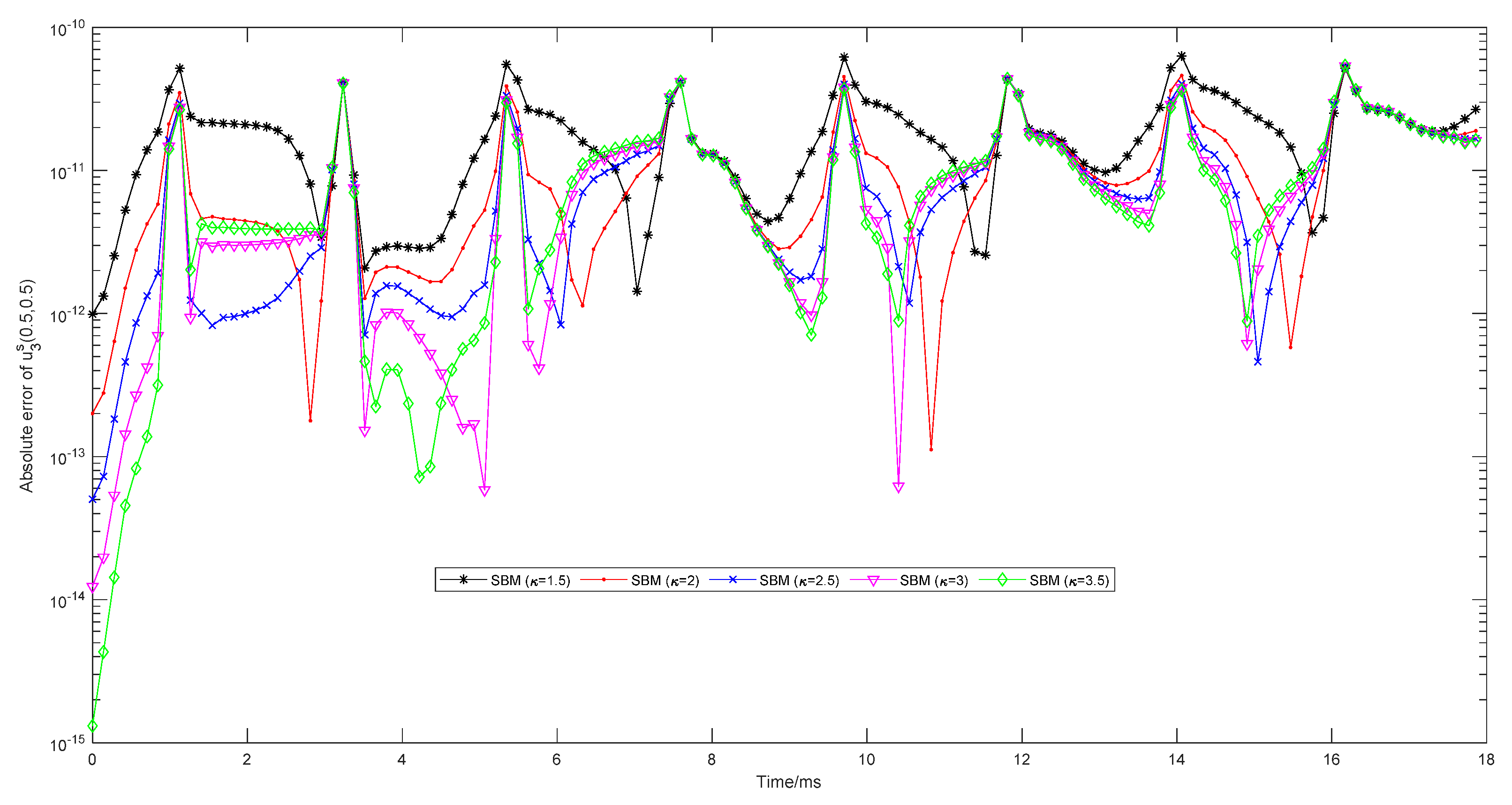
- Determine the shifting constant according to the numerical experiments and experience aswhere denote the damping coefficient, and is recommended;
- (3)
- Construct a desired damping system with scaling the variables ( and ) with the scaling function as . Bring new variables into the governing equations, and a novel frequency-domain boundary value problem Equations (6) and (7) with is obtained.
- (4)
- Simultaneously, the boundary condition is scaled into , and the frequency-domain boundary condition can be obtained via discretized Fourier transformwhere .
- (5)
- Perform the SBM to evaluate the solutions of the frequency-domain problems at the frequencies . The remaining of results can be obtained through conjugate symmetric property as
- (6)
- Perform the IFFT with the inverse DFT with Hanning window function , and obtain the time-domain solutions asThe Hanning window function is used to alleviate the Gibbs oscillations.
- (7)
- Descale the time-domain solutions and obtain the solutions of the original problems as
5. Numerical Examples
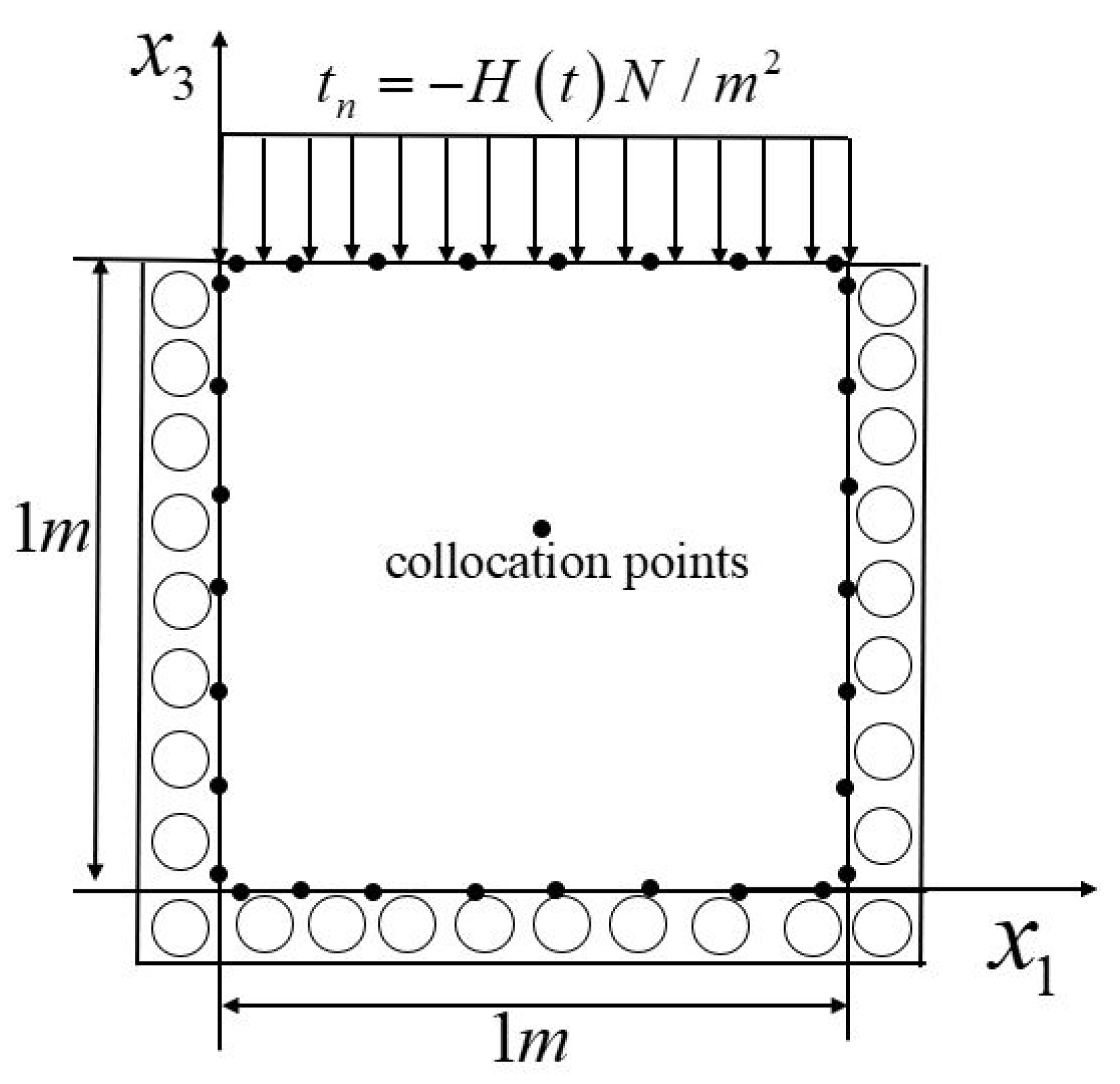
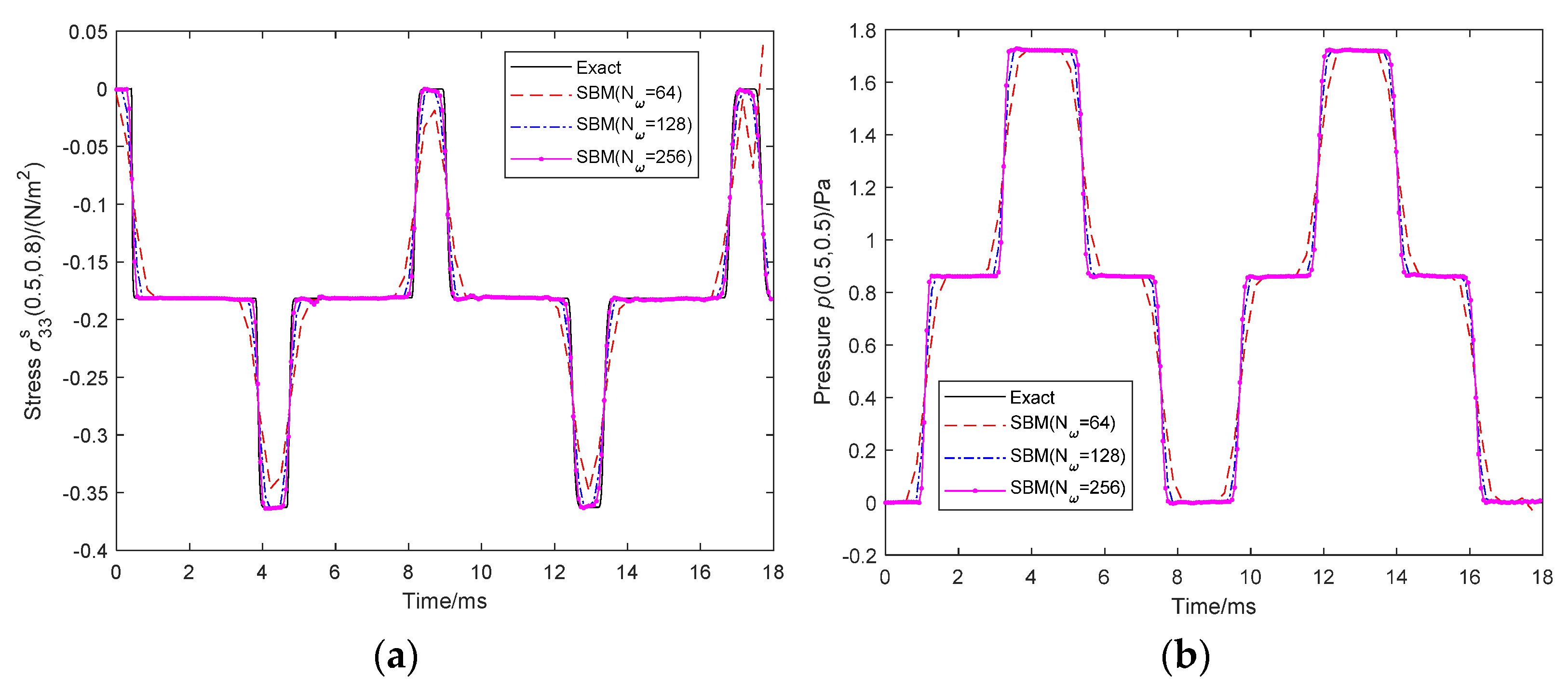
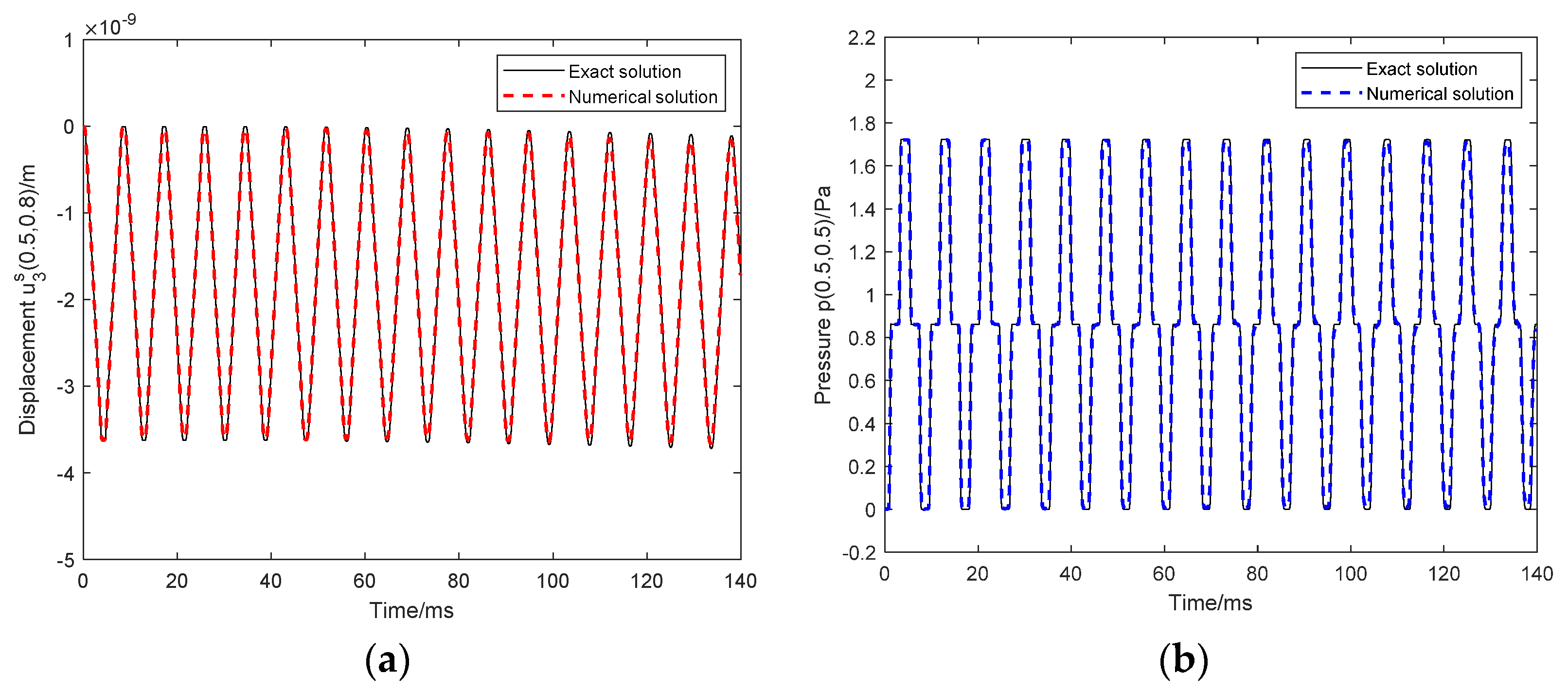
5.1. Verification of the Proposed SBM-EWM Method
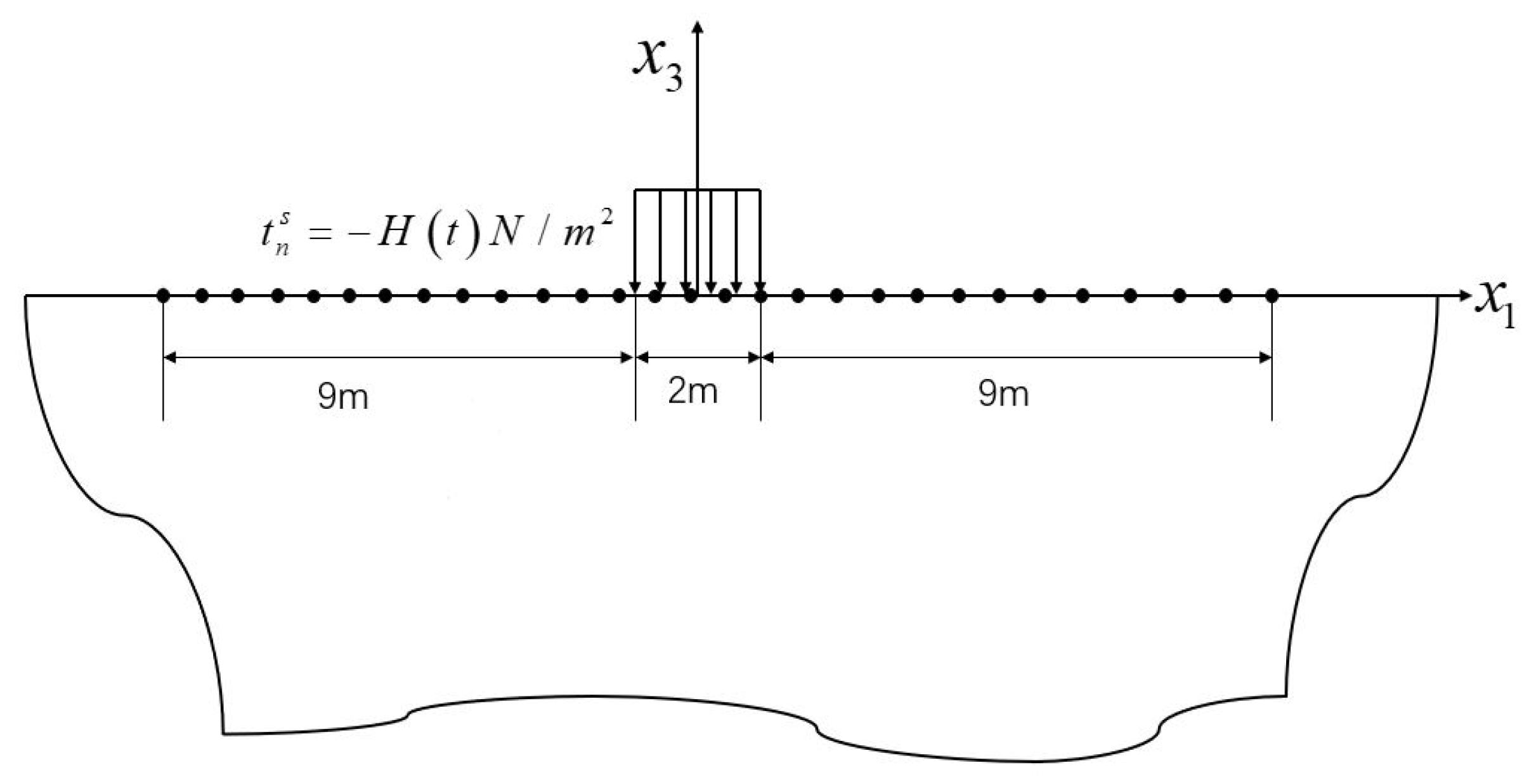
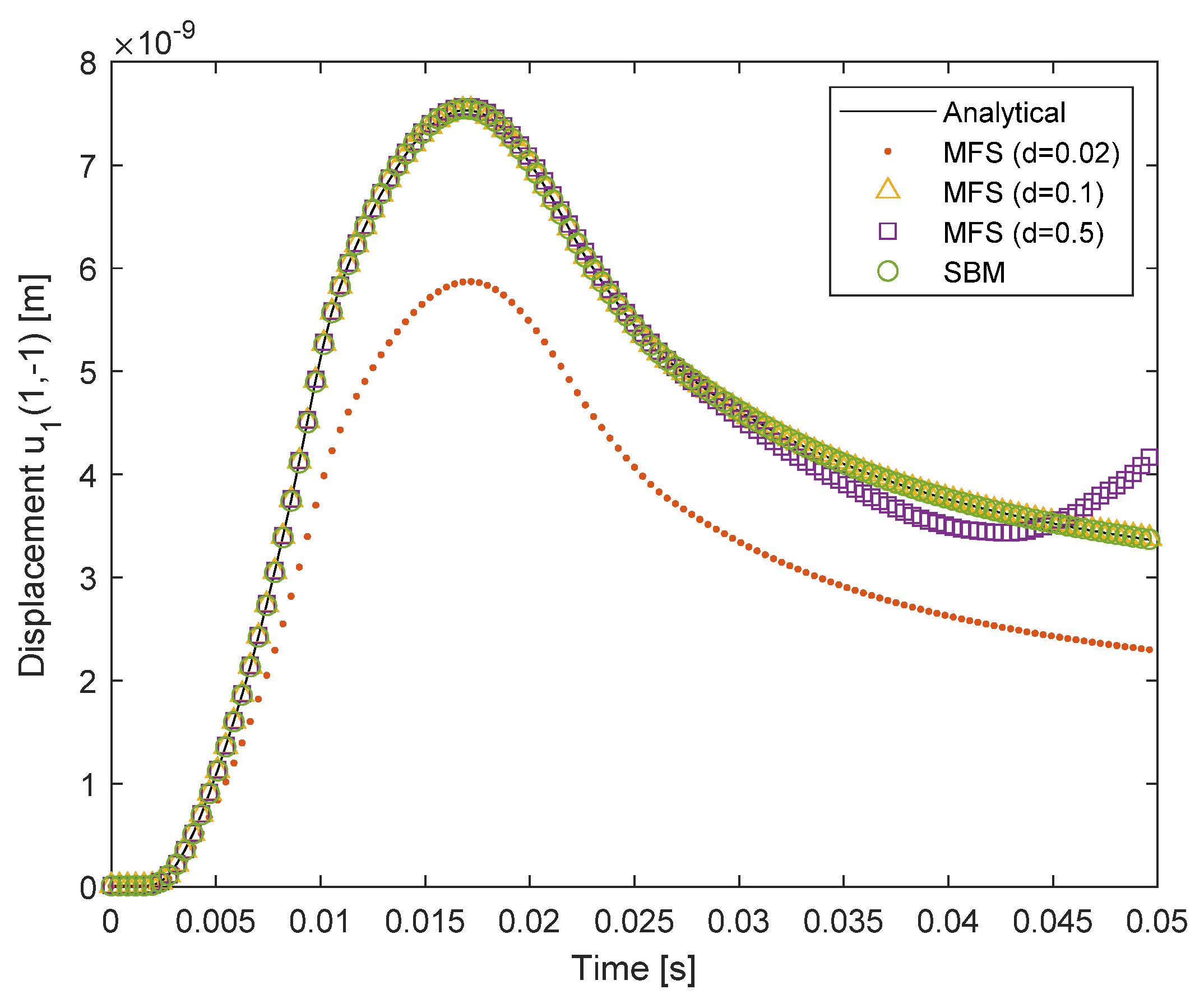
5.2. A Half-Space Problem Subjected to a Transient Load
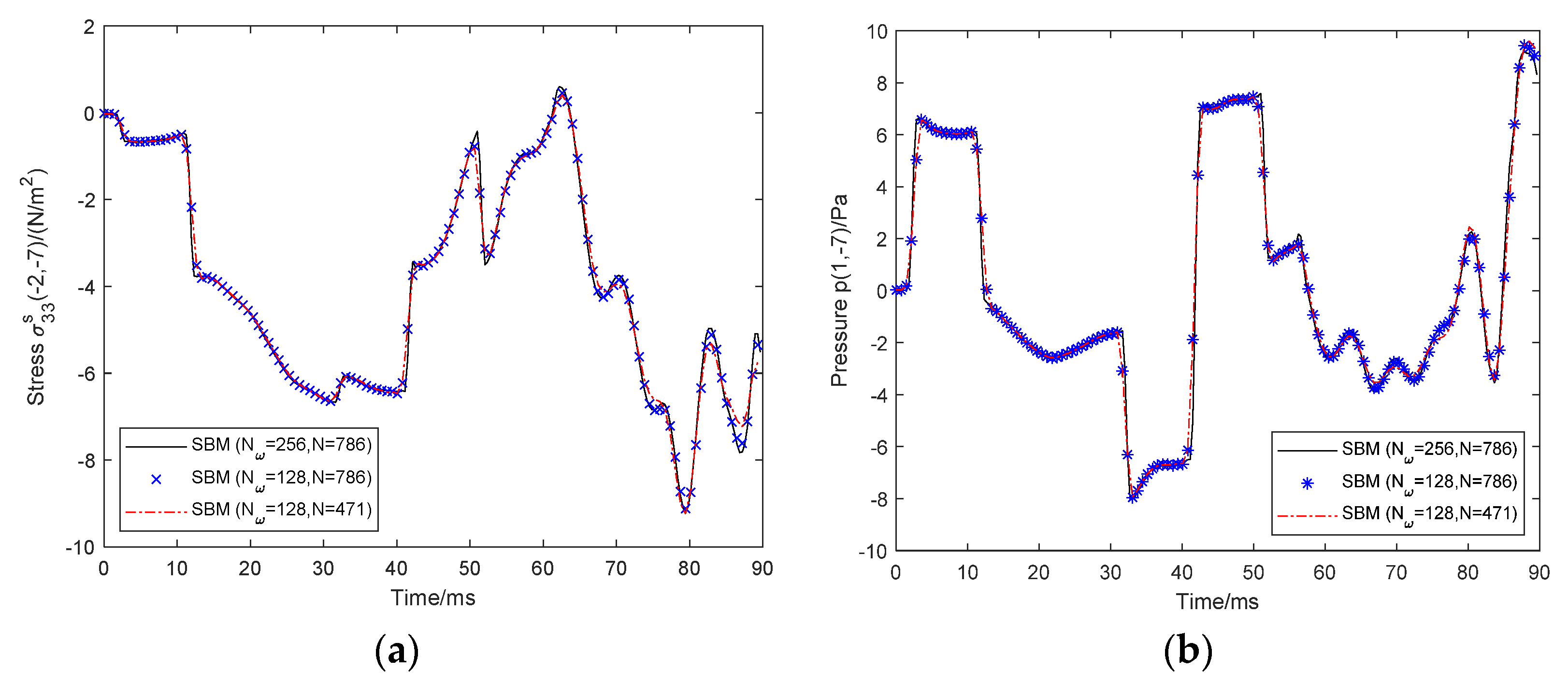
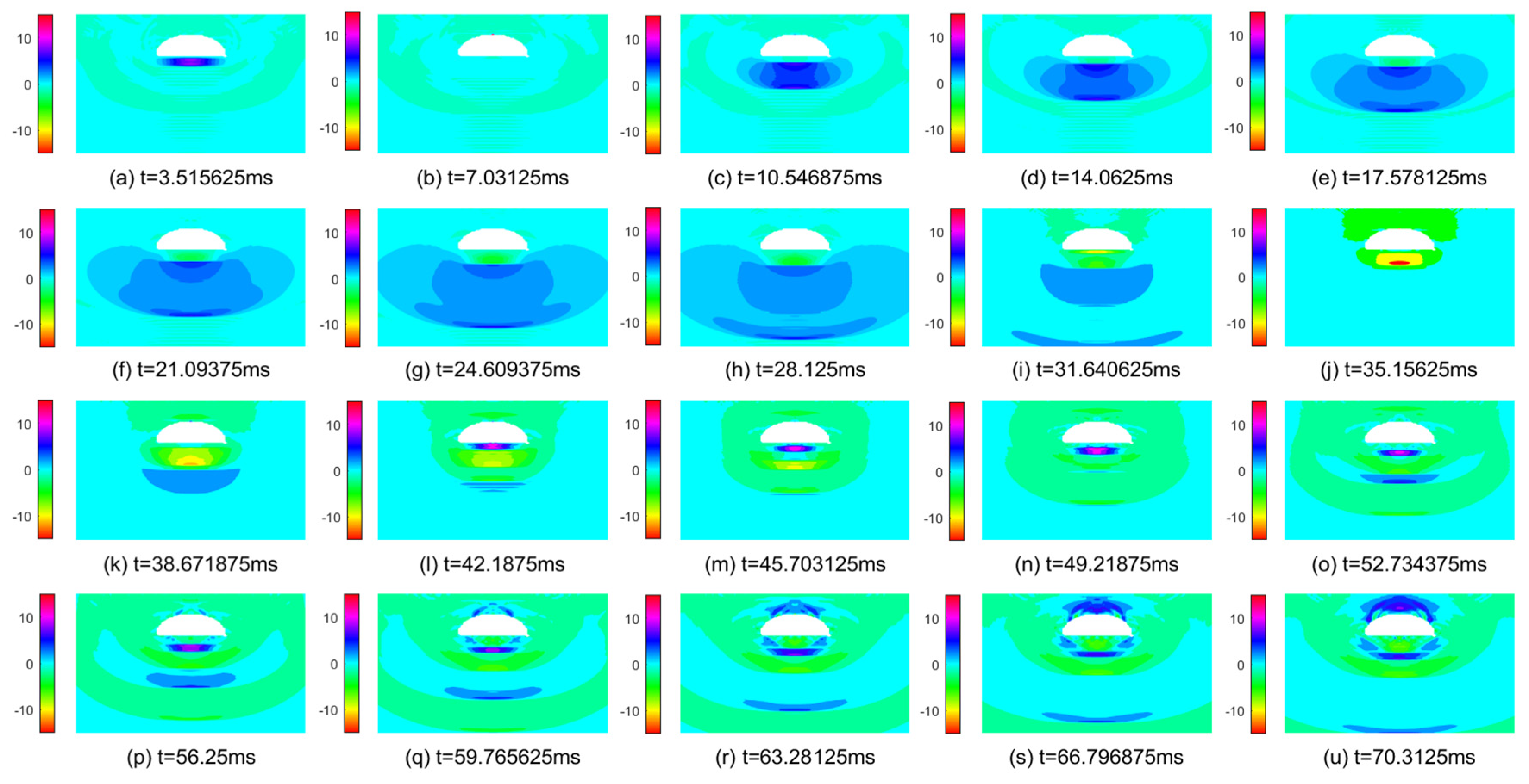
5.3. A Tunnel Embedded in a Saturated Poroelastic Half-Space
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Detailed Derivations of the 2D Fundamental Solutions
- (1)
- Solid loads
- (2)
- Fluid load
Appendix B. The of OIFs for 2D Saturated Poroelastic Problems
References
- Chen, G.; Yang, J.; Liu, Y.; Kitahara, T.; Beer, M. An energy-frequency parameter for earthquake ground motion intensity measure. Earthq. Eng. Struct. Dyn. 2022, 1–14. [Google Scholar] [CrossRef]
- Chen, G.; Li, Q.-Y.; Li, D.-Q.; Wu, Z.-Y.; Liu, Y. Main frequency band of blast vibration signal based on wavelet packet transform. Appl. Math. Model. 2019, 74, 569–585. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Q.; Gui, Q.; Chai, Y. A Coupled FE-Meshfree Triangular Element for Acoustic Radiation Problems. Int. J. Comput. Methods 2021, 18, 2041002. [Google Scholar] [CrossRef]
- Chai, Y.; Li, W.; Liu, Z. Analysis of transient wave propagation dynamics using the enriched finite element method with interpolation cover functions. Appl. Math. Comput. 2022, 412, 126564. [Google Scholar] [CrossRef]
- Pled, F.; Desceliers, C. Review and Recent Developments on the Perfectly Matched Layer (PML) Method for the Numerical Modeling and Simulation of Elastic Wave Propagation in Unbounded Domains. Arch. Comput. Methods Eng. 2022, 29, 471–518. [Google Scholar] [CrossRef]
- Fu, Z.-J.; Xie, Z.-Y.; Ji, S.-Y.; Tsai, C.-C.; Li, A.-L. Meshless generalized finite difference method for water wave interactions with multiple-bottom-seated-cylinder-array structures. Ocean Eng. 2020, 195, 106736. [Google Scholar] [CrossRef]
- Kythe, P.K. Fundamental Solutions for Differential Operators and Applications; Birkhauser: Basel, Switzerland, 1996. [Google Scholar]
- Chen, C.S.; Karageorghis, A.; Smyrlis, Y.S. The Method of Fundamental Solutions: A Meshless Method; Dynamic Publishers: Atlanta, GA, USA, 2008. [Google Scholar]
- Wei, X.; Chen, W.; Chen, B. An ACA accelerated MFS for potential problems. Eng. Anal. Bound. Elem. 2014, 41, 90–97. [Google Scholar] [CrossRef]
- Chen, Z.; Sun, L. A boundary meshless method for dynamic coupled thermoelasticity problems. Appl. Math. Lett. 2022, 134, 108305. [Google Scholar] [CrossRef]
- Wang, M.Z.; Xu, B.X.; Gao, C.F. Recent General Solutions in Linear Elasticity and Their Applications. Appl. Mech. Rev. 2008, 61, 030803–030820. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, C.; Yu, Y. A boundary knot method for 3D time harmonic elastic wave problems. Appl. Math. Lett. 2020, 104, 106210. [Google Scholar] [CrossRef]
- Xu, W.-Z.; Fu, Z.-J.; Xi, Q. A novel localized collocation solver based on a radial Trefftz basis for thermal conduction analysis in FGMs with exponential variations. Comput. Math. Appl. 2022, 117, 24–38. [Google Scholar] [CrossRef]
- Xi, Q.; Fu, Z.; Zhang, C.; Yin, D. An efficient localized Trefftz-based collocation scheme for heat conduction analysis in two kinds of heterogeneous materials under temperature loading. Comput. Struct. 2021, 255, 106619. [Google Scholar] [CrossRef]
- Li, Z.C.; Lu, T.T.; Hu, H.Y.; Cheng, A.H.D. Trefftz and Collocation Methods; WIT Press: Boston, UK, 2008. [Google Scholar]
- Sun, L.; Wei, X.; Chu, L. A 2D frequency-domain wave based method for dynamic analysis of orthotropic solids. Comput. Struct. 2020, 238, 106300. [Google Scholar] [CrossRef]
- Karageorghis, A.; Lesnic, D.; Marin, L. A survey of applications of the MFS to inverse problems. Inverse Probl. Sci. Eng. 2011, 19, 309–336. [Google Scholar] [CrossRef]
- Šarler, B. Solution of potential flow problems by the modified method of fundamental solutions: Formulations with the single layer and the double layer fundamental solutions. Eng. Anal. Bound. Elem. 2009, 33, 1374–1382. [Google Scholar] [CrossRef]
- Chen, W. Singular boundary method: A novel, simple, meshfree, boundary collocation numerical method. Chin. J. Solid Mech. 2009, 30, 592–599. [Google Scholar]
- Wei, X.; Chen, W.; Chen, B.; Sun, L. Singular boundary method for heat conduction problems with certain spatially varying conductivity. Comput. Math. Appl. 2015, 69, 206–222. [Google Scholar] [CrossRef]
- Wei, X.; Chen, W.; Sun, L.; Chen, B. A simple accurate formula evaluating origin intensity factor in singular boundary method for two-dimensional potential problems with Dirichlet boundary. Eng. Anal. Bound. Elem. 2015, 58, 151–165. [Google Scholar] [CrossRef]
- Wei, X.; Chen, W.; Fu, Z.J. Solving inhomogeneous problems by singular boundary method. J. Mar. Sci. Technol. Taiwan 2013, 21, 8–14. [Google Scholar] [CrossRef]
- Wei, X.; Sun, L.; Yin, S.; Chen, B. A boundary-only treatment by singular boundary method for two-dimensional inhomogeneous problems. Appl. Math. Model. 2018, 62, 338–351. [Google Scholar] [CrossRef]
- Wei, X.; Sun, L. Singular boundary method for 3D time-harmonic electromagnetic scattering problems. Appl. Math. Model. 2019, 76, 617–631. [Google Scholar] [CrossRef]
- Wei, X.; Huang, A.; Sun, L. Singular boundary method for 2D and 3D heat source reconstruction. Appl. Math. Lett. 2020, 102, 106103. [Google Scholar] [CrossRef]
- Wei, X.; Luo, W. 2.5D singular boundary method for acoustic wave propagation. Appl. Math. Lett. 2021, 112, 106760. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, F.; Li, P.-W.; Qu, W. Singular boundary method for 2D and 3D acoustic design sensitivity analysis. Comput. Math. Appl. 2022, 119, 371–386. [Google Scholar] [CrossRef]
- Fu, Z.; Xi, Q.; Li, Y.; Huang, H.; Rabczuk, T. Hybrid FEM–SBM solver for structural vibration induced underwater acoustic radiation in shallow marine environment. Comput. Methods Appl. Mech. Eng. 2020, 369, 113236. [Google Scholar] [CrossRef]
- Wei, X.; Rao, C.; Chen, S.; Luo, W. Numerical simulation of anti-plane wave propagation in heterogeneous media. Appl. Math. Lett. 2023, 135, 108436. [Google Scholar] [CrossRef]
- Sun, L.; Wei, X. A frequency domain formulation of the singular boundary method for dynamic analysis of thin elastic plate. Eng. Anal. Bound. Elem. 2019, 98, 77–87. [Google Scholar] [CrossRef]
- Sun, L.; Chen, W.; Cheng, A.H.D. Singular boundary method for 2D dynamic poroelastic problems. Wave Motion 2016, 61, 40–62. [Google Scholar] [CrossRef]
- Sun, L.; Wei, X.; Chen, B. A meshless singular boundary method for elastic wave propagation in 2D partially saturated poroelastic media. Eng. Anal. Bound. Elem. 2020, 113, 82–98. [Google Scholar] [CrossRef]
- Li, W.; Wang, F. Precorrected-FFT Accelerated Singular Boundary Method for High-Frequency Acoustic Radiation and Scattering. Mathematics 2022, 10, 238. [Google Scholar] [CrossRef]
- Li, J.; Gu, Y.; Qin, Q.-H.; Zhang, L. The rapid assessment for three-dimensional potential model of large-scale particle system by a modified multilevel fast multipole algorithm. Comput. Math. Appl. 2021, 89, 127–138. [Google Scholar] [CrossRef]
- Li, J.; Zhang, L.; Qin, Q. A regularized fast multipole method of moments for rapid calculation of three-dimensional time-harmonic electromagnetic scattering from complex targets. Eng. Anal. Bound. Elem. 2022, 142, 28–38. [Google Scholar] [CrossRef]
- Li, J.; Fu, Z.; Gu, Y.; Qin, Q. Recent advances and emerging applications of the singular boundary method for large-scale and high-frequency computational acoustics. Adv. Appl. Math. Mech. 2022, 14, 315–343. [Google Scholar] [CrossRef]
- Qu, W.; Chen, W.; Zheng, C. Diagonal form fast multipole singular boundary method applied to the solution of high-frequency acoustic radiation and scattering. Int. J. Numer. Methods Eng. 2017, 111, 803–815. [Google Scholar] [CrossRef]
- Fu, Z.; Tang, Z.; Xi, Q.; Liu, Q.; Gu, Y.; Wang, F. Localized collocation schemes and their applications. Acta Mech. Sin. 2022, 38, 422167. [Google Scholar] [CrossRef]
- Li, W. Localized method of fundamental solutions for 2D harmonic elastic wave problems. Appl. Math. Lett. 2021, 112, 106759. [Google Scholar] [CrossRef]
- Zhu, T.; Zhang, J.D.; Atluri, S.N. A local boundary integral equation (LBIE) method in Comput. Mech., and a meshless discretization approach. Comput. Mech. 1998, 21, 223–235. [Google Scholar] [CrossRef]
- Sun, L.; Fu, Z.; Chen, Z. A localized collocation solver based on fundamental solutions for 3D time harmonic elastic wave propagation analysis. Appl. Math. Comput. 2023, 439, 127600. [Google Scholar] [CrossRef]
- Zhang, Y.; Dang, S.; Li, W.; Chai, Y. Performance of the radial point interpolation method (RPIM) with implicit time integration scheme for transient wave propagation dynamics. Comput. Math. Appl. 2022, 114, 95–111. [Google Scholar] [CrossRef]
- Qu, W.; He, H. A spatial–temporal GFDM with an additional condition for transient heat conduction analysis of FGMs. Appl. Math. Lett. 2020, 110, 106579. [Google Scholar] [CrossRef]
- Gao, X.-W.; Zheng, B.-J.; Yang, K.; Zhang, C. Radial integration BEM for dynamic coupled thermoelastic analysis under thermal shock loading. Comput. Struct. 2015, 158, 140–147. [Google Scholar] [CrossRef]
- Kuhlman, K. Review of inverse Laplace transform algorithms for Laplace-space numerical approaches. Numer. Algorithms 2013, 63, 339–355. [Google Scholar] [CrossRef]
- Xiao, J.; Ye, W.; Cai, Y.; Zhang, J. Precorrected FFT accelerated BEM for large-scale transient elastodynamic analysis using frequency-domain approach. Int. J. Numer. Methods Eng. 2012, 90, 116–134. [Google Scholar] [CrossRef]
- Phan, A.V.; Gray, L.J.; Salvadori, A. Transient analysis of the dynamic stress intensity factors using SGBEM for frequency-domain elastodynamics. Comput. Methods Appl. Mech. Eng. 2010, 199, 3039–3050. [Google Scholar] [CrossRef]
- Marrero, M.; Domínguez, J. Numerical behavior of time domain BEM for three-dimensional transient elastodynamic problems. Eng. Anal. Bound. Elem. 2003, 27, 39–48. [Google Scholar] [CrossRef]
- Qu, W.; Gao, H.W.; Gu, Y. Integrating Krylov deferred correction and generalized finite difference methods for dynamic simulations of wave propagation phenomena in long-time intervals. Adv. Appl. Math. Mech. 2021, 13, 1398–1417. [Google Scholar]
- Kausel, E.; Roësset, J.M. Frequency Domain Analysis of Undamped Systems. J. Eng. Mech. 1992, 118, 721–734. [Google Scholar] [CrossRef]
- Tong, L.H.; Ding, H.B.; Yan, J.W.; Xu, C.; Lei, Z. Strain gradient nonlocal Biot poromechanics. Int. J. Eng. Sci. 2020, 156, 103372. [Google Scholar] [CrossRef]
- Tong, L.; Yu, Y.; Hu, W.; Shi, Y.; Xu, C. On wave propagation characteristics in fluid saturated porous materials by a nonlocal Biot theory. J. Sound Vib. 2016, 379, 106–118. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. II. Higher Frequency Range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Lu, J.F.; Jeng, D.S.; Williams, S. A 2.5-D dynamic model for a saturated porous medium: Part I. Green’s function. Int. J. Solids Struct. 2008, 45, 378–391. [Google Scholar] [CrossRef]
- Wei, X.; Liu, D.; Luo, W.; Chen, S.; Sun, L. A half-space singular boundary method for predicting ground-borne vibrations. Appl. Math. Model. 2022, 111, 630–643. [Google Scholar] [CrossRef]
- Gu, Y.; Chen, W.; Zhang, C.-Z. Singular boundary method for solving plane strain elastostatic problems. Int. J. Solids Struct. 2011, 48, 2549–2556. [Google Scholar] [CrossRef]
- Ariza, M.P.; Dominguez, J. General BE approach for three-dimensional dynamic fracture analysis. Eng. Anal. Bound. Elem. 2002, 26, 639–651. [Google Scholar] [CrossRef]
- Xiao, J.; Ye, W.; Wen, L. Efficiency improvement of the frequency-domain BEM for rapid transient elastodynamic analysis. Comput. Mech. 2013, 52, 903–912. [Google Scholar] [CrossRef]
- Ba, Z.; Kang, Z.; Lee, V.W. Plane strain dynamic responses of a multi-layered transversely isotropic saturated half-space. Int. J. Eng. Sci. 2017, 119, 55–77. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Wei, X.; Li, C.; Han, C.; Cheng, X.; Sun, L. Transient Dynamic Response Analysis of Two-Dimensional Saturated Soil with Singular Boundary Method. Mathematics 2022, 10, 4323. https://doi.org/10.3390/math10224323
Liu D, Wei X, Li C, Han C, Cheng X, Sun L. Transient Dynamic Response Analysis of Two-Dimensional Saturated Soil with Singular Boundary Method. Mathematics. 2022; 10(22):4323. https://doi.org/10.3390/math10224323
Chicago/Turabian StyleLiu, Dongdong, Xing Wei, Chengbin Li, Chunguang Han, Xiaxi Cheng, and Linlin Sun. 2022. "Transient Dynamic Response Analysis of Two-Dimensional Saturated Soil with Singular Boundary Method" Mathematics 10, no. 22: 4323. https://doi.org/10.3390/math10224323
APA StyleLiu, D., Wei, X., Li, C., Han, C., Cheng, X., & Sun, L. (2022). Transient Dynamic Response Analysis of Two-Dimensional Saturated Soil with Singular Boundary Method. Mathematics, 10(22), 4323. https://doi.org/10.3390/math10224323




