Exponential Graph Regularized Non-Negative Low-Rank Factorization for Robust Latent Representation

Abstract

Non-negative matrix factorization (NMF) is a fundamental theory that has received much attention and is widely used in image engineering, pattern recognition and other fields. However, the classical NMF has limitations such as only focusing on local information, sensitivity to noise and small sample size (SSS) problems. Therefore, how to develop the NMF to improve the performance and robustness of the algorithm is a worthy challenge. Based on the bottlenecks above, we propose an exponential graph regularization non-negative low-rank factorization algorithm (EGNLRF) combining sparseness, low rank and matrix exponential. Firstly, based on the assumption that the data is corroded, we decompose a given raw data item with a data error fitting noise matrix, applying a low-rank constraint to the denoising data. Then, we perform a non-negative factorization on the resulting low-rank matrix, from which we derive the low-dimensional representation of the original matrix. Finally, we use the low-dimensional representation for graph embedding to maintain the geometry between samples. The graph embedding terms are matrix exponentiated to cope with SSS problems and nearest neighbor sensitivity. The above three steps will be incorporated into a joint framework to validate and optimize each other; therefore, we can learn latent data representations that are undisturbed by noise and preserve the local structure of known samples. We conducted simulation experiments on different datasets and verified the effectiveness of the algorithm by comparing the proposed with the lasting ones related to NMF, low rank and graph embedding.

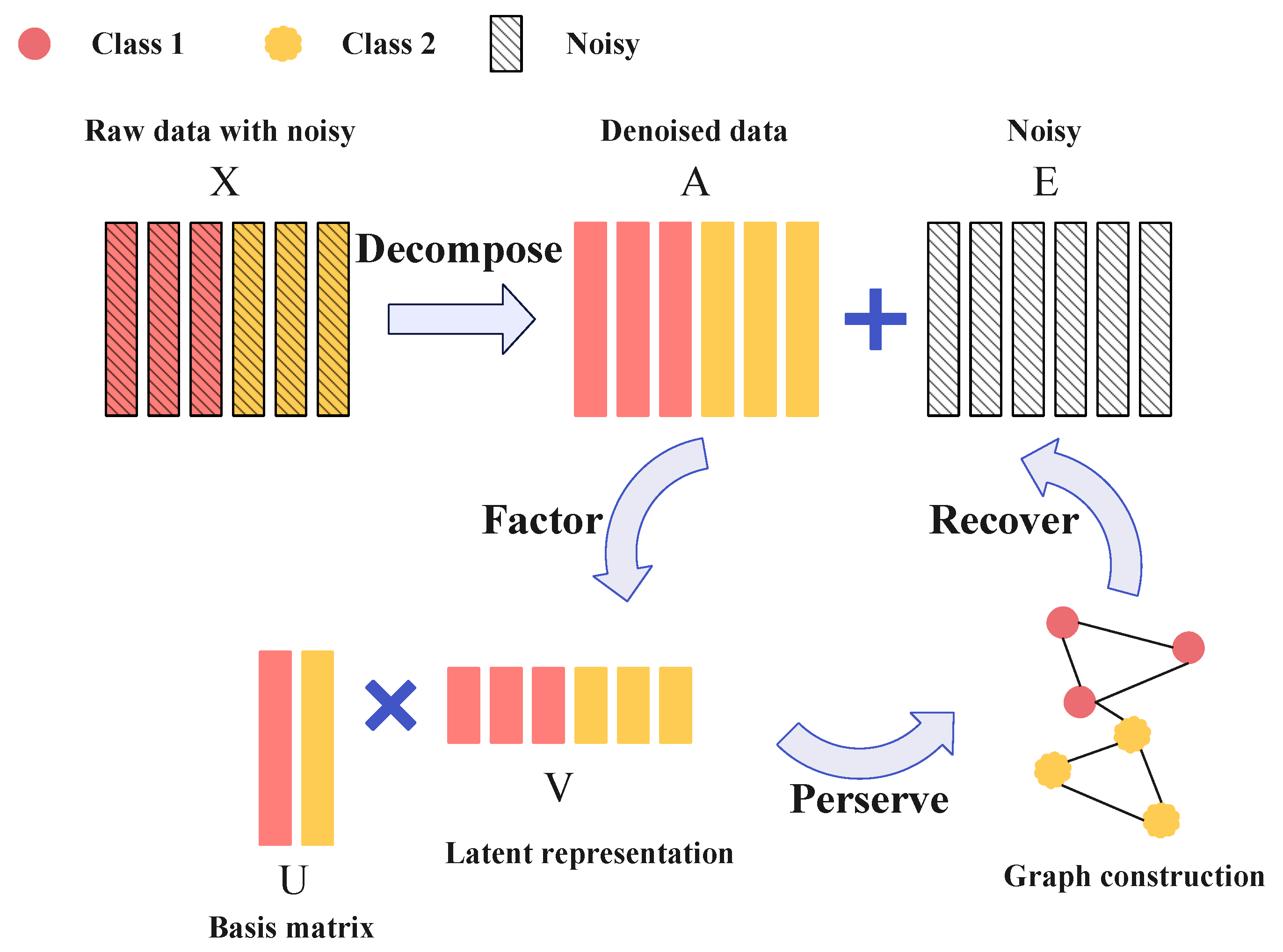
1. Introduction

With the continuous development of science and technology, various electronic devices are constantly bringing forth new ideas, the volume of data obtained is growing explosively and the “dimensionality curse” is becoming more and more significant [1,2]. Therefore, how to efficiently obtain effective feature representations from massive data has always been the focus of research. In addition, the practical application scenario is usually a typical small sample size (SSS) scenario [3,4,5]: abundant unlabeled data and a small amount of labeled data, which undoubtedly brings huge challenges to the multivariate data conversion algorithm. Generally speaking, a good data transformation method will have the basic characteristics of making the data structure clearer and reducing the data dimension. The more classic data dimensionality reduction algorithms include principal component analysis (PCA) [6], linear discriminant analysis (LDA) [7], locality preserving projections (LPP) [8], independent component analysis (ICA) [9], projection pursuit (PP) [10] and non-negative matrix factorization (NMF) [11], etc., which lead to differences in statistical properties due to different constraints imposed.

NMF stands out due to its natural non-negativity and its part-based representation properties. On the one hand, in many real-world data, negative values are meaningless; on the other hand, the theory that the perception of the whole is made up of the perception of the parts that make up the whole captures, in a sense, the essence of intelligent data description [12]. Due to the enhancement of semantic interpretability under non-negativity and the resulting sparsity that restrains the adverse effects of external changes to a certain extent, NMF has become a basic tool for multivariate data analysis and has been successfully applied to research in image engineering [13], pattern recognition [14], data mining [15], spectral data analysis [16], complex networks analysis [17] and other fields. However, the disadvantages of NMF are also significant. Non-negative constraints may help some models learn part-based representations, but this does not mean that only non-negative constraints are sufficient; NMF uses Euclidean distance as a measure of loss, resulting in sensitivity to noise or corrosion in the original data; the processing objects of NMF are essentially vectors, which makes encountering SSS problems inevitable [5].

Many NMF-based extension efforts have been developed to address these challenges. Generally, adding a regularization term based on the NMF framework, called constrained NMF, can bring about the effect of improving performance. Li et al. [18] presented a local learning NMF (LNMF) which, based on the NMF framework, defines an objective function to impose localization constraints for learning spatial localization. Immediately after, Hoyer et al. [19] proposed to combine the concept of sparseness to improve NMF and made relevant theoretical proofs and algorithm implementations. Wang et al. [20] imposed Fisher constraints on the NMF algorithm and proposed a fisher NMF (FNMF) to encode the discriminative information of classification problems. Since the above only considers the Euclidean space structure and related literature find that data generally have potential popular structures in high-dimensional data, NMF has a new direction for improvement. Cai et al. [21] proposed a graph regularization NMF (GNMF) that encodes geometric information by constructing an affinity graph. However, the way GNMF constructs graphs only considers the relationship between pairs of points, ignoring the higher-order relationship between multiple points. Zeng et al. [22] developed an improved GNMF, which introduced the concept of a hypergraph, called hypergraph regularization NMF (HNMF).

Soon, it was discovered that the original data contained many disturbances or corrosions, for which the NMF algorithm exhibited extremely unstable performance [23]. Hence, a robust NMF is on the agenda. Kong et al. [24] proposed an NMF model using the $L_{2,1}$ norm loss function to handle noise and outliers with its sparsity. Since the aforementioned algorithms [23,24] are based on local learning and global information is superior to local information in robustness, Lu et al. [25] consider an NMF extension that integrates global information and partial information. Different from sparse representation-based algorithms [26], low-rank representation (LRR) [27] aims to find the lowest rank representation of a vector set, which can capture global information well. There are many LRR-based extensions in the field of feature extraction and data transformation [28,29]. Inspired by LRR, they proposed a new low-rank nonnegative factorization (LRNF) method and used the L1 norm to sparsely constrain the assumed noise matrix. Further, to consider the label information of the samples, Lu et al. [30] introduced structural incoherence into LRNF and proposed a new algorithm called SILR-NMF. Li et al. [31] provided a unified framework of graph regularization non-negative low-rank matrix factorization (GNLMF) to improve the algorithm’s robustness to noise and popular structures. However, in its essence, it is only simple addition of low rank and GNMF and the two parts are not closely related. Recently, to learn a graph that can better represent the similar relationship between samples, Lu et al. [32] proposed a low-rank adaptive neighborhood graph embedding. He et al. [33] proposed low-rank NMF (LNMFS) based on the Stiefel manifold, using orthogonal constraints and graph smoothness to improve algorithm robustness.

Most of the algorithms mentioned above add various constraints to NMF, such as sparsity, low rank, graph embedding, linear discrimination, etc., while little is mentioned about how to improve NMF to improve its robustness to few-shot scenarios. These improve the algorithm’s performance, but NMF is carried out in the case of converting samples to column vectors, which inevitably faces the problem of SSS. In addition, we cannot ignore the graph structure of the sample and the global information, both of which can obtain distinct information from the original data and the combination of the two can achieve a win–win situation. The nearest neighbor-sensitive problem cannot be ignored when adding graph-related constraints to NMF to preserve geometric structure information. Since the above problems are more significant in dimensionality reduction algorithms such as LDA and LPP, and these algorithms have also been maturely developed  [34,35,36], the introduction of matrix exponential seems to bring unexpected benefits [37,38].

Inspired by the above, this paper combines low rank, graph embedding, matrix exponential and sparsity to propose a new robust NMF, called exponential graph regularization non-negative low-rank factorization (EGNLRF). Figure 1 performs the framework of the EGNLRF. Firstly, we incorporate low-rank into the NMF framework and use the $L_{2,1}$ norm to sparsely constrain the noise terms in the low-rank restoration. Secondly, we introduce graph embeddings using a regularization term to exploit local relations between samples as well as label information. To further improve the robustness of the algorithm in SSS scenarios, we perform matrix exponential processing on the graph embedding terms. Finally, we develop an alternating iterative algorithm to optimize the latent representation of denoised low-rank data.

The main contributions of this paper are as follows.

• The matrix exponent operation is carried out in the graph embedding items to expand the SSS scenarios’ application and increase the robustness of the algorithm. The attribute characteristic of the matrix index enables it to solve the matrix singularity problem.
• The nearest neighbor sensitivity caused by the introduction of graph structure can be alleviated because of the power series definition of the matrix exponent itself. Furthermore, the matrix index also provides more information for the algorithm, such as the potential hyper-order geometric structure among samples. The matrix index can spread the distance between samples and expand the margin between labels for classification.
• An exponential graph regularization non-negative low-rank decomposition algorithm is proposed, which incorporates graph regularization and low rank into the NMF framework for joint optimization. The algorithm integrates the global and local information of samples; not only can it learn latent representations that are not disturbed by noise but it can also maintain the local structure of known samples.
• The optimization process of the EGNLRF algorithm is derived in detail and its convergence is proved. Compared with other methods, the superiority of EGNLRF was verified by a simulation comparison experiment using the nearest neighbor classifier recognition rate as an evaluation index.

2. Related Work

NMF is one of the classical matrix factorization methods, which focuses on finding non-negative representations of factor matrices that approximate the original matrix.

Given an original data matrix $X=[x_1,x_2,\dots ,x_n]\in {\mathbb{R}}_{+}^{m\times n}$, composed of n sample data column vectors. NMF aims to find two non-negative matrix factors $U\in {\mathbb{R}}^{m\times k}$ and $V\in {\mathbb{R}}^{n\times k}$ that can approximate the original matrix X, which can be described as

$$X\approx U{V}^T$$

(1)

For the convenience of calculation, the square of the F-norm of the difference between the two matrices is generally used as the loss function to quantify the performance.

$$F_{loss}={\Vert X-U{V}^T\Vert }_F^2$$

(2)

In practical applications, NMF usually has $k\ll m$ and $k\ll n$ and the theory limits it to only an additive combination of basis vectors, so NMF essentially finds a partial-based latent low-dimensional representation of the original matrix. At present, this method has shown excellent performance in image engineering [13], pattern recognition [14] and other fields and has been widely used based on its simple and effective advantages.

Related research [39,40] shows that NMF algorithms can learn part-based representations, similar to how the brain perceives the world. In practical applications, to meet different needs, related scholars have studied the variants of NMF. This section will briefly introduce some representative NMF variant algorithms.

The geometric structure information of the samples is considered first. To reveal the hidden semantics, the GNMF algorithm that respects the local geometry between samples is proposed

$$\underset{U,V\ge 0}{min}{∥X-U{V}^T∥}_F^2+\lambda tr\left(V^{T}LV\right).$$

(3)

where $tr\left(V^{T}LV\right)$ is the graph regularization term and L is the Laplacian matrix. Similarly, Zeng et al. [22] also proposed an improved algorithm for NMF from a geometrical point of view. GNMF uses affinity graphs to encode geometric information, but simple graphs can only represent relationships between pairs of points, ignoring higher-order information between multiple points. Therefore, they introduce hypergraphs and propose HNMF

$$\underset{U,V\ge 0}{min}{∥X-U{V}^T∥}_F^2+\lambda tr\left(V^T{L}_{hyper}V\right).$$

(4)

where $L_{hyper}$ is the hyper-graph Laplacian matrix.

Furthermore, since the above algorithms are sensitive to noise and have low robustness, some robust NMF has gradually entered people’s field of vision. The global representation of data is more robust than the part-based representation, so Lu et al. [25] proposed an LRNF algorithm that can learn both part- and global-based.

$$\begin{array}{cc}\hfill & \underset{A,E,U,V}{min}{∥A-U{V}^T∥}_F^2+\alpha {∥A∥}_{*}+\beta {∥E∥}_1\hfill \\ \hfill & s.t.X=A+E,U,V\ge 0.\hfill \end{array}$$

(5)

where E is the noise matrix and A is the clean data matrix after denoising. Similar work was conducted by Li et al. [31], who proposed an NMF algorithm based on low-rank recovery. To further improve the robustness of the algorithm to popular geometric structures, the GNLMF algorithm is proposed.

$$\begin{array}{cc}\hfill \underset{A,E,U,V}{min}& {∥X-A-E∥}_F^2+\alpha tr\left(V^{T}LV\right)+\beta tr\left(U{U}^T\right)\hfill \\ \hfill s.t.& A=U{V}^T,A,U,V\ge 0\hfill \\ \hfill & rank\left(A\right)\le r,card\left(E\right)\le s\hfill \end{array}$$

(6)

where $tr\left(V^{T}LV\right)$ is the graph embedding regularization term and $tr\left(U{U}^T\right)$ is the Tikhonov regularization term of U. GNLMF only incorporates the graph embedding into the objective function, while the low-rank restoration is only a constraint of the objective function. In essence, GNLMF is a simple combination of low-rank recovery and GNMF, without joint optimization of the objective function.

It is undeniable that the above methods all improve NMF from different angles. However, they either do not consider geometric information or do not take into account the noise sensitivity. GNLMF takes all of these into account, but only in simple combinations and is incapable of dealing with the problem of SSS. In addition, a series of problems brought about by the introduction of graph embeddings [38,41], such as nearest neighbor sensitivity and matrix singularity, have not been taken seriously. In response to these issues, we propose an exponential graph regularization non-negative low-rank factorization algorithm combining sparseness, low rank and matrix exponential.

3. Exponential Graph Regularized Non-Negative Low-Rank Factorization

In this section, we first introduce the composition process of the objective function of EGNLRF. Then, the optimization algorithm of the function and the solution process are given. Finally, we analyze the time complexity and convergence of the algorithm.

3.1. Formulations and Problem Setting

In the real world, the original image information is often more or less corroded by noise, illumination or occlusion, etc. Hence, a related robust NMF algorithm is proposed. To improve the robustness of the algorithm, GNMF, LRNF and GNLMF combine different algorithm methods to explore the improvement and performance optimization of NMF from different angles. GNMF combines graph embedding and NMF to consider the local relationship between training data; LRNF introduces noise terms and low rank into NMF, which mainly focuses on global information. GNLMF synthesizes global information and local relations, but it simply combines low-rank and graph regularization NMF without joint optimization on the objective function.

Given an original data matrix $X=[x_1,x_2,\dots ,x_n]\in {\mathbb{R}}_{+}^{m\times n}$, NMF decomposes it into two non-negative factor matrices. Related research has proved that the extended regularization term in NMF can improve the robustness of NMF. Therefore, inspired by the above algorithms, we combine sparse, low-rank and graph embeddings to obtain NMF variants as shown below

$$\begin{array}{cc}\hfill & \underset{A,E,U,V}{min}{∥A-U{V}^T∥}_F^2+\alpha rank\left(A\right)+\beta card\left(E\right)\hfill \\ \hfill & +\lambda tr\left(V^{T}LV\right)\hfill \\ \hfill & s.t.X=A+E,U,V\ge 0.\hfill \end{array}$$

(7)

It is assumed that the noise is sparse, which means that the sparseness of the noise term is a key factor affecting the performance of the algorithm. Therefore, the noise matrix E is sparsely constrained using the $L_{2,1}$ norm. In addition, since Equation (7) belongs to the NP problem, this paper uses a convex optimization problem to replace it

$$\begin{array}{cc}\hfill & \underset{A,E,U,V}{min}{∥A-U{V}^T∥}_F^2+\alpha {∥A∥}_{*}+\beta {∥E∥}_{2,1}\hfill \\ \hfill & +\lambda tr\left(V^{T}LV\right)\hfill \\ \hfill & s.t.X=A+E,U,V\ge 0.\hfill \end{array}$$

(8)

The above three algorithms all have their problems when finding low-rank latent representations. The LRNF algorithm does not consider the information from the original training samples. When experiments are performed on the same dataset, the latent representation obtained with LRNF does not change under the division of different training sets and test sets. This can be improved by introducing graph embeddings. GNMF and GNLMF algorithms introduce graph embedding to extract local information of samples, but the SSS problem, nearest neighbor sensitivity and matrix singularity brought by the introduction of graph embedding have not been solved. In addition, graph embedding only considers the relationship between pairs of points, ignoring the higher-order information between multiple points. Therefore, we introduce exponential matrices into graph embeddings to address these challenges.

3.2. Matrix Exponential

As a theory widely used in ordinary differential equations, Markov chain analysis and other fields, the exponential matrix also occupies an important seat in pattern recognition’s image matrix correlation algorithm. This section will briefly introduce the definition and properties of exponential matrices that are closely related to this paper. Given a square matrix H of order n, ts exponential form is expanded as follows:

$$\begin{array}{c}\hfill exp\left(H\right)=I+H+\frac{H_2}{2!}+\cdots +\frac{H_m}{m!}+\cdots \end{array}$$

(9)

where I is the identity matrix of order n. According to Equation (9), we can obtain some properties of the matrix exponential function.

• Firstly, if matrix H has eigenvectors $v_1,v_2,\dots ,v_n$ corresponding to the eigenvalues ${\lambda }_1,{\lambda }_2,\dots ,{\lambda }_n$, then $exp\left(H\right)$ has the same eigenvectors $v_1,v_2,\dots ,v_n$ corresponding to the eigenvalues $e^{{\lambda }_1},e^{{\lambda }_2},\dots ,e^{{\lambda }_n}$. This means that $exp\left(V^{T}LV\right)$ can preserve and enhance the pivotal information of the graph, which is the key to matrix $V^{T}LV$ being replaced by $exp\left(V^{T}LV\right)$.
• Secondly, $exp\left(H\right)$ is a finite full-rank matrix. The matrix singularity problem will be solved easily after introducing the matrix exponential function.
• Finally, if D is a nonsingular matrix, we have

  $$exp\left(D^{-1}HD\right)=D^{-1}exp\left(H\right)D.$$
  Since symmetric matrices are diagonalizable, the Laplacian matrix exponent optimizes the operation by this property.

Furthermore, the power series definition of matrix exponents strongly suggests that $exp\left(V^{T}LV\right)$ can improve small-shot problems and nearest-neighbor-sensitive problems and obtain hidden higher-order graph structure information. Hence, after introducing the matrix index, the objective function can be obtained as follows:

$$\begin{array}{cc}\hfill & \underset{A,E,U,V}{min}{∥A-U{V}^T∥}_F^2+\alpha {∥A∥}_{*}+\beta {∥E∥}_{2,1}\hfill \\ \hfill & +\lambda tr\left(exp\left(V^{T}LV\right)\right)\hfill \\ \hfill & s.t.X=A+E,U\ge 0,V\ge 0.\hfill \end{array}$$

(10)

The model synthesizes the global and local information of the samples, along with low-rank constraints, noise sparsity and exponential Laplacian matrices. The clean data matrix A, noise matrix E and NMF factor matrices U, V are obtained with Equation (10) and we use $U^{T}A$ or $V^T$ as the underlying representation for all instances as appropriate. The resulting latent representation will be used as the EGNLRF classification result for standard classification.

3.3. Optimization and Solution

There are four variables in Equation (10), which is not a joint convex optimization problem and cannot be solved directly. This paper considers using the alternating direction method of multipliers (ADMM) [42] or the augmented Lagrange multipliers (ALM) [43] to solve the multivariable optimization non-convex matter in Equation (10). To solve the nuclear norm problem, we first convert Equation (10) into an equivalent problem as follows:

$$\begin{array}{cc}\hfill & \underset{A,E,U,V}{min}{∥A-U{V}^T∥}_F^2+\alpha {∥J∥}_{*}+\beta {∥E∥}_{2,1}\hfill \\ \hfill & +\lambda tr\left(exp\left(V^{T}LV\right)\right)\hfill \\ \hfill & s.t.X=A+E,A=J,U,V\ge 0.\hfill \end{array}$$

(11)

which can be disposed of with the ALM function as shown below.

$$\begin{array}{c}\hfill \mathcal{L}(A,J,E,U,V,Y_1,Y_2,\mu )\\ \hfill =& {∥A-U{V}^T∥}_F^2+\alpha {∥J∥}_{*}+\beta {∥E∥}_{2,1}\hfill \\ \hfill & +\lambda tr\left(exp\left(V^{T}LV\right)\right)+\frac{\mu }{2}{∥X-A-E+\frac{Y_1}{\mu }∥}_F^2\hfill \\ \hfill & +\frac{\mu }{2}{∥A-J+\frac{Y_2}{\mu }∥}_F^2-\frac{1}{2\mu }({∥Y_1∥}_F^2+{∥Y_2∥}_F^2).\hfill \end{array}$$

(12)

It can be observed that the ALM function is convex on any one variable when the rest of the variables are fixed in Equation (12). Therefore, the optimization problem can be solved by alternating iterative updates. Next, each variable’s solution details and updated formulation are given separately.

3.3.1. Update A, with Remaining Variables Fixed

When the remaining variables are fixed to compute A, the objective function is

$$\begin{array}{cc}\hfill \underset{A}{min}& {∥A-U{V}^T∥}_F^2+\frac{\mu }{2}{∥A-X+E-\frac{Y_1}{\mu }∥}_F^2\hfill \\ \hfill & +\frac{\mu }{2}{∥A-J+\frac{Y_2}{\mu }∥}_F^2.\hfill \end{array}$$

(13)

Using the Lagrangian method to find the local optimal solution, we can obtain

$$A=\frac{2U{V}^T+\mu \left(X-E+J+\frac{Y_1}{\mu }-\frac{Y_2}{\mu }\right)}{2+2\mu }$$

(14)

3.3.2. Update J, with Remaining Variables Fixed

It can be observed that when the remaining variables are fixed, the problem is transformed into a convex relaxation of the rank minimization problem and Equation (15) can be obtained.

$$\underset{J}{min}\frac{\alpha }{\mu }{∥J∥}_{*}+\frac{1}{2}{∥J-\left(A+\frac{Y_2}{\mu }\right)∥}_F^2.$$

(15)

Aiming at this kind of problem, Cai et al. [44] proposed a singular value thresholding algorithm and proved its effectiveness and convergence. Therefore, J can be iterated through the following steps.

First, we give $Q_1=A+\frac{Y_2}{\mu }$ and then perform a singular value decomposition operation on $Q_1$.

$$Q_1=U_{svd}\Sigma V_{svd}^{*},\Sigma =diag\left({\left\{{\sigma }_i\right\}}_{1\le i\le r}\right).$$

(16)

Then, for $\forall \tau >0$, the soft threshold operator ${\mathcal{D}}_{\tau }$ has the following definition

$${\mathcal{D}}_{\tau }\left(\Sigma \right):=diag\left({\left\{{\sigma }_i-\tau \right\}}_{+}\right).$$

(17)

Thus, the iterative update rule for J is given by Equation (18).

$$J=U_{svd}{\mathcal{D}}_{\frac{\alpha }{\mu }}\left(\Sigma \right)V_{svd}^{*},$$

(18)

3.3.3. Update E, with Remaining Variables Fixed

After fixing the rest of the variables except E, we obtain the following function

$$\underset{E}{min}\frac{\beta }{\mu }{∥E∥}_{2,1}+\frac{1}{2}{∥X-A-E+\frac{Y_1}{\mu }∥}_F^2.$$

(19)

For convex problems such as Equation (19), relevant scholars [27] have proved the existence of closed solutions. If E is the optimal solution of Equation (19), then each column of E is calculated as

$$E(:,i)=\left\{\begin{array}{cc}\frac{∥q_i∥-\lambda }{∥q_i∥}{q}_i,\hfill & \mathrm{if}\frac{\beta }{\mu }<∥q_i∥,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(20)

where $Q_2=[q_1,q_2,\dots ,q_i,\dots ]=X-A+\frac{Y_1}{\mu }$.

3.3.4. Update U, with Remaining Variables Fixed

Fixing the remaining variables to solve U, we can obtain the following function

$$\underset{U}{min}{∥A-U{V}^T∥}_F^2,$$

(21)

which is similar to the objective function of NMF. Therefore, we can directly obtain the update rule of U:

$$u_{ik}\leftarrow u_{ik}\frac{{\left(XV\right)}_{ik}}{{\left(U{V}^{T}V\right)}_{ik}}.$$

(22)

3.3.5. Update V, with Remaining Variables Fixed

When the remaining variables are fixed to solve V, the objective function is

$$\underset{V}{min}{∥A-U{V}^T∥}_F^2+\lambda tr\left(exp\left(V^{T}LV\right)\right).$$

(23)

This formula is different from Equation (21), but it is still a convex function, which can be solved by a simple calculation.

Let $\varphi$ be the Lagrange multiplier; the function can be obtained as

$$\begin{array}{cc}\hfill \mathcal{L}\left(V\right)=& tr\left(A{A}^T\right)-2trtr\left(AV{U}^T\right)+tr\left(U{V}^{T}V{U}^T\right)\hfill \\ \hfill & +\lambda tr\left(exp\left(V^{T}LV\right)\right)+tr\left(\varphi V^T\right).\hfill \end{array}$$

(24)

Taking the partial derivative concerning $\mathcal{L}\left(V\right)$ and using the KKT condition, it can be obtained that

$${\left(V{U}^{T}U\right)}_{jk}{v}_{jk}+\lambda {\left(LVexp\left(V^{T}LV\right)\right)}_{jk}{v}_{jk}={\left(X^{T}V\right)}_{jk}{v}_{jk}.$$

(25)

This results in the following update rule:

$$v_{jk}\leftarrow v_{jk}\frac{{\left(X^{T}V+WVexp\left(V^{T}LV\right)\right)}_{jk}}{{\left(V{U}^{T}U+\lambda DVexp\left(V^{T}LV\right)\right)}_{jk}}.$$

(26)

For the uncertainty of the solution of the NMF objective function, the constraint that the Euclidean length of each column vector in the matrix U (or V) is 1 is generally added in practice. We add that restriction to U, which can be achieved in the following ways:

$$u_{ik}\leftarrow \frac{u_{ik}}{\sqrt{{\sum }_i{u}_{ik}^2}},v_{jk}\leftarrow v_{jk}\sqrt{\sum _i{u}_{ik}^2}$$

(27)

Algorithm 1 summarizes the iterative process of the EGNLRF algorithm. Among them, U and V are initialized by random matrixes.

Algorithm 1 EGNLRF

Require:  Data matrix X, parameter $\alpha ,\beta ,\lambda$ in objective function and the maximum number of iterations $ma{x}_t$; Initialize:  U, V, $E=0$, $J=0$, $Y_1=Y_2=0$, $\mu >0$, $\rho >0$ and $t=1$; 1: repeat 2:     Update A by Equation (14); 3:     Update J by Equation (18); 4:     Update E by Equation (20); 5:     Update U by Equation (22); 6:     Update V by Equation (26); 7:     Update Lagrange multipliers as follows:             $Y_1\leftarrow Y_1+\mu (X-A-E)$;             $Y_2\leftarrow Y_2+\mu (A-J)$; 8:     $\mu$←$min(\rho \mu ,max\mu )$; 9:     t←$t+1$; 10: until $t>ma{x}_t$ or Convergence 11: Normalize each column of U, keeping $U{V}^T$ unchanged 12: Return the optional solution $(A,J,E,U,V)$

3.4. Convergence and Computational Complexity

Problem (11) is a non-convex function on all variables, which is a typical NP-hard problem, so we consider iterative optimization to approximate it. Hence, the corresponding convergence requirements are relaxed appropriately, which requires that the value of the objective function does not increase during the iterations. When the input data is non-negative, it can be known that the objective function in Equation (11) is non-negative and has a lower bound. In the five steps of the iterative algorithm, the ADMM is used to decrease the value of the objective function. Steps 3 and 4 have been proven to have closed solutions [27,44], which are decreasing and convergent. The convergence proof of step 2 is similar to the study by Lu et al. [25], while the convergence of steps 5 and 6 is proved by Cai et al. [21]. To more intuitively reflect the convergence of the proposed algorithm, we verified it on different datasets, as shown in Figure 2. We can observe that the polyline of FERET in Figure 2 has an upward perturbation at the beginning of the iteration. Our zero-initialization of matrices J and E, which are values that J and E do not end up with, creates a situation where the objective function value is abnormally small in the first few iterations.

In addition, the time complexity of the algorithm is also worth paying attention to. In Algorithm 1, the time complexity of step 2 is $O\left(m{n}^2\right)$. The time cost of step 3 is $O\left(n^3\right)$, which has an SVD operation. The computational complexity of step 4 is $O\left(mn\right)$ and the time complexity of steps 5 and 6 is $O(n^{2}k+k^3+mnk)$ which is only a simple matrix multiplication operation in these steps. In general, there are some explicit $m>>k,n>>k$ in the data transformation. Therefore, the overall time complexity of the algorithm is $O\left(t(m{n}^2+n^3)\right)$, where t is the number of iterations.

3.5. Discussion of Other Optimizations

The ADMM optimization method described above is only the most common method for solving non-convex problems at present, which is applied in many fields. The alternating nonnegative least squares (ANLS) algorithm is also an effective way to solve the non-convex problem of NMF. Many scholars have made innovations and developments in the ANLS framework, such as the projected gradient method, active-set-like method, hierarchical alternating least squares, etc. However, the key difference from ADMM is that there is no constraint between the variables that are solved alternately in ANLS. For the application of the objective function with additional constraints in the ANLS framework, the easiest way is to convert the constraints into corresponding regularization terms and add them to the objective function. The ADMM optimization method described above is only the most common method for solving non-convex problems at present, which is applied in many fields. The alternating nonnegative least squares (ANLS) framework [45,46,47] is also an effective way to solve the non-convex problem of NMF. Many scholars have made innovations and developments in the ANLS framework, such as the projected gradient method [45], active-set-like method [46], hierarchical alternating least squares [47], etc. However, the key difference from ADMM is that there is no constraint between the variables that are solved alternately in ANLS. For the application of the objective function with additional constraints in the ANLS framework, the easiest way is to convert the constraints into corresponding regularization terms and add them to the objective function.

4. Experiments and Evaluations

In this section, we use real-world datasets to verify the performance of the proposed algorithm. Furthermore, experiments include tests of different degrees of corrosion such as noise, occlusion, etc.

4.1. Real World Data Sets

We evaluate EGNLRF on four public datasets: object recognition (COIL20 [48]), palmprint recognition (PolyU palmprint database [49]) and face recognition (AR [50] and FERET [51]). Some of the original images for these four datasets are shown in Figure 3. It can be observed that AR is a dataset with natural occlusion. To verify the robustness of the algorithm, we add different erosions to the dataset for testing.

• COIL Data Set [48]: The COIL20 database contains 20 objects, each with 72 gray images taken from different viewpoints.
• AR Data Set [50]: The AR database contains more than 4000 facial images of 126 people, including frontal views with different facial expressions, lighting conditions and occlusions. The pictures are collected in two sessions two weeks apart and 120 individuals participated in both sessions.
• FERET Data Set [51]: The FERET database contains 200 people, each with seven photos with different lighting conditions.
• PolyU palmprint Data Set [49]: The PolyU palmprint database contains six palmprint photos of 100 people in varying shades of light.

4.2. Baseline Algorithms

The following are the selected benchmark algorithms for comparison with EGNLRF.

• NMF [11]: NMF is a classical matrix factorization algorithm that achieves nonlinear dimensionality reduction through non-negative constraints.
• ELPP [38]: ELPP is an improved algorithm of LPP to avoid matrix singularity.
• GNMF [21]: GNMF takes into account the local structure between samples by combining affinity graph encoding and NMF.
• LRNF [25]: LRNF enables the learning of partial and global latent representations by incorporating low-rank into the NMF framework.
• LNMFS [33]: LNMFS algorithm based on the Stiefel manifold is proposed, which considers orthogonal constraints and image smoothness.
• LRAGE [32]: LRAGE is an unsupervised feature extraction method using adaptive probabilistic neighborhood graph embedding and low-rank constraints.

Table 1. Objective functions and algorithm time complexity of seven algorithms.

Algorithm	Objective Function	Time Complexity *
NMF	${\Vert X-U{V}^T\Vert }_F^2$	$O\left(tmnk\right)$
ELPP	$P^{T}exp\left(X^{T}LX\right)P$ **	$O(m^{2}n+m{n}^2+n^3)$
LRNF	${∥A-U{V}^T∥}_F^2+\alpha {∥A∥}_{*}+\beta {∥E∥}_1$	$O\left(t(m^3+m{n}^2)\right)$
GNMF	${∥X-U{V}^T∥}_F^2+\lambda tr\left(V^{T}LV\right)$	$O(tmnk+m{n}^2)$
LNMFS	${∥X-U{V}^T∥}_F^2+\alpha {∥V∥}_F^2+\beta tr\left(V^{T}LV\right)$	$O\left(t(mnk+n^{2}k)\right)$
LRAGE	${\sum }_{i,j}{∥X_i^T-X_j^{T}PR∥}_2^2{W}_{ij}+\alpha {∥W∥}_F^2+\beta {∥PR∥}_{2,1}$ ***	$O\left(t(m^{2}n+m{n}^2+m^3)\right)$
EGNLRF	${∥A-U{V}^T∥}_F^2+\alpha {∥A∥}_{*}+\beta {∥E∥}_{2,1}+\lambda tr\left(exp\left(V^{T}LV\right)\right)$	$O\left(t(m{n}^2+n^3)\right)$

* m >> k, n >> k. ** P is a mapping transformation matrix of size m × k. *** R is a regression matrix of size k × m and W is the graph affinity matrix of size n × n.

presents the objective functions and algorithm time complexity of these baseline algorithms. It is clearly observed that NMF has the lowest time complexity and the simplest objective function. The remaining algorithms either add various constraints or introduce special operations, resulting in more or less an increase in algorithm complexity. Among them, the time requirements of GNMF are always relatively small, while the time requirements of other algorithms will produce different sorting according to different m and n. In the SSS scenario, which is in the case of $m>n$ or $m>>n$, ELPP, LRNF and LRAGE will have a high time cost. Since V is used for graph embedding and exponentiating, EGNLRF keeps the time cost at a moderate level.

4.3. Experimental Setup

Before reporting detailed experimental results, how to tune the hyperparameters of the algorithm must be explained. In the above comparison algorithms, GNMF, LNMFS and LRAGE have one parameter while LRNF has two parameters. We select the values of these parameters from $\{{10}^{-3},{10}^{-2},{10}^{-1},1,10,{10}^2,{10}^3\}$ by referring to the article proposing these algorithms. In EGNLRF, this paper selects the three parameters $\alpha$, $\beta$ and $\lambda$ from $\{{10}^{-4},{10}^{-3},{10}^{-2},{10}^{-1},1,10,{10}^2,{10}^3,{10}^4\}$ through cross-validation. In the experiment, the nearest neighbor classification is used to calculate the recognition rate of the samples in the test set. Figure 4 shows the recognition rate on the COIL20 data set as a function of one parameter while the rest of the parameters are fixed. When conducting experiments in different databases, p samples will be randomly selected as training samples according to the size of the database and the rest constitute the test set. Among them, $p=2,3,4$ in PolyU palmprint database and $p=9,12,15$ in AR database. In FERET and COIL20 database, $p=2,3,4,5$ and $p=20,30,40,50$, respectively. In specific experiments, the initialization of several algorithms will randomly generate U and V matrices. Hence, we uniformly initialize U and V matrices and input them into the algorithm as a fixed parameter to control variables.

4.4. Experimental Results

In this subsection, the EGNLRF algorithm will be tested on FERET, AR, COIL20 and PolyU palmprint, which cover diversified fields, such as face recognition, object recognition and palmprint recognition.

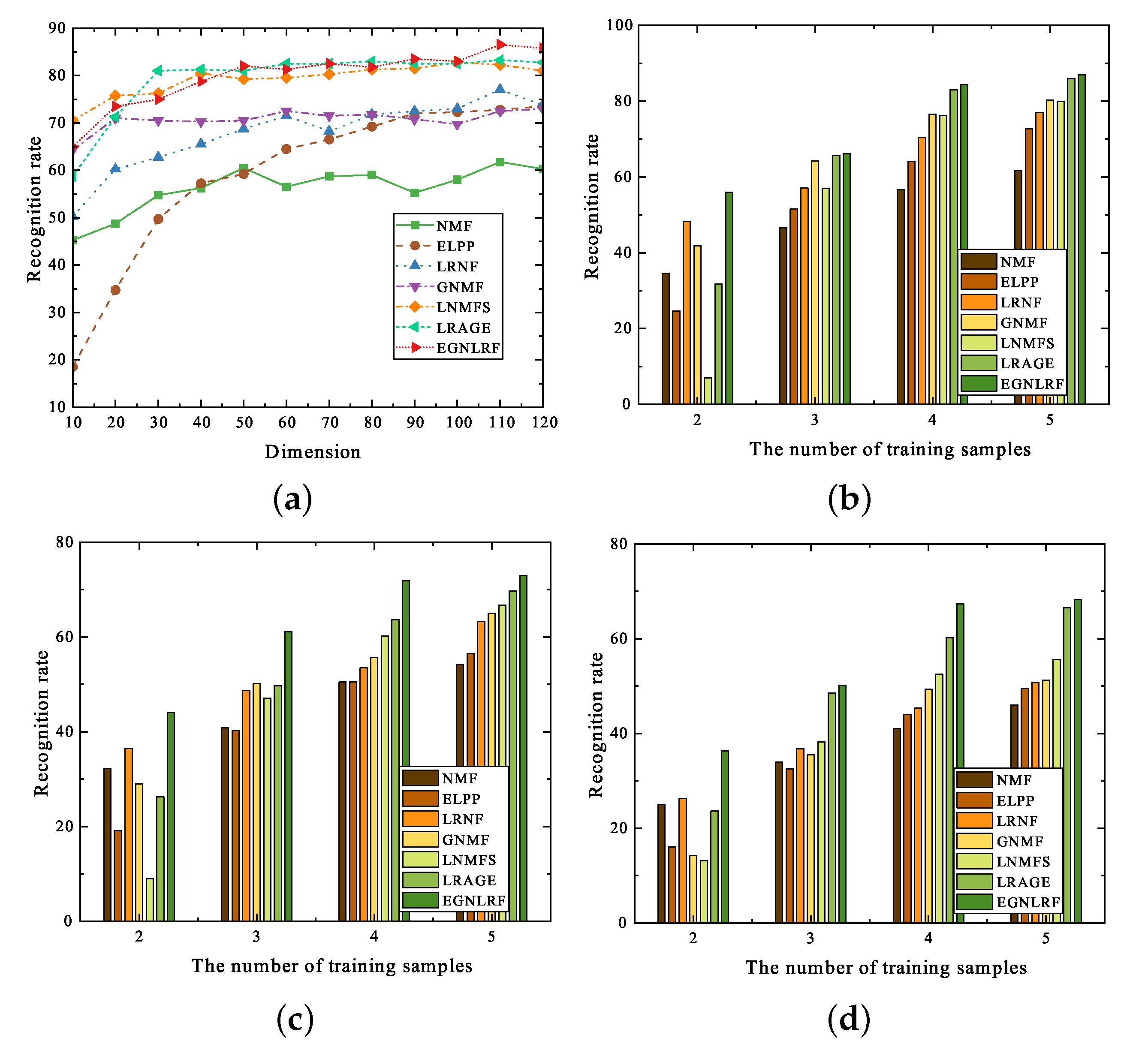
First, we conduct experiments on the FERET database. Face recognition does not require very high accuracy in the image, but it is usually corrupted by a variety of noise. The FERET database is a typical database used to verify whether the algorithm is robust to different lighting and camera angles. Furthermore, we added Gaussian noise of different densities to the images of the FERET database for experiments. Figure 5 shows part of the image of FERET with noise and the experimental results are shown in Figure 6. It can be observed that the image recognition rates of LNMFS, LRAGE and EGNLRF algorithms are at a superior level under different dimensionality reductions. As for the three figures with the number of training samples on the horizontal coordinate, the EGNLRF algorithm always has an advantage over the comparison algorithm, which is more obvious when the number of training samples is low or the image contains noise. Another common corrosion of images is occlusion.

In addition, the setting of the nearest neighbor parameter is a key point worth noting, so we give the algorithms with different nearest neighbor parameters for comparison. The nearest neighbor was evaluated from 2 to 10 on the FERET database and a boxplot is drawn using the result, as shown in Figure 7.

Considering more realistic scenarios, we choose to conduct experiments on face database AR containing natural occlusions, such as scarves and sunglasses, rather than adding occlusions randomly. Figure 5 shows part of the image of AR with noise. It can be observed in

Table 2. Recognition accuracy (%) of different algorithms on the AR dataset and with different dimensions.

Dimension	10	20	30	40	50	60	70	80	90	100	110	120
NMF	36.02	39.26	45.37	46.30	46.85	50.09	53.24	56.11	58.98	57.04	57.31	58.98
ELPP	15.83	29.47	37.73	45.91	49.92	51.59	53.33	54.32	56.36	57.88	57.73	59.62
LRNF	36.30	51.02	56.94	63.52	63.70	67.13	68.61	71.48	74.54	71.39	73.98	72.59
GNMF	59.17	68.06	69.44	71.48	72.22	72.59	73.89	72.87	73.80	72.04	74.81	72.41
LNMFS	61.67	67.22	70.28	71.30	70.74	71.11	73.70	72.96	73.06	72.59	74.54	73.89
LRAGE	44.26	58.80	63.43	66.57	68.89	71.67	71.57	72.69	75.00	75.74	75.93	75.74
EGNLRF	65.00	69.07	71.48	74.44	75.37	77.04	77.41	78.70	80.00	80.19	81.02	82.04

and

Table 3. Recognition accuracy (%) of different algorithms on the AR dataset and with different density noisy.

Algrithms	Raw Database			Gaussion Noisy (Density = 0.1)			Gaussion Noisy (Density = 0.5)
	9	12	15	9	12	15	9	12	15
NMF	47.70	52.74	63.71	40.29	46.79	55.15	33.15	38.64	45.64
ELPP	46.23	57.02	64.55	34.41	39.88	45.83	42.16	47.62	54.17
LRNF	58.87	60.60	75.90	59.17	61.31	74.09	48.43	57.44	64.62
GNMF	62.60	69.17	74.85	56.96	67.20	72.48	35.05	54.52	67.65
LNMFS	53.24	72.38	79.09	46.67	66.55	76.29	35.98	59.82	69.47
LRAGE	61.67	68.10	75.61	57.89	65.89	71.97	57.94	62.62	69.70
EGNLRF	69.61	76.85	87.88	67.35	74.94	86.36	54.71	68.15	76.21

that the performance of the proposed algorithm is superior in the face database with natural occlusion, which demonstrates that the EGNLRF algorithm is robust to occlusion corrosion. And we can obviously obtain that algorithms with low-rank constraints will outperform other algorithms without it in the performance of the AR database. The low-rank recovery framework can better deal with occlusion corrosion because the low-rank constraint can restore the occluded part to a certain extent.

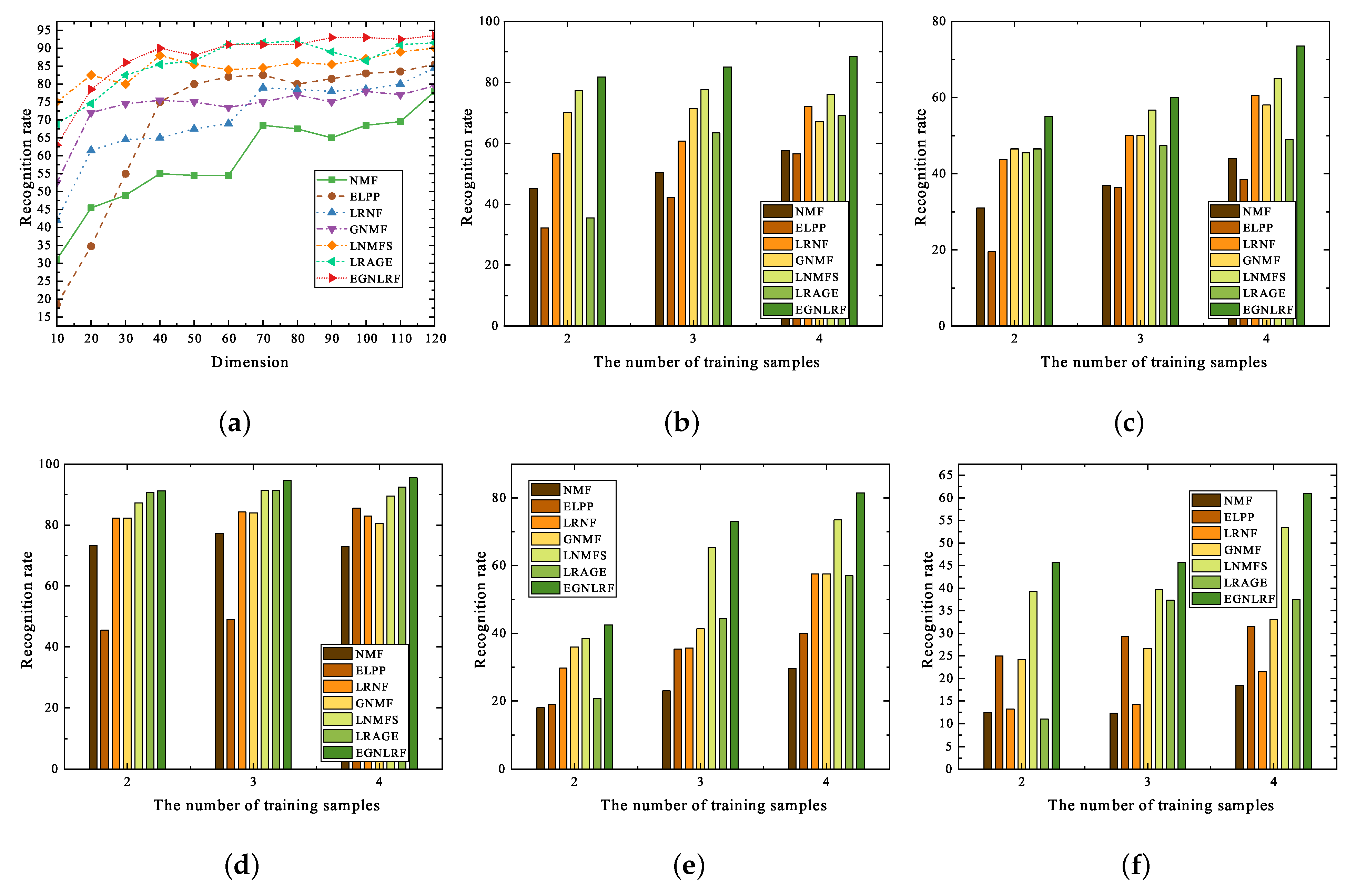
Furthermore, to verify the algorithm’s effectiveness in data conversion, we also conducted comparative experiments on the COIL20 object and PolyU palmprint databases. Inevitably, we add noise corrosion or occlusion corrosion to the original database to verify the robustness of the algorithm, concerning which Figure 8 and Figure 9 show some images. The results of all the experiments on COIL20 and PolyU palmprint are shown in Figure 10 and Figure 11. We can find that EGNLRF is always in the dominant position in the original database, whether it changes with the dimension or with the number of training samples. It is undeniable that the algorithms LRNF, GNMF, LNMFS and LRAGE all show good anti-corrosion ability in COIL20 in (b) and (c) of Figure 10, while the performance of NMF and ELPP algorithms fluctuates sharply with the addition of noise or occlusion. However, the anti-jamming ability of the proposed algorithm is better than that of the contrast algorithms, which is theoretically due to the synthesis of a variety of regular term constraints. It is also reflected in (e) and (f) of Figure 10 and the gap in recognition rate will increase with the increase of interference. In the experiment of the palmprint database, because the palmprint itself has high similarity, it is more sensitive to noise and the requirements for data conversion are the most stringent in these databases. Hence, the corrosion parameter setting of the robustness experiment becomes smaller accordingly. It is easy to observe that the performance of most comparison algorithms changes dramatically with the addition of corrosion in Figure 11. LNMFS can avoid the significant degradation of its performance, while the proposed algorithm is better. By comparing all the subgraphs in Figure 11, it can be found that if there is only a piece of single geometric structure in a low-rank recovery structure or non-negative matrix decomposition structure in the algorithm, it can only deal with less noise corrosion and occlusion corrosion. Only by merging these three into a joint framework can we deal with more serious corrosion, such as (e) and (f) in Figure 11.

4.5. Observations and Discussions

Generally speaking, by observing and comparing Figure 6, Figure 7, Figure 10 and Figure 11 and Table 2 and Table 3 above, we can draw the following summaries.

In most cases, LNMFS and LRAGE perform better than earlier algorithms because they employ more considerations or improvements concerning data conversion than before. Most of these algorithms share the same theoretical basis, such as NMF, graph embedding and low rank. The addition of these regularization terms will improve the performance of the algorithm.

Joint optimization with multiple constraints has higher classification accuracy than single constraints such as NMF and ELPP. The part-based information of the image and the geometric structure information of the image are both important parts of the image. This implies that the combination of multiple constraints that can obtain different distinct image information can obtain a highly robust and efficient data conversion algorithm.

LNMFS incorporates a variety of constraints into the objective function, but it is still not as superior as the proposed algorithm. This is because the algorithm that proposes the indexed graph regularization can alleviate the SSS problems and improve the nearest neighbor-sensitive problem. In addition, the exponential graph regularization term can also improve the hidden high-order geometric structure information for the algorithm, which is determined by the definition of its power series.

5. Conclusions

The robustness of data transformation or feature representation is not strong and the matrix singularity problem in SSS scenarios is always a research bottleneck. To solve these problems, this paper considers a low-rank recovery graph embedded NMF framework and introduces matrix exponential to alleviate the SSS problems and nearest neighbor sensitivity and obtain more high-order geometric structure information. Simulation experiments show that the proposed algorithm has absolute advantages over the comparison algorithm in most cases of the four databases, which is especially obvious when the images are subjected to various corrosions. For future work, we expect to design a more concise federation framework to realize automatic and efficient data transformation, which can simplify self-service parameter tuning.