Thin Right Triangle Convexity

Abstract

Let $\mathcal{F}$ be a family of sets in ${\mathbb{R}}^d$ (always $d\ge 2$). A set $M\subset {\mathbb{R}}^d$ is called $\mathcal{F}$-convex, if for any pair of distinct points $x,y\in M$, there is a set $F\in \mathcal{F}$, such that $x,y\in F$ and $F\subset M$. A thin right triangle is the boundary of a non-degenerate right triangle in ${\mathbb{R}}^2$. The aim of this paper is to introduce and begin investigating the thin right triangle convexity for short trt-convexity, which is obtained when $\mathcal{F}$ is the family of all thin right triangles. We investigate the $trt$-convexity of unbounded sets, convex surfaces and planar geometric graphs.

1. Introduction

Let $\mathcal{F}$ be a family of sets in a space ${\mathbb{R}}^d(d\ge 2$). A set $M\subset {\mathbb{R}}^d$ is called $\mathcal{F}$-convex if for any pair of distinct points $x,y\in M$, there is a set $F\in \mathcal{F}$ such that $x,y\in F$ and $F\subset M$.

The investigation of this very general kind of convexity was proposed in 1974 at a meeting on convexity in Oberwolfach by the third author.

Usual convexity, affine linearity, arc-wise connectedness and polygonal connectedness are examples of $\mathcal{F}$-convexity (for suitably chosen families $\mathcal{F}$).

Blind, Valette and the third author [1], and Böröczky Jr. [2] investigated the rectangular convexity, the case when $\mathcal{F}$ contains all non-degenerate rectangles. The last two authors [5] presented a discretization of rectangular convexity, the right quadruple convexity (for short, $rq$-convexity), where $\mathcal{F}$ is the family of all rectangular quadruples, which are vertex sets of rectangles. They are also currently studying another generalization, the thin rectangular convexity, by taking all thin rectangles (boundaries of rectangles) as $\mathcal{F}$.

It became clear that these generalizations revealed many interesting families of sets, leading far beyond the horizon of convexity.

In [6], the third author studied right convexity, the case when $\mathcal{F}$ consists of all right triangles, and the last two authors [4] investigated the right triple convexity for short rt-convexity, where $\mathcal{F}$ contains all triples $\{x,y,z\}\subset {\mathbb{R}}^d$ with $\angle xyz=\pi /2$.

Wang and the last two authors [3], generalizing in another way, investigated the poidge-convexity (the case with $\mathcal{F}$ consisting of all unions $\left\{x\right\}\cup \sigma$, called poidges, where x is a point, $\sigma$ a line segment, and $\mathrm{conv}\left(\right\{x\}\cup \sigma )$ a right triangle).

A thin right triangle is the boundary of a non-degenerate right triangle in ${\mathbb{R}}^2$. The aim of this paper is to introduce and begin investigating the thin right triangle convexity for short trt-convexity, which is obtained when $\mathcal{F}$ is the family of all thin right triangles.

Two points in M are said to enjoy the trt-property in M, if they belong to some thin right triangle included in M. Thus, M is trt-convex if any pair of its points enjoy the trt-property. Obviously, $trt$-convexity implies $rt$-convexity.

For convex sets, right convexity, $rt$-convexity, poidge-convexity and trt-convexity are equivalent. Not every poidge-convex set is trt-convex, not even $rt$-convex, but every rightly convex set is $rt$-convexity, poidge-convex and trt-convexity.

In order to obtain results describing $trt$-convex sets different from those provided by the initial study of right convexity, we must focus on sets which are essentially non-convex.

2. Definitions and Notation

For $M\subset {\mathbb{R}}^d$, we denote by $\complement M$ its complement, by $\overline{M}=\mathrm{aff}M$ its affine hull and by $\mathrm{conv}M$ its convex hull; further, $\mathrm{int}M$, $\mathrm{cl}M$ and $\mathrm{bd}M$ denote its topological interior, closure and boundary, respectively, considered in $\mathrm{aff}M$.

For distinct $x,y\in {\mathbb{R}}^d$, let $\overline{xy}$ be the line through $x,y$, $xy$ the line segment from x to y, and $H_{xy}$ the hyperplane through x orthogonal to $\overline{xy}$. If L, $L^{\prime }$ are affine subspaces of ${\mathbb{R}}^d$, $L\Vert L^{\prime }$ means that they are parallel and $L\perp L^{\prime }$ that they are orthogonal. In addition, ${\pi }_L\left(x\right)$ denotes the orthogonal projection of x onto L.

For any compact set $C\subset {\mathbb{R}}^d$, let $S_C$ be the smallest hypersphere containing C in its convex hull.

Let M be a closed convex set in ${\mathbb{R}}^d$ ($d\ge 2$). A point x in M is called an extreme point of M if there exists no non-degenerate line segment in M that contains x in its relative interior. The set of extreme points of M is denoted by $\mathrm{ext}M$.

A convex body is a compact convex set in ${\mathbb{R}}^d$ with a non-empty interior. The intersection of a convex body with a supporting hyperplane is called a face. A facet is a face of dimension $d-1$.

Let h denote the Pompeiu–Hausdorff distance (also called Hausdorff distance) between compact sets.

For $a_1,\cdots ,a_n\in {\mathbb{R}}^d$, put $a_1\cdots a_n=\mathrm{conv}\{a_1,\cdots ,a_n\}$.

3. Unbounded trt-Convex Sets

We now investigate the trt-convexity of unbounded sets in ${\mathbb{R}}^d$.

Theorem 1. 

The complement of a connected bounded set $M\subset {\mathbb{R}}^2$ which equals intclM is trt-convex if and only if $\mathrm{cl}M$ is a right or an acute triangle.

Proof. 

The “if” part is obvious.

Suppose $\complement M$ is trt-convex. Let $Q=\mathrm{conv}\mathrm{cl}M$.

First, we show that $\mathrm{bd}Q\subset \mathrm{bd}M$. If the inclusion is not true, we choose $x\in$ $\left(\mathrm{bd}Q\right)\backslash \mathrm{bd}M$. There are $y,z\in \mathrm{bd}M$ such that x lies in the line segment $yz$, and $\overline{yz}$ is a supporting line of Q. The line $H_{xy}$ is orthogonal to $yz$ and cuts $\mathrm{bd}M$ in at least two points. Let $uv$ be the longest line segment with $u,v\in H_{xy}\cap \mathrm{bd}M$. Then any thin right triangle containing $u,v$ meets M, contradiction.

Now we prove that M is convex. Indeed, otherwise we choose $x\in \left(\mathrm{int}Q\right)\backslash M$, $y\in M$. The line $\overline{xy}$ cuts $\mathrm{bd}Q$ in two points, $u,v$. Assume that the order on $\overline{xy}$ is $u,x,y,v$. Then, $x,v$ do not enjoy the trt-property in $\complement M$.

We claim that $\mathrm{bd}M$ does not contain parallel non-degenerate line segments.

Indeed, if $\mathrm{bd}M$ contains such line segments, then there is no thin right triangle in $\complement M$ containing their midpoints.

Let $L_1,L_2,L_3,L_4,L_5$ be supporting lines of $\mathrm{cl}M$, parallel to the sides of a regular pentagon. Choose $a_i\in L_i\cap \mathrm{cl}M(i=1,\cdots ,5)$. Let $A_1$ be the arc in $\mathrm{bd}M$ from $a_1$ to $a_2$ not containing $a_3$. If $A_1\ne a_1{a}_2$, for any $b\in A_1$ distinct from $a_1,a_2$, $\angle a_{1}b{a}_2\ge 3\pi /5$. Let $c_i\in A_1$ lie between $a_i$ and $b(i=1,2)$, such that a supporting line at $c_i$ be parallel to $\overline{a_{i}b}$. Obviously, $c_1,c_2$ do not enjoy the trt-property in $\complement M$. Hence, $\mathrm{cl}M=a_1{a}_2{a}_3{a}_4{a}_5$, where some of the $a_i$’s may not be distinct.

Assume that an angle of the polygon $\mathrm{cl}M$ is obtuse. Then, the midpoints of its sides do not enjoy the trt-property in $\complement M$. Hence, $\mathrm{cl}M$ has no obtuse angle and must consequently be a rectangle or a non-obtuse triangle. As $\mathrm{bd}M$ contains no parallel line segments, the proof is finished. □

Theorem 2. 

The complement of a connected bounded open set M in ${\mathbb{R}}^d$, where $d\ge 3$, is trt-convex, if for every $x,y\in \mathrm{bd}M$, there exist two non-parallel hyperplanes $H_x,H_y$ disjoint from M, with $x\in H_x,y\in H_y$.

Proof. 

We claim that M is convex.

Indeed, otherwise there exist two points $u,v\in M$ such that $uv\cap \mathrm{bd}M\ne \varnothing$. Choose $w\in uv\cap \mathrm{bd}M$. Since $u\notin H_w$, $H_w$ separates u from v. So $H_w\cap M\ne \varnothing$, a contradiction.

Now, we choose $x,y\in \complement M$.

If $x,y\in \mathrm{bd}M$, consider the two non-parallel hyperplanes $H_x,H_y$ at x and y, respectively. Take a line $L\subset H_x\cap H_y$. Choose $z\in L$, such that $\angle xzy<\pi /2$. There exist $x^{\prime }\in \overline{zx}$, $y^{\prime }\in \overline{zy}$ far away, yielding a right triangle $z{x}^{\prime }{y}^{\prime }$ with $x\in z{x}^{\prime }$, $y\in z{y}^{\prime }$ and $x^{\prime }{y}^{\prime }\cap M=\varnothing$. Then, $x^{\prime }{y}^{\prime }$, $x^{\prime }z$, $y^{\prime }z$ form a thin right triangle containing $x,y$.

If $x\in \mathrm{bd}M$, $y\notin \mathrm{bd}M$, consider the point $z\in \mathrm{cl}M$ closest from y. Let $H_x\ni x$ and $H_z\ni z$ be the hyperplanes given by the statement. Let $H\ni y$ be parallel to $H_z$. It follows that $H_x$ and H are not parallel. The proof continues as before. We proceed similarly if $x,y\notin \mathrm{bd}M$. □

The connectedness condition in Theorem 2 is in fact not necessary. We prove the following strengthening.

Theorem 3. 

The complement of a bounded open set M in ${\mathbb{R}}^d$, with at most two components and $d\ge 3$, is trt-convex, if for every $x,y\in \mathrm{bd}M$, there exist two non-parallel hyperplanes $H_x,H_y$ disjoint from M, with $x\in H_x,y\in H_y$.

Proof. 

For M connected, we apply Theorem 2.

Suppose now that M has the components $M_1,M_2$. Like in the proof of Theorem 2, it can be shown that both $M_1,M_2$ are convex.

Consider $x,y\in \complement M$. If $x,y\in \mathrm{bd}M$, we proceed like in the preceding proof.

Assume now $x\notin \mathrm{bd}M$.

Case 1.$xy\cap M=\varnothing$.

Then, close to x a point z can be found such that $\angle xzy=\pi /2$ and $xyz\cap M=\varnothing$.

Case 2.$xy\cap M_1\ne \varnothing$.

Let $\{u,v\}=xy\cap \mathrm{bd}{M}_1$. (It is easily seen that this intersection has two points.) By hypothesis, there exist non-parallel hyperplanes $H_u\ni u,H_v\ni v$ disjoint from M. Put $H=H_u\cap H_v$.

$M_2$ can lie in only one of the four half spaces determined by $H_u\cup H_v$ in ${\mathbb{R}}^d$. This implies that at most one of the sets $\mathrm{conv}\left(\right\{x\}\cup H)$, $\mathrm{conv}\left(\right\{y\}\cup H)$ meets $M_2$, say the latter.

Consider an arbitrary line $L\subset H$ and the plane $P=\mathrm{aff}\left(\right\{y\}\cup L)$. Clearly, $y\notin Y$, where

$$Y=M_2\cap \mathrm{conv}(\left\{y\right\}\cup H).$$

There exists a half-line $L^{\prime }\subset L$ such that, for each $z\in L^{\prime }$, $\overline{yz}\cap M_2=\varnothing$. Now, choose $z^{\prime }\in L^{\prime }$ far away, so that $\angle x{z}^{\prime }y<\pi /2$. Another pair of points $x^{\prime },y^{\prime }$ can be chosen on $\overline{x{z}^{\prime }},\overline{y{z}^{\prime }}$, respectively, such that $x\in x^{\prime }{z}^{\prime },y\in y^{\prime }{z}^{\prime },\angle x^{\prime }{y}^{\prime }{z}^{\prime }=\pi /2$, and bd$\left(x^{\prime }{y}^{\prime }{z}^{\prime }\right)\cap M=\varnothing$. □

Remark 1. 

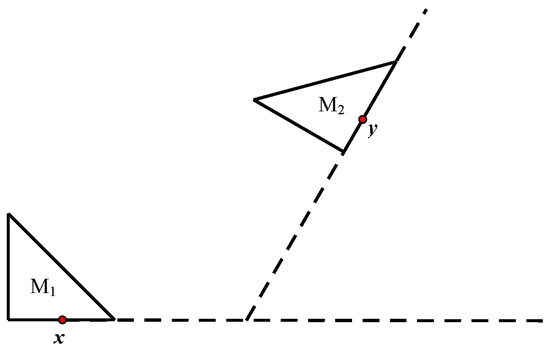
The $d\ge 3$ in Theorem 3 is the best possible. When $d=2$, we may consider $M=M_1\cup M_2,$ where both cl$M_1$ and cl$M_2$ are right triangles. However, $x\in \mathrm{bd}{M}_1$ and $y\in \mathrm{bd}{M}_2$ do not enjoy the $trt$-property in $\complement M$. See Figure 1.

Figure 1. Illustration of Remark 1.

A planar convex set having the union of two half-lines with a common end point as boundary is called a digon.

Theorem 4. 

The complement of a bounded open set M in ${\mathbb{R}}^d$, with at most three components and $d\ge 4$, is trt-convex, if for every $x,y\in \mathrm{bd}M$, there exist two non-parallel hyperplanes $H_x,H_y$ disjoint from M, with $x\in H_x,y\in H_y$.

Proof. 

We proceed like in the preceding proof until Case 1, including it.

Case 2. We again take $u,v,H_u$ and $H_v$ as before. The affine subspace $H=H_u\cap H_v$ has dimension $d-2\ge 2$. Consider an arbitrary plane $P\subset H$ and the 3-dimensional affine subspaces $E_x=\mathrm{aff}(\left\{x\right\}\cup P)$, $E_y=\mathrm{aff}(\left\{y\right\}\cup P)$.

It is again true that at most one of $\mathrm{conv}\left(\right\{x\}\cup H)$, $\mathrm{conv}\left(\right\{y\}\cup H)$ meets $M_2$, say the first.

If $E_x\cap M_2\ne \varnothing$ (notice that this may not be the case), consider $K_x=\mathrm{cl}(E_x\cap M_2)$. Let $\Pi$ be the plane through x parallel to P. If $\Pi \cap K_x\ne \varnothing$ (again, this may not happen), take the two supporting lines $L_1,L_2$ of $\Pi \cap K_x$ passing through x. Take $x_1\in L_1\cap K_x,x_2\in L_2\cap K_x$. Let $P_{x_i}$ be the supporting plane of $K_x$ at $x_i(i=1,2)$.

The set $(P_{x_1}\cap P)\cup (P_{x_2}\cap P)$ includes two half-lines determining a digon ${\Delta }_x$ with the following property. Every half-line starting at x and containing a point of $K_x$ either misses P or meets P inside ${\Delta }_x$.

We proceed in the same way with $M_3$. It meets conv$\left(\right\{x\}\cup H)$ or conv$\left(\right\{y\}\cup H)$ or none of them. In the first case, we consider $E_x$, in the second $E_y$. Going analogously ahead, we find a digon ${\Delta }_y\subset P$, such that every half-line from y through a point of $K_y$ either misses P or meets P inside ${\Delta }_y$.

Now, choose a half-line $L^{\prime }\subset P\backslash ({\Delta }_x\cup {\Delta }_y)$, and continue as in the preceding proof. □

Question 1. 

Is Theorem 2 valid without any condition regarding connectedness?

4. trt-Convexity of Convex Surfaces

Can convex surfaces be trt-convex?

A tetrahedron in ${\mathbb{R}}^3$ having a vertex, at which the angles of all three facets are right, will be called right.

Theorem 5. 

For a convex body $P\subset {\mathbb{R}}^3$, $\mathrm{bd}P$ is trt-convex if and only if P is a right tetrahedron.

Proof. 

For the “if” implication, let $\mathbf{0}abc$ be a tetrahedron with all three angles at $\mathbf{0}$ right. We show that bd$\left(\mathbf{0}abc\right)$ is trt-convex.

Let $x,y\in \mathrm{bd}\left(\mathbf{0}abc\right)$. We have four essentially different situations.

Case 1.  $x,y\in \mathbf{0}ab$.

This case follows from the right convexity of any right triangle.

Case 2.  $x,y\in abc$.

Similarly, $abc$ being an acute triangle, it must be rightly convex.

Case 3.  $x\in \mathbf{0}ab$, $y\in \mathbf{0}bc$.

Assume without loss of generality that y is not closer than x from $\overline{\mathbf{0}ac}$. Then,

$$\overline{{\pi }_{\overline{\mathbf{0}b}}\left(x\right)y}\cap \mathrm{bd}\left(\mathbf{0}bc\right)\subset bc.$$

Denote by z this intersection. Put $\left\{u\right\}=\overline{x{\pi }_{\overline{\mathbf{0}b}}\left(x\right)}\cap ab$. The points u, ${\pi }_{\overline{\mathbf{0}b}}\left(x\right)$ and z are the vertices of a thin right triangle included in bd$\left(\mathbf{0}abc\right)$.

Case 4.  $x\in \mathbf{0}ab$, $y\in abc$.

Consider the point u from Case 3 and $\left\{v\right\}=\overline{x{\pi }_{\overline{\mathbf{0}a}}\left(x\right)}\cap ab$. Clearly,

$$abc=acv\cup bcu.$$

If $y\in acv$, then $\overline{vy}\cap ac\ne \varnothing$. If $y\in bcu$, then $\overline{uy}\cap bc\ne \varnothing$.

So, if $y\in acv$, then $x,y$ lie in a thin right triangle with vertices $v,{\pi }_{\overline{\mathbf{0}a}}\left(x\right),\overline{vy}\cap ac$, included in $\mathrm{bd}\left(\mathbf{0}abc\right)$. Analogously, for $y\in bcu$.

Now, let us prove the “only if” implication.

Let $Q=\mathrm{ext}P$.

Claim 1. If two crossing line segments belong to bdP, then they lie in a facet of P.

Indeed, let $uv,xy$ be the two line segments, and $\left\{z\right\}=uv\cap xy$. Being a convex body, P is not included in the plane $\overline{xuz}$, supposed horizontal. Let $s\in P\backslash \overline{xuz}$, below $\overline{xuz}$, say. Take $t\in \mathrm{int}\left(xuz\right)$ and assume that $t\in \mathrm{int}\left(s{s}^{\prime }\right)$ for some $s^{\prime }\in P$. Then, $z\in \mathrm{int}\left(s{s}^{\prime }vy\right)$, which contradicts $z\in \mathrm{bd}P$. Hence, there exist no such points $s^{\prime }$, and consequently $xuz\subset \mathrm{bd}P$.

Analogously, $uzy\subset \mathrm{bd}P,yzv\subset \mathrm{bd}P,vzx\subset \mathrm{bd}P$ and $uxvy$ is a facet of P. Claim 1 is proven.

For any $u,v\in Q$, we have $uv\subset \mathrm{bd}P$. Indeed, otherwise there is no thin right triangle in bdP containing $u,v$.

We now prove that P has a facet. Assume that P has no facet.

Consider three extreme points $u_1,u_2,u_3\in Q$. We have $u_1{u}_2\cup u_2{u}_3\cup u_3{u}_1\subset \mathrm{bd}P$. Put $\overline{u_1{u}_2{u}_3}=\Pi$. Then, $u_1{u}_2{u}_3\subset \Pi \cap P$.

Since P contains no facet, $\Pi$ is not a supporting plane of P. Hence, $\Pi$ divides P into two parts $P_1,P_2$.

Choose $v_1\in Q\cap P_1\backslash \Pi ,v_2\in Q\cap P_2\backslash \Pi$. We have $v_1{v}_2\subset \mathrm{bd}P$.

Consider the non-degenerate polytope $u_1{u}_2{u}_3{v}_1{v}_2$. By Radon’s theorem, either one vertex is in the tetrahedron determined by the other four, or one line segment $\Sigma$ joining two vertices meets the triangle $\Delta$ formed by the other three. The first possibility is excluded, the vertices being in Q. Since $\Sigma \subset \mathrm{bd}P$, $\Sigma \cap \Delta$ avoids intP, whence $\Sigma$ meets bd$\Delta$, and Claim 1 provides a facet of P, which contradicts our assumption.

Let E be a facet of P.

Claim 2.  $Q\cap \mathrm{bd}E$ is nowhere dense in bdE.

Suppose, in contrast, there exists a non-degenerate arc $A\subset Q\cap \mathrm{bd}E$. Choose $w\in Q\backslash E$ and put $\left\{x\right\}={\pi }_{\overline{E}}\left(w\right)$. For $y,z\in A$ close to each other, but different from x, $\angle ywz$ is small. If $\angle wyz=\pi /2$, then $\angle xyz=\pi /2$ and $\angle wzy<\pi /2$. Then, choose $z^{\prime }\in A$ close to z, such that still $\angle w{z}^{\prime }y<\pi /2$. Since $y,z,z^{\prime }$ are not collinear, being in Q, $\angle xy{z}^{\prime }\ne \pi /2$, whence $\angle wy{z}^{\prime }\ne \pi /2$.

Hence, either the triangle $wyz$ is not right, or we find the triangle $wy{z}^{\prime }$ which is not right. Obviously, the midpoints of the two long sides do not have the $trt$-property.

Claim 3. There are no disjoint line segments in bdE.

Suppose, on the contrary, $S,T$ are such line segments, assumed maximal (with respect to inclusion). Let $S^{*}$ be the component of $\left(\mathrm{bd}P\right)\backslash \mathrm{bd}\mathrm{conv}\left(\right\{w\}\cup S)$ not containing T, and $T^{*}$ the component of $\left(\mathrm{bd}P\right)\backslash \mathrm{bd}\mathrm{conv}\left(\right\{w\}\cup T)$ not containing S. Since points in $S^{*}$ and $T^{*}$ have the $trt$-property, we must have $\mathrm{cl}{S}^{*}=\mathrm{conv}(\left\{w\right\}\cup S)$ and $\mathrm{cl}{T}^{*}=\mathrm{conv}(\left\{w\right\}\cup T)$.

Thus, the triangles $wab=\mathrm{cl}{S}^{*}$ and $wcd=\mathrm{cl}{T}^{*}$ are facets of P.

Now, we easily find $p\in \mathrm{int}\left(wab\right)$, $q\in \mathrm{int}\left(wcd\right)$, such that $\angle pwq\ne \pi /2$. Put $\left\{p^{\prime }\right\}=\overline{wp}\cap ab$ and $\left\{q^{\prime }\right\}=\overline{wq}\cap cd$. We can arrange the triangle $w{p}^{\prime }{q}^{\prime }$ not to be right. Indeed, if, for example $\angle w{p}^{\prime }{q}^{\prime }=\pi /2$, $\overline{w{p}^{\prime }}\perp \overline{E}$ or not. In the first case, for any choice of a point $p^{″}\ne {\pi }_{\overline{ab}}\left(q^{\prime }\right)$ very close to $p^{\prime }$ on $ab$, the triangle $w{p}^{″}{q}^{\prime }$ is not right. In the second case, for any choice of a point $q^{″}$ very close to q on $cd$, the triangle $w{p}^{\prime }{q}^{″}$ is not right.

Hence, we may suppose the triangle $w{p}^{\prime }{q}^{\prime }$ not to be right. However, then p and q do not enjoy the $trt$-property. Claim 3 is verified.

From Claims 2 and 3, it follows that E is a triangle $ijk$. In fact, every facet of P is a triangle. Moreover, $wi,wj,wk$ are edges of P. Suppose $wij$ is not a facet of P. Then, some point $m\in Q$ is separated from k by $\overline{wij}$. However, then $mk$ meets $wij$, which means that $mk\cap \mathrm{bd}\left(wij\right)\ne \varnothing$, as all four points belong to Q and $mk\subset \mathrm{bd}P$. By Claim 1, P has a quadrilateral facet, and a contradiction is found. Therefore, $P=wijk$.

It remains to prove that the tetrahedron P is right.

We call a tetrahedron $abcd$quasiright, if for any pair of opposite edges, such as $ab$, $cd$, we have $\overline{ab}\perp \overline{acd}$ or $\overline{ab}\perp \overline{bcd}$ or $\overline{cd}\perp \overline{abc}$ or $\overline{cd}\perp \overline{abd}$. Notice that a right tetrahedron is quasiright. We first show that P is quasiright.

Choose arbitrarily the pair of opposite edges $ij$ and $kw$ of P. Choose $x\in \mathrm{int}\left(ij\right)$ and $y\in \mathrm{int}\left(wk\right)$. Then, the only triangle boundaries in bdP containing $x,y$ are bd$\left(wxk\right)$ and bd$\left(ijy\right)$.

If $\overline{ij}\perp \overline{iwk}$ or $\overline{ij}\perp \overline{jwk}$, then the condition for P to be quasiright is fulfilled at $ij$, $kw$. Otherwise, card$(H_{ij}\cap wk)\le 1,\mathrm{card}(H_{ji}\cap wk)\le 1$ and card$(S_{ij}\cap wk)\le 2$, so $ijy$ is not right for any $y\in \mathrm{int}\left(wk\right)\backslash (H_{ij}\cup H_{ji}\cup S_{ij})$. Fix such a point y. Since $x,y$ have the $trt$-property in bdP, $wxk$ is right for any $x\in \mathrm{int}\left(ij\right)$. So $\angle kwx=\pi /2$ or $\angle wkx=\pi /2$ for all $x\in \mathrm{int}\left(ij\right)\backslash S_{wk}$. Suppose without loss of generality $\angle kwx=\pi /2$ and $\angle wkx<\pi /2$. Choose $x^{\prime }\in \mathrm{int}\left(ij\right)$ close to x such that $\angle wk{x}^{\prime }<\pi /2$. We also have $\angle kw{x}^{\prime }=\pi /2$. So $\overline{wk}\perp \overline{ijw}$. Again, the condition for P to be quasiright is fulfilled at $ij$, $kw$.

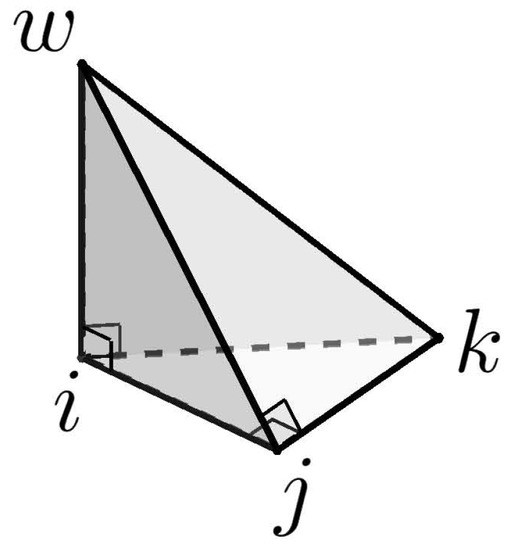
Hence, P is quasiright. If it is not right, it must look like in Figure 2. However, then, the midpoint of $ij$ and a point close to w on $wk$ do not enjoy the $trt$-property. □

Figure 2. A tetrahedron $wijk$.

5. trt-Convexity of Planar Geometric Graphs

A Jordan curve in ${\mathbb{R}}^d$ is the image of an injective continuous map of a circle into ${\mathbb{R}}^d$.

A Jordan arc in ${\mathbb{R}}^d$ is the image of an injective continuous map of an interval $[a,b]$ into ${\mathbb{R}}^d$.

A geometric graph D is a set containing finitely many points in ${\mathbb{R}}^d$ called vertices, which form a set $V\left(D\right)$, and including the union of finitely many Jordan arcs, each joining two vertices, called edges.

A planar geometric graph is a geometric graph in ${\mathbb{R}}^2$, the edges of which have pairwise no points in common, other than vertices of both.

Theorem 6. 

A planar geometric graph is trt-convex if and only if it is a thin right triangle or such a triangle plus its height corresponding to the hypotenuse.

Proof. 

Let $D\subset {\mathbb{R}}^2$ be a planar geometric graph. The bounded components of ${\mathbb{R}}^2\backslash D$ will be called regions.

The “if” part is obvious. Let us prove the other implication.

Clearly, D is connected. Each region F of D has a closed Jordan curve as boundary, consisting of two or more edges.

A broken line with at most three line segments and no obtuse angle will be called a 3-path.

Claim 1. Each edge is a 3-path .

Indeed, let E be an edge between the vertices v, w. Take $v^{\prime }\in E$ close to v and $w^{\prime }\in E$ close to w. The trt-property of $v^{\prime },w^{\prime }$ yields the existence of a thin right triangle $T\subset D$, to which $v^{\prime },w^{\prime }$ belong. Hence, the subarc $E^{\prime }\subset E$ from $v^{\prime },w^{\prime }$ is included in T. Therefore it is a 3-path . By letting $v^{\prime },w^{\prime }$ converge to $v,w$, respectively, we obtain the existence of a 3-path from v to w in E, whence E is a 3-path .

Let F be a region of D and $E\subset \mathrm{bd}F$ an edge.

Claim 2. If the 3-path E has an angle (measured toward F) $\alpha \ne \pi$ at some point, then $\alpha <\pi$.

Indeed, suppose at some point $y\in E$, the angle is $\alpha >\pi$. Take $x\in \left(\mathrm{bd}F\right)\backslash \left\{y\right\}$ such that $yx$ bisects that angle. The trt-property at $x,y$ is clearly violated.

An important consequence of Claim 2 is that each edge lying between two regions is a line segment.

Let $a,b$ determine the diameter of D. The trt-property of $a,b$ yields the existence of a thin right triangle $T\subset D$ with vertices $a,b,c$ and the right angle at c.

For $D=T$, we have already the first case of the statement.

Another important consequence of Claim 2 is that each region is convex. Let Y be the polygonal boundary of a region F or of the unbounded component $D^{\prime }$ of $\complement D$. Let v be a vertex of Y, not necessarily in $V\left(D\right)$, and $\beta$ the angle at v toward F, respectively $\complement D^{\prime }$.

Claim 3.  $\beta \le \pi /2$.

Indeed, assume $\beta >\pi /2$. Take $u,u^{\prime }$ on the two sides of Y which meet at v, close to v. Clearly, the trt-property is violated at $u,u^{\prime }$.

From Claim 3 it follows that Y has at most four sides. Moreover, if Y has four sides, then $\mathrm{conv}Y$ must be a rectangle. However, then, the trt-property is violated at midpoints of opposite sides. Hence, Y is a triangle. So $\complement D^{\prime }=abc$, and D is a triangulation.

Claim 4. If the edges $J^{\prime }$, $J^{″}$ of D have a common vertex v, then the angle at v equals $\pi$ or is not obtuse.

Indeed, if that angle is obtuse but not $\pi$, the trt-property at points on $J^{\prime }$, $J^{″}$, close to v is not enjoyed.

Remark 2. If D has a vertex $v\in \mathrm{bd}\left(abc\right)$ distinct from $a,b,c$, then, by Claim 4, v has degree 3 and some edge $vw$ of D is orthogonal to $\mathrm{bd}\left(abc\right)$ at v.

Remark 3. If D has a vertex $v\in \mathrm{int}\left(abc\right)$, then v has degree four and the four edges at v are pairwise collinear or orthogonal. This also follows from Claim 4.

It is clear that a belongs to a triangle $apq$ of the triangulation, with $p\in ab$.

By Remark 2, $apq$ has its right angle at p, so either $q\in \mathrm{int}\left(abc\right)$ and Remark 3 is contradicted, or $q\in ac$ and Remark 2 is contradicted, except for the case when $q=c$, which corresponds to the second case of the statement.

The proof is complete. □