A Quantum-Behaved Particle Swarm Optimization Algorithm on Riemannian Manifolds
Abstract
1. Introduction
- The iteration operation on the Riemannian manifold can reduce the modeling error and improve the expression ability of nonlinear problems;
- It can make full use of the intrinsic geometric structure of the objective function and embed the constraints into the search space to solve the unconstrained optimization problems based on the constrained search space, such as the low-rank matrix constraint problems and the positive semidefinite programming problems [11];
- Solving the target directly on the Riemannian manifold can reduce the damage to the original structural information caused by the vectorization of high-dimensional data.
2. Preliminaries
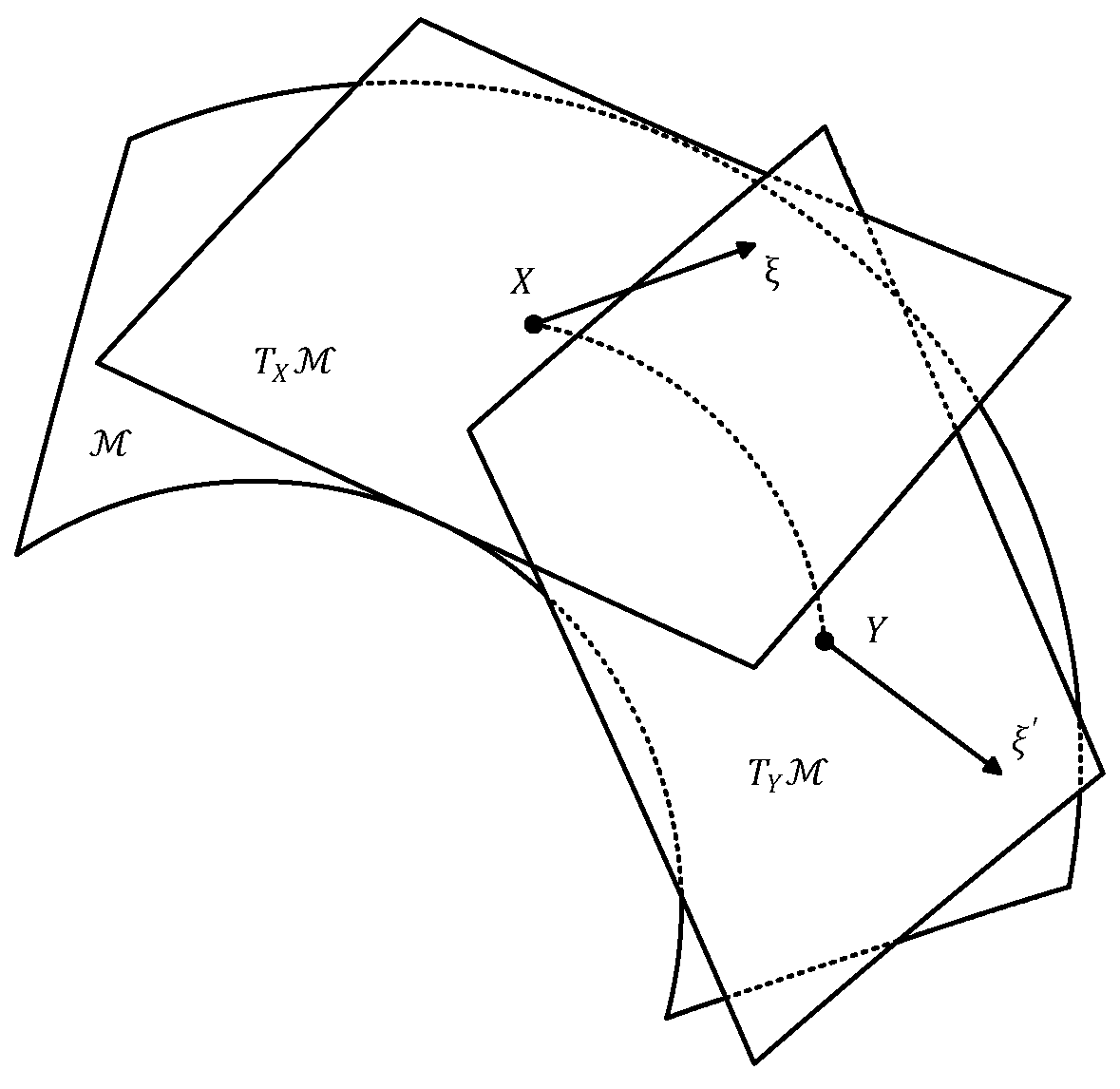
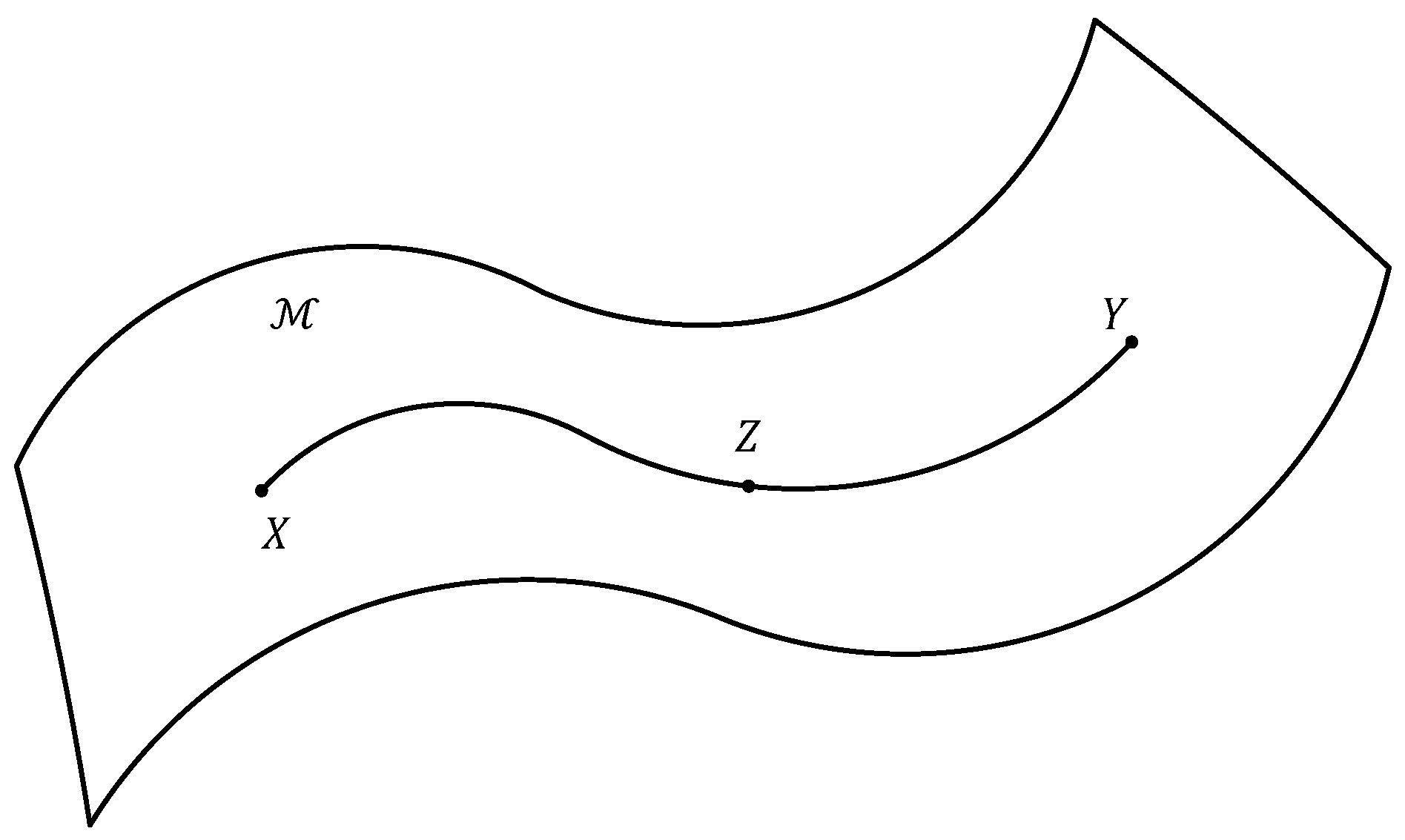
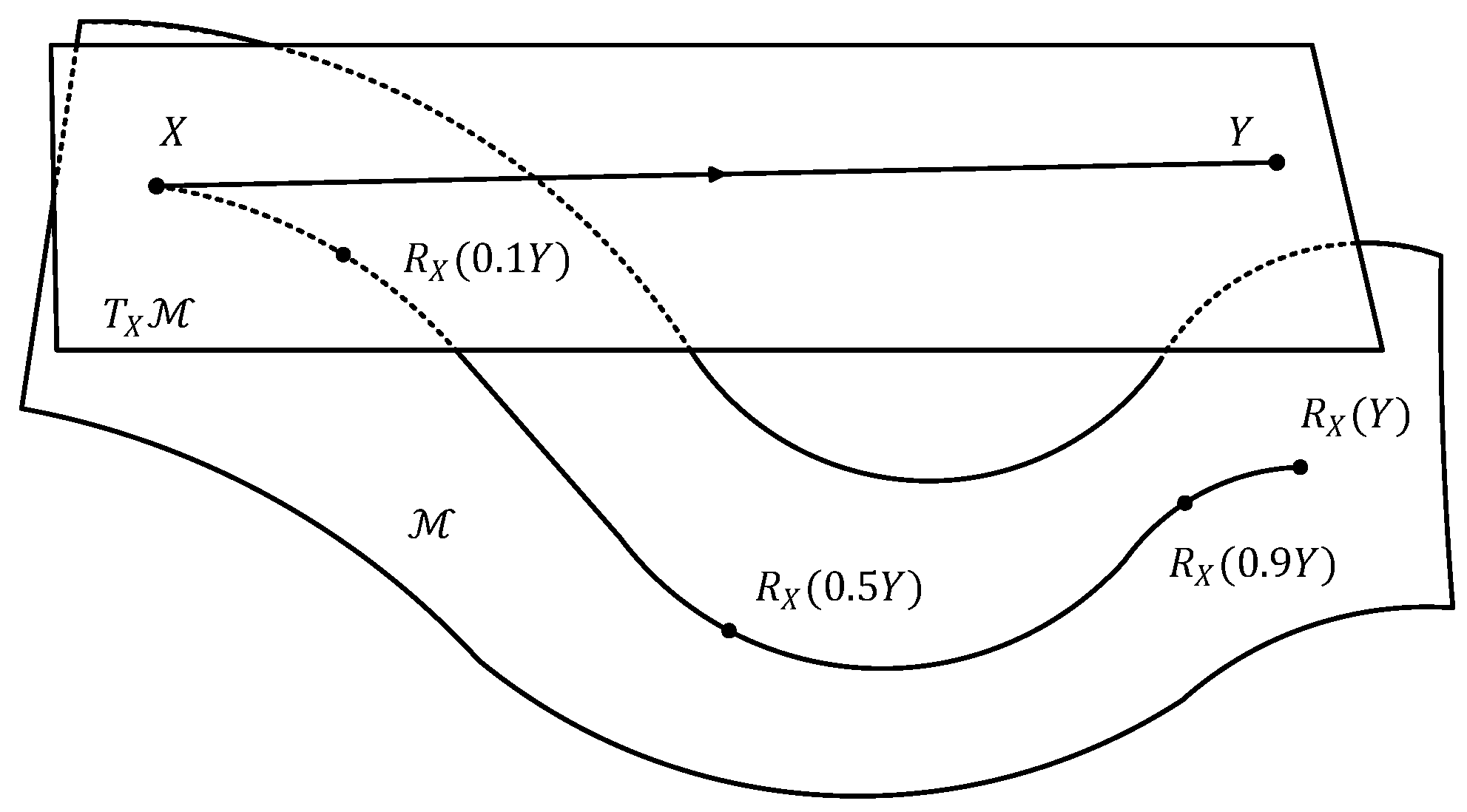
2.1. The Riemannian Manifold
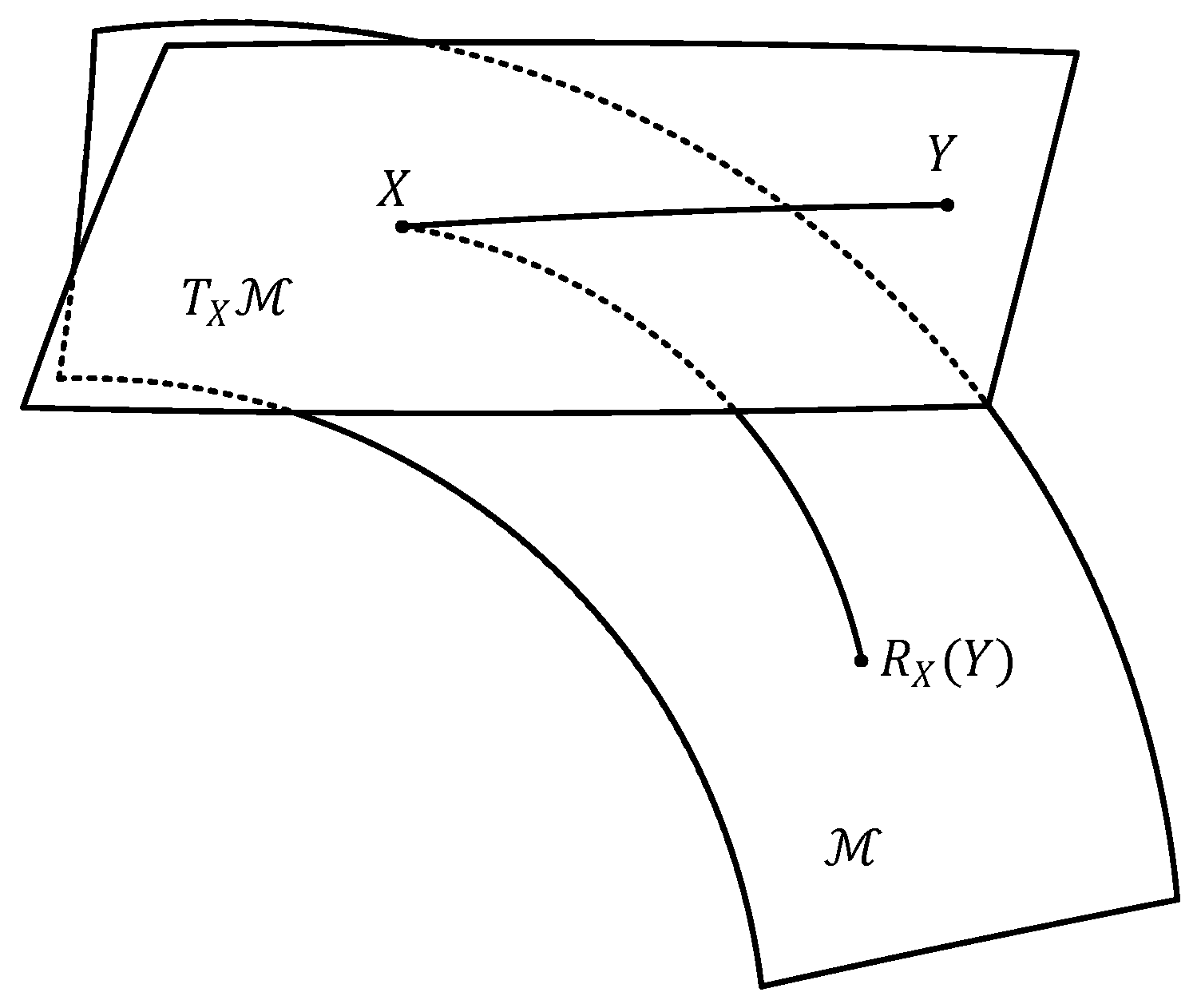
2.2. Basic Operators on Manifold
2.3. Test Problems
2.3.1. Semidefinite Programming Problem
2.3.2. Secant-Based Data Dimensionality Reduction Problem
2.3.3. Robust Principal Component Analysis
2.4. The Quantum-Behaved Particle Swarm Optimization Algorithm
3. The Proposed RQPSO Algorithm
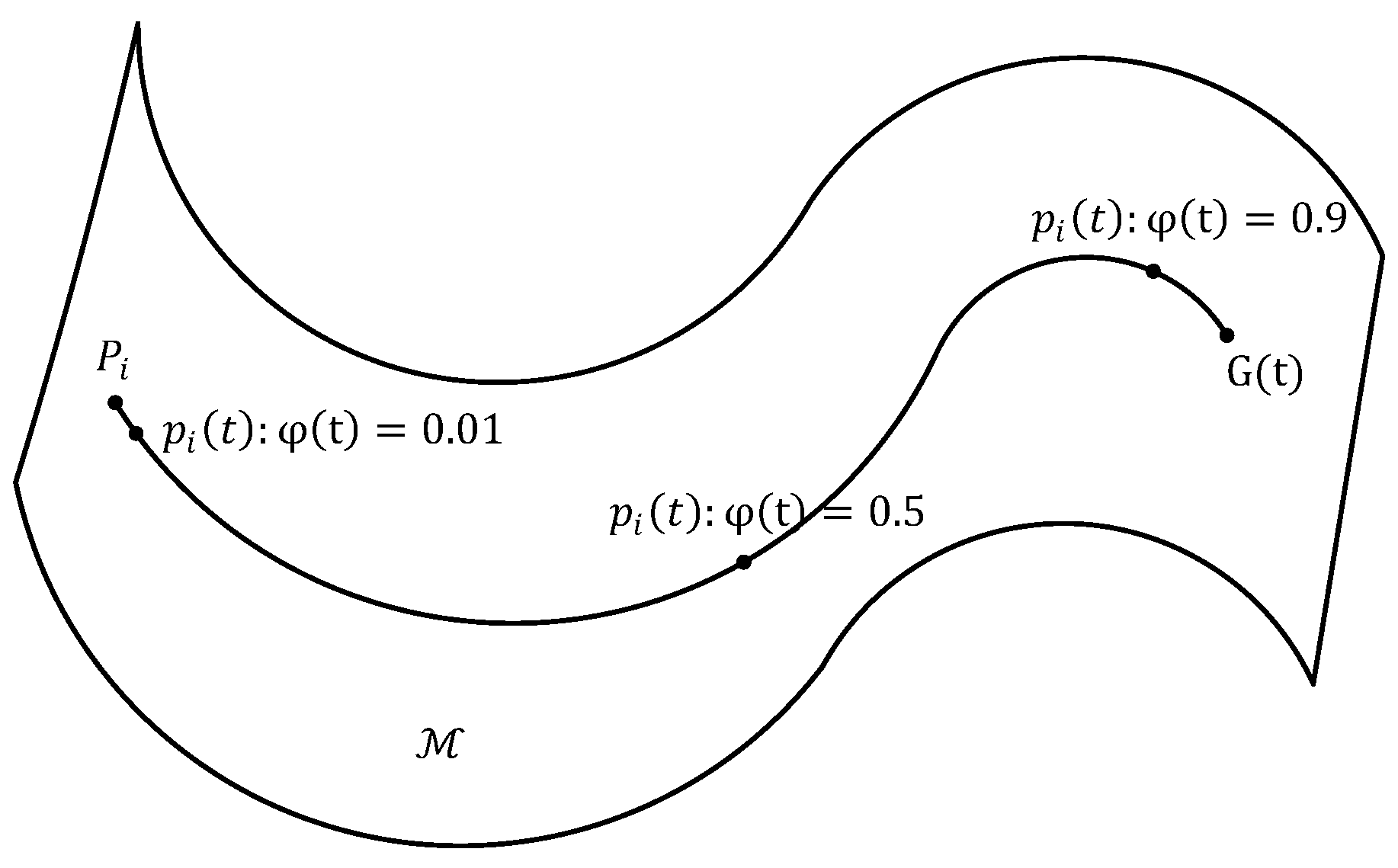
3.1. The QPSO Algorithm on Riemannian Manifold
- 1.
- Randomly select a point from the population as the mean best position ;
- 2.
- For particle , randomly select a point along the geodesic line between and . Generate a tangent from to , and then randomly select a point on the tangent and retract it to on the manifold;
- 3.
- Generate a tangent in the same direction as that from to at the point produced in (2). Then, retract to on the manifold at point and obtain a new population.
| Algorithm 1 Quantum Particle Swarm Optimization on Riemannian Manifold (RQPSO) |
|
3.2. Quantum Behavior of the RQPSO Algorithm
4. Experimental Studies
4.1. Parameters Analysis
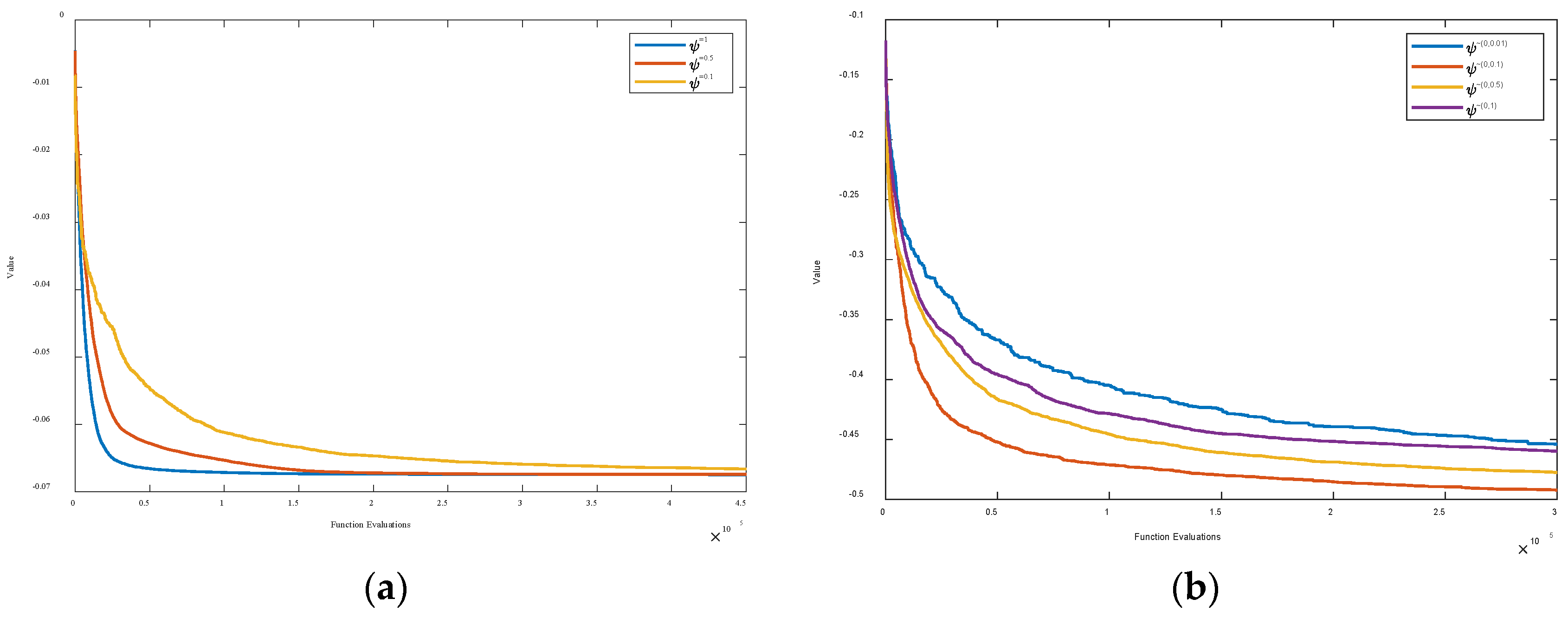
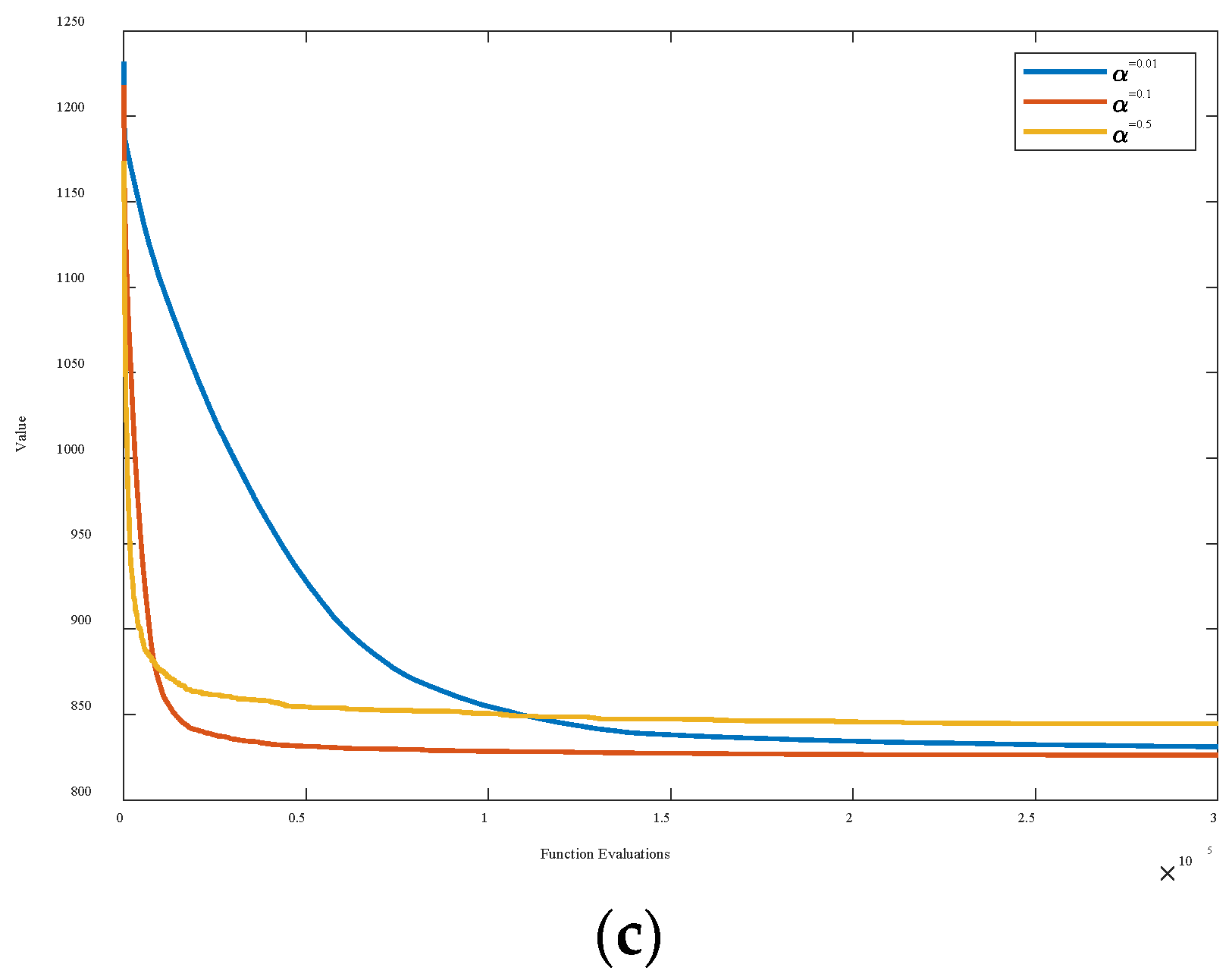
4.1.1. The Effect of on the Performance of RQPSO
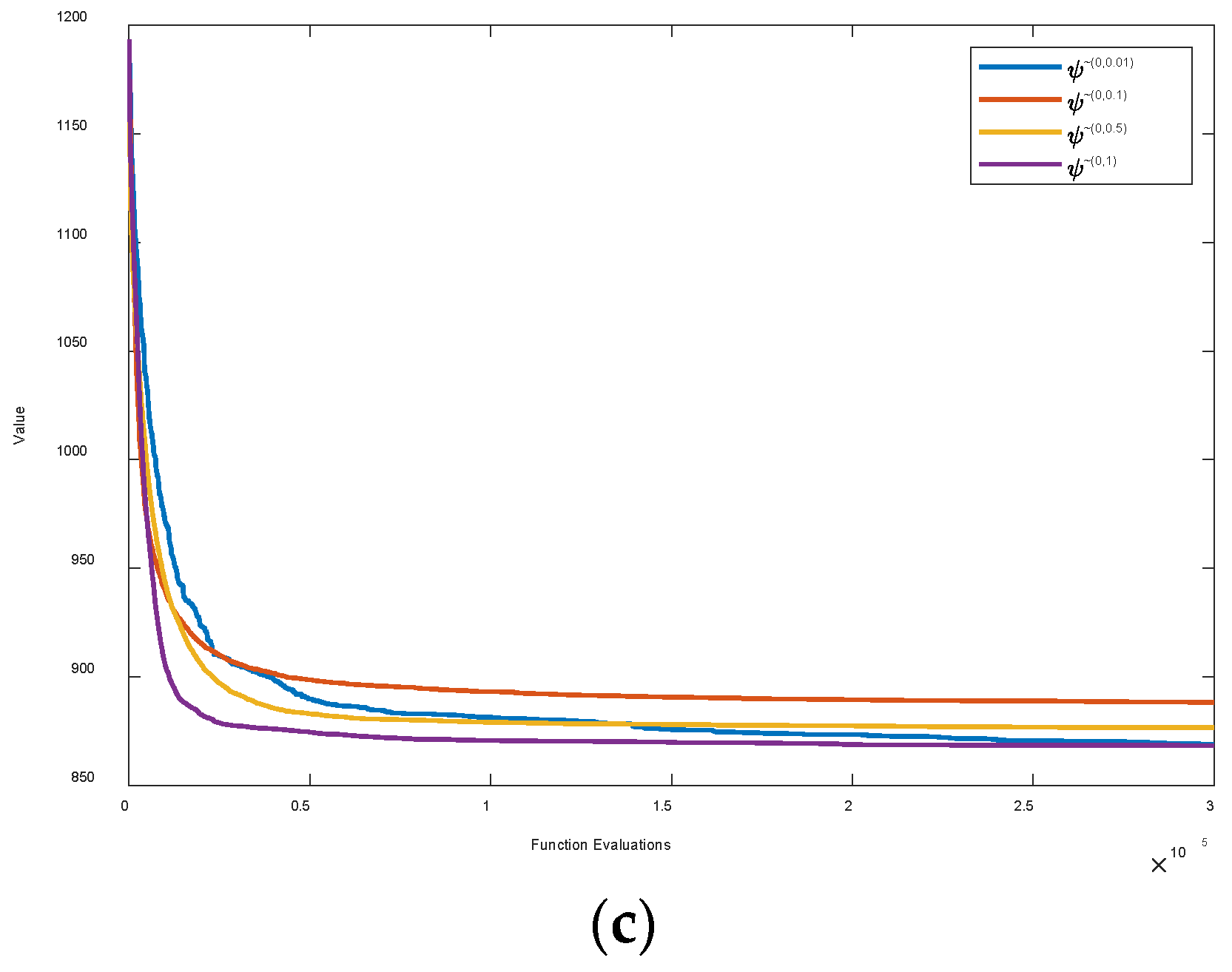
4.1.2. The Effect of on the Performance of RQPSO
4.1.3. The Effect of Parameters on the Performance of RQPSO
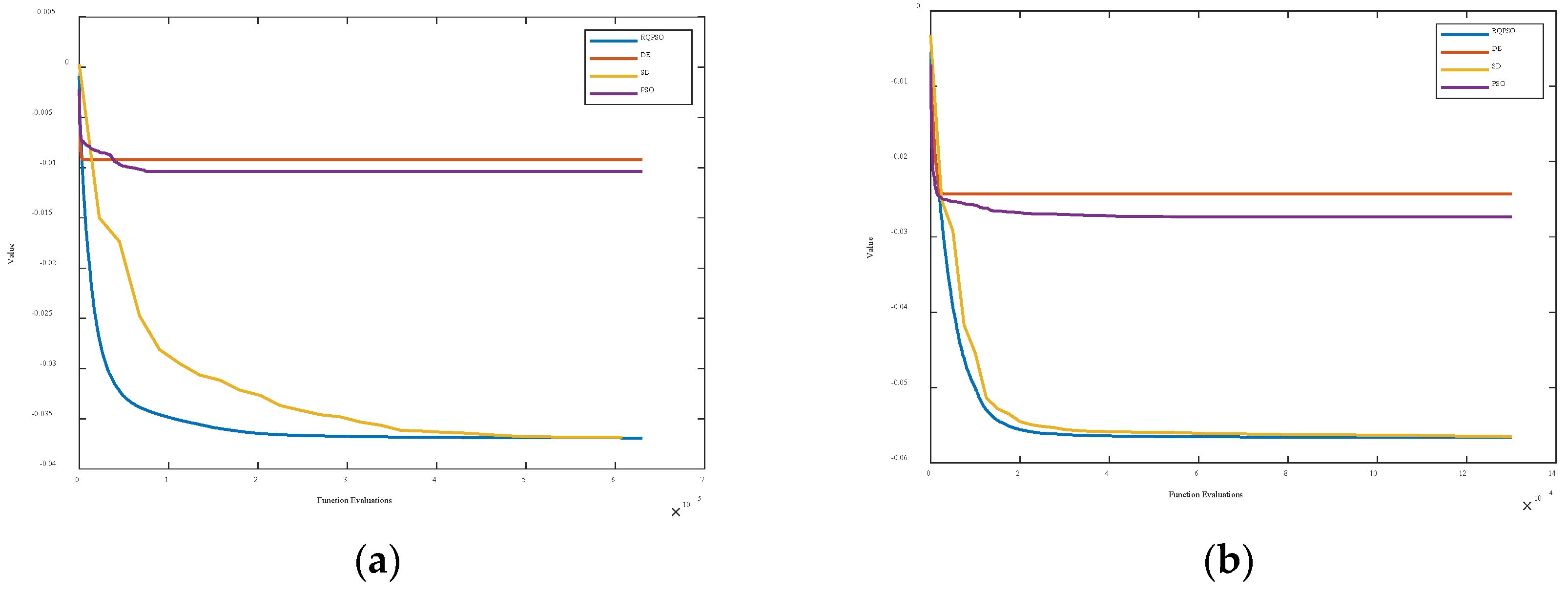
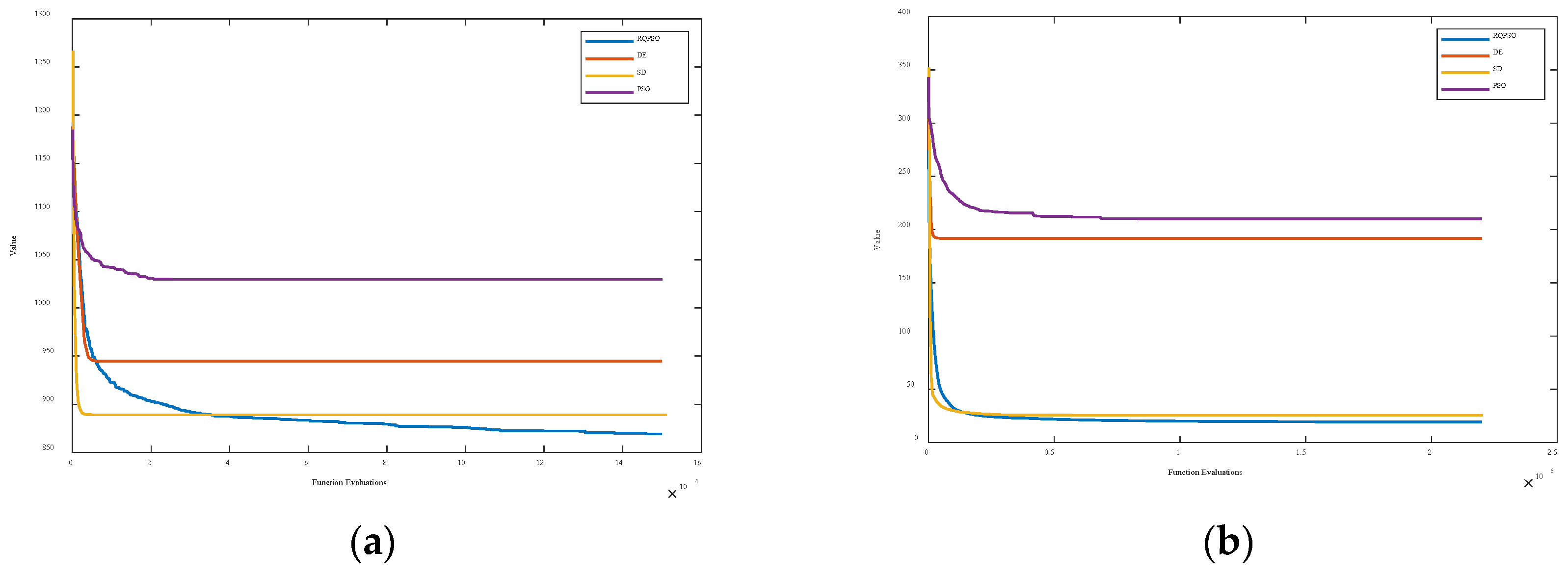
4.2. Comparison Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nocedal, J.; Warght, S.J. Numerical Optimization, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Sun, W.; Yuan, Y.X. Optimization Theory and Methods: Nonlinear Programming: Volume 1; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Sirković, P.; Kressner, D. Subspace acceleration for large-scale parameter-dependent Hermitian eigenproblems. SIAM J. Matrix Anal. Appl. 2016, 37, 695–718. [Google Scholar] [CrossRef]
- Agarwal, N.; Boumal, N.; Bullins, B.; Cartis, C. Adaptive regularization with cubics on manifolds with a first-order analysis. arXiv 2018, arXiv:1806.00065. [Google Scholar]
- Sarkis, M.; Diepold, K. Camera-pose estimation via projective Newton optimization on the manifold. IEEE Trans. Image Process. 2012, 21, 1729–1741. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Lai, M.J.; Lu, Z.S.; Fan, W.; Davulcu, H.; Ye, J. Orthogonal rank-one matrix pursuit for low rank matrix completion. SIAM J. Sci. Comput. 2014, 37, 488–514. [Google Scholar] [CrossRef]
- Liu, T.; Shi, Z.; Liu, Y. Visualization of the Image Geometric Transformation Group Based on Riemannian Manifold. IEEE Access 2019, 7, 105531–105545. [Google Scholar] [CrossRef]
- Lee, K.C.; Ho, J.; Kriegman, D.J. Acquiring Linear Subspaces for Face Recognition under Variable Lighting. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 684–698. [Google Scholar]
- Tuzel, O.; Porikli, F.; Meer, P. Region Covariance: A Fast Descriptor for Detection and Classification; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Absil, P.A.; Mahony, R.; Sepulchre, R. Optimization Algorithms on Matrix Manifolds; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Zhang, H.Y.; He, W.; Zhang, L.P.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- Smith, S.T. Optimization Techniques on Riemannian Manifolds. Mathematics 2014, 158, 328–342. [Google Scholar]
- Harandi, M.; Hartley, R.; Shen, C.; Lovell, B.; Sanderson, C. Extrinsic methods for coding and dictionary learning on Grassmann manifolds. Int. J. Comput. Vis. 2015, 114, 113–136. [Google Scholar] [CrossRef]
- Wang, R.; Shan, S.; Chen, X.; Gao, W. Manifold-manifold distance with application to face recognition based on image set. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2008), Anchorage, AK, USA, 23–28 June 2008; Volume 9, pp. 2940–2947. [Google Scholar]
- Li, Z.Z.; Zhao, D.L.; Lin, Z.C.; Chang, E.Y. A new retraction for accelerating the Riemannian three-factor low-rank matrix completion algorithm. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4530–4538. [Google Scholar]
- Gabay, D. Minimizing a differentiable function over a differential manifold. J. Optim. Theory Appl. 1982, 37, 177–219. [Google Scholar] [CrossRef]
- Zhao, Z.; Bai, Z.J.; Jin, X.Q. A Riemannian Newton Algorithm for Nonlinear Eigenvalue Problems. Siam J. Matrix Anal. Appl. 2015, 36, 752–774. [Google Scholar] [CrossRef]
- Shang, G.; Jing, Y. Swarm Intelligence Algorithm and Its Application; China Water Resources and Hydropower Press: Beijing, China, 2006. [Google Scholar]
- Borckmans, P.B.; Ishteva, M.; Absil, P.A. A Modified Particle Swarm Optimization Algorithm for the Best Low Multilinear Rank Approximation of Higher-Order Tensors; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Colutto, S.; Fruhauf, F.; Fuchs, M.; Scherzer, O. The CMA-ES on Riemannian Manifolds to Reconstruct Shapes in 3-D Voxel Images. IEEE Trans. Evol. Comput. 2010, 14, 227–245. [Google Scholar] [CrossRef]
- Arnold, D.V. On the use of evolution strategies for optimization on spherical manifolds. In Proceedings of the Parallel Problem Solving from Nature—PPSN XIII, Ljubljana, Slovenia, 13–17 September 2014; pp. 882–891. [Google Scholar]
- Arnold, D.V.; Lu, A. An evolutionary algorithm for depth image based camera pose estimation in indoor environments. In IEEE Congress on Evolutionary Computation (CEC); IEEE: New York, NY, USA, 2016. [Google Scholar]
- Sun, J.; Feng, B.; Xu, W. Particle swarm optimization with particles having quantum behavior. In Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No.04TH8753), Beijing, China, 19–23 June 2004; pp. 325–331. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Sun, J.; Liu, J.; Xu, W. Using quantum-behaved particle swarm optimization algorithm to solve non-linear programming problems. Int. J. Comput. Math. 2007, 84, 261–272. [Google Scholar] [CrossRef]
- Omkara, S.; Khandelwala, R.; Ananthb, T.; Naika, G.N.; Gopalakrishnana, S. Quantum behaved particle swarm optimization (QPSO) for multi-objective design optimization of composite structures. Expert Syst. Appl. 2009, 36, 11312–11322. [Google Scholar] [CrossRef]
- Li, S.-Y.; Wang, R.-G.; Hu, W.-W.; Sun, J. A new QPSO based BP neural network for face detection. In Fuzzy Information and Engineering; Cao, B.-Y., Ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 355–363. [Google Scholar]
- Mikki, S.; Kishk, A. Quantum particle swarm optimization for electromagnetics. IEEE Trans. Antennas Propag. 2006, 54, 2764–2775. [Google Scholar] [CrossRef]
- Lei, X.; Fu, A. Two-dimensional maximum entropy image segmentation method based on quantum-behaved particle swarm optimization algorithm. In Proceedings of the Fourth International Conference on Nature Computation, Mieres, Spain, 15–16 December 2015; pp. 692–696. [Google Scholar]
- Sun, J.; Fang, W.; Wang, D.; Xu, W. Solving the economic dispatch problem with a modified quantum-behaved particle swarm optimization method. Energy Convers. Manag. 2009, 50, 2967–2975. [Google Scholar] [CrossRef]
- Boumal, N.; Voroninski, V.; Bandeira, A. The non-convex Burer-Monteiro approach works on smooth semidefinite programs. Adv. Neural Inf. Process. Syst. 2016, 29, 2765–2773. [Google Scholar]
- Absil, P.A.; Hosseini, S. A Collection of Nonsmooth RIEMANNIAN Optimization Problems; ICTEAM Institute: Ottignies-Louvain-la-Neuve, Belgium, 2017. [Google Scholar]
- Ding, C.; Zhou, D.; He, X.; Zha, H. R1-PCA: Rotational Invariant L1-Norm Principal Component Analysis for Robust Subspace Factorization; ACM Press: New York, NY, USA, 2006; pp. 281–288. [Google Scholar]
- Vandenberghe, L.; Boyd, S. Semidefinite programming. SIAM Rev. 1996, 38, 49–95. [Google Scholar] [CrossRef]
- Broomhead, D.S.; Kirby, M.J. Dimensionality Reduction Using Secant-Based Projection Methods: The Induced Dynamics in Projected Systems. Nonlinear Dyn. 2005, 41, 47–67. [Google Scholar] [CrossRef]
- He, X.; Zhou, Y.; Chen, Z.; Jiang, S. An evolutionary approach to black-box optimization on matrix manifolds. Appl. Soft Comput. 2020, 97, 106773. [Google Scholar] [CrossRef]
- Sun, J.; Xu, W.; Feng, B. A global search strategy of quantum-behaved particle swarm optimization. IEEE Conf. Cybern. Intell. Syst. 2004, 1, 111–116. [Google Scholar] [CrossRef]
- Jun, S.; Fang, W.; Wu, X.; Palade, V.; Xu, W. Quantum-Behaved Particle Swarm Optimization: Analysis of Individual Particle Behavior and Parameter Selection. Evol. Comput. 2012, 20, 349–393. [Google Scholar]
- Sun, J.; Xu, W.; Feng, B. Adaptive parameter control for quantum-behaved particle swarm optimization on individual level. In Proceedings of the 2005 International Conference on Systems, Man and Cybernetics, Hefei, China, 12 October 2005; Volume 4, pp. 3049–3054. [Google Scholar]
- Cohen-Tannoudji, C.; Diu, B.; Laloe, F. Quantum Mechanics; John Wiley: New York, NY, USA, 1997; Volume 1. [Google Scholar]
- Rosa, J.L.; Robin, A.; Silva, M.B.; Baldan, C.A.; Peres, M.P. Electrodeposition of copper on titanium wires: Taguchi experimental design approach. J. Mater. Process. Technol. 2009, 209, 1181–1188. [Google Scholar] [CrossRef]
- Polak, E. Optimization: Algorithms and Consistent Approximations; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Boumal, N.; Mishra, B.; Absil, P.A.; Sepulchre, R. Manopt, a matlab toolbox for optimization on manifolds. J. Mach. Learn. Res. 2014, 15, 1455–1459. [Google Scholar]
- Das, S.; Suganthan, P.N. Differential Evolution: A Survey of the State-of-the-Art. IEEE Trans. Evol. Comput. 2011, 15, 4–31. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A Cooperative Approach to Particle Swarm Optimization. Trans. Evol. Comput. 2004, 8, 225–239. [Google Scholar] [CrossRef]
- Maučec, M.S.; Brest, J. A review of the recent use of Differential Evolution for Large-Scale Global Optimization: An analysis of selected algorithms on the CEC 2013 LSGO benchmark suite. Swarm Evol. Comput. 2019, 50, 100428. [Google Scholar] [CrossRef]

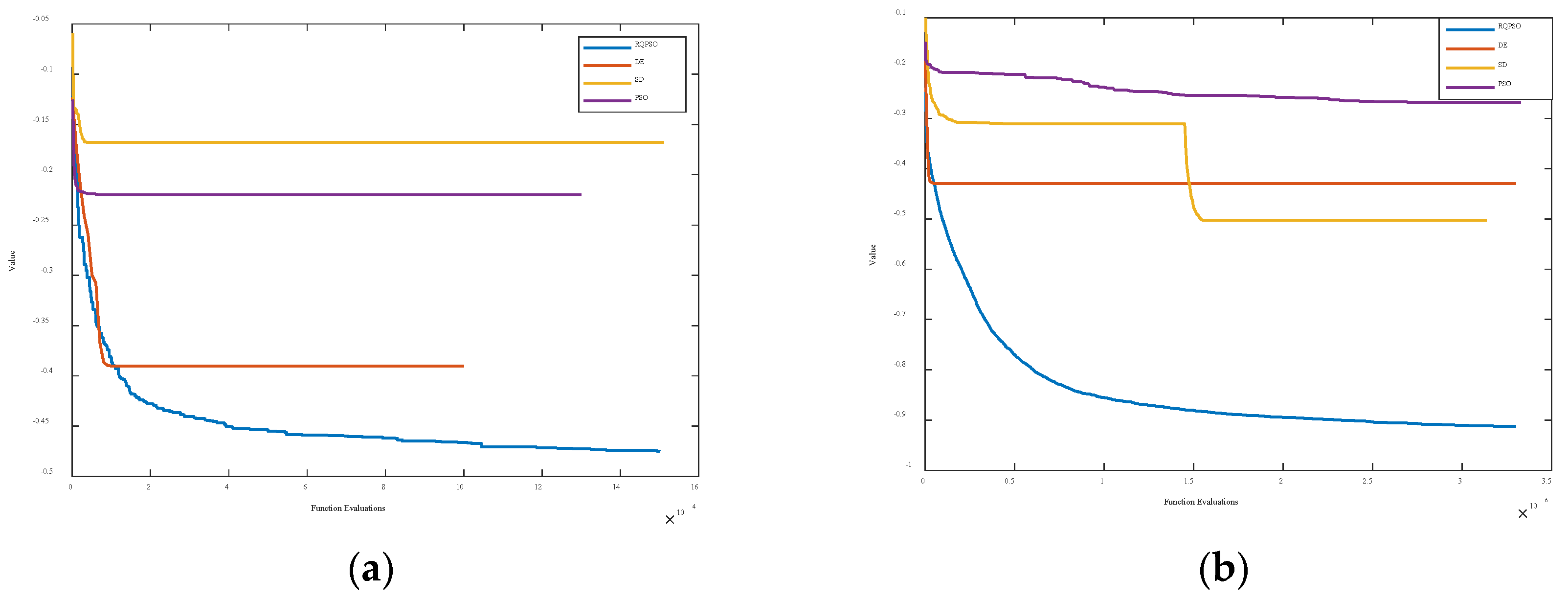
| 0.01 | 0.05 | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 | 1 | Average | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.01 | 8.19 × 102 | 7.94 × 102 | 7.73 × 102 | 8.89 × 102 | 8.90 × 102 | 8.14 × 102 | 7.59 × 102 | 8.60 × 102 | 8.25 × 102 | |
| 0.05 | 7.90 × 102 | 8.16 × 102 | 8.54 × 102 | 8.50 × 102 | 8.74 × 102 | 9.46 × 102 | 8.38 × 102 | 8.38 × 102 | 8.51 × 102 | |
| 0.1 | 7.86 × 102 | 8.87 × 102 | 8.59 × 102 | 8.77 × 102 | 8.41 × 102 | 8.06 × 102 | 8.33 × 102 | 7.55 × 102 | 8.30 × 102 | |
| 0.3 | 8.94 × 102 | 8.32 × 102 | 8.12 × 102 | 8.04 × 102 | 8.16 × 102 | 7.89 × 102 | 8.48 × 102 | 8.85 × 102 | 8.35 × 102 | |
| 0.5 | 8.32 × 102 | 9.04 × 102 | 8.16 × 102 | 7.42 × 102 | 7.99 × 102 | 7.98 × 102 | 8.37 × 102 | 7.67 × 102 | 8.12 × 102 | |
| 0.7 | 9.15 × 102 | 8.22 × 102 | 8.46 × 102 | 8.38 × 102 | 8.56 × 102 | 7.47 × 102 | 8.74 × 102 | 8.82 × 102 | 8.48 × 102 | |
| 0.9 | 9.33 × 102 | 9.30 × 102 | 8.65 × 102 | 8.22 × 102 | 9.00 × 102 | 8.46 × 102 | 8.96 × 102 | 8.35 × 102 | 8.79 × 102 | |
| 1 | 9.78 × 102 | 9.26 × 102 | 8.13 × 102 | 8.44 × 102 | 8.30 × 102 | 9.07 × 102 | 9.75 × 102 | 8.98 × 102 | 8.97 × 102 | |
| Average | 8.68 × 102 | 8.64 × 102 | 8.30 × 102 | 8.33 × 102 | 8.51 × 102 | 8.32 × 102 | 8.58 × 102 | 8.40 × 102 | ||
| RQPSO | DE | PSO | SD | ||
|---|---|---|---|---|---|
| 50 | 3 | −6.1752 × 10−2(4.9 × 10−3) | −2.6914 × 10−2(3.2 × 10−3) | −2.6504 × 10−2(3.0 × 10−3) | −6.1607 × 10−2(4.7 × 10−3) |
| 50 | 5 | −1.0293 × 10−1(5.9 × 10−3) | −4.0609 × 10−2(5.1 × 10−3) | −3.5358 × 10−2(6.4 × 10−3) | −1.0289 × 10−1(5.8 × 10−3) |
| 50 | 7 | −1.4504 × 10−1(9.9 × 10−3) | −5.0532 × 10−2(8.0 × 10−3) | −4.3870 × 10−2(5.4 × 10−3) | −1.4231 × 10−1(1.2 × 10−2) |
| 50 | 9 | −1.9149 × 10−1(1.1 × 10−2) | −5.8637 × 10−2(1.4 × 10−2) | −5.2653 × 10−2(1.0 × 10−2) | −1.9150 × 10−1(1.1 × 10−2) |
| 100 | 3 | −4.5067 × 10−2(1.3 × 10−3) | −1.5092 × 10−2(2.3 × 10−3) | −1.2780 × 10−2(1.4 × 10−3) | −4.4553 × 10−2(1.0 × 10−3) |
| 100 | 5 | −7.2857 × 10−2(3.0 × 10−3) | −1.9977 × 10−2(3.8 × 10−3) | −1.8332 × 10−2(2.0 × 10−3) | −7.2205 × 10−2(3.2 × 10−3) |
| 100 | 7 | −1.0462 × 10−1(3.9 × 10−3) | −2.9372 × 10−2(3.2 × 10−3) | −2.5277 × 10−2(8.0 × 10−4) | −1.0509 × 10−1(3.9 × 10−3) |
| 100 | 9 | −1.3619 × 10−1(6.0 × 10−4) | −3.1572 × 10−2(4.5 × 10−3) | −2.8639 × 10−2(9.0 × 10−4) | −1.3589 × 10−1(1.1 × 10−3) |
| 150 | 3 | −3.6335 × 10−2(1.3 × 10−3) | −8.6850 × 10−3(1.0 × 10−3) | −8.8120 × 10−3(9.0 × 10−4) | −3.5789 × 10−2(1.3 × 10−3) |
| 150 | 5 | −6.0190 × 10−2(2.6 × 10−3) | −1.2079 × 10−2(1.6 × 10−3) | −1.2042 × 10−2(1.4 × 10−3) | −5.9307 × 10−2(2.8 × 10−3) |
| 150 | 7 | −8.6039 × 10−2(7.0 × 10−4) | −1.6084 × 10−2(5.3 × 10−3) | −1.6833 × 10−2(2.2 × 10−3) | −8.4907 × 10−2(2.0 × 10−3) |
| 150 | 9 | −1.1066 × 10−1(2.8 × 10−3) | −2.1269 × 10−2(3.2 × 10−3) | −1.9045 × 10−2(3.0 × 10−4) | −1.0970 × 10−1(2.6 × 10−3) |
| 200 | 3 | −3.1323 × 10−2(1.0 × 10−3) | −6.9490 × 10−3(1.7 × 10−3) | −7.1720 × 10−3(3.0 × 10−4) | −3.0667 × 10−2(9.0 × 10−4) |
| 200 | 5 | −5.3004 × 10−2(2.0 × 10−3) | −9.8660 × 10−3(2.2 × 10−3) | −9.9820 × 10−3(1.4 × 10−3) | −5.1632 × 10−2(3.4 × 10−3) |
| 200 | 7 | −7.2677 × 10−2(1.9 × 10−3) | −1.1306 × 10−2(2.7 × 10−3) | −1.2830 × 10−2(1.1 × 10−3) | −7.2031 × 10−2(1.9 × 10−3) |
| 200 | 9 | −9.3857 × 10−2(3.2 × 10−3) | −1.2133 × 10−2(3.7 × 10−3) | −1.5398 × 10−2(1.4 × 10−3) | −9.2505 × 10−2(4.1 × 10−3) |
| 250 | 3 | −2.8527 × 10−2(5.0 × 10−4) | −5.6330 × 10−3(1.6 × 10−3) | −5.8580 × 10−3(9.0 × 10−4) | −2.7597 × 10−2(1.1 × 10−3) |
| 250 | 5 | −4.7342 × 10−2(1.0 × 10−3) | −7.0910 × 10−3(1.5 × 10−3) | −8.5570 × 10−3(1.1 × 10−3) | −4.6141 × 10−2(1.2 × 10−3) |
| 250 | 7 | −6.5982 × 10−2(4.0 × 10−3) | −1.0577 × 10−2(9.0 × 10−4) | −1.0990 × 10−2(2.0 × 10−4) | −6.5406 × 10−2(4.3 × 10−3) |
| 250 | 9 | −8.4324 × 10−2(4.0 × 10−4) | −1.1266 × 10−2(3.4 × 10−3) | −1.3213 × 10−2(1.6 × 10−3) | −8.5312 × 10−2(4.0 × 10−4) |
| RQPSO | DE | PSO | SD | ||
|---|---|---|---|---|---|
| 50 | 3 | −5.1412 × 10−1(3.6 × 10−2) | −3.6914 × 10−1(3.9 × 10−2) | −2.2311 × 10−1(3.7 × 10−2) | −1.5535 × 10−1(4.0 × 10−2) |
| 50 | 5 | −7.2470 × 10−1(4.3 × 10−2) | −5.4939 × 10−1(4.4 × 10−2) | −3.4967 × 10−1(3.9 × 10−2) | −2.9375 × 10−1(1.3 × 10−1) |
| 50 | 7 | −8.4877 × 10−1(2.4 × 10−2) | −6.4097 × 10−1(4.4 × 10−2) | −4.2784 × 10−1(3.7 × 10−2) | −3.7782 × 10−1(1.4 × 10−1) |
| 50 | 9 | −9.5784 × 10−1(2.5 × 10−2) | −6.4802 × 10−1(2.5 × 10−2) | −4.7087 × 10−1(4.2 × 10−2) | −4.5747 × 10−1(2.7 × 10−2) |
| 50 | 11 | −9.7983 × 10−1(4.8 × 10−3) | −7.6750 × 10−1(3.8 × 10−2) | −5.2336 × 10−1(2.5 × 10−2) | −5.4464 × 10−1(5.9 × 10−2) |
| 100 | 3 | −4.5088 × 10−1(6.3 × 10−2) | −2.7348 × 10−1(2.8 × 10−2) | −1.6399 × 10−1(2.9 × 10−2) | −1.2822 × 10−1(6.4 × 10−2) |
| 100 | 5 | −7.0184 × 10−1(5.8 × 10−2) | −3.9794 × 10−1(3.5 × 10−2) | −2.3570 × 10−1(1.6 × 10−2) | −2.1470 × 10−1(5.6 × 10−2) |
| 100 | 7 | −8.4863 × 10−1(3.8 × 10−2) | −4.8878 × 10−1(5.2 × 10−2) | −2.8928 × 10−1(4.1 × 10−2) | −3.2030 × 10−1(1.2 × 10−1) |
| 100 | 9 | −9.3729 × 10−1(9.1 × 10−3) | −5.6107 × 10−1(5.5 × 10−2) | −3.3634 × 10−1(2.7 × 10−2) | −4.0881 × 10−1(6.0 × 10−2) |
| 100 | 11 | −9.6894 × 10−1(2.1 × 10−2) | −5.7446 × 10−1(2.5 × 10−2) | −3.6837 × 10−1(3.9 × 10−2) | −3.9402 × 10−1(3.8 × 10−2) |
| 150 | 3 | −4.5232 × 10−1(4.0 × 10−2) | −2.1901 × 10−1(1.5 × 10−2) | −1.3250 × 10−1(3.0 × 10−2) | −1.0771 × 10−1(4.3 × 10−2) |
| 150 | 5 | −7.1913 × 10−1(3.6 × 10−2) | −3.5151 × 10−1(2.1 × 10−2) | −1.8971 × 10−1(2.0 × 10−2) | −2.2270 × 10−1(4.9 × 10−2) |
| 150 | 7 | −8.4141 × 10−1(5.1 × 10−2) | −4.4002 × 10−1(1.7 × 10−2) | −2.4282 × 10−1(3.1 × 10−2) | −2.6939 × 10−1(1.5 × 10−1) |
| 150 | 9 | −9.3148 × 10−1(2.7 × 10−2) | −4.6331 × 10−1(2.5 × 10−2) | −2.6749 × 10−1(1.9 × 10−2) | −3.507 × 10−1(6.2 × 10−2) |
| 150 | 11 | −9.5823 × 10−1(1.9 × 10−2) | −5.4493 × 10−1(2.9 × 10−2) | −3.0970 × 10−1(2.1 × 10−2) | −3.9021 × 10−1(1.0 × 10−1) |
| 200 | 3 | −4.5178 × 10−1(4.9 × 10−2) | −1.8594 × 10−1(1.7 × 10−2) | −1.1556 × 10−1(1.9 × 10−2) | - 9.438 × 10−2(3.1 × 10−2) |
| 200 | 5 | −7.0589 × 10−1(4.6 × 10−2) | −3.0637 × 10−1(1.3 × 10−2) | −1.6907 × 10−1(1.2 × 10−2) | −1.9180 × 10−1(6.6 × 10−2) |
| 200 | 7 | −8.4805 × 10−1(4.5 × 10−2) | −3.8202 × 10−1(2.7 × 10−2) | −2.1149 × 10−1(1.3 × 10−2) | −2.5795 × 10−1(1.1 × 10−1) |
| 200 | 9 | −9.1661 × 10−1(4.3 × 10−2) | −4.2616 × 10−1(2.2 × 10−2) | −2.3520 × 10−1(2.9 × 10−2) | −3.1237 × 10−1(8.2 × 10−2) |
| 200 | 11 | −9.5415 × 10−1(2.1 × 10−2) | −4.3796 × 10−1(2.0 × 10−2) | −2.6385 × 10−1(2.2 × 10−2) | −3.1408 × 10−1(7.2 × 10−2) |
| 250 | 3 | −4.4076 × 10−1(5.2 × 10−2) | −1.6892 × 10−1(1.2 × 10−2) | −1.0321 × 10−1(2.2 × 10−2) | −1.1178 × 10−1(5.2 × 10−2) |
| 250 | 5 | −7.1519 × 10−1(6.4 × 10−2) | −2.6108 × 10−1(2.1 × 10−2) | −1.4771 × 10−1(1.7 × 10−2) | −1.6973 × 10−1(8.9 × 10−2) |
| 250 | 7 | −8.2571 × 10−1(4.9 × 10−2) | −3.4541 × 10−1(3.7 × 10−2) | −1.8112 × 10−1(1.2 × 10−2) | −2.3421 × 10−1(9.1 × 10−2) |
| 250 | 9 | −9.1166 × 10−1(5.3 × 10−2) | −3.7130 × 10−1(2.6 × 10−2) | −2.1360 × 10−1(2.2 × 10−2) | −2.8784 × 10−1(7.0 × 10−2) |
| 250 | 11 | −9.4470 × 10−1(3.3 × 10−2) | −3.9195 × 10−1(1.6 × 10−2) | −2.3519 × 10−1(2.0 × 10−2) | −3.1495 × 10−1(5.8 × 10−2) |
| 300 | 3 | −4.3421 × 10−1(4.8 × 10−2) | −1.5870 × 10−1(1.1 × 10−2) | −8.8721 × 10−2(1.9 × 10−2) | −1.0580 × 10−1(6.7 × 10−2) |
| 300 | 5 | −7.1296 × 10−1(3.0 × 10−2) | −2.5536 × 10−1(1.0 × 10−2) | −1.3469 × 10−1(2.6 × 10−2) | −2.0357 × 10−1(1.1 × 10−1) |
| 300 | 7 | −8.4278 × 10−1(4.1 × 10−2) | −3.1615 × 10−1(1.5 × 10−2) | −1.7673 × 10−1(2.4 × 10−2) | −2.4069 × 10−1(1.2 × 10−1) |
| 300 | 9 | −9.1008 × 10−1(2.5 × 10−2) | −3.6700 × 10−1(2.1 × 10−2) | −1.8787 × 10−1(2.5 × 10−2) | −2.2254 × 10−1(6.7 × 10−2) |
| 300 | 11 | −9.2532 × 10−1(1.6 × 10−2) | −3.6645 × 10−1(1.4 × 10−2) | −2.1657 × 10−1(1.6 × 10−2) | −2.9021 × 10−1(7.4 × 10−2) |
| RQPSO | DE | PSO | SD | |||
|---|---|---|---|---|---|---|
| 0.1 | 50 | 3 | 7.5654 × 102(5.4 × 101) | 8.7453 × 102(9.1 × 101) | 9.6618 × 102(1.0 × 102) | 7.6972 × 102(5.1 × 101) |
| 0.1 | 50 | 5 | 5.8195 × 102(5.3 × 101) | 7.1959 × 102(6.7 × 101) | 9.2457 × 102(5.4 × 101) | 5.9085 × 102(3.4 × 101) |
| 0.1 | 50 | 7 | 5.2952 × 102(6.0 × 101) | 6.8135 × 102(8.3 × 101) | 9.5001 × 102(9.1 × 101) | 5.0008 × 102(4.6 × 101) |
| 0.1 | 50 | 9 | 4.1113 × 102(2.1 × 101) | 5.4901 × 102(6.1 × 101) | 8.2810 × 102(5.6 × 101) | 3.8311 × 102(3.6 × 101) |
| 0.1 | 50 | 11 | 3.3373 × 102(3.1 × 101) | 4.9010 × 102(7.4 × 101) | 8.0673 × 102(7.6 × 101) | 3.2929 × 102(8.3 × 101) |
| 0.1 | 100 | 3 | 1.3832 × 103(1.3 × 102) | 1.56508 × 103(1.3 × 102) | 1.6717 × 103(1.2 × 102) | 1.3888 × 102(9.8 × 101) |
| 0.1 | 100 | 5 | 1.1628 × 103(8.3 × 101) | 1.4193 × 103(1.2 × 102) | 1.7113 × 103(1.4 × 102) | 1.1765 × 103(5.6 × 101) |
| 0.1 | 100 | 7 | 9.1449 × 102(1.5 × 102) | 1.2066 × 103(1.6 × 102) | 1.5274 × 103(1.9 × 102) | 9.1183 × 102(1.4 × 102) |
| 0.1 | 100 | 9 | 8.3650 × 102(1.8 × 102) | 1.1813 × 103(1.2 × 102) | 1.5791 × 103(1.4 × 102) | 8.3439 × 102(1.1 × 102) |
| 0.1 | 100 | 11 | 7.2025 × 102(6.1 × 101) | 1.0461 × 103(6.2 × 10¹) | 1.5885 × 103(1.3 × 102) | 6.9774 × 102(3.5 × 101) |
| 0.1 | 150 | 3 | 1.9575 × 103(9.6 × 101) | 2.2522 × 103(8.3 × 101) | 2.3563 × 103(6.9 × 101) | 1.9948 × 103(4.8 × 101) |
| 0.1 | 150 | 5 | 1.6554 × 103(2.1 × 102) | 2.0202 × 103(1.8 × 102) | 2.2774 × 103(1.7 × 102) | 1.6435 × 102(2.3 × 102) |
| 0.1 | 150 | 7 | 1.4248 × 103(9.2 × 101) | 1.8835 × 103(2.0 × 102) | 2.2789 × 103(2.3 × 102) | 1.4109 × 103(1.4 × 102) |
| 0.1 | 150 | 9 | 1.1981 × 103(1.1 × 102) | 1.7073 × 103(1.3 × 102) | 2.1912 × 103(2.0 × 102) | 1.2012 × 103(8.1 × 101) |
| 0.1 | 150 | 11 | 1.0890 × 102(1.4 × 102) | 1.6137 × 103(1.5 × 102) | 2.1808 × 103(1.9 × 102) | 1.1446 × 103(1.5 × 102) |
| 0.1 | 200 | 3 | 2.4460 × 103(3.2 × 102) | 2.7945 × 103(4.1 × 102) | 2.9424 × 103(3.7 × 102) | 2.4734 × 103(3.3 × 102) |
| 0.1 | 200 | 5 | 2.1402 × 103(6.3 × 101) | 2.6536 × 103(1.8 × 102) | 2.9612 × 103(1.4 × 102) | 2.1360 × 103(6.9 × 102) |
| 0.1 | 200 | 7 | 1.8318 × 103(9.5 × 101) | 2.4882 × 103(1.2 × 102) | 2.8832 × 103(2.5 × 102) | 1.8842 × 103(1.3 × 102) |
| 0.1 | 200 | 9 | 1.6339 × 103(1.8 × 102) | 2.3872 × 103(1.8 × 102) | 2.9148 × 103(1.8 × 102) | 1.6754 × 103(9.6 × 101) |
| 0.1 | 200 | 11 | 1.4853 × 103(1.3 × 102) | 2.3016 × 103(4.9 × 101) | 2.8639 × 103(5.4 × 101) | 1.6038 × 103(1.5 × 102) |
| 0.01 | 50 | 3 | 7.1973 × 101(2.6 × 101) | 1.5195 × 102(1.1 × 101) | 2.0471 × 102(2.8 × 101) | 7.4976 × 101(3.1 × 101) |
| 0.01 | 50 | 5 | 5.1583 × 101(3.2 × 101) | 1.0843 × 102(2.5 × 101) | 1.7699 × 102(1.5 × 101) | 6.2757 × 101(3.0 × 101) |
| 0.01 | 50 | 7 | 4.7165 × 101(2.6 × 101) | 8.3367 × 101(2.4 × 101) | 1.7559 × 102(1.7 × 101) | 5.9280 × 101(2.8 × 101) |
| 0.01 | 50 | 9 | 2.9900 × 101(1.2 × 101) | 5.5275 × 101(1.1 × 101) | 1.3470 × 102(4.2 × 101) | 3.7299 × 101(1.3 × 101) |
| 0.01 | 50 | 11 | 3.2033 × 101(1.3 × 101) | 4.9114 × 101(1.5 × 101) | 1.0878 × 102(1.7 × 101) | 4.0297 × 101(1.4 × 101) |
| 0.01 | 100 | 3 | 1.2717 × 102(2.6 × 101) | 2.6042 × 102(3.9 × 101) | 2.9370 × 102(2.3 × 101) | 1.3677 × 101(1.6 × 101) |
| 0.01 | 100 | 5 | 9.7236 × 101(3.5 × 101) | 2.0219 × 102(7.3 × 101) | 2.7024 × 102(7.7 × 101) | 1.1542 × 102(2.5 × 101) |
| 0.01 | 100 | 7 | 7.3738 × 101(2.4 × 101) | 1.5125 × 102(1.9 × 101) | 2.3166 × 102(6.2 × 101) | 9.2338 × 101(1.2 × 101) |
| 0.01 | 100 | 9 | 6.9656 × 101(2.7 × 101) | 1.5284 × 102(5.0 × 101) | 2.8383 × 102(7.4 × 101) | 8.5461 × 101(2.1 × 101) |
| 0.01 | 100 | 11 | 5.6931 × 101(2.5 × 101) | 1.1947 × 102(2.1 × 101) | 2.1254 × 102(4.6 × 101) | 9.1455 × 101(3.0 × 101) |
| 0.01 | 150 | 3 | 1.7892 × 102(6.9 × 101) | 3.5798 × 102(8.2 × 101) | 4.0475 × 102(1.1 × 102) | 1.9433 × 102(8.0 × 101) |
| 0.01 | 150 | 5 | 1.4577 × 102(2.6 × 101) | 2.8052 × 102(5.1 × 101) | 3.4794 × 102(5,0 × 101) | 1.6277 × 102(2.9 × 101) |
| 0.01 | 150 | 7 | 1.5671 × 102(4.2 × 101) | 2.8247 × 102(3.7 × 101) | 3.6967 × 102(4.2 × 101) | 1.7908 × 102(4.9 × 101) |
| 0.01 | 150 | 9 | 1.1167 × 102(1.9 × 101) | 2.2275 × 102(3.4 × 101) | 3.1155 × 102(4.2 × 101) | 1.4133 × 102(1.4 × 101) |
| 0.01 | 150 | 11 | 1.0527 × 102(1.4 × 101) | 1.9597 × 102(2.3 × 101) | 2.9205 × 102(5.1 × 101) | 1.4177 × 102(2.1 × 101) |
| 0.01 | 200 | 3 | 2.0611 × 102(3.8 × 101) | 4.2597 × 102(1.7 × 102) | 4.4865 × 102(1.4 × 102) | 2.1420 × 102(4.6 × 101) |
| 0.01 | 200 | 5 | 1.5747 × 102(6.1 × 101) | 3.2010 × 102(2.7 × 101) | 3.5707 × 102(2.4 × 101) | 1.7202 × 102(6.8 × 101) |
| 0.01 | 200 | 7 | 1.5383 × 102(6.8 × 101) | 3.0628 × 102(8.2 × 101) | 3.9345 × 102(1.3 × 102) | 1.7395 × 102(6.3 × 101) |
| 0.01 | 200 | 9 | 1.6872 × 102(3.1 × 101) | 3.4866 × 102(8.1 × 101) | 4.3993 × 102(5.9 × 101) | 2.1596 × 102(3.5 × 101) |
| 0.01 | 200 | 11 | 1.6727 × 102(3.2 × 101) | 2.8346 × 102(4.4 × 101) | 3.5677 × 102(1.7 × 101) | 2.0155 × 102(6.7 × 101) |
| 0.001 | 50 | 3 | 2.5855 × 101(9.3 × 100) | 1.2590 × 102(3.6 × 101) | 1.5201 × 102(3.4 × 101) | 3.4484 × 101(1.7 × 101) |
| 0.001 | 50 | 5 | 8.3620 × 100(7.0 × 100) | 6.1819 × 101(2.1 × 101) | 1.2659 × 102(2.2 × 101) | 9.3607 × 100(1.1 × 101) |
| 0.001 | 50 | 7 | 6.7883 × 100(5.5 × 100) | 3.8484 × 101(6.1 × 100) | 1.0937 × 102(1.1 × 101) | 6.4283 × 100(1.1 × 101) |
| 0.001 | 50 | 9 | 6.4813 × 100(4.4 × 100) | 2.5437 × 101(8.9 × 100) | 9.5061 × 101(3.0 × 101) | 6.5565 × 100(1.0 × 101) |
| 0.001 | 50 | 11 | 3.6024 × 100(1.4 × 100) | 1.1593 × 101(2.4 × 100) | 7.9012 × 101(4.3 × 101) | 2.1094 × 100(7.7 × 10−1) |
| 0.001 | 100 | 3 | 2.8134 × 101(1.3 × 101) | 1.9378 × 102(6.1 × 101) | 2.3001 × 102(4.5 × 101) | 2.9517 × 101(1.4 × 101) |
| 0.001 | 100 | 5 | 1.5818 × 101(5.3 × 100) | 1.8256 × 102(4.2 × 101) | 2.4844 × 102(5.2 × 101) | 2.1447 × 101(8.4 × 100) |
| 0.001 | 100 | 7 | 1.1198 × 101(5.6 × 100) | 1.1245 × 102(3.5 × 101) | 1.7682 × 102(2.7 × 101) | 1.2736 × 101(9.5 × 100) |
| 0.001 | 100 | 9 | 1.3117 × 10¹(5.5 × 100) | 9.3403 × 101(4.7 × 101) | 1.8227 × 102(8.1 × 101) | 1.8515 × 101(1.4 × 101) |
| 0.001 | 100 | 11 | 7.6223 × 100(4.7 × 100) | 6.2281 × 101(1.4 × 101) | 1.4409 × 102(3.1 × 101) | 1.0546 × 101(1.0 × 101) |
| 0.001 | 150 | 3 | 3.7829 × 101(1.0 × 101) | 2.2759 × 102(1.1 × 102) | 2.5950 × 102(1.1 × 102) | 4.2692 × 101(1.4 × 101) |
| 0.001 | 150 | 5 | 2.7834 × 101(1.5 × 101) | 2.1556 × 102(6.3 × 101) | 2.7175 × 102(6.7 × 101) | 4.0423 × 101(2.5 × 101) |
| 0.001 | 150 | 7 | 1.4826 × 101(1.2 × 101) | 1.3634 × 102(3.1 × 101) | 1.9849 × 102(5.9 × 101) | 1.9988 × 101(1.5 × 101) |
| 0.001 | 150 | 9 | 1.6358 × 101(6.0 × 100) | 1.5928 × 102(3.5 × 101) | 2.4219 × 102(8.5 × 101) | 3.1013 × 101(1.6 × 101) |
| 0.001 | 150 | 11 | 1.8158 × 101(5.1 × 100) | 1.2162 × 102(2.6 × 101) | 1.9174 × 102(3.0 × 101) | 2.4575 × 101(8.0 × 100) |
| 0.001 | 200 | 3 | 3.2492 × 101(8.1 × 100) | 2.6359 × 102(1.0 × 102) | 2.8572 × 102(9.5 × 101) | 3.8216 × 101(1.6 × 101) |
| 0.001 | 200 | 5 | 2.6752 × 101(9.8 × 100) | 2.1531 × 102(9.5 × 101) | 2.5783 × 102(1.1 × 102) | 3.6128 × 101(1.7 × 101) |
| 0.001 | 200 | 7 | 2.6361 × 101(1.9 × 101) | 1.8300 × 102(1.4 × 102) | 2.2845 × 102(1.6 × 102) | 3.4054 × 101(2.6 × 101) |
| 0.001 | 200 | 9 | 1.8149 × 101(8.3 × 100) | 1.6877 × 102(6.9 × 101) | 2.1808 × 102(1.0 × 102) | 2.7946 × 101(1.1 × 101) |
| 0.001 | 200 | 11 | 2.2633 × 101(5.2 × 100) | 1.5670 × 102(3.5 × 101) | 2.0801 × 102(4.1 × 101) | 3.0098 × 101(3.9 × 100) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halimu, Y.; Zhou, C.; You, Q.; Sun, J. A Quantum-Behaved Particle Swarm Optimization Algorithm on Riemannian Manifolds. Mathematics 2022, 10, 4168. https://doi.org/10.3390/math10224168
Halimu Y, Zhou C, You Q, Sun J. A Quantum-Behaved Particle Swarm Optimization Algorithm on Riemannian Manifolds. Mathematics. 2022; 10(22):4168. https://doi.org/10.3390/math10224168
Chicago/Turabian StyleHalimu, Yeerjiang, Chao Zhou, Qi You, and Jun Sun. 2022. "A Quantum-Behaved Particle Swarm Optimization Algorithm on Riemannian Manifolds" Mathematics 10, no. 22: 4168. https://doi.org/10.3390/math10224168
APA StyleHalimu, Y., Zhou, C., You, Q., & Sun, J. (2022). A Quantum-Behaved Particle Swarm Optimization Algorithm on Riemannian Manifolds. Mathematics, 10(22), 4168. https://doi.org/10.3390/math10224168






