Abstract
Fractional Galilei invariant advection–diffusion (GIADE) equation, along with its more general version that is the GIADE equation with nonlinear source term, is discretized by coupling weighted and shifted Grünwald difference approximation formulae and Crank–Nicolson technique. The new version of the backward substitution method, a well-established class of meshfree methods, is proposed for a numerical approximation of the consequent equation. In the present approach, the final approximation is given by the summation of the radial basis functions, the primary approximation, and the related correcting functions. Then, the approximation is substituted back to the governing equations where the unknown parameters can be determined. The polynomials, trigonometric functions, multiquadric, or the Gaussian radial basis functions are used in the approximation of the GIADE. Moreover, a quasilinearization technique is employed to transform a nonlinear source term into a linear source term. Finally, three numerical experiments in one and two dimensions are presented to support the method.
Keywords:
weighted Grünwald difference; irregular domain; nonlinear functional diffusion problem; quasilinearization technique MSC:
26A33; 65M22; 65N22; 65T40
1. Introduction
The problem of diffusion has drawn significant interest and wide recognition in the scientific community in the past decade [1,2,3,4,5]. Fractional calculus has played an important role in obtaining advection–diffusion equations. The method of separation of variables, as well as the theory of eigenvalues and eigenfunctions when constructing a solution to an advection–diffusion equation, is studied in [6]. The analytical and numerical solution of a space–time fractional advection–diffusion equation with first-order accuracy in the temporal direction and second-order accuracy in the spatial direction is discussed in [7]. Moreover, the enhanced unconditionally positive finite difference method investigates the solutions to the linear and nonlinear advection–diffusion–reaction (ADR) to reduce the degree of freedom of the ADR equations [8]. A possible realization of the fractional Galilei invariant advection–diffusion (GIADE) equation is the transport of material in an external velocity or force field [9,10]. More precisely, we study the following fractional GIADE equation with the nonlinear source term
where , , the Laplacian operator is defined as , , and are specific functions, and is a real constant with the nonlinear source term . is a domain in the plane or with the boundary .
The symbol is the Riemann–Liouville fractional derivative operator of order with respect to t with the starting point at and is defined as
where is the gamma function. Chen et al. [11] have presented an implicit difference approximation with second-order spatial accuracy and first-order temporal accuracy for a variable-order GIADE equation in one dimension. Zaky et al. [12] have studied the existence and uniqueness solutions to nonlinear tempered fractional boundary value problems. Moreover, they have proved that the convergence rate for nonsmooth solutions can be enhanced by using a suitable smoothing transformation [13]. In [9], the fractional GIADE equation has been investigated by interpolating a stabilized element-free Galerkin method with the order of convergence . Moreover, in the numerical results, the effect of the advection coefficient and the smoothness of the numerical solution has been studied. There is also a wealth of literature regarding numerical solutions to the GIADE equation [14,15]. Therefore, it is more challenging to consider numerical schemes and related numerical analyses for the problem in a more general form. This article aims to describe, for the first time, a backward substitution method (BSM) for numerical approximation of a fractional problem with a coupled weighted and shifted Grünwald difference (WSGD) approximation formula and the Crank–Nicolson (C-N) technique.
First, the standard WSGD formula has been discussed in detail and successfully applied to solve fractional equations [16]. In [17], stability and consistency results for higher-order Grünwald-type formulae have been used to space fractional partial differential equations (PDEs). Finite difference schemes and the quasicompact difference schemes by shifted WSGD operators for discretizing the Riemann–Liouville fractional derivative have been established to solve the fractional diffusion equations numerically [18,19]. However, the 3-WSGD operator that was applied in [19] failed to solve the time-dependent fractional equations with unconditional stability. Wang [20] took advantage of the WSGD operator and analyzed a finite difference scheme for solving the nonlinear complex fractional Ginzburg–Landau equation. Meerschaert et al. [21,22] explored consistency and stability for numerical schemes for fractional PDEs using a shifted Grünwald formula to approximate the fractional derivative. Hence, we adopt the shifted formula to discretize the time-fractional derivative. In real applications, analytical methods cannot work well on most PDEs, but there have been many techniques to solve PDEs covered by Laplace transform method [23], the Green function method [24,25], factorization method [26,27] and so on [28,29]. This paper makes an important contribution to the literature by expressing the solution by BSM at each time step utilizing the WSGD operator. Reutskiy [30] applied the BSM based on the Fourier series expansion for solving initial and boundary value problems for fractional PDEs in one dimension. In [31], the combination of the C-N method with the BSM for solving space-fractional advection–diffusion reaction equations in one dimension has been considered. Safari and Azarsa [32] took advantage of the Müntz polynomials and numerically solved nonlinear space-fractional PDEs with meshless BSM.
Because of the nonlocal operator of the fractional derivative, it is challenging to harness using the BSM as a meshfree method for the fractional problem. So, the algorithm of the method contains two stages. First, the WSGD operator to discretize the involved fractional derivative is used. Then, the expression of the approximation is obtained by the sum of two parts, which includes the free parameters and already satisfies all the boundary conditions of the original problem but does not satisfy the equation. The parameters are determined in the second stage by the backward substitution into the original equation. The first part of the approximate solution, which is called primary approximation, is obtained from the boundary conditions, and the second part are the corrected basis functions, which consist of trigonometric functions and radial basis functions (RBFs).
It should be noted here that, for the first time, the method for the numerical approximation of fractional problems in two dimensions and three dimensions in the near future is applied. The approach consists of the advantages of RBFs in reducing the condition number of the matrix [33,34]. However, unlike the singular boundary method, the approach can be applied to problems in which equations contain a nonlinear term with variable coefficients [1,35]. Furthermore, the method of fundamental solutions is applied to solve the mentioned problem [36,37]. However, the truth of the real-world problems is that the determination of the optimal sources in the method has remained an open issue.
To solve the fractional GIADE equation, first, a mesh and discretization of the general equation in time is introduced, then the C-N scheme and the WSGD operator to discretize the involved fractional derivative (Section 2) are coupled. Next, in Section 3, the numerical scheme’s BSM to solve the consequent equation is proposed. Finally, in Section 4, the results of some numerical experiments, including a two-dimensional GIADE equation with nonlinear source term highlighting the efficiency of the BSM is given.
2. The Time Discretization Approximation
In this section, we introduce the concepts that are applied for discretization of the time variable. For a fixed positive number , the grid points in the time interval are labeled . It is well known that the approximation of the first-order derivative is as follows:
Second-order approximations of the Riemann–Liouville fractional derivative (the WSGD operators), which is important for the numerical approximation of fractional differential equations, are given as follows [18,38,39]
where are the normalized Grünwald weights and the coefficients of the series of the function and can be evaluated as
and
Denoting the approximations of , , and by , , and , respectively, omitting the truncation error and using the C-N technique for time discretization of Equation (1), we obtain the following equation for
Using the Grünwald formula in Equation (4) and rearranging Equation (7), we obtain the following equations:
Now, we apply the quasilinearization technique [40] which makes to a linear function of . Suppose that are the given functions of , which are the initial approximations of the corresponding exact values at the steps. Then, we have the relations . Assuming that are small values, the linearization of G is
By substitution Equation (9) in Equation (8), we have
We denote the left-hand side of the Equation (8) as , then the above equation can be written as
with the boundary equation , in Equation (1) where
Notice that for , from Equation (8) and initial condition , we have
We are now ready to introduce the BSM method for solving Equation (11) in the next section. We extend the BSM approach for governing Equation (11) in each step time. This extension is based on RBFs and a particular solution method. We later discuss the method for one-dimensional and two-dimensional cases.
3. Description of the BSM Method
Now, the meshless BSM method is described as a numerical tool for the solution of Equation (11). The approach for solving the inhomogeneous problem is to express the solution by the sum of two parts of a particular solution and as
where approximates the boundary condition Equation (11)
and is the correcting solution of the problem with the homogeneous boundary condition as follows:
To obtain the approximate solution, we consider the series
where are the multiquadric or the Gaussian RBFs on , is a defined correcting function that can be approximated by using basis functions, and are unknown coefficients. Moreover, is taken in such a way that satisfy the boundary condition
In order to approximate and , we chose a system of trigonometric functions in a one-dimensional problem and a two-dimensional problem , such that , therefore,
where and are the unknown coefficients which can be determined by enforcing the Equation (19) on the boundary nodes as
where the number of boundary collocation nodes K is larger than the number of basis function .
Substituting a set of collocation points into Equation (21), can be achieved.
4. Numerical Results in Two Space Dimensions
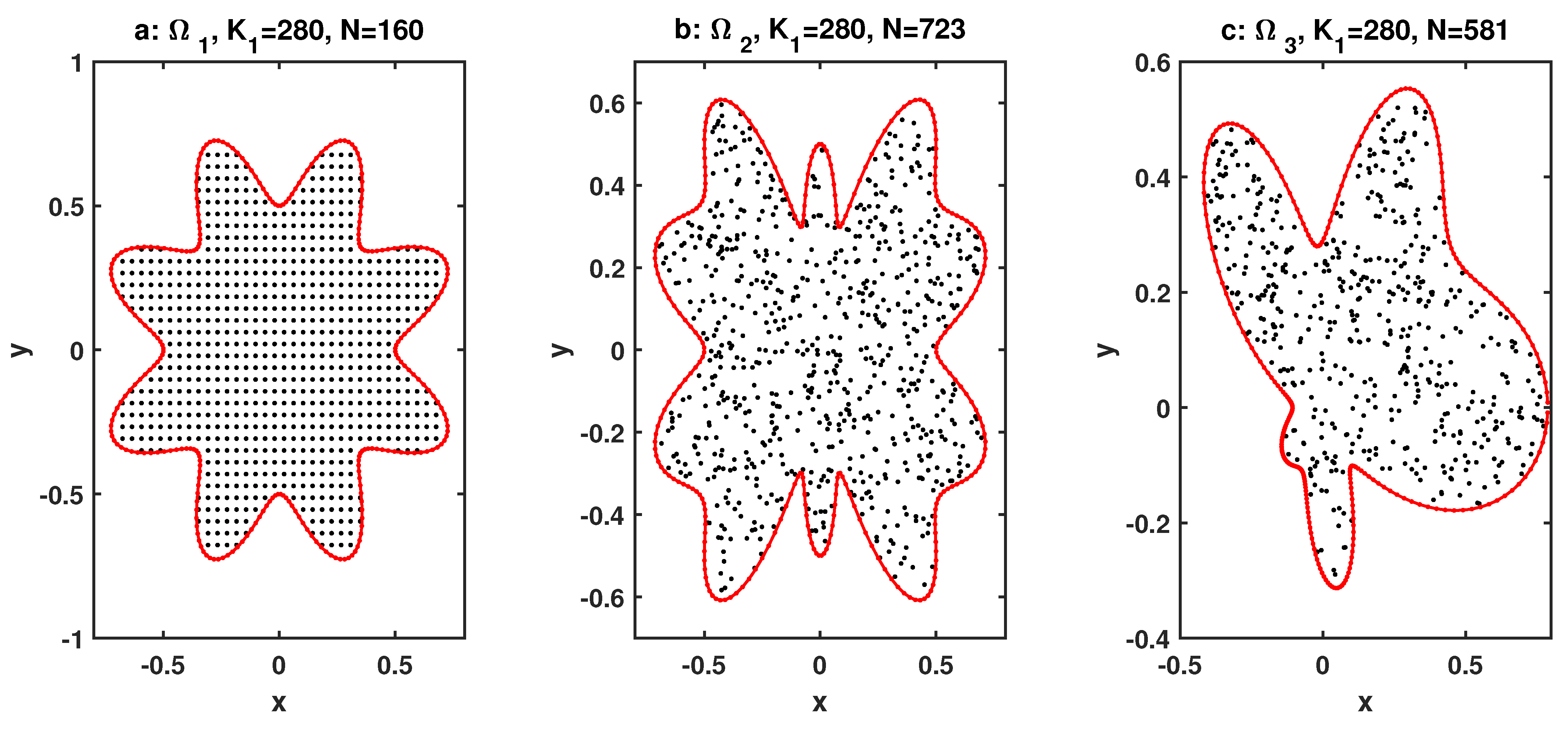
In this section, we present numerical results for the fractional GIADE (1) with and on the domains, as shown in Figure 1. Figure 1a is the star domain which is discretized with uniform distribution. The boundary of the irregular domain is determined by , where and m are assumed to be 8. Figure 1b,c are shown to be irregular geometries where and define the irregular domains and with an irregular distribution of nodes, respectively. In these examples, we report the following error indicators:
where u and are analytical and numerical solutions, respectively. The computational order of the new technique is computed by
in which and are errors corresponding to grids with mesh sizes and , respectively.
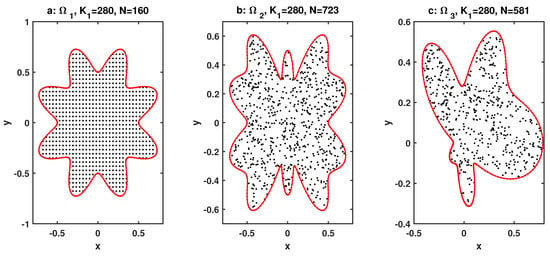
Figure 1.
Irregular domain for Examples 2 and 3.
Remark 1.
We have performed our calculations by applying MATLAB software with a Core i7-8565 PC with a 1.80 GHz CPU and 8-GB RAM.
Example 2.

We consider the fractional GIADE (1) with . The initial value is given by
We apply the new approach to obtain the solution on the domains , , and . To investigate the effect of the chosen basis function and domain on the accuracy of the proposed method, the results obtained using two different RBFs are shown in Table 1.

Table 1.
and for the BSM method and the effect of the chosen basis function and domain at times for Example 2 where , , , , , , , , .
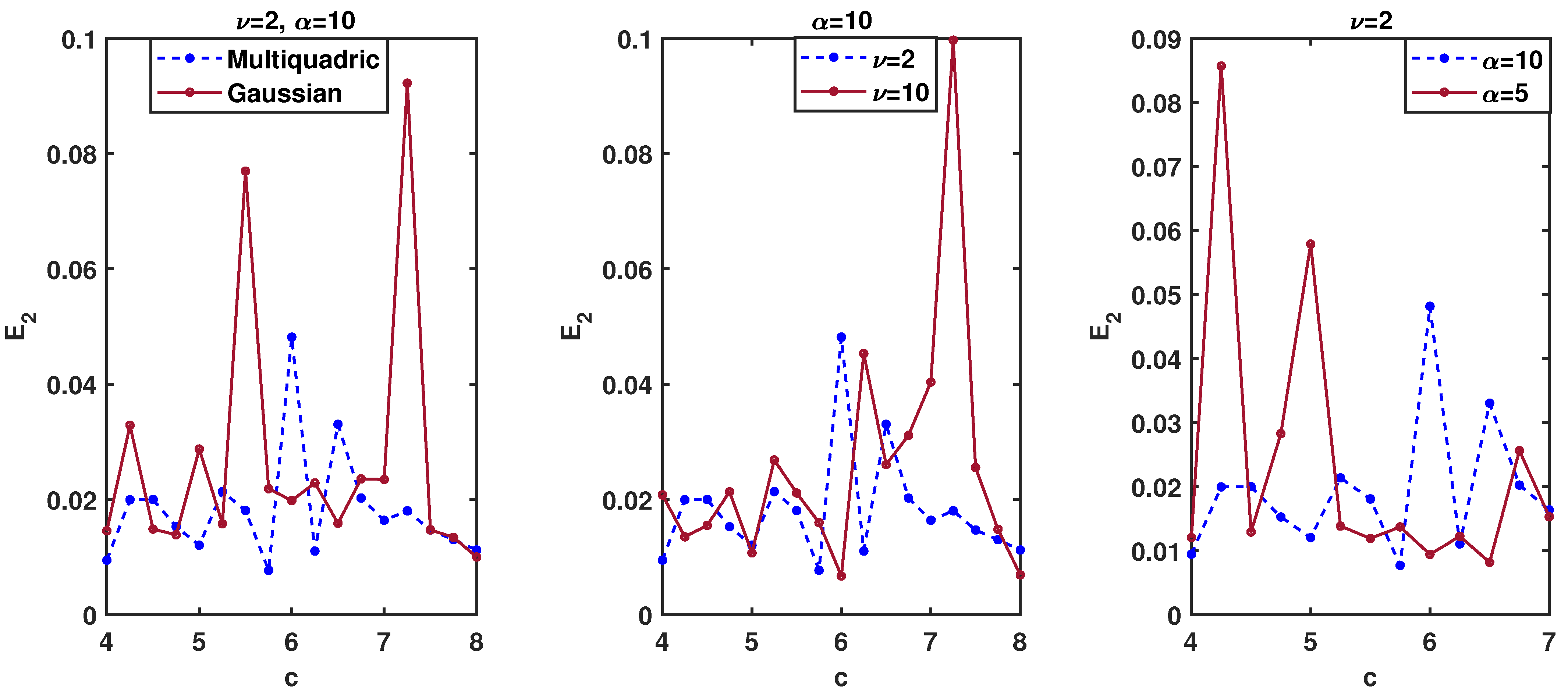
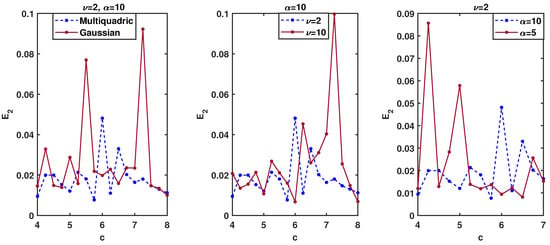
When running our algorithms using the same parameters as in Table 1, we obtain the results depicted in Figure 2 for different shape parameters c on the domains . It can be observed that the errors for Multiquadric and Gaussian basis functions decrease with the increase in c, even in the case of the multiquadric RBF for advection coefficients and , and and . It should be remarked that the optimal shape parameter is very difficult to determine. However, for the best accuracy of the method that is sensitive to the shape parameter c, we chose for the multiquadrics and the Gaussian RBF.

Figure 2.
Comparison with respect to the shape parameter c on the domains at time for Example 2 where .
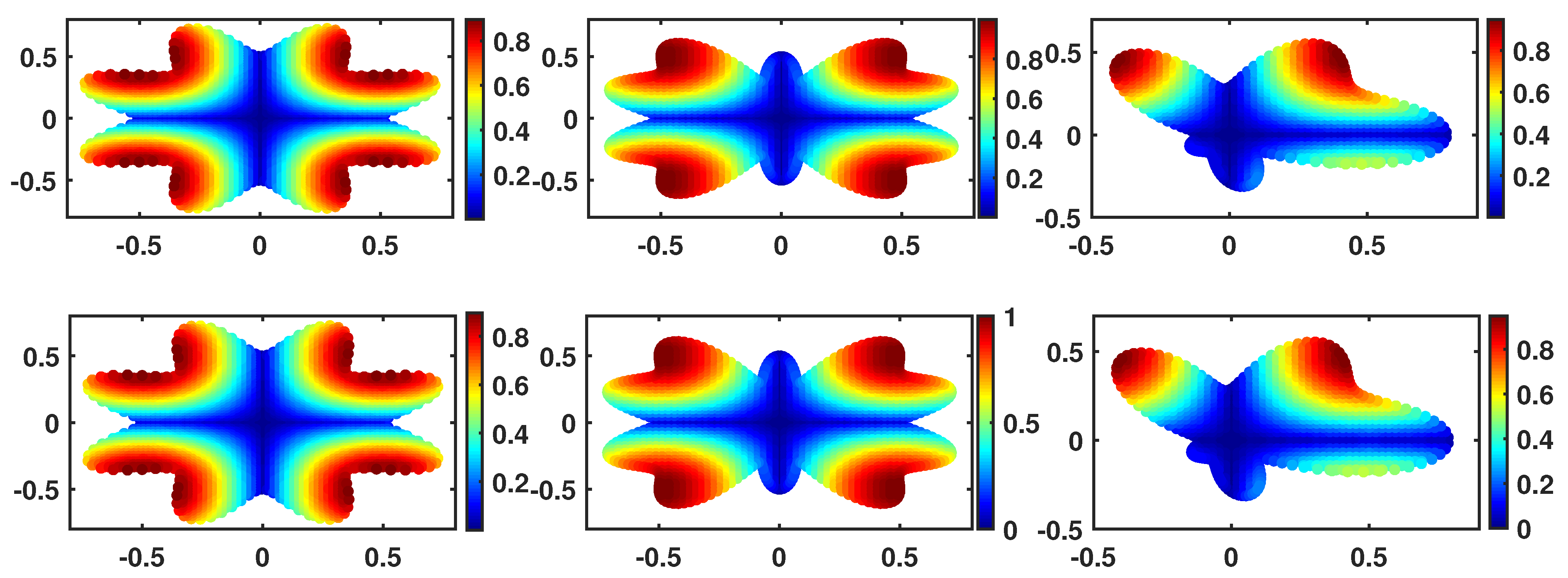
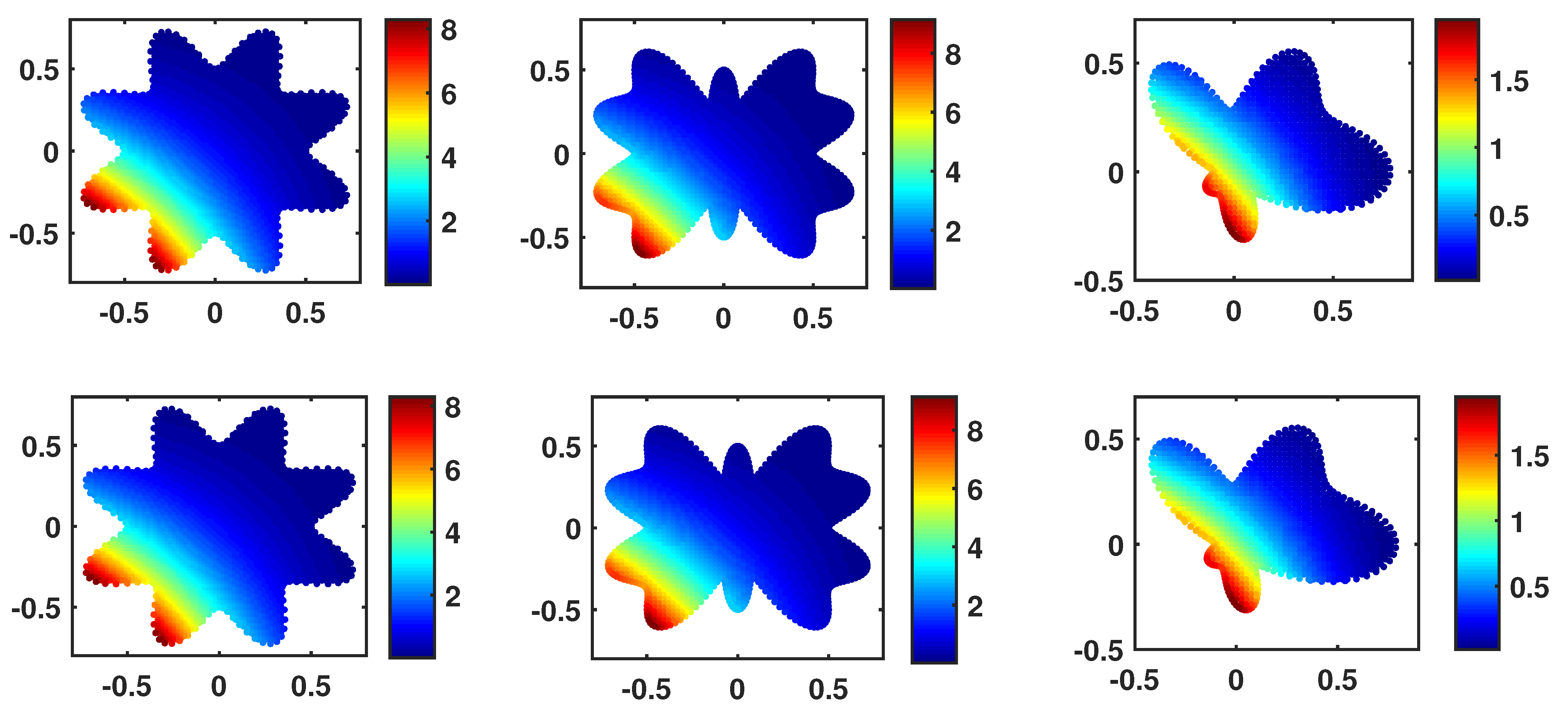
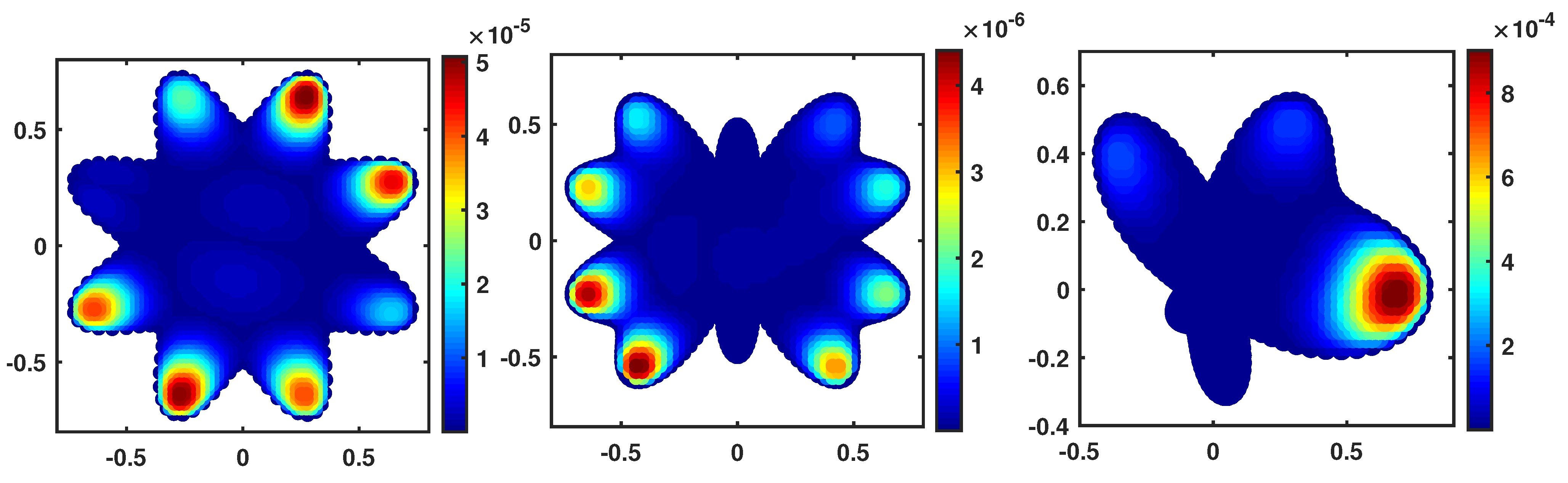
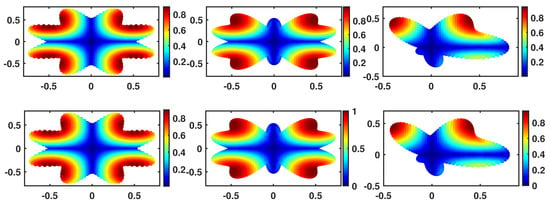
The numerical and analytical solutions and error function for the Gaussian basis function are shown in Figure 3 and Figure 4. The first row of Figure 3 is the numerical solution, and the second one is the analytical solution. It is easy to find that the error in the middle of the domain tends to decrease. We can even observe the effect of the distributed nodes inside the domains and the behavior of the error from this figure.

Figure 3.
Numerical and analytical solution at with in , , and for Example 2.

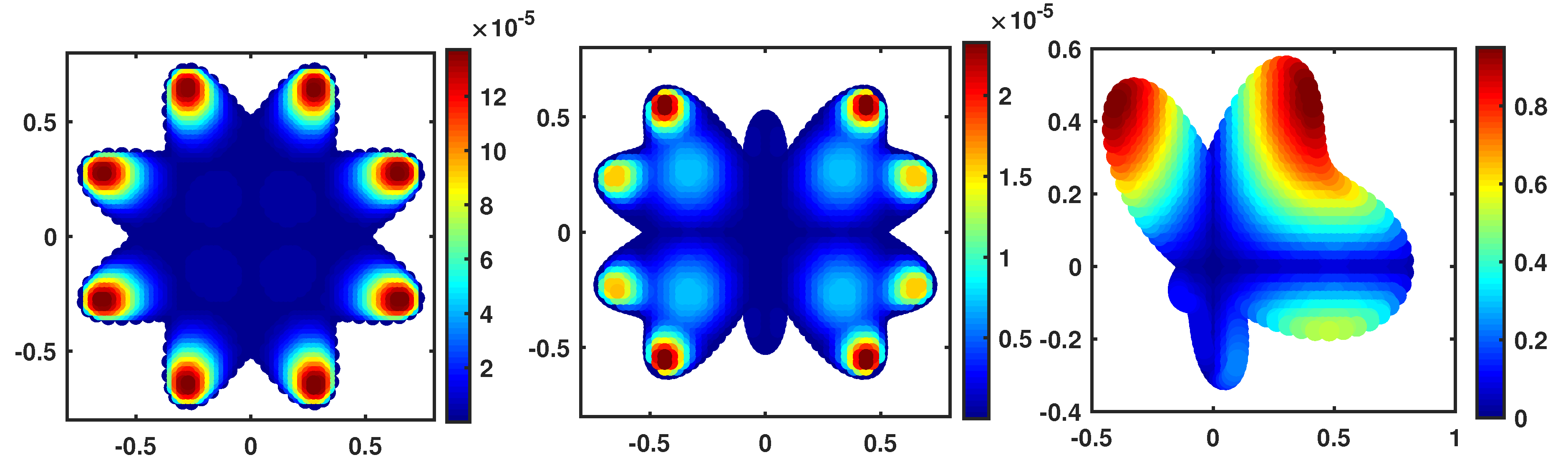
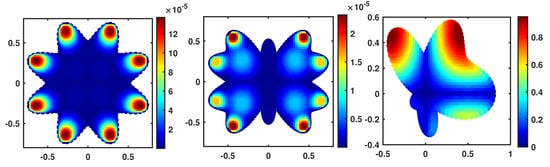
Figure 4.
–error function at with in , , and for Example 2.
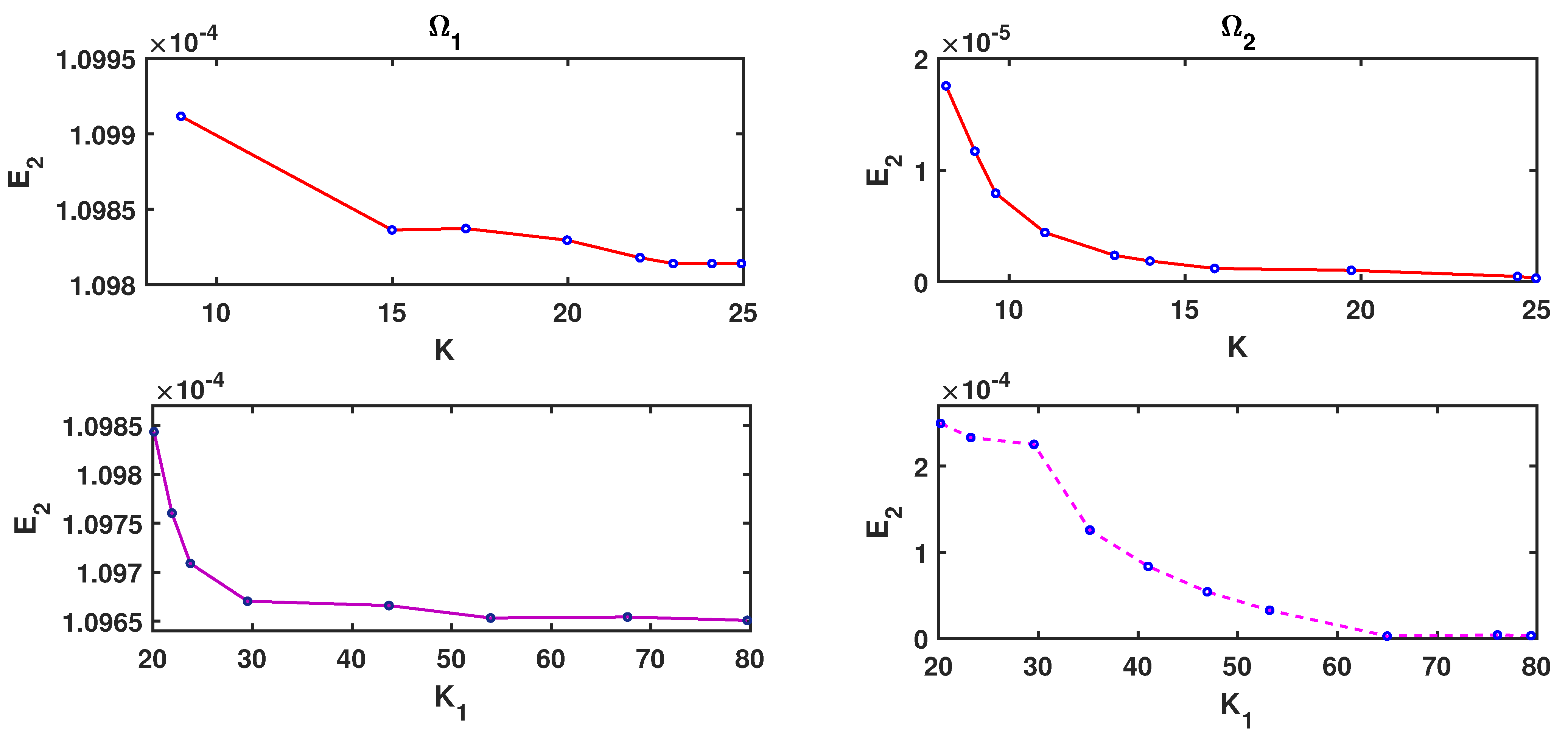
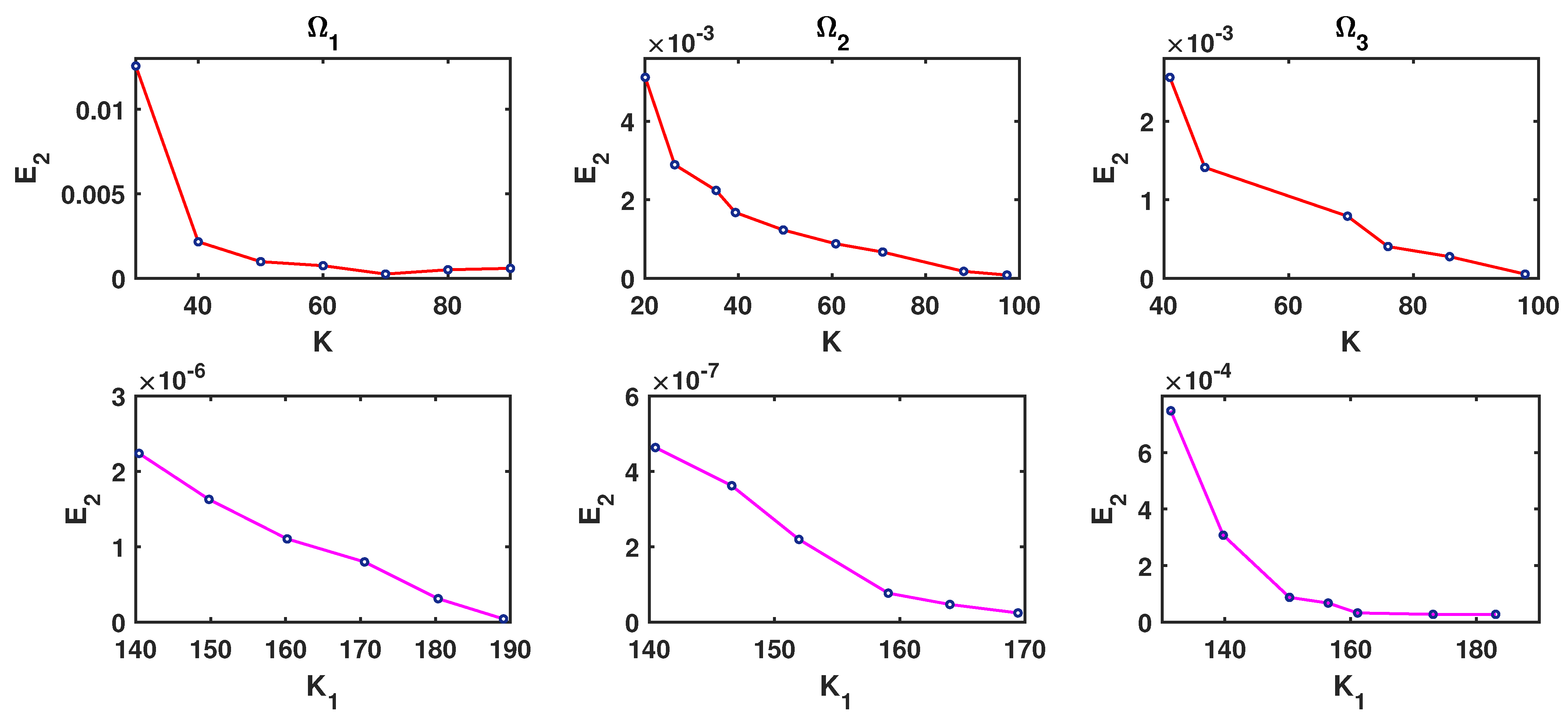
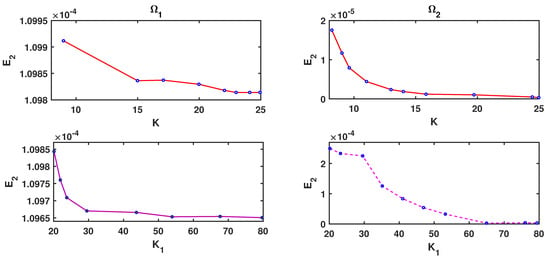
Different factors affect the convergence rate of the proposed methods. Obviously, increasing the number of K and improves the accuracy of the method. Now, we test the problems with multiquadric basis function for two types of geometries to show the result of our method. The errors are depicted in Figure 5, which show a little better results as we increase the number of K or . Figure 6a shows and errors and the effect of the fractional order at in . We can see that the error drops with the increase in fractional order γ. Moreover, from Figure 6b, it can be observed that the error value has an increasing trend for different time t.

Figure 5.
–errors and convergence for Example 2 in different domains at , where , , , , , , , (red) , and (pink) .

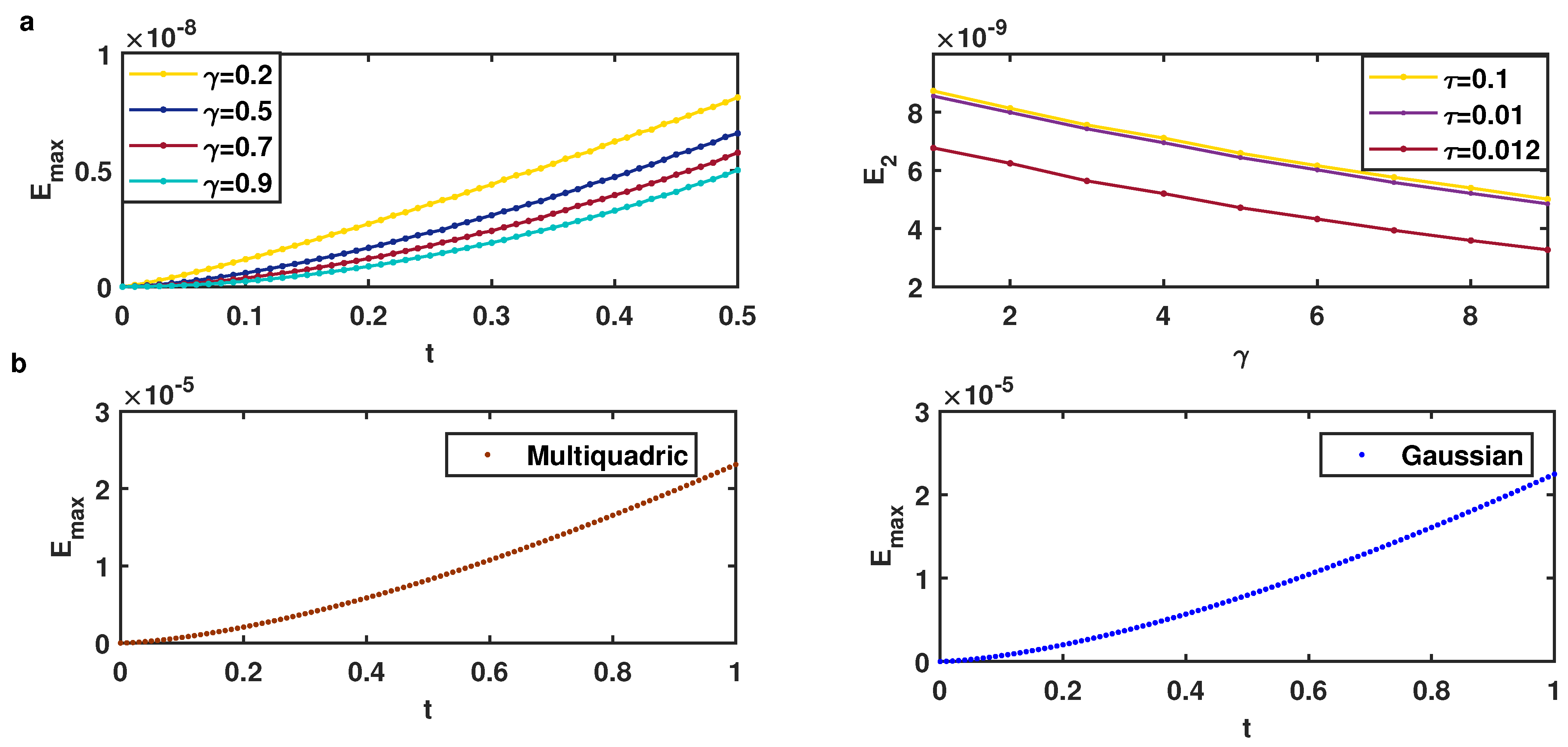
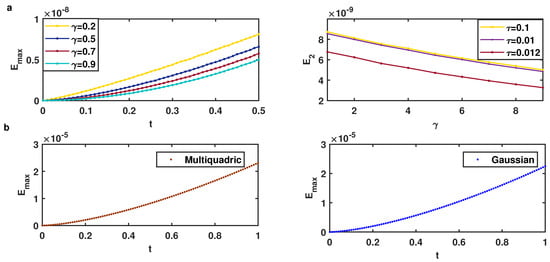
Figure 6.
and and the effect of the fractional order in time for Example 2, where (a) , , , , , , , , and (b) .
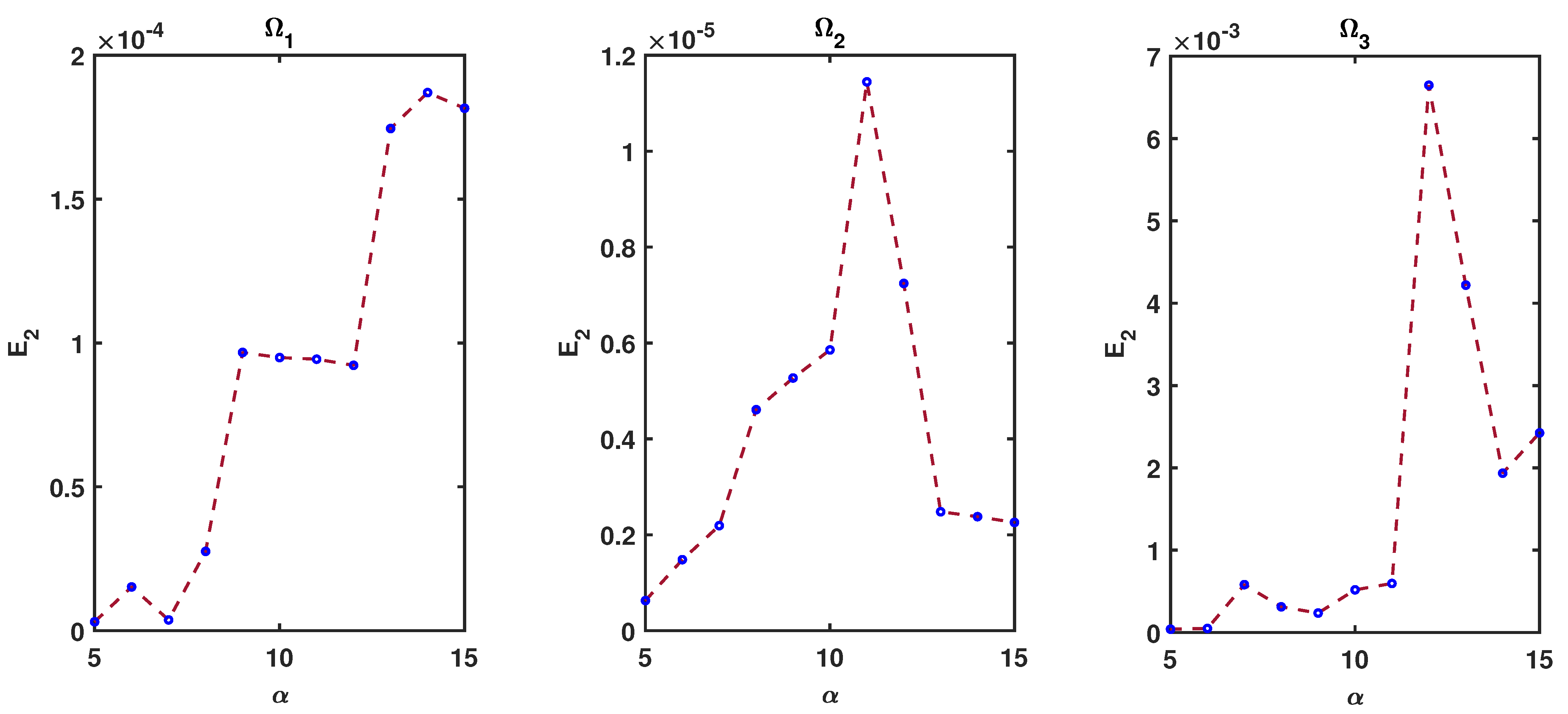
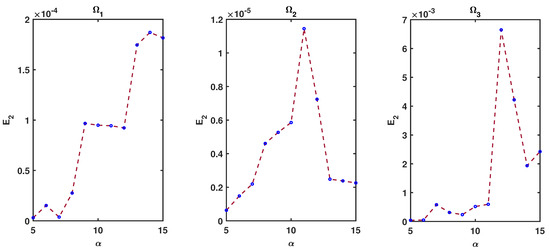
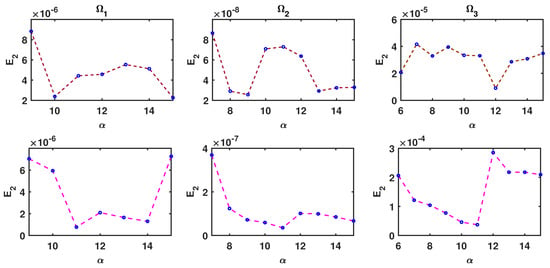
The values of errors yielded from the proposed method via different values of α and domains are reported for multiquadric basis functions in Figure 7. These figures confirm that the accuracy of the method improves by a small enough α.

Figure 7.
errors in different at and , , , , , , , and for Example 2.
Example 3.


The following fractional GIADE with an analytical solution is considered:
We chose a suitable right-hand-side function f such that the exact solution to (26) is [9]. First, we investigated the effect of the time, time step, and domain on the accuracy of the proposed method. In Table 2, we list the evolution of the solution at time and with . Next, we investigated the effect of the time steps and domain on the maximum errors. A comparison of numerical solutions using the BSM method and ISEFG method that is introduced in [9,41,42] is listed in Table 3. The stability of the present method and ISEFG method can be seen from the obtained results. However, the error reduction with decreasing time steps is negligible in our results.

Table 2.
and for the BSM method and the effect of time and domain for Example 3, where , , , , , , , , and .

Table 3.
and the effect of the time steps and domain at times for Example 3, where , , , , , , , and .
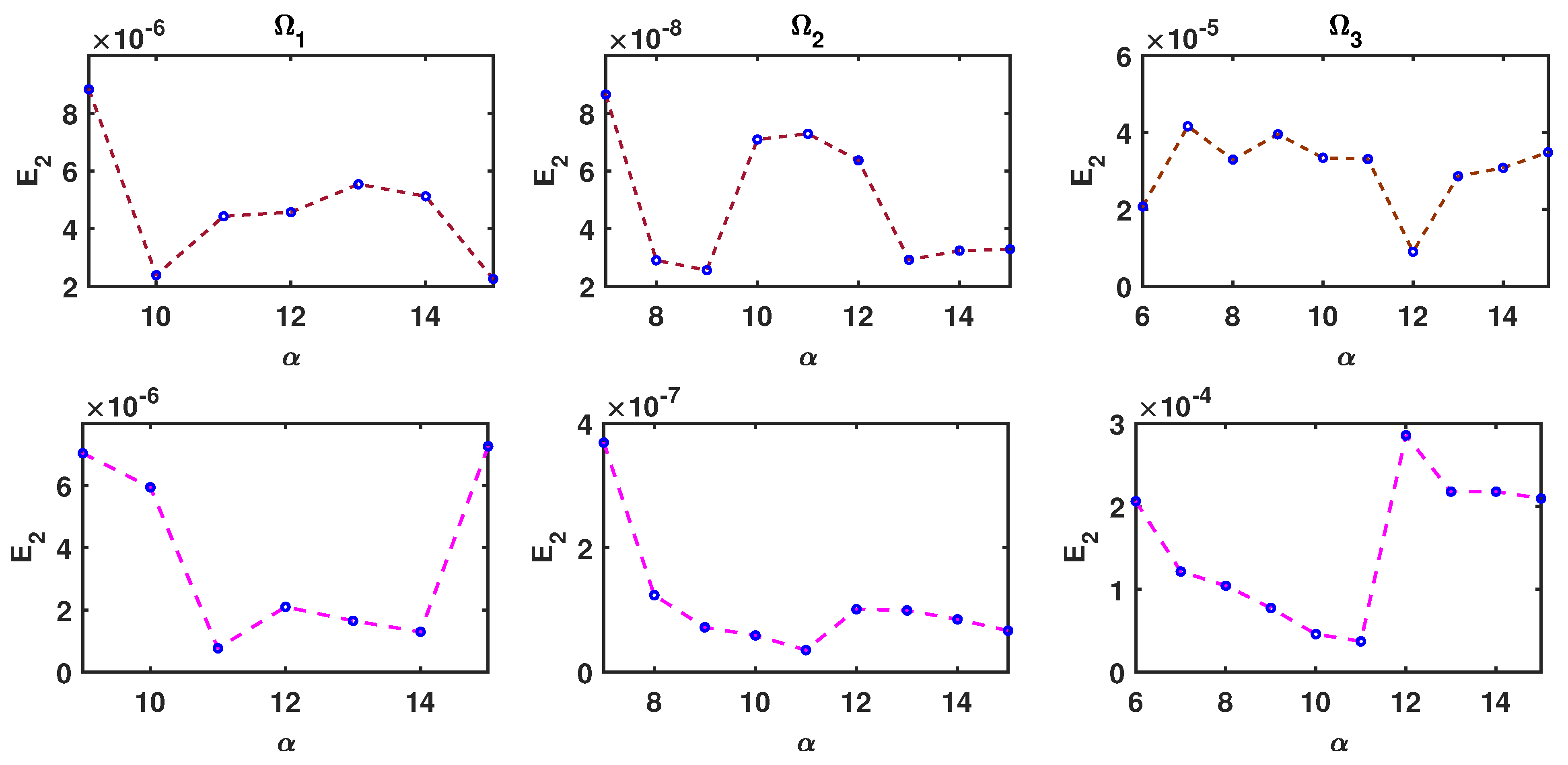
The values of errors yielded from the proposed method via different values of α and domains are reported for multiquadric basis functions in Figure 8. Using the same parameters as in Figure 8 and the best choice of α in every domain, graphs of errors for different values of K and for multiquadric functions are shown in Figure 9. Hence, we observe that the convergence rate will be better when K and are big enough. A contour plot for the behavior of numerical and analytical solutions and the error function for the multiquadric basis function are shown in Figure 10 and Figure 11. We can even observe the effect of distributed nodes inside the domains and the behavior of the error from these figures. When running our algorithms using the same parameters as in Figure 9, different shape parameter c and the order of the Riemann–Liouville fractional derivatives γ and M and N do not play any significant role in the solution quality in this example.

Figure 8.
–errors with respect to at , where (red) , (pink) , , , , , , , , and for Example 3.

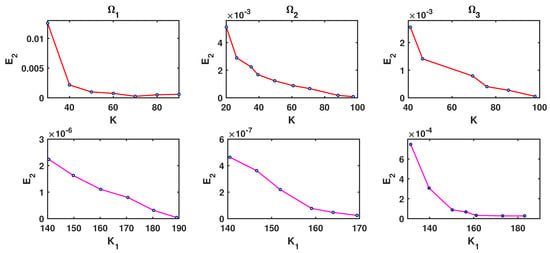
Figure 9.
–errors and convergence for Example 3 in different domains at , where , , , , , , , (red) , and (pink) .

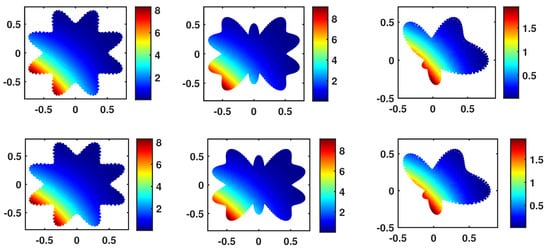
Figure 10.
Contour plot of (first row) numerical and (second row) analytical solutions at , with in , , and for Example 3.

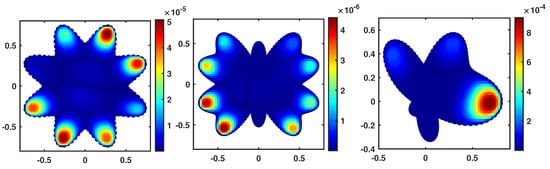
Figure 11.
–error function at with in , , and for Example 3.
To verify the theoretical results and show the efficiency and applicability of the proposed schemes, as well as the extension of the proposed schemes to the corresponding one-dimensional problems and even three-dimensional problems, a fractional GIADE with a nonhomogeneous source term in one-space dimension is presented in the next example.
Example 4.

We consider the fractional GIADE with a nonhomogeneous source term on the domain
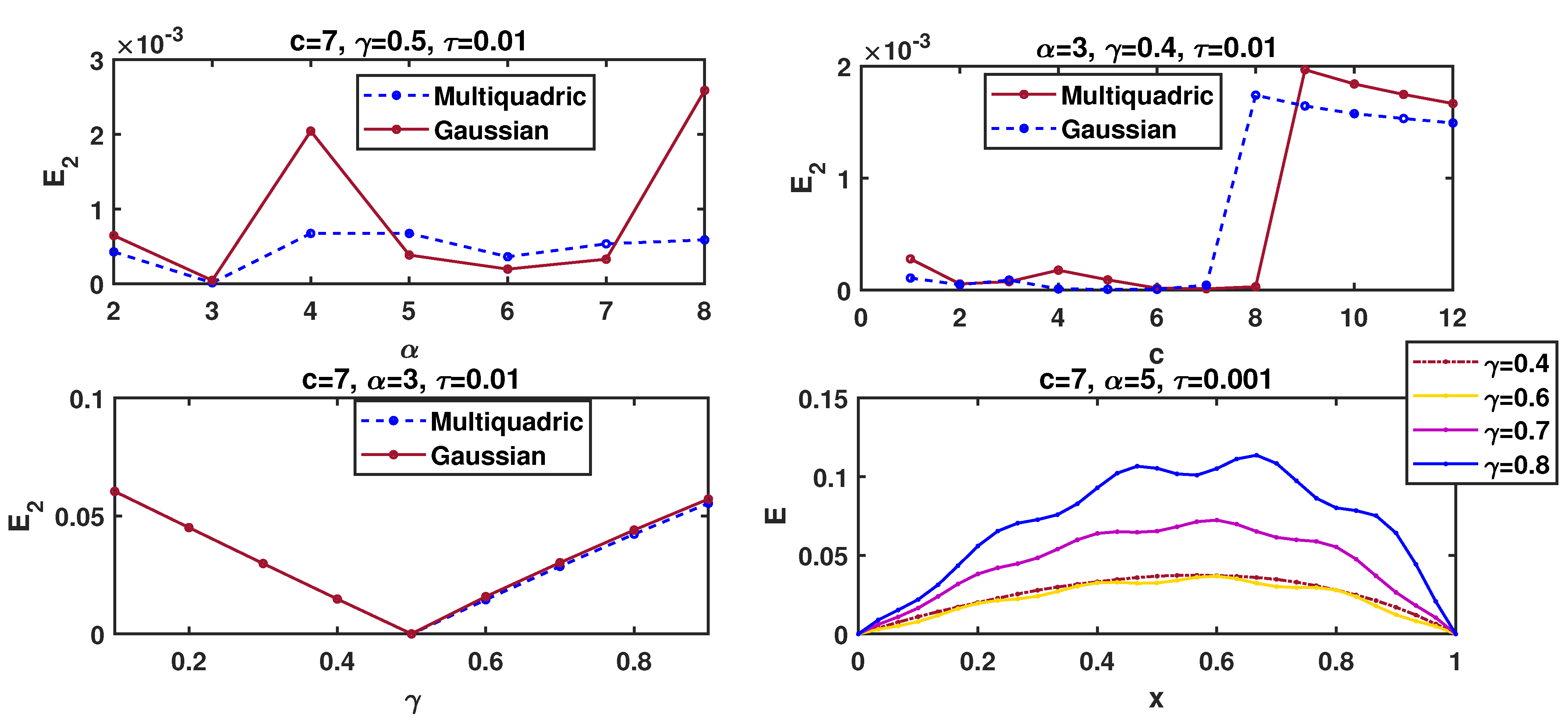
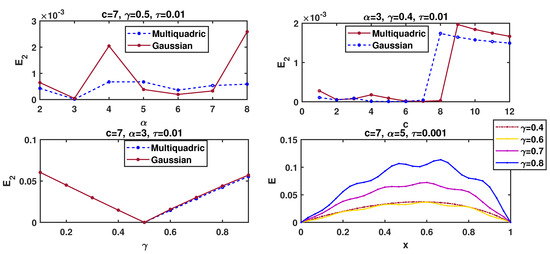
The exact solution of the problem (27) is . Similar to the previous example, the boundary and initial condition are obtained from the exact solution. First, we solve the problem by using the different parameters. Figure 12 illustrates how the shape parameters c and α play a significant role in the solution quality. It can be observed that the errors for multiquadric and Gaussian basis functions increase with the increase in c, and the good shape parameter range is between 1 and 7. Moreover, from the second row of the figure, it can be observed that the error value has an increasing trend when γ is arising from γ = 0.5.

Figure 12.
Comparison errors with respect to , c, and at time for Example 4, where , , , and .
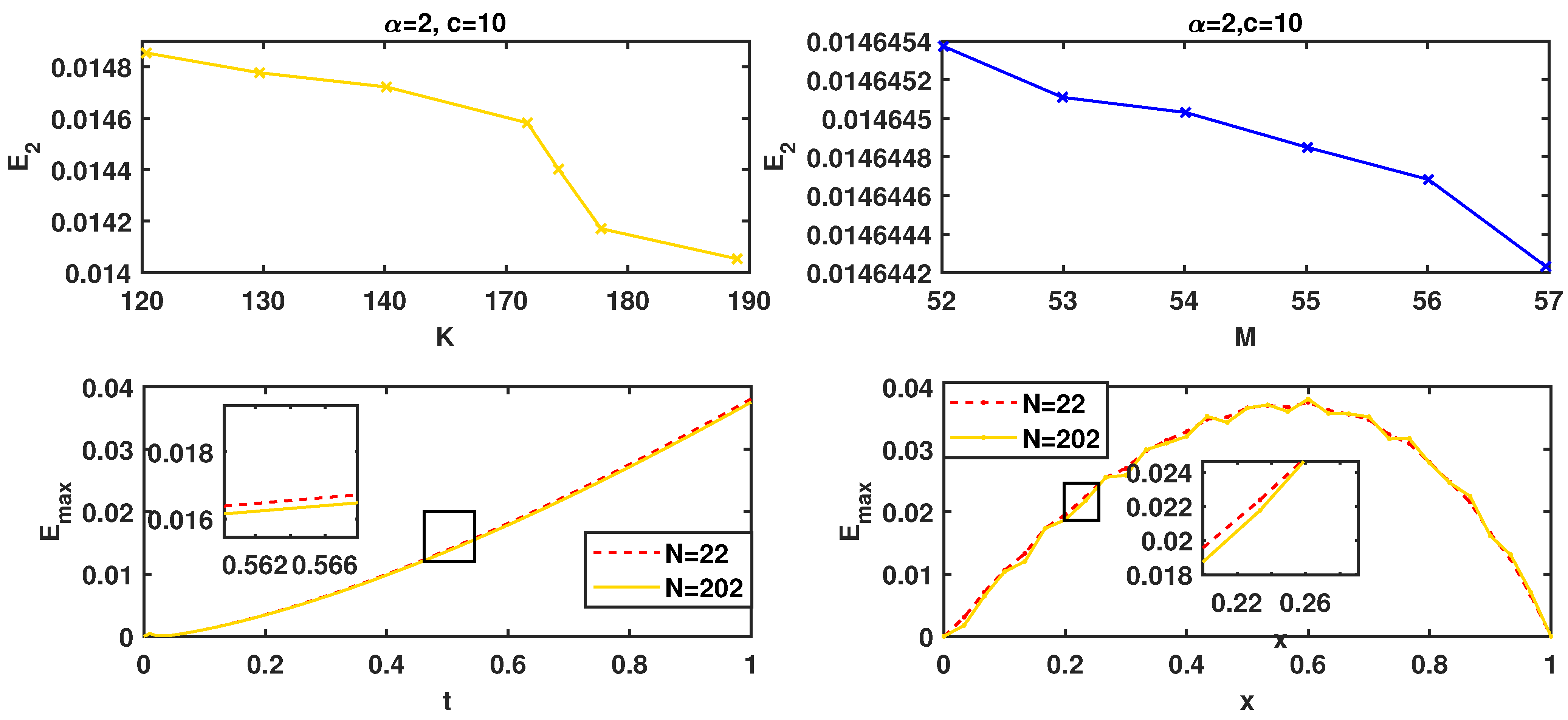
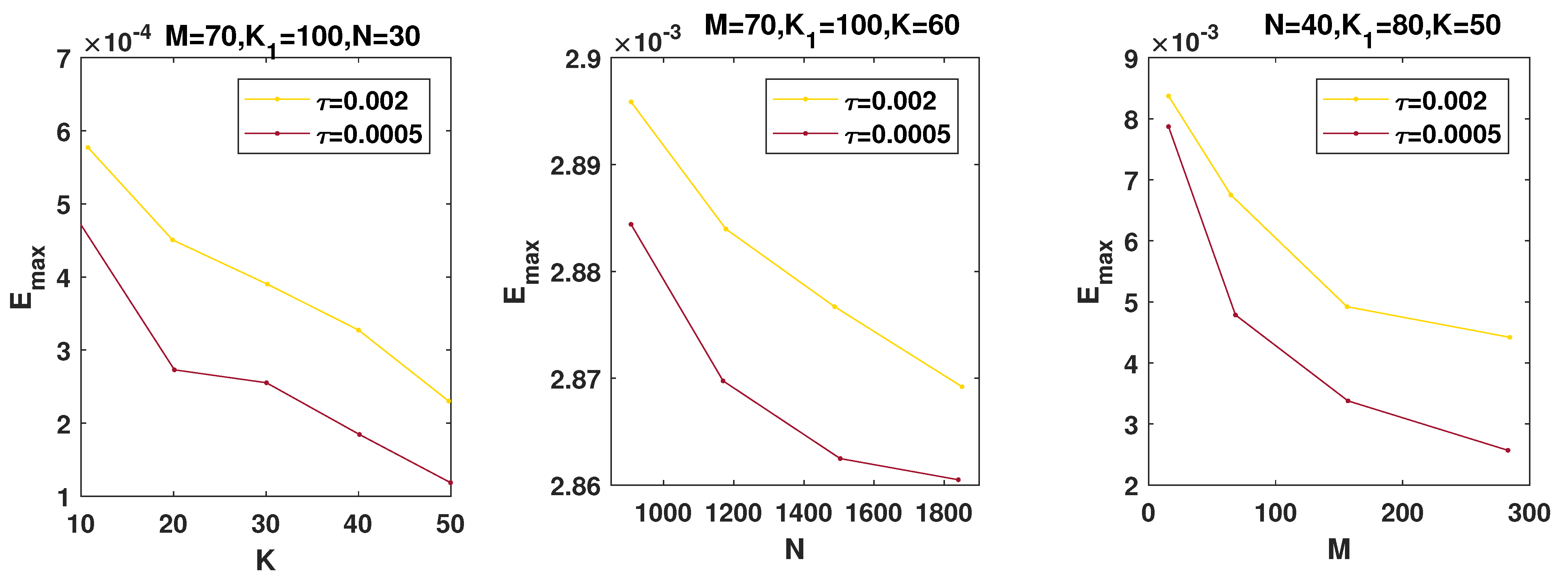
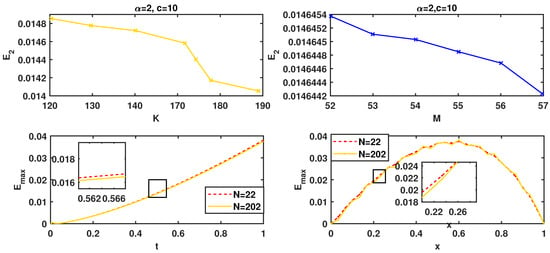
Now, we investigate convergence in time and space. In Figure 13, we illustrate the effect of the number of collocation points for this problem with τ, γ, and M fixed. It should be remarked that error reduction is negligible in our results. To evaluate the approximate solution of the problem, we illustrate Figure 14 to show the effect of the fractional order in both time and space. So, the different shape parameter c and the order of Riemann–Liouville fractional derivative γ and K played a significant role in the solution quality in this example.

Figure 13.
errors and convergence for Example 4 at , where , , , (first row) , , and , (second row) , and .

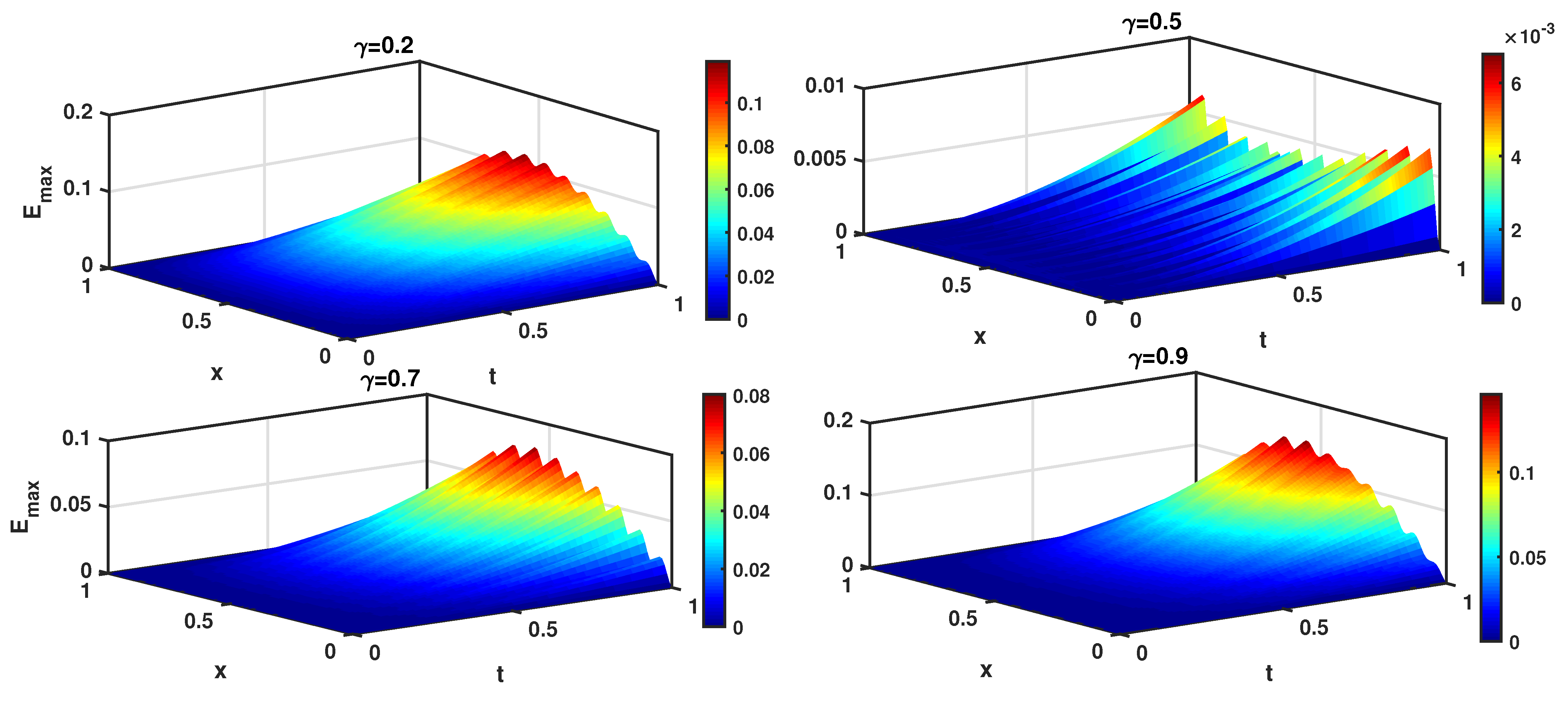
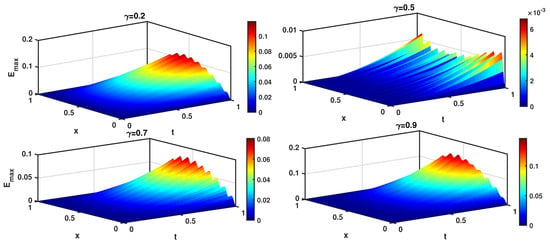
Figure 14.
Evolution of the with respect to for Example 4 at where , , , , and .
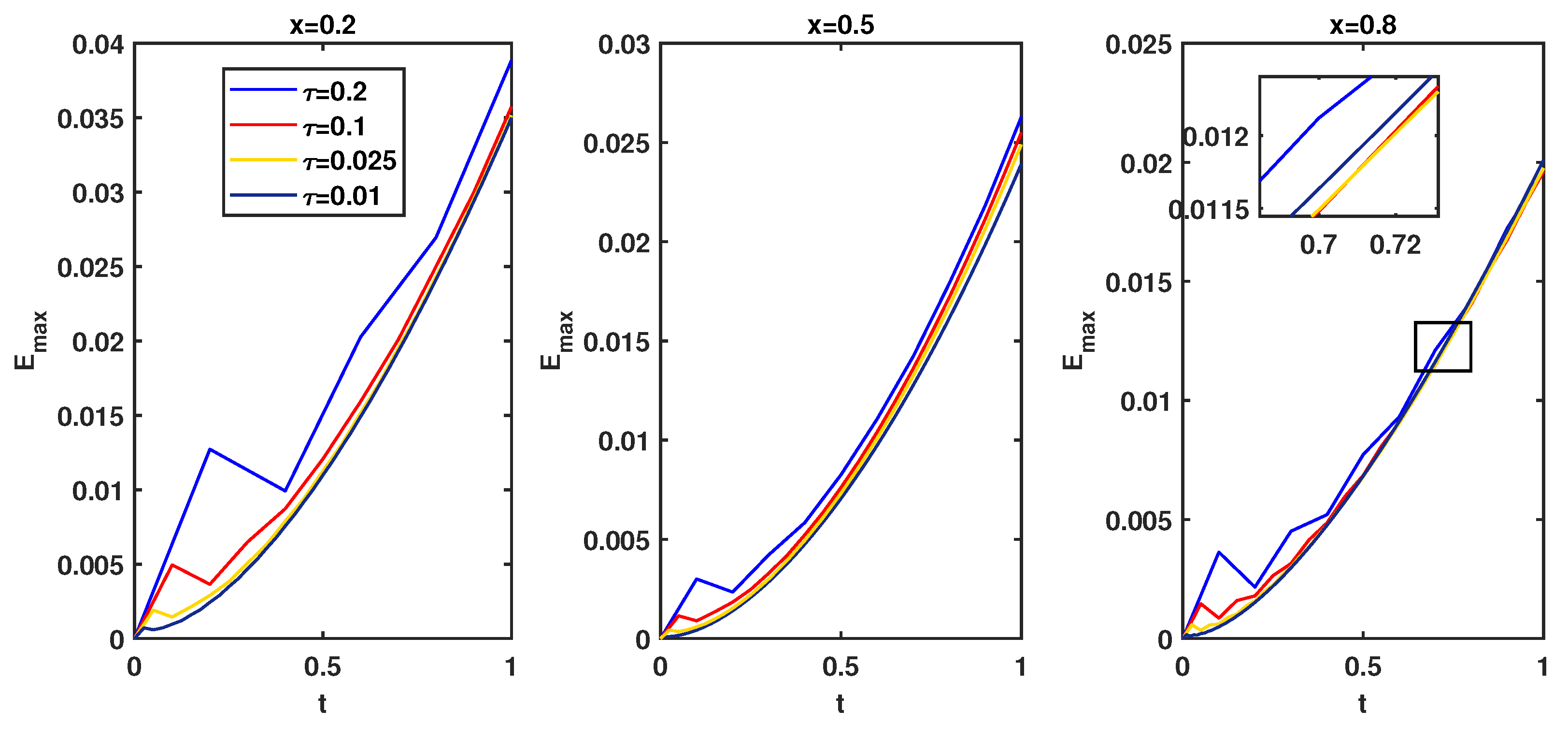
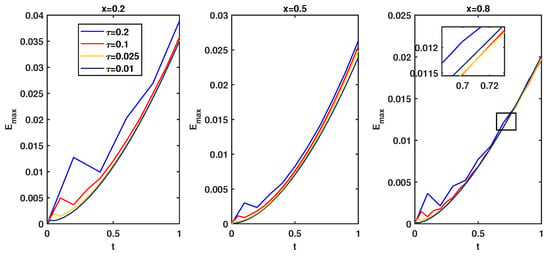
Finally, a comparison of our method by means of multiquadric basis functions is listed. Table 4 shows all the methods are numerically stable in terms of error when the first-order finite difference scheme [11], ISEFG method [9], and BSM method are applied to the problem. In addition, in Figure 15, the evolution of the solution at space , , with different time step is illustrated. Obviously, the present schemes are numerically stable.

Table 4.
and the effect of the time steps at times for Example 4, where , , , , , and .

Figure 15.
Evolution of the with respect to time step for Example 4 at , where , , , , , , and .
Example 5.

We consider the fractional GIADE with a nonhomogeneous source term on the domain
The initial and boundary conditions are as follows:
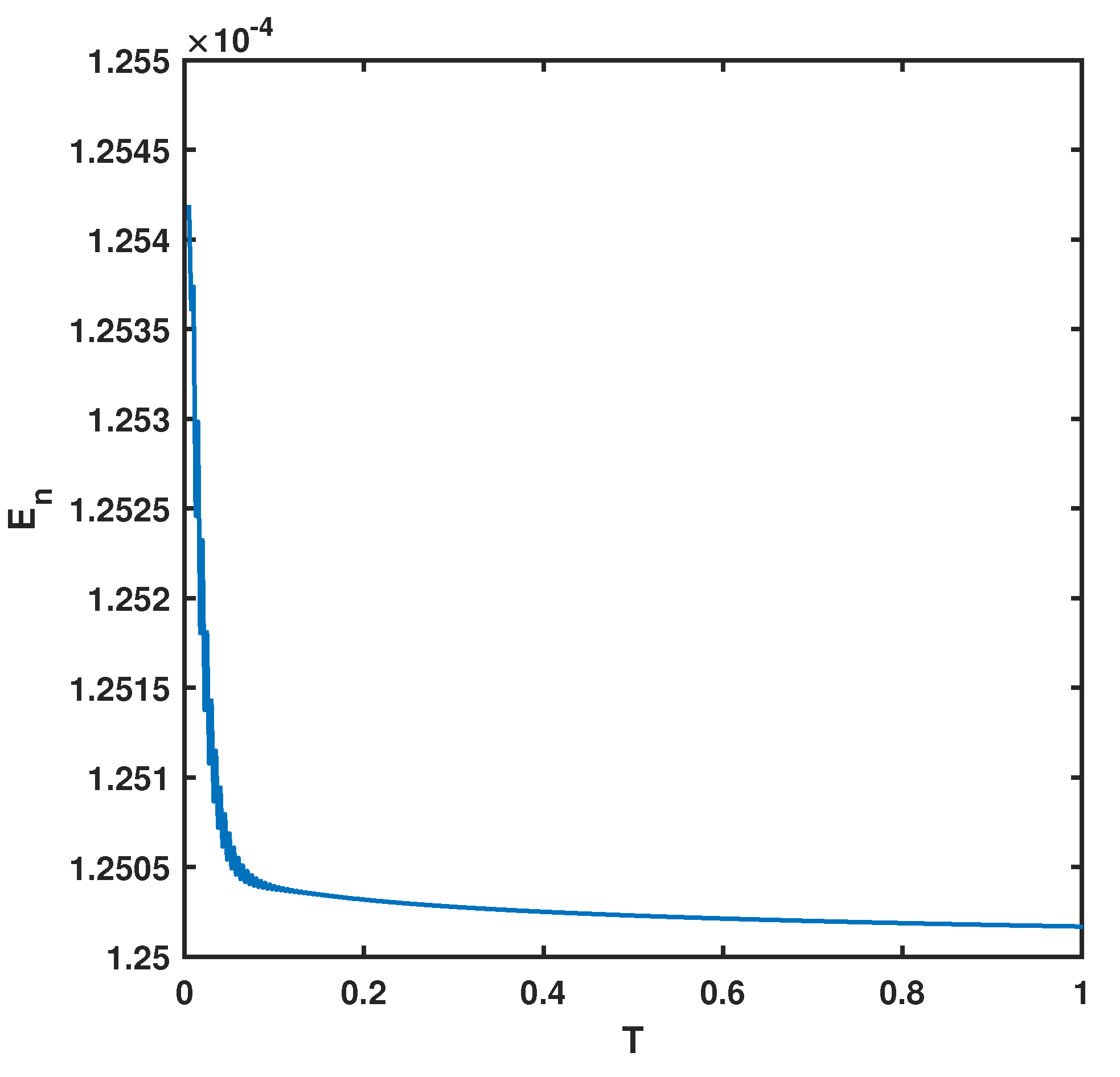
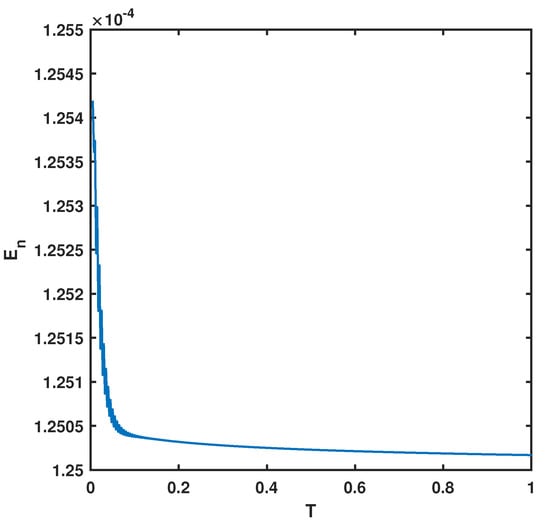
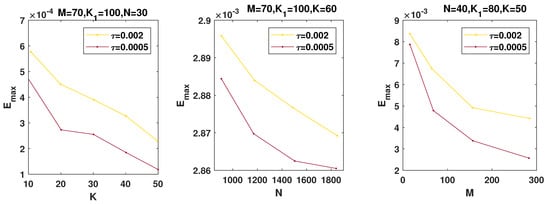
The numerical solutions are listed in Table 5, with , , , , , , and . We define to measure the stability of the time discretization scheme where , . The stability of the time discretization scheme at is presented in Figure 16. According to the lack of known reference solutions of the example, we validate the convergence rates by producing a numerical reference solution at . The convergence of time discretization scheme at is presented in Figure 17.

Table 5.
The numerical solution for Example 5, where , , , , , , and .

Figure 16.
–error using , , , , , , and for Example 5.

Figure 17.
–error of at , , , and for Example 5.
5. Conclusions
We coupled the WSGD approximation formula and the C-N technique that succeed in discretization of the involved fractional derivative of the GIADE equation along with its more general version, which is the GIADE equation with nonlinear source term. Next, we proposed the new version of the BSM, a well-established class of meshfree methods, to solve the consequent equation. In the present approach, the final approximation is given by the summation of the RBFs; the primary approximation satisfies only the boundary conditions. Moreover, a quasilinearization technique was employed to transform a nonlinear source term into a linear source term. From the verification of the efficiency and applicability of the proposed schemes, as well as an extension of the proposed schemes to the corresponding one- and two-dimensional problems, we observed acceptable accuracy depending on the shape parameter, the grid size, the domain of the problem, and the other potential factors.
Author Contributions
Formal analysis, F.S.; supervision, F.S. and Q.T.; project administration, Q.T.; data curation, Z.T. and J.L.; writing—original draft and writing—review and editing, F.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work was supported by the general project of Hunan Province Education Department (18C0220).
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Safari, F.; Chen, W. Coupling of the improved singular boundary method and dual reciprocity method for multi-term time-fractional mixed diffusion-wave equations. Comput. Math. Appl. 2019, 78, 1594–1607. [Google Scholar] [CrossRef]
- Shojaei, A.; Hermann, A.; Cyron, C.J.; Seleson, P.; Silling, S.A. A hybrid meshfree discretization to improve the numerical performance of peridynamic models. Comput. Methods Appl. Mech. Eng. 2022, 391, 114544. [Google Scholar] [CrossRef]
- Seleson, P.; Gunzburger, M.; Parks, M.L. Interface problems in nonlocal diffusion and sharp transitions between local and nonlocal domains. Comput. Methods Appl. Mech. Eng. 2013, 266, 185–204. [Google Scholar] [CrossRef]
- Shojaei, A.; Hermann, A.; Seleson, P.; Cyron, C.J. Dirichlet absorbing boundary conditions for classical and peridynamic diffusion-type models. Comput. Mech. 2020, 66, 773–793. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, Z.; Mehrmashhadi, J.; Bobaru, F. Construction of a peridynamic model for transient advection-diffusion problems. Int. J. Heat Mass Transf. 2018, 126, 1253–1266. [Google Scholar] [CrossRef]
- Aleroev, T.; Orlov, V. On One Approximate Method of a Boundary Value Problem for a One-Dimensional Advection–Diffusion Equation. Axioms 2022, 11, 541. [Google Scholar] [CrossRef]
- Mahmoud, E.I.; Aleroev, T.S. Boundary Value Problem of Space-Time Fractional Advection Diffusion Equation. Mathematics 2022, 10, 3160. [Google Scholar] [CrossRef]
- Ndou, N.; Dlamini, P.; Jacobs, B.A. Enhanced Unconditionally Positive Finite Difference Method for Advection–Diffusion–Reaction Equations. Mathematics 2022, 10, 2639. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. The Crank-Nicolson/interpolating stabilized element-free Galerkin method to investigate the fractional Galilei invariant advection-diffusion equation. Math. Methods Appl. Sci. 2021, 44, 2752–2768. [Google Scholar] [CrossRef]
- Kumar, S.; Pandey, P.; Das, S. Gegenbauer wavelet operational matrix method for solving variable-order non-linear reaction–diffusion and Galilei invariant advection–diffusion equations. Comput. Appl. Math. 2019, 38, 162. [Google Scholar] [CrossRef]
- Chen, C.; Liu, F.; Anh, V.; Turner, I. Numerical simulation for the variable-order Galilei invariant advection diffusion equation with a nonlinear source term. Appl. Math. Comput. 2011, 217, 5729–5742. [Google Scholar] [CrossRef]
- Zaky, M.A. Existence, uniqueness and numerical analysis of solutions of tempered fractional boundary value problems. Appl. Numer. Math. 2019, 145, 429–457. [Google Scholar] [CrossRef]
- Zaky, M.A. Recovery of high order accuracy in Jacobi spectral collocation methods for fractional terminal value problems with non-smooth solutions. J. Comput. Appl. Math. 2019, 357, 103–122. [Google Scholar] [CrossRef]
- Le Vot, F.; Abad, E.; Metzler, R.; Yuste, S.B. Continuous time random walk in a velocity field: Role of domain growth, Galilei-invariant advection-diffusion, and kinetics of particle mixing. New J. Phys. 2020, 22, 73048. [Google Scholar] [CrossRef]
- Zaky, M.A.; Baleanu, D.; Alzaidy, J.F.; Hashemizadeh, E. Operational matrix approach for solving the variable-order nonlinear Galilei invariant advection–diffusion equation. Adv. Differ. Equ. 2018, 2018, 102. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for fractional advection–dispersion flow equations. J. Comput. Appl. Math. 2004, 172, 65–77. [Google Scholar] [CrossRef]
- Baeumer, B.; Kovács, M.; Sankaranarayanan, H. Higher order Grünwald approximations of fractional derivatives and fractional powers of operators. Trans. Am. Math. Soc. 2015, 367, 813–834. [Google Scholar] [CrossRef]
- Tian, W.; Zhou, H.; Deng, W. A class of second order difference approximations for solving space fractional diffusion equations. Math. Comput. 2015, 84, 1703–1727. [Google Scholar] [CrossRef]
- Zhou, H.; Tian, W.; Deng, W. Quasi-compact finite difference schemes for space fractional diffusion equations. J. Sci. Comput. 2013, 56, 45–66. [Google Scholar] [CrossRef]
- Wang, P.; Huang, C. An implicit midpoint difference scheme for the fractional Ginzburg–Landau equation. J. Comput. Phys. 2016, 312, 31–49. [Google Scholar] [CrossRef]
- Tadjeran, C.; Meerschaert, M.M. A second-order accurate numerical method for the two-dimensional fractional diffusion equation. J. Comput. Phys. 2007, 220, 813–823. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Tadjeran, C. Finite difference approximations for two-sided space-fractional partial differential equations. Appl. Numer. Math. 2006, 56, 80–90. [Google Scholar] [CrossRef]
- Kazem, S.; Dehghan, M. Semi-analytical solution for time-fractional diffusion equation based on finite difference method of lines (MOL). Eng. Comput. 2019, 35, 229–241. [Google Scholar] [CrossRef]
- Dehghan, M.; Abbaszadeh, M. The solution of nonlinear Green–Naghdi equation arising in water sciences via a meshless method which combines moving kriging interpolation shape functions with the weighted essentially non–oscillatory method. Commun. Nonlinear Sci. Numer. Simul. 2019, 68, 220–239. [Google Scholar] [CrossRef]
- Karamali, G.; Dehghan, M.; Abbaszadeh, M. Numerical solution of a time-fractional PDE in the electroanalytical chemistry by a local meshless method. Eng. Comput. 2019, 35, 87–100. [Google Scholar] [CrossRef]
- Jafari, H.; Sadeghi, J.; Safari, F.; Kubeka, A. Factorization method for fractional Schrödinger equation in D-dimensional fractional space and homogeneous manifold SL(2,C)/GL(1,C). Comput. Methods Differ. Equ. 2019, 7, 199–205. [Google Scholar]
- Safari, F. The solution of the Schrödinger equation for Makarov potential and homogeneous manifold SL(2,C)/GL(1,C). Pramana 2020, 94, 59. [Google Scholar] [CrossRef]
- Lin, J.; Xu, Y.; Zhang, Y. Simulation of linear and nonlinear advection–diffusion–reaction problems by a novel localized scheme. Appl. Math. Lett. 2020, 99, 106005. [Google Scholar] [CrossRef]
- Lin, J.; Feng, W.; Reutskiy, S.; Xu, H.; He, Y. A new semi-analytical method for solving a class of time fractional partial differential equations with variable coefficients. Appl. Math. Lett. 2021, 112, 106712. [Google Scholar] [CrossRef]
- Reutskiy, S.Y. A new semi-analytical collocation method for solving multi-term fractional partial differential equations with time variable coefficients. Appl. Math. Model. 2017, 45, 238–254. [Google Scholar]
- Reutskiy, S.Y.; Lin, J. A semi-analytic collocation method for space fractional parabolic PDE. Int. J. Comput. Math. 2018, 95, 1326–1339. [Google Scholar] [CrossRef]
- Safari, F.; Azarsa, P. Backward substitution method based on Müntz polynomials for solving the nonlinear space fractional partial differential equations. Math. Methods Appl. Sci. 2020, 43, 847–864. [Google Scholar] [CrossRef]
- Lin, J.; Reutskiy, S. A cubic B-spline semi-analytical algorithm for simulation of 3D steady-state convection-diffusion-reaction problems. Appl. Math. Comput. 2020, 371, 124944. [Google Scholar] [CrossRef]
- Hong, Y.; Lin, J.; Chen, W. A typical backward substitution method for the simulation of Helmholtz problems in arbitrary 2D domains. Eng. Anal. Bound. Elem. 2018, 93, 167–176. [Google Scholar] [CrossRef]
- Safari, F.; Sun, H. Improved singular boundary method and dual reciprocity method for fractional derivative Rayleigh–Stokes problem. Eng. Comput. 2020, 37, 3151–3166. [Google Scholar] [CrossRef]
- Reutskiy, S.; Lin, J. A semi-analytic collocation technique for steady-state strongly nonlinear advection-diffusion-reaction equations with variable coefficients. Int. J. Numer. Methods Eng. 2017, 112, 2004–2024. [Google Scholar] [CrossRef]
- Safari, F.; Chen, W. Numerical approximations for space–time fractional Burgers’ equations via a new semi-analytical method. Comput. Math. Appl. 2021, 96, 55–66. [Google Scholar] [CrossRef]
- Zhuang, P.; Liu, F.; Anh, V.; Turner, I. Numerical methods for the variable-order fractional advection-diffusion equation with a nonlinear source term. SIAM J. Numer. Anal. 2009, 47, 1760–1781. [Google Scholar] [CrossRef]
- Wang, Z.; Vong, S. Compact difference schemes for the modified anomalous fractional sub-diffusion equation and the fractional diffusion-wave equation. J. Comput. Phys. 2014, 277, 1–15. [Google Scholar] [CrossRef]
- Lin, J.; Reutskiy, S.Y.; Lu, J. A novel meshless method for fully nonlinear advection–diffusion-reaction problems to model transfer in anisotropic media. Appl. Math. Comput. 2018, 339, 459–476. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Dehghan, M. Numerical and analytical investigations for neutral delay fractional damped diffusion–wave equation based on the stabilized interpolating element free Galerkin (IEFG) method. Appl. Numer. Math. 2019, 145, 488–506. [Google Scholar] [CrossRef]
- Zhang, T.; Li, X. Variational multiscale interpolating element-free Galerkin method for the nonlinear Darcy–Forchheimer model. Comput. Math. Appl. 2020, 79, 363–377. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).