Abstract
A quantum model of a free-electron laser (FEL) is considered. Two different approaches for the exploration of the the FEL system are considered. In the first case, the Heisenberg equations of motion are mapped on the basis of the initial wave functions, which consists of the photon coherent states and many-dimensional electron coherent states. This mapping is an exact procedure, which makes it possible to obtain an exact equation of motion for the intensity of the laser field in a closed form. The obtained equation is controlled by a Koopman operator. The analytical expression for the evolution of the FEL intensity is obtained in the framework of a perturbation theory, which is constructed for a small time scale. The second way of the consideration is based on the construction of the many-dimensional path integrals for the evolution of the wave function. This method also makes it possible to estimate the time evolution and the gain of the FEL intensity.
Keywords:
free-electron laser; Heisenberg equations of motion; coherent states; Koopman operator; path integral; super-radiance MSC:
81S40; 37M99
1. Introduction
In this paper, we discuss a quantum model of a free-electron laser (FEL). Experimental implementation and theoretical description of the FEL is a long-lasting problem that started in the seventies of the last century. This extensively studied phenomenon is well described and reviewed in [1,2,3,4], to mention a few. Contemporary studies are also reflected in recent publications and related to both classical and quantum descriptions [5,6], including application of fractional calculus to the FEL model [7,8]. In the present study, our interest to the model relates to a quantum description of the quantum FEL model with the quantum Hamiltonian of an electromagnetic field interacting with a system of N electrons [5,9,10,11]
Here, summation relates to the positions and momenta of electrons with the mass m and the wave number k. The position–momentum commutation rule is . The laser mode is described by the photon annihilation and creation operators and , respectively, with the commutation rule . The interaction parameter g couples the electron dynamics to the photon laser field. The Hamiltonian (1) has been obtained from the consideration of a non-relativistic electron in an electromagnetic field [9,10]; see also ref. [5]. Note also that the starting point of inferring the Hamiltonian (1) is the classical relativistic Hamiltonian [5,10]; see also Appendix A, where some grounds of the applicability of the model are explained.
It is worth stressing that, discussing the dynamics of the system, we also set the notation for the operators considered here. Namely, for any time-dependent operator , its initial value is denoted by . The same is concerned with its average values denoting and , where . The only exclusion is for the Hamiltonian, since it is the integral of motion and, correspondingly, .
The paper relates to mathematical aspects of the quantum mechanical treatment of the system (1) in the framework of two different approaches. The first one is the Koopman operator construction by mapping the Heisenberg equation of motion on the basis of the coherent states. The second approach is the Schrödinger–Feynman consideration of the Green function in the framework of the path integral. The main issue in the task is the laser field intensity. It is shown that both methods lead to the consistent results for the laser field output.
The dynamics of the intensity of the laser field in the operator form is described by the Heisenberg equation of motion
In this approach, our main concern is a technical consideration of the Heisenberg Equation (2) and finding the evolution of the averaged value of the laser field intensity in the form
where is a so-called Koopman operator [12]; see also, e.g., [13,14]. Another approach developed in the paper is the investigation of the evolution of the initial wave function, which relates to the construction of the evolution operator by means of the path integrals [15,16]. For the latter example, the initial wave functions are the direct product of the photon and electron wave functions
where the coherent states are chosen for the photon wave function [17], while the electron wave function is , where .
The paper is organized as follows. In Section 2, the Koopman operator is constructed by mapping the Heisenberg equations of motion for the intensity of the photon laser field on the basis of the coherent states, both photon and electron. The obtained equation is exact and determines the dynamics of the laser field intensity. The second approach to the system is the description in the framework of the Schrödinger–Feynman consideration, which is presented in Section 3 and Section 4. The path integral is constructed to describe both the evolution of the initial wave function and the intensity of the laser field. The obtained results and the consistency of the two suggested methods are discussed in Section 5. Concluding remarks are presented in Section 6. Appendix A is devoted to some details of the construction and the applicability of the Hamiltonian (1). The path integral construction and its evaluation in the framework of the stationary-phase approximation are presented in Appendix B and Appendix C, respectively.
2. Quantum Evolution according to Koopman Operator
For the quantum mechanical analysis of the Heisenberg equations of motion, we use a technique of mapping the Heisenberg equations on a basis of the coherent states [18,19,20,21,22]. Note that the Hamiltonian is the time-independent integral of motion, . Therefore, the Hamiltonian in the Heisenberg equations can be mapped on a basis of the coherent states and , constructed at the initial moment . First, we construct the basis of the photon coherent states. That is, at the initial moment , one introduces the coherent states vector as the eigenfunction of the annihilation operators , such that and, correspondingly, . The coherent state can also be constructed from a vacuum state as follows [23]
Then, defining the c-number function as an average value of the photon field operator
one maps the Heisenberg equation of motion (2) on the basis of the coherent states as follows
As admitted, the Hamiltonian is the integral of motion , therefore the mapping rules (7a) and (7b) yield the equation of motion (6) for in the form
where the photon–electron operator reads
while the commutator related to the electron part of the Hamiltonian (defined on the test function ) reads
Note that both operators and are Hermitian.
The next step is the averaging procedure for the electron part of the Hilbert space. To this end, we construct a basis of the electron coherent states at the initial moment . We admit that the electron system in the Hamiltonian (1) is considered as a system of free spinless particles, and their commutation rules corresponds to a so-called Heisenberg–Weyl group [23]. Therefore, introducing creation and annihilation operators:
where , we introduce the coherent state basis as follows:
which belongs to the Hilbert space of electrons.
Introducing the double average
and using properties (7a) and (7b) for both and operators, and taking into account the commutator (10), we obtain the “Koopman equation”
where the Hermitian Koopman operator reads
The Koopman operator consists of two parts: . The first part , described by Equation (15a), corresponds to the kinetic part of free electrons, while the second part describes the electron–photon interaction, as in Equation (15b).
The solution of the Koopman Equation (14) for the initial condition is presented in the exponential form
We take into account that electrons spend a very short time inside the laser size, namely , which results from the fact that the laser size is finite and electron velocity is close to the speed of light. Then, we should take into account only a few first terms in the expansion (16), and we limit ourselves by the second order of . Obviously, for , the zero-order term corresponds to the initial condition: . Correspondingly, the first-order term for reads
At this step, the action of the Koopman operator reduces to differentiation with respect to and only. The derivatives and do not “work” here. The situation changes for the second-order term, for which we obtain
We restrict the expansion by the second order in Equation (18). The last term is the main contribution to the laser field intensity
and it is the first main result, which is discussed in Section 5. It is also interesting to admit that in the coherent states, the averaged energy of electrons is conserved that immediately follows from the specific form of the Koopman operator (15) and the transformations (11). Namely, , then . This situation is a pure quantum effect. It can be explained by coherent Cherenkov radiation, which is described just by the same Hamiltonian as in Equation (1) [10]; see also Appendix A.
3. Evolution of Initial Wave Function
It is also instructive to obtain an analytical expression for the evolution operator , which determines the evolution of the initial wave function , where can be an arbitrary suitable function. We consider defined in Equation (3). The evolution operator can be presented in the form of the path integral related to the electron Hilbert space. In this case, the interaction term in the Hamiltonian (1) plays the role of the potential, which is however the operator valued the function of the operators and .
We follow the standard procedure [15,16] partitioning the time interval at the condition , while , where the boundary (initial and finite) conditions for the path integral defined at and are and . The procedure is presented in Appendix B. Then, the path integral arises from this partition as follows (A9):
Here, . The last line in Equation (21) describes the shift of the coherent states by means of the shift operator , where . It transforms one coherent state to another [23,24]:
In Equations (20)–(22), the shift operator in the photon Hilbert space is
Correspondingly, the shifted coherent state in Equation (22) at time t reads
Note that the wave function in Equation (24) reflects the electron–photon interaction. Substituting Equation (24) in Equation (21), we obtain the wave function in the formal form. Eventually, the exact expression for the evolution of the wave function reads as follows:
where the initial wave function is defined in Equation (3). The path integration is performed in the semiclassical or the stationary-phase approximation, defined by the path integral as follows:
where . Note that it is instructive to apply the stationary-phase approximation for the averages, namely for the intensity of the laser field.
4. Evolution of the FEL Intensity
Let us estimate the evolution of the intensity of the laser field , which is
To perform this calculation, we first map the photon operator on the shifted coherent states in Equation (26) that yields the averaged value
The term with is estimated by the stationary phase approximation, which is , where
The dynamics of are controlled by a physical pendulum with the principle Hamiltonian function of a j-th electron and the constant energy , determined at the initial time , while is a constant resulted from the Gaussian integration, which corresponds to the second variation at the stationary point. Note that the principle Hamiltonian function results from the first variation . Details of the calculation are shown in Appendix C.
The dynamics are described by the elliptic functions with a separatrix, which separates unlimited flight trajectories from the confined elliptic ones. Therefore, the stationary points are determined by the elliptic amplitude function , [25], where is defined in Equation (A23). Therefore, .
Our main concern, however, is the path integration of the interaction term
This part of the FEL intensity is presented in the form of the dimensional functional integration. Therefore, the main part (M.P.) of the averaged value is defined as follows:
The stationary-phase approximation in Equation (29) is performed according to Equation (28). It is reasonable to take the stationary solution for at the the asymptotic times, according to Figure A1 in Appendix C. Therefore, we obtain that . Eventually, we obtain
5. Discussion
We collect some physical consequences of the calculations of the laser intensity and discuss them in this section. The main contribution to the intensity of the laser photon field is due to the interaction term in the Hamiltonian (1), that is
Two different approaches for the evaluation of the laser intensity are suggested in the framework of the Heisenberg and the Schrödinger representations of quantum mechanics.
In the first approach, the Heisenberg equations of motion are mapped on the basis of the coherent states, which are constructed at the initial moment of time for both the photon laser field and electrons. Since the algebras of the photon and electron operators belong to the same Heisenberg–Weyl algebras, the analytical forms of the coherent states (as the eigenstates of the annihilation operators) are the same, although the wave functions and belong to the different Hilbert spaces. The Heisenberg equations of motions for the laser photon field intensity are exactly mapped on the basis of the coherent states and the obtained “Koopman equation”. The work in (14) describes the gain process, and it is controlled by the Koopman operator . The main advantage of this approach is that the gain intensity can be easily obtained by the small-time perturbation theory, (19), which yields
If initially all coherent states are just the same, that is , then according to Equation (11), the distributions of the initial conditions and are such that , which is defined as points on the hyper-sphere in the -dimensional phase space. In other words, all and are independent initial values defined on the hyper-sphere, which is just the direct product of N circles for the non-interacting electrons. In this case, the gained intensity is
which is superradiance. Note that super-radiance supposes that the intensity gain is of the order of .
The second approach relates to the construction of the path integral for the evolution operator in Equation (20). This makes it possible to estimate the FEL intensity according to the interaction term. This procedure is performed in the stationary-phase approximation. A detailed analysis is presented in Appendix C. The maximum gain effect is estimated for the large-time asymptotics of the stationary-phase solution for . This result is described by Equation (30) and eventually coincides with Equation (32). This corresponds to super-radiance as well.
Note also that the scalar product of the wave function in Equation (25) is
Therefore, in the stationary-phase approximation, the scalar product
for the stationary-phase solution , which is valid for all physical values of and and time .
6. Conclusions
A quantum model of a free-electron laser (FEL) is considered. Two different approaches for the evaluation of the laser field intensity are suggested, and these are the Heisenberg and the Schrödinger representations of quantum mechanics. In the first case, the Heisenberg equations of motion are mapped on the many-dimensional basis, which consists of the photon coherent states and many-dimensional electron coherent states. This mapping is an exact procedure, which makes it possible to obtain an equation of motion for the laser intensity in a closed form. The obtained equation is controlled by a Koopman operator. The analytical expression for the evolution of the FEL intensity is obtained in the framework of a perturbation theory, which is constructed for a small time scale.
The second way of the solution is based on the construction of the many-dimensional path integral for the evolution of the wave function. This method also makes it possible to estimate the time evolution and the gain of the FEL intensity.
It should be admitted that the laser field outputs presented in Equations (30) and (32) obtained by these different methods are mathematically consistent. However, the description of the electron dynamics underlying the FEL is completely different. In particular, in the path integral consideration, the laser field intensity is estimated by the stationary-phase approximation, where the electron dynamics are controlled by a physical pendulum and described semiclassically by the elliptic functions. Contrary to that, the Koopman operator describes the electron dynamics exactly, and the latter is a free-particle dynamic. This phenomenon is pure quantum and can be explained by the Cherenkov radiation, which is another scenario of the FEL [10]. It should be admitted that this behavior cannot be explained by the wiggler mechanism of interaction. Citing from the Tamm and Frank’s paper [26], we note that “if one takes in account the fact that an electron moving in a medium does radiate light even if it is moving uniformly provided that its velocity is greater than the velocity of light in the medium”. (See also [27]).
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. Quantum FEL Hamiltonian
The basic Hamiltonian (1), which governs a variety of different situations has been inferred in refs. [9,10]. We also follow ref. [5]. The starting point is the classical relativistic Hamiltonian
which describes a single electron, with the rest mass and the elementary charge e interacting with two electromagnetic plane wave fields . The laser field
travels in positive z-direction, while the wiggler field
propagates in the opposite direction. Here, are amplitudes of the vector potentials, and c is the speed of light while the circular polarization is chosen, when and . In a so-called Bambini–Renieri frame [28,29], the wave numbers and coincide, a.e, .
The non-relativistic approximation is performed by expanding the relativistic square root and neglecting the relativistic terms that yield [5]
where is the shifted mass with the wiggler parameter [5,30]
Appendix A.1. Quantization
In the quantization procedure of the classical Hamiltonian (A5), both the electron dynamics and the laser field are quantized. Therefore, the electron coordinate and the momentum are operators , where their commutation relation is . Then, treating the laser field amplitude as the quantized field, the photon annihilation and creation operators are introduced, and the commutation relation is . Then, the quantized amplitudes of the laser field are defined by the substitutions
where is the amplitude of the quantized laser field. However, the wiggler field is considered as an external classical parameter [5,10].
Appendix A.2. Cherenkov Radiation Scenario of the FEL
A slightly different consideration has been suggested in ref. [10], which is also suitable for the Cherenkov radiation (CR) scenario of the FEL. In the case of stimulated CR, the wiggler is replaced by a medium with a refractive index . Since , the interaction term is due to the transverse canonical momentum of the electron , while linear polarization is supposed in Equation (A2). The relativistic Hamiltonian now reads
As shown in ref. [10], quantization of the Hamiltonian (A8) for the N electrons systems yields
where is the frequency of the laser field. The coupling constant now is , while ,10].
In the interaction representation
and re-scaling , one arrives at the Hamiltonian in Equation (1), obtained by means of the commutation rule [31],
where over-brace contains n operators . Taking into account that , while , we obtain
Appendix B. Path Integral
We follow the standard procedure [15,16] partitioning the time interval at the condition , while . Then, the path integral arises from this partition as follows:
Here, is the Hamiltonian (1), such that
The operator leads to shifts in photon Hilbert space, while in the electron Hilbert space it is just the multiplication operator, which is diagonal and behaves like a potential
Note that it can also be taken at the middle point that, however, yields the same result in the limit [15].
To estimate the matrix elements , we insert a complete set of momentum states
From Equation (A13), this yields
Eventually, we arrive at the expression
which defines the evolution of the initial state according to the Hamiltonian. The boundary condition of the integration for is this initial state. Taking the limit , we arrive at the path integral
Appendix C. Stationary-Phase Approximation
Let us estimate the integral (26) in the framework of the stationary-phase approximation.
where . This approximation yields
where the Hamilton principal function results from the first variation , which yields . Correspondingly, is the extreme trajectory determined by the Euler–Lagrange equation
where , while and the energy
is determined by the initial position and the momentum of electrons. In the classical limit, without restriction of generality, we can set the energy . Therefore, for all j, we obtain the solutions in the form of the elliptic integral as follows:
where . The solutions are described by the elliptic functions with a separatrix where , which separates unlimited flight trajectories with from the confined elliptic ones with . The physical solutions are for , which are amplitude functions , [25]. Therefore,
It is instructive to set , which yields Equation (A23) in the form of the topological solution [32] as follows:
Then, we have
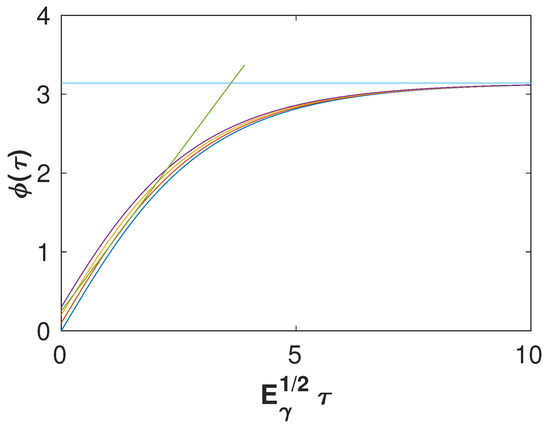
Figure A1.
The solution in Equation (A26) for and . The linear fitting plots correspond to the initial and the large time asymptotes, which are and .
Figure A1.
The solution in Equation (A26) for and . The linear fitting plots correspond to the initial and the large time asymptotes, which are and .
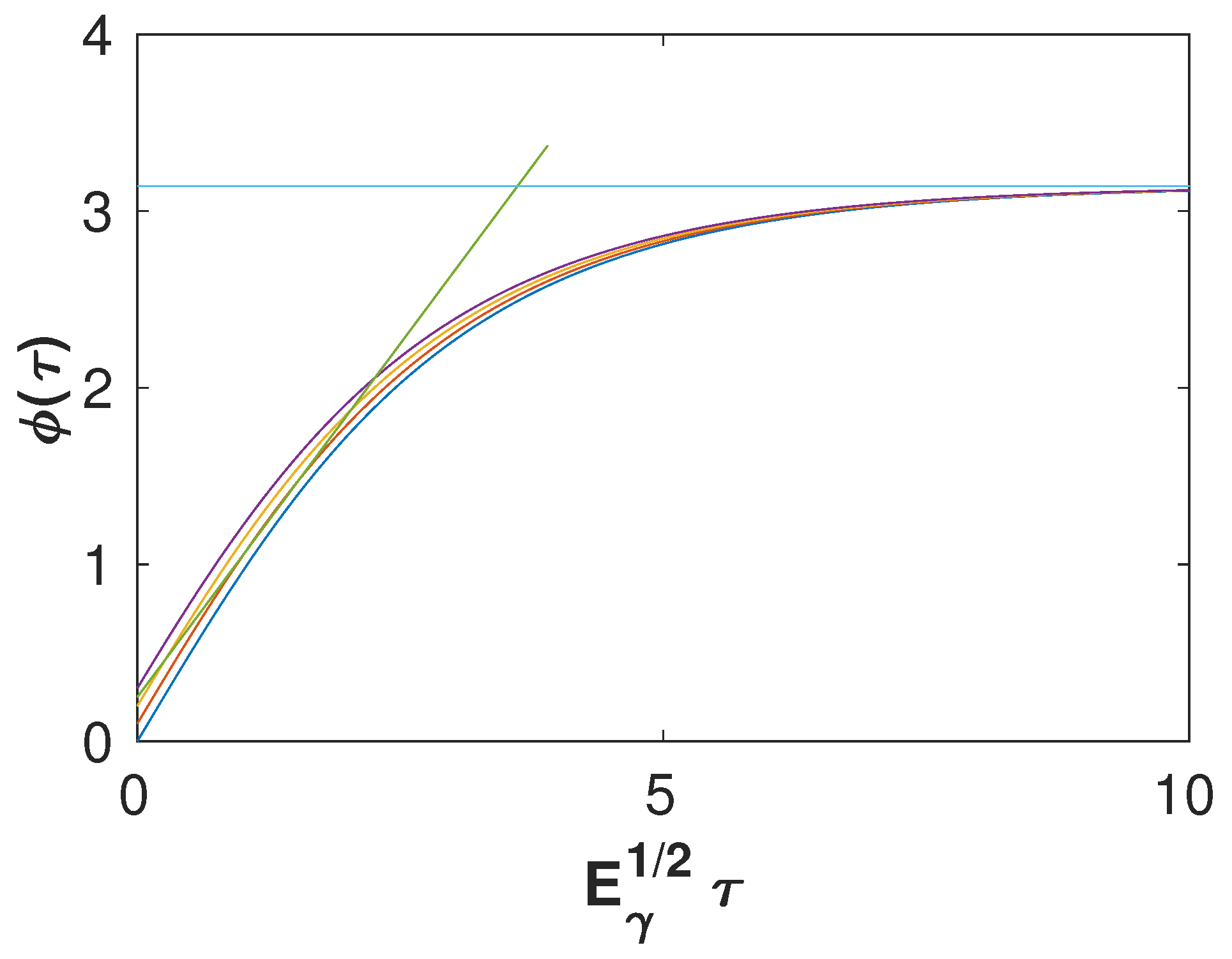
A graphical representation of the solution is presented in Figure A1. As it follows from the plots, the initial solution for is well fitted by the linear approximation, which is . In the opposite case, when , the solution is a constant value .
Gaussian Integration
The second step of the approximation is calculation of from the second variation , which leads to the Gaussian integration [16,33]. Therefore, accounting for the extremum solution , we perform the variable change , where . Then, Equation (A20) reads
with
For the extreme solution, we set the asymptotic one with . Therefore, . It is supposed that for [16] that determines the quantum fluctuations in the vicinity of the classical extreme trajectory. Eventually, we arrive at the dynamics in the inverted potential , whose path integral can be easily related to the linear “oscillator” with imaginary . In this case, the result of the path integration (for ) is well known [15,16] and reads
References
- Bonifacio, R.; Casagrande, F.; Cerchioni, G.; De Salvo Souza, L.; Pierini, P.; Piovella, N. Physics of the high-gain FEL and superradiance. Riv. Del Nuovo C. 1990, 13, 2–69. [Google Scholar] [CrossRef]
- Colson, W. Classical Free Electron Laser theory. In Laser Handbook; Colson, W., Pellegrini, C., Renieri, A., Eds.; North Holland: Amsterdam, The Netherlands, 1990; Volume VI. [Google Scholar]
- Dattoli, G.; Renieri, A.; Torre, A. Lectures on the Free Electron Laser Theory and Related Topics; World Scientific: Singapore, 1993. [Google Scholar] [CrossRef]
- Saldin, E.; Schneidmiller, E.; Yurkov, M. The Physics of Free Electron Laser; Springer: Heidelberg/Berlin, Germany, 2000. [Google Scholar]
- Kling, P.; Giese, E.; Endrich, R.; Preiss, P.; Sauerbrey, R.; Schleich, W.P. What defines the quantum regime of the free-electron laser? New J. Phys. 2015, 17, 123019. [Google Scholar] [CrossRef]
- Piovella, N.; Volpe, L. A review of high-gain free-electron laser theory. Atoms 2021, 9, 28. [Google Scholar] [CrossRef]
- Artioli, M.; Dattoli, G.; Licciardi, S.; Pagnutti, S. Fractional Derivatives, Memory Kernels and Solution of a Free Electron Laser Volterra Type Equation. Mathematics 2017, 5, 73. [Google Scholar] [CrossRef] [Green Version]
- Iomin, A. Fox H-Functions in Self-Consistent Description of a Free-Electron Laser. Fractal Fract. 2021, 5, 263. [Google Scholar] [CrossRef]
- Becker, W.; McIver, J.K. Fully quantized many-particle theory of a free-electron laser. Phys. Rev. A 1983, 27, 1030–1043. [Google Scholar] [CrossRef]
- Becker, W.; McIver, J. Many-particle quantum theory for a class of free-electron devices. Phys. Rep. 1987, 154, 205–245. [Google Scholar] [CrossRef]
- Kling, P.; Giese, E.; Carmesin, C.M.; Sauerbrey, R.; Schleich, W.P. High-gain quantum free-electron laser: Emergence and exponential gain. Phys. Rev. A 2019, 99, 053823. [Google Scholar] [CrossRef] [Green Version]
- Koopman, B.O. Hamiltonian Systems and Transformation in Hilbert Space. Proc. Natl. Acad. Sci. USA 1931, 17, 315–318. [Google Scholar] [CrossRef] [PubMed]
- Gaspard, P. Chaos, Scattering and Statistical Mechanics; Cambridge University Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Cvitanović, P.; Artuso, R.; Mainieri, R.; Tanner, G.; Vattay, G. Chaos: Classical and Quantum; ChaosBook.org; 2022. [Google Scholar]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Schulman, L. Techniques and Applications of Path Integration; Wiley: New York, NY, USA, 1981. [Google Scholar]
- Becker, W.; Scully, M.O.; Zubairy, M.S. Generation of Squeezed Coherent States via a Free-Electron Laser. Phys. Rev. Lett. 1982, 48, 475–477. [Google Scholar] [CrossRef]
- Sinitsyn, Y.A.; Tsukernik, V.M. Manifestation of quantum properties in evolution of physical quantities for nonlinear Hamiltonian systems. Phys. Lett. A 1982, 90, 339–341. [Google Scholar] [CrossRef]
- Berman, G.; Iomin, A.; Zaslavsky, G. Method of quasiclassical approximation for c-number projection in coherent states basis. Phys. D Nonlinear Phenom. 1981, 4, 113–121. [Google Scholar] [CrossRef]
- Berman, G.P.; Iomin, A.M.; Kolovsky, A.R.; Tarkhanov, N.N. On dynamics of four-wave interactions in nonlinear quantum chain. Kirensky Inst. Physics. Krasn. 1986. (In Russian) [Google Scholar] [CrossRef]
- Iomin, A. Quantum continuous time random walk in nonlinear Schrödinger equation with disorder. Chaos Solitons Fractals 2016, 93, 64–70. [Google Scholar] [CrossRef]
- Iomin, A. Subdiffusion in classical and quantum nonlinear Schrödinger equations with disorder. Comput. Math. Appl. 2017, 73, 914–930. [Google Scholar] [CrossRef] [Green Version]
- Perelomov, A. Generalized Coherent States and Their Applications; Springer: Berlin, Germany, 1986. [Google Scholar]
- Carruthers, P.; Nieto, M.M. Phase and Angle Variables in Quantum Mechanics. Rev. Mod. Phys. 1968, 40, 411–440. [Google Scholar] [CrossRef] [Green Version]
- Abramovitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover Publications: New York, NY, USA, 1972. [Google Scholar]
- Frank, I.; Tamm, I. Coherent radiation of fast electrons in a medium. Dokl. Akad. Nauk SSSR 1937, 14, 109–114. [Google Scholar]
- Tamm, I.E. Selected Papers; Bolotovskii, B.M., Frenkel, V.Y., Eds.; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Bambini, A.; Renieri, A. The Free Electron Laser: A Single-Particle Classical Model. Lett. Nuovo Cimento 1978, 21, 399–404. [Google Scholar] [CrossRef]
- Bambini, A.; Renieri, A.; Stenholm, S. Classical theory of the free-electron laser in a moving frame. Phys. Rev. A 1979, 19, 2013–2025. [Google Scholar] [CrossRef]
- Schmüser, P.; Dohlus, M.; Rossbach, J. Ultraviolet and Soft X-ray Free-Electron Lasers; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Louisell, W.H. Quantum Statistical Properties of Radiation; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Rajaraman, R. Solitons and Instantons; North-Holland Publishing Company: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Gel’fand, I.M.; Yaglom, A.M. Integration in function spaces and its application to quantum physics. Uspekhi Mat. Nauk 1956, 11, 77–114. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
