A Combined Control Scheme of Direct Torque Control and Field-Oriented Control Algorithms for Three-Phase Induction Motor: Experimental Validation
Abstract
1. Introduction
2. Theoretical Background of the DTC Algorithm
3. DTRFC Versus DTSFC in Terms of Pull-Out Torque
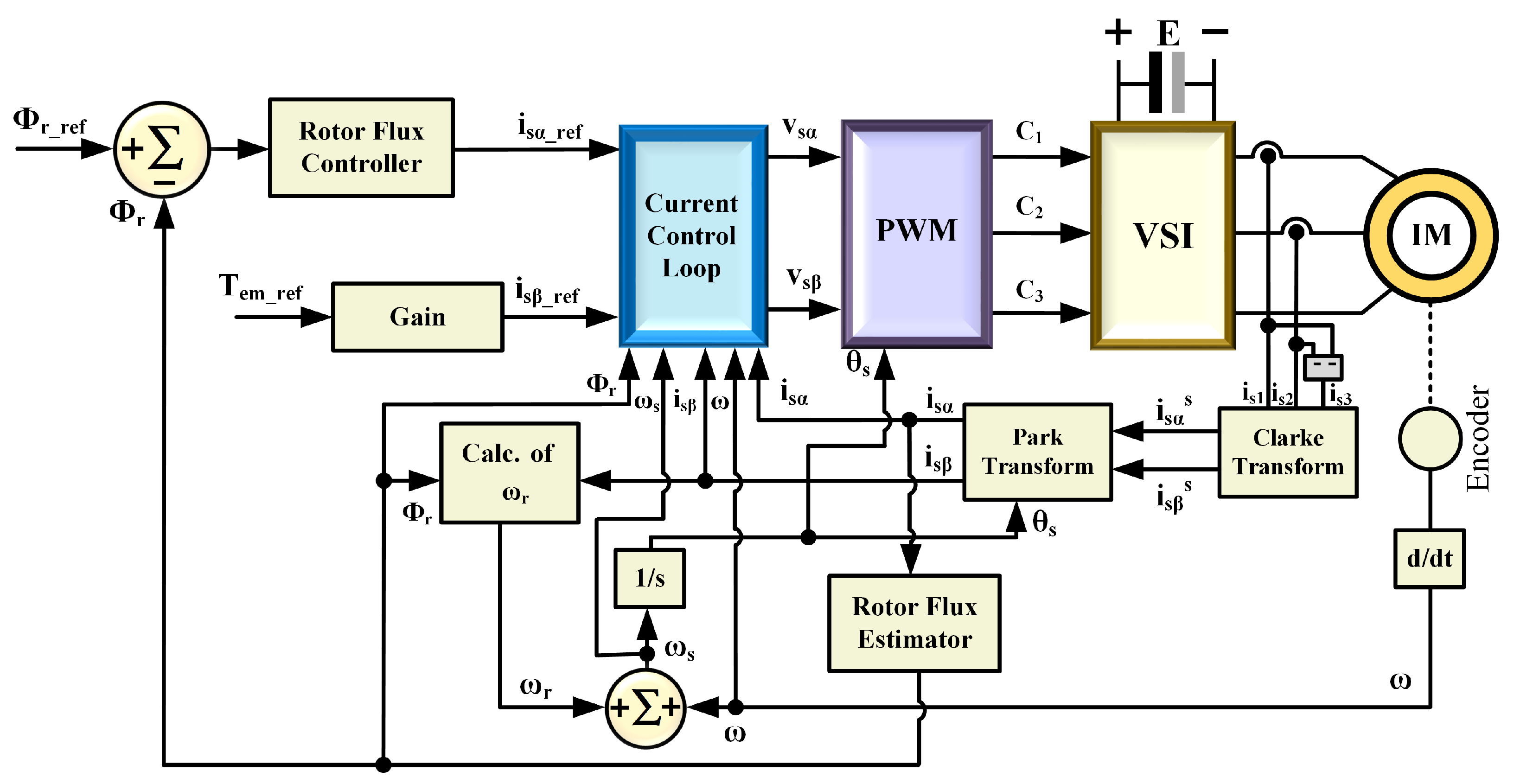
4. Theoretical Background of the FOC Algorithm
4.1. Working Principle
4.2. Setting Gain Controls of the FOC Algorithm
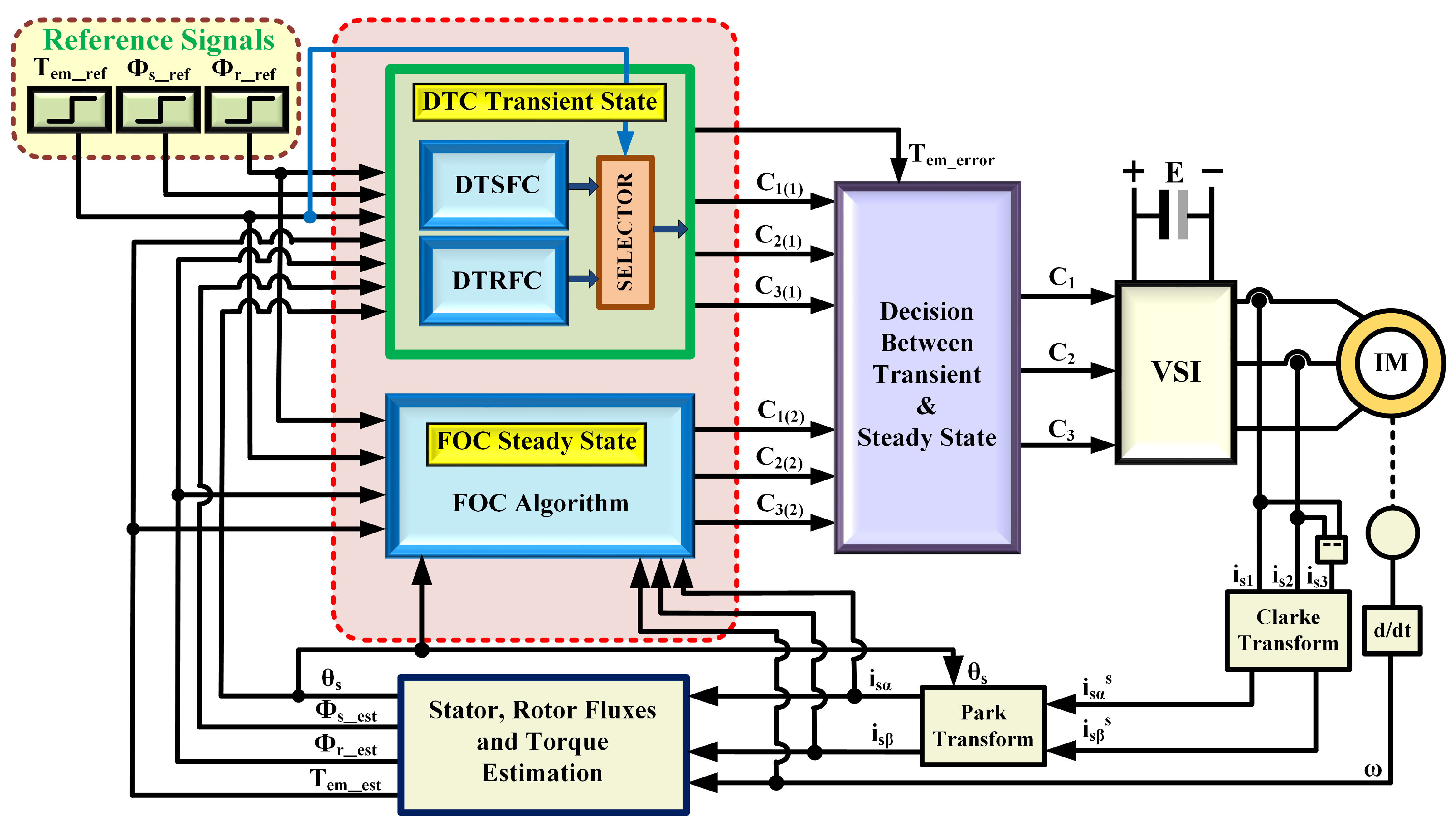
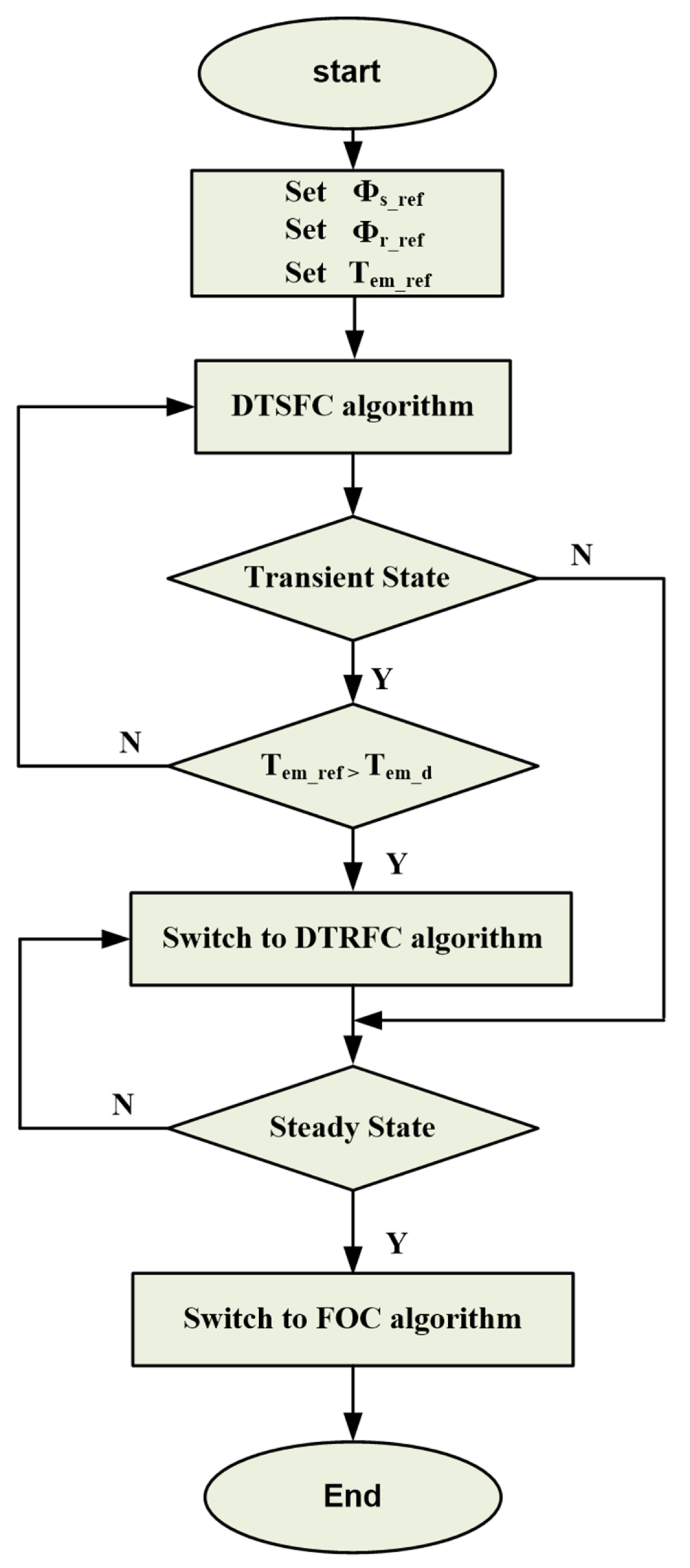
5. The Proposed Combined FOC and DTC Algorithms over a Wide Torque Operation Range
6. Simulation Results and Implementation
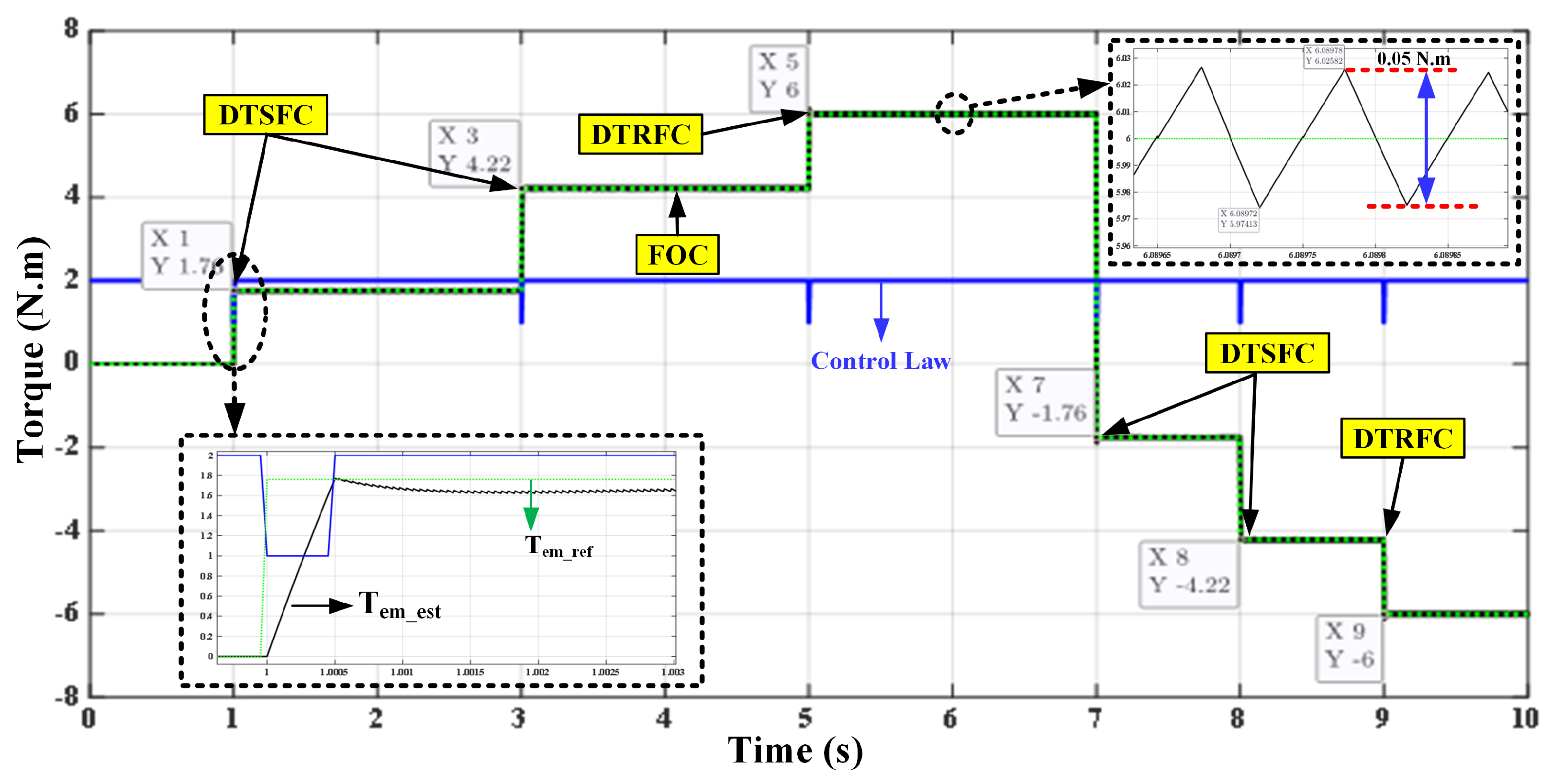
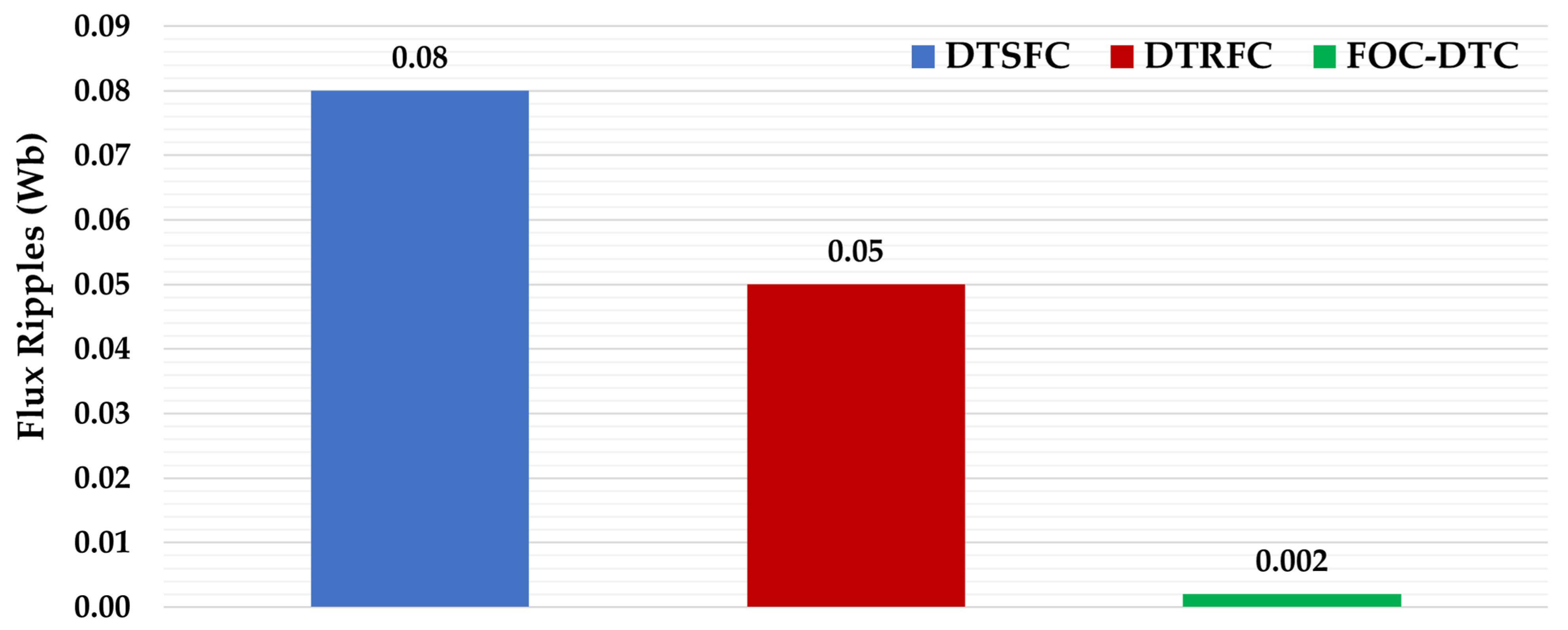
6.1. Simulation Results of DTRFC Versus DTSFC
6.2. Simulation Results of FOC with Rotor Flux Vector Orientation towards
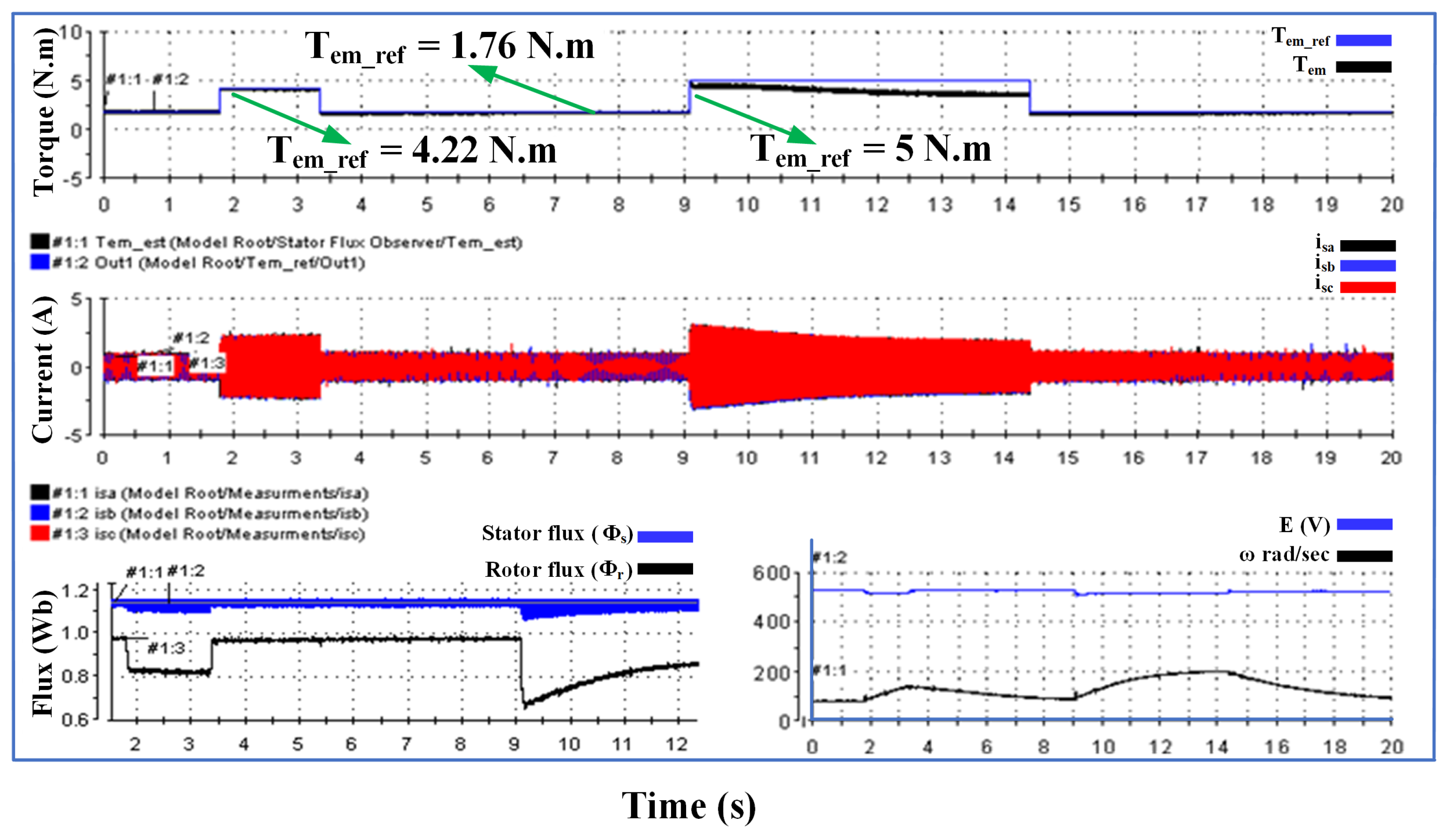
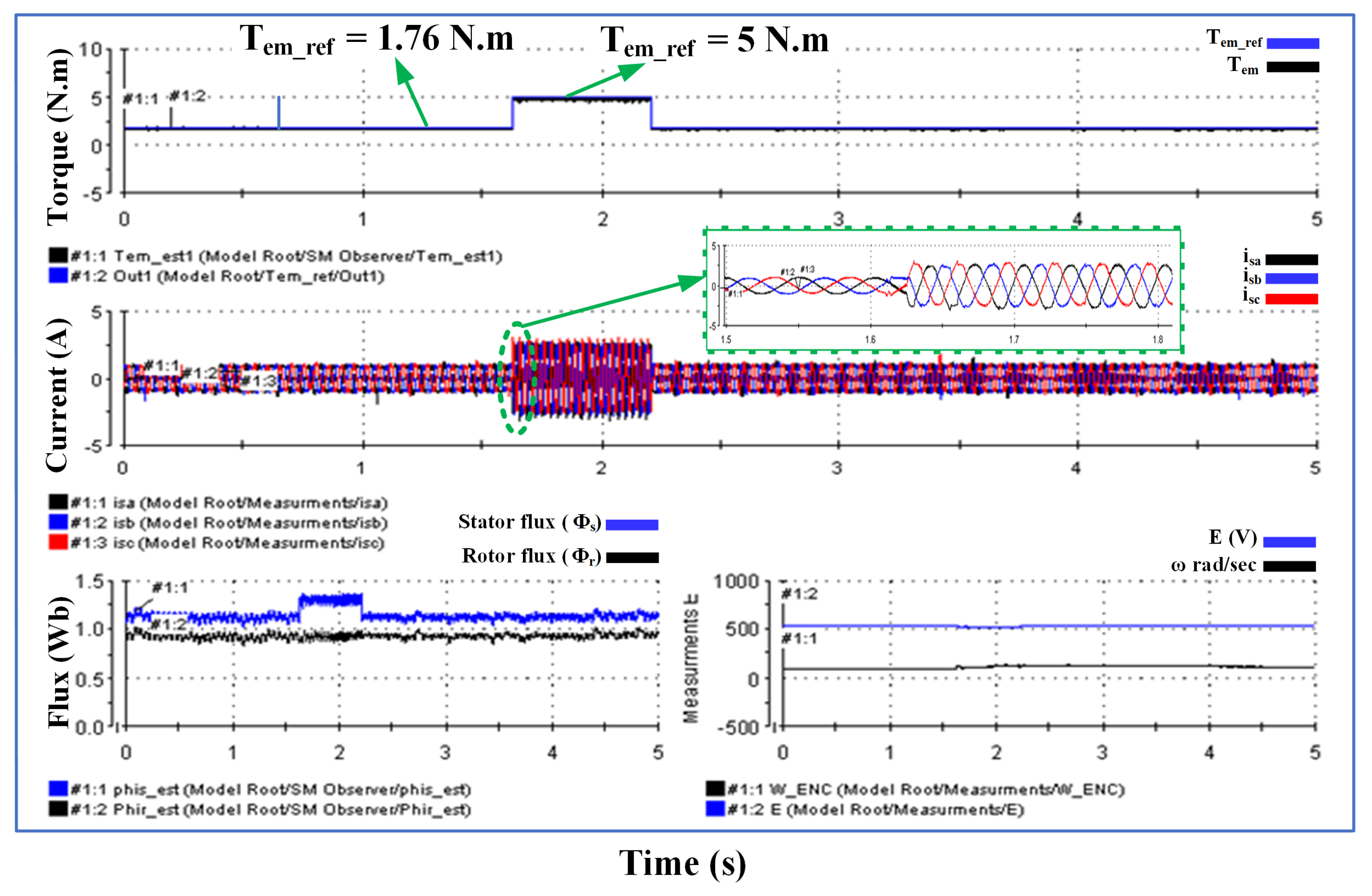
6.3. Simulation Results of the Combined FOC and DTC Algorithm
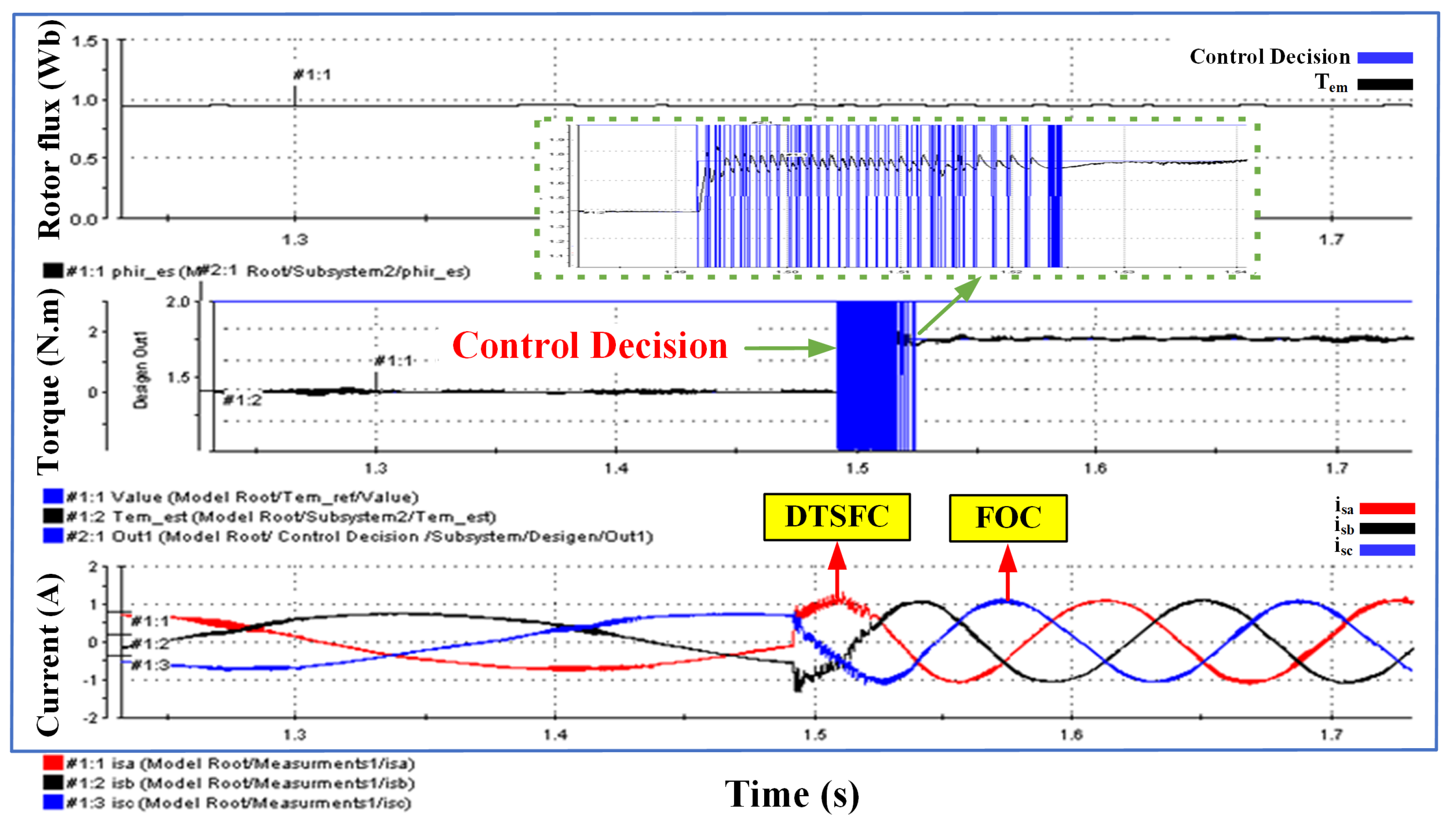
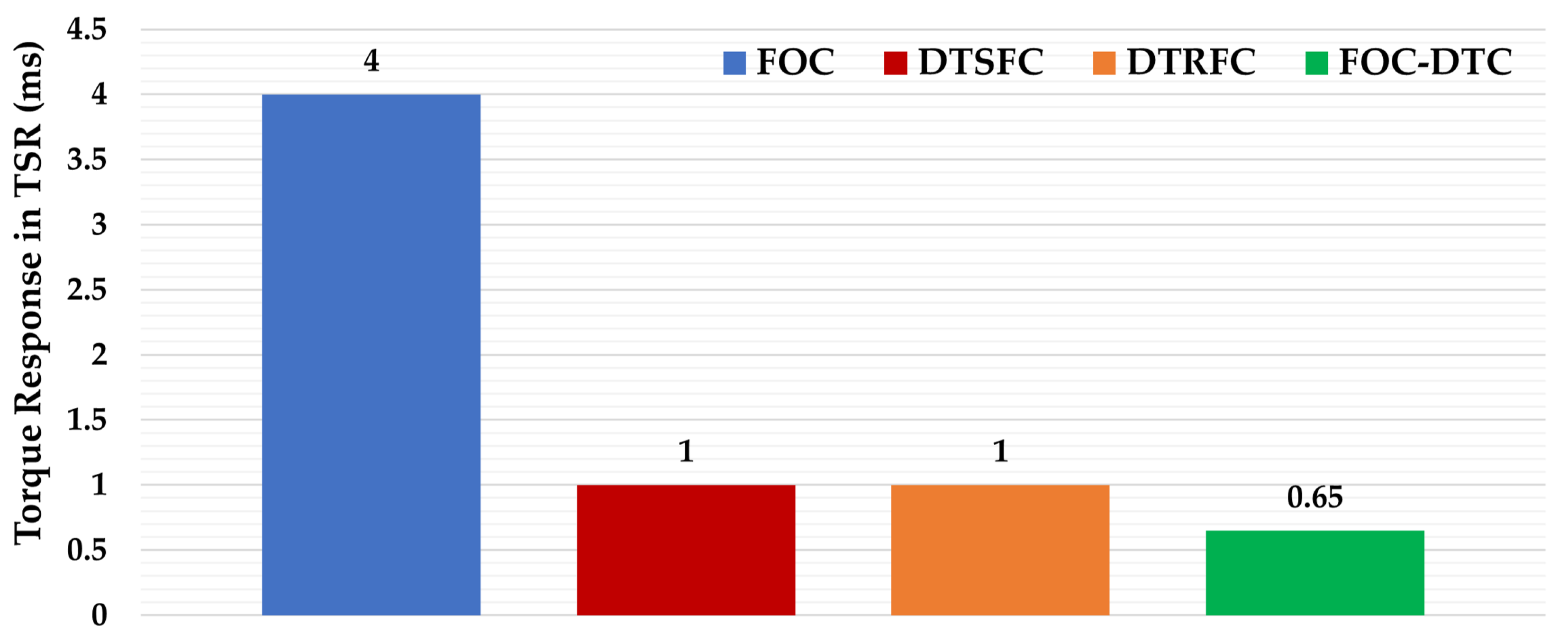
6.4. Transition Case Results between FOC and DTC Algorithms
6.4.1. Case 1: Assuming a Positive Torque Error
6.4.2. Case 2: Voltage Vector Switching Is Higher
7. Experimental Results Using a dSPACE-DS1103-Based Platform
8. Robustness and Evaluation against Previous and Recent Related Techniques
9. Conclusions
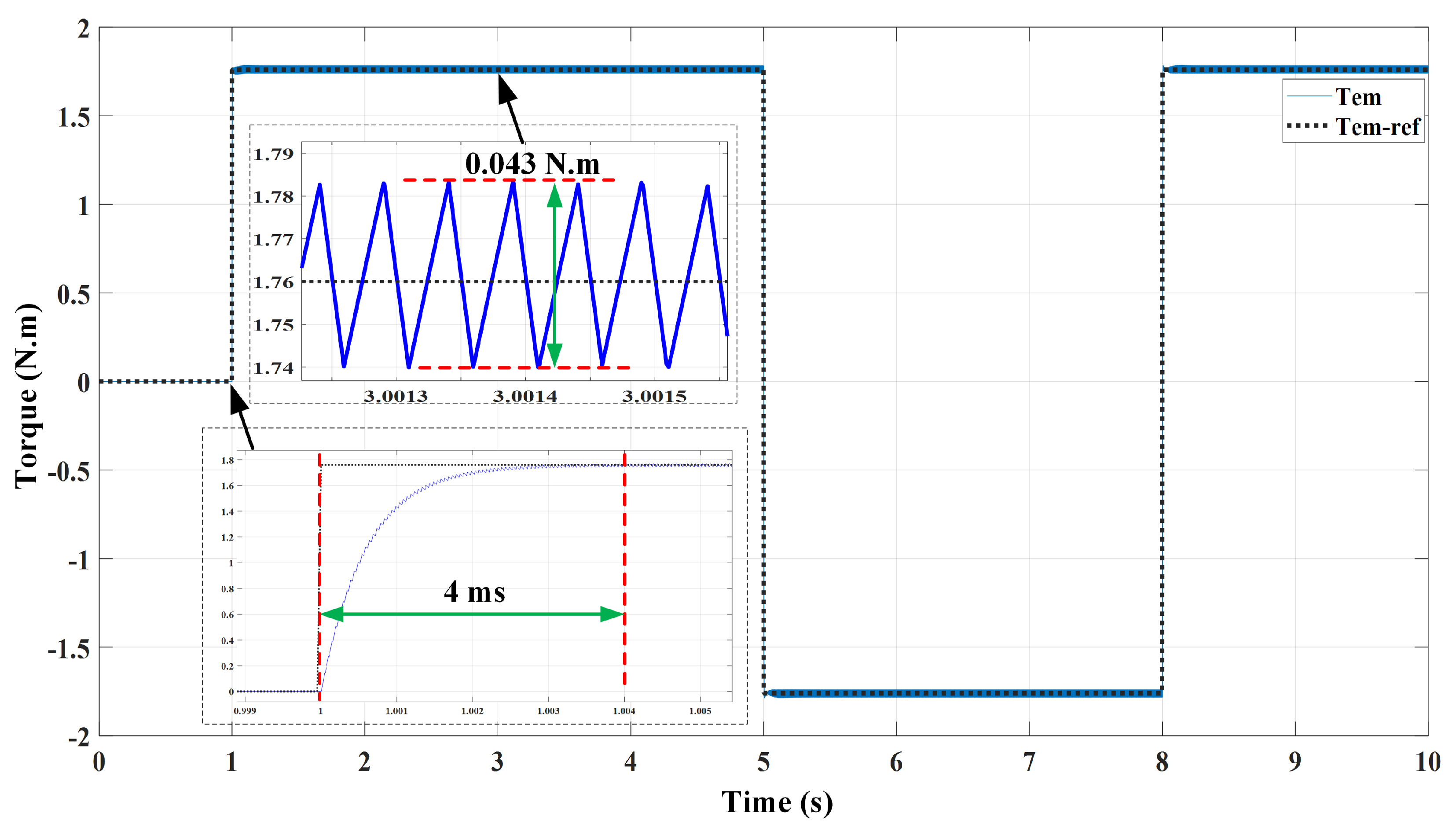
- Offered high dynamics of flux and torque due to the use of the DTSFC algorithm within the nominal torque range of 0.5 ms.
- Enabled the generation of high torque beyond the breakdown torque due to the use of the DTRFC algorithm 6/1.76 N.m * 100 = 340% T.
- Excellent, low steady-state error of torque and torque ripple that was reduced to a great extent due to the use of the FOC algorithm at 0.05 N.m and 0.028% T.
- Excellent transition between the transient state and steady state with the best values of switch-on= 0.5 N.m, switch-off = 0.1 N.m.
- Constant switching frequency was achieved at f = 10 kHz due to the use of the FOC algorithm during the steady-state condition.
- The results of the experiment distinguished the findings of the proposed study, which provided full validation for the adopted methodology and were in complete agreement with the simulated outcomes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variable | Unit Value |
|---|---|
| Nominal voltage | 230/400 V |
| Phase resistance stator | = 45.83 |
| Phase resistance rotor | = 31 |
| Phase inductance stator | = 1.24 H |
| Phase inductance rotor | = 1.11 H |
| Mutual inductance | = 1.05 H |
| Inertia | J = 0.006 kg.m |
| Friction factor | f = 0.001 N.m. sec/rad |
| Number of poles pairs | p = 2 |
| Nominal stator flux | = 1.14 Wb |
| Nominal rotor flux | = 0.945 Wb |
| Nominal power | = 0.25 kW |
| Nominal frequency | F = 50 Hz |
| Nominal speed | = 282 rad/s |
| Nominal torque | = 1.76 N.m |
Appendix B
| Kp and Ki Gains for Frame | Calculation of Kp and Ki Gains |
|---|---|
| = 100 | = |
| = 100, 200, 300 and 400. | = |
Appendix C. Motor Constants
Appendix D
| Abbreviation | Definition |
|---|---|
| IM | Induction Motor |
| DTSFC | Direct Torque ans Stator Flux Control |
| DTRFC | Direct Torque and Rotor Flux Control |
| FOC | Field-Oriented Control |
| VSI | Voltage Source Inverter |
| VEs | Voltage Vectors |
| HCs | Hysteresis Controllers |
| LUT | Lookup Table |
| PWM | Pulse Width Modulation |
| TSR | Transient State Response |
| SSR | Steady State Response |
| Ref | Reference |
Appendix E
References
- Priyanka, C.P.; Jagadanad, G. Inter-Turn Fault Analysis of Three Phase Induction Motor. In Proceedings of the 2020 IEEE 9th Power India International Conference (PIICON), Sonepat, India, 28 February–1 March 2020. [Google Scholar] [CrossRef]
- Shukla, S.; Singh, B. Single-Stage PV Array Fed Speed Sensorless Vector Control of Induction Motor Drive for Water Pumping. IEEE Trans. Ind. Appl. 2018, 54, 3575–3585. [Google Scholar] [CrossRef]
- Boulmane, A.; Zidani, Y.; Belkhayat, D.; Bouchouirbat, M. A GA-based adaptive mechanism for sensorless vector control of induction motor drives for urban electric vehicles. Turk. J. Electr. Eng. Comput. Sci. 2020, 28, 1731–1746. [Google Scholar] [CrossRef]
- Petri, A.M.; Petreus, D. Vector Control of Induction Machine Used in Electric Vehicle. In Proceedings of the 2020 43rd International Spring Seminar on Electronics Technology (ISSE), Demanovska Valley, Slovakia, 14–15 May 2020. [Google Scholar] [CrossRef]
- Aktas, M.; Awaili, K.; Ehsani, M.; Arisoy, A. Direct torque control versus indirect field-oriented control of induction motors for electric vehicle applications. Eng. Sci. Technol. Int. J. 2020, 23, 1134–1143. [Google Scholar] [CrossRef]
- Benbouhenni, H.; Bizon, N. Improved Rotor Flux and Torque Control Based on the Third-Order Sliding Mode Scheme Applied to the Asynchronous Generator for the Single-Rotor Wind Turbine. Mathematics 2021, 9, 2297. [Google Scholar] [CrossRef]
- Casadei, D.; Profumo, F.; Serra, G.; Tani, A. FOC and DTC: Two viable schemes for induction motors torque control. IEEE Trans. Power Electron. 2002, 17, 779–787. [Google Scholar] [CrossRef]
- Idris, N.R.N.; Yatim, A.H.M. Direct torque control of induction machines with constant switching frequency and reduced torque ripple. IEEE Trans. Ind. Electron. 2004, 51, 758–767. [Google Scholar] [CrossRef]
- Fekih, A.; Mobayen, S.; Chen, C.C. Adaptive robust fault-tolerant control design for wind turbines subject to pitch actuator faults. Energies 2021, 14, 1791. [Google Scholar] [CrossRef]
- Korkmaz, F.; Topaloğlu, İ.; Çakir, M.F.; Gürbüz, R. Comparative performance evaluation of FOC and DTC controlled PMSM drives. In Proceedings of the 2020 IEEE 4th International Conference on Power Engineering, Energy and Electrical Drives, Istanbul, Turkey, 13–17 May 2013. [Google Scholar] [CrossRef]
- Al-Mamoori, D.H.; Al-Tameemi, Z.H.; Jumaa, F.A.; Neda, O.M.; Al-Ghanimi, M.G. A Comparative Study of DTC-SVM and FOC-SVM Control Techniques of Induction Motor Drive. J. Eng. Appl. Sci. 2019, 14, 2135–2140. [Google Scholar] [CrossRef][Green Version]
- Meesala, R.E.K.; Thippiripati, V.K. An improved direct torque control of three-level dual inverter fed open-ended winding induction motor drive based on modified look-up table. IEEE Trans. Power Electron. 2020, 35, 3906–3917. [Google Scholar] [CrossRef]
- Wang, M.; Sun, D.; Ke, W.; Nian, H. A Universal Lookup Table-Based Direct Torque Control for OW-PMSM Drives. IEEE Trans. Power Electron. 2021, 36, 6188–6191. [Google Scholar] [CrossRef]
- Suresh, S.; Rajeevan, P.P. Virtual Space Vector-Based Direct Torque Control Schemes for Induction Motor Drives. IEEE Trans. Ind. Appl. 2020, 56, 2719–2728. [Google Scholar] [CrossRef]
- Yang, G.; Yang, J.; Li, S.; Wang, Y.; Hussain, H.; Deng, R.; Yan, L. A Sequential Direct Torque Control Scheme for Seven-Phase Induction Machines Based on Virtual Voltage Vectors. IEEE Trans. Ind. Appl. 2021, 57, 3722–3734. [Google Scholar] [CrossRef]
- Muduli, U.R.; Behera, R.K.; Hosani, K.A.; Moursi, M.S.E. Direct Torque Control With Constant Switching Frequency for Three-to-Five Phase Direct Matrix Converter Fed Five-Phase Induction Motor Drive. IEEE Trans. Power Electron. 2022, 37, 11019–11033. [Google Scholar] [CrossRef]
- Deng, W.; Li, H.; Rong, J. A Novel Direct Torque Control of Matrix Converter-Fed PMSM Drives Using Dynamic Sector Boundary for Common-Mode Voltage Minimization. IEEE Trans. Ind. Electron. 2021, 68, 70–80. [Google Scholar] [CrossRef]
- Fan, B.; Fu, Z.; Liu, L.; Fu, J. The full-order state observer speed-sensorless vector control based on parameters identification for induction motor. Meas. Control 2019, 52, 202–211. [Google Scholar] [CrossRef]
- Khan, M.R.; Iqbal, A. Experimental investigation of five-phase induction motor drive using extended Kalman-filter. Asian Power Electron. J. 2009, 3, 1–7. [Google Scholar]
- Khadar, S.; Abu-Rub, H.; Kouzou, A. Sensorless Field-Oriented Control for Open-End Winding Five-Phase Induction Motor With Parameters Estimation. IEEE Open J. Ind. Electron. Soc. 2021, 1, 266–279. [Google Scholar] [CrossRef]
- Wang, F.; Mei, X.; Tao, P.; Kennel, R.; Rodriguez, J. Predictive field-oriented control for electric drives. Chin. J. Electr. Eng. 2017, 3, 73–78. [Google Scholar] [CrossRef]
- Farhan, N.S.; Humod, A.T.; Hasan, F. Field Oriented Control of AFPMSM for Electrical Vehicle Using Adaptive Neuro-Fuzzy Inference System (ANFIS). Eng. Technol. J. 2021, 39, 1571–1582. [Google Scholar] [CrossRef]
- Monmasson, E.; Robyns, B.; Mendes, E.; Fornel, B.D. Dynamic reconfiguration of control and estimation algorithms for induction motor drives. In Proceedings of the Industrial Electronics, ISIE 2002, IEEE International Symposium; L’Aquila, Italy, 8–11 July 2002. [CrossRef]
- Naassani, A.A.; Monmasson, E.; Louis, J.P. Synthesis of direct torque and rotor flux control algorithms by means of sliding-mode theory. IEEE Trans. Ind. Electron. 2005, 52, 785–799. [Google Scholar] [CrossRef]
- Vaez-Zadeh, S.; Jalali, E. Combined vector control and direct torque control method for high performance induction motor drives. Energy Convers. Manag. 2007, 48, 3095–3101. Available online: https://www.sciencedirect.com/science/article/pii/S0196890407001409 (accessed on 24 September 2007). [CrossRef]
- Jiang, Z.; Hu, S.; Cao, W. A New Fuzzy Logic Torque Control Scheme Based on Vector Control and Direct Torque Control for Induction Machine. In Proceedings of the 2008 3rd International Conference on Innovative Computing Information and Control, Dalian, China, 18–20 June 2008. [Google Scholar] [CrossRef]
- Elgbaily, M.; Anayi, F.; Packianather, M. Performance Improvement Based Torque Ripple Minimization for Direct Torque Control Drive Fed Induction Motor Using Fuzzy Logic Control, Control, Instrumentation and Mechatronics: Theory and Practice; Springer Nature Singapore Pte Ltd.: Singapore, 2022; pp. 416–428. [Google Scholar]
- Vaez-Zadeh, S.; Daryabeigi, E. Combined vector and direct torque control methods for IPM motor drives using emotional controller (BELBIC). In Proceedings of the 2011 2nd Power Electronics, Drive Systems and Technologies Conference, Tehran, Iran, 16–17 February 2011. [Google Scholar] [CrossRef]
- Boulghasoul, Z.; Elbacha, A.; Elwarraki, E.; Yousfi, D. Combined Vector Control and Direct Torque Control an experimental review and evaluation. In Proceedings of the 2011 International Conference on Multimedia Computing and Systems, Washington, DC, USA, 7–9 April 2011. [Google Scholar] [CrossRef]
- El Kharki, A.; Boulghasoul, Z.; Et-Taaj, L.; Elbacha, A. A New Intelligent Control Strategy of Combined Vector Control and Direct Torque Control for Dynamic Performance Improvement of Induction Motor Drive. J. Electr. Eng. Technol. 2022. Available online: https://link.springer.com/article/10.1007/s42835-022-01086-3 (accessed on 24 September 2007). [CrossRef]
- Talib, M.H.N.; Ibrahim, Z.; Rahim, N.A.; Yaakop, N.M. Development of combined vector and Direct Torque Control methods for independent two induction motor drives. In Proceedings of the 2012 IEEE International Power Engineering and Optimization Conference Melaka, Melaka, Malaysia, 6–7 June 2012. [Google Scholar] [CrossRef]
- Vasarhelyi, J.; Imecs, M.; Szabo, C.; Incze, I.I. Run-Time Reconfiguration of Tandem Inverter for Induction Motor Drives. In Proceedings of the 2020 IEEE 12th International Power Electronics and Motion Control Conference, Nanjing, China, 29 November–2 December 2020. [Google Scholar] [CrossRef]
- Vasarhelyi, J.; Incze, I.I.; Imecs, M.; Szabo, C. Improved Starting of the Induction Motor Fed by a Run-Time Reconfigurable Frequency Converter. In Proceedings of the 2006 International Conference on Intelligent Engineering Systems, International Conference on Intelligent Engineering Systems, London, UK, 26–28 June 2006. [Google Scholar] [CrossRef]
- Mahfoud, S.; Derouich, A.; Iqbal, A.; El Ouanjli, N. ANT-colony optimization-direct torque control for a doubly fed induction motor: An experimental validation. Energy Rep. 2022, 8, 81–98. [Google Scholar] [CrossRef]
- Elgbaily, M.; Anayi, F.; Packianather, M. Genetic and particle swarm optimization algorithms based direct torque control for torque ripple attenuation of induction motor. Mater. Today Proc. 2022, 67, 577–590. [Google Scholar] [CrossRef]
- Alsofyani, I.M.; Idris, N.R.N.; Lee, K. Dynamic Hysteresis Torque Band for Improving the Performance of Lookup-Table-Based DTC of Induction Machines. IEEE Trans. Power Electron. 2018, 33, 7959–7970. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, K. Implementation of a direct control algorithm for induction motors based on discrete space vector modulation. IEEE Trans. Power Electron. 2000, 15, 769–777. [Google Scholar] [CrossRef]
- Hajian, M.; Soltani, J.; Markadeh, G.A.; Hosseinnia, S. Adaptive Nonlinear Direct Torque Control of Sensorless IM Drives With Efficiency Optimization. IEEE Trans. Ind. Electron. 2010, 57, 975–985. [Google Scholar] [CrossRef]
- Lai, Y.-S.; Chen, J.-H. A new approach to direct torque control of induction motor drives for constant inverter switching frequency and torque ripple reduction. IEEE Trans. Energy Convers. 2001, 16, 220–227. [Google Scholar] [CrossRef]
- Buja, Y.G.; Menis, R. Steady-State Performance Degradation of a DTC IM Drive Under Parameter and Transduction Errors. IEEE Trans. Ind. Electron. 2008, 55, 1749–1760. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, A. Steady-state and transient performance evaluation of a DTC scheme in the low speed range. IEEE Trans. Power Electron. 2001, 16, 846–851. [Google Scholar] [CrossRef]
- Casadei, D.; Serra, G.; Tani, A.; Zarri, L. Assessment of direct torque control for induction motor drives. Bull. Pol. Acad. Sci. Tech. Sci. 2006, 54, 237–254. [Google Scholar]
- Ambrozic, V.; Buja, G.S.; Menis, R. Band-constrained technique for direct torque control of induction motor. IEEE Trans. Ind. Electron. 2004, 51, 776–784. [Google Scholar] [CrossRef]
- Mathapati, S.; Bocker, J. Analytical and Offline Approach to Select Optimal Hysteresis Bands of DTC for PMSM. IEEE Trans. Ind. Electron. 2013, 60, 885–895. [Google Scholar] [CrossRef]
- Shin, M.-H.; Hyun, D.-S.; Cho, S.-B. Maximum torque control of stator-flux-oriented induction machine drive in the field-weakening region. IEEE Trans. Ind. Appl. 2002, 38, 117–122. [Google Scholar] [CrossRef]
- Hiware, R.S.; Chaudhari, J.G. Indirect Field Oriented Control for Induction Motor. In Proceedings of the 2011 4th International Conference on Emerging Trends in Engineering & Technology, Mauritius, 18–20 November 2011. [Google Scholar] [CrossRef]
- Kabache, N.; Moulahoum, S.; Houassine, H. FPGA Implementation of direct Rotor Field Oriented Control for Induction Motor. In Proceedings of the 2013 18th International Conference on Methods & Models in Automation & Robotics (MMAR), Miedzyzdroje, Poland, 26–29 August 2013. [Google Scholar] [CrossRef]
- Bahrani, B.; Kenzelmann, S.; Rufer, A. Multivariable-PI-Based dq Current Control of Voltage Source Converters With Superior Axis Decoupling Capability. IEEE Trans. Ind. Electron. 2011, 58, 3016–3026. [Google Scholar] [CrossRef]
- Acevedo, G.; Hernando; Vargas, N.; Hernando, G.M.; Torres, C.; Jairo, J. Design of Rotor Flux Oriented Vector Control Systems for Induction Motor. In Proceedings of the 7th International Power Electronics and Motion Control Conference, Budapest, Hungary, 2–4 September 1996. [Google Scholar] [CrossRef]
- Pjetri, A.; Luga, Y.; Bardhi, A. Sensorless Speed rotor flux oriented control of three phase induction motor. Eur. Sci. J. 2015, 11, 1857–7881. [Google Scholar]
- Consoli, A.; Scarcella, G.; Testa, A. Slip-frequency detection for indirect field-oriented control drives. IEEE Trans. Ind. Appl. 2004, 40, 194–201. [Google Scholar] [CrossRef]
- Abad, G.; Rodriguez, M.Á.; Poza, J. Two-Level VSC Based Predictive Direct Torque Control of the Doubly Fed Induction Machine With Reduced Torque and Flux Ripples at Low Constant Switching Frequency. IEEE Trans. Power Electron. 2008, 23, 1050–1061. [Google Scholar] [CrossRef]
- Hodel, A.S.; Hall, C.E. Variable-structure PID control to prevent integrator windup. IEEE Trans. Ind. Electron. 2001, 48, 442–451. [Google Scholar] [CrossRef]
- Kumar, S.; Negi, R. A comparative study of PID tuning methods using anti-windup controller. In Proceedings of the 2012 2nd International Conference on Power, Control & Embedded Systems, Allahabad, Uttar Pradesh, India, 17–19 December 2012. [Google Scholar] [CrossRef]
- Okada, Y.; Yamakawa, Y.; Yamazaki, T.; Kurosu, S. Tuning Method of PI Controller for Given Damping Coefficient. In Proceedings of the 2006 SICE-ICASE International Joint Conference, Busan, Korea, 18–21 October 2006. [Google Scholar] [CrossRef]
- Dincel, E.; Yıldırım, U.; Söylemez, M.T. Modeling and control of under-damped second order systems with dead-time and inverse response. In Proceedings of the 2013 IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 29 November–1 December 2013. [Google Scholar] [CrossRef]
- Jose, J.; Goyal, G.N.; Aware, M.V. Improved inverter utilisation using third harmonic injection. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems & 2010 Power India, New Delhi, India, 20–23 December 2010. [Google Scholar] [CrossRef]
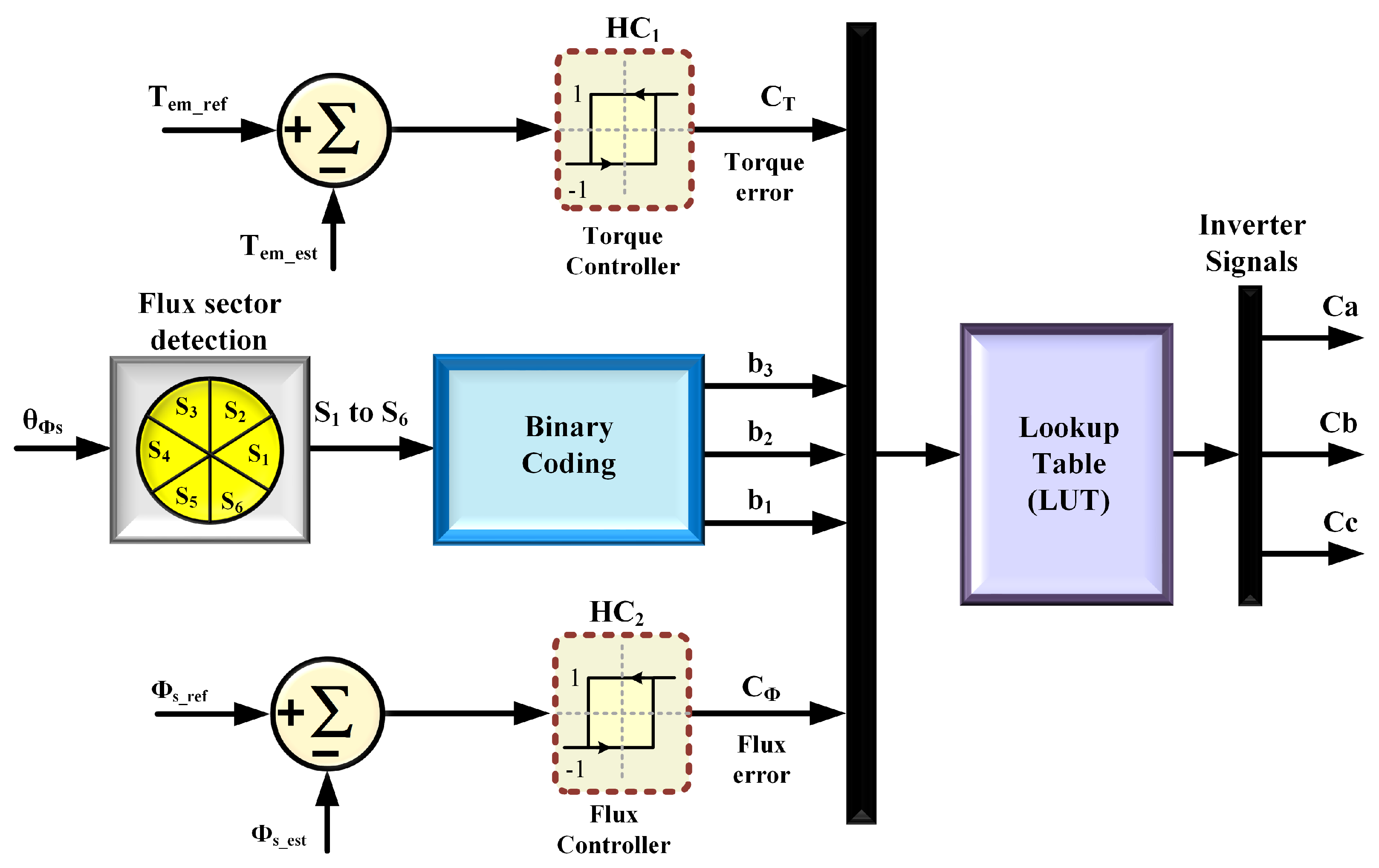



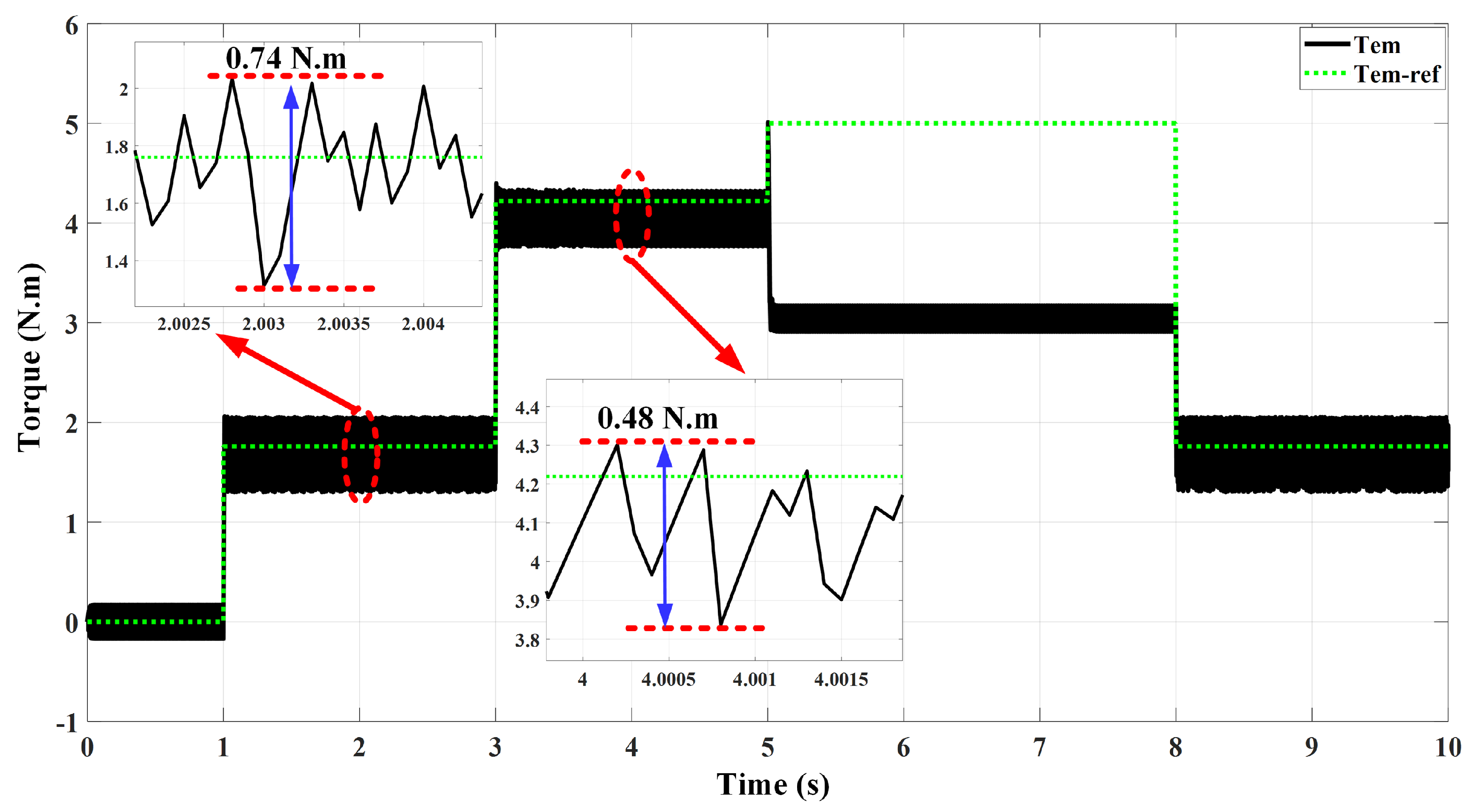
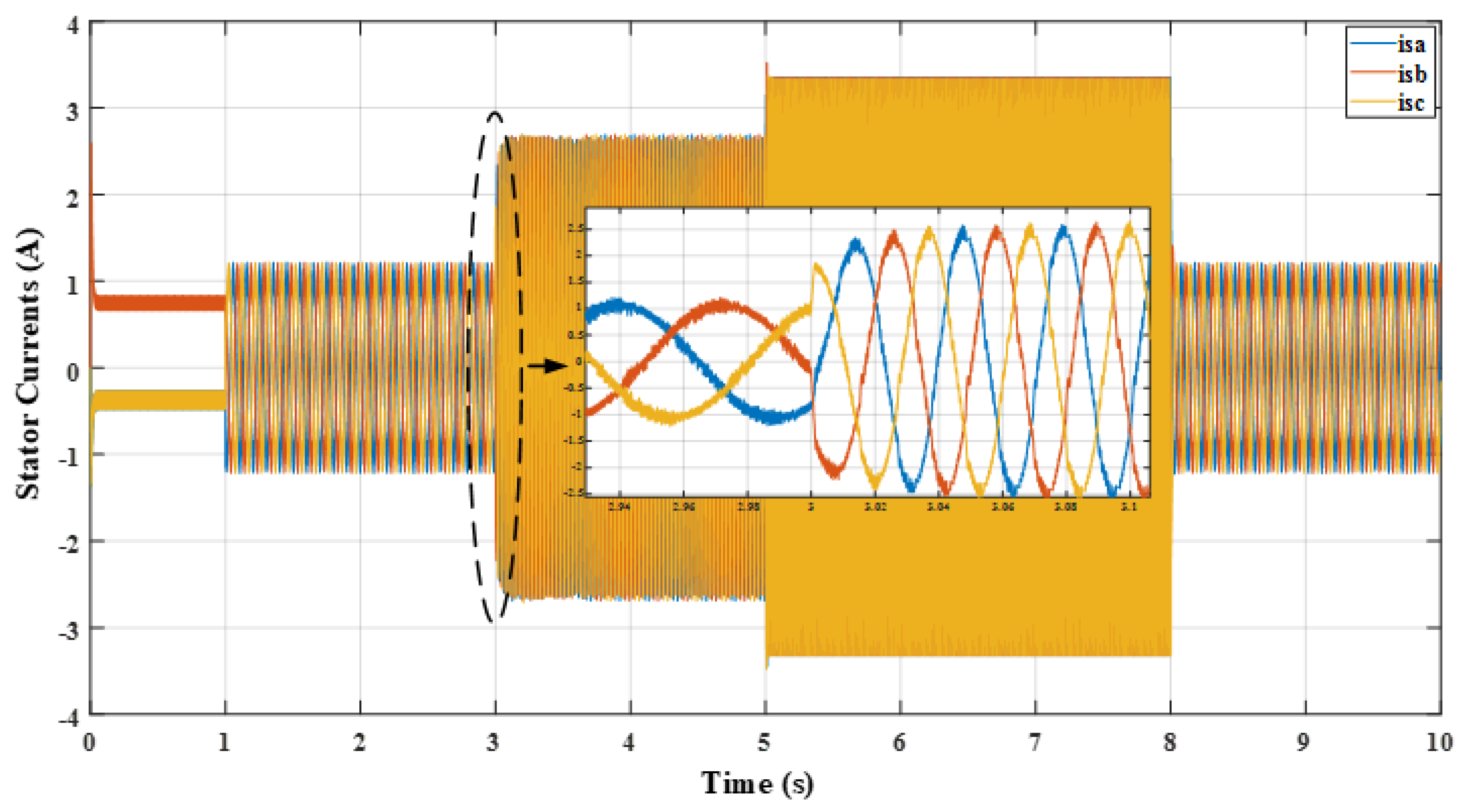
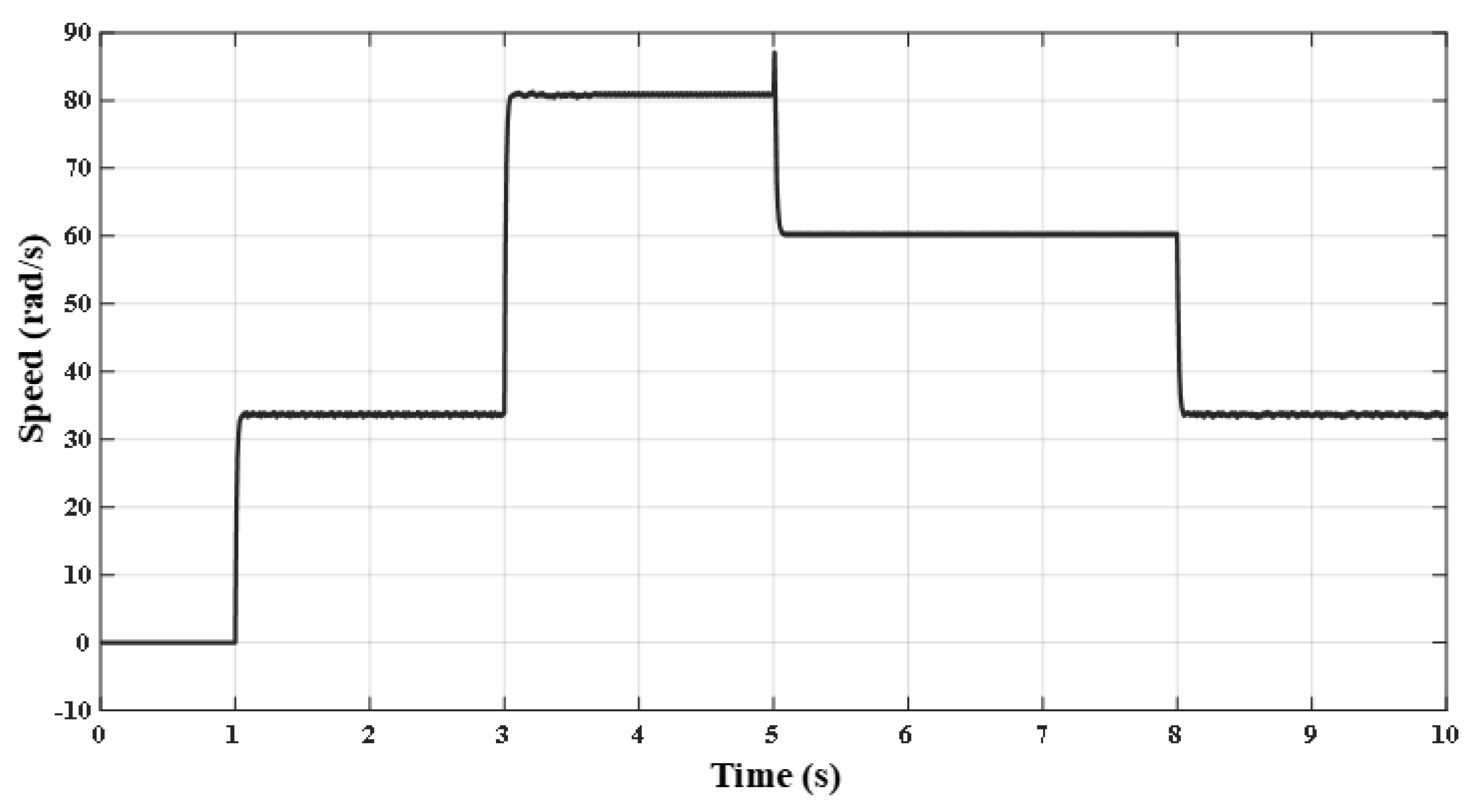
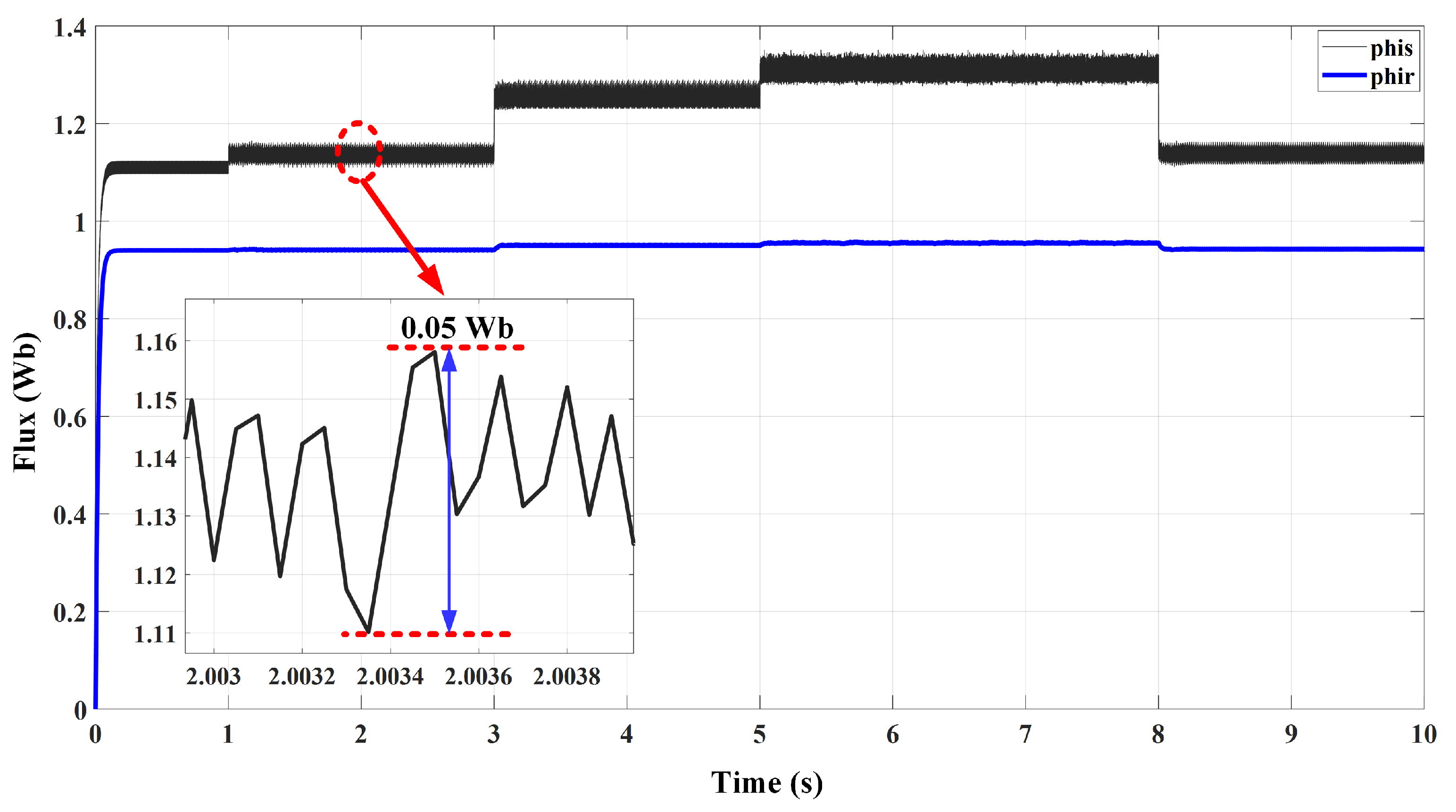

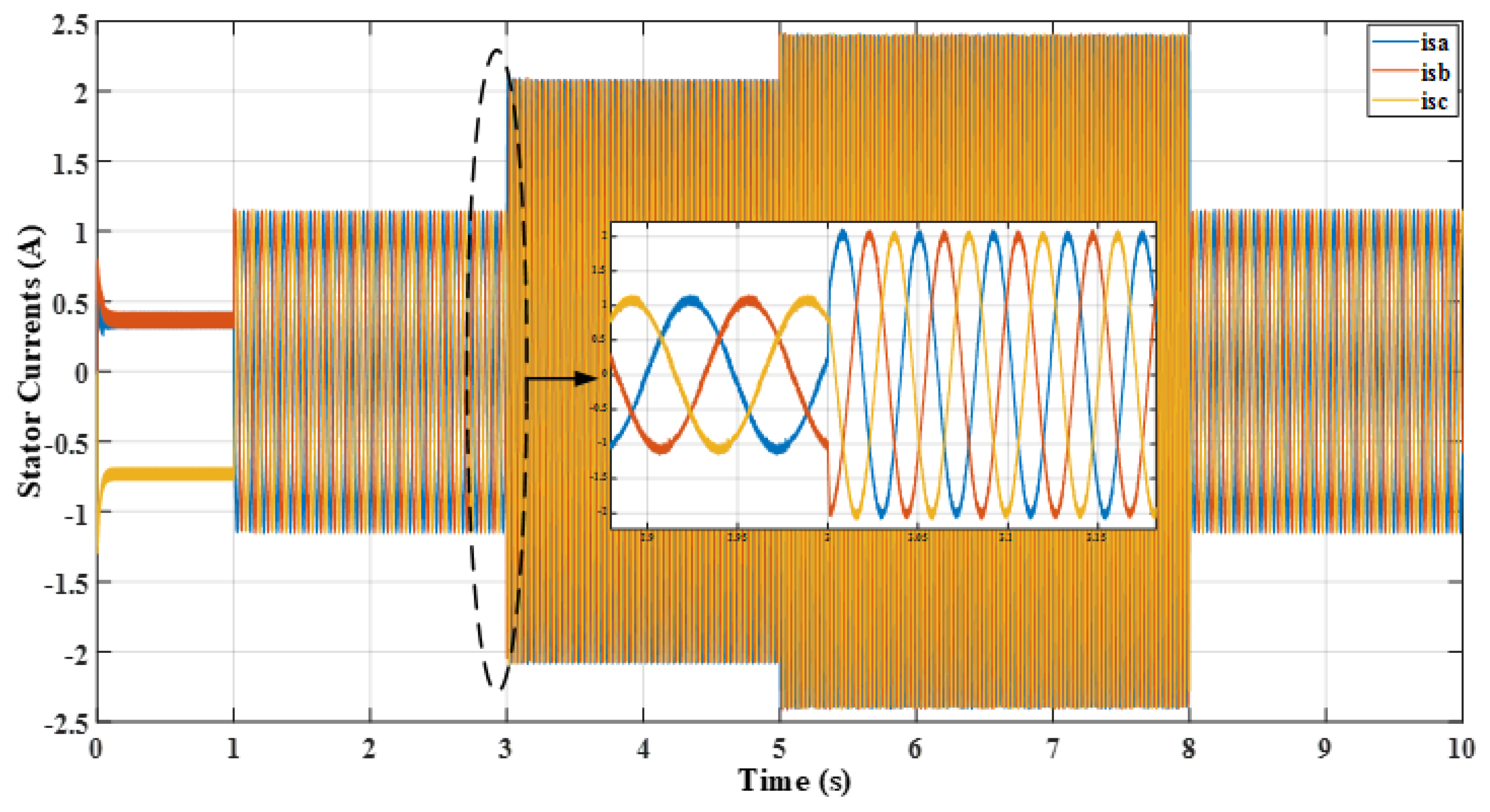
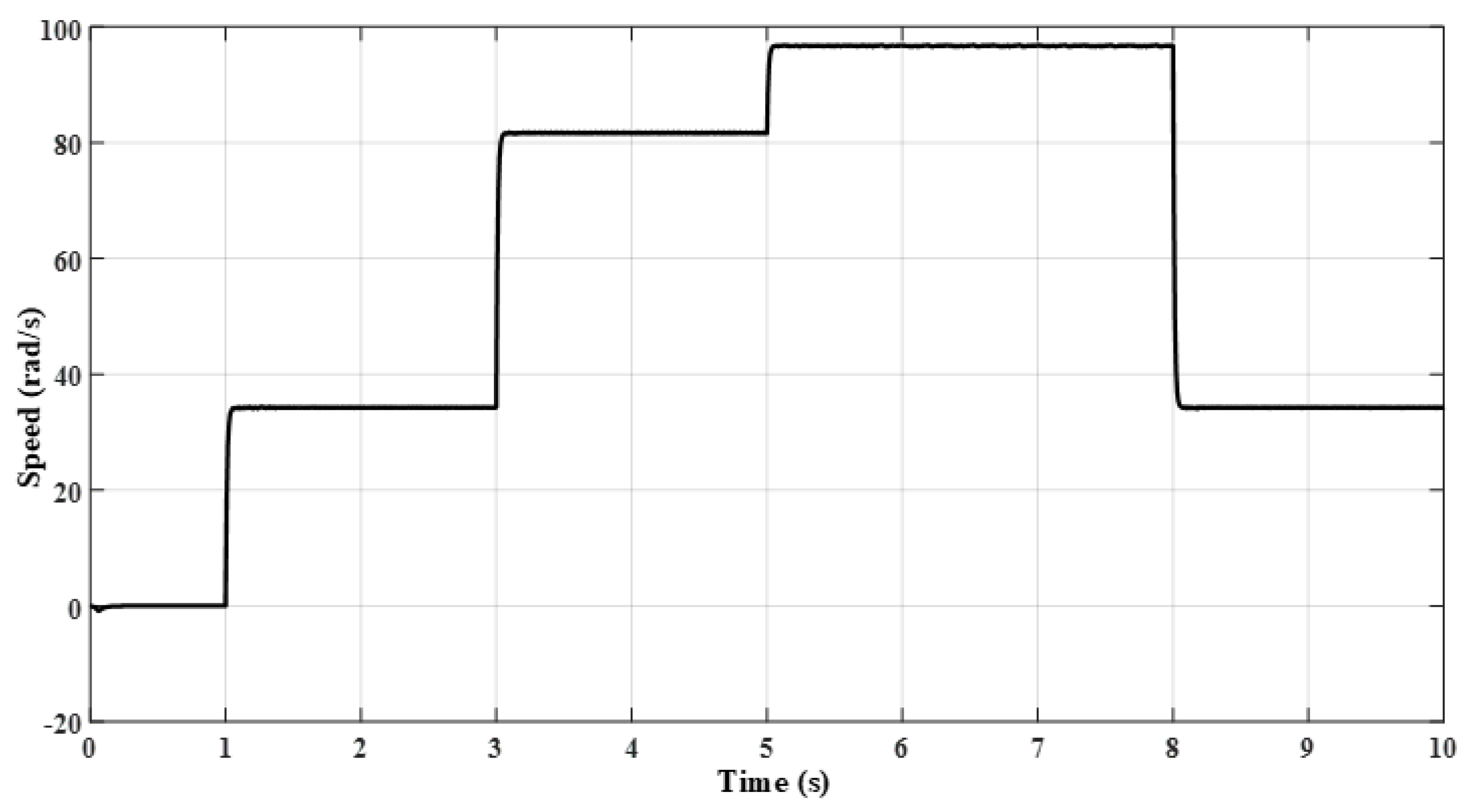


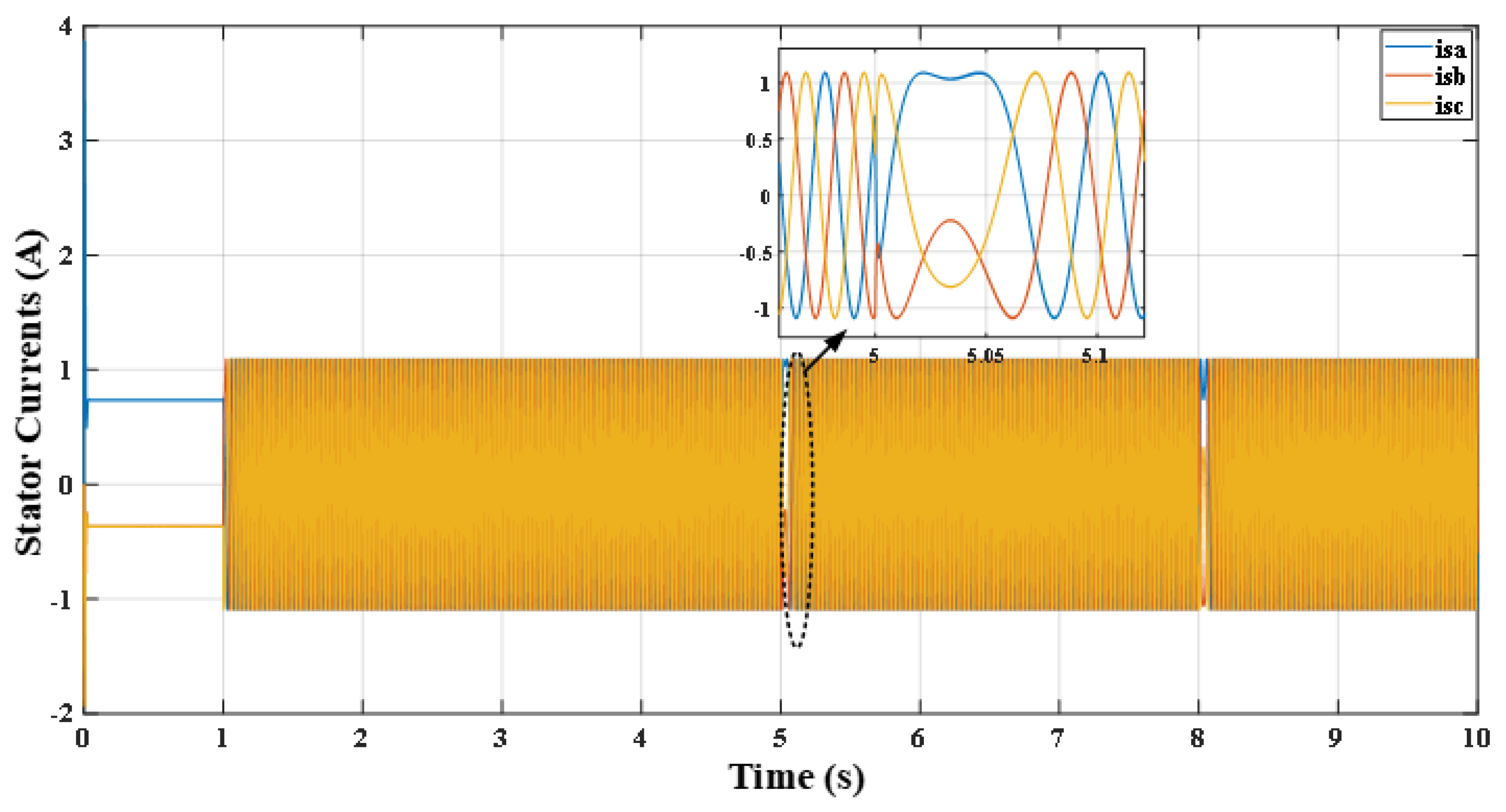
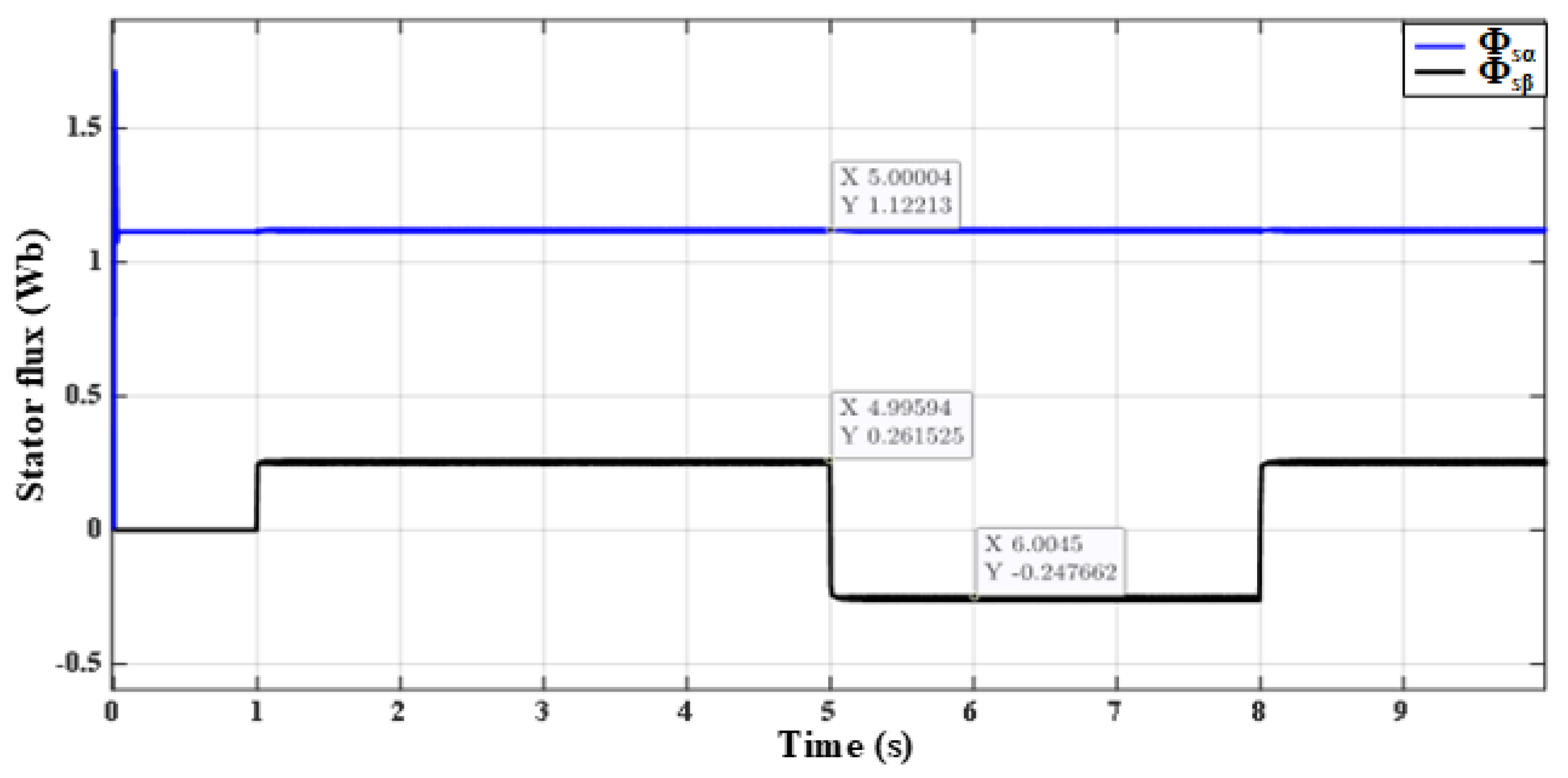

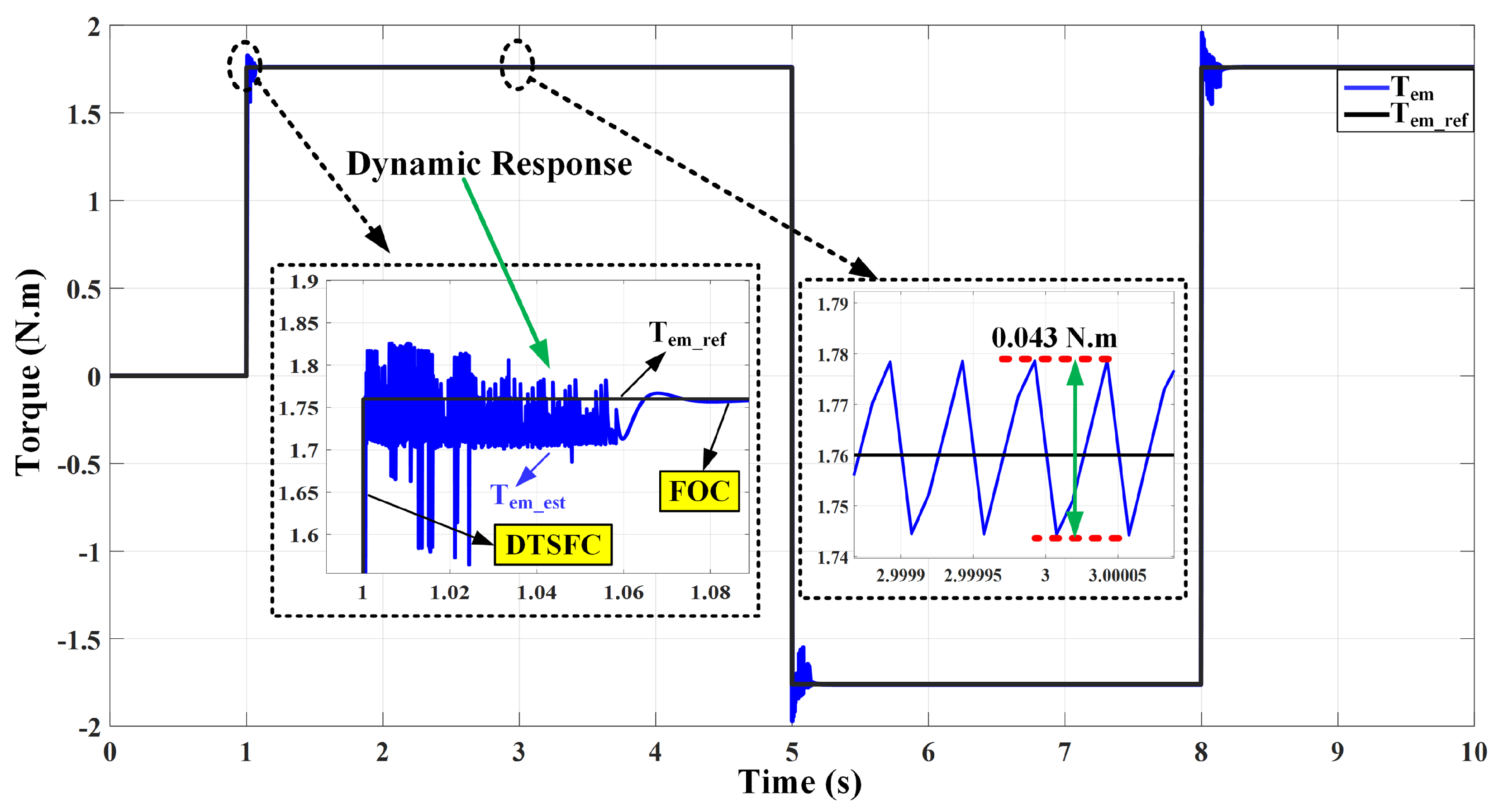


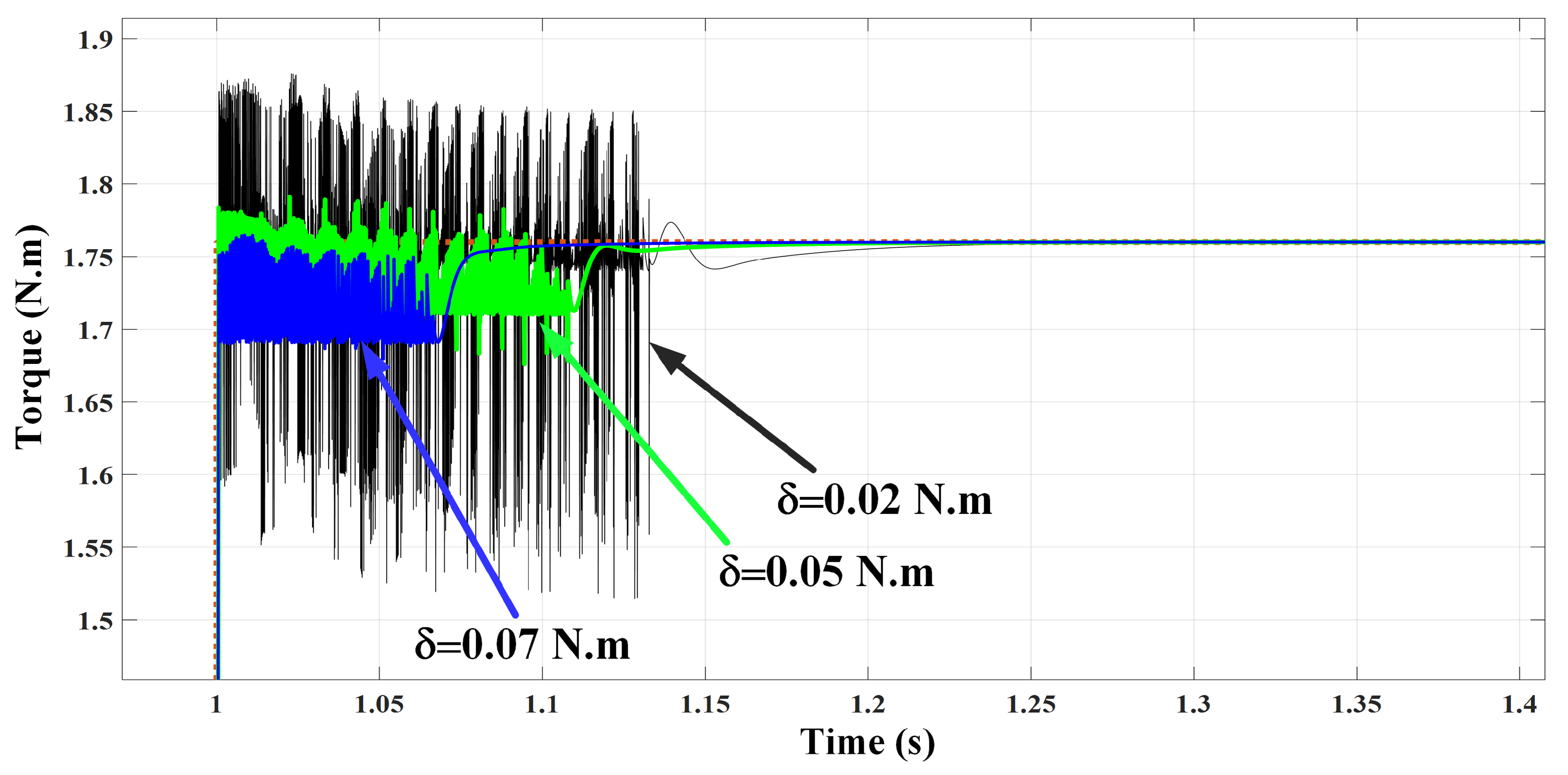
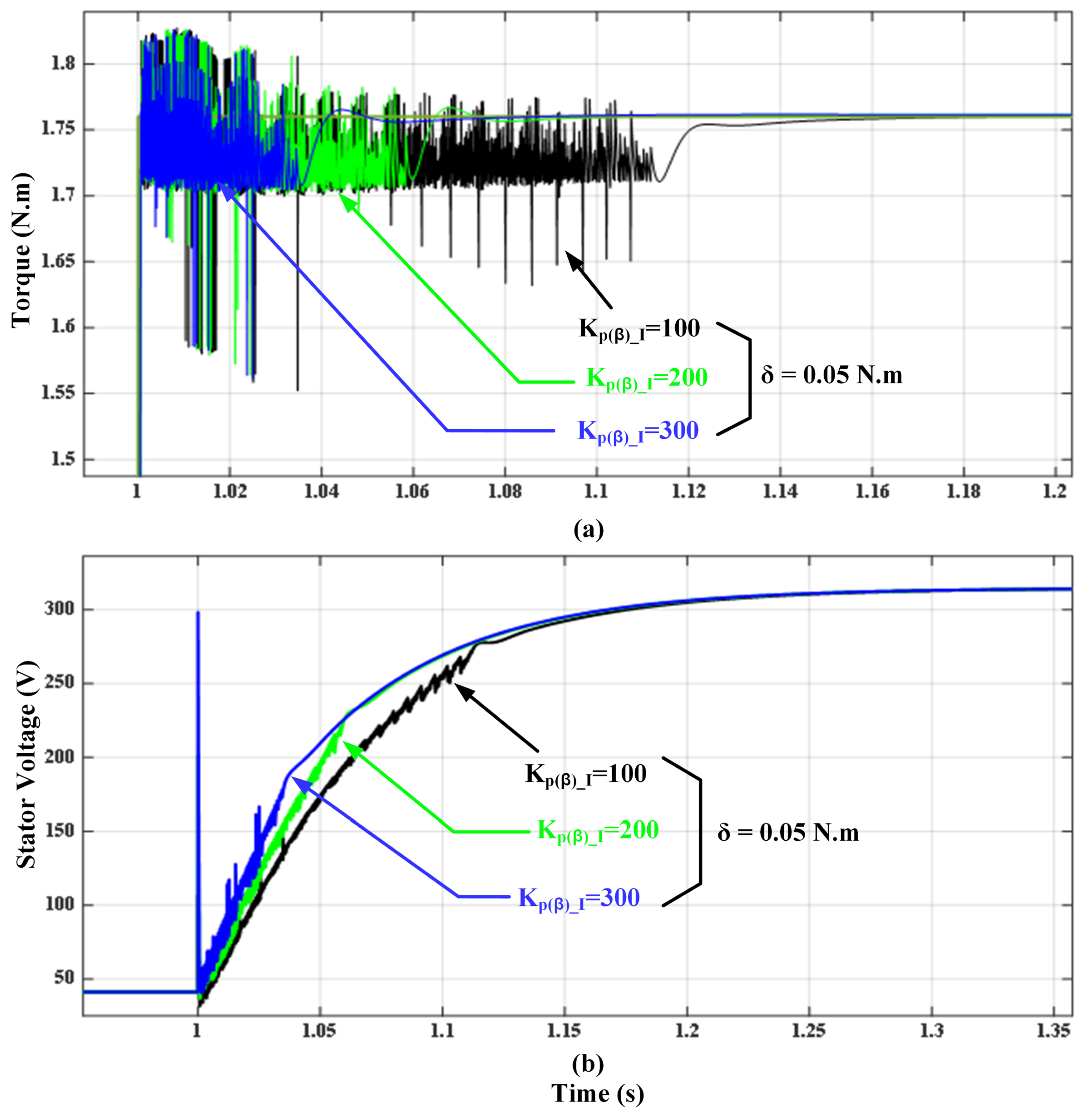
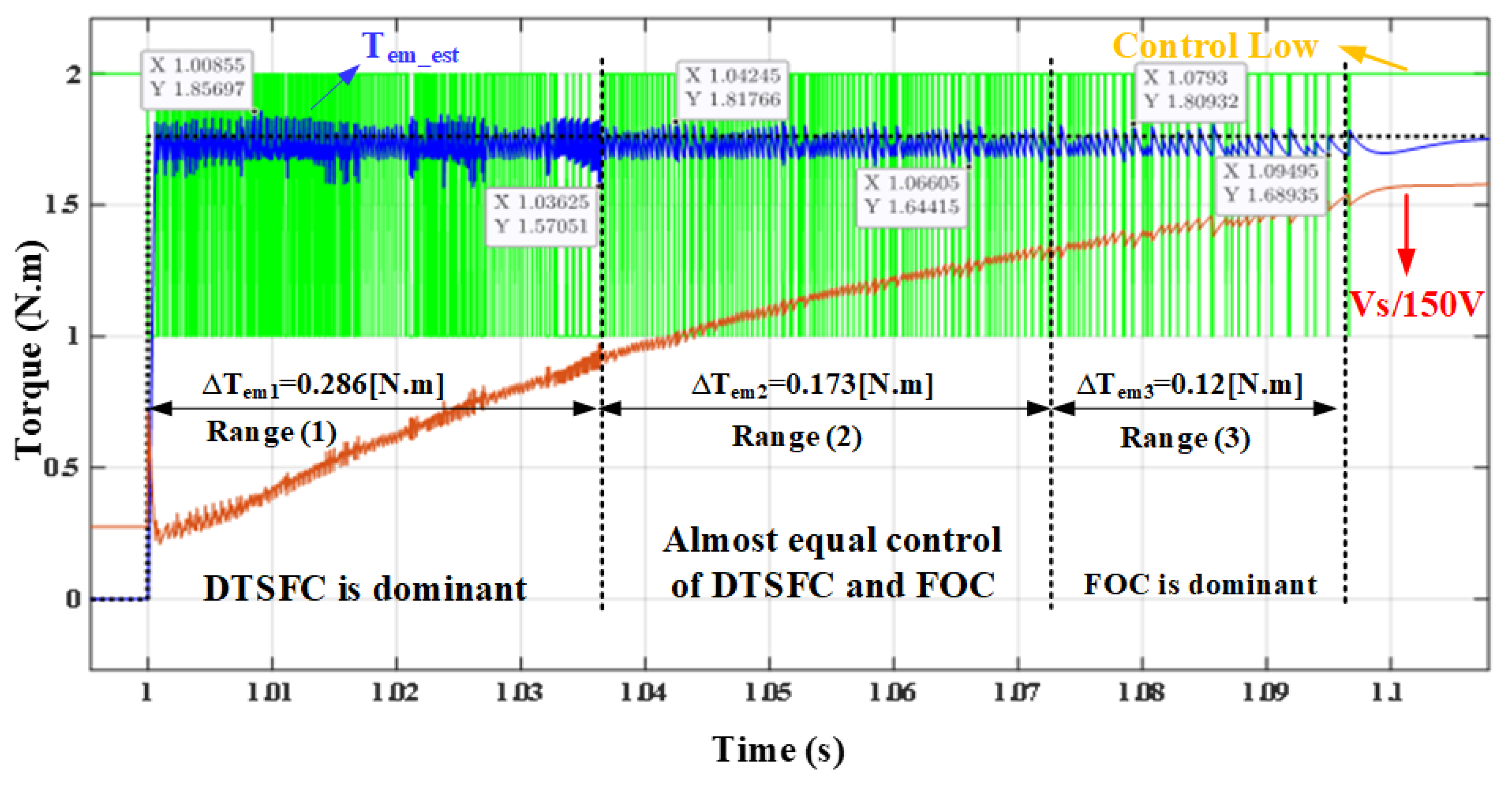
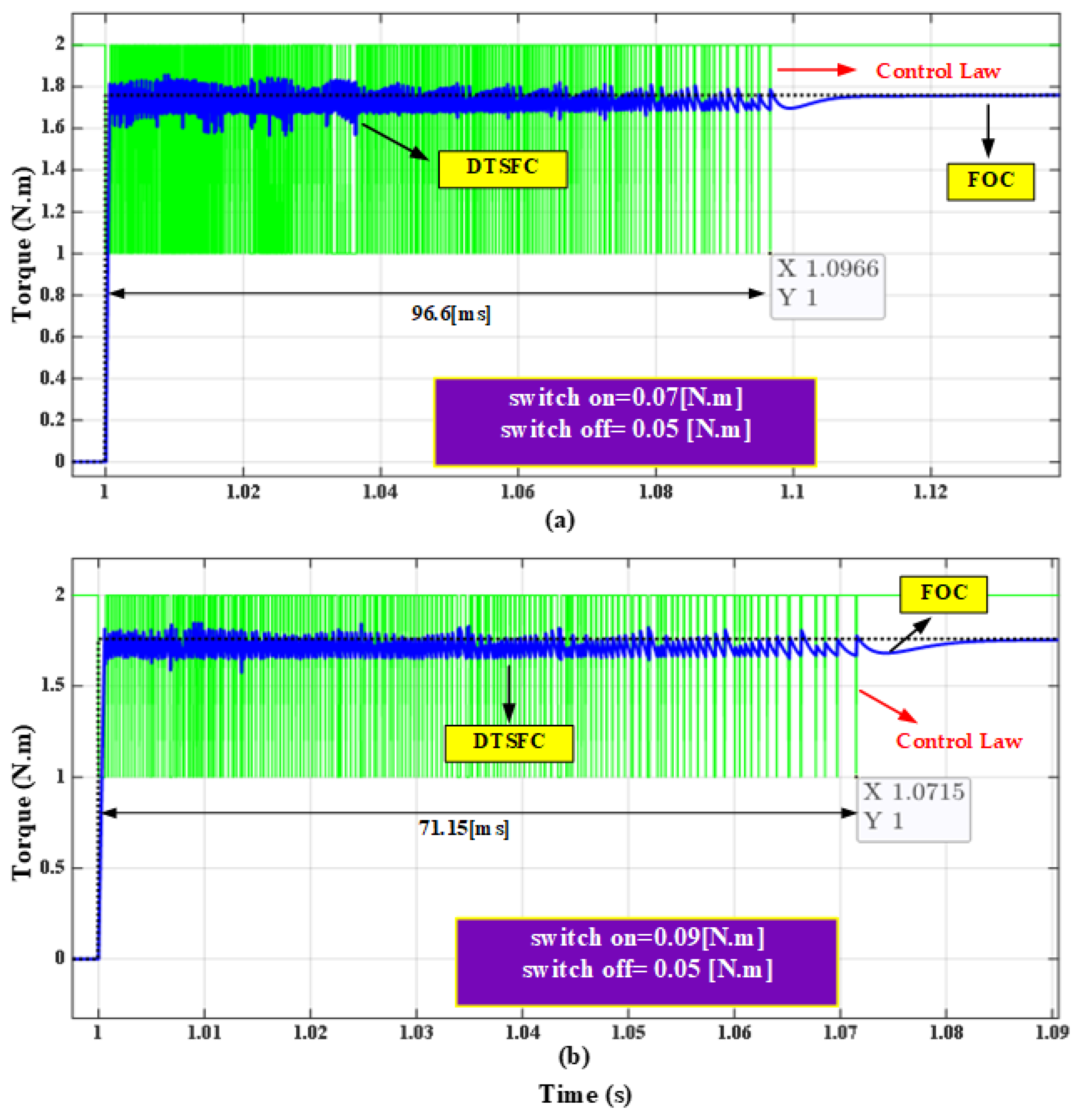
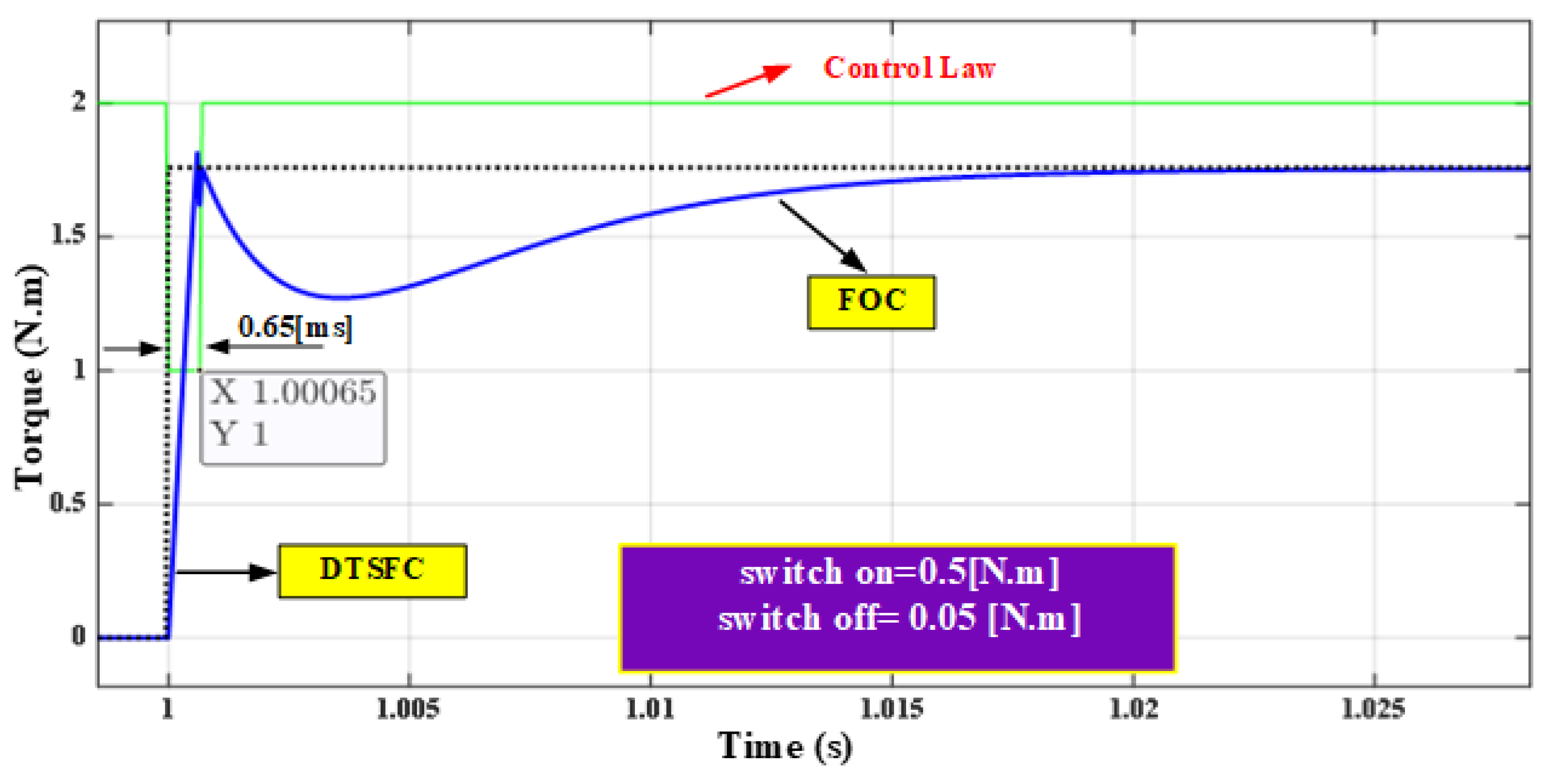
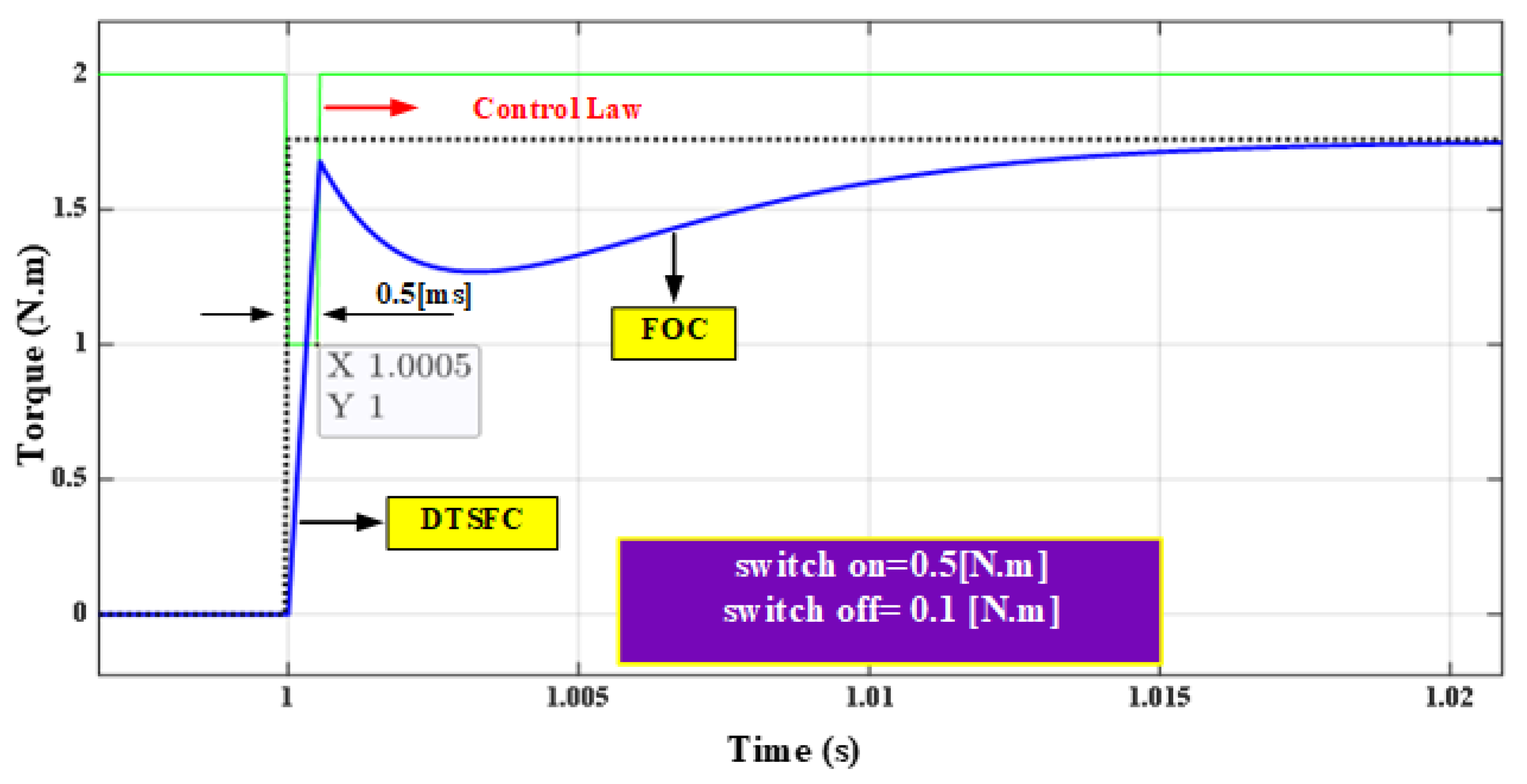




| Hysteresis Level | Applied Inverter Voltage Space Vectors | |||
|---|---|---|---|---|
| ↓ | ↑ | ↓ | ↑ | |
| ↓ | ↓ | ↑ | ↑ | |
| i = 1 | ||||
| i | ||||
| Unit with Time | Command Torque Sequence | |||||
|---|---|---|---|---|---|---|
| Time (s) | 1 | 3 | 5 | 7 | 8 | 9 |
| T (N.m) | 1.76 | 4.22 | 6 | −1.76 | −4.22 | −6 |
| Used Method | Flux Ripples | Torque Response for (TSR) | Torque Response for (SSR) | High Torque Prod. | Switching Frequency | Optional Gains |
|---|---|---|---|---|---|---|
| Proposed | Lower | 0.65 ms | Lower | Yes | Constant | 2 |
| Ref. [24] | Low | 1 ms | Low | Yes | Constant | 4 |
| Ref. [25] | High | 4 ms | High | No | Variable | - |
| Ref. [26] | No plot | 10 ms | Low | No | Variable | Unknown |
| Ref. [28] | High | 1 ms | Low | No | Variable | - |
| Ref. [29] | High | 10 ms | High | No | Variable | - |
| Ref. [30] | Low | 10 ms | Low | No | Constant | - |
| Ref. [31] | High | 1 ms | High | No | Variable | 12 |
| Ref. [34] | Low | 16 ms | Low | No | Variable | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elgbaily, M.; Anayi, F.; Alshbib, M.M. A Combined Control Scheme of Direct Torque Control and Field-Oriented Control Algorithms for Three-Phase Induction Motor: Experimental Validation. Mathematics 2022, 10, 3842. https://doi.org/10.3390/math10203842
Elgbaily M, Anayi F, Alshbib MM. A Combined Control Scheme of Direct Torque Control and Field-Oriented Control Algorithms for Three-Phase Induction Motor: Experimental Validation. Mathematics. 2022; 10(20):3842. https://doi.org/10.3390/math10203842
Chicago/Turabian StyleElgbaily, Mohamed, Fatih Anayi, and Mussaab M. Alshbib. 2022. "A Combined Control Scheme of Direct Torque Control and Field-Oriented Control Algorithms for Three-Phase Induction Motor: Experimental Validation" Mathematics 10, no. 20: 3842. https://doi.org/10.3390/math10203842
APA StyleElgbaily, M., Anayi, F., & Alshbib, M. M. (2022). A Combined Control Scheme of Direct Torque Control and Field-Oriented Control Algorithms for Three-Phase Induction Motor: Experimental Validation. Mathematics, 10(20), 3842. https://doi.org/10.3390/math10203842







