A Computational Framework for Exploring SARS-CoV-2 Pharmacodynamic Dose and Timing Regimes
Abstract
1. Introduction
2. Materials and Methods
Linear Stability Analysis
3. Results
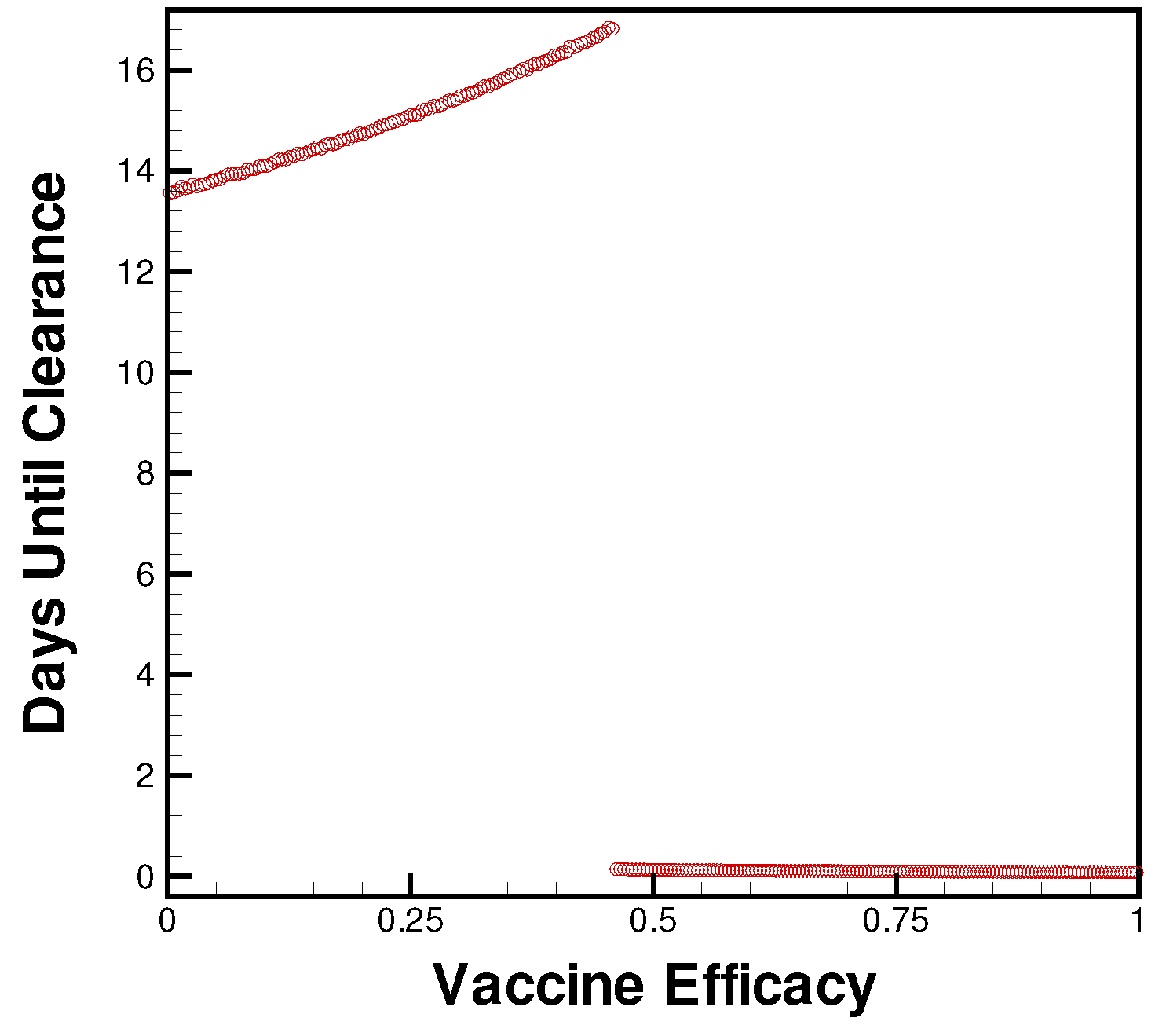
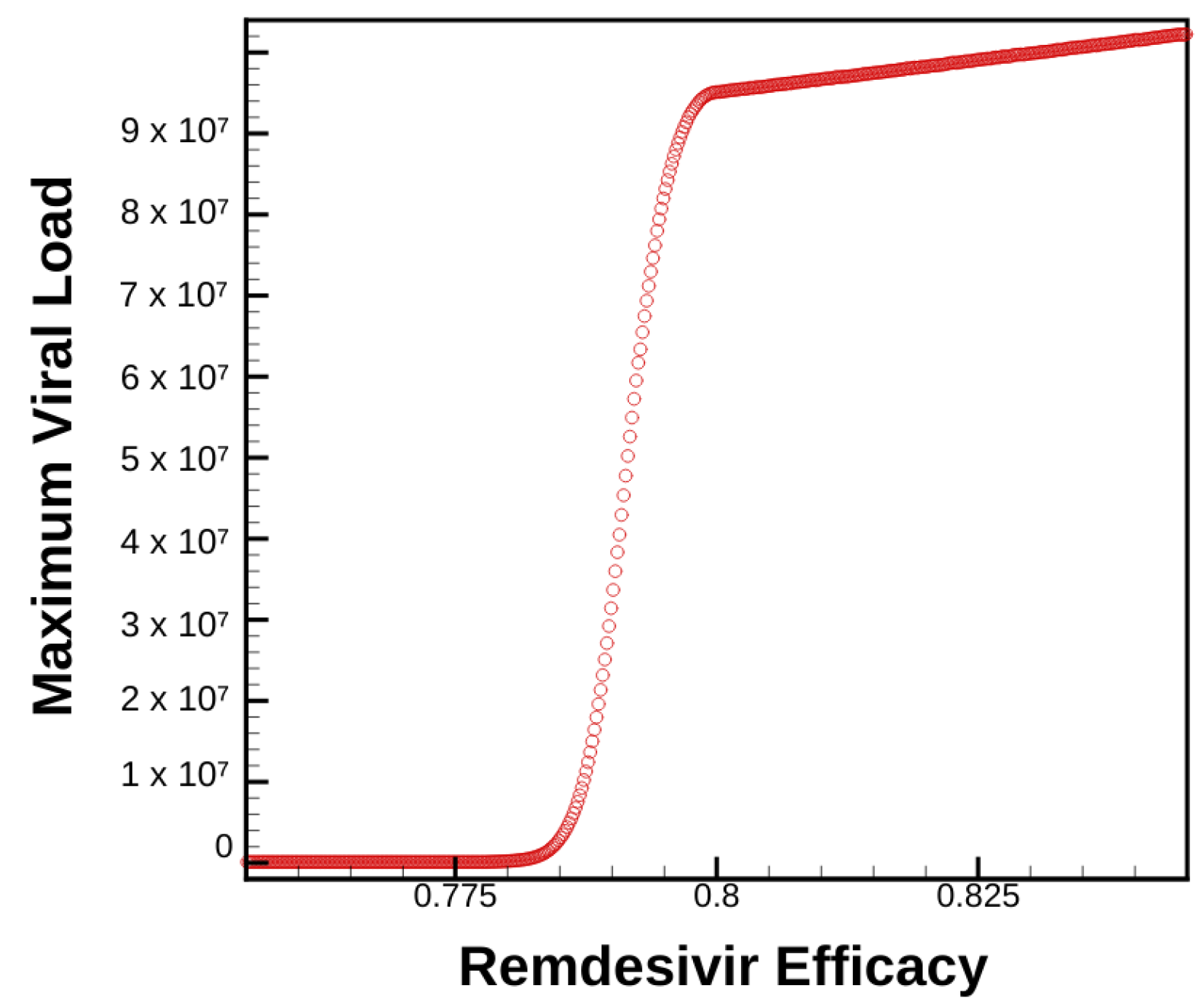
3.1. Singular Therapies
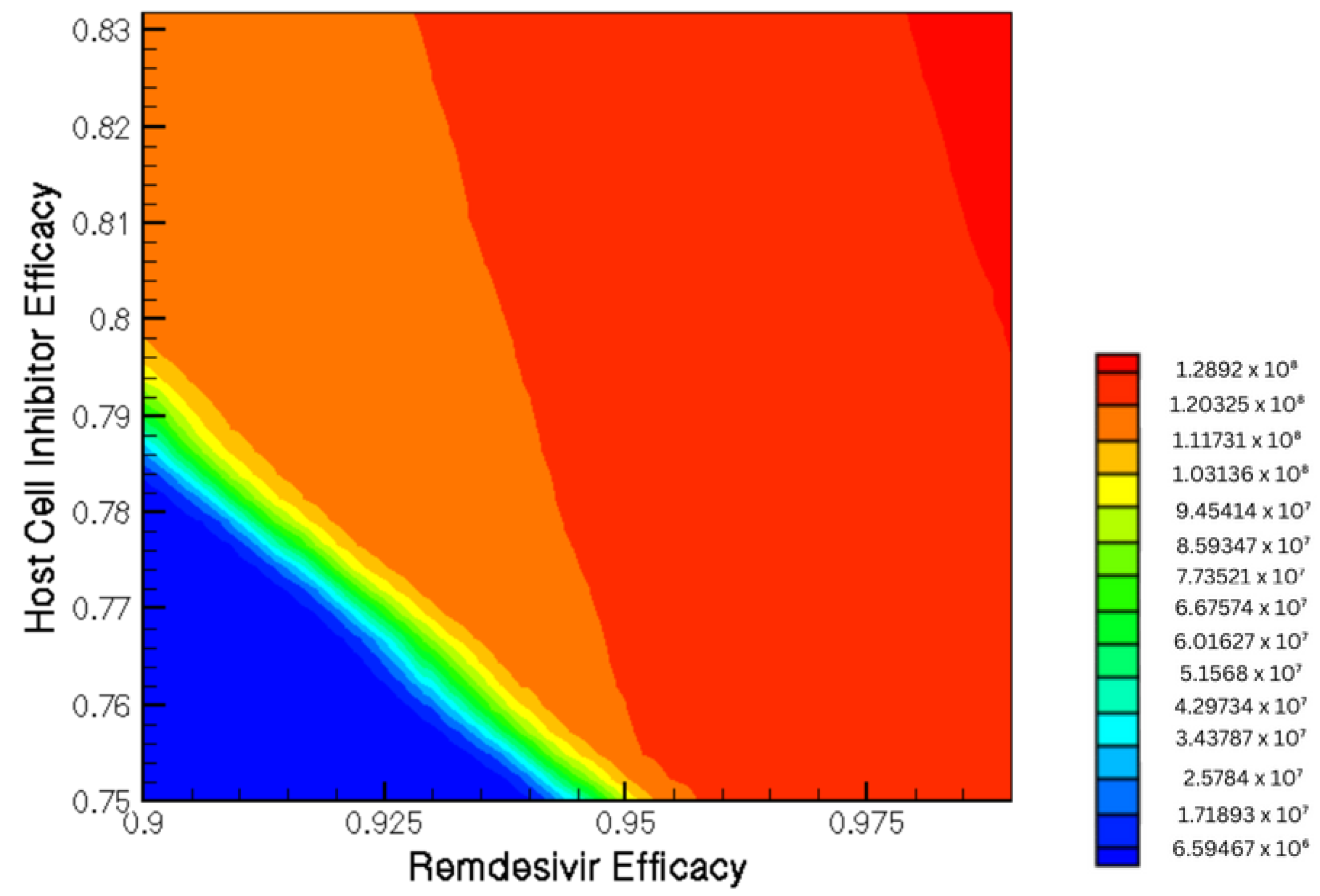
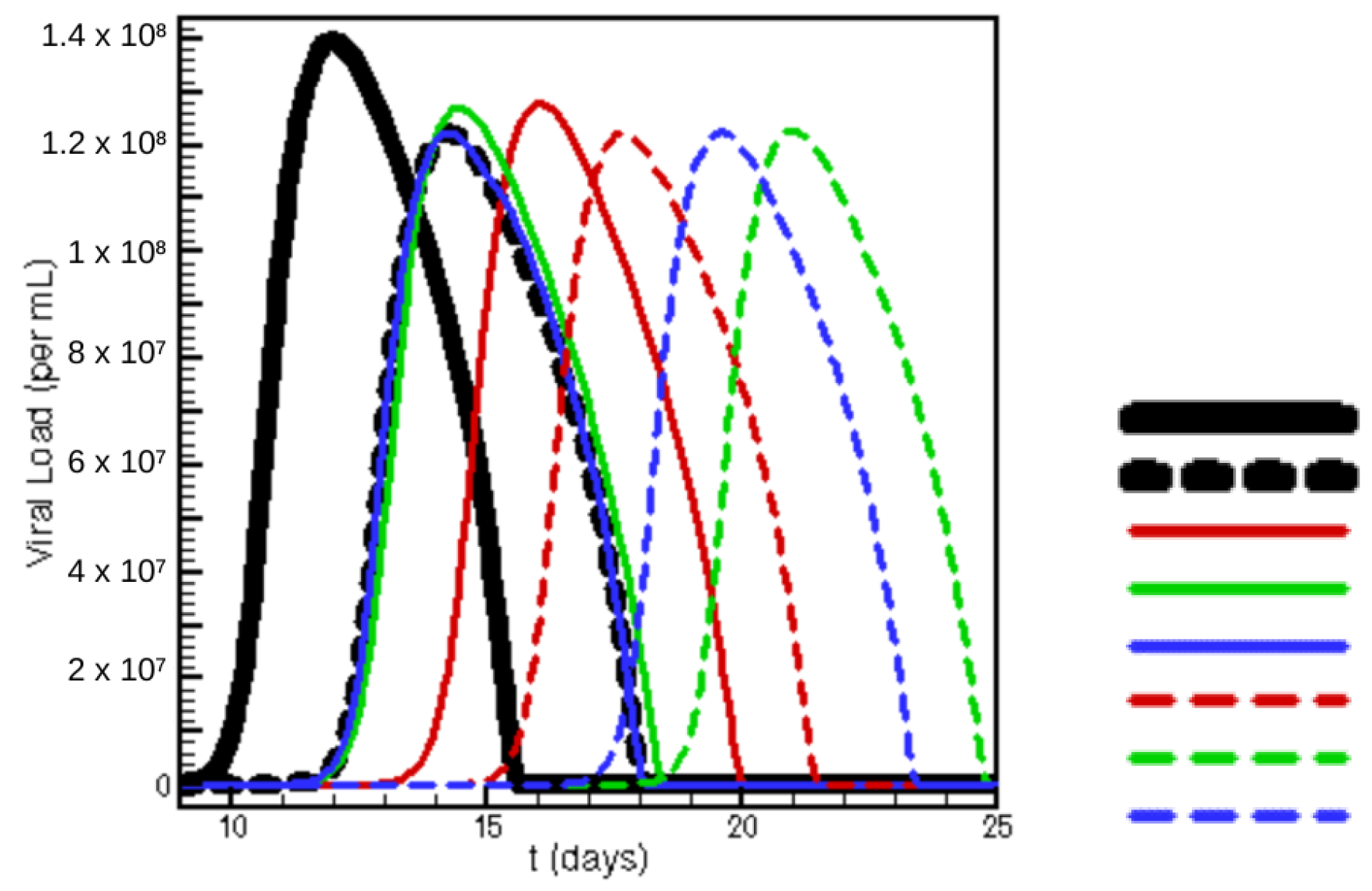
3.2. Combination Therapy
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ejima, K.; Kim, K.S.; Bento, A.I.; Iwanami, S.; Fujita, Y.; Aihara, K.; Shibuya, K.; Iwami, S. Estimation of timing of infection from longitudinal SARS-CoV-2 viral load data: Mathematical modelling study. BMC Infect. Dis. 2022, 22, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.S.; Ejima, K.; Ito, Y.; Iwanami, S.; Ohashi, H.; Koizumi, Y.; Asai, Y.; Nakaoka, S.; Watashi, K.; Thompson, R.N.; et al. Modelling SARS-CoV-2 dynamics: Implications for therapy. medRxiv 2020. [Google Scholar] [CrossRef]
- Chatterjee, B.; Singh Sandhu, H.; Dixit, N.M. Modeling recapitulates the heterogeneous outcomes of SARS-CoV-2 infection and quantifies the differences in the innate immune and CD8 T-cell responses between patients experiencing mild and severe symptoms. PLoS Pathog. 2022, 18, e1010630. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Vargas, E.A.; Velasco-Hernandez, J.X. In-host mathematical modelling of COVID-19 in humans. Annu. Rev. Control. 2020, 50, 448–456. [Google Scholar] [CrossRef] [PubMed]
- Almocera, A.E.S.; Quiroz, G.; Hernandez-Vargas, E.A. Stability analysis in COVID-19 within-host model with immune response. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105584. [Google Scholar] [CrossRef] [PubMed]
- Sanche, S.; Cassidy, T.; Chu, P.; Perelson, A.S.; Ribeiro, R.M.; Ke, R. A simple model of COVID-19 explains disease severity and the effect of treatments. Sci. Rep. 2022, 12, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Sadria, M.; Layton, A.T. Use of Angiotensin-Converting Enzyme Inhibitors and Angiotensin II Receptor Blockers During the COVID-19 Pandemic: A Modeling Analysis. PLoS Comput. Biol. 2020, 16, e1008235. [Google Scholar] [CrossRef]
- Wang, M.; Cao, R.; Zhang, L.; Yang, X.; Liu, J.; Xu, M.; Shi, Z.; Hu, Z.; Zhong, W.; Xiao, G. Remdesivir and chloroquine effectively inhibit the recently emerged novel coronavirus (2019-nCoV) in vitro. Cell Res. 2020, 30, 269–271. [Google Scholar] [CrossRef]
- Mahmoud, I.S.; Jarrar, Y.B.; Alshaer, W.; Ismail, S. SARS-CoV-2 entry in host cells-multiple targets for treatment and prevention. Biochimie 2020, 175, 93–98. [Google Scholar] [CrossRef] [PubMed]
- Chemaitelly, H.; Abu-Raddad, L.J. Waning effectiveness of COVID-19 vaccines. Lancet 2022, 399, 771–773. [Google Scholar] [CrossRef]
- Morrisette, T.; Lodise, T.P.; Scheetz, M.H.; Goswami, S.; Pogue, J.M.; Rybak, M.J. The pharmacodynamic and pharmacodynamic properties of hydroxychloroquine and dose selection for COVID-19: Putting the cart before the horse. Infect. Dis. Ther. 2020, 9, 561–572. [Google Scholar] [CrossRef]
- Pertinez, H.; Rajoli, R.K.; Khoo, S.H.; Owen, A. pharmacodynamic modelling to estimate intracellular favipiravir ribofuranosyl-5’-triphosphate exposure to support posology for SARS-CoV-2. J. Antimicrob. Chemother. 2021, 76, 2121–2128. [Google Scholar] [CrossRef] [PubMed]
- Ghasemiyeh, P.; Borhani-Haghighi, A.; Karimzadeh, I.; Mohammadi-Samani, S.; Vazin, A.; Safari, A.; Qureshi, A.I. Major neurologic adverse drug reactions, potential drug–drug interactions and pharmacodynamic aspects of drugs used in covid-19 patients with stroke: A narrative review. Ther. Clin. Risk Manag. 2020, 16, 595. [Google Scholar] [CrossRef]
- Kumar, A.A.; Lee, S.W.Y.; Lock, C.; Keong, N.C. Geographical variations in host predisposition to COVID-19 related Anosmia, Ageusia, and Neurological syndromes. Front. Med. 2021, 8, 527. [Google Scholar] [CrossRef]
- Jenner, A.L.; Aogo, R.A.; Alfonso, S.; Crowe, V.; Deng, X.; Smith, A.P.; Morel, P.A.; Davis, C.L.; Smith, A.M.; Craig, M. COVID-19 virtual patient cohort suggests immune mechanisms driving disease outcomes. PLoS Pathog. 2021, 17, e1009753. [Google Scholar] [CrossRef] [PubMed]
- Ordonez-Jimenez, F.; Blanco-Rodríguez, R.; Almocera, A.E.; Chinney-Herrera, G.; Hernandez Vargas, E.A. Quantifying antibody dynamics of severe and non-severe patients with COVID-19. medRxiv 2022. [Google Scholar] [CrossRef]
- Venisse, N.; Peytavin, G.; Bouchet, S.; Gagnieu, M.C.; Garraffo, R.; Guilhaumou, R.; Solas, C.; ANRS-AC43 Clinical Pharmacology Committee. Concerns about pharmacodynamic (PK) and pharmacodynamic-pharmacodynamic (PK-PD) studies in the new therapeutic area of COVID-19 infection. Antivir. Res. 2020, 181, 104866. [Google Scholar] [CrossRef]
- Sadria, M.; Layton, A.T. Modeling Within-host SARS-CoV-2 Infection Dynamics and Potential Treatments. Viruses 2021, 13, 1141. [Google Scholar] [CrossRef]
- Hancioglu, B.; Swigon, D.; Clermont, G. A dynamical model of human immune response to influenza A virus infection. J. Theor. Biol. 2007, 246, 70–86. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, D.; Yang, P.; Poon, L.L.; Wang, Q. Viral load of SARS-CoV-2 in clinical samples. Lancet Infect. Dis. 2020, 20, 411–412. [Google Scholar] [CrossRef]
- Wolfel, R.; Corman, V.M.; Guggemos, W.; Seilmaier, M.; Zange, S.; Müller, M.A.; Niemeyer, D.; Jones, T.C.; Vollmar, P.; Rothe, C.; et al. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 581, 465–469. [Google Scholar] [CrossRef] [PubMed]
- Sayama, H. Introduction to the Modeling and Analysis of Complex Systems; Open SUNY Textbooks; Geneseo: New York, NY, USA, 2015. [Google Scholar]
- Ghosh, P.; Vaidya, A.; Kumar, A.; Rangachari, V. Determination of critical nucleation number for a single nucleation amyloid-β aggregation model. Math. Biosci. 2016, 273, 70–79. [Google Scholar] [CrossRef] [PubMed]
- Ghag, G.; Ghosh, P.; Mauro, A.; Rangachari, V.; Vaidya, A. Stability analysis of 4-species Aβ aggregation model: A novel approach to obtaining physically meaningful rate constants. Math. Biosci. 2013, 224, 205–215. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Alós, L.; Armenteros, J.J.A.; Madsen, J.R.; Hansen, C.B.; Jarlhelt, I.; Hamm, S.R.; Heftdal, L.D.; Pries-Heje, M.M.; Møller, D.L.; Fogh, K.; et al. Modeling of waning immunity after SARS-CoV-2 vaccination and influencing factors. Nat. Commun. 2022, 13, 1–11. [Google Scholar] [CrossRef]
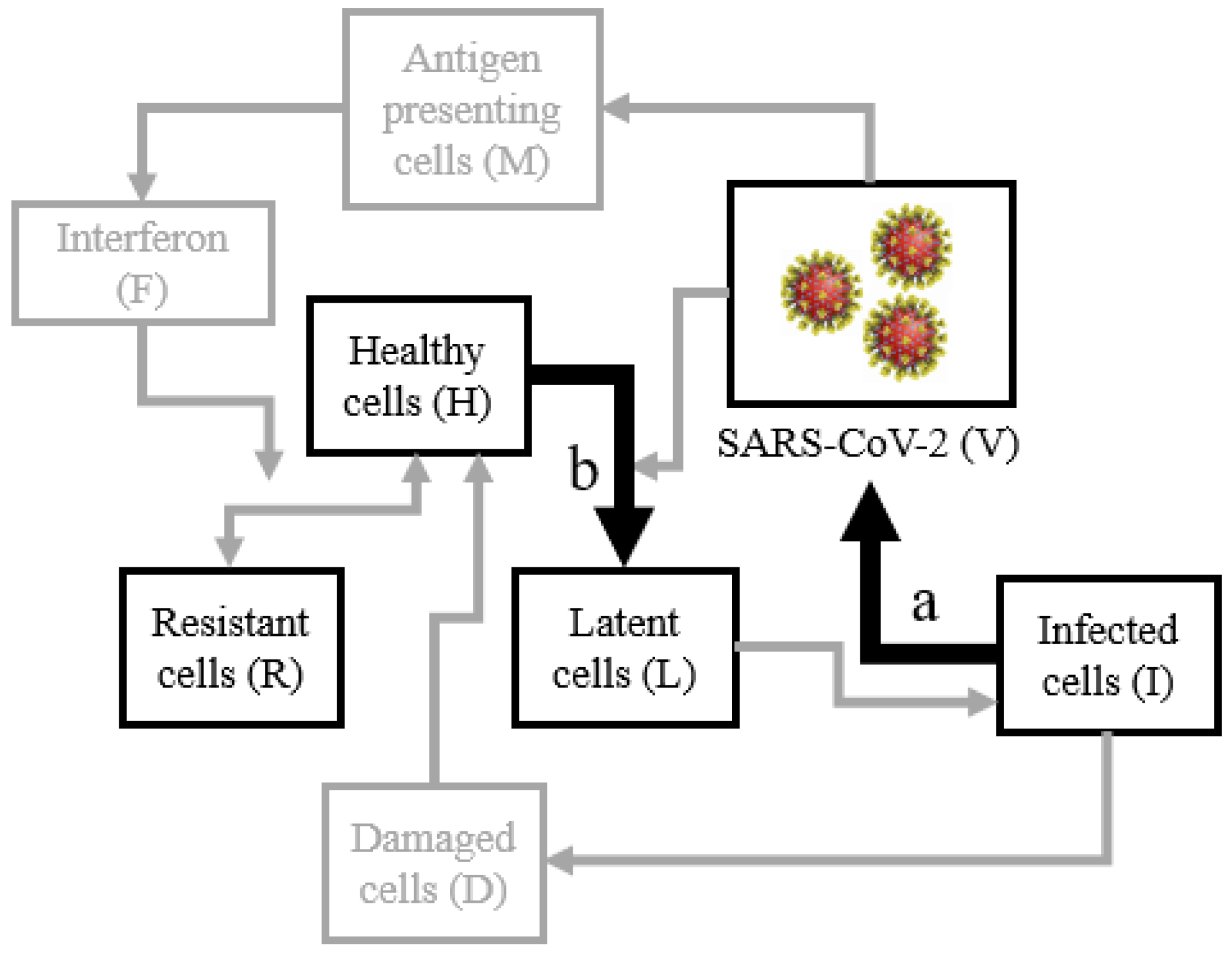
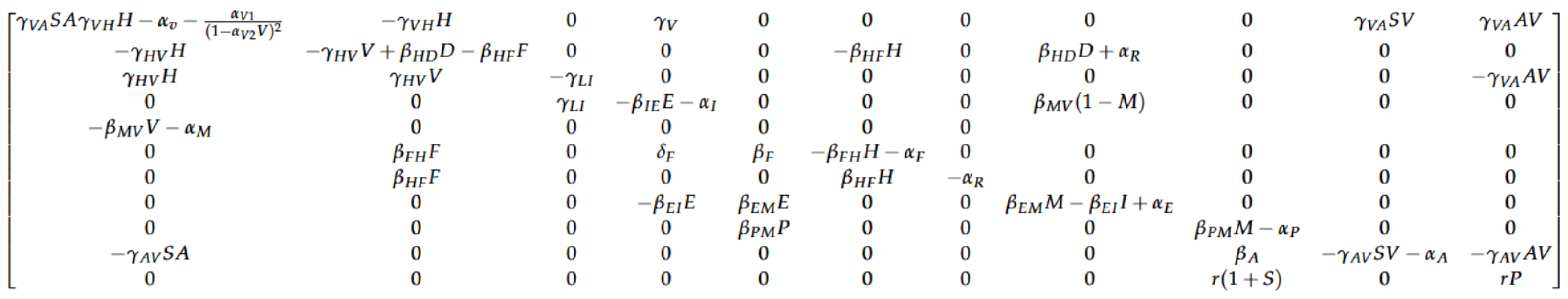
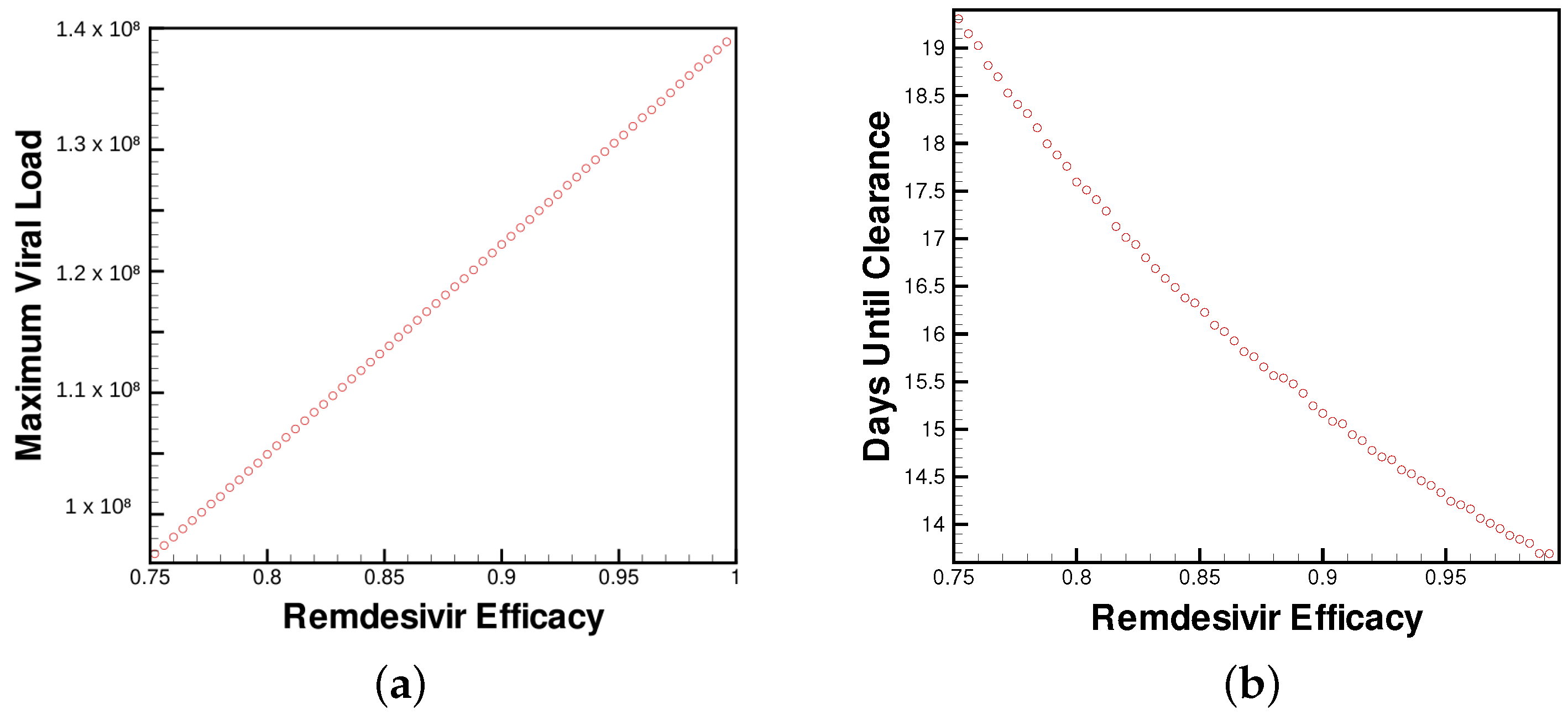
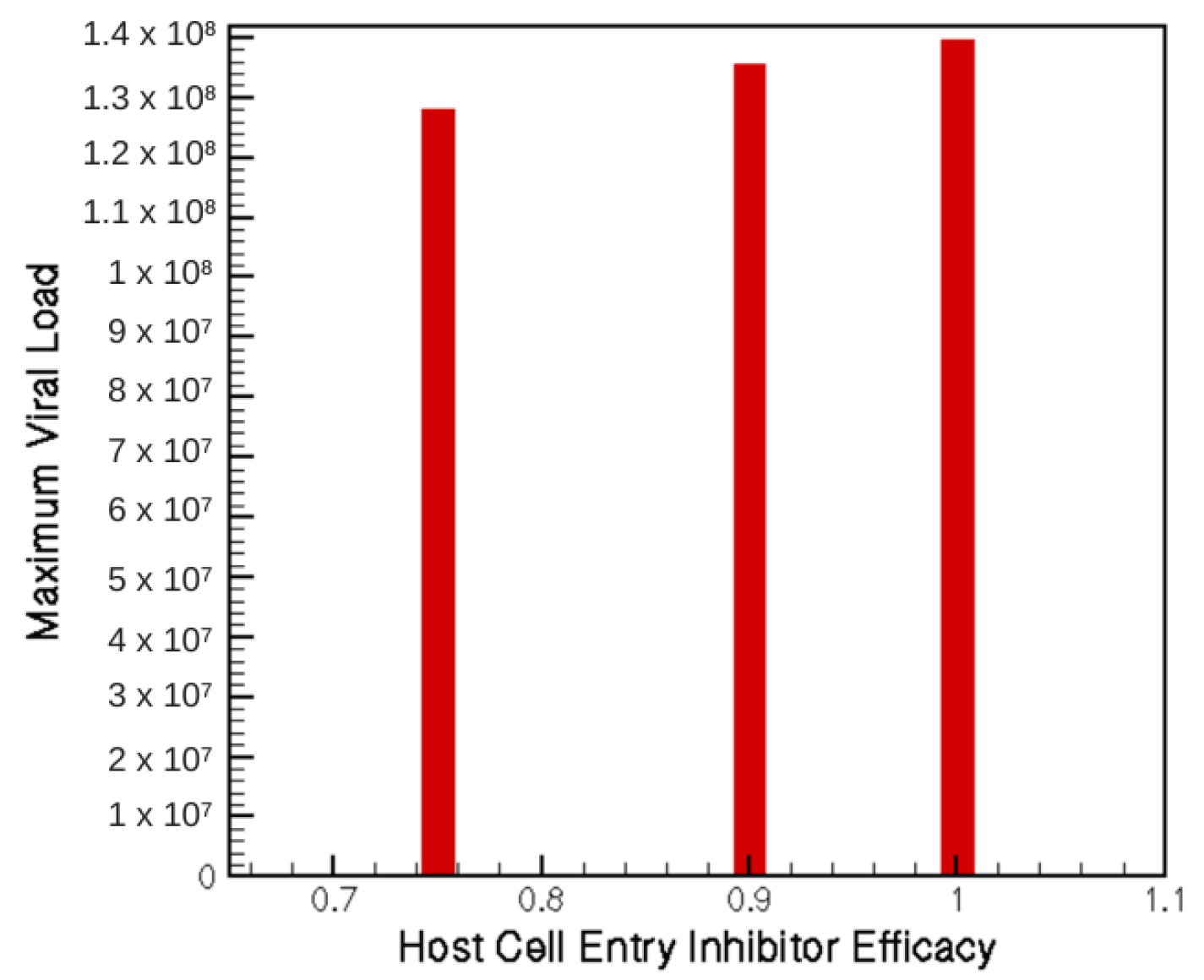


| V | Viral load |
| M | Population of antigen-presenting cells |
| F | Interferon |
| S | Antigenic compatibility |
| Respiratory Epithelial Cells | |
| H | Population of healthy, susceptible cells |
| D | Population of damaged cells |
| I | Population of infected cells |
| L | Population of latently infected cells |
| R | Population of resistant cells |
| Innate Immune System | |
| E | Population of effector cells |
| Adaptive Immune System | |
| P | Population of plasma cells |
| A | Antibodies |
| Parameter | Description |
|---|---|
| Virus reproduction rate in infected cells | |
| Virus elimination rate by antibodies | |
| Rate by which virus enters healthy cells | |
| Natural virus degradation rate | |
| Max. rate of virus removal | |
| = 23,000 | Michaelis–Menten constant in virus removal |
| Rate by which cells enter latent eclipse phase | |
| Epithelial cell regeneration rate | |
| Rate of virus resistance loss | |
| Cell infection rate by virus | |
| Rate by which susceptible cells gain resistance | |
| Rate by which infected cells are removed by immune effector cells | |
| Infected cell natural death rate | |
| Rate of producing antigen-presenting cells by damaged cells | |
| Rate of producing antigen-presenting cells stimulation by virus | |
| Antigen-presenting cell natural death rate | |
| = 125,000 | Interferon production rate by antigen-presenting cell |
| Interferon production rate by infected cell | |
| Rate by which interferon binds to healthy cells | |
| Interferon natural decay rate | |
| Rate by which effector cells are produced by antigen-presenting cells | |
| Rate of effector cell death by infected cell | |
| Effector cell natural death rate | |
| Plasma cell production rate | |
| Plasma cell natural death rate | |
| Antibody production rate by plasma cells | |
| Rate by which antibody binds to virus | |
| Antibody natural death rate | |
| Rate of antibody specificity change |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pateras, J.; Ghosh, P. A Computational Framework for Exploring SARS-CoV-2 Pharmacodynamic Dose and Timing Regimes. Mathematics 2022, 10, 3739. https://doi.org/10.3390/math10203739
Pateras J, Ghosh P. A Computational Framework for Exploring SARS-CoV-2 Pharmacodynamic Dose and Timing Regimes. Mathematics. 2022; 10(20):3739. https://doi.org/10.3390/math10203739
Chicago/Turabian StylePateras, Joseph, and Preetam Ghosh. 2022. "A Computational Framework for Exploring SARS-CoV-2 Pharmacodynamic Dose and Timing Regimes" Mathematics 10, no. 20: 3739. https://doi.org/10.3390/math10203739
APA StylePateras, J., & Ghosh, P. (2022). A Computational Framework for Exploring SARS-CoV-2 Pharmacodynamic Dose and Timing Regimes. Mathematics, 10(20), 3739. https://doi.org/10.3390/math10203739






