A Computational Framework for Exploring SARS-CoV-2 Pharmacodynamic Dose and Timing Regimes

Abstract

Emerging diseases—and none as recently or devastatingly impactful toward humans as COVID-19—pose an immense challenge to researchers concerned with infectious disease. This study is tasked with expanding the computational probe of treatment regimes in a differential equations-based model of the SARS-CoV-2 host–virus interaction. Parameters within the model are tweaked to simulate dose specifications. Further, parametric variations are introduced in a timed manner to infer the importance of dose timing. Arming in silico testing, and eventually, clinical testing, with abundant information on simulated therapeutic regimes is the overall contribution of this pharmacodynamic model; thus, a wide range of dose and timing combinations are examined. Therapeutic interventions that block viral replication inhibit viral entry into host cells, and vaccination-induced antibodies are all studied alone and in combination. Especially during early detection, exhaustive parameter sweeps of well-suited within-host models are often the first step in the clinical response to a novel disease.

1. Introduction

Model-based analyses play a very important role in informing the human struggle with infectious diseases. This has become increasingly important as the emergence of the SARS-CoV-2 virus has renewed urgency in epidemiological research. The terrible burden of COVID-19 has been mitigated expediently with the adaptation of antiviral therapies and the inclusion of novel immunization techniques. In this context, in-host modeling is one way to discuss the efficacy of immune response to therapy at the cellular level. An in-host model allows researchers to probe a patient’s response to viral exposition and therapies based on timing, dosage, individual mitigating factors or patient-specific co-morbidities.

Mathematical in-host models allow researchers to model as many in-vivo metrics as the modeler prescribes. Exerting control over metrics describing rates of viral replication, antiviral agents and other key host–virus interactions allows conclusions concerning the utility of various treatment regimes to be analyzed by the pharmacodynamic model. Increasing the predictive performance of such differential equation-based models is important as clinicians face uncertainty in treating novel diseases. Within-host dynamical models are arguably the first and best weapon against novel pathogens—serving as an intermediary between therapeutic discovery and/or adaptation and clinical intervention.

Differential equation-based models have been used to estimate the time-to-infection, to differentiate secondary infections from imported strains, and to inform potential therapies [1,2]. Other models intensively represent the interactions between virus and components of the host’s immune response, with a focus on T-cell interactions [3,4]. Bifurcation analyses have been employed to conclude how extremely rapid SARS-CoV-2 replication overcomes T-cell response [5]. Sanche et al. provide a framework that focuses on viral interactions leading to disease-progressing inflammation [6]. The interaction of angiotensin-converting enzyme inhibitors and angiotensin II receptor blockers with COVID-19 is also modeled thoroughly by within-host models [7]. In this paper, the effects of three COVID-19 therapies—which emerged as top prospects in combating the disease during our early understanding of it—are studied: Remdesivir [8], Host-cell entry inhibitors [9] and antibody/vaccination treatments. To simulate Remdesivir treatment, which inhibits viral transcription rate, we throttle the rate in our model, which describes the replication of infected cells. To simulate host-cell entry inhibitor antiviral therapy types, we throttle the rates that describe how the virus interacts with healthy cells to produce latently infected (termed as latent cells from hereon) and then infected cells. Finally, to model vaccination, we introduce an alternate antibody agent in the model to capture the presence of vaccine-induced antibodies. The inclusion of vaccination efficacy in the framework is crucial for interpreting patient-specific simulations. Chemaitelly and Abu-Raddad [10] study waning immunity provided by vaccination as a function of time since vaccination and many other personal patient characteristics such as: age, sex, place of birth and existing co-morbidities. Similar host–virus models have probed the effectiveness of other potential treatments, such as hydroxychloroquine [11] or favipiravir [12]. Additionally, the importance of patient-specific characteristics is highlighted by the simulation of adverse neurological reactions to certain COVID-19 treatment regimens in stroke patients [13] or as a function of a patient’s geographic location [14]. Jenner et al. explore patient-specific outcomes using within-host models to describe individual patients’ predisposition to produce infected cell-derived interferon [15]. Ordonez-Jimenez et al. describe patient-specific reactions as a function of initial infection severity [16]. Finally, it must be noted that pharmacodynamic models are subject to limitations imposed by modeling choices. Venisse et al. [17] discuss the need for existing host–virus models for SARS-CoV-2 to reduce the possibility of unreliable conclusions and call urgently for the development of further pharmacodynamic models. The results presented herein widen explored therapeutic parameter regimes while being still limited by computational cost. Further collaboration with clinical studies being needed to bridge the gap between purely computational probes and clinically informative numerical simulation.

This work provides a framework to probe large treatment doses and timing regimes in the context of treating emerging diseases. In the case of the novel coronavirus, key in-host viral dynamics have been studied [18]. This study sweeps various parameter combinations to provide insights into how dose, therapy combination, and vaccination status can affect an individual’s response to treatment. The novelty of large parameter sweeps, including timed administration simulation, is a useful tool for computational, clinical integrative treatment design. Further, the inclusion of vaccination-induced antibodies and the vaccination efficacy parameter, $\eta$, allow for explicitly patient-specific modeling as a function of time since vaccination. Additionally, a stability analysis to conclude the neutral stability of the system is performed.

2. Materials and Methods

The within-host SARS-CoV-2 viral model is probed with potential therapeutic interventions. The effect of widely used Remdesivir, a monophosphoroamidate prodrug that is utilized to inhibit the viral transcription rate, is modeled by controlling the parameter associated with viral replication. The potential use of host-cell inhibitors is modeled by controlling the parameters that inhibit the virus’s ability to catalyze the transformation of healthy cells to latent cells. A summary of the key viral interactions in the within-host model, first described by Sadria and Layton [18], is given in Figure 1.

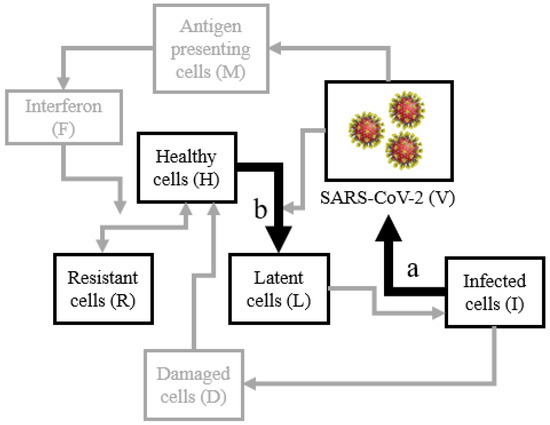
Figure 1. The key interactions of the in-host model where Remdesivir therapy are modeled by controlling the rate parameter at interaction (a) and host-cell entry inhibition therapy is modeled by interaction (b).

The entire in-host model is governed by Equations (1)–(12). The system is solved employing MATLAB function ode15s: a variable-step, variable-order multistep solver based on numerical differential formulae of order 1–5 by default. The model’s components are summarized in Table 1. The parameters and their values are displayed in Table 2. Original parameter values are borrowed from precursor work modeling influenza infection in-host model also derived from clonal selection theory, law of mass–action, interaction characteristics and natural cell creation–death balances [19]. Model parameters are then tuned to fit observational COVID-19 infection data. In brief, the model describes interactions between viral infection, respiratory epithelial cells, and the host’s immune system. The model allows the control of key parameters to simulate therapeutic intervention. Model parameters are scaled such that viral load clearance is realized in about three weeks, which is quite typical in COVID-19 patients.

$$\begin{array}{ccc}\hfill \frac{dV}{dt}& =& {\gamma }_{V}I-{\gamma }_{VA}SAV-{\gamma }_{VH}HV-{\alpha }_{V}V-\frac{{\alpha }_{V1}V}{1+{\alpha }_{V2}V}\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill \frac{dH}{dt}& =& -{\gamma }_{HV}VH+{\beta }_{HD}D(H+R)+{\alpha }_{R}R-{\beta }_{HF}FH\hfill \end{array}$$

(2)

$$\begin{array}{ccc}\hfill \frac{dL}{dt}& =& {\gamma }_{HV}VH-{\gamma }_{LI}L\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \frac{dI}{dt}& =& {\gamma }_{LI}L-{\beta }_{IE}EI-{\alpha }_{I}I\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill \frac{dM}{dt}& =& ({\beta }_{MD}D+{\beta }_{MV}V)(1-M)-{\alpha }_{M}M\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill \frac{dF}{dt}& =& {\beta }_{F}M+{\delta }_{F}I-{\beta }_{FH}HF-{\alpha }_{F}F\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill \frac{dR}{dt}& =& {\beta }_{HF}FH-{\alpha }_{R}R\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill \frac{dE}{dt}& =& {\beta }_{EM}ME-{\beta }_{EI}IE+{\alpha }_E(1-E)\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill \frac{dP}{dt}& =& {\beta }_{PM}MP+{\alpha }_P(1-P)\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill \frac{dA}{dt}& =& {\beta }_{A}P-{\gamma }_{AV}SAV-{\alpha }_{A}A\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill \frac{dS}{dt}& =& rP(1-S)\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill D& =& 1-H-R-L-I\hfill \end{array}$$

(12)

Table 1. The major components of the in-host SARS-CoV-2 infection model with a brief description.

V	Viral load
M	Population of antigen-presenting cells
F	Interferon
S	Antigenic compatibility
	Respiratory Epithelial Cells
H	Population of healthy, susceptible cells
D	Population of damaged cells
I	Population of infected cells
L	Population of latently infected cells
R	Population of resistant cells
	Innate Immune System
E	Population of effector cells
	Adaptive Immune System
P	Population of plasma cells
A	Antibodies

Table 2. The parameters of the in-host SARS-CoV-2 infection model. Parameter values are validated by comparison with clinical COVID-19 testing [20,21]. A brief description of the parameters is given.

Parameter	Description
${\gamma }_V=255$	Virus reproduction rate in infected cells
${\gamma }_{VA}=309.6$	Virus elimination rate by antibodies
${\gamma }_{VH}=0.51$	Rate by which virus enters healthy cells
${\alpha }_V=0.85$	Natural virus degradation rate
${\alpha }_{V1}=50$	Max. rate of virus removal
${\alpha }_{V2}$= 23,000	Michaelis–Menten constant in virus removal
${\gamma }_{LI}=6$	Rate by which cells enter latent eclipse phase
${\beta }_{HD}=2$	Epithelial cell regeneration rate
${\alpha }_R=0.5$	Rate of virus resistance loss
${\gamma }_{HV}=0.17$	Cell infection rate by virus
${\beta }_{HF}=0.005$	Rate by which susceptible cells gain resistance
${\beta }_{IE}=0.033$	Rate by which infected cells are removed by immune effector cells
${\alpha }_I=0.775$	Infected cell natural death rate
${\beta }_{MD}=0.5$	Rate of producing antigen-presenting cells by damaged cells
${\beta }_{MV}=0.00185$	Rate of producing antigen-presenting cells stimulation by virus
${\alpha }_M=0.75$	Antigen-presenting cell natural death rate
${\beta }_F$ = 125,000	Interferon production rate by antigen-presenting cell
${\delta }_F=1000$	Interferon production rate by infected cell
${\beta }_{FH}=8.5$	Rate by which interferon binds to healthy cells
${\alpha }_F=4$	Interferon natural decay rate
${\beta }_{EM}=4.15$	Rate by which effector cells are produced by antigen-presenting cells
${\beta }_{EI}=1.36$	Rate of effector cell death by infected cell
${\alpha }_E=0.2$	Effector cell natural death rate
${\beta }_{PM}=5.75$	Plasma cell production rate
${\alpha }_P=0.2$	Plasma cell natural death rate
${\beta }_A=0.0225$	Antibody production rate by plasma cells
${\gamma }_{AV}=73.1$	Rate by which antibody binds to virus
${\alpha }_A=0.0215$	Antibody natural death rate
$r=0.000015$	Rate of antibody specificity change

Ultimately, a modeling paradigm to include vaccination is also introduced. The model in Figure 1 already includes a general antibody agent, A. Sadria and Layton present an additional agent, $A^{\prime }$ where $\frac{d{A}^{\prime }}{dt}={\beta }_A^{\prime }-{\gamma }_{AV}{A}^{\prime }V-{\alpha }_A{A}^{\prime }$. Here, ${\beta }_A^{\prime }$ is the rate by which antibodies are introduced through plasma donor treatment. A proportional change in Equation (1) would be observed to reflect additional viral elimination due to $A^{\prime }$. The case of ${\beta }_A^{\prime }=0$ and initial value $A^{\prime }=A_0^{\prime }$ can be abstracted as exposure to some initial concentration of antibodies through vaccination. While in the case $A_0^{\prime }=0$, ${\beta }_A^{\prime }\ne 0$ is the rate of incoming antibodies through infusion.

An additional modeling modification is introduced to examine the effect that newly developed vaccines have on SARS-CoV-2 within-host interactions. To abstract vaccine efficacy, parameter $\eta$ is introduced. $\eta$ is a scaling parameter that affects the rate by which vaccine-induced antibodies are effective: allowing the study of the patient outcome as a function of waning immunity. $\eta =0$ implies no vaccination or complete loss of immunity, while $\eta =1$ implies that vaccine-induced antibodies, X, are equally as effective as regular antibodies, A. Thus, to model patient outcome, when vaccines are introduced, Equation (1) becomes:

$$\frac{dV}{dt}={\gamma }_{V}I-{\gamma }_{VA}S(A+\eta X)V-{\gamma }_{VH}HV-{\alpha }_{V}V-\frac{{\alpha }_{V1}V}{1+{\alpha }_{V2}V}$$

Linear Stability Analysis

In order to discuss the stability of the solutions under the conditions prescribed in Section 2, a linear stability analysis [22,23,24] is performed. Let the system of differential Equations (1)–(11) be represented by $F\left(x\right)$. The model is evaluated at equilibrium, where $F\left(x_{eq}\right)=0$. Small perturbations are introduced around such equilibrium and variables are replaced where $x=x_{eq}+\Delta x$. Thus, $\frac{d\Delta x}{dt}$ is approximated by $F\left(x_{eq}\right)+J\Delta x$. This implies

$$\frac{d\Delta x}{dt}\approx J\Delta x$$

where J is the Jacobian matrix of F where $x=x_{eq}$ is given by Figure 2

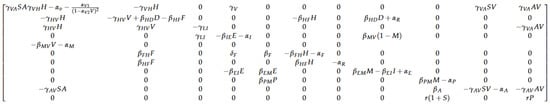
Figure 2. Parametric values of the Jacobian matrix: to be evaluated at equilibrium.

The value of the Jacobian’s eigenvalues are examined to infer the stability of the model parameters. The eleven eigenvalues ${\lambda }_i$ where $i=0,1,...,11$ are calculated with the equilibrium values attained by numerically integrating with ode15s for 75 time steps. Eigenvalues calculated with MATLAB’s eigen function are given by

$$\begin{array}{cc}{\lambda }_i& =\left[\begin{array}{c}-4.0+0.00i\\ -0.5+0.00i\\ -1.2+441.3i\\ -1.2-441.4i\\ 0.0005+0.00i\\ -0.81+0.00i\\ 0.31+0.00i\\ -0.05+0.22i\\ -0.05-0.22i\\ -0.50+0.00i\\ 0.06+0.00i\end{array}\right]\hfill \end{array}$$

Thus, the system is determined to be at least neutrally stable, with each eigenvalue containing real components taken to be equal to or less than zero. In other words, for small changes in initial parameters, one can still reasonably expect the robustness of equilibrium solutions.

3. Results

Viral load within the simulated host throughout infection is modeled as a function of therapy type, treatment efficacy and treatment timing. Treatment efficacy is described on a $[1,0]$ scale—vaccine efficacy describes a boost in antibody effectiveness, while simulated therapies represent a decrease in viral replication rate, Remdesivir or host-cell entry inhibition with a decrease in viral infectiousness rates, ${\gamma }_{HV}$ and ${\gamma }_{VH}$. For instance, in the modeling of Remdesivir and entry-inhibition therapy, efficacy $=0.9$ means the associated rate constant has been reduced to $90\%$ of its normal value; thus, ${\gamma }_{HV}$ is $90\%$ of its original value, resulting in a lower cell infection rate by the virus. An efficacy of 1 implies no administered treatment, while lower values of efficacy correspond to the treatment regime with either lower cell infection rates or lower rates of entering the healthy cells by the virus. In other words, here, efficacy denotes the reduction in the associated rate constants and does not directly equate to the overall efficiency of the treatment. The simulations are 25 days in duration. The viral load on day 1 is set to 30,000 parts per mL, simulating a relatively early detection of the virus. Efficacy is most readily abstracted as treatment dosage, and the two terms are used interchangeably henceforth. However, efficacy quantification implies a more general approach to therapeutic modeling, which could include an individual patient’s predisposition to certain treatment types or to model other factors that may affect in-host interactions.

3.1. Singular Therapies

First, the dependence of maximum viral load on treatment efficacy is examined. Remdesivir treatment efficacy of $0.9$—decreasing the viral transcription rate by 90%—corresponds to the efficacy of about $5\mathsf{\mu }$M Remdesivir [8]. Efficacy is varied around this value from $0.75$ to $0.99$ in steps of $0.01$.

Host-cell entry inhibitor therapy is modeled for a range of inhibition efficacy. This therapy is modeled by toggling rate constants, which govern the effect the virus’s presence has on producing latent cells. Practically, many potential therapies that inhibit viral entry into host cells could be modeled by the wide range of efficacy values chosen as $0.75$ or $0.90$ and values between $0.50$ and $0.80$ in steps of $0.01$ to produce contours.

Finally, the effects of vaccination effectiveness are also discussed through the modified system. Chosen values are in the range between 0 and 1 in steps of $0.01$.

Figure 3 clearly shows the patient’s simulated outcome is dependent upon the paradigm of modeled treatment efficacy. In both the case of Remdesivir and host-cell entry inhibition, increased efficacy results in decreased maximum viral load. Additionally, the time until clearance metric, the time passed to clear two-thirds of the initial viral load, is also dependent on Remdesivir dosage.

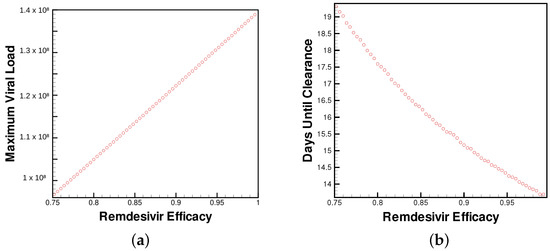
Figure 3. (a) Maximum viral load and (b) time until viral clearance observed by patients for varying levels of Remdesivir treatment.

Figure 4 displays the dependence of the maximum viral load on the efficacy of host-cell entry inhibitor therapy. However trivial, the dependence on viral load and time until clearance on treatment efficacy is an important foundation for the combination treatments discussed later and for future exploratory studies.

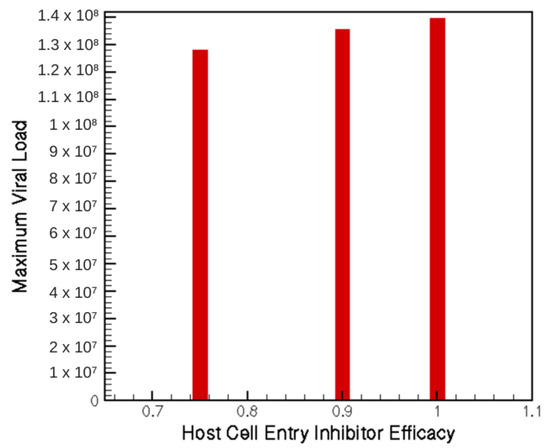
Figure 4. Maximum viral load for three potential levels of host-cell entry inhibition treatment.

Most interestingly, the effect of vaccine antibodies seems to have a cut-off, by which the introduced viral load is cleared immediately, whereas less capable antibodies result in nearly full-term infection duration (as shown in Figure 5). Further study into this phase transition will help uncover the understanding of how waning immunity affects in-host interactions. The rate at which vaccine effectiveness is lost and the efficacy of vaccination against SAR-CoV-2 variants are of paramount concern as we continue developing novel treatments. Comparing the exploratory study of parameter choice to emerging models of waning vaccine immunity [25] can help inform therapy regimens as dependent upon vaccination status or time since the last booster.

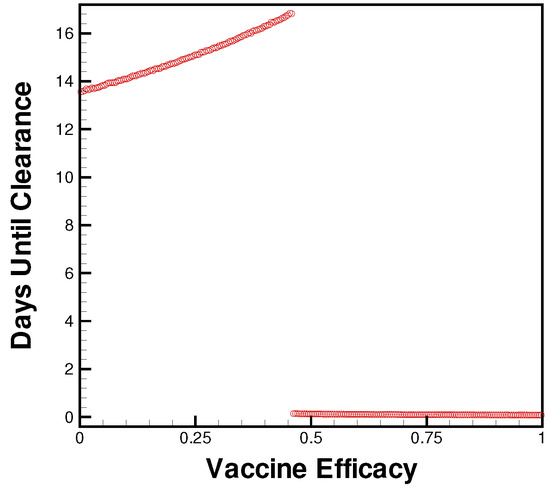
Figure 5. Days until clearance for levels of vaccine efficacy from no immunity (0) to natural antibody levels of immunity (1).

3.2. Combination Therapy

Here, multiple treatments are applied contemporaneously for the entire treatment window (Figure 6 and Figure 7), or in time-dependent dosing schedules (Figure 8). The results of combination therapy tests are of paramount importance to this study—the specific case study of COVID-19 allows modelers to inform clinical studies by describing the interaction of various dose and treatment timings to provide individual treatment suggestions. This is especially important when existing drugs are being repurposed for emerging diseases and when new treatments are being developed; thus, the important interactions between novel treatment techniques beg large-scale investigation. The proposed generic treatment efficacy model suggests a course of action for clinicians.

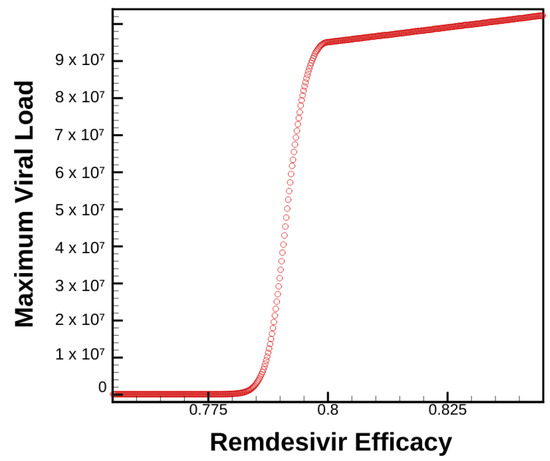
Figure 6. Maximum viral load as a function of time for varying levels of Remdesivir treatment combined with 75% efficacious host-cell entry inhibitor therapy

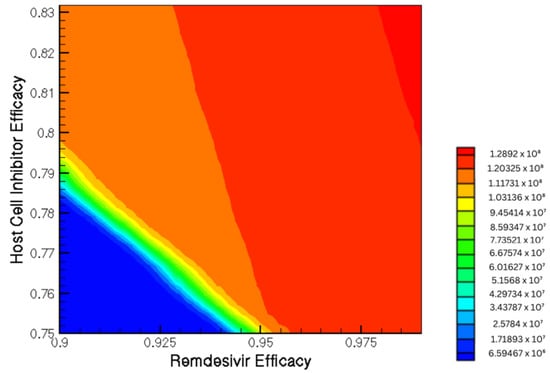
Figure 7. Contour plot shows the viral load as a function of Remdesivir and host-cell entry inhibition combination therapy.

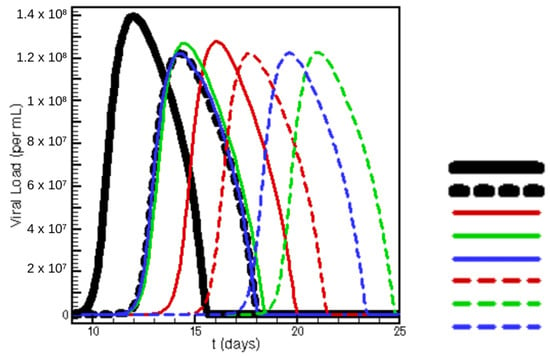
Figure 8. Viral load as a function of time for various treatment regimens. Each efficacy is 90% for Remdesivir (Rem.) and 75% for entry inhibition (HC). In descending order, the legend describes treatment regimens: 0–25 no treatment, 0–25 Rem., 0–5 Rem. 5–25 HC, 0–10 Rem. 10–25 HC, 0–15 Rem. 15–25 HC, 0–5 HC 5–25 Rem., 0–10 HC 10–25 Rem., 0–15 HC 15–25 Rem., where the number ranges describe the range of simulation days at which each therapy is administered.

Compared with Figure 3a, we can see how the introduction of host-cell therapy greatly affects a patient’s viral load dependence on Remdesivir dosage. The shift from a linearly shaped curve in Figure 3 to the S-shaped curve in Figure 6 suggests interesting phase transitions when studying concurrent treatment regimens. This is an important conclusion in that it suggests to clinicians that treatment plans do not respond linearly when varying dosage and timing—again begging further study before administering treatment.

Figure 7 displays the varying dependence of viral load on both treatments. One important conclusion suggests that the effect Remdesivir has on patient maximum viral load is dependent on the efficacy of concurrent host-cell entry inhibitor treatments. The nonlinearity further suggests the importance of broad-ranging parametric sweeps.

Additionally, timing and treatment efficacy are varied between dosing regimens in Figure 8. The relationship between timing a $5\mathsf{\mu }$M Remdesivir treatment with a host-cell entry treatment is displayed. Both time to viral peak and maximum viral load are dependent heavily on dose timing. Where the dose is constant, timing is still shown to produce important results in viral load and clearance rate.

Next, the combination of vaccination and both proposed therapeutics is examined. This highlights again the effect that individual patient characteristics have on treatment outcome. In this case, the patient-specific information is vaccination status. However, broadly speaking, this model could be extrapolated to include other patient-specific predispositions to treatment.

Many important conclusions can be drawn from Figure 9 and Figure 10. First, the introduction of treatment greatly affects the range of efficacy by which vaccines produce near-instantaneous clearance. The apparently step-wise phase transition dependency on treatment dosage offers insight into the level of treatment needed for a patient depending on time since vaccination.

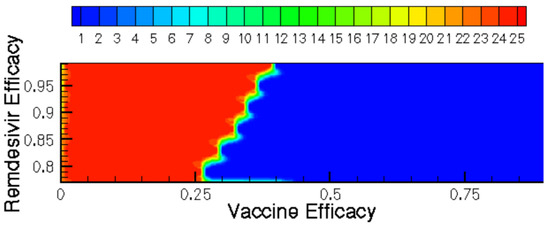
Figure 9. Time until clearance (days) displayed as a contour function of vaccine and Remdesivir efficacy.

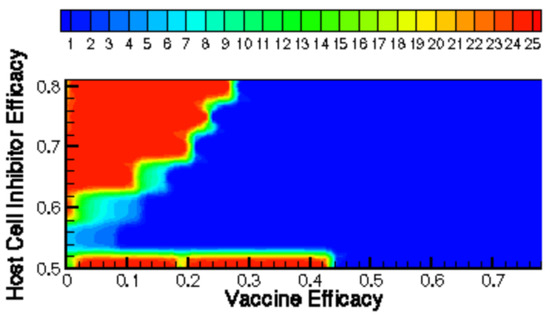
Figure 10. Time until clearance (days) displayed as a contour function of vaccine and host-cell entry inhibitor efficacy.

Finally, the results of various timed treatment combinations in key vaccination efficacy regimes are explored to highlight the differing outcomes. In other words, depending on patient predisposition, the “best” treatment—in terms of maximum viral load—is not always the same treatment timing and combination choice. This is most apparent in Figure 11, where identical treatment regimes are tested for various vaccination efficacies, and the mixed results for producing maximum viral load are reported.

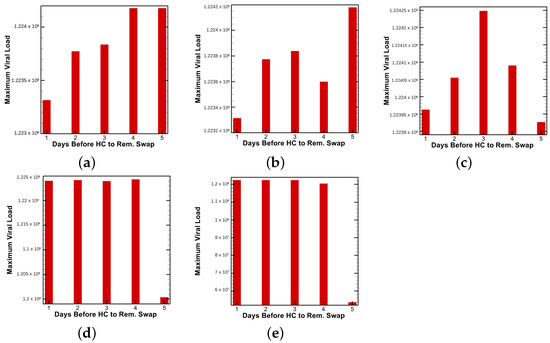
Figure 11. Maximum viral load observed for various treatment timing configuration of host-cell entry inhibitor followed by Remdesivir with patient vaccine efficacies of (a) 0.1, (b) 0.125, (c) 0.150, (d) 0.1625 and (e) 0.175.

Figure 9 and Figure 10 show how the time until clearance varies drastically as a function of both time since vaccination and intervention dose. Figure 11 further examines how optimal treatment timing depends upon vaccine efficacy. The effects on viral load in the first five days of treatment are observed in Figure 12. The host’s viral load is shown to depend closely upon dose timing. Figure 11, in conjunction with the maximum viral loads reported in Figure 11 and time until clearance reported in Figure 9 and Figure 10, illuminates the diversity of outcomes attainable by small differentiations in dose and timing. The diversity of outcomes further stresses the utility of pharmacodynamic models in integrative clinical treatment regimens.

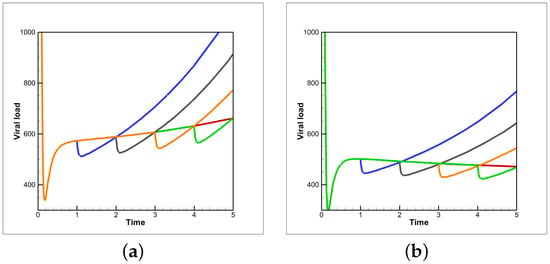
Figure 12. Viral load as a function of time for various treatment timing configurations of host-cell entry inhibitor followed by Remdesivir with patient vaccine efficacies of (a) 0.1 and (b) 0.15. Colored lines describethe time before the entry-inhibitor to Remdesivir therapy swap. Blue, black, orange, green and red correspond to one, two, three, four and five days, respectively.

4. Conclusions

The in-host model of SARS-CoV-2 infection is shown to be sensitive to parameter conditions describing the dose, timing and efficacy of various COVID-19 therapies. This correlation is drastically important to understanding how COVID-19 patients should be treated. COVID-19, a novel disease with rapidly evolving treatments, requires exploratory studies of treatment regimens.

The results presented include modeling the effect of Remdesivir or host-cell entry inhibition on a patient’s viral load. The clear dependence on small increments in treatment efficacy underscores the importance of in-host models in informing clinical explorations.

Further investigation of how different vaccinations can interact with different therapies needs only minor tweaks to the modeling paradigm and available data on vaccines and outcomes. Furthermore, the parameters in Table 2 remain widely unchanged as they represent the average patient. However, systemic parametric changes could be made to describe underlying differences in patient populations. Pre-existing conditions and co-morbidities could be added to the model through informed parameters. Importantly, in-host COVID-19 therapy models must continue to adapt to challenges presented by treatment design and patient condition modeling.