Abstract
A single-valued neutrosophic set (SVNS) is a subcategory of neutrosophic set that is used to represent uncertainty and fuzziness in three tiers, namely truthfulness, indeterminacy, and falsity. The measure of entropy of a SVNS plays an important role to determine the ambiguity in a variety of situations. The knowledge measure is a dual form of entropy and is helpful in certain counterintuitive situations. In this paper, we introduce a knowledge measure for the SVNS and contrast the same with existing measures. The comparative study reveals that the proposed knowledge measure is more effective in modeling the structured linguistic variables. We provide the relations of the proposed knowledge measure with single valued neutrosophic similarity and distance measures. We also investigate the application of the proposed measure in multi-attribute group decision making (MAGDM). The proposed MAGDM model is helpful when the decision makers in the group have varied background and the hiring organization is unable to assign the level of importance or weight to a decision-maker.
Keywords:
single valued neutrosophic set; knowledge measure; MAGDM; correlation coefficient; neutrosophic similarity MSC:
03E72; 90B50; 03E75
1. Introduction
The first successful attempt to model the imprecision or ambiguity of human reasoning in a mathematical framework was put forward by Zadeh [1]. The quantitative representation of the linguistic knowledge of the human observations or cognition was investigated under the notion of fuzzy theory. Atanassov [2] further extended the theory and introduced ‘Intuitionistic Fuzzy Set’ in which an element of the universal set belongs or does not belong to a set to a certain extent. In both these concepts, we get a set single-valued and 2-tuple quantitative representation of the vagueness associated with an element of the universal set. However, there are some complex situations in real life where these two representations are not sufficient to handle such situations. Smarandache [3] brings out the notion of a neutrosophic set (NS) from a philosophical point of view to investigate the indeterminate or inconsistent information that commonly occurs in real-life circumstances. The neutrosophic set is based on three tiers—belongingness, indeterminacy, and non-belongingness. In short, the neutrosophic set is beyond the fuzzy set and intuitionistic fuzzy set. Most of the attributes in a complex situation where decision-makers use linguistic variables can be easily expressed with the help of a neutrosophic value. Wang et al. [4] introduced a subclass of neutrosophic set and termed it as a single-valued neutrosophic set. Various operations (union, intersection, complement) have been studied. Since the advent of the neutrosophic set, major work especially in the field of multi-attribute decision-making and pattern-recognition played a vital role. Ma et al. [5] studied Archimedean t-norm or t-conorom using intuitionistic fuzzy aggregation operator for multi-criteria decision making. Symmetric intuitionistic fuzzy weighted mean operators concerning extensive weighted Archimedean t-norm and t-conorom put forward for dealing with membership and non-membership information. Wu et al. [6] discussed the entropy, similarity measure, and cross-entropy of information measure in SVNSs. The given information measure was used to handle MADM problems to check the effectiveness. Similarity measures and entropy of single-valued neutrosophic sets was proposed by Qin and Wang [7]. Smarandache [8] proposed a neutrosophic hedge algebra. Different operations in neutrosophic hedge algebra were also studied to aggregate the neutrosophic linguistic value. Hanafy [9] proposed a correlation coefficient formula for neutrosophic data. Singh et al. [10] studied the correlation coefficient in an intuitionistic fuzzy set. In the application part, a generalized correlation coefficient was used to solve MADM. Normalized correlation efficiency was considered as the weight of decision-makers. Biswas et al. [11] proposed a new technique concerning the TOPSIS method in the single-valued neutrosophic environment. Jin et al. [12] proposed an information measure for SVN entropy and similarity measure based on sine and cosine function. Comparative analysis was studied to check the effectiveness and rationality of the given method. Knowledge measure in a fuzzy set was given by Singh et al. [13] to check the effectiveness of the proposed method. In a hesitant fuzzy set, knowledge measure was computed by Lalotra and Singh [14]. The knowledge concerning the attributes in context with some available alternatives can be represented in various frameworks. A neutrosophic theory equips us with a kind of representation of the knowledge base that removes certain pitfalls of the fuzzy and intuitionistic fuzzy representation. The neutrosophic entropy provides a valuation of the uncertainty or ambiguity entailed in a given neutrosophic set. In the MADM problems, the neutrosophic entropy is utilized to compute the objective weights of the attribute. Sometimes, the entropy measures suffer from certain counterintuitive situations and render inappropriate results. The counterintuitive situations arise when an entropy/knowledge measure cannot distinguish two different neutrosophic sets. Moreover, the problems of multi-attribute group decision making if the higher organization is not aware of the expertise and knowledge base of decision-makers. Then how to assign the weightage to the decision experts. These two reasons motivated us to derive an alternative entropy-like measure for objective weight computation and to propose some mechanism for the weight assigned to the decision-makers. The main contribution of this paper is as follows:
- We propose an entropy-like measure in the neutrosophic settings and termed it a single-valued neutrosophic knowledge measure.
- We also discuss certain properties of the neutrosophic knowledge measure and establish its connection with the single-valued neutrosophic similarity and dissimilarity measure.
- An algorithm of MAGDM is proposed and implemented with the help of a numerical example.
- Comparative analysis to check the effectiveness of the proposed knowledge measure has also been presented.
The remaining part of the paper is organized is as follows: Section 2 presents the fundamental concepts regarding this paper. In Section 3, we propose a knowledge measure in the single-valued neutrosophic environment. Section 4 presents the relation of single valued neutrosophic similarity and distance measure with the single-valued neutrosophic knowledge measure. In Section 5, we consider an algorithm for the MAGDM problem. Section 6 deals with the comparative studies. Finally, concluding remarks are given in Section 7.
2. Preliminaries
In this section, we present some definitions and concepts concerning single-valued neutrosophic sets.
Definition 1.
([1]). Letbe the universal set then a fuzzy set in Y is defined as
wheredetermines the truth membership of y in B. The value ofgives the degree of belongingness of y in B.
Definition 2.
([2]). Intuitionistic fuzzy set B on a universal set Y is defined
whereanddetermines the degree of membership and degree of non—membership respectively with the conditionand the value ofandgives the value of membership and non-membership of y in B, respectively.
Definition 3.
([3,4]). A single-valued neutrosophic set on a universal set B is defined as
where,andassigns the degree of membership, degree of indeterminacy and degree of non—membership respectively with the condition. andgives the degree of truth membership, degree of indeterminacy, and degree of false membership respectively in [0, 1].
Remark 1:
Further in this paper, for a particular elementthe 3-tuplewill be termed as a single–valued neutrosophic element (SVNE) or single-valued neutrosophic value (SVNV).
Operations on single-valued neutrosophic values (SVNVs) [4]:
Let and be two SVNVs then, we have the following operations.
Union:
Intersection: .
Complement:
Definition 4.
Let N(Y) be the set of all single-valued neutrosophic elements on a universal set Y. Letandbe two member of N(Y) s.tiff,.
Then is a partially ordered set also, if
and then and are and , respectively. Therefore, N(Y) is a lattice.
This lattice is used to describe the valuation of the single-valued neutrosophic knowledge measure.
Definition 5.
([9]). The correlation coefficientbetween two neutrosophic sets B and C is defined as
Now we define correlation efficiency and normalized correlation efficiency for the determination of objective weights of decision makers in the MAGDM problem.
Definition 6.
The correlation efficiency of a SVNVwith respect to SVNVs, m, k = 1, 2, 3, …, n is defined as
Definition 7.
Normalized correlation efficiency ofis defined as
Definition 8.
([12]). The similarity measure S between two neutrosophic sets B and C is a functionwhich satisfies the given condition:
- NSM1:0S (B, C)1;
- NSM2:S (B, C) = 1 if B = C;
- NSM3:S (B, C) = S (C, B);
- NSM4:S (A, C)S (A, B); S (A, C)S (B, C), if AB.
Definition 9.
([6]). An entropy E on a single-valued neutrosophic element,is a functionwhich satisfies the following condition:
- NSE1:ENS () = 0 ifis a crisp set i.e.,
- NSE2:ENS ()= 1 if () = (0.5, 0.5, 0.5);
- NSE3:ENS ()ENS (ifis more uncertain;
- NSE4:E () = E (where.
Remark 2:
Letandbe two single-valued neutrosophic elements in N(Y) thenand() independently assumes their values in [0, 1].
In fuzzy theory, a fuzzy set is said to be a sharpened (less uncertain) version of a fuzzy set A with membership function if
for i.e.,
and for i.e., .
Based on similar logic, a single-valued neutrosophic elements is more uncertain than if for 0 and for 0 where .
3. A Knowledge Measure on Single-Valued Neutrosophic Set
We provide the following axiomatic framework for defining a knowledge measure of SVNV. Let N(Y) be the set of all single-valued neutrosophic values, then a knowledge measure on a single-valued neutrosophic value/element is a function K: N(Y) [0, 1] that satisfies the following conditions:
- NSK1: K () = 1 if and only if or ; t = 1, 2, 3;
- NSK2:K ( = 0 if and only if () = (0.5, 0.5, 0.5);
- NSK3: K ( = K (;
- NSK4: K ( K ( if is more uncertain than i.e., when 0; t = 1, 2, 3 or when .
We propose a knowledge measure for SVNV as
The following theorem establishes the validity of the proposed knowledge measure.
Theorem 1.
K () given in Equation (1) is a valid knowledge measure for SVNV.
Proof.
For this, it is sufficient to show that K ( satisfies the axiomatic requirements NSK1—NSK4.
- NSK1: We have . Let us suppose that = 0 or = 1 then = 1 or = −1 for t = 1, 2, 3.Using (1), we have K () = 1.On the other hand, we assume that K ( = 1then, = = − 1.[−1, 1].Therefore, every term in the summation of (1) is positive. As K () =1, then every term in this summation should be equal to one, i.e.,and Equation (2) holds if and only if = −1 or = 1 for t =1, 2, 3.Hence, K ( = 1 if and only if = 0 or = 1 for t = 1, 2, 3.
- NSK2: If () = (0.5, 0.5, 0.5), we have = 0. Then, from Equation (1), K ( = 0. On the other hand, from the above analysis, we have [−1, 1], it is obvious that 0 K () 1.If K () = 0 then = 0 for t = 1, 2, 3.It follows that = 0.5, t = 1, 2, 3 i.e., () = (0.5, 0.5, 0.5).
- NSK3: Since = (1 − ) then = Thus,Therefore, K () = K ().
- NSK4: Assume that is more uncertain than . Therefore, in view of Remark 2, we have two cases: for 0 and , when 0; .
Case 1: Let for 0;
Since 0 .
Using (3) and (4), we have
Further, [−1, 0] .
Using (A) and (B), we have
Note that, the generating function of the knowledge measure defined in Equation (1) is a decreasing function of x in [−1, 0].
Therefore, in view of Equations (1) and (C), we have
Case II: Let for 0; .
On the same lines as that of Case I, we can obtain
This shows that whenever is more uncertain than , we have
K () K () and hence the proof of axiom NSK4. □
Theorem 2.
Let K () and K () be a knowledge measure of single-valued neutrosophic elementandin the lattice N(Y) (Definition 4) then
Proof.
Here, we have two cases:
Case 1: when . Then, from Equation (1), we have
From (5) and (6) we get,
Case 2: when , then Equation (1) gives the similar results as that of Case I, i.e.,
□
In the next section, we establish the connections between similarity/distance measure for single-valued neutrosophic sets and the single-valued neutrosophic knowledge measure.
4. Single-Valued Neutrosophic Similarity Measure and Distance Measure
4.1. Single-Valued Neutrosophic Similarity Measure
Suppose and are two single-valued neutrosophic sets. The similarity S ( ) between should satisfy the following requirements [15].
- NS1: S () = 0 if and only if = 1 or . = −1, t = 1, 2, 3;
- NS2: S () = 1 if and only if () = (); t = 1, 2, 3;
- NS3: S () = S ();
- NS4: S () S (), S () S () if or , t = 1, 2, 3.
Theorem 3.
Letbe a SVNE, then 1 − S () is a single—valued neutrosophic knowledge measure i.e.,
Proof.
It is sufficient to show that 1 − S () satisfies the requirement NSK1–NSK4.
- (a)
- K () = 1 if and only if 1 − S () = 1 which implies S () = 0 if and only if = 1 or i.e., K () = 1 if and only if = 1 or .
- (b)
- K (() = 0 which implies that 1 − S () = 0 if and only if S () = 1 and S () = 1 if and only i.e., K () = 0 if and only if () =, i.e., K (() = 0 if and only if (.
- (c)
- K () = 1 − S (,) which implies K () = 1 − S (, ) = K ().
- (d)
- Let be two SVNEs. Suppose that when − 0 then 1 − 0 i.e., 1 − and we havei.e.,
Therefore, by definition of the similarity measure of SVNE (NS4), it is deduced that
S () S ()
or 1 − S () 1 − S ()
or 1 − S () 1 − S ().
which implies, K () K ().
Similarly, K () K () when − 0. □
4.2. Single-Valued Neutrosophic Distance Measure
If and are two SVNVs then the distance measure between and should satisfy the given conditions [16]:
NSD1:d () = d (, );
NSD2: d () = 1 if and only if = 0 or = 1 for t = 1, 2, 3;
NSD3: d () = 0 if and only if ;
NSD4: d () d (); d if or
Theorem 4.
Letbe a SVNV, then d () is a single-valued neutrosophic knowledge measure i.e., K () = d () is a single-valued neutrosophic knowledge measure.
Proof.
It is sufficient to show that d () satisfies the requirement NSD1–NSD4.
NSD1: As we know K(() = 1 which implies d () = 1 if and only if − = 1 or . − = −1 i.e., = 1 or = −1 and this equation holds if and only = 0 or = 1.
NSD 2: K () = 0 which implies that d () = 0 if and only if () = () or () = () or = 1 − which implies = 0.5 for t = 1, 2, 3 i.e., () = (0.5, 0.5, 0.5).
NSD 3: K () = d () which implies d () = K () = K ().
NSD 4: Let be two SVNEs. Suppose that when − 0 then 0 or 1 − and we have, . or . Therefore, by NSD4
d ()d ()d ()
i.e., d ()d ().
K ()
Consequently, K () K () for − 0. □
In the next section, we investigate the application of the proposed knowledge measure in MAGDM problem.
5. The MAGDM Problem
Suppose we are given m attributes of each of the n available alternatives and a person or an organization seeks the best alternative with the help of k decision-makers. Let, …, attributes be the attributes pertaining to the alternatives and be the decision-makers. Then, each decision-maker gives neutrosophic ratings based on satisfaction level to the attribute in context of the available alternative. Objective weights of attributes are computed using entropy/knowledge measure.
This problem can be considered as multiple attribute group decision-making (MAGDM). The theory of neutrosophy provides an alternative and an efficient tool to design decision-making models with vague information. Such a mechanism is more practical and sophisticated for obtaining the reasonable and appropriate solution of MAGDM problem.
A framework based on cognitive logic to solve an MAGDM problem requires the following information.
- (1)
- Decision matrices/table based on the neutrosophic knowledge-base of each decision maker.
- (2)
- A unified decision table aggregating the opinion of the decision makers with different knowledge and background. The procedure of opinion aggregation essentially needs to consider the level of expertise of each of the decision-makers. Therefore, some level of importance or weight should be assigned to each decision expert. The weight computed in this manner may be considered as the level of expertise. Now question arises how to compute this weight. In such a scenario, the objective weights of decision-makers can be obtained using some mathematical procedure connecting the information base of the decision-makers. The correlation coefficient among the neutrosophic knowledge base of experts gives the linear association or degree of agreement in the opinion of the experts. The normalized correlation efficiency computes the relative agreement level of each of the expert at normalized scale. Thus, normalized correlation efficiency can be perceived as the weight to the expertise of a decision-maker.
- (3)
- The weights of the decision-makers are utilized to obtain the collective decision matrix. The fusion of decision matrices also requires a suitable aggregation operator. In the present scenario, we use a single-valued neutrosophic weighted averaging operator.
- (4)
- Finally, the rating of alternatives can be obtained.
On the basis of this discussion, we developed the flowchart given in Figure 1 and the following algorithm.
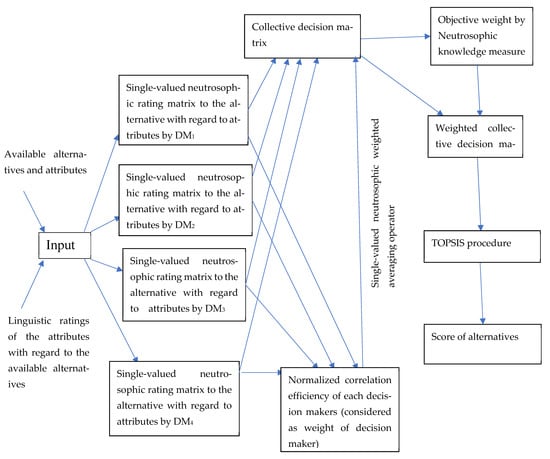
Figure 1.
Flowchart for algorithm following in the MADM problem.
5.1. Algorithm for MADM Problem in Neutrosophic Set
- Step 1: There may be lots of attributes in a decision-making problem. Among them, only some of the attributes are appropriate and technically sound. Therefore, appropriate attributes are identified with the help of the domain experts.
- Step 2: Different alternatives may be good in different attributes. On the basis of their performance level, some ratings are given to each alternative with regard to each attribute by decision-makers and these scores are given in the form of linguistic terms. The alternatives with neutrosophic ratings of attributes are shown in the following decision matrix D:In the given matrix represent degree of truthness, indeterminacy, and falsity respectively.
- Step 3: In the next step, we construct decision matrices for k decision-maker with the help of linguistic term. It is necessary to find out the weights of each decision-makers because each decision-maker has their own significance. For this, the linguistic terms for each decision-maker are rated with the help of neutrosophic number . Using the correlation coefficient formula given in Definition 5 between each decision-maker helps us to find the correlation measure and correlation coefficient between linguistic opinions of the decision-makers. The correlation efficiency of each decision-maker can be considered as a more realistic weight of the decision-maker as it computes the objective and subjective assessments.
- Step 4: Correlation efficiency concerning the intuitionistic fuzzy sets was computed by Singh et al. [10]. Analogously, we compute the correlation efficiency and normalized correlation efficiency N in the neutrosophic environment in Definition 6 and Definition 7. The normalized correlation efficiency of each decision maker was considered as the weights of the decision-maker.
- Step 5: With the help of the decision-maker’s assessment, construct the aggregated single-valued neutrosophic decision matrix was constructed with the help of SVNWA (single-valued neutrosophic weighted averaging) operator (Biswas et al. [11])where p is no. of decision-makers and is the weight of a decision-maker.
- Step 6: The knowledge measure of the selected attribute is calculated using Equation (1). From the knowledge measure of attributes, we can find the weight of an attribute as follows.
- Step 7: Aggregation-weighted neutrosophic decision matrix is constructed for each alternative with respect to each attribute with the help of the given formula:
- Step 8: Obtain relative neutrosophic positive ideal (RNPIS) and relative neutrosophic negative ideal solution (RNNIS) for each attribute from aggregated single neutrosophic decision matrix as follows.
- Step 9: The distance measure of each alternative from RNPIS () and RNNIS () is determined with the help of the given formula:where are the max. and min. value of truth membership, are the max. and min. value of indeterminacy, and are the max. and min. value of falsity membership.
- Step 10: Finally, the relative closeness coefficient to the neutrosophic ideal solution is obtained which is defined as follows:The larger relative closeness coefficient value depicts the most suitable and appropriate alternative.
5.2. Numerical Example Based on MADM (Multiple Attribute Decision-Making)
Suppose there are four decision-makers in a selection committee and they want to select the most suitable and deserving candidate for the managerial position in an organization. Let there be four candidates (alternatives) , , , for the post. The candidates have been selected based on four attributes , , , where : Hardworker, Leadership, : Domain knowledge, and : Visionary. Based on these attribute decision-makers , , , and select the most suitable candidate. Now, we implement the proposed algorithm with the help of the numerical example:
- Step 1: Each attribute attains its own significance. Some are very major and some are not. Similarly, each decision-maker has their own importance according to their background knowledge base, power, and position in an organization. The importance of attributes is expressed by linguistic term and these terms are rated as single-valued neutrosophic numbers as shown below in Table 1:
 Table 1. Ranking of attributes and decision makers with linguistic terms.Table 1. Ranking of attributes and decision makers with linguistic terms.
Table 1. Ranking of attributes and decision makers with linguistic terms.Table 1. Ranking of attributes and decision makers with linguistic terms.Linguistic Term SVNNs Extremely good (1.0, 0.0, 0.0) Very good (0.95, 0.15, 0.05) Good (0.75, 0.25, 0.10) Medium (0.50, 0.40, 0.30) Bad (0.20, 0.60, 0.60) Very bad (0.10, 0.80, 0.95) - Step 2: The linguistic term taken from Table 2 can be expressed as single-valued neutrosophic number using Table 1 for rating the opinion of each decision-maker. We present these ratings in the form of four decision matrices which subsequently helps to assess the objective weights of the decision-makers. The correlation measures of the neutrosophic values were calculated between each possible pair of decision-makers as shown in Table 3. In Table 4, the correlation coefficient between each pair of decision-makers is obtained with the help of the formula given in Definition 5. Further, we determine the correlation efficiency and normalized correlation efficiency as shown in Table 5 and Table 6 by using the formula given in Definition 6 and Definition 7. We consider the normalize correlation efficiency of each decision-maker as the weights of decision-makers.
 Table 2. Linguistic rating for four attributes for the four available alternatives by decision-makers.Table 2. Linguistic rating for four attributes for the four available alternatives by decision-makers.
Table 2. Linguistic rating for four attributes for the four available alternatives by decision-makers.Table 2. Linguistic rating for four attributes for the four available alternatives by decision-makers.Alternative Decision-Maker C1 C2 C3 C4 A1 DM1
DM2
DM3
DM4G
VG
G
VGG
G
VG
GG
A
VG
AG
G
A
VGA2 DM1
DM2
DM3
DM4VG
VG
VG
VGG
A
VG
AA
G
G
GA
G
G
GA3 DM1
DM2
DM3
DM4VG
G
A
GVG
G
A
VGVG
G
A
VGVG
G
A
GA4 DM1
DM2
DM3
DM4G
A
VG
GG
A
G
GG
G
G
GG
G
G
GFor decision-maker DM1, DM2, DM3, DM4 linguistic term are given as below:For decision-maker DM1For decision-maker DM2For decision-maker DM3For decision-maker DM4For decision-maker DM1, DM2, DM3, DM4 single-valued neutrosophic values corresponding to linguistic terms areFor decision maker DM2, the single-valued neutrosophic value corresponding to linguistic terms isFor decision maker DM3, the single-valued neutrosophic value corresponding to linguistic terms isFor decision maker DM4, the single-valued neutrosophic value corresponding to linguistic terms is Table 3. Correlation measures of neutrosophic pair for each decision-maker.Table 3. Correlation measures of neutrosophic pair for each decision-maker.
Table 3. Correlation measures of neutrosophic pair for each decision-maker.Table 3. Correlation measures of neutrosophic pair for each decision-maker.11.336 10.262 10.193 10.984 10.262 10.194 9.65 10.562 10.193 9.65 10.939 10.118 10.984 10.562 10.118 11.341  Table 4. Correlation coefficient of single-valued neutrosophic sets.Table 4. Correlation coefficient of single-valued neutrosophic sets.
Table 4. Correlation coefficient of single-valued neutrosophic sets.Table 4. Correlation coefficient of single-valued neutrosophic sets.1 0.954 0.915 0.968 0.954 1 0.914 0.982 0.915 0.914 1 0.908 0.968 0.982 0.908 1  Table 5. Correlation efficiency of decision-makers.Table 5. Correlation efficiency of decision-makers.
Table 5. Correlation efficiency of decision-makers.Table 5. Correlation efficiency of decision-makers.Decision-Maker Correlation Efficiency DM1 0.945 DM2 0.95 DM3 0.912 DM4 0.952  Table 6. Normalized correlation efficiency of decision-makers.Table 6. Normalized correlation efficiency of decision-makers.
Table 6. Normalized correlation efficiency of decision-makers.Table 6. Normalized correlation efficiency of decision-makers.Decision-Maker Normalized Correlation Efficiency DM1 0.251 DM2 0.252 DM3 0.242 DM4 0.253 Where 0.251, 0.252, 0.242, and 0.253 are weights of decision-makers. Take 1 = 2 = 3 = 0.242, and 4 = 0.253. - Step 3: We construct aggregated neutrosophic decision matrix as given in Table 7 with the help of SVNWA (single-valued neutrosophic weighted averaging aggregation operator).
 Table 7. Aggregated neutrosophic decision matrix.Table 7. Aggregated neutrosophic decision matrix.
Table 7. Aggregated neutrosophic decision matrix.Table 7. Aggregated neutrosophic decision matrix.C1 C2 C3 C4 A1 (0.889, 0.192, 0.070) (0.830, 0.221, 0.084) (0.759, 0.280, 0.147) (0.803, 0.246, 0.109) A2 (0.949, 0.149, 0.050) (0.759, 0.280, 0.147) (0.702, 0.281, 0.131) (0.702, 0.281, 0.131) A3 (0.802, 0.246, 0.109) (0.868, 0.216, 0.092) (0.764, 0.278, 0.144) (0.803, 0.246, 0.109) A4 (0.798, 0.248, 0.111) (0.702, 0.281, 0.132) (0.750, 0.250, 0.100) (0.750, 0.250, 0.100) The weights of the attributes are determined with the help of Equation (8), i.e., , . - Step 4: We construct an aggregated weighted neutrosophic decision matrix using Equation (9) and present in Table 8.
 Table 8. Aggregated weighted neutrosophic decision matrix.Table 8. Aggregated weighted neutrosophic decision matrix.
Table 8. Aggregated weighted neutrosophic decision matrix.Table 8. Aggregated weighted neutrosophic decision matrix.C1 C2 C3 C4 A1 (0.278, 0.060, 0.021) (0.204, 0.054, 0.020) (0.157, 0.057, 0.030) (0.186, 0.057, 0.025) A2 (0.297, 0.046, 0.015) (0.186, 0.068, 0.036) (0.145, 0.058, 0.027) (0.162, 0.065, 0.030) A3 (0.251, 0.076, 0.034) (0.213, 0.053, 0.022) (0.158, 0.057, 0.029) (0.186, 0.057, 0.025) A4 (0.249, 0.077, 0.034) (0.172, 0.069, 0.032) (0.155, 0.051, 0.020) (0.174, 0.058, 0.023) Step 5: The neutrosophic relative positive ideal solution and relative negative solution is obtained from aggregated weighted neutrosophic decision matrix given in Equations (10) and (11).Neutrosophic relative positive ideal solution (Qi+):Neutrosophic relative positive ideal solution (Qi−): - Step 6: The distance measures () of each alternative from RNPIS and RNNIS are determined with the help of normalized Euclidean distance measure given in Equations (12) and (13). Finally, we obtain the relative closeness coefficient (Ci*) with the help of formula given in Equation (14).The largest relative closeness value indicates the most suitable and appropriate alternative. From Table 9, it can be seen that the largest value of relative closeness coefficient is corresponding to . Hence, A1 is the most suitable alternative.
 Table 9. Closeness coefficients of the alternatives.Table 9. Closeness coefficients of the alternatives.
Table 9. Closeness coefficients of the alternatives.Table 9. Closeness coefficients of the alternatives.Alternatives Ci* A1 0.0079 0.0173 0.6865 A2 0.0134 0.0178 0.5705 A3 0.0170 0.0157 0.4801 A4 0.0220 0.0065 0.2280
Using the VIKOR method (Kamal et al. [17]) to the data of the numerical problem considered in this section, the ranking results are . We observe that the best alternative due to the VIKOR Method and proposed method remains the same. Therefore, the proposed method is consistent with VIKOR method for finding the best alternative.
6. Comparative Study
In this section, we investigate the effectiveness of the proposed knowledge measure in MCDM problems and comparative study of proposed similarity measure.
6.1. Effectiveness of the Proposed Knowledge Measure against Different Existing Entropies
To check the usefulness of our proposed knowledge measure in MCDM problems, we consider the numerical example given in Section 5.2. We calculate the weight of the attribute with the help of the proposed single-valued neutrosophic knowledge measure. We use a same numerical problem and calculate the weight of the attributes by using different existing entropies as shown in Table 10.

Table 10.
Ranking result using existing entropies and the proposed knowledge measure.
From Table 10, we observe that the best alternative using the existing single valued entropy measures and our proposed knowledge measure remains same, i.e., . However, overall ranking of the alternatives is different due to our proposed measure. Moreover, as pointed out in the Section 5, the ranking of alternatives using VIKOR method is which is consistent with the ranking due to single-valued neutrosophic entropy measures (i = 1, 2, 3, 4), since the VIKOR method is suitable for the problems with conflicting criteria as it gives the compromise-type solutions. Thus, in view of these facts, we can say that the existing entropy measures are more suitable to MAGDM problems with conflicting criteria and our proposed measure is suitable to the problems with non-conflicting criteria.
6.2. Comparison between the Existing Entropies of the Neutrosophic Sets and the Proposed Knowledge Measure of Neutrosophic Sets on the Basis of Linguistic Hedges
In this subsection, we compare the existing entropies of single-valued neutrosophic sets and proposed knowledge measure on the basis of linguistic hedges.
Zadeh [19] introduced the notion of the linguistic hedge in two parts: 1. Very, much, more, or less which are used in direct situations; 2. hedges essentially, practically, techniques are used in complex situations. Zadeh gave different types of operations, two of which are concentration and dilation. The concentration is defined as
and dilation is the somehow opposite of concentration and is defined as
Singh et al. [13] also investigated the superiority of the fuzzy knowledge measure using structured linguistic framework.
The entropy for a fuzzy set A on the basis of mathematical operation should follow the order as
Because of this, knowledge measure of fuzzy set, should follow the order
Neutrosophy is a broader sense of capturing the vagueness, so, the inequality order given in Equations (15) and (16) must also be followed by an entropy and a knowledge measure, respectively, in the single-valued neutrosophic framework. To analyze the practicality of the proposed measure, we consider the following empirical scenario.
Let be a SVNS in which , assumes three values, each of which can be regarded as membership value, indeterminacy, and non-membership value. Here, we consider A as linguistic hedge good, as average, as very good, and as extremely good. The modifier for the NS(A) is given as
(Wu et al. [6])
(Jin et al. [12])
(Elshabshery and Fattouh [18])
(Aydogdu [15])
(Qin and Wang [7])
(Majumdar and Samanta [20])
(Thao and Smarandache [21])
(Aydogdu and Sahin [22])
The comparative results for the following entropies of SVNS are given in Table 11.

Table 11.
Computed entropies/knowledge measures of SVNSs.
Now, from Table 11, we observed that
EY1(A1/2) > EY1(A) < EY1(A2) < EY1(A3)
EY2(A1/2) > EY2(A) > EY2(A2) > EY2 (A3)
EY3(A1/2) > EY3(A) < EY3(A2) < EY3 (A3)
EY4(A1/2) > EY4(A) > EY4(A2) > EY4 (A3)
EY5(A1/2) > EY5(A) > EY5(A2) > EY5 (A3)
EY6(A1/2) > EY6(A) > EY6(A2) < EY6 (A3)
EY7(A1/2) > EY7(A) > EY7(A2) > EY7 (A3)
EY8(A1/2) > EY8(A) > EY8(A2) > EY8 (A3)
K(A1/2) < K(A) < K(A2) < K(A3).
From the above result, it has been observed that entropies follow the pattern given in Equation (15). The knowledge measure of the neutrosophic set is also shown above, which satisfies the order given in Equation (16). Now, we consider another example of a NS.
The entropies and knowledge measure table of the given NSs is shown below
From the Table 11 and Table 12, it was observed that our proposed knowledge measure produces theoretical valid results, i.e., K(A1/2) < K(A) < K(A2) < K(A3), while SVN entropies produce unreasonable results in different instances. Therefore, the performance of our knowledge measure is better than the conventional entropy measures in the neutrosophic settings.

Table 12.
Computed entropies/knowledge measures of SVNSs.
7. Conclusions
In this paper, we have proposed a knowledge measure in the single-valued neutrosophic framework. The single-valued neutrosophic knowledge measure has been found to have a general relationship with the similarity and distance measures. Comparative studies demonstrated that the given knowledge measure is more effective and suitable than the existing entropy measure while dealing with the linguistic hedges and in MADM problems. We have also developed a mechanism to handle a MAGDM problem incorporating the proposed single-valued knowledge measure, an existing correlation measure, and an aggregation operator. This algorithm is found novel in sense that it identifies the level of expertise of each decision maker in the group even if the hiring organization has no information about their domain knowledge. The investigation of a problem related to MAGDM using the proposed method improves upon the existing methods in two ways. It offers independent choice of truthiness, falsity, and indeterminacy to the decision-makers for creating numerical data from the vague knowledge base and derives the weightage to decision-makers from the model itself. However, the current study demonstrates the practical applications using artificially generated data; the creation of real single-valued neutrosophic database seems to make this study more pragmatic. Our future studies will focus on some other areas of applications such as pattern recognition, image processing, etc., where the single-valued neutrosophic information seems to play a significant role.
Author Contributions
Conceptualization, S.S. (Sonam Sharma) and S.S. (Surender Singh); Formal analysis, S.S. (Sonam Sharma); Investigation, S.S. (Sonam Sharma); Methodology, S.S. (Surender Singh); Project administration, S.S. (Surender Singh); Resources, S.S. (Sonam Sharma) and S.S. (Surender Singh); Supervision, S.S. (Surender Singh); Visualization, S.S. (Sonam Sharma); Writing—original draft, S.S. (Sonam Sharma); Writing—review & editing, S.S. (Surender Singh). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Authors are highly thankful to anonymous referee and the editor for their critical and constructive suggestions to bring this article in the present form.
Conflicts of Interest
Authors declare that they have no conflict of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic Set-A Generalization of the Intuitionistic Fuzzy Set. Int. J. Pure Appl. Math. 2005, 24, 287–297. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single valued neutrosophic sets. In Multispace & Multistructure-Neutrosophic Transdisciplinarity (100 Collected Papers of Sciences); North-European Scientific Publishers: Hanko, Finland, 2010; pp. 410–413. [Google Scholar]
- MA, M.Z.; Yang, W. Symmetric Intuitionistic Fuzzy Weighted Mean Operators Based on Weighted Archimedian t-Norm and t-Conorms for Multi-Criteria Decision Making. Informatica 2020, 3, 89–112. [Google Scholar] [CrossRef]
- Wu, H.; Yuan, Y.; Wei, L.; Pei, L. On entropy, similarity measure and cross entropy of single–valued neutrosophic sets and their application in multi–attribute decision making. Soft Comput. 2018, 22, 7367–7376. [Google Scholar] [CrossRef]
- Qin, K.; Wang, L. New similarity and entropy measures of single–valued neutrosophic sets with applications in multi–attribute decision making. Soft Comput. 2020, 24, 16165–16176. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic Hedge Algebras. Broad Res. Artif. Intell. Neurosci. 2019, 10, 117–123. [Google Scholar]
- Hanafy, I.; Salama, A.; Mahfouz, K. Correlation of Neutrosophic Data. Int. J. Eng. Sci. 2012, 1, 39–43. [Google Scholar]
- Singh, S.; Sharma, S.; Lalotra, S. Generalized Correlation Coefficients of Intuitionistic Fuzzy Sets with Application to MAGDM and Clustering Analysis. Int. J. Fuzzy Syst. 2020, 22, 1582–1595. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B. TOPSIS method for multi–attribute group decision–making under single–valued neutrosophic environment. Neural Comput. Appl. 2016, 27, 727–737. [Google Scholar] [CrossRef]
- Jin, F.; Ni, Z.; Zhu, X.; Chen, H.; Langari, R.; Mao, X.; Yuan, H. Single-valued neutrosophic entropy and similarity measures to solve supplier selection problems. J. Intell. Fuzzy Syst. 2018, 35, 6513–6523. [Google Scholar] [CrossRef]
- Singh, S.; Lalotra, S.; Sharma, S. Dual concepts in fuzzy theory: Entropy and knowledge measure. Int. J. Intell. Syst. 2019, 34, 1034–1059. [Google Scholar] [CrossRef]
- Lalotra, S.; Singh, S. Knowledge measure of hesitant fuzzy set and its application in multi–attribute decision–making. Comp. Appl. Math. 2020, 39, 1–31. [Google Scholar] [CrossRef]
- Aydogdu, A. On Similarity and Entropy of Single Valued Neutrosophic Sets. ICSRS 2015, 29, 67–74. [Google Scholar]
- Chai, J.S.; Selvachandran, G.; Smarandache, F.; Gerogiannis, V.C.; Son, L.H.; Bui, Q.; Vo, B. New similarity measures for single-valued neutrosophic sets with applications in pattern recognition and medical diagnosis problems. Complex Intell. Syst. 2021, 7, 703–723. [Google Scholar] [CrossRef]
- Kamal, N.L.A.M.; Abdullah, L.; Yee, F.M.; Abdullah, I.; Vafaei, N. Single Valued Neutrosophic VIKOR and Its Application to Wastewater Treatment Selection. Neutrosophic Sets Syst. 2021, 47, 251–272. [Google Scholar]
- Elshabshery, A.; Fattouh, M. On some Information Measures of Single–Valued Neutrosophic Sets and their Applications in MCDM Problems. Int. J. Eng. Res. Technol. 2021, 10, 406–415. [Google Scholar]
- Zadeh, L.A. A Fuzzy–Set–Theoretic Interpretation of Linguistic Hedges. J. Cybern. 1972, 2, 4–34. [Google Scholar] [CrossRef]
- Majumdar, P.; Samanta, S.K. On Similarity and entropy of neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 1245–1252. [Google Scholar] [CrossRef]
- Thao, N.X.; Smarandache, F. Apply new entropy-based similarity measures of single valued neutrosophic sets to select supplier material. J. Intell. Fuzzy Syst. 2020, 39, 1005–1019. [Google Scholar] [CrossRef]
- Aydodgu, A.; Sahin, R. New entropy measures based on neutrosophic set and their applications to multi -criteria decision making. Suleyman Demirel Univ. Fen Bilim. Enst. Derg. 2019, 23, 40–45. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).