Multi-User Massive MIMO System with Adaptive Antenna Grouping for Beyond 5G Communication Network

Abstract

Error-correcting codes with limited errors and higher spectral efficiency are the main concern for wireless communications. In the current situation, research is increasing daily to satisfy the growing demand for users with improved QoS. Adaptive Antenna Grouping (AAG) with a multilevel space–time trellis coding scheme in the Multi-User Massive MIMO system is the better option to provide flexible data transfer speeds, encoding gains, and gain in diversity with improved spectral efficiency and low decoding complexity, including the power optimization by reduced SNR at the same Symbol Error Rate/Frame Error Rate (SER/FER). The prior aim of maintaining spectral efficiency is achieved by using Massive MIMO. This paper presents the AAG according to the channel state information in the Massive MIMO scenario. The impact of the proposed model on standard ITU-R M.2135 scenarios is also demonstrated in this paper.

1. Introduction

In today’s technological age, multipath fading is one of the leading causes of erroneous signal propagation in wireless communication. A study group has researched various error-correcting codes to curb the adverse multipath fading effects. Multilevel (ML) coding is a new technique that uses numerous error-correcting codes for signal transmission. [1]. The ML coding method aims to provide versatile data transfer rates and greater spectral efficiency. The method works as follows: First, several sub-data streams break the stream of input data. To generate error-correcting codes, these sub-data streams are sorted out in parallel through a series of encoders known as element codes. Each section code is mapped to symbols of the constellation of an extended signal. The mapping requires splitting the constellation of these signals into subsets unless a single constellation point is contained in the subset. This particular method of partitioning the constellation of signals has been implemented and is called set partitioning [2]. The mapped symbols are modulated and combined to build complex codes called ML codes; ultimately, ML codes are transmitted over a wireless interface. Trellis codes are a form of channel codes commonly used to achieve efficient data transmission in wireless communication. The convolution encoder performs the input data stream conversion with the encoder’s impulse response [3]. This paper uses the trellis as component codes for information encoding at ML. The ML coding scheme with convolution/trellis codes as element codes can provide a better data transfer rate, encoding gains and the maximum gain in diversity with the desired error performance [4,5,6].

As the radio spectrum is limited, more efficient signaling techniques can be the only way to obtain a higher data rate. A multiple inputs multiple-output (MIMO) system uses various antennas at the transmitting and receiver side, which improves the enactment of the system through antenna diversity, as compared with one antenna system through multiplexing and attaining a high data rate. A system with multiple antennas is called a MIMO system, which uses multiple inputs/outputs at both the transmitting and receiving ends. Thus, the capacity of the wireless systems is improved as the number of antennas used increases, along with additional bandwidth and increased power requirements [7].

Extensive work has been carried out on MIMO systems with antenna selection and grouping to enhance the error efficiency of space–time codes further. Antenna selection is an exciting strategy with easy encoding and decoding algorithms and reduced complexity, providing high potential diversity order. The collection of antennas is carried out at both the transmitter and the receiver. Based on the assumption of perfect channel state information (CSI) accessible both at the receiver and in the transmitter, the current works described above on antenna selection for MIMO systems were completed. It has been demonstrated that this further boosts the efficiency and ability of the space–time coded method.

The selection of adaptive transmit antenna for MIMO coded systems selects a suitable group of transmitting antennas, according to CSI. The adaptive section provides a substantial advantage compared to the antenna selection method with a defined number of antennas in the collection sub-set. Wireless communications demand is expected to grow rapidly in the coming years. Massive MIMO is one potential technology to meet this demand. Massive MIMO is a popular strategy as a multiuser multiple antenna network for current-century wireless networks. The idea of Massive MIMO entails installing base stations with a very large number of antenna arrays, utilizing probably hundreds of transceiver components to maximize network bandwidth, boost stability, and minimize the total transmitted strength [8].

In Massive MIMO technology, the set of antennas is used on the transmission and reception sides to distinguish the individual channels in a multipath scenario. It is found that noise and fading are reduced on a small scale; the energy required for transmitting each bit decreases to zero because the range of antennas within the base station approaches infinity. This conclusion is based on the speculation of random matrices. With real propagation support, an information rate of 17 Mbps is often achieved with an average rate of 730 Mbps for individual cells and a spectral efficiency of 26.5 Mbps per hertz in a 20 MHz channel [9]. As the number of antennas is as high as the number of consumers, it provides more degrees of freedom to eliminate interference. However, the framework tends to become complex, so well-defined algorithms are required.

The growth of the individual Massive MIMO antennas should reduce the transmitted power in proportion to the antennas used in the base station, containing information about the CSI, because the base antenna with CSI is not very precise. For this reason, the Massive MIMO is more effective than any other configuration of an antenna. As it evolves, the problem of traffic congestion arises, which requires greater spectrum efficiency. Moreover, the spectral frequencies tend to remain limited. The orthogonal frequency division multiplexing based on the cyclic prefix and space–time (ST) coding is found in the fourth generation (4G) and the long-term evolution (LTE) as the main signal.

The key benefit is the efficient separation of the channels for multiple accesses, which reduces the complexity of the cyclic prefix when aligning to face the fading of the channel in several routes. However, performance is only achieved when the orthogonality is maintained between the subcarriers and synchronized correctly. Massive MIMO is an exciting field of 5G wireless research. It promises significant benefits for next-generation wireless data networks, which allow them to accommodate more users with higher data rates, higher reliability, and lower power consumption.

Motivation

While numerous research techniques in the literature address the above-mentioned problems, as shown in Table 1, the implementation of Adaptive Antenna Grouping (AAG) in Massive MIMO has not been improved, and no article for application in a real-world scenario has yet been realized. There is also a need to extend the AAG mechanism to individual users in various parts of the world, according to their requirements. The article attempts to fill the gap between agricultural, metropolitan, and suburban users, according to standard ITU-R M.2135. This paper presents an adaptive grouping algorithm for an antenna after being inspired by the above facts, which is then applied to various parts of the world in a Massive MIMO scenario. The main inspiration behind this research is summarized as follows:

Table 1. Investigation of space–time coding, antenna grouping, and their applications.

Ref.	Space–Time Coding Application	Methodology	Limitations/Contributions
[1]	Introduction of multilevel in error-correcting codes.	A new coding system called multilevel coding has been implemented that utilizes multiple error-correcting codes for signal transmission.	No antenna grouping/Massive MIMO/spectral efficiency based on multilevel in error-correcting codes.
[2]	Mapping by set partitioning in trellis code.	Signal constellation partitioning has been implemented and is referred to as set partitioning. Modulate and combine the mapped symbols to create complicated codes called multilevel codes.	No antenna grouping/Massive MIMO/spectral efficiency, but through mapping, create multilevel codes.
[4,5,6]	Multilevel codes in conjunction with iterative decoding of the block and convolutional code, and calculation of diversity and coding gain.	The multilevel coding scheme can deliver a preferred information transmission rate, error performance and coding, and diversity gain.	No antenna grouping/Massive MIMO/spectral efficiency. The major contributions are iterative decoding.
[10]	Multiple inputs and a single output are used with two transmitting and one receiving antenna and are applied with a diversity scheme in block coding.	A diversity scheme of two-branch simple transmission has been presented. The system uses two antennas for transmitting and one antenna for receiving. This has the same order of variety combined with one transmitting antenna and two receiving antennas as the max unit. With two transmitting antennas and the receiving M antennas, the scheme can be easily generalized to give a range of 2 M diversity. The novel idea does not need bandwidth expansion or input from the receiver to the transmitter, and the measurement complexity is close to the maximum combination of the receiver.	No antenna grouping/Massive MIMO/spectral efficiency. The key impact is the establishment of the diversity scheme.
[11]	Multiple inputs and a single output are used with two transmitting and one receive antenna and are applied with a diversity scheme in trellis coding.	The design procedure for choosing trellis codes with a simple transmit diversity scheme is described. Using this method, both diversity and coding gain can be achieved using two transmitting and one receiving antenna.	No antenna grouping/Massive MIMO/spectral efficiency, but the use of the diversity scheme in the trellis code, which benefits both coding and diversity, is a significant addition.
[12]	Multiple inputs and single output by optimal set partitioning are used with the designed multilevel super-orthogonal trellis coding.	A space–time code, known as space–time super-orthogonal trellis codes, with the new class, is presented. These codes symmetrically combine the allocated collection and modified space–time orthogonal codes to provide a better coding advantage and maximum diversity gain for the overall performance of previous STTCC codes. Moreover, the optimality of the parcel collection has been tested and the coding gain investigation has been evaluated. The perfect environment was used to schedule various quantities of states with codes running at different data rates up to a relatively high conceivable rate.	No Adaptive Antenna Grouping/Massive MIMO/spectral efficiency. The essential contribution is in trellis coding; the idea of orthogonality has been introduced.
[13]	Multiple inputs and a single output using four transmitting and one receiving antenna in terms of a cooperative diversity scheme are applied in orthogonal trellis coding.	In a cooperative diversity setting, a new family space–time trellis code is introduced, which extends the space–time super-orthogonal trellis codes intensively attributed to transmission antennas. A group of semi-orthogonal trellis codes is in use as building components in the new trellis codes. In space–time coding, multilevel coding will be further enhanced in its diversity plus coding gain. As a combination of MLC with STTCs, MLSTTCs are planned. MLSTTCs enhance the efficiency of the bandwidth, enhance diversity and coding gain and decrease decoding complexity, particularly for larger groups.	No Adaptive Antenna Grouping/Massive MIMO/spectral efficiency. However, the principle of super orthogonality has been introduced.
[14]	Multiple inputs and multiple outputs are used with four transmitting antennas and a different number of receiving antennas with Multilevel space-time trellis coding.	This paper presents a new code termed adaptively grouped MLSTTCs. This code is designed to perform better than traditional space-time trellis coding because it incorporates the advantages of MLC, STTC, antenna grouping, and CSIT simultaneously.	No Adaptive Antenna Grouping/Massive MIMO/Spectral efficiency. A noteworthy contribution is the introduction of antenna grouping.
[15]	Path-loss models in a standard.	Path-loss models have been standardized in this paper for different transmission models, such as the ITU-R M.2135 standard rural, suburban, and urban macro models.	No Adaptive Antenna Grouping major contribution works on path-loss model.
[16]	Multiple inputs and multiple outputs used two transmitting and two receiving antennas with multilevel pseudo-space–time trellis code.	In terms of its output difference with Shannon-bound sphere packing (a simple performance assessment tool), this paper shows that short block lengths of the code architecture show better results with convolution codes for point-to-point channels and the suggested MLPSTTCC.	No Massive MIMO. The main impact of cooperative diversity scheme implementation.

• Sending error-free data with improved network performance and increased spectral efficiency for better use of a limited spectrum for communication networks of the next decade.
• To examine the proposed method on different deployment scenarios of the ITU-R M.2135 standard.

2. Background and Scope of the Study

A brief introduction to the work and the scope of AAG in Massive MIMO is given in this subsection. The analysis of various procedures for multilevel space–time trellis codes (MLSTTC) has enhanced the situation over the past few years by achieving both the benefits of coding and the added diversity, including spectral efficiency. The trellis code was designed for high-speed data transmission in wireless communications, and multiple transmitting antenna channel codes were created to improve the rate of data transfer and communication efficiency over fading channels. The data are encoded with a channel code, and the encoded data are split into several streams that are transmitted concurrently using several transmission antennas. A linear combination of a sequence of transmitted signals interrupted by noise is the signal received at each receiving antenna. By using multiple transmitting antennas on the transmitter and receiver, spatio-temporal lattice codes [17] dramatically increase the performance of multiple wireless inputs and outputs. The essential parameters are the rank and the code-word distance matrix in slowly fading channels. The rank is used to obtain the maximum diversity gain, while the determinant is a criterion for obtaining the maximum code gain.

A diversity scheme of two simple branch transmissions has been presented. The system uses two antennas for transmitting and one antenna for receiving. This has the same order of variety combined with one transmitting antenna and two receiving antennas as the max unit [10,11,12,13]. The focus of the research was the further improvement of the ST code error. The focus is on the beam-forming MIMO method, antenna selection, and antenna grouping to improve the error performance. The scheme, which regulates the ST code by the number of antennas [18], helps the transmitter to adjust its rendering to the channel state information (CSI) by applying the pilot carriers to find the information about the channel behavior. The required information is applied where the number of transmission antennas is greater. The code selection scheme has been proven to provide a performance benefit in compromising complexity. Channel phase feedback was used to select the internal code. The internal code selection criteria are based on decoded low peak-to-average power ratio and can be easily applied without review [19]. The adaptive code selection method defined in [20] improves the ratio of signal to noise at the destination, using four-bit feedback at the destination, and on the transmitter side, it has suitable channel status information.

In an antenna transmitting a convolutional code with an ST code, for example, TAS/STBC [21,22] then TAS/STTC [23] to select the antenna, the antenna must be modified to become a comprehensively optimized antenna so that it is the better choice when considering all of the antennas available, without any restrictions. Furthermore, given this TAS/STBC/STTC function, it is recommended that this antenna has better code availability and error performance. In the grouped multilevel space–time trellis coding (GMLSTTC) scheme, transmit antennas are divided into small subgroups; the STCs from a separate transmitter were used to transmit information from each subset of transmit antennas. For decoding, a linear array processing method was used to suppress the signal transmitted from another antenna array since all other signals are treated as interference. The antenna on the transmitter side divides the antennas into lesser groups [24]; STCs are used individually to transmit data from every group of transmitting antennas. The linear array processing technique decodes a separate ST code that suppresses the signal transmitted over other antennas, considering interference. An adaptive antenna selection occurs at the transmitter in which an antenna grouping according to the CSI [25] is applied.

Individually, the ST information block adaptively chooses the corresponding group of transmitting antennas by the channel state information. This is represented by grouping an adaptive antenna [26]. The collection of transmitting antennas is made by selecting transmitting antennas by the feedback on the channel status.

STTCs and beamforming codes were combined in [27,28] to calculate WSTTC. The results show that this method enables the achievement of additional temporal separation with full spatial separation, as well as the additional receiver/signal amplifier gain, and better coding gain compared to STTC.

The bandwidth efficiency of the AWGN channel is enhanced by introducing multilevel coding using various error correction codes. This coding method creates a complex code from a combination of simple codes. This method [29] was applied for both modulation and error correction coding to select the constellation transmission points using constituent codes. The decoding of ML codes is performed in different stages [30,31,32], so the decoded information can pass from further stages. Multilevel coding and multilevel decoding provide high spectral efficiency and a great advantage in coding with reduced decoding complexity. In combination with ST codes, by [14], multi-level codes can be increasingly developed. Multilevel space–time trellis code (MLSTTC) [33] is developed using multilevel coding in STTC and MRM. It is proficient in increasing bandwidth efficiency, with lower decoding complexity, particularly for bigger groups and higher throughput. After the invention of MIMO technology, the grouping of antennas provides better performance with increased throughput, and the gain in diversity, named grouped multilevel space–time trellis code (GMLSTTC) [34], is developed using an amalgamation of MLSTTC with CSI. GMLSTTC uses CSI, which provides an improved error performance compared to MLSTTC [34,35,36]. An analysis of adaptive grouping according to the CSI is an effective and promising solution for the next generation [37].

MIMO development provides significant efficiency enhancements in terms of the speed and reliability of wireless communications systems [38]. Recently, the Massive MIMO device has been called a modern mechanism of the cellular network [39,40,41]. It provides a very high energy output by raising the strength of the radiated power. A base station (BS) mounted with a set of N antenna elements must transmit just 1/N of power to reach the average peak speed relative to a base station antenna; if certain components in the antenna array malfunction, the output of an extensive MIMO network would not be dramatically impacted [42]. Such devices also reach reasonable average speeds as they reduce user interference. Both these ventures analyzed the efficiency of large MIMO systems with single antenna users or regarded multiple antennas per operator as actual individual users when many antennas existed [39]. MIMO starts with some initial antennas and then extends to many others, a technology called Massive MIMO.

An investigation of broadcasting in Massive MIMO [43] frameworks with a partial coherence interim are displayed. The base station, for example, does not send channel state information to the terminals when transmitting basic data, such as the control signal. This paper suggests that the base station uses an orthogonal space–time block code (OSTBC) to communicate these standard data. This code is mapped to the massive antenna. Massive MIMO technology has been shown to have significant potential in meeting the ever-increasing demand for transmission-based communication systems with higher spectral efficiency. Although this exponential expansion of mobile communications remains the root cause of improved spectral efficiency, the rise of additional services, including machine-to-machine communication, Internet banking, the Internet of Things (IoT), and others, have become fundamental necessities of modern life [42,43,44,45].

Multi-User MIMO offers enormous points of interest over a traditional point-to-point (P2P) MIMO [46,47,48,49,50]; Massive MIMO uses a huge overabundance of service antennas over dynamic terminals and time-division duplex activity to separate from current practice. The additional antenna helps achieve broad throughput and energy efficiency by centering vitality in ever-smaller areas of the building. For the wireless system, the Massive MIMO technology was examined. Massive MIMO uses a wide range of antennas, and the duplex time division feature was used to focus energy in increasingly restricted spaces and boost energy efficiency technologies. The numerous advantages of Massive MIMO include the large use of low-power economic resources, reduced latency, improved MAC layer, and jamming robustness.

The number of users upturns significantly in the current scenario, but in the restricted range, data speed and connection quality play a major role in improving service quality. This paper attempts to explore the solution by introducing space–time coding to Massive MIMO. By applying the model in a real-time environment, this paper also takes the initiative to help industries update their equipment accordingly.

2.1. Contribution

A comparative analysis of pre-existing work on space–time coding with the proposed method is shown in Table 2. At the same time, the article’s contributions revolve around the proposed AAG in the Multi-User Massive MIMO system (AAG-3M).

Table 2. Comparative analysis of pre-existing work on space–time coding with the proposed method.

Ref.	Multi-Levelling	Antenna Grouping	AAG	Massive MIMO	Spectral Efficiency Analysis	Application in ITU-R M.2135 Standard
[1]	Yes	×	×	×	×	No
[2]	No	×	×	×	×	No
[6]	Yes	×	×	×	×	No
[11]	Yes	×	×	×	×	No
[13]	Yes	✓	×	×	×	No
[14]	Yes	✓	×	×	×	No
[16]	Yes	✓	✓	×	×	No
AAG-3M	Yes	✓	✓	✓	✓	Yes

The existing system still cannot achieve the requisite spectral efficiency with the advent of ideas such as IoT, machine-to-machine communication, virtual environments, and artificial intelligence. The ultimate purpose of this paper is to increase error-free transmission with better communication quality and spectral performance; the system’s link quality is improved by implementing multilevel coding in STTC. The network’s spectral performance is improved by using AAG in the base station with MIMO/Massive MIMO. Massive MIMO systems have shown improved spectrum efficiency, proving their usefulness.

It is also assumed that perfect channel information is necessary to acquire AAG and that this supports interference coordination. This paper further discusses the impact of introducing the Massive MIMO and various implementation scenarios, such as the metropolitan macro heterogeneous deployment scenario in the traditional 3GPP LTE, and the industrial, suburban and rural macro deployment scenarios in the typical ITUWireless R M.2135.

2.2. Organization

The organization of this paper is as follows. Section 1 discuss the introduction. Section 2 explores the existing literature and the scope of the work. Section 3 describes the system model for AAG for Multi-User Massive MIMO. Section 4 analyzes the simulation parameters and results of the proposed work. Section 5 proves the future scope and concludes this paper.

3. System Model and Problem Description

3.1. AAG-3M System Overview

ML coding in ST increased its diversity and the gain in coding, reduced the complexity of decoding, and increased the throughput even for a bigger group. MLSTTCs are conceived to combine ML coding with STTCs. The MLSTTCs increase bandwidth efficiency, enhance diversity and encode gain. Antenna grouping implemented in a multilevel multi-user trellis code in Massive MIMO (AAG-3M) offers a higher performance in data rate with much higher diversity gains or link quality.

The adaptive grouping of an antenna according to the CSI will give more weight to each grouping. At the receiving end, a multistage Viterbi decoder is used to increase the likelihood, as illustrated in Figure 1. The structure of AAG-3M is depicted in Figure 2. The device not only provides the diversity and coding gain, but also assorts the extended spectral enhancement if the particular approach is associated with Massive-MIMO. It can also eliminate radio spectrum shortage, retain control in situations of slower information rates, and avoid switching from higher quality channels. With better use of usable bandwidth, AAG-3M offers higher throughput.

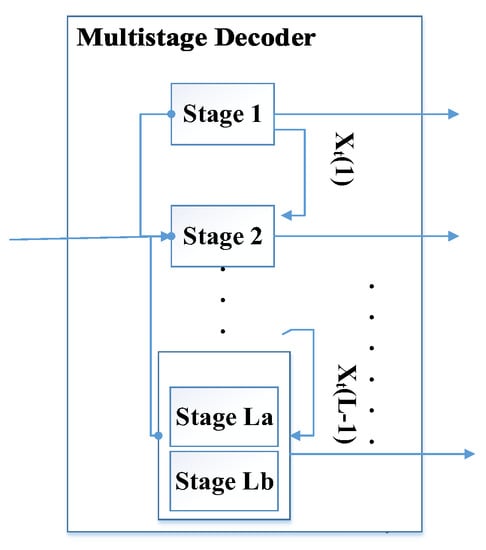
Figure 1. Multistage decoder.

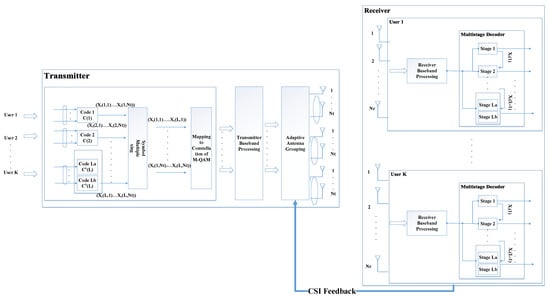
Figure 2. Proposed AAG in Multi-User Massive MIMO systems.

Implementing Massive-MIMO networks in real-world application scenarios is another significant feature of the proposed research plan. The resulting technology assessment must be sufficiently comprehensive. This is so the findings can be used to endorse policy changes based on the latest innovations for the better allocation of higher-throughput spectrum resources.

Encoding

The information bits are received from the transmitter and pass through individual STTC encoders of $\mathcal{L}$ levels. The STTC encoder performs the coding on the information bits. Level $1 to \mathcal{L}-1$ performs the full diversity operation and transmits it from all $N_t$ transmitting antenna.

The STTC encode $\mathcal{L}$ at level $\ell$ is expressed as:

$$\complement \left(l\right)=x_t{l}^1,x_t{l}^2,\dots \dots \dots x_t{l}^{N_t} where l=1,2,\dots \dots L-1$$

(1)

To increase the throughput, more than one data symbol has been used at a particular time slot by the combination of the antenna. In Figure 2, in this particular level, two STTC encoders ${\mathcal{L}}_a$ and ${\mathcal{L}}_b$ are used in parallel; at the same time, the antenna $N_t$ is divided into groups as the CSI (at the transmitter).

Let $N_t$; the transmitting antennas are divided into clusters according to the CSI. The grouping of an antenna may be different in number at each level. The transmitting antennas $N_t$ (at level L) are divided into two groups, and each group has an equivalent transmitting antenna i.e., $N_t/2$. The output for the encoder ${\mathcal{L}}_a$ is given by

$$\complement \left({\mathcal{L}}_a\right)=x_t{\left({\mathcal{L}}_a\right)}^1,x_t{\left({\mathcal{L}}_a\right)}^2,\dots \dots \dots x_t{\left({\mathcal{L}}_a\right)}^{N_t/2}$$

(2)

The encoder ${\mathcal{L}}_b$ uses the remaining antennas from $\left(\left(N_t/2\right)+1\right)$ to $N_t$ antennas, and the output is provided by:

$$\complement \left({\mathcal{L}}_b\right)=x_t{\left({\mathcal{L}}_b\right)}^{\left(\frac{N_t}{2}\right)+1},x_t{\left({\mathcal{L}}_b\right)}^{\left(\frac{N_t}{2}\right)+2},\dots \dots \dots x_t{\left({\mathcal{L}}_b\right)}^{N_t}$$

(3)

The output at level $\mathcal{L}$ is given as:

$$\begin{gathered} \complement \left(\mathcal{L}\right)=x_t{\left({\mathcal{L}}_a\right)}^1,x_t{\left({\mathcal{L}}_a\right)}^2,\dots x_t{\left({\mathcal{L}}_a\right)}^{\frac{N_t}{2}}, x_t{\left({\mathcal{L}}_b\right)}^{\left(\frac{N_t}{2}\right)+1}, \\ {x}_t{\left({\mathcal{L}}_b\right)}^{\left(\frac{N_t}{2}\right)+2},\dots x_t{\left({\mathcal{L}}_b\right)}^{N_t} \end{gathered}$$

(4)

For 4-QAM constellation output symbols, $x_t\left(1\right) to x_t\left(\mathcal{L}\right)$ are represented in complex form as:

$$x_t\left(l\right)=a+jb, a,b \in \left\{1,-1\right\}$$

(5)

Separately produced STTC is recycled as a constituent code in the MLC. The MLSTTC divides the base signal spectrum into the next hierarchical sequence of subsets. The data input is transmitted via L data sources, utilizing a serial-to-parallel converter, and the cluster has its subgroups. Multilevel coding delivers up to L resolution for the M-QAM scheme, with $M=4^L$. For $\mathcal{L}=2$ it is 16QAM (Figure 3).

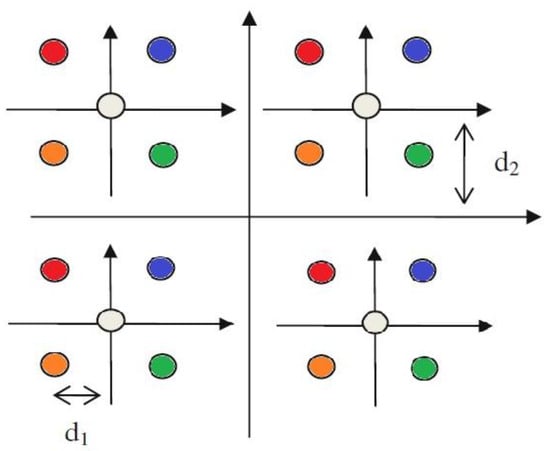
Figure 3. Partitioning of 16-QAM utilizing (N = 4)-way segments and 𝐿 = 2.

However, the array has been increased to make the constellation points for 64 QAM. This system should require three levels of encoding. It increases the complexity as it requires a minimum of four encoders at the transmitter, but it is manageable even for a bigger constellation; hence, it increases the throughput that is one of the required parameters for the QoS in the latest scenario. As the level of modulation increases to 128 QAM or even more as it provides higher throughput and spectral efficiency, at the same time, there are some limitations, i.e., the complexity and less resilience to the noise of higher-order modulation. For higher-order constellations, the distance between the constellation points becomes closer and more sensitive to noise, and the error rate is increased as compared to lower-order modulation. Therefore, the system requires a balance between the information error rates. The use of AAG in STTC creates the balance between error performance spectral efficiency and complexity. Using the AAG in STTC for 64 QAM or 128QAM, the error performance is comparable to STTC with reduced complexity.

The outputs of the level $L$, $\complement \left(1\right),\dots ..\complement \left(\mathcal{L}\right)$ are functional to the symbol converter to produce $M-QAM$ symbols. These $M-QAM$ symbols are designated by

$$\complement \left(1\right)=x_t{\left(1\right)}^1,x_t{\left(2\right)}^1,\dots \dots \dots x_t{\left({\mathcal{L}}_a\right)}^1$$

(6)

$$\complement \left(N\right)=x_t{\left(1\right)}^{N_t},x_t{\left(2\right)}^{N_t},\dots \dots \dots x_t{\left({\mathcal{L}}_b\right)}^{N_t}$$

(7)

The $N_t$-interpreted symbols are plotted to the $M-QAM$ signal constellations. The plotted signals use $N_t$ antennas to transmit. The time t is indicated as $Q_t^j$ and the symbol is transmitted by the jth transmitting antenna.

$$Q_t^j=d_{\left(1\right)}{x}_t{\left(1\right)}^j+d_{\left(2\right)}{x}_t{\left(2\right)}^j+\dots +d_{\left(\mathcal{L}\right)}{({\mathcal{L}}_{\left(a or b\right)})}^j$$

(8)

where $j=1,\dots \dots \dots ,N and d_{\left(1\right)},\dots \dots \dots d_{\left(\mathcal{L}\right)},$ the subsection is distanced equivalent to $x_t\left(1\right)\dots \dots \dots x_t\left(\mathcal{L}\right)$.

The algorithm for adaptive selection of antennas for grouping in described as algorithm 1 below.

Algorithm 1: Adaptive selection of antennas for grouping.

Step 1: Power gain calculation amongst ith transmitting antenna and all the received antennas j. ${\mathbb{P}}_i={\displaystyle \sum }_{j=1}^M{\left|h_{ij}^t\right|}^2$$1\le i\le N_t$ Step 2: Reorganize the random variables${\mathbb{P}}_i$ in to ascending order. $P_i\left(l\right), \mathrm{where} 1 \le \left(l\right)\le { N}_t \mathrm{and} P\left(1\right)\le P\left(2\right)\dots \dots . \le P\left(N_t\right).$ ‘l’ is the ordinal antenna number of the antenna correlated with P(l). The $P\left(N_t\right)$ associated transmitting antenna is considered the best antenna among $N_t$ antennas. Step 3: Selection of the first two antennas The dual antennas, known as r and s, are identified by $\left\{r,s\right\}=\mathrm{argmax}\left(\left\{{\mathbb{P}}_r+{\mathbb{P}}_s\right\}\right)$$1\le r,s\le N_t,r\ne s$ This implies the twin antennas are linked to each other. $\mathbb{P}\left(N\right) \mathrm{and} \mathbb{P}\left(N_t-1\right) \mathrm{are} \mathrm{selected}.$ Step 4: Selection of the rest of the antenna Similarly, pick the next two antennas, the transmitting antennas, from the group. This process continues until all the transmission antennas are clustered.

3.2. Decoding (ML)

At the receiving end, the received signal is the superposition of all $N_t$ transmitted signals. The received signal is very noisy in the Rayleigh fading version.

The received signal by the specific antenna ith at time t is written by

$$r_t^i={\displaystyle \sum }_{j=1}^M{h}_{ij}^t{Q}_t^j+n_t^i$$

(9)

$n_t^i$ shows the noise related to the received antenna $i$ at time $t$, and $h_{ij}^t$ is the channel established between the $j^{th}$ relay and the $i^{th}$ received antenna $1 \le j \le M, 1 \le i \le N_t$.

Substituting the Equation (8) in Equation (11)

$$r_t^i={\displaystyle \sum }_{\ell =1}^{\mathcal{L}}{\displaystyle \sum }_j^M{h}_{ij}^t{d}_{\ell }{x}_t{\left(\ell \right)}^j+n_t^i$$

(10)

The multistage Viterbi decoder is used at the receiving end, as shown in Figure 1. In step 1, the component code is decoded by the stage 1 decoder of the signal generated from encoder 1. Through the searching, the operation maximizes the probability function in the hypothesized values of ${\widehat{x}}_t\left(1\right)$. In the next decoding stage, the estimated values ${\widehat{x}}_t\left(1\right)$ are transmitted to decrypt the values of ${\widehat{x}}_t\left(\mathcal{L}-1\right)$ etc. In the final step, the decoder employs the estimates obtained from different levels, $1 to \left(\mathcal{L}-1\right)$ to obtain ${\widehat{x}}_t\left(\mathcal{L}\right)$.

For the purpose of analysis, by assuming four antennas and two groups:

Level-1 uses all $N_t$ antennas.

A single full diversity $ℂ\left(1\right)$ is generated.

Level-2 uses $N_t/2$ antennas:

$\complement \left({\mathcal{L}}_a\right)$ for antenna groups 1, and $\complement \left({\mathcal{L}}_b\right)$, for antennas group 2.

The antennas chosen for each group are calculated by:

$$\mathrm{Group} 1= \mathrm{antennas}\left\{r,s\right\}=\mathrm{argmax}\left(\left\{{\mathbb{P}}_r+{\mathbb{P}}_s\right\}\right)) 1\le r,s\le 4,r\ne s$$

(11)

$$\mathrm{Group} 2=\mathrm{antennas}\left\{u,v\right\}=\arg \left(\left\{{\mathbb{P}}_u+{\mathbb{P}}_v\right\}\right)) 1\le u,v\le 4,u\ne v, \mathrm{argmax}\left(\left\{{\mathbb{P}}_r+{\mathbb{P}}_s\right\}\right)>\arg \left(\left\{{\mathbb{P}}_u+{\mathbb{P}}_v\right\}\right)$$

(12)

The signal received at time $t$ from the $i^{th}$ received antenna is specified by

$$r_t^i={\displaystyle \sum }_{j=1}^N{h}_{ij}^t{d}_{x\left(1\right)}{x}_t\left(1,j\right)+{\displaystyle \sum }_{j=1}^N{h}_{i,j}{}^t{d}_{x\left(2\right)}{x}_t\left(2,j\right)+n_t^i$$

(13)

The encoder output probability density function with the channel matrix of $r_t$ is given by:

$$P\left(r_t|x_t\right)\left(1\right),x_t\left(2\right),H_t$$

(14)

In the first stage, aim to decode the $x_t\left(1\right)$. To find this, hypothesize the value of $x_t\left(1\right)$ using the Viterbi algorithm and the decoder of this stage to maximize the likelihood function over the hypothesized values of $x_t\left(1\right)$, since at this stage $x_t\left(2\right)$ is unknown. Hence, assume them as “nuisance” variables and average them out. The probability density function can be written as:

$$P\left(r_t|x_t\right)\left(1\right),H_t={\displaystyle {{\displaystyle \sum }}_{\begin{array}{c}{x}_{t\left(\ell \right)} \\ \ell =1,2 \end{array}}}P\left(x_t\left(2\right)|x_t(1\right),H_t)P\left(r_t|x_t(2\right),H_t)$$

(15)

By assuming that the encoder components $x_t\left(1\right)$ and $x_t\left(2\right)$ are strictly exclusive, the channel also has part codes. The transmitted probability is the same for different values of $x_t\left(1\right)$. The first right-hand side expression of the right-hand side $P\left(x_t\left(2\right)|x_t(1\right),H_t)$ of Equation (17) is treated as a constant. Now focusing only on the second term, the equation can now be written as:

$$P\left(r_t|x_t\right)\left(1\right),H_t=\frac{1}{\left(\sqrt{2\pi }{\sigma }_n^2\right)}exp[\frac{{\left|r_t^i-{{\displaystyle \sum }}_{jr.s}{h}_{ij}^t{d}_2{\tilde{x}}_t^a{\left(2\right)}^j-{{\displaystyle \sum }}_{ju.v}{h}_{ij}^t{d}_2{\tilde{x}}_t^b{\left(2\right)}^j-{{\displaystyle \sum }}_{j=1}^N{h}_{ij}^t{d}_1{x}_t{\left(1\right)}^j\right|}^2}{2{\sigma }_n^2}]$$

(16)

From Equations (17) and (18), ignoring the constant term, the likelihood function is in the form

$$\begin{gathered} \mathcal{L}(x_{t)}\left(1\right))=P\left(r_t|x_t\right)\left(1\right),H_t)\propto \\ exp[\frac{{\left|r_t^i-{{\displaystyle \sum }}_{jr.s}{h}_{ij}^t{d}_2{\tilde{x}}_t^a{\left(2\right)}^j-{{\displaystyle \sum }}_{ju.v}{h}_{ij}^t{d}_2{\tilde{x}}_t^b{\left(2\right)}^j-{{\displaystyle \sum }}_{j=1}^N{h}_{ij}^t{d}_1{x}_t{\left(1\right)}^j\right|}^2}{2{\sigma }_n^2}] \end{gathered}$$

(17)

Hence, at level 1, the branch metric for $ℂ\left(1\right)$ is specified by

$$\underset{\begin{array}{c}{\tilde{x}}_t^a\left(2\right)\in \left\{x_t^a\left(2\right)\right\},\\ {\tilde{x}}_t^b\left(2\right)\in \left\{x_t^b\left(2\right)\right\}\end{array}}{max}{\displaystyle \sum }_{i=1}^M{\left|r_t^i-{\displaystyle \sum }_{j=r,s}{h}_{ij}^t{d}_2{\tilde{x}}_t^a{\left(2\right)}^j-{\displaystyle \sum }_{j=r,s}{h}_{i,j}^t{d}_2{\tilde{x}}_t^b{\left(2\right)}^j-{\displaystyle \sum }_{j=r,s}{h}_{i,j}^t{d}_1{x}_t{\left(1\right)}^j\right|}^2$$

(18)

Two simultaneous Viterbi decoders are used in the second stage to decode both $\complement \left({\mathcal{L}}_a\right)$ (for the group 1 antenna) and $\complement \left({\mathcal{L}}_b\right)$ (for the group 2 antenna).

At level 2:

(for antenna group 1)

The subdivision metric for $\complement \left({\mathcal{L}}_a\right)$ is specified as:

$$\underset{{\tilde{x}}_t^b\left(2\right)\in \left\{x_t^b\left(2\right)\right\}}{max}{\displaystyle \sum }_{i=1}^{N_r}{\left|r_t^i-{\displaystyle \sum }_{j=r,s}{h}_{ij}^t{d}_2{x}_t^a{\left(2\right)}^j-{\displaystyle \sum }_{j=u,v}{h}_{ij}^t{d}_2{\tilde{x}}_t^b{\left(2\right)}^j-{\displaystyle \sum }_{j=1}^N{h}_{ij}^t{d}_1{\widehat{x}}_t{\left(1\right)}^j\right|}^2$$

(19)

(for antenna group 2)

The subdivision metric for $\complement \left({\mathcal{L}}_b\right)$ is specified as:

$$\underset{{\tilde{x}}_t^a\left(2\right)\in \left\{x_t^a\left(2\right)\right\}}{max}{\displaystyle \sum }_{i=1}^{N_r}{\left|r_t^i-{\displaystyle \sum }_{j=r,s}{h}_{ij}^t{d}_2{\tilde{x}}_t^a{\left(2\right)}^j-{\displaystyle \sum }_{j=u,v}{h}_{ij}^t{d}_2{x}_t^b{\left(2\right)}^j-{\displaystyle \sum }_{j=1}^N{h}_{ij}^t{d}_1{\widehat{x}}_t{\left(1\right)}^j\right|}^2$$

(20)

3.3. Massive MIMO with Perfect CSI (System Model)

By considering the Multi-User MIMO system in which the base station is equipped with $N_{mt}=L{N}_t$ transmitting antennas, the total number of receiving antennas at the receiver side is $N_{mr}=K{N}_r .$ At a particular time, BS transmits the signal to K independent multiple-antenna users, as shown in Figure 2, with $K{N}_{mr}\le N_{mt}$. AAG provides full spatial diversity and coding gain with higher throughput.

In AAG-3M channels with perfect CSI

$$\mathcal{H}=\left[\begin{array}{c}{\mathcal{H}}_1\\ {\mathcal{H}}_2\\ \begin{array}{c}⋮\\ {\mathcal{H}}_k\end{array}\end{array}\right]$$

(21)

where ${\mathcal{H}}_k\in {\complement }^{N_r\times L{N}_t}$, $k=1,2,\dots ,K$.

The precoding matrix is

$$\mathbb{Z}=\beta {\mathcal{H}}_k^H\left({\left.{\mathcal{H}}_k{\mathcal{H}}_k^H\right)}^{-1}\right.$$

(22)

where ${(.)}^H$ denotes the conjugate transposition, and $\beta$ is the normalized coefficient, defined as

$$\beta =\sqrt{\frac{L{N}_t}{tr\left[\left({\left.{\mathcal{H}}_k{\mathcal{H}}_k^H\right)}^{-1}\right.\right]}}$$

(23)

where tr[.] denotes the trace of a matrix.

Let $X\in {\complement }^{KL{N}_r\times T}$ represent the STTC matrix constructed in the base station transmitter for all users during 𝑇 time intervals. After transmitter precoding, the received transmitted matrix $\mathbb{N}\in {\complement }^{L{N}_r\times T}$ can be written as

$$\mathbb{N}=\mathbb{Z}X$$

(24)

where $\mathbb{Z}\in {\complement }^{L{N}_r\times KL{N}_r}$ is the precoding matrix expressed in the resulting matrix $\mathcal{Y}\in {\complement }^{K{N}_r\times T}$ and may be written as

$$\mathcal{Y}=\sqrt{\frac{E_x}{L{N}_T{N}_0}}\left(\mathcal{H}\odot \mathcal{D}\right)\mathbb{N}+\mathcal{W}$$

(25)

where $\mathbb{N}\in {\complement }^{L{N}_t\times T}$, and the codeword is the transmitted matrix;

$\mathcal{W}\in {\complement }^{K{N}_r\times T}$ is the noise matrix; $\mathcal{H}\in {\complement }^{K{N}_r\times L{N}_t}$ is the channel transfer matrix; and $\mathcal{D}\in {\complement }^{K{N}_r\times L{N}_t}$ is a matrix of random binary numbers representing the losses incurred during transmission, as indicated earlier. Figure 2 depicts AAG-3M.

Now, let $s_m^k$ denote the symbol to be transmitted for the kth user, and the character is pre-encoded in BSTx, so that data without fading are received at the $mth$ user antenna, $m=1,2,\dots \dots \dots N_r;$ then, the symbol obtained can be defined as

$$Y_k=\left\{\begin{array}{c}\beta s_i^k+w_i^k if i=m\\ v_i^k+w_i^k if i\ne m\end{array}\right.$$

(26)

where $w_i^k$ represents the Gaussian noise for the $k^{th}$ user at the $i^{th}$ receiving antenna, and $v_i^k={{\displaystyle \sum }}_n^{L{N}_t}{h}_k^{in}\widehat{s},i\ne m$ is the effect of fading of the channel and multiuser interference. For user 𝑘, the detection process of ML detection can be described as

$${\tilde{\mathbb{Z}}}_k^i=\mathrm{argmin}\Vert \frac{1}{\beta }{Y}_k-{\mathbb{Z}}_k^i{\Vert }_F^2$$

(27)

where ${\tilde{\mathbb{Z}}}_k^i$ is the k^th user’s estimated matrix at the antenna i^th.

Although the applied algorithm used precoding to eliminate interference, the lossy channel does not completely suppress interference. Therefore, MUI cannot eliminate whenever there are lossy links in the data transmission, and this should be considered a mass MIMO system. As the losses are introduced, this affects the precoding matrix expressed in (24). Consequently, the Euclidean distance determined by the formula (12) will be less, as compared with the lossless case, and the system performance will deteriorate. Introducing the effects of loss in (11), the adopted symbol can now be rewritten as

$$Y_k=\left\{\begin{array}{c}\beta s_k^i+w_k^i+z_k^i if i=m\\ {\displaystyle {\displaystyle \sum }_n^{L{N}_t}}{h}_k^{in}\widehat{s}+w_i^k if i\ne m\end{array}\right.$$

(28)

4. Simulation Parameters and Results

This section includes the simulation parameters used to implement the model castoff in this article. The block diagram offered in Figure 2 shows the scenario and model included in this article to evaluate the performance of STTCs techniques. The parameters used to realize the model used in this paper are shown in Table 3 [48].

Table 3. System Parameters for MIMO Application Context.

Parameter	Values
Channel-specific bandwidth	20 MHz
Sampling frequency	30.72 MS/s
FFT size	2048
Utilized subcarriers in number	1200
Blocks of resources	100
OFDM symbol count per slot	7
Length of CyclicPrefix (samples)	160 (first symbol) 144 (six following symbols)
$\mathrm{Frame} \mathrm{lifetime}$	$10 \mathrm{ms}$
$\mathrm{Subframe} \mathrm{lifetime}$	$1 \mathrm{ms}$
$\mathrm{Slot} \mathrm{lifetime}$	$0.5 \mathrm{ms}$
Cell radius	60 m (Indoor hotspot) 200 m (Ultra-Dense Urban) 500 m (Urban) 1299 m (Suburban) 1732 m (Rural)
Transmission bandwidth	40 × 106 (Indoor hotspot) 20 × 106 (Others)

The channel that was used to evaluate various STTCs techniques across multiple deployment scenarios is similar to the multi-path Rayleigh fading channel model, and the rural, suburban, and urban macro deployment scenarios in the typical ITU-R M.2135 [15]. Path-loss models have been optimized for various transmission scenarios in [51,52]. The selected bandwidth is 2–6 GHz, where the models/schemes will work, and for different antenna lengths. This proposed scheme will operate from 450 MHz to 6 GHz in rural areas. With convolution codes for point-to-point channels, the code design’s short block lengths display better results in light of its performance gap with Shannon-bound sphere packing (a fundamental performance assessment tool) and the proposed MLPSTTCC [16].

In a wireless situation, which has been compromised due to multi-path propagation, there is a need to enhance the link quality of the connections. To boost the consistency of the connections, various STCs techniques are implemented on the relay side in the Massive MIMO scenario [53,54]. We evaluate the output of various STCs techniques in terms of FER and SER in Rayleigh fading scenario multi-path propagation. From all the results shown in Figure 4, Figure 5, Figure 6 and Figure 7, it is clear that AAG with ML (AAG) performs better with Massive MIMO related to the other techniques, because it can provide a better benefit in coding, improve the efficiency of diversity, and, eventually, improve the spectral efficacy.

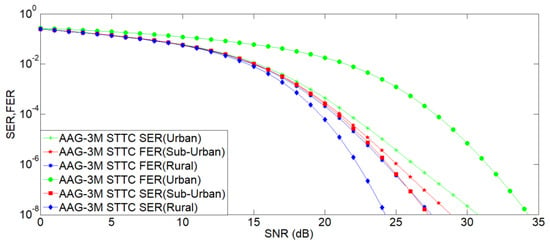
Figure 4. Comparison of urban, suburban, and rural deployment for AAG-3M STTC in terms of FER and SER.

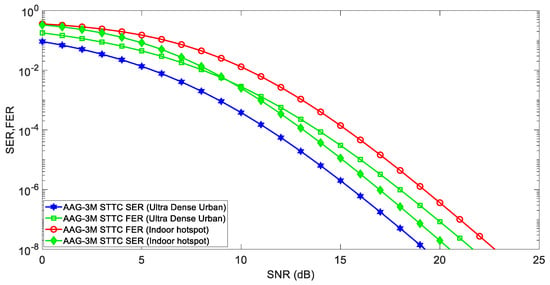
Figure 5. Comparison of Indoor hotspot and Ultra-Dense Urban deployment for AAG-3M STTC with Massive MIMO in terms of FER and SER.

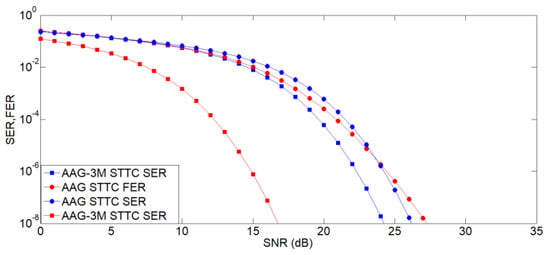
Figure 6. Comparison of AAG for urban Scenario with and without Massive MIMO in terms of SER and FER.

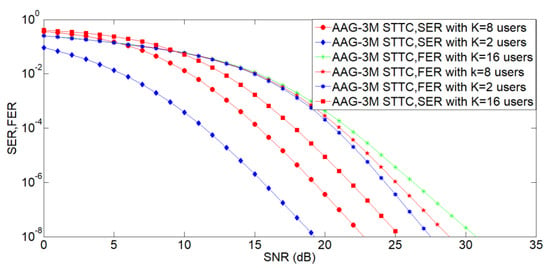
Figure 7. Comparison of AAG-3M with different number of users in terms of SER and FER.

The goal is achieved by grouping antennas and accomplishing more than one data symbol per time slot at certain levels by utilizing different STTCs for each category.

4.1. Comparison of Different Deployment Scenarios in AAG in Multilevel Massive MIMO (AAG-3M)

Multistage encoding is used; any number of receiving antennas can be used. AAG-3M uses ML encoding and partitioning of the antenna.

Different implementation scenarios of advanced operating environments IMT are used in this section. Such scenarios help to assess the channel coding effect and the signal intensity. The precision of channel models is a guideline for broadband networks to be found in the days ahead and is essential as RF transmission. Furthermore, it is important for multi-input multi-output systems where the radio channel can be used in some way to make it cheap and usable and to increase the bit rate.

Effect of Multipath Propagation Scenario

This paper considered three types of IMT-based scenarios: urban, suburban, and rural.

• For the urban deployment scenario

In the urban macro-cell incidence, diffraction possibilities exist; hence, the height of the BTS (Base Trans Receiver Station) is kept slightly higher than the heights of the surrounding workplaces. The BTS is usually located in the outer urban areas where the tablets shape a grid-type system or may have various locations at least five stories higher. Mostly homogeneous structures are created in these cases, keeping in mind the density of the area and the size of the buildings. In the urban scenario, the non-line of sight propagation and the base station are marginally above the surrounding building heights due to the diffraction above the roof. At street level, a mobile station is situated outside, while the building blocks are more chaotic, with a height of more than four stories. The height and density of the building in this scenario are largely homogeneous.

2.

For the sub-urban deployment scenario

For suburban settings, MS is deployed at street level for remote areas, while BTS is positioned at a higher point at the peak of the buildings to enhance coverage. Compared to the urban areas, the number of floors here is low; secondly, there is an additional number of grounds available for homes and workplaces far from one another; therefore, it is spacious. The pattern of streets is also unpredictable because they do not follow a grid pattern, and the lack of vegetation is also less.

3.

For rural deployment scenario (high-speed deployment scenario)

A macro cell would not be able to sustain a large velocity system because this would lead to impairments in transmission. Because of a wider coverage area, large-speed cars are assisted in this program, and thus, focus on wider cells. As there are fewer buildings and the length of BTS is high, LOS is achievable in rural areas.

As the SER and FER are developed, Figure 4 compares the outcomes for rural, urban, and sub-urban macro deployment scenarios in the ITU-R M.2135 standard for AAG-3M STTC in the Massive MIMO scenario. In comparison to urban and suburban settings, it has been shown that the mistake rate has decreased. Due to a larger service area, the rural model system supports high-speed vehicles. As a result, it concentrates on bigger cells. Additionally, LOS is feasible in rural places due to the lower density of buildings and the longer BTS. In suburban areas, MS is placed at street level, whereas BTS is maintained at a level higher, i.e., on rooftops, to provide better coverage. In comparison to metropolitan regions, the number of floors is modest; second, houses and offices are separated from one another. There are more grounds available; therefore, it is larger. As they do not follow a grid layout, street patterns are random, and foliage loss is lower than in metropolitan areas. In this model, building height and density are substantially higher than in suburban and rural areas, resulting in higher losses.

Further, the extremely demanding quest and energy applications that are anticipated for use of the 5G communications infrastructure will be made possible by the ultra-dense deployments of small cells running at mmWave frequencies, as well as a high user density, high user throughput indoor environment with separate office cells or hotspots for pedestrian or stationary users.

Since Massive MIMO is anticipated to play a significant role in delivering better data rates in future mmWave systems, a high user-density indoor environment with separate office cells or hotspots for pedestrian or stationary users is advised. The article compares the Indoor hotspot and Ultra-Dense Urban deployment for AAG-3M STTC with Massive MIMO in terms of FER and SER in Figure 5. In comparison to the Indoor hotspot, Ultra-Dense Urban deployment has better SER/FER. This is because of the multipath fading and interference between the different signals of the BS antennas.

4.2. Comparison of the Only AAG

Finally, the AAG scheme is implemented in contrast to the results for urban scenarios with and without Massive MIMO mode. It is clear from the findings shown in Figure 6. The Massive MIMO mode results better in all schemes, i.e., for SER and FER.

4.3. Comparison of AAG-3M with Different Numbers of Users

In this section, the paper analyzes the performance of AAG-3M with different numbers of users for (K = 2,8 and 16) with a fixed number of base station antennas ($L{N}_t$ = 64, as shown in Figure 7) in an urban scenario. The performance in terms of SER and FER degraded as the number of users increased because more signal power is required as the number of users increases.

4.4. Comparison of Spectral Efficiency AAG with and without Massive MIMO

This section analyses the effect of spectral efficiency in the urban scenario; as the number of antennas increases, so does the number of antenna groupings, hence, the spectral efficiency shown in Figure 8.

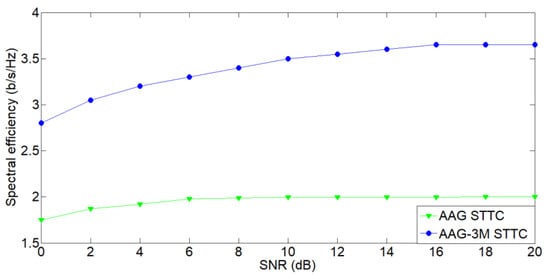
Figure 8. Comparison of spectral efficiency of AAG and AAG-3M STTC.

As the SNR is increased, the gain in spectral efficiency increases in each step, as shown in Table 4. Further, if we compare the SER performance of AAG-3M with Massive MIMO of Figure 8, the analysis shows that the SER performance also improves for the particular value of SNR.

Table 4. Spectral efficiency of AAG with and without Massive MIMO.

SNR (dB)	Spectral Efficiency (b/s/Hz) of AAG with Massive MIMO	Spectral Efficiency (b/s/Hz) of AAG without Massive MIMO	Diversity Gain
2	2.6	1.87	0.73
4	2.8	1.92	0.88
6	2.95	1.98	0.97
8	3.1	1.99	1.11
10	3.2	1.995	1.205
12	3.3	1.998	1.302
14	3.35	1.999	1.351
16	3.37	1.999	1.371
18	3.38	2.00	1.38
20	3.38	2.00	1.38

5. Challenges and Future Scope

The more advantageous option to offer variable data transfer speeds, coding gains, and gain in diversity with improved spectral efficiency and low decoding complexity, including the power optimization by reduced SNR at the same SER/FER, is Adaptive Antenna Grouping (AAG) with a multilevel space–time trellis coding scheme.

It has been observed that the certainty of network services will be strengthened beyond the 5G era to adapt to diverse scenarios of various sectors. Next-generation networks require the certainty of providing low latency and high reliability. This article attempts to address this specific difficulty. Challenges that need to be tackled in channel coding should be addressed after obtaining results from the proposed model and noticing patterns, which may assist other authors in future directions.

First, although Massive MIMO is implemented in AAG, it yields good experimental results in different scenarios regarding spectral efficiency. However, one of the major problems of the scarcity of available spectrum performance analysis can be solved by applying STTC-based code in Massive MIMO under cognitive radio scenarios.

Second, to solve other problems according to the latest technologies, AAG-3M may be applied in filter bank techniques to achieve better results.

The third and final aspect is to analyze and find the optimal hardware requirement for the implementation of the proposed codes.

Developing AAG-3M with Massive MIMO simultaneously provides diversity gain, spectral efficiency, and coding gain. QoS is the major aspect of today’s technology for a limited spectrum. If this particular scheme can be applied for cooperative spectrum sensing in the CR scenario, the CR can use cooperative spectrum sensing, increasing spectral efficiency. By combining Massive MIMO technologies used in the 5G network with CR, the throughput and link quality can further improve.