Abstract
The research community still faces challenges with respect to understanding and promoting mathematics teachers’ knowledge related to integrating technology into their instruction. This study’s goals are: (1) to examine the relations between the various components of pedagogical technology knowledge (PTK), (2) to examine whether teachers’ PTK differed significantly after their participation in a professional development (PD) program designed to enhance Community of Inquiry (CoI) practices, and (3) to examine the effect of teachers’ personal characteristics on PTK components and on their development. This study involved 42 middle school mathematics teachers. The data, collected using Thomas and Palmer’s PTK questionnaire, underwent a statistical analysis. Through the quantitative analysis, scores for each PTK component were computed and appropriate statistical tests were run. The results indicate that, aside from knowledge of mathematical content, all the components of PTK and PTK itself demonstrate strong correlations. In addition, the results showed that teachers’ PTK components differed significantly after they participated in a CoI PD program, except for the knowledge of mathematical content component. The background variables had significant effects on some PTK components’ scores and on their development among the participants.
Keywords:
teachers’ knowledge; technology integration; professional development; community of inquiry MSC:
97U50
1. Introduction
Technology integration in schools is quite limited and the potential of digital technologies in mathematics classrooms has been poorly utilized [1,2]. Earlier research concerning technology integration in the mathematics classroom was aimed at students’ mathematical learning processes and outcomes. It has become widely accepted, however, that changes in classroom practices have not been widespread as a result of teachers’ slow uptake of technology [3]. Many studies have suggested the “teacher barrier” as one of the main reasons for the failure to change classroom practices while integrating technology [4,5]. Therefore, it is crucial to understand how to advance, as part of PD programs, teachers’ knowledge and practices towards using technology in their teaching [4].
Moreover, in the last decade, researchers appear to have been paying attention to the need to analyze mathematics teachers’ knowledge related to incorporating digital technologies in the classroom [6,7,8]. The need to further research mathematics teachers’ degree of knowledge required for integrating technology in classroom practices is driven by the complexity of this knowledge, which in turn is the result of the need to construct a didactic situation that involves the organization of a large number of educational relationships—this requires a change in teachers’ thinking [9]. To accomplish such a change in thinking, teachers’ knowledge must develop. The Community of Inquiry (CoI) framework has been proposed for designing a PD program aiming at promoting mathematics teachers’ knowledge related to technology integration [9]. The present study seeks to examine teachers’ PTK and its development in the context of a CoI PD program by means of two core themes: (1) teachers’ knowledge and (2) PD program design. This paper is structured as follows: firstly, in Section 2, we examine the literature discussing the related themes in light of technology integration and present the research questions and goals. Then, in Section 3, we describe the adopted methodology; we then progress to presenting the results in Section 4; and finally, in Section 5, we conclude and discuss the results and attempt to interpret them.
2. Literature Review
2.1. Mathematics Teachers’ Knowledge
It has long been recognized that teachers’ knowledge is key to implementing change in classroom practices [10], which is why educational research has been focused on teachers’ knowledge, particularly in the last three decades [11]. The following is an overview of several attempts to identify frameworks for teachers’ knowledge, ordered as follows: frameworks for teachers’ knowledge, and frameworks for teachers’ knowledge connected to the affective domain.
2.1.1. Teachers’ Knowledge
One important professional knowledge framework was suggested by Shulman [12]. Shulman’s framework proposes that teaching knowledge is divided into seven domains. Within this framework, the pedagogical content knowledge (PCK) domain drastically changed researchers’ thinking, linking content and pedagogical knowledge bases (Figure 1).
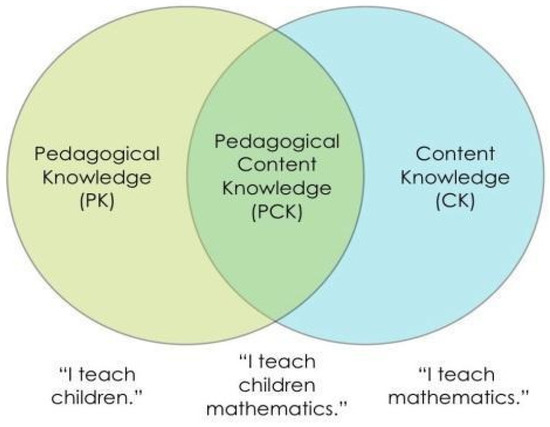
Figure 1.
Shulmans’ [12] domain of pedagogical content knowledge.
In particular, PCK continued to be developed by researchers. For example, Ball, Thames, and Phelps [13] observed that Shulman’s categorization was theoretical rather than empirical. This observation resulted in suggesting the Mathematics Knowledge for Teaching model (the MKT model), which was subdivided into six categories (Figure 2).
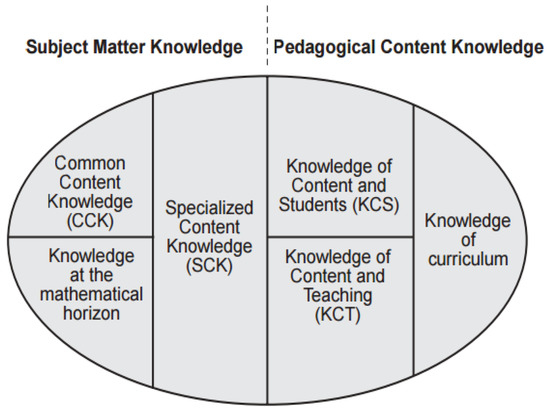
Figure 2.
The MKT model of Ball et al. [13].
Shulman’s PCK also influenced proposed theoretical frameworks for teachers’ knowledge with respect to integrating technology into the teaching practice in the classroom. One of these frameworks is the technological-pedagogical content knowledge (TPACK) framework. The TPACK framework defines the knowledge and skills needed for integrating technology in the classroom [14], though it is not specific to mathematics education. The TPACK model describes the interactions between the three main domains of teachers’ knowledge: content, pedagogy, and technology. New types of teachers’ knowledge resulted from these interactions, namely, pedagogical content knowledge (PCK), technological content knowledge (TCK), technological pedagogical knowledge (TPK), and, especially, TPACK (Figure 3).
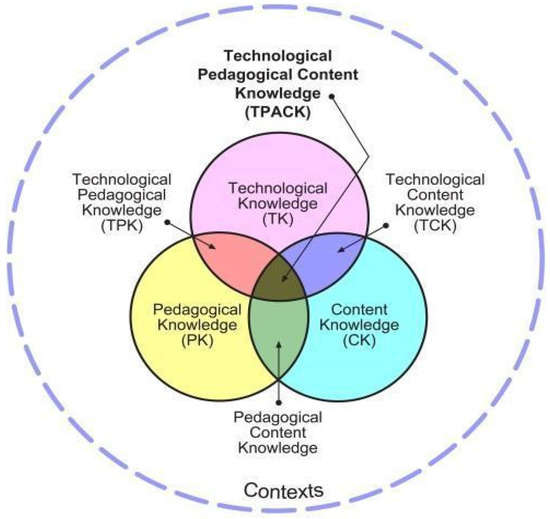
Figure 3.
The TPACK Model of Koehler and Mishra [14].
Thomas and Palmer [9] proposed a theoretical framework in parallel to TPACK to describe teachers’ knowledge with respect to integrating technology into mathematics classrooms—the PTK framework.
According to these researchers, PTK is a combination of several components (Figure 4): MKT, technology instrumental genesis, personal orientations. The MKT component involves knowledge of pedagogical and mathematical content. Technology instrumental genesis refers to teachers performing mathematics using technology, as well as their organization of technology-based learning conditions for their students, in particular, by designing appropriate tasks that exploit technology [15]. The personal orientations component influences teachers’ goal setting and decision making. It includes teachers’ beliefs, attitudes, values, preferences, etc. In the present research, we considered two measures of teachers’ personal orientation: teachers’ confidence in using technology and their perceived value of using technology. This consideration was due to Thomas and Palmer’s [9] argument that these two subcomponents are crucial to technology integration. The present study utilizes the PTK framework.
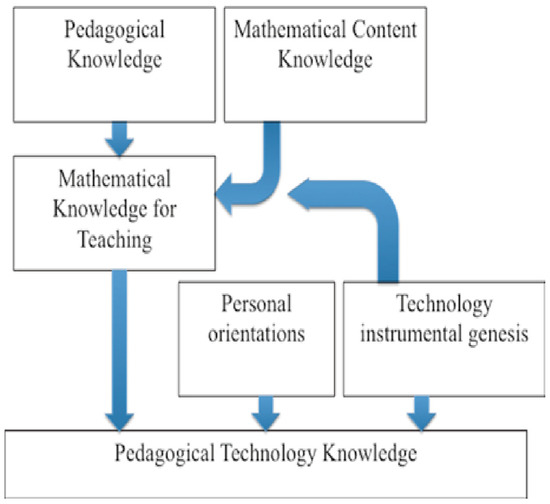
Figure 4.
The PTK framework proposed by Thomas and Palmer [9].
2.1.2. The Affective Domain of Teachers’ Knowledge
Researchers interested in the knowledge teachers require for teaching mathematics suggested that in addition to the cognitive knowledge of teaching, an examination of the affective domain of teaching is also needed (e.g., [16]). Schoenfeld [17] developed a theoretical framework to explain why teachers’ affective domain should be taken into account when considering teachers’ knowledge. Schoenfeld [17], within his framework, emphasized teachers’ orientations towards their teaching practice. Hence, the relations between teachers’ affective domain and their knowledge were examined by researchers (e.g., [18]). Thus, Ball’s et al. [13] framework was expanded by Beswick et al. [18] to include teachers’ confidence. Similarly, Barton [19] argued that mathematics teachers’ knowledge should include their attitudes and orientations toward mathematics, which he defined as the way teachers understand mathematics and how they relate to it.
Some researchers were concerned with the affective aspect in mathematics education in general, and others with mathematics teachers’ affective domain related to technology integration in teaching. Thus, researchers were interested in examining teachers’ orientations as a component of teachers’ knowledge, especially beliefs about technology’s value, the nature of learning mathematics, and teachers’ confidence in using technology [9]. Thomas and Palmer’s PTK framework, mentioned earlier, was developed based on Schoenfeld’s framework, which includes a teacher’s orientation as a main factor influencing teachers’ PTK (Figure 4). The present study utilizes this framework to achieve several goals: examining the relationship between the different components of PTK, assessing whether teachers’ PTK differed significantly after they participated in a CoI PD program, and examining the effect of teachers’ personal characteristics on PTK scores and on their development.
2.2. Professional Development of Mathematics Teachers
In Clark-Wilson et al.’s [3] view, “professional development” refers to how teachers acquire their professional identity and associated practices over time.
This section describes two aspects: (a) PD frameworks and (b) the characteristics and design of effective PD programs.
2.2.1. PD Frameworks
In the absence of a “big” theory for teachers’ PD [20], researchers have attempted to identify frameworks for the PD of mathematics teachers. For example, Schoenfeld [21] introduced a framework that included teachers’ knowledge, goals, and beliefs, focusing primarily on the individual teacher. Krainer [22] introduced a four-dimensional framework of teachers’ professional practice based on individual and the social aspects: action, reflection, autonomy, and networking. Llinares and Krainer [23] also emphasized both the individual and social aspects, pointing out that analyzing teachers’ professional development involves discussing the issue at the individual, social, and organizational levels. Another framework that considered social and organizational aspects is that of Clark-Wilson et al. [3], who identified five aspects related to mathematics teacher’s PD with respect to integrating technology: (a) the institutional context; (b) the PD programs’ design of mathematics teachers; (c) the PD activities of teachers with technologies, as part of formal PD programs or outside of them; (d) teachers’ use of technology in their classrooms; and (e) meta-level reflections by teachers and researchers on how digital technologies facilitate PD. The present PD program utilizes the CoI notion related to Wenger’s community of practice notion [24]. The notion of a CoI is related to the community whose participants work collaboratively on a joint enterprise to develop their knowledge by examining their practice with questioning attitudes [25]. Furthermore, Goodchild, Fuglestad, and Jaworski [26] argue that inquiry is about “asking questions and seeking answers, recognizing problems and seeking solutions, exploring and investigating to find out more about what we do that can help us do it better” (p. 396). Thus, a CoI is a community where the previous practices occur. In our case, the CoI consists of mathematics teachers whose practice is the preparation and implementation of mathematics lessons that integrate technology. By doing so, they engage in inquiry—in terms of Goodchild et al.’s framework [26]—about the preparation and implementation of technology-based mathematics lessons.
2.2.2. PD Program Characteristics and Designs
The research identified the characteristics of professional development programs that make these programs effective or ineffective. First, we review the characteristics of effective PD programs, then those of ineffective ones. Then, we refer to PD program designs.
Some characteristics of effective PD programs were described by Watson et al. [27] and by Rösken-Winter et al. [28]. These characteristics include a shared purpose; the evidence-based recognition of best practices; ownership by participants; connection to the school context; sustainment over time; the development of theoretical understandings and connections to practices that extend teachers’ knowledge; the balance of individual learning needs in a community of practice; the evaluation of student learning; a focus on improving participants’ competences; the active involvement of participants; switching between phases of attendance, self-study, and e-learning; and the continuous encouragement of participants to reflect on their conceptions, attitudes, and practices.
Highlighting the factors that hinder successful in-service teachers’ PD, previous research underscored the influence of a previous teaching style, teachers’ knowledge and beliefs, and systemic constraints [28].
The researchers identified two types of PD programs that affect teachers’ learning and development: those that are based on both content and process, and those that are only process-based (e.g., [29]). Mathematical and pedagogical knowledge, skills, and dispositions were originally promoted by programs that were based on both content and process (ibid.). An example of a process-only PD program design is the lesson study (LS) design. The LS design was developed in Japan. Through the LS design, teachers and their educators are encouraged to collaborate and share their knowledge and expertise. The LS design has an iterative nature, as illustrated in Figure 5.
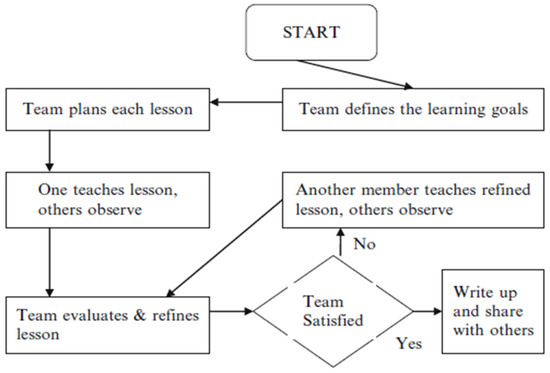
Figure 5.
LS cycle [30] (p. 568).
Jaworski [25] proposed a PD design based on inquiry that is parallel to the LS method and specifically geared for mathematics education. The inquiry takes place through an inquiry cycle of planning, acting, and observing; reflection and analysis; and feedback.
Referring to PD programs aiming to promote technology use by mathematics teachers, Thomas and Palmer [9] contended that teachers should engage in a PD practice where they become members in a supportive CoI. The CoI provides its members with opportunities to observe, practice, and reflect on their practices of integrating technology in the classroom. They suggested organizing small heterogeneous groups of teachers in which each teacher, in turn, presents a technology-based lesson. The community members discuss and reflect upon that technology-based lesson. In this way, the community takes advantage of those teachers who have a high level of PTK. The present study adopts this suggestion and implements the entire inquiry cycle.
Several studies have investigated the PD of mathematics teachers within a CoI. For example, Jaworski [25] described the central role of this inquiry with respect to sharing knowledge and expertise among teachers. In addition, she described the inquiry component as follows: “inquiry was evident in the planning process, in ways in which teachers took workshop ideas back to schools and tried out ideas in classrooms and in the developing relationships between the participants as activity progressed (p. 318)”.
The current study continues the line of investigation from these previous studies while considering mathematics teachers’ knowledge related to technology integration. The study adopts the suggestion of Thomas and Palmer [9] and uses the inquiry cycle to develop the PTK of mathematics teachers who work within a CoI [20]. In more detail, the participating mathematics teachers were expected to engage in discussing their teaching methods with the other teachers and reflecting on their practices. The participants were also expected to negotiate their practices and beliefs with other participants, which we expected would align these practices and beliefs according to the participants’ reflective practice and thereby affect the communal PTK knowledge.
2.3. Research Rationale, Design and Goals
Firstly, we begin this section by addressing the reasons that drove us to conduct the present study; then, we present the research design and goals.
In the last decade, researchers appear to have been paying attention to the need to analyze mathematics teachers’ knowledge with respect to incorporating digital technologies in the classroom. In addition, we have a limited understanding of how to advance—as part of PD programs—teachers’ knowledge towards using technology in their teaching [4]. Whereas previous research has pointed that the most prevalent inhibitory factor affecting teachers’ integration of technology is the lack of PD programs that may develop teachers’ knowledge related to technology integration [31,32]. On the other hand, researchers pointed out that teachers’ participation in professional communities that provide them with opportunities to reflect on their teaching scenarios and beliefs and promote designing tasks and lessons collaboratively, such as the CoIs, can enhance their integration of technology [33,34,35,36,37]. The previously mentioned factors affecting teachers’ implementation of technology were one reason for our initiative to invite middle school mathematics teachers to a PD program in which they were engaged as communities of inquiry (CoI). Thus, we wanted to examine, mainly, the effect of this PD program design on teachers’ pedagogical technology knowledge development, which was expected to influence their integration of technology in their classrooms. Our use of the CoI framework is consistent with Jaworski [20], who used it as a context for inquiry practices related to teaching and learning mathematics. We used the CoI framework to acknowledge that mathematics teachers are not homogenous; therefore, the design of PD cannot be based on a “one size fits all” method, especially when it considers promoting the use of dynamic technologies [3,36]. By adopting the CoI framework, we encouraged the participating teachers to engage in various roles (learner, teacher, and researcher) as part of the PD activities of the CoI [37]. Few PD programs have utilized the CoI framework as a context for teachers’ PD in conjunction with integrating technology in their classroom practices. At the same time, few studies have examined the effect of CoI practices on mathematics teachers’ PD with respect to integrating technology into their classroom practices. The present research attempts to fill this lacuna.
The participating teachers worked in groups based on the grade level they taught. The CoI encouraged collaborative practices of the teachers, especially planning the mathematics lessons, discussing how to integrate technology into their lessons and how to teach the lessons in the classrooms, and reflecting on their teaching, including on how to improve the lesson plans and their implementation. The design of the PD program was expected to be conducive to encouraging the participating teachers to integrate technology into their teaching of mathematics as well as develop their knowledge.
The present study’s goals are as follows: to examine the relationship between the different components of PTK, to assess whether teachers’ PTK differed significantly after they participated in a CoI PD program, and to examine the effect of teachers’ personal characteristics on PTK scores and on their development.
2.4. Research Questions
- Are there statistically significant relationships between the different components of PTK: pedagogical knowledge, knowledge of mathematical content, technology instrumental genesis, teachers’ confidence in using technology, and teachers’ beliefs about the value of technology; and PTK itself?
- Are there statistically significant differences in the PTK level according to seniority, technology-integration level, and employment status?
- Do teachers’ PTK scores differ significantly after they participate in a PD program based on a CoI framework?
- Do background variables (seniority, previous technology integration level, and employment status) affect changes in the PTK components from pre- to post-measurement among participants in the CoI PD program?
3. Research Methodology
3.1. Research Context and Participants
3.1.1. The Intervention: The PD Program
Funding for the PD program was provided by the Trump Fund and approved by the Israel Ministry of Education. It was conducted during the academic years 2017–2019. The PD program aimed to enhance the use of educational technology among middle school mathematics teachers. Warner, Bell, and Odom [38] defined educational technology as a collection of tools that enhance learning. Williams [39] (p. 3) presented a practical definition of educational technology: “educational technology is traditionally thought of as computers, video projectors, the internet, and other technologies that are placed in the classroom for the purpose of enhancing teaching and learning”. Here, technology use refers to the use of several devices, namely, the specific software that teachers and students use to advance the learning of mathematics. Within the scope of this study, the emphasis is on digital technologies.
The PD program was entirely process-based [29] on CoI processes [20,25]. Over the course of six months, the participants met for two academic hours once every two weeks (10 meetings). Participating teachers worked in two ways in the PD program: with the whole group and with smaller groups divided by the grade in which they did most of their teaching (seventh, eighth, or ninth). This division was intended to enable better collaborative work between the participants. Working in groups, teachers engaged in three inquiry cycles. Each inquiry cycle includes several processes, which are presented in Figure 6.
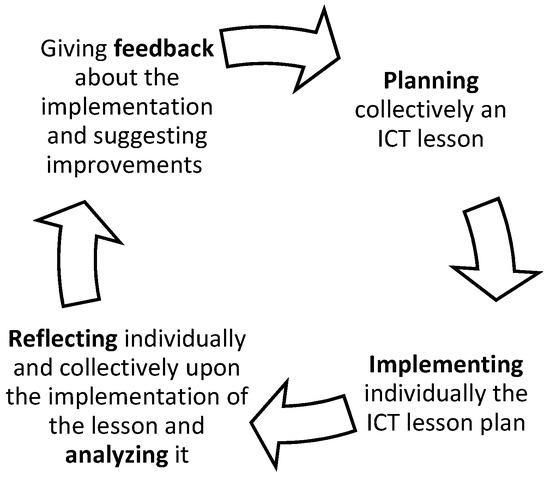
Figure 6.
The inquiry cycle processes.
During the PD sessions, the inquiry cycle processes were facilitated by participants videotaping their lessons and discussing them with the members of their groups. The participants had no prior experience working in a CoI PD program.
The researchers facilitated the PD program to ensure the achievement of the PD goals as adequately possible. Facilitating the PD was expected to help the researcher in discussing the research findings. The facilitator organized the PD program to ensure that the different groups engaged in three inquiry cycles (at least). She tried not to affect the lessons’ planning processes that occurred within the different groups. Thus, she tried not to influence the development of the groups regarding technology use, and to let each group development affected mainly by its members. So, generally speaking, the facilitator designed and organized the structure of the PD meetings, proposed tasks (a template for a lesson plan and templates for individual/collective reflections), kept discussions focused, problematized discussions, gave feedback, and guided the reflections of the teachers without expressing her point of view. The teachers were inquirers who plan, implement, explore, and analyze their teaching practices.
The above approach of the PD program was maintained according to the inquiry processes of the CoI. Teachers asked questions, conducted investigations, acquired information, and searched for knowledge [34]. To describe these processes, Jaworski [40] referred to Wells’ “dialogic inquiry”, that is, to the “willingness to wonder, to ask questions, and to seek to understand by collaborating with others in the attempt to make answers to them” [41] (p. 122).
3.1.2. The Participants
The participants included 42 mathematics middle school teachers who formed 12 teams from 12 schools in average socioeconomic areas in Israel. The participating teachers’ classrooms were equipped with at least a computer and a projector.
Twenty-three of the participants were enrolled in a course titled Technology in Mathematics Education as part of their M.A degree in teaching mathematics. The rest were enrolled in a PD program aimed at increasing the level of technology integration in their classroom practices. The participants differed in their seniority: ten of them had been teaching for 0–5 years, eleven had been teaching 6–10 years, eleven had been teaching 11–15 years, and ten had been teaching more than 15 years. Moreover, the participants differed in their previous level of technology integration: 8 reported a low level of technology integration, 17 a medium level, and 17 a high level. Moreover, nine of the participants were ICT coordinators.
3.2. Research Collecting Tools
We used a PTK questionnaire as the data collection instrument. The questionnaire was used both before and after the PD program. It consists of two parts. Personal information was collected in the first part, including seniority, employment status, and previous technology-integration level. The second part was composed of four scales: (1) personal orientation measuring two constructs—teacher’s beliefs regarding the value of technology (26 items) and teacher’s confidence in integrating technology in teaching mathematics (7 items); (2) pedagogical knowledge (10 items); (3) technology instrumental genesis (5 items); 4) knowledge of mathematical content (6 items). Some of the scales (personal orientations, pedagogical knowledge, and technology instrumental genesis) were borrowed from Thomas and Palmer [9], while the knowledge of mathematical content scale was developed by Hill, Schilling, and Ball [42]. Note that the scales by Thomas and Palmer were originally intended to examine teachers’ confidence in using graphing calculators. In the present study, the word “technology” is replaced “graphing calculators”. Responses were rated on a 5-point Likert scale, ranging from 1 (strongly disagree) to 5 (strongly agree). Since the scales had been translated, they underwent face validity testing. In addition, the reliability of each scale was analyzed by computing its Cronbach’s alpha based on the teachers’ scores on the PTK questionnaire. These computations yielded Cronbach alphas ranging between 0.71 and 0.82, which are considered acceptable reliability scores. Examples of items each subscale are presented below:
- An example of an item in teacher’s beliefs regarding technology’s value scale—“Mathematics students need to know how to use technology”.
- An example of an item in teachers’ confidence in using technology scale—“Learning how to use technological tools is difficult for me”.
- An example on an item on pedagogical knowledge scale—“Technology can be used as a tool to solve problems students could not solve without it”.
- An example of an item on technology instrumental genesis scale—“I usually know how to set up the technological tool to find answers I want”.
- An example on an item on knowledge of mathematical content scale—“Mrs. Yosef is looking through her textbook for problems and solution methods that use the distributive property as their primary justification. Which of these familiar situations can she use to demonstrate the distributive property of multiplication over addition [i.e., a (b + c) = ab + ac]? (Indicate Applies, Does not apply, or I’m not sure for each item) (Figure 7)”.
 Figure 7. An example on an item on knowledge of mathematical content scale.
Figure 7. An example on an item on knowledge of mathematical content scale.
3.3. Research Analysis Tools
In line with Thomas and Palmer [9], the scores for PTK components (knowledge of mathematical content, pedagogical knowledge, teachers’ beliefs about technology’s value, teachers’ confidence in using technology, and technology instrumental genesis) for each teacher before and after the PD program were computed as the average of the scores for the relevant items. The teachers’ confidence in using technology component was included in computing PTK level according to Thomas and Palmer recommendation. In addition, the PTK levels for each teacher before and after the PD program were computed as the average of the PTK components’ scores. PTK levels were classified into very low, low, normal, good, and very good, using Daher and Saifi’s [43] method.
Question 1 was answered using Pearson correlations and regressions analysis. Question 2 was answered using independent sample t-test and ANOVA. To answer Question 3, we used paired-samples t-test. Finally, for answering Question 4, two-way repeated measures ANOVA tests were used. To this end, two-way repeated measures ANOVAs were run with each of the background variables (seniority, previous technology-integration level, and employment status) as a between-subjects factor and the PD program intervention as a within-subjects factor. The PD program intervention was represented in SPSS by the time of the two values: 1 for pre-intervention measurements and 2 for post-intervention measurements. Next, for the interaction analysis we ran post-hoc tests in SPSS with Bonferroni corrections, using the code ‘EMMEANS = TABLES(A * B) compare(A) ADJ (Bonferroni)’. For example, in examining the interaction between PD program intervention and seniority, we used the code: ‘EMMEANS = TABLES (PD_time * seniority) compare (seniority) ADJ (Bonferroni)’.
4. Results
Below, we present the findings for the first, second, third, and fourth research questions.
4.1. Relations between PTK Scores
To assess the relationship between the PTK components (pedagogical knowledge, knowledge of mathematical content, teachers’ confidence in using technology, teachers’ beliefs about the value of technology, and technology instrumental genesis) and PTK itself, a Pearson product–moment correlation coefficient was computed. There was a positive correlation between all the components except the knowledge of mathematical content component, which was related only with PTK (see Figure 8). Note that the r value indicates a weak correlation when its value is 0.3–0.5, a moderate correlation when its value is 0.5–0.7, and a strong correlation when its value is more than 0.7.
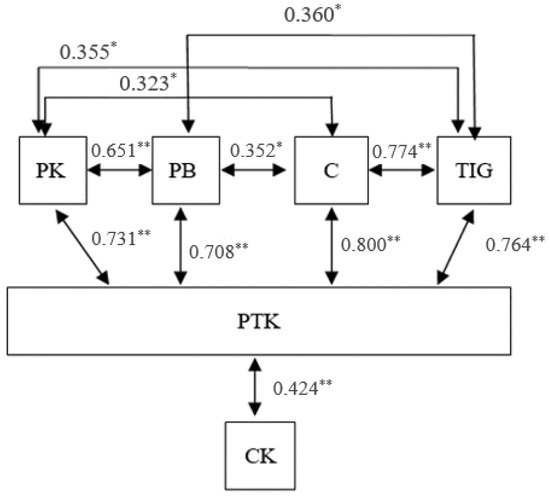
Figure 8.
Correlation between the PTK components and PTK itself. PK—Pedagogical Knowledge; PB—Personal Beliefs about the Value of Technology; C—Teachers’ Confidence in using Technology; TIG—Technology Instrumental Genesis; PTK—Pedagogical Technology Knowledge; CK—Knowledge of mathematical content. * p < 0.05; ** p < 0.01.
The Pearson’s correlation showed strong positive correlations between the PTK as a construct and the different components of PTK, except for the knowledge of mathematical content component, where a moderate positive correlation was found between said component and PTK. It also showed weak to moderate correlations between the different components of PTK except for teachers’ confidence in using technology and technology instrumental genesis, which had a strong positive correlation.
By using a multiple linear regression analysis, we developed a model for predicting teachers’ PTK from their pedagogical knowledge, personal beliefs about technology’s value, confidence in using technology, technology instrumental genesis, and knowledge of mathematical content. Table 1 shows basic descriptive statistics and regression coefficients. As in the last column, the predictor variables all had a significant (p < 0.01) partial effects on PTK. The Standardized Coefficients Beta Column shows that technology instrumental genesis and teachers’ confidence in using technology had the strongest effect on PTK. The values appear in T column shows that, for the most part, these results did not occur by chance.

Table 1.
Values of Beta appropriate for predicting teachers’ PTK from its components.
4.2. The Effect of Teachers’ Personal Characteristics on Their PTK Components’ Scores
Firstly, for each of the participating teachers we computed his\her initial level of PTK. The mean of the group was 3.8 (0.37). Characterizing their level of PTK (following Daher and Saifi [35]) indicated that six teachers had normal PTK levels, thirty had good PTK levels, and six had very good PTK levels.
The effect of employment status on the PTK level and on its components was examined using a t-test. The results show that the scores for the different components of PTK did not differ significantly. In addition, the differences between PTK and its components’ scores according to seniority were examined using ANOVA. The results show a significant effect of seniority on the PTK level [F(3,38) = 5.281, p = 0.004]. A post hoc analysis using Scheffe’s test showed that the PTK of teachers whose seniority was less than ten years was significantly more than that of teachers whose seniority was more than 15 years. The ANOVA results also showed a significant effect of seniority on teachers’ confidence in using technology [F(3,38) = 12.84, p < 0.000]. The post hoc analysis using Scheffe’s method showed that the confidence of teachers whose seniority was more than 15 years is significantly more than the rest of the teachers. Moreover, a significant effect was found for seniority with respect to technology instrumental genesis [F(3,38) = 5.423, p = 0.003]. Here, Scheffe’s test showed that the participants whose seniority was between 5–10 years had a significantly higher score on technology instrumental genesis than the participants whose seniority was more than 15 years.
The differences between PTK and its components’ scores according to the technology-integration level (low, medium, and high levels) were examined using ANOVA. The results showed that the technology-integration level had a significant effect of on PTK the level [F(2,39) = 4.463, p = 0.018]. Post hoc analysis using Scheffe’s method showed that the PTK of teachers whose technology-integration level was high was significantly greater than the teachers whose technology-integration level was low. The ANOVA results also showed a significant effect of the technology-integration level on the teachers’ confidence in using technology [F(2,39) = 8.101, p =0.001]. The post hoc analysis using Scheffe’s method showed that the confidence in using technology of teachers whose technology-integration level was low was significantly less than the rest of the teachers. Moreover, a significant effect was found for technology-integration level in relation to technology instrumental genesis [F(2,39) = 6.958, p = 0.003]. Here, Scheffe’s method showed that the participants whose technology-integration level was high had a significantly higher score on technology instrumental genesis than the rest of the participants.
4.3. The Effect of Teachers’ Participation in a PD Program Based on CoI on Their PTK Level
A paired-samples t-test was conducted to compare the teachers’ PTK levels and PTK’s components before and after their participation in a PD program. Table 2 shows the means, standard deviations, and standard error means for the PTK components of the participating teachers before and after the PD program. Table 2 indicates that the mean scores of the participating teachers after the PD program were higher than those before the PD program for all PTK components. To discover whether these differences were significant, a paired-samples t-test was conducted. The results are shown in Table 3, indicating that the PD program yielded significantly higher means on all the components of the participating teachers’ PTK, except for the knowledge of mathematical content score.

Table 2.
Means, standard deviations, and standard error means for participating teachers’ knowledge components (N = 42).

Table 3.
Paired-samples t-test between participants’ scores before and after PD program.
4.4. Effect of Teachers’ Personal Caracteristics on PTK Components’ Development
Each PTK component that exhibited different levels of the background variables (seniority, previous technology-integration level, and employment status) was measured before and after the PD program. Two-way repeated measures ANOVAs were run with each of the background variables as a between-subjects factor and the PD program intervention as a within-subjects factor.
The interaction between the PD program intervention and the ‘employment status’ background variable did not yield significant results for any of the different PTK component scores (confidence: F(1,39) = 0.86, p = 0.36; pedagogic knowledge: F(1,39) = 0.86, p = 0.36; technology instrumental genesis: F(1,39) = 0.77, p = 0.39, beliefs about the value of technology: F(1,39) = 0.84, p = 0.31). The significant interactions between the PD program intervention and the other background variables are reported below.
4.4.1. Effect of Seniority on PTK Components’ Development
The results of a two-way repeated measures ANOVA revealed a statistically significant effect of seniority on teachers’ confidence (F(1,39) = 10.11, p < 0.01). Before the PD program, the confidence of teachers with a level of seniority of ten years or less was significantly higher than that of teachers with a seniority level of more than ten years (mean difference = 0.91, p < 0.001). This mean difference decreased significantly after the PD program (mean difference = 0.48, p < 0.001).
In addition, the analysis revealed that the interaction between the PD program intervention and seniority had a significant effect on pedagogical knowledge (F(1,39) = 4.23, p < 0.05). Before the PD program, the pedagogical knowledge of teachers with more than ten years of seniority was significantly higher than that of teachers with ten years or less of seniority (mean difference = 0.33, p < 0.05). After the PD program, the participants’ pedagogical knowledge did not differ significantly (mean difference = 0.11, p = 0.33).
Moreover, the analysis revealed that the interaction between the PD program intervention and seniority had a significant effect on teachers’ instrumental genesis (F(1,39) = 9.04, p < 0.01). Before the PD program, the instrumental genesis of teachers with ten years or less of seniority was significantly higher than that of teachers with more than ten years of seniority (mean difference = 0.80, p < 0.001). After the PD program, the mean difference still showed a higher level of instrumental genesis among the teachers with ten years or less of seniority, but the difference had become lower and not significant (mean difference = 0.32, p = 0.09).
4.4.2. Effect of Previous Technology Integration Level on PTK Components’ Development
The two-way repeated measures ANOVA analysis revealed that the interaction between the PD program and previous technology-integration level (F(2,38) = 3.47, p < 0.05) had a significant effect on teachers’ confidence in using technology. Before the PD program, the confidence in using technology of teachers with a high level of previous technology integration was significantly higher than among those with a low technology-integration level (mean difference = 0.91, p < 0.05), and significantly higher than among teachers whose previous use was at an intermediate level (mean difference = 0.63, p < 0.05). After the PD program, the confidence in using technology for the teachers with a high technology-integration level and for those with a low technology-integration level did not differ significantly (mean difference = 0.42, p = 0.18).
In addition, the analysis revealed that the interaction between the previous technology-integration level and the PD program intervention (F(2,38) = 4.64, p < 0.05) had a significant impact on pedagogic knowledge. Before the PD program, teachers with a high level of technology integration exhibited significantly higher pedagogic knowledge than teachers with an intermediate level of previous technology integration (mean difference = 0.45, p < 0.05) as well as a higher pedagogic knowledge than teachers with a low level of technology integration, though the difference was not significant (mean difference = 0.02, p = 1.00). After the PD program, the teachers with a high previous technology integration level still showed an advantage in pedagogic knowledge over those with a low level (mean difference = 0.04, p = 1.00) and those with an intermediate level of technology-integration (mean difference = 0.08, p = 1.0), but this difference became lower and not significant.
5. Discussion and Conclusions
The present study aims to examine, among other things, the relationship between the components of PTK. The statistics revealed that PTK’s components and PTK itself had strong correlations, except for the knowledge of mathematical content, which had a moderate correlation with PTK. So, the PTK framework proposed by Thomas and Palmer [9] is emphasized here. These results agree with those of Roig-Vila et al. [44] who reported a non-strong correlations between the knowledge of mathematical content and teachers’ knowledge for integrating technology. In Roig-Vila et al. [44] study, the TPACK framework was utilized. In terms of correlations between the PTK components, the results showed mostly weak to moderate correlations between the different components of PTK, except for the knowledge of mathematical content, which had no correlation with the other PTK components. According to these results, it seems that the different components of the PTK framework are correlated. A more extensive study is needed to verify this interesting finding.
Additionally, this study examined the effect of the background variables—seniority, employment status, and technological-integration level—on the PTK scores. Significant differences in PTK, teachers’ confidence in using technology, and technology instrumental genesis were found, where these differences are related to seniority and technology-integration level. On the other hand, according to Pearson’s correlations these two components exhibited strong positive correlations. It could be argued that these PTK components are flexible, which means that education or experience related to ICT integration can influence them. In addition, the effect of seniority on teacher’s knowledge related to technology integration was also reported by other researchers, such as Saltan and Arslan [45] and Roig-Vila et al. [44]. This reveals the lack of PTK in teachers with the highest seniority.
The third goal of the current study was to assess whether teachers’ PTK changed significantly after they participated in a CoI PD program. The statistical analysis showed significantly higher means for PTK and all of its components after participation in the PD program, except for the knowledge of mathematical content component. These results support the suggestion of Thomas and Palmer [9] regarding the designing of a CoI PD program to develop teachers’ PTK. These results seem to indicate that most PTK components can be influenced by experience related to technology integration, an interesting finding that needs to be verified through more extensive research. These results are in line with those of Baya’a et al. [46], who examined teachers’ TPACK development as a result of a preparation program. Baya’a et al. [46] reported a significant improvement in the TPACK level.
The insignificant change in the participants’ CK scores may be explained by the initial high scores of the participating teachers in this component (M = 4.05, SD = 0.43). Moreover, the non-significant difference in the CK scores may be explained by the teachers’ goals and practices during the PD program. Through their participation in the CoI PD program, the teachers aimed to optimize their practices with technology, and they accomplished this goal using limited mathematical topics (three topics in three lessons), which did not significantly influence their knowledge of the mathematical content. It is notable that the insignificant change in the mean CK score did not influence the development of the other PTK components. This phenomenon may be related to the correlations between the different components of PTK, where weak to moderate correlations between CK and teachers’ knowledge with respect to integrating technology were found.
The fourth goal of this study examined whether background variables affected the development of PTK components among the participants in a CoI PD program. The results for seniority showed that the scores of teachers’ confidence in using technology and technology instrumental genesis increased significantly for the teachers with more than ten years of experience than teachers with a seniority of ten years or less. On the other hand, the scores of the pedagogical knowledge component increased significantly for the teachers with less than ten years’ experience than in those with more than ten years’ experience. The inquiry processes that the participants carried out in the course of the PD program appears to have enabled them to share knowledge between themselves, in accordance with Jaworski’s findings [25], who argued that inquiry is central in sharing knowledge and critical for building new knowledge within a community. Moreover, the teachers’ confidence in using technology may have developed as a result of the support in technology integration that those with less seniority provided to their more experienced colleagues [47]. Recent studies reported that more senior teachers had lower scores in technological knowledge components but higher scores in pedagogical knowledge components than the less senior teachers [48,49].
Moreover, we found no significant effect of seniority on teachers’ beliefs about technology’s value. This shows that all the participating teachers increased their “beliefs about technology’s value” at a similar rate. As a result of participating in the CoI PD program, both seniority groups became more aware of the value of technology. The increase in the belief scores is consistent with the findings of studies indicating that beliefs are subject to modification (e.g., [50]), showing a strong association between stronger beliefs and the more frequent and effective use of technology [51]. The participating teachers’ practices with technology appear to have resulted in meaningful learning outcomes, which increased their beliefs about the value of technology [52].
The results also showed that fewer and more senior teachers had close initial scores with respect to “beliefs about the value of technology,” which explains why both groups developed similarly. The same level of development of fewer and more senior teachers supports Perrotta’s [53] finding that teachers’ perceptions of technology’s benefits are more influenced by institutional factors than by individual characteristics.
The results for the background variable of ‘previous technology-integration level’ showed that teachers with a low level of previous technology-integration showed a significant increase in their confidence in using technology as well as in their pedagogical knowledge regarding technology integration. It appears that conforming to the inquiry cycle can support teachers in their pedagogy, especially those with a low PTK. This support is provided by the sharing of the technological knowledge among the CoI members [25].
The results showed that PTK components and their development are significantly affected by seniority and previous technology integration levels. These results are consistent with previous studies that suggested that these background variables play key roles in teachers’ knowledge and in knowledge development [54].
The present study examined the influence of the employment status background variable on teachers’ knowledge development as a consequence of participating in the CoI program. Scarce research has been conducted that studys the effect of employment status on technology integration [55]. We found no significant effect for this background variable on the development of the participating teachers’ knowledge. This may be related to what was found in Lavicza’s [56] investigation, where mathematics teachers’ personal characteristics affected their use of technology. These findings show that their computer proficiency, which may be related to the employment status variable, did not interact with the teachers’ use of technology.
Finally, according to the results of the current study, we argue that PTK development occurred by taking advantage of the high degree of PTK among teachers whose participation is valuable to the community [9].
Author Contributions
Conceptualization, M.T.; Data curation, A.A.; Formal analysis, A.A.; Funding acquisition, M.T.; Methodology, M.T. and A.A.; Project administration, M.T.; Supervision, M.T.; Validation, M.T.; Writing—original draft, A.A.; Writing—review & editing, M.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Trump Fund.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tabach, M. Competencies for Teaching Mathematics in the Digital Era: Are We Ready to Characterize Them? In Proceedings of the 44th Conference of the International Group for the Psychology of Mathematics Education, Khon Kaen, Thailand, 19–22 July 2021; pp. 32–47. [Google Scholar]
- Haspekian, M. Teachers’ Instrumental Genesis when Integrating Spreadsheet Software. In The Mathematics Teacher in the Digital Era; Clark Wilson, A., Robutti, O., Sinclair, N., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 241–275. [Google Scholar]
- Clark-Wilson, A.; Robutti, O.; Sinclair, N. The Mathematics Teacher in the Digital Era: An International Perspective on Technology Focused Professional Development; Springer: Dordrecht, The Netherlands, 2014; Volume 2. [Google Scholar]
- Hegedus, S.; Laborde, C.; Brady, C.; Dalton, S.; Siller, H.-S.; Tabach, M.; Trgalova, J.; Moreno-Armella, L. Uses of Technology in Upper Secondary Mathematics Education; Gabriele, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Ruthven, K. Teachers, Technologies and the Structures of Schooling. In Proceedings of the Fifth Congress of the European Society for Research in Mathematics Education, Larnaca, Cyprus, 22–26 February 2007; pp. 52–67. [Google Scholar]
- Bozkurt, G.; Ruthven, K. The activity structure of technology-based mathematics lessons: A case study of three teachers in English secondary schools. Res. Math. Educ. 2018, 20, 254–272. [Google Scholar] [CrossRef]
- Bozkurt, G.; Uygan, C. Lesson hiccups during the development of teaching schemes: A novice technology-using mathematics teacher’s professional instrumental genesis of dynamic geometry. ZDM 2020, 52, 1349–1363. [Google Scholar] [CrossRef]
- Chorney, S. Classroom practice and craft knowledge in teaching mathematics using Desmos: Challenges and strategies. Int. J. Math. Educ. Sci. Technol. 2021, 1–25.–25. [Google Scholar] [CrossRef]
- Thomas, M.O.J.; Palmer, J.M. Teaching with Digital Technology: Obstacles and Opportunities. In The Mathematics Teacher in the Digital Era. An International Perspective on Technology Focused Professional Development; Clark-Wilson, A., Robutti, O., Sinclair, N., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 71–89. [Google Scholar]
- Fennema, E.; Franke, M.L. Teachers’ Knowledge and Its Impact. In Handbook of Research on Mathematics Teaching and Learning; Grouws, D.A., Ed.; Macmillan: New York, NY, USA, 1992; pp. 147–164. [Google Scholar]
- Jaworski, B. Research practice into/influencing mathematics teaching and learning development: Towards a theoretical framework based on co-learning partnerships. Educ. Stud. Math. 2003, 54, 249–282. [Google Scholar] [CrossRef]
- Shulman, L. Knowledge and teaching: Foundations of the new reform. Harv. Educ. Rev. 1987, 56, 1–22. [Google Scholar] [CrossRef]
- Ball, D.L.; Thames, M.; Phelps, G. Content knowledge for teaching: What makes it special? J. Teach. Educ. 2008, 59, 389–407. [Google Scholar] [CrossRef]
- Koehler, M.J.; Mishra, P.; Yahya, K. Tracing the development of teacher knowledge in a design seminar: Integrating content, pedagogy and technology. Comput. Educ. 2007, 49, 740–762. [Google Scholar] [CrossRef]
- Haspekian, M. Computer Science in Mathematics’ New Curricula at Primary School: New Tools, New Teaching Practices? In Proceedings of the 13th International Conference on Technology in Mathematics Teaching, Lyon, France, 3–6 July 2017; pp. 23–31. [Google Scholar]
- Tatto, M.T.; Schwille, J.; Senk, S.; Ingvarson, L.; Peck, R.; Rowley, G. Teacher Education and Development Study in Mathematics (TEDS-M): Conceptual Framework; College of Education, Michigan State University: East Lansing, MI, USA, 2008. [Google Scholar]
- Schoenfeld, A.H. How We Think: A Theory of Goal-Oriented Decision Making and Its Educational Applications; Routledge: New York, NY, USA, 2010. [Google Scholar]
- Beswick, K.; Callingham, R.; Watson, J. The nature and development of middle school mathematics teachers’ knowledge. J. Math. Teach. Educ. 2011, 15, 131–157. [Google Scholar] [CrossRef]
- Barton, B. Being Mathematical, Holding Mathematics: Further Steps in Mathematical Knowledge for Teaching. In Proceedings of the 32nd Annual Conference of the Mathematics Education Research Group of Australasia, Wellington, New Zealand, 5–9 July 2009; pp. 4–10. [Google Scholar]
- Jaworski, B. Theory and practice in mathematics teaching development: Critical inquiry as a mode of learning in teaching. J. Math. Teach. Educ. 2006, 9, 187–211. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. Toward a theory of teaching-in-context. Issues Educ. 1998, 4, 1–94. [Google Scholar] [CrossRef]
- Krainer, K. Investigation into Practice as a Powerful Means of Promoting (Student) Teachers’ Professional Growth. In Proceedings of the Second Conference of the European Society for Research in Mathematics Education, Charles University, Prague, Czech Republic, 24–27 February 2001; pp. 281–291. [Google Scholar]
- Llinares, S.; Krainer, K. Professional Aspects of Teaching Mathematics. In Handbook of Research on the Psychology of Mathematics Education. Past, Present and Future; Gutiérrez, A., Boero, P., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2006; pp. 429–459. [Google Scholar]
- Wenger, E. Communities of Practice: Learning, Meaning and Identity; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Jaworski, B. Building and Sustaining Enquiry Communities in Mathematics Teaching Development: Teachers and Didacticians in Collaboration. In Participants in Mathematics Teacher Education: Individuals, Teams, Communities and Networks; Krainer, K., Wood, T., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2008; pp. 309–330. [Google Scholar]
- Goodchild, S.; Fuglestad, A.B.; Jaworski, B. Critical alignment in inquiry-based practice in developing mathematics teaching. Educ. Stud. Math. 2013, 84, 393–412. [Google Scholar] [CrossRef]
- Watson, J.M.; Beswick, K.; Brown, N. Educational Research and Professional Learning in Changing Times: The MARBLE Experience; Sense Publisher: Rotterdam, The Netherlands, 2012. [Google Scholar]
- Rösken-Winter, B.; Schüler, S.; Stahnke, R.; Blömeke, S. Effective CPD on a large scale: Examining the development of multipliers. ZDM 2015, 47, 13–25. [Google Scholar] [CrossRef]
- Simon, M. The Challenge of Mathematics Teacher Education in an Era of Mathematics Education Reform. In The International Handbook of Mathematics Teacher Education; Wood, T., Jaworski, B., Krainer, K., Tirosh, D., Sullivan, P., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2008; pp. 17–30. [Google Scholar]
- White, A.L.; Lim, C.S. Lesson Study in a Global World. In Meeting the Challenges of Developing Quality Mathematics Education: Proceedings of the Fourth East Asia Regional Conference on Mathematics Education; University Sains Malaysia: Penang, Malaysia, 2007; pp. 567–573. [Google Scholar]
- Thomas, M.O.J.; Chinnappan, M. Teaching and Learning with Technology: Realising the Potential. In Research in Mathematics Education in Australasia 2004–2007; Forgasz, H., Barkatsas, A., Bishop, A., Clarke, B., Keast, S., Seah, W.-T.P., Sullivan, P., Eds.; Sense Publishers: Sydney, Australia, 2008; pp. 167–194. [Google Scholar]
- Forgasz, H. Factors that encourage and inhibit computer use for secondary mathematics teaching. J. Comput. Math. Sci. Teach. 2006, 25, 77–93. [Google Scholar]
- Lauer, P.A.; Christopher, D.E.; Firpo-Triplett, R.; Buchting, F. The impact of short-term professional development on participant outcomes: A review of the literature. Prof. Dev. Educ. 2013, 40, 207–227. [Google Scholar] [CrossRef]
- Thurm, D.; Barzel, B. Micro-Teaching of Landmark Jobs—Fostering Self-Efficacy for Teaching Mathematics with Technology. In Proceedings of the 14th International Congress in Mathematics Education (ICME14), Shanghai, China, 11–18 July 2021. [Google Scholar]
- Drijvers, P.; Monaghan, J.; Thomas, M.; Trouche, L. Use of Technology in Secondary Mathematics. Final Report for the International Baccalaureate; International Baccalaureate: Geneva, Switzerland, 2015. [Google Scholar]
- Pierce, R.; Ball, L. Perceptions that may affect teachers’ intention to use technology in secondary mathematics classes. Educ. Stud. Math. 2009, 71, 299–317. [Google Scholar] [CrossRef]
- Healy, L.; Lagrange, J.B. Section 3 Teachers and Technology. In Proceedings of the Mathematics Education and Technology—Rethinking the Terrain: The 17th ICMI Study, Berlin, Germany, 3–8 December 2009; pp. 287–345. [Google Scholar]
- Warner, C.K.; Bell, C.V.; Odom, A.L. Defining technology for learning: Cognitive and physical tools of inquiry. Middle Grades Rev. 2018, 4, 2. [Google Scholar]
- Williams, B. The Degree to which the Reliability of Educational Technology Affects its Use in the Classroom. Ph.D. Thesis, University Sains Malaysia, Penang, Malaysia, 2009. [Google Scholar]
- Jaworski, B. Teaching Better Mathematics: What, how and why? Tidssk. FoU Praksis 2010, 4, 9–21. [Google Scholar]
- Wells, G. Dialogic Inquiry: Towards a Socio-Cultural Practice and Theory of Education; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Hill, H.C.; Schilling, S.G.; Ball, D.L. Developing measures of teachers’ mathematics knowledge for teaching. Elem. Sch. J. 2004, 105, 11–30. [Google Scholar] [CrossRef]
- Daher, W.; Saifi, A. Democratic practices in a constructivist science classroom. Int. J. Sci. Math. Educ. 2016, 16, 221–236. [Google Scholar] [CrossRef]
- Roig-Vila, R.; Mengual-Andres, S.; Quinto-Medrano, P. Primary teachers’ technological, pedagogical and content knowledge. Comunicar 2015, 45, 151–159. [Google Scholar] [CrossRef]
- Saltan, F.; Arslan, K. A comparison of in-service and pre-service teachers’ technological pedagogical content knowledge self-confidence. Cogent Educ. 2017, 4, 1311501. [Google Scholar] [CrossRef]
- Baya’a, N.; Daher, W.; Anabousy, R.; Anabousy, A. The Development of Pre-Service Teachers’ TPACK for the Use of Digital Tools. In Proceedings of the CERME 10, Dublin, Ireland, 1–5 February 2017. [Google Scholar]
- Thomas, M.O.; Hong, Y.Y. Teacher Integration of Technology into Mathematics Learning. Int. J. Tech. Math. Educ. 2013, 20, 69–84. [Google Scholar]
- Hsu, C.-Y.; Tsai, M.-J.; Chang, Y.-H.; Liang, J.-C. Surveying in-service teachers’ beliefs about game based learning and perceptions of Technological Pedagogical and Content Knowledge of Games. J. Educ. Techno. Soc. 2017, 20, 134–143. [Google Scholar]
- Cheng, S.-L.; Xie, K. The relations among teacher value beliefs, personal characteristics, and TPACK in intervention and non-intervention settings. Teach. Teach. Educ. 2018, 74, 98–113. [Google Scholar] [CrossRef]
- Wilkins, J.L.; Brand, B.R. Change in preservice teachers’ beliefs: An evaluation of a mathematics methods course. Sch. Sci. Math. 2004, 104, 226–232. [Google Scholar] [CrossRef]
- Thurm, D.; Barzel, B. Self-efficacy—The Final Obstacle on Our Way to Teaching Mathematics with Technology? In Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education, Utrecht, The Netherlands, 6–10 February 2019; pp. 2749–2757. [Google Scholar]
- Ertmer, P.; Ottenbreit-Leftwich, A.; Sadik, O.; Sendurur, E.; Sendurur, P. Teacher beliefs and technology integration practices: A critical relationship. Comput. Educ. 2012, 59, 423–435. [Google Scholar] [CrossRef]
- Perrotta, C. Do school-level factors influence the educational benefits of digital technology? A critical analysis of teachers’ perceptions. Br. J. Educ. Technol. 2013, 44, 314–327. [Google Scholar] [CrossRef]
- Uslu, Ö. Factors Associated with Technology Integration to Improve Instructional Abilities: A Path Model. Aust. J. Teach. Educ. 2018, 43, 31–50. [Google Scholar] [CrossRef]
- McCulloch, A.W.; Hollebrands, K.; Lee, H.; Harrison, T.; Mutlu, A. Factors that influence secondary mathematics teachers’ integration of technology in mathematics lessons. Comput. Educ. 2018, 123, 26–40. [Google Scholar] [CrossRef]
- Lavicza, Z. Factors influencing the integration of Computer Algebra Systems into university-level mathematics education. Int. J. Tech. Math. Educ. 2007, 14, 121. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).