Estimation of the Six Sigma Quality Index

Abstract

The measurement of the process capability is a key part of quantitative quality control, and process capability indices are statistical measures of the process capability. Six Sigma level represents the maximum achievable process capability, and many enterprises have implemented Six Sigma improvement strategies. In recent years, many studies have investigated Six Sigma quality indices, including $Q_{pk}$. However, $Q_{pk}$ contains two unknown parameters, namely $\delta$ and $\gamma$, which are difficult to use in process control. Therefore, whether a process quality reaches the k sigma level must be statistically inferred. Moreover, the statistical method of sampling distribution is challenging for the upper confidence limits of $Q_{pk}$. We address these two difficulties in the present study and propose a methodology to solve them. Boole’s inequality, Demorgan’s theorem, and linear programming were integrated to derive the confidence intervals of $Q_{pk}$, and then the upper confidence limits were used to perform hypothesis testing. This study involved a case study of the semiconductor assembly process in order to verify the feasibility of the proposed method.

1. Introduction

The measurement of the process capability is crucial for quantitative quality control, and process capability indices (PCIs) are statistical measures of the process capability [1]. Many PCIs have been proposed in recent decades, and they have been widely applied in various industries [2,3,4]. For example, the $C_p$ index, which was proposed by Juran [5], is defined as follows:

$$C_p=\frac{USL-LSL}{6\sigma }=\frac{d}{3\sigma }$$

(1)

where USL and LSL are the upper and lower specification limits, respectively, d refers to half of the length of the specification interval, and σ denotes the process standard deviation for an in-control process. However, because this index lacks a measure of the process mean $\mu$, the deviation of the process mean is not included in the value of $C_p$. Therefore, for processes with equal standard deviations σ but different means $\mu$, the values of $C_p$ are equal. However, a larger difference in the process means $\mu$ corresponds to a greater probability of exceeding the process specification; this results in a loss of accuracy in the evaluation of the process capability.

Consequently, Kane [6], proposed another process capability index, $C_{pk}$, which is defined as follows:

$$C_{pk}=Min\left\{\frac{USL-\mu }{3\sigma },\frac{\mu -LSL}{3\sigma }\right\}=\frac{d-|\mu -T|}{3\sigma }$$

(2)

where $T=\left(USL+LSL\right)/2$ denotes target value and $d=\left(USL-LSL\right)/2$. Boyles [7] described the $C_{pk}$ index as a bilateral specification process capability index based on process yield. Assuming that the quality characteristic $X$ has a normal distribution, the inequality $Yield\%\ge 2\mathsf{\Phi }\left(3C_{pk}\right)-1$ holds, where $\mathsf{\Phi }(\cdot )$ refers to the cumulative distribution function of $N\left(0,1\right)$. Because the $C_{pk}$ index fully reflects the characteristics of the process yield, it is widely used in many manufacturing industries to measure the potential process capability in practical applications [8].

Six Sigma is a statistical tool that has been used by companies to improve process capability [9]. The main goal of Six Sigma is to improve the process capability to Six Sigma level for all “critical to quality” characteristics. When the process capability reaches Six Sigma level, the output of the process is only 3.4 ppm defective [10,11]. To measure the quality level of the process capability, a corresponding process capability index must be defined. In recent years, many studies have focused on the topic of quality indices for Six Sigma. These studies have investigated the relationships of PCIs with Six Sigma level of process capability, and they have utilized the multicharacteristic process quality analysis chart to determine whether the quality of a process meets customers’ expectations [12,13,14,15,16,17,18].

According to Aldowaisana et al. [8], Linderman et al. [19], and Chen et al. [20], a process capability can reach Six Sigma level if the process mean $\mu$ is no more than 1.5σ from the target value, where the process standard deviation is defined as $\sigma =d/6$. In other words, the process capability reaches Six Sigma level when $|\mu -T|\le 1.5\sigma$ and $6\sigma =d$. Chen et al. [21] defined $Y=\left(X-T\right)/d$, and assumed that Y has a normal distribution with a mean $\delta$ and variance ${\gamma }^2$ (i.e., $Y~N\left(\delta ,{\gamma }^2\right)$). The estimate of $\gamma$ is also the square root of MSE [22]. They then proposed the following quality index:

$$Q_{pk}=\frac{1-|\delta |}{\gamma }+1.5$$

(3)

where $\delta =\left(\mu -T\right)/d$ and $\gamma =\sigma /d$. Chen et al. [21] noted that when a process reaches k sigma level, it obeys the following conditions:

$$Q_{pk}\ge Q_{pk}(k)=\frac{1-|1.5/k|}{1/k}+1.5=k,$$

(4)

$$Yield\%\ge 2\mathsf{\Phi }(Q_{pk}-1.5).$$

(5)

This quality index for Six Sigma fully indicates the process quality level and process yield. Thus, it is a convenient and effective tool for assessing whether a process capability reaches Six Sigma level. However, the $Q_{pk}$ index includes the two unknown parameters of $\delta$ and $\gamma$. Hence, to determine whether the process capability reaches the k sigma level, these parameters must be inferred through statistical methods. Moreover, the statistical method of sampling distribution is difficult for the upper confidence limit of $Q_{pk}$. The purpose of the present study was to address these two difficulties and develop a simple operational procedure.

The remainder of this paper is organized as follows: Section 2 derives the expected value, bias, and mean square error of the natural estimator for the Six Sigma quality index. Boole’s inequality, Demorgan’s theorem, and linear programming are integrated to derive the confidence intervals of $Q_{pk}$ in Section 3. Section 4 details the process of statistical hypothesis testing for the upper confidence limits of $Q_{pk}$ in this study. Section 5 presents a case study from the semiconductor assembly process for verification of the statistical hypothesis testing results. Conclusions are presented in Section 6.

2. Point Estimation for the Six Sigma Quality Index

Let $\left(Y_1,Y_2,\cdots ,Y_n\right)$ be a random sample from $N\left(\delta ,{\gamma }^2\right)$; the sample mean and sample standard deviation are then defined as follows:

$$\widehat{\delta }=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{Y}_i}, \widehat{\gamma }=\sqrt{\frac{1}{n-1}{\displaystyle {\sum }_{i=1}^n{\left(Y_i-\overline{Y}\right)}^2}}.$$

Thus, the estimator of $Q_{pk}$ can be written as follows:

$${\widehat{Q}}_{pk}=\frac{1-|\widehat{\delta }|}{\widehat{\gamma }}+1.5$$

(6)

Under the assumption of normality, let $\theta =\sqrt{n}\delta /\gamma$,

$$Z^{\prime }=\frac{\sqrt{n}\widehat{\delta }}{\gamma }, \mathrm{and} K=\frac{\left(n-1\right){\widehat{\gamma }}^2}{{\gamma }^2};$$

$Z^{\prime }$ and $K$ have distributions of $N\left(\theta ,1\right)$ and ${\chi }_{n-1}^2$, respectively. Hence,

$${\widehat{Q}}_{pk}=\frac{1-|\widehat{\delta }|}{\widehat{\gamma }}+1.5=\frac{\frac{\sqrt{n}}{\gamma }-\frac{|\sqrt{n}\widehat{\delta }|}{\gamma }}{\sqrt{\frac{n}{n-1}K}}+1.5=K^{-1/2}\left(\frac{\sqrt{n-1}}{\gamma }-\sqrt{\frac{n-1}{n}}|Z^{\prime }|\right)+1.5.$$

(7)

To obtain the expected value of ${\widehat{Q}}_{pk}$, the following calculations are first performed:

$$E\left[|Z^{\prime }|\right]=\sqrt{\frac{2}{\pi }}\exp \left(-\frac{{\theta }^2}{2}\right)+|\theta |\left(1-2\mathsf{\Phi }(-|\theta |)\right)$$

(8)

$$E\left[K^{-1/2}\right]=\frac{\mathsf{\Gamma }\left((n-2)/2\right)}{\mathsf{\Gamma }\left((n-1)/2\right)}\times \frac{1}{\sqrt{2}}.$$

(9)

The expected value of ${\widehat{Q}}_{pk}$ can subsequently be obtained as follows:

$$\begin{array}{l}E\left[{\widehat{Q}}_{pk}\right]=E\left[K^{-1/2}\right]\left\{\frac{\sqrt{n-1}}{\gamma }-\sqrt{\frac{n-1}{n}}\left[E|Z^{\prime }|\right]\right\}+1.5\\ \hspace{1em}\hspace{1em}\hspace{1em} =A\left(n\right)\left\{\frac{1}{\gamma }-\frac{1}{\sqrt{n}}\left(\sqrt{\frac{2}{\pi }}\exp \left(-\frac{{\theta }^2}{2}\right)+|\theta |\left[1-2\mathsf{\Phi }\left(-|\theta |\right)\right]\right)\right\}+1.5\\ \hspace{1em}\hspace{1em}\hspace{1em} =A\left(n\right)\left\{\left(\frac{1}{\gamma }-\frac{|\theta |}{\sqrt{n}}\right)-\sqrt{\frac{2}{n\pi }}\exp \left(-\frac{{\theta }^2}{2}\right)+2\frac{|\theta |}{\sqrt{n}}\mathsf{\Phi }\left(-|\theta |\right)\right\}+1.5\end{array},$$

where

$$A\left(n\right)=\frac{\mathsf{\Gamma }\left[\left(n-2\right)/2\right]\sqrt{n-1}}{\mathsf{\Gamma }\left[\left(n-1\right)/2\right]\sqrt{2}}.$$

(10)

Because $\theta =\sqrt{n}\delta /\gamma$, this can be rewritten as

$$E\left[{\widehat{Q}}_{pk}\right]=A_n\left\{\left(Q_{pk}-1.5\right)+\left(2\frac{|\delta |}{\gamma }\mathsf{\Phi }\left(-\frac{\sqrt{n}|\delta |}{\gamma }\right)-\sqrt{\frac{2}{n\pi }}\exp \left(-\frac{n{\delta }^2}{2{\gamma }^2}\right)\right)\right\}+1.5$$

(11)

${\widehat{Q}}_{pk}$ is a biased estimator of $Q_{pk}$, and its bias can be computed as follows:

$$\begin{array}{l}Bias\left[{\widehat{Q}}_{pk}\right]=\left(Q_{pk}-1.5\right)\left(A_n-1\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +A_n\left\{2\frac{|\delta |}{\gamma }\mathsf{\Phi }\left(-\frac{\sqrt{n}|\delta |}{\gamma }\right)-\sqrt{\frac{2}{n\pi }}\exp \left(-\frac{n{\delta }^2}{2{\gamma }^2}\right)\right\}\end{array}.$$

(12)

Furthermore, the mean square error of ${\widehat{Q}}_{pk}$ can be computed as follows:

$$\begin{array}{l}MSE\left[{\widehat{Q}}_{pk}\right]=E\left[{\left({\widehat{Q}}_{pk}-Q_{pk}\right)}^2\right]\\ \hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em} =E\left[{\left(\left(1-|\widehat{\delta }|\right)/\widehat{\gamma }-\left(1-|\delta |/\gamma \right)\right)}^2\right]\\ \hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em} =E\left[{\left(\left[{\widehat{Q}}_{pk}-1.5\right]-\left[Q_{pk}-1.5\right]\right)}^2\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =E\left[{\left({\widehat{Q}}_{pk}-1.5\right)}^2\right]-2\left(Q_{pk}-1.5\right)E\left[{\widehat{Q}}_{pk}-1.5\right]+{\left(Q_{pk}-1.5\right)}^2\end{array}.$$

(13)

Based on Equation (11) and Appendix A, the procedure of deriving the mean square error of ${\widehat{Q}}_{pk}$.

$$\begin{array}{l}E\left[{\widehat{Q}}_{pk}-1.5\right]=A_n\left\{\left(Q_{pk}-1.5\right)+\left(2\frac{|\delta |}{\gamma }\mathsf{\Phi }\left(-\frac{\sqrt{n}|\delta |}{\gamma }\right)-\sqrt{\frac{2}{n\pi }}\exp \left(-\frac{n{\delta }^2}{2{\gamma }^2}\right)\right)\right\},\\ \hspace{1em}\hspace{1em}\hspace{1em}E\left[{\left({\widehat{Q}}_{pk}-1.5\right)}^2\right]=\frac{n-1}{n-3}\times \{{\left(Q_{pk}-1.5\right)}^2+\frac{1}{n}-\frac{2}{\gamma }\\ \hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em} \hspace{1em} \times \left(2\frac{|\delta |}{\gamma }\mathsf{\Phi }\left(-\frac{\sqrt{n}|\delta |}{\gamma }\right)-\sqrt{\frac{2}{n\pi }}\exp \left(-\frac{n{\delta }^2}{2{\gamma }^2}\right)\right)\}\end{array}.$$

(14)

Thus,

$$\begin{array}{l}MSE\left[{\widehat{Q}}_{pk}\right]\\ =\frac{n-1}{n-3}\times \left\{{\left(Q_{pk}-1.5\right)}^2+\frac{1}{n}-\frac{2}{\gamma }\times \left(2\frac{|\delta |}{\gamma }\mathsf{\Phi }\left(-\frac{\sqrt{n}|\delta |}{\gamma }\right)-\sqrt{\frac{2}{n\pi }}\exp \left(-\frac{n{\delta }^2}{2{\gamma }^2}\right)\right)\right\}\\ +2A_n\left(Q_{pk}-1.5\right)\left\{\left(Q_{pk}-1.5\right)+\left(2\frac{|\delta |}{\gamma }\mathsf{\Phi }\left(-\frac{\sqrt{n}|\delta |}{\gamma }\right)-\sqrt{\frac{2}{n\pi }}\exp \left(-\frac{n{\delta }^2}{2{\gamma }^2}\right)\right)\right\}\\ +{\left(Q_{pk}-1.5\right)}^2\end{array}.$$

(15)

$Bias\left[{\widehat{Q}}_{pk}\right] \mathrm{a}\mathrm{n}\mathrm{d} MSE\left[{\widehat{Q}}_{pk}\right]$ can be computed following Equations (12) and (15) under the assumption that the value of k is 6, 5, 4, or 3 and the sample size (n) is 10, 20, 30, 40, 50, 60, or 70. The results of these calculations are shown in

Table 1. Bias and MSE for various ${\widehat{Q}}_{pk}$.

K	n	δ = 0		δ = 1/4		δ = 1/2		δ = 3/4
		Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE
6	10	0.1480	91.1658	0.4241	90.7310	0.4241	90.7310	0.4241	90.7310
	20	0.0021	85.2514	0.1879	85.1295	0.1879	85.1295	0.1879	85.1295
	30	−0.0288	83.6844	0.1207	83.6224	0.1207	83.6224	0.1207	83.6224
	40	−0.0397	82.9602	0.0889	82.9212	0.0889	82.9212	0.0889	82.9212
	50	−0.0442	82.5433	0.0704	82.5160	0.0704	82.5160	0.0704	82.5160
	60	−0.0461	82.2724	0.0582	82.2518	0.0582	82.2518	0.0582	82.2518
	70	−0.0467	82.0825	0.0497	82.0663	0.0497	82.0663	0.0497	82.0663
5	10	0.0536	55.2756	0.3298	54.9375	0.3298	54.9375	0.3298	54.9375
	20	−0.0397	51.6150	0.1462	51.5202	0.1462	51.5202	0.1462	51.5202
	30	−0.0557	50.6487	0.0939	50.6005	0.0939	50.6005	0.0939	50.6005
	40	−0.0595	50.2029	0.0692	50.1726	0.0692	50.1726	0.0692	50.1726
	50	−0.0599	49.9466	0.0547	49.9253	0.0547	49.9253	0.0547	49.9253
	60	−0.0590	49.7801	0.0453	49.7641	0.0453	49.7641	0.0453	49.7641
	70	−0.0578	49.6634	0.0386	49.6509	0.0386	49.6509	0.0386	49.6509
4	10	−0.0405	28.3338	0.2347	28.0949	0.2356	28.0923	0.2356	28.0923
	20	−0.0815	26.3809	0.1044	26.3132	0.1044	26.3132	0.1044	26.3132
	30	−0.0825	25.8686	0.0671	25.8341	0.0671	25.8341	0.0671	25.8341
	40	−0.0792	25.6328	0.0494	25.6112	0.0494	25.6112	0.0494	25.6112
	50	−0.0755	25.4975	0.0391	25.4823	0.0391	25.4823	0.0391	25.4823
	60	−0.0720	25.4097	0.0323	25.3983	0.0323	25.3983	0.0323	25.3983
	70	−0.0688	25.3482	0.0276	25.3393	0.0276	25.3393	0.0276	25.3393
3	10	−0.1347	10.3404	0.1245	10.2241	0.1414	10.1955	0.1414	10.1955
	20	−0.1232	9.5491	0.0606	9.5112	0.0626	9.5085	0.0626	9.5085
	30	−0.1093	9.3439	0.0399	9.3236	0.0402	9.3232	0.0402	9.3232
	40	−0.0990	9.2499	0.0296	9.2370	0.0296	9.2369	0.0296	9.2369
	50	−0.0911	9.1961	0.0234	9.1870	0.0235	9.1870	0.0235	9.1870
	60	−0.0849	9.1613	0.0194	9.1544	0.0194	9.1544	0.0194	9.1544
	70	−0.0799	9.1369	0.0166	9.1316	0.0166	9.1316	0.0166	9.1316

. Figure 1 illustrates the relationship between $Bias\left[{\widehat{Q}}_{pk}\right]$ and sample size (n) for δ = 1/4. As the sample size increases, $Bias\left[{\widehat{Q}}_{pk}\right]$ tends to decrease to the same stable value for all k. Figure 2 presents the relationship between $MSE\left[{\widehat{Q}}_{pk}\right]$ and sample size for δ = 1/4. As the sample size increases, $MSE\left[{\widehat{Q}}_{pk}\right]$ tends to decrease to the same stable value for all k.

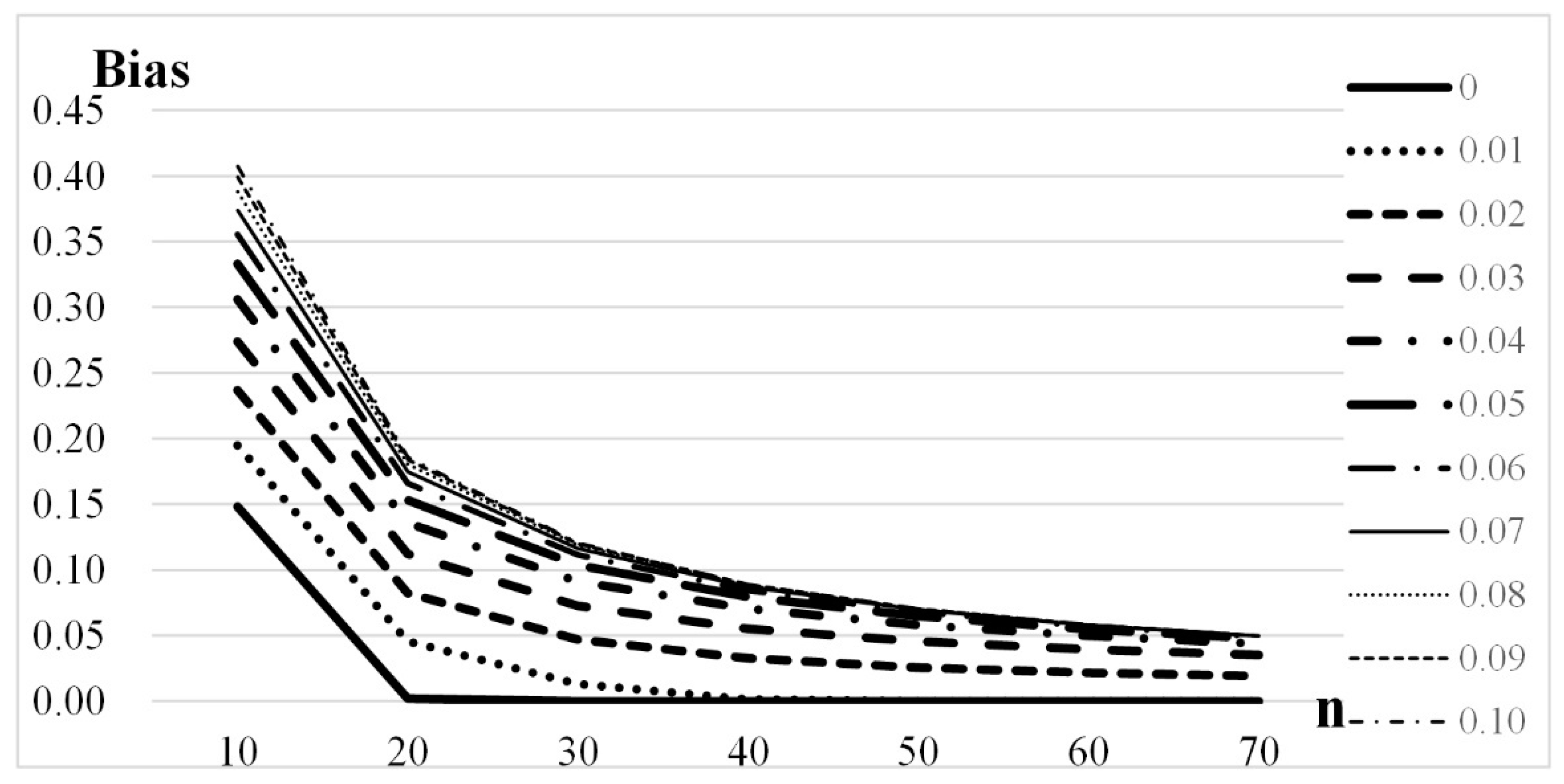
In addition, the influence of a small change in δ on $Bias\left[{\widehat{Q}}_{pk}\right]$ and $MSE\left[{\widehat{Q}}_{pk}\right]$ is also worth discussing. Therefore, we calculate $Bias\left[{\widehat{Q}}_{pk}\right] \mathrm{a}\mathrm{n}\mathrm{d} MSE\left[{\widehat{Q}}_{pk}\right]$ with δ increments of 0.01 according to Equations (12) and (15) for k values of 6, 5, 4, or 3 and sample sizes of 10, 20, 30, 40, 50, 60, or 70. The results are shown in

Table 2. Bias and MSE for various ${\widehat{Q}}_{pk}$ (δ increment is 0.01).

K	n	δ = 0		δ = 0.01		δ = 0.02		δ = 0.03		δ = 0.04		δ = 0.05
		Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE
6	10	0.148	91.166	0.195	91.116	0.237	91.066	0.274	91.017	0.306	90.969	0.333	90.925
6	20	0.002	85.251	0.046	85.237	0.082	85.220	0.112	85.202	0.136	85.185	0.153	85.170
6	30	−0.0288	83.684	0.013	83.677	0.047	83.667	0.073	83.656	0.091	83.646	0.104	83.638
6	40	−0.0397	82.960	0.001	82.956	0.033	82.949	0.055	82.941	0.070	82.934	0.079	82.929
6	50	−0.0442	82.543	−0.0039	82.541	0.026	82.535	0.046	82.529	0.058	82.524	0.065	82.520
6	60	−0.0461	82.272	−0.0065	82.271	0.022	82.266	0.040	82.261	0.050	82.257	0.055	82.254
6	70	−0.0467	82.083	−0.0077	82.081	0.019	82.077	0.035	82.073	0.044	82.070	0.048	82.068
K	n	δ = 0.06				δ = 0.07		δ = 0.08		δ = 0.09		δ = 0.10
		Bias		MSE		Bias	MSE	Bias	MSE	Bias	MSE	Bias	MSE
6	10	0.356		90.885		0.374	90.850	0.388	90.821	0.399	90.796	0.407	90.777
6	20	0.166		85.157		0.175	85.148	0.180	85.141	0.184	85.136	0.186	85.133
6	30	0.112		83.632		0.116	83.628	0.119	83.625	0.120	83.624	0.120	83.623
6	40	0.085		82.925		0.087	82.923	0.088	82.922	0.089	82.922	0.089	82.921
6	50	0.068		82.518		0.070	82.517	0.070	82.516	0.070	82.516	0.070	82.516
6	60	0.057		82.253		0.058	82.252	0.058	82.252	0.058	82.252	0.058	82.252
6	70	0.049		82.067		0.050	82.067	0.050	82.066	0.050	82.066	0.050	82.066

. Figure 3 illustrates the relationship between $Bias\left[{\widehat{Q}}_{pk}\right]$ and sample size for k = 6. As the sample size increases, $Bias\left[{\widehat{Q}}_{pk}\right]$ tends to decrease to the same stable value for all k. Figure 4 shows the relationship between $MSE\left[{\widehat{Q}}_{pk}\right]$ and sample size for k = 6. As the sample size increases, $MSE\left[{\widehat{Q}}_{pk}\right]$ tends to decrease to the same stable value for all k.

3. Upper Confidence Limits of the Six Sigma Quality Index

As mentioned, under the assumption of normality, $K$ follows the ${\chi }_{n-1}^2$ distribution. Therefore,

$$p\left\{\chi \le {\chi }_{1-\alpha /2;n-1}^2\right\}=p\left\{\frac{(n-1){\widehat{\gamma }}^2}{{\gamma }^2}\le {\chi }_{1-\alpha /2;n-1}^2\right\}=p\left\{\gamma \ge \sqrt{\frac{n-1}{{\chi }_{1-\alpha /2;n-1}^2}}\widehat{\gamma }\right\}=1-\frac{\alpha }{2}.$$

Furthermore, when we let

$$T=\frac{\sqrt{n}\left(\widehat{\delta }-\delta \right)}{\widehat{\gamma }},$$

(16)

T follows a $t_{n-1}$ distribution. Thus, we have

$$p\left\{-t_{\alpha /4;n-1}\le T\le t_{\alpha /4;n-1}\right\}=p\left\{\widehat{\delta }-t_{\alpha /4;n-1}\times \frac{\widehat{\gamma }}{\sqrt{n-1}}\le \delta \le \widehat{\delta }+t_{\alpha /4;n-1}\times \frac{\widehat{\gamma }}{\sqrt{n-1}}\right\}=1-\frac{\alpha }{2}.$$

To derive the $\left(1-\alpha \right)\times 100\%$ upper confidence limit on $Q_{pk}$, some events are defined as follows:

$$E_{\delta }=\left\{\widehat{\delta }-t_{\alpha /4;n-1}\times \frac{\widehat{\gamma }}{\sqrt{n-1}}\le \delta \le \widehat{\delta }+t_{\alpha /4;n-1}\times \frac{\widehat{\gamma }}{\sqrt{n-1}}\right\}$$

(17)

and

$$E_{\gamma }=\left\{{\gamma }^2\ge \frac{n-1}{{\chi }_{1-\alpha /2;n-1}^2}{\widehat{\gamma }}^2\right\},$$

(18)

where $t_{\alpha /4;n-1}$ is the upper $\alpha /4$ quintile of $t_{n-1}$, ${\chi }_{1-\alpha /2;n-1}^2$ is the lower $1-\alpha /2$ quintile of ${\chi }_{n-1}^2$, and $\alpha$ is the confidence level. In fact, $P\left(E_{\delta }\right)=P\left(E_{\gamma }\right)=1-\left(\alpha /2\right)$ and $P\left(E_{\delta }^C\right)=P\left(E_{\gamma }^C\right)=\alpha /2$. Based on Boole’s inequality and Morgan’s theorem,

$$P\left(E_{\delta }\cap E_{\gamma }\right)\ge 1-P\left(E_{\delta }^C\right)-P\left(E_{\gamma }^C\right)=1-\alpha .$$

(19)

This is equivalent to

$$p\left\{\widehat{\delta }-e_t\le \delta \le \widehat{\delta }+e_t,\gamma \ge \sqrt{\frac{n-1}{{\chi }_{1-\alpha /2;n-1}^2}}\widehat{\gamma }\right\}\ge 1-\alpha ,$$

(20)

where

$$e_t=t_{\alpha /4;n-1}\frac{\widehat{\gamma }}{\sqrt{n}}.$$

(21)

Therefore, the $100\left(1-\alpha \right)\%$ confidence interval of $\left(\delta ,\gamma \right)$ can be calculated as follows:

$$CR=\left\{\left(\delta ,\gamma \right)|\widehat{\delta }-e_t\le \delta \le \widehat{\delta }+e_t,\gamma \ge \sqrt{\frac{n-1}{{\chi }_{1-\alpha /2;n-1}^2}}\widehat{\gamma }\right\}$$

(22)

$Q_{pk}$ is a function of parameter $\delta$ and $\gamma$. According to Chen et al. [21], mathematical programming can be used to compute the upper confidence limit of $Q_{pk}$.

In this computation method, $Q_{pk}$ is treated as the objective function, and the confidence region is regarded as the feasible solution area. Therefore, parameters $\delta$ and $\gamma$ are the two decision variables of this objective function. The optimization problem can then be defined as follows:

$$\{\begin{array}{l}U{Q}_{pk}=Max Q_{pk}\left(\delta ,\gamma \right)=Max\frac{1-|\delta |}{\gamma }+1.5\\ s.t.\\ \hspace{1em}\widehat{\delta }-e_t\le \delta \le \widehat{\delta }+e_t\\ \hspace{1em}\gamma \ge \sqrt{\frac{n-1}{{\chi }_{1-\alpha /2;n-1}^2}}\widehat{\gamma }\end{array}$$

(23)

The feasible solution area in this problem is a rectangle (convex set), and when $\delta$ is closer to 0, $Q_{pk}$ increases because $1-|\delta |$ becomes closer to 1. Similarly, the value of $Q_{pk}\left(\delta \right)$ increases as the value of γ decreases. Therefore, $Q_{pk}$ increases as $\left(\delta ,\gamma \right)$ approaches the origin. The maximum of $Q_{pk}$ is obtained at the bottom of the rectangle. Therefore, the feasible solution area in this problem is a line segment (convex set). Thus, mathematical programming can be applied to determine the upper confidence limit of $Q_{pk}$. Consequently, the model for the index $U{Q}_{pk}$ can be rewritten as follows:

$$\{\begin{array}{l}U{Q}_{pk}=Max Q_{pk}\left(\delta \right)=\sqrt{\frac{{\chi }_{1-\alpha /2;n-1}^2}{n-1}}\frac{1-|\delta |}{\widehat{\gamma }}+1.5\\ s.t.\\ \hspace{1em}\widehat{\delta }-e_t\le \delta \le \widehat{\delta }+e_t\end{array}$$

(24)

$Q_{pk}\left(\delta \right)$ can be simplified to a function of $\delta$ as follows:

$$Q_{pk}\left(\delta \right)=\sqrt{\frac{{\chi }_{1-\alpha /2;n-1}^2}{n-1}}\frac{1-|\delta |}{\widehat{\gamma }}+1.5$$

(25)

Equation (25) shows that $Q_{pk}\left(\delta \right)$ increases as $\delta$ becomes closer to 0.

Furthermore, the maximum value of $U{Q}_{pk}$ is closely related to $\widehat{\delta }$ and $e_t$. Hence, we consider three cases for $\widehat{\delta }$ and $e_t$ in this study.

Case 1: 

$0\in \left[\widehat{\delta }-e_t,\widehat{\delta }+e_t\right]$

Because $0\in \left[\widehat{\delta }-e_t,\widehat{\delta }+e_t\right]$, the maximum of $U{Q}_{pk}$ is obtained for $Q_{pk}\left(\delta =0\right)$; this maximum is defined as

$$U{Q}_{pk}=Q_{pk}\left(\delta =0\right)=\sqrt{\frac{{\chi }_{1-\alpha /2;n-1}^2}{n-1}}\frac{1}{\widehat{\gamma }}+1.5$$

(26)

Case 2: 

$\widehat{\delta }-e_t>0$

Because $\widehat{\delta }-e_t>0$, $\delta >\widehat{\delta }-e_t>0$. Therefore, the maximum of $U{Q}_{pk}$ is obtained for $Q_{pk}\left(\delta =\widehat{\delta }-e_t\right)$:

$$U{Q}_{pk}=Q_{pk}\left(\delta =\widehat{\delta }-e_t\right)=\sqrt{\frac{{\chi }_{1-\alpha /2;n-1}^2}{n-1}}\frac{1-\widehat{\delta }+e_t}{\widehat{\gamma }}+1.5$$

(27)

Case 3: 

$\widehat{\delta }+e_t<0$

Because $\widehat{\delta }+e_t<0$, $\delta <\widehat{\delta }+e_t<0$. Therefore, the maximum of $U{Q}_{pk}$ is obtained for $Q_{pk}\left(\delta =\widehat{\delta }+e_t\right)$:

$$U{Q}_{pk}=Q_{pk}\left(\delta =\widehat{\delta }+e_t\right)=\sqrt{\frac{{\chi }_{1-\alpha /2;n-1}^2}{n-1}}\frac{1-\widehat{\delta }-e_t}{\widehat{\gamma }}+1.5$$

(28)

On the basis of the relationships described in Equations (26)–(28), we define

$$I=\{\begin{array}{l}0 if 0\in \left[\widehat{\delta }-e_t,\widehat{\delta }+e_t\right]\\ 1 if \widehat{\delta }-e_t>0 or \widehat{\delta }+e_t<0\end{array}$$

and

$$i=\{\begin{array}{l}0 if \widehat{\delta }-e_t>0\\ 1 if \widehat{\delta }+e_t<0\end{array}$$

Subsequently, the $100\left(1-\alpha \right)\%$ upper confidence limit of $C_{pmh}$ can be obtained as follows:

$$U{Q}_{pk}=\sqrt{\frac{{\chi }_{1-\alpha /2;n-1}^2}{n-1}}\frac{1}{\widehat{\gamma }}\times {\left(\frac{1-\widehat{\delta }+{(-1)}^i{e}_t}{\widehat{\gamma }}\right)}^I+1.5$$

(29)

4. Hypothesis Testing

As defined previously, $U{Q}_{pk}$ is a function of the process parameters $\widehat{\delta }$ and $\widehat{\gamma }$. To determine whether the process quality level reaches the k sigma level, statistical hypothesis testing was conducted. The relationship between $Q_{pk}$ and $k$ should be constructed and then verified using a hypothesis test. A case study is presented to verify the proposed inferences in Section 5.

Hypothesis testing entails the following steps:

Step 1: 

Determine the required process quality level.

The process quality level is assumed to be k sigma.

Step 2: 

Propose the null hypothesis $H_0$ and the alternative hypothesis $H_1$.

The null and alternative hypotheses are as follows:

• Null hypothesis $H_0: Q_{pk}\ge k$
• Alternative hypothesis $H_1: Q_{pk}<k$

The upper confidence limit $U{Q}_{pk}$ can then be obtained through statistical testing, and the hypotheses are judged as follows:

(1)

If $U{Q}_{pk}\ge k$, then do not reject $H_0$ and conclude that $Q_{pk}\ge k$

(2)

If $U{Q}_{pk}<k$, then reject $H_0$ and conclude that $Q_{pk}<k$

Step 3: 

Design the sampling plan.

The sample size and significance level α are assigned. Random sampling should then be conducted during the process control.

Step 4: 

Compute $\widehat{\delta }$ and $e_t$ to determine the suitable formula for $U{Q}_{pk}$.

The suitable formula for $U{Q}_{pk}$ can be determined on the basis of the three for $\widehat{\delta }$ and $e_t$ after these two parameters have been calculated from the original measurement data.

$$\widehat{\delta }=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{Y}_i}, \mathrm{where} Y_i=\left(X_i-T\right)/d$$

$$e_t=t_{\alpha /4;n-1}\frac{\widehat{\gamma }}{\sqrt{n}}, \mathrm{where} \widehat{\gamma }=\sqrt{\frac{1}{n-1}{\displaystyle {\sum }_{i=1}^n{\left(Y_i-\overline{Y}\right)}^2}}$$

Step 5: 

Compare $U{Q}_{pk}$ and k.

After $U{Q}_{pk}$ has been computed, k and $U{Q}_{pk}$ can be compared. The process capability is considered to reach Six Sigma level if $U{Q}_{pk}\ge 6$.

5. A Case Study

This article proposed a new Six Sigma index, which can quickly and easily determine the process capability by simply calculating the value of the collected data. For managers and engineers, this index can be used to monitor the process in real time, taking into account the economy and immediacy.

To demonstrate the suitability of the proposed method for practical application, a case study from the semiconductor assembly process is presented as an example for statistical testing. A chip package with a leadframe carrier must pass through the plating process to provide protection for the metal plating layer and the medium, which are required for the subsequent surface-mounted technology (SMT) process. Because the plating thickness affects the SMT quality, process control is crucial at the plating stage. The plating layer on the outer lead of the leadframe is an important medium, providing a mechanical and electrical connection between the package and the printed circuit board (PCB). The composition and thickness of the plating layer affect the soldering quality between the package and the PCB. When the plating thickness exceeds the specification, the package body and the PCB cannot be effectively joined, resulting in an open-circuit or short-circuit current. In this study, the thickness specification for the plating layer was 550 ± 150 μm; that is, T = 550 μm and d = 150 μm.

The statistical testing procedure accords with the five steps defined in the previous section:

Step 1:

Determine the required process quality level.

Six Sigma level (k = 6) is the desired process quality level for this case.

Step 2:

Propose the null hypothesis $H_0$ and the alternative hypothesis $H_1$.

The null and alternative hypotheses are as follows:

• Null hypothesis $H_0: Q_{pk}\ge 6$
• Alternative hypothesis $H_1: Q_{pk}<6$

The upper confidence limit $U{Q}_{pk}$ can be obtained through statistical testing, and the hypotheses are judged as follows:

(1)

If $U{Q}_{pk}\ge 6$, then do not reject $H_0$ and conclude that $Q_{pk}\ge 6$

(2)

If $U{Q}_{pk}<6$, then reject $H_0$ and conclude that $Q_{pk}<6$

Step 3: 

Design the sampling plan.

The sample size (n) and the significance level α are defined as 70 and 0.05, respectively.

Step 4: 

Compute $\widehat{\delta }$ and $e_t$ to determine the suitable formula for $U{Q}_{pk}$.

$$\widehat{\delta }=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{Y}_i=-0.1955},$$

$$\widehat{\gamma }=\sqrt{\frac{1}{n-1}{\displaystyle {\sum }_{i=1}^n{\left(Y_i-\overline{Y}\right)}^2}}=0.1900, \mathrm{where} e_t=t_{\alpha /4;n-1}\frac{\widehat{\gamma }}{\sqrt{n}}=0.00489.$$

Thus,

$$\widehat{\delta }-e_t=-0.20039<0, \widehat{\delta }+e_t=-0.19061<0$$

Because $\widehat{\delta }-e_t$ and $\widehat{\delta }+e_t$ are both less than 0.00, I and i are both 1.00, according to Equation (25). Finally,

$$U{Q}_{pk}=\sqrt{\frac{{\chi }_{1-\alpha /2;n-1}^2}{n-1}}\frac{1}{\widehat{\gamma }}\times {\left(\frac{1-\widehat{\delta }+{(-1)}^i{e}_t}{\widehat{\gamma }}\right)}^I+1.5=8.48.$$

Step 5: 

Compare $U{Q}_{pk}$ and k.

Because $U{Q}_{pk}=8.48>6$, do not reject $H_0$ and conclude that $Q_{pk}\ge k=6$. This result is consistent with the assumption that $U{Q}_{pk}\ge k$. That is, the minimum value of $U{Q}_{pk}$ is 8.48, but it exceeds the required value of k (6) for a sample size of 70. Hence, statistical testing reveals that $Q_{pk}\ge k=6$, and the process capability is considered to reach Six Sigma level.

6. Conclusions

A PCI is necessary for determining whether a process capability meets Six Sigma level, which is indicative of an extremely good process capability.

Following the research of Chen et al. [21], this study employed $Q_{pk}$ as a measure of process capability. However, $Q_{pk}$ includes unknown parameters $\widehat{\delta }$ and $\widehat{\gamma }$. Therefore, statistical inference was used to verify $Bias\left[{\widehat{Q}}_{pk}\right] \mathrm{a}\mathrm{n}\mathrm{d} MSE\left[{\widehat{Q}}_{pk}\right]$ for different k values and sample sizes (n). Finally, the results revealed that $Bias\left[{\widehat{Q}}_{pk}\right] \mathrm{a}\mathrm{n}\mathrm{d} MSE\left[{\widehat{Q}}_{pk}\right]$ exhibit stable convergence trends. Furthermore, we derived the upper limit of $Q_{pk}$. First, Boole’s inequality and Morgan’s theorem were used to compute the error $e_t$, and linear programming was then applied to calculate the upper confidence limit $U{Q}_{pk}$ of $Q_{pk}$.

The maximum value of $Q_{pk}$ was separated into three categories based on the relationship between $\widehat{\delta }$ and $e_t$.

The maximum value of $U{Q}_{pk}$ was determined from a comparison of the combination of $\widehat{\delta }$ and $e_t$ with 0.00. Three combinations of $\widehat{\delta }$ and $e_t$ were explored in this study. For each combination, we obtained a general formula for $U{Q}_{pk}$.

Finally, a case study from the semiconductor assembly process was employed to verify the hypotheses of the Six Sigma quality index. For this case, $U{Q}_{pk}$ was deduced to be 8.48 for k = 6 and n = 70. Therefore, $U{Q}_{pk}\ge k$ was a valid hypothesis. That is, the process capability reached Six Sigma level.

This study utilized $Q_{pk}$ as a Six Sigma quality index to make statistical inferences, and the upper limits of the confidence intervals of point estimations were then obtained. The integrated definition of $U{Q}_{pk}$ is simple and convenient for industrial application.