An Efficient Zero-Knowledge Dual Membership Proof Supporting Pos-and-Neg Membership Decision

Abstract

In this paper, we address the problem of secure decision of membership. We present a Zero-Knowledge Dual Membership Proof (ZKDMP) protocol, which can support positive and negative (Pos-and-Neg) membership decisions simultaneously. To do it, two secure aggregation functions are used to compact an arbitrarily-sized subset into an element in a cryptographic space. By using these aggregation functions, a subset can achieve a secure representation, and the representation size of the subsets is reduced to the theoretical lower limit. Moreover, the zeros-based and poles-based secure representation of the subset are used to decide Pos-and-Neg membership, respectively. We further verify the feasibility of combining these two secure representations of the subset, so this result is used to construct our dual membership decision cryptosystem. Specifically, our ZKDMP protocol is proposed for dual membership decisions, which can realize a cryptographic proof of strict Pos-and-Neg membership simultaneously. Furthermore, the zero-knowledge property of our construction ensures that the information of the tested element will not be leaked during the implementation of the protocol. In addition, we provide detailed security proof of our ZKDMP protocol, including positive completeness, negative completeness, soundness and zero-knowledge.

1. Introduction

With the development of cryptography research, some basic math skills and concepts are becoming more and more significant in the last decade. For instance, set theory, as one of theoretical foundations of computer science and engineering, has been widely used in database design [1], large-scale data processing [2], fault diagnosis [3] and other areas. Wherein, the problem of determining whether or not an element belongs to a set is called set membership decision. It is not only the basis of set theory but also a common problem on the Internet, and has been widely concerned and applied in many fields, such as e-auction, blacklist and whitelist mechanism, anonymous certificate systems, and so forth [4,5,6,7]. For example, as a common access control technology, the blacklist mechanism allows access to any user in the system except those explicitly mentioned. This mechanism is essentially used to determine whether the user is in the blacklist set.

A naive method to solve the set membership decision problem is to compare a tested element x with all elements in a set S one-by-one. However, this method is very ineffective and does not meet the needs of large-scale membership determination on the Internet. In order to improve efficiency, Bloom Filter (BF) [8] and Cryptographic Accumulator (CA) [9] are applied to the membership decision by compressing the set into a compact representation. Usually, the following points need to be considered for a cryptographic membership decision scheme:

• Representing the set S and the element x into specific cryptographic forms;
• Deciding whether or not x belongs to S in terms of the relationship between x and S’s representation.

Specifically, the BF-based method maps each element in the set into k positions on an array by k different hash functions and sets the bits of these positions to 1. This array is called the representation of the set. When testing, the tested element is first mapped by the above k hash functions, the tested element must not be in the set if one of these mapped positions in the array is 0; otherwise, the tested element is likely to be in the set if these positions are all 1. The CA-based method works as follows. It first accumulates all of the elements in the set to a random value as the representation of the set. In the decision stage, a verifier can determine whether the tested element belongs to the set based on the algebraic relationship between the element’s witness and published accumulative value.

In the above methods, the way to solve the membership decision problem is one-time testing between the tested element and the compressed form of the set. Obviously, they are more efficient in comparison with one-by-one testing in the naive method. In order to further protect the privacy of tested element, Zero-Knowledge Proof (ZKP) technology [10,11,12] is considered in [7,13,14]. In these schemes, zero-knowledge property allows one to prove that a tested element belongs to a set without revealing its information. This feature has bright application prospects. For example, in the financial supervision, a user can prove to a bank that they belong to a public user set without disclosing their identity information, which will reduce the disclosure of the user’s privacy.

Although many remarkable results have been made on the membership decision and related problems, there are still some challenges, especially under the requirements of complex applications and the security required by large-scale and dynamic networks. For example, although the existing set representation has a certain compression feature, the more detailed and secure set compact representation still needs to be further studied to meet the needs of large-scale network applications. Furthermore, the research on cryptographic protocol supporting privacy protection remains a challenge for protecting a sensitive tested element in the membership decision.

In view of the above challenges, this paper aims to construct a secure representation of the set and design a Zero-Knowledge Dual Membership (Dual membership denotes two opposite set membership, i.e., ∈ and ∉, = and ≠) Proof (ZKDMP) protocol. The highlights of this paper can be described as follows: (a) defining the cryptographic representation of the set and formalizing its security, (b) proposing the concept of Secure Decision of Membership to decide the Pos-and-Neg membership, and (c) constructing the ZKDMP protocol to support strict Pos-and-Neg membership decisions.

1.1. Related Works

Bloom Filter (BF) is an efficient tool that can be used to test whether an element is a member of a set. In 2009, Nojima and Kadobayashi [15] proposed a cryptographically secure privacy protection BF protocol. They adopted the blind signature and oblivious pseudorandom function to enhance the privacy of bit information in the array, and gave a simple security definition and analysis. Subsequently, Ramezanian [16] enhanced the above work by using Goldwasser–Micali homomorphic encryption and blind RSA signature. Furthermore, he also proposed several membership testing schemes with privacy protection.

In 1993, Cryptographic Accumulator (CA) was introduced in [9]. It accumulates a set of elements into a short commitment and generates a short witness for all the accumulated elements. These witnesses can be publicly verified with commitments, so as to prove the relationship between elements and sets. On this basis, Papamanthou et al. [17] presented a q-strong multilinear Diffie–Hellmann (q-SMDH) accumulator construction. They combined this accumulator with a constant-depth tree in a nested way and proposed a cryptographic protocol for determining the membership of sets. Then, Papamanthou et al. [18] further improved the above scheme and gave an accumulator based on bilinear mapping, as well as a more strict definition and security proof. Additionally, Derler et al. [19] revised the concept of the accumulator by introducing indiscriminability and proposed an undeniable universal accumulator. Ghosh et al. [20] paid attention to the privacy of accumulator and proposed a zero-knowledge accumulator, which would not disclose the information of the set in the execution process.

At the same time, CA is also used to decide the non-membership. Li et al. introduced the concept of the universal accumulator in [21], different from traditional accumulative machines, this scheme can efficiently compute the non-membership witness for all elements that have not been accumulated. Furthermore, this scheme is proved to be secure under the strong RSA (sRSA) assumption. After that, Damgård and Triandopoulos [22] completed the above scheme and presented a new accumulator construction based on bilinear mapping, which supports the proof of a set non-membership. The security of this scheme is reduced to the q-strong Diffie–Hellman (q-SDH) assumption. Then, Yu et al. [23] constructed the first universal accumulator from the small integer solution (SIS) assumption in a standard lattice. Their scheme could not only generate short witnesses for non-accumulators but also made a zero-knowledge proof for non-accumulator witnesses.

Recently, some ZKP protocols for membership are proposed to prove that an element in or not a public set without disclosing the element. In 2008, Camenisch et al. [24] presented two new approaches to building set-membership zero-knowledge proofs based on q-SDH and RSA assumption, respectively. Furthermore, their protocols can be used to range proof in zero-knowledge. After that, Peng et al. [25] constructed two new non-membership proof protocols to prove that a committed element is not in a finite set. Benarroch et al. [7] also proposed an efficient ZKP protocol supporting membership or non-membership decisions based on the strong RSA (sRAS) assumption.

In addition, there are many other studies on membership decision. Guo et al. proposed a membership encryption scheme in [26,27]. By adding a set of tokens to the ciphertext, their scheme required the user to hold the token belonging to the token set when decrypting the message. In terms of design, their scheme adopted a construction based on polynomial root-value decision, which can be regarded as an extension of the broadcast encryption. Arfaoui et al. [28] applied membership proof to Near-Field Communication and proposed a secure mobile ticketing protocol for the public transportation. This protocol ensured the anonymity of users, so as to prevent service providers from tracking users’ tracks. According to the zero-knowledge set membership proof, Baza et al. [29] proposed a time-locked deposit protocol for ride sharing in order to ensure the privacy of both drivers and riders. Locher and Haenni [30] also proposed an Internet voting protocol based on the same technology, which can ensure the anonymity of voting without authority. In summary, in the

Table 1. Comparison between related literature and our protocol.

Literature	Technology	Decision Mode	Zero-Knowledge	Hardness Assumption
Benarroch et al. [7]	Merkle trees	Dual membership	Yes	–
Ramezanian [16]	Bloom filter	Membership	No	RSA
Papamanthou et al. [17]	CA	Membership	No	q-SMDH
Damgård et al. [22]	CA	Non-membership	No	t-SDH
Camenisch et al. [24]	Digital signature, CA	Membership	Yes	q-SDH, RSA
Peng et al. [25]	Commitment	Non-membership	Yes	sRSA
ZKDMP	Aggregation functions	Dual membership	Yes	t-SDH

, we list the comparison results between some related works [7,16,17,22,24,25] and ours in terms of technology, decision mode, zero-knowledge and hardness assumptions.

1.2. Our Contributions

The purpose of this work is to construct a novel Zero-Knowledge Dual Membership Proof (ZKDMP) protocol, which can support Pos-and-Neg membership decisions simultaneously. To that end, a new security representation of a subset using aggregation functions is introduced to achieve a secure membership decision. The contributions of this paper are listed below.

• We first formalize the security requirements of the aggregator based on our previous work [31], which refers to the security properties in easy or hard to compute aggregated values for a given set and a certain element. Based on them, two aggregation functions, ZeroAggr and PoleAggr, can achieve a secure representation of a subset in terms of zero-pole interpolation and reach the theoretical lower limit for the representation size of subsets. Moreover, the security of our aggregation functions are proved under the t-SDH assumption (see Section 3 and Section 4).
• We propose the concept of Secure Decision of Membership (SDM) and use the zeros-based and poles-based secure representation of the subset to decide the Pos-and-Neg membership, respectively. Thus, the security of membership decisions can be reduced to the security of ZeroAggr and PoleAggr. Furthermore, we verify the feasibility of combining these two secure representations of subset, so this kind of combination could act as the foundation for constructing a dual membership decision cryptosystem (see Section 5).
• Following the approach of the SDM, we construct a ZKDMP protocol for the dual membership decision, which can realize a cryptographic proof of the strict Pos-and-Neg membership. In contrast with a single membership decision, the proposed protocol can prevent elements outside the system from affecting the decision result. Furthermore, the zero-knowledge property of our protocol ensures that the information of the tested element will not be leaked during the interactive proof of the protocol. Moreover, we provide the complete security proofs of the ZKDMP protocol, including positive completeness, negative completeness, soundness and zero-knowledge (see Section 6).

In addition, in our secure representation of the subset, there is no limit to the number of elements in the universal set (in fact, when the system parameter $p=2^{512}$, the number of elements in the universal set is about ${10}^{51}$ and a set with so many elements can be considered almost infinite in a practical application). Finally, the performance evaluations show that our protocol has a simple and easy-to-understand structure.

1.3. Organization

Our approach for cryptographic Pos-and-Neg memberships is presented in Section 2. Zeros-based and poles-based representation of the subset are introduced in Section 3 and Section 4, respectively. Moreover, the secure membership decision is discussed in Section 5. We present the ZKDMP protocol and its security analysis in Section 6. The performance evaluations are given in Section 7. Finally, our conclusion is presented in Section 8.

2. Our Approach

This paper aims to construct a new zero-knowledge protocol that can support dual membership (positive and negative, Pos-and-Neg) decisions, simultaneously. The basis of constructing such a protocol is to realize a secure representation of subsets. Next, we first show the core idea for designing cryptographic construction of a set-membership (∈ or ∉). The notations and abbreviations used throughout the paper are shown in

Table 2. Notation table.

Symbol	Description
$\mathcal{P}\left(\mathcal{U}\right)$	the power set of the set $\mathcal{U}$
$\mathcal{A}$	a probabilistic polynomial-time adversary
$R_e$	a cryptographic representation of element e
$C_{\mathcal{S}}$	a cryptographic representation of set $\mathcal{S}$
B	bilinear pairing operation
$e(·,·)$	a bilinear mapping
PPT	probabilistic polynomial-time
$\overline{\mathcal{S}}$	the relative complement of $\mathcal{S}$ in $\mathcal{U}$, $\mathcal{U}\setminus \mathcal{S}$
ZeroAggr	zeros-based aggregation
PoleAggr	poles-based aggregation

.

2.1. Secure Representation of the Subset (SRS)

Our basic idea is to cryptographically represent the subset by using the aggregation function. In fact, based on the aggregation function (in short, Aggregator) proposed in our previous work [31], we can further define the security properties of the aggregation function, so as to take the output of the Aggregator as the security representation of the subset (SRS). Specifically, for any set $\mathcal{U}$, an Aggregator is a cryptographic function if it can map any subset of $\mathcal{U}$ into a fixed-size value. The specific definition of the aggregation function is described below.

Definition 1

(Aggregator). Given a set $\mathcal{U}=\{e_1,e_2,\cdots ,e_n\}$, let $\mathcal{P}\left(\mathcal{U}\right)$ be the power set of $\mathcal{U}$, $\mathcal{PK}$ that denotes the public key space. The algorithm $Aggregator:\mathcal{PK}\times \mathcal{P}\left(\mathcal{U}\right)\to \mathbb{G}$ satisfies:

$$Aggregator(mpk,\mathcal{S})=R_{\mathcal{S}},$$

(1)

where $mpk\in \mathcal{PK}$ is the public key, $\mathcal{S}$ is a subset of $\mathcal{U}$ and $R_{\mathcal{S}}\in \mathbb{G}$ is a random element.

Note that the aggregation function is a publicly computable function because the public key is used as input of the Aggregator. Moreover, there is no restriction on the size of the set $\mathcal{U}$ or the subset $\mathcal{S}$. In addition, this definition only presents the functional requirement of the Aggregator, and is not related to its security requirements. We give a simple description of the secure Aggregator with two security properties as follows.

Definition 2

(Secure Aggregator). Given a subset $\mathcal{S}$, a secure aggregation function can compress $\mathcal{S}$ into a constant-size random element, and satisfies the following security properties.

• Easy to compute the aggregated value for normal input, i.e.,

  -

  try to add an element into $\mathcal{S}$ where the element is not in $\mathcal{S}$; or

  -

  try to delete from $\mathcal{S}$ an element which is already present in $\mathcal{S}$.

• Hard to compute the aggregated value for abnormal input, i.e.,

  -

  try to add an element into $\mathcal{S}$ where the element is already present in $\mathcal{S}$; or

  -

  try to delete from $\mathcal{S}$ an element which is not in $\mathcal{S}$.

2.2. Roadmap for SRS

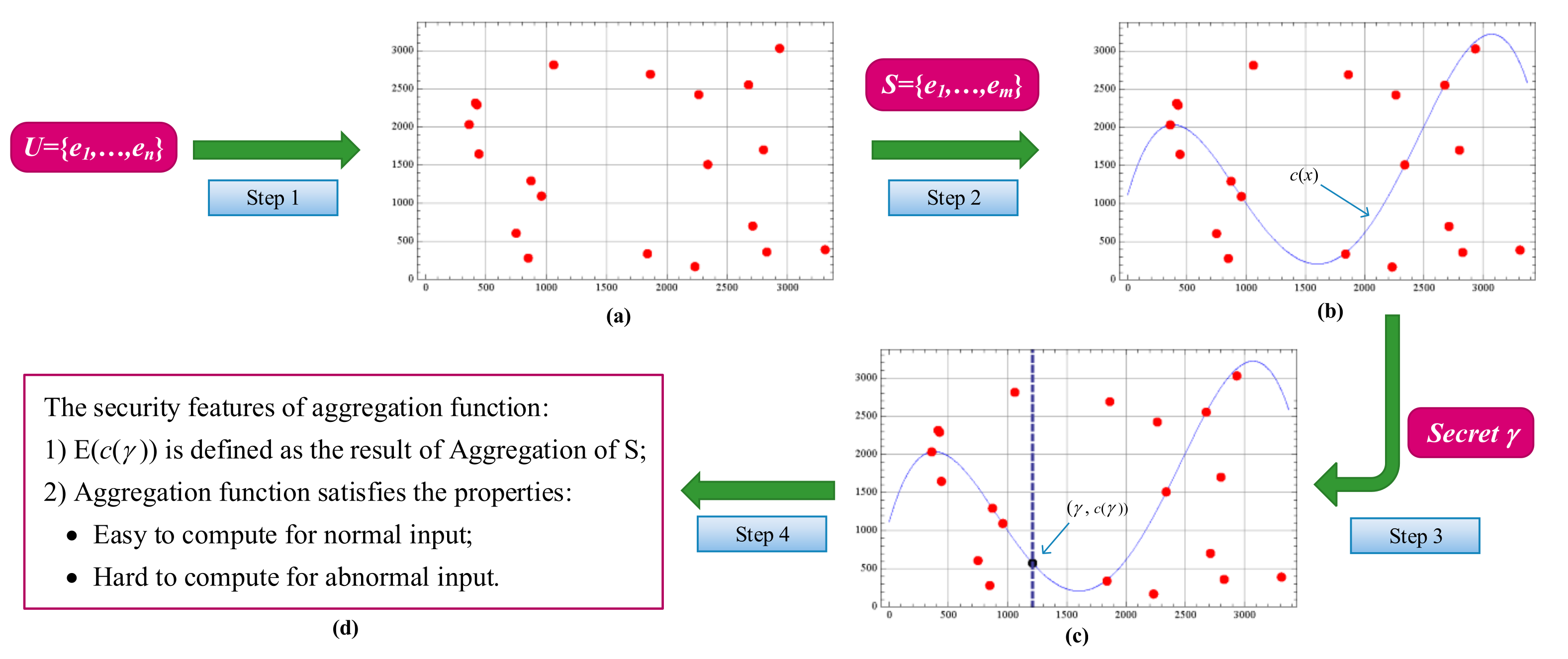
According to the security properties of the aggregate function defined in the last section, it is challenging to design a secure aggregation function for the security representation of the subset, especially for a subset of any size. We here present our intuition to solve this challenging problem. Our approach will be used to construct two secure aggregation functions in Section 3 and Section 4. For the convenience of explanation, as shown in Figure 1, we describe this approach as follows.

• For $\mathcal{U}=\{e_1,e_2,\cdots ,e_n\}$, $\forall e_i\in \mathcal{U}$ is mapped to a random point in a cryptographic space. In this step, we also pick partial information of these mapped points and publish them as public keys $mpk$;
• For a subset $\mathcal{S}\subset \mathcal{U}$, we construct a curve $c\left(x\right)$ through random points mapped from elements in $\mathcal{S}$;
• We pick a secret $\gamma$ and define the output of the aggregation function as an encapsulation of the point $(\gamma ,c(\gamma \left)\right)$, $E\left(c\right(\gamma \left)\right)\leftarrow Aggregator(mpk,\mathcal{S})$, where $E(·)$ denotes a cryptographic encapsulation function;
• Two security features of the aggregate function are defined to ensure that the aggregation is secure against malicious adversary attacks.

According to secure aggregation functions, we can achieve a secure representation of subsets. Before introducing secure aggregate functions, we first recall the definitions of zeros and poles in rational polynomials.

Definition 3

(Zeros and Poles). Let $H\left(x\right)=\frac{P\left(x\right)}{Q\left(x\right)}$ be a rational polynomial. Then, z is called a zero of the polynomial $H\left(x\right)$ if $P\left(z\right)=0$, and z is a pole of the polynomial $H\left(x\right)$ if $Q\left(z\right)=0$.

3. Zeros-Based Representation of Subset

Given a polynomial-sized set of elements $\mathcal{U}=\{e_1,\cdots ,e_n\}$, we first translate these elements into some random points in a one-dimensional plane; that is, $(x_1,x_2\cdots ,x_n)=(hash\left(e_1\right),\cdots ,hash\left(e_n\right))\in {\mathbb{Z}}_p^n$, where we assume each element $e_i$ is denoted as a binary string and $hash$ is a collision-resistant hash function. We utilize the cryptographic hash to ensure that all points are distributed uniformly in the whole space ${\mathbb{Z}}_p$ and each point is unique and nonzero, i.e., $x_i\ne x_j$ and $x_i\ne 0$ for all $i,j\in [1,n]$, $i\ne j$. Since the size of $\mathcal{U}$ is usually far less than that of ${\mathbb{Z}}_p$, we do not limit the size of $\mathcal{U}$ (e.g., $p>2^{512}$ for a secure elliptic curve).

Next, for $\mathcal{S}=\{e_1^{\prime },e_2^{\prime },\cdots ,e_m^{\prime }\}\subset \mathcal{U}$, we wish to find an effective method to compress the corresponding points $(hash\left(e_1^{\prime }\right),\cdots ,hash\left(e_m^{\prime }\right))$ in $\mathcal{S}$ into a random point $(x,y)$ in a two-dimensional plane. To do so, an $(m+1)$-order polynomial $f_{\mathcal{S}}\left(x\right)$ is defined over $\mathcal{S}$.

$$f_{\mathcal{S}}\left(x\right)=x(x+x_1^{\prime })\cdots (x+x_m^{\prime })=x\prod _{e_i^{\prime }\in \mathcal{S}}(x+x_i^{\prime })(modp)$$

(2)

It is easy to find that $f_{\mathcal{S}}\left(x\right)$ will be different if a different subset $\mathcal{S}$ is used. We map the subset $\mathcal{S}$ into a point $(x,y)=(x,f_{\mathcal{S}}\left(x\right))$. Given an unknown and random x, $f_{\mathcal{S}}\left(x\right)$ is random and unpredictable. An adversary cannot guess the correct value when x is unknown.

We further introduce the Discrete Logarithm Problem (DLP) into the above-mentioned construction in order to guarantee the privacy of x and the unpredictability of $f_{\mathcal{S}}\left(x\right)$. That is, given a multiplicative cyclic group $\mathbb{G}$, where g is a generator of $\mathbb{G}$, we map the subset $\mathcal{S}$ into the point $(g^x,g^{f_{\mathcal{S}}\left(x\right)})$ rather than $(x,f_{\mathcal{S}}\left(x\right))$. Based on the assumption of DLP, the privacy of x, as well as the unpredictability of $g^{f_{\mathcal{S}}\left(x\right)}$, will be guaranteed even when $g^x$ keeps public.

For a secret $\gamma$ and a subset $\mathcal{S}$, we next define the aggregation function by the above based on the above polynomial $f_{\mathcal{S}}\left(x\right)$. Since the hash values of all elements in the subset $\mathcal{S}$ are used for the (negative) zeros in $f_{\mathcal{S}}\left(x\right)$ ($f_{\mathcal{S}}\left(x\right)=x{\prod }_{e_i^{\prime }\in \mathcal{S}}(x-(-x_i^{\prime }))=x{\prod }_{e_i^{\prime }\in \mathcal{S}}(x+x_i^{\prime })(modp).$), this aggregation function is named Zeros-based Aggregator (ZeroAggr). In addition, it can aggregate all elements of $\mathcal{S}$ to $g^{f_{\mathcal{S}}(\gamma )}$.

Definition 4

(ZeroAggr). Let g be a generator in the group $\mathbb{G}$ and $\mathcal{S}\subset \mathcal{U}$. The Zeros-based Aggregator (ZeroAggr) inputs the public key $mpk$ and a subset $\mathcal{S}$ outputs an element in $\mathbb{G}$ as follows.

$$G_{\mathcal{S}}=\mathrm{ZeroAggr}(mpk,\mathcal{S})=g^{f_{\mathcal{S}}(\gamma )}=g^{\gamma ·{\prod }_{e_i\in \mathcal{S}}(\gamma +x_i)}$$

(3)

where γ is the secret, the public key $mpk={\{g_i=g^{{\gamma }^i}\}}_{i\in [1,|\mathcal{U}\left|\right]}$ and $x_i=hash\left(e_i\right)$.

Security Definition and Analysis

Let $f\left(x\right)$ be a polynomial, we make use of a simple polynomial division with monomial in order to remove a certain (negative) zero $x_i$ from this polynomial, i.e., $\frac{f\left(x\right)}{x+x_i}$. Two cases may arise. In the first case, $x_i$ is not a root of $f\left(x\right)$, such that we define $f\left(x\right)=(x+x_i)q\left(x\right)+r\left(x\right)$ and $\frac{f\left(x\right)}{x+x_i}=q\left(x\right)+\frac{r\left(x\right)}{x+x_i}$, where $q\left(x\right)$ and $r\left(x\right)$ are two polynomials and the remainder $r\left(x\right)\ne 0$. In the second case, $x_i$ is a root of $f\left(x\right)$, such that the remainder is equal to 0. Hence, we are able to convert the decisional problem of membership into a new problem: whether or not the remainder $r\left(x\right)$ is equal to 0?

According to the above-mentioned discussions, we define the set subtraction as ${\mathcal{S}}_{-}=\mathcal{S}\setminus \left\{e_i\right\}$ and the corresponding subtraction of the Zeros-based aggregation is expressed as:

$$G_{{\mathcal{S}}_{-}}=G_{\mathcal{S}\setminus \left\{e_i\right\}}=g^{\gamma ·{\prod }_{e_k\in \mathcal{S}\setminus \left\{e_i\right\}}(\gamma +x_k)}=g^{\frac{f_{\mathcal{S}}(\gamma )}{\gamma +x_i}},$$

(4)

where $x_i=hash\left(e_i\right)$. Let $\frac{f_{\mathcal{S}}\left(x\right)}{x+x_i}=q\left(x\right)+\frac{r\left(x\right)}{x+x_i}$. According to $e_i\in \mathcal{S}$ or $e_i\notin \mathcal{S}$, we have the two following cases:

• Case$e_i\in \mathcal{S}$ means that $(x+x_i)|f_{\mathcal{S}}\left(x\right)$ and $r\left(x\right)=0$, such that $G_{{\mathcal{S}}_{-}}=g^{q(\gamma )}$;
• Case$e_i\notin \mathcal{S}$ means that $x_i$ is not one root of $f_{\mathcal{S}}\left(x\right)$ and $r\left(x\right)\ne 0$, such that $G_{{\mathcal{S}}_{-}}=g^{q(\gamma )}·g^{\frac{r(\gamma )}{\gamma +x_i}}$.

It is easy to find that $G_{{\mathcal{S}}_{-}}$ can be computed by zeros-based aggregation algorithm for $e_i\in \mathcal{S}$, otherwise we must have the ability to compute $g^{\frac{r(\gamma )}{\gamma +x_i}}$ from $mpk={\{g_i=g^{{\gamma }^i}\}}_{i\in [1,|\mathcal{U}\left|\right]}$. Hence, we continue to transfer the problem of set membership into a computational problem: whether or not $G_{{\mathcal{S}}_{-}}$ can be computed in a polynomial time.

Based on the above discussion, the security definition of zeros-based aggregation under the dividing polynomial with a monomial is defined below.

Definition 5

(Security of ZeroAggr). Given an element $e_i\in \mathcal{U}$ and a subset $\mathcal{S}\subset \mathcal{U}$, a ZeroAggr function on $\mathcal{S}$ is called a secure zeros-based aggregation if it has the following two properties:

• Easy to compute $G_{{\mathcal{S}}_{-}}$ for $e_i\in \mathcal{S}$. The value of $G_{{\mathcal{S}}_{-}}=g^{\frac{f_{\mathcal{S}}(\gamma )}{\gamma +x_i}}$ can be computed by the ZeroAggr algorithm within a polynomial time, that is,

  $$Pr[ZeroAggr(mpk,S_{-})=G_{S_{-}}|e_i\in S]>1-ϵ.$$

  (5)
• Hard to compute $G_{{\mathcal{S}}_{-}}$ for $e_i\notin \mathcal{S}$. Any probabilistic polynomial-time adversary $\mathcal{A}$ computing $G_{{\mathcal{S}}_{-}}=g^{\frac{f_{\mathcal{S}}(\gamma )}{\gamma +x_i}}$ succeeds with negligible probability ϵ, that is,

  $$Pr[\mathcal{A}(mpk,e_i,S)=G_{S_{-}}|e_i\notin \mathcal{S}]<ϵ.$$

  (6)

We next prove that our ZeroAggr function is a secure zeros-based aggregation under the Strong Diffie–Hellman (SDH) assumption. The following is the description of the t-SDH problem [32].

Definition 6

(t-SDH Problem). Given some elements $(G,G^{\alpha },\cdots ,$$G^{{\alpha }^t})$ in $\mathbb{G}$, find a pair $(c,G^{1/(\alpha +c)})$ such that $c\ne 0(modp)$.

The SDH assumption holds in some infinite family of groups, if the aforementioned t-SDH problem is hard for any t that is polynomially bounded in the security parameter, where the group size p grows exponentially with the security parameter. According to this assumption, we prove the security of ZeroAggr in a straightforward manner.

Theorem 1.

Our ZeroAggr function is a secure zeros-based aggregator under the t-SDH assumption.

Proof. 

Let $(G,G^{\alpha },G^{{\alpha }^2},\cdots ,G^{{\alpha }^t})\to (c,G^{1/(\alpha +c)})$ be an instance of t-SDH. We convert this instance into a ZeroAggr function: let $g=G$ and $\gamma =\alpha$ ($\alpha$ is an unknown secret), such that we have $g_i=g^{{\gamma }^i}=G^{{\alpha }^i}$ and $mpk={\left\{g_i\right\}}_{i\in [1,t]}$, where we assume that $t\ge \left|\mathcal{U}\right|$. We have the two following cases for any $e_i\in \mathcal{U}$ and $\mathcal{S}\subset \mathcal{U}$ ($\left|\mathcal{S}\right|=k$):

• Easy to compute ${\mathbf{G}}_{\mathcal{S}-}$ for$e_i\in \mathcal{S}$. Given a subset $\mathcal{S}$ and an element $e_i\in \mathcal{S}$, we define $f_{{\mathcal{S}}_{-}}\left(x\right)=x{\prod }_{e_k\in \mathcal{S},e_k\ne e_i}(x+x_k)={\sum }_{i=0}^{k-1}{c}_i{x}^{i+1}$ based on $(x+x_i)|f_{\mathcal{S}}\left(x\right)$. This information is sufficient to compute the value:

  $$G_{{\mathcal{S}}_{-}}=g^{f_{{\mathcal{S}}_{-}}(\gamma )}=g^{{\sum }_{i=0}^{k-1}{c}_i{\gamma }^{i+1}}={\prod }_{i=1}^k{\left(G^{{\alpha }^i}\right)}^{c_{i-1}}.$$

  (7)
• Hard to compute ${\mathbf{G}}_{\mathcal{S}-}$ for$e_i\notin \mathcal{S}$. If there is a PPT algorithm $\mathcal{A}$ can compute $G_{{\mathcal{S}}_{-}}=g^{\frac{f_{\mathcal{S}}(\gamma )}{\gamma +x_i}}$ but $(x+x_i)\nmid f_{\mathcal{S}}\left(x\right)$. Then we can solve the SDH problem as follows. Let $\frac{f_{\mathcal{S}}\left(x\right)}{x+x_i}=q\left(x\right)+\frac{r\left(x\right)}{x+x_i}$ be defined as above, where $q\left(x\right)={\sum }_{i=0}^k{d}_i{x}^i$ and $r\left(x\right)=r$ are two known polynomials. Hence, we can compute:

  $$G^{1/(\alpha +x_i)}={(G_{{\mathcal{S}}_{-}}/{\prod }_{i=0}^k{\left(G^{{\alpha }^i}\right)}^{d_i})}^{1/r}$$

  (8)

  because we have $G^{\frac{f_{\mathcal{S}}(\gamma )}{\gamma +x_i}}=G^{q(\gamma )}·G^{\frac{r}{\gamma +x_i}}$ and $G^{q(\gamma )}={\prod }_{i=0}^k{\left(G^{{\alpha }^i}\right)}^{d_i}$. This means we forge a valid solution $(x_i,G^{1/(\alpha +x_i)})$ for the t-SDH problem. However, this is a contradiction with the t-SDH assumption.

Thus, the ZeroAggr function is secure under the t-SDH assumption.    □

4. Poles-Based Representation of Subset

We have presented an effective approach to deal with the decisional problem of positive membership (∈) based on zeros-based aggregation, but it is not enough to realize the decisional problem of negative membership (∉). To solve this problem, we expect to build a “conversely” aggregation function that is easy to compute for $e\notin \mathcal{S}$ but hard to compute for $e_i\in \mathcal{S}$. We will use the poles-based aggregation to deal with this problem in this section.

Similar to zeros-based aggregation, we next show the construction of the Poles-based Aggregator (PoleAggr). For $\mathcal{R}=\{e_1^{\prime },\cdots ,e_m^{\prime }\}\subset \mathcal{U}$, this function can compress elements of $\mathcal{R}$ into a random point $(x,y)$ even if the size of $\mathcal{R}$ is large. Then, we use hash values of elements in the subset $\mathcal{R}$ as the poles of the polynomial, such that the m-order polynomial $g_{\mathcal{R}}\left(x\right)$ is defined as follows, where $m=\left|\mathcal{R}\right|$.

$$g_{\mathcal{R}}\left(x\right)=\frac{1}{(x+x_1^{\prime })\cdots (x+x_m^{\prime })}=\frac{1}{{\prod }_{e_i^{\prime }\in \mathcal{R}}(x+x_i^{\prime })}(modp)$$

(9)

In the above polynomial, $x_i^{\prime }$ is the results of $hash\left(e_i^{\prime }\right)$. The output of $g_{\mathcal{R}}\left(x\right)$ is random and unpredictable for a unknown and random x. Note that give a random value x, the probability of collision between x and all cryptographic hash values ${\left\{h\left(e_i^{\prime }\right)\right\}}_{i=1}^m$ is negligible when p is large enough. This means that the probability of $x+x_i^{\prime }=0$ or division by zero errors is also negligible.

We next define the PoleAggr based on the above-mentioned polynomial $g_{\mathcal{R}}\left(x\right)$. In this definition, we let h be a generator in the cyclic group $\mathbb{G}$. Our goal is to compute $h^{g_{\mathcal{R}}(\gamma )}$ for a secret $\gamma$ in terms of the public parameter $mpk$. This definition is expressed as follows:

Definition 7

(PoleAggr). Let h be a generator in the group $\mathbb{G}$ and $\mathcal{R}\subset \mathcal{U}$. The Poles-based Aggregator ($PoleAggr$) inputs the public key $mpk$ and the subset $\mathcal{R}$, outputs an element in $\mathbb{G}$ as follows.

$$H_{\mathcal{R}}=\mathrm{PoleAggr}(mpk,\mathcal{R})=h^{g_{\mathcal{R}}(\gamma )}=h^{\frac{1}{{\prod }_{e_i\in \mathcal{R}}(\gamma +x_i)}},$$

(10)

where γ is the secret, the public key $mpk={\{h_i=h^{\frac{1}{\gamma +x_i}}\}}_{i\in [1,|\mathcal{U}\left|\right]}$ and $x_i=hash\left(e_i\right)$.

When $h_i$ and $h_j$ are known, we can easily obtain:

$$\begin{array}{cc}\hfill H_{\{e_i,e_j\}}& ={\left(\frac{h_j}{h_i}\right)}^{\frac{1}{x_i-x_j}}={(h^{\frac{1}{\gamma +x_j}}/h^{\frac{1}{\gamma +x_i}})}^{\frac{1}{x_i-x_j}}=h^{\frac{1}{(\gamma +x_i)(\gamma +x_j)}}\hfill \end{array}$$

(11)

iff $x_i\ne x_j$ (or $e_i\ne e_j$).

Security Definition and Analysis

We define the addition of the set and element as ${\mathcal{R}}_{+}=\mathcal{R}\cup \left\{e_i\right\}$ and the corresponding addition of poles-based aggregation is expressed as the equation:

$$H_{{\mathcal{R}}_{+}}=H_{\mathcal{R}\cup \left\{e_i\right\}}=h^{g_{\mathcal{R}}(\gamma )·\frac{1}{\gamma +x_i}}=h^{\frac{1}{(\gamma +x_i)·{\prod }_{e_k\in \mathcal{R}}(\gamma +x_k)}},$$

(12)

where $x_i=hash\left(e_i\right)$. Depending on whether $e_i$ is an element of $\mathcal{R}$ or not, we have the following two cases:

• Case$e_i\notin \mathcal{R}$. This means that $hash\left(e_i\right)\ne hash\left(e_k\right)$ for all $e_k\in \mathcal{R}$ and a collision-resistant $hash(·)$, such that $H_{{\mathcal{R}}_{+}}=h^{g_{{\mathcal{R}}_{+}}(\gamma )}=h^{\frac{1}{(\gamma +x_i)·{\prod }_{e_k\in \mathcal{R}}(\gamma +x_k)}}$;
• Case$e_i\in \mathcal{R}$. This means that $x_i$ is a double pole of $g_{{\mathcal{R}}_{+}}\left(x\right)$, such that $H_{{\mathcal{R}}_{+}}=h^{g_{{\mathcal{R}}_{-}}(\gamma )·\frac{1}{{(\gamma +x_i)}^2}}=h^{\frac{1}{{(\gamma +x_i)}^2{\prod }_{e_k\in \mathcal{R}\setminus \left\{e_i\right\}}(\gamma +x_k)}}$.

It is easy to find that $H_{{\mathcal{R}}_{+}}$ can be computed by the poles-based aggregation algorithm for $e_i\notin \mathcal{R}$, otherwise we must have ability to compute the value $h^{g_{{\mathcal{R}}_{-}}\left(x\right)·\frac{1}{{(\gamma +x_i)}^2}}$ from the public parameter $mpk={\{h_i=h^{\frac{1}{\gamma +x_i}}\}}_{e_i\in \mathcal{U}}$. However, it is improbable to calculate this value by Equation (11) because of the “divided by zero” exception. We will provide a rigorous proof in the proof of Theorem 2. Therefore, the following is a security definition of poles-based aggregation by dividing the polynomial with the monomial.

Definition 8

(Security of PoleAggr). Given an element $e_i\in \mathcal{U}$ and a subset $\mathcal{R}\subset \mathcal{U}$, a PoleAggr function on $\mathcal{R}$ is called a secure poles-based aggregation if it has the following two properties:

• Easy to compute $H_{{\mathcal{R}}_{+}}$ for $e_i\notin \mathcal{R}$. The value of $H_{{\mathcal{R}}_{+}}=h^{\frac{g_{\mathcal{R}}(\gamma )}{\gamma +x_i}}$ can be computed by PoleAggr algorithm within a polynomial time, that is,

  $$Pr[PoleAggr(mpk,{\mathcal{R}}_{+})=H_{{\mathcal{R}}_{+}}|e_i\notin \mathcal{R}]>1-ϵ.$$

  (13)
• Hard to compute $H_{{\mathcal{R}}_{+}}$ for $e_i\in \mathcal{R}$. Any probabilistic polynomial-time adversary $\mathcal{A}$ computing $H_{{\mathcal{R}}_{+}}=h^{\frac{g_{\mathcal{R}}(\gamma )}{\gamma +x_i}}$ succeeds with negligible probability ϵ, that is,

  $$Pr[\mathcal{A}(mpk,e_i,\mathcal{R})=H_{{\mathcal{R}}_{+}}|e_i\in \mathcal{R}]<ϵ.$$

  (14)

Although the two functions, ZeroAggr and PoleAggr, are dramatically different in form, they have the same security foundation, called the strong Diffie–Hellman (SDH) assumption. We can prove the security of PoleAggr in a more subtle way, where the value $G^{f(\gamma )}$, built on the polynomial $f\left(x\right)={\prod }_{i=1}^n(x+x_i)$, could be used as a generator in $\mathbb{G}$.

Theorem 2.

Our PoleAggr function is a secure poles-based aggregator under the t-SDH assumption.

Proof. 

Let $(G,G^{\alpha },G^{{\alpha }^2},\cdots ,G^{{\alpha }^t})\to (c,G^{1/(\alpha +c)})$ be an instance of t-SDH. We convert this instance into a PoleAggr function: Let $\mathcal{U}=\{e_1,\cdots ,e_n\}$ and $f\left(x\right)={\prod }_{i=1}^n(x+x_i)$ for $n\le t$. We define $h=G^{f(\gamma )}$ and $\gamma =\alpha$ ($\alpha$ is an unknown secret), such that we have $h_i=h^{1/(\gamma +x_i)}=G^{f_i(\gamma )}$ and $mpk={\left\{h_i\right\}}_{i\in [1,n]}$, where $f_i\left(x\right)=f\left(x\right)/(x+x_i)={\sum }_{i=0}^{n-1}{d}_i{x}^i$ and $G^{f_i(\gamma )}={\prod }_{i=0}^{n-1}{\left(G^{{\alpha }^i}\right)}^{d_i}$ for all $e_i\in \mathcal{U}$. We have the two following cases for any $e_i\in \mathcal{U}$ and $\mathcal{R}\subset \mathcal{U}$ ($\left|\mathcal{R}\right|=k$):

• Easy to compute $H_{{\mathcal{R}}_{+}}$ for $e_i\notin \mathcal{R}$. Given a subset $\mathcal{R}$ and an element $e_i\notin \mathcal{R}$, we define:

  $$f\left(x\right)·g_{{\mathcal{R}}_{+}}\left(x\right)=\frac{f\left(x\right)}{{\prod }_{e_k\in {\mathcal{R}}_{+}}(x+x_k)}={\prod }_{e_k\in \mathcal{U}\setminus (\mathcal{R}\cup \left\{e_i\right\})}(x+x_i)={\sum }_{i=0}^{n-k-1}{c}_i{x}^i$$

  (15)

  based on $(x+x_i)|f\left(x\right)$. Such that, we can compute the value of $H_{{\mathcal{R}}_{+}}$ by using:

  $$H_{{\mathcal{R}}_{+}}=h^{g_{{\mathcal{R}}_{+}}(\gamma )}=G^{f\left(x\right)·g_{{\mathcal{R}}_{+}}\left(x\right)}=G^{{\sum }_{i=0}^{n-k-1}{c}_i{\gamma }^i}={\prod }_{i=0}^{n-k-1}{\left(G^{{\alpha }^i}\right)}^{c_i}.$$

  (16)
• Hard to compute ${\mathbf{H}}_{{\mathcal{R}}_{+}}$ for ${\mathbf{e}}_{\mathbf{i}}\in \mathcal{R}$. Assume that there exists a PPT algorithm $\mathcal{A}$ can compute the value $H_{{\mathcal{R}}_{+}}=h^{\frac{g_{\mathcal{R}}(\gamma )}{\gamma +x_i}}=G^{\frac{f\left(x\right)·g_{\mathcal{R}}(\gamma )}{\gamma +x_i}}$ but $(x+x_i)\nmid f\left(x\right)·g_{\mathcal{R}}\left(x\right)$, where $f\left(x\right)·g_{\mathcal{R}}\left(x\right)={\prod }_{e_k\in \mathcal{U}\setminus \mathcal{R}}(x+x_i)$. We construct a PPT algorithm solving the SDH problem as follows: Let $\frac{f\left(x\right)·g_{\mathcal{R}}\left(x\right)}{x+x_i}=q\left(x\right)+\frac{r\left(x\right)}{x+x_i}$ be defined as above, where $q\left(x\right)={\sum }_{i=0}^{n-k-1}{d}_i{x}^i$ and $r\left(x\right)=r$ are two known polynomials. Hence, we can compute the value:

  $$G^{1/(\alpha +x_i)}={(H_{{\mathcal{R}}_{+}}/{\prod }_{i=0}^{n-k-1}{\left(G^{{\alpha }^i}\right)}^{d_i})}^{1/r}$$

  (17)

  because we have $G^{\frac{f(\gamma )·g_{\mathcal{R}}(\gamma )}{\gamma +x_i}}=G^{q(\gamma )}·G^{\frac{r}{\gamma +x_i}}$ and $G^{q(\gamma )}={\prod }_{i=0}^{n-k-1}{\left(G^{{\alpha }^i}\right)}^{d_i}$. The value $(x_i,G^{1/(\alpha +x_i)})$ is a valid output of the t-SDH problem, but it is contradiction with SDH assumption.

Therefore, the PoleAggr function is secure under the t-SDH assumption.    □

5. Secure Decision of Membership

The zeros-based and poles-based representation of the subset have exhibited an ability for the decision of (positive and negative) membership. In this section, we further show that our method is able to provide a clear and concise form for the decision problem of either positive or negative membership when both representations of the subset are used together.

We first present a simple definition for the membership predicate, which is the fundamental principle in our construction of the dual membership decision protocol. Informally, a predicate $P(·)$ is a statement that may be true or false according to the values of its variables. Generally, a predicate over membership is defined as follows:

Definition 9

(Membership Predicate). For $\mathcal{U}=\{e_1,\cdots ,e_N\}$, a membership predicate is a binary function $P:\mathcal{U}\times \mathcal{P}\left(\mathcal{U}\right)\to \{0,1\}$ whose result represents the truth or falsehood of the condition $e\in \mathcal{S}$ ($P_{\in }(e,\mathcal{S})=1$) or $e\notin \mathcal{S}$ ($P_{\notin }(e,\mathcal{S})=1$), where $e\in \mathcal{U}$, $\mathcal{S}\in \mathcal{P}\left(\mathcal{U}\right)$ and the subscript of P denotes the set-membership.

If the condition is defined as $e\in \mathcal{S}$, it is called a positive membership predicate $P_{\in }$. Similarly, if the condition is $e\notin \mathcal{S}$, it is called a negative membership predicate $P_{\notin }$. Next, we define the cryptographic decision problem of positive and negative membership below.

Definition 10

(Secure Decision of Membership, SDM). Let $P(e,\mathcal{S})$ denote a membership predicate for ∈ or ∉. Given an element e and a subset $\mathcal{S}$, we say that a probabilistic polynomial time (PPT) algorithm ${Verify}_P$ is a secure decision of membership if,

• Completeness: if $P(e,\mathcal{S})=1$ holds, then the verifier will accept the proof, that is,

  $$Pr[Verif{y}_P(R_e,C_{\mathcal{S}})=1|P(e,\mathcal{S})=1]=1$$

  (18)
• Soundness: if $P(e^{*},\mathcal{S})=0$ holds, then the verifier will accept the proof with negligible probability ϵ, that is,

  $$Pr[Verif{y}_P(R_{e^{*}},C_{\mathcal{S}})=1|P(e^{*},\mathcal{S})=0]<ϵ$$

  (19)

where, $R_e$ denotes a cryptographic representation of element e and $C_{\mathcal{S}}$ is a cryptographic representation of subset $\mathcal{S}\subset \mathcal{U}$.

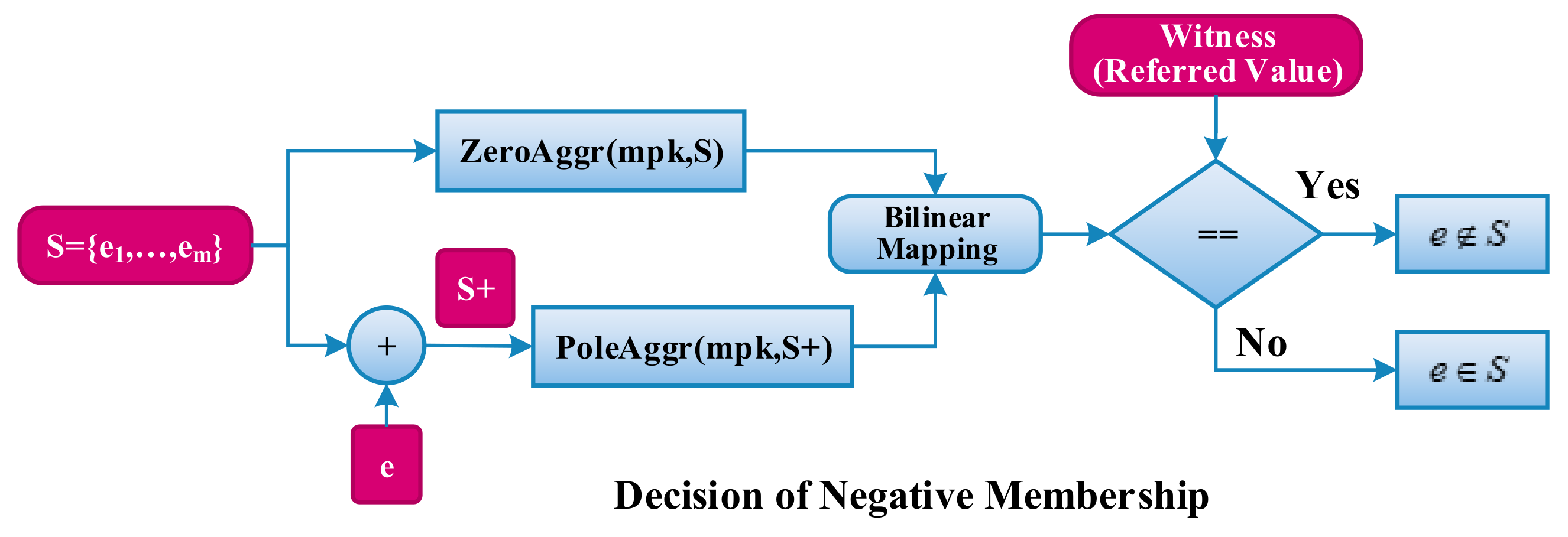
Before discussing the SDM problem, we can observe the fact that ‘zeros’ and ‘poles’ in a rational polynomial function could cancel each other out if and only if zeros and poles are equal. It is this fundamental truth that compels us to combine ZeroAggr and PoleAggr functions together, such that we can verify whether or not the same ‘zeros’ and ‘poles’ exist in these two functions.

We now show how to put zeros-based aggregation and poles-based aggregation together. We use a bilinear mapping $e:\mathbb{G}\times \mathbb{G}\mapsto {\mathbb{G}}_T$ to implement this combination. For any generators $g,h$ in $\mathbb{G}$ and any elements $a,b$ in ${\mathbb{Z}}_p^{*}$, then we have $e(g^a,h^b)=e{(g,h)}^{ab}$. Therefore, let ZeroAggr and PoleAggr work in the group $\mathbb{G}$ in such a bilinear system, so that we integrate two aggregation functions into an element in ${\mathbb{G}}_T$. Such a result value will be further used to make the decision of set-membership.

5.1. SDM for Positive Membership

We now present a practical solution for the SDM problem on positive membership. This solution is built on three algorithms, Setup, Extract, and Verify ${}_{\in }$, as follows:

• Setup: this is a probabilistic algorithm that generates the public key and a secure representation of subset $\mathcal{S}$; that is, $(mpk,H_{\mathcal{S}})\leftarrow Setup(\mathbb{S},\mathcal{U},\mathcal{S})$, where $\mathbb{S}=\{p,\mathbb{G},{\mathbb{G}}_T,e,g,h\}$. Firstly, we randomly pick a secret $\gamma \in {\mathbb{Z}}_p^{*}$ and a positive integer $n\in {\mathbb{Z}}^{+}$, and then generate the public key:

  $$mpk=(g^{\gamma },\cdots ,g^{{\gamma }^n}),$$

  (20)

  as well as the private key $sk=(\gamma )$. Next, given the arbitrary subset $\mathcal{S}=\{e_1,\cdots ,e_m\}$ and $m<n$, we make use of the poles-based aggregation function to compute the value:

  $$H_{\mathcal{S}}\leftarrow PoleAggr(sk,\mathcal{S})=h^{g_{\mathcal{S}}(\gamma )}$$

  (21)

  where $g_{\mathcal{S}}\left(x\right)=\frac{1}{{\prod }_{e_k\in \mathcal{S}}(x+x_k)}$ and $x_k=hash\left(e_k\right)$.
• Extract: this is an algorithm that yields the witness of an arbitrary element $e_i$. We can extract the witness $W_i$ of $e_i$ from the private key $sk$ by using the equation $W_i\leftarrow Extract(sk,e_i)=e{(g,h)}^{\frac{\gamma }{\gamma +x_i}}$.
• Verify ${}_{\in }$: this is a verification algorithm that tests membership of an element $e_i$ that is in the subset $\mathcal{S}$, that is, $Verif{y}_{\in }(W_i,H_{\mathcal{S}})$, where $W_i$ is the witness of $e_i$ and $H_{\mathcal{S}}$ is secure representation of $\mathcal{S}$.

  -

  Firstly, we check the relation $e_i\in \mathcal{S}$. If it holds, we compute ${\mathcal{S}}_{-}=\mathcal{S}\setminus \left\{e_i\right\}$ and:

  $$G_{{\mathcal{S}}_{-}}\leftarrow ZeroAggr(mpk,{\mathcal{S}}_{-})=g^{f_{{\mathcal{S}}_{-}}(\gamma )}=g^{\gamma \frac{{\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}{\gamma +x_i}}.$$

  (22)

  -

  Secondly, we check whether or not the witness $W_i$ is equal to $e(G_{{\mathcal{S}}_{-}},H_{\mathcal{S}})$, that is:

  $$W_i\stackrel{?}{=}e(G_{{\mathcal{S}}_{-}},H_{\mathcal{S}}).$$

  (23)

  If the above equation holds, we say that $e_i\in \mathcal{S}$; otherwise, we say that $e_i\notin \mathcal{S}$.

The above solution for SDM over the positive membership is described by Figure 2. Firstly, the poles-based representation of subset $H_{\mathcal{S}}$ is generated by using $PoleAggr\left(\mathcal{S}\right)$ for a given subset $\mathcal{S}$. Secondly, given an element $e_i$, we extract the value $W_i\leftarrow Extract(sk,e_i)$ as the witness of $e_i$. Next, the zeros-based representation $G_{{\mathcal{S}}_{-}}$ of ${\mathcal{S}}_{-}=\mathcal{S}\setminus \left\{e_i\right\}$ is also yielded if $e_i$ is in $\mathcal{S}$. Then, the bilinear map between $H_{\mathcal{S}}$ and $G_{{\mathcal{S}}_{-}}$ is used to remove all of the same elements between the two corresponding subsets, $\mathcal{S}$ and ${\mathcal{S}}_{-}$. Finally, the final decision is realized by matching the above result of the bilinear map and witness $W_i$.

In this solution, any adversary cannot cheat or forge the final decisional result based on the theorem below.

Theorem 3.

The above construction is a secure decision of positive membership if the ZeroAggr function is a secure zeros-based aggregator.

Proof. 

According the Definition 10, we prove that our construction satisfies the two following properties:

• Completeness: When $e_i\in \mathcal{S}$, the Equation (23) holds for all valid $G_{{\mathcal{S}}_{-}}$ in terms of:

  $$e(G_{{\mathcal{S}}_{-}},H_{\mathcal{S}})=e(g^{f_{{\mathcal{S}}_{-}}(\gamma )},h^{g_{\mathcal{S}}(\gamma )})=e(g^{\gamma \frac{{\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}{\gamma +x_i}},h^{\frac{1}{{\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}})=e{(g,h)}^{\frac{\gamma }{\gamma +x_i}}=W_i.$$

  (24)
• Soundness: According to the precondition of this theorem, we assume that the ZeroAggr function is a secure zeros-based aggregation. This means that for every PPT adversary $\mathcal{A}$ (see Definition 5), then:

  $$Pr[\mathcal{A}(mpk,e_i^{*},\mathcal{S})=G_{{\mathcal{S}}_{-}}|e_i^{*}\notin \mathcal{S}]<ϵ$$

  (25)

  for any given element $e_i^{*}\notin \mathcal{S}$. We will prove that the verifier accepts the verification with negligible probability $ϵ$; that is, $Pr[Verif{y}_{\in }(W_i,H_{\mathcal{S}})=1]<ϵ$, where $W_i$ and $H_{\mathcal{S}}$ are two assured and unchanged values. We also know that $W_i=e{(g,h)}^{\frac{\gamma }{\gamma +x_i^{*}}}$ and $H_{\mathcal{S}}=h^{\frac{1}{{\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}}$, where $x_i^{*}=hash\left(e_i^{*}\right)$. This means that the adversary can forge a valid $G^{*}$ to meet the equation: $Pr[Verif{y}_{\in }(W_i,H_{\mathcal{S}})=1]=Pr[e{(g,h)}^{\frac{\gamma }{\gamma +x_i^{*}}}=e(G^{*},h^{\frac{1}{{\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}})]$. Without loss of generality, let $G^{*}=g^z$, so that we have the probability:

  $$\begin{array}{c}{\displaystyle Pr[Verif{y}_{\in }(W_i,H_{\mathcal{S}})=1]}\hfill \\ =Pr[e{(g,h)}^{\frac{\gamma }{\gamma +x_i^{*}}}=e(G^{*},h^{\frac{1}{{\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}})]\hfill \\ \stackrel{G^{*}=g^z}{=}Pr\left[\begin{array}{c}e(g,h)=e{(g,h)}^{\frac{z(\gamma +x_i^{*})}{\gamma {\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}}|\\ g^z\leftarrow \mathcal{A}(mpk,e_i^{*},\mathcal{S})\end{array}\right]·Pr[g^z\leftarrow \mathcal{A}(mpk,e_i^{*},\mathcal{S})]\hfill \\ =Pr\left[\mathcal{A}(mpk,e_i^{*},\mathcal{S})\to g^z=g^{\gamma \frac{{\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}{\gamma +x_i^{*}}}\right]\hfill \\ =Pr[\mathcal{A}(mpk,e_i^{*},\mathcal{S})=G_{S_{-}}|e_i^{*}\notin \mathcal{S}]<ϵ.\hfill \end{array}$$

  (26)
  In this equation, we require the relation $\frac{z(\gamma +x_i^{*})}{\gamma {\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}=1$ to make:

  $$Pr\left[e(g,h)=e{(g,h)}^{\frac{z(\gamma +x_i^{*})}{\gamma {\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}}\right]=1.$$

  (27)
  In this case, $z=\gamma \frac{{\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}{\gamma +x_i^{*}}$ and $G_{{\mathcal{S}}_{-}}=g^z$.

This means that the adversary’s advantage to break a secure decision of positive membership is equal to the advantage of breaking the secure zeros-based aggregator.    □

5.2. SDM for Negative Membership

We next present a practical solution for the SDM problem over negative membership. This solution is similar to the previous SDM over positive membership. We also present this solution by the three following algorithms:

• Setup: this algorithm generates the public key and a secure representation of subset $\mathcal{S}$; that is, $(mpk,G_{\mathcal{S}})\leftarrow Setup(\mathbb{S},\mathcal{U},\mathcal{S})$. Firstly, we randomly pick a secret $\gamma \in {\mathbb{Z}}_p^{*}$ and a positive integer $n\in {\mathbb{Z}}^{+}$, and generates the public key:

  $$mpk=(h^{\frac{1}{\gamma +x_1}},\cdots h^{\frac{1}{\gamma +x_n}}),$$

  (28)

  as well as the private key $sk=(\gamma )$. Next, given an arbitrary subset $\mathcal{S}=\{e_1,\cdots ,e_m\}$, we make use of the zeros-based aggregation function to compute the value:

  $$G_{\mathcal{S}}\leftarrow ZeroAggr\left(\mathcal{S}\right)=g^{f_{\mathcal{S}}(\gamma )},$$

  (29)

  where $f_{\mathcal{S}}(\gamma )=\gamma {\prod }_{e_k\in \mathcal{S}}(x+x_k)$ and $x_k=hash\left(e_k\right)$.
• Extract: this is an algorithm that yields the witness of element $e_i$. We can extract the witness $W_i$ of $e_i$ from $sk$ as $W_i\leftarrow Extract(sk,e_i)=e{(g,h)}^{\frac{\gamma }{\gamma +x_i}}$.
• Verify ${}_{\notin }$: this is a verification algorithm that tests the membership of an element $e_i$ that is in the subset $\mathcal{S}$; that is, $Verif{y}_{\notin }(W_i,G_{\mathcal{S}})$, where $W_i$ is the witness of $e_i$ and $G_{\mathcal{S}}$ is a secure representation of $\mathcal{S}$.

  -

  Firstly, we check the relation $e_i\notin \mathcal{S}$. If it holds, we compute ${\mathcal{S}}_{+}=\mathcal{S}\cup \left\{e_i\right\}$ and:

  $$H_{{\mathcal{S}}_{+}}\leftarrow PoleAggr(mpk,{\mathcal{S}}_{+})=h^{g_{{\mathcal{S}}_{+}}(\gamma )}=h^{\frac{1}{(\gamma +x_i)·{\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}}.$$

  (30)

  -

  Secondly, we check whether or not the witness $W_i$ is equal to $e(G_{{\mathcal{S}}_{+}},H_{\mathcal{S}})$, that is:

  $$W_i\stackrel{?}{=}e(G_{\mathcal{S}},H_{{\mathcal{S}}_{+}}).$$

  (31)

  If the above equation holds, we say that $e_i\notin \mathcal{S}$; otherwise, we say that $e_i\in \mathcal{S}$.

As shown above, Figure 3 has almost the same structure as that in Figure 2. It is an important property to help us combine them (SDMP and SDMN) into one cryptographic protocol (see our membership decision ZKP protocol in next section). However, when we carefully inspect the details, there also exist two differences between SDM for Pos-and-Neg membership. One is that both positions of two aggregation functions, ZeroAggr and PoleAggr, are swapped with each other; and another is that the ‘+’ operation in Figure 3 takes the place of the ‘–’ operation in Figure 2.

Next, we prove that our solution is secure against cheating or forgery according to the theorem below.

Theorem 4.

The above construction is a secure decision of negative membership if the PoleAggr function is a secure poles-based aggregator.

Proof. 

In terms of the definition of SDM, we prove tha our construction satisfies the two following properties:

• Completeness: When $e_i\notin \mathcal{S}$, the Equation (31) holds for all valid $H_{{\mathcal{S}}_{+}}$ in terms of:

  $$\begin{array}{c}\hfill e(G_{\mathcal{S}},H_{{\mathcal{S}}_{+}})=e(g^{f_{\mathcal{S}}(\gamma )},h^{g_{{\mathcal{S}}_{+}}(\gamma )})=e(g^{\gamma {\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)},h^{\frac{1}{(\gamma +x_i)·{\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}})=e{(g,h)}^{\frac{\gamma }{\gamma +x_i}}=W_i.\end{array}$$

  (32)
• Soundness: According to the precondition of this theorem, we assume that the ZeroAggr function is a secure zeros-based aggregation. This means that for every PPT adversary $\mathcal{A}$ (see Definition 8):

  $$Pr[\mathcal{A}(mpk,e_i^{*},\mathcal{S})=H_{{\mathcal{S}}_{+}}|e_i^{*}\in \mathcal{S}]<ϵ$$

  (33)

  for a given element $e_i^{*}\in \mathcal{S}$. We will prove that the verifier accepts the verification with negligible probability $ϵ$; that is, $Pr[Verif{y}_{\notin }(W_i,G_{\mathcal{S}})=1]<ϵ$, where $W_i$ and $G_{\mathcal{S}}$ are two assured and unchanged values. We also know that $W_i=e{(g,h)}^{\frac{\gamma }{\gamma +x_i^{*}}}$ and $G_{\mathcal{S}}=g^{\gamma {\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}$, where $x_i^{*}=hash\left(e_i^{*}\right)$. In this case, the adversary can forge a valid $H^{*}$ to meet the equation: $Pr[Verif{y}_{\notin }(W_i,G_{\mathcal{S}})=1]=Pr[e{(g,h)}^{\frac{\gamma }{\gamma +x_i^{*}}}=e(g^{\gamma {\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)},H^{*})]$. Without loss of generality, we let $H^{*}=h^z$, so that:

  $$\begin{array}{c}{\displaystyle Pr[Verif{y}_{\notin }(W_i,G_{\mathcal{S}})=1]}\hfill \\ =Pr[e{(g,h)}^{\frac{\gamma }{\gamma +x_i^{*}}}=e(g^{\gamma {\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)},H^{*})]\hfill \\ \stackrel{H^{*}=h^z}{=}Pr\left[\begin{array}{c}e{(g,h)}^{\frac{\gamma }{\gamma +x_i^{*}}}=e{(g,h)}^{z\gamma {\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}|\\ h^z\leftarrow \mathcal{A}(mpk,e_i^{*},\mathcal{S})\end{array}\right]·Pr[h^z\leftarrow \mathcal{A}(mpk,e_i^{*},\mathcal{S})]\hfill \\ =Pr\left[\mathcal{A}(mpk,e_i^{*},\mathcal{S})\to h^z=h^{\frac{1}{(\gamma +x_i^{*}){\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}}\right]\hfill \\ =Pr[\mathcal{A}(mpk,e_i^{*},\mathcal{S})=H_{{\mathcal{S}}_{+}}|e_i^{*}\in \mathcal{S}]<ϵ.\hfill \end{array}$$

  (34)
  In this equation, we require the relation $\frac{\gamma }{\gamma +x_i^{*}}=z\gamma {\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)$ to make the probability $Pr\left[e{(g,h)}^{\frac{\gamma }{\gamma +x_i^{*}}}=e{(g,h)}^{z\gamma {\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}\right]=1$, such that $z=\frac{1}{(\gamma +x_i^{*}){\prod }_{e_k\in \mathcal{S}}(\gamma +x_k)}=\frac{1}{{(\gamma +x_i^{*})}^2{\prod }_{e_k\in \mathcal{S}\setminus \left\{e_i^{*}\right\}}(\gamma +x_k)}$ and $H_{{\mathcal{S}}_{+}}=h^z$.

This means that the adversary’s advantage to break secure decisions of negative membership is equal to the advantage of breaking secure poles-based aggregation.    □

Based on the above security analysis of SDM, the computational complexity of $\alpha$ is $\mathcal{O}(logp·(\sqrt{(p/d)}+d))$ operations in the group $\mathbb{G}$ and the complexity of space is $\mathcal{O}(max\{\sqrt{p/d},\sqrt{d}\})$, where p is the order of the group $\mathbb{G}$ and d is a factor of $p+1$. Obviously, the number of elements in the subset is determined by d, and the security of the SDM is ensured by p, which contains a large factor (e.g., $d\le p^{1/3}$). For example, when $p\approx 2^{512}$ and $d\approx 2^{170}$, the complexity of recovering the secret in the private key is still $\mathcal{O}\left(2^{170}\right)$. At this time, the number of elements in the set can reach $2^{170}\approx {10}^{51}$, which means that the number of elements is unlimited in practical applications.

In all, it is easy to see that the decision problems of Pos-and-Neg membership are converted into the problems of effective computation of $G_{{\mathcal{S}}_{-}}$ and $H_{{\mathcal{S}}_{+}}$ from the two above-mentioned solutions. More importantly, these two solutions have nearly the same structure from the view of Figure 2 and Figure 3, for the reason that we easily combine the predicate ∈ and ∉ into a cryptosystem. In the next section, we also apply for this approach to construct a dual membership proof protocol.

6. Zero-Knowledge Dual Membership Proof Protocol

Our ZKDMP protocol is described by an interactive proof system between the prover and verifier. We assume that the verifier holds a public set of elements $\mathcal{S}$ and the prover owns a secret element e. The prover proves to the verifier the element $e\in \mathcal{S}$ or $e\notin \mathcal{S}$ without revealing the element itself.

Definition 11.

Given two parties, Prover (P) and Verifier (V), the protocol is a secure membership decision over the universal set $\mathcal{U}$ for a certain element e and a subset $\mathcal{S}\subset \mathcal{U}$, if it satisfies the three following properties:

• Positive Completeness: For the positive membership $e\in \mathcal{S}$ and the honest prover, the verifier outputs $True$ with probability at least $1-ϵ$ after interacting with prover, where ϵ is a neglectable probability, i.e.,

  $$Pr[\langle P(e),V(\mathcal{S})\rangle =True|e\in \mathcal{S}]\ge 1-ϵ.$$

  (35)
• Negative Completeness: For the negative membership $e\in \overline{\mathcal{S}}$ ($e\notin \mathcal{S}$ and $e\in \mathcal{U}$) and the honest prover, the verifier outputs $False$ with probability at least $1-{ϵ}^{\prime }$ after interacting with prover, where ${ϵ}^{\prime }$ is a neglectable probability, i.e.,

  $$Pr[\langle P\left(e\right),V\left(\mathcal{S}\right)\rangle =False|e\in \overline{\mathcal{S}}]\ge 1-{ϵ}^{\prime }.$$

  (36)
• Soundness: For any inefficient $e^{*}\notin \mathcal{U}$ and any prover $P^{*}$, the verifier outputs $True$ or $False$ with probability at most ${ϵ}^{″}$ after interacting with prover, where ${ϵ}^{″}$ is a neglectable probability, i.e.,

  $$Pr[\langle P^{*}\left(e^{*}\right),V\left(\mathcal{S}\right)\rangle =True\vee False|e^{*}\notin \mathcal{U}]<{ϵ}^{\prime \prime }.$$

  (37)
  We define a new output state ⊥ that denotes $e^{*}$ is irrelevant to the set $\mathcal{U}$. Hence, according to the soundness property, we define this state as the output of the interactive proof system under $e^{*}\notin \mathcal{U}$, i.e.,

  $$Pr[\langle P^{*}\left(e^{*}\right),V\left(\mathcal{S}\right)\rangle =\perp |e^{*}\notin \mathcal{U}]\ge 1-{ϵ}^{\prime \prime }.$$

  (38)
• Zero-knowledge [33]: For any verifier $V^{*}$, there is a PPT machine ${\mathcal{M}}^{*}$ such that the following two probability distributions are statistically indistinguishable.

  -

  $\left\{\langle P,V^{*}\rangle \left(e\right)\right\}$ denotes the output of the interactive proof system in the $V^{*}$ view on common input e.

  -

  $\left\{{\mathcal{M}}^{*}\left(e\right)\right\}$ is the output of machine ${\mathcal{M}}^{*}$ on input e.

  The statistical indistinguishability of the above two probability distributions can be denoted as $\left\{\langle P,V^{*}\rangle \left(e\right)\right\}\cong \left\{{\mathcal{M}}^{*}\left(e\right)\right\}$.

Note that the output of ZKDMP protocol involves three cases: $True$ denotes positive membership ($e\in \mathcal{S}$), $False$ denotes negative membership ($e\notin \mathcal{S}$ and $e\in \mathcal{U}$) and ⊥ denotes invalid membership ($e\notin \mathcal{U}$). We call it a strict Pos-and-Neg membership decision.

6.1. The Proposed Protocol

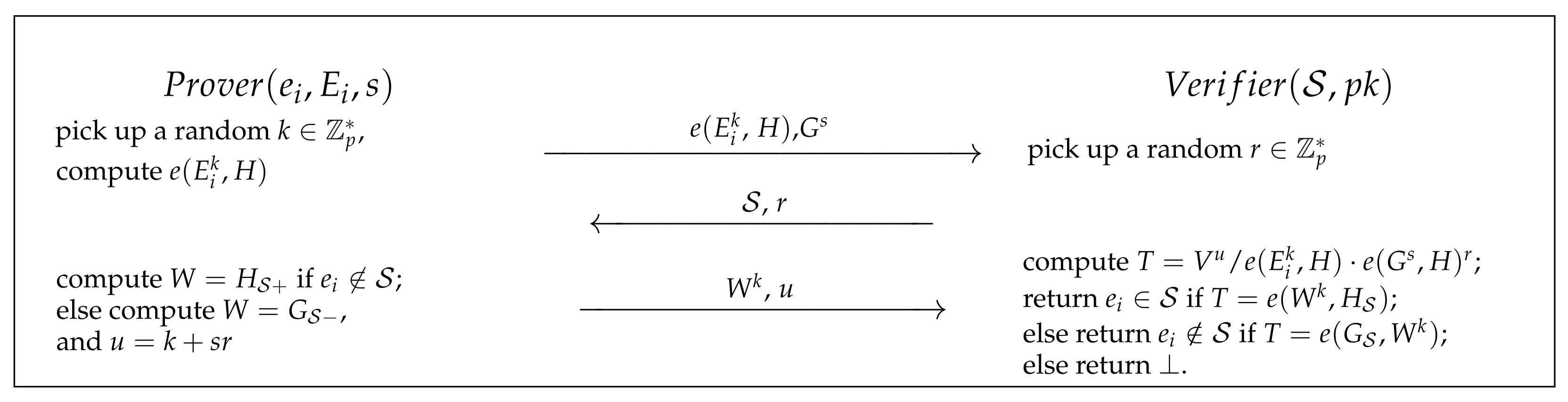
In our ZKDMP protocol, as shown in Figure 4, we choose $\mathbb{S}=(p,\mathbb{G},{\mathbb{G}}_T,e(·,·))$, G is a generator in $\mathbb{G}$ and the prime p is the order of the group. Furthermore, for any identity $e_i\in {\{0,1\}}^{*}$, the hash function can compute $hash\left(e_i\right)=x_i\in {\mathbb{Z}}_p^{*}$, where a collision-resistant hash function is used to prevent two different elements from mapping into a same value, i.e., for any $e_i\ne e_j$, $hash\left(e_i\right)\ne h\left(e_j\right)$. Detailed construction of our protocol can be found below.

• Setup ($\mathbb{S},\mathcal{U}$). Let G denote a generator in $\mathbb{G}$, the Setup algorithm chooses $\delta$ in ${\mathbb{Z}}_p^{*}$, then it sets $H=G^{\delta }$ and $V=e(G,H)$. Furthermore, the algorithm picks $\gamma$ in ${\mathbb{Z}}_p^{*}$ and sets $G_j=G^{{\gamma }^j}$ for $j\in [1,|\mathcal{U}\left|\right]$. For any $e_i\in \mathcal{U}$, this algorithm computes $x_i=hash\left(e_i\right)$ and $H_i=H^{\frac{1}{\gamma +x_i}}$ and outputs the master key $msk=(\delta ,\gamma ,G)$. Finally, it publishes $mpk=\left\{\mathbb{S},\mathcal{U},{\left\{G_j\right\}}_{j\in [1,|\mathcal{U}\left|\right]},{\left\{H_i\right\}}_{e_i\in \mathcal{U}},H,V\right\}.$
• Protocol. The complete protocol is divided into the following three stages:
  Initial stage: The prover random chooses $e_i\in \mathcal{U}$ and $s\in {\mathbb{Z}}_p^{*}$, then the manager computes the witness $E_i=G^{\frac{x_i}{\gamma +x_i}}$ and the commitment $G^s$ by using the master key. Finally, the manager sends $E_i$ and $G_s$ to the prover and the verifier, respectively. The verifier also chooses a subset $\mathcal{S}$ from the universal set $\mathcal{U}$.
  Interactive-proof stage: Based on the three-move structure in $\Sigma$-protocols, our proposed protocol is described below.

  -

  Commitment: Prover randomly picks $k\in {\mathbb{Z}}_p^{*}$ and computes $e(E_i^k,H)$, then it sends this calculation result to the verifier;

  -

  Challenge: Verifier randomly selects r in ${\mathbb{Z}}_p^{*}$, then sends $(\mathcal{S},r)$ to the prover;

  -

  Response: Prover computes $(u,W^k)$ and sends them to the verifier as the responses, where $u=k+sr$,

  $$W=\left\{\begin{array}{cc}{G}_{\mathcal{S}-}=ZeroAggr(mpk,\mathcal{S}\setminus \left\{e_i\right\})& e_i\in \mathcal{S},\\ H_{\mathcal{S}+}=PoleAggr(mpk,\mathcal{S}\cup \left\{e_i\right\})& e_i\notin \mathcal{S}.\end{array}\right.$$

  (39)

  Verification stage: The verifier computes $T=V^u/e(E_i^k,H)·e(G_s^r,H)$, and returns True if $T=e(W^k,H_{\mathcal{S}})$, else False if $T=e(G_{\mathcal{S}},W^k)$, otherwise ⊥, where $G_{\mathcal{S}}=ZeroAggr(mpk,\mathcal{S})$ and $H_{\mathcal{S}}=PoleAggr(mpk,\mathcal{S})$.

6.2. Security Analysis

According the Definition 11, we prove that the proposed membership decision protocol satisfies the following four properties.

(1) Positive Completeness: When $e_i\in \mathcal{S}$, we have the following equation:

$$\begin{array}{cc}\hfill & e(E_i^k,H)·e(G_s^r,H)·e(W^k,H_{\mathcal{S}})\hfill \\ \hfill =& e(G^{\frac{x_i·k}{\gamma +x_i}},H)·e(G^{sr},H)·e(G_{\mathcal{S}-}^k,H_{\mathcal{S}})\hfill \\ \hfill =& e(G^{\frac{x_i·k}{\gamma +x_i}},H)·e(G^{sr},H)·e(G^{\frac{f_{\mathcal{S}}(\gamma )k}{\gamma +x_i}},H^{\frac{1}{g_{\mathcal{S}}(\gamma )}})\hfill \\ \hfill =& e{(G,H)}^{k+sr}=V^u\hfill \end{array}$$

(40)

Then, the verifier can output $True$ with probability:

$$\begin{array}{c}\hfill Pr[\langle P\left(e\right),V\left(\mathcal{S}\right)\rangle =True|e\in \mathcal{S}]=Pr[e(E_i^k,H)·e(G_s^r,H)·e(W^k,H_{\mathcal{S}})=V^u|e\in \mathcal{S}]=1.\end{array}$$

(41)

(2) Negative Completeness: When $e_i\in \overline{\mathcal{S}}$, we have the following equation:

$$\begin{array}{cc}\hfill & e(E_i^k,H)·e(G_s^r,H)·e(G_{\mathcal{S}},W^k)\hfill \\ \hfill =& e(G^{\frac{x_i·k}{\gamma +x_i}},H)·e(G^{sr},H)·e(G_{\mathcal{S}},H_{\mathcal{S}+}^k)\hfill \\ \hfill =& e(G^{\frac{x_i·k}{\gamma +x_i}},H)·e(G^{sr},H)·e(G^{f_{\mathcal{S}(\gamma )}},H^{\frac{k}{g_{\mathcal{S}}(\gamma )·(\gamma +x_i)}})\hfill \\ \hfill =& e{(G,H)}^{k+sr}=V^u\hfill \end{array}$$

(42)

Then, the verifier can output $False$ with probability:

$$Pr[\langle P\left(e\right),V\left(\mathcal{S}\right)\rangle =False|e\in \overline{\mathcal{S}}]=Pr[e(E_i^k,H)·e(G_s^r,H)·e(G_{\mathcal{S}},W^k)|e\in \overline{\mathcal{S}}]=1.$$

(43)

(3) Soundness: Before proving the soundness of the proposed protocol, we firstly define the following events.

• Event $A_1$ denotes $\langle P^{*}\left(e^{*}\right),V\left(\mathcal{S}\right)\rangle =True$.
• Event $A_2$ denotes $\langle P^{*}\left(e^{*}\right),V\left(\mathcal{S}\right)\rangle =False$.
• Event A denotes $A_1\cup A_2$.
• Event $B_1$ denotes $e^{*}\notin \mathcal{S}$.
• Event $B_2$ denotes $e^{*}\notin \overline{\mathcal{S}}$, i.e., $(e^{*}\in \mathcal{S})\cup (e^{*}\notin \mathcal{U})$.
• Event B denotes $e^{*}\notin \mathcal{U}$, i.e., B is the joint of events $B_1$ and $B_2$, $B=B_1{B}_2$.

In this case, $A_1$ and $A_2$ are mutual exclusive events, i.e., $A_1{A}_2=\varnothing$, the Equation (37) can be written as:

$$\begin{array}{cc}\hfill & Pr[\langle P^{*}\left(e^{*}\right),V\left(\mathcal{S}\right)\rangle =True\vee False|e^{*}\notin \mathcal{U}]\hfill \\ \hfill =& Pr\left[A\right|B]=Pr\left[(A_1\cup A_2)\right|B]\hfill \\ \hfill =& \frac{Pr\left[(A_1\cup A_2)B\right]}{Pr\left[B\right]}=\frac{Pr[\left(A_{1}B\right)\cup \left(A_{2}B\right)]}{Pr\left[B\right]}\hfill \\ \hfill =& \frac{Pr\left[A_{1}B\right]+Pr\left[A_{2}B\right]}{Pr\left[B\right]}.\hfill \end{array}$$

(44)

For any $e^{*}\notin \mathcal{U}$, we get $Pr\left[B\right]=1$. Thus, the above equation:

$$Pr\left[A\right|B]=(Pr\left[A_{1}B\right]+Pr\left[A_{2}B\right])/Pr\left[B\right]=Pr\left[A_1{B}_1{B}_2\right]+Pr\left[A_2{B}_1{B}_2\right]\le Pr\left[A_1{B}_1\right]+Pr\left[A_2{B}_2\right].$$

(45)

Let $Pr\left[A_1{B}_1\right]={ϵ}_1$ and $Pr\left[A_2{B}_2\right]={ϵ}_2$. Assuming that both ${ϵ}_1$ and ${ϵ}_2$ are neglectable, then $Pr\left[A\right|B]$ is also neglectable. In this case, the soundness of our protocol can be proven. In the following, we show that the above assumption is correct, i.e., both $Pr\left[A_1{B}_1\right]={ϵ}_1$ and $Pr\left[A_2{B}_2\right]={ϵ}_2$ are neglectable.

Proof. 

For any $e^{*}\notin \mathcal{U}$, we have $Pr\left[B_1\right]=1$ and $Pr\left[A_1{B}_1\right]=\frac{Pr\left[A_1\right|B_1]}{Pr\left[B_1\right]}=Pr\left[A_1\right|B_1]$. Thus, we have:

$$Pr\left[A_1{B}_1\right]=Pr\left[A_1\right|B_1]=Pr[\langle P\left(e^{*}\right),V\left(\mathcal{S}\right)\rangle =\mathrm{True}|e^{*}\notin \mathcal{S}]=Pr[T=e(W^k,H_{\mathcal{S}})|e^{*}\notin \mathcal{S}]={ϵ}_1.$$

(46)

  

We prove that the verifier accepts the positive verification with probability ${ϵ}_1$ for the given $e^{*}\notin \mathcal{S}$. It means that a PPT adversary $\mathcal{A}$ can forge W to make the verifier successfully verify $T=e(W^k,H_{\mathcal{S}})$ with probability ${ϵ}_1$. We know that $H_{\mathcal{S}}=H^{\frac{1}{f_{\mathcal{S}}(\gamma )}}$ is an assured and unchanged value. This means that the adversary $\mathcal{A}$ can forge a valid W to meet the equation: $Pr[T=e(W^k,H_{\mathcal{S}})]=Pr[V^u/e(E_{*}^k,H)e(G_s^r,H)=e(W^k,H_{\mathcal{S}})]$. Without loss of generality, let $W=G^z$, so we have the following probability.

$$\begin{array}{c}{\displaystyle Pr[T=e(W^k,H_{\mathcal{S}})]}\hfill \\ =Pr[V^u/e(E_{*}^k,H)e(G_s^r,H)=e(W^k,H_{\mathcal{S}})]\hfill \\ =Pr[V^u=e(W^k,H_{\mathcal{S}})·e(E_{*}^k,H)·e(G_s^r,H)]\hfill \\ =Pr[e{(G,H)}^{k+sr}=e(W^k,H^{\frac{1}{f_{\mathcal{S}}(\gamma )}})·e(G^{\frac{x_{*}k}{\gamma +x_{*}}},H)·e(G^{sr},H)]\hfill \\ \stackrel{W=G^z}{=}Pr\left[\begin{array}{c}e{(G,H)}^{k+sr}=e{(G,H)}^{\frac{zk}{f_{\mathcal{S}}(\gamma )}+\frac{x^{*}k}{\gamma +x^{*}}+sr}|\\ G^z\leftarrow \mathcal{A}(mpk,e^{*},\mathcal{S})\end{array}\right]·Pr[G^z\leftarrow \mathcal{A}(mpk,e^{*},\mathcal{S})]\hfill \\ =Pr\left[\mathcal{A}(mpk,e^{*},\mathcal{S})\to G^z=G^{\frac{\gamma f_{\mathcal{S}}(\gamma )}{\gamma +x^{*}}}\right]\hfill \\ =Pr[\mathcal{A}(mpk,e^{*},\mathcal{S})=G_{{\mathcal{S}}_{-}}|e^{*}\notin \mathcal{S}]={ϵ}_1.\hfill \end{array}$$

(47)

In the above equation, we require $\frac{zk}{f_{\mathcal{S}}(\gamma )}+\frac{x^{*}k}{\gamma +x^{*}}=k$ to make:

$$Pr\left[e{(G,H)}^u=e{(G,H)}^{\frac{zk}{f_{\mathcal{S}}(\gamma )}+\frac{x^{*}k}{\gamma +x^{*}}+sr}\right]=1,$$

(48)

such that $z=\frac{\gamma f_{\mathcal{S}}(\gamma )}{\gamma +x^{*}}$ and $G_{{\mathcal{S}}_{-}}=G^z=W$. If the probability ${ϵ}_1$ is non-neglectable, this means that the adversary $\mathcal{A}$ can secure zeros-based aggregation with a non-neglectable advantage ${ϵ}_1$, that is contradictory to the Theorem 1. Thus, ${ϵ}_1$ is neglectable.

For any $e^{*}\notin \mathcal{U}$, we have $Pr\left[B_2\right]=1$ and $Pr\left[A_2{B}_2\right]=\frac{Pr\left[A_2\right|B_2]}{Pr\left[B_2\right]}=Pr\left[A_2\right|B_2]$, so that we have the probability:

$$Pr\left[A_2{B}_2\right]=Pr\left[A_2\right|B_2]=Pr[\langle P\left(e^{*}\right),V\left(\mathcal{S}\right)\rangle =\mathrm{False}|e^{*}\notin \overline{\mathcal{S}}]=Pr[T=e(G_{\mathcal{S}},W^k)|e^{*}\notin \overline{\mathcal{S}}]={ϵ}_2.$$

(49)

We next prove that the verifier accepts the negative verification with probability ${ϵ}_2$ for given $e^{*}\notin \overline{\mathcal{S}}$, i.e., $e^{*}\in \mathcal{S}$ or $e^{*}\notin \mathcal{U}$. It means that a PPT adversary $\mathcal{A}$ can forge W to make the verifier successfully verify $T=e(G_{\mathcal{S}},W^k)$ with probability ${ϵ}_2$. We know that $G_{\mathcal{S}}=G^{\gamma f_{\mathcal{S}}(\gamma )}$ is an assured and unchanged value. This means that the adversary $\mathcal{A}$ can forge a valid W to meet the equation: $Pr[T=e(G_{\mathcal{S}},W^k)]=Pr[V^u/e(E_{*}^k,H)e(G_s^r,H)=e(G_{\mathcal{S}},W^k)]$. Without loss of generality, let $W=H^z$, that we have the following probability.

$$\begin{array}{cc}\hfill & Pr\left[T=e(G_{\mathcal{S}},W^k)\right]\hfill \\ \hfill =& Pr\left[V^u/e(E_{*}^k,H)e(G_s^r,H)=e(G_{\mathcal{S}},W^k)\right]\hfill \\ \hfill =& Pr\left[V^u=e(G_{\mathcal{S}},W^k)·e(E_{*}^k,H)·e(G_s^r,H)\right]\hfill \\ \hfill =& Pr[e{(G,H)}^{k+sr}=e(G^{\gamma f_{\mathcal{S}}(\gamma )},W^k)·e(G^{\frac{x^{*}k}{\gamma +x^{*}}},H)·e(G^{sr},H)]\hfill \\ \hfill & \stackrel{W=H^z}{=}Pr\left[\begin{array}{c}e{(G,H)}^{k+sr}=e{(G,H)}^{\gamma f_{\mathcal{S}}(\gamma )zk+\frac{x^{*}k}{\gamma +x^{*}}+sr}|\\ G^z\leftarrow \mathcal{A}(mpk,e^{*},\mathcal{S})\end{array}\right]·Pr\left[G^z\leftarrow \mathcal{A}(mpk,e^{*},\mathcal{S})\right]\hfill \\ \hfill =& Pr\left[\mathcal{A}(mpk,e^{*},\mathcal{S})\to H^z=H^{\frac{1}{(\gamma +x^{*})f_{\mathcal{S}}(\gamma )}}\right]\hfill \\ \hfill =& Pr\left[\mathcal{A}(mpk,e^{*},\mathcal{S})=H_{{\mathcal{S}}_{+}}|e^{*}\notin \overline{\mathcal{S}}\right]={ϵ}_2.\hfill \end{array}$$

(50)

In this equation, we require $\gamma f_{\mathcal{S}}(\gamma )zk+\frac{x^{*}k}{\gamma +x^{*}}=k$ to make:

$$Pr\left[e{(G,H)}^k=e{(G,H)}^{zk\gamma f_{\mathcal{S}}(\gamma )+\frac{x^{*}k}{\gamma +x^{*}}}\right]=1,$$

(51)

such that $z=\frac{1}{(\gamma +x^{*})f_{\mathcal{S}}(\gamma )}$ and $H_{{\mathcal{S}}_{-}}=H^z=W$. For any $e^{*}\notin \overline{\mathcal{S}}$ ($e^{*}\in \mathcal{S}$ or $e^{*}\notin \mathcal{U}$) the Equation (50) holds. If $e^{*}\in \mathcal{S}$ and the probability ${ϵ}_2$ is non-neglectable, this means that the adversary $\mathcal{A}$ can break secure poles-based aggregation with a non-neglectable advantage ${ϵ}_2$, that is contradictory to the Theorem 2. Thus, ${ϵ}_2$ is neglectable.

Therefore, ${ϵ}_1$ and ${ϵ}_2$ are neglectable, so $Pr\left[A\right|B]\le {ϵ}_1+{ϵ}_2$ is also neglectable, it means that:

$$Pr[\langle P^{*}\left(e^{*}\right),V\left(\mathcal{S}\right)\rangle =True\vee False|e^{*}\notin \mathcal{U}]\le {ϵ}_1+{ϵ}_2.$$

(52)

The soundness of our ZKDMP protocol is proved.    □

(4) Zero-knowledge: The zero-knowledge of our membership decision protocol implies that the verifier cannot learn any information of the tested element e beyond that $e\in \mathcal{S}$, $e\in \overline{\mathcal{S}}$ or $e\notin \mathcal{U}$.

Theorem 5.

The proposed dual membership decision is a zero-knowledge proof protocol.

Proof. 

Let $Vie{w}_{V^{*}}\left(e_i\right)$ be the output of the interactive proof system in $V^{*}$ view on common input $e_i$, the distribution of $Vie{w}_{V^{*}}\left(e_i\right)$ during the correct executing of our protocol can be denoted as:

$$Vie{w}_{V^{*}}\left(e_i\right)=\left\{\langle P,V^{*}\rangle \left(e_i\right)\right\}=\{Y,\mathcal{S},r,W^k,u\}{\in }_R\{{\mathbb{G}}_T,\mathcal{P}\left(\mathcal{U}\right),{\mathbb{Z}}_p^{*},\mathbb{G},{\mathbb{Z}}_p^{*}\}.$$

(53)

In the above equation, $Y=e(E_i^k,H)$ and $\mathcal{P}\left(\mathcal{U}\right)$ is the power set of $\mathcal{U}$. Next, we construct the PPT machine ${\mathcal{M}}^{*}$ as follows.

• Randomly pick a subset $\mathcal{S}{\in }_R\mathcal{P}\left(\mathcal{U}\right)$.
• Randomly pick $r{\in }_R{\mathbb{Z}}_p^{*}$.
• Randomly pick $W{\in }_R\mathbb{G}$, $k{\in }_R{\mathbb{Z}}_p^{*}$, then it computes $W^k$ and $u=k+rs$.
• Compute Y as follows:

  $$Y=\left\{\begin{array}{c}\begin{array}{cc}\frac{V^u}{e(G_{\mathcal{S}}^r,H)·e(W^k,H_{\mathcal{S}})}\hfill & e_i\in \mathcal{S},\hfill \\ \frac{V^u}{e(G_{\mathcal{S}}^r,H)·e(G_{\mathcal{S}},W^k)}\hfill & e_i\in \overline{\mathcal{S}},\hfill \\ y\hfill & e_i\notin \mathcal{U}.\hfill \end{array}\hfill \end{array}\right.$$

  (54)

In the above equation, y is a random element chosen in ${\mathbb{G}}_T$. Obviously, the above construction ${\mathcal{M}}^{*}\left(e\right)=\{Y,\mathcal{S},r,W^k,u\}$ is a valid protocol simulation. Y has always been a random element in ${\mathbb{G}}_T$ no matter $e_i\in \mathcal{S}$, $e_i\in \overline{\mathcal{S}}$ or $e_i\notin \mathcal{U}$. Therefore, we have ${\mathcal{M}}^{*}\left(e_i\right){\in }_R\{{\mathbb{G}}_T,\mathcal{P}\left(\mathcal{U}\right),{\mathbb{Z}}_p^{*},\mathbb{G},{\mathbb{Z}}_p^{*}\}$ and $\left\{\langle P,V^{*}\rangle \left(e_i\right)\right\}\cong \left\{{\mathcal{M}}^{*}\left(e_i\right)\right\}$. Thus, the zero-knowledge property of our ZKDMP protocol is proved.    □

7. Performance Evaluation

As shown in

Table 3. Computation and communication overheads of related protocols and ours.

	Computation Overheads		Communication Overheads
Protocol	Prover	Verifier	Prover	Verifier
[24]	$3E_{\mathbb{G}}+M_{\mathbb{G}}+2E_{{\mathbb{G}}_T}+M_{{\mathbb{G}}_T}+2B$	$(n+4)E_{\mathbb{G}}+2M_{\mathbb{G}}+3E_{{\mathbb{G}}_T}+2M_{{\mathbb{G}}_T}+3B$	$2l_{\mathbb{G}}+l_{{\mathbb{G}}_T}+3l_{{\mathbb{Z}}_p^{*}}$	$(n+1)l_{\mathbb{G}}+l_{{\mathbb{Z}}_p^{*}}$
[25]	$n{E}_{\mathbb{G}}$	$2n{E}_{\mathbb{G}}+n{M}_{\mathbb{G}}$	$n{l}_{\mathbb{G}}+4n{l}_{{\mathbb{Z}}_p^{*}}$	$n{l}_{\mathbb{G}}$
[28]	$9E_{\mathbb{G}}+4M_{\mathbb{G}}$	$(n+7)E_{\mathbb{G}}+4M_{\mathbb{G}}$	$4l_{\mathbb{G}}+4l_{{\mathbb{Z}}_p^{*}}$	$n{l}_{\mathbb{G}}+l_{{\mathbb{Z}}_p^{*}}$
[34]	$4E_{\mathbb{G}}+M_{\mathbb{G}}+2E_{{\mathbb{G}}_T}+M_{{\mathbb{G}}_T}+2B$	$(n+6)E_{\mathbb{G}}+3M_{\mathbb{G}}+3E_{{\mathbb{G}}_T}+2M_{{\mathbb{G}}_T}+3B$	$2l_{\mathbb{G}}+l_{{\mathbb{G}}_T}+3l_{{\mathbb{Z}}_p^{*}}$	$(n+1)l_{\mathbb{G}}$
Our protocol	$\left(\frac{n^2+n}{2}+2\right)E_{\mathbb{G}}+\left(\frac{n^2+n}{2}\right)D_{\mathbb{G}}+B$   for $e_i\notin \mathcal{S}$; $(n+1)E_{\mathbb{G}}+(n-1)M_{\mathbb{G}}+B$   for $e_i\in \mathcal{S}$	$E_{{\mathbb{G}}_T}+M_{{\mathbb{G}}_T}+3B$	$2l_{\mathbb{G}}+l_{{\mathbb{G}}_T}+l_{{\mathbb{Z}}_p^{*}}$	$(n+1)l_{{\mathbb{Z}}_p^{*}}$

, the comparisons of computation and communication overheads are provided between four existing zero-knowledge membership proof protocols [24,25,28,34] and ours. In this paper, n, $E_{\mathbb{G}}$ and $E_{{\mathbb{G}}_T}$ denote the number of elements in $\mathcal{S}$, exponentiation operations in $\mathbb{G}$ and ${\mathbb{G}}_T$, respectively. $M_{\mathbb{G}}$ and $D_{\mathbb{G}}$ are multiplication and devision operations in $\mathbb{G}$. $M_{{\mathbb{G}}_T}$ and B are multiplication operation in ${\mathbb{G}}_T$ and the bilinear pairing operation, respectively. The lengths of elements in $\mathbb{G}$, ${\mathbb{G}}_T$ and ${\mathbb{Z}}_p^{*}$ are defined as $l_{\mathbb{G}}$, $l_{{\mathbb{G}}_T}$ and $l_{{\mathbb{Z}}_p^{*}}$, respectively. In addition, the operations in ${\mathbb{Z}}_p^{*}$, multiplication in $\mathbb{G}$ and hash take less time than the other operations, we neglect them in our evaluation.

In terms of computation overheads, the prover’s costs in [24,28,34] are constants. However, computation costs of the verifier are linear with the number of elements in the subset. In our protocol, for positive membership decisions, i.e., $e_i\in \mathcal{S}$, the prover’s computation cost is exponential with the number of elements in $\mathcal{S}$; for negative membership decisions, i.e., $e_i\notin \mathcal{S}$, the prover’s computation overheads are linear with the number of elements in $\mathcal{S}$. However, the computation costs of our verifier is constant for either the positive or negative set membership. Furthermore, let us turn our attention to communication costs. Obviously, in Table 3, all of the provers’ communication costs are constants in [24,28,34] and ours, while that of the verifiers are linear with the number of elements in the subset.

In order to evaluate the performance of membership decision protocols in [24,25,28,34] and ours, we implement them based on the Java Pairing Based Cryptography Library (JPBC) and IntelliJ IDEA 2020.3.3. All programs run on a 64-bit Windows 10 PC with Intel Core i5-4590S processor (Qual Core, 3.00 GHz). Moreover, we choose the SHA-256 cryptographic algorithm as the hash function in our experiments. Let the tested set, $\mathcal{U}=\{e_1,e_2,\cdots ,e_{150}\}$, be any $e_i$ in a random arbitrary-length string, i.e., $e_i\in {\{0,1\}}^{*}$. Note that in order to reduce the experimental error, all of our experiments are repeated 100 times arithmetically averaging the final results. The simulation parameters are shown in

Table 4. Parameters setting.

Simulation Parameters	Value
Security strength	128 bit
The type of the pairing	Type-A
Elliptic curve	$y^2=x^3+x$
The order of the pairing group	160 bit
Warm Up	5 rounds

.

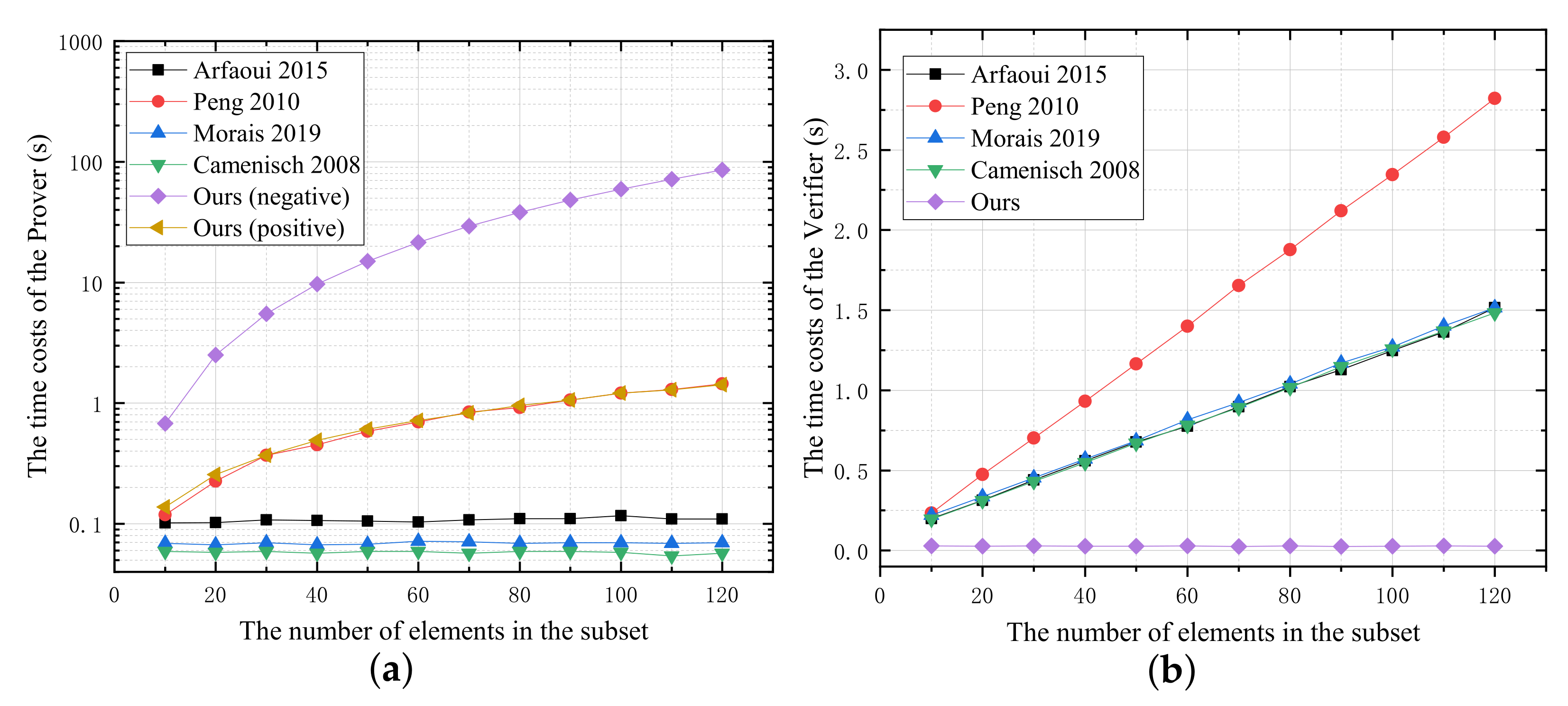
As shown in Figure 5, we compare the computation overheads of these protocols in the experiments. From Figure 5a, it is obvious that the time costs of the prover in the negative membership decision in our protocol is more expensive than those of the others. The reason is that the prover in our interactive protocol will compute the poles-based aggregation function, which requires a lot of exponentiation operations in $\mathbb{G}$. In our positive membership decision, the time costs of the prover are similar to that in [25], which is higher than that in [24,28,34]. In the other hand, as shown in Figure 5b, the time costs of our verifier are constant and less than that of the other four protocols, which are consistent with the theoretical analysis.

By using the aforementioned setup and tools, we simulate the aggregation algorithms (see [31]) and show the results of experiments in Figure 6. As shown in this figure, our poles-based aggregation takes longer than the zeros-based aggregation for the same number of elements in the subset. This is because, the PoleAggr needs to perform more exponential operations than that of ZeroAggr and this operation is more time-consuming than others. Specifically, in the PoleAggr, the number of exponential operations is exponentially related to the number of subset elements, however, that of ZeroAggr is linear with the number of subset elements.

Our ZKDMP is executed by a three-move interaction between a prover and a verifier. In order to clearly describe the protocol, we split the interaction into three functions, i.e., $Commit$, $Respond$ and $Verify$. Specifically, the first two functions are run by the prover and the last one is by the verifier. The details of these three functions are described in Algorithms 1 and 2. The pseudocodes of our protocol is provided in Algorithm 3. It is not difficult to see that three aforementioned functions are simple and concise. Therefore, our ZKDMP protocol (Algorithm 4) has a simple and easy-to-understand structure.

Algorithm 1:$Commit(e_i,msk,mpk)$

1: randomly pick $k,s\in {\mathbb{Z}}_p^{*}$ 2: $x_i\leftarrow Hash\left(e_i\right)$ 3: $E_i\leftarrow G^{\frac{x_i}{\gamma +x_i}}$ 4: $comm\leftarrow (e(E_i^k,H),G^s)$

Algorithm 2:$Respond(e_i,r,\mathcal{S},msk,mpk)$

1: if$e_i\in \mathcal{S}$then 2:    $W\leftarrow PoleAggr(mpk,{\mathcal{S}}_{-})$ 3: else 4:    $W\leftarrow ZeroAggr(mpk,{\mathcal{S}}_{+})$ 5: end if 6: $u\leftarrow k+sr$ 7: $resp\leftarrow (W^k,u)$

Algorithm 3:$Verify(resp,comm,\mathcal{S},mpk)$

1: $T\leftarrow \frac{e{(G,H)}^u}{e(E_i^k,H)e(G_{\mathcal{S}}^r,H)}$ 2: if$T=e(W^k,H_{\mathcal{S}})$then 3:    $out\leftarrow True$ $T=e(W^k,G_{\mathcal{S}})$ 4:    $out\leftarrow False$ 5: else 6:    $out\leftarrow \perp$ 7: end if

Algorithm 4:$ZKDMP(e_i,\mathcal{S},resp,comm,mpk)$

1: Prover runs $Commit(e_i,msk,mpk)$ and sends $comm$ to Verifier 2: Verifier randomly picks $r\in {\mathbb{Z}}_p^{*}$ and subset $\mathcal{S}$ and sends them to Prover 3: Prover runs $Respond(e_i,r,\mathcal{S},msk,mpk)$ and sends $resp$ to Verifier 4: Verifier runs $Verify(resp,comm,mpk)$ and outputs $out$

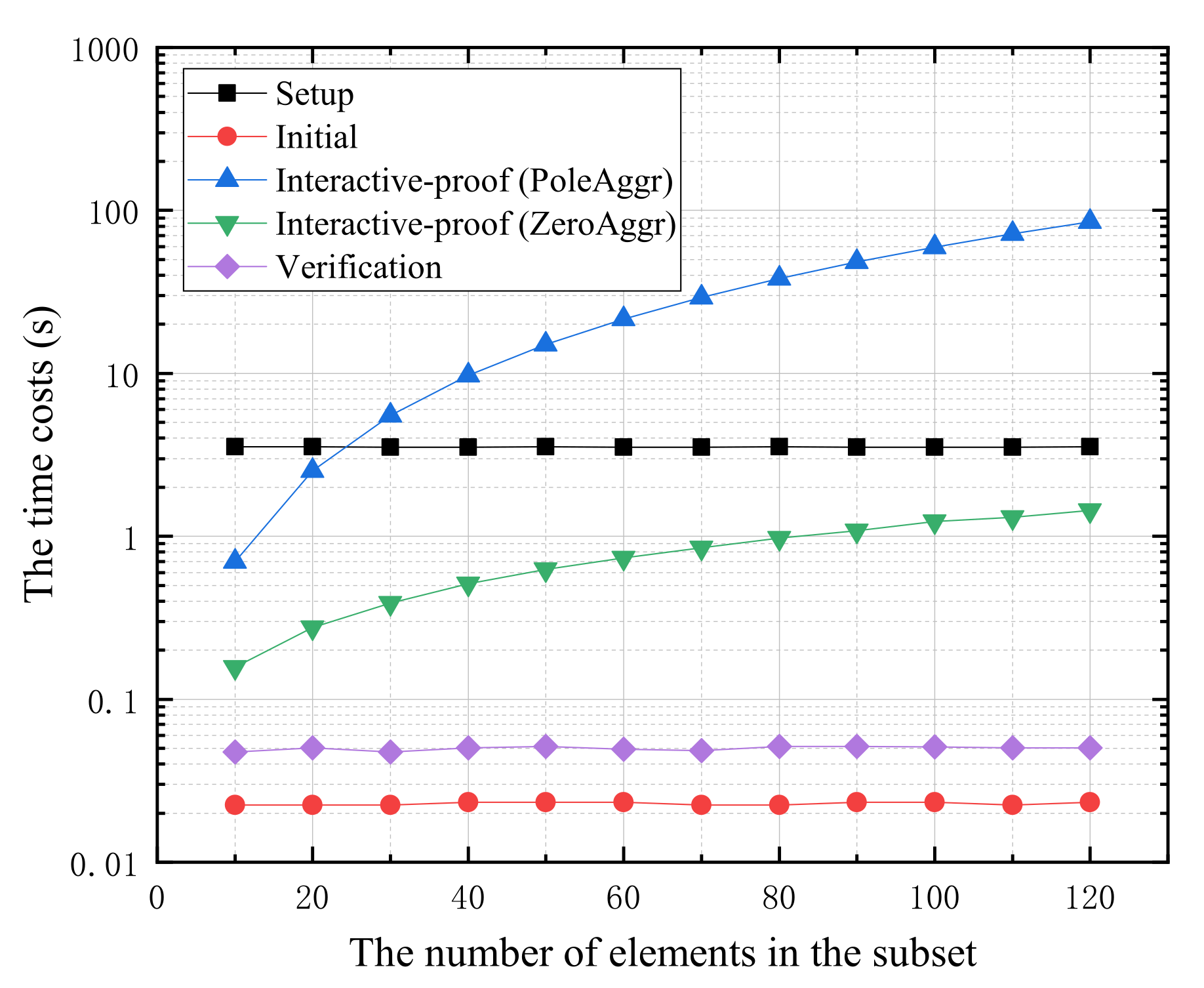
Moreover, we implement our ZKDMP and evaluate the overheads of the Setup and three stages in the interactive protocol, including initial, interactive-proof and verification. As shown in Figure 7, the time costs of the Setup, initial and verification are constants. In the interactive-proof stage, the main overheads come from the calculation of the aggregation functions. Specifically, the time costs of the positive set membership is exponential with the number of elements in $\mathcal{S}$, that of negative set membership is linear with the number of elements in $\mathcal{S}$.

8. Conclusions

In this paper, we focus on the cryptographic principle and construction for secure membership decision in set theory. Firstly, we formalize the security of the aggregator, and then use ZeroAggr and PoleAggr to compress an arbitrary-size subset into an element in the cryptospace for achieving the secure representation of the subset. Secondly, this paper provides the concept of SDM and uses the zeros-based and poles-based secure representation of the subset to decide the Pos-and-Neg membership, respectively. Finally, we propose the ZKDMP protocol for supporting strict Pos-and-Neg membership decisions. In addition, our aggregation functions are proved to be secure under the t-SDH assumption and the proposed ZKDMP protocol has positive completeness, negative completeness, soundness and zero-knowledge. Moreover, the performance evaluation shows that the ZKDMP protocol has a simple and easy-to-understand structure. In future work, the aggregation complexity will be optimized, i.e., parallelized algorithm, to improve the decision efficiency of the ZKDMP protocol. On the other hand, the secure aggregation functions should be widely applied to construct other cryptosystems, such as attribute-based encryption, broadcast encryption and role-based encryption.