Pattern Dynamics of Cross Diffusion Predator–Prey System with Strong Allee Effect and Hunting Cooperation
Abstract
1. Introduction
2. Analysis of Self Diffusion Model
2.1. Existence of Equilibrium Point
- (1)
- The model (5) has a semi trivial equilibrium point .
- (2)
- The model (5) has a semi trivial equilibrium point .
- (3)
- When and , the model (5) has a unique positive equilibrium point .
- (4)
- When and , the model (5) has has two positive equilibrium points and . Where , , .
- (5)
- When and or , the model (5) has no positive equilibrium point.
2.2. Stability of Equilibrium Point
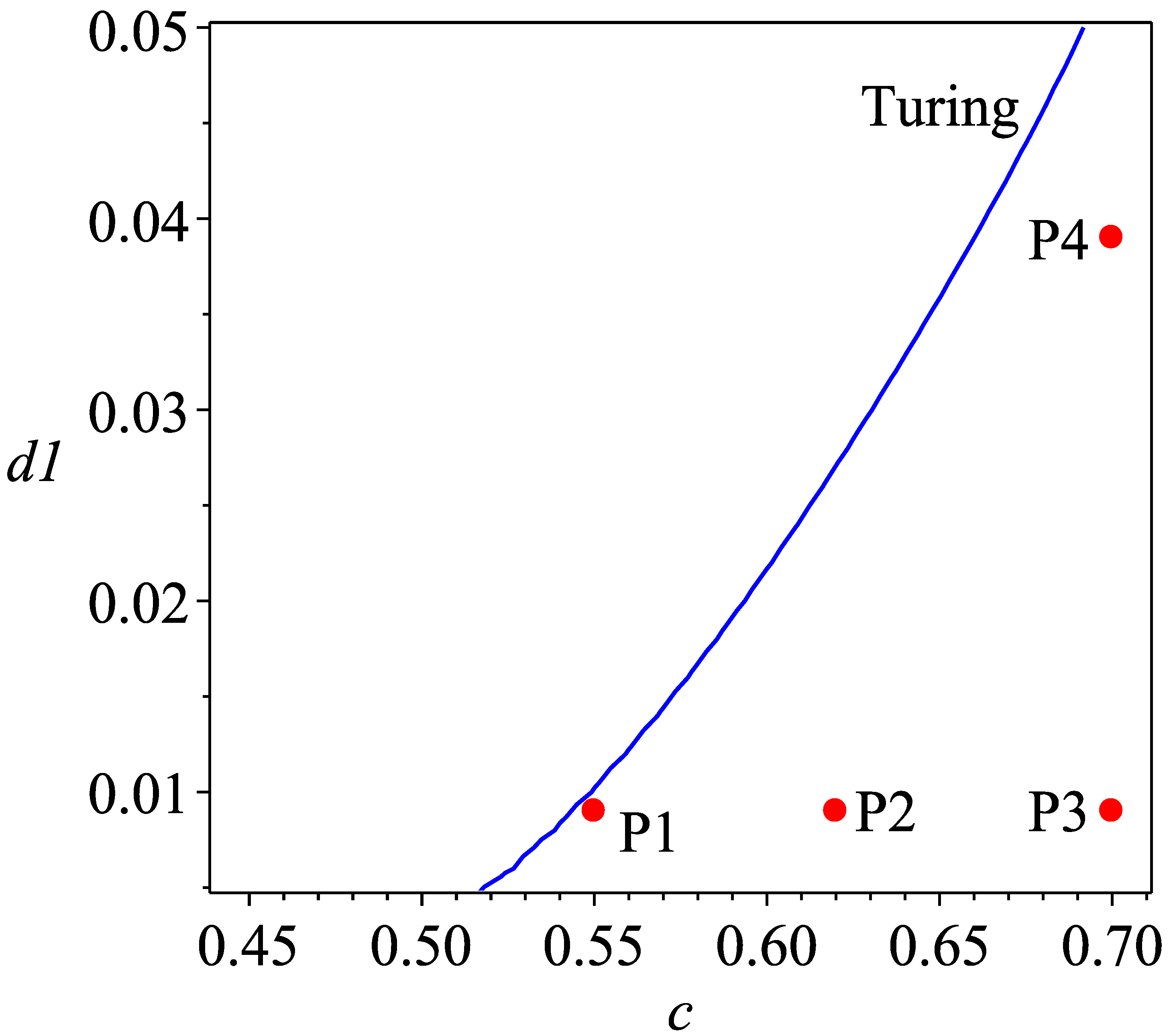
2.3. Turing Instability
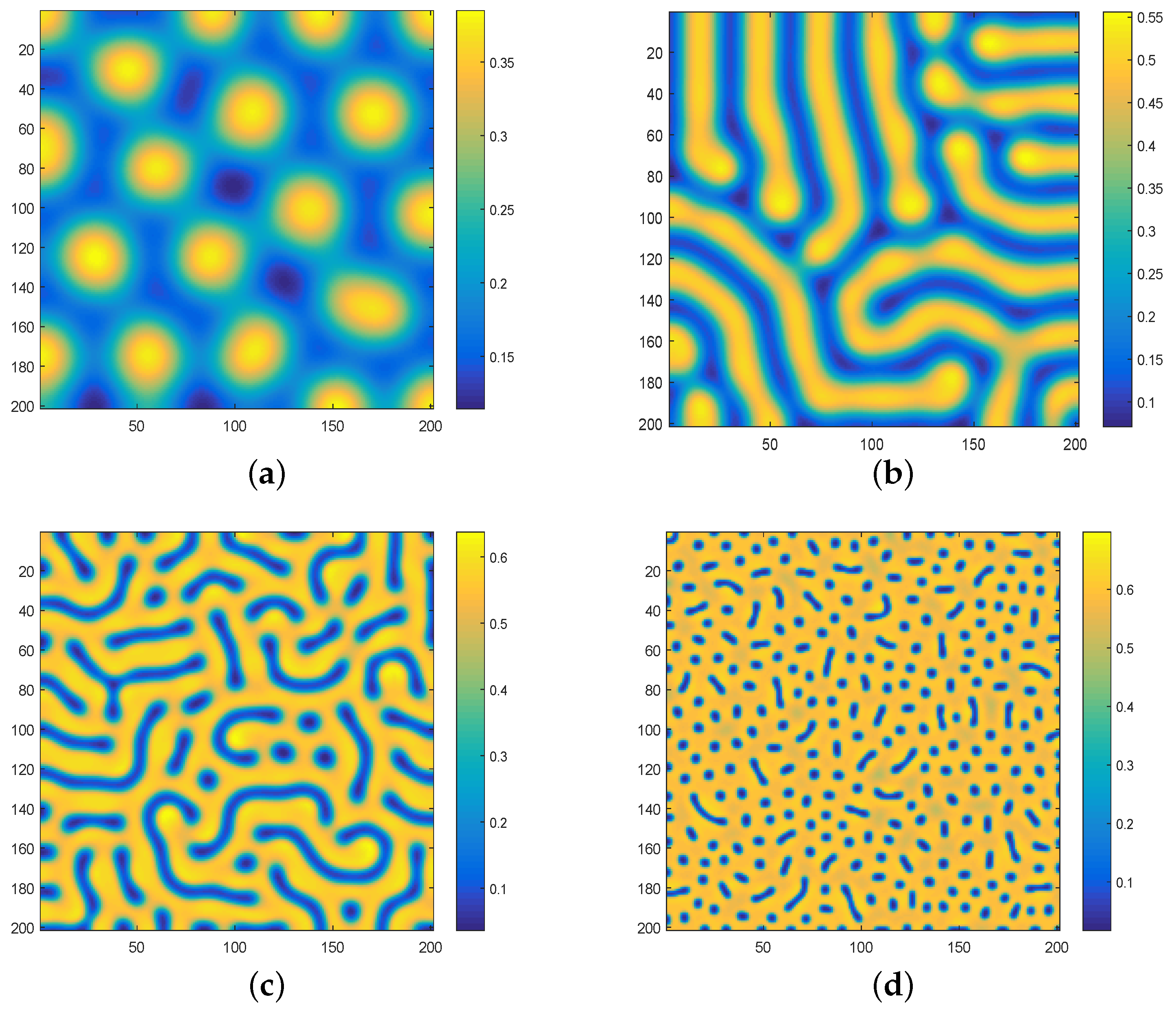
2.4. Diffusion Induced Pattern
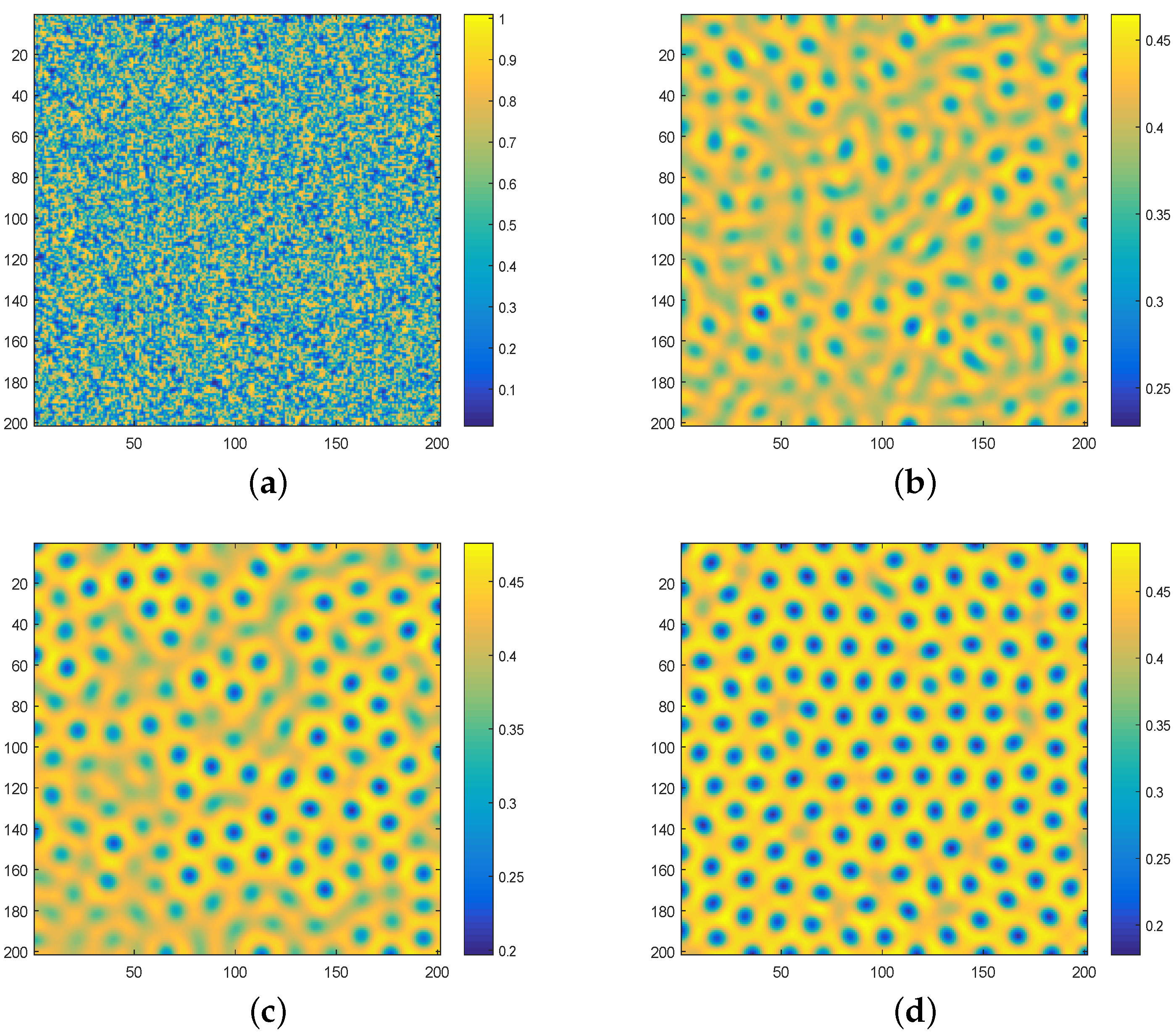

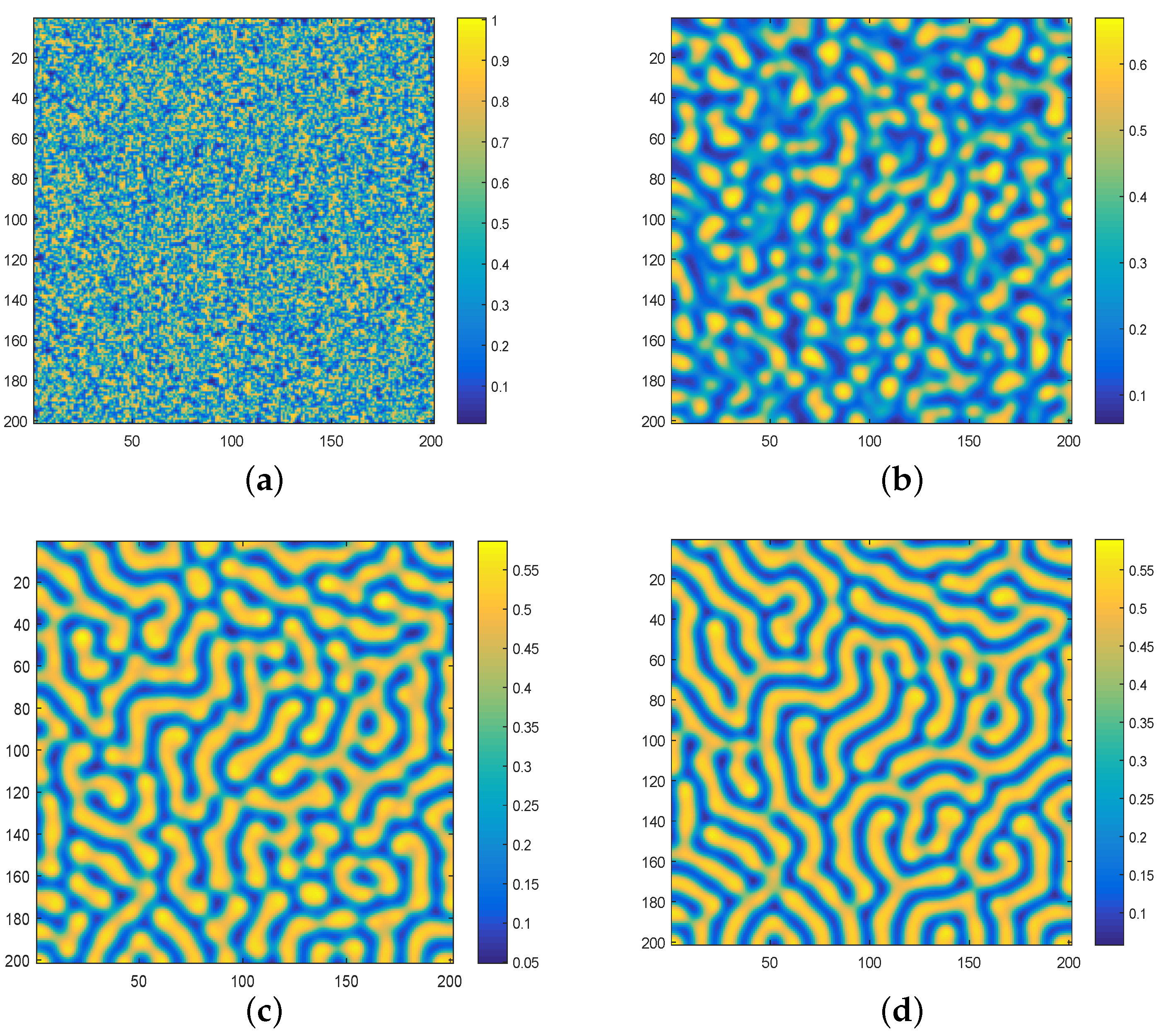
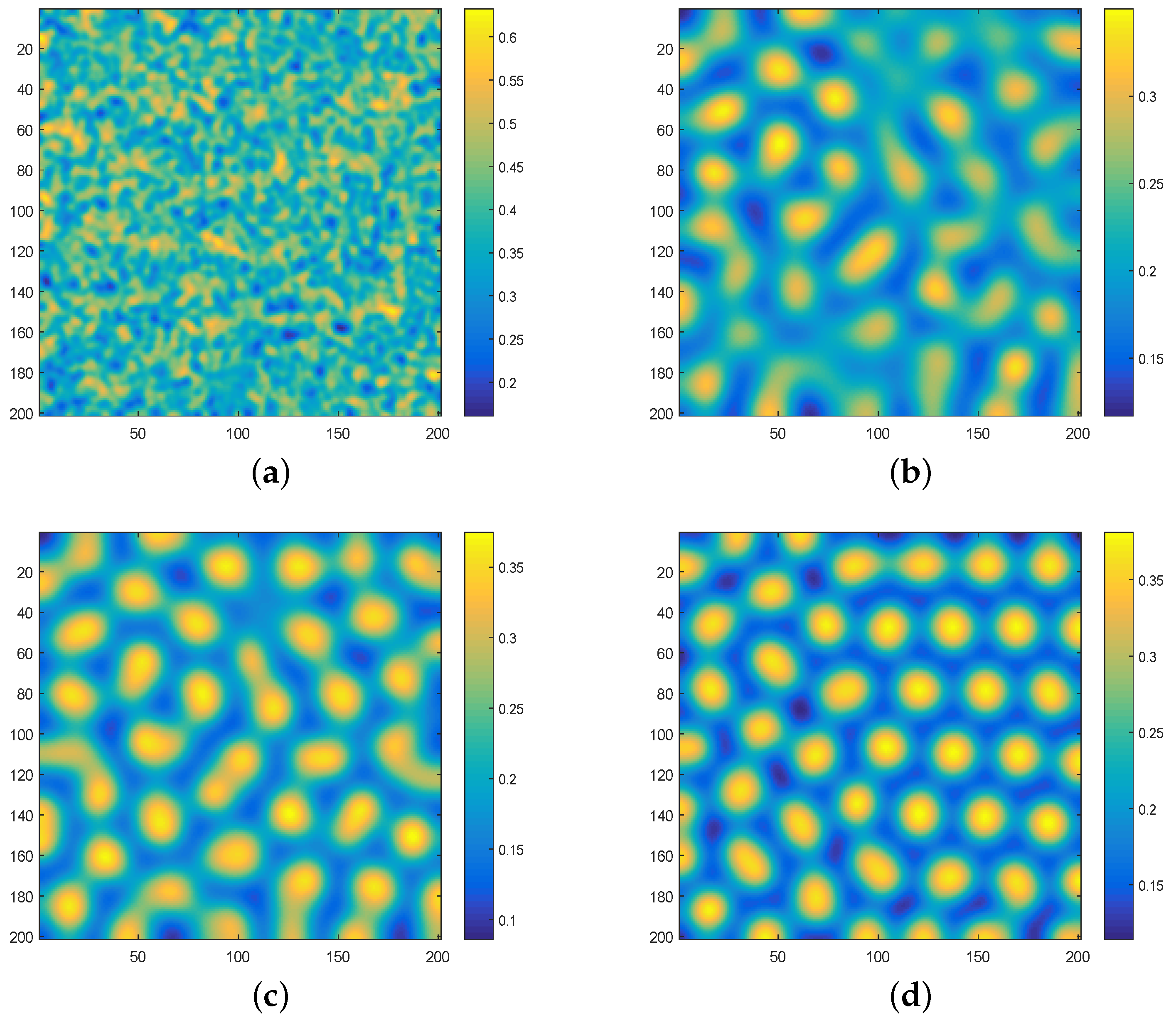
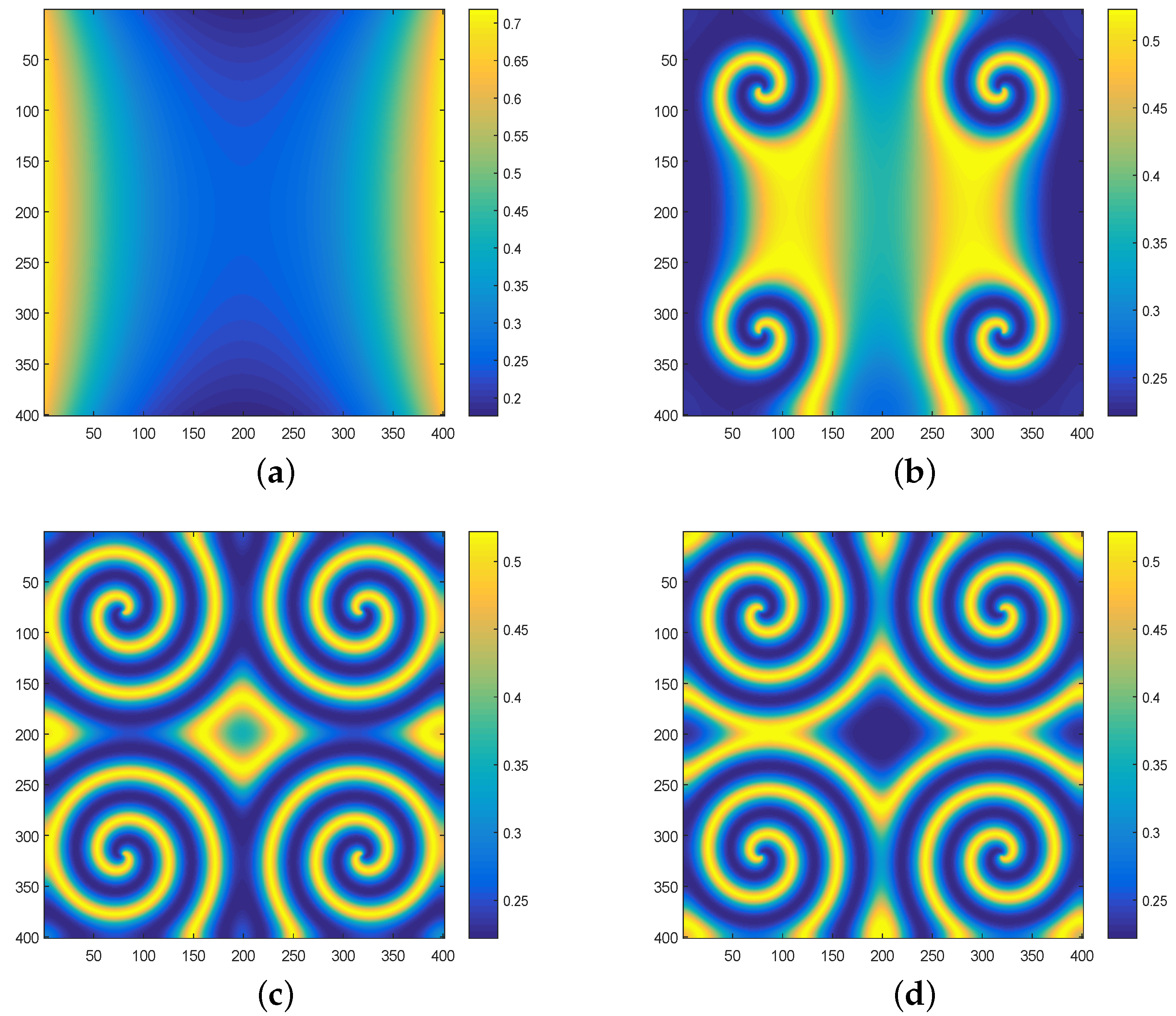
3. Analysis of Cross Diffusion Model
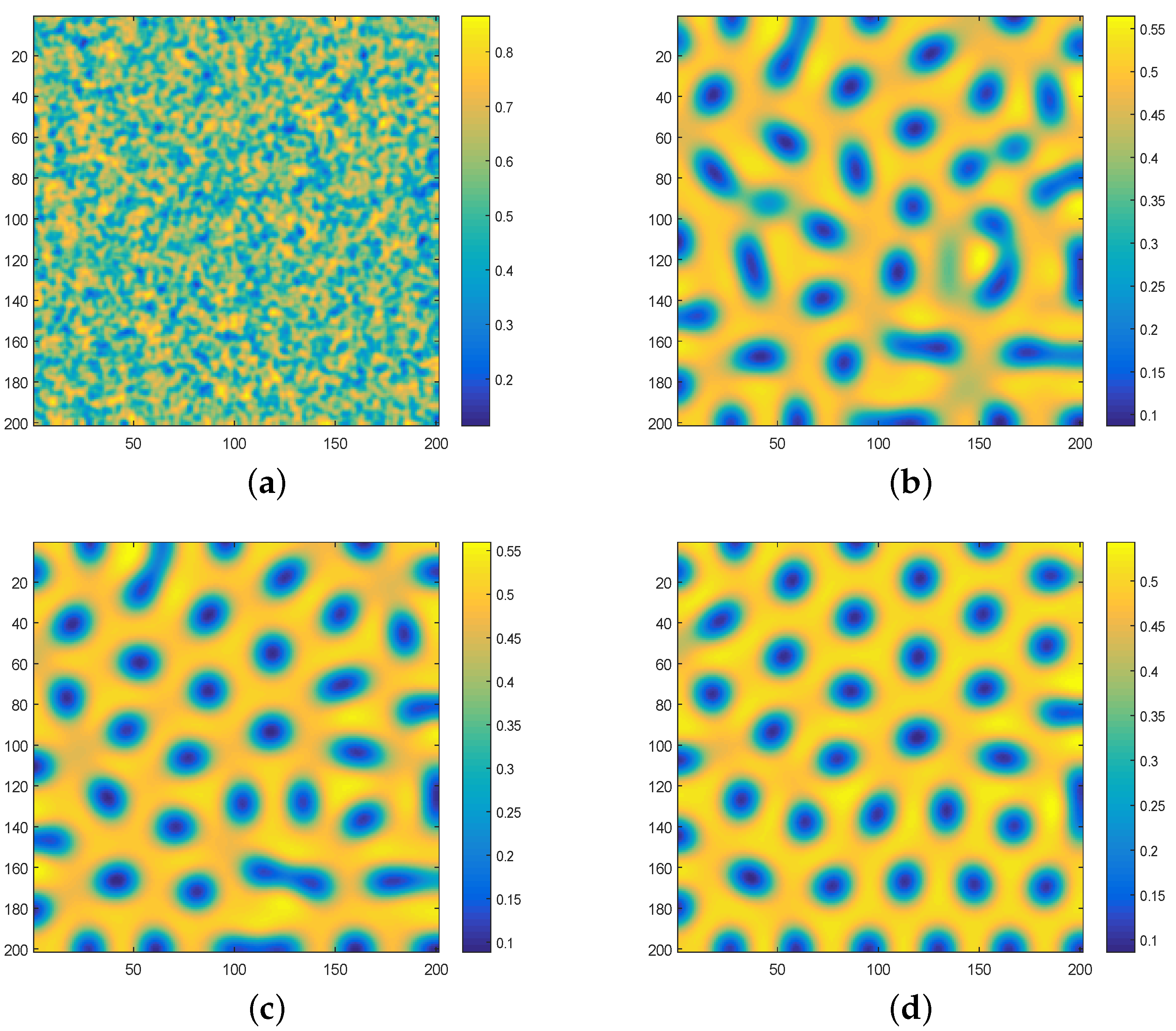
3.1. Turing Instability Induced by Cross Diffusion
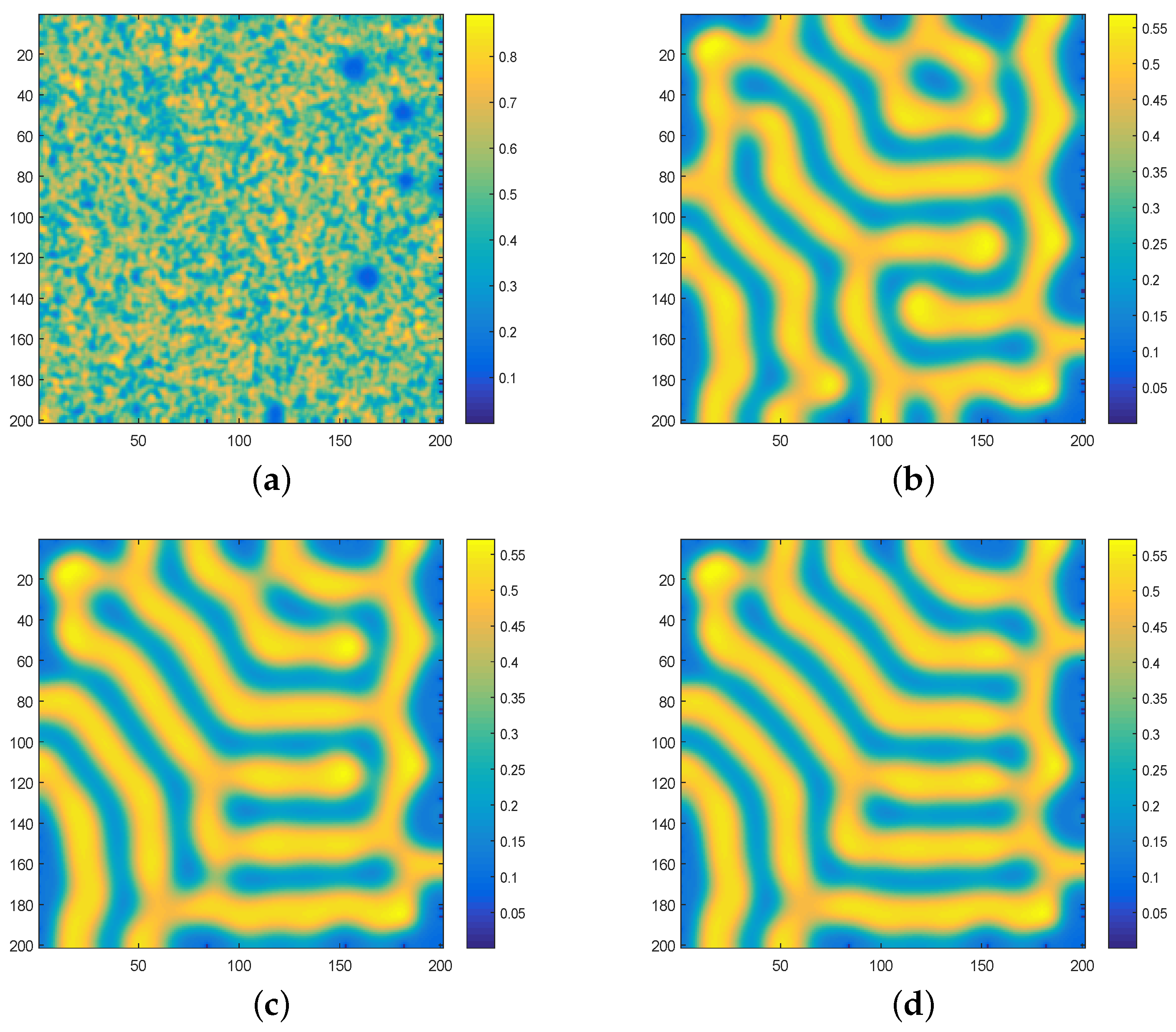
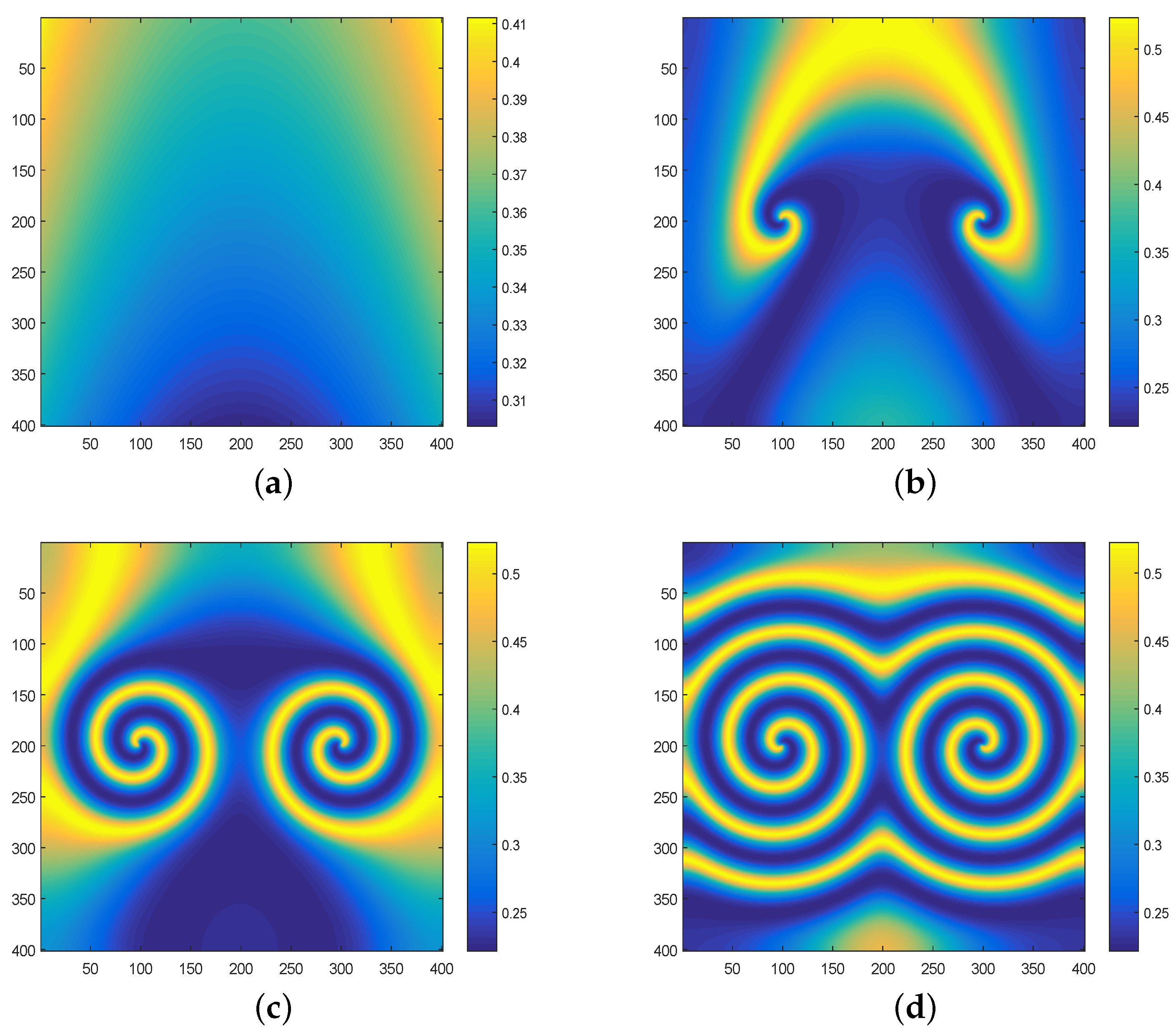
3.2. Pattern Formation Induced by Self Diffusion and Cross Diffusion
4. Conclusions and Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Leslie, P.H.; Gower, J.C. The properties of a stochastic model for the predator-prey type of interaction between two species. Biometrika 1960, 47, 219–234. [Google Scholar] [CrossRef]
- Holling, C.S. The functional response of invertebrate predators to prey density. Mem. Entomol. Soc. Can. 1966, 98, 1–86. [Google Scholar] [CrossRef]
- Tanner, J.T. The stability and the intrinsic growth rates of prey and predator populations. Ecology 1975, 56, 855–867. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, T.; Lan, J.; Wong, G. Application of animal models to compare and contrast the virulence of current and future potential SARS-CoV-2 variants. Biosaf. Health 2022, 4, 154–160. [Google Scholar] [CrossRef] [PubMed]
- Ho, L.V.; Nguyen, D.H.; Mousavi, M.; De Roeck, G.; Bui-Tien, T.; Gandomi, A.H.; Wahab, M.A. A hybrid computational intelligence approach for structural damage detection using marine predator algorithm and feedforward neural networks. Comput. Struct. 2021, 252, 106568. [Google Scholar] [CrossRef]
- Hamadneh, N.N.; Tahir, M.; Khan, W.A. Using Artificial Neural Network with Prey Predator Algorithm for Prediction of the COVID-19: The Case of Brazil and Mexico. Mathematics 2021, 9, 180. [Google Scholar] [CrossRef]
- Allee, W.C. Animal Aggregations. Q. Rev. Biol. 1927, 2, 367–398. [Google Scholar] [CrossRef]
- Courchamp, F.; Berec, L.; Gascoigne, J. Allee effects in ecology and conservation. Environ. Conserv. 2018, 36, 80–85. [Google Scholar]
- Zhang, C.; Yang, W. Dynamic behaviors of a predator-prey model with weak additive Allee effect on prey. Nonlinear Anal. Real World Appl. 2020, 55, 103137. [Google Scholar] [CrossRef]
- Rebelo, C.; Soresina, C. Coexistence in seasonally varying predator-prey systems with Allee effect. Nonlinear Anal. Real World Appl. 2020, 55, 103140. [Google Scholar] [CrossRef]
- Shi, Y.; Wu, J.; Cao, Q. Analysis on a diffusive multiple Allee effects predator-prey model induced by fear factors. Nonlinear Anal. Real World Appl. 2021, 59, 103249. [Google Scholar] [CrossRef]
- Liu, P.; Yang, B.W. Dynamics analysis of a reaction-diffusion system with Beddington-DeAngelis functional response and strong Allee effect. Nonlinear Anal. Real World Appl. 2020, 51, 102953. [Google Scholar] [CrossRef]
- Shang, Z.C.; Qiao, Y.H. Bifurcation analysis of a Leslie-type predator-prey system with simplified Holling type IV functional response and strong Allee effect on prey. Nonlinear Anal. Real World Appl. 2022, 64, 103453. [Google Scholar] [CrossRef]
- Ni, W.; Wang, M. Dynamical properties of a leslie-gower prey-predator model with strong allee effect in prey. Discret. Contin. Dyn. Syst.-B 2017, 22, 3409. [Google Scholar] [CrossRef][Green Version]
- Mukherjee, D.; Maji, C. Bifurcation analysis of a holling type II predator-prey model with Refuge. Chin. J. Phys. 2020, 65, 153–162. [Google Scholar] [CrossRef]
- Aguirre, P.; Flores, J.D.; González-Olivares, E. Bifurcations and global dynamics in a predator-prey model with a strong allee effect on the prey and a ratio-dependent functional response. Nonlinear Anal. Real World Appl. 2014, 16, 235–249. [Google Scholar] [CrossRef]
- Kar, T.K.; Matsuda, H. Global dynamics and controllability of a harvested prey-predator system with Holling type III functional response. Nonlinear Anal. Hybrid Syst. 2007, 1, 59–67. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Yang, H.Z. Hopf bifurcation in a delayed predator-prey system with modified leslie-gower and Holling type III schemes. Acta Autom. Sin. 2013, 39, 610–616. [Google Scholar] [CrossRef]
- Sarwardi, S.; Haque, M.; Mandal, P.K. Persistence and global stabiligty of Bazykin predator-prey model with Beddington-deangelis response function. Commun. Nonlinear Sci. Numer. Simulate 2014, 19, 189–209. [Google Scholar] [CrossRef]
- Chen, X.; Du, Z. Existence of positive periodic solutions for a neutral delay predator-prey model with Hassell-Varley type functional response and impulse. Qual. Theory Dyn. Syst. 2018, 17, 67–80. [Google Scholar] [CrossRef]
- Dai, Y.; Zhao, Y. Hopf cyclicity and global dynamics for a predator-prey system of leslie type with simplified Holling type IV functional response. Int. J. Bifur. Chaos 2018, 28, 1850166. [Google Scholar] [CrossRef]
- Shang, Z.C.; Qiao, Y.H.; Duan, L.J.; Miao, J. Stability and bifurcation analysis in a nonlinear harvested predator-prey model with simplified Holling type IV functional response. Int. J. Bifurc. Chaos 2020, 30, 2050205. [Google Scholar] [CrossRef]
- Shang, Z.C.; Qiao, Y.H.; Duan, L.J.; Jun, M. Bifurcation analysis in a predator-prey system with an increasing functional response and constant-yield prey harvesting. Math. Comput. Simul. 2021, 190, 976–1002. [Google Scholar] [CrossRef]
- Alves, M.T.; Hilker, F.M. Hunting cooperation and allee effects in predators. J. Theor. Biol. 2017, 419, 13–22. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Jia, D.; Zhang, T.; Yuan, S. Pattern dynamics in a diffusive predator-prey model with hunting cooperations. Chaos Solitons Fractals 2020, 130, 109428. [Google Scholar] [CrossRef]
- Sen, D.; Ghorai, S.; Banerjee, M. Allee effect in prey versus hunting cooperation on predator-enhancement of stable coexistence. Int. J. Bifurc. Chaos 2019, 29, 1950081. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, M. Qualitative analysis for a diffusive predator-prey model with hunting cooperative. Phys. A Stat. Mech. Appl. 2019, 515, 299–309. [Google Scholar] [CrossRef]
- Pal, S.; Pal, N.; Chattopadhyay, J. Hunting cooperation in a discrete-time predator-prey system. Int. J. Bifurc. Chaos 2018, 28, 1850083. [Google Scholar] [CrossRef]
- Ye, P.H.; Wu, D.Y. Impacts of strong Allee effect and hunting cooperation for a Leslie-Gower predator-prey system. Chin. J. Phys. 2020, 68, 49–64. [Google Scholar] [CrossRef]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. Biol. Sci. 1952, 237, 37–72. [Google Scholar]
- Liu, X.; Zhang, T.; Meng, X.; Zhang, T. Turing-Hopf bifurcations in a predator-prey model with herd behavior quadratic mortality and prey-taxis. Phys. A 2018, 496, 446–460. [Google Scholar] [CrossRef]
- Lian, X.Z.; Wang, H.L.; Wang, W.M. Delay-driven pattern formation in a reaction-diffusion predator-prey model incorporating a prey refuge. J. Stat. Mech. Theory Exp. 2013, 2013, P04006. [Google Scholar] [CrossRef]
- Chen, M.X.; Wu, R.C.; Liu, B.; Chen, L.P. Pattern selection in a predator-prey model with Michaelis-Menten type nonlinear predator harvesting. Ecol. Complex. 2018, 36, 239–249. [Google Scholar] [CrossRef]
- Biktashev, V.; Brindley, J.; Holden, A.; Tsyganov, M. Pursuit-evasion predator-prey waves in two spatial dimensions. Chaos 2004, 14, 988–994. [Google Scholar] [CrossRef] [PubMed]
- Shukla, J.; Verma, S. Effects of convective and dispersive interactions on the stability of two species. Bull. Math. Biol. 1981, 43, 593–610. [Google Scholar] [CrossRef]
- Kerner, E. Further considerations on the statistical mechanics of biological associations. Bull. Math. Biophys. 1959, 21, 217–255. [Google Scholar] [CrossRef]
- Song, D.; Li, C.; Song, Y. Stability and cross-diffusion-driven instability in a diffusive predatorCprey system with hunting cooperation functional response. Nonlinear Anal. Real World Appl. 2020, 54, 103106. [Google Scholar] [CrossRef]
- Ma, T.; Meng, X.; Hayat, T.; Hobiny, A. Stability analysis and optimal harvesting control of a cross-diffusion prey-predator system. Chaos 2021, 152, 111418. [Google Scholar] [CrossRef]
- Peng, Y.; Ling, H. Pattern formation in a ratio-dependent predator-prey model with cross-diffusion. Appl. Math. Comput. 2018, 331, 307–318. [Google Scholar] [CrossRef]
- Meng, Q.; Yang, L.L. Steady state in a cross-diffusion predator-prey model with the Beddington-DeAngelis functional response. Nonlinear Anal. Real World Appl. 2019, 45, 401–413. [Google Scholar] [CrossRef]
- Lian, X.Z.; Yue, Y.H.; Wang, H.L. Pattern Formation in a Cross-Diffusive Ratio-Dependent Predator-Prey Model. Discret. Dyn. Nat. Soc. 2012, 2012, 814069. [Google Scholar] [CrossRef]
- Yang, R.Z.; Zhang, C.R. Dynamics in a diffusive modified Leslie-Gower predator-prey model with time delay and prey harvesting. Nonlinear Dyn. 2017, 87, 863–878. [Google Scholar] [CrossRef]
- Cao, J.; Sun, H.; Hao, P.; Wang, P. Bifurcation and turing instability for a predator-prey model with nonlinear reaction cross-diffusion. Appl. Math. Model. 2021, 89, 1663–1677. [Google Scholar] [CrossRef]
- Yan, X.; Maimaiti, Y.; Yang, W. Stationary pattern and bifurcation of a Leslie-Gower predator-prey model with prey-taxis. Math. Comput. Simul. 2022, 201, 163–192. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, M.; Li, J.; Lian, X. Pattern Dynamics of Cross Diffusion Predator–Prey System with Strong Allee Effect and Hunting Cooperation. Mathematics 2022, 10, 3171. https://doi.org/10.3390/math10173171
Zhu M, Li J, Lian X. Pattern Dynamics of Cross Diffusion Predator–Prey System with Strong Allee Effect and Hunting Cooperation. Mathematics. 2022; 10(17):3171. https://doi.org/10.3390/math10173171
Chicago/Turabian StyleZhu, Meng, Jing Li, and Xinze Lian. 2022. "Pattern Dynamics of Cross Diffusion Predator–Prey System with Strong Allee Effect and Hunting Cooperation" Mathematics 10, no. 17: 3171. https://doi.org/10.3390/math10173171
APA StyleZhu, M., Li, J., & Lian, X. (2022). Pattern Dynamics of Cross Diffusion Predator–Prey System with Strong Allee Effect and Hunting Cooperation. Mathematics, 10(17), 3171. https://doi.org/10.3390/math10173171