Abstract
GIM Lie algebras are the generalizations of Kac–Moody Lie algebras. However, the structures of GIM Lie algebras are more complex than the latter, so they have encountered many new difficulties to study their representation theory. In this paper, we classify all finite dimensional simple modules over the GIM Lie algebra as well as those over .
MSC:
17B10; 17B65; 17B66; 17B68
1. Introduction
A generalized intersection matrix (GIM) is a matrix with integer entries, 2’s along the diagonal, and either or if . Slodowy [1] used these matrices to define the GIM Lie algebras that encompassed all Kac–Moody Lie algebras.
Definition 1
([1,2]). Given a GIM . The GIM Lie algebra is a Lie algebra over generated by the elements
subject to the generating relations
Slodowy [1] and, later, Berman [3] showed that every GIM Lie algebra is isomorphic to the fixed point subalgebra of involution on some larger Kac–Moody Lie algebra.
The GIM Lie algebras play important roles in the classification of the root-graded Lie algebras (see [4,5,6,7]) and are closely related to the representations of tilted algebras via Ringel–Hall algebras (see [8,9]). Their quantized analogues are isomorphic to the Hopf co-ideals of some Kac–Moody quantum groups (see [10,11,12,13]).
For any , let be the GIM whose entries are given by
which corresponds to the Dynkin diagram:
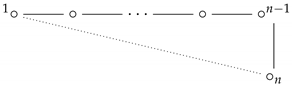
For convenience, we denote the GIM Lie algebra by , and we say that it is of type . should be the simplest oriented GIM Lie algebra because it is the fixed point subalgebra of affine Kac–Moody Lie algebra . Roughly, a GIM Lie algebra is called oriented if it is not a Kac–Moody Lie algebra. In [14], all finite dimensional simple modules over are constructed and classified.
For , let be the GIM Lie algebra defined via the structural matrix
We say that is of type . As in the definition above, we assume that is generated by the ’s, ’s, ’s. Then, is identified as the Lie subalgebra generated by . In particular, the Dynkin diagram of is
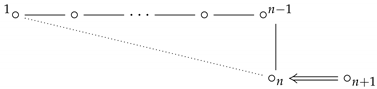
In this paper, our main purpose is to classify all finite dimensional simple modules over for all . As a surprised byproduct, we also obtain the classification of all finite dimensional simple modules over a class of ‘larger’ oriented GIM Lie algebras (see Definition 2 below).
We use the word larger with quotation marks, because seems to be isomorphic to some fixed-point subalgebra of . However, we can only give an epimorphism from to . Quite fortunately, this epimorphism is sufficient for our purpose.
Throughout the paper, we denote the set of complex numbers, the set of integers, the set of positive integers and the set of non-negative integers using , respectively.
2. GIM Lie Algebras
2.1. Lie Algebra
For any , let be the GIM such that
Definition 2.
The Lie algebra is the GIM Lie algebra over generated by the elements
subject to the generating relations
The affine Lie algebra can be identified to be the Lie subalgebra generated by the elements . Moreover, also is simply-laced and its Dynkin diagram is
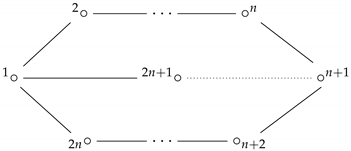
2.2. An Involution of
Define a map such that
Lemma 1.
The map σ defines an automorphism of .
Proof.
It is straightforward. □
There is no confusion to denote this automorphism by . In particular, is an involution as well as its restriction .
Lemma 2
(see [3]). The fixed-point subalgebra of is isomorphic to .
2.3. The Fixed-Point Subalgebra
Let be the fixed-point subalgebra of the involution . Then, it can be generated by the elements
Lemma 3.
For , the map ξ
defines a Lie algebra epimorphism from to .
Proof.
By Lemma 2, it is sufficient to check the generating relationships for . Notice that the elements generate a Lie algebra of type . In fact, the restriction is a diagram automorphism. Then there is a fixed-point subalgebra of type (or ), and the lemma follows. □
3. Basics and Main Results
Lemma 4
(see [14]). Let V be a finite dimensional vector space and a GIM Lie algebra. Then, V is a simple -module if, and only if, there exists an ideal I of such that is finite dimensional semi-simple, and V is a simple -module.
Note that, for a general Lie algebra, the quotient perhaps contains a one dimensional direct summand. However, this situation doesn’t happen for GIM Lie algebras (of course, for Kac–Moody Lie algebras).
Let denote the Lie subalgebra of generated by the elements
Similar to the above, we say that is of type . In particular, .
Lemma 5.
For , the Lie algebra has no nontrivial finite dimensional module.
Proof.
The Dynkin diagram of is a subdiagram of . It is sufficient to prove it for .
Note that the subalgebra generated by the elements , is of type . So
is the fundamental central element of (see Table Aff1 and §6.2 in [15]). Let V be a finite dimensional module over , then it is a module over . This implies . However, . It forces . Then . □
Define the loop Lie algebra
which has the bracket
The following two lemmas are well-known for all loop Lie algebras.
Lemma 6.
If for some , the quotient has a nontrivial nilpotent ideal.
Proof.
It is straightforward. For example, let , it is clearly an ideal, and . However, . □
Lemma 7.
Suppose for pairwise different constants , we have
Proof.
Since has no multiple root, any common divisor of all , must be a constant. Then there exist some constants such that
Due to the fact that for each i, we have
□
Lemma 8.
Let V be a finite dimensional vector space.
(1) For , the Lie algebra has no nontrivial finite dimensional simple module.
(2) V is a simple module over if, and only if, it is a module over for some .
(3) V is a simple module over if, and only if, it is a module over for some .
(4) V is a simple module over if, and only if, it is a module over for some .
Proof.
By Lemma 5, has no nontrivial finite dimensional simple module for .
For , let I be the ideal such that is finite dimensional semi-simple. It is easy to find some monic polynomial with such that . By Lemma 6, we may assume
such that for all .
For , we have by Lemma 7.
For , we have by Lemma 7.
For , we have by Lemma 7. Moreover, each summand is the untwisted affine Lie algebra. It is known that its semi-simple quotient is a multiple of .
The lemma follows. □
Next, we list our main results as follows.
Theorem 1.
- (1)
- For , has some nontrivial finite dimensional simple modules.
- (2)
- A finite dimensional vector space V is a simple -module if, and only if, it is a simple -module for some .
- (3)
- A finite dimensional vector space V is a simple -module if, and only if, it is a simple -module for some .
- (4)
- A finite dimensional vector space V is a simple -module if, and only if, it is a simple -module for some .
Theorem 2.
- (1)
- For , has some nontrivial finite dimensional simple modules.
- (2)
- A finite dimensional vector space V is a simple module over if, and only if, it is a simple module over for some and .
- (3)
- A finite dimensional vector space V is a simple module over if, and only if, it is a simple module over for some .
Immediately, from above theorems we can get the following result directly.
Corollary 1.
- (1)
- Let I be a maximal ideal of the finite co-dimension of . Then
- (2)
- Let I be a maximal ideal of finite co-dimension of . Then
4. Proof of Theorem 1
Let , and . It is easy to check that
Lemma 9.
There exists an epimorphism of Lie algebras
defined by
Proof.
First, the elements
generate the loop algebra .
It is sufficient to check the serre relations involving . Explicitly, we have
and
□
Corollary 2.
Any simple -module is a simple -module.
Lemma 10.
Any finite dimensional simple -module must be a simple -module.
Proof.
Assume that I is an ideal of such that is finite dimensional and semi-simple. Let , then . In particular, is a central element, and . For convenience, we can regard as the map defined over . For this situation, is injective.
Due to the the fact that is finite dimensional, there exists a polynomial such that
Let , then is an ideal of S. In addition, is the direct summand of S, since S is semi-simple. Let be the canonical projection. Then implies . In other words, has an ideal such that and . It is easy to get and . So . Moreover, .
By Lemma 4, we have finished the proof. □
Construction 1.
Let J be the ideal ofgenerated by a polynomialwith pairwise distinct constants. Then, by Lemma 8,
Letbe the natural projection and letbe a finite dimensional simple representation. Thendefines a simple finite dimensional representation. In particular, the image ofis as described in Theorem 1.
Proof of Theorem 1.
Corollary 2 and Lemma 10 imply that a finite vector space V is a simple module over if, and only if, it is a simple module over . Then Theorem 1 holds by Lemma 8 and Construction 1. □
5. Proof of Theorem 2
Similar to the previous section, we regard as the map defined over . It is easy to see that , so is still injective.
Lemma 11.
Any finite dimensional simple module over is a simple module over .
Proof.
Suppose that I is an ideal, such that is finite dimensional and semi-simple. Let . Then is an ideal of . Moreover, there exists such that
In fact, it holds that
For details, one is referred to page 4806 of [14].
Similar to the proof of Lemma 10, we have
Moreover, S is isomorphic to some quotient of , and hence some quotient of . □
Corollary 3.
Let V be a finite dimensional vector space. Then V is a simple -module if, and only if, it is a simple -module.
Corollary 4.
Suppose that I is an ideal, such that is finite dimensional and semi-simple. Then S is a subquotient of .
Proof.
It follows from the fact that is a subalgebra of . □
Lemma 12.
If for some , then the quotient has a nontrivial nilpotent ideal.
Lemma 13.
Suppose for some positive integer p and pairwise distinct constants , we have
for some and .
Proof .
(i) .
By the main result of [14], we have
for some and .
Moreover, if , we infer that
the quotient Lie algebra .
If , the quotient Lie algebra
If , the quotient Lie algebra
(ii) .
By the main result of [14], we have
for some and .
If , the quotient Lie alpha
If , the quotient Lie algebra
If , the quotient Lie algebra
□
Lemma 14.
- (1)
- A finite dimensional vector space V is a simple module over if, and only if, it is a simple module over for some and .
- (2)
- A finite dimensional vector space V is a simple module over if, and only if, it is a simple module over for some .
Proof .
(1) holds by Lemma 13.
Notice that any semi-simple quotient of is a multiple of , any semi-simple quotient of is a multiple of , and the semi-simple quotient of is a multiple of . Thus (2) also holds by Lemma 13. □
Construction 2.
Consider the map in Construction 1, let I be the kernel of the map
as in Theorem 2 for. Then any finite dimensional simple modules overcan be constructed directly. Those are simple-modules in the natural way.
Proof of Theorem 2.
For , contains a Lie subalgebra generated by the elements
which is of type . In particular, is a central element. If V is a finite dimensional module over , we have . Due to the fact that , we have , and . It is easy to obtain .
Assume . Then it holds by Corollary 3, Lemma 14, and Construction 2. The theorem is proved. □
6. Conclusions
In conclusion, all finite dimensional simple modules over the GIM Lie algebra as well as those over are classified in this paper (Theorems 1 and 2). Meanwhile, such research for was completed in [14]. Certainly, the study of finite dimensional modules over GIM Lie algebras is still in its infancy.
Author Contributions
Conceptualization, L.X. and D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the National Natural Science Foundation of China (Grant Nos. 11871249, 12071405, 11971315 and 12171155).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declared that they have no conflict of interest to this work.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of Open-Access Journals |
| TLA | Three-Letter Acronym |
| LD | Linear Dichroism |
References
- Slodowy, P. Beyond Kac–Moody algebras and inside. Can. Math. Soc. Conf. Proc. 1986, 5, 361–371. [Google Scholar]
- Berman, S.; Moody, R.V. Lie algebras graded by finite root systems and the intersection matrix algepbras of Slowdowy. Invent. Math. 1992, 108, 323–347. [Google Scholar] [CrossRef]
- Berman, S. On generators and relations for certain involutory subalgebras of Kac–Moody Lie algebras. Comm. Alg. 1989, 17, 3165–3185. [Google Scholar] [CrossRef]
- Benkart, G.; Zelmanov, E. Lie algebras graded by finite root systems and intersection matrix algebras. Invent. Math. 1996, 126, 1–45. [Google Scholar] [CrossRef]
- Berman, S.; Jurisich, E.; Tan, S. Beyond Borcherds Lie algebras and inside. Trans. Amer. Math. Soc. 2001, 353, 1183–1219. [Google Scholar] [CrossRef][Green Version]
- Gao, Y. Involutive Lie algebras graded by finite root systems and compact forms of IM algebras. Math. Z. 1996, 223, 651–672. [Google Scholar] [CrossRef]
- Neher, E. Lie algebras graded by 3-graded root systems and Jordan pairs covered by grids. Am. J. Math. 1996, 118, 439–491. [Google Scholar] [CrossRef]
- Xu, M.; Peng, L. Symmetrizable intersection matrix Lie algebras. Algebra Colloq. 2011, 18, 639–646. [Google Scholar] [CrossRef]
- Xia, L.; Hu, N. A class of Lie algebras arising from intersection matrices. Front. Math. China 2015, 10, 185–198. [Google Scholar] [CrossRef][Green Version]
- Gao, Y.; Hu, N.; Xia, L. Quantized GIM algebras and their images in quantized Kac–Moody algebras. Algebra Represent. Theory 2021, 24, 565–584. [Google Scholar] [CrossRef]
- Kolb, S. Quantum symmetric Kac–Moody pairs. Adv. Math. 2014, 267, 395–469. [Google Scholar] [CrossRef]
- Tan, Y. Quantized GIM Lie algebras and their Lusztig symmetries. J. Algebra 2005, 289, 214–276. [Google Scholar] [CrossRef][Green Version]
- Tan, Y. Drinfel’d-Jimbo coproduct of quantized GIM Lie algebras. J. Algebra 2007, 313, 617–641. [Google Scholar] [CrossRef][Green Version]
- Gao, Y.; Xia, L. Finite-dimensional representations for a class of generalized intersection matrix Lie algebras. Comm. Algebra 2016, 44, 4794–4810. [Google Scholar] [CrossRef]
- Kac, V. Infinite-Dimensional Lie Algebras, 3rd ed.; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).