A (2+1)-Dimensional Fractional-Order Epidemic Model with Pulse Jumps for Omicron COVID-19 Transmission and Its Numerical Simulation
Abstract
:1. Introduction
2. Fractional-Order Model with Pulse Jumps
3. Inverse Problem
| Algorithm 1 Gradient descent. |
| Require: Starting point , , , a function , step size , tolerance 1: repeat 2: Calculate , 3: Update and 4: until for 10 iterations in sequence Ensure: some hopefully minimizing , , |
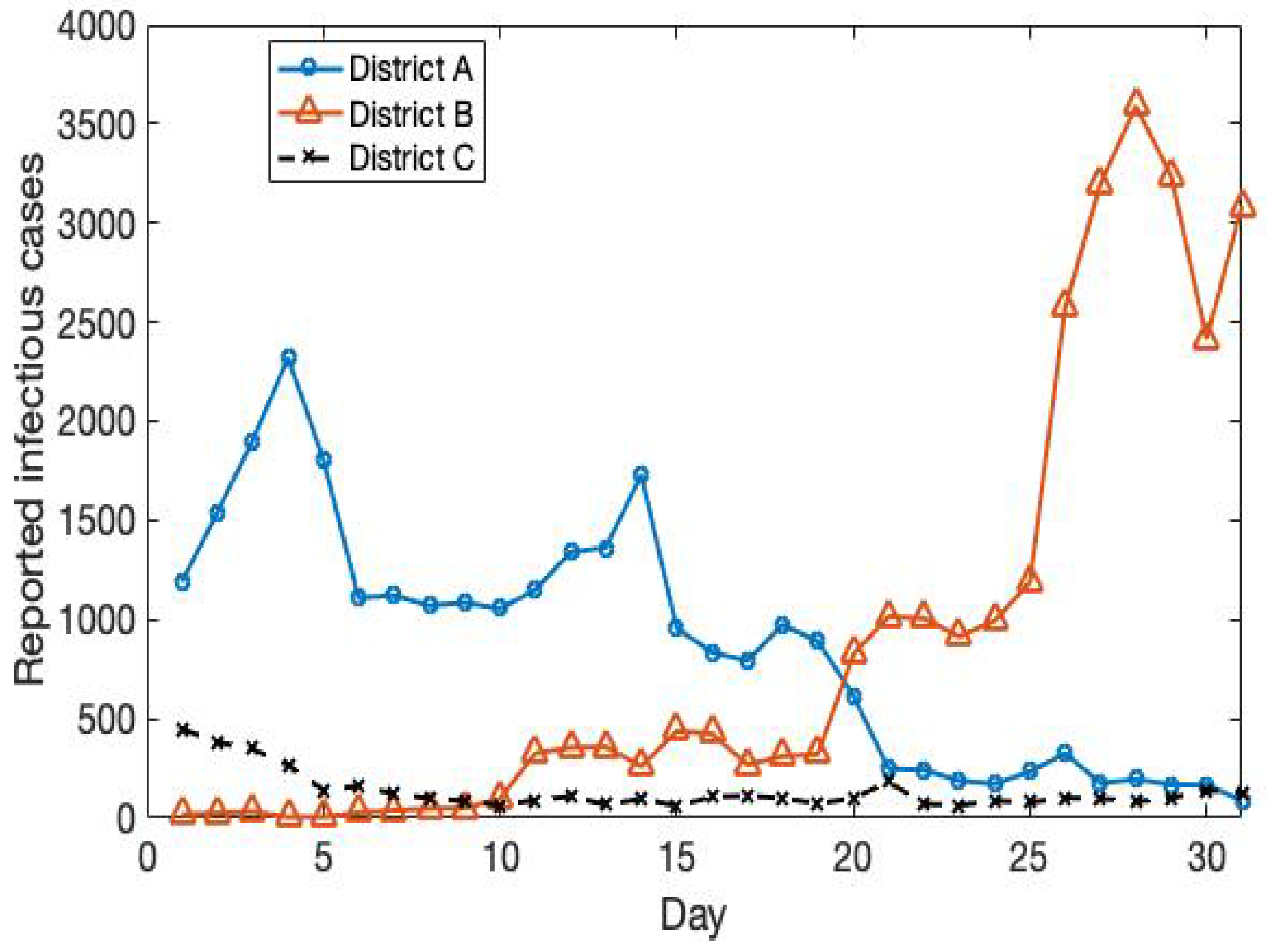
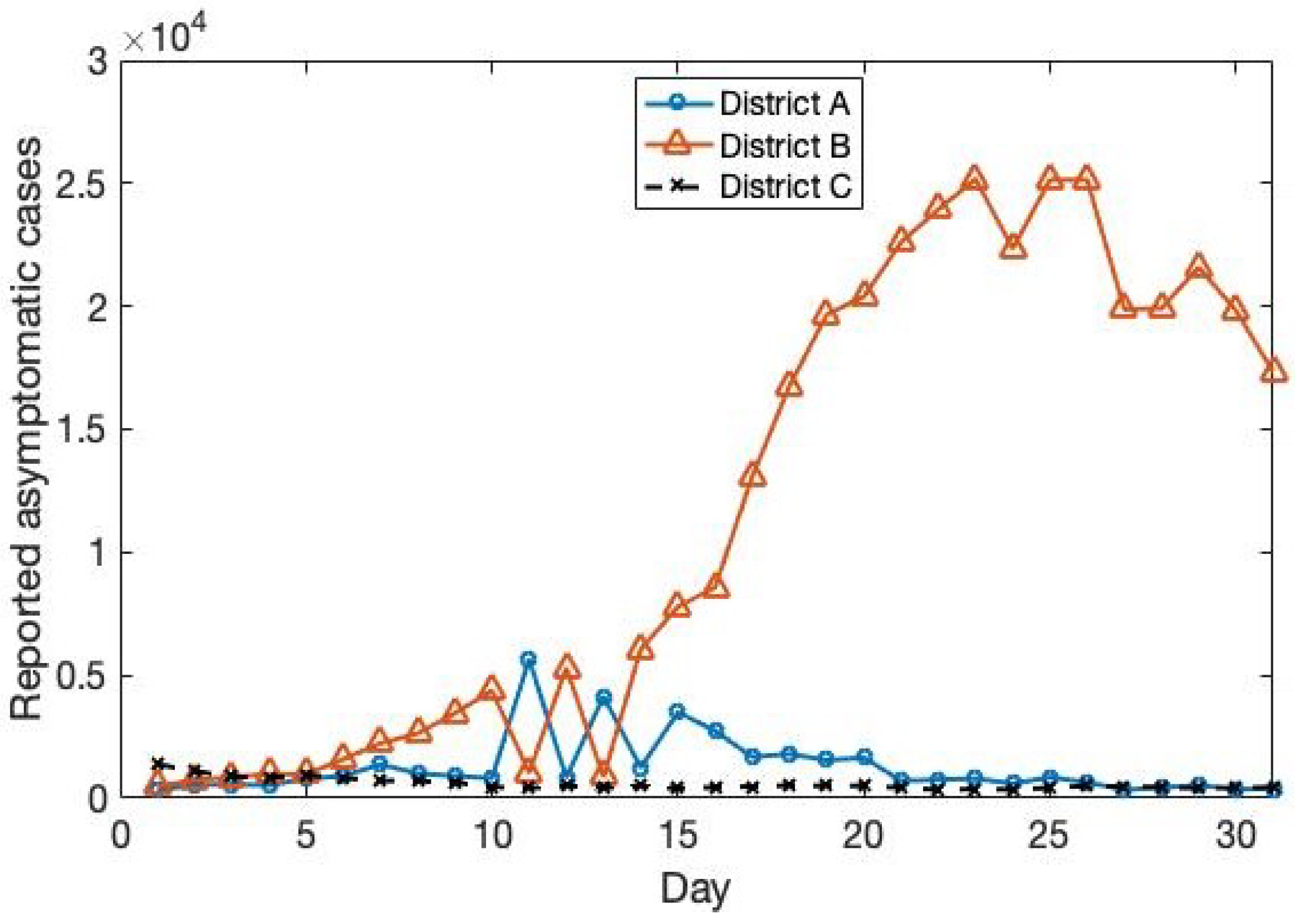
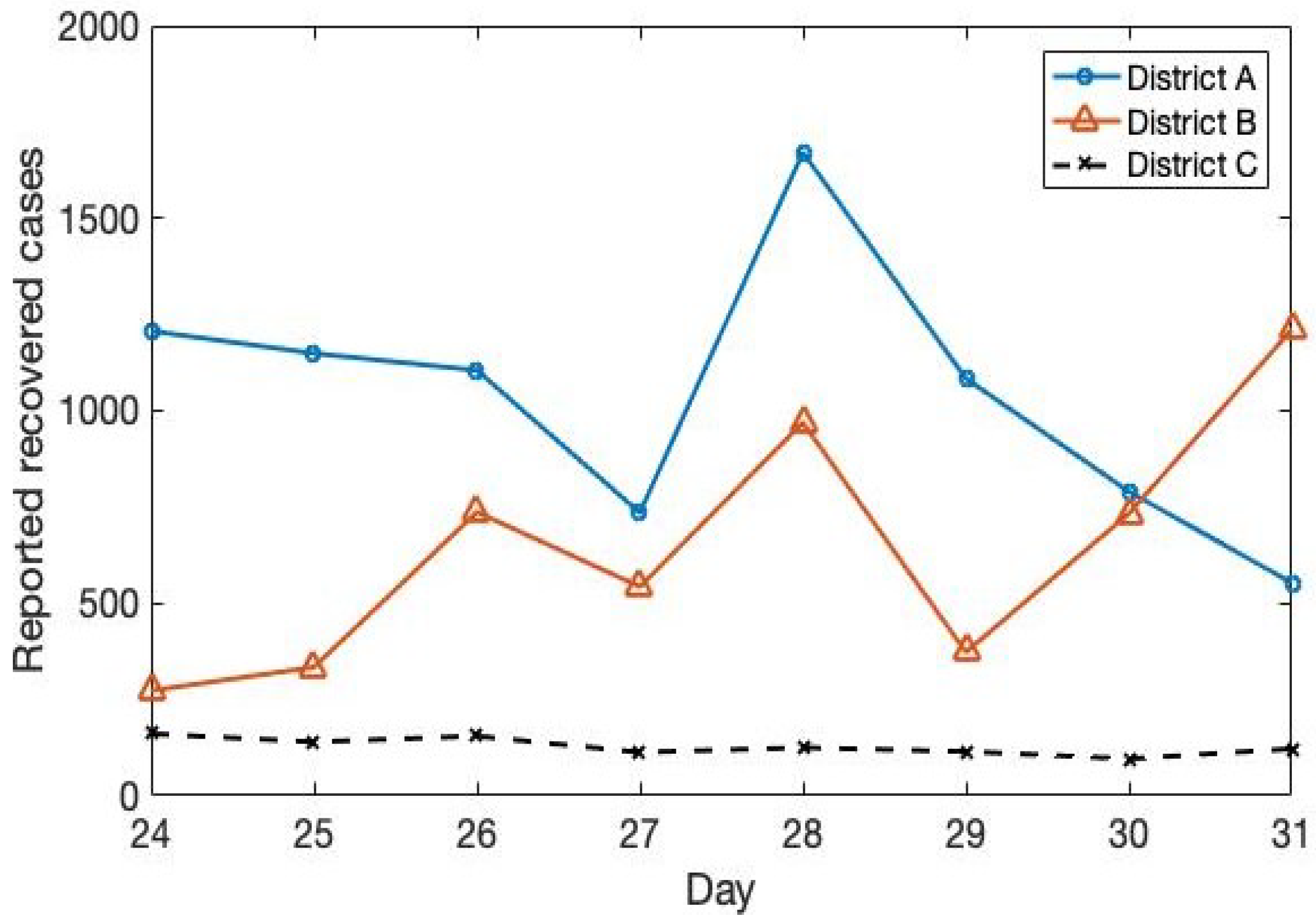
4. Numerical Simulation
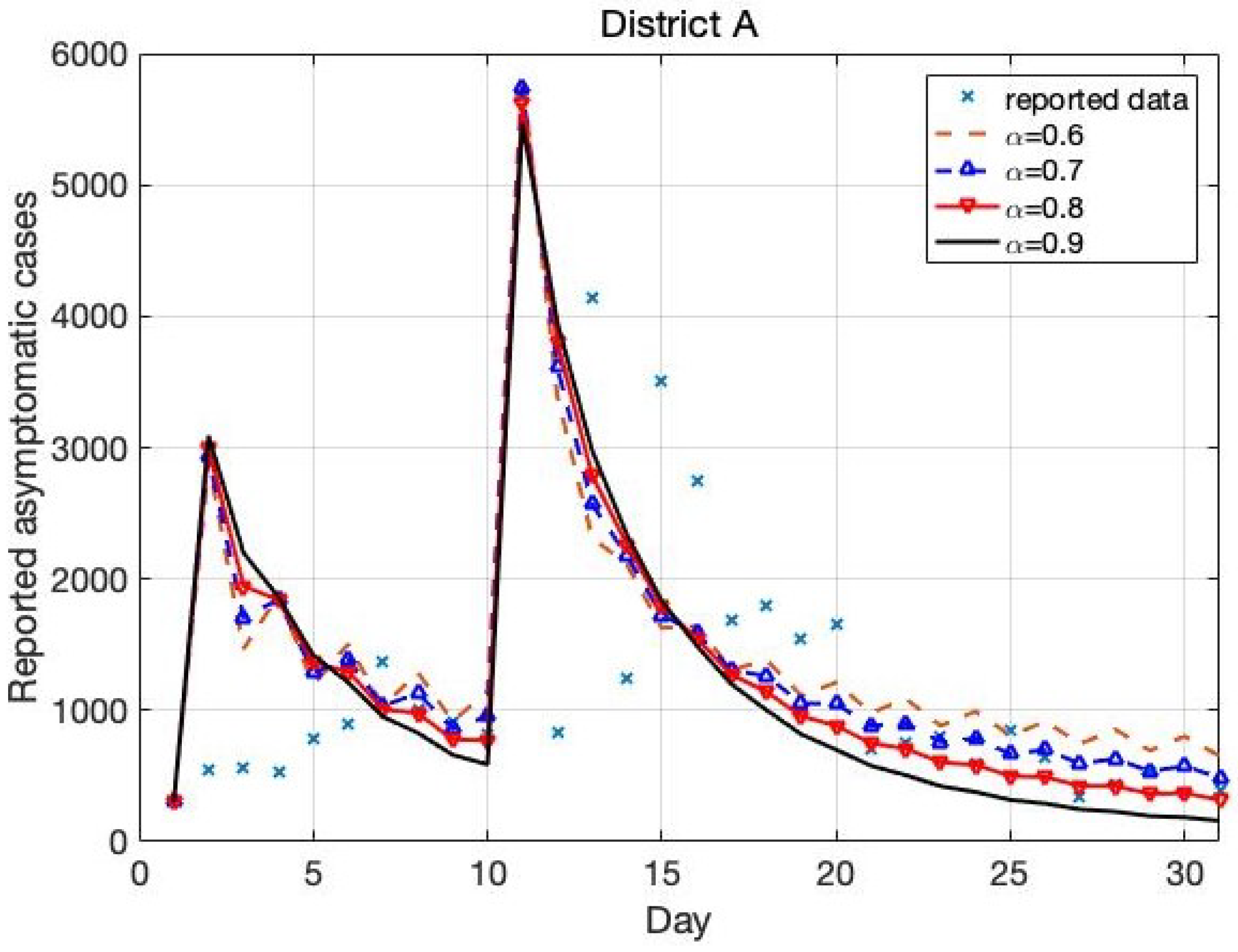
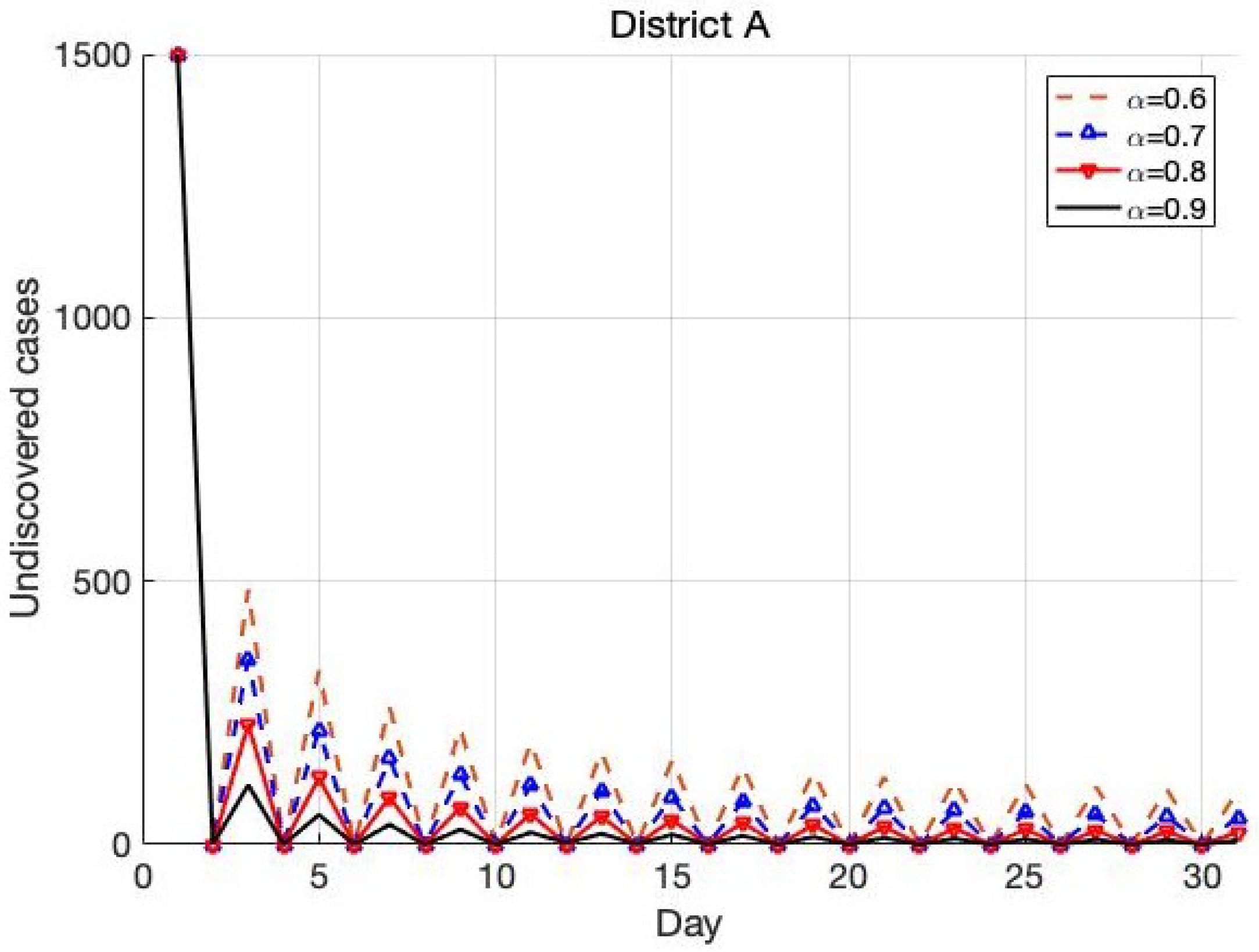
4.1. The Trend in District A
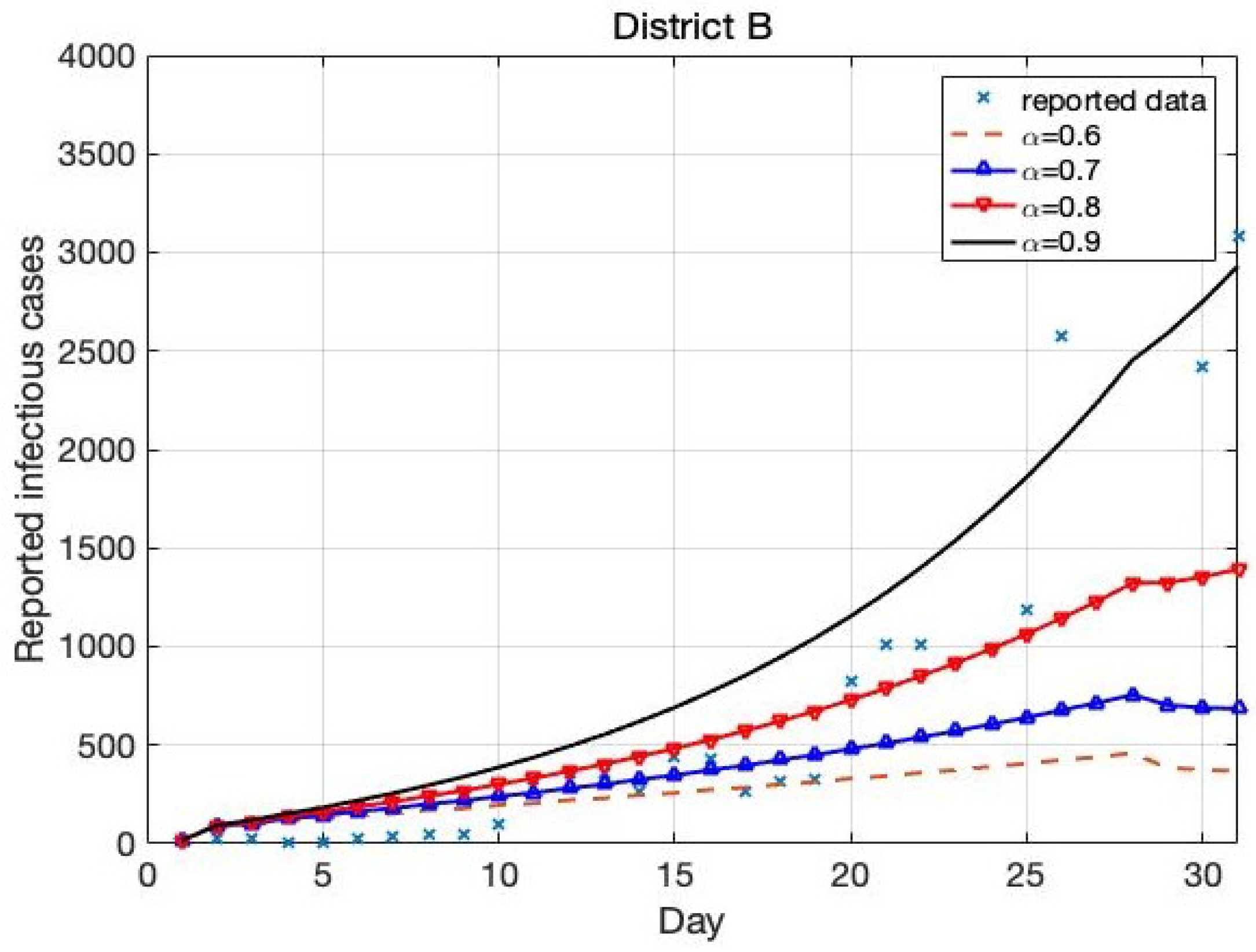
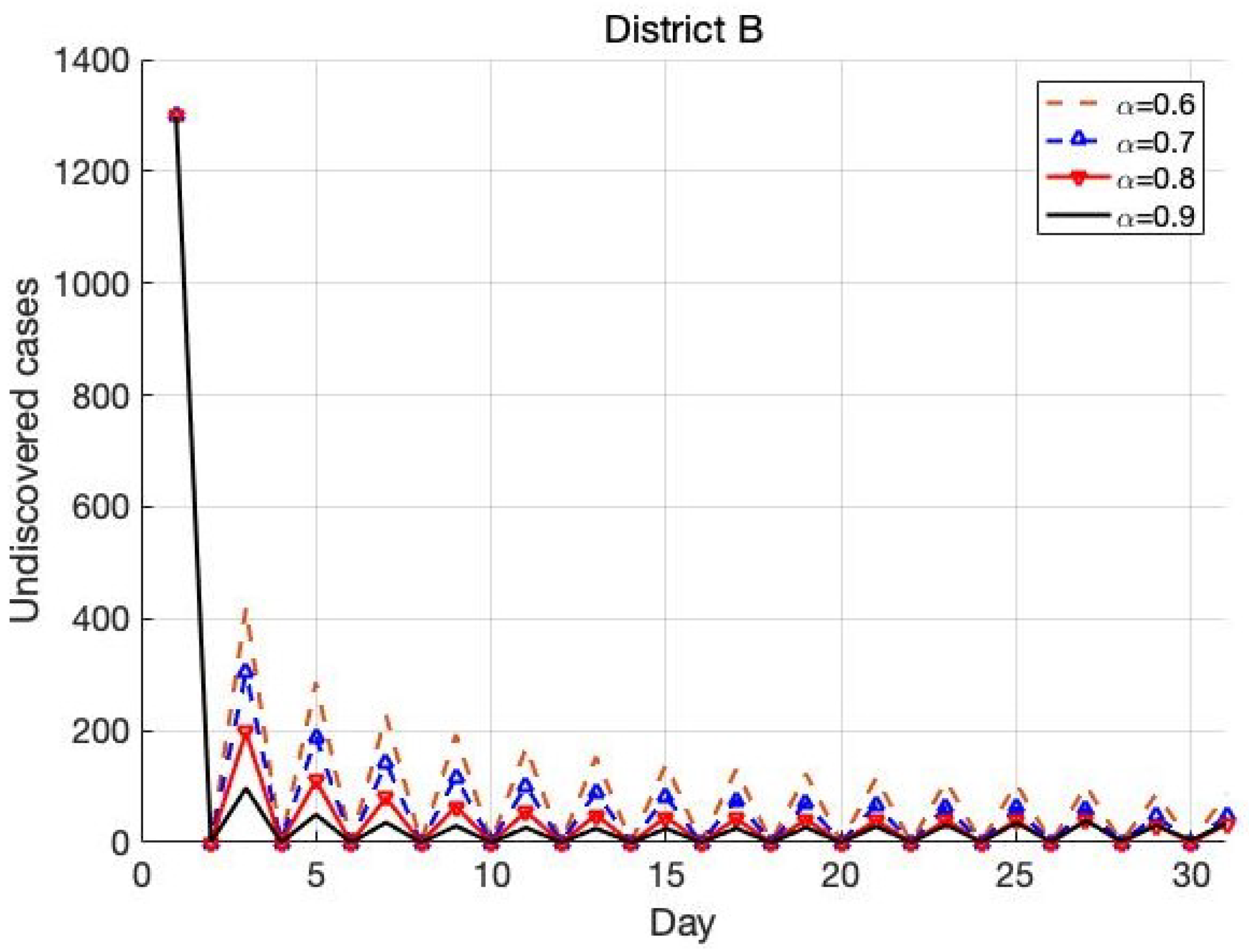
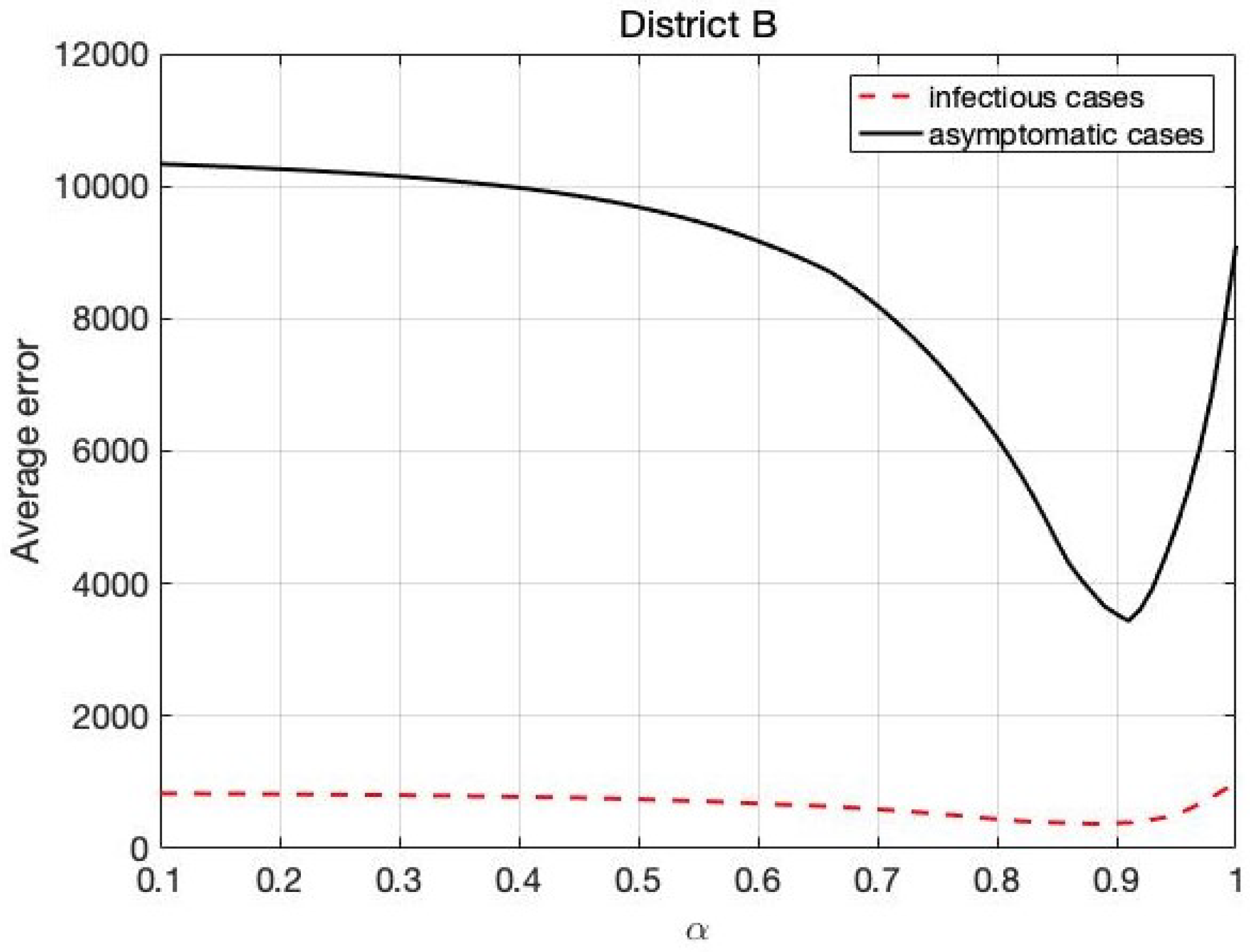
4.2. The Trend in District B
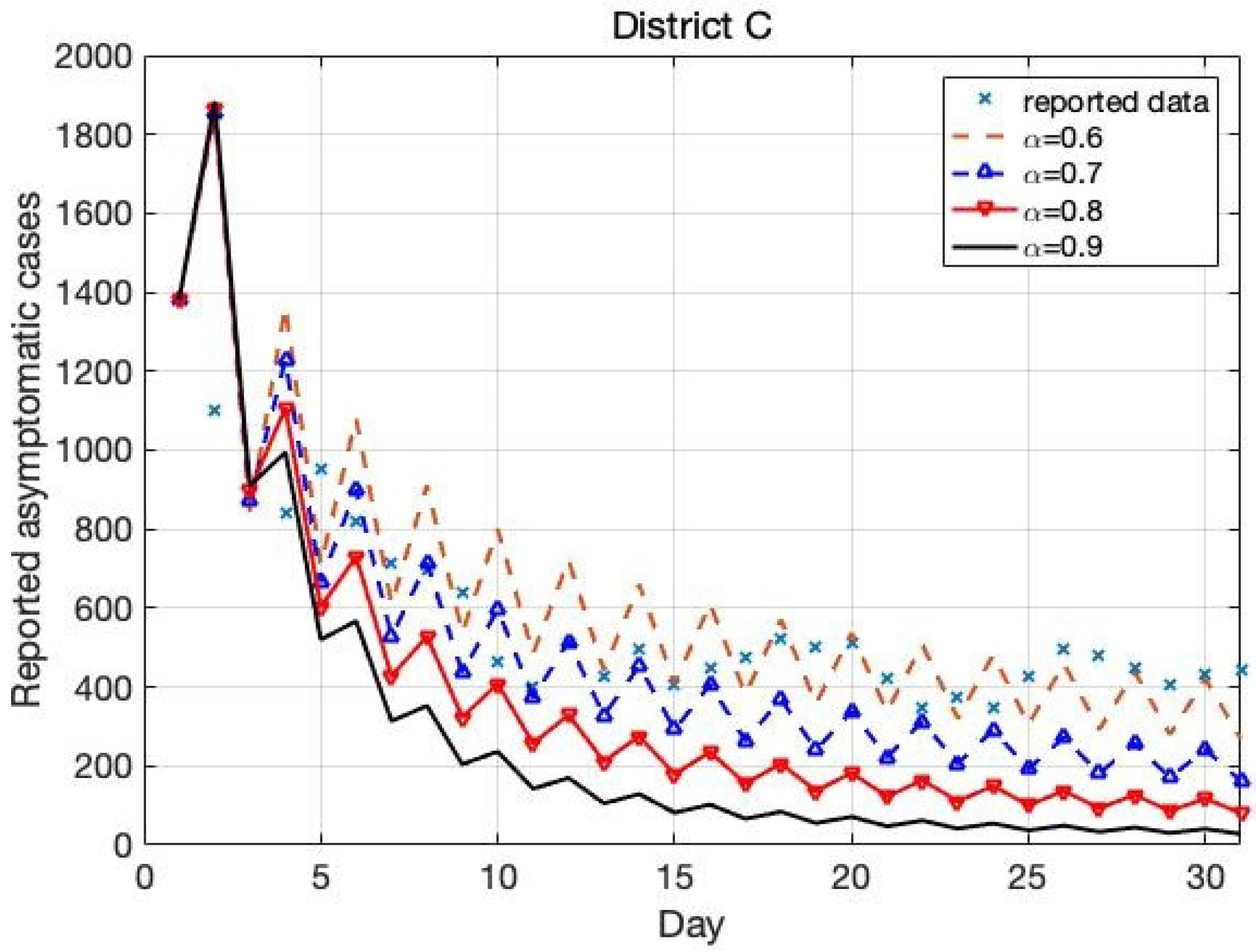
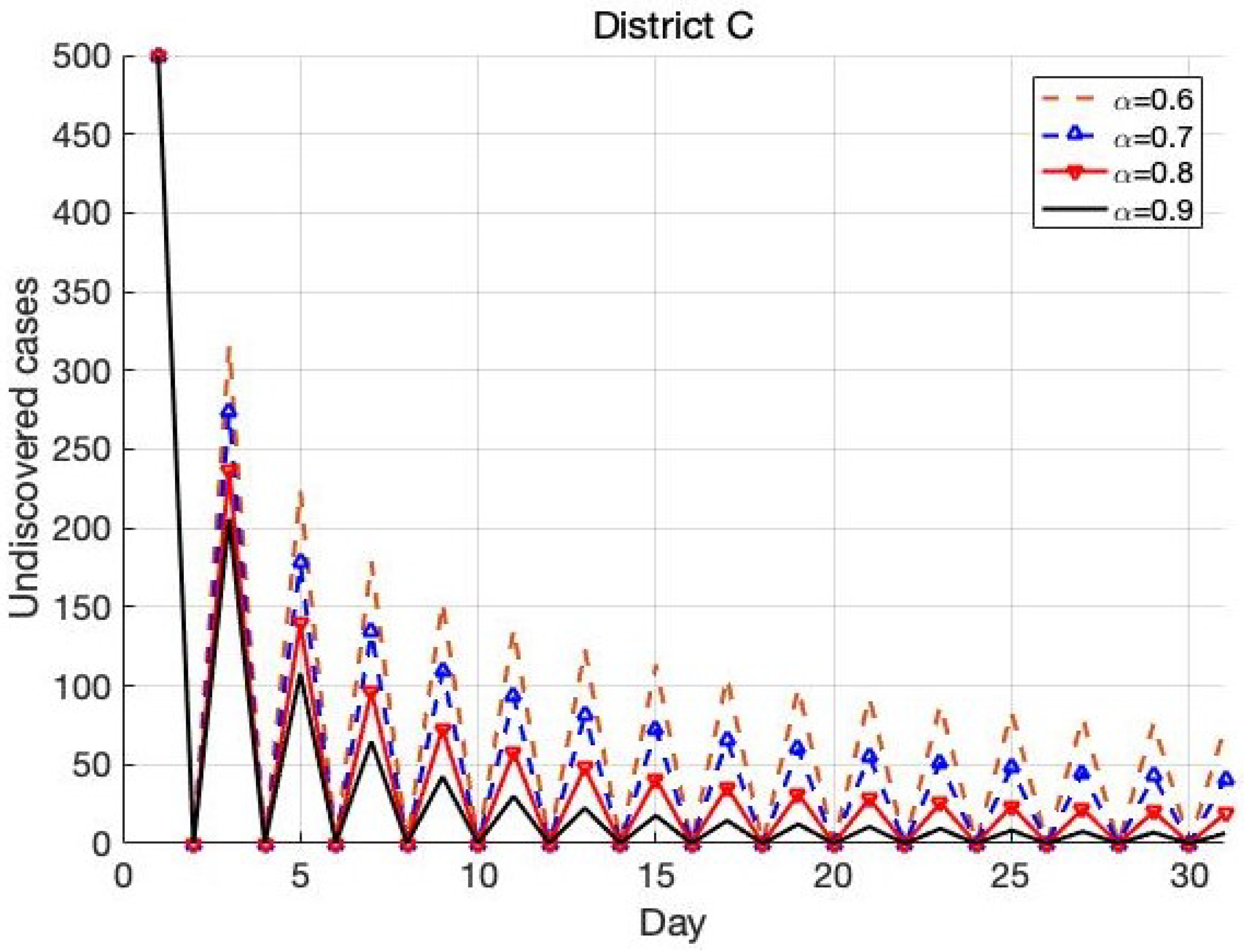
4.3. The Trend in District C
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shin, H.Y. A multi-stage SEIR(D) model of the COVID-19 epidemic in Korea. Ann. Med. 2021, 53, 1159–1169. [Google Scholar] [CrossRef]
- Annas, S.; Pratama, M.I.; Rifandi, M.; Sanusi, W.; Side, S. Stability analysis and numerical simulation of SEIR model for pandemic COVID-19 spread in Indonesia. Chaos Solitons Fractals 2020, 139, 110072. [Google Scholar] [CrossRef]
- Paul, S.; Mahata, A.; Ghosh, U.; Roy, B. Study of SEIR epidemic model and scenario analysis of COVID-19 pandemic. Ecol. Genet. Genom. 2021, 19, 100087. [Google Scholar] [CrossRef]
- Quintero, Y.; Ardila, D.; Camargo, E.; Rivas, F.; Aguilar, J. Machine learning models for the prediction of the SEIRD variables for the COVID-19 pandemic based on a deep dependence analysis of variables. Comput. Biol. Med. 2021, 134, 104500. [Google Scholar] [CrossRef]
- Li, J.; Zhong, J.; Ji, Y.M.; Yang, F. A new SEIAR model on small-world networks to assess the intervention measures in the COVID-19 pandemics. Results Phys. 2021, 25, 104283. [Google Scholar] [CrossRef]
- Zhu, W.J.; Shen, S.F. An improved SIR model describing the epidemic dynamics of the COVID-19 in China. Results Phys. 2021, 25, 104289. [Google Scholar] [CrossRef]
- Inc, M.; Acay, B.; Berhe, H.W.; Yusuf, A.; Khan, A.; Yao, S.W. Analysis of novel fractional COVID-19 model with real-life data application. Results Phys. 2021, 23, 103968. [Google Scholar] [CrossRef]
- Omar, O.A.M.; Elbarkouky, R.A.; Ahmed, H.M. Fractional stochastic modelling of COVID-19 under wide spread of vaccinations: Egyptian case study. Alex. Eng. J. 2022, 61, 8595–8609. [Google Scholar] [CrossRef]
- Kolebaje, O.T.; Vincent, O.R.; Vincent, U.E.; McClintock, P.V.E. Nonlinear growth and mathematical modelling of COVID-19 in some African countries with the Atangana-Baleanu fractional derivative. Commun. Nonlinear Sci. Numer. Simul. 2022, 105, 106076. [Google Scholar] [CrossRef]
- Zhou, J.C.; Salahshour, S.; Ahmadian, A.; Senu, N. Modeling the dynamics of COVID-19 using fractal-fractional operator with a case study. Results Phys. 2022, 33, 105103. [Google Scholar] [CrossRef]
- Omame, A.; Abbas, M.; Onyenegecha, C.P. A fractional-order model for COVID-19 and tuberculosis co-infection using Atangana-Baleanu derivative. Chaos Solitons Fractals 2021, 15, 111486. [Google Scholar] [CrossRef]
- Omame, A.; Abbas, M.; Onyenegecha, C.P. A fractional order model for the co-interaction of COVID-19 and Hepatitis B virus. Results Phys. 2022, 37, 105498. [Google Scholar] [CrossRef]
- Omame, A.; Isah, M.E.; Abbas, M.; Abdel-Aty, A.H.; Onyenegecha, C.P. A fractional order model for Dual Variants of COVID-19 and HIV co-infection via Atangana-Baleanu derivative. Alex. Eng. J. 2022, 61, 9715–9731. [Google Scholar] [CrossRef]
- Meng, X.Z.; Chen, L.S.; Song, Z.T. Global dynamics behaviors for new delay SEIR epidemic disease model with vertical transmission and pulse vaccination. Appl. Math. Mech. 2007, 28, 1259–1271. [Google Scholar] [CrossRef]
- Sekiguchi, M.; Ishiwata, E. Dynamics of a discretized SIR epidemic model with pulse vaccination and time delay. J. Comput. Appl. Math. 2011, 236, 997–1008. [Google Scholar] [CrossRef] [Green Version]
- Ling, L.; Jiang, G.R.; Long, T.F. The dynamics of an SIS epidemic model with fixed-time birth pulses and state feedback pulse treatments. Appl. Math. Model. 2015, 39, 5579–5591. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Okyere, E.; Abidemi, A.; Moore, S.E.; Sun, G.Q.; Jin, Z.; Acheampong, E.; Gordon, J.F. Optimal control and comprehensive cost-effectiveness analysis for COVID-19. Results Phys. 2022, 33, 105177. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Jin, Z.; Sun, G.Q.; Seidu, B.; Yankson, E.; Abidemi, A.; Oduro, F.T.; Moore, S.E.; Okyere, E. Sensitivity assessment and optimal economic evaluation of a new COVID-19 compartmental epidemic model with control interventions. Chaos Solitons Fractals 2021, 146, 110885. [Google Scholar] [CrossRef]
- Acheampong, E.; Okyere, E.; Iddi, S.; Bonney, J.H.; Asamoah, J.K.K.; Wattis, J.A.; Gomes, R.L. Mathematical modelling of earlier stages of COVID-19 transmission dynamics in Ghana. Results Phys. 2022, 34, 105193. [Google Scholar] [CrossRef]
- Asamoah, J.K.K.; Owusu, M.A.; Jin, Z.; Oduro, F.T.; Abidemi, A.; Gyasi, E.O. Global stability and cost-effectiveness analysis of COVID-19 considering the impact of the environment: Using data from Ghana. Chaos Solitons Fractals 2020, 140, 110103. [Google Scholar]
- Ssebuliba, J.; Nakakawa, J.N.; Ssematimba, A.; Mugisha, J.Y.T. Mathematical modelling of COVID-19 transmission dynamics in a partially comorbid community. Partial. Differ. Equ. Appl. Math. 2022, 5, 100212. [Google Scholar] [CrossRef]
- Paul, S.; Mahata, A.; Mukherjee, S.; Roy, B. Dynamics of SIQR epidemic model with fractional order derivative. Partial. Differ. Equ. Appl. Math. 2022, 5, 100216. [Google Scholar] [CrossRef]
- Rezapour, S.; Mohammadi, H.; Samei, M.E. SEIR epidemic model for COVID-19 transmission by Caputo derivative of fractional order. Adv. Differ. Equ. 2020, 2020, 490. [Google Scholar] [CrossRef]
- Delshad, S.S.; Asheghan, M.M.; Beheshti, M.H. Robust stabilization of fractional-order systems with interval uncertainties via fractional-order controllers. Adv. Differ. Equ. 2010, 2010, 984601. [Google Scholar] [CrossRef] [Green Version]
- Arenas, A.J.; Gonzlez-Parra, G.; Chen-Charpentier, B.M. Construction of nonstandard finite difference schemes for the SI and SIR epidemic models of fractional order. Math. Comput. Simul. 2016, 121, 48–63. [Google Scholar] [CrossRef]
- Sene, N. Introduction to the fractional-order chaotic system under fractional operator in Caputo sense. Alex. Eng. J. 2021, 60, 3997–4014. [Google Scholar] [CrossRef]
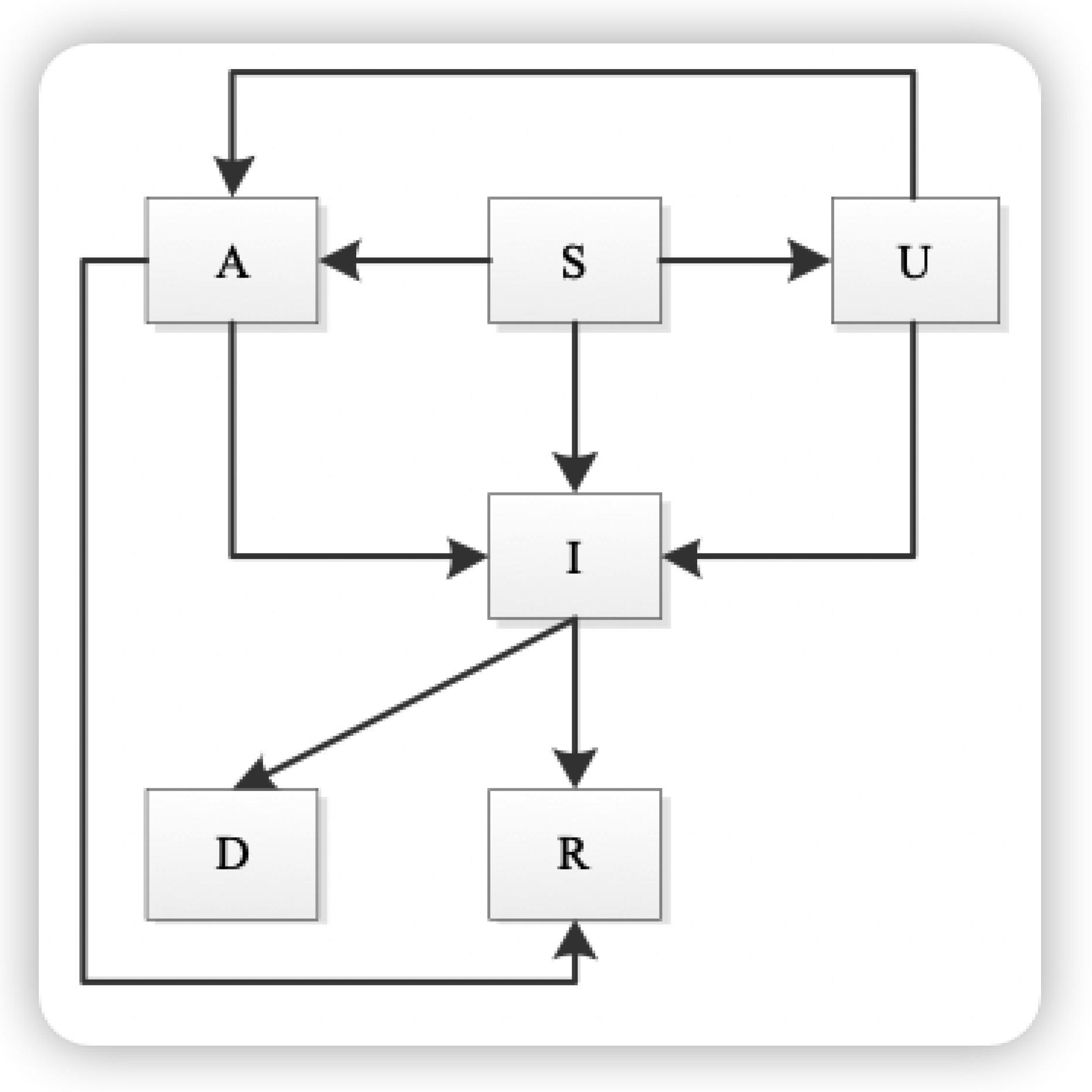





| Symbols | Description |
|---|---|
| Transmission rate from S group in other considered locations | |
| Transmission rate from U group in other considered locations | |
| Transmission rate from S to I group | |
| Transmission rate from S to A group | |
| Transmission rate from S to U group | |
| Transmission rate from A to I group | |
| Transmission rate from U to I group | |
| Recovery rate of I group | |
| Omicron COVID-19 death rate | |
| Recovery rate of A group | |
| Transmission rate from U to A group |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.-J.; Shen, S.-F.; Ma, W.-X. A (2+1)-Dimensional Fractional-Order Epidemic Model with Pulse Jumps for Omicron COVID-19 Transmission and Its Numerical Simulation. Mathematics 2022, 10, 2517. https://doi.org/10.3390/math10142517
Zhu W-J, Shen S-F, Ma W-X. A (2+1)-Dimensional Fractional-Order Epidemic Model with Pulse Jumps for Omicron COVID-19 Transmission and Its Numerical Simulation. Mathematics. 2022; 10(14):2517. https://doi.org/10.3390/math10142517
Chicago/Turabian StyleZhu, Wen-Jing, Shou-Feng Shen, and Wen-Xiu Ma. 2022. "A (2+1)-Dimensional Fractional-Order Epidemic Model with Pulse Jumps for Omicron COVID-19 Transmission and Its Numerical Simulation" Mathematics 10, no. 14: 2517. https://doi.org/10.3390/math10142517
APA StyleZhu, W.-J., Shen, S.-F., & Ma, W.-X. (2022). A (2+1)-Dimensional Fractional-Order Epidemic Model with Pulse Jumps for Omicron COVID-19 Transmission and Its Numerical Simulation. Mathematics, 10(14), 2517. https://doi.org/10.3390/math10142517







