Near-Record Values in Discrete Random Sequences

Abstract

Given a sequence $\left(X_n\right)$ of random variables, $X_n$ is said to be a near-record if $X_n\in (M_{n-1}-a,M_{n-1}]$, where $M_n=max\{X_1, \dots , X_n\}$ and $a>0$ is a parameter. We investigate the point process $\eta$ on $[0,\infty )$ of near-record values from an integer-valued, independent and identically distributed sequence, showing that it is a Bernoulli cluster process. We derive the probability generating functional of $\eta$ and formulas for the expectation, variance and covariance of the counting variables $\eta \left(A\right),A\subset [0,\infty )$. We also derive the strong convergence and asymptotic normality of $\eta \left(\right[0,n\left]\right)$, as $n\to \infty$, under mild regularity conditions on the distribution of the observations. For heavy-tailed distributions, with square-summable hazard rates, we prove that $\eta \left(\right[0,n\left]\right)$ grows to a finite random limit and compute its probability generating function. We present examples of the application of our results to particular distributions, covering a wide range of behaviours in terms of their right tails.

1. Introduction

Outstanding achievements and world records in athletics events such as the 100 m sprint always make headlines and arouse widespread admiration. Similarly, considerable media attention and public concern are attached to record figures (often bad) relating to the economy, the weather or healthcare systems. Crucial social questions arise when we are faced with a steady flow of records, which are presented as ominous signs of dramatic underlying phenomena. It is therefore unsurprising that the term “record” has become such a constant in our modern everyday life and in a wide range of specialist domains. The probabilistic theory and statistical analysis of record breaking data can be helpful in assessing the seriousness of these issues.

The mathematical theory of records is well developed, especially for data generated by independent and identically distributed (i.i.d.) random variables (r.v.) with a continuous underlying distribution function. As is well known, in this setting, one can only expect about log n record values among n observations, which means that records are rare. The reader interested in the theory of records can consult the monographs [1,2,3]. For statistical inference from record data, see [4].

Concepts of “quasi-records” emerged as natural extensions of records and have proven to be worthwhile from a mathematical as well as an applied perspective. The general idea of values close to records was translated into a variety of definitions that were theoretically analysed and applied in widely different contexts. Near-records were introduced in [5] for applications in finance, and their properties were analysed in [6,7]. In addition, the related concept of the $\delta$-record was introduced in [8] and later studied in [9,10,11,12]. These objects have practical applications in the case of negative $\delta$, since $\delta$-records are more numerous than records. So, by considering samples of $\delta$-records for statistical inference, we address the problem of the scarcity of records while keeping the extremal nature of the data. Indeed, it has been shown in [9] and in references therein that inferences based on $\delta$-records outperform those based on records only.

The main objects of interest in this work are near-records. An observation is a near-record if it is not a record but is at a distance of less than $a>0$ units from the last record; that is, it falls short of being a record by less than a units. While the number of records in an i.i.d. sequence of continuous r.v. grows with the logarithm of the number of observations, the number of near-records grows at speeds depending on the distribution of the observations. In fact, for heavy-tailed distributions, there are fewer near-records than records (in extreme cases, only a finite number of near-records can be observed along the whole sequence), while for light-tailed distributions, near-records outnumber records; see [13] for details.

Another interesting aspect of near-records is related to their values. It is well known that record values of an i.i.d. sequence behave as the so-called Shorrock process [14], which is a mixture of a non-homogeneous Poisson process and a Bernoulli process. In the particular case of non-negative integer-valued r.v., k is a record value with probability $\mathbb{P}(X_1=k|X_1\ge k)$, and the events wherein $\{k$ is a record value} are independent.

In this paper, we focus on the process of near-record values for i.i.d. sequences of r.v., taking non-negative integer values. The case of continuous r.v., analysed in [13], showed that near-record values follow a Poisson cluster point process, where records are the centres of the clusters and near-records are the points in each cluster. The main characteristics of this process, including its asymptotic behaviour, were derived from the properties of the Poisson cluster process, which has been thoroughly studied in the literature. In the discrete setting of the present paper, we prove that near-record values also behave as a cluster process, with centres following a Bernoulli process. We fully characterise the process by giving an expression for its probability generating functional. In particular, we find the exact distribution of the number of times that k is a near-record, which turns out to be a mixture of a point mass at 0 and a geometric distribution. We also characterise the distribution of the total number of near-records for heavy-tailed distributions. Moreover, we study the limiting behaviour of the number of near-records with values less than n, as n goes to infinity, by giving laws of large numbers and central limit theorems. Rather than relying on properties of cluster processes, as done in [13], here, we use a more direct approach that consists of approximating the sequences under study by a sum of independent r.v. We give several examples of applications of our results to particular families, ranging from heavy-tailed distributions, with a finite number of near-records, to light-tailed ones, such as the Poisson distribution.

The paper is organised as follows: notations and first definitions are presented in Section 2. The process of near-record values is studied in Section 3, while in Section 4, we consider the eventual finiteness of the total number of near-records, followed by asymptotic results in Section 5. Finally, illustrative examples are shown in Section 6 and Appendix A is devoted to technical results.

2. Notation and Preliminary Definitions

The sets of real and positive real numbers are denoted by $\mathbb{R}$ and ${\mathbb{R}}_{+}$, respectively. The sets of positive and non-negative integers are denoted by $\mathbb{N}$ and ${\mathbb{Z}}_{+}$, respectively. Sequences in $\mathbb{R}$ are indexed by $\mathbb{N}$ and are written in lower-case letters, between parentheses, such as $\left(x_n\right), \left(y_k\right)$, etc. All r.v. are assumed to be defined on a common probability space $(\Omega ,\mathcal{F},\mathbb{P})$. The indicator r.v. of an event $B\in \mathcal{F}$, taking the value 1 on B and 0 otherwise, is denoted by ${\mathbf{1}1}_B$. The indicator function of $A\subseteq \mathbb{R}$, equal to 1 on A and 0 on $\mathbb{R}\backslash A$, is denoted by ${\mathbf{1}1}_A$.

When referring to a geometric r.v. or distribution throughout the paper, we assume 0 as the starting value. The probability generating function (p.g.f.) of an r.v. X, taking values in ${\mathbb{Z}}_{+}$, is defined as ${\phi }_X\left(t\right)=\mathbb{E}\left(t^X\right)={\sum }_{k=0}^{\infty }{t}^k\mathbb{P}(X=k)$, for all $t\in \mathbb{R}$, such that the series is absolutely convergent.

Sequences of r.v. are also indexed by $\mathbb{N}$ and are written in upper-case letters, such as $\left(X_n\right), \left(Y_k\right)$, etc. The convergence of deterministic sequences to a limit L is denoted by $x_n\to L$ or $lim{x}_n=L$, and it is implicitly understood as $n\to \infty$, unless otherwise stated. The notation $x_n\sim y_n$ stands for $x_n/y_n\to 1$. The same notation applies to random sequences, where the mode of convergence (almost sure $\stackrel{\mathrm{a}.\mathrm{s}.}{⟶}$ or in distribution $\stackrel{\mathcal{D}}{⟶}$) is indicated over the arrow. The $\sigma$-algebra of Borel subsets of ${\mathbb{R}}_{+}$ is denoted by ${\mathcal{B}}_{+}$.

Definition 1. 

Let $\left(X_n\right)$ be a sequence of r.v. and let a be a positive parameter. Then, for $n\in \mathbb{N}$,

• $X_n$ is a record if $X_n>M_{n-1}$, and
• $X_n$ is near-record if $M_{n-1}-a<X_n\le M_{n-1},$

where $M_n=max\{X_1, \cdots , X_n\}$, with $M_0=-\infty$, by convention.

From the above definitions, it is clear that a near-record is not a record, but it can take the value of the current record. Other random sequences of interest related to records are record times $\left(L_n\right)$, defined as

$$L_n=min\{k\in \mathbb{N}|k>L_{n-1}, X_k>M_{L_{n-1}}\},$$

for $n\ge 1$, with $L_0=0$, and record values $\left(R_n\right)$, given by $R_n=X_{L_n}=M_{L_n}$, for $n\ge 1$. Additionally, we consider the set of record values as a point process on $\mathbb{R}$, which can be described by the random counting measure $\xi$, defined by

$$\xi \left(A\right)=card\{n\in \mathbb{N}|R_n\in A\}, A\in {\mathcal{B}}_{+}.$$

(1)

We also define $I_n:=\xi \left(\left\{n\right\}\right)$—the indicator of the event for which a record takes the value n.

Observe that record times $L_n$ are the jump times of the sequence of partial maxima and that record values $R_n$ are the (strictly increasing) subsequence of partial maxima $\left(M_n\right)$, sampled at those jump times. However, without further probabilistic assumptions on $\left(X_n\right)$, it may happen that $L_n=\infty$, from some value of n on, which is equivalent to the existence of a final record. Furthermore, we have to ensure that the counting measure $\xi$ is boundedly finite in the sense of being finite on bounded sets.

Similarly, the sequence $\left(L_n^a\right)$ of near-record times is defined by

$$L_n^a=min\{k\in \mathbb{N}|k>L_{n-1}^a, M_{k-1}-a<X_k\le M_{k-1}\},$$

for $n\ge 1$, with $L_0^a=0$, and near-record values $\left(R_n^a\right)$ are given by $R_n^a=X_{L_n^a}$, for $n\ge 1$. We define the counting measure of near-record values by

$$\eta \left(A\right)=card\{n\in \mathbb{N}|R_n^a\in A\}, A\in {\mathcal{B}}_{+},$$

(2)

and define the related r.v. $\eta \left(n\right)=\eta \left(\right[0,n\left]\right)$ and ${\eta }_n=\eta \left(\left\{n\right\}\right)$, for $n\in {\mathbb{Z}}_{+}$.

As for records, assumptions are needed in order to ensure that near-record times and values are well defined. Additionally, in order to characterise $\eta$ as a cluster point process, we consider a classification of near-records in terms of their proximity to records.

Definition 2. 

(a) For$m,n\in \mathbb{N}$, the n-th near-record value $R_n^a$is said to be associated to the m-th record value$R_m$if$L_m<L_n^a<L_{m+1}$.

(b) For$m\in \mathbb{N}$, the point process$\eta (·|R_m)$of near-record values associated to$R_m$is defined by the random counting measure

$$\eta \left(A\right|R_m)=card\{n\in \mathbb{N}|R_n^a\in A, L_m<L_n^a<L_{m+1}\}, A\in {\mathcal{B}}_{+}.$$

(3)

We state here the probabilistic assumptions regarding $\left(X_n\right)$, which hold throughout the paper. We assume that $\left(X_n\right)$ is a sequence of i.i.d. r.v., taking non-negative integer values, with $p_k:=\mathbb{P}(X_1=k), y_k:=\mathbb{P}(X_1>k), k\in {\mathbb{Z}}_{+}$. For convenience, we define $p_k=0$ and $y_k=1$ for $k<0$.

In addition, let

$$r_k=\frac{p_k}{y_{k-1}}=\mathbb{P}(X_1=k|X_1\ge k), k\in {\mathbb{Z}}_{+},$$

(4)

be the hazard or failure rates, and

$$q_k=\frac{y_k}{y_{k-a}}=\mathbb{P}(X_1>k|X_1>k-a), k\in {\mathbb{Z}}_{+}.$$

(5)

Note that $y_k={\prod }_{i=0}^k(1-r_i)$, $k\in {\mathbb{Z}}_{+}$.

In order to ensure that no final record exists and thus that all record times are well defined, we assume that $y_k>0, \forall k\in {\mathbb{Z}}_{+}$. This, in particular, implies $r_k<1, \forall k\in {\mathbb{Z}}_{+}$. In addition, to avoid unnecessary complications, we assume $a\in \mathbb{N}$.

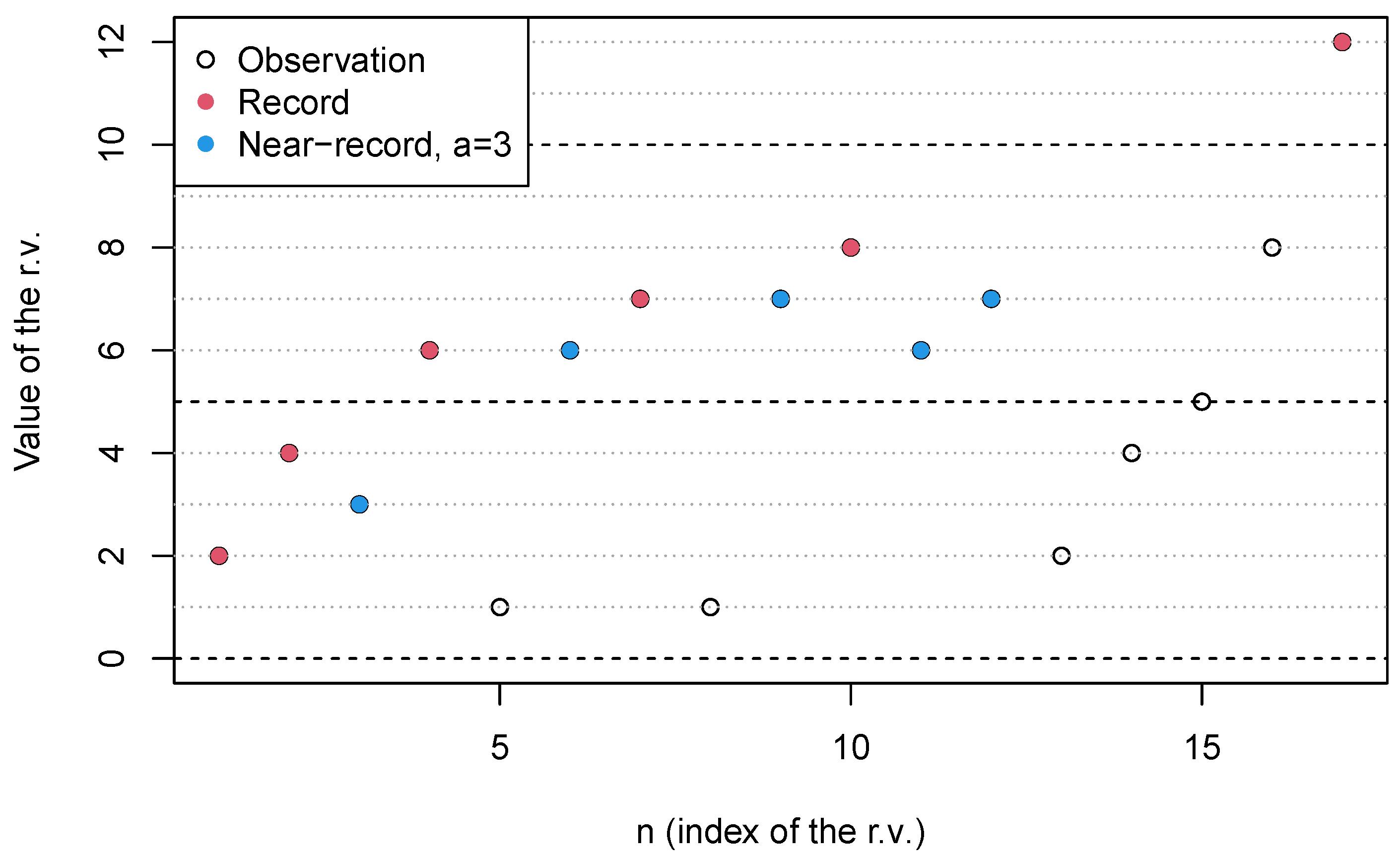
Example 1 (Records and near-records).

Let us consider a near-record parameter $a=3$ and the following sequence of 17 observations: $2, 4, 3, 6, 1, 6, 7, 1, 7, 8, 6, 7, 2, 4, 5, 8, 12, \cdots$. See Figure 1.

• The sequence of partial maxima is $M_1=2$, $M_2=4$, $M_3=4$, $M_4=6$, $M_5=6\cdots$.
• For the record value sequence, we have $R_1=2$, $R_2=4$, $R_3=6$, $R_4=7$, $R_5=8$, $R_6=12$.
• According to Definition 2, there are no near-records associated to $R_1$, there is one near-record (with value 3) associated to $R_2$, one near-record (with value 6) associated to $R_3$, one near record (with value 7) associated to $R_4$ and two near-records (with values 6 and 7) associated to $R_5$. Note also that, as $X_{17}=R_6=12$ and $a=3$, there will be no near-records with value smaller than 10 after observation 17. Thus, $\eta \left(\right[0,9\left]\right)$, the number of near-records with value in the interval $[0,9]$, is equal to 5.

Figure 1. Representation of the sequence given in Example 1. Red dots represent record observations, while blue dots are near-record observations with parameter $a=3$.

Figure 1. Representation of the sequence given in Example 1. Red dots represent record observations, while blue dots are near-record observations with parameter $a=3$.

3. The Point Process of Near-Record Values

We recall that a point process N on ${\mathbb{R}}_{+}$ can be seen as a random measure and has a probability generating functional (p.g.fl.) defined by ${\mathbb{G}}_N\left[h\right]=\mathbb{E}(\exp (\int \log h\left(x\right)N\left(dx\right)\left)\right)$, under appropriate conventions regarding the logarithm of 0, where $h:{\mathbb{R}}_{+}\to [0,1]$ is a measurable function equal to 1 outside some bounded subset of ${\mathbb{R}}_{+}$ (such functions are referred to as “suitable”). Alternative formulas for the p.g.fl., in the form of a product–integral or a product are given by

$${\mathbb{G}}_N\left[h\right]=\mathbb{E}\left(\prod _{x\in {\mathbb{R}}_{+}}h{\left(x\right)}^{N\left(dx\right)}\right)=\mathbb{E}\left(\prod _{{}_{x:N\left(\right\{x\left\}\right)>0}}h{\left(x\right)}^{N\left(\right\{x\left\}\right)}\right).$$

(6)

In this section, we show that the near-record process $\eta$ is a discrete cluster process. Indeed, since $\eta \left(A\right)={\sum }_{m=1}^{\infty }\eta \left(A\right|R_m),A\in {\mathcal{B}}_{+}$, process $\eta$ can be seen as a superposition of a denumerable family of point processes which, by Proposition 1 (c) below, are conditionally independent. Moreover, since the r.v. $X_n$ take values in ${\mathbb{Z}}_{+}$, we find that, for every bounded A, $\eta \left(A\right)\le L_{K+a}$, where $K\in \mathbb{N}$ is an upper bound of A, the process $\eta$ is boundedly finite.

We characterise $\eta$ by means of its p.g.fl. and compute its first moments and other quantities of interest. To that end, we first present some useful results about records and near-records.

Lemma 1. 

(a) The point process ξ of record values has its atoms in ${\mathbb{Z}}_{+}$, and the r.v. $I_n$ are independent Bernoulli, with $\mathbb{E}\left(I_n\right)=r_n,n\in {\mathbb{Z}}_{+}.$

(b) For any suitable function h,

$${\mathbb{G}}_{\xi }\left[h\right]=\prod _{n=0}^{\infty }\left(1-r_n(1-h\left(n\right))\right).$$

(7)

Proof. 

For a proof of (a), see, for instance, Theorem 16.1 in [3]. To prove (b), from (a) and the second formula in (6), we obtain, noting that $h=0$ outside a bounded set, and using the convention $0^0=1$,

$$\begin{array}{cc}\hfill {\mathbb{G}}_{\xi }\left[h\right]& =\mathbb{E}\left(\prod _{n=0}^{\infty }h{\left(n\right)}^{\xi \left(\right\{n\left\}\right)}\right)\hfill \\ \hfill & =\mathbb{E}\left(\prod _{n=0}^{\infty }h{\left(n\right)}^{I_n}\right)\hfill \\ \hfill & =\prod _{n=0}^{\infty }\mathbb{E}\left(h{\left(n\right)}^{I_n}\right)\hfill \\ \hfill & =\prod _{n=0}^{\infty }\left(1-r_n+r_{n}h\left(n\right)\right).\hfill \end{array}$$

□

Proposition 1. 

(a)

Let $S_m=\eta \left({\mathbb{R}}_{+}\right|R_m)$ be the number of near-records associated to record $R_m,m\in \mathbb{N}$, according to Definition 2. Then,

$$\mathbb{P}(S_m=s|R_m)={(1-q_{{}_{R_m}})}^s{q}_{{}_{R_m}},s\in {\mathbb{Z}}_{+}.$$

(8)

That is, $S_m$ is geometrically distributed, conditionally on $R_m$.

(b)

Let $L_{n_1}^a<\cdots <L_{n_{{}_{S_m}}}^a$ be the near-record times associated to $R_m$. Then, conditionally on $R_m, S_m$, the near-record values $Y_{m,j}:=X_{L_{n_j}^a}, j=1, \dots , S_m$ are i.i.d. with

$$\mathbb{P}(Y_{m,1}=k_1, \dots , Y_{m,S_m}=k_{S_m}\mid R_m,S_m)=\prod _{j=1}^{S_m}\pi (k_j,R_m),$$

(9)

where $\pi (k,i):=\frac{p_k}{y_{i-a}-y_i}{\mathbf{1}1}_{(i-a,i]}\left(k\right), i,k\in {\mathbb{Z}}_{+}$.

Moreover, conditionally on $R_m,S_m$, the r.v. $N_{m,k}:=\eta \left(\left\{k\right\}\right|R_m)={\sum }_{j=1}^{S_m}{\mathbf{1}1}_{\{Y_{m,j}=k\}}$, for $k\in (R_m-a,R_m]\cap {\mathbb{Z}}_{+}$, are multinomially distributed, with parameters $S_m,\pi (k,R_m)$.

(c)

The σ-algebras ${\mathcal{F}}_m:=\sigma \{R_m,S_m,Y_{m,j},j=1, \dots , S_m\},m\in \mathbb{N}$ are independent, conditionally on $\mathcal{R}:=\sigma \left\{R_m\right|m\in \mathbb{N}\}$.

Proof. 

(a)

Note that the r.v. $X_n, n>L_m,$ are independent and identically distributed as $X_1$. Define the subsequence $\left(X_{k_n}\right)$, with $k_1=min\{k>L_m|X_k>R_m-a\}$ and $k_n=min\{k>k_{n-1}|X_k>R_m-a\},n\ge 2$. Then, conditionally on $R_m$, the sequence $\left(X_{k_n}\right)$ is also i.i.d., but their common (conditional) distribution is $\mathbb{P}(X_1\le x|X_1>R_m-a)$. Lastly, $S_m$ is the number of terms $X_{k_n}$ up to (but no including) the first $X_{k_n}>R_m$. Hence, conditionally on $R_m$, $S_m$ is geometrically distributed, as stated.

(b)

The near-record values $Y_{m,j}$ are precisely the $X_{k_n}$ before the next record. So, conditionally on $R_m,S_m$, they are i.i.d. with probabilities $\pi (k,R_m)$. In addition, from the arguments above, it is clear that the $N_{m,k}$ are (conditionally) multinomial.

(c)

Note that, since the $\left(X_n\right)$ are i.i.d, the $\sigma$-algebras ${\mathcal{G}}_m=\sigma \{X_k,L_m\le k<L_{m+1}\},m\in \mathbb{N}$ are independent, conditionally on $\mathcal{R}$. Then, since the r.v. $S_m$, $Y_{m,j}$, $j=1, \dots , S_m$ are $\mathcal{G}$-measurable, the result follows.

□

We compute below the p.g.fl. of the point process $\eta (·|R_m)$, which is obtained from (6) by taking the conditional expectation. That is,

$${\mathbb{G}}_{\eta (·|R_m)}\left[h\right]:=\mathbb{E}\left(\prod _{k=0}^{\infty }h{\left(k\right)}^{\eta \left(\left\{k\right\}\right|R_m)}|R_m\right).$$

(10)

For $h:{\mathbb{R}}_{+}\to [0,1]$ measurable, $A\in {\mathcal{B}}_{+}$ and $i\in {\mathbb{Z}}_{+}$, let

$${\alpha }_i\left(h\right)=\frac{1}{y_i}\sum _{k=i-a+1}^i{p}_k(1-h\left(k\right)), {\alpha }_i\left(A\right)=\frac{1}{y_i}\sum _{k=i-a+1}^i{p}_k{\mathbf{1}1}_A\left(k\right).$$

(11)

Additionally, let ${\alpha }_i\left(n\right)={\alpha }_i\left([0,n]\right),n\in {\mathbb{Z}}_{+}$.

Proposition 2. 

For a suitable function h,

$${\mathbb{G}}_{\eta (·|R_m)}\left[h\right]=\frac{1}{1+{\alpha }_{{}_{R_m}}\left(h\right)}.$$

(12)

Proof. 

Suppose $R_m=i$, for some $m\in \mathbb{N}$. From (10) and (b) of Proposition 1, we get

$$\begin{array}{cc}\hfill {\mathbb{G}}_{\eta (·|R_m)}\left[h\right]& =\mathbb{E}\left(\mathbb{E}\left(\prod _{k=0}^{\infty }h{\left(k\right)}^{\eta \left(\left\{k\right\}\right|R_m)}|R_m,S_m\right)|R_m\right)\hfill \\ \hfill & =\mathbb{E}\left(\mathbb{E}\left(\prod _{k=0}^{\infty }h{\left(k\right)}^{N_{m,k}}|R_m,S_m\right)|R_m\right)\hfill \\ \hfill & =\mathbb{E}\left({\left(\sum _{k=0}^{\infty }\pi (k,R_m)h\left(k\right)\right)}^{S_m}|R_m\right)\hfill \\ \hfill & =\frac{q_{{}_{R_m}}}{1 - (1 - q_{{}_{R_m}}){\displaystyle \sum _{k=0}^{\infty }}\pi (k,R_m)h\left(k\right)}\hfill \\ \hfill & =\frac{y_{{}_{R_m}}}{y_{{}_{R_m-a}} - {\displaystyle \sum _{k=R_m-a+1}^{R_m}}h\left(k\right)p_k}\hfill \\ \hfill & =\frac{1}{1 + {\alpha }_{{}_{R_m}}\left(h\right)},\hfill \end{array}$$

where the third and fourth equalities, as shown above, follow from the expressions of the p.g.f. of the multinomial and geometric distributions, respectively. □

Definition 3 

(Definition 6.3.I in [15]). A (boundedly finite) point process N is a cluster point process on ${\mathbb{R}}_{+}$, with the centre process $N_c$ on ${\mathbb{R}}_{+}$ and component processes the family of point processes $\{N(·|y):y\in {\mathbb{R}}_{+}\}$ if, for every bounded $A\in {\mathcal{B}}_{+}$,

$$N\left(A\right)=\sum _{y\in {\mathbb{R}}_{+}}N\left(A\right|y){\mathbf{1}1}_{\{N_c\left(\left\{y\right\}\right)>0\}}.$$

(13)

Definition 4. 

For $i\in {\mathbb{Z}}_{+}$, let ${\zeta }_i$ be the point process with p.g.fl. given by

$${\mathbb{G}}_{{\zeta }_i}\left[h\right]=\frac{1}{1+{\alpha }_i\left(h\right)},$$

where h is a suitable function and ${\alpha }_i\left(h\right)$ is defined in (11).

Theorem 1. 

(a)

The point process η of near-records is a cluster process on ${\mathbb{Z}}^{+}$, with the centre process ξ and independent components processes $\{{\zeta }_i,i\in {\mathbb{Z}}^{+}\}$.

(b)

For a suitable function h,

$${\mathbb{G}}_{\eta }\left[h\right]=\prod _{i=0}^{\infty }\frac{1+(1-r_i){\alpha }_i\left(h\right)}{1+{\alpha }_i\left(h\right)}.$$

(14)

In particular, taking $h\left(k\right)=t^{{\mathbf{1}1}_A\left(k\right)},t\in [0,1]$ and $A\in {\mathcal{B}}_{+}$ bounded, we obtain the p.g.f. of $\eta \left(A\right)$, given by

$${\phi }_{\eta \left(A\right)}\left(t\right)=\prod _{i=0}^{\infty }\frac{1+(1-r_i)(1-t){\alpha }_i\left(A\right)}{1+(1-t){\alpha }_i\left(A\right)}.$$

(15)

(c)

For every bounded $A,B\in {\mathcal{B}}_{+}$,

• $\mathbb{E}\left(\eta \left(A\right)\right)={\sum }_{i=0}^{\infty }{\alpha }_i\left(A\right)r_i<\infty$,
• $Var\left(\eta \left(A\right)\right)={\sum }_{i=0}^{\infty }{\alpha }_i^2\left(A\right)r_i(2-r_i)+\mathbb{E}\left(\eta \left(A\right)\right)<\infty$,
• $\mathrm{Cov}(\eta \left(A\right),\eta \left(B\right))={\sum }_{i=0}^{\infty }{\alpha }_i\left(A\right){\alpha }_i\left(B\right)r_i(2-r_i)$, for $A\cap B=\varnothing$.

Proof. 

(a) Observe that

$$\eta \left(A\right)=\sum _{m=1}^{\infty }\eta \left(A\right|R_m)=\sum _{i=0}^{\infty }{\zeta }_i\left(A\right)I_i.$$

(16)

So, according to Definition 3, $\eta$ is a cluster point process, as asserted. Independence of component processes follows from (c) in Proposition 1, because $\eta \left(A\right|R_m)$ is ${\mathcal{F}}_m$-measurable, for any $m\in \mathbb{N}$.

(b) For h, a suitable function, let $\tilde{h}:{\mathbb{Z}}_{+}\to [0,1]$ be defined as $\tilde{h}\left(i\right)=G_{{\zeta }_i}\left[h\right]=\frac{1}{1 + {\alpha }_i\left(h\right)}$, which is also a suitable function. From 6.3.6 in [15], we have ${\mathbb{G}}_{\eta }\left[h\right]=G_{\xi }\left[\tilde{h}\right]$. Therefore, by Lemma 1 (b) and Proposition 2,

$$\begin{array}{cc}\hfill {\mathbb{G}}_{\eta }\left[h\right]& =\prod _{i=0}^{\infty }\left(1-r_i\left(1-\frac{1}{1+{\alpha }_i\left(h\right)}\right)\right)\hfill \\ \hfill & =\prod _{i=0}^{\infty }\frac{1+(1-r_i){\alpha }_i\left(h\right)}{1+{\alpha }_i\left(h\right)}\hfill \\ \hfill & =\prod _{i=0}^{\infty }\left(\frac{r_i}{1+{\alpha }_i\left(h\right)}+1-r_i\right).\hfill \end{array}$$

For ${\phi }_{\eta \left(A\right)}\left(t\right)$ we replace h by $t^{{\mathbf{1}1}_A}$ in (14) and get (15), noting that ${\alpha }_i\left(t^{{\mathbf{1}1}_A}\right)=(1-t){\alpha }_i\left(A\right)$.

(c1) Observe that $\eta \left(A\right)={\sum }_{k\in A}{\sum }_{m=1}^{\infty }\eta \left(\left\{k\right\}\right|R_m)={\sum }_{k\in A}{\sum }_{m=1}^{\infty }{N}_{m,k}$ and recall that $N_{m,k}$ is binomial, conditional on $R_m, S_m$, with parameters $S_m, \pi (k,R_m)$, and that $S_m$ is geometric, conditional on $R_m$, with parameter $q_{{}_{R_m}}$.

Moreover, $N_{m,A}:={\sum }_{k\in A}{N}_{m,k}$ is binomial, conditional on $R_m, S_m$, with parameters $S_m, \pi (A,R_m)$, where $\pi (A,R_m):={\sum }_{k\in A\cap {\mathbb{Z}}_{+}}\pi (k,R_m)$, hence

$$\begin{array}{cc}\hfill \mathbb{E}\left(N_{m,A}\right)& =\mathbb{E}\left(\mathbb{E}\left(N_{m,A}\right|R_m,S_m)\right)\hfill \\ \hfill & =\mathbb{E}\left(S_m\pi (A,R_m)\right)\hfill \\ \hfill & =\mathbb{E}\left(\mathbb{E}\left(S_m\pi (A,R_m)\right|R_m)\right)\hfill \\ \hfill & =\mathbb{E}\left(\pi (A,R_m)\mathbb{E}\left(S_m\right|R_m)\right)\hfill \\ \hfill & =\mathbb{E}\left(\pi (A,R_m)\frac{1 - q_{{}_{R_m}}}{q_{{}_{R_m}}}\right).\hfill \end{array}$$

(17)

So, noticing that $\pi (A,i)\frac{1 - q_i}{q_i}={\alpha }_i\left(A\right)$,

$$\mathbb{E}\left(\eta \left(A\right)\right)=\mathbb{E}\left(\sum _{m=1}^{\infty }{\alpha }_{{}_{R_m}}\left(A\right)\right)=\mathbb{E}\left(\sum _{i=0}^{\infty }{\alpha }_i\left(A\right)I_i\right)=\sum _{i=0}^{\infty }{\alpha }_i\left(A\right)r_i,$$

(18)

which is finite since ${\alpha }_i\left(A\right)>0$ only for a finite set of i values.

(c2) From the computations above, it is clear that

$$\mathbb{E}\left(\eta \left(A\right)\right|\mathcal{R})=\sum _{m=1}^{\infty }{\alpha }_{{}_{R_m}}\left(A\right)=\sum _{i=0}^{\infty }{\alpha }_i\left(A\right)I_i.$$

Hence, the variance of the conditional expectation is

$$Var\left(\mathbb{E}\left(\eta \left(A\right)\right|\mathcal{R})\right)=\sum _{i=0}^{\infty }{\alpha }_i^2\left(A\right)r_i(1-r_i).$$

We compute next the expectation of the conditional variance, namely $\mathbb{E}\left(Var\right(\eta \left(A\right)\left|\mathcal{R}\right))$. Observe that, because of the conditional independence of the $\eta \left(A\right|R_n),n\in \mathbb{N}$, we have

$$Var\left(\eta \left(A\right)\right|\mathcal{R})=\sum _{m=1}^{\infty }Var\left(\eta \left(A\right|R_m)\right|\mathcal{R})=\sum _{m=1}^{\infty }Var\left(N_{m,A}\right|R_m).$$

Moreover,

$$\begin{array}{cc}\hfill Var\left(N_{m,A}\right|R_m)& =\mathbb{E}\left(Var\left(N_{m,A}\right|R_m,S_m)\right|R_m)+Var\left(\mathbb{E}\left(N_{m,A}\right|R_m,S_m)\right|R_m)\hfill \\ \hfill & =\mathbb{E}\left(S_m\pi (A,R_m)(1-\pi (A,R_m))\right|R_m)+Var\left(S_m\pi (A,R_m)\right|R_m)\hfill \\ \hfill & =\frac{1 - q_{{}_{R_m}}}{q_{{}_{R_m}}}\pi (A,R_m)(1-\pi (A,R_m))+\frac{1 - q_{{}_{R_m}}}{q_{{}_{R_m}}^2}{\pi }^2(A,R_m)\hfill \\ \hfill & ={\alpha }_{{}_{R_m}}\left(A\right)(1-\pi (A,R_m))+{\alpha }_{{}_{R_m}}\left(A\right)\frac{\pi (A,R_m)}{q_{{}_{R_m}}}\hfill \\ \hfill & ={\alpha }_{{}_{R_m}}\left(A\right)\left(1+\pi (A,R_m)\left(\frac{1 - q_{{}_{R_m}}}{q_{{}_{R_m}}}\right)\right)\hfill \\ \hfill & ={\alpha }_{{}_{R_m}}\left(A\right)(1+{\alpha }_{{}_{R_m}}\left(A\right)).\hfill \end{array}$$

Therefore, $Var\left(\eta \left(A\right)\right|\mathcal{R})={\sum }_{m=1}^{\infty }Var\left(N_{m,A}\right|R_m)={\sum }_{i=0}^{\infty }{\alpha }_i\left(A\right)(1+{\alpha }_i\left(A\right))I_i$ and so, $\mathbb{E}\left(Var\left(\eta \left(A\right)\right|\mathcal{R})\right)={\sum }_{i=0}^{\infty }{\alpha }_i\left(A\right)(1+{\alpha }_i\left(A\right))r_i$. Collecting terms from the expressions above and using the formula $Var\left(\eta \right(A\left)\right)=Var\left(\mathbb{E}\right(\eta \left(A\right)\left|\mathcal{R}\right))+\mathbb{E}(Var\left(\eta \right(A\left)\right|\mathcal{R}\left)\right)$, we obtain

$$\begin{array}{cc}\hfill Var\left(\eta \right(A\left)\right)& =\sum _{i=0}^{\infty }{\alpha }_i^2\left(A\right)r_i(1-r_i)+\sum _{i=0}^{\infty }{\alpha }_i\left(A\right)(1+{\alpha }_i\left(A\right))r_i\hfill \\ \hfill & =\sum _{i=0}^{\infty }{\alpha }_i^2\left(A\right)r_i(2-r_i)+\mathbb{E}\left(\eta \left(A\right)\right).\hfill \end{array}$$

(19)

(c3) The covariance $Cov\left(\eta \right(A), \eta (B\left)\right)$, when $A\cap B=\varnothing$, follows immediately from the formula for the variance, noting that $\eta (A\cup B)=\eta \left(A\right)+\eta \left(B\right)$. □

Corollary 1. 

For $N\in {\mathbb{Z}}_{+}$, the r.v. ${\eta }_N$ (the number of near-records taking the value N) is distributed as a mixture of a point mass at 0, with probability $\frac{1 - c}{1 + d}$, and a geometric distribution, with a success probability equal to $\frac{1}{1 + d}$. That is,

$$\mathbb{P}({\eta }_N=0)=\frac{1+c}{1+d}, \mathbb{P}({\eta }_N=k)=\frac{(d-c)d^{k-1}}{{(1+d)}^{k+1}},k\ge 1,$$

(20)

where $c=r_N$ and $d=r_N/q_{N+a-1}$. Moreover,

$$\begin{array}{cc}\hfill \mathbb{E}\left({\eta }_N\right)& =p_N{\displaystyle \sum _{i=N}^{N+a-1}}\frac{r_i}{y_i},\hfill \\ \hfill Var\left({\eta }_N\right)& =p_N^2{\displaystyle \sum _{i=N}^{N+a-1}}\frac{r_i(2-r_i)}{y_i^2}+p_N{\displaystyle \sum _{i=N}^{N+a-1}}\frac{r_i}{y_i},\hfill \\ \hfill Cov({\eta }_N,{\eta }_{N+1})& =p_N{p}_{N+1}{\displaystyle \sum _{i=N+1}^{N+a-1}}\frac{r_i(2-r_i)}{y_i^2}.\hfill \end{array}$$

(21)

Proof. 

After simple computations, we obtain the p.g.f.,

$${\phi }_{{\eta }_N}\left(t\right)=\prod _{i=N}^{N+a-1}\frac{1+\frac{p_N}{y_{i-1}}(1-t)}{1+\frac{p_N}{y_i}(1-t)}=\frac{1+c(1-t)}{1+d(1-t)},$$

(22)

which yields the probability mass function (p.m.f.) (20). Formulas in (21) follow from Theorem 1 (c), observing that ${\alpha }_i\left(\left\{N\right\}\right)=\frac{p_N}{y_i}{\mathbf{1}1}_{[N,N+a-1]}\left(i\right)$, for $i,N\in {\mathbb{Z}}_{+}$. □

Remark 1. 

Note that ${\alpha }_i\left(A\right)=\frac{1}{y_i}{\sum }_{k\in [i-a+1,i]\cap A}{p}_k$, which implies $Cov\left(\eta \right(A),\eta (B\left)\right)=0$, if A and B are at least a units apart; that is, if

$$min\left\{\right|i-j|:i\in A,j\in B\}\ge a.$$

In fact, the r.v. ${\eta }_N$ and ${\eta }_M$ are independent if $|M-N|\ge a$, due to the independence of the r.v. $I_n$. In other words, the r.v. ${\eta }_N$ are $(a-1)$-dependent.

4. Finiteness of the Number of Near-Records

Theorem 2. 

If ${\sum }_{i=0}^{\infty }{r}_i^2<\infty$, then $\eta \left({\mathbb{R}}_{+}\right)<\infty$ a.s; that is, the number of near-records in the whole sequence $\left(X_n\right)$ is finite a.s. Moreover, $\eta \left({\mathbb{R}}_{+}\right)$ has the finite expectation

$$\mathbb{E}\left(\eta \left({\mathbb{R}}_{+}\right)\right)=\sum _{i=0}^{\infty }{\alpha }_i\left({\mathbb{R}}_{+}\right)r_i$$

(23)

and p.g.f. given by

$${\phi }_{\eta \left({\mathbb{R}}_{+}\right)}\left(t\right)=\prod _{i=0}^{\infty }\frac{1+(1-r_i)(1-t){\alpha }_i\left({\mathbb{R}}_{+}\right)}{1+(1-t){\alpha }_i\left({\mathbb{R}}_{+}\right)},$$

(24)

with ${\alpha }_i\left({\mathbb{R}}_{+}\right)=\frac{y_{i-a}}{y_i}-1$.

Proof. 

From Proposition 1, we have

$$\sum _{m=1}^{\infty }\mathbb{P}(S_m>0|\mathcal{R})=\sum _{m=1}^{\infty }(1-q_{{}_{R_m}})=\sum _{i=0}^{\infty }\left(1-\frac{y_i}{y_{i-a}}\right)I_i.$$

Taking the expectation above, we obtain

$$\begin{array}{cc}\hfill \sum _{m=1}^{\infty }\mathbb{P}(S_m>0)& =\sum _{i=0}^{\infty }\left(1-\frac{y_i}{y_{i-a}}\right)r_i\hfill \\ \hfill & =\sum _{i=0}^{\infty }\left(1-\prod _{j=i-a+1}^i(1-r_j)\right)r_i\hfill \\ \hfill & \le \sum _{i=0}^{\infty }\sum _{j=i-a+1}^i{r}_j{r}_i\hfill \\ \hfill & =\sum _{j=0}^{a-1}\sum _{i=j}^{\infty }{r}_{i-j}{r}_i\hfill \\ \hfill & \le a\sum _{i=0}^{\infty }{r}_i^2.\hfill \end{array}$$

(25)

where the final term in the display above follows from the Cauchy–Schwarz inequality. Therefore, by the Borel–Cantelli lemma, $\mathbb{P}(S_m>0\mathrm{i}.\mathrm{o}.)=0$, which yields the result.

In order to compute the p.g.f. of $\eta \left({\mathbb{R}}_{+}\right)$, we observe that $\eta \left(n\right)\stackrel{\mathrm{a}.\mathrm{s}.}{⟶}\eta \left({\mathbb{R}}_{+}\right)$, and so, by the monotone convergence theorem, ${\phi }_{\eta \left(n\right)}\left(t\right)\to {\phi }_{\eta \left({\mathbb{R}}_{+}\right)}\left(t\right)$, for $t\in [0,1]$. Furthermore, from (15), we have

$${\phi }_{\eta \left({\mathbb{R}}_{+}\right)}\left(t\right)=\underset{n\to \infty }{lim}\prod _{i=0}^{\infty }\frac{1+(1-r_i)(1-t){\alpha }_i\left(n\right)}{1+(1-t){\alpha }_i\left(n\right)}=\prod _{i=0}^{\infty }\frac{1+(1-r_i)(1-t){\alpha }_i\left({\mathbb{R}}_{+}\right)}{1+(1-t){\alpha }_i\left({\mathbb{R}}_{+}\right)}.$$

(26)

The interchange of the limit and product above is justified by the monotone convergence theorem, after taking logarithms, since the sequence inside the product decreases with n.

Finally, (23) is obtained, for example, from the derivative of ${\phi }_{\eta \left({\mathbb{R}}_{+}\right)}\left(t\right)$ at $t=1^{-}$ or as the limit of $\mathbb{E}\left(\eta \right(n\left)\right)$. Finiteness follows from the bound $1-q_i\le {\sum }_{j=i-a+1}^i{r}_j$, used in (25), which implies $q_i\to 1$. Indeed, for sufficiently large i, we have $q_i\ge 1/2$ and

$${\alpha }_i\left({\mathbb{R}}_{+}\right)=\frac{1}{y_i}\sum _{j=i-a+1}^i{p}_j=\frac{y_{i - a}}{y_i}-1=\frac{1-q_i}{q_i}\le 2(1-q_i).$$

The conclusion ${\alpha }_i\left({\mathbb{R}}_{+}\right)<\infty$ is obtained after arguing as in (25). □

5. Asymptotic Behaviour

We now focus on the asymptotic behaviour of $\eta \left(n\right)$. From Theorem 2, we know that if ${\sum }_{i=0}^{\infty }{r}_i^2<\infty$, then ${lim}_{n\to \infty }\eta \left(n\right)$ is finite a.s. In this section, we obtain laws of large numbers and a central limit theorem for $\eta \left(n\right)$ under the assumption ${\sum }_{i=0}^{\infty }{r}_i^2=\infty$.

Lemma 2. 

The random variables

$$Z_i=\sum _{m=1}^{\infty }{S}_m{\mathbf{1}1}_{\{R_m=i\}},i\in {\mathbb{Z}}_{+},$$

(27)

are independent with p.g.f.

$${\phi }_{{}_{Z_i}}\left(s\right)=1-r_i+\frac{q_i{r}_i}{1 - (1 - q_i)s},s\in [0,1].$$

(28)

Proof. 

For simplicity, we prove pairwise independence since the argument extends easily to the general case, but details are somewhat laborious. We compute the joint p.g.f. of $Z_i,Z_j$ as follows: for $s,t\in [0,1]$,

$$\begin{array}{cc}\hfill {\phi }_{Z_i,Z_j}(s,t)& =\mathbb{E}\left(s^{Z_i}{t}^{Z_j}\right)\hfill \\ \hfill & =\mathbb{E}\left(s^{{\sum }_{m=1}^{\infty }{S}_m{\mathbf{1}1}_{\{R_m=i\}}}{t}^{{\sum }_{m=1}^{\infty }{S}_m{\mathbf{1}1}_{\{R_m=j\}}}\right)\hfill \\ \hfill & =\mathbb{E}\left(\mathbb{E}\left(\prod _{m=1}^{\infty }{s}^{S_m{\mathbf{1}1}_{\{R_m=i\}}}{t}^{S_m{\mathbf{1}1}_{\{R_m=j\}}}|\mathcal{R}\right)\right)\hfill \\ \hfill & =\mathbb{E}\left(\prod _{m=1}^{\infty }\mathbb{E}\left(s^{S_m{\mathbf{1}1}_{\{R_m=i\}}}{t}^{S_m{\mathbf{1}1}_{\{R_m=j\}}}|\mathcal{R}\right)\right)\hfill \\ \hfill & =\mathbb{E}\left(\prod _{m=1}^{\infty }\frac{q_{{}_{R_m}}}{1 - (1 - q_{{}_{R_m}})s^{{\mathbf{1}1}_{\{R_m=i\}}}{t}^{{\mathbf{1}1}_{\{R_m=j\}}}}\right)\hfill \\ \hfill & =\mathbb{E}\left(\frac{q_i{I}_i}{1 - (1 - q_i)s}\frac{q_j{I}_j}{1 - (1 - q_j)t}+\frac{q_i{I}_i(1 - I_j)}{1 - (1 - q_i)s}+\frac{q_j(1 - I_i)I_j}{1 - (1 - q_j)t}+(1-I_i)(1-I_j)\right)\hfill \\ \hfill & =\frac{q_i{r}_i}{1 - (1 - q_i)s}\frac{q_j{r}_j}{1 - (1 - q_j)t}+\frac{q_i{r}_i(1 - r_j)}{1 - (1 - q_i)s}+\frac{q_j(1 - r_i)r_j}{1 - (1 - q_j)t}+(1-r_i)(1-r_j).\hfill \end{array}$$

From the formula above, we get ${\phi }_{Z_i,Z_j}(s,1)={\phi }_{Z_i}\left(s\right)$, as in (28). In addition, ${\phi }_{Z_i,Z_j}(s,t)={\phi }_{Z_i,Z_j}(s,1){\phi }_{Z_i,Z_j}(1,t)$, which implies the independence of $Z_i,Z_j$ because the interval of convergence of the p.g.f. of $Z_i$ can be extended from $[0,1]$ to $[0,{(1-q_i)}^{-1})$. □

Remark 2. 

Note that $Z_i$ in (27) is the number of near-records associated to i if i is a record value and is equal to 0 otherwise. Indeed, (28) shows that $Z_i$ is distributed as a mixture of a point mass at 0 and a geometric random variable of parameter $q_i$, with respective weights $1-r_i, r_i$.

Our interest in the variable $Z_i$ arises from the following inequalities, which are easily verified:

$$\sum _{i=0}^n{Z}_i\le \eta \left(n\right)\le \sum _{i=0}^{n+a-1}{Z}_i.$$

(29)

The strategy of the proof is to establish the desired asymptotic results for the sum of $Z_i$s, which are then transferred to $\eta$. For that purpose, we assume some minimal conditions on the hazard rates $r_n$, besides ${\sum }_{i=0}^{\infty }{r}_i^2=\infty$.

The following proposition gathers some useful facts about the variable $Z_i$.

Proposition 3. 

(a) $\mathbb{E}\left(Z_i\right)=\frac{1 - q_i}{q_i}{r}_i$, $Var\left(Z_i\right)=\frac{1 - q_i}{q_i^2}{r}_i\left((1-q_i)(1-r_i)+1\right)$.

(b) If${\sum }_{i=0}^{\infty }{r}_i^2=\infty$then${\sum }_{i=0}^{\infty }\mathbb{E}\left(Z_i\right)={\sum }_{i=0}^{\infty }Var\left(Z_i\right)=\infty$.

(c) If either

(i) 

${\sum }_{i=0}^{\infty }{r}_i^2=\infty$and$lim\; sup{r}_n<1$or

(ii) 

$lim{r}_n=1$and$lim\frac{1-r_n}{1-r_{n-1}}=1$

hold, then

(c1) 

$lim\frac{\mathbb{E}\left(Z_{n+k}\right)}{{\sum }_{i=0}^n\mathbb{E}\left(Z_i\right)}=lim\frac{Var\left(Z_{n+k}\right)}{{\sum }_{i=0}^{n}Var\left(Z_i\right)}=0,\forall k\in \mathbb{N}$,

(c2) 

$\frac{Z_{n+k}}{\sqrt{{\sum }_{i=0}^{n}Var\left(Z_i\right)}}\stackrel{\mathbb{P}}{⟶}0,\forall k\in \mathbb{N}.$

Proof. 

(a) The (factorial) moments of $Z_i$ are computed by differentiating the p.g.f. in (28).

(b) From (a) we have

$$\begin{array}{cc}\hfill \sum _{i=0}^{\infty }\mathbb{E}\left(Z_i\right)& =\sum _{i=0}^{\infty }\frac{1-q_i}{q_i}{r}_i\hfill \\ \hfill & \ge \sum _{i=0}^{\infty }(1-q_i)r_i\hfill \\ \hfill & =\sum _{i=0}^{\infty }\left(1-\prod _{j=i-a+1}^i(1-r_j)\right)r_i\hfill \\ \hfill & \ge \sum _{i=0}^{\infty }{r}_i^2.\hfill \end{array}$$

(30)

For the variance, we obtain from (a) and the divergence of expectations that

$$\sum _{i=0}^{\infty }Var\left(Z_i\right)\ge \sum _{i=0}^{\infty }\frac{1 - q_i}{q_i^2}{r}_i\ge \sum _{i=0}^{\infty }\frac{1 - q_i}{q_i}{r}_i=\infty .$$

(c) Suppose that (i) holds. Then, $lim\; inf{q}_n>0$, which implies that expectations $\mathbb{E}\left(Z_n\right)$ and variances $Var\left(Z_n\right)$ are bounded above. Hence, from (b), the limits in (c1) hold.

Suppose now that (ii) holds, then $q_n={\prod }_{i=n-a+1}^n(1-r_i)\to 0$, and also,

$$lim\frac{q_n}{q_{n+1}}=lim\frac{{\prod }_{i=n-a+1}^n(1 - r_i)}{{\prod }_{i=n-a+2}^{n+1}(1 - r_i)}=lim\frac{1 - r_{n-a+1}}{1 - r_{n+1}}=1,$$

hence

$$lim\frac{\mathbb{E}\left(Z_{n+1}\right)}{\mathbb{E}\left(Z_n\right)}=lim\frac{(1 - q_{n+1})q_n{r}_{n+1}}{q_{n+1}(1 - q_n)r_n}=lim\frac{q_n}{q_{n+1}}=1.$$

(31)

The same argument applies to prove that $Var\left(Z_{n+1}\right)/Var\left(Z_n\right)\to 1$ and so, claim (c1) follows from Lemma A1. Finally, convergence in (c2) is obtained from (c1) and Markov’s inequality, noting that, from (a), we have ${\left(\mathbb{E}\left(Z_{n+k}\right)\right)}^2\le Var\left(Z_{n+k}\right)$. □

Theorem 3. 

If either

(i) 

${\sum }_{i=0}^{\infty }{r}_i^2=\infty$ and ${lim\; sup}_n{r}_n<1$ or

(ii) 

${lim}_n{r}_n=1$ and ${lim}_n{n}^{\beta }(1-\frac{1 - r_n}{1 - r_{n-1}})=0$, for some $\beta \in (1/2,1)$,

then

$$\frac{\eta \left(n\right)}{\mathbb{E}\left(\eta \right(n\left)\right)}\stackrel{\mathrm{a}.\mathrm{s}.}{⟶}1.$$

Proof. 

By (29) and (c1) in Proposition 3, the result follows if we show that

$$\frac{{\sum }_{i=0}^n{Z}_i}{{\sum }_{i=0}^n\mathbb{E}\left(Z_i\right)}\stackrel{\mathrm{a}.\mathrm{s}.}{⟶}1.$$

(32)

By the strong law of large numbers for sequences of i.i.d. r.v., (32) follows if we prove that

$$\sum _{n=0}^{\infty }\frac{Var\left(Z_n\right)}{{\left({\sum }_{i=0}^n\mathbb{E}\left(Z_i\right)\right)}^2}<\infty .$$

(33)

Suppose first that (i) holds. Note that $Var\left(Z_i\right)\le 2\mathbb{E}\left(Z_i\right)/q_i,i\in {\mathbb{Z}}_{+}$ and also that ${lim\; inf}_n{q}_n>0$. Hence, there exists a positive constant $\gamma$ such that $q_n>\gamma$, for $n\in {\mathbb{Z}}_{+}$. So,

$$\sum _{n=0}^{\infty }\frac{Var\left(Z_n\right)}{{\left({\sum }_{i=0}^n\mathbb{E}\left(Z_i\right)\right)}^2}\le 2{\gamma }^{-1}\sum _{n=0}^{\infty }\frac{\mathbb{E}\left(Z_n\right)}{{\left({\sum }_{i=0}^n\mathbb{E}\left(Z_i\right)\right)}^2}<\infty ,$$

(34)

where convergence in the right-hand side of (34) follows from Abel-Dini’s Theorem A1.

On the other hand, if condition (ii) holds, then it is easy to see that $q_n\to 0$ and ${lim}_n{n}^{\beta }(1-\frac{q_n}{q_{n-1}})=0$. In addition, $q_n\mathbb{E}\left(Z_n\right)\to 1$ and $q_n^{2}Var\left(Z_n\right)\to 1$. Therefore, (33) is equivalent to

$$\sum _{n=0}^{\infty }\frac{q_n^{-2}}{{\left({\sum }_{i=0}^n{q}_i^{-1}\right)}^2}<\infty ,$$

which follows from Proposition A1, thus proving the stated result. □

Theorem 4. 

If either

(i) 

${\sum }_{i=0}^{\infty }{r}_i^2=\infty$ and ${lim\; sup}_n{r}_n<1$ or

(ii) 

${lim}_n{r}_n=1$ and ${lim}_n\frac{1 - r_n}{1 - r_{n-1}}=1$,

then

$$\frac{\eta \left(n\right)-\mathbb{E}\left(\eta \right(n\left)\right)}{\sqrt{Var\left(\eta \right(n\left)\right)}}\stackrel{\mathcal{D}}{⟶}N(0,1),$$

(35)

where $N(\mu ,{\sigma }^2),\mu \in \mathbb{R},\sigma >0$ stands for the normal distribution with expectation μ and variance ${\sigma }^2$.

Proof. 

First, we prove asymptotic normality for ${\sum }_{i=1}^n{Z}_i$ and then transfer the result to $\eta \left(n\right)$. To that end, we show that the following Lyapunov condition holds:

$$\frac{1}{s_n^3}\sum _{i=0}^n\mathbb{E}\left(\right|Z_i-\mathbb{E}\left(Z_i\right){|}^3)\to 0,$$

(36)

where $s_n^2={\sum }_{i=0}^{n}Var\left(Z_i\right)$. Indeed, from the elementary inequality $\mid a-b{\mid }^3<a^3+b^3$, for $a,b\ge 0$, we get

$$\mathbb{E}\left(\right|Z_i-\mathbb{E}\left(Z_i\right){|}^3)\le \mathbb{E}\left(Z_i^3\right)+{\left(\mathbb{E}\left(Z_i\right)\right)}^3=r_i\frac{(1 - q_i)}{q_i^3}(q_i^2-6q_i+6)+r_i^3{\left(\frac{1 - q_i}{q_i}\right)}^3.$$

(37)

Note first that $Var\left(Z_i\right)\ge \mathbb{E}\left(Z_i\right)$. Moreover, if (i) holds, then $lim\; inf{q}_n>0$, and from (37) above, we obtain $\mathbb{E}\left(\right|Z_i-\mathbb{E}\left(Z_i\right){|}^3)\le K\mathbb{E}\left(Z_i\right),i\in \mathbb{N}$, where $K>0$ is a generic constant. So, the sequence in (36) is bounded above by $K{\left({\sum }_{i=1}^n\mathbb{E}\left(Z_i\right)\right)}^{-1/2}$, which tends to 0, because of Proposition 3 (b).

If (ii) holds, then $q_n\to 0$, which implies $\mathbb{E}\left(\right|Z_i-\mathbb{E}\left(Z_i\right){|}^3)\le K_1{q}_i^{-3}$ and $Var\left(Z_i\right)\ge K_2{q}_i^{-2}$, for sufficiently large $i\in \mathbb{N}$, where $K_1,K_2>0$ are generic constants. Then, the Lyapunov condition in (36) holds if

$${\lambda }_n:=\frac{{\sum }_{i=0}^n{q}_i^{-3}}{{\left({\sum }_{i=0}^n{q}_i^{-2}\right)}^{3/2}}\to 0.$$

From the Cauchy–Schwarz inequality, we have ${\sum }_{i=0}^n{q}_i^{-3}\le {\left({\sum }_{i=0}^n{q}_i^{-2}{\sum }_{i=0}^n{q}_i^{-4}\right)}^{1/2}$, and so,

$${\lambda }_n^2\le \frac{{\sum }_{i=0}^n{q}_i^{-2}{\sum }_{i=0}^n{q}_i^{-4}}{{\left({\sum }_{i=0}^n{q}_i^{-2}\right)}^3}=\frac{{\sum }_{i=0}^n{q}_i^{-4}}{{\left({\sum }_{i=0}^n{q}_i^{-2}\right)}^2}\to 0.$$

(38)

Convergence to 0 in (38) is obtained from Lemma A2, since $q_{n-1}/q_n\to 1$.

From the Lyapunov central limit theorem, we conclude that

$$\frac{{\sum }_{i=0}^n{Z}_i-{\sum }_{i=0}^n\mathbb{E}\left(Z_i\right)}{s_n}\stackrel{\mathcal{D}}{⟶}N(0,1),$$

which, by (29) and Proposition 3 (c2), implies that

$$\frac{\eta \left(n\right)-{\sum }_{i=0}^n\mathbb{E}\left(Z_i\right)}{s_n}\stackrel{\mathcal{D}}{⟶}N(0,1).$$

(39)

Now, taking expectations in (29), we have ${\sum }_{i=0}^n\mathbb{E}\left(Z_i\right)\le E\left(\eta \left(n\right)\right)\le {\sum }_{i=0}^{n+a-1}\mathbb{E}\left(Z_i\right)$. In addition, from (a) in Proposition 3, we have ${\left(\mathbb{E}\left(Z_{n+k}\right)\right)}^2\le Var\left(Z_{n+k}\right)$, and so

$$\frac{\eta \left(n\right) - \mathbb{E}\left(\eta \right(n\left)\right)}{s_n}\stackrel{\mathcal{D}}{⟶}N(0,1),$$

(40)

by (b) and (c1) in Proposition 3. To conclude the proof, we must show that

$$\frac{Var\left(\eta \right(n\left)\right)}{s_n^2}\to 1.$$

(41)

From Theorem 1 (c), we have $Var\left(\eta \left(n\right)\right)={\sum }_{i=0}^{\infty }{\alpha }_i\left(n\right)r_i({\alpha }_i\left(n\right)(2-r_i)+1)$, and noting that

$${\alpha }_i\left(n\right)=\left\{\begin{array}{cc}(y_{i-a}-y_i)/y_i\hfill & \mathrm{for}i\le n,\hfill \\ (y_{i-a}-y_n)/y_i\hfill & \mathrm{for}n<i\le n+a-1,\hfill \\ 0\hfill & \mathrm{for}i>n+a-1,\hfill \end{array}\right.$$

we obtain

$$Var\left(\eta \left(n\right)\right)=\sum _{i=0}^n\frac{y_{i-a} - y_i}{y_i}{r}_i\left(\frac{y_{i-a} - y_i}{y_i}(2-r_i)+1\right)+\sum _{i=n+1}^{n+a-1}\frac{y_{i-a} - y_n}{y_i}{r}_i\left(\frac{y_{i-a} - y_n}{y_i}(2-r_i)+1\right).$$

(42)

In addition, from Proposition 3 (a), we get

$$\begin{array}{cc}\hfill Var\left(Z_i\right)& =\frac{1 - q_i}{q_i}{r}_i\left(\frac{1 - q_i}{q_i}(1-r_i)+\frac{1}{q_i}\right)\hfill \\ \hfill & =\frac{y_{i-a} - y_i}{y_i}{r}_i\left(\frac{y_{i-a} - y_i}{y_i}(2-r_i)-\frac{y_{i-a} - y_i}{y_i}+\frac{y_{i-a}}{y_i}\right)\hfill \\ \hfill & =\frac{y_{i-a} - y_i}{y_i}{r}_i\left(\frac{y_{i-a} - y_i}{y_i}(2-r_i)+1\right),\hfill \end{array}$$

and, from (42), we have $Var\left(\eta \left(n\right)\right)-s_n^2\ge 0$ and

$$\begin{array}{cc}\hfill Var\left(\eta \left(n\right)\right)-s_n^2& =\sum _{i=n+1}^{n+a-1}\frac{y_{i-a} - y_n}{y_i}{r}_i\left(\frac{y_{i-a} - y_n}{y_i}(2-r_i)+1\right)\hfill \\ \hfill & \le \sum _{i=n+1}^{n+a-1}\frac{y_{i-a} - y_i}{y_i}{r}_i\left(\frac{y_{i-a} - y_i}{y_i}(2-r_i)+1\right)\hfill \\ \hfill & =\sum _{i=n+1}^{n+a-1}Var\left(Z_i\right).\hfill \end{array}$$

From the inequalities above, (41) is a direct consequence of (c1) in Proposition 3. □

6. Examples

In this section, we present some examples of application of our results to particular distributions. For each distribution, we consider the r.v. ${\eta }_N$ analysed in Corollary 1. In particular, we give formulas for $\mathbb{E}\left({\eta }_N\right)$, $Var\left({\eta }_N\right)$ and the correlation $\rho ({\eta }_N,{\eta }_{N+1})$. We also study the asymptotic behaviour of $\eta \left(n\right)$.

The distributions that we consider in this section are very different in terms of their right tails. Example 2 is devoted to a heavy-tailed distribution, similar to the Zeta distribution (see Example 3.1 in [16]), which is the discrete counterpart of the Pareto distribution. Example 3 deals with the geometric distribution, which has an exponential-like tail, while Example 4 is about the Poisson distribution, which is light-tailed.

Example 2 

(Heavy-tailed distribution). Let $p_k={\left(k(k+1)\right)}^{-1}$, hence $y_k={(k+1)}^{-1}$ and $r_k={(k+1)}^{-1},k\in \mathbb{N}$. Then, from (21) we have

$$\begin{array}{cc}\hfill \mathbb{E}\left({\eta }_N\right)& =\frac{a}{N(N + 1)},\hfill \\ \hfill Var\left({\eta }_N\right)& =a\frac{N^2 + 3N + a}{N^2{(N + 1)}^2},\hfill \\ \hfill Cov({\eta }_N,{\eta }_{N+1})& =\frac{(a - 1)(a + 2N + 1)}{N{(N + 1)}^2(N + 2)},\hfill \end{array}$$

$$\rho ({\eta }_N,{\eta }_{N+1})=\frac{(a - 1)(a + 2N + 1)}{a\sqrt{(N^2 + 3N + a)(N^2 + 5N + a + 4)}}.$$

Note that $\rho ({\eta }_N,{\eta }_{N+1})\sim \frac{2(a-1)}{a}\frac{1}{N}$, as $N\to \infty$, for every $a\ge 1$. The p.m.f. of ${\eta }_N$ can be obtained from (20) by noting that $c=\frac{1}{N + 1}$ and $d=\frac{N + a}{N(N + 1)}$.

Regarding the asymptotic behaviour of $\eta \left(n\right)$, we observe that ${\sum }_{k=0}^{\infty }{r}_k^2<\infty$ and so, from Theorem 2, $\eta \left(n\right)\to \eta \left({\mathbb{R}}_{+}\right)<\infty$ a.s. We now compute the main characteristics of this r.v. For the expectation, note that ${\alpha }_i\left({\mathbb{R}}_{+}\right)=i$, for $i<a$, and ${\alpha }_i\left({\mathbb{R}}_{+}\right)=\frac{a}{i - a + 1}$, for $i\ge a$. So, from (23), we obtain

$$\mathbb{E}\left(\eta \left({\mathbb{R}}_{+}\right)\right)=\sum _{i=0}^{a-1}\frac{i}{i + 1}+\sum _{i=a}^{\infty }\frac{a}{(i + 1)(i - a + 1)}=a.$$

It is interesting to see that the expected total number of near-records is equal to the near-record parameter a. For the variance, we use (19) to obtain

$$Var\left(\eta \left({\mathbb{R}}_{+}\right)\right)=\mathbb{E}\left(\eta \left({\mathbb{R}}_{+}\right)\right)+\sum _{i=0}^{a-1}{i}^2{r}_i(2-r_i)+\sum _{i=a}^{\infty }{\left(\frac{a}{i - a + 1}\right)}^{{}_2}{r}_i(2-r_i),$$

which, after some algebra (see Appendix B), yields

$$Var\left(\eta \left({\mathbb{R}}_{+}\right)\right)=a^2-3a+2\left(1+\frac{1}{a}\right)\sum _{i=1}^a\frac{1}{i}+(a-1)\frac{{\pi }^2}{3}.$$

(43)

In addition, the p.g.f. of $\eta \left({\mathbb{R}}_{+}\right)$ is easily computed from (24) as

$${\phi }_{{\mathbb{R}}_{+}}\left(t\right)=\prod _{i=1}^a\left(1-\frac{(i - 1)(1 - t)}{i + (i - 1)i(1 - t)}\right)\prod _{i=a+1}^{\infty }\left(1-\frac{a(1 - t)}{(i - a)i + ai(1 - t)}\right).$$

(44)

The p.m.f. of $\eta \left({\mathbb{R}}_{+}\right)$ can be obtained from (44). For instance, taking $t=0$, we get

$$P(\eta \left({\mathbb{R}}_{+}\right)=0)={\phi }_{{\mathbb{R}}_{+}}\left(0\right)=\prod _{i=1}^{\infty }\left(1-\frac{min\{a,i-1\}}{i^2}\right).$$

Example 3 

(Geometric distribution). The geometric distribution has $p_k=p{(1-p)}^k$, $y_k={(1-p)}^{k+1}$, $r_k=p$, for $k\in {\mathbb{Z}}_{+}$, with $p\in (0,1)$. From (21), it is easy to see that

$$\begin{array}{cc}\hfill \mathbb{E}\left({\eta }_N\right)& =p\left(\frac{1}{{(1 - p)}^a}-1\right),\hfill \\ \hfill Var\left({\eta }_N\right)& =p^2\left(\frac{1}{{(1 - p)}^{2a}}-1\right)+p\left(\frac{1}{{(1-p)}^a}-1\right),\hfill \\ \hfill Cov({\eta }_N,{\eta }_{N+1})& =\frac{p^2}{1 - p}\left(\frac{1}{{(1 - p)}^{2(a-1)}}-1\right).\hfill \end{array}$$

Observe that none of the quantities above depend on N. The p.m.f. of ${\eta }_N$ is given by (20), with $c=p$, $d=\frac{p}{{(1 - p)}^a}$.

Since $r_k=p,k\in {\mathbb{Z}}_{+}$, hypothesis $\left(i\right)$ of Theorems 3 and 4 holds, and so we have a strong law of large numbers and a central limit theorem for $\eta \left(n\right)$. For Theorem 3 note that $\eta \left(n\right)={\sum }_{N=0}^n{\eta }_N$ and therefore,

$$\frac{\eta \left(n\right)}{n}\stackrel{\mathrm{a}.\mathrm{s}.}{⟶}p\left(\frac{1}{{(1 - p)}^a}-1\right).$$

For the central limit theorem, as shown in the proof of Theorem 4, we can replace $Var\left(\eta \right(n\left)\right)$ by ${\sum }_{i=0}^{n}Var\left(Z_i\right)$ in the denominator of (35). Since $q_i={(1-p)}^a$, for $i\ge a$, from Proposition 3 (a), we get

$${\sigma }^2:=Var\left(Z_i\right)=\frac{1 - {(1 - p)}^a}{{(1 - p)}^{2a}}p((1-{(1-p)}^a)(1-p)+1).$$

Therefore,

$$\frac{\eta \left(n\right)-p\left(\frac{1}{{(1 - p)}^a}-1\right)n}{\sqrt{n}}\stackrel{\mathcal{D}}{⟶}N(0,{\sigma }^2).$$

(45)

Example 4 

(Poisson distribution). The Poisson distribution has $p_k=e^{-\lambda }{\lambda }^k/k!$ for $k\in {\mathbb{Z}}_{+}$. Although there is not a manageable form of $y_k$ and $r_k$, the following bound, taken from [17], are useful:

$$\frac{\lambda }{k + 1}-{\left(\frac{\lambda }{k + 1}\right)}^2\le 1-r_k\le \frac{\lambda }{k + 1}, k\in {\mathbb{Z}}_{+}.$$

(46)

Explicit expressions for the quantities in (21) can be written out, but they shed little light on their dependence on $\lambda$ and N. Instead, we analyse their asymptotic behaviour for large N. By (46), $r_k\to 1$, so $y_k/y_{k-1}\to 0$. Therefore, ${\sum }_{i=N}^{N+a-1}{r}_i/y_i\sim 1/y_{N+a-1}$ and

$$\frac{p_N}{y_{N+a-1}}=\frac{r_N}{(1 - r_N)\cdots (1 - r_{N+a-1})}\sim {\left(\frac{N}{\lambda }\right)}^a,$$

as $N\to \infty$. This immediately yields the asymptotic behaviour of the formulas in (21):

$$\begin{array}{cc}\hfill \mathbb{E}\left({\eta }_N\right)& \sim {\left(\frac{N}{\lambda }\right)}^a,\hfill \\ \hfill Var\left({\eta }_N\right)& \sim {\left(\frac{N}{\lambda }\right)}^{2a},\hfill \\ \hfill Cov({\eta }_N,{\eta }_{N+1})& \sim {\left(\frac{N}{\lambda }\right)}^{2a-1},\hfill \end{array}$$

and $\rho ({\eta }_N,{\eta }_{N+1})\sim \lambda /N$. Hence, as in Example 2, the correlation coefficient between ${\eta }_N$ and ${\eta }_{N+1}$ converges to 0 as $N\to \infty$.

For the asymptotic behavior of $\eta \left(n\right)$, note that (46) guarantees that ${lim}_n{r}_n=1$ and, moreover, $|r_n-r_{n-1}|\le C/n^2$ and $1-r_n\ge D/n$, for all large enough values of n and some positive constants C and D. Hence, condition $\left(ii\right)$ in Theorem 3 holds, with $\beta =3/4$, and so does condition $\left(ii\right)$ in Theorem 4. In order to apply Theorem 3 note that, since $\mathbb{E}\left({\eta }_N\right)\sim {(N/\lambda )}^a$, we have $\mathbb{E}\left(\eta \left(n\right)\right)={\sum }_{N=0}^n\mathbb{E}\left({\eta }_N\right)\sim \frac{n^{a+1}}{{\lambda }^a(a + 1)}$ and

$$\frac{\eta \left(n\right)}{n^{a+1}}\stackrel{\mathrm{a}.\mathrm{s}.}{⟶}\frac{1}{{\lambda }^a(a + 1)}.$$

For the central limit theorem, as in Example 3, the scaling sequence can be taken as ${\left({\sum }_{i=0}^{n}Var\left(Z_i\right)\right)}^{1/2}$. Since $q_i={\prod }_{j=i-a+1}^i(1-r_j)\to 0$, we have $Var\left(Z_i\right)\sim q_i^{-2}\sim {(i/\lambda )}^{2a}$, so

$$\sum _{i=0}^{n}Var\left(Z_i\right)\sim \frac{n^{2a+1}}{{\lambda }^{2a}(2a+1)}.$$

In addition, from the proof of Theorem 4, the centring sequence in the central limit theorem can be chosen as ${\sum }_{i=0}^n\mathbb{E}\left(Z_i\right)$, which in turn can be replaced by ${\sum }_{i=a}^n{q}_i^{-1}$. Indeed, for $i\ge a$,

$$e_i:=\left|\mathbb{E}\left(Z_i\right)-\frac{1}{q_i}\right|=\frac{1}{q_i}|r_i-r_i{q}_i-1|\le 1+\frac{1-r_i}{q_i}=1+\prod _{j=i-a+1}^{i-1}\frac{1}{1-r_j}.$$

Thus, by (46), ${\sum }_{i=0}^n{e}_i\le n+C{n}^a$, for a given constant $C>0$, which implies

$$\frac{{\sum }_{i=0}^n{e}_i}{{\left({\sum }_{i=0}^{n}Var\left(Z_i\right)\right)}^{1/2}}\to 0.$$

We can further replace ${\sum }_{i=a}^n{q}_i^{-1}$ by $\frac{n^{a+1}}{(a + 1){\lambda }^a}$ since, by (46), it can be shown that

$$\left|\frac{1}{q_i}-{\left(\frac{i}{\lambda }\right)}^a\right|<C{i}^{a-1},$$

for all $i\ge a$ and some constant $C>0$. Therefore, we conclude

$$\frac{\eta \left(n\right)-\frac{n^{a+1}}{(a + 1){\lambda }^a}}{n^{a+1/2}}\stackrel{\mathcal{D}}{⟶}N(0,{\sigma }^2),$$

(47)

where $\sigma =\frac{1}{{\lambda }^a\sqrt{2a + 1}}$.

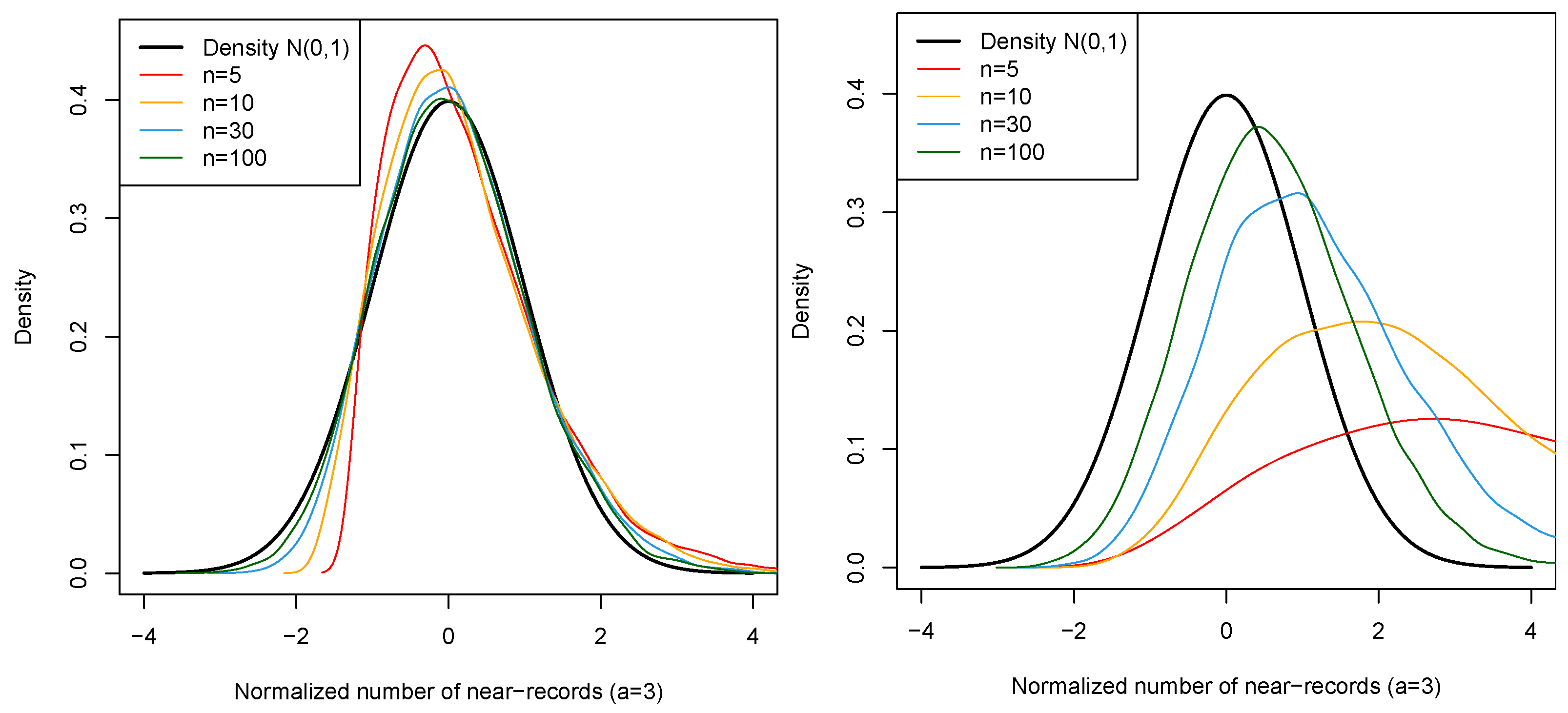
Remark 3. 

In Examples 3 and 4 above, we observe that the normalising sequences in the law of large numbers and central limit theorem depend on the right-tail behaviour of the parent distribution of the observations. This is also the case for the speed of convergence of $\eta \left(n\right)$ to the normal distribution in the central limit theorem, as shown in Figure 2. Convergence is very fast for the geometric distribution, while it is much slower in the Poisson distribution (the distribution of $\eta \left(30\right)$ in the geometric distribution is closer to the normal than the distribution of $\eta \left(100\right)$ in the Poisson).

7. Conclusions and Future Work

In this paper, we have studied the point process of near-record values from a sequence of independent and identically distributed discrete random variables. Near-records arise as a natural complement of records, with applications in statistical inference.

We have shown that this process is a Bernoulli cluster process and obtained its probability generating functional, as well as formulas for the expectation, variance, covariance and probability generating functions for related counting processes.

We have given a condition for the finiteness of the total number of near-records along the whole sequence of observations. This condition is provided in terms of convergence of the squared hazard rates series. In addition, the explicit expression of its probability generating function is obtained.

In the case where the total number of near-records is not finite, strong convergence and central limit theorems for the number of record values in growing intervals are derived under mild regularity conditions. Finally, we have presented examples of the application of our results to particular families, which show that the asymptotics of near-record values depends critically on the right-tail behaviour of the parent distribution.

Some interesting questions remain open, such as a more detailed analysis of the sequence $\eta \left(n\right)$, including the law of the iterated logarithm and large deviations, or departures from the i.i.d. hypothesis (e.g., linear trend model). They will be addressed in future work.