Abstract
Students’ graph understanding was chosen for the research because teachers, especially physics teachers, tend to use graphs as a second language, assuming that their students can extract most of the information from them. This research aims to determine the differences between Serbian and North Macedonian students’ graph understanding of kinematics and their perceived mental effort. Differences in physics curricula in the Republic of Serbia and Republic of North Macedonia are taken into account and compared as well as students’ achievement on the TUG-K knowledge test to find explanations of potential differences and guidelines for change in the approaches to physics teaching. The sample includes 630 first-grade grammar school students (313 students from Serbia and 317 from North Macedonia) from randomly selected classes. Mann–Whitney U-test determined possible differences in student achievement and perceived mental effort. The main results indicate a difference in students perceived mental effort. North Macedonian students perceived less mental effort than Serbian ones, which leads to higher instructional efficiency of teaching approaches applied in North Macedonia than in Serbia. Based on the results, the recommendation for improving the Serbian education system lies in reducing mental effort through efficient allocation of teaching hours.
Keywords:
cross-country comparison; instructional efficiency; mental effort; understanding kinematics graphs MSC:
97B20; 97B70; 97C30; 97G30
1. Introduction
Contemporary society problems, such as the COVID-19 pandemic and trends in world stock exchanges, emphasize the importance of understanding a different kinds of numerical graphs. People need to know how to make those numbers talk [1] (p. 299) and how to read the data as well as between and beyond the data [2] (p. 36). Researchers’ interest in graphs dates back to 1875 [3].
Graphs are powerful visual pattern-recognition tools to see trends and spot subtle differences in shape [4,5]. In physics, graphs are used to visualize the mutual dependencies between physical quantities [1] (p. 299). Therefore, physics teachers tend to use graphs as a second language, assuming that their students can extract most of their rich information content, but it is often an incorrect assumption [4,6]. To participate in physics and be a critical consumer of scientific knowledge, students need to understand the message communicated by graphs [7].
One of the physics topics that abounds in graphs is kinematics. Kinematics includes the concepts of position, displacement, velocity, speed, and acceleration and discusses straight motion without considering the causes of motion, defined as forces [8]. Position vs. time, velocity vs. time, and acceleration vs. time are the three main kinematics graphs [5,9,10]. Students can obtain most of the kinematics formulas by using these graphs [5]. The importance of kinematics is reflected in its relationship with other areas of physics. Manurung noted that lack of understanding of the kinematics concept results in students’ poor comprehension of further physics concepts [8] (p. 180). The importance of understanding the graphs can be seen in correlation with students’ spatial ability. According to Kozhevnikov et al., spatial ability might be necessary for visualizing invisible phenomena and processes such as electric or magnetic field lines or electric current [1] (p. 301). Therefore, it is crucial to find an appropriate teaching approach that will cause higher student achievement. Students’ achievement can be increased by reducing the cognitive load. Generally, the cognitive load can be defined as a required working memory resource necessary for fulfilling the goals of the cognitive activities in certain situations [11]. Reflecting the relationship between the structure of information and the cognitive characteristics of students, cognitive load is affected by the nature of teaching and learning material and by the manner in which such material is presented to the students [12,13].
If the cognitive load value is not considered, it can exceed the value of working memory and thus disrupt the learning process. In that case, part of the information, due to overload, will not be adopted. Therefore, the information of cognitive load indicates whether a student can process the information and properly integrate it into his/her cognitive system or not. Cognitive load is characterized by two dimensions: causal, which relates to the interaction of the task and cognitive characteristics of an individual, and measurable, which relates to measurable concepts of cognitive load: mental load, mental effort, and performance [14]. Mental effort is an aspect of a cognitive load that is related to the cognitive capacities allocated for processing the demands imposed by the task [15]. In this research, mental effort was used as an estimator of cognitive load.
Based on the information of the standardized value of mental effort (R) and students’ achievement (P), it is possible to calculate the instructional efficiency (E) of the teaching approach as [16]. The sign of the instructional efficiency is determined graphically (Figure 1).
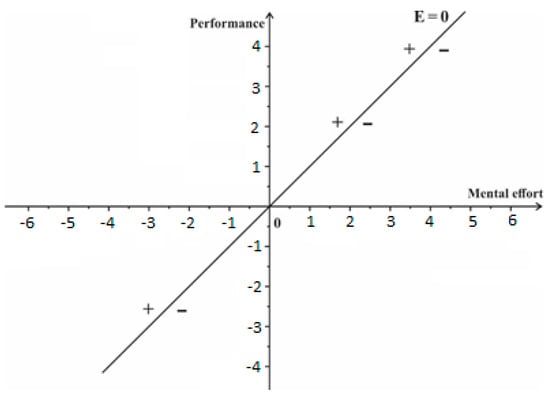
Figure 1.
Graphical representation of instructional efficiency (adapted according to [17]).
If the point that represents the effect of the applied teaching approach is above the curve P = R, then E > 0, and the applied approach is suitable for students, while if the point is below the curve, then E < 0, and it is considered that such an approach causes too much mental effort, and the total load exceeds the limit of the working memory.
2. Materials and Methods
2.1. The Aim and Tasks of Research
Until 1991, the Republic of Serbia and the Republic of North Macedonia were two of the six constituents countries of the Socialist Federative Republic of Yugoslavia, and they were parts of one joint education system. Both countries reconstructed their educational system, and some more significant changes were introduced into Science. Therefore, this research focuses on students’ graph understanding in kinematics as an essential part of physics, chemistry, and mathematics. This research aims to determine the potential differences in students’ understanding of graphs in kinematics and their perceived mental effort in the Republic of Serbia and the Republic of North Macedonia to find a better approach for students. According to the authors’ knowledge, this is the first cross-country comparison study of two countries using the TUG-K test.
In line with the aim, the following research questions were formulated:
- Are there differences in the curriculum of physics (curricula, syllabi, national standards, textbooks, and a number of teaching hours) in lower secondary school (age from 12 to 15 years)?
- Are there differences in students’ achievement?
- Are there differences in the perceived mental effort of students?
- Are there differences in instructional efficiency?
2.2. Research Instruments
To test student achievement, a standardized knowledge test, the Test of Understanding Graphs and Kinematics (TUG-K), created by Bob Beichner, was applied. The test can be found on the site https://www.physport.org/assessments/assessment.cfm?A=TUGK&S=4 (accessed on 19 January 2017). The test consists of 26 questions. The question was indexed with 1 for correct, i.e., with 0 for an incorrect answer. The psychometric values of the test have been confirmed in numerous papers. In our research, the Cronbach’s alpha was 0.715, which shows that the test is reliable and can be used for further analysis. The TUG-K test includes nine concepts related to students’ understanding of graphs in kinematics: position, velocity, acceleration, graph reading, slope velocity, slope acceleration, area displacement graph, area velocity graph, and one-point slope (Table 1).

Table 1.
Distribution of questions according to concepts.
With each question on the TUG-K test, Likert’s 5-point scale was added, which the students applied to determine the perceived mental effort needed to solve the given task, starting from 1, which denotes the smallest mental effort, up to 5, which is for highest mental effort. Therefore, students do not perceive their knowledge about the topic, which is quite different from the Dunning–Kruger effect. In this research, students perceived the effort that they needed for solving the problems. This method of determining perceived mental effort is considered reliable [11,12,14,15,16,17]. The standardized value of Cronbach’s alpha for the mental effort in our research was 0.927.
The original version of the test analysis omitted the questions from 22–26. In this research, omitted questions were added to existing concepts. Therefore, all the questions given by this test were used.
2.3. The Research Sample
The research sample includes 630 first-grade secondary school students (age of 15): 313 students from Serbia and 317 students from North Macedonia. The North Macedonian sample consisted of students from the third generation of the new reformed education. According to the Raosoft sample size calculator application (http://www.raosoft.com/samplesize.html (accessed on 22 June 2017), the sample represents a convenience sample.
The students were informed that the test was only for scientific purposes, and there was no additional motivation directed to students during the test. Students voluntarily participated in the research. The students who did not agree to participate in the research participated equally in all activities, but their tests were not evaluated and not taken into statistical data processing. All students completed the test anonymously. Whole classes were included in the research, but classes were randomly selected.
Data were collected during September and the first half of October 2017 in both countries before students learn graphs in secondary school. Therefore, their knowledge and skills from the primary and lower secondary school level were tested.
2.4. Statistical Data Processing
To determine differences in student achievement and perceived mental effort, SPSS 20.0 was applied to perform a Mann–Whitney U-test. Table 2 shows descriptive statistics, while the Shapiro–Wilk test (W = 0.888 (df = 630), p < 0.001 for knowledge test, and W = 0.988 (df = 630), p < 0.001 for mental effort) indicated that non-parametric statistics should be applied.

Table 2.
Descriptive statistics.
3. Results and Discussion
According to the set of research tasks, the research results were divided into four sections.
3.1. Difference in Physics Curriculum in the Republic of Serbia and the Republic of North Macedonia
Until 1991, the Republic of Serbia and the Republic of North Macedonia were two of the six constituents countries of the Socialist Federative Republic of Yugoslavia, and they were parts of one joint education system. Both systems consist of three levels, namely compulsory primary, secondary, and higher education, and up to 2006, the structure of compulsory education was the same.
In the Republic of Serbia, compulsory primary education consists of two cycles and lasts eight years [18]. Children start at the age of 6–7 years. Within the first cycle of compulsory education (the first four years), one teacher teaches all subjects regardless of subjects’ diversity. With some basic physics concepts, students are introduced to subjects about the world around us (for first and second grades) and nature and society (for third and fourth grades). The second cycle of compulsory education is held within the subject teaching, where different teachers teach each subject. Within the second cycle of compulsory education, students start studying physics in the sixth grade (age of 12–13) and continue in the seventh and eighth grades (age of 14–15). After finishing primary school, students can enroll in secondary school for three or four years (18–19 years).
In the academic 2006/2007 year, the Republic of North Macedonia started with a new reformed educational system [19]. This reform added one more year to primary education, starting at the age of 5–6. Compulsory education is organized in primary education, which now lasts 9 years, and four-year secondary education, which together lasts 13 years (at age 18–19). Elements of physics are taught in the subject of science beginning from first to sixth grade. Physics as a separate subject is taught in the last two years of primary school (eighth and ninth, at age 13 to 14) and three or four years in secondary school, depending on the students’ choice.
Since the test was administered in the first semester of the first grade of higher secondary school, it can be assumed that the knowledge and skills the students showed during the research are the result of the knowledge they obtained in primary and lower secondary school. Hence, to better understand the possible differences in students’ graph understanding, a comparative analysis of the lower secondary school physics curricula was made. According to this analysis, there were no significant differences in the teaching content of the physics curricula for lower secondary schools (Appendix A).
A deeper content analysis showed the difference in the number of teaching hours. In the North Macedonian eighth-grade physics curriculum, when students learn about motion, they have 11 classes for work with graphs: presenting data with graphs, reading data from graphs, calculating path and speed, comparing various motions, etc. [20], while in Serbia, students in physics classes have only two hours in sixth grade and four hours in seventh grade to learn the graphical representation of physics laws. Therefore, North Macedonian students have more classes for exercising, analyzing graphs, and discussing concepts.
Moreover, by analyzing and comparing curricula, syllabi, national standards, and textbooks, other differences were found. Serbian documents show that graphs are mentioned in the sixth grade physics curriculum for the first time but only in additional activities for high-performing students (at the age of 12–13). The seventh-grade physics curriculum introduces two outcomes related to graphs. Students should:
- -
- Use and analyze experimental data of various quantities and present them in tables and graphs;
- -
- Solve qualitative, quantitative, and graph problems (kinematics and dynamics of motion, friction, the balance of lever, buoyancy, conservation laws, etc.).
In the additional outcomes for high-performing students, recommendation is given for using graph presentation of relationships between quantities, as it initiates thinking.
The eighth-grade physics curriculum does not define special classes dedicated to graphs. Yet, graph representation is planned to be applied in the experimental work. It is explicitly noted in the outcomes that students should master graph representation of experimental data. Finally, the Serbian National standards for physics at the end of lower secondary education [21] stipulate mastering the following knowledge and skills:
- -
- Students should know to apply graphs and to organize experimental data into graphs.
- -
- Students should be able to make relevant conclusions from graphs, for example, to estimate values, recognize the existence of dependence between two quantities, or find the value of the independent quantity for zero value of the dependent quantity.
- -
- Students should recognize wavelength from graph representation of the wave.
National standards stipulate calculations and experimental activities, as they are an important part of physics education.
One of the physics textbooks explains distance as an area below the curve in velocity vs. time graph, which is interesting, as such questions appear in the TUG-K test.
In North Macedonia, graphs are introduced for the first time in fourth grade in the subject science, which is three years earlier than in Serbia. The curriculum does not explicitly mention graphs in the content or activity section, but it gives directions to teachers to “visually” represent data and information. On the other hand, the science curriculum for fourth grade says that the content is following the III-A.30 national standard, which states that “pupils should be able to organize and represent quantitative data with tables and graphs, diagrams and sketches and to interpret data from various areas, presented in various ways”. The textbook includes activities where pupils use bar charts to represent multiple measurements. They construct their own charts, mainly in the biology section.
In the physics section, they watch graphs of visualized sound, i.e., graph voltage vs. time, and analyze the loudness (volume) and pitch (frequency). Yet, they do not know that it is graph voltage vs. time, but they analyze the shape of the curve and make conclusions.
North Macedonian national standards for fifth and higher grades are not adopted yet. However, learning outcomes and teacher’s guide notes included in the science curriculum for fifth and sixth grade say that pupils should be able to represent experimental data with bar charts and line graphs.
According to the fifth grade science textbook, pupils use bar charts to represent the melting point for various substances. They use graphs to represent the dependence of the light intensity vs. distance from the light source.
It is not explicitly mentioned that pupils should read data from graphs and interpret them. It is left to the teacher to decide what activities will give to the pupils. However, if teachers follow the outcomes defined in the curriculum, they should provide to the pupils corresponding activities.
According to sixth-grade curriculum, pupils use bar charts to represent reaction time and measurements for air drag. Textbook proposes activities for investigation of solubility and construction graph solubility vs. temperature. There are many activities involving measurements and investigating dependences. It is left to the teachers to decide what they will do with the results (organize them in tables, graphs, etc.).
In addition to the previous knowledge and skills defined in the science curriculum, the eighth-grade physics curriculum introduces interpreting simple graphs of distance vs. time and velocity vs. time. Out of 22 classes dedicated to motion, nine are explicitly provided for work with graphs, and an additional five classes are left to the teacher to decide how to use them. The textbook offers many activities that correspond with the outcomes with a special section for graphs of distance vs. time. Students construct graphs, read values from the curve, construct and explain graphs for complex motions, interpret the slope of the curve as velocity, calculate velocity from the x-t graph, transfer table data to graph and vice versa, and transfer x-t graph into v-t graph and vice versa. They perform same activities for motion with constant speed and motion with constant acceleration.
Further, the basics of dynamics are taught (including friction, air resistance, and free-fall and energy). Again, there are activities with graphs.
Later, when Hooke’s law is investigated, the curriculum stipulates graph presentation of experimental data. It is interesting that there is a section in the textbook explaining elasticity constant as the slope of the curve in the graph extension vs. force. However, the activities are not explained in details, and it is left to teachers to get the activities in line with the outcomes and content defined in the curriculum.
Although there are not graphs and dependence measurements in the energy unit, at the end-unit questions, graphs temperature vs. time are given for analysis and interpretation.
In the optics section, graphs are again mentioned when investigating shadows but without further and detailed direction on what to measure.
Therefore, it can be concluded that North Macedonian physics curricula involve more hours than Serbian ones devoted to practical examples, work with graphs, analysis of motions, and open discussion. These differences could cause a change in student performance.
3.2. Students’ Achievement on the Knowledge Test
Table 3 shows descriptive statistics and the Mann–Whitney U-test for Serbian and North Macedonian students’ achievement on the TUG-K test.

Table 3.
Descriptive statistics and the Mann–Whitney U-test for Serbian and North Macedonian students’ achievement on the TUG-K test.
Questions in TUG-K test put students in new situations where they must think “out-of-the-box”. Students’ achievements in both countries were about 5 points, which is around 20% of the maximum (26 points). Therefore, the low results can be understood as students’ lower ability to think critically: they cannot apply their knowledge in new unknown situations given by the questions. This can be a problem because when teachers want to give students a complete idea of phenomena and processes described and interpreted in physics, they use graphs for that [1]. Therefore, in order to participate in physics classes, students need to understand the message communicated by graphs [7].
Students’ lower understanding of graphs was noticed in other research [1,22]. Brassel and Rowe found that at least one-fifth of the students do not have adequate graphing skills [22] (p. 1394). They found that students have difficulties with linking graphs and verbal descriptions of a given event, and they do not understand graphs as a means of representing functional relationships between variables. Lichtenberger et al. [23] found that the students may know how to use formulas and calculate certain numerical problems, but they still fail to comprehend the physics concepts.
McDermott et al. identified two categories of student difficulties related to kinematics graphs: (1) difficulties in connecting graphs to physics concepts and (2) difficulties in connecting graphs to the real world [9] (p. 1129); [4] (p. 2). The first category includes difficulties with discriminating between slope and height, interpreting changes in height and changes in slope, and interpreting the area under a graph curve, for example. Confirmations of the existence of these difficulties can be found in the papers by [8,24,25,26], etc. According to [24], the area under a curve is a difficult concept for students; therefore, more attention should be given to this. Some of the difficulties included in the second category are representing continuous motion by a continuous line; representing negative velocity on a v vs. t graph, or representing constant acceleration on a v vs. t graph [4,9]. For example, students use two principal approaches to explain speed constancy. The first one is by the straight line and by the constancy of the slope or the derivative, while the second one is the interval reasoning [27].
Table 4 shows the differences in understanding various physics concepts between Serbian and North Macedonian students and the difficulties in understanding these concepts.

Table 4.
The value of Mann–Whitney U-test for comparison differences in understanding physics concepts of Serbian and North Macedonian students in the TUG-K test.
As shown in Table 4, significant differences in students’ achievement were found for three concepts: graph reading, area velocity graph, and one-point slope. For graph reading and area velocity graph, North Macedonian students have higher achievement than Serbian students. One physics concept is tested by more than one question. The analysis shows that students answer some of the questions correctly but answer incorrectly other questions that test the same physics concept and skill. In other words, it seems that the knowledge is content-dependent. Thus, almost the same misconceptions appear in both groups. For example, students misunderstood the shape of the curve graph-as-picture (GAP) misconception [28] when constant acceleration with decreasing velocity vs. time is represented. The most common incorrect answers are that the object is moving with uniformly decreasing acceleration (75% Serbian students and 19% North Macedonian students), and the object is moving with uniformly increasing velocity (7% of Serbian students and 21% North Macedonian students). Furthermore, when the graph represents constant acceleration as a function of time, they think that velocity is constant (49% of Serbian students and 45% of North Macedonian students). This is related to the curve’s shape: if the curve goes up, then the velocity increases or the opposite; if the curve goes down, everything decreases. Students very often do not see what is represented on the axes. Similar results are obtained for other concepts. Regardless of the country, students do not perceive the traveled distance as the area under the v-t diagram curve, which is indicated by the lower students achievement for both Serbian and North Macedonian students. Further analysis of students’ responses to other questions reveals that, in order to calculate velocity, students read the data from one point in the graph instead of using slope. The students are misled by the text in the question since it says “…velocity at t = 3 s”. Hence, they read the data at t = 3 s and forget that the slope represents the velocity. Therefore, it is a clear indication that the responses are context-dependent.
Students’ failure to observe scales can be represented by Woolnough’s findings: “In math, the scales are the same, even when doing motion” [29] (p. 264). Similarly, Planinic et al. [22] noticed that students calculate slope instead of area. They do not recognize the meaning of area under kinematics graph curves or distinguish between distance, velocity, and acceleration [9]. Additionally, they often believe that the graph of these variables should be identical and appear to readily switch axis labels from one variable to another without recognizing that the graphed line should also change. Beichner pointed out that the most common students’ errors are thinking that the graph is a literal picture of the situation and confusing the meaning of the slope of a line and the height of a point on the line [4] (p. 2). Erceg and Aviani [30] emphasized that students often do not know how to apply mathematical knowledge to graphs in physics. On the other side, Ergül [31] found that they cannot see that the equation in mathematics (p. 143), , has the same structure as in physics, or . This is positively correlated with the result of Woolnough [29], which emphasizes that inappropriate transfer of concepts from mathematics to physics can adversely affect the development of physics concepts. According to [29] (p. 264), students emphasize that “Dealing with gradients wasn’t a problem in Math, but it is in Physics”, and “You shouldn’t have units in slope”.
3.3. Perceived Mental Effort
Table 5 shows the mean values of the students’ perceived mental effort and the Mann–Whitney U-test value. According to Cohen criteria, the value of r-estimator of impact size (r = −0.168) indicated the low-to-medium size of the conventional teaching approach effect students’ perceived mental effort.

Table 5.
Perceived mental effort during knowledge test.
As shown in Table 5, students from North Macedonia perceived less mental effort than students from Serbia. In unstructured group interviews with a few physics teachers from Serbia, it was confirmed that students have difficulties with understanding graphs, and because of that, some of them repeat these instructions in other classes, which should be focused on other teaching units, but it is not enough.
Figure 2 shows the distribution of the perceived mental effort of students.
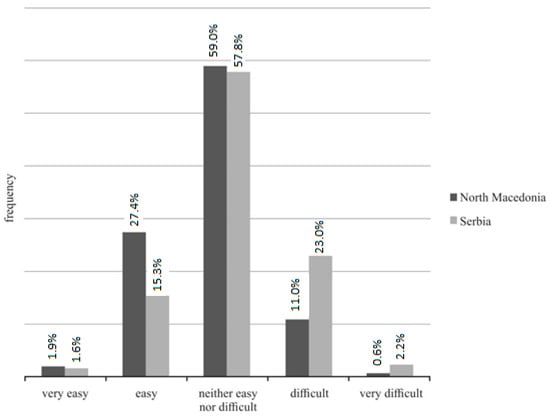
Figure 2.
Students perceived mental effort of both countries.
As shown in Figure 2, most of the students of both countries characterized the questions as neither easy nor difficult. Differences have emerged within the categories easy and difficult. A higher percentage of Serbian students than North Macedonian ones assessed the same questions as difficult. It means that Serbian students had to occupy working memory capacity more by invoking information from the long-term and short-term memory to solve the task successfully. Therefore, they had to make more effort to solve the questions than North Macedonian students. It can be assumed that the reasons are in the difference in teaching hours and more practice for North Macedonian students. By devoting more time to the graphs’ analysis and discussion, students better understand the causal relationships, and the teaching material was more accessible for them because they are used to working with graphs.
Table 6 shows the differences in Serbian and North Macedonian students’ perceived mental effort for observed concepts.

Table 6.
The values of the Mann–Whitney U-test for comparing differences in the perceived mental effort of Serbian and North Macedonian students for observed concepts.
As shown in Table 6, there are no statistically significant differences in students’ mental effort only for the concept area velocity graph. Therefore, these data indicate that Serbian students invest much more effort in all concepts except the one-point slope to correctly understand the graphic representation of a body’s speed and acceleration. The most significant differences were obtained for position and slope velocity. This is in line with the previous misconception analysis, which revealed more misconceptions for Serbian students than North Macedonian ones. Thus, it is expected to obtain that Serbian students perceived higher mental effort for these concepts.
3.4. Instructional Efficiency
Figure 3 shows both countries’ instructional efficiency (E) of applied teaching approaches. The standardized value for Serbian students’ achievement is −0.02, while for North Macedonian students, it is 0.03. Standardized mental effort for Serbian students is 0.23, while for North Macedonian students is −0.23. Using the Van Gog and Paas formula, it is obtained that the instructional efficiency of the learning process in Serbia is ES = −0.177, while that for North Macedonia is ENM = 0.184.
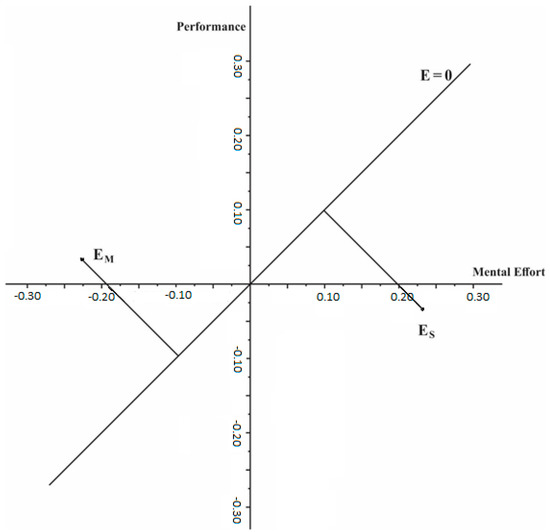
Figure 3.
Instructional efficiency.
The values of instructional efficiency indicated that the teaching approach applied in North Macedonia is more efficient for students because it causes less mental effort. This means that the Serbian students meet more difficulties in the process of learning than the North Macedonian ones. Lower mental effort enables students with a higher free capacity of working memory. The students’ correct understanding of the graphical representation of results, reading values, and interpretation is an essential basis for a proper understanding of kinematics, mathematics, and other fields of science.
As a consequence of this research, we expect the use and application of positive experience as guidelines for change in physics teaching approaches to be the final outcome. Therefore, to make recommendations for improvement of the educational system, it is necessary to determine the predictor’s contribution, perceived mental effort, and applied approaches to explain the student achievement variable, more precisely, students’ exceptional achievement on TUG-K test. Since the predictor correlates with each other, r = 0.230, p < 0.001, a neural network model is applied. In our neural network model, the overall percentage of correctly classified students in the training sample was 98.4%, while this percentage in the test sample was 97.9%. The AUROC (area under the ROC curve) showed the model’s accuracy of 0.612. Table 7 shows each predictor’s importance and normalized importance in determining the neural network.

Table 7.
Importance and the normalized importance of each predictor of students’ achievement.
As can be seen, the achievement of exceptional achievements on the TUG-K test is influenced by both predictors, with the significant impact of perceived mental effort. Mental effort as a measurable part of cognitive load is influenced by teaching approaches and the complexity of teaching content. Therefore, the recommendation for improving the Serbian education system lies in the efficient allocation of time and in including more practice for students’ work with graphs.
4. Conclusions
By analyzing curricula and syllabi, some differences were revealed. North Macedonian students start learning and applying graphs much earlier than Serbian students. Starting in fourth grade, the number and level of activities with graphs defined in the curriculum and offered in the textbook increases, reaching its maximum in eighth grade. Even more, the North Macedonian eighth-grade physics curriculum defines special classes for working with graphs and gives detailed instruction. Serbian outcomes and directions for activities are somewhat more general and provide teacher freedom in creating activities, which means that not all teachers will work with graphs and give the students the same or similar activities or activities with similar level.
By analyzing the results from TUG-K test, it was obtained that regardless of the country, students do not perceive the distance as the area under the v-t diagram curve, which is indicated by the lower students’ achievement. Differences in students’ understanding were obtained only for graph reading and area velocity graph, where North Macedonian students had higher achievement than Serbian ones. Examples of misinterpreting graphs, as the shape of the curve, were more noticed by Serbian students. Research results [1] imply that students do not have enough skills to work with graphs, emphasizing the need for more classes for graph reading practice. Therefore, the obtained results indicate the need to apply the same recommendations as in research [1].
In terms of mental effort, Serbian students perceived higher mental effort during the TUG-K test than North Macedonian students. North Macedonian students are used to working with graphs. After they leave lower secondary school, they already have six years of experience, which makes them relaxed, comfortable, and unencumbered when they complete tasks with graphs. Therefore, they feel it as a routine, and they perceive lower mental effort.
These differences in perceived mental effort cause the difference in instructional efficiency, which is higher for the North Macedonian teaching approach than for Serbian ones. Therefore, the recommendation for improving the Serbian education system lies in the efficient allocation of time and in including more practice for students’ work with graphs.
Even though the research was obtained from a large sample, further research should take into account other neighboring countries that have the same former educational system in order to better elucidate the changes. In addition, further research should consider classroom equipment and other potential differences and apply new methods such as eye-tracking.
Author Contributions
Conceptualization, B.R. and O.Z.; methodology, B.R. and M.S.; validation, M.S., S.G.-Z. and J.S.; formal analysis, B.R. and S.G.-Z.; investigation, B.R., M.S., O.Z. and S.G.-Z.; writing—original draft preparation, B.R., M.S., O.Z., S.G.-Z. and J.S. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge financial support of the Ministry of Education, Science, and Technological Development of the Republic of Serbia (Grant No. 451-03-68/2022-14/200125).
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by Director of the Department of Physics, Faculty of Sciences, University of Novi Sad (date of approval 19 May 2017). The students were voluntarily participating in the research, and informed consent to participate in the research was obtained from each participant.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
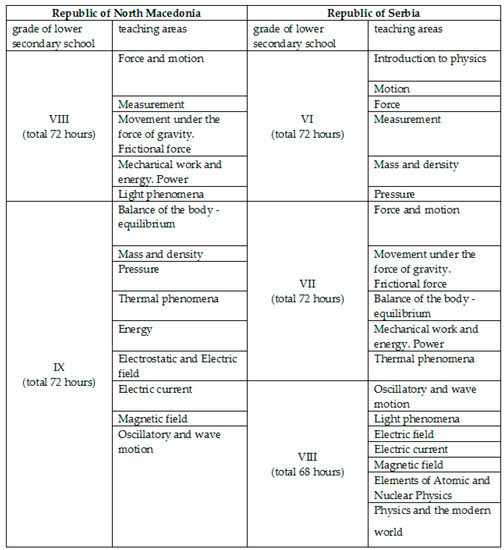
Figure A1.
Comparative overview of the studied teaching areas in physics for lower secondary school.
References
- Skrabankova, J.; Popelka, S.; Beitlova, M. Students’ ability to work with graphs in physics studies related to three typical student groups. J. Balt. Sci. Educ. 2020, 19, 298–316. [Google Scholar] [CrossRef]
- Delport, D.H. Teaching first-year statistics students with COVID-19 real-world data: Graphs. Teach. Stat. 2021, 43, 36–43. [Google Scholar] [CrossRef]
- Vose, G.L. Graphic Method for Solving Certain Algebraic Problems; D. Van Nostrand Publisher: New York, NY, USA, 1875. [Google Scholar]
- Eshach, H. The use of intuitive rules in interpreting students’ difficulties in reading and creating kinematic graphs. Can. J. Phys. 2014, 92, 1–8. [Google Scholar] [CrossRef]
- Bektasli, B.; White, A.L. The relationships between logical thinking, gender, and kinematics graph interpretation skills. Eurasian J. Educ. Res. 2012, 48, 1–19. [Google Scholar]
- Zajkov, O.; Jonoska, M. Graph and graphic understanding among secondary school students. In Proceedings of the Fifth General Conference of the Balkan Physical Union, Vrnjacka Banja, Serbia, 25–29 August 2003; Jokić, S., Milošević, I., Balaž, A., Nikolić, Z., Eds.; Serbian Physical Society: Belgrade, Serbia, 2003; pp. 1849–1854. [Google Scholar]
- Nixon, R.S.; Godfrey, T.J.; Mayhew, N.T.; Wiegert, C.C. Undergraduate student construction and interpretation of graphs in physics lab activities. Phys. Rev. Phys. Educ. Res. 2016, 12, 010104. [Google Scholar] [CrossRef]
- Amin, B.D.; Sahib, E.P.; Harianto, Y.I.; Patandean, A.J.; Herman, H.; Sujiono, E.H. The interpreting ability on science kinematics graphs of senior high school students in South Sulawesi, Indonesia. J. Pendidik. IPA Indones. 2020, 9, 179–186. [Google Scholar] [CrossRef]
- Araujo, I.S.; Veit, E.A.; Moreira, M.A. Physics students’ performance using computational modelling activities to improve kinematics graphs interpretation. Comput. Educ. 2008, 50, 1128–1140. [Google Scholar] [CrossRef]
- Doorman, L.M.; Gravemeijer, K.P.E. Emergent modeling: Discrete graphs to support the understanding of change and velocity. Zero Downtime Migr. 2009, 41, 199–211. [Google Scholar] [CrossRef][Green Version]
- Radulović, B.; Stojanović, M.; Županec, V. The effects of laboratory inquire-based experiments and computer simulations on high school students’ performance and cognitive load in physics teaching. Zb. Inst. Pedagos. Istraz. 2016, 48, 264–283. [Google Scholar] [CrossRef]
- Choi, H.H.; Van Merriënboer, J.J.; Paas, F. Effects of the physical environment on cognitive load and learning: Towards a new model of cognitive load. Educ. Psychol. Rev. 2014, 26, 225–244. [Google Scholar] [CrossRef]
- Horvat, S.A.; Rončević, T.N.; Arsenović, D.Z.; Rodić, D.D.; Segedinac, M.D. Validation of the procedure for the assessment of cognitive complexity of chemical technology problem tasks. J. Balt. Sci. Educ. 2020, 19, 64–75. [Google Scholar] [CrossRef]
- Sweller, J.; Ayres, P.; Kalyuga, S. Cognitive Load Theory; Springer: New York, NY, USA, 2011. [Google Scholar]
- Paas, F.; Tuovinen, J.E.; Tabbers, H.; Van Gerven, P.W.M. Cognitive load measurement as a means to advance cognitive load theory. Educ. Psychol. 2003, 38, 63–71. [Google Scholar] [CrossRef]
- van Gog, T.; Paas, F. Instructional efficiency: Revisiting the original construct in educational research. Educ. Psychol. 2008, 43, 16–26. [Google Scholar] [CrossRef]
- Clark, R.C.; Nguyen, F.; Sweller, J. Efficiency in Learning: Evidence-Based Guidelines to Manage Cognitive Load; John Wiley & Sons: San Francisco, CA, USA, 2011. [Google Scholar]
- Radulović, B.; Gajić, O.; Španović, S.; Lungulov, B. Challenges of initial teacher education in the context of higher education reform in Serbia. Educ. Self Dev. 2019, 14, 34–39. [Google Scholar] [CrossRef]
- Zajkov, O.; Gegovska-Zajkova, S.; Mitrevski, B. Textbook-caused misconceptions, inconsistencies, and experimental safety risks of a grade 8 physics textbook. Int. J. Sci. Math. Educ. 2017, 15, 837–852. [Google Scholar] [CrossRef]
- Bureau for Development of Education, Physics Curriculum for 8th Grade. 9-Year Primary Education. Skopje, Macedonia: Ministry of Education and Science, Bureau for Development of Education. Available online: https://www.bro.gov.mk/wp-content/uploads/2018/02/Nastavna_programa-Fizika-VIII_odd-mkd.pdf (accessed on 18 March 2019).
- Educational Standards for End of Compulsory Education; Ministry of Education of the Republic of Serbia, Institute for Evaluation of Education and Upbringing Quality: Belgrade, Serbia. 2010. Available online: https://ceo.edu.rs/wp-content/uploads/obrazovni_standardi/kraj_obaveznog_obrazovanja/Predlog%20standarda.pdf (accessed on 20 February 2019).
- Planinic, M.; Milin-Sipus, Z.; Katic, H.; Susac, A.; Ivanjek, L. Comparison of student understanding of line graph slope in physics and mathematics. Int. J. Sci. Math. Educ. 2012, 10, 1393–1414. [Google Scholar] [CrossRef]
- Lichtenberger, A.; Vaterlaus, A.; Wagner, C. Analysis of student concept knowledge in Kinematics. In Proceedings of the ESERA the 2013th E-Book Conference: Teaching and Coherence in Learning Science Education Research for Evidence Based, Nicosia, Cyprus, 2–7 September 2013; Volume 11, pp. 38–50. [Google Scholar]
- Susac, A.; Bubic, A.; Kazotti, E.; Planinic, M.; Palmovic, M. Student understanding of graph slope and area under a graph: A comparison of physics and nonphysics students. Phys. Rev. Phys. Educ. Res. 2018, 14, 020109. [Google Scholar] [CrossRef]
- Planinic, M.; Ivanjek, L.; Susac, A.; Milin-Sipus, Z. Comparison of university students’ understanding of graphs in different contexts. Phys. Rev. Spec. Top. Phys. Educ. Res. 2013, 9, 020103. [Google Scholar] [CrossRef]
- Klein, P.; Küchemann, S.; Brückner, S.; Zlatkin-Troitschanskaia, O.; Kuhn, J. Student understanding of graph slope and area under a curve: A replication study comparing first-year physics and economics students. Phys. Rev. Phys. Educ. Res. 2019, 15, 020116. [Google Scholar] [CrossRef]
- Bollen, L.; De Cock, M.; Zuza, K.; Guisasola, J.; van Kampen, P. Generalizing a categorization of students’ interpretations of linear kinematics graphs. Phys. Rev. Phys. Educ. Res. 2016, 12, 010108. [Google Scholar] [CrossRef]
- Garcia, G.G.; Cox, R. “Graph-as-Picture” Misconceptions in young students. In Proceedings of the International Conference on Theory and Application of Diagrams, Portland, OR, USA, 9–11 August 2010; Goel, A.K., Jamnik, M., Narayanan, N.H., Eds.; Springer: Berlin, Heidelberg, 2010; pp. 310–312. [Google Scholar] [CrossRef]
- Woolnough, J. How do students learn to apply their mathematical knowledge to interpret graphs in physics? Res. Sci. Educ. 2000, 30, 259–267. [Google Scholar] [CrossRef]
- Erceg, N.; Aviani, I. Students’ understanding of velocity-time graphs and the sources of conceptual difficulties. Croat. J. Educ. Hrvat. Časopis Odgoj. Obraz. 2014, 16, 43–80. [Google Scholar]
- Ergül, N.R. Pre-Service Science Teachers’ Construction and Interpretation of Graphs. Univers. J. Educ. Res. 2018, 6, 139–144. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).