On Some Properties of a Class of Eventually Locally Mixed Cyclic/Acyclic Multivalued Self-Mappings with Application Examples

Abstract

In this paper, a multivalued self-mapping is defined on the union of a finite number of subsets $p\left(\ge 2\right)$ of a metric space which is, in general, of a mixed cyclic and acyclic nature in the sense that it can perform some iterations within each of the subsets before executing a switching action to its right adjacent one when generating orbits. The self-mapping can have combinations of locally contractive, non-contractive/non-expansive and locally expansive properties for some of the switching between different pairs of adjacent subsets. The properties of the asymptotic boundedness of the distances associated with the elements of the orbits are achieved under certain conditions of the global dominance of the contractivity of groups of consecutive iterations of the self-mapping, with each of those groups being of non-necessarily fixed size. If the metric space is a uniformly convex Banach one and the subsets are closed and convex, then some particular results on the convergence of the sequences of iterates to the best proximity points of the adjacent subsets are obtained in the absence of eventual local expansivity for switches between all the pairs of adjacent subsets. An application of the stabilization of a discrete dynamic system subject to impulsive effects in its dynamics due to finite discontinuity jumps in its state is also discussed.

1. Introduction

There are abundant results on the best proximity points available in the background literature for different kinds of cyclic contractions and quasi-contractions. For instance, in [1], an important investigation is performed for 2-cyclic contractive self-mappings on the union of a set of non-empty, closed and convex subsets, which do not necessarily intersect at a uniformly convex Banach space. It is also found that the sequences built with the iterations of the self-mapping converge to unique best proximity points. On the other hand, an algorithm is provided to find the best proximity points in [2]. See also [3] for some related discussion on best proximity point results for some contractive mappings in uniform spaces. Some results on cyclic quasi-contractions and strong-quasi-contractions are given in [4,5,6,7,8,9] and some of the references therein. On the other hand, in [10], quasi non-expansive results for metric-like spaces were obtained. Additionally, best proximity point theorems for $p\left(\ge 2\right)$-cyclic Meir–Keeler contractions are given in [11] for uniformly convex Banach spaces. Sufficient-type conditions for the existence of a best proximity point and the convergence of sequences to it are also given in this paper. Furthermore, a useful notion of cyclic orbital Meir–Keeler contractions is given together with sufficient conditions for the existence of best proximity points and fixed points in [12]. This work generalizes previous results obtained in [13], which, in turn, generalizes some mentioned results of [1] to Meir–Keeler cyclic contractions. On the other hand, some general cyclic contraction mappings of the rational type are discussed in [14,15], including a particular study of the case when the involved subsets intersect. Additionally, the problem of the existence of best proximity point results in multivalued non-self-mappings is focused on in [16,17] by using optimization tools. In particular, this problem is investigated in [17] for contraction multivalued non-self-mappings in metric spaces as well as for non-expansive ones in Banach spaces which have an appropriate geometric property.

On the other hand, a solution of a Fredholm integral equation in b-metric-like spaces is found in [18] through the involvement of a particular of a technique based on the use of rational contractive mappings.

In [19], an existence and uniqueness result for a common solution of a second-order two-point boundary differential system based on the properties of the study’s newly introduced concept of cyclic $p$-contraction pairs. Additionally, best proximity results are proved in that paper concerned with mappings defined on proximally complete pairs of subsets of a metric space. This research extends a previous one reported in [20] on the proposed new concept of $p$-contractions. It is also proved in [20] that any $p$-contraction self-mapping possesses a unique fixed point in a complete metric space.

It is well-known that sometimes differential or difference dynamic systems can be subject to different parameterizations which describe the dynamical behavior around different operation points. When the parameterization of the differential system changes abruptly, there are discontinuities in the differential equations which describe the system dynamics. If the state has finite jump-type discontinuities, then the differential system is impulsive and vice-versa. See, for instance, [21]. Therefore, some typical control problems, such as, for instance, controllability or stabilization, become much more difficult to solve in the presence of either state discontinuities or impulsive controls at certain time instants. Some phenomena are sometimes associated with parameterization jumps or state discontinuities related to practical requirements. This often happens, for instance, in dynamics of chemical engineering processes along different phases of processing and monitoring a complete complex process or in discrete dynamic systems when the sampling rate is non-uniform, as in [22,23]. Therefore, the stabilization problem under either configurations or state switches has received important attention in the study of continuous-time, discrete-time, hybrid and time-delayed systems. Close problems often appear concerning the properties of the controllability and reachability of dynamic systems. See, for instance, [24,25,26,27,28] and some of the references therein as well as the recent works [29,30,31,32,33,34].

In this paper, we define and study a very general class of multivalued self-mappings defined on the union of a finite set of subsets of a metric space which is of a mixed cyclic and acyclic nature. The mixed nature is that the mappings can generate iterations in one of the subsets before eventual switching to their right adjacent one. The main purpose of defining and addressing such a mapping is to have in mind its potential application to the stabilization of dynamic systems submitted to state discontinuities in their state, which causes the differential systems of the equations which describe their dynamics to become impulsive at certain time instants.

The considered self-mapping has the following specific characteristics in the most general formal setting:

(a)

It is multivalued since it applies to each subset in the union set of itself with its right adjacent one and each domain point can have, in general, several image points in both such subsets;

(b)

It is of mixed cyclic and acyclic nature since it can perform several consecutive iterations within each of the subsets before switching to its right adjacent one;

(c)

The number of such consecutive iterations within each of the subsets before switching to its right adjacent one may vary dynamically around each cycle of complete running of the self-mapping on all the subsets. This fact facilitates the formal use of monitored iteration-dependent switches in stabilization applications;

(d)

It is not necessarily contractive between all the pairs of adjacent subsets of the configuration, although the most relevant properties are proved if the switches related to at least one of the pairs of adjacent subsets are contractive;

(e)

It can have also local non-expansive (being, furthermore, non-contractive) local properties between some of the pairs of adjacent subsets or even local expansive ones for some of the switches between the pairs of adjacent subsets;

(f)

The contractive, non-expansive or expansive constants associated with each of the subsets and in-between adjacent subsets which characterize the mapping are not necessarily identical and the distances between each pair of adjacent subsets are not necessarily identical either. Some of the results concerning the boundedness and the asymptotic boundedness of the distances between orbital points generated by the self-mapping iteration do not require specific conditions such as closeness or convexity on the involved subsets of the metric space or the uniform convexity of this one.

The paper is organized as follows. Section 2 gives a preliminary study for the mixed 2-cyclic/acyclic multivalued mapping (that is, being defined on two subsets of the metric space). The asymptotic boundedness of distances in the orbits from initial points in the union of sets are proved under certain global contractivity conditions of the whole mapping for groups of non-necessarily constant numbers of consecutive iterations. That property is proved without requiring that the involved subsets are closed. Section 3 extends and completes the former results for mixed $p\left(\ge 2\right)$-cyclic/acyclic multivalued mappings. Some specific related results are presented in Section 4 on the convergence of iterated sequences to best proximity points. The particular cases focused on in this section are that of the absence of local expansivity and the one of potential statement of monitored switching between adjacent subsets. Such a monitoring process is governed by a switching rule which operates in tandem with mixed $p$-cyclic/acyclic self-mapping and which establishes the iterations for switching between adjacent subsets to take place. Afterwards, some numerical examples concerned with an application for the stabilization of a discrete dynamic system subject to impulsive controls with monitored switching are discussed in Section 5. Finally, our conclusions end the paper.

Notation

$${\mathit{Z}}_{0+}=\left\{z\in \mathit{Z}:z\ge 0\right\}, {\mathit{Z}}_{+}=\left\{z\in \mathit{Z}:z>0\right\}, \overline{n}=\left\{1,2,\dots ,n\right\};$$

$${\mathit{R}}_{0+}=\left\{r\in \mathit{R}:r\ge 0\right\}, {\mathit{R}}_{+}=\left\{r\in \mathit{R}:r>0\right\};$$

• $cl\hspace{0.17em}A$ denotes the closure of a set $A$ and $cardA$ is the cardinal of the set $A$;
• if $T:{\displaystyle {\cup }_{i\in \overline{p}}{A}_i}\to {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ is multivalued then $Tx$ is the image set of $x\in {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ through $T$ which is, in particular, a singleton if $T$ is single-valued. In the same way, ${\left(Tx\right)}_i\subset A_i$ is the image set of $x$ in $A_i$ through $T$;
• distances between points and distances between sets under a metric $d:X\times X\to {\mathit{R}}_{0+}$ in a metric space $\left(X,d\right)$ are denoted with the same notation, i.e., $d\left(x,y\right)$ for $x,y\in X$ and $d\left(A,B\right)=\underset{x\in A,y\in B}{inf}d\left(x,y\right)$ for $A,B$ being subsets of $X$.

2. Problem Statement for Two Subsets of Metric Space

Following [1], we define the following concepts for non-empty subsets $A_1,A_2\subset X$, where $\left(X,d\right)$ is a metric space:

$$P_{A_i}\left(x\right)=\left\{y\in X:d\left(x,y\right)=d\left(x,A_i\right)\right\} \mathrm{for} i=1,2$$

$$D=d\left(A_1,A_2\right)=inf\left\{d\left(x,y\right):x\in A_1,y\in A_2\right\}$$

$$A_{01}=\left\{x\in A_1:d\left(x,y\right)=D\hspace{0.17em}\mathrm{for}\hspace{0.17em}\mathrm{some}\hspace{0.17em}y\in A_2\right\}$$

$$A_{02}=\left\{y\in A_2:d\left(x,y\right)=D\hspace{0.17em}\mathrm{for}\hspace{0.17em}\mathrm{some}\hspace{0.17em}x\in A_1\right\}$$

Thus, $P_{A_1}\left(A_{02}\right)=\left\{y\in X:d\left(A_{02},y\right)=d\left(A_{02},A_1\right)\right\}$ and $P_{A_2}\left(A_{01}\right)=\left\{y\in X:d\left(A_{01},y\right)=d\left(A_{01},A_2\right)\right\}$. Note that, for the sake of simplicity, the distances between sets and the distances from a point to a set via the $d$-metric are referred to with the same notation $d\left(.,.\right)$ as the one used for distance between points. The sets of best proximity points $A_{01}\subseteq A_1$ and $A_{02}\subseteq A_2$ are non-empty if $A_1$ is compact and $A_2$ is approximatively compact with respect to $A_1$, that is, every sequence ${\left\{x_n\right\}}_{n=0}^{\infty }\subset A_2$, such that $d\left(y,x_n\right)\to d\left(y,A_2\right)$ as $n\to \infty$ for some $y\in A_1$, has a convergent subsequence. It can be pointed out that there are examples where $A_{02}$ or $B_{02}$ may be empty even if $A_1$ and $A_2$ are non-empty. See, for instance, [2,3]. The following definition is quoted from the cyclic mappings in [1,2,3,4,5,6,7,8,9,10,11,12,13] and renamed “ad hoc” by indicating with “2” the particular cyclic context involving just two subsets of the metric space and the contraction constant.

Definition 1

([3,4,5,6]). Let $A_1$ and $A_2$ non-empty subsets of a metric space $\left(X,d\right)$ and let $T:A_1\cup A_2\to A_1\cup A_2$, such that $D=d\left(A_1,A_2\right)$, and $T\left(A_1\right)\subseteq A_2$ and $T\left(A_2\right)\subseteq A_1$. Then, $T$ is said to be a $2$-cyclic contraction if, for all $x\in A_1$ and $y\in A_2$ and some $k\in \left[0,1\right)$,

$$d\left(Ty,Tx\right)\le k\hspace{0.17em}d\left(y,x\right)+\left(1-k\right)D$$

(1)

In the same way, if$k=1$then$d\left(Tx,Ty\right)\le d\left(x,y\right)$and$T:A_1\cup A_2\to A_1\cup A_2$is non-expansive and if$d\left(Tx,Ty\right)>d\left(x,y\right)$, then$T:A_1\cup A_2\to A_1\cup A_2$is expansive.

We now investigate some properties of boundedness and convergence of sequences of a multi-valued self-mapping $T:A\to A$, where $A=A_1\cup A_2$ with non-empty sets $A_1$ and $A_2$ being subsets of a metric space $\left(X,d\right)$. Note that self-mapping $T:A\to A$ is not, in general, cyclic since the constraints $T\left(A_1\right)\subseteq A_2$ and $T\left(A_2\right)\subseteq A_1$ do not hold in such a way that each generated sequence through $T$ from any initial point in $A$ can have several successive iterated points in either $A_1$ or $A_2$ before switching either to $A_2$ or to $A_1$. Therefore, the mapping is mixed cyclic and acyclic. Assume through the manuscript that $T:A\to A$ satisfies the subsequent stipulations for $x,y\in A$:

$$Tx=\left\{{\left(Tx\right)}_1,{\left(Tx\right)}_2\right\}; {\left(Tx\right)}_i\left(\ne \varnothing \right)\subset A_i \mathrm{for} i=1,2; \forall x\in A$$

(2)

$$k_0\hspace{0.17em}d\left(y,x\right)\le d\left(x{{}^{\prime }}_1,y{{}^{\prime }}_1\right)=d\left({\left(Ty\right)}_1,{\left(Tx\right)}_1\right)\le k_1\hspace{0.17em}d\left(y,x\right)$$

(3)

for some $k_0,k_1\left(\ge k_0\right)>1$ if $x,y\in A_1$ for some $x{{}^{\prime }}_1\in {\left(Tx\right)}_1,y{{}^{\prime }}_1\in {\left(Ty\right)}_1$,

$$d\left(x{{}^{\prime }}_2,y{{}^{\prime }}_2\right)=d\left({\left(Ty\right)}_2,{\left(Tx\right)}_2\right)\le k_2\hspace{0.17em}d\left(y,x\right)$$

(4)

for some $k_2\in \left[0,1\right)$ if $x,y\in A_2$ for some $x{{}^{\prime }}_2\in {\left(Tx\right)}_2,y{{}^{\prime }}_2\in {\left(Ty\right)}_2$,

$$d\left(x{{}^{\prime }}_3,y{{}^{\prime }}_3\right)=d\left({\left(Ty\right)}_2,{\left(Tx\right)}_1\right)\le k_{12}\hspace{0.17em}d\left(y,x\right)+\left(1-k_{12}\right)D$$

(5)

for some $k_{12}\in \left[0,1\right]$ if $x,y\in A_1$ for some $\left(x{{}^{\prime }}_3,y{{}^{\prime }}_3\right)\in {\left(Tx\right)}_1\times {\left(Ty\right)}_2\cup {\left(Tx\right)}_2\times {\left(Ty\right)}_1$ provided that $d\left(x,y\right)\ge D$,

$$d\left(x{{}^{\prime }}_4,y{{}^{\prime }}_4\right)=d\left({\left(Ty\right)}_1,{\left(Tx\right)}_2\right)\le k_{21}\hspace{0.17em}d\left(y,x\right)+\left(1-k_{21}\right)D$$

(6)

for some $k_{21}\in \left[0,1\right]$ if $x,y\in A_2$ for some $\left(x{{}^{\prime }}_4,y{{}^{\prime }}_4\right)\in {\left(Tx\right)}_1\times {\left(Ty\right)}_2\cup {\left(Tx\right)}_2\times {\left(Ty\right)}_1$ provided that $d\left(x,y\right)\ge D$,

$$d\left(x{{}^{\prime }}_5,y{{}^{\prime }}_5\right)=d\left({\left(Ty\right)}_1,{\left(Tx\right)}_2\right)\le k_{c}d\left(y,x\right)+\left(1-k_c\right)D$$

(7)

for some $k_c\in \left[0,1\right]$ if $\left(x,y\right)\in A_1\times A_2\cup A_2\times A_1$ for some $\left(x{{}^{\prime }}_5,y{{}^{\prime }}_5\right)\in {\left(Tx\right)}_1\times {\left(Ty\right)}_2\cup {\left(Tx\right)}_2\times {\left(Ty\right)}_1$.

Then, given $\left(x,y\right)\in A\times A$, we can choose $\left(x{}^{\prime },y{}^{\prime }\right)\in {\left(Tx\right)}_i\times {\left(Tx\right)}_j\subset Tx\times Ty\subset A_1\times A_2\cup A_2\times A_1$ for $i,j=1,2$, which satisfies one of the inequalities (3) to (6). The constraint (2) implies that each point in $A$ has at least one image in $A_1$ and one image in $A_2$ through $T:A\to A$.

It is also assumed in the sequel that the best proximity sets of $A_i$ with respect to $A_j$; $i,j\left(\ne i\right)=1,2$ are non-empty, that is, $A_{0j}=\left\{x\in A_j:d\left(x,y\right)=D\hspace{0.17em}\mathrm{for}\hspace{0.17em}\mathrm{some}\hspace{0.17em}y\in A_i;\hspace{0.17em}i,j\left(\ne i\right)=1,2\right\}\ne \varnothing$; $j=1,2$.

The following technical assumption is made through the manuscript:

Assumption 1.

The metric$d:X\times X\to {\mathit{R}}_{0+}$of the metric space$\left(X,d\right)$is assumed to be homogeneous.

The above assumption is not necessary for the whole set of obtained results, in particular, for those referred to the upper-bounds of the distances associated with the mappings through the iterated calculations. However, it facilitates some of the mathematical proofs, in particular, those referred to excluding potential asymptotic unboundedness of distances from the implication that bounded distances can imply that of the sequences of points of $X$ involved in the calculations of such distances. In particular, it can be pointed out that homogeneous and translation-invariant distances are norm-induced distances. A metric is said to be homogeneous if $d\left(\alpha x,\alpha y\right)=\left|\alpha \right|d\left(x,y\right)$ for $\alpha \in \mathit{R}$ and $\forall x,y\in X$. It is said to be translation-invariant if $d\left(x+z,y+z\right)=d\left(x,y\right)$; $\forall x,y,z\in X$ properties are jointly fulfilled, for instance, by norm-induced metrics on linear or vector spaces $X$ since:

$$d\left(\alpha \left(x+z\right),\alpha \left(y+z\right)\right)=\left|\alpha \right|‖x+z-\left(y+z\right)‖=\left|\alpha \right|d\left(x,y\right)=\left|\alpha \right|‖x-y‖; \forall x,y,z\in X, \alpha \in \mathit{R}.$$

Typical widely-used metrics in applications such as, for instance, Euclidean and taxi-cab metrics fulfill those joint properties. Note also that the property that distances can asymptotically grow, leading to infinity limits (if some of the involved sequence of the points of $X$ involved in their calculations is unbounded), is intuitively attractive and very useful in practical problems. This property is fulfilled by many usual distances, such as Euclidean distance, taxi-cab distance, Minkowski’s distance and others, but it is not inherent to the definition of distance. For instance, the discrete metric is never unbounded, irrespective of the involved pairs of points, since it is not greater than unity by definition. However, a homogenous distance is characterized by the property $d\left(\alpha x,\alpha y\right)=\left|\alpha \right|d\left(x,y\right)$ so that $d\left(\alpha x,y\right)=\left|\alpha \right|d\left(x,y/\left|\alpha \right|\right)\to \left|\alpha \right|d\left(x,0\right)=\left|\alpha \right|‖x‖$ and to infinity as $\alpha \to \pm \infty$. Note that homogeneous distances are termed as absolutely homogeneous distances in some of the background literature.

Remark 1.

The above constraints (2)–(7) imply that the mapping is expansive on$A_1$, contractive on$A_2$and cyclic contractive for switchings between both sets if both$k_{ij}\in \left[0,1\right)$. If$k_{ij}=1$, then the switching from$A_i$to$A_j$when building the iteration step is not necessarily contractive, but it is non-expansive. Note that$d\left(T^{i+2}x,T^{i+1}x\right)=\underset{1\le i,j\le 2}{min}d\left({\left(T^{i+1}x\right)}_i,{\left(T^{i+1}x\right)}_j\right)$;$\forall i\in {\mathit{Z}}_{0+}$;$j,k=1,2$for any$x\in A$. In particular, (3) is expansive, which applies to the images in$A_1$of$T:A\to A$of the couples of the points$x,y$in$A_1$, while (4) is a contraction which applies to the images in$A_2$of$T:A\to A$of the couples of the points$x,y$in$A_2$. Equation (5) is non-expansive, since$k_{12}\le 1$, in particular, contractive if$k_{12}<1$, for the images of two points$x,y$in$A_1$, which are one in$A_1$and the other one in$A_2$. In the same way, the non-expansive (6) applies for images of the two points$x,y$in$A_2$, which are one in$A_1$and the other one in$A_2$. Finally, (7) is a non-expansive or contractive rule which applies to points$x,y$, each in one of the sets$A_1$and$A_2$with images each in one of the sets but not necessarily alternated with respect to each of the original points. In the particular case that the images are alternated, the mapping is also cyclic according to (7).

Remark 2.

The various orbits$O\left(x_0\right)=\left\{x_0,x_1,x_2,\dots \right\}$of initial point$x_0\in A$might be generated according to$x_{i+1}\in {\left(T{x}_i\right)}_j\subset T{x}_i\subset T^{i+1}{x}_0$for some$j\in \left\{1,2\right\}$,$\forall i\in {\mathit{Z}}_{0+}$with$T:A\to A$being subject to one of the stipulations (2)–(7) for each successive iteration.

Note from (5) and (6) that if$x,y\in A_1$or if$x,y\in A_2$, then switches of$T:A\to A$the form$\left(Tx,Ty\right)\in A_1\times A_2$do not take place if$d\left(x,y\right)<D$, implying that both$x$and$y$are either in$A_1$or in$A_2$, since, in this case, (5) and (6) would lead to the contradiction$d\left(Tx,Ty\right)<D$if$k_{12}\in \left(0,1\right]$or, respectively,$k_{21}\in \left(0,1\right]$. In order to also allow switchings of$T:A\to A$when$d\left(x,y\right)<D$(requiring necessarily$x,y\in A$or$x,y\in B$) so that the constraint$d\left(x,y\right)\ge D$is removed from (5) and (6) while keeping$T:A\to A$to be non-expansive at$\left(x,y\right)$, except if$d\left(x,y\right)<D$, the stipulations (5) and (6) on$T:A\to A$can be changed to the following ones:

$$\begin{array}{c}\left[\left(\left(x,y\right)\in A\right)\wedge \left(\left({\left(Tx\right)}_1,{\left(Ty\right)}_2\right)\in A_1\times A_2\right)\wedge \left(d\left(x,y\right)\ge D\right)\right]\Rightarrow d\left({\left(Ty\right)}_2,{\left(Tx\right)}_1\right)\le k_{12}d\left(y,x\right)+\left(1-k_{12}\right)D\\ \mathrm{for} \mathrm{some} k_{12}\in \left[0,1\right]\end{array}$$

(8)

$$\begin{array}{c}\left[\left(\left(x,y\right)\in A\right)\wedge \left(\left({\left(Tx\right)}_2,{\left(Ty\right)}_1\right)\in A_2\times A_1\right)\wedge \left(d\left(x,y\right)\ge D\right)\right]\Rightarrow d\left({\left(Ty\right)}_1,{\left(Tx\right)}_2\right)\le k_{21}d\left(y,x\right)+\left(1-k_{21}\right)D\\ \mathrm{for} \mathrm{some} k_{21}\in \left[0,1\right]\end{array}$$

(9)

$${\left[\left(\left(x,y\right)\in A\right)\wedge \left(\left(x{}^{\prime },y{}^{\prime }\right)\in Tx\times Ty\right)\wedge \left(d\left(x,y\right)<D\right)\right]}^{}\Rightarrow {\left[\left(x{}^{\prime },y{}^{\prime }\right)\in {\left(Tx\right)}_1\times {\left(Tx\right)}_2\cup \left(T{x}_2\right)\times {\left(Tx\right)}_1\right]}^{}$$

(10)

Note that, since$d\left(x,y\right)<D$implies that both$Tx$and$Ty$are in the same subset$A_1$or$A_2$, Equation (9) is identically expressed as follows:

$$\left[\left(\left(x,y\right)\in A_1\times A_1\cup A_2\times A_2\right)\wedge \left(\left(Tx,Ty\right)\in A_1\times A_2\cup A_2\times A_1\right)\wedge \left(d\left(x,y\right)<D\right)\right]\Rightarrow d\left(Ty,Tx\right)\ge D.$$

In the following, the main results are conducted under the stipulations (2)–(6) for the sake of exposition simplicity. Let us denote the sequel $K_i$ as the $i$-iteration constant for a sequence generated from any initial point in $A$ and which can take any of the values $k_1$, $k_2$, $k_{12}$ and $k_{21}$. Then, the following result holds for boundedness and convergence of distances between iterates of an orbit $O\left(x_0\right)=\left(x_0,x_1,x_2,\dots \right)$ of $x_0\in A$ for some sequence ${\left\{x_{i+1}\left(\in T{x}_i\right)\right\}}_{i=0}^{\infty }$; $\forall i\in {\mathit{Z}}_{0+}$.

Theorem 1.

Consider the orbits$O\left(x_0\right)=\left\{x_0,x_1,x_2,\dots \right\}$of$x_0\in A=A_1\cup A_2$generated according to$x_{i+1}\in {\left(T{x}_i\right)}_j\subset T{x}_i\subset T^{i+1}{x}_0$for some$j\in \left\{1,2\right\}$,$\forall i\in {\mathit{Z}}_{0+}$with$T:A\to A$being subject to the stipulations (2)–(7). Then, the following properties hold:

(i) 

$$d\left(x_{i+1},x_i\right)\le K\left(i,1\right)d\left(x_0,x_1\right)+M\left(i,1\right)\le K\left(i,1\right)d\left(x_0,x_1\right)+\left(1-K\left(i,1\right)\right)D; \forall i\in {\mathit{Z}}_{+}$$

(11)

where

$$K\left(i,1\right)={\displaystyle {\prod }_{k=1}^i\left[K_k\right]}; M\left(i,1\right)={\displaystyle {\sum }_{k=1}^i\left({\displaystyle {\prod }_{\ell =k+1}^i\left[K_{\ell }\right]}\right)}{M}_k; \forall i\in {\mathit{Z}}_{+}$$

(12)

where:

(a) 

$K_i=k_j$and$M_i=0$if$x_i,x_{i+1}\in A_j$;$j=1,2$,

(b) 

$K_i=k_{\ell j}$and$M_i=\left(1-k_{\ell j}\right)D$if$x_i,x_{i+1}\in A_j$and$\left(x_{i+1},x_i\right)\in {\left(T{x}_i\right)}_j\times {\left(T{x}_{i-1}\right)}_{\ell }\subset A_j\times A_{\ell }$;$\ell ,j\left(\ne \ell \right)\in \left\{1,2\right\}$,

(c) 

$K_i=k_c$and$M_i=\left(1-k\right)D$if$\left(x_{i-1},x_i\right)\in A_1\times A_2\cup A_2\times A_1$and$\left(x_{i+1},x_i\right)\in {\left(T{x}_i\right)}_1\times {\left(T{x}_{i-1}\right)}_2\cup {\left(T{x}_{i-1}\right)}_2\times {\left(T{x}_i\right)}_1\subset A_1\times A_2\cup A_2\times A_1$.

(ii) 

If Assumption 1 holds, then${\left\{d\left(x_{i+1},x_i\right)\right\}}_{i=0}^{\infty }$is bounded for$x_0\in A$such that$d\left(x_0,x_1\right)$is finite and

$$max\left\{\underset{i\in {\mathit{Z}}_{+}}{sup}\hspace{0.17em}K\left(i,1\right),\underset{i\in {\mathit{Z}}_{+}}{sup}\hspace{0.17em}M\left(i,1\right)\right\}<+\infty ; max\left\{\underset{i\to \infty }{lim sup}\hspace{0.17em}K\left(i,1\right),\underset{i\to \infty }{lim sup}\hspace{0.17em}M\left(i,1\right)\right\}<+\infty$$

(13)

(iii) 

If Assumption 1 holds and$d\left(x_0,x_1\right)$is finite, then${\left\{d\left(x_{i+1},x_i\right)\right\}}_{i=0}^{\infty }$is bounded if it does not exist, a strictly increasing sequence of positive integers${\left\{N_k\right\}}_{k=1}^{\infty }$with$N_1$finite such that$d\left(x_{N_{k+1}},x_{N_k}\right)>d\left(x_{N_k+1},x_{N_k}\right)$;$\forall N_j\in {\left\{N_j\right\}}_{j=1}^{\infty }$. Otherwise, if one such a sequence${\left\{N_k\right\}}_{k=1}^{\infty }$exists, then${\left\{d\left(x_{i+1},x_i\right)\right\}}_{i=0}^{\infty }$is unbounded.

(iv) 

Under Assumption 1, assume that$d\left(x_0,x_1\right)$is finite. Then${\left\{d\left(x_{i+1},x_i\right)\right\}}_{i=0}^{\infty }$is bounded if the following constraints hold:

(C1) it exists a finite set or a sequence${\left\{N_k\right\}}_{k=1}^{\chi }\subset {\mathit{Z}}_{+}$, with$N_1$being finite and$1\le \chi \le \infty$such that

(C1a) the incremental sequence${\left\{N_{k+1}-N_k\right\}}_{k=1}^{\chi -1}$is bounded if$\chi \le \infty$, and$N_{\chi }-N_{\chi -1}$is bounded if$\chi <\infty$, while$N_{\chi }-N_{\chi -1}$is infinity if$\chi =\infty$(implying that$N_{\chi }=\infty$) and

$$\left(C1b\right)\hspace{0.17em}M\left(N_{k+1},N_k\right)\le \left(1-K\left(N_{k+1},N_k\right)\right)D\le \left(1-K\left(N_{k+1},N_k\right)\right)d\left(x_{N_k+1},x_{N_k}\right); \forall k\in \overline{\chi }$$

(14)

under the necessary condition$K\left(N_{k+1},N_k\right)\le 1$;$\forall k\in \overline{\chi }$. A sufficient condition for (14) to hold if$D\ne 0$is

$$M\left(N_{k+1},N_k\right)/D\le 1-K\left(N_{k+1},N_k\right); \forall k\in \overline{\chi }$$

(15)

where

$$K\left(N_{k+1},N_k\right)={\displaystyle {\prod }_{j=N_k}^{N_{k+1}}\left[K_j\right]}; M\left(N_{k+1},N_k\right)={\displaystyle {\sum }_{i=N_k}^{N_{k+1}}\left({\displaystyle {\prod }_{\ell =N_k+1}^{N_{k+1}}\left[K_{\ell }\right]}\right)}{M}_i; \forall k\in \overline{\chi }$$

(16)

(C2) Furthermore, if$\chi <\infty$then${\left\{T^{i}x\right\}}_{i\ge N_{\chi }+m}\subset A\cup B_0$for some positive integer$m$.

(v) 

If$d\left(x_0,x_1\right)$is finite for a given$x_0\in A_2,x_1\in {\left(T{x}_0\right)}_2\subset A_2$and$x_{i+1}\in {\left(T{x}_i\right)}_2\subset {\left(T^{i+1}{x}_0\right)}_2\subset A_2$;$\forall i\in {\mathit{Z}}_{0+}$then${\left\{d\left(x_{i+1},x_i\right)\right\}}_{i=0}^{\infty }$is bounded and$d\left(x_{i+1},x_i\right)\to 0$as$i\to \infty$. The same property holds for the sequence of distances between consecutive points on an orbit$O\left(x_0\right)=\left\{x_0,x_1,\dots ,x_N,x_{N+1},\dots \right\}$if$x_0\in A_2$is such that$d\left(x_0,{\left(T{x}_0\right)}_2\right)$is finite with$x_i\in {\left(T^i{x}_0\right)}_1\cup {\left(T^i{x}_0\right)}_2$for$i\in N$and$x_i\in {\left(T^i{x}_0\right)}_2$;$\forall i\left(>N\right)\in {\mathit{Z}}_{0+}$for some finite nonnegative integer$N$.

Proof. 

One obtains from (2)–(7) that

$$d\left(y_i,x_i\right)=d\left({\left(T^i{y}_0\right)}_j,{\left(T^i{x}_0\right)}_k\right)\le K_{i}d\left(y_{i-1},x_{i-1}\right)+M_i; \forall i\in {\mathit{Z}}_{+}; \forall x,y\in A; j,k=1,2$$

(17)

where $T^0$ is the identity map and

(1)

$K_i=k_j$ and $M_i=0$ if $x_{i-1}\in {\left(T{x}_{i-2}\right)}_j\subset {\left(T^{i-1}{x}_0\right)}_j\subset A_j,y_{i-1}\in {\left(T{y}_{i-2}\right)}_j\subset {\left(T^{i-1}{y}_0\right)}_j\subset A_j$ with $x_i\in {\left(T{x}_{i-1}\right)}_j\subset {\left(T^i{x}_0\right)}_j\subset A_j,y_i\in {\left(T{y}_{i-2}\right)}_j\subset {\left(T^i{y}_0\right)}_j\subset A_j$ for some $j=1,2$.

(2)

$K_i=k_{\ell j}$ and $M_i=\left(1-k_{\ell j}\right)D$ if $x_{i-1}\in {\left(T{x}_{i-2}\right)}_j\subset {\left(T^{i-1}{x}_0\right)}_j\subset A_j,y_{i-1}\in {\left(T{y}_{i-2}\right)}_j\subset {\left(T^{i-1}{y}_0\right)}_j\subset A_j$ for some $j=1,2$ with $\left(x_i,y_i\right)\in {\left(T^i{x}_0\right)}_1\times {\left(T^i{y}_0\right)}_2\cup {\left(T^i{x}_0\right)}_2\times {\left(T^i{y}_0\right)}_1\subset A_1\times A_2\cup A_2\times A_1$

(3)

$K_i=k_c$ and $M_i=\left(1-k\right)D$ if $\left(x_{i-1},y_{i-1}\right)\in {\left(T{x}_{i-2}\right)}_1\times {\left(T{y}_{i-2}\right)}_2\cup {\left(T{x}_{i-2}\right)}_2\times {\left(T{y}_{i-2}\right)}_1\subset A_1\times A_2\cup A_2\times A_1$ with $\left(x_i,y_i\right)\in {\left(T{x}_{i-1}\right)}_1\times {\left(T{y}_{i-1}\right)}_2\cup {\left(T{x}_{i-1}\right)}_2\times {\left(T{y}_{i-1}\right)}_1\subset {\left(T^i{x}_0\right)}_1\times {\left(T^i{y}_0\right)}_2\cup {\left(T^i{x}_0\right)}_2\times {\left(T^i{y}_0\right)}_1\subset A_1\times A_2\cup A_2\times A_1$

In the same way, one obtains by taking $y_0\in T{x}_0$,

$$\begin{array}{c}d\left(x_{i+1},x_i\right)=d\left({\left(T^{i+1}{x}_0\right)}_j,{\left(T^i{x}_0\right)}_k\right)\le K_{i}d\left(x_i,x_{i-1}\right)+M_i=K_{i}d\left(x_{i-1},{\left(T{x}_{i-1}\right)}_k\right)+M_i;\\ \forall x_0\in A, \forall i\in {\mathit{Z}}_{+}; j,k=1,2\end{array}$$

(18)

where $x_i\in {\left(T^i{x}_0\right)}_k$ and $x_{i+1}\in {\left(T^{i+1}{x}_0\right)}_j$ for $j,k\in \left\{1,2\right\}$ and $M_i=0$ and $K_i=k_j$ if $j=k$ and $M_i=\left(1-k_{kj}\right)D$ or $M_i=\left(1-k_{jk}\right)D$ or $M_i=\left(1-k_c\right)D$ if $j\ne k$ in view of (5)–(7) depending on the allocations in $A_1$ or in $A_2$ of the images of the original points and on the fact that those original points are in the same or in distinct sets $A_1$ or $A_2$ according to (5)–(7). Then, one obtains recursively from (17) that:

$$\begin{array}{c}d\left(y_i,x_i\right)\le K_i\left(K_{i-1}d\left(y_{i-2},x_{i-2}\right)+M_{i-1}\right)+M_i\\ =K_i\left(K_{i-1}d\left({\left(T^{i-1}y\right)}_j,{\left(T^{i-1}x\right)}_k\right)+M_{i-1}\right)+M_i\end{array}$$

(19)

$$\begin{array}{c}\Rightarrow d\left(y_i,x_i\right)\le K_i\left(i,i-1\right)d\left(y_{i-2},x_{i-2}\right)+M\left(i,i-1\right)\\ \le \dots \le K\left(i,1\right)d\left(x_0,y_0\right)+M\left(i,1\right); \forall x_0,y_0\in A, i\in {\mathit{Z}}_{+}; j,k=1,2\end{array}$$

(20)

with $K\left(i,i-1\right)=K_i{K}_{i-1}$ and $M\left(i,i-1\right)=K_{i-1}{M}_{i-1}+M_i$ and one obtains (11), from (20) via (14), by taking $y_0=x_1\in {\left(T{x}_0\right)}_j$, some $j\in \left\{1,2\right\}$. Then, properties (i) and (ii) follow directly. Property (iii) is direct since if ${\left\{N_j\right\}}_{j=1}^{\infty }$ exists with $d\left(x_{N_{k+1}+1},x_{N_k}\right)>d\left(x_{N_k+1},x_{N_k}\right)$, then ${\left\{d\left(x_{i+1},x_i\right)\right\}}_{i=0}^{\infty }$ is unbounded since it has one strictly increasing subsequence ${\left\{d\left(x_{N_k+1},x_{N_k}\right)\right\}}_{k=0}^{\infty }$. Otherwise, if no such a sequence ${\left\{N_j\right\}}_{j=0}^{\infty }$ exists such that $d\left(x_{N_{k+1}+1},x_{N_k}\right)>d\left(x_{N_k+1},x_{N_k}\right)$, then ${\left\{d\left(x_{i+1},x_i\right)\right\}}_{i=0}^{\infty }$ is bounded if $d\left(x_0,x_1\right)=d\left(x_0,{\left(T{x}_0\right)}_j\right)$ is finite for some $x_1\in {\left(T{x}_0\right)}_j$ and some $j\in \left\{1,2\right\}$, being the second point of the orbit of $x_0$ since all its subsequences are bounded. To prove property (iv), note that if ${\left\{d\left(x_{i+1},x_i\right)\right\}}_{i=0}^{\infty }$ is bounded, then it has (at least) a finite maximum $d\left(x_{N_1+1},x_{N_1}\right)$ at a finite iteration step $N_1$. If such a maximum is zero, then the sequence is identically zero and the proof follows directly. Assume now that $d\left(x_{N_1+1},x_{N_1}\right)$, while it also has to exist that either a finite set or an infinity sequence of nonnegative integers ${\left\{N_k\right\}}_{k=1}^{\chi }\subset {\mathit{Z}}_{+}$ $1\le \chi \le \infty$, with the incremental sequence ${\left\{N_{k+1}-N_k\right\}}_{k=1}^{\chi }$ being bounded if $\chi =\infty$ and ${\left\{N_{k+1}-N_k\right\}}_{k=1}^{\chi -1}$ being bounded and $N_{\chi }=\infty$, is bounded if $\chi <\infty$ so that

$$\begin{array}{c}d\left(x_{N_{k+1}+1},x_{N_k}\right)\le K\left(N_{k+1},N_k\right)d\left({\left(T^{N_{k+1}}{x}_0\right)}_j,{\left(T^{N_k}{x}_0\right)}_{\ell }\right)+M\left(N_{k+1},N_k\right)\le d\left(x_{N_k+1},x_{N_k}\right)\\ \le d\left(x_{N_1+1},x_{N_1}\right)=\underset{i\in {\mathit{Z}}_{0+}}{max}\left(d\left(x_0,x_1\right)\right); \forall k\in \overline{\chi }\end{array}$$

(21)

for some $j,\ell \in \left\{1,2\right\}$ since $d\left(x_{N_1+1},x_{N_1}\right)$ is the finite maximum of consecutive distances between points of the orbit $O\left(x_0\right)=\left\{x_0,x_1,x_2,\dots \right\}$ of the initial point $x_0$, where $K\left(N_{k+1},N_k\right)$ and $M\left(N_{k+1},N_k\right)$ are defined in (17). In order that (21) holds, the following constraint is required:

$$M\left(N_{k+1},N_k\right)\le \left(1-K\left(N_{k+1},N_k\right)\right)d\left(x_{N_{}+1},x_{N_k}\right); \forall k\in \overline{\chi }$$

(22)

Since $M\left(N_{k+1},N_k\right)\ge 0$ with $M\left(N_{k+1},N_k\right)=0$ if and only if $D=0$, that is, if and only if $cl\hspace{0.17em}{A}_1\cap cl\hspace{0.17em}{A}_2=\varnothing$; $\forall k\in \overline{\chi }$ and then (22) also holds under the stronger condition:

$$M\left(N_{j+1},N_j\right)\le \left(1-K\left(N_{j+1},N_j\right)\right)D\le \left(1-K\left(N_{j+1},N_j\right)\right)d\left(T^{N_j+1}x,T^{N_j}x\right); \forall j\in \overline{\chi -1}$$

(23)

then, if $K\left(N_{k+1},N_k\right)\le 1$; $\forall k\in \overline{\chi }$ and, furthermore, $M\left(N_{k+1},N_k\right)/D\le 1-K\left(N_{k+1},N_k\right)$; $\forall j\in \overline{\chi }$ if $D\ne 0$. Property (iv) has been proved. The proof of property (v) follows directly from property (iv) since there is no switch from $A_2$ to $A_1$, then $K\left(i,1\right)=k_2^i<1$, $M\left(i,1\right)=0$; $\forall i\in {\mathit{Z}}_{+}$, $K\left(i,1\right)\to 0$ as $i\to \infty$. The same property also holds for any orbit which does not contain points of the mapping iterates in $A_2$, after some finite number of iterations, for any given initial point $x_0$ in $A$ such that $d\left(x,{\left(Tx\right)}_2\right)$ is finite generates the sequence. □

Remark 3.

For the distance sequences generated from any finite initial point$x_0\in A_1\cup A_2$, some intuitive consequences of Theorem 1 are:

(1) 

It is not relevant that the sets$A_1$and$A_2$be necessarily either bounded or closed for the eventual boundedness of any iterated sequence of distances generated from any point$x_0\in A_1\cup A_2$such that$d\left(x_0,x_1\right)=d\left(x_0,{\left(T{x}_0\right)}_j\right)$is finite for some$x_1\in {\left(T{x}_0\right)}_j$and some$j\in \left\{1,2\right\}$. This is an “a priori” hypothesis, equivalent in fact to the initial distance to be defined in order to give conditions for the sequence of distances between consecutive iterates not to be unbounded.

(2) 

The distance sequences is unbounded if$x_0\in A_1$and$T\left(A_1\right)\subseteq A_1$, i.e., all the iterations are in$A_1$from (3) since, from (14),$K\left(i,1\right)=k_1^i>1$and$M\left(i,1\right)=0$;$\forall i\in {\mathit{Z}}_{+}$and$K\left(i,1\right)\to \infty$as$i\to \infty$. The same happens if all the iterations are in$A_1$after a finite iteration step$N$.

(3) 

The distance sequence is bounded and convergent to zero if$x_0\in A_2$and$T\left(A_2\right)\subseteq A_2$, i.e., all the iterations are in$A_2$from (4) since, from (14),$K\left(i,1\right)=k_2^{i1}<1$and$M\left(i,1\right)=0$;$\forall i\in {\mathit{Z}}_{+}$and$K\left(i,1\right)\to 0$as$i\to \infty$. The same happens if all the iterations are in$A_2$after a finite step$N$.

(4) 

The distance sequence is bounded if, after some finite iteration step$N$, each member alternates switches iteration-to-iteration from$A_1$to$A_2$and from$A_2$to$A_1$since the distance is bounded after the finite number$N$of iterations prior to the first switching (if the initial generating point$x_0^{}$is such that$d\left(x_0,x_1\right)$is finite) and since the mapping$T:A_1\cup A_2\to A_1\cup A_2$is both non-expansive and cyclic for the successive iterations$i>N$from (5) and (6) since$k_{ij}\le 1$for$i,j=1,2$so that

$$\begin{array}{c}D\le d\left(x_{i+1},x_i\right)=d\left(x_i,{\left(T{x}_i\right)}_j\right)=d\left({\left(T{x}_{i-1}\right)}_k,{\left(T{x}_i\right)}_j\right)\le d\left(x_i,x_{i-1}\right)=d\left({\left(T{x}_{i-1}\right)}_k,x_{i-1}\right)\ge D\\ x_{i+1}\in {\left(T{x}_i\right)}_j, x_i\in \left(T{x}_{i-1}\right), \forall x_0\in A, j,k\left(\ne j\right)\in \left\{1,2\right\},i\left(>N\right)\in {\mathit{Z}}_{+}.\end{array}$$

(5) 

In order for (15) to hold for some sequence${\left\{N_k\right\}}_{k=1}^{\chi }\subset {\mathit{Z}}_{+}$with$N_1$finite,$1\le \chi \le \infty$, with the incremental sequence${\left\{N_{k+1}-N_k\right\}}_{k=1}^{\chi }$being bounded such that the distance sequence boundedness conditions (15) or (16) hold, it is sufficient that:

(a) 

either the mapping becomes cyclic after a finite number of steps (see the above Remark 3(4)), or

(b) 

it remains confined to iterations within$A_2$after a finite number of steps or, if there are non-successive switches from$A_1$to$A_2$and from$A_2$to$A_1$, then switches are ruled to satisfy the conditions (15) or (16) of Theorem 1 (iv).

(6) 

The condition C2 of Theorem 1(iv),${\left\{T^i{x}_0\right\}}_{i\ge N_{\chi }+m}\subset A_2\cup A_{01}$if$\chi <\infty$, means that, after a finite number of iterations, the successive iterates only are in$A$or in the best proximity set of$A_1$with respect to$A_2$. In other words, if infinitely many iterates of$\left\{T^i{x}_0\right\}$are alternated in$A_2$and$A_1\backslash A_{01}$, then$\chi =\infty$, that is, the sequence${\left\{N_k\right\}}_{k=1}^{\chi }$is infinite to ensure the boundedness of the distance sequence.

The following result gives explicit conditions on particular conditions for successive iterates for Theorem 1 (iv) to hold:

Proposition 1.

Under Assumption 1, assume also that$d\left(x_0,x_1\right)$is finite for a given$x_0\in A$and consider orbits$O\left(x_0\right)=\left\{x_0,x_1,x_2,\dots \right\}$of$x_0\in A$generated by$x_{i+1}\in {\left(T{x}_i\right)}_j\subset T{x}_i\subset T^{i+1}{x}_0$for some$j\in \left\{1,2\right\}$,$\forall i\in {\mathit{Z}}_{0+}$, with$T:A\to A$being subject to the stipulations (2)–(7).

(1) 

Let$p_{jk}\in {\mathit{Z}}_{0+}$be the total number of (non-necessarily consecutive) iterations${\left(T^i{x}_0\right)}_j$from$x_{i-1},x_i\in A_j$to$x_{i+1}\in A_j$;$j\in \left\{1,2\right\}$for iteration indices$i\in {\left[N_k,N_{k+1}\right]}^{}$,$k\in \overline{\chi }$according to (3) and (4);

(2) 

let$p_{j\ell k}\in {\mathit{Z}}_{0+}$be the total number of iterations from$x_{i-1},\hspace{0.17em}{x}_i\in A_{\ell }$to$x_{i+1}\in A_j$for$\ell ,j\left(\ne \ell \right)=1,2$for iteration indices$i\in {\left[N_k,N_{k+1}\right]}^{}$,$k\in \overline{\chi }$satisfying the constraints (5) and (6); and

(3) 

let$p_{ck}\in {\mathit{Z}}_{0+}$be the total number of (non-necessarily consecutive) iterations${\left(T^i{x}_0\right)}_j$from$\left(x_{i-1},x_i\right)\in A_1\times A_2$to$x_{i+1}\in A_1$and from$\left(x_{i-1},x_i\right)\in A_2\times A_1$to$x_{i+1}\in A_2$for iteration indices$i\in {\left[N_k,N_{k+1}\right]}^{}$,$k\in \overline{\chi }$according to (7).

Then,${\left\{d\left(x_{i+1},x_i\right)\right\}}_{i=0}^{\infty }$is bounded if, for some real constant$0\le a\le 1$, there exists a non-negative real sequence${\left\{a_k\right\}}_{k=1}^{\chi }\subset \left[0,a\right]$such that

$$p_{1k}\le \frac{1}{ln{k}_1}\left(p_{2k}\left|ln{k}_2\right|+p_{12k}\left|ln{k}_{12}\right|+p_{21k}\left|ln{k}_{21}\right|+p_{ck}\left|ln{k}_c\right|-ln\left|a_k\right|\right); \forall k\in \overline{\chi }$$

(24)

if$D=0$or if$D>0$and$p_{12k}=p_{21k}=p_{ck}=0$;$\forall k\in \overline{\chi }$, and

$$p_{1k}<\frac{1}{ln{k}_1}\left(p_{2k}\left|ln{k}_2\right|+p_{12k}\left|ln{k}_{12}\right|+p_{21k}\left|ln{k}_{21}\right|+p_{ck}\left|ln{k}_c\right|-ln\left|a_k\right|\right); \forall k\in \overline{\chi }$$

(25)

if$D>0$and$p_{12k}+p_{21k}+p_{ck}>0$;$\forall k\in \overline{\chi }$.

Proof. 

Note from (12) and (17), and $K\left(N_{k+1},N_k\right)\le 1$; $\forall k\in \overline{\chi }$ in Theorem 1 (iv) that

$$K\left(N_{k+1},N_k\right)={\displaystyle {\prod }_{j=N_k}^{N_{k+1}}\left[K_j\right]}=k_1^{p_{1k}}{k}_2^{p_{2k}}{k}_{12}^{p_{12k}}{k}_{21}^{p_{21k}}{k}_c^{p_{ck}}\le 1; \forall k\in \overline{\chi }$$

(26)

subject to the constraint:

$$N_{k+1}-N_k+1=p_{1k}+p_{2k}+p_{12k}+p_{21k}+p_{ck}; \forall k\in \overline{\chi }$$

(27)

where $p_{1k},p_{2k},p_{12k},p_{21k},p_{ck}\in \overline{N_{k+1}-N_k+1}\cup \left\{0\right\}$ are the respective non-necessarily consecutive numbers of iterations ${\left(T^i{x}_0\right)}_j$ for $i\in {\left[N_k,N_{k+1}\right]}^{}$, $j\in \left\{1,2\right\}$; $\forall k\in \overline{\chi }$ satisfying the constraints (1)–(7). Define also:

$$\overline{K}\left(N_{k+1},N_k\right)={\overline{k}}_1^{p_{1k}}{\overline{k}}_2^{p_{2k}}{\overline{k}}_{12}^{p_{12k}}{\overline{k}}_{21}^{p_{21k}}{\overline{k}}_c^{p_{ck}}; \forall k\in \overline{\chi }$$

(28)

with ${\overline{k}}_j=1$, ${\overline{k}}_c=k_c$, ${\overline{k}}_{\ell j}=k_{lj}$; $\ell ,j\left(\ne \ell \right)=1,2$, which allows us to rewrite compactly $M\left(N_{k+1},N_k\right)$ as

$$M\left(N_{k+1},N_k\right)=k_1^{p_{1k}}{k}_2^{p_{2k}}\left(1-\overline{K}\left(N_{k+1},N_k\right)\right)D=k_1^{p_{1k}}{k}_2^{p_{2k}}\left(1-{\overline{k}}_{12}^{p_{12k}}{\overline{k}}_{21}^{p_{21k}}\right)D; \forall k\in \overline{\chi }$$

(29)

after rewriting the upper-bounds of (2)–(7) under the equivalent forms:

$$k_j\hspace{0.17em}d\left(y,x\right)+\left(1-{\overline{k}}_j\right)D; k_{\ell j}\hspace{0.17em}d\left(y,x\right)+\left(1-{\overline{k}}_{\ell j}\right)D; \ell ,j\left(\ne \ell \right)=1,2; k_c\hspace{0.17em}d\left(y,x\right)+\left(1-{\overline{k}}_c\right)D$$

(30)

since $\overline{K}\left(N_{k+1},N_k\right)=k_{12}^{p_{12k}}{k}_{21}^{p_{21k}}$ if $p_{12k}+p_{21k}+p_{ck}>0$ and $\overline{K}\left(N_{k+1},N_k\right)=1$ if $p_{12k}+p_{21k}+p_{ck}=0\left(\iff p_{12k}=p_{21k}=p_{ck}=0\right)$; $\forall k\in \overline{\chi }$.

The constraint (15) with $K\left(N_{k+1},N_k\right)\le 1$ of Theorem 1 (iv) for guaranteeing the boundedness of the distance sequences are $k_1^{p_{1k}}{k}_2^{p_{2k}}{k}_{12}^{p_{12k}}{k}_{21}^{p_{21k}}{k}_c^{p_{ck}}\le a\left(N_k\right)\le a\le 1$, from (26) by taking into account that $ln{k}_2=-\left|ln{k}_2\right|$, $ln{k}_c=-\left|ln{k}_c\right|$ and $ln{k}_{j\ell }=-\left|ln{k}_{lj}\right|$ for $j,\ell \left(\ne j\right)\in \left\{1,2\right\}$, or equivalently from (24), provided that $D=0$, that is, $cl{A}_1\cap cl{A}_2\ne \varnothing$, or under the strict inequality $k_1^{p_{1k}}{k}_2^{p_{2k}}{k}_{12}^{p_{12k}}{k}_{21}^{p_{21k}}{k}_c^{p_{ck}}<a\left(N_k\right)<a\le 1$, equivalent to (25), provided that both $D>0$, that is, $cl{A}_1\cap cl{A}_2=\varnothing$, and $p_{12j}=p_{21j}=p_{ck}=0$, so that $\overline{K}\left(N_{k+1},N_k\right)=0$ in (27), implying that there is no crossed iteration from $A_1$ to $A_2$ or vice-versa. □

It turns out that Proposition 1 still holds under the non-strict inequality (24) if the total number of crossed iterations from $A_1$ to $A_2$ or vice-versa are finite. Thus, one has the subsequent direct extension of Proposition 1:

Proposition 2.

Under Assumption 1,${\left\{d\left(x_{i+1},x_i\right)\right\}}_{i=0}^{\infty }$is bounded under the stipulations of Proposition 1 if, for some real constant$0\le a\le 1$, there exists a non-negative real sequence${\left\{a_k\right\}}_{k=1}^{\chi }\subset \left[0,a\right]$such that (24) holds and$D=0$or, if$D>0$and${\displaystyle {\sum }_{k=1}^{\infty }\left(p_{12k}+p_{21k}\right)}<\infty$.

It turns out that, in order for the sequences of distances between consecutive points of any orbit for some initial point $x_0\in A$, it is necessary that $T:A\to A$ can have image points in $A_2$ for such a $x_0\in A_1$.

Proposition 3.

A multi-valued mapping$T:A\to A$which has bounded distance sequences according to Proposition 1, or to Theorem 1(iv), for any orbit$O\left(x_0\right)=\left\{x_0,x_1,x_2,\dots \right\}$from some given initial point$x_0\in A_1$has to fulfill$T^{N_1}{x}_0\cap A_2\ne \varnothing$for some finite integer$N_1=N_1\left(x_0\right)$. The above property holds for any orbit$O\left(x_0\right)=\left\{x_0,x_1,x_2,\dots \right\}$from any given initial point$x_0\in A_1$if and only if$T^{N_1\left(x_0\right)}{x}_0\cap A_2\ne \varnothing$for finite integer$N_1=N_1\left(x_0\right)$depending on each$x_0\in A_1$.

Proof. 

It follows since if $T^n{x}_0\in A_1$ for $x_0\notin F\left(T\right)\cap A_1$, $n\ge N$ and any finite non-negative integer $N$, then ${\left\{d{\left({\left(T^{i+1}{x}_0\right)}_1,\left(T^i{x}_0\right)\right)}_1\right\}}_{i=0}^{\infty }\to \infty$, since $k_0^{i-N}d\left({\left(T^N{x}_0\right)}_1,{\left(T^{N+1}{x}_0\right)}_1\right)\to \infty$ as $i\to \infty$ $N$ so that it is not possible to fulfill either the constraints (24) and (25) of Proposition 1 or the conditions of Theorem 1 (iv). □

Definition 2.

The partial orbit$O_{\left[0,i\right]}\left(x_0\right)$of the orbit$O\left(x_0\right)$of$x_0\in A$through$T:A\to A$is an ordered set defined recursively by$O_{\left[0,i\right]}\left(x_0\right)=\left\{O_{\left[0,i\right]}\left(x_0\right),x_i\right\}$for some$x_i\in T^i{x}_0$with$O_{\left[0,0\right]}\left(x_0\right)=\left\{x_0\right\}=\left\{T^0{x}_0\right\}$;$\forall i\in {\mathit{Z}}_{+}$.

Remark 4.

Note that if$T^i{x}_0$belongs to$A_{\ell }$and$T^{i+1}{x}_0$belongs to$A_j$;$j,\ell \left(\ne j\right)\in \left\{1,2\right\}$, then the partial orbit$O_{\left[0,i+1\right]}\left(x_0\right)=\left\{O_i\left(x_0\right),x_{i+1}\right\}$$x_{i+1}\in {\left(T^{i+1}{x}_0\right)}_j\subset T^{i+1}{x}_0$with$O_{\left[0,0\right]}\left(x_0\right)=\left\{x_0\right\}=\left\{T^0{x}_0\right\}$;$\forall i\in {\mathit{Z}}_{0+}$has a switch of set in the generation of its last member. Thus, one of the non-expansive constraints (5) or (6) has been used to incorporate the new element of the orbit. Note also that unconditional switchings from$A_1$to$A_2$or vice-versa are not allowed at any arbitrary iteration if$T:A\to A$is single-valued. Therefore, the results of Theorem 1 and Propositions 1–3 concerning the boundedness and the convergence of the distance sequences cannot be monitored towards the fulfilment of Theorem 1or Propositions 1–3.

It turns out that the particular cases $k_{21}=k_1>1$ and $k_{12}=k_2=k_c<1$ are also covered by the above more general formulation. This suggests that switchings from $A_2$ to $A_1$ are expansive as they are the successive iterates within $A_1$, while switchings from $A_1$ to $A_2$ are contractive as they are the successive iterates within $A_2$. The lost on non-expansivity of switches from $A_2$ to $A_1$ does not modify the essence of the above given results. This is seen in short as follows. Assume that $k_{21}=k_1>1$ and take $x_0\in A$, $x_1\in {\left(T{x}_0\right)}_2$ and $x_2\in {\left(T{x}_1\right)}_1$ that satisfy:

$$d\left(x_2,x_1\right)\le k_{1}d\left(x_1,x_0\right)+\left(1-k_1\right)D=k_{1}d\left(x_1,x_0\right)-\left(k_1-1\right)D$$

The necessary condition $d\left(x_2,x_1\right)\ge D$ is compatible with the above upper-bound since $k_{1}d\left(x_1,x_0\right)-\left(k_1-1\right)D\ge D\iff \left(k_1-1\right)D\ge 0$. At the same time the fact that the mapping is expansive from $x_1$ to $x_2$ such that

$$d\left(x_1,x_0\right)<d\left(x_2,x_1\right)\le k_{1}d\left(x_1,x_0\right)-\left(k_1-1\right)D$$

agrees with $d\left(x_1,x_0\right)>D$, while it keeps as locally non-expansive if $d\left(x_2,x_1\right)=d\left(x_1,x_0\right)=D$, i.e., if $x_1\in {\left(T{x}_0\right)}_2\cap A_{02}$, and $x_2\in {\left(T{x}_1\right)}_1\cap A_{01}$ under the necessary assumption that ${\left(T{x}_0\right)}_j\cap A_{0j}\ne \varnothing$ for $j=1,2$. Thus, once a switching to $A_2$ holds which is expansive if $d\left(x_1,x_0\right)>D$, it can remain in $A_2$ leading to the orbit to be contractive in $A_2$ and converging to some $x_2\in F\left(T\right)$ if $F\left(T\right)\cap A_2\ne \varnothing$ and $A_2$ is closed.

3. Problem Statement for p Subsets of a Metric Space

Now, define $p$ non-empty subsets $A_i\subset X$ with $D_i=d\left(A_i,A_{i+1}\right)$ for $i\in \overline{p}$ and $A_{p+1}\equiv A_p$ $\left(p\ge 2\right)$, where $\left(X,d\right)$ is a metric space and consider a self-mapping $T:{\displaystyle {\cup }_{i\in \overline{p}}{A}_i}\to {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$. The terminology is used such that $A_i$ and $A_{i+1}$ are adjacent subsets, $A_{i+1}$ is the right adjacent subset to $A_i$, while $A_i$ is the left adjacent subset to $A_{i+1}$; $\forall i\in \overline{p}$. In order to keep a simple notation, we will denote in the sequel by $T:A_i\to \left(A_i\cup A_{i+1}\right)$ for any given $i\in \overline{p}$ the restricted multivalued map from a set to the union to itself with its right adjacent one $T:\left({\displaystyle {\cup }_{j\in \overline{p}}{A}_j}\right)|A_i\to {\displaystyle {\cup }_{j\in \overline{p}}{A}_j}|\left(A_i\cup A_{i+1}\right)$.

Through this section, the main ideas of the former section are kept but, in order to simplify the exposition, the following assumptions are made:

(A1) The multivalued mapping $T:{\displaystyle {\cup }_{i\in \overline{p}}{A}_i}\to {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ is mixed $p$-cyclic/acyclic in the sense that $T\left(A_i\right)\subseteq A_i\cup A_{i+1}$ for $i\in \overline{p}$ with $A_{p+1}\equiv A_1$ such that for each $x_0\in A_i$ and each $i\in \overline{p}$, $T{x}_0=\left\{{\left(T{x}_0\right)}_i,{\left(T{x}_0\right)}_{i+1}\right\}$ with ${\left(T{x}_0\right)}_i\left(\ne \varnothing \right)\subset A_i$.

(A2) A finite number $n_i\in {\mathit{Z}}_{0+}$ of iterated images of $x_0$ in $A_i$ may happen before switching to its right adjacent subset $A_{i+1}$ when constructing an orbit. That is, a partial orbit $O_{\left[0,n_i+1\right]}\left(x_0\right)$ with initial point $x_0$ in $A_i$ is $O_i\left(x_0\right)=\left(x_0,x_1,\dots ,x_{n_i},x_{n_i+1}\right)$, where $x_j\in {\left(T^j{x}_0\right)}_i$ for $j\in {\overline{n}}_i$, $x_0={\left(T^0{x}_0\right)}_i$ and $x_{n_i+1}\in {\left(T^{n_i+1}{x}_0\right)}_{i+1}$. If $n_i$ is infinity, then $A_i$ is the terminal set with no further switchings of $T:A_i\to \left(A_i\cup A_{i+1}\right)|A_i$ to its right adjacent subset.

The number $n_i$ is admitted to be varying for each cycle of $T:{\displaystyle {\cup }_{i\in \overline{p}}{A}_i}\to {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ running all the subsets $A_i$; $\forall i\in \overline{p}$.

(A3) $\overline{p}=p_c\cup p_{ne}\cup p_e$ with $p_e,\hspace{0.17em}{p}_{ne}$ and $p_c$ being pair-wise disjoint defined by:

$$p_c=\left\{i\in \overline{p} \mathrm{such} \mathrm{that} T:A_i\to A_i\cup A_{i+1} \mathrm{satisfies} \mathrm{condition} C_c\right\}\subset \overline{p}$$

$$p_{ne}=\left\{i\in \overline{p} \mathrm{such} \mathrm{that} T:A_i\to A_i\cup A_{i+1} \mathrm{satisfies} \mathrm{condition} C_{ne}\right\}\subset \overline{p}$$

$$p_e=\left\{\hspace{0.17em}i\in \overline{p} \mathrm{such} \mathrm{that} T:A_i\to A_i\cup A_{i+1} \mathrm{satisfies} \mathrm{condition} C_e\right\}\subset \overline{p}$$

which are indexing the disjoint subsets $S_c=\left\{A_i:i\in p_c\right\}$, $S_{ne}=\left\{A_i:i\in p_{ne}\right\}$ and $S_e=\left\{A_i:i\in p_e\right\}$, where $T:A_i\to \left(A_i\cup A_{i+1}\right)|A_i$ are contractive, non-expansive being non-contractive and expansive, respectively, where:

(a)

the contraction condition $C_c$ is defined as follows:

$$\begin{array}{c}d\left({\left(Tx\right)}_i,{\left(Ty\right)}_i\right)\le k_{i}d\left(x,y\right); max\left(d\left({\left(Tx\right)}_{i+1},{\left(Ty\right)}_i\right),d\left({\left(Tx\right)}_i,{\left(Ty\right)}_{i+1}\right)\right)\le k_{i}d\left(x,y\right)+\left|1-{k^{\prime }}_i\right|D_i;\\ \forall x,y\in A_i \mathrm{for} i\in p_c \mathrm{and} \mathrm{some} \mathrm{real} \mathrm{constants} k_i\in \left[0,1\right), {k^{\prime }}_i\in \left[k_i,{\overline{k}}_i\right); \forall i\in p_c\end{array}$$

(31)

(b)

the non-expansivity condition is defined as follows:

$$\begin{array}{c}d\left({\left(Tx\right)}_i,{\left(Ty\right)}_i\right)\le k_{i}d\left(x,y\right); max\left(d\left({\left(Tx\right)}_{i+1},{\left(Ty\right)}_i\right),d\left({\left(Tx\right)}_i,{\left(Ty\right)}_{i+1}\right)\right)\le k_{i}d\left(x,y\right)+\left|1-{k^{\prime }}_i\right|D_i;\\ \forall x,y\in A_i \mathrm{for} i\in p_{ne} \mathrm{and} \mathrm{some} \mathrm{real} \mathrm{constants} k_i=1, {k^{\prime }}_i\in \left[1,{\overline{k}}_i\right); \forall i\in p_{ne}\end{array}$$

(32)

(c)

the expansivity condition $C_e$ is defined as follows:

$$\begin{array}{c}{k}_{0i}d\left(x,y\right)\le d\left({\left(Tx\right)}_i,{\left(Ty\right)}_i\right)\le k_{i}d\left(x,y\right);\\ k_{0i}d\left(x,y\right)+\left({k^{\prime }}_{0i}-1\right)D_i\le \mathit{min}\left(d\left({\left(Tx\right)}_{i+1},{\left(Ty\right)}_i\right),d\left({\left(Tx\right)}_i,{\left(Ty\right)}_{i+1}\right)\right)\\ \le max\left(d\left({\left(Tx\right)}_{i+1},{\left(Ty\right)}_i\right),d\left({\left(Tx\right)}_i,{\left(Ty\right)}_{i+1}\right)\right)\le k_{i}d\left(x,y\right)+\left({k^{\prime }}_i-1\right)D_i;\\ \forall x,y\in A_i \mathrm{for} i\in p_e \mathrm{and} \mathrm{some} \mathrm{real} \mathrm{constants} k_{0i},k_i\left(\ge k_{0i}\right)>1, {k^{\prime }}_i\in \left[k_i,{\overline{k}}_i\right), {k^{\prime }}_{0i}\in \left[{k^{\prime }}_i,{{\overline{k}}^{\prime }}_{0i}\right); \forall i\in p_e\end{array}$$

(33)

(d)

The switching from $A_i$ to its right adjacent subset $A_{i+1}$ in (33), and in (31) and (32) if $k_i{}^{\prime }>1$, are performed only provided that $d\left(x,y\right)>\frac{k_i{}^{\prime }-1}{k_i{}^{\prime }}{D}_i$ if $x,y\in A_i$ for any $i\in \overline{p}$.

Note that, in order to simplify the exposition, the contractive or expansive constants for iterations within subsets $k_{\left(.\right)}$ are assumed identical to their counterparts related to switching from a subset to its right adjacent one. Note also that, although contractive conditions are also inherently non-expansive, we consider each one of them, in the above characterization, specifically as “contractive· or as “non expansive” according to the constant $k_i$ being either less than unity or unity. Thus, by convenience, the set $S_c$ is not included in the set $S_{ne}$ so that $S_c\cap S_{ne}\ne \varnothing$. It turns out that from the above constraints the restricted images of $T:A_i\to \left(A_i\cup A_{i+1}\right)|A_i$ (i.e., the mapping $T$ from the respective subset A_i to itself) are contractive, non-expansive and expansive, respectively. However, the respective restrictions to each reach right adjacent subset $T:A_i\to \left(A_i\cup A_{i+1}\right)|A_{i+1}$ are not guaranteed to be contractive or non-expansive since ${\overline{k}}_i$ can exceed unity. This tries to reflect the practical fact that switching actions from a subset to its right adjacent one can have an instability cost due to the switching itself even if iterations within that right adjacent subset are contractive. We can think here, for instance, about the modeling through ordinary differential equations of a dynamical system subject to impulsive controls which can make the state norm to grow by huge amounts at the sampling instants where impulses happen.

Note that the condition $d\left(x,y\right)>\frac{k_i-1}{k_i}{D}_i$ if $x,y\in A_i$ for switching to $A_{i+1}$ any $i\in \overline{p}$ ensures that the upper-bounds in the conditions (31)–(33) are well posed since ${k^{\prime }}_{i}d\left(x,y\right)+\left|1-{k^{\prime }}_i\right|D_i>0$ for any $i\in \overline{p}$.

Proposition 4.

A sufficient condition guaranteeing that the expansivity condition$C_e$is well posed is that, for any$A_i\in S_e$, Assumption A4 below holds:

(A4) $diam{A}_{i+1}\le {k^{\prime }}_{0i}diam{A}_i$ if ${k^{\prime }}_{0i}=2$

$$D_i\ge max\left(0,\frac{{k^{\prime }}_{0i}diam\hspace{0.17em}{A}_i-diam{A}_{i+1}}{2-{k^{\prime }}_{0i}}\right) \mathrm{if} {k^{\prime }}_{0i}\ne 2$$

Proof. 

It follows since, for the first inequality of (33) to hold in the worst case, that is, for the largest possible value of $d\left(x,y\right)$ for $x,y\in A_i$, which is $d\left(x,y\right)=\underset{x,y\in A_i}{sup}d\left(x,y\right)=diam\hspace{0.17em}{A}_i$, it is sufficient that for $\left(i\in P_e\right)\iff \left(A_i\in S_e\right)$: ${k^{\prime }}_{0i}diam\hspace{0.17em}{A}_i+\left({k^{\prime }}_{0i}-1\right)D_i\le diam{A}_{i+1}+D_i$ which gives the result. □

Remark 5.

Since we will usually work only with conditions for the boundedness and convergence of sequences, only the upper-bound of (24) will be addressed through the constants$k_i$and$k_i{}^{\prime }$. However, note that the upper-bound does not guarantee directly that the mapping$T:A_i\to A_i\cup A_{i+1}$is expansive but just that it is not guaranteed to be non-expansive.

Now, consider an orbit $O\left(x_0\right)$ from an initial point $x_0\in {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ such that $x_0=T^0{x}_0$, $x_{j+1}\in {\left(T{x}_j\right)}_i\cup {\left(T{x}_j\right)}_{i+1}\subset T^j{x}_0\subset {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ provided that $x_j\in A_i$ for some $i\in \overline{p}$; $\forall j\in {\mathit{Z}}_{0+}$. Denote the partial orbit of $O_{\left[k,k+N_k\right]}\left(x_0\right)$ on $\left[k,k+N_k\right]$ for some $N_k\in {\mathit{Z}}_{0+}$ and a given $k\in {\mathit{Z}}_{0+}$ as $O_{\left[k,k+N_k\right]}\left(x_0\right)=\left(x_k,x_{k+1},\dots ,x_{k+N_k}\right)$. Then, all the points of the partial orbit belong to $A_{\ell },A_{l+1},\dots ,A_j$ for some $\ell ,j\left(\ge \ell \right)\in \overline{p}$ with eventual $n_i=n_i\left(x_0\right)\in {\mathit{Z}}_{0+}$ iterations within of the various sets $A_i$, for each $i\in \left[\ell ,j\right]$, together with eventual iteration switches $i\to i+1$ to their right adjacent ones.

The following result holds which implies that the sequence of distances is bounded provided that $p_e$ is non-empty, that is, there is at least one subset $A_i$ for $i\in \overline{p}$, where $T:A_i\to \left(A_i\cup A_{i+1}\right)|A_i^{}$ is contractive, according to (31), and that each cycle has a sufficiently large number of iterations in $S_c=\left\{A_i:i\in p_c\right\}$.

Theorem 2.

Under Assumptions A1 to A4, the following properties hold:

(i) 

Consider a complete cycle of$N_k$consecutive iterations on all the subsets$A_i$,$\forall i\in \overline{p}$on the integer interval$\left[k,k+N_k\right]$starting from$x_k\in {\left(T^k{x}_0\right)}_{\ell }\subset T^k{x}_0\cap A_{\ell }$for some$x_0\in {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$, some$\ell =\ell \left(k\right)\in \overline{p}$and some$k\in {\mathit{Z}}_{0+}$which has$n_i\left(k,k+N_k\right)$consecutive iterations within$A_i$before switching to$A_{i+1}$for each$i\in \overline{p}$. Thus, one has for the partial orbit$O_{{}_{\left[k,k+N_k\right]}}\left(x_0\right)$on$\left[k,k+N_k\right]$the following relation of distances:

$$d\left(x_{k+N_k+1},x_{k+N_k}\right)\le K_1\left(k,k+N_k\right)d\left(x_{k+1},x_k\right)+{\displaystyle {\sum }_{i=1}^p{K}_{i+\ell }\left(k,k+N_k\right)\left|1-{k^{\prime }}_{i+\ell -1}\right|D_{i+\ell -1}}$$

(34)

$$\le K_1\left(k,k+N_k\right)\left(d\left(x_{k+1},x_k\right)+\widehat{D}\left({\displaystyle {\sum }_{i=1}^{p}1}/\left({\displaystyle {\prod }_{j=1}^{i-1}\left[k_j^{n_j\left(k,k+N_k\right)}{k^{\prime }}_j\right]}\right)\right)\right)$$

(35)

under the identities$k_{i+\ell }=k_{i+\ell -p}$,${k^{\prime }}_{i+\ell }={k^{\prime }}_{i+\ell -p}$and$D_{i+\ell }=D_{i+\ell -p}$, if$i+\ell >p$;$\forall i,\ell \in \overline{p}$, where$N_k=p+{\displaystyle {\sum }_{i=1}^p{n}_i\left(k,k+N_k\right)}$and

$$K_i\left(k,k+N_k\right)={\displaystyle {\prod }_{j=i}^p\left[k_j^{n_j\left(k,k+N_k\right)}{k^{\prime }}_j\right]}=K_1\left(k,k+N_k\right)/\left({\displaystyle {\prod }_{j=1}^{i-1}\left[k_j^{n_j\left(k,k+N_k\right)}{k^{\prime }}_j\right]}\right); \forall i\in \overline{p}$$

(36)

(ii) 

Assume, in addition, that${\left\{N_{k+j-1}\right\}}_{j=0}^{\chi }\subset {\mathit{Z}}_{+}$$\left(\chi \le \infty \right)$with$N_{k-1}=k$for the given$k\in {\mathit{Z}}_{0+}$is the sequence of integers with the associated incremental sequence${\left\{N_{k+j}-N_{k+j-1}\right\}}_{j=0}^{\chi }$, which contains element-to-element the number of iterations, each of them being associated with a complete cycle on all the subsets$A_i$for$i\in \overline{p}$, that is,$N_{k+1}=N_k+p+{\displaystyle {\sum }_{i=1}^p{n}_i\left(N_k,N_{k+1}\right)}$with$N_k,N_{k+1},N_{k+2}\in {\left\{N_{k+j-1}\right\}}_{j=0}^{\chi }$and

$$1\le {\delta }_k=\delta +{\displaystyle {\sum }_{i=\ell }^{\ell +\delta }{n}_i\left(N_{k+1},N_{k+1}+{\delta }_k\right)}<N_{k+2}-N_{k+1}$$

(37)

where$\delta \in \overline{p-1}$contains$\delta$switches between right adjacent subsets and${\delta }_k$is the total number of switches which have happened since the iteration$N_{k+1}$.

Then, the distances$d\left(x_{N_{k+1}+1},x_{N_{k+1}}\right)$and$d\left(x_{N_{k+1}+\delta },x_{N_{k+1}+1}\right)$for$\delta \in \overline{p-1}$, related to the two pairs of elements$\left(x_{N_{k+1}+1},x_{N_{k+1}}\right)$and$\left(x_{N_{k+1}+\delta },x_{N_{k+1}+1}\right)$of the partial orbit$O_{{}_{\left[N_k,N_{k+1}+\delta \right]}}\left(x_0\right)$on$\left[N_k,N_{k+1}+\delta \right]$, satisfy the constraints:

$$\begin{array}{c}d\left(x_{N_{k+1}+1},x_{N_{k+1}}\right)\le K_1\left(N_k,N_{k+1}\right)d\left(x_{N_k+1},x_{N_k}\right)+{\displaystyle {\sum }_{i=1}^p{K}_{i+\ell }\left(N_k,N_{k+1}\right)\left|1-{k^{\prime }}_{i+\ell -1}\right|D_{i+\ell -1}}\\ =K_1\left(N_k,N_{k+1}\right)d\left(x_{k+1},x_k\right)+{\displaystyle {\sum }_{i=\ell }^{\ell +p-1}{K}_{i+1}\left(N_k,N_{k+1}\right)\left|1-{k^{\prime }}_i\right|D_i}\end{array}$$

(38)

$$\begin{array}{c}d\left(x_{N_{k+1}}+{\delta }_k,x_{N_{k+1}}+{\delta }_k-1\right)\le K_1\left(N_{k+1},N_{k+1}+{\delta }_k\right)d\left(x_{N_{k+1}+1},x_{N_{k+1}}\right)+{\displaystyle {\sum }_{i=1}^{\delta }{K}_{i+\ell }}\left(N_{k+1},N_{k+1}+\delta \right)\left|\hspace{0.17em}1-{k^{\prime }}_{i+\ell -1}\right|D_{i+\ell -1}\\ =K_1\left(N_{k+1},N_{k+1}+{\delta }_k\right)d\left(x_{N_{k+1}+1},x_{N_{k+1}}\right)+{\displaystyle {\sum }_{i=\ell }^{\ell +\delta -1}{K}_{i+1}\left(N_{k+1},N_{k+1}+{\delta }_k\right)\left|1-{k^{\prime }}_i\right|D_i}\end{array}$$

(39)

for$x_{N_k},x_{N_{k+1}}\in {\left(T^{N_k}{x}_0\right)}_{\ell }\subset T^{N_k}{x}_0\subset A_{\ell }$; some$\ell \in \overline{p}$,$\forall k\in {\mathit{Z}}_{0+}$, where:

$$K_{i+\ell }\left(N_k,N_{k+1}\right)={\displaystyle {\prod }_{j=i+\ell }^{\ell +p-1}\left[k_j^{n_j\left(N_k,N_{k+1}\right)}{k^{\prime }}_j\right]}; \forall i\in \overline{p}, \forall \ell \in \overline{p}$$

(40)

$$K_{i+\ell }\left(N_{k+1},N_{k+1}+{\delta }_k\right)={\displaystyle {\prod }_{j=i+\ell }^{\ell +\delta -1}\left[k_j^{n_j\left(N_{k+1},N_{k+1}+{\delta }_k\right)}{k^{\prime }}_j\right]}; \forall i\in \overline{p},\hspace{0.17em}\forall \ell \in \overline{p}, \delta \in \overline{p-1}$$

(41)

(iii) 

Assume furthermore that, for the sequence${\left\{N_{k+j-1}\right\}}_{j=0}^{\chi }\subset {\mathit{Z}}_{+}$of property (ii),$\underset{\ell \in {\mathit{Z}}_{0+}}{sup}\hspace{0.17em}{K}_1\left(N_{j+\ell -2},N_{j+\ell -1}\right)\le 1-\epsilon$, for some$\epsilon \in \left(0,1\right)$, and assume also that

$$d\left(x_{k+1},x_k\right)\ge \underset{\ell \in {\mathit{Z}}_{0+}}{sup}\frac{K_1\left(N_{k+\ell -2},N_{k+\ell -1}\right)\widehat{D}}{1-K_1\left(N_{k+\ell -2},N_{k+\ell -1}\right)}\left({\displaystyle {\sum }_{j=1}^{i-1}\frac{1}{{\displaystyle {\prod }_{j=1}^{i-1}\left[k_j^{n_j\left(N_{k+\ell -2},N_{k+\ell -1}\right)}{k^{\prime }}_j\right]}}}\right)$$

(42)

with$N_{k-1}=k$for the given$k\in {\mathit{Z}}_{0+}$such that$x_k\in {\left(T^k{x}_0\right)}_{\ell }\subset T^k{x}_0\cap A_{\ell }$for some$\ell =\ell \left(k\right)\in \overline{p}$and assume also that$d\left(x_0,x_k\right)$is finite. Then,$\underset{\ell \in {\mathit{Z}}_{0+}}{sup}\hspace{0.17em}d\left(x_{N_{k+l}+1},x_{N_{k+l}}\right)\le d\left(x_{k+1},x_k\right)$. If$\underset{j\in {\mathit{Z}}_{0+}}{sup}\hspace{0.17em}d\left(x_{N_{k+j}+1},x_{N_{k+j}}\right)\le d\left(x_{k+1},x_k\right)$and if

(1) 

either$\underset{j\in {\mathit{Z}}_{0+}}{sup} {\displaystyle {\sum }_{i=1}^p{n}_i\left(N_{k+j-2},N_{k+j+1}\right)}\le \overline{n}<\infty$and$\chi =\infty$(i.e., there are infinity many switches from a subset to its right adjacent one but not infinitely many iterations in a subset$A_i$prior to switching to the right adjacent one), or

(2) 

if$\chi <\infty$and there are infinitely many iterations$n_i$within in a final set$A_i$being either non-expansive (including the contractive case) subject, furthermore, to$k_i^{{}^{\prime }}\le 1$,

Then the sequence of distances${\left\{d\left(x_i,x_{i+1}\right)\right\}}_{i=0}^{\infty }$for adjacent points of the orbit$O\left(x_0\right)$is bounded. Furthermore,

$$\underset{j\to \infty }{lim sup}\hspace{0.17em}d\left(x_{N_{k+j}+1},x_{N_k}\right)\le \frac{1}{\epsilon }{\displaystyle {\sum }_{i=1}^p\underset{j\in \overline{\chi }}{sup}\left(K_{i+\ell }\left(N_j,N_{j+1}\right)\left|\hspace{0.17em}1-{k^{\prime }}_{i+\ell -1}\right|D_{i+\ell -1}\right)}<+\infty$$

(43)

As a result, all sequences of distances${\left\{d\left(x_i,x_{i+j}\right)\right\}}_{i=0}^{\infty }$;$\forall j\in {\mathit{Z}}_{0+}$are also bounded.

Proof. 

Properties [(i) and (ii)] follow directly from the application of (31)–(34) where $k\in {\mathit{Z}}_{0+}$ is arbitrary, with $d\left(x_0,x_k\right)$, being finite and $\ell =\ell \left(k\right)\in \overline{p}$ is such that $x_k\in {\left(T^k{x}_0\right)}_{\ell }\subset T^k{x}_0\cap A_{\ell }$, and ${\left\{N_j\right\}}_{j=0}^{\chi }\subset {\mathit{Z}}_{+}$ $\left(\chi \le \infty \right)$, with $N_0=k,$ is the sequence of complete iterations along the $p$ subsets $A_i$. Property (iii) follows since (42) under the constraint $K_1\left(N_{k+\ell -2},N_{k+\ell -1}\right)\le 1-\epsilon$ yields $\underset{\ell \in {\mathit{Z}}_{0+}}{sup}\hspace{0.17em}d\left(x_{N_{k+\ell }+1},x_{N_{k+\ell }}\right)\le d\left(x_{k+1},x_k\right)$. Furthermore, if $\underset{j\in {\mathit{Z}}_{0+}}{sup}\hspace{0.17em}{\displaystyle {\sum }_{i=1}^p{n}_i\left(N_{k+j-2},N_{k+j+1}\right)}\le \overline{n}<\infty$ and $\chi =\infty$, then the sequence of distances ${\left\{d\left(x_i,x_{i+1}\right)\right\}}_{i=0}^{\infty }$ cannot be unbounded for intermediate iterations within the sequence of finite intervals ${\left\{N_{k+1}-N_k\right\}}_{k=0}^{\chi }$ so that it is bounded. It also follows from (38) that

$$\begin{array}{c}d\left(x_{N_{k+j}+1},x_{N_k}\right)\le K_1^j\left(N_k,N_{k+1}\right)d\left(x_{N_{k+1}},x_{N_k}\right)\\ +{\displaystyle {\sum }_{\ell =1}^{j-1}{\displaystyle {\sum }_{i=1}^p{K}_1^{\ell }\left(N_k,N_{k+1}\right)\underset{j\in \overline{\chi }}{sup}\left(K_{i+\ell }\left(N_j,N_{j+1}\right)\left|1-{k^{\prime }}_{i+\ell -1}\right|D_{i+\ell -1}\right)}}\\ \le {\left(1-\epsilon \right)}^{j}d\left(x_{N_k+1},x_{N_k}\right)\end{array}$$

(44)

$$+\frac{1-{\left(1-\epsilon \right)}^j}{\epsilon }{\displaystyle {\sum }_{i=1}^p\underset{j\in \overline{\chi }}{sup}\left(K_{i+\ell }\left(N_j,N_{j+1}\right)\left|\hspace{0.17em}1-{k^{\prime }}_{i+\ell -1}\right|D_{i+\ell -1}\right)}$$

(45)

and (43) holds since ${\left(1-\epsilon \right)}^j\to 0$ as $j\to \infty$. A similar result is found if $\chi <\infty$, that is there is some subset $A_i$ for $i\in \overline{p}$ where infinitely many terminal iterations take place with no later switch to its right adjacent one $A_{i+1}$ under the assumption that $max\left(k_i,k_i^{{}^{\prime }}\right)\le 1$, that is, the terminal iterations are non-expansive (eventually contractive) with $k_i^{{}^{\prime }}\le 1$. □

Note that the conditions $\underset{\ell \in {\mathit{Z}}_{0+}}{sup}\hspace{0.17em}{K}_1\left(N_{j+\ell -2},N_{j+\ell -1}\right)\le 1-\epsilon$ and $\underset{j\in {\mathit{Z}}_{0+}}{sup}\hspace{0.17em}{\displaystyle {\sum }_{i=1}^p{n}_i\left(N_{k+j-2},N_{k+j+1}\right)}\le \overline{n}<\infty$ are key stipulations for the boundedness of the distances between consecutive points of the orbit $O\left(x_0\right)$ in Theorem 2 (iii). This can be fulfilled with at least one of the subsets in $S_c=\left\{A_i:i\in p_c\right\}$ and a sufficiently large $n_i$, for $A_i\in S_c$, compared to $\overline{n}$ being dependent on the value of the contractivity condition $k_i\in \left[0,1\right)$. On the other hand, note that any distances ${\left\{d\left(x_i,x_{i+j+1}\right)\right\}}_{i=0}^{\infty }$ for any finite $j\in {\mathit{Z}}_{0+}$ are bounded from the use of the triangle inequality for distances and the above proved property $\underset{\ell \in {\mathit{Z}}_{0+}}{sup}\hspace{0.17em}d\left(x_{N_{k+\ell }+1},x_{N_{k+\ell }}\right)\le d\left(x_{k+1},x_k\right)$ for the given $k\in {\mathit{Z}}_{0+}$ since for some finite real constant $M>1$:

$$d\left(x_{i+j+1},x_i\right)\le {\displaystyle {\sum }_{\ell =0}^{j}d\left(x_{i+\ell +1},x_{i+\ell }\right)}\le Md\left(x_{N_{k+m+1}},x_{N_{k+m}}\right)\le Md\left(x_{k+1},x_k\right)<+\infty$$

for some $m=m\left(i,j\right)\in {\mathit{Z}}_{0+}$ and some $N_k\in {\left\{N_k\right\}}_{k=0}^{\overline{\chi }}$. However, according to (43), the above result also holds for any (even infinity) $j\in {\mathit{Z}}_{0+}$.

Example 1.

Note that$d\left(x_{N_{k+j}+1},x_{N_k}\right)$in (43) has to be not smaller than the corresponding distance between adjacent subsets provided that the involved points belong to adjacent subsets. For instance, assume that$p=2$,$k_1=k_1{}^{\prime }\ge {k^{\prime }}_{01}>1$and$k_2={k^{\prime }}_2<1$, that is, the mapping$T:A_1\cup A_2\to A_1\cup A_2$is expansive in$A_1$and contractive in$A_2$. Assume that all the cycles have the same number of iterations en each of the subsets taken as$n_1=0$within$A_1$and$n_2=1$within$A_2$. Under Theorem 2 (iii),$K_1=k_2^2{k}_1<1$for each cycle of iterations on both subsets to be contractive. Identifying$d\left(x_{N_{k+j}+1},x_{N_k}\right)$with$d\left(x_{j+1},x_j\right)$with one of each points within one subset, one obtains from (43) that

$$\underset{j\to \infty }{lim\hspace{0.17em}sup}d\left(x_{j+1},x_j\right)\ge \widehat{D}=\frac{k_2^2\left(k_1-1\right)+1-k_2}{1-k_2^2{k}_1}D\ge d\left(A_1,A_2\right)=D$$

under the necessary assumption that$k_2\left(2k_1-1\right)\ge 1$, which, together with$k_2^2{k}_1<1$, yields$1/\sqrt{k_1}>k_2\ge 1/\left(2k_1-1\right)$, subject to$1<k_1<{\left(2k_1-1\right)}^2$.

Now, consider the alternative problem without iterations within neither$A_1$nor$A_2$so that$n_1=n_2=0$. In this case,$k_2<1/k_1$and an “ad hoc” redefinition of$\widehat{D}$leads to$\widehat{D}=\frac{k_2\left(k_1-1\right)+1-k_2}{1-k_2{k}_1}D\ge D$under the necessary condition$k_2\left(2k_1-2\right)\ge 0$, which holds since$k_1>1$if$k_2<1/k_1<1$. It turns out that the maximum allowable$k_2$is smaller than the one for the above case.

Example 2.

Consider$p=3$for subsets$A_i$with none internal iterations within any of the subsets before switching to each right adjacent subset, i.e.,$n_i=0$for$i\in \overline{3}$, subject to$k_1=k_1{}^{\prime }\ge {k^{\prime }}_{01}>1$and$0<k_i={k^{\prime }}_i<1$for$i=2,3$. Assume four possible cases to guarantee that$\widehat{D}=\underset{1\le i\le 3}{max}{D}_i$:

(a) 

$D_i=D=d\left(A_i,A_{i+1}\right)$;$\forall i\in \overline{3}$with$A_4\equiv A_1$. Then,

$$\widehat{D}=\frac{k_3{k}_2\left(k_1-1\right)+k_3\left(1-k_2\right)+1-k_3}{1-k_3{k}_2{k}_1}D\ge D$$

which holds trivially identical to$2k_3{k}_2\left(k_1-1\right)\ge 0$since$k_1>1$.

(b) 

$D_i=d\left(A_i,A_{i+1}\right)$can be eventually distinct subject to$D_1\ge D_2=D_3$so that

$$\widehat{D}=\frac{k_3{k}_2\left(k_1-1\right)D_1+\left(1-k_3{k}_2\right)D_2}{1-k_3{k}_2{k}_1}\ge D_1$$

which holds if

$$\left(k_3{k}_2\left(k_1-1\right)+k_3{k}_2{k}_1-1\right)D_1+\left(1-k_3{k}_2\right)D_2\ge 0$$

for which it is sufficient that, since$D_1\ge D_2$,$k_3{k}_2\left(k_1-1\right)+k_3{k}_2{k}_1-k_3{k}_2\ge 0$, which holds directly since$k_1>1$.

(c) 

$D_1<D_2=D_3$so that$\widehat{D}\ge D_2>D_1$so that

$$\widehat{D}=\frac{k_3{k}_2\left(k_1-1\right)D_1+\left(1-k_3{k}_2\right)D_2}{1-k_3{k}_2{k}_1}\ge D_2>D_1$$

which holds if

$$k_3{k}_2\left(k_1-1\right)D_1+\left(1-k_3{k}_2\right)D_2-D_2+k_3{k}_2{k}_1{D}_2\ge 0$$

for which it is sufficient, since$D_2>D_1$,$k_3{k}_2\left(k_1-1\right)D_1+k_3{k}_2{D}_1+k_3{k}_2{k}_1{D}_1\ge 0$, which holds directly since$2k_1{D}_1\ge 0$.

(d) 

Now assume that$k_i={k^{\prime }}_i=k<1$for$i\in \overline{3}$so that the redefined$\widehat{D}$is

$$\widehat{D}=\frac{k^2\left(1-k\right)+k\left(1-k\right)+1-k}{1-k^3}D=\frac{k^2-k^3+k-k^2+1-k}{1-k^3}D=\frac{1-k^3}{1-k^3}D=D$$

which is a known property of$3$-cyclic contractions.

Example 3.

The convergence of the distances to the best proximity points is not possible if the mapping is expansive for switching actions from a set to its adjacent one, and there is one expansive contraction that is not possible for the case of only two sets$A_1$and$A_2$, i.e.,$p=2$when the closures of such sets (or themselves if they are closed) do not intersect; i.e., the constraint$\widehat{D}=D_1=D$is not feasible. Note that at the limit for infinitely many iterations, the subsequent relations

$${k^{\prime }}_{01}D+\left({k^{\prime }}_{01}-1\right)D\le \widehat{D}\le \underset{i=1,2}{min}\left({k^{\prime }}_{i}D+\left(1-{k^{\prime }}_i\right)D\right)={k^{\prime }}_{2}D+\left(1-{k^{\prime }}_2\right)D=D$$

should hold, that is$2\left({k^{\prime }}_{01}-1\right)D\le 0$, which only holds if and only if$D=0$, i.e., if and only if$cl{A}_1\cap cl{A}_2\ne \varnothing$since${k^{\prime }}_{01}>1$.

If there are three involved sets$A_1$,$A_2$and$A_3$, i.e.,$p=3$, with one expansive mapping$T:A_1\cup A_2\cup A_3\to A_1\cup A_2\cup A_3$for the switches from$A_1$to$A_2$, while those from$A_2$to$A_3$and from$A_1$to$A_3$are contractive, one has the following limit constraint relations to guarantee the eventual convergence of the distances for$\widehat{D}=D_2$if$D_2=D_3=\lambda D$,$D_1=D$:

$${k^{\prime }}_{01}D+\left({k^{\prime }}_{01}-1\right)D\le \widehat{D}\le \lambda \hspace{0.17em}\underset{i=1,2}{min}\left({k^{\prime }}_{i}D+\left(1-{k^{\prime }}_i\right)D\right)=\lambda \left({k^{\prime }}_{2}D+\left(1-{k^{\prime }}_2\right)D\right)=\lambda D$$

implying that$2\left({k^{\prime }}_{01}-\lambda \right)D\le 0$so that either$D=0$, that is,$cl{A}_1\cap cl{A}_2\ne \varnothing$, or$\lambda >{k^{\prime }}_{01}$so that$D_2=D_3=\lambda D>{k^{\prime }}_{01}D$so that, even, if$\widehat{D}=D_2=D_3$, then$\widehat{D}\ne D_1=D$, and then the convergence of the distances to$D_1$or that of the involved points to the best proximity points of$A_1$and$A_2$is not possible.

Note that Theorem 2 (iii) also implies the boundedness of the elements of any orbit $O\left(x_0\right)$, what is now termed as such an orbit being bounded, as it is now specifically addressed:

Theorem 3.

Under Assumptions A1 to A4, consider any orbit$O\left(x_0\right)$with bounded initial point$x_0=T^0{x}_0\in {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$,$x_{j+1}\in {\left(T{x}_j\right)}_i\cup {\left(T{x}_j\right)}_{i+1}\subset T^j{x}_0\subset {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$. If Theorem 2 (iii) holds, then such an orbit$O\left(x_0\right)$is bounded.

Proof. 

It is obvious from generation of the orbit $O\left(x_0\right)$, for some given initial point $x_0\in {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$, that $x_j\in {\left(T^j{x}_0\right)}_{\ell }\subset T^j{x}_0\subset A_{{\ell }_j}$ for some ${\ell }_j=\ell \left(j\right)\in \overline{p}$, $j\in \overline{k}$ and any given finite $k\in {\mathit{Z}}_{0+}$. The partial orbit $O_{\left[0,k\right]}\left(x_0\right)=\left\{O_{k-1}\left(x_0\right),x_k\right\}$ is bounded since $k\in {\mathit{Z}}_{0+}$ is finite and $x_0$ is bounded. Since $k$ is finite then $d\left(x_0,x_k\right)$ is finite. Now, assume that there is some sequence ${\left\{x_n\right\}}_{n=0}^{\infty }\subset {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ which has an unbounded subsequence ${\left\{x_{n_m}\right\}}_{m=0}^{\infty }$ with $n_0\ge k$. Since $\underset{j\to \infty }{lim sup} d\left(x_{N_{k+j}+1},x_{N_k}\right)<\infty$, take $N_k$ to be sufficiently closer to $n_k$ by taking the advantage that the incremental sequence ${\left\{N_{k+j}-N_{k+j-1}\right\}}_{j=0}^{\chi }$ with $N_{k-1}=k$, for the given $k\in {\mathit{Z}}_{0+}$, is bounded and one obtains also from (43) that if the subsequence ${\left\{x_{n_m}\right\}}_{m=0}^{\infty }\subset {\left\{x_n\right\}}_{n=0}^{\infty }$ is unbounded, then the following contradiction holds since $x_k\in {\left(T^k{x}_0\right)}_{\ell }\subset T^k{x}_0\subset A_{\ell }$ for some $\ell =\ell \left(k\right)\in \overline{p}$ and some finite $k\in {\mathit{Z}}_{0+}$, so that $x_k$ is finite:

$$+\infty =\underset{m\to \infty }{lim\hspace{0.17em}sup}\hspace{0.17em}d\left(x_{n_m},x_k\right)\le \underset{m\to \infty }{lim\hspace{0.17em}sup}\hspace{0.17em}d\left(x_{n_m},x_{N_m}\right)+\underset{m,j\to \infty }{lim sup}\hspace{0.17em}d\left(x_k,x_{N_{n_m}}\right)\le \underset{m\to \infty }{lim sup}\hspace{0.17em}d\left(x_{n_m},x_{N_m}\right)+C<+\infty$$

Therefore, any sequence ${\left\{x_n\right\}}_{n=0}^{\infty }\subset {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ is bounded. □

Note that Theorem 2 (iii) assumes that $d\left(x_0,x_k\right)$ is finite as an “a priori” stipulation for the boundedness of the sequence of distances in-between adjacent elements of the orbit $O\left(x_0\right)$. However, Theorem 3 assumes that the initial point $x_0$ of the considered orbits is finite in order to guarantee that the partial orbit of a finite number of elements starting by $x_0$ is bounded. This assumption would not be invoked if the subsets $A_i$ for $i\in \overline{p}$ were bounded.

4. Some Particular Results: The Case of Non-Expansivity and That of Monitored Switching

It is proved for $p=2$ in [1] (Lemma 3.8 based on Lemma 3.8), irrespective of the properties of the single-valued contractive 2-cyclic mapping $T:A_1\cup A_2\to A_1\cup A_2$, that if $\left(X,‖‖\right)$ is an uniformly convex Banach space and the subsets $A_1$ and $A_2$ of $X$ are non-empty, closed and convex then:

$$\begin{gathered} {\left[\left({\left\{x_n\right\}}_{n=0}^{\infty }\subset A_i\right)\wedge \left({\left\{z_n\right\}}_{n=0}^{\infty }\subset A_i\right)\wedge \left({\left\{y_n\right\}}_{n=0}^{\infty }\subset A_2\right)\wedge \left({\left\{‖x_n-y_n‖\right\}}_{n=0}^{\infty }\to D\right),\left({\left\{‖z_n-y_n‖\right\}}_{n=0}^{\infty }\to D\right)\right]}^{} \\ \Rightarrow \left({\left\{‖z_n-y_n‖\right\}}_{n=0}^{\infty }\to 0\right); \forall i\in \overline{p} \end{gathered}$$

(46)

Such a property holds irrespective of the mapping being single-valued or multivalued and without invoking whether it is contractive or not. It is also proved in [1] that if, furthermore, $T:A_1\cup A_2\to A_1\cup A_2$ is single-valued and 2-cyclic contractive then there is a unique best proximity point $z\in A_1$ such that $‖z-Tz‖=D$ and if $z_0\in A_1$ then ${\left\{T^{2n}{z}_0\right\}}_{n=0}^{\infty }\to z$ and ${\left\{T^{2n+1}{z}_0\right\}}_{n=0}^{\infty }\to Tz$, and ${\left\{T^{2n}{z}_0\right\}}_{n=0}^{\infty }$ and ${\left\{T^{2n+1}{z}_0\right\}}_{n=0}^{\infty }$ are Cauchy sequences.

The subsequent result firstly establishes some best proximity results in the case that there are no iterations of the mixed $p$-cyclic/acyclic multivalued mapping $T:{\displaystyle {\cup }_{i\in \overline{p}}{A}_i}\to {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$, $p\ge 2$, within each of the subsets $A_i$ provided that the complete metric space that the subsets $A_i$ for $i\in \overline{p}$ belong to is a uniformly convex Banach space and that the mapping is contractive at least from one switching of one of the subsets to its right adjacent one in the event that it is not expansive from any of the subsets to its right adjacent one. Since there are no iterations between each subset before switching to its right adjacent one, the $p$-cyclic/acyclic mapping $T:{\displaystyle {\cup }_{i\in \overline{p}}{A}_i}\to {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ is, in particular, a multivalued $p$-cyclic mapping due to the absence of internal iterations within each of the subsets. Later on, in the second property of the theorem, a new result generalizes the results to the case when $T:{\displaystyle {\cup }_{i\in \overline{p}}{A}_i}\to {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ has iterations within the subsets before switching to the right adjacent ones (i.e., it is of cyclic/acyclic nature) under certain conditions of Theorem 2.

Theorem 4.

Assume that:

(A1)$\left\{A_i:i\in \overline{p}\right\}$are non-empty closed and convex subsets of a uniformly convex Banach space$\left(X,‖‖\right)$.

(A2) Assume that$T:{\displaystyle {\cup }_{i\in \overline{p}}{A}_i}\to {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$is a mixed$p$-cyclic/acyclic mapping, subject to$T\left(A_i\right)\subseteq A_i\cup A_{i+1}$;$\forall \in \overline{p}$with respect to the norm-induced metric$d:X\times X\to {\mathit{R}}_{0+}$;$\forall i\in \overline{p}$, by the norm of$\left(X,‖‖\right)$, which satisfies (31) and (32), under the constraints$S_c=\left\{A_i:i\in p_c\right\}\ne \varnothing$,$S_e=\left\{A_i:i\in p_e\right\}=\varnothing$(so that${\displaystyle {\cup }_{i\in \overline{p}}{A}_i}=S_c\cup S_{ne}$and$\overline{p}=p_c\cup p_{ne}$),$k_i={k^{\prime }}_i<1$;$\forall i\in p_c$,$D_i=D$,$n_i\left(k,N_k\right)=0$;$\forall i\in \overline{p}$,$\forall k\in {\mathit{Z}}_{0+}$such that for each$x\in A_i$and each$i\in \overline{p}$,$Tx={\left(Tx\right)}_{i+1}$with${\left(Tx\right)}_{i+1}\left(\ne \varnothing \right)\subset A_{i+1}$;$\forall i\in \overline{p}$.

Then, the following properties hold:

(i) 

There is a best proximity point$z_i$in$A_i$with respect to$A_{i+1}$, that is,$d\left(z_i,{\left(T{z}_i\right)}_{i+1}\right)=D$;$\forall i\in \overline{p}$. Furthermore, for any$i\in \overline{p}$, if$x\in A_i$, then${\left\{{\left(T^{pn+j}x\right)}_{i+j}\right\}}_{n=0}^{\infty }\to z_{i+j}\in A_{i+j}$for$j\in \overline{p-1}$is a best proximity point in$A_{i+j}$with respect to$A_{i+j+1}$, and$z_i\in {\left(T^p{z}_i\right)}_i$is also a fixed point in$A_i$of the composite mappings$T^p:{\displaystyle {\cup }_{i\in \overline{p}}{A}_i}|A_j\to {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}|A_j$;$\forall j\in \overline{p}$.

(ii) 

If Assumption A2 holds under the subsequent generalizations: (a)$n_i\left(N_k,N_{k+1}\right)\ge 0$;$\forall i\in \overline{p}$, for some given$k\in {\mathit{Z}}_{0+}$with$N_{k-1}=k$,${\left\{N_j\right\}}_{j=0}^{\infty }\subset {\mathit{Z}}_{0+}$being strictly increasing and the incremental sequence${\left\{N_j-N_{j-1}\right\}}_{j=0}^{\infty }\subset {\mathit{Z}}_{0+}$being uniformly bounded and covering a whole cycle of iterations covering all the subsets$A_i$for$i\in \overline{p}$, such that for each$x\in A_i$and each$i\in \overline{p}$,$Tx=\left\{{\left(Tx\right)}_i,{\left(Tx\right)}_{i+1}\right\}$with${\left(Tx\right)}_{i+1}\left(\ne \varnothing \right)\subset A_{i+1}$,$\forall i\in \overline{p}$and${\left(Tx\right)}_{i1}\left(\ne \varnothing \right)\subset A_i$in the case when$n_i\left(N_k,N_{k+1}\right)>0$for some$N_k\in {\left\{N_k\right\}}_{k=0}^{\infty }$; and

$$\underset{N_k\in {\left\{N_j\right\}}_{j=0}^{\infty }}{sup}\frac{ln{K}_1\left(N_k,N_{k+1}\right)}{p}<0$$

(47)

where$K_1\left(N_k,N_{k+1}\right)={\displaystyle {\prod }_{j=1}^p\left[k_j^{n_j\left(N_k,N_{k+1}\right)+1}\right]}$.

Proof. 

Since $S_c=\left\{A_j:j\in P_c\right\}\ne \varnothing$, it exists $A_i\in S_c$ for some $i\in \overline{p}$. Consider, with no loss in generality, initial points $x_1,y_1\in A_i$ of the sequences ${\left\{T^{np+j}{x}_1\right\}}_{n=0}^{\infty }\subset A_{i+j}$ and ${\left\{T^{np+j}{y}_1\right\}}_{n=0}^{\infty }\subset A_{i+j}$; $\forall j\in \overline{p-1}\cup \left\{0\right\}$ generated by $T:{\displaystyle {\cup }_{i\in \overline{p}}{A}_i}\to {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ under the constraint $n_i=0$; $\forall i\in \overline{p}$, which makes $T\left(A_i\right)\subseteq A_i\cup A_{i+1}$ become $T\left(A_i\right)\subseteq A_{i+1}$; $\forall i\in \overline{p}$. The choice of $x_1$ and $y_1$ in $A_i$ is without loss of generality since for any given $x_{01},y_{01}\in {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$, there are nonnegative integers $j,k\in \overline{p}$ such that one can fix $x_1\in T^j{x}_{01}\subset A_i$ and $y_1\in T^k{x}_{01}\subset A_i$ for any prefixed subset $A_i\in S_c$ of ${\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$. Since $A_i\in S_c$, ${k^{\prime }}_j=k_j$, $\forall j\in \overline{p}$ and ${\displaystyle {\cup }_{i\in \overline{p}}{A}_i}=S_c\cup S_{ne}$, it turns out that ${\displaystyle {\prod }_{j=1}^p\left[k_j\right]}\le k_i<1$ so that:

$$d\left(T^{np+j}{x}_1,T^{np+j+1}{y}_1\right)\le k_i^{n}d\left(x_1,y_1\right)+\left(1-k_i^n\right)D$$

(48)

$$d\left(T^{\left(n+k\right)p+j}{y}_1,T^{\left(n+k\right)p+j+1}{y}_1\right)\le k_i^{n+k}d\left(T{y}_1,y_1\right)+\left(1-k_i^{n+k}\right)D$$

(49)

Then, ${\left\{d\left(T^{np+j}{x}_1,T^{np+j+1}{y}_1\right)\right\}}_{n=0}^{\infty }\to D$ and ${\left\{d\left(T^{\left(n+k\right)p+j}{y}_1,T^{\left(n+k\right)p+j+1}{y}_1\right)\right\}}_{n=0}^{\infty }\to D$ for any given $x_1,y_1\left(\ne x_1\right)\in A_i$, $\forall k\in {\mathit{Z}}_{0+}$ with ${\left\{T^{\left(n+k\right)p+j+1}{x}_1\right\}}_{k=0}^{\infty }\subset A_{i+j+1}$ and ${\left\{T^{\left(n+k\right)p+j+1}{y}_1\right\}}_{k=0}^{\infty }\subset A_{i+j+1}$ for any $k\in {\mathit{Z}}_{0+}$. Since $\left(X,‖‖\right)$ is a uniformly Banach space, and $A_j\left(j\in \overline{p}\right)$ are closed and convex and $A_i\in S_c$, one concludes also that ${\left\{d\left(T^{np}{x}_1,T^{\left(n+k\right)p}{y}_1\right)\right\}}_{n=0}^{\infty }\to 0$ and that ${\left\{T^{\left(n+k\right)p}{x}_1\right\}}_{n=0}^{\infty }\to z_i\in A_i$ is a Cauchy sequence. It also holds that $z_i\in A_i$ is a fixed point of the composite mapping $T^p:{\displaystyle {\cup }_{j\in \overline{p}}{A}_j}|A_j\to {\displaystyle {\cup }_{j\in \overline{p}}{A}_j}|A_i$, then $z_i\in {\left(T^p{z}_i\right)}_i$. As a result, $z_{i+j}\in {\left(T^{p+j}{z}_i\right)}_{i+j}={\left(T^p\left(T^j{z}_i\right)\right)}_{i+j}={\left(T^p{z}_{i+j}\right)}_{i+j}\in A_{i+j}$; $\forall j\in \overline{p}$ and $z_{i+j}\in {\left(T^j{z}_i\right)}_{i+j}\subset {\left(T^p{z}_{i+j}\right)}_{i+j}$ is a fixed point of $T^p:{\displaystyle {\cup }_{k\in \overline{p}}{A}_k}|A_{i+j}\to {\displaystyle {\cup }_{k\in \overline{p}}{A}_k}|A_{i+j}$ in $A_{i+j}$ and also a best proximity point in $A_{i+j}$ of $A_{i+j-1}$ since $d\left(z_{i+j-1},z_{i+j}\right)=D$ because $A_j\in S_{ne}\cup S_c$; $\forall j\in \overline{p}$ implies that $D=d\left(A_i,A_{i+1}\right)\ge d\left(A_{i-j},A_{i-j+1}\right)=D$; $\forall j\in \overline{p}$ and the given $i\in {\overline{p}}_c$ such that $A_i\in S_c$.

${\left\{T^{\left(n+k\right)p+j}{x}_1\right\}}_{n=0}^{\infty }\to z_{i+j}\in A_{i+j}$ and that ${\left\{T^{\left(n+k\right)p+j}{x}_1\right\}}_{n=0}^{\infty }$ are convergent and Cauchy sequences; $\forall j\in \overline{p}$. Note that, since $\left\{T^{\left(n+k\right)p}{x}_1\right\}\to z_i\in A_i$ if $A_i\in S_c$ since $A_i$ is closed, and the sequences $\left\{T^{\left(n+k\right)p-1}{x}_1\right\}$ and $\left\{T^{\left(n+k\right)p-1}{y}_1\right\}$ for any given $k\in {\mathit{Z}}_{0+}$ fulfill that ${\left\{d\left(T^{\left(n+k\right)p-1}{x}_1,T^{\left(n+k\right)p}{x}_1\right)\right\}}_{n=0}^{\infty }\to D$ and ${\left\{d\left(T^{\left(n+k\right)p-1}{y}_1,T^{\left(n+k\right)p}{x}_1\right)\right\}}_{k=0}^{\infty }\to D$, one obtains that ${\left\{d\left(T^{\left(n+k\right)p-1}{x}_1,T^{\left(n+k\right)p-1}{y}_1\right)\right\}}_{n=0}^{\infty }\to 0$ for any given $x_1,y_1\in A_1$ and ${\left\{T^{\left(n+k\right)p-1}{x}_1\right\}}_{n=0}^{\infty }$ is convergent to ${z^{\prime }}_{i-1}\in A_{i-1}\equiv A_{p+i-1}$ since $A_{i-1}$ is closed. Continuing with this process, one obtains that ${\left\{T^{\left(n+k\right)p-j}{x}_1\right\}}_{n=0}^{\infty }\to {z^{\prime }}_{i-j}\in A_{i-j}\equiv A_{p+i-j}$; $\forall j\in \overline{p-1}\hspace{0.17em}$. Assume that ${z^{\prime }}_{i-1}\ne z_{i-1}\in A_i$. Then, one obtains that ${\left\{d\left(T^{\left(n+k\right)p-1}{y}_1,T^{\left(n+k\right)p}{x}_1\right)\right\}}_{k=0}^{\infty }\to D$ and ${\left\{d\left(T^{\left(n+k\right)p-1}{x}_1,T^{\left(n+k\right)p-1}{y}_1\right)\right\}}_{n=0}^{\infty }\to 0$ with convergent sequences ${\left\{T^{\left(n+k\right)p-1}{x}_1\right\}}_{n=0}^{\infty }\to z_{i-1}$ and ${\left\{T^{\left(n+k\right)p-1}{y}_1\right\}}_{n=0}^{\infty }\to {z^{\prime }}_{i-1}$. However, then $\underset{n\to \infty }{lim inf}{\left\{d\left(T^{\left(n+k\right)p-1}{x}_1,T^{\left(n+k\right)p-1}{y}_1\right)\right\}}_{n=0}^{\infty }>0$ which is a contradiction to ${\left\{d\left(T^{\left(n+k\right)p-1}{x}_1,T^{\left(n+k\right)p-1}{y}_1\right)\right\}}_{n=0}^{\infty }\to 0$ then $z_{i-1}={z^{\prime }}_{i-1}$. Continuing in the same way with this process for $i-p+1\le j\le i-1$, one concludes that $z_i\in A_i$ are unique best proximity points in $A_i$ of $A_{i+1}$, which are fixed points of the composite mapping $T^p$. As a result, property (i) is proved.

To prove property (ii), note that under Assumption 1 and the given generalized Assumption 2, and, since ${k^{\prime }}_j=k_j\le 1$; $\forall j\in \overline{p}$ and $\underset{N_k\in {\left\{N_j\right\}}_{j=0}^{\infty }}{sup}\frac{ln\hspace{0.17em}{K}_1\left(N_k,N_{k+1}\right)}{p}<0$, then

$$K_1\left(N_k,N_{k+1}\right)={\displaystyle {\prod }_{j=1}^p\left[k_j^{n_j\left(N_k,N_{k+1}\right)}{k^{\prime }}_j\right]}={\displaystyle {\prod }_{j=1}^p\left[k_j^{n_j\left(N_k,N_{k+1}\right)+1}\right]}\le k_i^{n_i\left(N_k,N_{k+1}\right)+1}<1$$

(50)

since $A_i\in S_c$ then $K_1\left(N_k,N_{k+1}\right)\le K^p<1$ for some real constant $K\in \left[0,1\right)$ and any given $k\in {\mathit{Z}}_{0+}$. According to Theorem 2, Equations (35) and (36), one concludes in the same way as getting (48) and (49) that, for any given $x_1,y_i\in A_i\in S_c$,

$$d\left(T^{{\displaystyle {\sum }_{\ell =k-1}^{k+n}\left(N_{\ell +1}-N_{\ell }\right)}+j}{x}_1,T^{{\displaystyle {\sum }_{\ell =k-1}^{k+n}\left(N_{\ell +1}-N_{\ell }\right)}+j+1}{y}_1\right)\le K^{n}d\left(x_1,y_1\right)+\left(1-K^n\right)D; \forall j\in \overline{p},\hspace{0.17em}\forall n\in {\mathit{Z}}_{0+}$$

(51)

$$d\left(T^{{\displaystyle {\sum }_{\ell =k-1}^{k+n}\left(N_{\ell +1}-N_{\ell }\right)}+j}{y}_1,T^{{\displaystyle {\sum }_{\ell =k-1}^{k+n}\left(N_{\ell +1}-N_{\ell }\right)}+j+1}{y}_1\right)\le K^{n}d\left(x_1,y_1\right)+\left(1-K^n\right)D; \forall j\in \overline{p},\hspace{0.17em}\forall n\in {\mathit{Z}}_{0+}$$

(52)

so that

$$\underset{j\in \overline{p}n\to \infty }{lim}\hspace{0.17em}d\left(T^{{\displaystyle {\sum }_{\ell =k-1}^{k+n}\left(N_{\ell +1}-N_{\ell }\right)}+j}{x}_1,T^{{\displaystyle {\sum }_{\ell =k-1}^{k+n}\left(N_{\ell +1}-N_{\ell }\right)}+j+1}{y}_1\right)=\underset{n\to \infty }{lim}\hspace{0.17em}d\left(T^{{\displaystyle {\sum }_{\ell =k-1}^{k+n}\left(N_{\ell +1}-N_{\ell }\right)}+j}{y}_1,T^{{\displaystyle {\sum }_{\ell =k-1}^{k+n}\left(N_{\ell +1}-N_{\ell }\right)}+j+1}{y}_1\right)=D$$

(53)

$$\underset{m\in {\mathit{Z}}_{0+},n\to \infty }{lim}\hspace{0.17em}d\left(T^{{\displaystyle {\sum }_{\ell =k-1}^{k+n}\left(N_{\ell +1}-N_{\ell }\right)}}{x}_1,T^{{\displaystyle {\sum }_{\ell =k-1}^{k+mn}\left(N_{\ell +1}-N_{\ell }\right)}}{y}_1\right)=0$$

(54)

The remaining of the proof of property (ii) follows in a similar way to that of property (i). □

Remark 6.

If$S_e\ne \varnothing$in Theorem 4 so that values of the constants$k_j>1$for$A_j\in S_e$are compensated by other contractive constant values$k_j<1$for$A_j\in S_c\cup S_{ne}$while (47) holds then (53) and (54) in Theorem 4 (ii) still hold. H, it cannot be proved, in general, the convergence of sequences to the best proximity points of adjacent subsets$A_i$and$A_{i+1}$for$i\in \overline{p}$of$X$.

The statements of the given results until now consider the event that the number of consecutive iterations within each subset $A_i$ before switching to $A_{i+1}$ is either pre-designed, including a fixed number of iterations, eventually being iteration-dependent, within each $A_i$, or monitored in the sense that the switching be decided by a switching rule $\sigma :{\mathit{Z}}_{0+}\to \overline{p}$ such that if $\sigma \left(k\right)=\sigma \left(k+1\right)=i\left(\in \overline{p}\right)$, then there is not a switch at the $k$-th iteration of $T$ from $A_i$ to $A_{i+1}$ for some $i\in \overline{p}$ and the partial orbit of any $x_0\in {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$ fulfills $O_{\left[0,k+1\right]}\left(x_0\right)=\left(O_{\left[0,k\right]}\left(x_0\right),x_{k+1}\right)$ with $O_{\left[0,k\right]}\left(x_0\right)=\left(x_0,x_1,\cdots ,x_k\right)$ satisfying $x_k\in {\left(T{x}_{k-1}\right)}_i\subset A_i$, $x_{k+1}\in {\left(T{x}_k\right)}_i\subset {\left(T^2{x}_{k-1}\right)}_i\subset A_i$.

On the other hand, if $\left(\overline{p}∍\right)i=\sigma \left(k\right)\ne \sigma \left(k+1\right)=i+1\left(\in \overline{p}\right)$, the mapping $T$ switches from $A_i$ to $A_{i+1}$ at the $k$-th iteration so that the partial orbit $O_{\left[0,k+1\right]}\left(x_0\right)=\left(O_{\left[0,k\right]}\left(x_0\right),x_{k+1}\right)=\left(O_{\left[0,k-1\right]}\left(x_0\right),x_k,x_{k+1}\right)$ exhibits a switch in the allocation set from $x_k\in A_i$ to $x_{k+1}\in A_{i+1}$.

The monitored strategy of switching between the subsets $A_i$; $\forall i\in \overline{p}$ of $X$ according some rule $\sigma :{\mathit{Z}}_{0+}\to \overline{p}$ is of interest in certain applications. For instance, if the stabilization of a discrete dynamic system cannot be achieved for successive iterations within a set because of inherent instability within it, then it is convenient to assign it along certain transients. Additionally, an instability problem could arise if a discrete system becomes unstable under its current parameterization. This drawback can be eventually solved by generating switches in its state, together eventually with parameterization switches, which lead again the trajectory to a stable region. See, for instance, [24,25,26,27,28,29,30]. The following immediate result establishes the convergence of sequences to a fixed point of any subset $A_i$, where the mapping is contractive, under any monitored switching rule which confines the successive iterations within such a subset after a finite number of iterations.

Theorem 5.

Consider a pair$\left(T,\sigma \right)$, where$T:{\displaystyle {\cup }_{i\in \overline{p}}{A}_i}\to {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$is a self-mapping under assumptions A1 and A2 of Theorem 4 and$\sigma :{\mathit{Z}}_{0+}\to \overline{p}$is a monitored switching rule between a subset$A_j$and its right adjacent one$A_{j+1}$;$\forall j\in \overline{p}$. Assume that for some finite$k_0\in {\mathit{Z}}_{0+}$,$\sigma \left(k_0+\ell \right)=\sigma \left(k_0\right)\in \overline{p}$;$\forall \ell \in {\mathit{Z}}_{0+}$such that$A_{\sigma \left(k_0\right)}\in S_c$. Then, any sequence${\left\{T^n{x}_0\right\}}_{n=0}^{\infty }\to g_i$where$g_i\in {\left(T{g}_i\right)}_i\subset T{g}_i\subset A_i$is a fixed point of$T$for any given$x_0\in {\displaystyle {\cup }_{i\in \overline{p}}{A}_i}$.

Proof. 

It is obvious since the monitored switching rule $\sigma :{\mathit{Z}}_{0+}\to \overline{p}$ determines that any partial orbit $O_{\left[k_0,k\right]}\left(x_0\right)=\left(x_{k_0},x_{k_0+1},\dots ,x_k\right)$ of the orbit $O\left(x_0\right)$ is confined within $A_i\in S_c$, which has a fixed point from since $A_i$ is closed and ${\left(Tx\right)}_i$ is closed for any $x\in A_i$. If $T:\left({\displaystyle {\cup }_{j\in \overline{p}}{A}_j}\right)|A_i\to {\displaystyle {\cup }_{j\in \overline{p}}{A}_j}|\left(A_i\cup A_{i+1}\right)$ is single-valued, then $g_i=T{g}_i$ is unique since $A_i$ is closed and convex. □

5. Numerical Simulations

This section is aimed at illustrating the previous obtained results concerning the boundedness of sequences and orbits of cyclic/acyclic contractive/non-contractive self-mappings. To this end, the case of a discrete-time dynamical system is discussed. Thus, consider the dynamic system given by:

$$x_{k+1}=x_k{y}_k$$

(55)

$$y_{k+1}=-x_k{y}_k$$

(56)

; $\forall k\in {\mathit{Z}}_{0+}$. The system is described by the self-mapping $T(x_k,y_k)=x_k{y}_k(1,-1)$. This self-mapping has a different behavior depending on $\left|x_k{y}_k\right|>1$, $\left|x_k{y}_k\right|=1$ or $\left|x_k{y}_k\right|<1$, generating the following three subsets:

$$\begin{array}{c}{A}_1=\left\{(x,y)\in R^2|\left|xy\right|>1\right\}=A_{11}\cup A_{21}\cup A_{31}\cup A_{41}\end{array}$$

$$\begin{array}{c}{A}_2=\left\{(x,y)\in R^2|\left|xy\right|<1\right\}=A_{12}\cup A_{22}; A_3=\left\{(x,y)\in R^2|\left|xy\right|=1\right\}\end{array}$$

(57)

with

$$A_{11}=\left\{(x,y)\in R^2|\left|xy\right|>1,x>0,y>0\right\}; A_{21}=\left\{(x,y)\in R^2|\left|xy\right|>1,x<0,y>0\right\}$$

$$A_{31}=\left\{(x,y)\in R^2|\left|xy\right|>1,x<0,y<0\right\}; A_{41}=\left\{(x,y)\in R^2|\left|xy\right|>1,x>0,y<0\right\}$$

$$A_{12}=\left\{(x,y)\in R^2|-\frac{1+\sqrt{5}}{2}<x<-\frac{2}{1+\sqrt{5}},y=-1/x\wedge -\frac{2}{1+\sqrt{5}}\le x\le 0,y=\frac{1+\sqrt{5}}{2}\right\}; A_{22}=A_2-A_{12}$$

(58)

The set A₁ is disconnected and can be represented by the union of four connected disjoint subsets. These subsets are called $A_{11}$, $A_{21}$, $A_{31}$ and $A_{41}$ as is displayed in Figure 1 where the blue lines depict the hyperbola $y=1/x$. On the other hand, the set A₂ is connected and it is split into two subsets, namely $A_{12}$ and $A_{22}$, as in Figure 1.

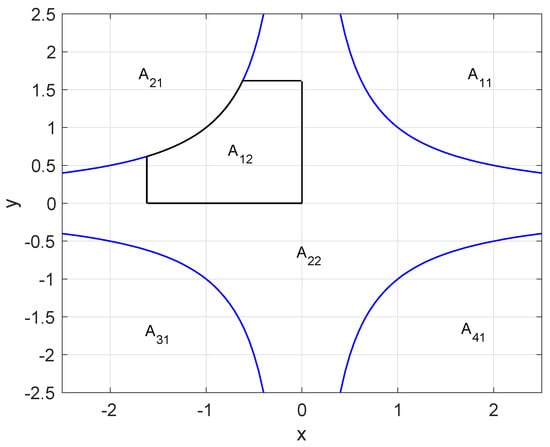
Figure 1. Different regions on the plane for the self-mapping (55) and (56).

Note that $A_1,\hspace{0.17em}{A}_2$ and $A_3$ are disjoint unbounded subsets of ${\mathit{R}}^2$, with $A_1$ and $A_2$ being open and $A_3$ being closed. Since those sets are disjoint, the sets of best proximity points between each pair of them are empty, but because of the asymptotes defined in blue lines which define the boundaries, the distances between adjacent subsets are zero. Note that $T$ is a self-mapping on ${\mathit{R}}^2=A_1\cup A_2\cup A_3$ so that $T:A_1\cup A_2\cup A_3\to A_1\cup A_2\cup A_3$ and $T\left(A_3\right)\subset A_3$. Note also from (55) and (56) that, for any given initial point $z_0=\left(x_0,y_0\right)\in {\mathit{R}}^2$, the Euclidean distance between consecutive points of iterations through $T$ satisfies with $z_k=\left(x_k,y_k\right)\in {\mathit{R}}^2$; $\forall k\in {\mathit{Z}}_{0+}$:

$$\begin{array}{c}d\left(z_{k+1},z_k\right)=\sqrt{{\left(x_{k+1}-x_k\right)}^2+{\left(y_{k+1}-y_k\right)}^2}=\sqrt{{\left(y_k-y_{k+1}\right)}^2+{\left(y_{k+1}-y_k\right)}^2}\\ =\sqrt{2}\left|y_{k+1}-y_k\right|=\sqrt{2}\left|y_k+x_k{y}_k\right|=\sqrt{2}\left|y_k\right|\left|1+x_k\right|\\ =\sqrt{2}\left|x_k\right|\left|1+x_k\right|=\sqrt{2}\left|y_k\right|\left|1-y_k\right|; \forall k\in {\mathit{Z}}_{+}\end{array}$$

(59)

which becomes asymptotically unbounded as $k\to \infty$ if $\left|x_k\right|\to \infty$, or if $\left|y_k\right|\to \infty$, as $k\to \infty$. We can define the contractivity-, non-expansivity- and expansivity-point-dependent constants as:

$$k\left(z_{k-1},z_k\right)=\frac{d\left(z_{k+1},z_k\right)}{d\left(z_k,z_{k-1}\right)}=\frac{\left|x_k\right|\left|1+x_k\right|}{\left|x_{k-1}\right|\left|1+x_{k-1}\right|}; \forall k\in {\mathit{Z}}_{+}$$

(60)

Thus, the Euclidean distances between consecutive points of arbitrary orbits being calculated via iterations through $T$ from finite initial points in ${\mathit{R}}^2$ are not necessarily asymptotically bounded. Then, some monitoring of switching between the three subsets $A_1$, $A_2$ and $A_3$ should be performed to guarantee their asymptotic boundedness. Note the following facts:

Fact 1.

One obtains from (55) and (56) that$x_k\le 0$and$y_k=-x_k\ge 0$;$\forall k\in {\mathit{Z}}_{+}$. Therefore, the second semi-open quadrant$\left(0,1\right]\times \left(0,1\right]$of${\mathit{R}}^2$is unreachable (or forbidden) for any sequence solution of (55) and (56) except for initial points$\left(x_0,y_0\right)$. As a result, there are forbidden subsets of$A_{11}$and$A_{22}$(see (57) and (58) and Figure 1) which are unreachable except for the initial conditions.

Fact 2.

If$\left(x_{k-1},y_{k-1}\right)\in A_2$, then$\left|x_{k-1}{y}_{k-1}\right|<1$and$x_{k-1}^2=y_{k-1}^2<1$since$x_k=-y_k$, and then$x_{k-1}\in \left(-1,0\right]$;$\forall k\left(\ge 2\right)\in {\mathit{Z}}_{+}$. Thus,$\left|x_k\right|\le \left|x_{k-1}\right|$since$\left|x_k\right|=x_{k-1}^2\le 1$;$\forall k\in {\mathit{Z}}_{+}$. Additionally,$\left|x_k\right|<\left|x_{k-1}\right|$and$x_{k-1}\in \left(-1,0\right]$;$\forall k\in {\mathit{Z}}_{+}$imply that$-1<x_{k-1}<x_k<0$;$\forall k\in {\mathit{Z}}_{+}$. Then, the sequence${\left\{x_k\right\}}_{k=1}^{\infty }$is non-positive and convergent to zero under a weak contraction. Since${\left\{x_k\right\}}_{k=1}^{\infty }$is non-positive convergent to zero,${\left\{y_k\right\}}_{k=1}^{\infty }$is non-negative and convergent to zero from (55) and (56).

Fact 3.

($T$ is weakly contractive in$A_{22}$and a strict contraction in$A_{12}$): One obtains from (55), (56), (60) that

$$k\left(z_{k-1},z_k\right)=\frac{\left|x_k\right|\left(1-\left|x_k\right|\right)}{\left|x_{k-1}\right|\left(1-\left|x_{k-1}\right|\right)}=\frac{\left|x_k\right|-{\left|x_k\right|}^2}{\left|x_{k-1}\right|-{\left|x_k-1\right|}^2}=\frac{{\left|x_{k-1}\right|}^2-{\left|x_{k-1}\right|}^4}{\left|x_{k-1}\right|-{\left|x_k-1\right|}^2}=\left|x_{k-1}\right|+{\left|x_{k-1}\right|}^2$$

Since${\left\{x_k\right\}}_{k=1}^{\infty }$is convergent for any initial condition in$A_{22}$, from Fact 2, for any given real constant$k_c\in \left[0,1\right)$, there is some finite$r=r\left(k_c\right)\in {\mathit{Z}}_{+}$such that$k\left(z_{k-1},z_k\right)\le k_c^{}<1$;$\forall k\left(\ge r\right)\in {\mathit{Z}}_{+}$. By checking the inequality$p\left(\left|x_{k-1}\right|\right)=\left|x_{k-1}\right|+{\left|x_{k-1}\right|}^2-1<0$with and since$p\left(\left|x_{k-1}\right|\right)$is a convex parabola, one concludes that$p\left(\left|x_{k-1}\right|\right)<0$with$x_{k-1}\le 0$if$x_{k-1}\in \left(-\frac{1+\sqrt{5}}{2},0\right]$. As a result, any sequence${\left\{x_k\right\}}_{k=0}^{\infty }$, with$\left(x_0,y_0\right)\in A_{22}$, is non-positive with strictly decreasing modulus and, from (55) and (56),${\left\{y_k\right\}}_{k=0}^{\infty }$is non-negative and strictly decreasing, both sequences being convergent to zero. This implies that$T$is weakly contractive in$A_{22}$and it enters into$A_{12}$after a finite number of iterations, where$T$is a (strict) contraction with the solution${\left\{\left(x_k,y_k\right)\right\}}_{k=0}^{\infty }\to 0$for any$\left(x_0,y_0\right)\in A_2$.

Fact 4.

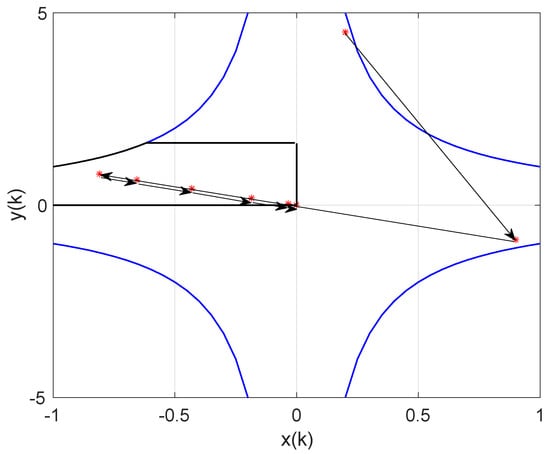
($\left(0,0\right)$is a fixed point of$T$and a global attractor of the solution for any initial condition in$A_{22}$). Additionally, if initial conditions are in the set A₁, then the self-mapping is expansive. The blue lines (set A₃) define the boundaries between regions, where the self-mapping is neither expansive nor contractive. The equilibrium points, which are the fixed points of$T$, are$\left(0,0\right)$and$\left(-1,1\right)$. Figure 2 displays the time evolution of the system when the initial conditions are in$A_{22}$and given by$x_0=0.2,y_0=4.5$. It is observed in Figure 2 how the sequence of iterates enters into$A_{12}$and converges to the equilibrium point (0, 0).

Figure 2. Evolution of the discrete-time dynamic system (55) and (56), when the initial conditions are $x_0=0.2,\hspace{0.17em}{y}_0=4.5$.

Fact 5.

($T$is expansive in$A_1$): For all$k\in {\mathit{Z}}_{+}$, if$\left(x_{k-1},y_{k-1}\right)\in A_1$, then$\left|x_{k-1}{y}_{k-1}\right|=1$,$x_{k-1}^2=y_{k-1}^2>1$since$x_k=-y_k$, which implies that$x_{k-1}<-1$and$x_{k-1}>1$. Therefore,$x_k=-\left|x_k\right|=-{\left|x_{k-1}\right|}^2<x_{k-1}=-\left|x_{k-1}\right|$so that$\frac{\left|x_k\right|}{\left|x_{k-1}\right|}>1$;$\forall k\in {\mathit{Z}}_{+}$. It can also be concluded that$y_k>y_{k-1}$and$\frac{\left|y_k\right|}{\left|k_{k-1}\right|}>1$;$\forall k\in {\mathit{Z}}_{+}$. Additionally,$x_k<x_{k-1}<-1$that$1+x_k<1+x_{k-1}<0$and$\left|1+x_k\right|>\left|1+x_{k-1}\right|$. Thus, one obtains from (60) that$T$is expansive in$A_1$since

$$k\left(z_{k-1},z_k\right)=\frac{\left|x_k\right|\left|1+x_k\right|}{\left|x_{k-1}\right|\left|1+x_{k-1}\right|}>\frac{\left|1+x_k\right|}{\left|1+x_{k-1}\right|}>\frac{\left|1+x_{k-1}\right|}{\left|1+x_{k-1}\right|}\ge \underset{k\in {\mathit{Z}}_{+}}{inf}\frac{\left|1+x_{k-1}\right|}{\left|1+x_{k-1}\right|}=1; \forall k\in {\mathit{Z}}_{+}.$$

Fact 6.

($T$is non-expansive and non-contractive in$A_3$). For all$k\in {\mathit{Z}}_{+}$, if$\left(x_{k-1},y_{k-1}\right)\in A_3$, then$\left|x_{k-1}{y}_{k-1}\right|=1$,$x_{k-1}^2=y_{k-1}^2=1$since$x_k=-y_k$, which implies that$\left|x_k\right|={\left|x_{k-1}\right|}^2=\left|x_{k-1}\right|=1$,$x_{k-1}=x_k<0$and$\frac{\left|x_k\right|}{\left|x_{k-1}\right|}=1$. Then,

$$k\left(z_{k-1},z_k\right)=\frac{\left|x_k\right|\left|1+x_k\right|}{\left|x_{k-1}\right|\left|1+x_{k-1}\right|}=\frac{\left|1+x_k\right|}{\left|1+x_{k-1}\right|}=\frac{\left|1-\left|x_k\right|\right|}{\left|1-\left|x_{k-1}\right|\right|}=\frac{\left|1-\left|x_{k-1}\right|\right|}{\left|1-\left|x_{k-1}\right|\right|}=1; \forall k\in {\mathit{Z}}_{+}$$

It is also observed that when the image of the self-mapping is included in $A_2$, the Euclidean distance between two consecutive iterations is bounded and the orbit converges to the origin, as corresponds to a contractive self-mapping, in accordance with Theorem 1. It should be to pointed out here that the distance between two consecutive iterations of the self-mapping is given by the length of the arrow depicted in Figure 2, which corresponds to the Euclidean distance. On the other hand, if initial conditions are in $A_{31}\subset A_1$, for instance, the self-mapping is expansive and the orbit diverges, as Figure 3 shows. Figure 3 displays how the length of the arrow increases resulting in an unbounded distance between consecutive iterations. This happens because the value K(i, 1) in Equation (12) from Theorem 1 is unbounded due to the expansive properties of the self-mapping.

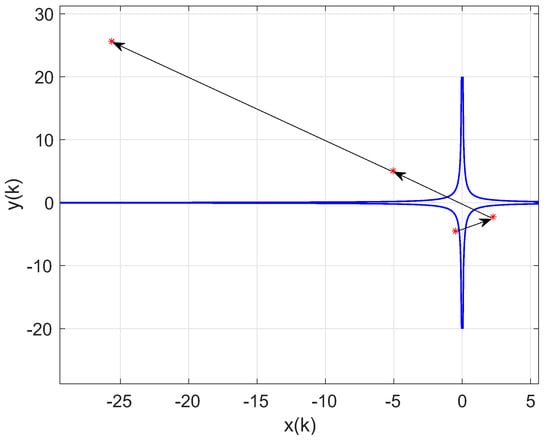
Figure 3. Evolution of the discrete-time dynamics system (55) and (56), when the initial conditions are $x_0=-0.5,\hspace{0.17em}{y}_0=-4.5$.

It can also be seen that the image of the self-mapping changes the subset from $A_{31}$ to $A_{34}$ and then to $A_{32}$, where it remains afterwards. This system can be stabilized in different ways. The clue to stabilizing this system is to include a mechanism in (55) and (56) to force the self-mapping to be cyclic, that is, to include a mechanism to make the self-mapping change its image from A₁ to A₂ so that any condition from Propositions 1, 2 or 3 is met. For instance, if we force the system to change its image to the set A₂ where it remains after a finite number of changes, then the orbit of the system and the distance between two consecutive iterations will both be bounded (Propositions 2 and 3, and their extensions to the general case, Theorems 2 and 3). Two mechanisms are presented in this section for this purpose: a feedback term added to this system and the impulsive control of states. Thus, a feedback term working in the following way is added:

$$x_{k+1}=x_k{y}_k-{\delta }_k\frac{x_k^2{y}_k^2}{1+x_k{y}_k}$$

(61)

$$x_{k+1}=-x_k{y}_k+{\delta }_k\frac{x_k^2{y}_k^2}{1+x_k{y}_k}$$

(62)

with

$${\delta }_k=\left\{\begin{array}{cc}1,\hfill & \left|x_k{y}_k\right|>1\hfill \\ 0,\hfill & otherwise\hfill \end{array}\right.$$

(63)

If the above feedback term is included in the system, the evolution of (55) and (56) changes to the one depicted in Figure 4.

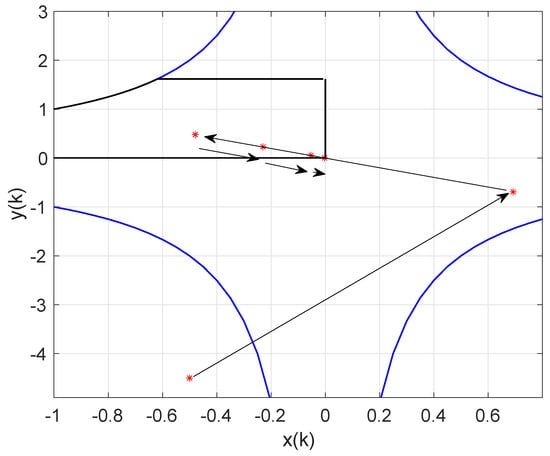
Figure 4. Evolution of the discrete-time dynamic system (61)–(63), when the initial conditions are $x_0=-0.5,\hspace{0.17em}{y}_0=-4.5$ and the feedback gain (63) is employed.

It is observed in Figure 4 that the feedback term acts moving the iteration from the set $A_{31}\subset A_1$, where the self-mapping is expansive, to the set $A_{22}\subset A_2$, and finally to $A_{12}\subset A_2$, where the self-mapping is contractive and where it remains. Consequently, according to Theorem 5, the distance between two consecutive iterations is bounded and converges to zero asymptotically, as seen in Figure 4 by the length of the arrows. Furthermore, this system could also be stabilized by applying an impulsive action to the states so that the controlled system reads:

$$x_{k+1}=x_k{y}_k$$

(64)

$$y_{k+1}=-x_k{y}_k$$

(65)

$$\left\{\begin{array}{c}{x}_k^{+}=0.4x_k^{-}\\ y_k^{+}=0.6y_k^{-}\end{array}\right., \left|x_k{y}_k\right|>1, k \mathrm{is} \mathrm{even}$$

(66)

where the value $x_k^{-}$ stands for the value of the state prior to the impulse, while $x_k^{+}$ represents the value immediately after the impulse. This case corresponds to the situation when the states of the system suffer an impulsive change whenever they are out of $A_2$ and the iteration is even. This is not the only impulsive action that could stabilize the system, but it is certainly one able to do so. Similarly, the effect of feedback, the impulsive action, causes the self-mapping to become cyclic, changing its image from set A₁ to A₂. The result of applying this impulsive action is portrayed in Figure 5.

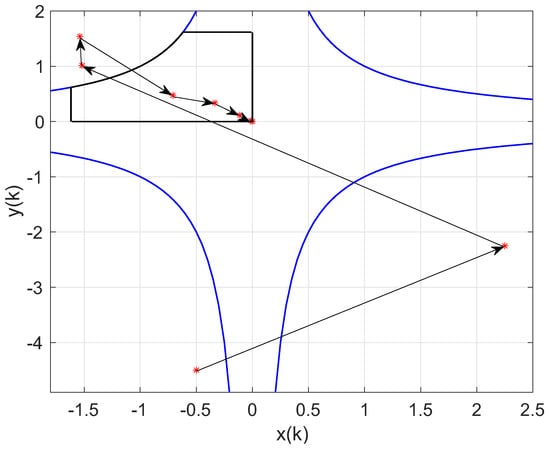
Figure 5. Evolution of the discrete-time dynamics system (64)–(66), when the initial conditions are $x_0=-0.5,\hspace{0.17em}{y}_0=-4.5$ and the impulsive action (66) is included in the system.

It is observed in Figure 5 how the impulsive action changes the image of the self-mapping and moves it from $A_{31}$ to $A_{41}$ and then to $A_{21}$ until it ends up in $A_{12}$, where it remains and the contractivity of the mapping causes the orbit to converge to the origin (0, 0). Since $A_{31}\cup A_{41}\cup A_{21}\subset A_1$ and $A_{12}\subset A_2$ then the monitored mixed cyclic/acyclic self-mapping T on $A_1\cup A_2\cup A_3$ satisfies $T\left(A_1\right)\subset A_1\cup A_2$, $T\left(A_2\right)\subset A_2$ and $T\left(A_3\right)\subset A_3$. It is also observed that the length of the arrows is bounded and converges to zero, as Theorem 5 predicts. Finally, we may consider the multivalued self-mapping given by:

$$x_{k+1}=\pm \sqrt{\left|x_k{y}_k\right|}$$

(67)

$$y_{k+1}=-\left|x_k\right|y_k$$

(68)

There are two branches in (67), one corresponding to the positive sign for the square root and another corresponding to the negative one. Figure 6 displays the evolution of the two images of the self-mapping when the initial conditions are given by $x_0=-0.5,y_0=-4.5$. The positive branch is depicted by asterisks in red, while the negative branch is portrayed with plus symbols.

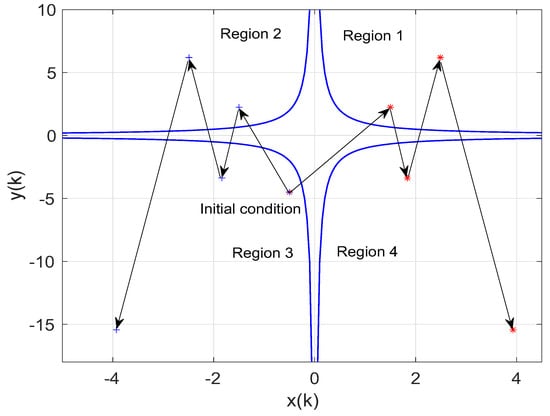
Figure 6. Evolution of the multi-valued discrete-time dynamic system (67) and (68), when the initial conditions are $x_0=-0.5,\hspace{0.17em}{y}_0=-4.5$. The positive branch is depicted by asterisks in red, while the negative branch is portrayed in blue plus symbols.

As Figure 6 shows, the multivalued mapping diverges and the distance between two successive iterations increases and is not asymptotically bounded. However, if an impulsive action is added to this system as:

$$x_{k+1}=\pm \sqrt{\left|x_k{y}_k\right|}$$

(69)

$$y_{k+1}=-\left|x_k\right|y_k$$

(70)

$$\left\{\begin{array}{c}{x}_k^{+}=0.4x_k^{-}\\ y_k^{+}=0.6y_k^{-}\end{array}\right., \left|x_k{y}_k\right|>1, k \mathrm{is} \mathrm{even}$$

(71)

Then, the system stabilizes, as Figure 7 depicts:

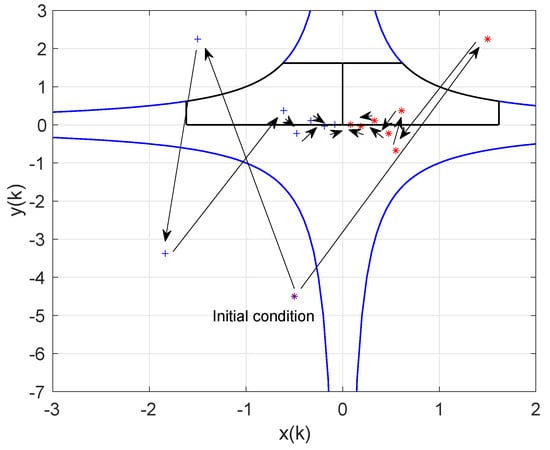
Figure 7. Evolution of the multi-valued discrete-time dynamic system (69)–(71), when the initial conditions are $x_0=-0.5,\hspace{0.17em}{y}_0=-4.5$ and the impulsive action (71) is included in the system. The positive branch is depicted by asterisks in red, while the negative branch is portrayed in blue plus symbols.

The effect of the impulsive action is to force the image of the mapping to move from $A_{31}\subset A_1$ to $A_{12}\subset A_2$, where the mapping is contractive. Under these circumstances, we are in the condition of applying Theorem 5, and the distance between two successive points reduces and the orbit converges to the origin and the stable equilibrium point of the system (0, 0) which is in $A_2$. There is another fixed point, $\left(-1,1\right)$, which is an unstable equilibrium point.

6. Conclusions

A multivalued self-mapping on the union of a finite number of subsets $p\left(\ge 2\right)$ of a metric space has been considered. Such a mapping might be of a mixed cyclic and acyclic nature being able to perform some iterations within each of the subsets before switching to its right adjacent one when generating orbits. The self-mapping is admitted to be either locally contractive, non-expansive/non-contractive and even locally expansive for different combinations of pairs of adjacent subsets. The properties of asymptotic boundedness of the distances associated with the elements of the orbits are proved under certain conditions of the global dominance of the contractivity for groups of consecutive iterations of the self-mapping, each of those groups of non-necessarily fixed size. If the metric space is a uniformly convex Banach space and the subsets are closed and convex, then some particular results on the convergence of the sequences of iterates to the best proximity points of the adjacent subsets are obtained in the absence of eventual local expansivity for switches between all the pairs of adjacent subsets. An application for the stabilization of a discrete dynamic system subject to impulsive effects in its dynamics due to finite discontinuity jumps in its state is also discussed. For that purpose, the iterations being run by the cyclic/acyclic self-mapping are subject to a monitoring process which is governed by a switching rule between adjacent subsets of the configuration in order to compensate for eventual instability of the solution under different system parameterizations and impulsive controls. Numerical examples were also given and discussed.