Verification of Approximate Initial-State Opacity for Control Systems via Neural Augmented Barrier Certificates
Abstract
1. Introduction
1.1. Research Motivation
- We define a new type of augmented barrier certificate, which can produce a weaker sufficient condition for the approximate initial-state opacity.
- We present a framework for synthesizing neural augmented barrier certificates. In the framework, a counterexample guided procedure is adopted to speed up the construction of networks, and the verification of Rectified Linear Unit (ReLU) networks can be efficiently performed via an MILP.
- We carry out proof-of-concept case studies to empirically show the efficiency and practicability of the approach.
1.2. Relate Work
2. An Augmented Barrier Certificate for Approximate Initial-State Opacity
2.1. Approximate Initial-State Opacity for Discrete-Time Control Systems
- , , andare the state set, control input set, and output set, respectively;
- , , andare the initial state set, secret state set, and non-secret state set, respectively, where, , ⊆ , and ⋂ = ∅;
- is the state transition function;
- is the output function.
2.2. A New Augmented Barrier Certificate for Approximate Initial-State Opacity
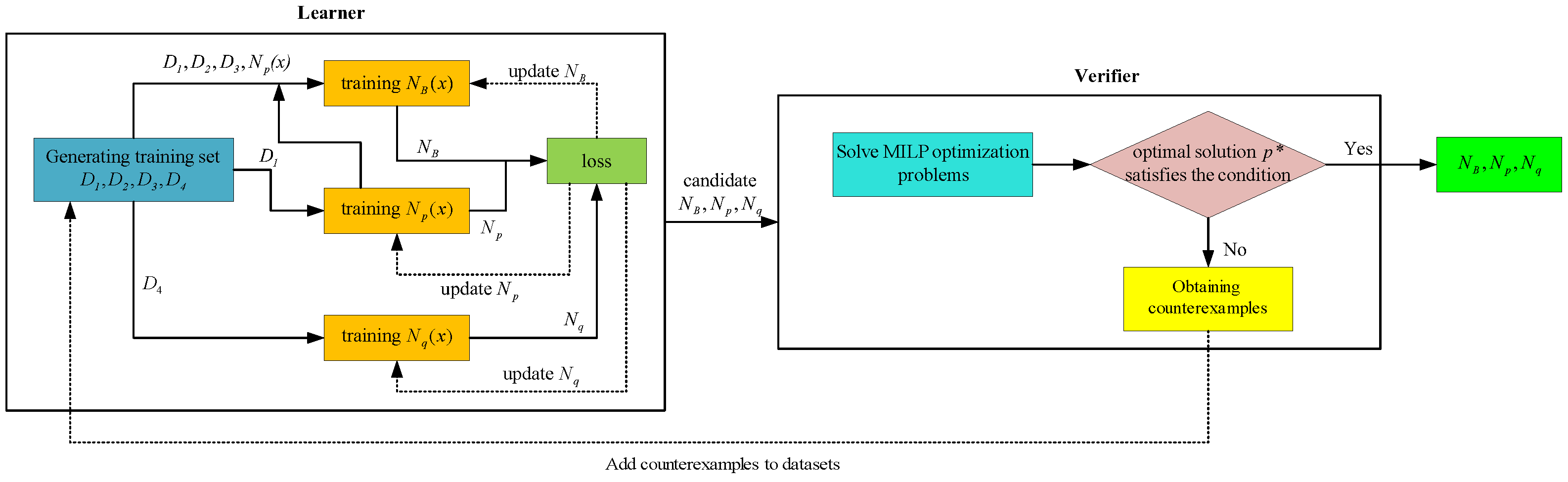
3. Synthesis of an Augmented Barrier Certificate via Learning and Verification
3.1. Neural Certificate Training
3.1.1. The Structure of Neural Networks
- One input layer, one output layer, and several hidden layers;
- The number of input neurons for , and q is , n, and , respectively;
- Both B and q have one output neuron, while p has n output neurons;
- The ReLU function is the only legal activation function.
3.1.2. Training Dataset Generation
3.1.3. Loss Function Encoding
3.2. Certificate Function Verification
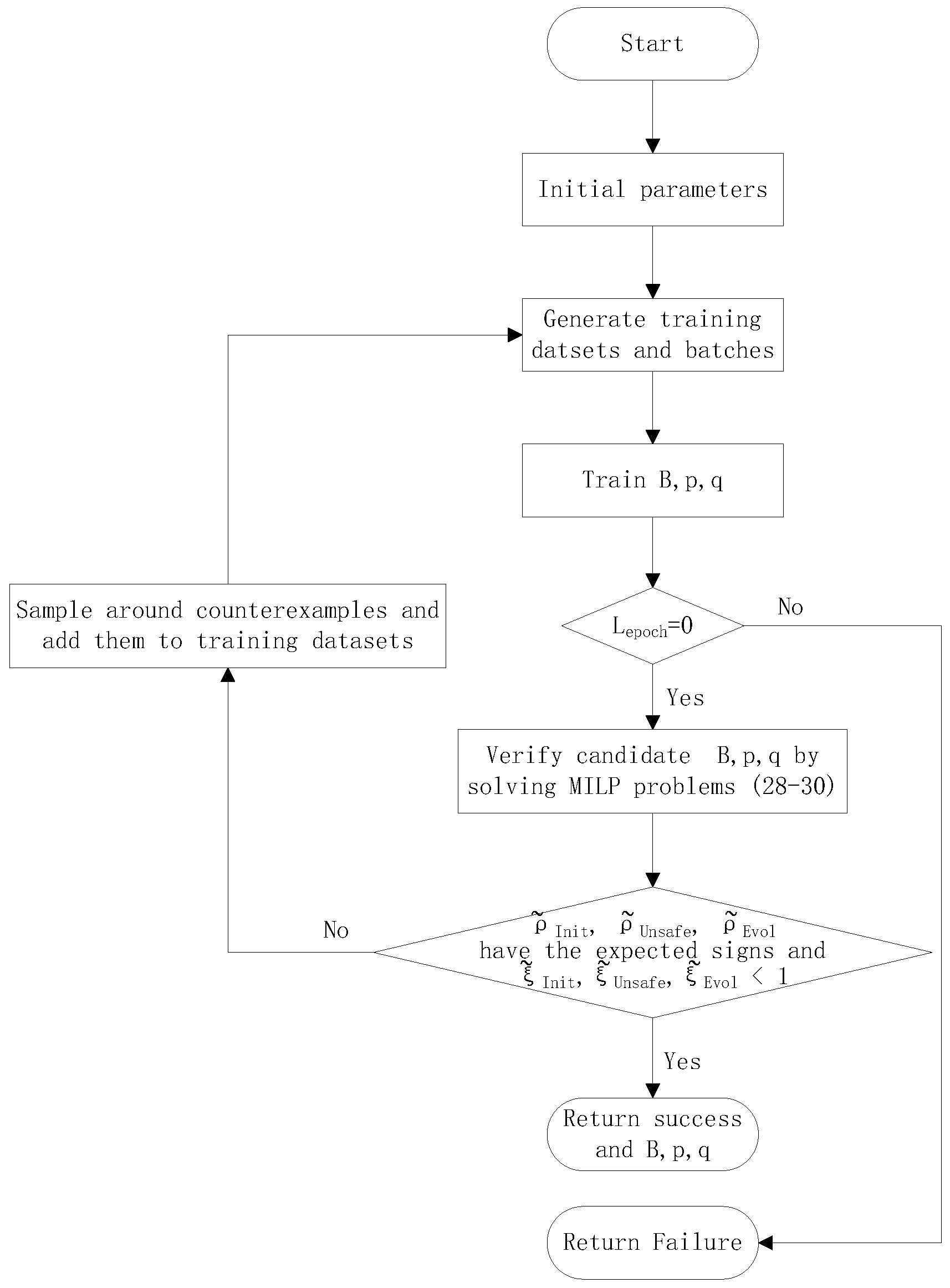
3.3. Algorithm
| Algorithm 1 Barrier certificate and relation function synthesis. |
Require:
Ensure:
|
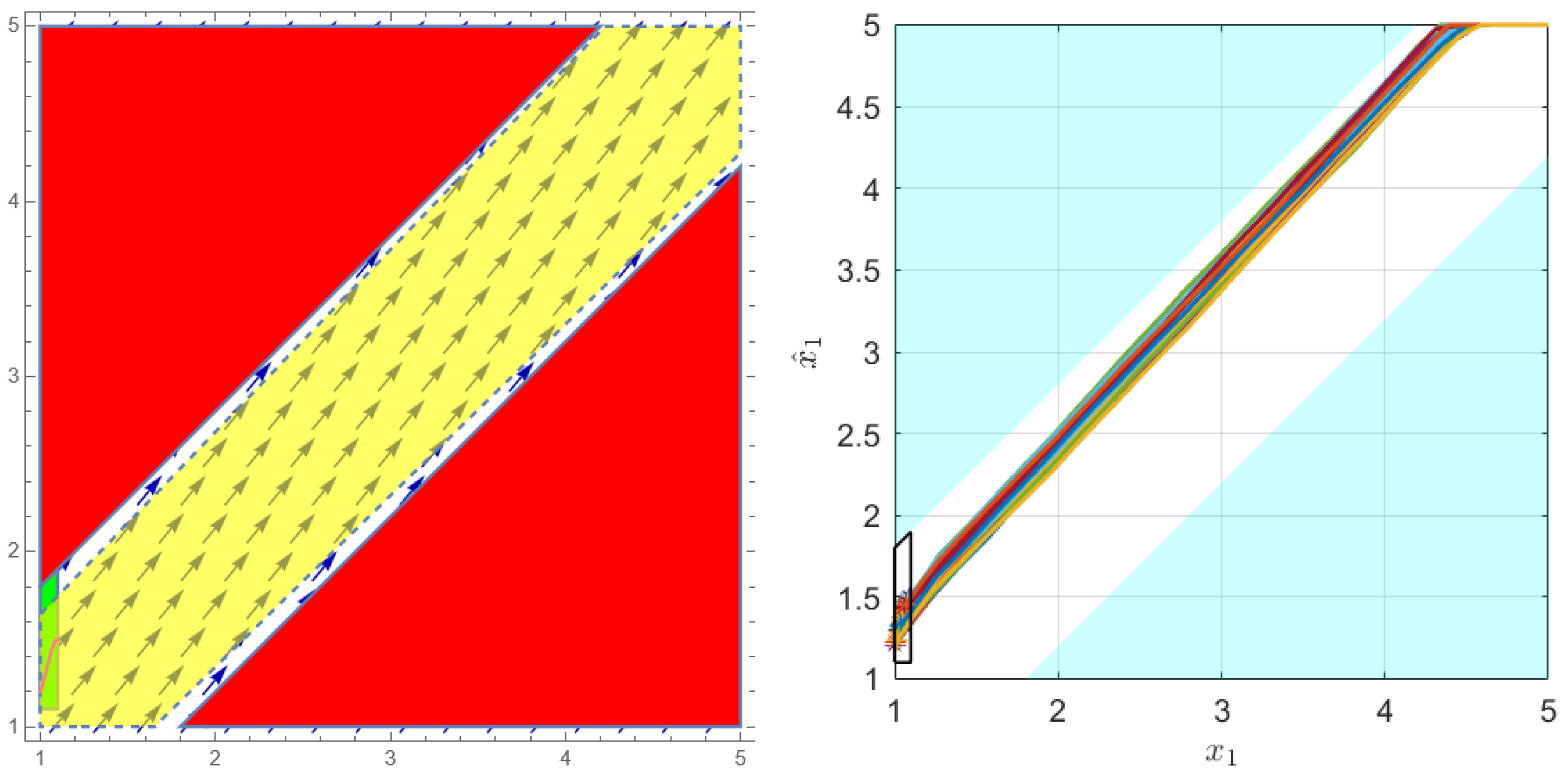
4. Experimental Results and Analysis
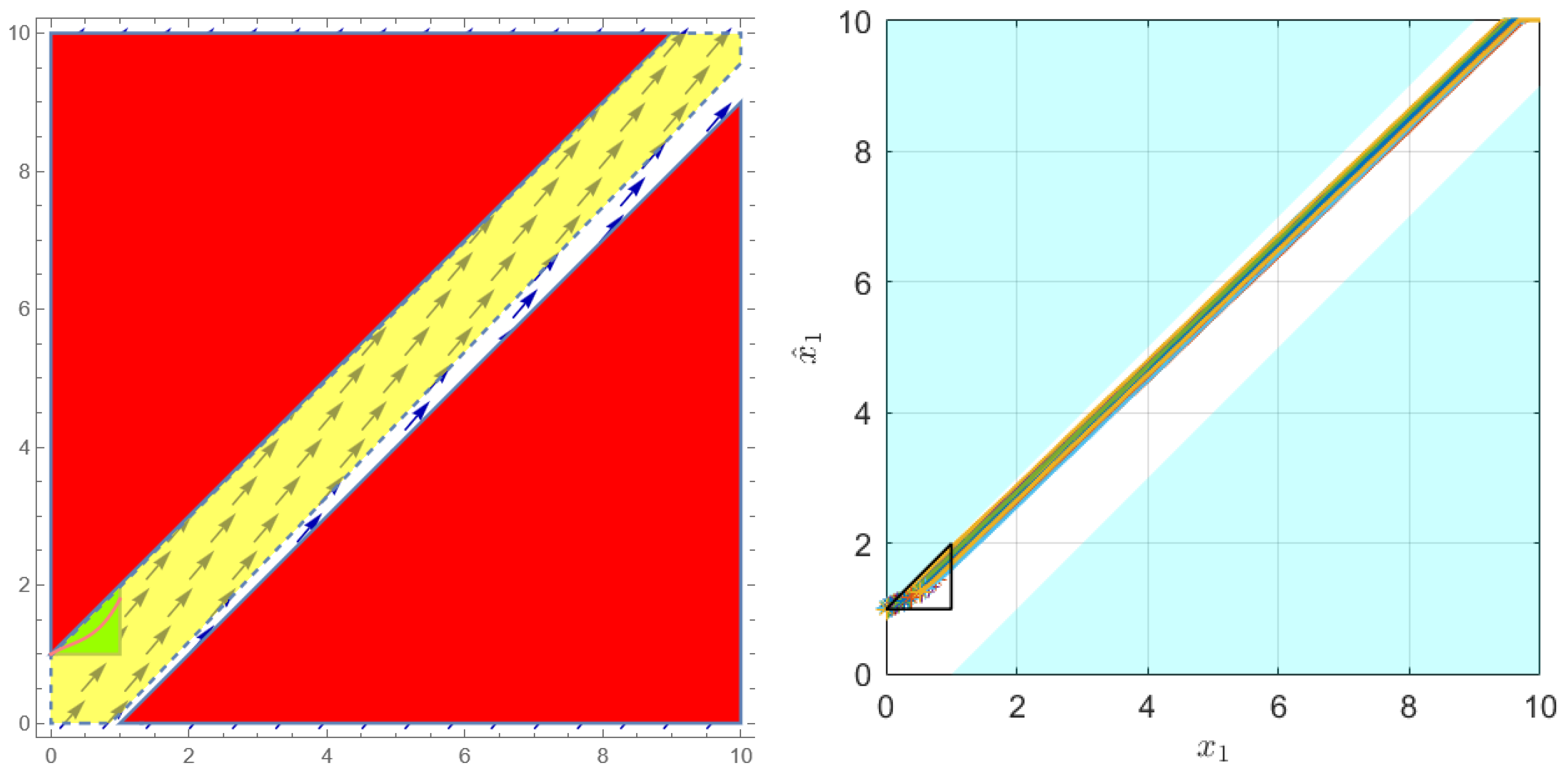
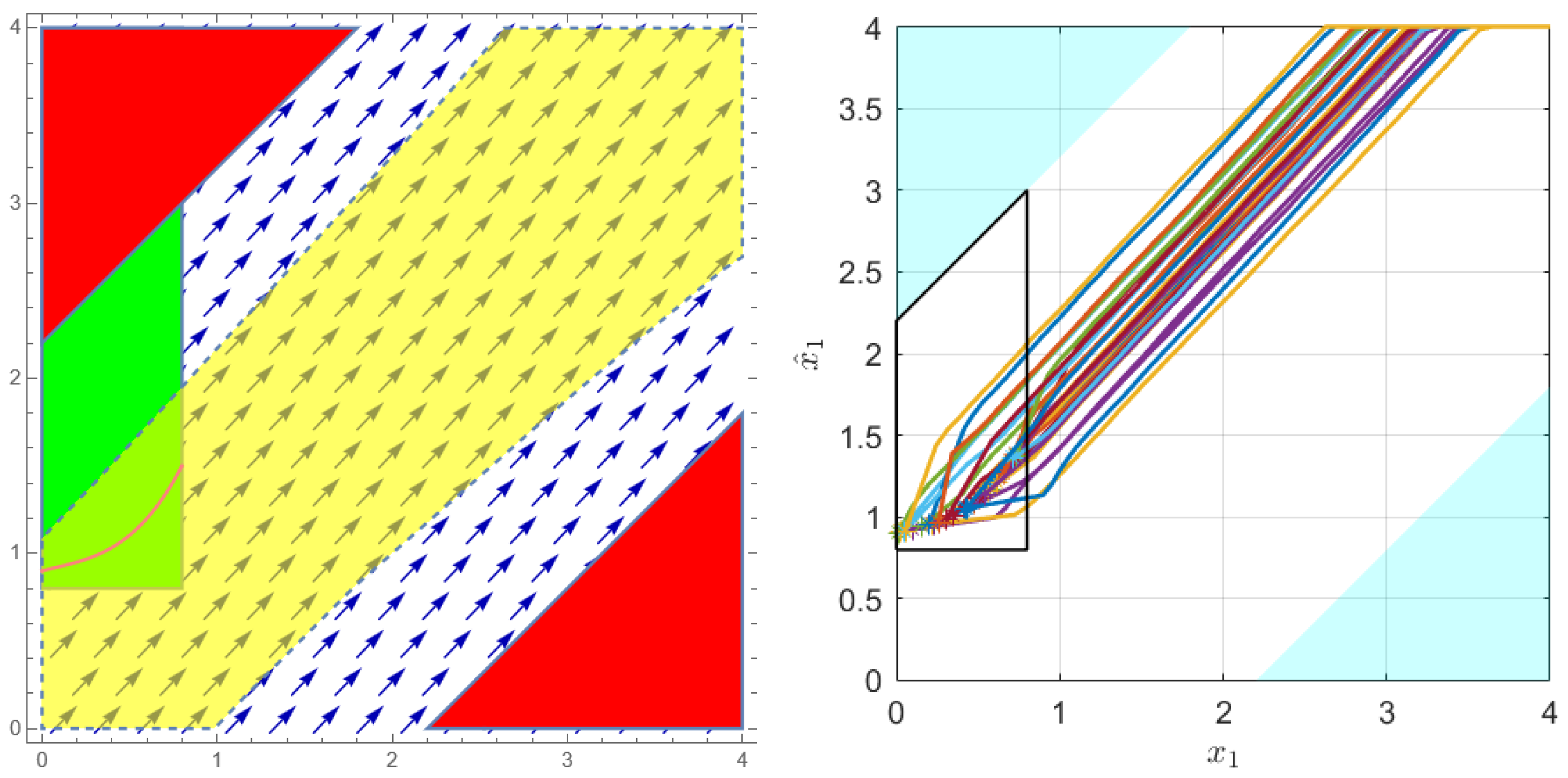
4.1. Examples
4.2. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, X.; Khedr, H.; Shoukry, Y. Formal verification of neural network controlled autonomous systems. In Proceedings of the 22nd ACM International Conference on Hybrid Systems: Computation and Control, Montreal, QC, Canada, 16–18 April 2019; pp. 147–156. [Google Scholar]
- Corsi, D.; Marchesini, E.; Farinelli, A. Formal verification of neural networks for safety-critical tasks in deep reinforcement learning. In Proceedings of the Uncertainty in Artificial Intelligence, PMLR, Virtual Event, 27–30 July 2021; pp. 333–343. [Google Scholar]
- Focardi, R.; Gorrieri, R. A taxonomy of trace-based security properties for CCS. In Proceedings of the Computer Security Foundations Workshop VII, Franconia, NH, USA, 14–16 June 1994; pp. 126–127. [Google Scholar]
- Sandberg, H.; Amin, S.; Johansson, K. Cyberphysical Security in Networked Control Systems: An Introduction to the Issue. Control Syst. IEEE 2015, 35, 20–23. [Google Scholar]
- Mazaré, L. Using unification for opacity properties. In Proceedings of the 4th IFIP WG1, Barcelona, Spain, 22–27 August 2004; Volume 7, pp. 165–176. [Google Scholar]
- Lafortune, S.; Lin, F.; Hadjicostis, C.N. On the history of diagnosability and opacity in discrete event systems. Annu. Rev. Control 2018, 45, 257–266. [Google Scholar] [CrossRef]
- Wu, Y.C.; Lafortune, S. Comparative analysis of related notions of opacity in centralized and coordinated architectures. Discret. Event Dyn. Syst. 2013, 23, 307–339. [Google Scholar] [CrossRef]
- Yin, X.; Zamani, M.; Liu, S. On approximate opacity of cyber-physical systems. IEEE Trans. Autom. Control 2020, 66, 1630–1645. [Google Scholar] [CrossRef]
- Yang, J.; Deng, W.; Qiu, D.; Jiang, C. Opacity of networked discrete event systems. Inf. Sci. 2021, 543, 328–344. [Google Scholar] [CrossRef]
- Balun, J.; Masopust, T. Comparing the notions of opacity for discrete-event systems. Discret. Event Dyn. Syst. 2021, 31, 553–582. [Google Scholar] [CrossRef]
- Liu, S.; Zamani, M. Verification of Approximate Opacity via Barrier Certificates. IEEE Control Syst. Lett. 2021, 5, 1369–1374. [Google Scholar] [CrossRef]
- Anand, M.; Murali, V.; Trivedi, A.; Zamani, M. Formal Verification of Control Systems against Hyperproperties via Barrier Certificates. arXiv 2021, arXiv:2105.05493. [Google Scholar]
- Prajna, S.; Jadbabaie, A. Safety verification of hybrid systems using barrier certificates. In Proceedings of the International Workshop on Hybrid Systems: Computation and Control, Philadelphia, PA, USA, 25–27 March 2004; pp. 477–492. [Google Scholar]
- Kong, H.; He, F.; Song, X.; Hung, W.N.; Gu, M. Exponential-condition-based barrier certificate generation for safety verification of hybrid systems. In Proceedings of the International Conference on Computer Aided Verification, Saint Petersburg, Russia, 13–19 July 2013; pp. 242–257. [Google Scholar]
- Ames, A.D.; Coogan, S.; Egerstedt, M.; Notomista, G.; Sreenath, K.; Tabuada, P. Control barrier functions: Theory and applications. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 3420–3431. [Google Scholar]
- Zhang, Y.; Yang, Z.; Lin, W.; Zhu, H.; Chen, X.; Li, X. Safety verification of nonlinear hybrid systems based on bilinear programming. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 2768–2778. [Google Scholar] [CrossRef]
- Zhao, Q.; Chen, X.; Zhang, Y.; Sha, M.; Yang, Z.; Lin, W.; Tang, E.; Chen, Q.; Li, X. Synthesizing ReLU neural networks with two hidden layers as barrier certificates for hybrid systems. In Proceedings of the 24th International Conference on Hybrid Systems: Computation and Control, Nashville, TN, USA, 19–21 May 2021; pp. 1–11. [Google Scholar]
- Peruffo, A.; Ahmed, D.; Abate, A. Automated and formal synthesis of neural barrier certificates for dynamical models. In Proceedings of the International Conference on Tools and Algorithms for the Construction and Analysis of Systems, Luxembourg, 27 March–1 April 2021; pp. 370–388. [Google Scholar]
- Feng, L. Opacity of discrete event systems and its applications. Automatica 2011, 47, 496–503. [Google Scholar]
- Saboori, A.; Hadjicostis, C.N. Verification of initial-state opacity in security applications of discrete event systems. Inf. Sci. 2013, 246, 115–132. [Google Scholar] [CrossRef]
- Saboori, A.; Hadjicostis, C.N. Verification of K-step opacity and analysis of its complexity. IEEE Trans. Autom. Sci. Eng. 2011, 8, 549–559. [Google Scholar] [CrossRef]
- Saboori, A.; Hadjicostis, C.N. Notions of security and opacity in discrete event systems. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 5056–5061. [Google Scholar]
- Saboori, A.; Hadjicostis, C.N. Verification of infinite-step opacity and complexity considerations. IEEE Trans. Autom. Control 2011, 57, 1265–1269. [Google Scholar] [CrossRef]
- Xie, Y.; Yin, X.; Li, S. Opacity enforcing supervisory control using non-deterministic supervisors. IEEE Trans. Autom. Control. 2021. [Google Scholar] [CrossRef]
- Xie, Y.; Yin, X.; Li, S. Optimal Synthesis of Opacity-Enforcing Supervisors for Qualitative and Quantitative Specifications. arXiv 2021, arXiv:2102.01402. [Google Scholar]
- Liu, S.; Swikir, A.; Zamani, M. Compositional verification of initial-state opacity for switched systems. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju Island, Korea, 14–18 December 2020; pp. 2146–2151. [Google Scholar]
- Noori-Hosseini, M.; Lennartson, B.; Hadjicostis, C. Compositional Visible Bisimulation Abstraction Applied to Opacity Verification. IFAC-PapersOnLine 2018, 51, 434–441. [Google Scholar] [CrossRef]
- Yin, X.; Li, Z.; Wang, W.; Li, S. Infinite-step opacity and K-step opacity of stochastic discrete-event systems. Automatica 2019, 99, 266–274. [Google Scholar] [CrossRef]
- Tong, Y.; Li, Z.; Seatzu, C.; Giua, A. Verification of state-based opacity using Petri nets. IEEE Trans. Autom. Control 2016, 62, 2823–2837. [Google Scholar] [CrossRef]
- Tasdighi Kalat, S.; Liu, S.; Zamani, M. Modular Verification of Opacity for Interconnected Control Systems via Barrier Certificates. IEEE Control Syst. Lett. 2022, 6, 890–895. [Google Scholar] [CrossRef]
- Chédor, S.; Morvan, C.; Pinchinat, S.; Marchand, H. Diagnosis and opacity problems for infinite state systems modeled by recursive tile systems. Discret. Event Dyn. Syst. 2015, 25, 271–294. [Google Scholar] [CrossRef][Green Version]
- Liu, S.; Yin, X.; Zamani, M. On a notion of approximate opacity for discrete-time stochastic control systems. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 5413–5418. [Google Scholar]
- Tjeng, V.; Xiao, K.; Tedrake, R. Evaluating robustness of neural networks with mixed integer programming. arXiv 2017, arXiv:1711.07356. [Google Scholar]
- Dutta, S.; Jha, S.; Sankaranarayanan, S.; Tiwari, A. Output range analysis for deep feedforward neural networks. In Proceedings of the NASA Formal Methods Symposium, Newport News, VA, USA, 17–19 April 2018; pp. 121–138. [Google Scholar]
- Zhao, H.; Zeng, X.; Chen, T.; Liu, Z.; Woodcock, J. Learning safe neural network controllers with barrier certificates. Form. Asp. Comput. 2021, 33, 437–455. [Google Scholar] [CrossRef]
- Katz, G.; Barrett, C.; Dill, D.L.; Julian, K.; Kochenderfer, M.J. Reluplex: An efficient SMT solver for verifying deep neural networks. In Proceedings of the International Conference on Computer Aided Verification, Heidelberg, Germany, 24–28 July 2017; pp. 97–117. [Google Scholar]
- Huang, X.; Kwiatkowska, M.; Wang, S.; Wu, M. Safety verification of deep neural networks. In Proceedings of the International Conference on Computer Aided Verification, Heidelberg, Germany, 24–28 July 2017; pp. 3–29. [Google Scholar]
- Rössig, A.; Petkovic, M. Advances in verification of ReLU neural networks. J. Glob. Optim. 2021, 81, 109–152. [Google Scholar] [CrossRef]
- Botoeva, E.; Kouvaros, P.; Kronqvist, J.; Lomuscio, A.; Misener, R. Efficient verification of relu-based neural networks via dependency analysis. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 3291–3299. [Google Scholar]
- Zhao, Q.; Chen, X.; Zhao, Z.; Zhang, Y.; Tang, E.; Li, X. Verifying Neural Network Controlled Systems Using Neural Networks. In Proceedings of the 25th ACM International Conference on Hybrid Systems: Computation and Control, Milan, Italy, 4–6 May 2022; pp. 1–11. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
| Ex | B | p | q | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ex 1 | 4 | 4-16-1 | 2-16-2 | 5-16-1 | 0.01 | 1.2 | 1 | 0 | 0.01 | 0.01 | 0.001 |
| Ex 2 | 6 | 6-16-16-1 | 3-10-3 | 7-10-1 | 0.1 | 1.5 | 1 | 0.01 | 0.05 | 0.01 | 0.001 |
| Ex 3 | 4 | 4-16-1 | 2-16-2 | 5-16-1 | 0.01 | 1.2 | 1 | 0.01 | 0.05 | 0.01 | 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Ding, M.; Lin, W.; Jia, Y. Verification of Approximate Initial-State Opacity for Control Systems via Neural Augmented Barrier Certificates. Mathematics 2022, 10, 2388. https://doi.org/10.3390/math10142388
Wang S, Ding M, Lin W, Jia Y. Verification of Approximate Initial-State Opacity for Control Systems via Neural Augmented Barrier Certificates. Mathematics. 2022; 10(14):2388. https://doi.org/10.3390/math10142388
Chicago/Turabian StyleWang, Shengpu, Mi Ding, Wang Lin, and Yubo Jia. 2022. "Verification of Approximate Initial-State Opacity for Control Systems via Neural Augmented Barrier Certificates" Mathematics 10, no. 14: 2388. https://doi.org/10.3390/math10142388
APA StyleWang, S., Ding, M., Lin, W., & Jia, Y. (2022). Verification of Approximate Initial-State Opacity for Control Systems via Neural Augmented Barrier Certificates. Mathematics, 10(14), 2388. https://doi.org/10.3390/math10142388






