Towards Explainable Machine Learning for Bank Churn Prediction Using Data Balancing and Ensemble-Based Methods
Abstract
1. Introduction
2. Related Work
- In which year was the paper published?
- Which ML algorithms were tested, which was the best and with what performance?
- What metrics were used to evaluate the proposed method(s)?
- Did the authors balance the data?
- Did the authors explain or interpret the ML models constructed?
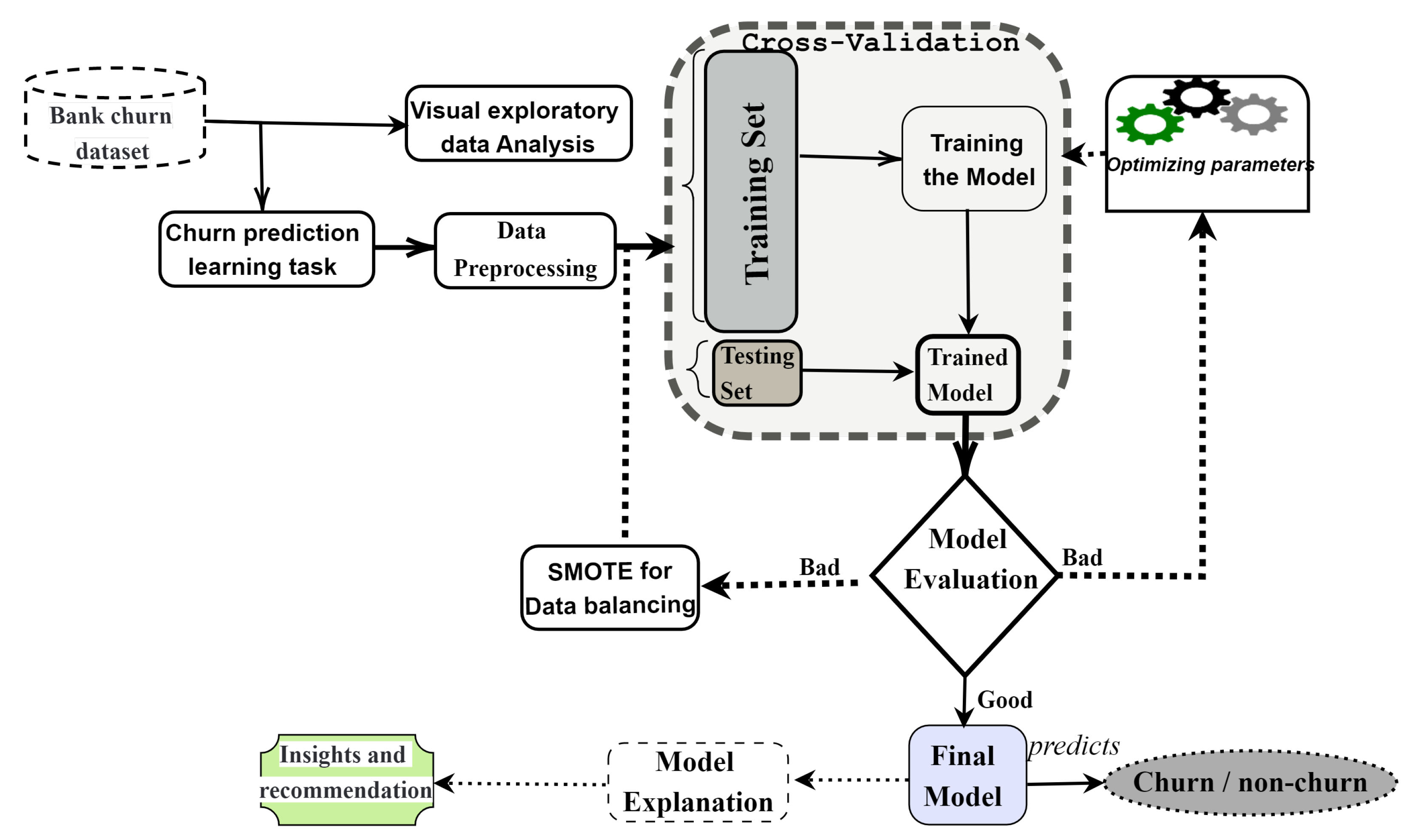
3. The Proposed Approach
3.1. Data Preprocessing
3.2. SMOTE Method for Data Balancing
| Algorithm 1 SMOTE algorithm [21] |
| Input: • N: the number of instances in the minority classes; |
| • n: the amount of SMOTE (in %); |
| • : the number of nearest neighbours; |
| • minority data where . |
| Output: D′: synthetic data from D; |
| 1: n ← (int)(n/100); |
| 2: for i = 1 to N do |
| 3: Find the k nearest neighbours of ; |
| 4: while do |
| 5: Select one of the k nearest neighbours of |
| 6: Select a random number [0, 1] |
| 7: x ← |
| 8: Append x to D′ |
| 9: end while |
| 10: end for |
3.3. Modelling and Prediction with Ensemble Methods
3.4. Model Explanation with Shapley Values and Feature Importance
4. Results Analysis and Discussion
4.1. Bank Churn Dataset
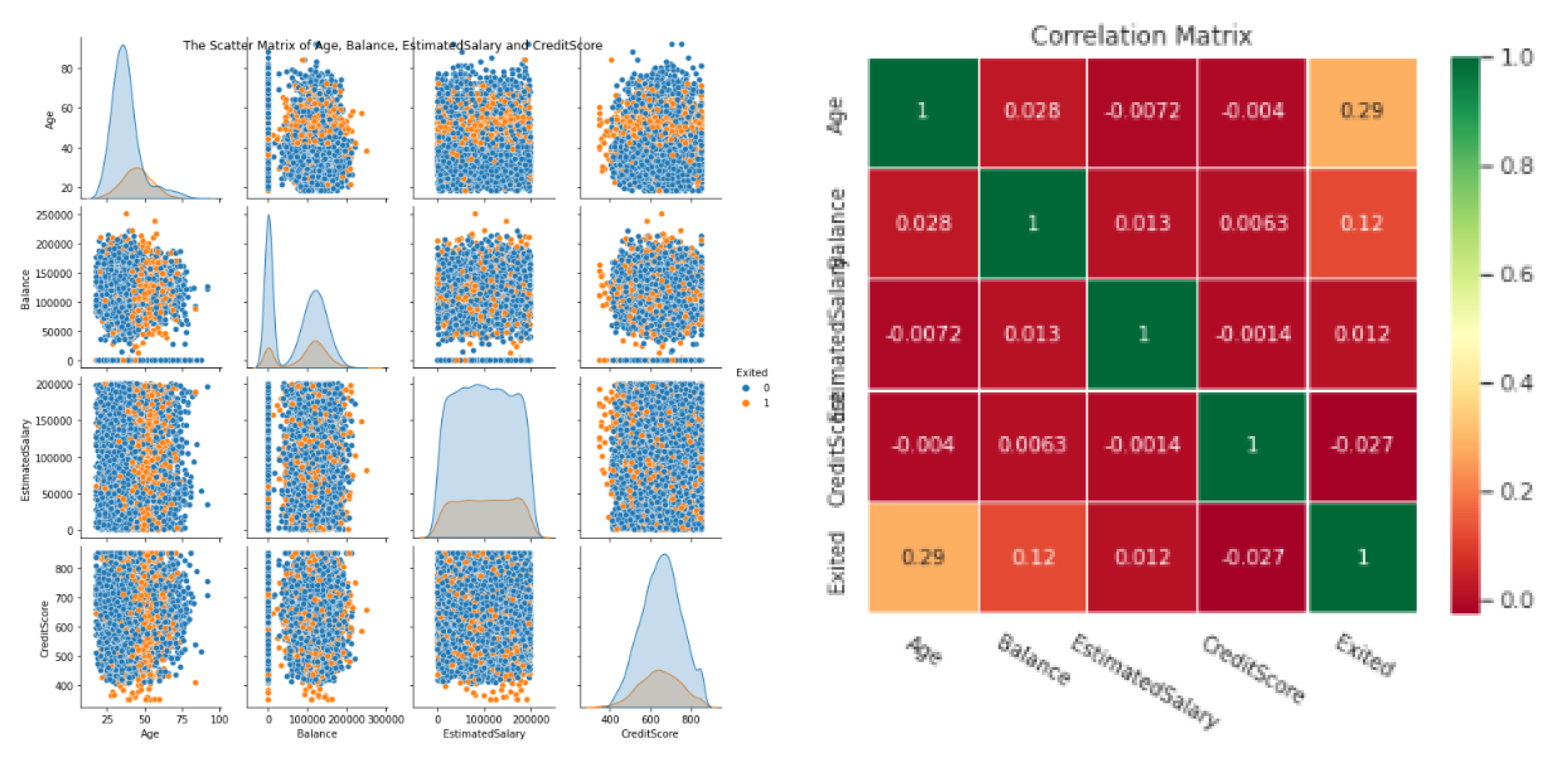
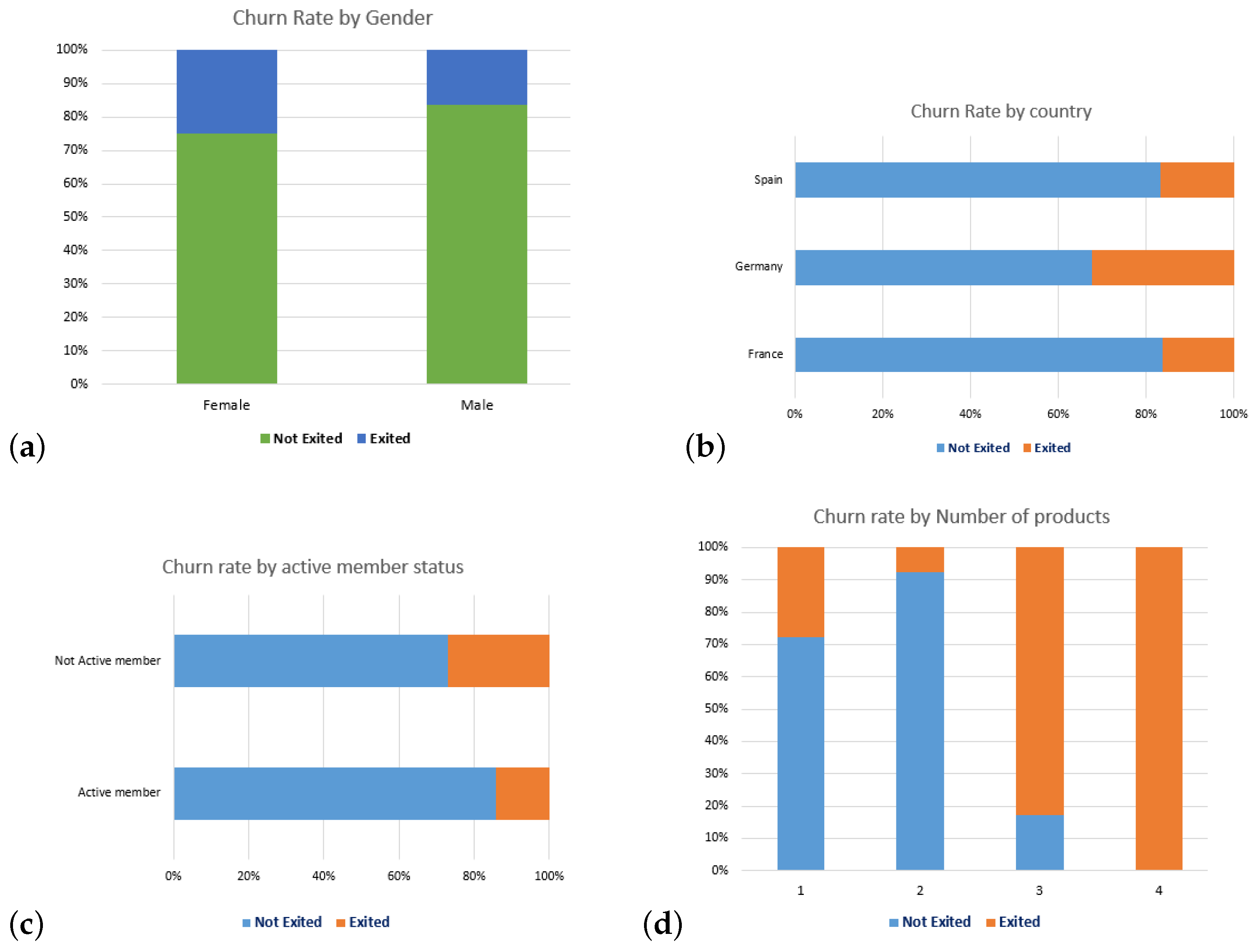
4.2. Visual Exploratory Data Analysis
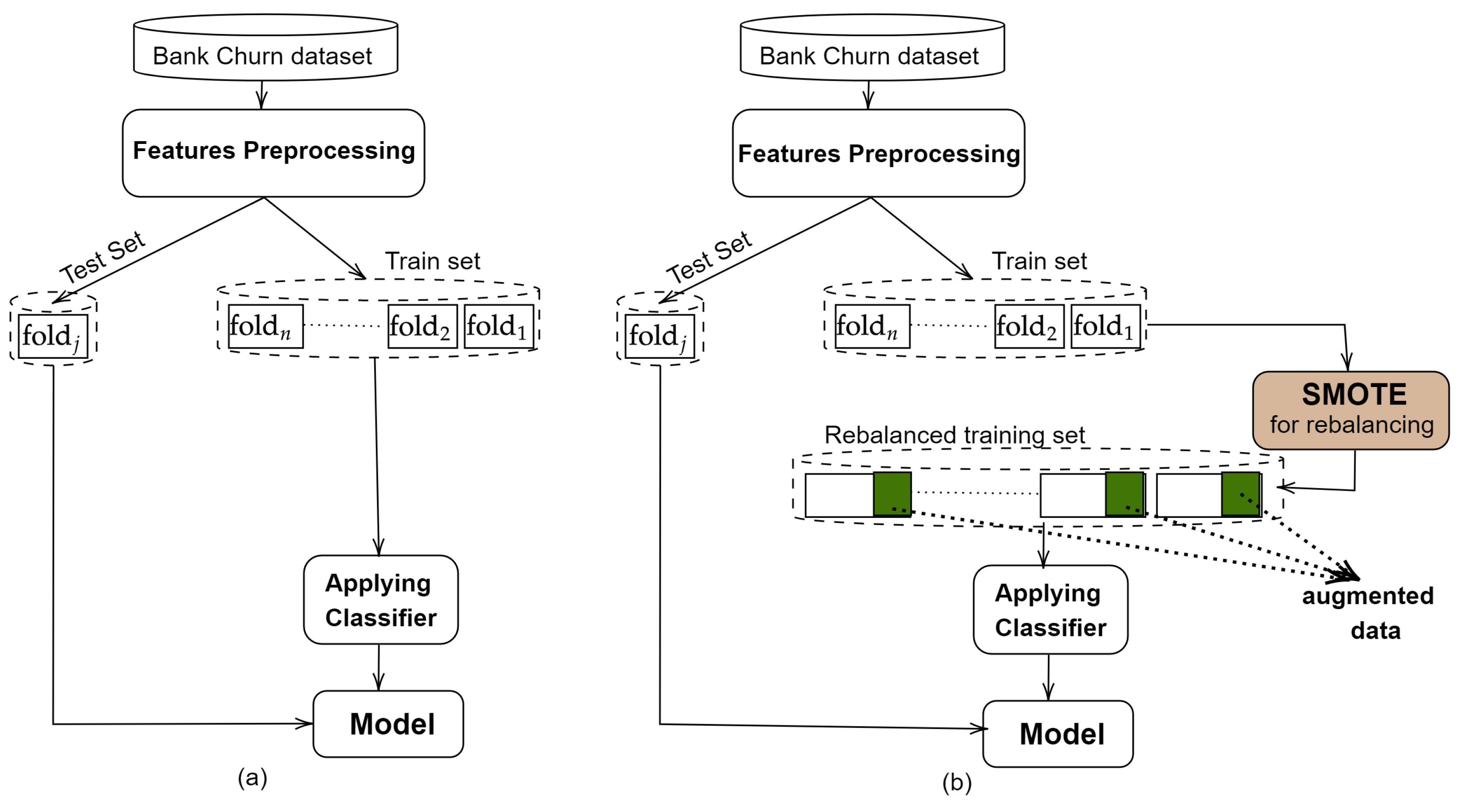
4.3. Experimental Protocol
Performance Measure
4.4. Results Analysis and Discussion
4.4.1. Cross-Validated Results without Balance Data
4.4.2. Optimizing Random Forest Performances Results
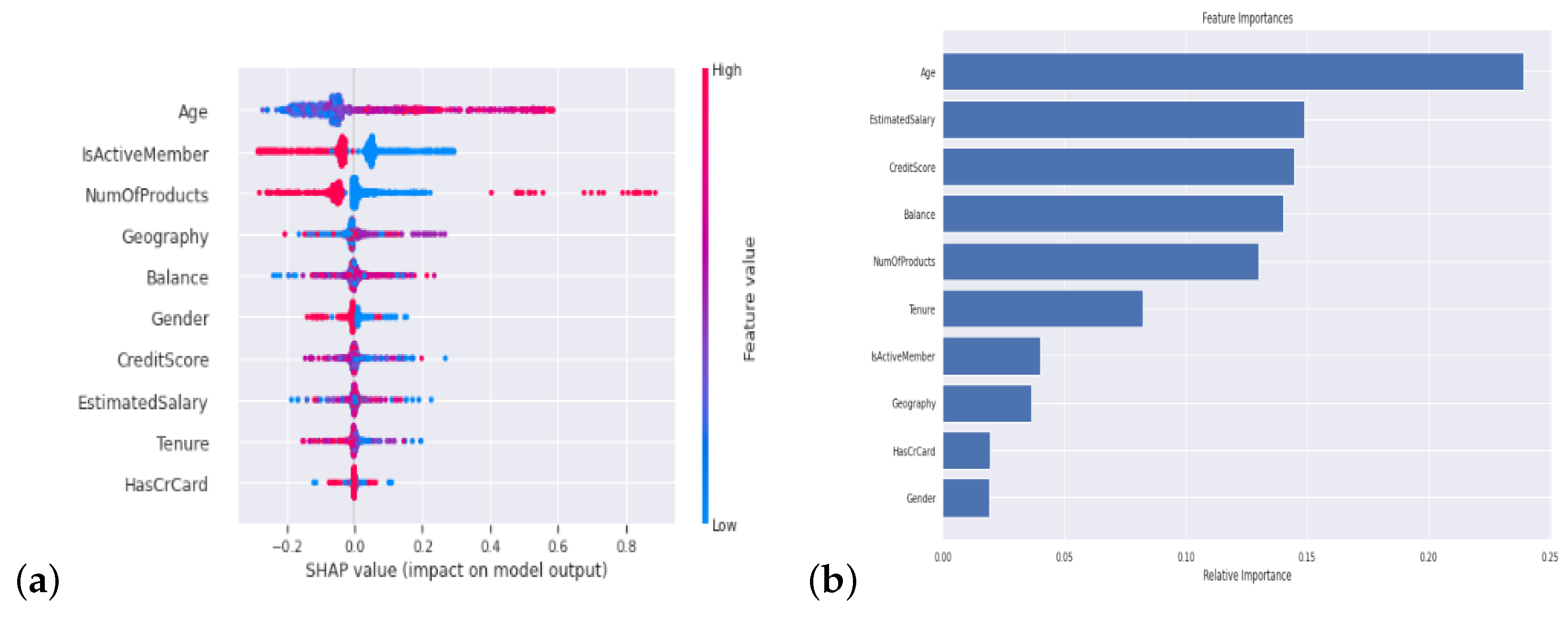
4.5. Model Explanation
4.6. Discussion and Insights
5. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ngai, E.W.; Xiu, L.; Chau, D.C. Application of data mining techniques in customer relationship management: A literature review and classification. Expert Syst. Appl. 2009, 36, 2592–2602. [Google Scholar] [CrossRef]
- Bahari, T.F.; Elayidom, M.S. An efficient CRM-data mining framework for the prediction of customer behaviour. Procedia Comput. Sci. 2015, 46, 725–731. [Google Scholar] [CrossRef]
- Ranjan, J.; Bhatnagar, V. Critical success factors for implementing CRM using data mining. J. Knowl. Manag. Pract. 2008, 1, 7. [Google Scholar] [CrossRef]
- Dick, A.S.; Basu, K. Customer loyalty: Toward an integrated conceptual framework. J. Acad. Mark. Sci. 1994, 22, 99–113. [Google Scholar] [CrossRef]
- Chaudhary, K.; Yadav, J.; Mallick, B. A review of fraud detection techniques: Credit card. Int. J. Comput. Appl. 2012, 45, 39–44. [Google Scholar]
- Bhattacharyya, S.; Jha, S.; Tharakunnel, K.; Westland, J.C. Data mining for credit card fraud: A comparative study. Decis. Support Syst. 2011, 50, 602–613. [Google Scholar] [CrossRef]
- Garver, M.S. Using data mining for customer satisfaction research. Mark. Res. 2002, 14, 8. [Google Scholar]
- Oralhan, B.; Kumru, U.; Oralhan, Z. Customer satisfaction using data mining approach. Int. J. Intell. Syst. Appl. Eng. 2016, 4, 63–66. [Google Scholar] [CrossRef][Green Version]
- Zhang, Z.; Lin, H.; Liu, K.; Wu, D.; Zhang, G.; Lu, J. A hybrid fuzzy-based personalized recommender system for telecom products/services. Inf. Sci. 2013, 235, 117–129. [Google Scholar] [CrossRef]
- Díez, J.; Martínez-Rego, D.; Alonso-Betanzos, A.; Luaces, O.; Bahamonde, A. Optimizing novelty and diversity in recommendations. Prog. Artif. Intell. 2019, 8, 101–109. [Google Scholar] [CrossRef]
- Au, W.H.; Chan, K.C.; Yao, X. A novel evolutionary data mining algorithm with applications to churn prediction. IEEE Trans. Evol. Comput. 2003, 7, 532–545. [Google Scholar]
- Wei, C.P.; Chiu, I.T. Turning telecommunications call details to churn prediction: A data mining approach. Expert Syst. Appl. 2002, 23, 103–112. [Google Scholar] [CrossRef]
- Verbeke, W.; Martens, D.; Baesens, B. Social network analysis for customer churn prediction. Appl. Soft Comput. 2014, 14, 431–446. [Google Scholar] [CrossRef]
- Vafeiadis, T.; Diamantaras, K.I.; Sarigiannidis, G.; Chatzisavvas, K.C. A comparison of machine learning techniques for customer churn prediction. Simul. Model. Pract. Theory 2015, 55, 1–9. [Google Scholar] [CrossRef]
- Karvana, K.G.M.; Yazid, S.; Syalim, A.; Mursanto, P. Customer churn analysis and prediction using data mining models in banking industry. In Proceedings of the 2019 International Workshop on Big Data and Information Security (IWBIS), Bali, Indonesia, 11 October 2019; pp. 33–38. [Google Scholar] [CrossRef]
- Hung, S.Y.; Yen, D.C.; Wang, H.Y. Applying data mining to telecom churn management. Expert Syst. Appl. 2006, 31, 515–524. [Google Scholar] [CrossRef]
- Tékouabou Koumétio, S.C.; Toulni, H. Improving KNN Model for Direct Marketing Prediction in Smart Cities. In Machine Intelligence and Data Analytics for Sustainable Future Smart Cities; Springer: Berlin/Heidelberg, Germany, 2021; pp. 107–118. [Google Scholar] [CrossRef]
- Koumétio, C.S.T.; Cherif, W.; Hassan, S. Optimizing the prediction of telemarketing target calls by a classification technique. In Proceedings of the 2018 6th International Conference on Wireless Networks and Mobile Communications (WINCOM), Marrakesh, Morocco, 16–19 October 2018; pp. 1–6. [Google Scholar]
- Cioca, M.; Ghete, A.I.; Cioca, L.I.; Gifu, D. Machine learning and creative methods used to classify customers in a CRM systems. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Bach, Switzerland, 2013; Volume 371, pp. 769–773. [Google Scholar]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Tékouabou, S.C.K.; Chabbar, I.; Toulni, H.; Cherif, W.; Silkan, H. Optimizing the early glaucoma detection from visual fields by combining preprocessing techniques and ensemble classifier with selection strategies. Expert Syst. Appl. 2022, 189, 115975. [Google Scholar] [CrossRef]
- Konstantinov, A.V.; Utkin, L.V. Interpretable machine learning with an ensemble of gradient boosting machines. Knowl.-Based Syst. 2021, 222, 106993. [Google Scholar] [CrossRef]
- Rodríguez-Pérez, R.; Bajorath, J. Interpretation of machine learning models using shapley values: Application to compound potency and multi-target activity predictions. J. Comput.-Aided Mol. Des. 2020, 34, 1013–1026. [Google Scholar] [CrossRef]
- Alphy, A.; Prabakaran, S. A dynamic recommender system for improved web usage mining and CRM using swarm intelligence. Sci. World J. 2015, 2015, 193631. [Google Scholar] [CrossRef]
- Chen, Y.L.; Hsu, C.L.; Chou, S.C. Constructing a multi-valued and multi-labeled decision tree. Expert Syst. Appl. 2003, 25, 199–209. [Google Scholar] [CrossRef]
- Elmandili, H.; Toulni, H.; Nsiri, B. Optimizing road traffic of emergency vehicles. In Proceedings of the 2013 International Conference on Advanced Logistics and Transport, Sousse, Tunisia, 29–31 May 2013; pp. 59–62. [Google Scholar]
- Lai, K.K.; Yu, L.; Wang, S.; Huang, W. An intelligent CRM system for identifying high-risk customers: An ensemble data mining approach. In International Conference on Computational Science; Springer: Berlin/Heidelberg, Germany, 2007; pp. 486–489. [Google Scholar]
- Farquad, M.; Ravi, V.; Raju, S.B. Analytical CRM in banking and finance using SVM: A modified active learning-based rule extraction approach. Int. J. Electron. Cust. Relatsh. Manag. 2012, 6, 48–73. [Google Scholar] [CrossRef]
- Keramati, A.; Ghaneei, H.; Mirmohammadi, S.M. Developing a prediction model for customer churn from electronic banking services using data mining. Financ. Innov. 2016, 2, 1–13. [Google Scholar] [CrossRef]
- Li, B.; Xie, J. Study on the Prediction of Imbalanced Bank Customer Churn Based on Generative Adversarial Network. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2020; p. 032054. [Google Scholar] [CrossRef]
- de Lima Lemos, R.A.; Silva, T.C.; Tabak, B.M. Propension to customer churn in a financial institution: A machine learning approach. Neural Comput. Appl. 2022, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Bilal Zorić, A. Predicting customer churn in banking industry using neural networks. Interdiscip. Descr. Complex Syst. 2016, 14, 116–124. [Google Scholar] [CrossRef]
- Boudhane, M.; Nsiri, B.; Toulni, H. Optical fish classification using statistics of parts. Int. J. Math. Comput. Simul. 2016, 10, 18–22. [Google Scholar]
- Muneer, A.; Ali, R.F.; Alghamdi, A.; Taib, S.M.; Almaghthawi, A.; Ghaleb, E.A.A. Predicting customers churning in banking industry: A machine learning approach. Indones. J. Electr. Eng. Comput. Sci. 2022, 26, 539–549. [Google Scholar] [CrossRef]
- Verma, P. Churn Prediction for Savings Bank Customers: A Machine Learning Approach. J. Stat. Appl. Probab. 2020, 9, 535–547. [Google Scholar] [CrossRef]
- Naveen Sundar, G.; Narmadha, D.; Jebapriya, S.; Malathy, M. Optimized Methodology for Hassle-Free Clustering of Customer Issues in Banking. In Cognitive Informatics and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2019; Volume 768, pp. 421–428. [Google Scholar] [CrossRef]
- Farquad, M.A.H.; Ravi, V.; Raju, S.B. Churn prediction using comprehensible support vector machine: An analytical CRM application. Appl. Soft Comput. 2014, 19, 31–40. [Google Scholar] [CrossRef]
- Deng, Y.; Li, D.; Yang, L.; Tang, J.; Zhao, J. Analysis and prediction of bank user churn based on ensemble learning algorithm. In Proceedings of the 2021 IEEE International Conference on Power Electronics, Computer Applications (ICPECA), Shenyang, China, 22–24 January 2021; pp. 288–291. [Google Scholar] [CrossRef]
- Feuerverger, A.; He, Y.; Khatri, S. Statistical significance of the Netflix challenge. Stat. Sci. 2012, 27, 202–231. [Google Scholar] [CrossRef]
- Roy, A.; Cruz, R.M.; Sabourin, R.; Cavalcanti, G.D. A study on combining dynamic selection and data preprocessing for imbalance learning. Neurocomputing 2018, 286, 179–192. [Google Scholar] [CrossRef]
- Xiao, J.; Xie, L.; He, C.; Jiang, X. Dynamic classifier ensemble model for customer classification with imbalanced class distribution. Expert Syst. Appl. 2012, 39, 3668–3675. [Google Scholar] [CrossRef]
- Woloszynski, T.; Kurzynski, M. A probabilistic model of classifier competence for dynamic ensemble selection. Pattern Recognit. 2011, 44, 2656–2668. [Google Scholar] [CrossRef]
- Alhamidi, M.R.; Jatmiko, W. Optimal Feature Aggregation and Combination for Two-Dimensional Ensemble Feature Selection. Information 2020, 11, 38. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In International Conference on Intelligent Computing; Springer: Berlin/Heidelberg, Germany, 2005; pp. 878–887. [Google Scholar] [CrossRef]
- Díez-Pastor, J.F.; Rodríguez, J.J.; García-Osorio, C.; Kuncheva, L.I. Random balance: Ensembles of variable priors classifiers for imbalanced data. Knowl.-Based Syst. 2015, 85, 96–111. [Google Scholar] [CrossRef]
- Faris, H.; Abukhurma, R.; Almanaseer, W.; Saadeh, M.; Mora, A.M.; Castillo, P.A.; Aljarah, I. Improving financial bankruptcy prediction in a highly imbalanced class distribution using oversampling and ensemble learning: A case from the Spanish market. Prog. Artif. Intell. 2020, 9, 31–53. [Google Scholar] [CrossRef]
- Wu, Y.; Ding, Y.; Feng, J. SMOTE-Boost-based sparse Bayesian model for flood prediction. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Barua, S.; Islam, M.M.; Yao, X.; Murase, K. MWMOTE—Majority Weighted Minority Oversampling Technique for Imbalanced Data Set Learning. IEEE Trans. Knowl. Data Eng. 2014, 26, 405–425. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Alonso-Betanzos, A. Ensembles for feature selection: A review and future trends. Inf. Fusion 2019, 52, 1–12. [Google Scholar] [CrossRef]
- Diez-Olivan, A.; Del Ser, J.; Galar, D.; Sierra, B. Data fusion and machine learning for industrial prognosis: Trends and perspectives towards Industry 4.0. Inf. Fusion 2019, 50, 92–111. [Google Scholar] [CrossRef]
- Kuncheva, L.I. A theoretical study on six classifier fusion strategies. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 281–286. [Google Scholar] [CrossRef]
- Padarian, J.; McBratney, A.B.; Minasny, B. Game theory interpretation of digital soil mapping convolutional neural networks. Soil 2020, 6, 389–397. [Google Scholar] [CrossRef]
- Arjunan, P.; Poolla, K.; Miller, C. EnergyStar++: Towards more accurate and explanatory building energy benchmarking. Appl. Energy 2020, 276, 115413. [Google Scholar] [CrossRef]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A.K. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, NIPS’17, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4768–4777. [Google Scholar]
- Bahnsen, A.C.; Aouada, D.; Ottersten, B. Example-dependent cost-sensitive decision trees. Expert Syst. Appl. 2015, 42, 6609–6619. [Google Scholar] [CrossRef]
- Verbraken, T.; Verbeke, W.; Baesens, B. A novel profit maximizing metric for measuring classification performance of customer churn prediction models. IEEE Trans. Knowl. Data Eng. 2012, 25, 961–973. [Google Scholar] [CrossRef]
- Raschka, S.; Mirjalili, V. Python Machine Learning: Machine Learning and Deep Learning with Python. In Scikit-Learn, and TensorFlow; Packt Publishing: Birmingham, UK, 2017. [Google Scholar]
- Marinakos, G.; Daskalaki, S. Imbalanced customer classification for bank direct marketing. J. Mark. Anal. 2017, 5, 14–30. [Google Scholar] [CrossRef]
- Chayjan, M.R.; Bagheri, T.; Kianian, A.; Someh, N.G. Using data mining for prediction of retail banking customer’s churn behaviour. Int. J. Electron. Bank. 2020, 2, 303–320. [Google Scholar] [CrossRef]



| Ref | Year | Algorithm | Metrics | Best Score | Balancing Data? | Explained Model? |
|---|---|---|---|---|---|---|
| [29] | 2016 | DT | Acc, pre, rec, f1 | 99.7, 91.8, 91.0, 90.96 | No | Yes |
| [32] | 2016 | ANN | Acc | 0.89 | No | No |
| [37] | 2014 | SVM | Acc, sen, spe | 83.1, 79.7, 83.7 | No | No |
| [15] | 2019 | SVM | recall | 0.73 | Yes | No |
| [38] | 2021 | RF | Acc, AUC, f1 | 0.92, 0.91, 0.92 | No | Yes |
| [35] | 2020 | RF | Acc, spe, sen, AUC | 0.8, 0.81, 0.79, 0.84 | No | Yes |
| [34] | 2022 | SVM, RF | Acc, f1 | 88.7, 91.90 | Yes | No |
| [31] | 2022 | DT, KNN, SVM, RF | AUC | 0.9 | No | Yes |
| [36] | 2019 | k-means, KHM | Acc | 91.4 | No | No |
| [30] | 2020 | RF, DT | pre, f1 | 0.99, 0.76 | Yes | No |
| N | Attribute | Description | Type | Role |
|---|---|---|---|---|
| 1 | IDclient | A unique identifier for each customer | Categorical | feature |
| 2 | Surname | The surname of the customer | Categorical | feature |
| 3 | CreditScore | This number is between 300 and 850 and depicts the creditworthiness of a consumer | Numerical | feature |
| 4 | Gender | The customer’s gender: Female (0) and Male (1) | Boolean | feature |
| 5 | Age | The client’s current age, at the time of being a customer | Numerical | feature |
| 6 | Tenure | The number of years the client has been with the bank. | Numerical | feature |
| 7 | Balance | The actual bank balance of the customer | Numerical | feature |
| 8 | NumOfProducts | The number of banking products used by the client | Numerical | feature |
| 9 | HasCrCard | The number of credit cards obtained from the bank by the client | Boolean | feature |
| 10 | IsActiveMember | Binary status indicating whether or not the client was active with the bank before he left it. | Boolean | feature |
| 11 | EstimatedSalary | The estimated customers’ salary | Numerical | feature |
| 12 | Exited | Binary flag stating if the customer closed an account with the bank or not. | Boolean | target |
| ML Model | ML Model | |||
|---|---|---|---|---|
| Model | Accuracy | f1-Score | Accuracy | f1-Score |
| KNN | 0.75 | 0.12 | 0.68 | 0.70 |
| SVM | 0.80 | 0.00 | 0.57 | 0.64 |
| DT | 0.79 | 0.50 | 0.80 | 0.80 |
| LR | 0.79 | 0.09 | 0.67 | 0.67 |
| ANN | 0.66 | 0.10 | 0.52 | 0.54 |
| NB | 0.79 | 0.13 | 0.72 | 0.74 |
| RF | 0.86 | 0.58 | 0.86 | 0.86 |
| B | 0.85 | 0.54 | 0.84 | 0.83 |
| GB | 0.87 | 0.59 | 0.84 | 0.84 |
| ET | 0.86 | 0.55 | 0.86 | 0.86 |
| AB | 0.86 | 0.57 | 0.83 | 0.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tékouabou, S.C.K.; Gherghina, Ș.C.; Toulni, H.; Mata, P.N.; Martins, J.M. Towards Explainable Machine Learning for Bank Churn Prediction Using Data Balancing and Ensemble-Based Methods. Mathematics 2022, 10, 2379. https://doi.org/10.3390/math10142379
Tékouabou SCK, Gherghina ȘC, Toulni H, Mata PN, Martins JM. Towards Explainable Machine Learning for Bank Churn Prediction Using Data Balancing and Ensemble-Based Methods. Mathematics. 2022; 10(14):2379. https://doi.org/10.3390/math10142379
Chicago/Turabian StyleTékouabou, Stéphane C. K., Ștefan Cristian Gherghina, Hamza Toulni, Pedro Neves Mata, and José Moleiro Martins. 2022. "Towards Explainable Machine Learning for Bank Churn Prediction Using Data Balancing and Ensemble-Based Methods" Mathematics 10, no. 14: 2379. https://doi.org/10.3390/math10142379
APA StyleTékouabou, S. C. K., Gherghina, Ș. C., Toulni, H., Mata, P. N., & Martins, J. M. (2022). Towards Explainable Machine Learning for Bank Churn Prediction Using Data Balancing and Ensemble-Based Methods. Mathematics, 10(14), 2379. https://doi.org/10.3390/math10142379







