Modified Inertial Subgradient Extragradient Method with Regularization for Variational Inequality and Null Point Problems

Abstract

The paper develops a modified inertial subgradient extragradient method to find a solution to the variational inequality problem over the set of common solutions to the variational inequality and null point problems. The proposed method adopts a nonmonotonic stepsize rule without any linesearch procedure. We describe how to incorporate the regularization technique and the subgradient extragradient method; then, we establish the strong convergence of the proposed method under some appropriate conditions. Several numerical experiments are also provided to verify the efficiency of the introduced method with respect to previous methods.

1. Introduction

Let H be a real Hilbert space with scalar product $\langle ·,·\rangle$ and generated norm $∥·∥$. Let $A:H\to H$ be a nonlinear operator. Recall that the variational inequality problem (VIP) for the operator A on C is described as follows:

$$\mathrm{Find}{v}^{*}\in C,\mathrm{such}\mathrm{that}\langle A{v}^{*},v-v^{*}\rangle \ge 0,\forall v\in C.$$

(1)

Denote by $VI(C,A)$ the set of solutions of the VIP (1). The VIP theory, which was first proposed independently by Fichera [1] and Stampacchia [2], is a  powerful and effective tool in mathematics. It has a vast application across several fields of study, such as engineering mechanics, nonlinear equations, necessary optimality conditions, fractional differential equations, economics, and so on  [3,4,5,6,7,8,9,10,11,12,13,14,15,16].

Let C be a nonempty, closed, and convex subset of a real Hilbert space H. A mapping $S:C\to H$ is:

(i)

monotone, if

$$\langle Sx-Sy,x-y\rangle \ge 0,\forall x,y\in C;$$

(ii)

$\alpha$- strongly monotone, if there exists a number $\alpha >0$ such that

$$\langle Sx-Sy,x-y\rangle \ge \alpha {∥x-y∥}^2,\forall x,y\in C;$$

(iii)

$\gamma$-inverse strongly monotone, if there exists a positive number $\gamma$ such that

$$\langle Sx-Sy,x-y\rangle \ge \gamma {∥Sx-Sy∥}^2,\forall x,y\in C;$$

(iv)

k- Lipschitz continuous, if there exists $k>0$ such that

$$∥Sx-Sy∥\le k∥x-y∥,\forall x,y\in C;$$

(v)

nonexpansive, if

$$∥Sx-Sy∥\le ∥x-y∥,\forall x,y\in C.$$

Remark 1. 

Notice that any γ-inverse strongly monotone mapping is $\frac{1}{\gamma }$-Lipschitz continuous, and both strongly monotone and inverse strongly monotone mappings are monotone. It is also known that the set of fixed points of a nonexpansive mapping is closed and convex.

For each $p\in H$, because C is nonempty, closed, and convex, then there exists a unique point in C, denoted by $P_{C}p$, which is the nearest to p. The mapping $P_C:H\to C$ is called the metric projection from H onto C. We give two explicit formulas to find the projection of any point onto a ball and a half-space.

• The projection of  p onto a ball $\mathcal{B}(u,r)=\{x:∥x-u∥\le r\}$ is computed by

  $$P_{\mathcal{B}(u,r)}=u+\frac{r}{max\{∥p-u∥,r\}}(p-u).$$
• The projection of p onto a half-space $H=\{x:\langle v,x-u\rangle \le 0\}$ is computed by

  $$P_H\left(p\right)=p-max\{\langle v,p-u\rangle /{∥v∥}^2,0\}v.$$

The problem, which will be studied in this work, is stated as follows:

$$\mathrm{Find}{u}^{*}\in VI(C,A)\bigcap S^{-1}0,\mathrm{such}\mathrm{that},\langle F{u}^{*},v-u^{*}\rangle \ge 0,\forall v\in VI(C,A)\bigcap S^{-1}0,$$

(2)

where S is inverse-strongly monotone, F is strongly monotone, and A is monotone.

Recently, many works of literature on iterative methods for solving variational inequality problems have been proposed and studied, see, e.g., [6,9,11,12,14,15] and the references therein. The simplest and oldest method is the projected-gradient method in which only one projection on a feasible set is performed. A convergence of the method, however, requires a strong hypothesis: strong monotonicity or inverse strong monotonicity on A. To weaken this strong hypothesis, Korpelevich [9] suggested the following extragradient method (EGM):

$$\left\{\begin{array}{c}{y}_n=P_C(x_n-\tau A{x}_n),\hfill \\ x_{n+1}=P_C(x_n-\tau A{y}_n),\hfill \end{array}\right.$$

(3)

where A is monotone and L-Lipschitz continuous. It is known that the sequence $\left\{x_n\right\}$ generated by the EGM converges weakly to a solution of the VIP provided that $VI(C,A)\ne \varnothing$. However, the EGM needs to  compute the projection onto the feasible set twice in each iteration. This may be expensive if  the feasible set C has a complicated structure. Furthermore, it might seriously affect the efficiency by using such a method. In 2011, Censor et al. [15] modified the EGM and first proposed the subgradient extragradient method (SEGM) (Algorithm 1):

Algorithm 1: The subgradient extragradient algorithm (SEGM).

Initialization: Set $\tau >0$, and let $x_0\in H$ be arbitrary. Step 1. Given $x_n(n\ge 0)$, compute $$y_n=P_C(x_n-\tau A{x}_n),$$ and construct the half-space $T_n$ the bounding hyperplane of which supports C at $y_n$, $$T_n:=\{w\in H\mid \langle (x_n-\tau A{x}_n)-y_n,w-y_n\rangle \le 0\}.$$ Step 2. Calculate the next iterate $$x_{n+1}=P_{T_n}(x_n-\tau A{y}_n).$$ Step 3. If $x_n=y_n$, then stop. Otherwise, set $n:=n+1$ and return to Step 1.

The main advantage of the SEGM is that it replaces the second projection from the convex and closed subset C to the half-space $T_n$, and this projection can be computed by an explicit formula. Notice that both EGM and SEGM have been proven to possess only weak convergence in real Hilbert spaces. It is worth noting that strong convergence is more desirable than weak convergence in infinite dimensional spaces. One the other hand, we point out here that the stepsize of the EGM and SEGM plays a  significant role in the convergence properties of the iterative methods. The stepsize defined by a constant is often very small and slows down the convergence rate. On the contrary, variable and appropriate stepsizes can often cause better numerical results. Recently, Yang et al. [17] introduced a self-adaptive subgradient extragradient method for solving the VIP.

It should be noted that strong convergence theorems can be obtained by using Algorithm 2 in real Hilbert spaces. However, the stepsize used in Algorithms 2 is monotonically decreasing, which may also affect the execution efficiency of such a method. Following the ideas of the EGM, the SEGM, and the  SSEGM, Tan and Qin [18] proposed the following inertial extragradient algorithm with nonmonotonic stepsizes for solving the monotone variational inequality problem in real Hilbert spaces.

Algorithm 2: Self-adaptive subgradient extragradient method (SSEGM).

Initialization: Set $\left\{{\tau }_n\right\}\subset (0,+\infty )$, $\left\{{\alpha }_n\right\}\subset (0,+\infty )$, and $\nu \subset \in (0,1)$, and let $x_0\in H$ be arbitrary. Step 1. Given $x_n$, compute $$y_n=P_C\left(x_n-{\tau }_{n}A{x}_n\right).$$ If $x_n=y_n$, then stop: $x_n$ is a solution. Otherwise, go to Step 2. Step 2. Construct the half-space $T_n$ the bounding hyperplane of which supports C at $y_n$, $$T_n:=\{w\in H\mid \langle x_n-{\tau }_{n}A{x}_n-y_n,w-y_n\rangle \le 0\},$$ and calculate $$z_n=P_{T_n}\left(x_n-{\tau }_{n}A{y}_n\right).$$ Step 3. Compute $$x_{n+1}={\alpha }_n{x}_0+(1-{\alpha }_n)z_n,$$ where $\left\{{\tau }_n\right\}$ is updated by $${\tau }_{n+1}=\left\{\begin{array}{c}min\{\frac{\nu {∥x_n-y_n∥}^2-{∥z_n-y_n∥}^2}{2\langle A{x}_n-A{y}_n,z_n-y_n\rangle },{\tau }_n\},\mathrm{if}\langle A{x}_n-A{y}_n,z_n-y_n\rangle \ne 0;\hfill \\ {\tau }_n,\mathrm{otherwise}.\hfill \end{array}\right.$$ Step 4. Set $n:=n+1$ and return to Step 1.

Under some suitable conditions, they proved that the iterative sequence $\left\{x_n\right\}$ constructed by Algorithm 3 converges strongly to a solution of the VIP (1).

Algorithm 3: Self adaptive viscosity-type inertial subgradient extragradient method with nonmonotonic stepsizes (SSEGMN).

Initialization: Set $\left\{{\tau }_n\right\}\subset (0,+\infty )$, $\left\{{\alpha }_n\right\}\subset (0,+\infty )$, $\nu \in (0,1)$, and $\varrho \in (0,+\infty )$, and let $x_0,x_1\in H$ be arbitrary. Step 1. Given $x_{n-1}$ and $x_n(n\ge 1)$, compute $$u_n=x_n+{\mu }_n(x_n-x_{n-1}),$$ where $${\mu }_n=\left\{\begin{array}{c}min\{\frac{{ϵ}_n}{∥x_n-x_{n-1}∥},\varrho \},\mathrm{if}{x}_n\ne x_{n-1};\hfill \\ \varrho ,\mathrm{otherwise}.\hfill \end{array}\right.$$ (4) Step 2. Compute $$y_n=P_C\left(u_n-{\tau }_{n}A{u}_n\right),$$ and construct the half-space $T_n$ the bounding hyperplane of which supports C at $y_n$, $$T_n:=\{w\in H\mid \langle u_n-{\tau }_{n}A{u}_n-y_n,w-y_n\rangle \le 0\}.$$ Step 3. Compute $$z_n=P_{T_n}\left(u_n-{\tau }_{n}A{y}_n\right).$$ Step 4. Compute $$x_{n+1}={\alpha }_{n}f\left(x_n\right)+(1-{\alpha }_n)z_n,$$ where $\left\{{\tau }_n\right\}$ is updated by $${\tau }_{n+1}=\left\{\begin{array}{c}min\{\frac{\nu ∥u_n-y_n∥}{∥A{u}_n-A{y}_n∥},{\tau }_n+{\xi }_n\},\mathrm{if}A{u}_n-A{y}_n\ne 0;\hfill \\ {\tau }_n+{\xi }_n,\mathrm{otherwise}.\hfill \end{array}\right.$$ (5) Step 5. Set $n:=n+1$ and return to Step 1.

Motivated by Korpelevich [9], Censor et al. [15], Yang et al. [17], and Tan and Qin [18], we introduce a modified inertial subgradient extragradient method with a nonmonotonic stepsize rule for finding a solution to the variational inequality problem over the set of common solutions to the variational inequality and null point problems. Different from the Halpern iteration and the viscosity methods, the strong convergence of the new method is based on the regularization technique. We also give some numerical examples to illustrate the efficiency of the proposed method over some existing ones.

2. Preliminaries

In this work, we denote the strong and weak convergence of $\left\{x_n\right\}$ by $x_n\to x$ and $x_n\rightharpoonup x$, respectively. We denote by $\mathrm{Fix}\left(S\right)$ the set of fixed points of a mapping $S:C\to H$ (i.e., $\mathrm{Fix}\left(S\right)=\{x\in C:Sx=x\}$). We use $\omega \left(x_n\right)=\{x:x_{n_j}\rightharpoonup x\}$ to denote the weak $\omega$-limit set of $\left\{x_n\right\}$. In view of  Alaoglu’s Theorem, we have: each bounded sequence $\left\{x_n\right\}$ in H has a subsequence that is weakly convergent (see [19]).

Lemma 1 

([20]). Let C be a nonempty closed convex subset of a real Hilbert space H. For $u\in H$ and $v\in C$, $v=P_{C}u$ if and only if $\langle u-v,w-v\rangle \le 0,\forall w\in C.$

Lemma 2 

([19]). Assume C is a nonempty closed convex subset of a real Hilbert space H, and $S:C\to H$ is a nonexpansive mapping. Then, the mapping $I-S$ is demiclosed, i.e., if $\left\{x_n\right\}$ is a sequence in C such that $x_n\rightharpoonup x$ and $(I-S)x_n\to y$, then $(I-S)x=y$.

Lemma 3 

([19]). Let $\left\{x_n\right\}$ be a sequence in H. If $x_n\rightharpoonup x$ and $∥x_n∥\to ∥x∥$, then $x_n\to x$.

Lemma 4 

([21]). Suppose $A:C\to H$ is a hemicontinuous and (pseudo) monotone operator; then, $v^{*}$ is a solution of the VIP (1) if and only if $v^{*}$ is a solution of the following problem:

$$\mathit{find}{v}^{*}\in C\mathit{such}\mathit{that}\langle Av,v-v^{*}\rangle \ge 0,\forall v\in C.$$

Lemma 5 

([22,23]). Let $\left\{a_n\right\}$ be a sequence of nonnegative real numbers. Assume that

$$a_{n+1}\le (1-{\beta }_n)a_n+{\gamma }_n,n\in \mathbb{N},$$

where $\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\}$ satisfy the conditions

(i) 

${\sum }_{n=1}^{\infty }{\beta }_n=\infty ,{lim}_{n\to \infty }{\beta }_n=0$,

(ii) 

${lim\; sup}_{n\to \infty }\frac{{\gamma }_n}{{\beta }_n}\le 0$.

Then, ${lim}_{n\to \infty }{a}_n=0$.

3. Main Results

In this section, let C be a nonempty, closed, and convex subset of H, $S:H\to H$ be $\rho$-inverse-strongly monotone, $F:H\to H$ be $\gamma$- strongly monotone, and k- Lipschitz continuous. Let $A:H\to H$ be L- Lipschitz continuous and monotone such that $\Omega :=VI(C,A)\bigcap S^{-1}0\ne \varnothing .$ It is easily seen that the mapping $I-\iota S$ is nonexpansive for any $\iota \in (0,2\rho ]$ (also, see [24]). Furthermore, one finds from Remark 1 that $S^{-1}0=\mathrm{Fix}(I-\iota S)$ is closed and convex. Since $VI(C,A)$ is closed and convex, then $\Omega$ is also closed and convex. These ensure the uniqueness of solutions $x^{†}$ to problem (2). Let $\mu \in (0,1)$ be a fixed positive real number. We now construct a regularization solution $x_{\alpha }$ for problem (2) by solving the following general variational inequality problem:

$$\mathrm{Find}{x}_{\alpha }\in C,\mathrm{such}\mathrm{that}\langle A{x}_{\alpha }+{\alpha }^{\mu }S{x}_{\alpha }+\alpha F{x}_{\alpha },v-x_{\alpha }\rangle \ge 0,\forall v\in C.$$

(6)

The following lemmas play an important role in proving the main results.

Lemma 6. 

For each $\alpha >0,$ the problem (6) has a unique solution $x_{\alpha }$.

Proof. 

Since A is monotone and Lipschitz continuous, S is inverse-strongly monotone, and F is strongly monotone and Lipschitz continuous, then we deduce that $A+{\alpha }^{\mu }S+\alpha F$ is strongly monotone and Lipschitz continuous. It is well-known that if a mapping A is Lipschitzian and strongly monotone, then the  VIP (1) has a unique solution (see [25] for more details). Hence, replacing A by $A+{\alpha }^{\mu }S+\alpha F$, we derive that the problem (6) has a unique solution $x_{\alpha }\in C$ for each $\alpha >0$. □

Lemma 7. 

It holds that ${lim}_{\alpha \to 0^{+}}∥x_{\alpha }-x^{†}∥=0$.

Proof. 

For every $q\in \Omega$, one has $\langle Aq,x_{\alpha }-q\rangle \ge 0$ and $Sq=0$. By (6), the monotone property of $A,S$, and F, one obtains

$$\begin{array}{ccc}\hfill \langle F{x}_{\alpha },q-x_{\alpha }\rangle & \ge & {\alpha }^{-1}\langle A{x}_{\alpha }+{\alpha }^{\mu }S{x}_{\alpha },x_{\alpha }-q\rangle \hfill \\ & =& {\alpha }^{-1}\langle A{x}_{\alpha },x_{\alpha }-q\rangle +{\alpha }^{\mu -1}\langle S{x}_{\alpha },x_{\alpha }-q\rangle \hfill \\ & \ge & {\alpha }^{-1}\langle Aq,x_{\alpha }-q\rangle +{\alpha }^{\mu -1}\langle Sq,x_{\alpha }-q\rangle \hfill \\ & \ge & 0.\hfill \end{array}$$

(7)

Noticing that

$$\begin{array}{c}\langle F{x}_{\alpha }-Fq,q-x_{\alpha }\rangle +\langle Fq,q-x_{\alpha }\rangle =\langle F{x}_{\alpha },q-x_{\alpha }\rangle ,\end{array}$$

(8)

this, together with the $\gamma$- strong monotonicity of F and (7), implies

$$\begin{array}{c}\hfill -\gamma {∥x_{\alpha }-q∥}^2+\langle Fq,q-x_{\alpha }\rangle \ge 0.\end{array}$$

Namely,

$$\begin{array}{c}\hfill \langle Fq,q-x_{\alpha }\rangle \ge \gamma {∥x_{\alpha }-q∥}^2.\end{array}$$

(9)

Since $\langle Fq,q-x_{\alpha }\rangle \le ∥Fq∥∥q-x_{\alpha }∥,$ by substituting it into (9), we find

$$\begin{array}{c}\hfill \gamma {∥x_{\alpha }-q∥}^2\le ∥Fq∥∥q-x_{\alpha }∥.\end{array}$$

If $∥x_{\alpha }-q∥\ne 0$, then it holds that

$$\begin{array}{c}\hfill \gamma ∥x_{\alpha }-q∥\le ∥Fq∥,\end{array}$$

which implies

$$\begin{array}{c}\hfill ∥x_{\alpha }∥\le ∥q∥+\frac{∥Fq∥}{\gamma },\forall q\in \Omega .\end{array}$$

If $∥x_{\alpha }-q∥=0$, then the above inequality obviously holds. Particularly, one also obtains

$$\begin{array}{c}\hfill ∥x_{\alpha }∥\le ∥x^{†}∥+\frac{∥F{x}^{†}∥}{\gamma }.\end{array}$$

(10)

Thus, we deduce that $\left\{x_{\alpha }\right\}$ is bounded. Furthermore, there is a subsequence $\left\{x_{{\alpha }_j}\right\}$ of $\left\{x_{\alpha }\right\}$ and some point $x^{*}$ such that $x_{{\alpha }_j}\rightharpoonup x^{*}(\mathrm{as}j\to \infty )$. Utilizing the inverse strongly monotone property of  S, the monotone property of A, and noting (6), one has

$$\begin{array}{ccc}\hfill {\alpha }_j^{\mu }\langle S{x}_{{\alpha }_j},x_{{\alpha }_j}-q\rangle & \le & \langle A{x}_{{\alpha }_j},q-x_{{\alpha }_j}\rangle +{\alpha }_j\langle F{x}_{{\alpha }_j},q-x_{{\alpha }_j}\rangle \hfill \\ & \le & \langle Aq,q-x_{{\alpha }_j}\rangle +{\alpha }_j\langle F{x}_{{\alpha }_j},q-x_{{\alpha }_j}\rangle \hfill \\ & \le & {\alpha }_j\langle Fq,q-x_{{\alpha }_j}\rangle ,\hfill \end{array}$$

which leads to

$$\begin{array}{c}\hfill \langle S{x}_{{\alpha }_j},x_{{\alpha }_j}-q\rangle \le {\alpha }_j^{1-\mu }\langle Fq,q-x_{{\alpha }_j}\rangle \to 0(\mathrm{as}j\to \infty ).\end{array}$$

(11)

By using the $\rho$-inverse-strongly monotone property of S, noticing $Sq=0$ and (11), one obtains

$$\begin{array}{ccc}\hfill \rho {∥S{x}_{{\alpha }_j}∥}^2& =& \rho {∥S{x}_{{\alpha }_j}-Sq∥}^2\hfill \\ & \le & \langle S{x}_{{\alpha }_j}-Sq,x_{{\alpha }_j}-q\rangle \hfill \\ & =& \langle S{x}_{{\alpha }_j},x_{{\alpha }_j}-q\rangle \to 0,\hfill \end{array}$$

which yields that

$$\underset{j\to \infty }{lim}S{x}_{{\alpha }_j}=0.$$

Since the mapping $S_{\iota }:=I-\iota S$ is nonexpansive for any $\iota \in (0,2\rho ]$ (see [24]), noting Lemma 2, one obtains that $S_{\iota }$ demiclosed at zero. Therefore, one deduces that $x^{*}\in \mathrm{Fix}\left(S_{\iota }\right),$ which implies

$$x^{*}\in S^{-1}0.$$

(12)

We now prove that $x^{*}\in VI(C,A)$. It follows from the monotonic property of A, S, F, and (6) that

$$\langle Av+{\alpha }_j^{\mu }Sv+{\alpha }_{j}Fv,v-x_{{\alpha }_j}\rangle \ge 0,\forall v\in C,$$

or, equivalently,

$$\langle Av,x_{{\alpha }_j}-v\rangle +{\alpha }_j^{\mu }\langle Sv,x_{{\alpha }_j}-v\rangle +{\alpha }_j\langle Fv,x_{{\alpha }_j}-v\rangle \le 0,\forall v\in C.$$

(13)

Since ${\alpha }_j\to 0^{+}$ as $j\to \infty$, one deduces from (13) that

$$\langle Av,x^{*}-v\rangle \le 0,\forall v\in C.$$

Hence, one obtains from Lemma 4 that $x^{*}\in VI(C,A)$. This together with (12) implies

$$x^{*}\in \Omega .$$

(14)

We prove $x_{\alpha }\to x^{*}$ ($\alpha \to 0^{+}).$ One deduces from  (9) that

$$\begin{array}{c}\hfill \langle Fq,q-x_{{\alpha }_j}\rangle \ge 0,\forall q\in \Omega .\end{array}$$

(15)

Passing to the limit in (15) as $j\to \infty$, and noting the fact $x_{{\alpha }_j}\rightharpoonup x^{*}(\mathrm{as}j\to \infty ),$ one infers

$$\begin{array}{c}\hfill \langle Fq,q-x^{*}\rangle \ge 0,\forall q\in \Omega ,\end{array}$$

which implies by Lemma 4 that $x^{*}$ is the solution of problem (2). Since the solution $x^{†}$ of problem (2) is unique, one deduces that $x^{*}=x^{†}.$ Thus, the set $\omega \left(x_{\alpha }\right)$ only has one element $x^{†}$; that is, $\omega \left(x_{\alpha }\right)=\left\{x^{†}\right\}.$ Therefore, the whole sequence $\left\{x_{\alpha }\right\}$ converges weakly to $x^{†}$. Again, using (9) with $q=x^{†}$, one finds

$$\begin{array}{c}\hfill {∥x_{{\alpha }_j}-x^{†}∥}^2\le \frac{1}{\gamma }\langle F{x}^{†},x^{†}-x_{{\alpha }_j}\rangle .\end{array}$$

(16)

Passing in (16) to the limit as $j\to \infty$, and noting the fact $x_{{\alpha }_j}\rightharpoonup x^{*}=x^{†}(\mathrm{as}j\to \infty ),$ one obtains

$$\begin{array}{c}\hfill \underset{j\to \infty }{lim}∥x_{{\alpha }_j}-x^{†}∥=0.\end{array}$$

We take another subsequence $\left\{x_{{\alpha }_k}\right\}$ of $\left\{x_{\alpha }\right\}$ and some point $\widehat{x}$ such that $x_{{\alpha }_k}\rightharpoonup \widehat{x}.$ By following a similar proof to the above, one derives ${lim}_{k\to \infty }{x}_{{\alpha }_k}=\widehat{x}$, and $\widehat{x}=x^{†}.$ Therefore, one deduces that ${lim}_{\alpha \to 0^{+}}∥x_{\alpha }-x^{†}∥=0$. This completes the proof.  □

Lemma 8. 

$∥x_{{\alpha }_1}-x_{{\alpha }_2}∥\le \frac{|{\alpha }_2-{\alpha }_1|}{{\alpha }_1{\alpha }_2}M$ for all ${\alpha }_1,{\alpha }_2\in (0,1)$, where $M=\frac{1}{\gamma }sup\{∥S{x}_{{\alpha }_2}∥+∥F{x}_{{\alpha }_2}∥\}$.

Proof. 

Suppose $x_{{\alpha }_1}$, $x_{{\alpha }_2}$ are two solutions of the problem (6). Without loss of generality, we assume that $0<{\alpha }_2<{\alpha }_1<1$. Then,

$$\langle A{x}_{{\alpha }_1}+{\alpha }_1^{\mu }S{x}_{{\alpha }_1}+{\alpha }_{1}F{x}_{{\alpha }_1},x_{{\alpha }_2}-x_{{\alpha }_1}\rangle \ge 0,$$

and

$$\langle A{x}_{{\alpha }_2}+{\alpha }_2^{\mu }S{x}_{{\alpha }_2}+{\alpha }_{2}F{x}_{{\alpha }_2},x_{{\alpha }_1}-x_{{\alpha }_2}\rangle \ge 0.$$

Summing up the above two inequalities, one finds that

$$\begin{array}{ccc}& & \langle A{x}_{{\alpha }_1}-A{x}_{{\alpha }_2},x_{{\alpha }_2}-x_{{\alpha }_1}\rangle +{\alpha }_1^{\mu }\langle S{x}_{{\alpha }_1}-S{x}_{{\alpha }_2},x_{{\alpha }_2}-x_{{\alpha }_1}\rangle +({\alpha }_1^{\mu }-{\alpha }_2^{\mu })\langle S{x}_{{\alpha }_2},x_{{\alpha }_2}-x_{{\alpha }_1}\rangle \hfill \\ & & +{\alpha }_1\langle F{x}_{{\alpha }_1}-F{x}_{{\alpha }_2},x_{{\alpha }_2}-x_{{\alpha }_1}\rangle +({\alpha }_1-{\alpha }_2)\langle F{x}_{{\alpha }_2},x_{{\alpha }_2}-x_{{\alpha }_1}\rangle \ge 0.\hfill \end{array}$$

Noting the monotonic property of A and S, one obtains

$$\begin{array}{c}\hfill ({\alpha }_2^{\mu }-{\alpha }_1^{\mu })\langle S{x}_{{\alpha }_2},x_{{\alpha }_1}-x_{{\alpha }_2}\rangle +{\alpha }_1\langle F{x}_{{\alpha }_1}-F{x}_{{\alpha }_2},x_{{\alpha }_2}-x_{{\alpha }_1}\rangle +({\alpha }_1-{\alpha }_2)\langle F{x}_{{\alpha }_2},x_{{\alpha }_2}-x_{{\alpha }_1}\rangle \ge 0,\end{array}$$

or, equivalently,

$$\begin{array}{ccc}& & ({\alpha }_2^{\mu }-{\alpha }_1^{\mu })\langle S{x}_{{\alpha }_2},x_{{\alpha }_1}-x_{{\alpha }_2}\rangle +({\alpha }_2-{\alpha }_1)\langle F{x}_{{\alpha }_2},x_{{\alpha }_1}-x_{{\alpha }_2}\rangle \ge {\alpha }_1\langle F{x}_{{\alpha }_1}-F{x}_{{\alpha }_2},x_{{\alpha }_1}-x_{{\alpha }_2}\rangle .\hfill \end{array}$$

It follows from the  $\gamma$- strong monotonicity of F that

$$\begin{array}{ccc}& & ({\alpha }_2^{\mu }-{\alpha }_1^{\mu })\langle S{x}_{{\alpha }_2},x_{{\alpha }_1}-x_{{\alpha }_2}\rangle +({\alpha }_2-{\alpha }_1)\langle F{x}_{{\alpha }_2},x_{{\alpha }_1}-x_{{\alpha }_2}\rangle \ge {\alpha }_1\gamma {∥x_{{\alpha }_1}-x_{{\alpha }_2}∥}^2,\hfill \end{array}$$

which yields

$$|{\alpha }_2^{\mu }-{\alpha }_1^{\mu }|∥S{x}_{{\alpha }_2}∥∥x_{{\alpha }_1}-x_{{\alpha }_2}∥+\left|{\alpha }_2-{\alpha }_1\right|∥F{x}_{{\alpha }_2}∥∥x_{{\alpha }_1}-x_{{\alpha }_2}∥\ge {\alpha }_1\gamma {∥x_{{\alpha }_1}-x_{{\alpha }_2}∥}^2.$$

Thus, one obtains

$$∥x_{{\alpha }_1}-x_{{\alpha }_2}∥\le \frac{|{\alpha }_2^{\mu }-{\alpha }_1^{\mu }|}{{\alpha }_1}\frac{∥S{x}_{{\alpha }_2}∥}{\gamma }+\frac{|{\alpha }_2-{\alpha }_1|}{{\alpha }_1}\frac{∥F{x}_{{\alpha }_2}∥}{\gamma }.$$

(17)

The mappings S and F are bounded due to the fact that they are Lipschitz. From the Lagrange’s mean-value theorem to a continuous function $f\left(x\right)=x^{\mu }$ on $(0,1)$, one deduces that

$$|{\alpha }_2^{\mu }-{\alpha }_1^{\mu }|={\alpha }_1^{\mu }-{\alpha }_2^{\mu }\le \mu {\alpha }_2^{\mu -1}({\alpha }_1-{\alpha }_2)\le \mu {\alpha }_2^{-1}({\alpha }_1-{\alpha }_2)\le {\alpha }_2^{-1}({\alpha }_1-{\alpha }_2).$$

This, together with (17), implies that

$$∥x_{{\alpha }_1}-x_{{\alpha }_2}∥\le \frac{|{\alpha }_2-{\alpha }_1|}{{\alpha }_1{\alpha }_2}\frac{∥S{x}_{{\alpha }_2}∥}{\gamma }+\frac{|{\alpha }_2-{\alpha }_1|}{{\alpha }_1{\alpha }_2}\frac{∥F{x}_{{\alpha }_2}∥}{\gamma }\le \frac{|{\alpha }_2-{\alpha }_1|}{{\alpha }_1{\alpha }_2}M,$$

(18)

where $M=\frac{1}{\gamma }sup\{∥S{x}_{{\alpha }_2}∥+∥F{x}_{{\alpha }_2}∥\}$. If $0<{\alpha }_1\le {\alpha }_2<1$, by interchanging ${\alpha }_1$ and ${\alpha }_2$ in the above proof, one can also obtain the same results. This finishes the proof.    □

Now, the iterative method is presented as follows:    

Lemma 9 

([18]). The sequence $\left\{{\tau }_n\right\}$ generated by (20) is well defined, and ${lim}_{n\to \infty }{\tau }_n=\tau$ and $\tau \in [min\{\frac{\nu }{L},{\tau }_0\},{\tau }_0+\zeta ]$, where $\zeta ={\sum }_{i=1}^{\infty }{\xi }_n.$

Assumption 1. 

(C1) 

$0<\nu +\tau {\rho }^{-1}<1$, where τ is that in Lemma 9;

(C2) 

${lim}_{n\to \infty }{\alpha }_n=0$, ${\sum }_{n=0}^{\infty }{\alpha }_n=\infty$;

(C3) 

${lim}_{n\to \infty }\frac{{\alpha }_n-{\alpha }_{n+1}}{{\alpha }_n^2{\alpha }_{n+1}}=0$;

(C4) 

${lim}_{n\to \infty }\frac{{ϵ}_n}{{\alpha }_n}=0$;

(C5) 

$\Omega :=VI(C,A)\bigcap S^{-1}0\ne \varnothing$.

Theorem 1. 

The sequence $\left\{x_n\right\}$ generated by Algorithm 4 converges strongly to the unique solutions $x^{†}$ of problem (2) under Assumption A1 (C1)–(C5).

Algorithm 4: Modified inertial subgradient extragradient method with regularization (MSEMR).

Initialization: Set $\left\{{\tau }_n\right\}\subset (0,+\infty )$, $\left\{{ϵ}_n\right\}\subset (0,+\infty )$, $\left\{{\alpha }_n\right\}\subset (0,+\infty )$, $\varrho >0$, $\mu \in (0,1)$, and $\nu \in (0,1)$. Choose a nonnegative real sequence $\left\{{\xi }_n\right\}$ such that ${\sum }_{n=0}^{\infty }{\xi }_n<\infty$. Let $x_0,x_1\in H$ be arbitrary. Step 1.Compute $$u_n=x_n+{\mu }_n(x_n-x_{n-1}),$$ where $${\mu }_n=\left\{\begin{array}{c}min\{\frac{{ϵ}_n}{∥x_n-x_{n-1}∥},\varrho \},\mathit{if}{x}_n\ne x_{n-1};\hfill \\ \varrho ,\mathit{otherwise}.\hfill \end{array}\right.$$ (19) Step 2.Compute $$y_n=P_C\left(u_n-{\tau }_n(A{u}_n+{\alpha }_n^{\mu }S{u}_n+{\alpha }_{n}F{u}_n)\right),$$ and construct the half-space $T_n$ the bounding hyperplane of which supports C at $y_n$, $$T_n:=\{w\in H\mid \langle u_n-{\tau }_n(A{u}_n+{\alpha }_n^{\mu }S{u}_n+{\alpha }_{n}F{u}_n)-y_n,w-y_n\rangle \le 0\}.$$ Step 3.Calculate $$x_{n+1}=P_{T_n}\left(u_n-{\tau }_n(A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n)\right),$$ where $\left\{{\tau }_n\right\}$ is updated by $${\tau }_{n+1}=\left\{\begin{array}{c}min\{\frac{\nu ∥u_n-y_n∥}{∥A{u}_n-A{y}_n∥},{\tau }_n+{\xi }_n\},\mathit{if}A{u}_n-A{y}_n\ne 0;\hfill \\ {\tau }_n+{\xi }_n,\mathit{otherwise}.\hfill \end{array}\right.$$ (20) Step 4.Set $n:=n+1$ and return to Step 1.

Proof. 

Denote by $x_{{\alpha }_n}$ the solution of the problem (6) with $\alpha ={\alpha }_n$. By (C2) and Lemma 7, one obtains $x_{{\alpha }_n}\to x^{†}$ as $n\to \infty$. Thus, it is sufficient to prove

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}∥x_n-x_{{\alpha }_n}∥=0.\end{array}$$

Setting $w_n=u_n-{\tau }_n(A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n)$, and noting $x_{{\alpha }_n}\in C\subset T_n$ for any $n\in \mathbb{N}$, one obtains

$$\begin{array}{ccc}\hfill {∥x_{n+1}-x_{{\alpha }_n}∥}^2& =& {∥P_{T_n}{w}_n-x_{{\alpha }_n}∥}^2\hfill \\ & =& \langle P_{T_n}{w}_n-x_{{\alpha }_n},P_{T_n}{w}_n-x_{{\alpha }_n}\rangle \hfill \\ & =& \langle P_{T_n}{w}_n-w_n+w_n-x_{{\alpha }_n},P_{T_n}{w}_n-w_n+w_n-x_{{\alpha }_n}\rangle \hfill \\ & =& {∥P_{T_n}{w}_n-w_n∥}^2+{∥w_n-x_{{\alpha }_n}∥}^2+2\langle P_{T_n}{w}_n-w_n,w_n-x_{{\alpha }_n}\rangle .\hfill \end{array}$$

(21)

It follows from Lemma 1 that

$$\begin{array}{c}\hfill 2{∥P_{T_n}{w}_n-w_n∥}^2+2\langle P_{T_n}{w}_n-w_n,w_n-x_{{\alpha }_n}\rangle =2\langle P_{T_n}{w}_n-w_n,P_{T_n}{w}_n-x_{{\alpha }_n}\rangle \le 0.\end{array}$$

(22)

This, together with (21), implies

$$\begin{array}{ccc}\hfill & & {∥x_{n+1}-x_{{\alpha }_n}∥}^2\hfill \\ & \le & {∥w_n-x_{{\alpha }_n}∥}^2-{∥P_{T_n}{w}_n-w_n∥}^2\hfill \\ & =& {∥u_n-{\tau }_n(A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n)-x_{{\alpha }_n}∥}^2-{∥u_n-{\tau }_n(A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n)-x_{n+1}∥}^2\hfill \\ & =& {∥(u_n-x_{{\alpha }_n})-{\tau }_n(A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n)∥}^2-{∥(u_n-x_{n+1})-{\tau }_n(A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n)∥}^2\hfill \\ & =& {∥u_n-x_{{\alpha }_n}∥}^2-{∥u_n-x_{n+1}∥}^2+2{\tau }_n\langle A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n,x_{{\alpha }_n}-x_{n+1}\rangle \hfill \\ & =& {∥u_n-x_{{\alpha }_n}∥}^2-{∥u_n-x_{n+1}∥}^2+2\langle u_n-y_n,y_n-x_{n+1}\rangle \hfill \\ & & +2{\tau }_n\langle A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n,x_{{\alpha }_n}-y_n\rangle \hfill \\ & & +2{\tau }_n\langle (A{y}_n+{\alpha }_n^{\mu }S{y}_n)-(A{u}_n+{\alpha }_n^{\mu }S{u}_n),y_n-x_{n+1}\rangle \hfill \\ & & +2\langle u_n-{\tau }_{n}A{u}_n-{\tau }_n{\alpha }_n^{\mu }S{u}_n-{\tau }_n{\alpha }_{n}F{u}_n-y_n,x_{n+1}-y_n\rangle .\hfill \end{array}$$

(23)

Noticing the definition of $T_n$ and $x_{n+1}$, one derives

$$\langle u_n-{\tau }_{n}A{u}_n-{\tau }_n{\alpha }_n^{\mu }S{u}_n-{\tau }_n{\alpha }_{n}F{u}_n-y_n,x_{n+1}-y_n\rangle \le 0.$$

(24)

Substituting (24) into (23), one obtains

$$\begin{array}{ccc}\hfill {∥x_{n+1}-x_{{\alpha }_n}∥}^2& \le & {∥u_n-x_{{\alpha }_n}∥}^2-{∥u_n-x_{n+1}∥}^2+2\langle u_n-y_n,y_n-x_{n+1}\rangle \hfill \\ & & +2{\tau }_n\langle A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n,x_{{\alpha }_n}-y_n\rangle \hfill \\ & & +2{\tau }_n\langle (A{y}_n+{\alpha }_n^{\mu }S{y}_n)-(A{u}_n+{\alpha }_n^{\mu }S{u}_n),y_n-x_{n+1}\rangle .\hfill \end{array}$$

As

$$2\langle u_n-y_n,y_n-x_{n+1}\rangle ={∥u_n-x_{n+1}∥}^2-{∥u_n-y_n∥}^2-{∥y_n-x_{n+1}∥}^2,$$

(25)

by substituting (25) into the former inequality, one obtains

$$\begin{array}{ccc}\hfill {∥x_{n+1}-x_{{\alpha }_n}∥}^2& \le & {∥u_n-x_{{\alpha }_n}∥}^2-{∥u_n-y_n∥}^2-{∥y_n-x_{n+1}∥}^2\hfill \\ & & +2{\tau }_n\langle A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n,x_{{\alpha }_n}-y_n\rangle \hfill \\ & & +2{\tau }_n\langle (A{y}_n+{\alpha }_n^{\mu }S{y}_n)-(A{u}_n+{\alpha }_n^{\mu }S{u}_n),y_n-x_{n+1}\rangle .\hfill \end{array}$$

(26)

It follows from (20) and the inverse-strongly monotonicity of S that

$$\begin{array}{ccc}& & 2{\tau }_n\langle (A{y}_n+{\alpha }_n^{\mu }S{y}_n)-(A{u}_n+{\alpha }_n^{\mu }S{u}_n),y_n-x_{n+1}\rangle \hfill \\ & \le & 2{\tau }_n(∥A{y}_n-A{u}_n∥+∥S{y}_n-S{u}_n∥)∥y_n-x_{n+1}∥\hfill \\ & \le & 2{\tau }_n\left(\frac{\nu }{{\tau }_{n+1}}∥y_n-u_n∥+{\rho }^{-1}∥y_n-u_n∥\right)∥y_n-x_{n+1}∥\hfill \\ & =& 2\left(\nu \frac{{\tau }_n}{{\tau }_{n+1}}+{\tau }_n{\rho }^{-1}\right)∥y_n-u_n∥∥y_n-x_{n+1}∥\hfill \\ & \le & {\left(\nu \frac{{\tau }_n}{{\tau }_{n+1}}+{\tau }_n{\rho }^{-1}\right)}^2{∥y_n-u_n∥}^2+{∥y_n-x_{n+1}∥}^2.\hfill \end{array}$$

This, together with (26), leads to

$$\begin{array}{ccc}\hfill {∥x_{n+1}-x_{{\alpha }_n}∥}^2& \le & {∥u_n-x_{{\alpha }_n}∥}^2-\left(1-{\left(\nu \frac{{\tau }_n}{{\tau }_{n+1}}+{\tau }_n{\rho }^{-1}\right)}^2\right){∥u_n-y_n∥}^2\hfill \\ & & +2{\tau }_n\langle A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n,x_{{\alpha }_n}-y_n\rangle .\hfill \end{array}$$

(27)

Now, we estimate the last term in inequality (27). Observe that

$$\begin{array}{ccc}\hfill & & 2{\tau }_n\langle A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n,x_{{\alpha }_n}-y_n\rangle \hfill \\ & =& 2{\tau }_n\langle A{y}_n-A{x}_{{\alpha }_n},x_{{\alpha }_n}-y_n\rangle +2{\tau }_n\langle A{x}_{{\alpha }_n}+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n,x_{{\alpha }_n}-y_n\rangle \hfill \\ & =& 2{\tau }_n\langle A{y}_n-A{x}_{{\alpha }_n},x_{{\alpha }_n}-y_n\rangle +2{\tau }_n\langle A{x}_{{\alpha }_n}+{\alpha }_n^{\mu }S{x}_{{\alpha }_n}+{\alpha }_{n}F{x}_{{\alpha }_n},x_{{\alpha }_n}-y_n\rangle \hfill \\ & & +2{\tau }_n{\alpha }_n^{\mu }\langle S{y}_n-S{x}_{{\alpha }_n},x_{{\alpha }_n}-y_n\rangle +2{\tau }_n{\alpha }_n\langle F{u}_n-F{x}_{{\alpha }_n},x_{{\alpha }_n}-y_n\rangle .\hfill \end{array}$$

(28)

Since S and A are monotone, and $x_{{\alpha }_n}$ is the solution of the problem (6) with $\alpha ={\alpha }_n,$ one finds that

$$\langle A{y}_n-A{x}_{{\alpha }_n},x_{{\alpha }_n}-y_n\rangle \le 0,\langle S{y}_n-S{x}_{{\alpha }_n},x_{{\alpha }_n}-y_n\rangle \le 0,$$

and $\langle A{x}_{{\alpha }_n}+{\alpha }_n^{\mu }S{x}_{{\alpha }_n}+{\alpha }_{n}F{x}_{{\alpha }_n},x_{{\alpha }_n}-y_n\rangle \le 0,$ which, by (28) and the  strongly monotonicity of F, imply that

$$\begin{array}{ccc}\hfill & & 2{\tau }_n\langle A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n,x_{{\alpha }_n}-y_n\rangle \hfill \\ & \le & 2{\tau }_n{\alpha }_n\langle F{u}_n-F{x}_{{\alpha }_n},x_{{\alpha }_n}-y_n\rangle \hfill \\ & \le & 2{\tau }_n{\alpha }_n\langle F{u}_n-F{x}_{{\alpha }_n},x_{{\alpha }_n}-u_n\rangle +2{\tau }_n{\alpha }_n\langle F{u}_n-F{x}_{{\alpha }_n},u_n-y_n\rangle \hfill \\ & \le & -2{\tau }_n{\alpha }_n\gamma {∥u_n-x_{{\alpha }_n}∥}^2+2{\tau }_n{\alpha }_n∥F{u}_n-F{x}_{{\alpha }_n}∥∥u_n-y_n∥\hfill \\ & \le & -2{\tau }_n{\alpha }_n\gamma {∥u_n-x_{{\alpha }_n}∥}^2+2{\tau }_n{\alpha }_{n}k∥u_n-x_{{\alpha }_n}∥∥u_n-y_n∥.\hfill \end{array}$$

(29)

Let ${\sigma }_1,{\sigma }_2$, and ${\sigma }_3$ be positive real numbers such that

$$2\gamma -{\sigma }_{1}k-{\sigma }_2-{\sigma }_3>0.$$

Noticing

$$\begin{array}{c}\hfill 2∥u_n-x_{{\alpha }_n}∥∥u_n-y_n∥\le {\sigma }_1{∥u_n-x_{{\alpha }_n}∥}^2+\frac{1}{{\sigma }_1}{∥u_n-y_n∥}^2,\end{array}$$

(30)

one obtains from  (29) and (30) that

$$\begin{array}{ccc}\hfill & & 2{\tau }_n\langle A{y}_n+{\alpha }_n^{\mu }S{y}_n+{\alpha }_{n}F{u}_n,x_{{\alpha }_n}-y_n\rangle \hfill \\ & \le & -2{\tau }_n{\alpha }_n\gamma {∥u_n-x_{{\alpha }_n}∥}^2+{\tau }_n{\alpha }_n{\sigma }_{1}k{∥u_n-x_{{\alpha }_n}∥}^2+\frac{{\tau }_n{\alpha }_{n}k}{{\sigma }_1}{∥u_n-y_n∥}^2.\hfill \end{array}$$

(31)

Combining (27) and (31), one finds

$$\begin{array}{ccc}\hfill {∥x_{n+1}-x_{{\alpha }_n}∥}^2& \le & (1-(2\gamma -{\sigma }_{1}k){\tau }_n{\alpha }_n){∥u_n-x_{{\alpha }_n}∥}^2\hfill \\ & & -\left(1-{\left(\nu \frac{{\tau }_n}{{\tau }_{n+1}}+{\tau }_n{\rho }^{-1}\right)}^2-\frac{{\tau }_n{\alpha }_{n}k}{{\sigma }_1}\right){∥u_n-y_n∥}^2.\hfill \end{array}$$

(32)

By virtue of Lemma 9, (C1), (C2), and (C4), there exists $n_0\ge 1$ such that

$$\begin{array}{ccc}\hfill & & 1-(2\gamma -{\sigma }_{1}k){\tau }_n{\alpha }_n>0,\left(1-{\left(\nu \frac{{\tau }_n}{{\tau }_{n+1}}+{\tau }_n{\rho }^{-1}\right)}^2-\frac{{\tau }_n{\alpha }_{n}k}{{\sigma }_1}\right)>0,\hfill \\ & & 1-{\sigma }_3{\tau }_n{\alpha }_n>0,{ϵ}_n\le {\sigma }_2{\tau }_n{\alpha }_n,\forall n\ge n_0.\hfill \end{array}$$

(33)

Thus, one derives from (32) and (33) that

$${∥x_{n+1}-x_{{\alpha }_n}∥}^2\le (1-(2\gamma -{\sigma }_{1}k){\tau }_n{\alpha }_n){∥u_n-x_{{\alpha }_n}∥}^2,\forall n\ge n_0.$$

(34)

It follows from definition of $u_n$, (4) and (33) that

$$\begin{array}{ccc}\hfill {∥u_n-x_{{\alpha }_n}∥}^2& =& {∥x_n+{\mu }_n(x_n-x_{n-1})-x_{{\alpha }_n}∥}^2\hfill \\ & \le & {(∥x_n-x_{{\alpha }_n}∥+{\mu }_n∥x_n-x_{n-1}∥)}^2\hfill \\ & \le & {∥x_n-x_{{\alpha }_n}∥}^2+{\mu }_n^2{∥x_n-x_{n-1}∥}^2+2∥x_n-x_{{\alpha }_n}∥{\mu }_n∥x_n-x_{n-1}∥\hfill \\ & \le & {∥x_n-x_{{\alpha }_n}∥}^2+{ϵ}_n^2+2∥x_n-x_{{\alpha }_n}∥{ϵ}_n\hfill \\ & \le & {∥x_n-x_{{\alpha }_n}∥}^2+{ϵ}_n^2+{∥x_n-x_{{\alpha }_n}∥}^2{ϵ}_n+{ϵ}_n\hfill \\ & \le & (1+{ϵ}_n){∥x_n-x_{{\alpha }_n}∥}^2+2{ϵ}_n\hfill \\ & \le & (1+{\sigma }_2{\tau }_n{\alpha }_n){∥x_n-x_{{\alpha }_n}∥}^2+2{ϵ}_n,\forall n\ge n_0.\hfill \end{array}$$

(35)

Observe that

$$2∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥∥x_{{\alpha }_{n+1}}-x_{n+1}∥\le \frac{1}{{\sigma }_3{\tau }_n{\alpha }_n}{∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2+{\sigma }_3{\tau }_n{\alpha }_n{∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2.$$

(36)

Hence, for each $n\ge n_0$, one deduces from (36) and Lemma 8 that

$$\begin{array}{ccc}& & {∥x_{{\alpha }_n}-x_{n+1}∥}^2\hfill \\ & =& {∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2+{∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2-2\langle x_{{\alpha }_{n+1}}-x_{{\alpha }_n},x_{{\alpha }_{n+1}}-x_{n+1}\rangle \hfill \\ & \ge & {∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2+{∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2-2∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥∥x_{{\alpha }_{n+1}}-x_{n+1}∥\hfill \\ & \ge & {∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2+{∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2-\frac{1}{{\sigma }_3{\tau }_n{\alpha }_n}{∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2-{\sigma }_3{\tau }_n{\alpha }_n{∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2\hfill \\ & \ge & (1-{\sigma }_3{\tau }_n{\alpha }_n){∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2-\frac{1-{\sigma }_3{\tau }_n{\alpha }_n}{{\sigma }_3{\tau }_n{\alpha }_n}{∥x_{{\alpha }_{n+1}}-x_{{\alpha }_n}∥}^2\hfill \\ & \ge & (1-{\sigma }_3{\tau }_n{\alpha }_n){∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2-\frac{1-{\sigma }_3{\tau }_n{\alpha }_n}{{\sigma }_3{\tau }_n{\alpha }_n}{\left(\frac{{\alpha }_{n+1}-{\alpha }_n}{{\alpha }_n{\alpha }_{n+1}}\right)}^2{M}^2\hfill \\ & =& (1-{\sigma }_3{\tau }_n{\alpha }_n){∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2-\frac{(1-{\sigma }_3{\tau }_n{\alpha }_n){({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\tau }_n{\alpha }_n^3{\alpha }_{n+1}^2}{M}^2,\hfill \end{array}$$

which implies

$${∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2\le \frac{1}{1-{\sigma }_3{\tau }_n{\alpha }_n}{∥x_{n+1}-x_{{\alpha }_n}∥}^2+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\tau }_n{\alpha }_n^3{\alpha }_{n+1}^2}{M}^2,\forall n\ge n_0.$$

(37)

It follows from (33), (34), (35), and (37) that

$$\begin{array}{ccc}\hfill & & {∥x_{{\alpha }_{n+1}}-x_{n+1}∥}^2\hfill \\ & \le & \frac{1-(2\gamma -{\sigma }_{1}k){\tau }_n{\alpha }_n}{1-{\sigma }_3{\tau }_n{\alpha }_n}{∥u_n-x_{{\alpha }_n}∥}^2+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\tau }_n{\alpha }_n^3{\alpha }_{n+1}^2}{M}^2\hfill \\ & \le & \frac{(1-(2\gamma -{\sigma }_{1}k){\tau }_n{\alpha }_n)(1+{\sigma }_2{\tau }_n{\alpha }_n)}{1-{\sigma }_3{\tau }_n{\alpha }_n}{∥x_n-x_{{\alpha }_n}∥}^2+\frac{1-(2\gamma -{\sigma }_{1}k){\tau }_n{\alpha }_n}{1-{\sigma }_3{\tau }_n{\alpha }_n}2{ϵ}_n\hfill \\ & & +\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\tau }_n{\alpha }_n^3{\alpha }_{n+1}^2}{M}^2\hfill \\ & \le & \frac{1-(2\gamma -{\sigma }_{1}k-{\sigma }_2){\tau }_n{\alpha }_n}{1-{\sigma }_3{\tau }_n{\alpha }_n}{∥x_n-x_{{\alpha }_n}∥}^2-\frac{(2\gamma -{\sigma }_{1}k){\sigma }_2{\tau }_n^2{\alpha }_n^2}{1-{\sigma }_3{\tau }_n{\alpha }_n}{∥x_n-x_{{\alpha }_n}∥}^2\hfill \\ & & +\frac{1-(2\gamma -{\sigma }_{1}k){\tau }_n{\alpha }_n}{1-{\sigma }_3{\tau }_n{\alpha }_n}2{ϵ}_n+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\tau }_n{\alpha }_n^3{\alpha }_{n+1}^2}{M}^2\hfill \\ & \le & \frac{1-(2\gamma -{\sigma }_{1}k-{\sigma }_2){\tau }_n{\alpha }_n}{1-{\sigma }_3{\tau }_n{\alpha }_n}{∥x_n-x_{{\alpha }_n}∥}^2+4{ϵ}_n+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\tau }_n{\alpha }_n^3{\alpha }_{n+1}^2}{M}^2\hfill \\ & =& (1-{\beta }_n){∥x_n-x_{{\alpha }_n}∥}^2+{\gamma }_n,\forall n\ge n_0,\hfill \end{array}$$

(38)

where ${\beta }_n=\frac{(2\gamma -{\sigma }_{1}k-{\sigma }_2-{\sigma }_3){\tau }_n{\alpha }_n}{1-{\sigma }_3{\tau }_n{\alpha }_n}$, and ${\gamma }_n=4{ϵ}_n+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\tau }_n{\alpha }_n^3{\alpha }_{n+1}^2}{M}^2.$ From (C2), one obtains that ${\beta }_n\to 0$ and ${\sum }_{n=1}^{\infty }{\beta }_n=+\infty$. Furthermore, one derives by (C3) and (C4) that

$$\frac{{\gamma }_n}{{\beta }_n}=\left(\frac{4{ϵ}_n}{{\alpha }_n}+\frac{{({\alpha }_{n+1}-{\alpha }_n)}^2}{{\sigma }_3{\tau }_n{\alpha }_n^4{\alpha }_{n+1}^2}{M}^2\right)\left(\frac{1-{\sigma }_3{\tau }_n{\alpha }_n}{(2\gamma -{\sigma }_{1}k-{\sigma }_2-{\sigma }_3){\tau }_n}\right)\to 0.$$

By using Lemma 5, one deduces ${lim}_{n\to \infty }∥x_n-x_{{\alpha }_n}∥=0$. Thus, one has ${lim}_{n\to \infty }∥x_n-x^{†}∥$$=0$.    □

Remark 2. 

Compared with Algorithm (3) ($\mathrm{EGM}$), Algorithm 1 ($\mathrm{SEGM}$), Algorithm 2 ($\mathrm{SSEGM}$), and Algorithm 3 ($\mathrm{SSEGMN}$), our Algorithm 4 ($\mathrm{MSEMR}$) is very different in the following aspects.

• The $\mathrm{MSEMR}$, used to find a solution to the problem (6), is more extensive than the $\mathrm{EGM}$, $\mathrm{SEGM}$, $\mathrm{SSEGM}$, and $\mathrm{SSEGMN}$ used to find a solution to the  VIP (1).
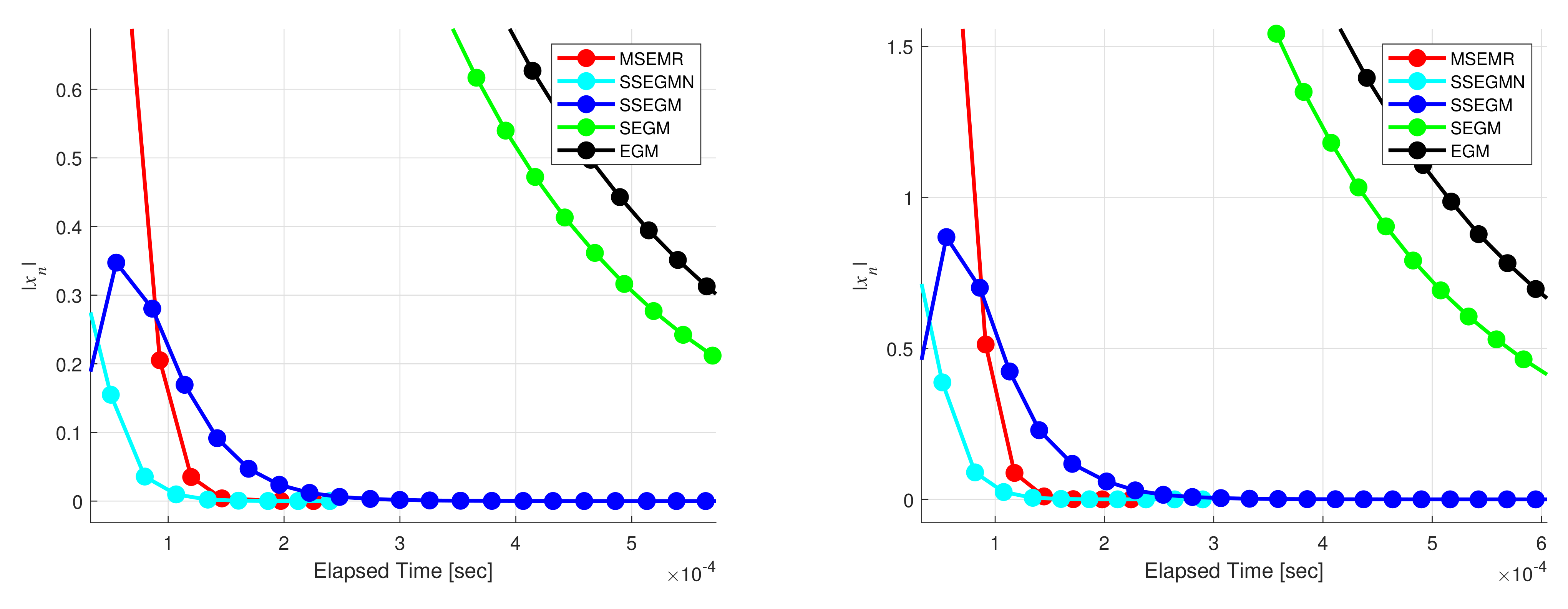
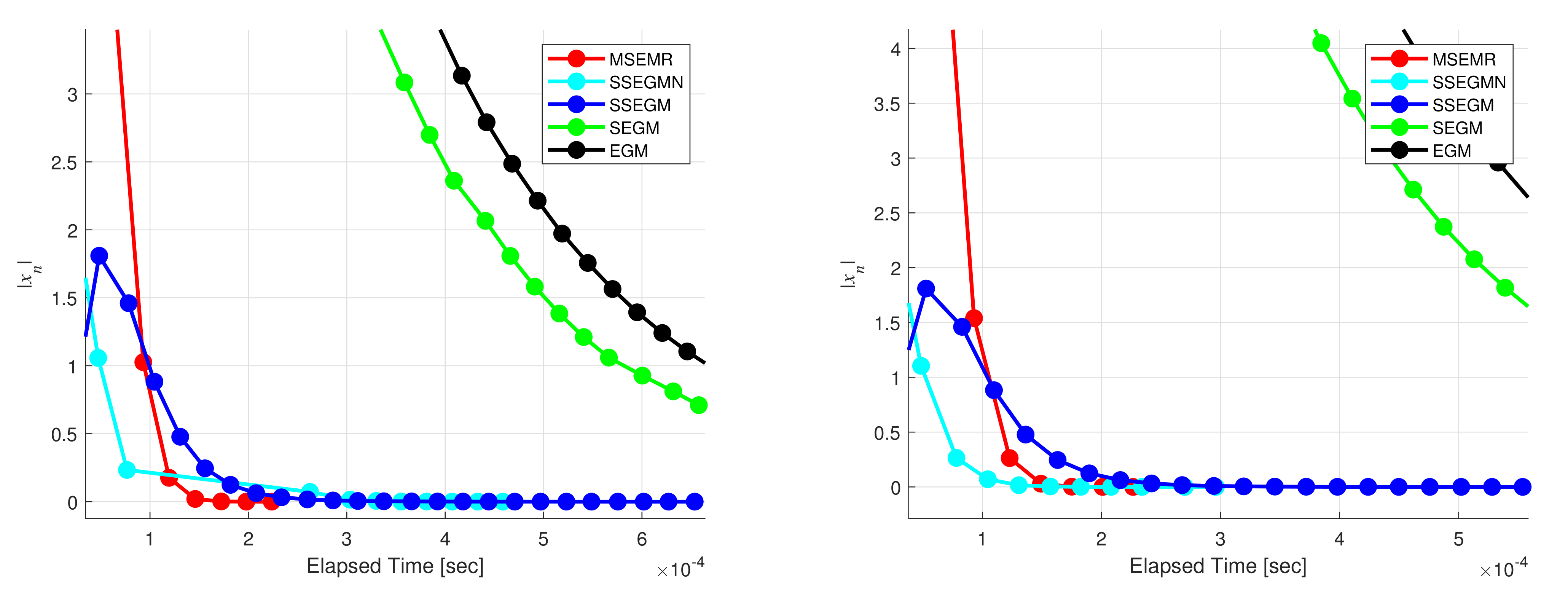
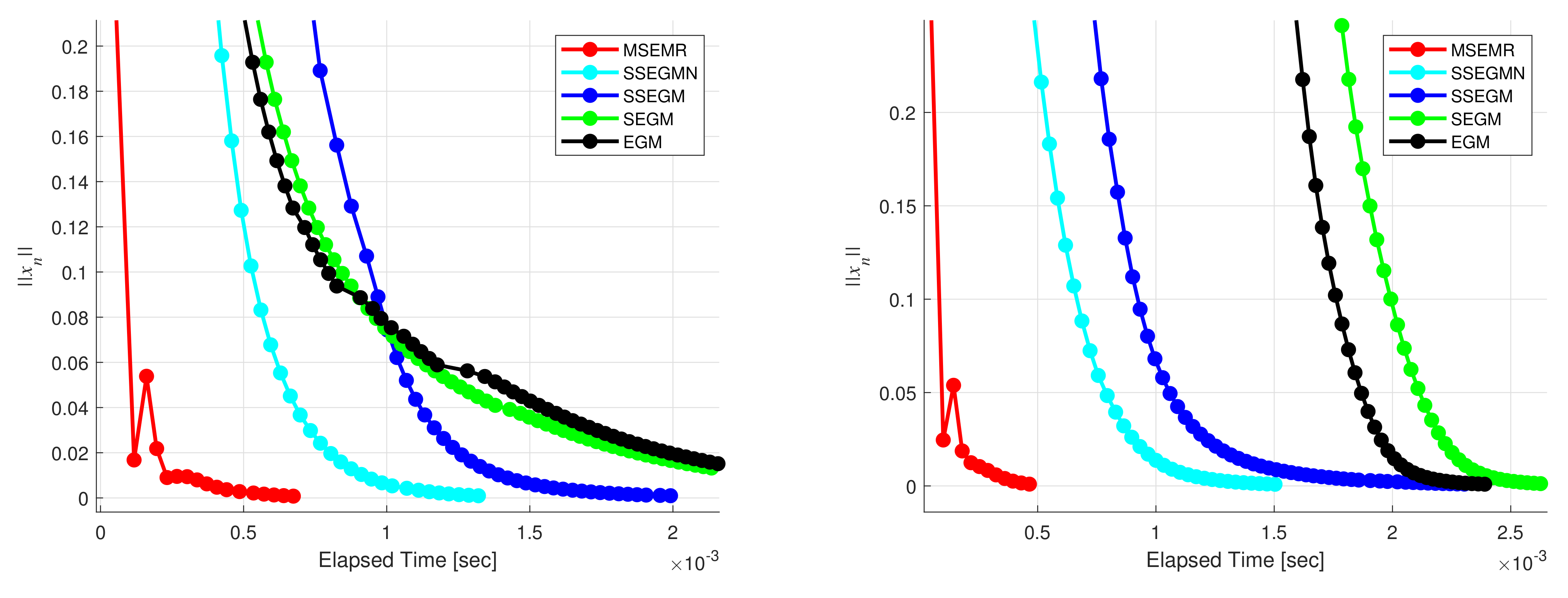
• Note that the stepsizes adopted in the $\mathrm{EGM}$, $\mathrm{SEGM}$, $\mathrm{SSEGM}$, and $\mathrm{SSEGMN}$ are monotonically decreasing, which may affect the execution efficiency of such methods. However, the $\mathrm{MSEMR}$ adopts a new nonmonotonic stepsize criterion that overcomes the drawback of the monotonically decreasing stepsize sequences generated by the other mentioned methods.
• One of the advantages of the $\mathrm{MSEMR}$ is its strong convergence, which is preferable to the weak convergence resulting from the $\mathrm{EGM}$ and $\mathrm{SEGM}$ in infinite dimensional spaces.
• The strong convergence of the $\mathrm{MSEMR}$ comes from the regularization technique, which is different to the Halpern iteration and the viscosity methods used in the $\mathrm{SSEGM}$ and $\mathrm{SSEGMN}$, respectively.

4. Application to Split Minimization Problems

Let C be a nonempty closed convex subset of H. The constrained convex minimization problem is to find a point $x^{*}\in C$ such that

$$f\left(x^{*}\right)=\underset{x\in C}{min}f\left(x\right),$$

(39)

where $f:C\to \mathbb{R}$ is a continuous differentiable function. The following lemma is useful to prove Theorem 2.

Lemma 10 

([26]). A necessary condition of optimality for a point $x^{*}\in C$ to be a solution to the minimization problem (39) is that $x^{*}$ solves the  inequality

$$\begin{array}{c}\hfill \langle \nabla f\left(x^{*}\right),y-x^{*}\rangle \ge 0,\forall y\in C.\end{array}$$

(40)

Equivalently, $x^{*}\in C$ solves the fixed point equation

$$\begin{array}{c}\hfill x^{*}=P_C(x^{*}-\tau \nabla f\left(x^{*}\right))\end{array}$$

for every constant $\tau >0$. If, in addition, f is convex, then the optimality condition (40) is also sufficient.

Theorem 2. 

Suppose $f:H\to H$ is a differentiable and convex function whose gradient is L-Lipschitz continuous. Assume that the optimization problem ${min}_{x\in C}f\left(x\right)$ is consistent, (i.e., its solution set is nonempty). Then, the sequence $\left\{x_n\right\}$ constructed by Algorithm 5 converges to the minimization problem (39) under Assumption 1 (C1)–(C4).

Algorithm 5: Modified inertial subgradient extragradient method to split minimization problems (MSESM).

Initialization: Set $\left\{{\tau }_n\right\}\subset (0,+\infty )$, $\left\{{ϵ}_n\right\}\subset (0,+\infty )$, $\left\{{\alpha }_n\right\}\subset (0,+\infty )$, $\varrho >0$, $\mu \in (0,1)$, and $\nu \in (0,1)$. Choose a nonnegative real sequence $\left\{{\xi }_n\right\}$ such that ${\sum }_{n=0}^{\infty }{\xi }_n<\infty$. Let $x_0,x_1\in H$ be arbitrary. Step 1.Compute $$u_n=x_n+{\mu }_n(x_n-x_{n-1}),$$ where $${\mu }_n=\left\{\begin{array}{c}min\{\frac{{ϵ}_n}{∥x_n-x_{n-1}∥},\varrho \},\mathit{if}{x}_n\ne x_{n-1};\hfill \\ \varrho ,\mathit{otherwise}.\hfill \end{array}\right.$$ Step 2.Compute $$y_n=P_C\left(u_n-{\tau }_n\nabla f{u}_n\right),$$ and construct the half-space $T_n$ the bounding hyperplane of which supports C at $y_n$, $$T_n:=\{w\in H\mid \langle u_n-{\tau }_n\nabla f{u}_n-y_n,w-y_n\rangle \le 0\}.$$ Step 3.Calculate $$x_{n+1}=P_{T_n}\left(u_n-{\tau }_n\nabla f{y}_n\right),$$ where $\left\{{\tau }_n\right\}$ is updated by $${\tau }_{n+1}=\left\{\begin{array}{c}min\{\frac{\nu ∥u_n-y_n∥}{∥\nabla f{u}_n-\nabla f{y}_n∥},{\tau }_n+{\xi }_n\},\mathit{if}\nabla f{u}_n-\nabla f{y}_n\ne 0;\hfill \\ {\tau }_n+{\xi }_n,\mathit{otherwise}.\hfill \end{array}\right.$$ Step 4.Set $n:=n+1$ and return to Step 1.

5. Numerical Illustrations

In the sequel, we provide some numerical experiments to demonstrate the advantages of the proposed method and compare it with the $\mathrm{EGM}$, $\mathrm{SEGM}$, $\mathrm{SSEGM}$, and $\mathrm{SSEGMN}$.

Example 3. 

Let $H=\mathbb{R}$, and $C=[0,50]$. Let $A:H\to H$ be given by $Ax=\frac{1}{2}x$ and $F:H\to H$ be given by $Fx=\frac{1}{3}x$ for all $x\in H$. It is not difficult to determine that 0 is the unique solution of problem (2). Let us choose $\varrho =0.3,\mu =0.5,{\tau }_1=1,\nu =0.9,{\alpha }_n=\frac{1}{\sqrt[3]{n+1}}$, and ${ϵ}_n=\frac{50}{{(n+1)}^2}.$ We test the $\mathrm{MSEMR}$ for different values of $x_0$ and $x_1$, see Figure 1 and Figure 2.

Example 4. 

Let $H={\mathbb{R}}^m$, and $C=\{x\in {\mathbb{R}}^m:0\le x_i\le 3,i=1,2,\dots ,m\}$. Assume the operator $A:{\mathbb{R}}^m\to {\mathbb{R}}^m$ is given by $Ax=x$, and $f:{\mathbb{R}}^m\to {\mathbb{R}}^m$ is given by $fx=\frac{9x}{10}$ for all $x\in {\mathbb{R}}^m$. It is obvious that A is monotone and Lipschitz continuous. For this experiment, in all the methods, we use the same starting points, which are randomly generated. The control parameters are chosen as $\varrho =0.3,\mu =0.5,{\tau }_1=1,\nu =0.9,{\alpha }_n=\frac{1}{\sqrt[3]{n+1}}$, and ${ϵ}_n=\frac{50}{{(n+1)}^2}.$ Figure 3 describes the numerical results for Example 4 in ${\mathbb{R}}^5$ and ${\mathbb{R}}^{10}$, respectively.

From Examples 3 and 4, one finds that the MSEMR seems better than the other mentioned methods. The reasonable use of inertial terms and new stepsize greatly improves the computational performance of the proposed method.

6. Conclusions

The paper proposed an inertial subgradient extragradient method for finding a solution to the variational inequality problem over the set of common solutions to the variational inequality and null point problems. The introduced method used a nonmonotonic stepsize rule without any linesearch procedure. This allowed the proposed method to perform without the prior knowledge of the Lipschitz constants. The regularization technique was incorporated into the proposed method to obtain the strong convergence. Finally, several numerical experiments were also provided to verify the efficiency of the introduced method with respect to previous methods.