On Finite/Fixed-Time Stability Theorems of Discontinuous Differential Equations
Abstract
:1. Introduction
2. Materials and Methods
- (i)
- FNTS, if it satisfies Lyapunov stability and finite-time attractiveness. Moreover, the finite-time attractiveness means that there exists a satisfying and for all , where is known as the ST.
- (ii)
- Uniformly FNTS, if it has uniform Lyapunov stability and finite-time attractiveness.
- (iii)
- Uniformly FXTS, if it is uniformly FNTS and is uniformly bounded with respect to , i.e., there exists a fixed constant for any initial state point values satisfying .
- (1)
- is positive definite,
- (2)
- is radially unbounded and
- (3)
- there exist , , such that
- (1)
- is positive definite,
- (2)
- is radially unbounded and
- (3)
- there exist , and , such that
3. Results
- (H1):
- (H2):
- , where ;
- (H3):
- there exists satisfying
- , where ;
- there exists such that
- : , where , .
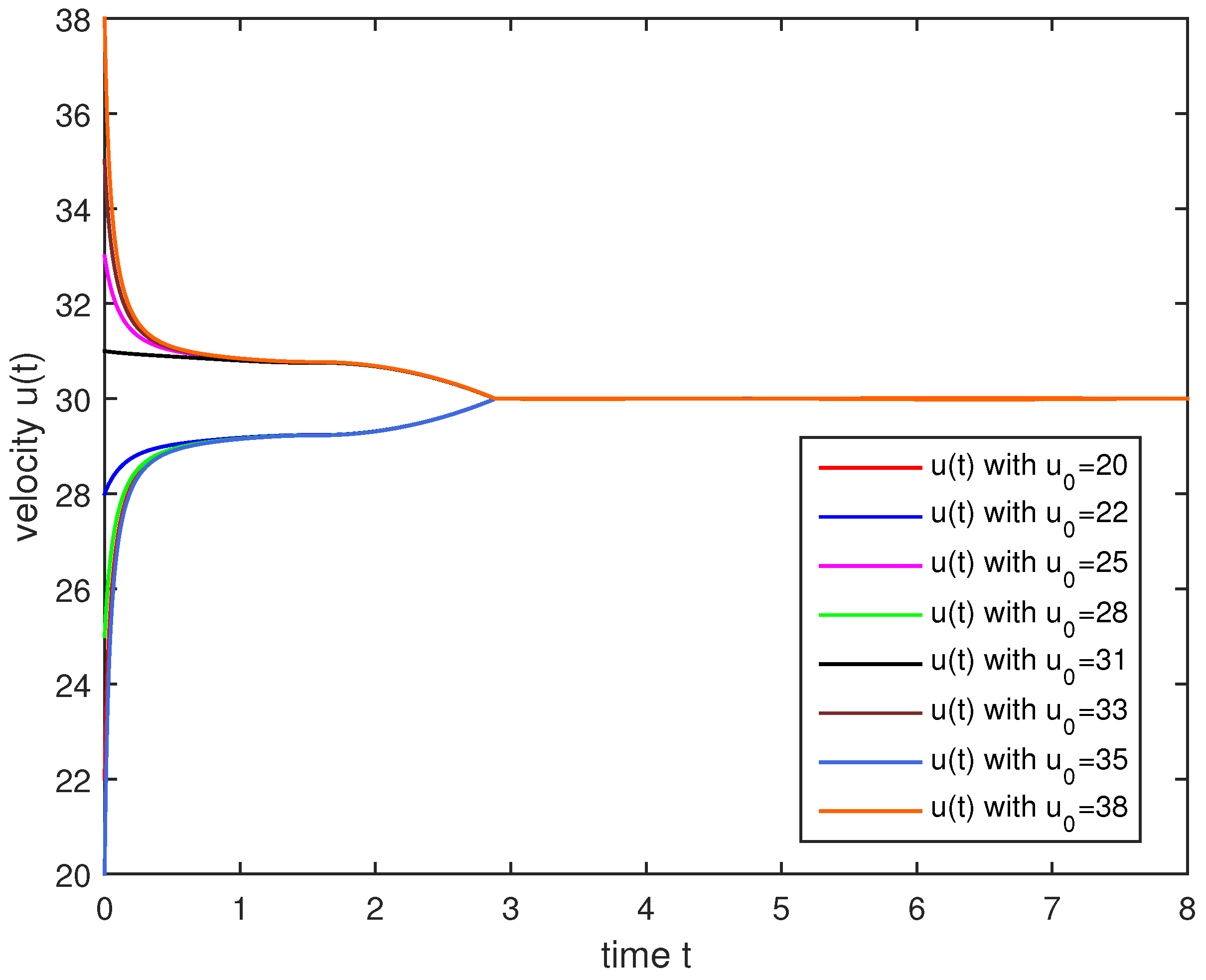
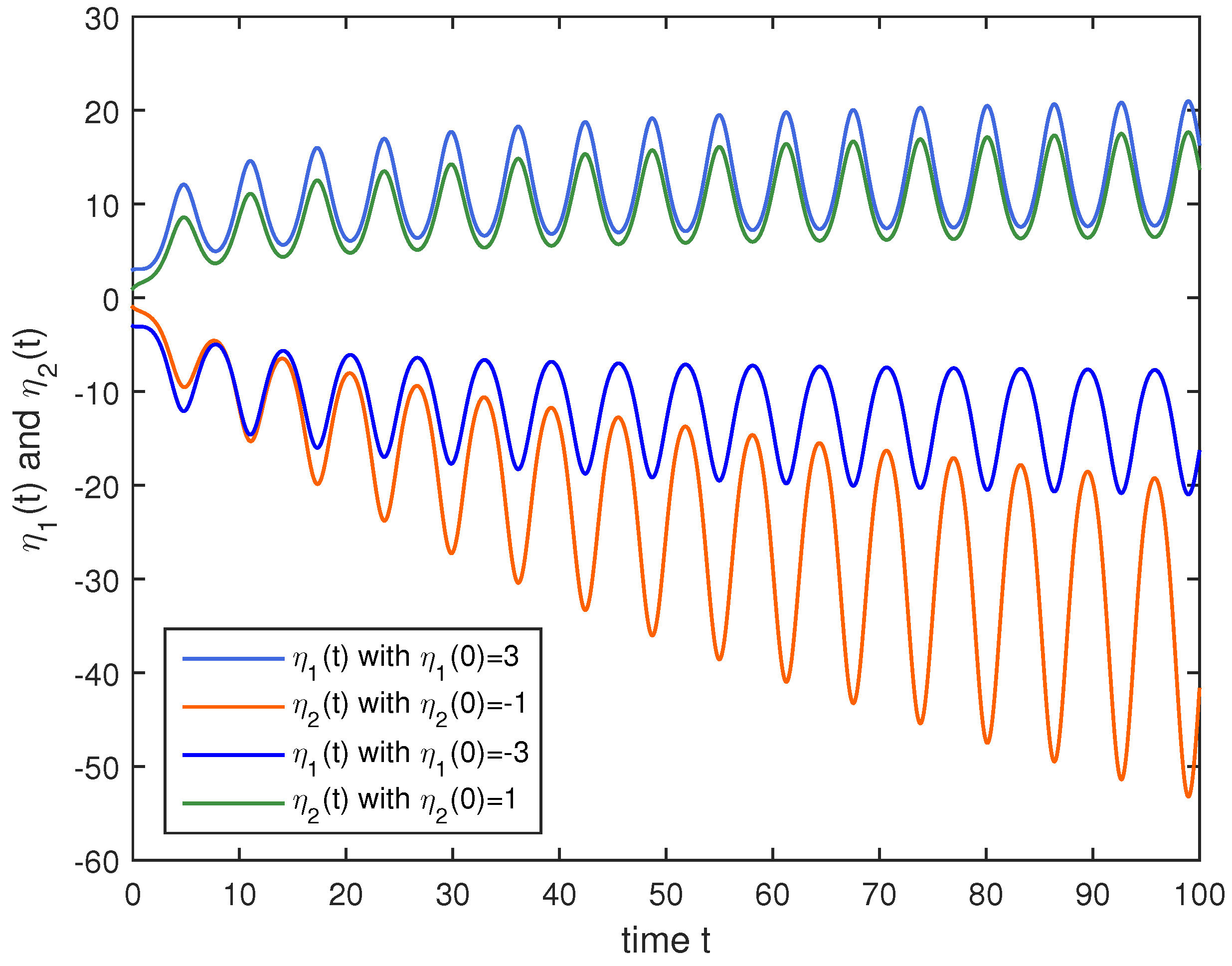
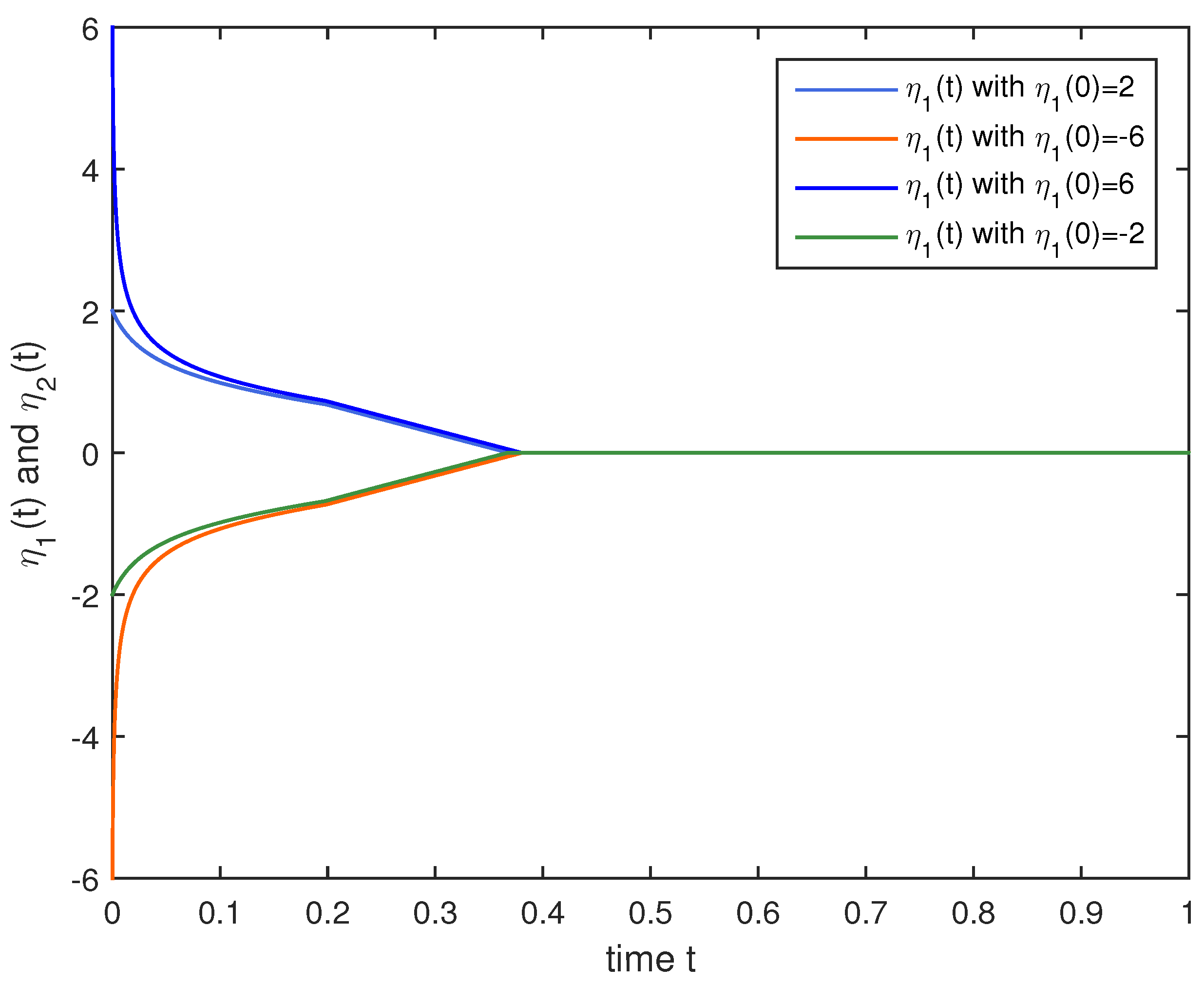
4. Numerical Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FNTS | finite time stability; |
| FXTS | fixed time stability; |
| DDE | discontinuous differential equation; |
| LF | Lyapunov function; |
| ST | settling time; |
| USC | upper semi-continuous; |
| DI | differential inclusion; |
| LLC | locally Lipschitz continuous. |
References
- Hong, Y.; Jiang, Z.; Feng, G. Finite-time input-to-state stability and applications to finite-time control design. SIAM J. Control Optim. 2010, 48, 4395–4418. [Google Scholar] [CrossRef]
- Nersesov, S.G.; Haddad, W.M. Finite-time stabilization of nonlinear impulsive dynamical systems. Nonlinear Anal. Hybrid Syst. 2008, 2, 832–845. [Google Scholar] [CrossRef]
- Bhat, S.; Bernstein, D. Finite-Time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Xi, Q.; Liang, Z.; Li, X. Uniform finite-time stability of nonlinear impulsive time-varying systems. Appl. Math. Model. 2021, 91, 913–922. [Google Scholar] [CrossRef]
- Wang, L.; Sun, S.; Xia, C. Finite-time stability of multi-agent system in disturbed environment. Nonlinear Dyn. 2012, 67, 2009–2016. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, X.; Wang, G.; Zuo, Z. Finite-time stability for continuous-time switched systems in the presence of impulse effects. IET Control Theory Appl. 2012, 6, 1741–1744. [Google Scholar] [CrossRef]
- Orlov, Y. Finite Time Stability and Robust Control Synthesis of Uncertain Switched Systems. SIAM J. Control Optim. 2005, 43, 1253–1271. [Google Scholar] [CrossRef]
- Yang, X.; Cao, J. Finite-time stochastic synchronization of complex networks. Appl. Math. Model. 2010, 34, 3631–3641. [Google Scholar] [CrossRef]
- Chen, G.; Yang, Y. Finite-time stability of switched nonlinear time-varying systems via indefinite Lyapunov functions. Int. J. Robust Nonlinear Control 2018, 28, 1901–1912. [Google Scholar] [CrossRef]
- Xu, J.; Sun, J. Finite-time stability of linear time-varying singular impulsive systems. IET Control Theory Appl. 2010, 4, 2239–2244. [Google Scholar] [CrossRef]
- Polyakov, A. Nonlinear feedback design for fixed-time stabilization of linear control systems. IEEE Trans. Autom. Control 2012, 57, 2106–2110. [Google Scholar] [CrossRef] [Green Version]
- Defoort, M.; Polyakov, A.; Demesure, G.; Djemai, M. Leader-follower fixed-time consensus for multi-agent systems with unknown non-linear inherent dynamics. IET Control Theory Appl. 2015, 9, 2165–2170. [Google Scholar] [CrossRef] [Green Version]
- Ni, J.; Liu, L.; Liu, C.; Hu, X.; Li, S. Fast fixed-time nonsingular terminal sliding mode control and its application to chaos suppression in power system. IEEE Trans. Circuits Syst. Express Briefs 2017, 64, 151–155. [Google Scholar] [CrossRef]
- Chen, C.; Sun, Z. Fixed-time stabilisation for a class of high-order non-linear systems. IET Control Theory Appl. 2018, 12, 2578–2587. [Google Scholar] [CrossRef]
- Yu, J.; Yu, S.; Li, J.; Yan, Y. Fixed-time stability theorem of stochastic nonlinear systems. Int. J. Control 2019, 92, 2194–2200. [Google Scholar] [CrossRef]
- Hu, J.; Sui, G.; Lv, X.; Li, X. Fixed-time control of delayed neural networks with impulsive perturbations. Nonlinear-Anal.-Model. Control 2018, 23, 904–920. [Google Scholar] [CrossRef] [Green Version]
- Cai, Z.; Huang, L.; Zhang, L. Finite-time synchronization of master-slave neural networks with time-delays and discontinuous activations. Appl. Math. Model. 2017, 47, 208–226. [Google Scholar] [CrossRef]
- Wang, Z.; Cao, J.; Cai, Z.; Abdel-Aty, M. A novel Lyapunov theorem on finite/fixed-time stability of discontinuous impulsive systems. Chaos 2020, 30, 013139. [Google Scholar] [CrossRef]
- Cai, Z.; Zhu, M.; Huang, L.; Wang, D. Finite-time stabilization control of memristor-based neural networks. Nonlinear Anal. Hybrid Syst. 2016, 20, 37–54. [Google Scholar] [CrossRef]
- Wang, D.; Huang, L.; Cai, Z. On the periodic dynamics of a general Cohen-Grossberg BAM neural networks via differential inclusions. Neurocomputing 2013, 118, 203–214. [Google Scholar] [CrossRef]
- Wang, D.; Huang, L. Periodicity and global exponential stability of generalized Cohen-Grossberg neural networks with discontinuous activations and mixed delays. Neural Netw. 2014, 51, 80–95. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Huang, L. Generalized Lyapunov method for discontinuous systems. Nonlinear Anal. Theory Methods Appl. 2009, 71, 3083–3092. [Google Scholar] [CrossRef]
- Filipov, A.F. Differential Equations with Discontinuous Right-Hand Side; Kluwer Academic Press: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Kim, S.J.; Ha, I.J. Existence of Carathe/spl acute/odory solutions in nonlinear systems with discontinuous switching feedback controllers. IEEE Trans. Autom. Control 2004, 49, 1167–1171. [Google Scholar] [CrossRef]
- Hu, C.; Yu, J.; Chen, Z.; Jiang, H.; Huang, T. Fixed-time stability of dynamical systems and fixed-time synchronization of coupled discontinuous neural networks. Neural Netw. 2017, 89, 74–83. [Google Scholar] [CrossRef]
- Ding, Z.; Zeng, Z.; Wang, L. Robust Finite-Time Stabilization of Fractional-Order Neural Networks with Discontinuous and Continuous Activation Functions Under Uncertainty. IEEE Trans. Neural Networks Learn. Syst. 2018, 29, 1477–1490. [Google Scholar] [CrossRef]
- Cai, Z.; Huang, L.; Wang, Z. Finite/Fixed-Time stability of nonautonomous functional differential inclusion: Lyapunov approach involving indefinite derivative. IEEE Trans. Neural Networks Learn. Syst. 2021. Early Access. [Google Scholar] [CrossRef] [PubMed]
- Clarke, F. Optimization and Nonsmooth Analysis; Wiley Press: Hoboken, NJ, USA, 1983. [Google Scholar]
- Kong, F.; Zhu, Q.; Huang, T. Fixed-Time Stability for Discontinuous Uncertain Inertial Neural Networks with Time-Varying Delays. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 4507–4517. [Google Scholar] [CrossRef]
- Hardy, G.H.; Littlewood, J.E.; Polya, G. Inequalities; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Parsegov, S.E.; Polyakov, A.E.; Shcherbakov, P. Nonlinear fixed-time control protocol for uniform allocation of agents on a segment. Dokl. Math. Vol. 2013, 87, 133–136. [Google Scholar] [CrossRef]
- Zuo, Z.; Tie, L. Distributed robust finite-time nonlinear consensus protocols for multi-agent systems. Int. J. Syst. Sci. 2016, 47, 1366–1375. [Google Scholar] [CrossRef]
- Li, N.; Wu, X.; Yang, Q. Fixed-Time Synchronization of Complex Dynamical Network with Impulsive Effects. IEEE Access 2020, 8, 33072–33079. [Google Scholar] [CrossRef]
- Wang, Z.; Cao, J.; Cai, Z.; Huang, L. Periodicity and fixed-time periodic synchronization of discontinuous delayed quaternion neural networks. J. Frankl. Inst. Eng. Appl. Math. 2020, 357, 4242–4271. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Wang, D. On Finite/Fixed-Time Stability Theorems of Discontinuous Differential Equations. Mathematics 2022, 10, 2221. https://doi.org/10.3390/math10132221
Li L, Wang D. On Finite/Fixed-Time Stability Theorems of Discontinuous Differential Equations. Mathematics. 2022; 10(13):2221. https://doi.org/10.3390/math10132221
Chicago/Turabian StyleLi, Luke, and Dongshu Wang. 2022. "On Finite/Fixed-Time Stability Theorems of Discontinuous Differential Equations" Mathematics 10, no. 13: 2221. https://doi.org/10.3390/math10132221
APA StyleLi, L., & Wang, D. (2022). On Finite/Fixed-Time Stability Theorems of Discontinuous Differential Equations. Mathematics, 10(13), 2221. https://doi.org/10.3390/math10132221




