Permutation Tests for Metaheuristic Algorithms
Abstract
:1. Introduction
2. Permutation Tests (P-Tests)
Example
3. P-Tests for Metaheuristics
| Algorithm 1 P-test for two algorithms |
|
4. Experimental Results
4.1. Descriptive Statistics and Plots
4.2. Permutation Tests
- SHADE vs. L-SHADE;
- HBA vs. JS; and
- SHADE vs. Jaya.
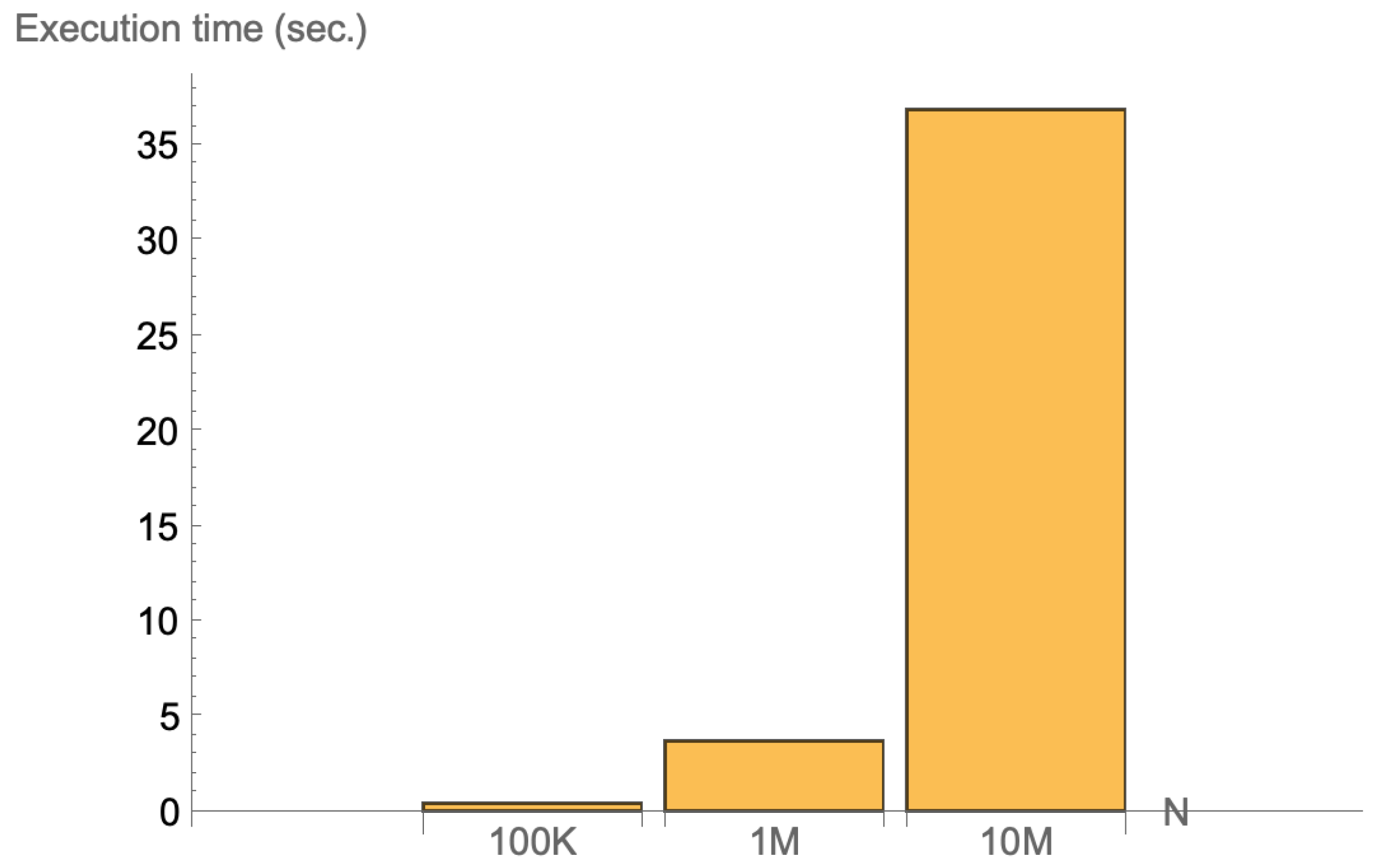
Permutation Tests Execution Time
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| PSO | Particle Swarm Optimization |
| DE | Differential Evolution |
| ACO | Ant Colony Optimization |
| HBA | Honey Badger Algoirthm |
| KS | Kolmogorov–Smirnov |
| JS | JellyFish Search |
| SD | Standard Deviation |
References
- Yang, X.S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Dorigo, G.D.C.M. The Ant Colony Optimization meta-heuristic. In New Ideas in Optimization; Corne, D., Dorigo, F.G.M., Eds.; McGraw Hill: London, UK, 1999; pp. 11–32. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces; Technical Report; ICSI: Berkeley, CA, USA, 1995. [Google Scholar]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Li, S.; Chen, H.; Wang, M.; Heidari, A.A.; Mirjalili, S. Slime mould algorithm: A new method for stochastic optimization. Future Gener. Comput. Syst. 2020, 111, 300–323. [Google Scholar] [CrossRef]
- Hosseini, E.; Ghafoor, K.Z.; Emrouznejad, A.; Sadiq, A.S.; Rawat, D.B. Novel metaheuristic based on multiverse theory for optimization problems in emerging systems. Appl. Intell. 2021, 51, 3275–3292. [Google Scholar] [CrossRef] [PubMed]
- Nabil, E. A Modified Flower Pollination Algorithm for Global Optimization. Expert Syst. Appl. 2016, 57, 192–203. [Google Scholar] [CrossRef]
- Han, F.; Zheng, M.; Ling, Q. An improved multiobjective particle swarm optimization algorithm based on tripartite competition mechanism. Appl. Intell. 2022, 52, 5784–5816. [Google Scholar] [CrossRef]
- Ning, Y.; Peng, Z.; Dai, Y.; Bi, D.; Wang, J. Enhanced particle swarm optimization with multi-swarm and multi-velocity for optimizing high-dimensional problems. Appl. Intell. 2019, 49, 335–351. [Google Scholar] [CrossRef]
- Chaitanya, K.; Somayajulu, D.V.L.N.; Krishna, P.R. Memory-based approaches for eliminating premature convergence in particle swarm optimization. Appl. Intell. 2021, 51, 4575–4608. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Improving the search performance of SHADE using linear population size reduction. In Proceedings of the Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1658–1665. [Google Scholar]
- Li, Y.; Wang, S.; Liu, H.; Yang, B.; Yang, H.; Zeng, M.; Wu, Z. A backtracking differential evolution with multi-mutation strategies autonomy and collaboration. Appl. Intell. 2022, 52, 3418–3444. [Google Scholar] [CrossRef]
- Zhong, X.; Cheng, P. An elite-guided hierarchical differential evolution algorithm. Appl. Intell. 2021, 51, 4962–4983. [Google Scholar] [CrossRef]
- Dos Santos Coelho, L.; Mariani, V.C. Use of chaotic sequences in a biologically inspired algorithm for engineering design optimization. Expert Syst. Appl. 2008, 34, 1905–1913. [Google Scholar] [CrossRef]
- Kayhan, A.H.; Ceylan, H.; Ayvaz, M.T.; Gurarslan, G. PSOLVER: A new hybrid particle swarm optimization algorithm for solving continuous optimization problems. Expert Syst. Appl. 2010, 37, 6798–6808. [Google Scholar] [CrossRef]
- Sörensen, K. Metaheuristics—The metaphor exposed. Int. Trans. Oper. Res. 2015, 22, 3–18. [Google Scholar] [CrossRef]
- Camacho-Villalón, C.L.; Stützle, T.; Dorigo, M. Success-history based parameter adaptation for differential evolution. In Proceedings of the Grey Wolf, Firefly and Bat Algorithms: Three Widespread Algorithms that Do Not Contain Any Novelty, ANTS Conference 2020, Auckland, New Zealand, 29 June–4 July 2020; pp. 121–133. [Google Scholar]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- LaTorre, A.; Molina, D.; Osaba, E.; Poyatos, J.; Ser, J.D.; Herrera, F. A Prescription of Methodological Guidelines for Comparing Bio-inspired Optimization Algorithms. Swarm Evol. Comput. 2021, 67, 100973. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Dunn, O. Multiple comparisons among means. J. Am. Can. Stat. Assoc. 1961, 56, 52–64. [Google Scholar] [CrossRef]
- Aickin, M.; Gensler, H. Adjusting for multiple testing when reporting research results: The Bonferroni vs Holm methods. Am. J. Public Health 1996, 86, 726–728. [Google Scholar] [CrossRef] [Green Version]
- Edgington, E. Randomization Tests; Marcel Dekker, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Knijnenburg, T.; Wessels, L.; Reinders, M.; Shmulevich, I. Fewer permutations, more accurate P-values. Bioinformatics 2009, 25, i161–i168. [Google Scholar] [CrossRef] [Green Version]
- Skiena, S. The Data Science Design Manual; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kunert-Graf, J.; Sakhanenko, N.; Galas, D. Optimized permutation testing for information theoretic measures of multi-gene interactions. BMC Bioinform. 2021, 22, 180. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Hussain, K.; Mabrouk, M.S.; Al-Atabany, W. Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems. Math. Comput. Simul. 2022, 192, 84–110. [Google Scholar] [CrossRef]
- Rao, R.V. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar]
- Chou, J.S.; Truong, D.N. A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean. Appl. Math. Comput. 2021, 389, 125535. [Google Scholar] [CrossRef]
- Tanabe, R.; Fukunaga, A. Success-history based parameter adaptation for differential evolution. In Proceedings of the Evolutionary Computation (CEC), Cancun, Mexico, 20–23 June 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 71–78. [Google Scholar]
- Yue, D.; Price, K.; P, S.; Liang, J.; Ali, M.; Qu, B.; Awad, N.; Biswas, P. Problem Definitions and Evaluation Criteria for CEC 2020 Competition on Single Objective Bound Constrained Numerical Optimization; Technical Report; Zhengzhou University: Zhengzhou, China; Nanyang Technological University: Singapore, 2019. [Google Scholar]





| Exam | Jane | John | (Sample) Average |
|---|---|---|---|
| Pre-Semester Test: | 70 | 75 | 72.5 |
| Final Exam: | 76 | 72 | 74.0 |
| Permutation i | 70 | 72 | 75 | 76 | |
|---|---|---|---|---|---|
| 1 | P | P | F | F | 4.5 |
| 2 | P | F | P | F | 1.5 (d) |
| 3 | P | F | F | P | 0.5 |
| 4 | F | P | P | F | −0.5 |
| 5 | F | P | F | P | −1.5 |
| 6 | F | F | P | P | −4.5 |
| Function | Type | Optimum Value |
|---|---|---|
| F1 | Unimodal function | 100 |
| F2 | Basic function | 1100 |
| F3 | Basic function | 700 |
| F4 | Basic function | 1900 |
| F5 | Hybrid function | 1700 |
| F6 | Hybrid function | 1600 |
| F7 | Hybrid function | 2100 |
| F8 | Composition function | 2200 |
| F9 | Composition function | 2400 |
| F10 | Composition function | 2500 |
| Function | Median | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| F1 | 3.65E + 03 | 3.95E + 03 | 2.94E + 03 | 1.00E + 02 | 9.28E + 03 |
| F2 | 2.69E + 03 | 2.73E + 03 | 6.18E + 02 | 1.68E + 03 | 4.55E + 03 |
| F3 | 7.83E + 02 | 7.86E + 02 | 1.83E + 01 | 7.52E + 02 | 8.39E + 02 |
| F4 | 1.90E + 03 | 1.90E + 03 | 1.93E + 00 | 1.90E + 03 | 1.91E + 03 |
| F5 | 5.86E + 04 | 6.52E + 04 | 3.84E + 04 | 5.43E + 03 | 1.95E + 05 |
| F6 | 1.80E + 03 | 1.80E + 03 | 0.00E + 00 | 1.80E + 03 | 1.80E + 03 |
| F7 | 1.83E + 04 | 4.13E + 04 | 1.46E + 05 | 3.69E + 03 | 1.06E + 06 |
| F8 | 2.30E + 03 | 2.62E + 03 | 9.36E + 02 | 2.30E + 03 | 7.07E + 03 |
| F9 | 2.91E + 03 | 2.95E + 03 | 9.99E + 01 | 2.84E + 03 | 3.25E + 03 |
| F10 | 2.96E + 03 | 2.96E + 03 | 3.51E + 01 | 2.90E + 03 | 3.02E + 03 |
| Function | Median | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| F1 | 2.20E + 09 | 2.28E + 09 | 4.85E + 08 | 1.43E + 09 | 3.83E + 09 |
| F2 | 4.93E + 03 | 4.87E + 03 | 3.49E + 02 | 4.01E + 03 | 5.61E + 03 |
| F3 | 8.88E + 02 | 8.92E + 02 | 1.80E + 01 | 8.61E + 02 | 9.40E + 02 |
| F4 | 1.91E + 03 | 1.91E + 03 | 1.49E + 00 | 1.91E + 03 | 1.92E + 03 |
| F5 | 1.08E + 06 | 1.24E + 06 | 8.39E + 05 | 1.32E + 05 | 3.36E + 06 |
| F6 | 1.74E + 03 | 1.74E + 03 | 4.55E − 13 | 1.74E + 03 | 1.74E + 03 |
| F7 | 3.49E + 05 | 4.61E + 05 | 3.14E + 05 | 1.29E + 05 | 1.46E + 06 |
| F8 | 2.59E + 03 | 4.18E + 03 | 2.02E + 03 | 2.43E + 03 | 7.09E + 03 |
| F9 | 2.94E + 03 | 2.94E + 03 | 1.09E + 01 | 2.91E + 03 | 2.96E + 03 |
| F10 | 3.02E + 03 | 3.03E + 03 | 4.51E + 01 | 2.97E + 03 | 3.23E + 03 |
| Function | Median | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| F1 | 6.00E + 02 | 1.20E + 03 | 1.73E + 03 | 1.00E + 02 | 8.65E + 03 |
| F2 | 2.33E + 03 | 2.44E + 03 | 5.69E + 02 | 1.35E + 03 | 3.55E + 03 |
| F3 | 8.02E + 02 | 8.03E + 02 | 1.93E + 01 | 7.61E + 02 | 8.64E + 02 |
| F4 | 1.91E + 03 | 1.91E + 03 | 4.61E + 00 | 1.90E + 03 | 1.92E + 03 |
| F5 | 9.20E + 04 | 9.77E + 04 | 3.79E + 04 | 3.52E + 04 | 2.11E + 05 |
| F6 | 1.68E + 03 | 1.68E + 03 | 0.00E + 00 | 1.68E + 03 | 1.68E + 03 |
| F7 | 2.38E + 04 | 2.99E + 04 | 1.90E + 04 | 4.53E + 03 | 1.02E + 05 |
| F8 | 2.30E + 03 | 2.30E + 03 | 8.10E − 01 | 2.30E + 03 | 2.30E + 03 |
| F9 | 2.85E + 03 | 2.85E + 03 | 1.80E + 01 | 2.82E + 03 | 2.91E + 03 |
| F10 | 3.00E + 03 | 2.98E + 03 | 2.37E + 01 | 2.91E + 03 | 3.02E + 03 |
| Function | Median | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| F1 | 1.00E + 02 | 1.00E + 02 | 0.00E + 00 | 1.00E + 02 | 1.00E + 02 |
| F2 | 1.64E + 03 | 1.64E + 03 | 1.54E + 02 | 1.26E + 03 | 1.86E + 03 |
| F3 | 7.42E + 02 | 7.42E + 02 | 4.18E + 00 | 7.34E + 02 | 7.54E + 02 |
| F4 | 1.90E + 03 | 1.90E + 03 | 6.24E − 01 | 1.90E + 03 | 1.90E + 03 |
| F5 | 1.97E + 03 | 1.96E + 03 | 1.16E + 02 | 1.74E + 03 | 2.32E + 03 |
| F6 | 2.05E + 03 | 2.05E + 03 | 0.00E + 00 | 2.05E + 03 | 2.05E + 03 |
| F7 | 2.27E + 03 | 2.28E + 03 | 1.03E + 02 | 2.13E + 03 | 2.56E + 03 |
| F8 | 2.30E + 03 | 2.30E + 03 | 0.00E + 00 | 2.30E + 03 | 2.30E + 03 |
| F9 | 2.83E + 03 | 2.83E + 03 | 5.60E + 00 | 2.82E + 03 | 2.84E + 03 |
| F10 | 2.91E + 03 | 2.91E + 03 | 5.08E − 01 | 2.91E + 03 | 2.91E + 03 |
| Function | Median | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| F1 | 1.00E + 02 | 1.00E + 02 | 0.00E + 00 | 1.00E + 02 | 1.00E + 02 |
| F2 | 1.37E + 03 | 1.38E + 03 | 1.06E + 02 | 1.17E + 03 | 1.59E + 03 |
| F3 | 7.27E + 02 | 7.27E + 02 | 1.87E + 00 | 7.24E + 02 | 7.32E + 02 |
| F4 | 1.90E + 03 | 1.90E + 03 | 2.30E − 01 | 1.90E + 03 | 1.90E + 03 |
| F5 | 1.87E + 03 | 1.87E + 03 | 8.39E + 01 | 1.73E + 03 | 2.06E + 03 |
| F6 | 2.05E + 03 | 2.05E + 03 | 0.00E + 00 | 2.05E + 03 | 2.05E + 03 |
| F7 | 2.13E + 03 | 2.15E + 03 | 5.53E + 01 | 2.10E + 03 | 2.31E + 03 |
| F8 | 2.30E + 03 | 2.30E + 03 | 0.00E + 00 | 2.30E + 03 | 2.30E + 03 |
| F9 | 2.81E + 03 | 2.81E + 03 | 2.77E + 00 | 2.80E + 03 | 2.82E + 03 |
| F10 | 2.91E + 03 | 2.91E + 03 | 1.83E − 02 | 2.91E + 03 | 2.91E + 03 |
| Function | Rank-Sum | KS | P-Test (100 K) | P-Test (1 M) | P-Test (10 M) |
|---|---|---|---|---|---|
| F1 | 1.00E + 00 | 1.00E + 00 | 1.00E + 00 | 1.00E + 00 | 1.00E + 00 |
| F2 | 1.59E − 12 | 1.32E − 10 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F3 | 6.86E − 18 | 1.98E − 29 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F4 | 8.72E − 18 | 9.81E − 26 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F5 | 1.23E − 04 | 5.82E − 04 | 3.10E − 04 | 4.09E − 04 | 3.96E − 04 |
| F6 | 1.00E + 00 | 1.00E + 00 | 1.00E + 00 | 1.00E + 00 | 1.00E + 00 |
| F7 | 3.99E − 11 | 1.32E − 10 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F8 | 1.00E + 00 | 1.00E + 00 | 1.00E + 00 | 1.00E + 00 | 1.00E + 00 |
| F9 | 7.28E − 18 | 1.98E − 27 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F10 | 2.96E − 02 | 1.79E − 01 | 6.45E − 02 | 6.46E − 02 | 6.48E − 02 |
| Function | Rank-Sum | KS | P-Test (100 K) | P-Test (1 M) | P-Test (10 M) |
|---|---|---|---|---|---|
| F1 | 3.86E − 06 | 4.93E − 07 | 1.00E − 05 | 4.00E − 06 | 4.90E − 06 |
| F2 | 3.09E − 02 | 2.17E − 02 | 6.85E − 02 | 6.75E − 02 | 6.76E − 02 |
| F3 | 1.64E − 05 | 3.80E − 05 | 0.00E + 00 | 4.00E − 06 | 5.10E − 06 |
| F4 | 3.89E − 13 | 5.02E − 12 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F5 | 2.69E − 05 | 9.91E − 05 | 2.00E − 05 | 2.40E − 05 | 2.87E − 05 |
| F6 | 6.86E − 18 | 1.98E − 29 | 8.42E − 01 | 8.42E − 01 | 8.42E − 01 |
| F7 | 1.26E − 02 | 6.78E − 02 | 6.32E − 02 | 6.35E − 02 | 6.34E − 02 |
| F8 | 7.88E − 01 | 2.83E − 03 | 1.08E − 01 | 1.07E − 01 | 1.08E − 01 |
| F9 | 3.38E − 10 | 2.62E − 09 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F10 | 3.86E − 06 | 4.93E − 07 | 1.00E − 04 | 8.30E − 05 | 9.04E − 05 |
| Function | Rank-sum | KS | P-Test (100 K) | P-Test (1 M) | P-Test (10 M) |
|---|---|---|---|---|---|
| F1 | 6.86E − 18 | 1.98E − 29 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F2 | 6.86E − 18 | 1.98E − 29 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F3 | 6.86E − 18 | 1.98E − 29 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F4 | 6.86E − 18 | 1.98E − 29 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F5 | 6.86E − 18 | 1.98E − 29 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F6 | 6.86E − 18 | 1.98E − 29 | 8.42E − 01 | 8.42E − 01 | 8.42E − 01 |
| F7 | 6.86E − 18 | 1.98E − 29 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F8 | 6.86E − 18 | 1.98E − 29 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F9 | 6.86E − 18 | 1.98E − 29 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
| F10 | 6.86E − 18 | 1.98E − 29 | 0.00E + 00 | 0.00E + 00 | 0.00E + 00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omran, M.G.H.; Clerc, M.; Ghaddar, F.; Aldabagh, A.; Tawfik, O. Permutation Tests for Metaheuristic Algorithms. Mathematics 2022, 10, 2219. https://doi.org/10.3390/math10132219
Omran MGH, Clerc M, Ghaddar F, Aldabagh A, Tawfik O. Permutation Tests for Metaheuristic Algorithms. Mathematics. 2022; 10(13):2219. https://doi.org/10.3390/math10132219
Chicago/Turabian StyleOmran, Mahamed G. H., Maurice Clerc, Fatme Ghaddar, Ahmad Aldabagh, and Omar Tawfik. 2022. "Permutation Tests for Metaheuristic Algorithms" Mathematics 10, no. 13: 2219. https://doi.org/10.3390/math10132219
APA StyleOmran, M. G. H., Clerc, M., Ghaddar, F., Aldabagh, A., & Tawfik, O. (2022). Permutation Tests for Metaheuristic Algorithms. Mathematics, 10(13), 2219. https://doi.org/10.3390/math10132219








