Tumour-Natural Killer and CD8+ T Cells Interaction Model with Delay
Abstract
1. Introduction
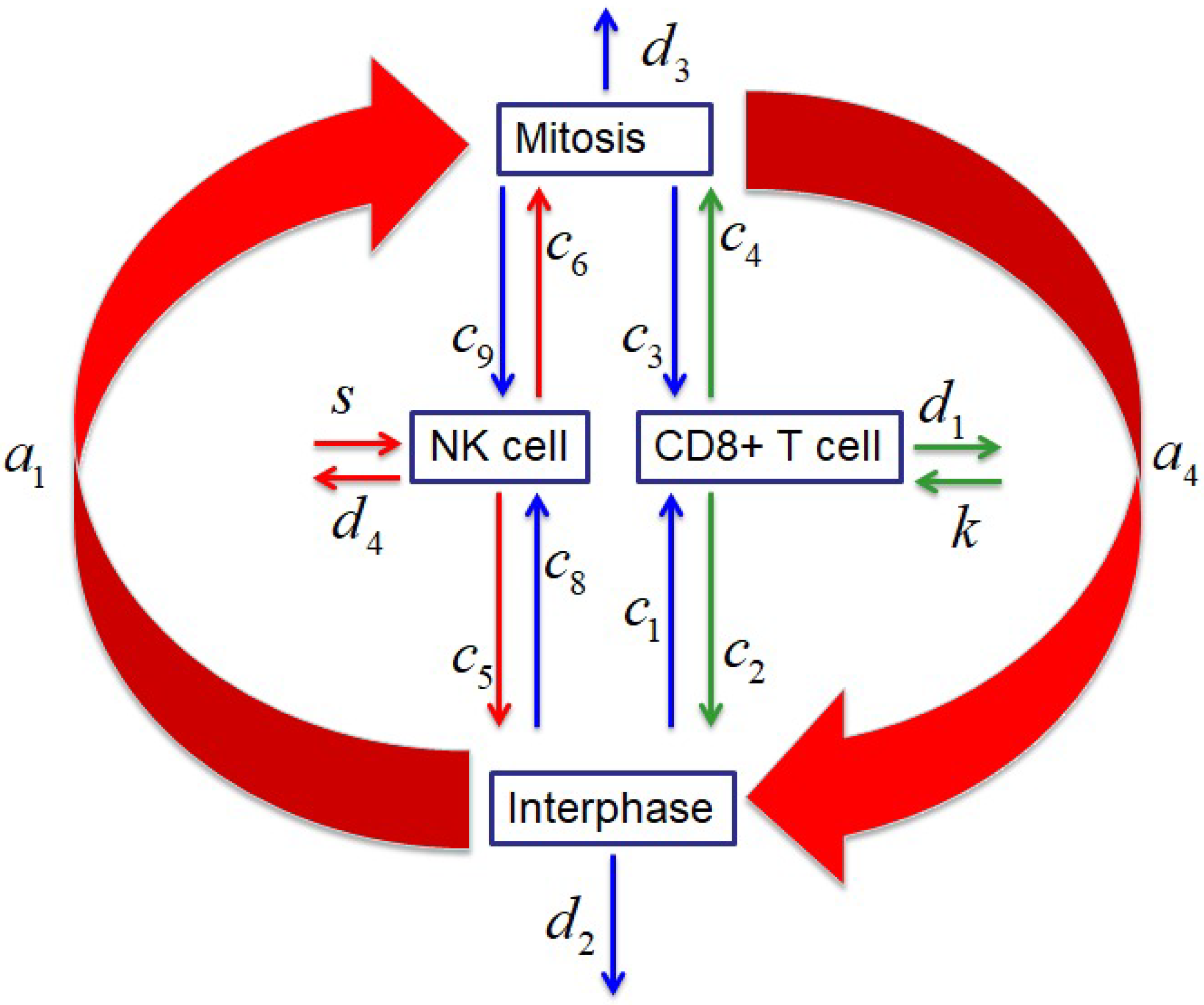
2. Construction of the Mathematical Model
- Tumour-specific CD T cell are initiated when tumour cells are detected [15].
- NK and CD T cells are assume to interact with cells from all phases
Parameter Values
3. Stability Analysis
3.1. Steady State and Stability Result
- (a)
- (b)
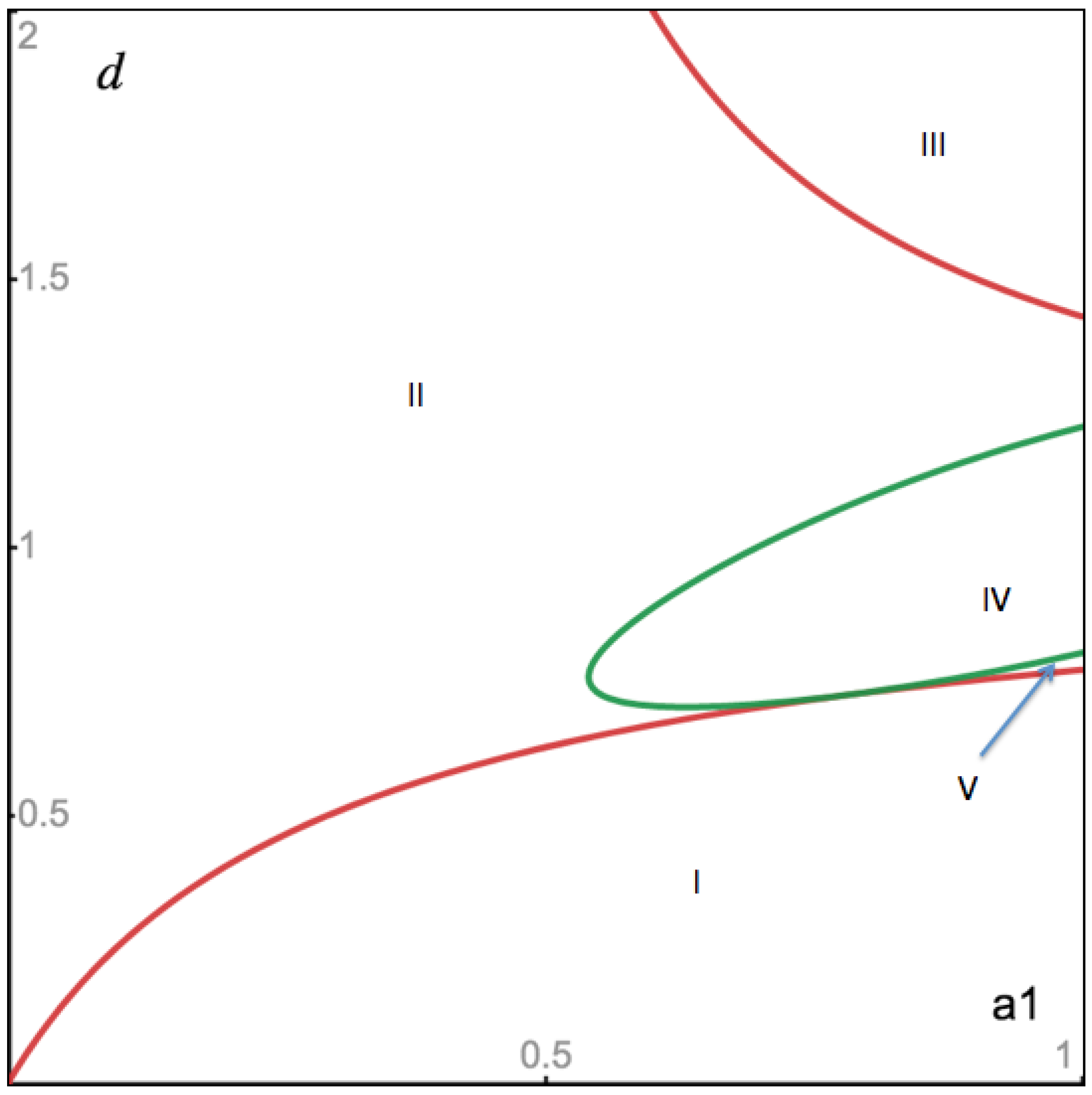
3.2. Stability Result of Tumour-Free Equilibrium Point,
- 1.
- and , and
- 2.
- either , or , and .
3.3. Stability Result of Tumour Equilibrium Point with Immune Responses
- a.
- ,
- b.
- c.
- , and
- d.
- .
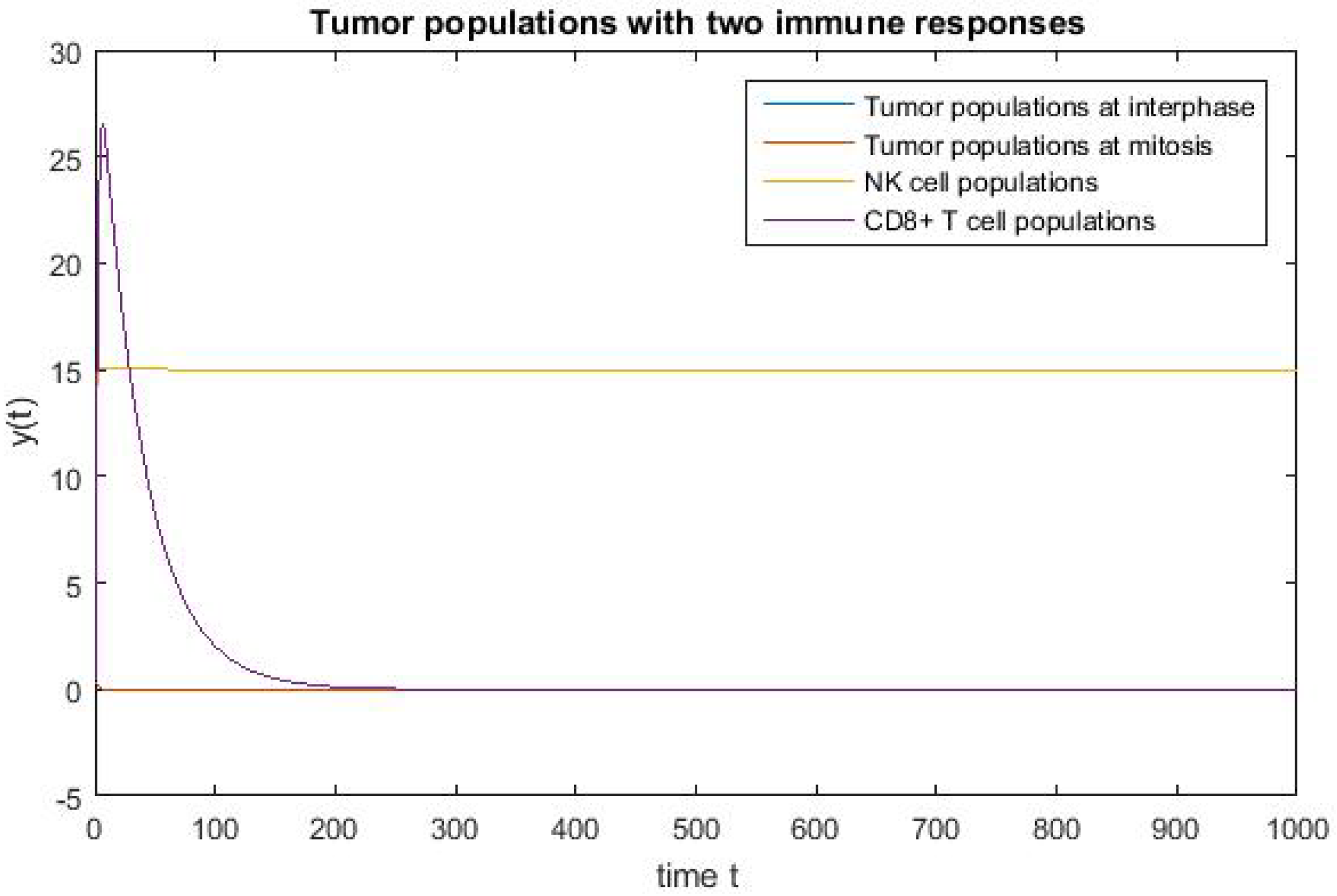
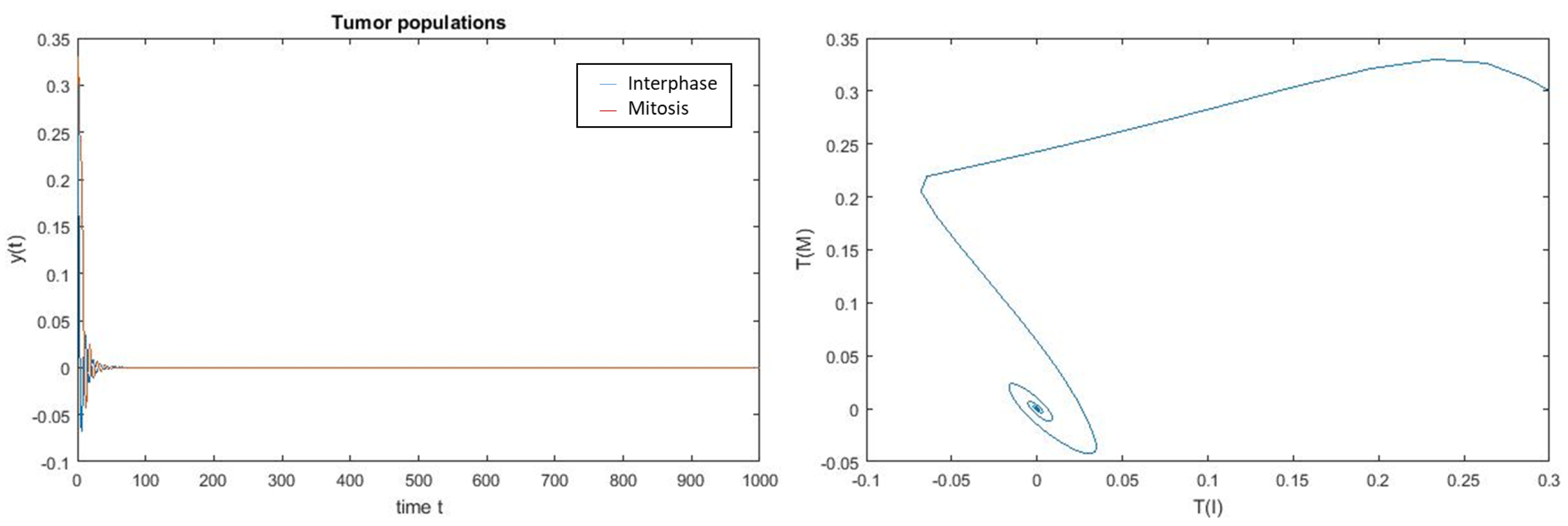
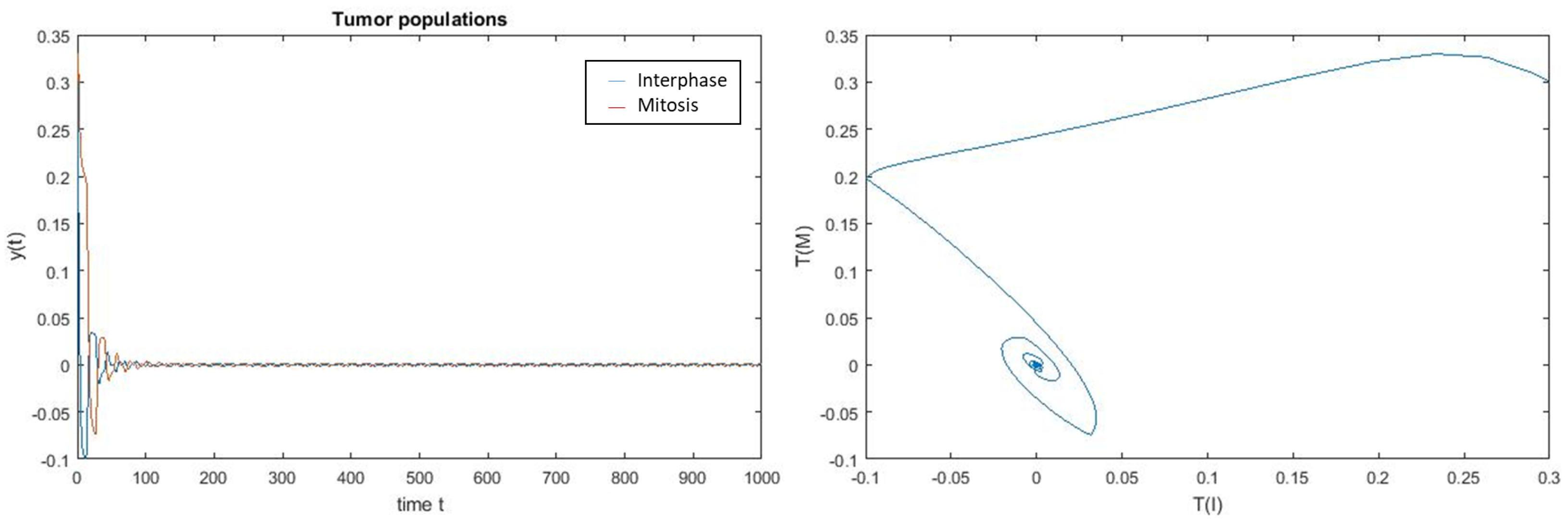
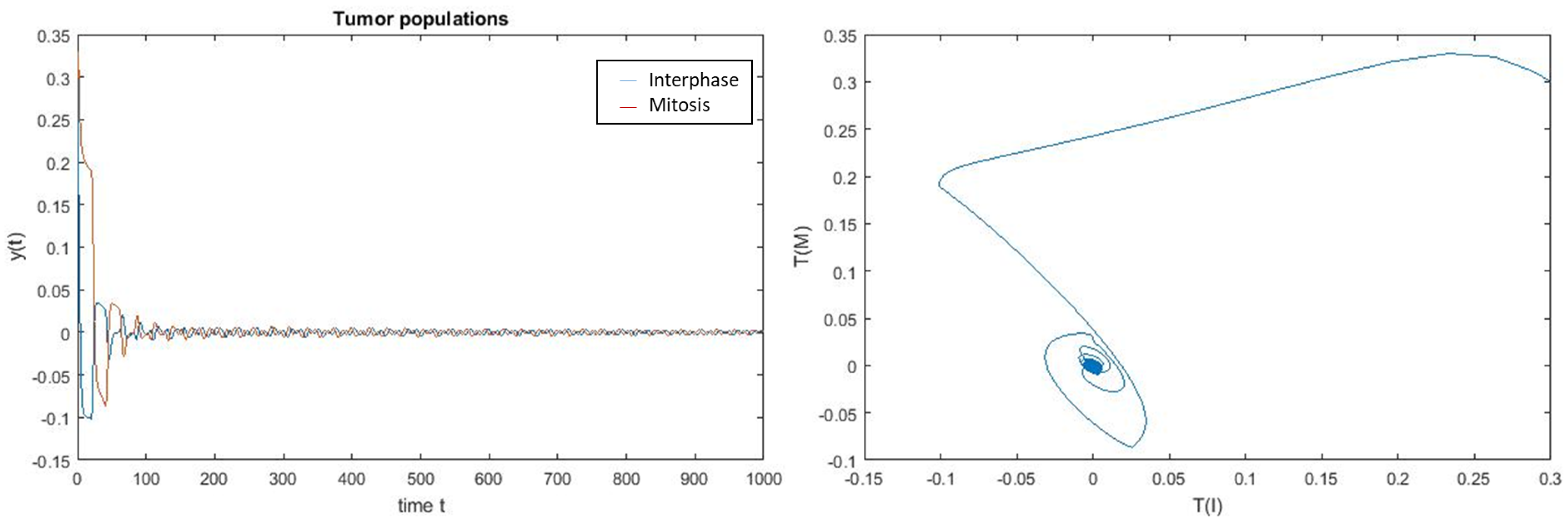
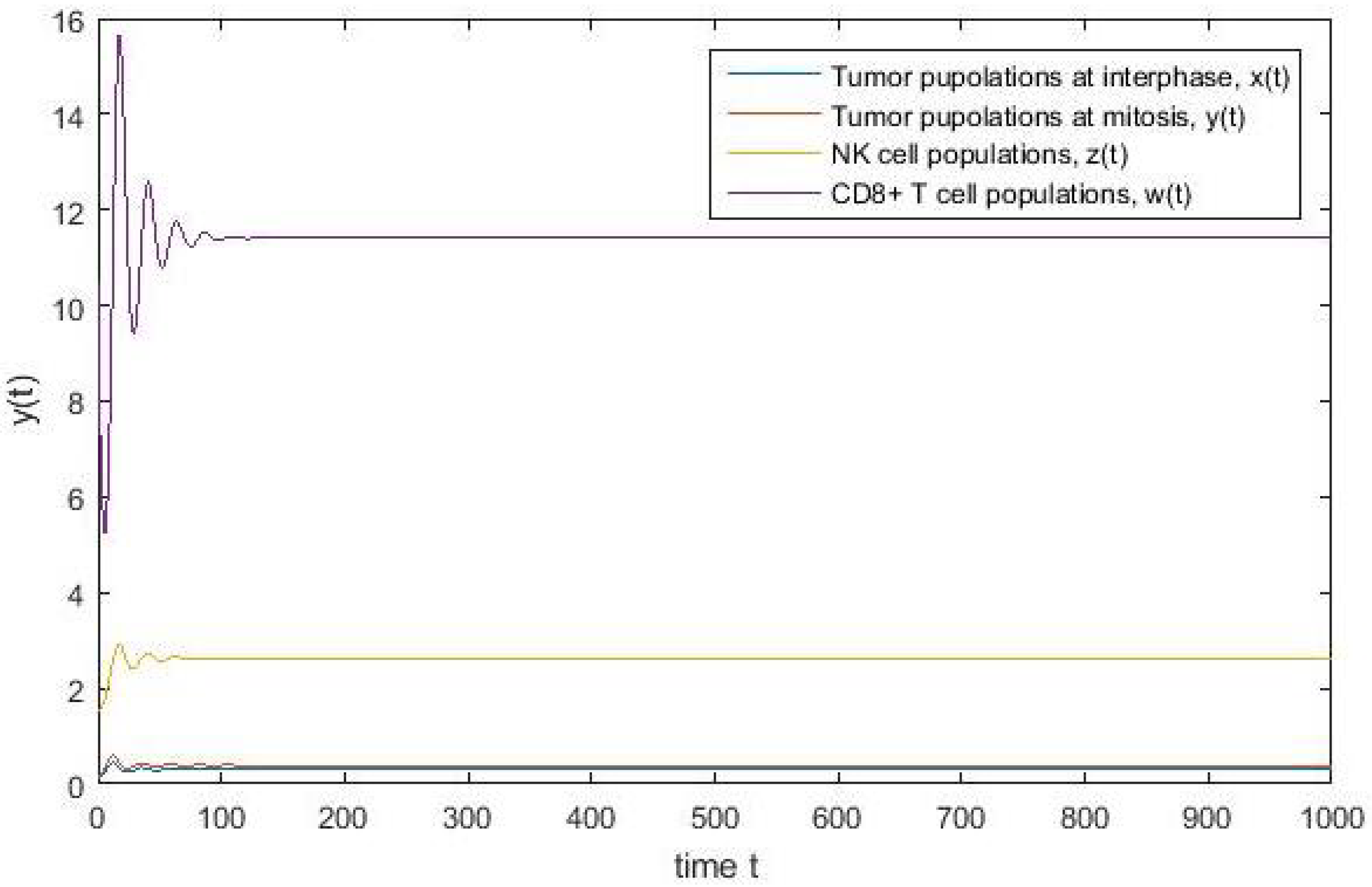
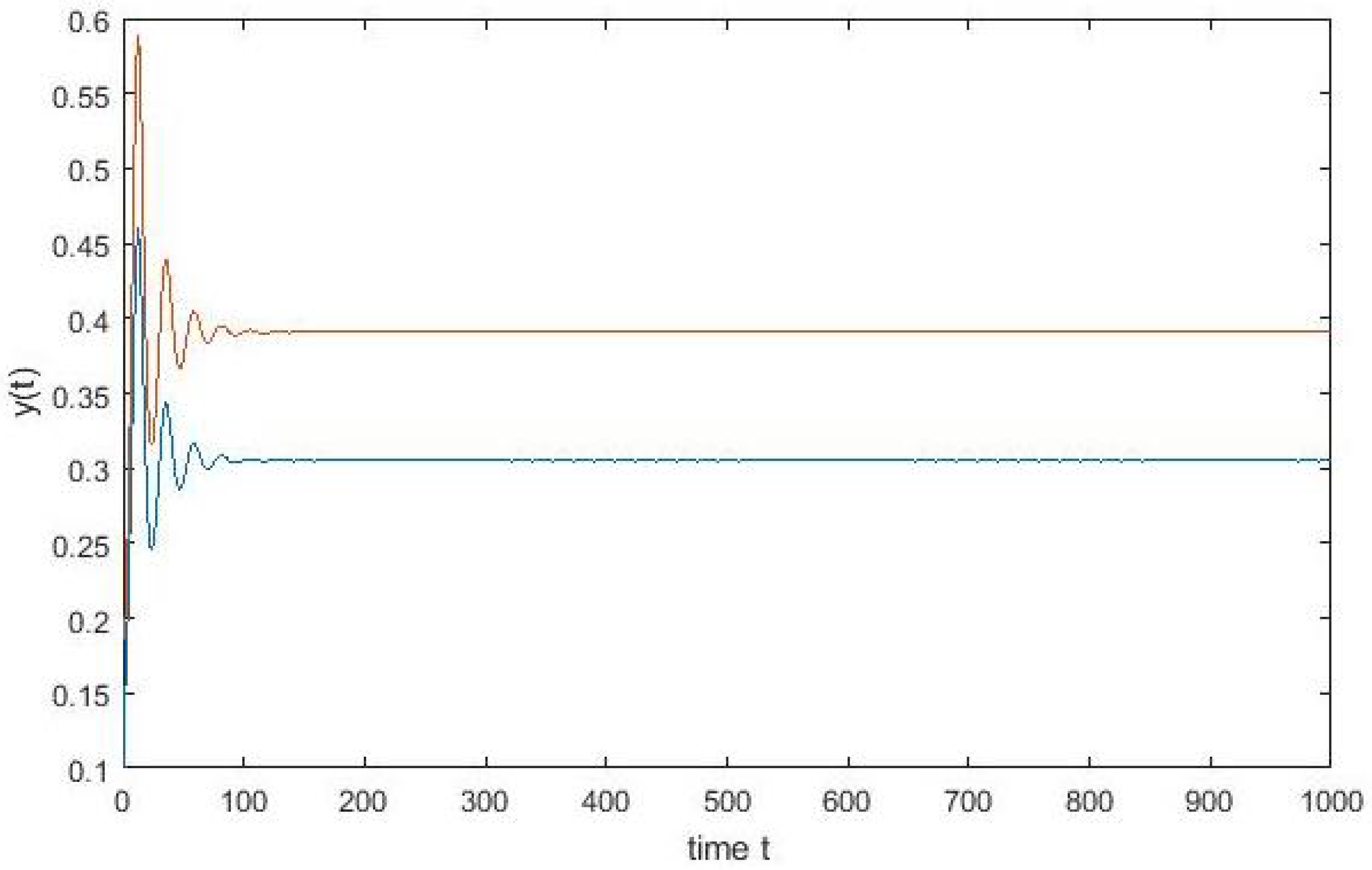
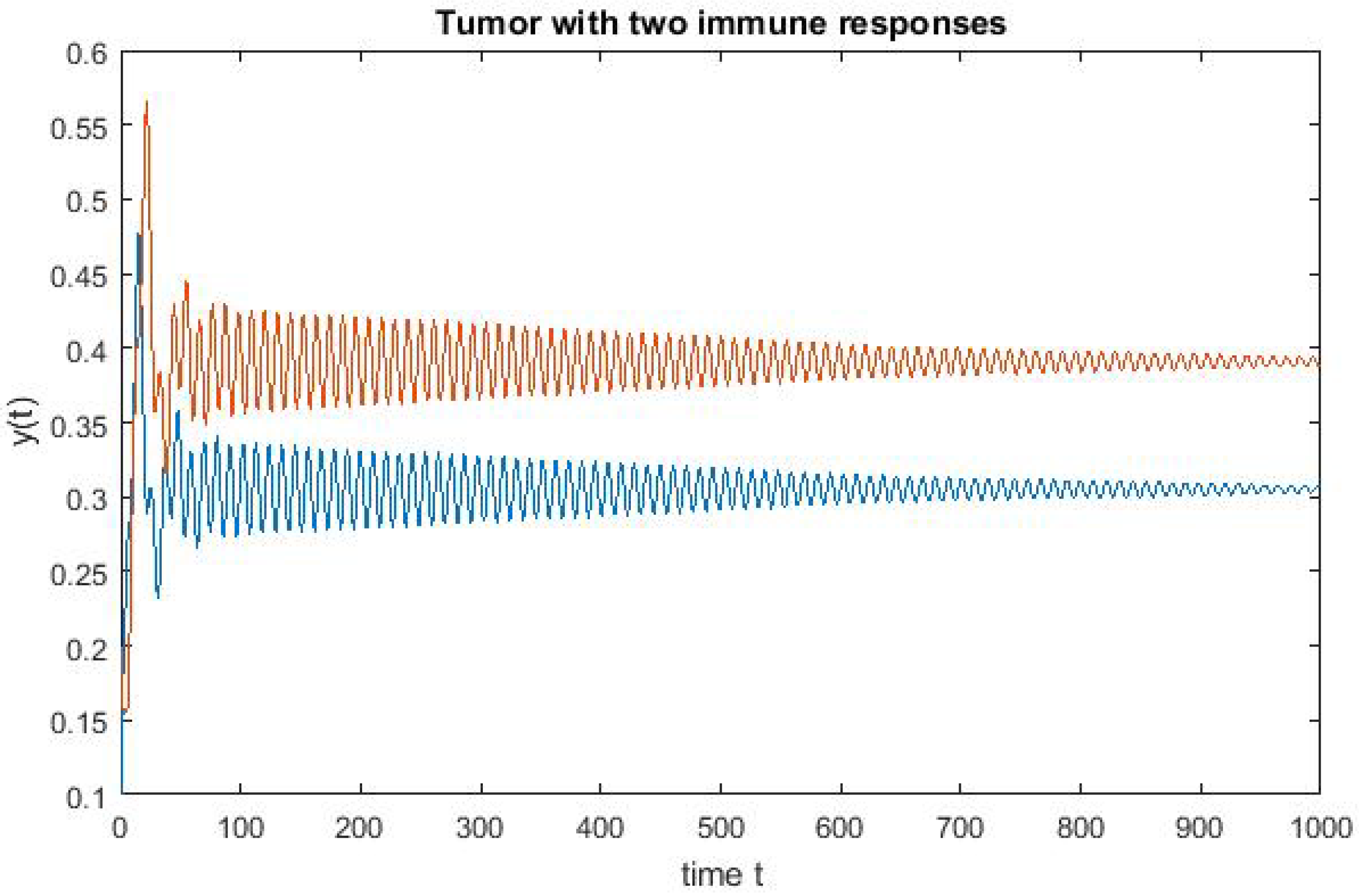
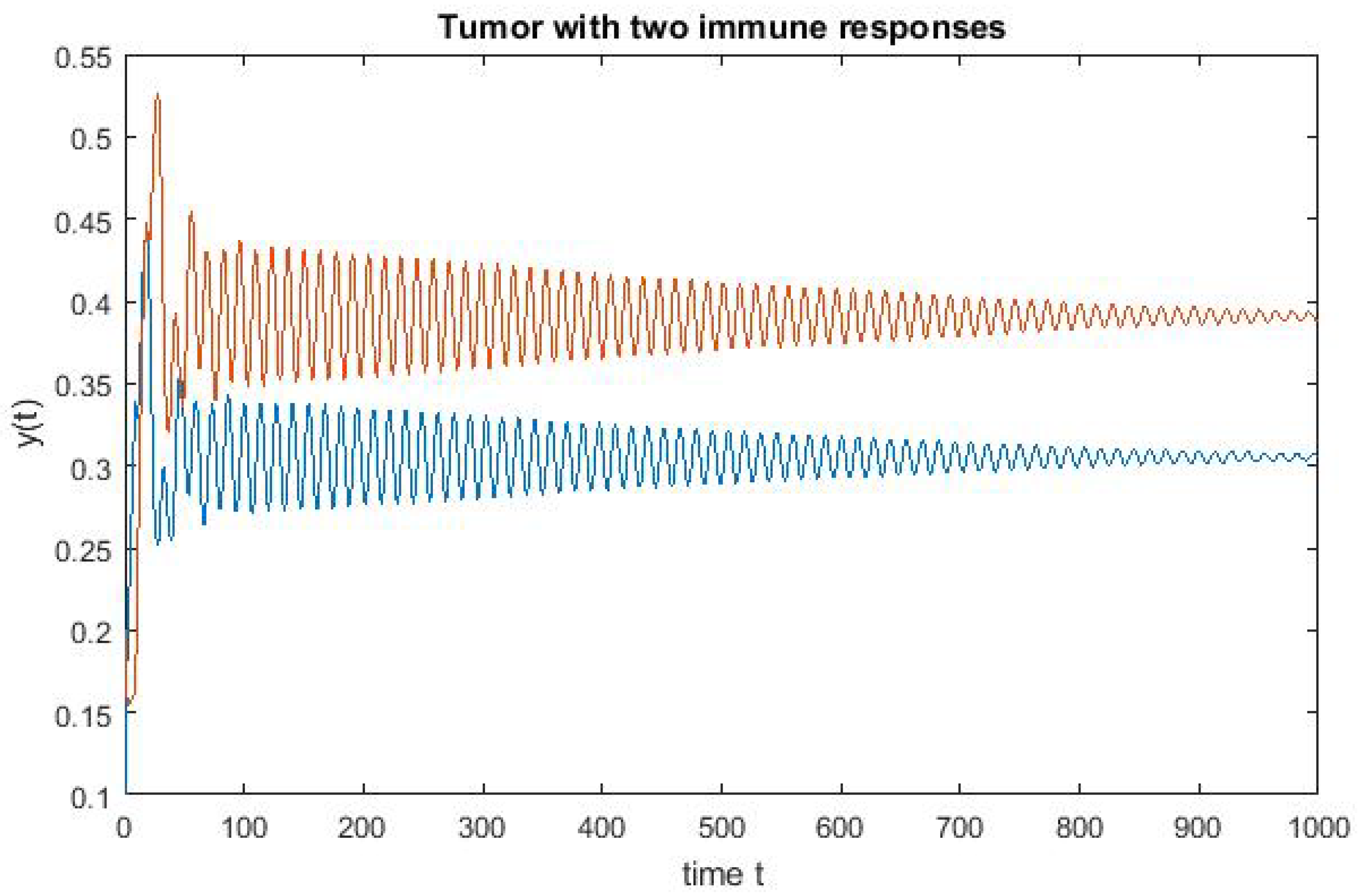
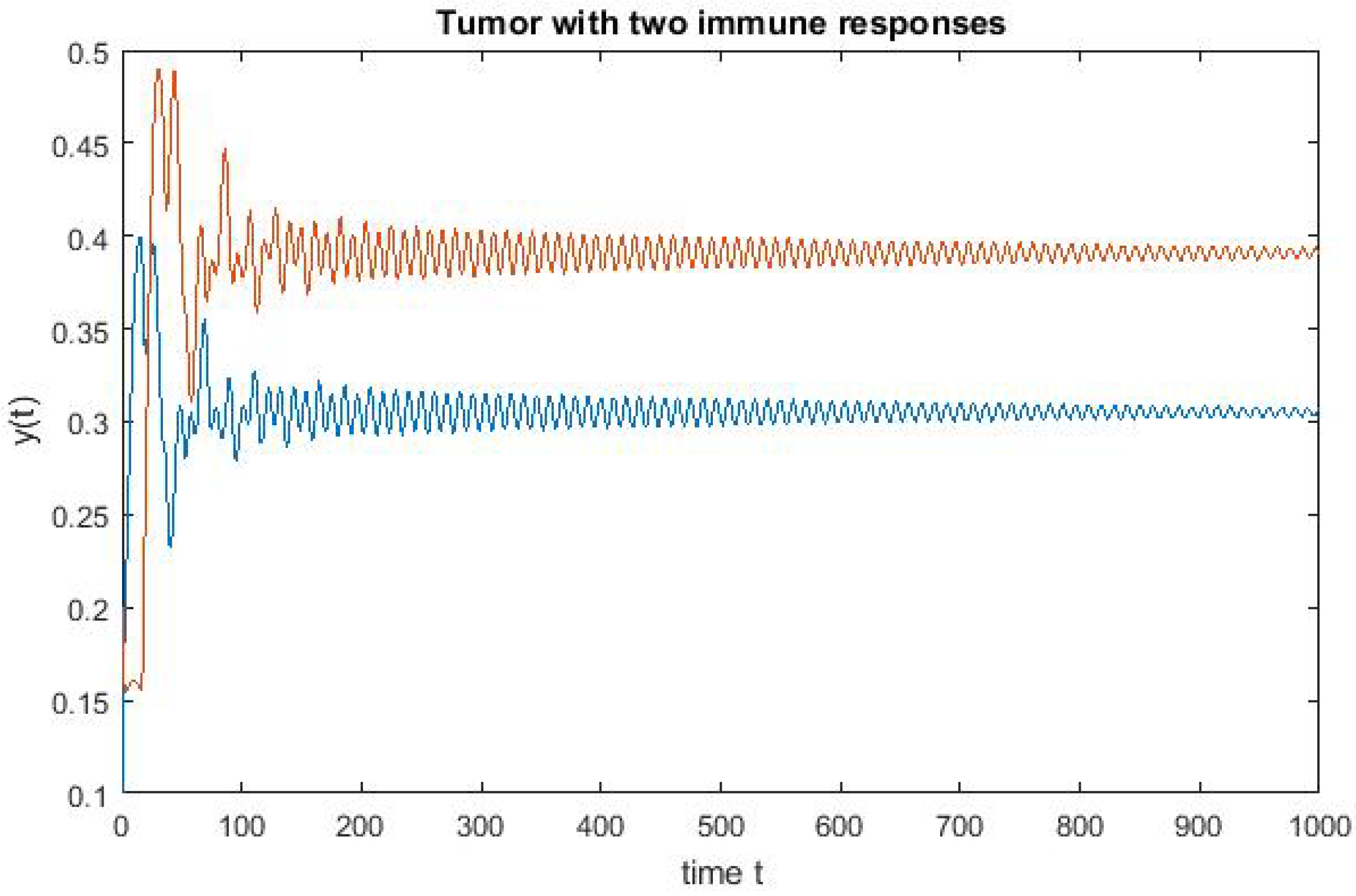
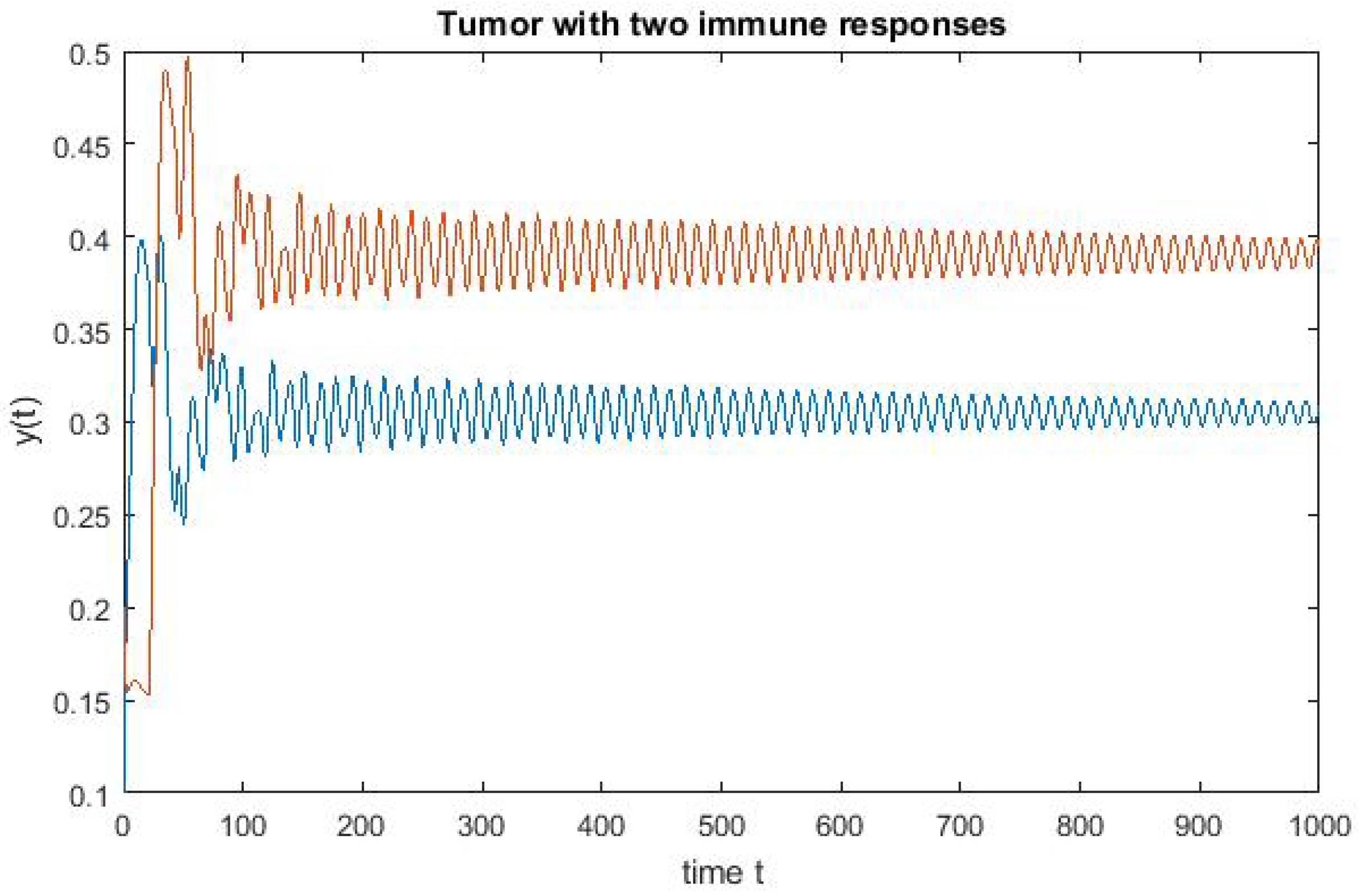
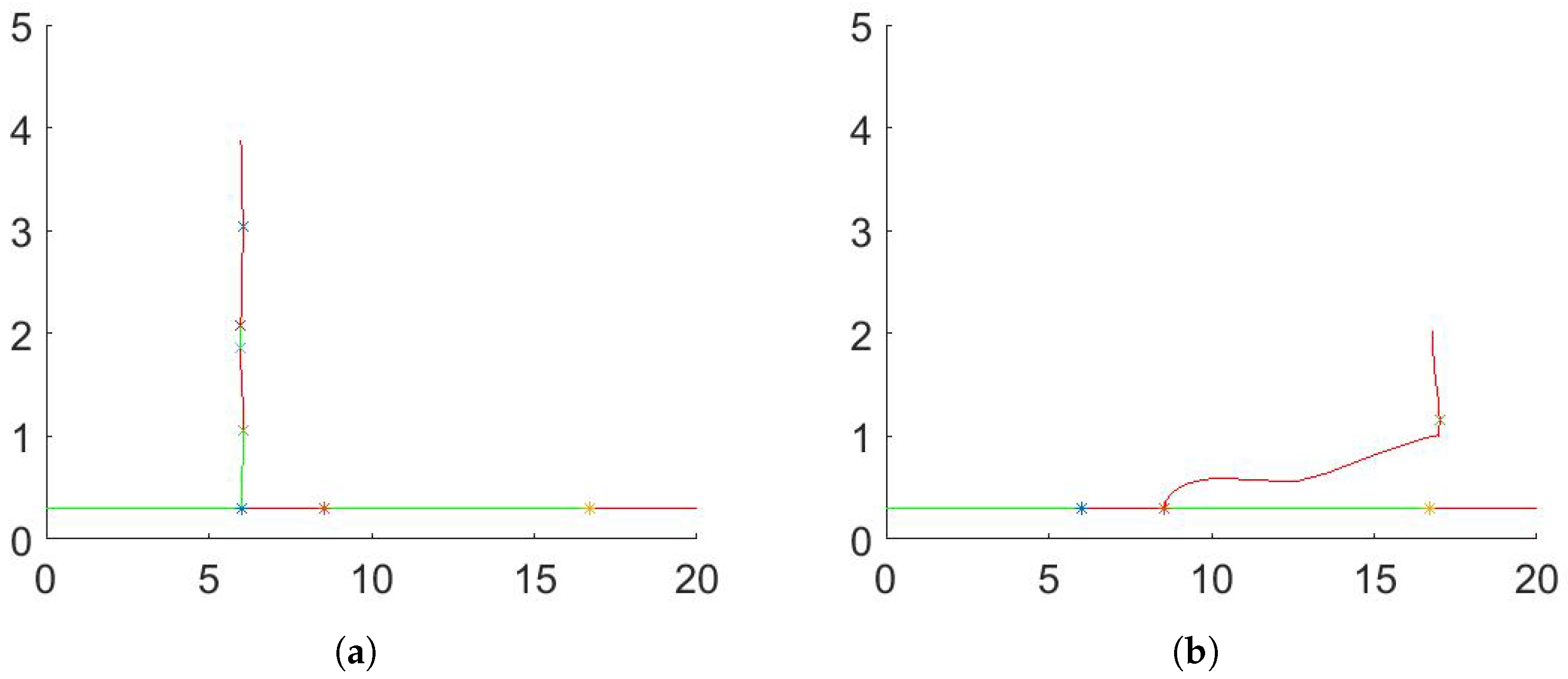
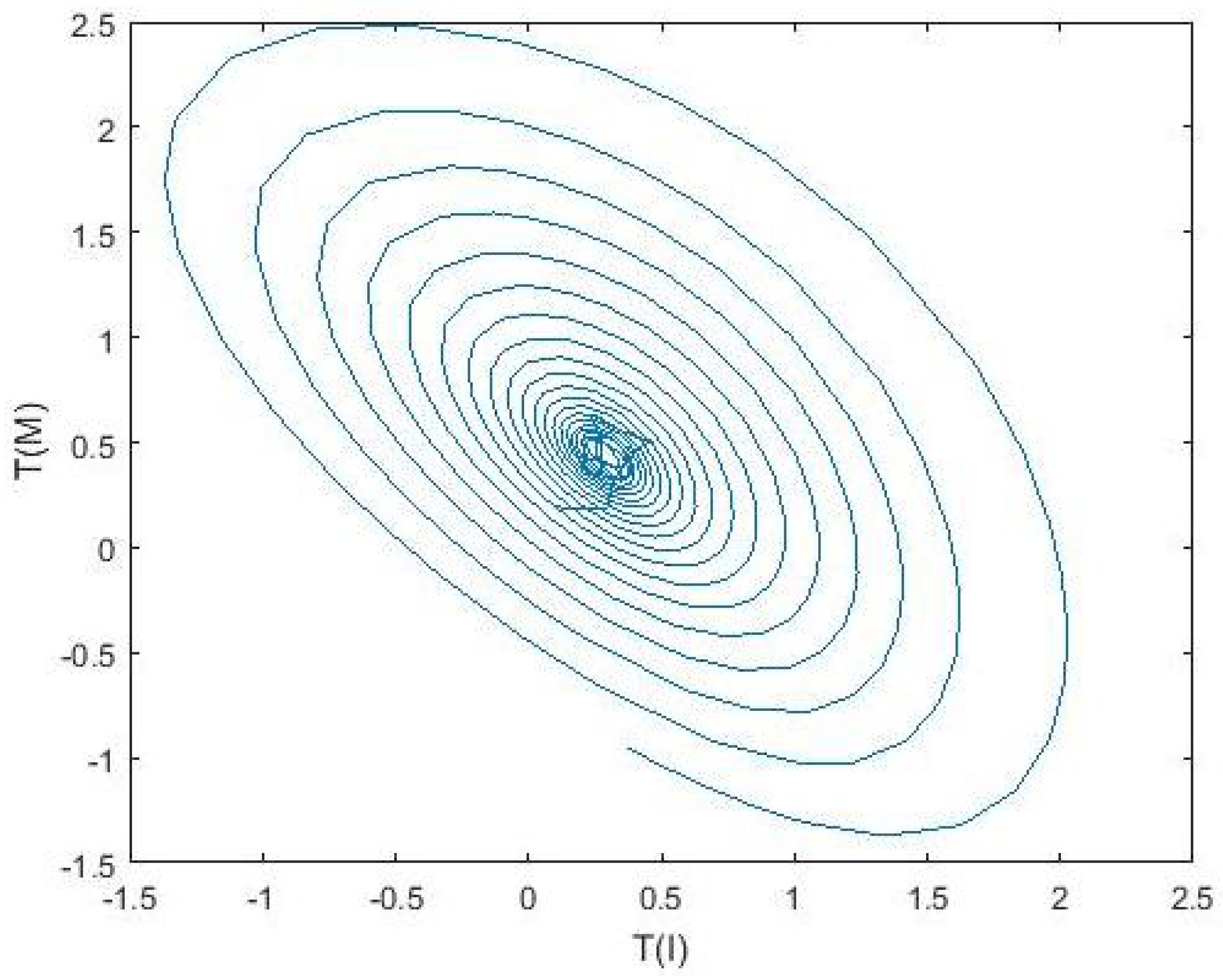
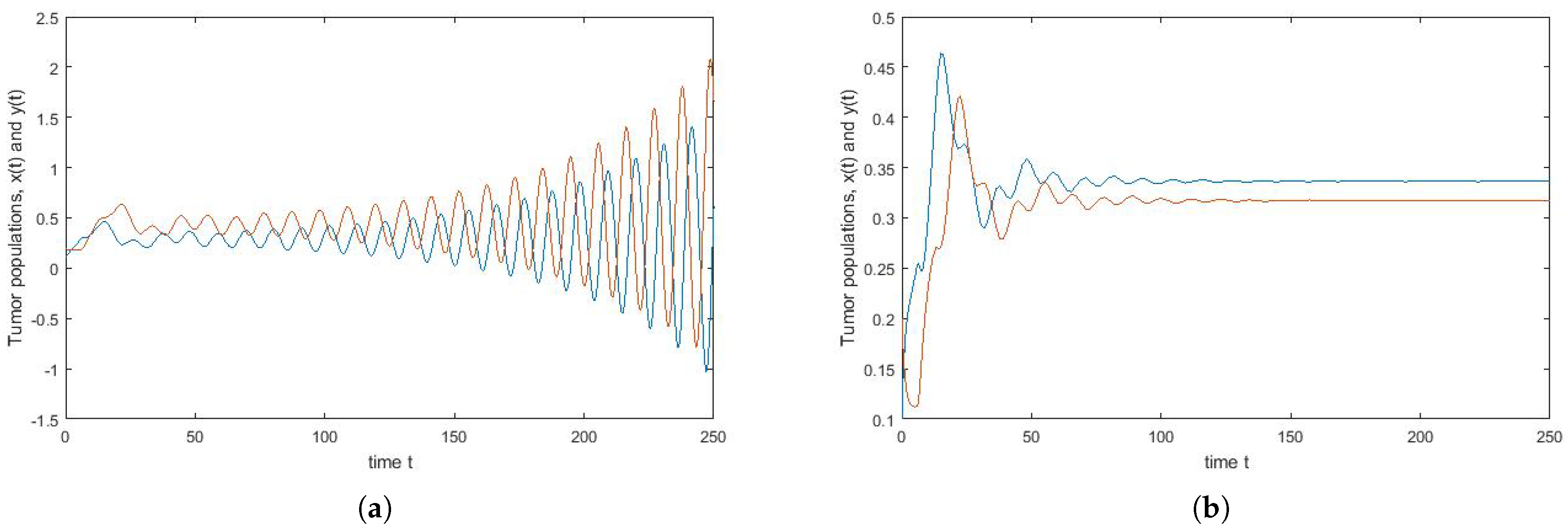
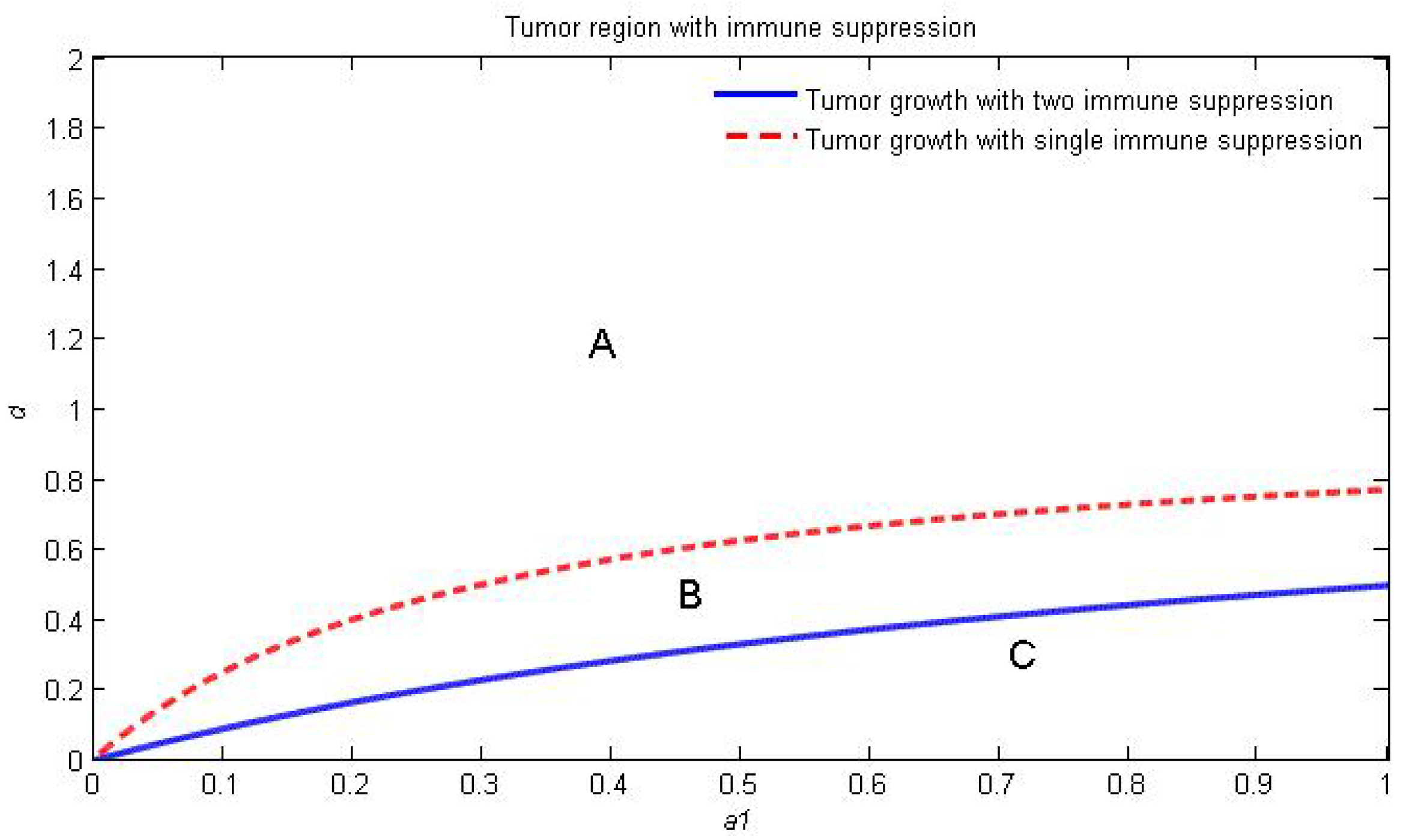
4. Numerical Simulation
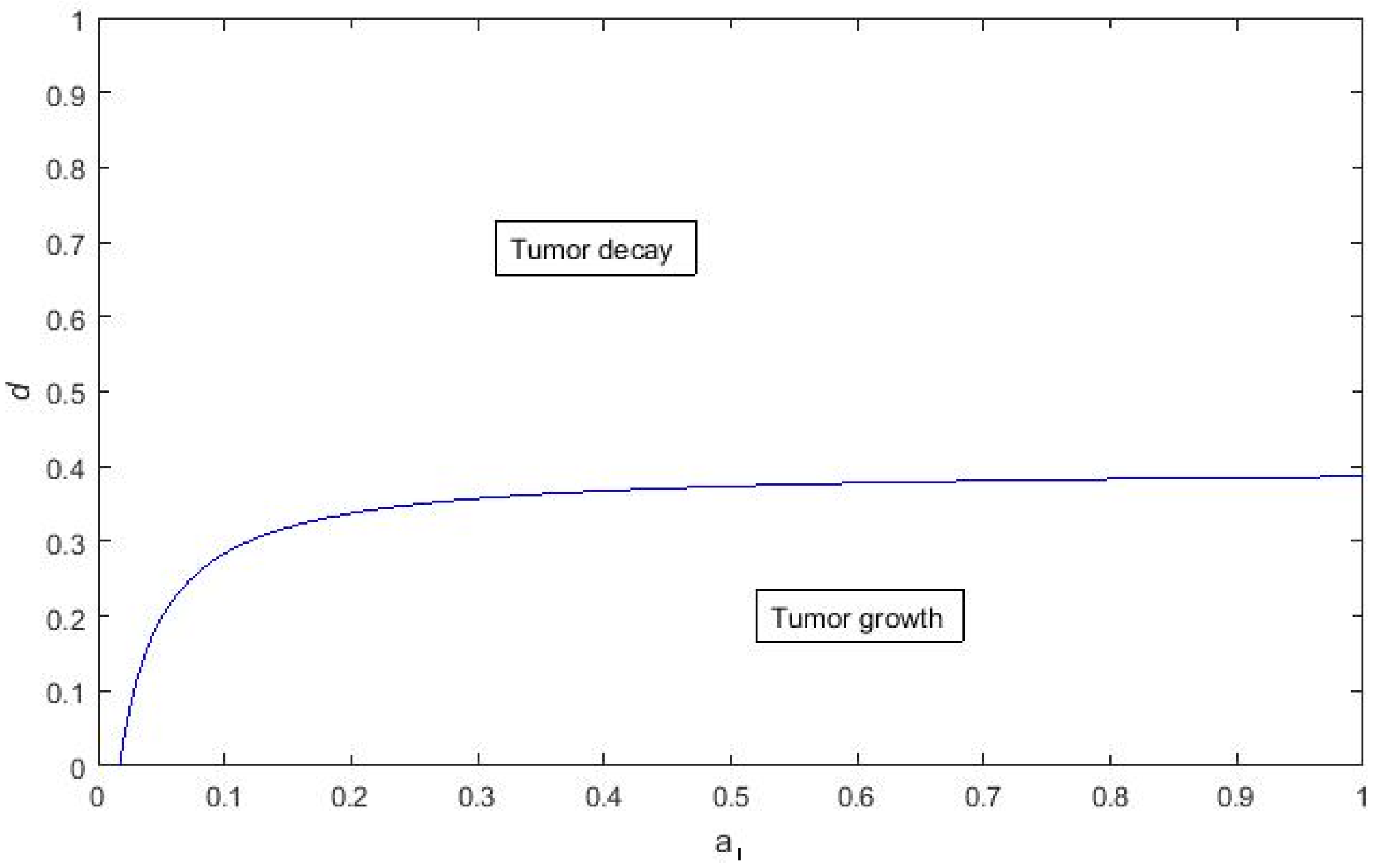
Varying Rate at Which Tumour Cell Enter Mitosis,
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- de Martel, C.; Georges, D.; Bray, F.; Ferlay, J.; Clifford, G.M. Global burden of cancer attributable to infections in 2018: A worldwide incidence analysis. Lancet Glob. Health 2020, 8, e180–e190. [Google Scholar] [CrossRef]
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Eftimie, R.; Bramson, J.L.; Earn, D.J. Interactions between the immune system and cancer: A brief review of non-spatial mathematical models. Bull. Math. Biol. 2011, 73, 2–32. [Google Scholar] [CrossRef] [PubMed]
- de Pillis, L.G.; Gu, W.; Radunskaya, A.E. Mixed immunotherapy and chemotherapy of tumors: Modeling, applications and biological interpretations. J. Theor. Biol. 2006, 238, 841–862. [Google Scholar] [CrossRef] [PubMed]
- d’Onofrio, A. A general framework for modeling tumor-immune system competition and immunotherapy: Mathematical analysis and biomedical inferences. Phys. D Nonlinear Phenom. 2005, 208, 220–235. [Google Scholar] [CrossRef]
- d’Onofrio, A. Metamodeling tumor–immune system interaction, tumor evasion and immunotherapy. Math. Comput. Model. 2008, 47, 614–637. [Google Scholar] [CrossRef]
- Burnet, F. Immunological aspects of malignant disease. Lancet 1967, 289, 1171–1174. [Google Scholar] [CrossRef]
- Kirschner, D.; Panetta, J.C. Modeling immunotherapy of the tumor–immune interaction. J. Math. Biol. 1998, 37, 235–252. [Google Scholar] [CrossRef]
- Kirkwood, J.M.; Butterfield, L.H.; Tarhini, A.A.; Zarour, H.; Kalinski, P.; Ferrone, S. Immunotherapy of cancer in 2012. CA Cancer J. Clin. 2012, 62, 309–335. [Google Scholar] [CrossRef]
- Esfahani, K.; Roudaia, L.; Buhlaiga, N.A.; Del Rincon, S.; Papneja, N.; Miller, W. A review of cancer immunotherapy: From the past, to the present, to the future. Curr. Oncol. 2020, 27, 87–97. [Google Scholar] [CrossRef]
- Fruci, D.; Lo, M.E.; Cifaldi, L.; Locatelli, F.; Tremante, E.; Benevolo, M.; Giacomini, P. T and NK cells: Two sides of tumor immunoevasion. J. Transl. Med. 2013, 11, 30. [Google Scholar] [CrossRef] [PubMed]
- Gajewski, T.F.; Schreiber, H.; Fu, Y.X. Innate and adaptive immune cells in the tumor microenvironment. Nat. Immunol. 2013, 14, 1014–1022. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.W.; Park, H.J.; Kim, N.; Hong, S. Natural Killer Dendritic Cells Enhance Immune Responses Elicited by α-Galactosylceramide-Stimulated Natural Killer T Cells. BioMed Res. Int. 2013, 2013, 460706. [Google Scholar] [CrossRef]
- Levy, E.M.; Roberti, M.P.; Mordoh, J. Natural killer cells in human cancer: From biological functions to clinical applications. BioMed Res. Int. 2011, 2011, 676198. [Google Scholar] [CrossRef] [PubMed]
- de Pillis, L.G.; Radunskaya, A.E.; Wiseman, C.L. A validated mathematical model of cell-mediated immune response to tumor growth. Cancer Res. 2005, 65, 7950–7958. [Google Scholar] [CrossRef]
- Admon, M.R.; Maan, N. Modelling tumor growth with immune response and drug using ordinary differential equations. J. Teknologi 2017, 79, 49–59. [Google Scholar] [CrossRef][Green Version]
- Awang, N.A.; Maan, N. Analysis of tumor populations and immune system interaction model. In Proceedings of the 23rd Malaysian National Symposium of Mathematical Sciences (SKSM23), Johor, Malaysia, 27–29 September 2016; Volume 1750, p. 030049. [Google Scholar]
- Admon, M.R.; Maan, N. Modelling of macrophage interactions in breast cancer by partial differential equations. Malays. J. Fundam. Appl. Sci. 2017, 13, 113–117. [Google Scholar]
- Abdulkareem, A.I.; Jemon, K.; Maan, N. Stability and Sensitivity Analysis of Tumor-induce immune Suppression with Time Delay. J. Adv. Res. Dyn. Control. Syst. 2020, 12, 1321–1331. [Google Scholar]
- de Pillis, L.; Radunskaya, A. A mathematical model of immune response to tumor invasion. In Computational Fluid and Solid Mechanics 2003; Elsevier Science Ltd.: Oxford, UK, 2003; pp. 1661–1668. [Google Scholar]
- Pang, L.; Liu, S.; Zhang, X.; Tian, T. Mathematical modeling and dynamic analysis of anti-tumor immune response. J. Appl. Math. Comput. 2020, 62, 473–488. [Google Scholar] [CrossRef]
- Kuznetsov, V.A.; Makalkin, I.A.; Taylor, M.A.; Perelson, A.S. Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar] [CrossRef]
- de Pillis, L.; Renee Fister, K.; Gu, W.; Collins, C.; Daub, M.; Gross, D.; Moore, J.; Preskill, B. Mathematical model creation for cancer chemo-immunotherapy. Comput. Math. Methods Med. 2009, 10, 165–184. [Google Scholar] [CrossRef]
- Villasana, M.; Radunskaya, A. A delay differential equation model for tumor growth. J. Math. Biol. 2003, 47, 270–294. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Hillen, T.; Freedman, H. A mathematical model for M-phase specific chemotherapy including the G0-phase and immunoresponse. Math. Biosci. Eng. 2007, 4, 239. [Google Scholar] [PubMed]
- Lodish, H.F.; Berk, A.; Kaiser, C.A.; Kaiser, C.; Krieger, M.; Scott, M.P.; Matsudaira, P. Molecular Cell Biology; Macmillan: New York, NY, USA, 2000; Volume 4. [Google Scholar]
- Kastan, M.B.; Bartek, J. Cell-cycle checkpoints and cancer. Nature 2004, 432, 316–323. [Google Scholar] [CrossRef]
- de Villegas, M.V. A Delay Differential Equation Model for Tumor Growth. Ph.D. Thesis, Claremont University, Claremont, CA, USA, 2001. [Google Scholar]
- Mahasa, K.J.; Ouifki, R.; Eladdadi, A.; de Pillis, L. Mathematical model of tumor–immune surveillance. J. Theor. Biol. 2016, 404, 312–330. [Google Scholar] [CrossRef]
- Matlab. Version 8.5.0.197613 (R2015a); The MathWorks Inc.: Natick, MA, USA, 2015. [Google Scholar]


| Parameter | Description | Estimated Value/Range | Source |
|---|---|---|---|
| Cell that enter interphase | 0–1 day | [25,28] | |
| Cell that enter mitosis | 0–1 day | [25,28] | |
| Natural death rate of NK cell | day cell | [29] | |
| Natural death rate of tumour cell | 0–1 day | [25,28] | |
| at interphase | |||
| Natural death rate of tumour cell | 0–1 day | [25,28] | |
| at mitosis | |||
| Natural death rate of CD T cell | day cell | [29] | |
| Rate at which NK cell destroy | day cell | [29] | |
| tumour at interphase | |||
| Loses due to encounter with NK cell | day cell | [29] | |
| at interphase | |||
| Rate at which NK cell destroy | day cell | [29] | |
| tumour at mitosis | |||
| Loses due to encounter with NK cell | day cell | [29] | |
| at mitosis | |||
| Loses due to encounter with CD T cell | day cell | [29] | |
| at interphase | |||
| Loses due to encounter with CD T cell | day cell | [29] | |
| at mitosis | |||
| Rate at which CD T cell destroy | day cell | [29] | |
| tumour at interphase | |||
| Rate at which CD T cell destroy | day cell | [29] | |
| tumour at mitosis | |||
| k | Constant source of NK cell | day cell | [25,28] |
| r | Rate at which tumour-specific | day cell | [28] |
| CD T cell are stimulated | |||
| Proportion of the growth of lymphocytes | day | [25,28] | |
| due to stimulus by tumour cell | |||
| Steepness coefficient of the NK | day cell | [25,28] | |
| and CD T cells recruitment curve |
| 1.69531 i | −1.68244 | ||
| 7.33207 + 1.69531 i | 5.64962 | ||
| 14.6641 + 1.69531 i | 12.9817 | ||
| 21.9962 + 1.69531 i | 20.3138 | ||
| 29.3283 + 1.69531 i | 27.6458 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awang, N.A.; Maan, N.; Sulain, M.D. Tumour-Natural Killer and CD8+ T Cells Interaction Model with Delay. Mathematics 2022, 10, 2193. https://doi.org/10.3390/math10132193
Awang NA, Maan N, Sulain MD. Tumour-Natural Killer and CD8+ T Cells Interaction Model with Delay. Mathematics. 2022; 10(13):2193. https://doi.org/10.3390/math10132193
Chicago/Turabian StyleAwang, Nor Aziran, Normah Maan, and Mohd Dasuki Sulain. 2022. "Tumour-Natural Killer and CD8+ T Cells Interaction Model with Delay" Mathematics 10, no. 13: 2193. https://doi.org/10.3390/math10132193
APA StyleAwang, N. A., Maan, N., & Sulain, M. D. (2022). Tumour-Natural Killer and CD8+ T Cells Interaction Model with Delay. Mathematics, 10(13), 2193. https://doi.org/10.3390/math10132193






